A cumulative frequency is the sum of frequency values of class or basic value. The frequency values are equal to the number of times the score or basic value or class is repeated. For Example, Class : 1 ,2, 1, 1, 1, 3,3, 3, 5, 5, 5, 6, 6, 7, 7, 7, 8, 8. The cumulative frequency of a value of a variable is the collection of data of a number of values less than or equal to the value of the variable. The cumulative frequency of a class interval that is overlapping or nonoverlapping is the sum of the frequencies of earlier class intervals and the concerned class interval.
| Class | Frequency | Cumulative Frequency |
|---|---|---|
| 1 | 4 | 4 |
| 2 | 1 | 5 (that is 4 +1) |
| 3 | 3 | 8 (that is 5 + 3) |
| 5 | 3 | 11 (that is (8 + 3) |
| 6 | 2 | 13 (that is 11 + 2) |
| 7 | 3 | 16 (that is 13 + 3) |
| 8 | 2 | 18 (that is 16 + 2) |
Also, Read: Medians and Altitudes of a Triangle
Cumulative Frequency Examples
1. The Following Table gives the frequency distribution of marks obtained by the 30 students. Find the Cumulative frequency based on the below values?

Solution: Based on the student’s marks and the frequency of the marks, we can easily find out the cumulative frequency. Cumulative frequency is the sum of the frequency of marks of the students. That is,
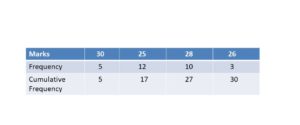
So, the cumulative frequency is 5, 17 ( 5 + 12), 27 (17 + 10), and 30 (27 + 3).
2. The below table gives the mass of 30 objects with the frequency. Find out the cumulative frequency for the objects?

Solution: As per the given information We have mass objects and the frequency of the mass of objects. The cumulative frequency is the sum of the frequency of mass of objects. That is
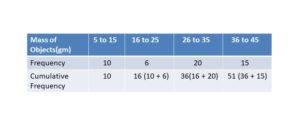
Finally, the cumulative frequency of the mass of objects is 10, 16, 36, and 51.
3. The below-given details are the ages of the employees in a particular company and the frequency of the ages of employees. Find the cumulative frequency for the given data?
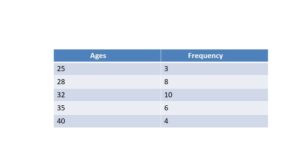
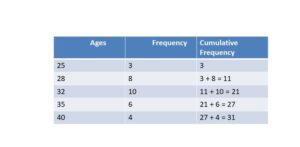
Solution: As per the given details,
Ages of the employees in a company and the frequency of ages of the employees are noted. The cumulative frequency of the ages of employees is
4. A cloth store contains different colors of clothes. The color details, the cumulative frequency of some colors, and the frequency of the colors are given below, find the final cumulative frequency?
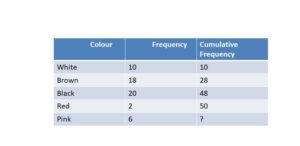
Solution: The given details are colors of cloths are white, brown, black, red, and pink.
The frequency of the colors is 10, 18, 20, 2, and 6.
The cumulative frequency of colors is the sum of the frequency of the colors. That is,
White – 10
Brown – 10 + 18 = 28
Black – 28+ 20 = 48
Red – 48 + 2 = 50
Pink – 50 + 6 = 56.
So, the final cumulative frequency of the colors is equal to 56.
5. For the collection of numbers 10, 12, 35, 10, 10, 12, 12, 35, 35, 35, 35, 10, 13, 11, 11, 13, 11, 13, and 10? What is the cumulative frequency of 13?
Solution: As per the given information
The given numbers are10, 12, 35, 10, 10, 12, 12, 35, 35, 35, 35, 10, 13, 11, 11, 13, 11, 13, and 10.
The frequency of the numbers is
Number – frequency
10 – 5
11 – 3
12 – 3
13 – 3
Cumulative frequency is equal to the sum of the frequency and the cumulative frequency of the 13 is equal to the sum of the frequency of less than or equal to 13. That is
5 + 3+ 3 + 3 = 14.
Therefore, the cumulative frequency of 13 is equal to 14.
6. The marks of 100 students are given below with the frequency. Find the cumulative frequency and answer the following questions.
(i) How many students obtain less than 41 % marks?
(ii) How many students obtain at least 51% marks?
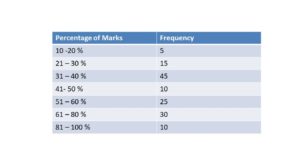
Solution: The cumulative frequency is
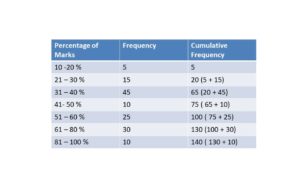
(i) How many students obtain less than 40 marks?
The number of students obtaining less than 41% of marks is 31 – 40% cumulative frequency = 65.
(ii) How many students obtain at least 51% marks?
The number of students obtaining at least 51% of marks =total number of students – the number of students obtaining less than or equal to 41 – 50%.
= 100 – 75 = 25.
So, the number of students obtaining at least 51% of marks is equal to 25.
