Different Types of Quadrilaterals – Definition, Properties

by

Depending upon the length and angles, quadrilaterals are classifieds in different ways. Let us check Different Types of Quadrilaterals and their definition, properties along with their diagrams. A quadrilateral can be explained using the below properties

  • The sum of the interior angles is 360 degrees in a quadrilateral.
  • A quadrilateral consists of 4 sides and 4 vertices, and also 4 angles.
  • The sum of the interior angle from the formula of the polygon using (n – 2) × 180 where n is equal to the number of sides of the polygon.

The main types in a quadrilateral are squares and rectangles, etc., with the same angles and sides.

Various Types of Quadrilaterals

Mainly quadrilaterals are classified into six types. They are

  1. Parallelogram
  2. Rhombus
  3. Rectangle
  4. Square
  5. Trapezium
  6. Kite

Parallelogram

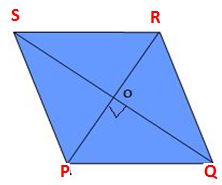
A quadrilateral is said to be a parallelogram when it has two pairs of parallel sides and opposite sides are parallel and equal in length. Also, the opposite angles are equal in a parallelogram. Let us take a parallelogram PQRS, then the side PQ is parallel to the side RS. Also, the side PS is parallel to a side QR.

Two diagonals are present in the parallelogram and they intersect each other at a midpoint. From the figure, PR and QS are two diagonals. Also, the diagonals are equal in length from the midpoint.

PQ ∥ RS and PS ∥ QR.

parallelogram 6

Rhombus

Rhombus is a quadrilateral when all the four sides of a quadrilateral having equal lengths. In a rhombus, opposite sides are parallel and opposite angles are equal.

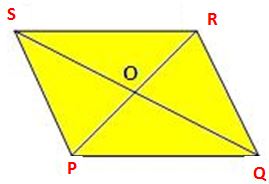
Rhombus

From the above figure, PQRS is a rhombus in which PQ ∥ RS, PS ∥ QR, and PQ = QR = RS = SP.

Rectangle

A quadrilateral is considered as a rectangle when all 4 angles of it are equal and each angle is 90 degrees. Also, both pairs of opposite sides of a rectangle are parallel and have equal lengths.

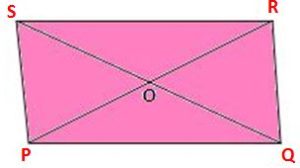
rectangle

From the above figure, PQRS is a quadrilateral in which PQ ∥ RS, PS ∥ QR and ∠P = ∠Q = ∠R = ∠S = 90°.

So, PQRS is a rectangle.

Square

A square is a quadrilateral consists all the sides and angles are equal. Also, every angle of a square is 90 degrees. The pairs of opposite sides of a square are parallel to each other.

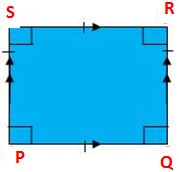
square

From the above figure, PQRS is a quadrilateral in which PQ ∥ RS, PS ∥ QR, PQ = QR = RS = SP and ∠P = ∠Q = ∠R = ∠S = 90°.

So, PQRS is a square.

Trapezium

A quadrilateral is called a trapezium when it has one pair of opposite parallel sides.

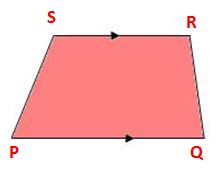
trapezium

From the above figure, PQRS is a quadrilateral in which PQ ∥ RS. So, PQRS is a trapezium. A trapezium its non-parallel sides are equal is called an isosceles trapezium.

Kite

A quadrilateral is said to be a kite that has two pairs of equal-length sides and the sides are adjacent to each other.

kite

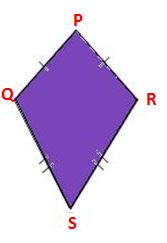
From the above figure, PQRS is a quadrilateral. PQ = PS, QR = RS, PS ≠ QR, and PQ ≠ RS.

So, PQRS is a kite.

Important Points to Remember for Quadrilaterals

Look at some of the important points need to remember about a quadrilateral.

  • A square is a rectangle and also it becomes a rhombus.
  • The rectangle and rhombus do not become a square.
  • A parallelogram is a trapezium.
  • Square, rectangle, and rhombus are types of parallelograms.
  • A trapezium is not a parallelogram.
  • Kite is not a parallelogram.

 

Leave a Comment