Practice with the help of enVision Math Common Core Grade 6 Answer Key Topic 2 Integers and Rational Numbers regularly and improve your accuracy in solving questions.
Envision Math Common Core 6th Grade Answers Key Topic 2 Integers and Rational Numbers
?Topic Essential Question What are integers and rational numbers? How are points graphed on a coordinate plane?
Answer:
An “Integer” can be written as a fraction by giving it a denominator of one. So, any integer is a rational number
“Rational numbers” are those numbers that are integers and can be expressed in the form of \(\frac{x}{y}\) where both numerator and denominator are integers
To graph or plot points, we use two perpendicular lines called the x-axis and the y-axis. The horizontal number line is the x-axis and the vertical line is the y-axis. Every point in the coordinate plane is represented by an ordered pair of x and y coordinates.
3-ACT MATH
The ULTIMATE THROW

The Ultimate Throw
Have you ever played ultimate? It’s a team sport played with a flying disc. The goal is to score the most points by passing the disc to your opponent’s end zone. Ultimate is played by millions of people across the globe, from casual games to professional leagues.

There are many ways to throw a flying disc. It takes a lot of practice to learn each type of throw. If you want the disc to travel a specific path and distance, you need to try different throws with different amounts of spin and power. Think about this during the 3-Act Mathematical Modeling lesson.
enVision STEM Project
Did You Know?
Your Task: Improve Your School
Now that you have defined the problem, or improvement needed, you and your classmates will apply the engineering design process to propose solutions.

Topic 2 GET READY!
Review What You Know!
Vocabulary
Choose the best term from the box to complete each definition.
decimal
denominator
fraction
numerator
Question 1.
A ____ names part of a whole, part of a set, or a location on a number line.
Answer:
We know that,
A “Fraction” names part of a whole, part of a set, or a location on a number line.
Hence, from the above,
We can conclude that
The best term that is suitable for the given definition is: Fraction
Question 2.
The number above the fraction bar that represents the part of the whole is the ____
Answer:
We know that,
The number above the fraction bar that represents the part of the whole is the “Numerator”
Hence, from the above,
We can conclude that
The best term that is suitable for the given definition is: Numerator
Question 3.
The number below the fraction bar that represents the total number of equal parts in one whole is the ____
Answer:
We know that,
The number below the fraction bar that represents the total number of equal parts in one whole is the “Denominator”
Hence, from the above,
We can conclude that
The best term that is suitable for the given definition is: Denominator
Fractions and Decimals
Write each fraction as a decimal.
Question 4.
\(\frac{2}{5}\)
Answer:
The given fraction is: \(\frac{2}{5}\)
Hence, from the above,
We can conclude that
The representation of the given fraction in the form of a decimal is:
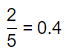
Question 5.
\(\frac{3}{4}\)
Answer:
The given fraction is: \(\frac{3}{4}\)
Hence, from the above,
We can conclude that
The representation of the given fraction in the form of a decimal is:
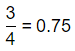
Question 6.
\(\frac{10}{4}\)
Answer:
The given fraction is: \(\frac{10}{4}\)
Hence, from the above,
We can conclude that
The representation of the given fraction in the form of a decimal is:
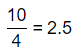
Question 7.
\(\frac{12}{5}\)
Answer:
The given fraction is: \(\frac{12}{5}\)
Hence, from the above,
We can conclude that
The representation of the given fraction in the form of a decimal is:
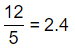
Question 8.
\(\frac{3}{5}\)
Answer:
The given fraction is: \(\frac{3}{5}\)
Hence, from the above,
We can conclude that
The representation of the given fraction in the form of a decimal is:

Question 9.
\(\frac{15}{3}\)
Answer:
The given fraction is: \(\frac{15}{3}\)
Hence, from the above,
We can conclude that
The representation of the given fraction in the form of a decimal is:
![]()
Division with Decimals
Divide.
Question 10.
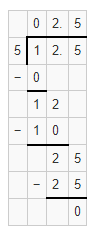
1.25 ÷ 0.5
Answer:
The given Division Expression is: 1.25 ÷ 0.5
Now,
By using the Long Division,
Hence, from the above,
We can conclude that
1.25 ÷ 0.5 = 2.5
Question 11.
13 ÷ 0.65
Answer:
The given Division Expression is: 13 ÷ 0.65
Now,
By using the Long Division,
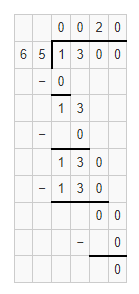
Hence, from the above,
We can conclude that
13 ÷ 0.65 = 20
Question 12.
12.2 ÷ 0.4
Answer:
The given Division Expression is: 12.2 ÷ 0.4
Now,
By using the Long Division,
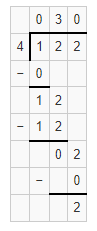
Hence, from the above,
We can conclude that
12.2 ÷ 0.4 = 30
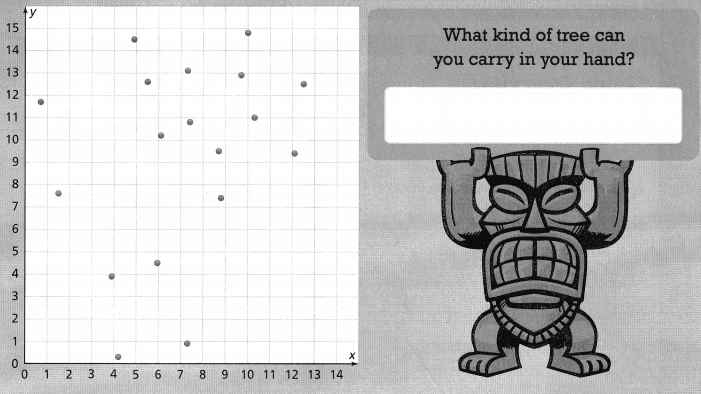
Ordered Pairs
Write the ordered pair for each point shown on the graph.
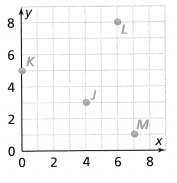
Question 13.
J
Answer:
The given coordinate plane is:

Now,
We know that,
“Ordered pairs” are often used to represent two variables. The number which corresponds to the value of x is called the x-coordinate and the number which corresponds to the value of y is called the y-coordinate.
Hence, from the above,
We can conclude that
The ordered pair J is: (4, 3)
Question 14.
K
Answer:
The given coordinate plane is:

Now,
We know that,
“Ordered pairs” are often used to represent two variables. The number which corresponds to the value of x is called the x-coordinate and the number which corresponds to the value of y is called the y-coordinate.
Hence, from the above,
We can conclude that
The ordered pair K is: (0, 6)
Question 15.
L
Answer:
The given coordinate plane is:

Now,
We know that,
“Ordered pairs” are often used to represent two variables. The number which corresponds to the value of x is called the x-coordinate and the number which corresponds to the value of y is called the y-coordinate.
Hence, from the above,
We can conclude that
The ordered pair L is: (6, 8)
Question 16.
M
Answer:
The given coordinate plane is:

Now,
We know that,
“Ordered pairs” are often used to represent two variables. The number which corresponds to the value of x is called the x-coordinate and the number which corresponds to the value of y is called the y-coordinate.
Hence, from the above,
We can conclude that
The ordered pair M is: (7, 1)
Plot each point on the coordinate plane.
Question 17.
A(6, 2)
Answer:
The given point is: A (6, 2)
Hence,
The representation of the given point in a coordinate plane is:
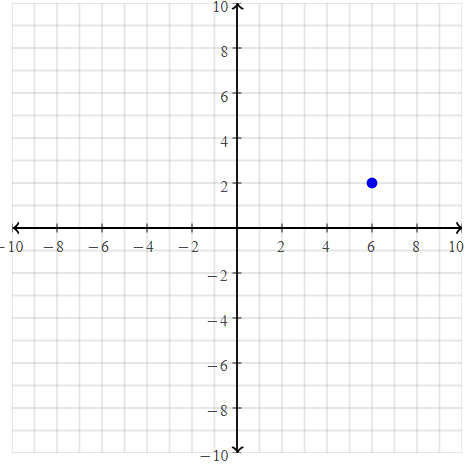
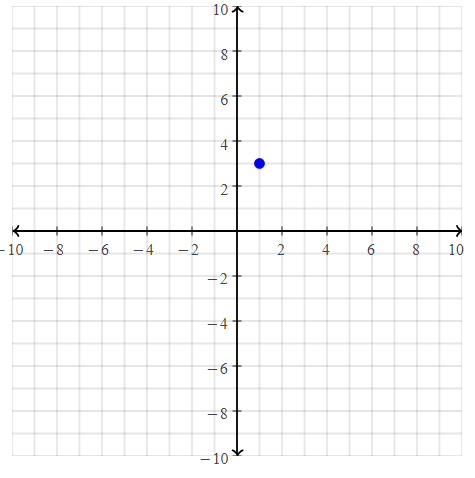
Question 18.
B(1, 3)
Answer:
The given point is: B (1, 3)
Hence,
The representation of the given point in a coordinate plane is:
Question 19.
C(5, 7)
Answer:
The given point is: C (5, 7)
Hence,
The representation of the given point in a coordinate plane is:

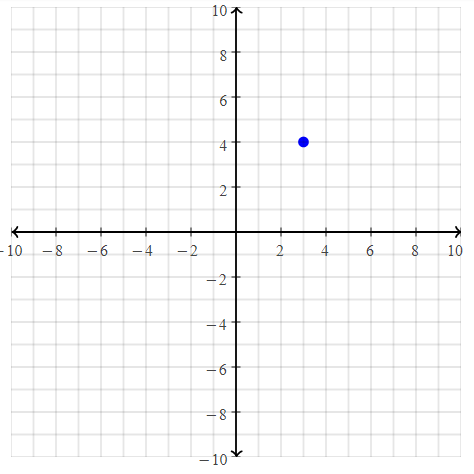
Question 20.
D(3, 4)
Answer:
The given point is: D (3, 4)
Hence,
The representation of the given point in a coordinate plane is:
Explain
Question 21.
Les said that the quotient of 3.9 ÷ 0.75 is 0.52. Explain how you know Les is incorrect without completing the division.
Answer:
It is given that
Les said that the quotient of 3.9 ÷ 0.75 is 0.52
Now,
The given Division Expression is: 3.9 ÷ 0.75
Now,
By using the Long Division,
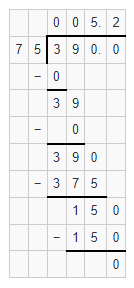
Now,
When we observe the numbers after the decimal point in the given division expression,
We can say that there are 2 numbers after the decimal point n the numerator and 1 number after the decimal point in the denominator
So,
The numbers after the decimal point in the quotient will be only 1 number
But,
There are 2 numbers after the decimal point
Hence, from the above,
We can conclude that Les is incorrect
Language Development
Use the graphic organizer to help you understand new vocabulary terms.

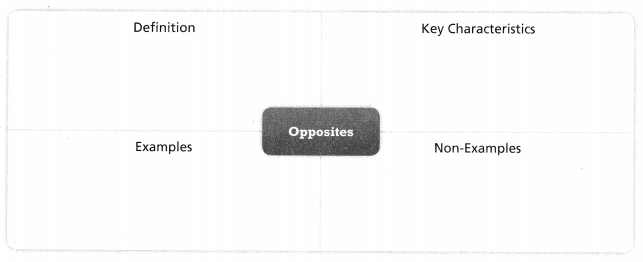
Answer:



Topic 2 PICK A PROJECT
PROJECT 2A
What places would you like to visit in the United States?
PROJECT: MAKE A TRAVEL BROCHURE

PROJECT 2B
If you were to solve a puzzle, what type would you choose?
PROJECT: DESIGN A CONNECT-THE-DOTS PUZZLE

PROJECT 2C
What are some exercises for staying fit and having fun?
PROJECT: RECORD AN EXERCISE VIDEO

PROJECT 2D
If you were going to make a commercial, what type of product would you feature?
PROJECT: WRITE YOUR OWN COMMERCIAL

Lesson 2.1 Understand Integers
ACTIVITY
Explain It!
Sal recorded the outdoor temperature as -4°F at 7:30 A.M. At noon, it was 22°F. Sal said the temperature changed by 18°F because 22 – 4 = 18.

A. Critique Reasoning is Sal right or wrong? Explain.
Answer:
It is given that
Sal recorded the outdoor temperature as -4°F at 7:30 A.M. At noon, it was 22°F. Sal said the temperature changed by 18°F because 22 – 4 = 18.
So,
The total temperature from 7:30 A.M to noon = (The temperature at 7:30 A.M) + (The temperature at noon
= -4 + 22
= 18° F
Hence, from the above,
We can conclude that Sal is right
B. Construct Arguments What was the total temperature change from 7:30 A.M. until noon? Use the thermometer to help justify your solution.
Answer:
It is given that
It is given that
Sal recorded the outdoor temperature as -4°F at 7:30 A.M. At noon, it was 22°F. Sal said the temperature changed by 18°F because 22 – 4 = 18.
Now,
The given figure is:

Now,
Using the thermometer,
The temperature at 7:30 A.M is: -4° F
Now,
The temperature at noon is: 18° F
So,
The change in temperature from 7: 30 A.M to until noon by using the thermometer is: 18° F
Hence, from the above,
We can conclude that
The total temperature change from 7:30 A.M. until noon is: 18° F
Focus on math practices
Reasoning 0°C is the temperature at which water freezes. Which is colder, 10°C or -10°C? Explain.
Answer:
It is given that
0°C is the temperature at which water freezes
Now,
We know that,
A temperature below 0°C is a negative temperature
Hence, from the above,
We can conclude that
-10°C is colder than 0°C
Visual Learning
? Essential Question What are integers and how are they used to represent real-world quantities?
Answer:
“Integers” are a set of numbers that include the positive whole numbers (1, 2, 3, 4, 5, …), their opposites (-1, -2, -3, -4, -5, …) and zero.
You can use integers to help represent many real-world situations, such as Increases and decreases in temperature
Try It!
Label the integers on the number line.
The opposite of 4 is![]() . The opposite of -4 is
. The opposite of -4 is![]() .
.
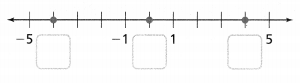
Answer:
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Now,
The completed number line is:
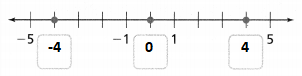
Hence, from the above,
We can conclude that
By using the given definition,
The opposite of 4 is: -4
The opposite of -4 is: 4
Convince Me! How do you know that two numbers are opposites?
Answer:
Two numbers are opposites if they have the same absolute value but different signs. Opposites are the same distance from 0 on a number line, and they are on opposite sides of 0
Try It!
Which number is greater, -4 or -2? Explain.
Answer:
The given numbers are: -4, and -2
Now,
We know that,
In the positive numbers i.e., the numbers that are to the right side of 0,
4 > 2
So,
In the negative numbers, i.e., the numbers that are to the left side of 0,
-4 < -2
Hence, from the above,
We can conclude that,
The greater number is: -2
Try It!
Which integer represents each situation?
a. A $10 debt
Answer:
We know that,
A “Debt” is a negative value
Hence, from the above,
We can conclude that
The representation of the given situation as an integer is: -$10
b. Six degrees below zero
Answer:
We know that,
In a vertical number line,
The numbers above zero are positive
The numbers below zero are negative
Hence, from the above,
We can conclude that
The representation of the given situation as an integer is: -6° C
c. Deposit of $25
Answer:
We know that,
A “Deposit” is a positive value
Hence, from the above,
We can conclude that
The representation of the given situation as an integer is: $25
KEY CONCEPT
Integers are all of the counting numbers, their opposites, and 0. Opposites are integers that are the same distance from 0 and on opposite sides of 0 on a number line.
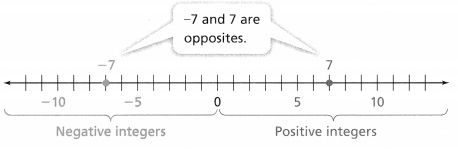
Do You Understand?
Question 1.
? Essential Question What are integers and how are they used to represent real-world quantities?
Answer:
“Integers” are a set of numbers that include the positive whole numbers (1, 2, 3, 4, 5, …), their opposites (-1, -2, -3, -4, -5, …) and zero.
You can use integers to help represent many real-world situations, such as Increases and decreases in temperature
Question 2.
Reasoning What do you know about two different integers that are opposites?
Answer:
Let us consider two integers a and b such that a > b (or) a < b
Now,
The opposites of the two integers are: -a and -b
Now,
In the number line,
The numbers after 0 increase from left to right
The numbers before 0 decrease from right to left
So,
We can conclude that
-a < -b (or) -a > -b
Hence, from the above,
We can conclude that
The two different integers that are opposites can be represented as:
-a < -b or -a > -b
Question 3.
How do you read -17?
Answer:
The given number is: -17
Hence,
We can conclude that
-17 can read as:
a. The opposite of 17
b. The number that is on the left side of the number line
Question 4.
Construct Arguments which amount represents a debt of two hundred fifty dollars, $250 or -$250? Explain.
Answer:
We know that,
A “Debt” is a negative number
Hence, from the above,
We can conclude that
The representation of a debt of two hundred fifty dollars in the form of an integer is: -$250
Question 5.
Generalize when comparing two negative integers, how can you determine which integer is the greater number?
Answer:
We know that,
In the number line,
The numbers that are on the left side of 0 are called “Negative Numbers”
The “Negative Numbers” decrease when moves from right to left
Hence, from the above,
We can conclude that
When comparing two negative integers,
The negative number that is nearest to zero is the greater number
Do You Know How?
In 6-17, write the opposite of each integer.
Question 6.
1
Answer:
The given integer is: 1
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of 1 is: -1
Question 7.
-1
Answer:
The given integer is: -1
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -1 is: 1
Question 8.
-11
Answer:
The given integer is: -11
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -11 is: 11
Question 9.
30
Answer:
The given integer is: 30
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of 30 is: -30
Question 10.
0
Answer:
The given integer is: 0
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
There is not any opposite value for 0
Hence, from the above,
We can conclude that
The opposite of 0 is: 0
Question 11.
-16
Answer:
The given integer is: -16
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -16 is: 16
Question 12.
-(-8)
Answer:
The given integer is: -(-8)
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -(-8) is: -8
Question 13.
28
Answer:
The given integer is: 28
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of 28 is: -28
Question 14.
-(-65)
Answer:
The given integer is: -(-65)
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -(-65) is: -65
Question 15.
98
Answer:
The given integer is: 98
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of 98 is: -98
Question 16.
100
Answer:
The given integer is: 100
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of 100 is: -100
Question 17.
-33
Answer:
The given integer is: -33
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -33 is: 33
In 18-20, write the integers in order from least to greatest.
Question 18.
2, -3, 0, -4
Answer:
The given integers are: 2, -3, 0, -4
Now,
We know that,
In a number line,
The numbers after zero increase from left to right i.e., the farthest number after zero will be a greater number
The numbers before zero decrease from right to left i.e., the nearest number to zero will be a greater number
Hence, from the above,
We can conclude that
The given integers from the least to the greatest is: -4, -3, 0, 2
Question 19.
4, 12, -12, -11
Answer:
The given integers are: 4, 12, -12, -11
Now,
We know that,
In a number line,
The numbers after zero increase from left to right i.e., the farthest number after zero will be a greater number
The numbers before zero decrease from right to left i.e., the nearest number to zero will be a greater number
Hence, from the above,
We can conclude that
The given integers from the least to the greatest is: -12, -11, 4, 12
Question 20.
-5, 6, -7, -8
Answer:
The given integers are: -5, 6, -7, -8
Now,
We know that,
In a number line,
The numbers after zero increase from left to right i.e., the farthest number after zero will be a greater number
The numbers before zero decrease from right to left i.e., the nearest number to zero will be a greater number
Hence, from the above,
We can conclude that
The given integers from the least to the greatest is: -8, -7, -5, 6
Practice & Problem Solving
Scan for Multimedia
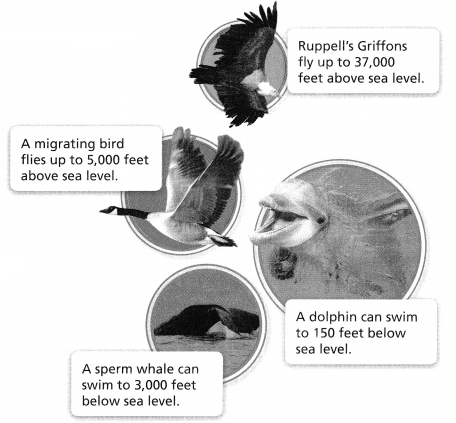
In 21-24, use the pictures at the right.
Question 21.
Generalize Which integer represents sea level? Explain.
Answer:
We know that,
We will represent the real-world situations always like above the sea level and below the sea level
Now,
When we observe a number line,
We will say the numbers above zero and the numbers below zero
Now,
When we compare the 2 definitions,
We can say that
The integer that represents the sea level is: zero
Hence, from the above,
We can conclude that
The integer that represents the sea level is: Zero
Question 22.
Use a negative integer to represent the depth to which a dolphin may swim.
Answer:
From the given figure,
We can observe that
A dolphin can swim to 150 feet below the sea level
Now,
We know that,
The values below the sea level are all “Negative numbers”
Hence, from the above,
We can conclude that
The representation of the depth to which a dolphin may swim in the form of an integer is: -150 feet
Question 23.
Which of these animals can travel at the greatest distance from sea level?
Answer:
We know that,
The values that are above the sea level are “Positive values” and the value that is farthest from the sea level is the greatest value
The values that are below the sea level are “Negative values” and the value that is nearest to the sea level is the greatest value
Hence, from the above,
We can conclude that
The animal that can travel at the greatest distance above sea level is: Griffon
The animal that can travel at the greatest distance below sea level is: Sperm whale
Question 24.
Order the elevations of the animals as integers from least to greatest.
Answer:
The given figure is:

Now,
We know that,
We know that,
The values that are above the sea level are “Positive values” and the value that is farthest from the sea level is the greatest value
The values that are below the sea level are “Negative values” and the value that is nearest to the sea level is the greatest value
Hence, from the above,
We can conclude that
The elevations of the animals as integers from the least to the greatest is:
Sperm whale, Dolphin, Migrating bird, Griffon
In 25-30, plot each point on the number line below.
Question 25.
G(-10)
Answer:
The given point is: G (-10)
Hence,
The representation of the given point on the number line is:

Question 26.
H(8)
Answer:
The given point is: H (8)
Hence,
The representation of the given point on the number line is:

Question 27.
I(-1)
Answer:
The given point is: I (-1)
Hence,
The representation of the given point on the number line is:

Question 28.
J(9)
Answer:
The given point is: J (9)
Hence,
The representation of the given point on the number line is:

Question 29.
K(6)
Answer:
The given point is: K (6)
Hence,
The representation of the given point on the number line is:

Question 30.
L(-3)
Answer:
The given point is: L (-3)
Hence,
The representation of the given point on the number line is:

In 31-36, write the integer value that each point represents. Then use the number line to help write its opposite.
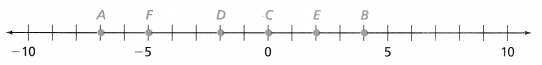
Question 31.
A
Answer:
The given number line is:
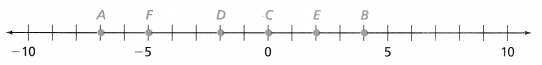
Now,
From the given figure,
We can observe that
The value of A is: -7
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
So,
The opposite value of A is: 7
Hence, from the above,
We can conclude that
The integer value that A represents is: -7
The opposite value of -7 is: 7
Question 32.
B
Answer:
The given number line is:
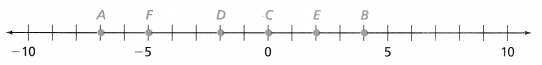
Now,
From the given figure,
We can observe that
The value of B is: 4
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
So,
The opposite value of B is: -4
Hence, from the above,
We can conclude that
The integer value that B represents is: 4
The opposite value of 4 is: -4
Question 33.
C
Answer:
The given number line is:
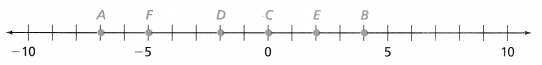
Now,
From the given figure,
We can observe that
The value of C is: 0
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
The opposite of 0 is 0 i.e., there is not any opposite value for 0
So,
The opposite value of C is: 0
Hence, from the above,
We can conclude that
The integer value that C represents is: 0
The opposite value of 0 is: 0
Question 34.
D
Answer:
The given number line is:
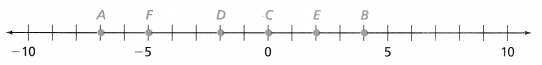
Now,
From the given figure,
We can observe that
The value of D is: -2
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
So,
The opposite value of D is: 2
Hence, from the above,
We can conclude that
The integer value that D represents is: -2
The opposite value of -2 is: 2
Question 35.
E
Answer:
The given number line is:
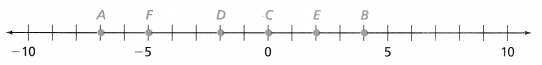
Now,
From the given figure,
We can observe that
The value of E is: 2
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
So,
The opposite value of E is: -2
Hence, from the above,
We can conclude that
The integer value that E represents is: 2
The opposite value of 2 is: -2
Question 36.
F
Answer:
The given number line is:
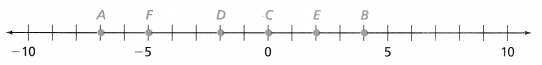
Now,
From the given figure,
We can observe that
The value of F is: -5
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
So,
The opposite value of F is: 5
Hence, from the above,
We can conclude that
The integer value that F represents is: -5
The opposite value of -5 is: 5
Question 37.
Write the opposite of each integer.
A. 5
Answer:
The given integer is: 5
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of 5 is: -5
B. -13
Answer:
The given integer is: -13
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -13 is: 13
C. -(-22)
Answer:
The given integer is: -(-22)
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -(-22) is: -22
D. -31
Answer:
The given integer is: -31
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -31 is: 31
E. -50
Answer:
The given integer is: -50
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -50 is: 50
F. -(-66)
Answer:
The given integer is: -(-66)
Now,
We know that,
The opposite of any integer ‘a’ is ‘−a‘ Similarly, the opposite of any integer ‘−a’ is ‘−(−a)’ = ‘a’
Hence, from the above,
We can conclude that
The opposite of -(-66) is: -66
Question 38.
Compare the integers and write the integer with the greater value.
A. -5, 1
Answer:
The given integers are: -5, 1
Now,
We know that,
In a number line,
The numbers that are after zero are “Positive numbers” and the numbers that are farthest to zero are the greater numbers
The numbers that are before zero are “Negative numbers” and the numbers that are nearest to zero are the least numbers
The “Positive numbers” are always greater than “Negative numbers”
Hence, from the above,
We can conclude that
1 > -5
The greater value is: 1
B. -6, -7
Answer:
The given integers are: -6, -7
Now,
We know that,
In a number line,
The numbers that are after zero are “Positive numbers” and the numbers that are farthest to zero are the greater numbers
The numbers that are before zero are “Negative numbers” and the numbers that are nearest to zero are the least numbers
The “Positive numbers” are always greater than “Negative numbers”
Hence, from the above,
We can conclude that
-6 > -7
The greater value is: -6
C. -9, 8
Answer:
The given integers are: -9, 8
Now,
We know that,
In a number line,
The numbers that are after zero are “Positive numbers” and the numbers that are farthest to zero are the greater numbers
The numbers that are before zero are “Negative numbers” and the numbers that are nearest to zero are the least numbers
The “Positive numbers” are always greater than “Negative numbers”
Hence, from the above,
We can conclude that
8 > -9
The greater value is: 8
D. -12, -(-10)
Answer:
The given integers are: -12, -(-10)
So,
The given integers are: -12, 10
Now,
We know that,
In a number line,
The numbers that are after zero are “Positive numbers” and the numbers that are farthest to zero are the greater numbers
The numbers that are before zero are “Negative numbers” and the numbers that are nearest to zero are the least numbers
The “Positive numbers” are always greater than “Negative numbers”
Hence, from the above,
We can conclude that
10 > -12
The greater value is: 10
E. -(-9), 11
Answer:
The given integers are: -(-9), 11
So,
The given integers are: 9, 11
Now,
We know that,
In a number line,
The numbers that are after zero are “Positive numbers” and the numbers that are farthest to zero are the greater numbers
The numbers that are before zero are “Negative numbers” and the numbers that are nearest to zero are the least numbers
The “Positive numbers” are always greater than “Negative numbers”
Hence, from the above,
We can conclude that
11 > 9
The greater value is: 11
F. -(-4), 3
Answer:
The given integers are: -(-4), 3
So,
The given integers are: 4, 3
Now,
We know that,
In a number line,
The numbers that are after zero are “Positive numbers” and the numbers that are farthest to zero are the greater numbers
The numbers that are before zero are “Negative numbers” and the numbers that are nearest to zero are the least numbers
The “Positive numbers” are always greater than “Negative numbers”
Hence, from the above,
We can conclude that
4 > 3
The greater value is: 4
Question 39.
The display at the right shows the daily low temperatures for several consecutive days in a New England city. Write the temperatures in order from least to greatest. On which day was it the coldest?

Answer:
It is given that
The display at the right shows the daily low temperatures for several consecutive days in a New England city.
Now,
The given temperatures are:

Now,
We know that,
In a number line,
The numbers that are after zero are “Positive numbers” and the numbers that are farthest to zero are the greater numbers
The numbers that are before zero are “Negative numbers” and the numbers that are nearest to zero are the least numbers
The “Positive numbers” are always greater than “Negative numbers”
So,
The temperatures in order from the last to the greatest is:
-7° < -5° < 4° < 7°
The coldest day from the given days is: Wednesday
Hence, from the above,
We can conclude that
The temperatures in order from the last to the greatest is:
-7° < -5° < 4° < 7°
The coldest day from the given days is: Wednesday
Question 40.
In a bank account, a paid-out expense is called a debit, and a deposit is called a credit. Would you use positive or negative integers to represent credits? Debits? Explain.
Answer:
It is given that
In a bank account, a paid-out expense is called a debit, and a deposit is called a credit.
Now,
We know that,
A “Paid-out expense” or “Debit” is a negative value
A “Deposit” or “Credit” is a positive value
Hence, from the above,
We can conclude that
We will use “Positive integers” to represent “Credits”
We will use “Negative integers” to represent “Debits”
Question 41.
Higher-Order Thinking Atoms have negatively charged particles called electrons and positively charged particles called protons. If an atom loses an electron, it has a positive electric charge. If it gains an electron, it has a negative electric charge. Which integer would represent the electric charge of an atom that has an equal number of electrons and protons?
Answer:
It is given that
Atoms have negatively charged particles called electrons and positively charged particles called protons. If an atom loses an electron, it has a positive electric charge. If it gains an electron, it has a negative electric charge.
Now,
We know that,
“Protons” and “Electrons” have the same values but opposite signs
So,
The value of the integer that has an equal number of electrons and protons = (The number of Protons) – (The number of Electrons)
= 0 (Since both have the same values but with opposite signs)
Hence, from the above,
We can conclude that
The value of the integer that has an equal number of electrons and protons is: 0
Assessment Practice
Question 42.
Marco goes on a recreational scuba diving expedition. What is a possible diving depth for his expedition?
A. 0 meters
B. 40 meters
C. 400 meters
D. -40 meters
Answer:
It is given that
Marco goes on a recreational scuba diving expedition.
Now,
In terms of sea level,
The “Height” represents the positive values
The “Depth” represents the negative values
Hence, from the above,
We can conclude that
The possible diving depth for Marco’s expedition is:

Question 43.
Fill in the bubbles to match each integer with its opposite.
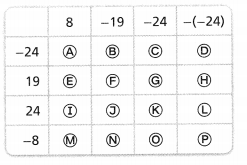
Answer:
The bubbles that matched with each integer and its opposite are:

Lesson 2.2 Represent Rational Numbers on the Number Line
ACTIVITY
Explore It!
The locations of four animals relative to sea level are shown.

A. What can you say about the animals and their positions relative to sea level?
Answer: It is given that
The locations of four animals relative to sea level are shown.
Now,
The given figure is:

Now,
We know that,
The sea level is considered as zero
The values above the sea level are positive
The values below the sea level are negative
Now,
From the given figure,
We can observe that
The animals that are below the sea level are: Dolphin, Sea Turtle, and Shark
The animals that are above sea level are: Seagull
Hence, from the above,
We can conclude that
The animals that are below the sea level are: Dolphin, Sea Turtle, and Shark
The animals that are above sea level are: Seagull
B. How can you use a number line to represent the locations of the animals?
Answer:
The given figure is:

Now,
In terms of a number line,
The sea level is considered zero
The values above zero (Sea level) are positive
The values below zero (Sea level) are negative
So,
The representations of the locations of the given animals in a number line are:
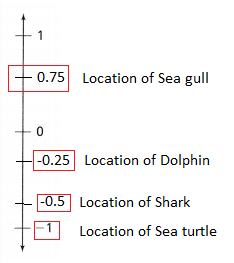
Hence, from the above,
We can conclude that
The representation of the locations of the animals in a number line is:

Focus on math practices
Generalize How is representing the locations of negative fractions and decimals like representing the locations of positive fractions and decimals? How is it different?
Answer:
We know that,
In a number line,
The values above zero are “Positive numbers”
The values below zero are “Negative numbers”
Hence,
If the fractions and decimals are positive, then they are above zero in a number line
If the fractions and decimals are negative, then they are below zero in a number line
Visual Learning
? Essential Question How can you plot, compare, and order rational numbers using a number line?
Answer:
Just as positive and negative integers can be represented on a number line, so can positive and negative rational numbers. You can use a number line to help you compare and order negative rational numbers.
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left
Try It!
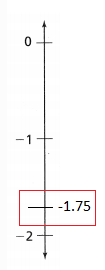
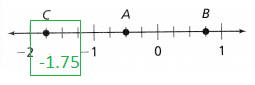
How can you find and position –\(\frac{5}{4}\) and -1.75 on the number lines? Write –\(\frac{5}{4}\) and -1.75 as mixed numbers, then plot the points on the number lines.

Answer:
The given numbers are: –\(\frac{5}{4}\) and -1.75
Now,
The representation of –\(\frac{5}{4}\) into a mixed number is:
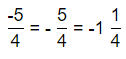
The representation of -1.75 into a mixed number is:
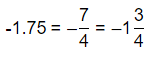
So,
The representation of –\(\frac{5}{4}\) on a number line is:
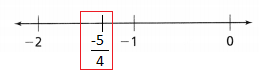
So,
The representation of -1.75 on a number line is:
Hence, from the above,
We can conclude that
The representation of the given numbers as mixed numbers are:
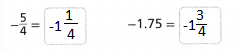
The representation of the given numbers on a number line is:
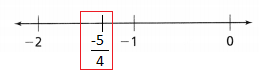

Convince Me! Why is it helpful to rename –\(\frac{5}{4}\) and -1.75 as mixed numbers when plotting these points on number lines?
Answer:
The given numbers are: –\(\frac{5}{4}\) and -1.75
Now,
The representations of the given numbers into mixed numbers are:
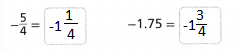
Now,
When we observe the fraction part in the mixed numbers,
We can draw a conclusion as to how much nearer to the whole numbers the fraction part is
Now,
We know that,
Between 2 numbers,
\(\frac{1}{4}\) is near to the previous number
\(\frac{1}{2}\) is between 2 numbers
\(\frac{3}{4}\) is near to the next number
Hence,
We will rewrite the numbers into mixed numbers to facilitate the marking of the numbers on the number line
Try It!
If \(\frac{1}{4}\) is ordered within the list of numbers in the example above, between which two numbers would it be placed?
Answer:
The given numbers in Example 2 are:
\(\frac{2}{3}\), 1.75 and -0.75
Now,
The given numbers from the given information will be:
\(\frac{2}{3}\), \(\frac{1}{4}\), 1.75 and -0.75
Now,
Convert all the given numbers into decimal numbers to compare the numbers from the least to the greatest
So,
The representation of the given fractions into decimal numbers are:
\(\frac{2}{3}\) = 0.66
\(\frac{1}{4}\) = 0.25
So,
The order of the given numbers from the least t the greatest is:
-0.75 < \(\frac{1}{4}\) < \(\frac{2}{3}\) < 1.75
Hence, from the above,
We can conclude that
\(\frac{1}{4}\) would be placed between -0.75 and \(\frac{2}{3}\)
Try It!
At 10:00 P.M. one winter night, the temperature was -3°C. At midnight, the temperature was -7°C. Use <, >, or = to compare the two temperatures and explain their relationship.
Answer:
It is given that
At 10:00 P.M. one winter night, the temperature was -3°C. At midnight, the temperature was -7°C.
Now,
We know that,
The values before zero are called “Negative Numbers”
The values before zero decrease as we move from right to left
The farthest value at the leftmost side of a number line is the “least value”
So,
-3° C > -7° C
Hence, from the above,
We can conclude that
The temperature at 10 P.M is greater than the midnight
KEY CONCEPT
A rational number can be expressed as a fraction in the form \(\frac{a}{b}\) and –\(\frac{a}{b}\) are integers and b is not 0.
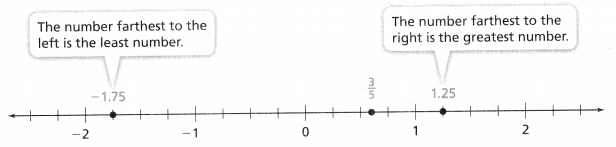
The numbers, in order from least to greatest, are: -1.75, \(\frac{3}{5}\), 1.25
Do You Understand?
Question 1.
? Essential Question How can you plot, compare, and order rational numbers using a number line?
Answer:
Just as positive and negative integers can be represented on a number line, so can positive and negative rational numbers. You can use a number line to help you compare and order negative rational numbers.
When comparing the values of two numbers, you can use a number line to determine which number is greater. The number on the right is always greater than the number on the left
Question 2.
Generalize Why are whole numbers rational numbers? Use 15 as an example.
Answer:
Rational numbers are the numbers that can be written in the form of \(\frac{p}{q}\) where q ≠ 0. “Whole numbers” are the numbers that start from 0 to ∞. Whole numbers can be written in the form of \(\frac{0}{1}\), \(\frac{1}{1}\), \(\frac{2}{1}\), etc. Thus, every whole number is a rational number but every rational number is not a whole number.
Example:
15 = \(\frac{15}{1}\)
We know that,
15 is a “Whole number”
So,
We can write 15 in the form of \(\frac{p}{q}\) i.e., a “Rational number”
Question 3.
Vocabulary Why are integers rational numbers? Give an example.
Answer:
An “Integer” can be written as a fraction by giving it a denominator of one, So, any integer is a rational number
Examples: 17 and -34 are integers as well as rational numbers
Question 4.
Reasoning Explain how the inequality -4°C > -9°C describes how the temperatures are related.
Answer:
The given inequality is: -4°C > -9°C
Now,
We know that,
In a number line,
The values before zero are “Negative values”
The negative values on a number line decrease from right to left
So,
In the negative values,
The large number will be a small number and vice-versa
Hence, from the above,
We can conclude that
-4° C is greater than -9° C
Do You Know How?
In 5-7, write the number positioned at each point.
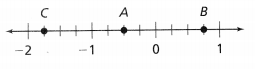
Question 5.
A
Answer:
The given number line is:
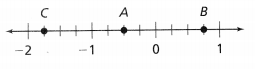
Hence,
The representation of the value of A on the given number line is:

Question 6.
B
Answer:
The given number line is:
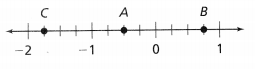
Hence,
The representation of the value of B on the given number line is:
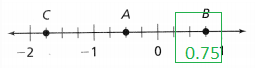
Question 7.
C
Answer:
The given number line is:
Hence,
The representation of the value of C on the given number line is:
In 8-11, plot the points on the number line below.

Question 8.
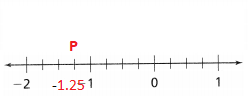
P at -1\(\frac{1}{4}\)
Answer:
The given point is: P (-1\(\frac{1}{4}\))
Now,
The representation of -1\(\frac{1}{4}\) into a decimal number is:
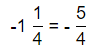
-1\(\frac{1}{4}\) = -1.25
Hence,
The representation of P on the given number line is:
Question 9.
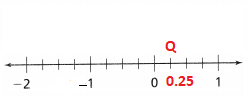
Q at 0.25
Answer:
The given point is: Q (0.25)
Hence,
The representation of Q on the given number line is:
Question 10.
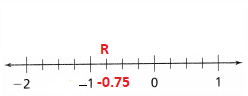
R at -0.75
Answer:
The given point is: R (-0.75)
Hence,
The representation of R on the given number line is:
Question 11.
S at –\(\frac{1}{4}\)
Answer:
The given point is: S (-\(\frac{1}{4}\))
Now,
The representation of –\(\frac{1}{4}\) into a decimal number is:
![]()
In 12-14, use the number line to help order the numbers from least to greatest.
![]()
Question 12.
1.25, –\(\frac{3}{2}\), -1.25, 1\(\frac{1}{2}\)
Answer:
The given numbers are:
1.25, –\(\frac{3}{2}\), -1.25, 1\(\frac{1}{2}\)
Now,
The representation of the given numbers into decimal numbers are:
1.25, -1.5, -1.25, 1.5
Hence, from the above,
We can conclude that
The numbers that are from the least to the greatest are: -1.5, -1.25, 1.25, 1.5
Question 13.
– 0.5, \(\frac{1}{2}\), -0.75, \(\frac{3}{4}\)
Answer:
The given numbers are:
– 0.5, \(\frac{1}{2}\), -0.75, \(\frac{3}{4}\)
Now,
The representation of the given numbers into decimal numbers are:
-0.5, 0.5, -0.75, 0.75
Hence, from the above,
We can conclude that
The numbers that are from the least to the greatest are: -0.75, -0.5, 0.5, 0.75
Question 14.
-1.5, -0.75, -1,2
Answer:
The given numbers are:
-1.5, -0.75, -1,2
Hence, from the above,
We can conclude that
The numbers that are from the least to the greatest are: -1.5, -1.2, -0.75
Practice & Problem Solving
Scan for Multimedia
In 15-20, write the number positioned at each point.
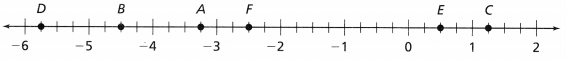
Question 15.
A
Answer:
The given number line is:
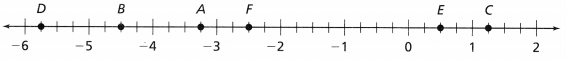
Now,
We know that,
Each line in the given number line represents 0.25 units
Hence, from the above,
We can conclude that
The value of A in the given number line is: -3.25
Question 16.
B
Answer:
The given number line is:
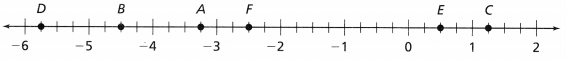
Now,
We know that,
Each line in the given number line represents 0.25 units
Hence, from the above,
We can conclude that
The value of B in the given number line is: -4.5
Question 17.
C
Answer:
The given number line is:
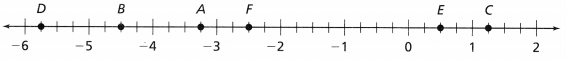
Now,
We know that,
Each line in the given number line represents 0.25 units
Hence, from the above,
We can conclude that
The value of C in the given number line is: 1.25
Question 18.
D
Answer:
The given number line is:
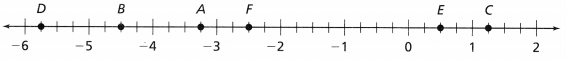
Now,
We know that,
Each line in the given number line represents 0.25 units
Hence, from the above,
We can conclude that
The value of D in the given number line is: -5.75
Question 19.
E
Answer:
The given number line is:
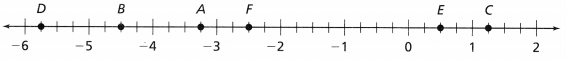
Now,
We know that,
Each line in the given number line represents 0.25 units
Hence, from the above,
We can conclude that
The value of E in the given number line is: 0.5
Question 20.
F
Answer:
The given number line is:
Now,
We know that,
Each line in the given number line represents 0.25 units
Hence, from the above,
We can conclude that
The value of F in the given number line is: -2.5
Question 21.
Plot the numbers on the number line below.

A. -5\(\frac{1}{2}\)
Answer:
The given fraction is: -5\(\frac{1}{2}\)
Now,
The given number line is:

Now,
The representation of the given fraction into a decimal number is: -5.5
From the given number line,
We can observe that
Each line in the number line represents 0.1 units
Hence,
The representation of the given fraction in the given number line is:
B. -6.3
Answer:
The given number is: -6.3
Now,
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the number line represents 0.1 units
Hence,
The representation of the given decimal number in the given number line is:
C. -5.8
Answer:
The given number is: -5.8
Now,
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the number line represents 0.1 units
Hence,
The representation of the given decimal number in the given number line is:

D. -6\(\frac{7}{10}\)
Answer:
The given fraction is: -6\(\frac{7}{10}\)
Now,
The given number line is:

Now,
The representation of the given fraction into a decimal number is: -6.7
From the given number line,
We can observe that
Each line in the number line represents 0.1 units
Hence,
The representation of the given fraction in the given number line is:
E. -4.9
Answer:
The given number is: -4.9
Now,
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the number line represents 0.1 units
Hence,
The representation of the given decimal number in the given number line is:

F. -6\(\frac{9}{10}\)
Answer:
The given fraction is: -6\(\frac{9}{10}\)
Now,
The given number line is:

Now,
The representation of the given fraction into a decimal number is: -6.9
From the given number line,
We can observe that
Each line in the number line represents 0.1 units
Hence,
The representation of the given fraction in the given number line is:

Question 22.
Use <, >, or = to compare.
A. \(\frac{1}{10}\) ![]() 0.09
0.09
Answer:
The given numbers are: \(\frac{1}{10}\), 0.09
Now,
Convert –\(\frac{1}{10}\) into a decimal number
So,
\(\frac{1}{10}\) = 0.10
Hence, from the above,
We can conclude that
![]()
B. –1.44 ![]() -1\(\frac{1}{4}\)
-1\(\frac{1}{4}\)
Answer:
The given numbers are: -1.44, -1\(\frac{1}{4}\)
Now,
Convert -1\(\frac{1}{4}\) into a decimal number
So,
1\(\frac{1}{4}\) = 1.25
Hence, from the above,
We can conclude that
![]()
C. –\(\frac{2}{3}\) ![]() -0.8
-0.8
Answer:
The given numbers are: -0.8, –\(\frac{2}{3}\)
Now,
Convert –\(\frac{2}{3}\) into a decimal number
So,
\(\frac{2}{3}\) = 0.66
Hence, from the above,
We can conclude that
![]()
D. 0.5 ![]() \(\frac{2}{4}\)
\(\frac{2}{4}\)
Answer:
The given numbers are: 0.5, \(\frac{2}{4}\)
Now,
Convert \(\frac{2}{4}\) into a decimal number
So,
\(\frac{2}{4}\) = 0.5
Hence, from the above,
We can conclude that
![]()
E. -2\(\frac{3}{4}\) ![]() -2.25
-2.25
Answer:
The given numbers are: -2\(\frac{3}{4}\), -2.25
Now,
Convert 2\(\frac{3}{4}\) into a decimal number
So,
2\(\frac{3}{4}\) = 2.75
Hence, from the above,
We can conclude that
![]()
F. –\(\frac{3}{5}\) ![]() -0.35
-0.35
Answer:
The given numbers are: –\(\frac{3}{5}\), -0.35
Now,
Convert \(\frac{3}{5}\) into a decimal number
So,
\(\frac{3}{5}\) = 0.60
Hence, from the above,
We can conclude that
![]()
Question 23.
Order the numbers from least to greatest.
A. -6, 8, -9, 13
Answer:
The given numbers are: -6, 8, -9, 13
Now,
We know that,
In a number line,
The positive values are greater than negative values
The positive values increase from left to right
The negative values decrease from right to left
Hence, from the above,
We can conclude that
The order of the given numbers from the least to the greatest is: -9, -6, 8, 13
B. –\(\frac{4}{5}\), –\(\frac{1}{2}\), 0.25, -0.2
Answer:
The given numbers are: –\(\frac{4}{5}\), –\(\frac{1}{2}\), 0.25, -0.2
Now,
We know that,
In a number line,
The positive values are greater than negative values
The positive values increase from left to right
The negative values decrease from right to left
Now,
The representation of the given numbers into a decimal number is: -0.8, -0.5, 0.25, -0.2
Hence, from the above,
We can conclude that
The order of the given numbers from the least to the greatest is: -0.8, -0.5, -0.2, 0.25
C. 4.75, -2\(\frac{1}{2}\), –\(\frac{8}{3}\), –\(\frac{9}{2}\)
Answer:
The given numbers are: 4.75, -2\(\frac{1}{2}\), –\(\frac{8}{3}\), –\(\frac{9}{2}\)
Now,
We know that,
In a number line,
The positive values are greater than negative values
The positive values increase from left to right
The negative values decrease from right to left
Now,
The representation of the given numbers into a decimal number is: 4.75, -2.5, -2.66, -4.5
Hence, from the above,
We can conclude that
The order of the given numbers from the least to the greatest is: -4.5, -2.66, -2.5, 4.75
D. 4, -3, -8, -1
Answer:
The given numbers are 4, -3, -8, -1
Now,
We know that,
In a number line,
The positive values are greater than negative values
The positive values increase from left to right
The negative values decrease from right to left
Hence, from the above,
We can conclude that
The order of the given numbers from the least to the greatest is: -8, -3, -1, 4
E. –\(\frac{1}{4}\), 0.5, \(\frac{3}{4}\), –\(\frac{1}{2}\)
Answer:
The given numbers are: –\(\frac{1}{4}\), 0.5, \(\frac{3}{4}\), –\(\frac{1}{2}\)
Now,
We know that,
In a number line,
The positive values are greater than negative values
The positive values increase from left to right
The negative values decrease from right to left
Now,
The representation of the given numbers into a decimal number is: -0.25, 0.5, 0.75, -0.5
Hence, from the above,
We can conclude that
The order of the given numbers from the least to the greatest is: -0.5, -0.25, 0.5, 0.75
F. –\(\frac{4}{5}\), –\(\frac{5}{4}\), –\(\frac{3}{2}\), 1.5
Answer:
The given numbers are: –\(\frac{4}{5}\), –\(\frac{5}{4}\), –\(\frac{3}{2}\), 1.5
Now,
We know that,
In a number line,
The positive values are greater than negative values
The positive values increase from left to right
The negative values decrease from right to left
Now,
The representation of the given numbers into a decimal number is -0.8, -1.25, -1.5, 1.5
Hence, from the above,
We can conclude that
The order of the given numbers from the least to the greatest is: -1.5, -1.25, -0.8, 1.5
Question 24.
Make Sense and Persevere What is the least number of points you must plot to have examples of all four sets of numbers, including at least one positive integer and one negative integer? Explain.

Answer:
Let’s define the sets:
Integers: The set of all whole numbers.
Rational numbers: Numbers that can be written as the quotient of two integer numbers.
Natural numbers: The set of positive integers.
Whole numbers: All the numbers that can be made by adding (or subtracting) 1 a given number of times.
Hence, from the above,
We can conclude that
We can use only one example for all four sets of numbers, including at least one positive integer and one negative integer
Question 25.
Reasoning Suppose you plot the locations of the animals on a number line. Which animal would be represented by the point farthest from 0 on the number line? Explain.
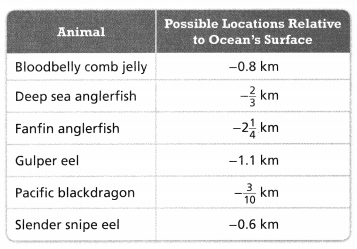
Answer:
It is given that
You plot the locations of the animals on a number line
Now,
The given table is:

Now,
The representation of the given data present in the table into a decimal number is:
Bloodbelly comb jelly – -0.8 km
Deep-sea anglerfish – -0.66 km
Fanfin anglerfish – -2.25 km
Gulper eel – -1.1 km
Pacific blackdragon – -0.3 km
Slender snipe eel – -0.6 km
Now,
We know that,
In a number line,
The negative decrease from right to left
The negative number that is at the end of the number line on the left side is the “Least number”
Hence, from the above,
We can conclude that
The animal which is farthest from 0 at the left side of the number line is: Fanfin anglerfish
The animal which is farthest from 0 at the right side of the number line is: Pacific blackdragon
Question 26.
Which animal is closest to a depth of -0.7 km?
Answer:
From Question 25,
The given information is:

Now,
The representation of the given data present in the table into a decimal number is:
Bloodbelly comb jelly – -0.8 km
Deep-sea anglerfish – -0.66 km
Fanfin anglerfish – -2.25 km
Gulper eel – -1.1 km
Pacific blackdragon – -0.3 km
Slender snipe eel – -0.6 km
Hence, from the above,
We can conclude that
The animal that is closest to a depth of -0.7 km is: Deep-sea anglerfish
Question 27.
The change in the value of a stock is represented by the rational number -5.90. Describe, in words, what this means.
Answer:
It is given that
The change in the value of a stock is represented by the rational number -5.90.
Now,
From the given information,
We can observe that
The given number is a negative number.
Now,
We know that,
When a stock is given by a negative number, it represents the decrease in stock and when a stock is given by a positive number, it represents the increase in stock.
As we are given number is a negative number,
We can just say that
The stock value is being decreased by 5.90.
Hence, from the above,
We can conclude that
The representation of the given information in words is:
The stock value is being decreased by 5.90.
Question 28.
Construct Arguments A classmate ordered these numbers from greatest to least. Is he correct? Construct an argument to justify your answer.
4.4, 4.2, -4.42, -4.24
Answer:
It is given that
A classmate ordered these numbers from greatest to least and the given order of these numbers is:
4.4, 4.2, -4.42, -4.24
Now,
We know that,
The positive values are greater than the negative values
In a number line,
The negative values decrease from right to left
The positive values increase from left to right
So,
The order of the numbers ordered by a classmate from the greatest to the least is:
4.4, 4.2, -4.24, -4.42
Hence, from the above,
We can conclude that
The classmate is not correct
Question 29.
Make Sense and Persevere Order -3.25, -3\(\frac{1}{8}\), -3\(\frac{3}{4}\), and -3.1 from least to greatest. Explain.
Answer:
The given numbers are: -3.25, -3\(\frac{1}{8}\), -3\(\frac{3}{4}\), and -3.1
Now,
The representation of the given numbers into a decimal number is:
-3.25, -3.12, -3.75, and -3.1
Hence, from the above,
We can conclude that
The order of the given numbers from the least to the greatest is:
-3.75, -3.25, -3.12, -3.1
Question 30.
Higher Order Thinking Suppose \(\frac{a}{b}\), \(\frac{c}{d}\), and \(\frac{e}{f}\) represent three rational numbers. If \(\frac{a}{b}\) is less than \(\frac{c}{d}\), and \(\frac{c}{d}\) is less than \(\frac{e}{f}\), compare \(\frac{a}{b}\) and \(\frac{e}{f}\). Explain.
Answer:
It is given that
Suppose \(\frac{a}{b}\), \(\frac{c}{d}\), and \(\frac{e}{f}\) represent three rational numbers. If \(\frac{a}{b}\) is less than \(\frac{c}{d}\), and \(\frac{c}{d}\) is less than \(\frac{e}{f}\)
Now,
According to the given information,
\(\frac{a}{b}\) < \(\frac{c}{d}\) and \(\frac{c}{d}\) < \(\frac{e}{f}\)
So,
\(\frac{a}{b}\) < \(\frac{c}{d}\) < \(\frac{e}{f}\)
Hence, from the above,
We can conclude that
\(\frac{a}{b}\) < \(\frac{e}{f}\)
Assessment Practice
Question 31.
Which could be a value for n?
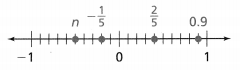
A. –\(\frac{1}{2}\)
B. –\(\frac{1}{3}\)
C. –\(\frac{1}{4}\)
D. –\(\frac{1}{6}\)
Answer:
The given number line is:

Now,
From the given figure,
We can observe that
Each line in the given number line is: 0.1 units
So,
The representation of the value of n on the given number line is:
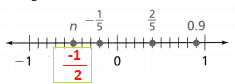
Hence, from the above,
We can conclude that
The value of n on the given number line is:
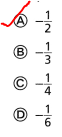
Question 32.
Which inequality does NOT represent the correct position of two numbers on a number line?
A. 4\(\frac{1}{2}\) > \(\frac{25}{4}\)
B. -4\(\frac{1}{2}\) > –\(\frac{25}{5}\)
C. -6 < -5
D. –\(\frac{1}{2}\) < \(\frac{1}{2}\)
Answer:
The given inequalities are:
A. 4\(\frac{1}{2}\) > \(\frac{25}{4}\)
B. -4\(\frac{1}{2}\) > –\(\frac{25}{5}\)
C. -6 < -5
D. –\(\frac{1}{2}\) < \(\frac{1}{2}\)
So,
The representation of the given inequalities in the form of a decimal number is:
A. 4.5 > 6.25
B. -9.5 > -5
C. -6 < -5
D. -0.5 < 0.5
Hence, from the above,
We can conclude that
The inequality that does not represent the correct position of two numbers on a number line is:

Lesson 2.3 Absolute Values of Rational Numbers
Solve & Discuss It!
A portion of a bank account statement is shown below How would you interpret the value of the ending balance? Explain.

Answer:
It is given that
A portion of a bank account statement is shown
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The Ending Balance is: -$30
Now,
We know that,
A negative balance in your Debit Account means you owe money to the bank. It probably means you have used more than what you had in your account
Hence, from the above,
We can conclude that
The Ending Balance of -$30 in your account statement represents a negative balance in your Debit Account which means you owe money to the bank. It probably means you have used more than what you had in your account
Focus on math practices
Reasoning What is an example of a bank account balance that represents an amount owed greater than $40?
Answer:
We know that,
The money owed should be represented as “Negative”
Now,
Let the bank account balance that represents an amount be x
So,
According to the given information,
x > -$40
Hence, from the above,
We can conclude that
The representation of the bank account balance that represents an amount greater than 40$ is:
x > -$40
Visual learning
? Essential Question
How are absolute values used to describe quantities?
Answer:
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Try It!
The students in a science class recorded the change in the water level of a local river. During which week did the water level change by the greatest amount?
Use absolute values to represent the change in the water level.

The water level changed by the greatest amount in Week![]() .
.
Answer:
It is given that
The students in a science class recorded the change in the water level of a local river
Now,
The given table is:

Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The representation of the changes in the water level is:

Hence, from the above,
We can conclude that

Convince Me! Can a lesser number represent a greater change in water level than a greater number? Explain.
Answer:
The given table is:

Now,
From the given table,
We can observe that
The greatest number in the given table represents the greatest change in the water level
Hence, from the above,
We can conclude that
A lesser number can not represent a greater change in water level than a greater number
Try It!
A bank has two customers with overdrawn accounts. Which balance is the greater number? Which balance is the lesser amount owed?

Answer:
It is given that
A bank has two customers with overdrawn accounts
Now,
The given information is:

Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute value of V.Wong’s Account’s balance is: $19.45
The absolute value of J.Olson’s Account’s balance is: $23.76
Now,
We know that,
In a number line,
The value of a negative number decrease from right to left and the negative number that is farthest to zero is the least number
We represent the amount of money owed as “Negative”
So,
The greater number is: $23.76
The balance that is the lesser amount owed is: $-19.45
Hence, from the above,
We can conclude that
The greater number is: $23.76
The balance that is the lesser amount owed is: $-19.45
KEY CONCEPT
The absolute value of a number is its distance from 0 on a number line. Distance is always positive. The absolute value of any number, n, is written |n|.

-4 and 4 are opposites as they are the same distance from 0.
Do You Understand?
Question 1.
? Essential Question How are absolute values used to describe quantities?
Answer:
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Question 2.
Construct Arguments Explain why – 7 has a greater absolute value than the absolute value of 6.
Answer:
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute value of -7 is:
|-7| = 7
So,
In the number line,
We know that,
The positive values increase from left to right
Hence, from the above,
We can conclude that
According to the Property of representation of Integers in a number line,
7 > 6
Question 3.
Reasoning Give an example of a balance that has a greater integer value than a balance of -$12 but represents a debt of less than $5.
Answer:
It is given that
Give an example of a balance that has a greater integer value than a balance of -$12 but represents a debt of less than $5.
Now,
Let x be the balance that has a greater integer value than a balance of -$12, but represents a debt of less than $5.
Now,
We are given that a balance that has a greater integer value than a balance of -$12
So,
x >-12
Now,
We are given that balance represents a debt of less than $5.
So,
Debt < -5
So,
x < -5
So,
-5 >x >-12
So,
x ∈ [-6,-11]
Hence, from the above,
We can conclude that
The balance that has a greater integer value than a balance of -$12, but represents a debt of less than $5 is:
-5 > x > -12
Question 4.
Of the three elevations, -2 feet, -12 feet, and 30 feet, which represents the least number? Which represents the farthest distance from sea level?
Answer:
It is given that
There are three elevations namely: -2 feet, -12 feet, and 30 feet
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute values of the three elevations are: 2 feet, 12 feet, and 30 feet
Now,
We know that,
In a number line,
The positive values increase from left to right
So,
The least number is: 2 feet
The farthest distance from the sea level is: 30 feet
Hence, from the above,
We can conclude that
The least number is: 2 feet
The farthest distance from the sea level is: 30 feet
Do You Know How?
In 5-14, find each absolute value.
Question 5.
|-9|
Answer:
The given number is |-9|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-9| is: 9
Question 6.
|5\(\frac{3}{4}\)|
Answer:
The given number is |5\(\frac{3}{4}\)|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |5\(\frac{3}{4}\)| is: 5\(\frac{3}{4}\)
Question 7.
|-5.5|
Answer:
The given number is |-5.5|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-5.5| is: 5.5
Question 8.
|82.5|
Answer:
The given number is |82.5|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |82.5| is: 82.5
Question 9.
|-14\(\frac{1}{3}\)|
Answer:
The given number is |-14\(\frac{1}{3}\)|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-14\(\frac{1}{3}\)| is: 14\(\frac{1}{3}\)
Question 10.
|-7.75|
Answer:
The given number is |-7.75|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-7.75| is: 7.75
Question 11.
|–19|
Answer:
The given number is |-19|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-19| is: 19
Question 12.
|-2\(\frac{1}{2}\)|
Answer:
The given number is |-2\(\frac{1}{2}\)|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-2\(\frac{1}{2}\)| is: 2\(\frac{1}{2}\)
Question 13.
|24|
Answer:
The given number is |24|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |24| is: 24
Question 14.
|35.4|
Answer:
The given number is |35.4|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |35.4| is: 35.4
In 15-17, use the absolute value of each account balance to determine which account has the greater overdrawn amount.
Question 15.
Account A: -$5.42
Account B: -$35.76
Answer:
The given information is:
Account A: -$5.42
Account B: -$35.76
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute value of each account balance is:
Account A: $5.42
Account B: $35.76
Now,
We know that,
In a number line,
The positive values increase from left to right
So,
The account that has the greater overdrawn amount is: Account B
Hence, from the above,
We can conclude that
The account that has the greater overdrawn amount is: Account B
Question 16.
Account A: – $6.47
Account B: -$2.56
Answer:
The given information is:
Account A: -$6.47
Account B: -$2.56
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute value of each account balance is:
Account A: $6.47
Account B: $2.56
Now,
We know that,
In a number line,
The positive values increase from left to right
So,
The account that has the greater overdrawn amount is: Account A
Hence, from the above,
We can conclude that
The account that has the greater overdrawn amount is: Account A
Question 17.
Account A: -$32.56
Account B: -$29.12
Answer:
The given information is:
Account A: -$32.56
Account B: -$29.12
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute value of each account balance is:
Account A: $32.56
Account B: $29.12
Now,
We know that,
In a number line,
The positive values increase from left to right
So,
The account that has the greater overdrawn amount is: Account A
Hence, from the above,
We can conclude that
The account that has the greater overdrawn amount is: Account A
Practice & Problem Solving
In 18-33, find each absolute value.
Question 18.
|-46|
Answer:
The given number is |-46|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-46| is: 46
Question 19.
|0.7|
Answer:
The given number is |0.7|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |0.7| is: 0.7
Question 20.
|-\(\frac{2}{3}\)|
Answer:
The given number is |-\(\frac{2}{3}\)|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-\(\frac{2}{3}\)| is: \(\frac{2}{3}\)
Question 21.
|-7.35|
Answer:
The given number is |-7.35|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-7.35| is: 7.35
Question 22.
|-4\(\frac{3}{4}\)|
Answer:
The given number is |-4\(\frac{3}{4}\)|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-4\(\frac{3}{4}\)| is: 4\(\frac{3}{4}\)
Question 23.
|-54.5|
Answer:
The given number is |-54.5|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-54.5| is: 54.5
Question 24.
|27\(\frac{1}{4}\)|
Answer:
The given number is |27\(\frac{1}{4}\)|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |27\(\frac{1}{4}\)| is: 27\(\frac{1}{4}\)
Question 25.
|–13.35|
Answer:
The given number is |-13.35|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-13.35| is: 13.35
Question 26.
|14|
Answer:
The given number is |14|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |14| is: 14
Question 27.
|-11.5|
Answer:
The given number is |-11.5|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-11.5| is: 11.5
Question 28.
|-6.3|
Answer:
The given number is |-6.3|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-6.3| is: 6.3
Question 29.
|3.75|
Answer:
The given number is |3.75|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |3.75| is: 3.75
Question 30.
|-8.5|
Answer:
The given number is |-8.5|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-8.5| is: 8.5
Question 31.
|15|
Answer:
The given number is |15|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |15| is: 15
Question 32.
|-6\(\frac{3}{4}\)|
Answer:
The given number is |-6\(\frac{3}{4}\)|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-6\(\frac{3}{4}\)| is: 6\(\frac{3}{4}\)
Question 33.
|-5.3|
Answer:
The given number is |-5.3|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
Hence, from the above,
We can conclude that
The absolute value of |-5.3| is: 5.3
In 34-37, order the numbers from least to greatest.
Question 34.
|-12|, |11\(\frac{3}{4}\)|, |-20.5|, |2|
Answer:
The given numbers are:
|-12|, |11\(\frac{3}{4}\)|, |-20.5|, |2|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute values of the given numbers are:
12, 11\(\frac{3}{4}\), 20.5, 2
So,
The absolute values of the given numbers in the decimal form are:
12, 11.75, 20.5, 2
Now,
We know that,
In a number line,
The positive values increase from left to right
Hence, from the above,
We can conclude that
The order of the numbers from the least to the greatest is:
2, 11.75, 12, 20.5
Question 35.
|10|, |-3|, |0|, |-5.25|
Answer:
The given numbers are:
|10|, |-3|, |0|, |-5.25|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute values of the given numbers are:
10, 3, 0, 5.25
Now,
We know that,
In a number line,
The positive values increase from left to right
Hence, from the above,
We can conclude that
The order of the numbers from the least to the greatest is:
0, 3, 5.25, 10
Question 36.
|-6|, |-4|, |11|, |0|
Answer:
The given numbers are:
|-6|, |-4|, |11|, |0|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute values of the given numbers are:
6, 4, 11, 0
Now,
We know that,
In a number line,
The positive values increase from left to right
Hence, from the above,
We can conclude that
The order of the numbers from the least to the greatest is:
0, 4, 6, 11
Question 37.
|4|, |-3|, |–18|, |-3.18|
Answer:
The given numbers are:
|4|, |-3|, |–18|, |-3.18|
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute values of the given numbers are:
4, 3, 18, 3.18
Now,
We know that,
In a number line,
The positive values increase from left to right
Hence, from the above,
We can conclude that
The order of the numbers from the least to the greatest is:
3, 3.18, 4, 18
Alberto and Rebecca toss horseshoes at a stake. Whoever’s horseshoe is closer to the stake wins a point.
Question 38.
Reasoning What integer best describes the location of Alberto’s horseshoe in relation to the stake? What integer best describes the location of Rebecca’s horseshoe?
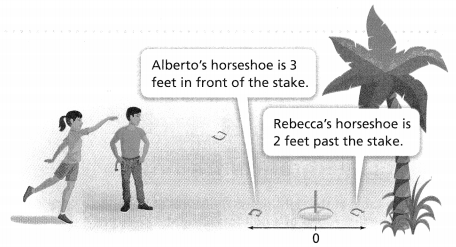
Answer:
It is given that
Alberto and Rebecca toss horseshoes at a stake. Whoever’s horseshoe is closer to the stake wins a point.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The stake is at zero position
The location of Alberto’s horseshoe is at: -3
The location of Rebecca’s horseshoe is at: 2
So,
The location of Alberto’s horseshoe is: 3 feet
The location of Reecca’s horseshoe is: 2 feet
Hence, from the above,
We can conclude that
The integer that best describes the location of Alberto’s horseshoe in relation to the stake is: 3 feet
The integer that best describes the location of Rebecca’s horseshoe is: 2 feet
Question 39.
Critique Reasoning Alberto says that -3 is less than 2, so he wins a point. Is Alberto correct? Explain.
Answer:
It is given that
Alberto says that -3 is less than 2, so he wins a point
Now,
The given figure is:

Now,
The number of points between Alberto’s horseshoe and Rebecca’s horseshoe = |(The location of Alberto’s horseshoe) + (The location of Rebecca’s horseshoe)|
= |-3 + 2|
= |-1|
= 1
Hence, from the above,
We can conclude that Alberto is correct
Question 40.
A model with Math
Find the distance from Alberto’s horseshoe to Rebecca’s horseshoe. Explain.
Answer:
The given figure is:

So,
The distance between Alberto’s horseshoe and Rebecca’s horseshoe = |(The location of Alberto’s horseshoe) + (The location of Rebecca’s horseshoe)|
= |-3 + 2|
= |-1|
= 1 feet
Hence, from the above,
We can conclude that
The distance from Alberto’s horseshoe to Rebecca’s horseshoe is: 1 feet
Question 41.
Higher-Order Thinking Let a = any rational number. Is the absolute value of a difference if a is a positive number or a negative number? Explain.
Answer:
It is given that
“a” is any rational number
Now,
Let
a = 6 (or) a = -5
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
|a| = |6| (or) |a| = |-5|
|a| = 6 (or) |a| = 5
So,
|6 – 5| = |1| =1
Hence, from the above,
We can conclude that
The absolute value of a difference is positive even if “a” is a positive number or a negative number
Question 42.
Construct Arguments Samuel and Leticia are playing a game. After the first round of the game, Samuel’s score was -19, and Leticia’s score was 21. The score with the greater absolute value wins each round. Who won the first round? Explain.
Answer:
It is given that
Samuel and Leticia are playing a game. After the first round of the game, Samuel’s score was -19, and Leticia’s score was 21. The score with the greater absolute value wins each round
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The abso;ute value of Samuel’s score was:
|-19| = 19
The absolute value of Leticia’s score was:
|21| = 21
Now,
We know that,
The positive values increase from left to right
So,
Leticia won the first round
Hence, from the above,
We can conclude that
Leticia won the first round
Question 43.
Use Structure Ana and Chuyen are exploring underwater sea life while on a helmet diving adventure. Ana’s location is -30 feet below sea level, and Chuyen’s location is -12 feet below sea level. Which girl is located farther from sea level?
Answer:
It is given that
Ana and Chuyen are exploring underwater sea life while on a helmet diving adventure. Ana’s location is -30 feet below sea level, and Chuyen’s location is -12 feet below sea level
Now,
We know that,
In a number line,
The negative values decrease from right to left
The negative value that is farthest to the number line is the least value
Hence, from the above,
We can conclude that
Ana is located farther from sea level
Question 44.
Marie’s account balance is – $45.62. Tom’s account balance is $42.55. Which balance represents the greater number? Which balance represents the lesser amount owed?
Answer:
It is given that
Marie’s account balance is – $45.62. Tom’s account balance is $42.55
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute value of Marie’s account balance is: $45.62
The absolute value of Tom’s account balance is: $42.55
So,
The balance that represents the greater number is: Marie’s account balance
The balance that represents the lesser amount owed is: Tom’s account balance
Hence, from the above,
We can conclude that
The balance that represents the greater number is: Marie’s account balance
The balance that represents the lesser amount owed is: Tom’s account balance
Question 45.
In New York, the Federal Reserve gold vault is located at a depth of |-80| feet below ground. The treasure at Oak Island is believed to be at a depth of |-134| feet. Which is farther below ground, the gold vault or the Oak Island treasure?
Answer:
It is given that
In New York, the Federal Reserve gold vault is located at a depth of |-80| feet below ground. The treasure at Oak Island is believed to be at a depth of |-134| feet
Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute value of the depth of the Federal reserve gold vault is: 80 feet
The absolute value of the depth of the treasure at Oak Island is: 134 feet
So,
The treasure at oak Island is farther below ground
Hence, from the above,
We can conclude that
The treasure at Oak Island is farther below ground
Question 46.
Two scuba divers are swimming below sea level. The locations of the divers can be represented by -30 feet and -42 feet. Which measure represents the location that is closest to sea level?
Answer:
It is given that
Two scuba divers are swimming below sea level. The locations of the divers can be represented by -30 feet and -42 feet
Now,
We know that,
In a number line,
The negative values decrease from left to right
Hence, from the above,
We can conclude that
The measure that represents the location that is closest to sea level is: -30 feet
Assessment Practice
Question 47.
The table at the right shows the scores at the end of the first round of a golf tournament. The scores are relative to par.
PART A
Par is represented as 0. Using absolute value, show the distance each score is from par.
Answer:
It is given that
The table at the right shows the scores at the end of the first round of a golf tournament. The scores are relative to par.
Now,
The given table is:

Hence,
The representation of the distance each score is from Par in a number line is:
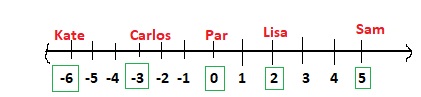
PART B
The golfer with the least score wins the round. Who won the first round of the tournament? Explain.
Answer:
It is given that
The golfer with the least score wins the round
The given table is:

Now,
From part (a),
The representation of the scores on a number line is:

Now,
From the given table,
We can observe that
The golfer who has the least score is: Kate
Hence, from the above,
We can conclude that
Kate won the first round of the tournament
Topic 2 MID-TOPIC CHECKPOINT
Question 1.
Vocabulary Describe the relative locations of the rational numbers -(-\(\frac{a}{b}\)) and \(\frac{a}{b}\) on a number line. Lessons 2.1 and 2.2
Answer:
The given rational numbers are: \(\frac{a}{b}\) and -(-\(\frac{a}{b}\))
Now,
We know that,
– × – = +
So,
The given rational numbers are: \(\frac{a}{b}\) and \(\frac{a}{b}\)
Now,
From the given fractions,
We can observe that both are positive rational numbers
Now,
We know that,
In a number line,
The values after zero are the “positive Values”
Hence, from the above,
We can conclude that
The relative locations of the given rational numbers on a number line are: At the right side of the number line
Question 2.
Marc deposited $175 in a new bank account. After buying some furniture, he was overdrawn by $55. Select all the true statements about Marc’s account. Lesson 2.1
![]() To start, Marc had a negative balance.
To start, Marc had a negative balance.
![]() In this situation, 0 represents an empty bank account.
In this situation, 0 represents an empty bank account.
![]() When Marc was overdrawn, he had a negative balance.
When Marc was overdrawn, he had a negative balance.
![]() After buying furniture, Marc had a positive balance.
After buying furniture, Marc had a positive balance.
![]() The lowest balance in the account was -$55.
The lowest balance in the account was -$55.
Answer:
It is given that
Marc deposited $175 in a new bank account. After buying some furniture, he was overdrawn by $55.
Hence, from the above,
We can conclude that
All the true statements about Marc’s account are:

Question 3.
What number is represented on the number line? Give your answer as a decimal and as a fraction. Lesson 2.2
Answer:
The given number line is:
Now,
From the given number line,
We can observe that
Each line in the given number line represents 0.25 units
So,
The number that is represented on the number line is: -2.25
Hence, from the above,
We can conclude that
The number that is represented on the number line as a decimal number is: -2.25
The number that is represented on the number line as a fraction is: -2\(\frac{1}{4}\)
Question 4.
The absolute value of a number is 52. Select all the integers that this number could be. Lesson 2.3
![]() -52
-52
![]() -25
-25
![]() 25
25
![]() –\(\frac{1}{52}\)
–\(\frac{1}{52}\)
![]() 52
52
Answer:
It is given that
The absolute value of a number is 52
Hence, from the above,
We can conclude that
All the integers that the number could be:
![]()
Question 5.
The table shows the location of four treasure chests relative to sea level. How can you use the number line to find the treasure chest that is farthest from sea level? Lesson 2.2

![]()
Answer:
It is given that
The table shows the location of four treasure chests relative to sea level
Now,
The given table is:

Now,
The representation of \(\frac{5}{4}\) feet in a decimal form is: 1.25 feet
Now,
The given number line is:
![]()
Now,
From the given number line,
We can observe that
Each unit represents 0.25 on the given number line
Hence,
The representation of the locations of the treasure chests on the given number line is:
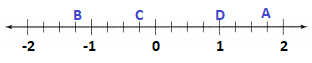
Question 6.
Three customers have accounts owing money. The table shows the account balances that represent what the customers owe. Which customer owes the least amount of money? Lesson 2.3
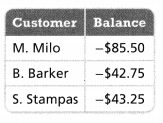
Answer:
It is given that
Three customers have accounts owing money. The table shows the account balances that represent what the customers owe.
Now,
The given table is:

Now,
We know that,
In a number line,
The negative value that is farthest from zero is the least value
The negative values decrease from right to left
Hence, from the above,
We can conclude that
The customet that owes the least amount of money is: B Barker
How well did you do on the mid-topic checkpoint? Fill in the stars. 
Topic 2 MID-TOPIC PERFORMANCE TASK
Warren and Natasha started a dog-walking business. During their first week, they paid $10 to make their business cards and $6 for a 4.5-pound box of doggie treats. Warren walked a dog for 15 minutes, and Natasha walked a dog for 30 minutes.
PART A
Which integers represent the dollar amounts either spent or earned during the first week Warren and Natasha were in business? Select all that apply.
![]() $5
$5
![]() -$5
-$5
![]() $10
$10
![]() -$10
-$10
![]() -$6
-$6

Answer:
It is given that
Warren and Natasha started a dog-walking business. During their first week, they paid $10 to make their business cards and $6 for a 4.5-pound box of doggie treats. Warren walked a dog for 15 minutes, and Natasha walked a dog for 30 minutes.
Now,
The given table is:

So,
The amount of money Warren and Natasha spent during the first week = (The amount spent on business cards) + 9the amount spent on a 4.5-pound box of doggie treats)
= $10 + $6
= $16
So,
The amount earned by Warren = $5
The amount earned by Natasha = $10
Hence, from the above,
We can conclude that
The integers that represent the dollar amounts either spent or earned during the first week Warren and Natasha were in business are:

PART B
At the end of each week, Warren records the weight in pounds of doggie treats eaten as a negative rational number. Plot the numbers of pounds eaten each week on the number line. Order the numbers from most pounds eaten to fewest pounds eaten.
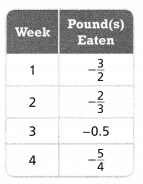
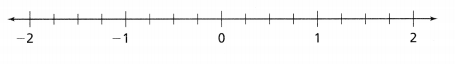
Answer:
It is given that
At the end of each week, Warren records the weight in pounds of doggie treats eaten as a negative rational number
Now,
The given table is:

Now,
The representation of the number of pounds eaten into a decimal number are:
–\(\frac{3}{2}\) = -1.5
–\(\frac{2}{3}\) = -0.6
–\(\frac{5}{4}\) = -1.25
Now,
We know that,
In a number line,
The negative numbers decrease from right to left
So,
The representation of the number of pounds eaten on a number line is:

So,
The order of the numbers from most pounds eaten to fewest pounds eaten is:
-1.5 < -1.25 < -0.66 < -0.5
–\(\frac{3}{2}\) < –\(\frac{5}{4}\) < –\(\frac{2}{3}\) < -0.5
Hence, from the above,
We can conclude that
The representation of the number of pounds eaten on a number line is:

The order of the numbers from most pounds eaten to fewest pounds eaten is:
–\(\frac{3}{2}\) < –\(\frac{5}{4}\) < –\(\frac{2}{3}\) < -0.5
PART C
Find the absolute value for the number of pounds of doggie treats eaten each week. Which two weeks had the greatest number of pounds eaten?
Answer:
The given table from part B is:

Now,
We know that,
“Absolute value” refers to a point’s distance from zero or origin on the number line, regardless of the direction. The absolute value of a number is always positive
So,
The absolute values for the number of pounds eaten are:
|-\(\frac{3}{2}\)| = \(\frac{3}{2}\)
|-\(\frac{2}{3}\)| = \(\frac{2}{3}\)
|-0.5| = 0.5
|-\(\frac{5}{4}\)| = \(\frac{5}{4}\)
So,
The representation of the absolute values for the number of pounds eaten into a decimal number is:
1.5, 0.66, 0.5, 1.25
Now,
From the given table,
We can observe that
Week 1 and Week 4 had the greatest number of pounds eaten
Hence, from the above,
We can conclude that
a. The absolute values for the number of pounds eaten are:
|-\(\frac{3}{2}\)| = \(\frac{3}{2}\)
|-\(\frac{2}{3}\)| = \(\frac{2}{3}\)
|-0.5| = 0.5
|-\(\frac{5}{4}\)| = \(\frac{5}{4}\)
b. Week 1 and Week 4 had the greatest number of pounds eaten
Lesson 2.4 Represent Rational Numbers on the Coordinate Plane
Solve & Discuss It!
Point B has the same x-coordinate as point A, but its y-coordinate is the opposite of the y-coordinate of point A. Plot point B and write its coordinates.
Answer:
It is given that
Point B has the same x-coordinate as point A, but its y-coordinate is the opposite of the y-coordinate of point A.
Now,
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that A (3, 5)
Now,
We know that,
The opposite of y-coordinate in the coordinate plane is: -y
So,
The coordinates for point B is: B (3, -5)
Hence, from the above,
We can conclude that
The coordinates for point B is: B (3, -5)
The representation of B (3, -5) in the coordinate plane is:
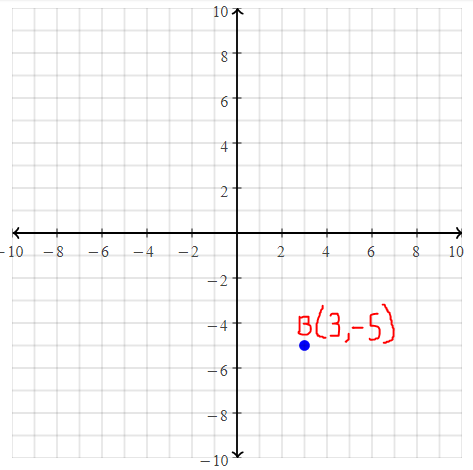
Make Sense and Persevere How can you use what you know about integers and graphing points on a coordinate plane to plot point B?
Answer:
From the above problem,
We know that,
The coordinates of point B are: B (3, -5)
Now,
We know that,
A coordinate plane consists of 2 number lines i.e., 1 horizontal number line and 1 vertical number line, and both intersect at zero
Now,
We know that,
In a number line,
The right side of zero and the upside of zero will be positive numbers
The left side of zero and the downside of zero will be negative numbers
Hence, from the above,
We can conclude that
B (3, -5) will be located on the right side of the horizontal number line and the downside of the vertical number line
Focus on math practices
Generalize Two points that have the same x-coordinate but opposite y-coordinates. Across which axis do they form mirror images of each other?
Answer:
It is given that
Two points that have the same x-coordinate but opposite y-coordinates.
So,
The representation of the point and its mirror image respectively are:
(x, y) ——–> (x, -y)
Hence, from the above,
We can conclude that
The mirror images of the given points will form across the x-axis
Visual Learning
? Essential Question How can you graph a point with rational coordinates on a coordinate plane?
Answer:
Graphing Points with Rational Number Coordinates:
a. Locate “a” on the x-axis.
b. From “a” on the x-axis, if “b” is positive, move up “b” units, and if “b” is negative, move down “b” units.
c. The location should now line up to “a” on the x-axis and to “b” on the y-axis, so we draw a point at the location. This is the point (a, b).
Try It!
Graph point P(-2, -3) on the coordinate plane shown.
Start at the origin![]() .
.
The x-coordinate is negative, so move![]() units to the left.
units to the left.
Then use y-coordinate to move![]() units down.
units down.
Draw and label the point.
Answer:
The given point is: P (-2, -3)
Now,
Hence,
The representation of the given point in the coordinate plane is:

Convince Me! How do the signs of the coordinates relate to the quadrant in which a point is located? Explain for each of the four quadrants.
Answer:
a. If both x and y are positive, then the point lies in the “First quadrant”
b. If x is negative and y is positive, then the point lies in the “Second quadrant”
c. If both x and y are negative, then the point lies in the “Third quadrant”
d. If x is positive and y is negative, then the point lies in the “Fourth quadrant”
Try It!
What landmark is located on the map at (2, \(\frac{1}{4}\))?
Answer:
The given point is: (2, \(\frac{1}{4}\)
Now,
The given figure is:

Now,
The representation of the given point in the decimal form is: (2, 0.25)
Now,
From the given map,
Locate the given point
So,
The location of the given point in the map is:
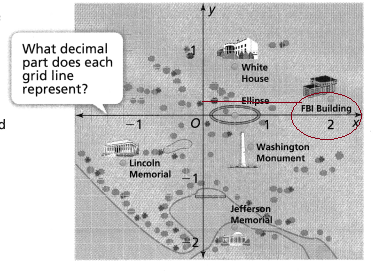
Hence, from the above,
We can conclude that
The landmark that is located on the map at (2, \(\frac{1}{4}\)) is: FBI Building
Try It!
The coordinates of point A are (-3, 5). What are the coordinates of point B, which is a reflection of point A across the x-axis?
Answer:
It is given that
The coordinates of point A are (-3, 5)
Now,
It is given that
Point B is the reflection of point A across the x-axis
Now,
We know that,
When (x, y) reflects across the x-axis, the point will become (x, -y)
Hence, from the above,
We can conclude that
The coordinates of point B, which is a reflection of point A across the x-axis is: (-3, -5)
KEY CONCEPT
A coordinate plane is a grid that contains number lines that intersect at right angles and divide the plane into four quadrants. The horizontal number line is called the x-axis, and the vertical number line is called the y-axis.
The location of a point on a coordinate plane is written as an ordered pair (x, y).
Do You Understand?
Question 1.
? Essential Question How can you graph a point with rational coordinates on a coordinate plane?
Answer:
Graphing Points with Rational Number Coordinates:
a. Locate “a” on the x-axis.
b. From “a” on the x-axis, if “b” is positive, move up “b” units, and if “b” is negative, move down “b” units.
c. The location should now line up to “a” on the x-axis and to “b” on the y-axis, so we draw a point at the location. This is the point (a, b).
Question 2.
What is the y-coordinate of any point that lies on the x-axis?
Answer:
Every point on the x-axis has no distance (zero distance) from the x-axis, therefore, the y – coordinate of every point lying on the x-axis is always “Zero”
Question 3.
Look for Relationships How are the points (4, 5) and (-4, 5) related?
Answer:
The given points are: (4, 5), and (-4, 5)
Now,
We know that,
The reflection of A (x, y) across the x-axis is: B(x, -y)
The reflection of A (x, y) across the y-axis is: B(-x, y)
Now,
From the given points,
We can observe that
(-4, 5) is the reflection of (4, 5) across the y-axis
Hence, from the above,
We can conclude that
(-4, 5) is the reflection of (4, 5) across the y-axis
Question 4.
Construct Arguments On a larger map, the coordinates for the location of another Washington, D.C. landmark are (8, -10). In which quadrant of the map is this landmark located? Explain.
Answer:
It is given that
On a larger map, the coordinates for the location of another Washington, D.C. landmark are (8, -10)
Now,
We know that,
a. If both x and y are positive, then the point lies in the “First quadrant”
b. If x is negative and y is positive, then the point lies in the “Second quadrant”
c. If both x and y are negative, then the point lies in the “Third quadrant”
d. If x is positive and y is negative, then the point lies in the “Fourth quadrant”
Hence, from the above,
We can conclude that
The location of another Washington D. C of the map is located in the fourth quadrant
In 5-7, graph and label each point on the coordinate plane.
Question 5.
A(-4, 1)
Answer:
The given point is: A (-4, 1)
Hence,
The representation of the given point in the coordinate plane is:
Question 6.
B(4, 3)
Answer:
The given point is: B (4, 3)
Hence,
The representation of the given point in the coordinate plane is:
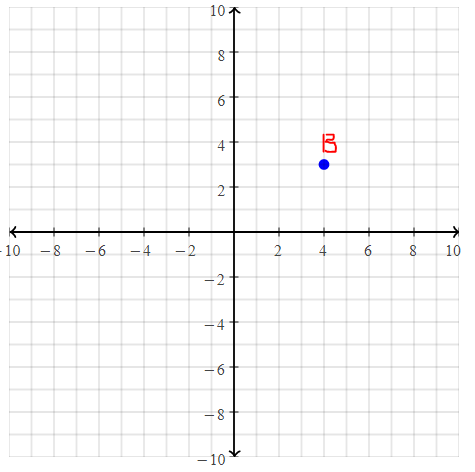
Question 7.
C(0, -2)
Answer:
The given point is: C (0, -2)
Hence,
The representation of the given point in the coordinate plane is:
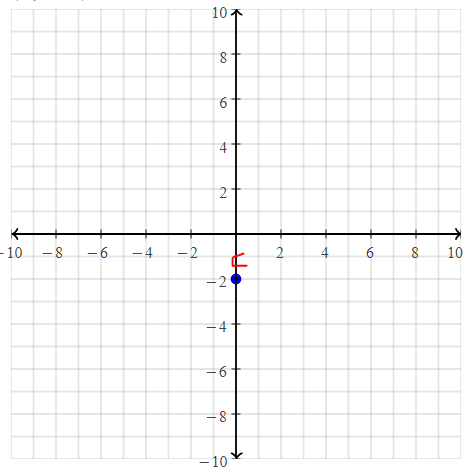
Question 8.
What ordered pair gives the coordinates of point P above?
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
Point P is in the 4th quadrant
The coordinates of point P is: P (3, -2)
Hence, from the above,
We can conclude that
The ordered pair that gives the coordinates of Point P is: P (3, -2)
In 9 and 10, use the map in Example 2 and write the ordered pair of each location.

Question 9.
White House
Answer:
The given map is:

Now,
From the given map,
We can observe that
The coordinates of the White House are: (1, 1)
Hence, from the above,
We can conclude that
The coordinates of the White House are: (1, 1)
Question 10.
Lincoln Memorial
Answer:
The given map is:

Now,
From the given map,
We can observe that
The coordinates of the Lincoln Memorial are: (-1, -0.5)
Hence, from the above,
We can conclude that
The coordinates of the White House are: (-1, -0.5)
In 11 and 12, use the map in Example 2 and write the landmark located at each ordered pair.
Question 11.
(0.5, 0)
Answer:
The given point is: (0.5, 0)
Now,
The given map is:

Now,
From the given map,
We can observe that
The landmark that is located at (0.5, 0) is: Ellipse
Hence, from the above,
We can conclude that
The landmark that is located at (0.5, 0) is: Ellipse
Question 12.
(\(\frac{3}{4}\), –\(\frac{1}{2}\))
Answer:
The given point is: (\(\frac{3}{4}\), –\(\frac{1}{2}\))
Now,
The given map is:

Now,
From the given map,
We can observe that
The landmark that is located at (\(\frac{3}{4}\), –\(\frac{1}{2}\)) is: Washington Monument
Hence, from the above,
We can conclude that
The landmark that is located at (\(\frac{3}{4}\), –\(\frac{1}{2}\)) is: Washington Monument
Practice & Problem Solving
In 13-20, graph and label each point.
Question 13.
A(1, -1)
Answer:
The given point is: A (1, -1)
Hence,
The representation of the given point in the coordinate plane is:
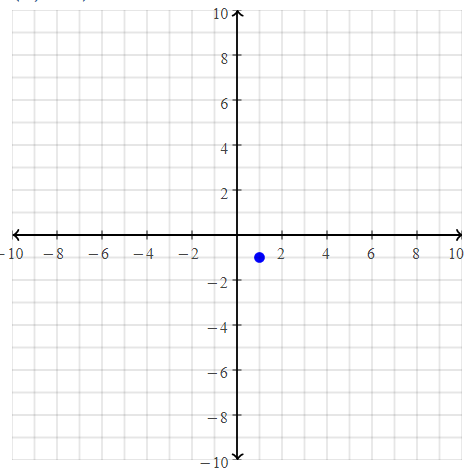
Question 14.
B(4, 3)
Answer:
The given point is: B (4, 3)
Hence,
The representation of the given point in the coordinate plane is:
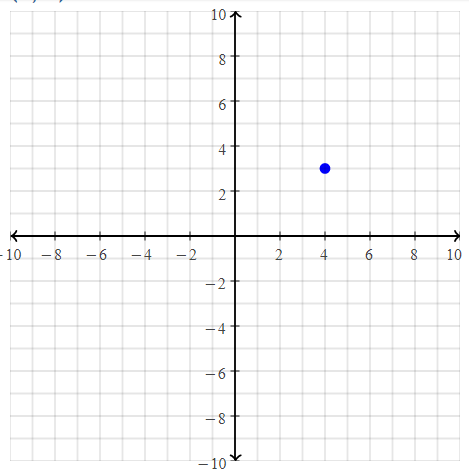
Question 15.
C(-4, 3)
Answer:
The given point is: C (-4, 3)
Hence,
The representation of the given point in the coordinate plane is:
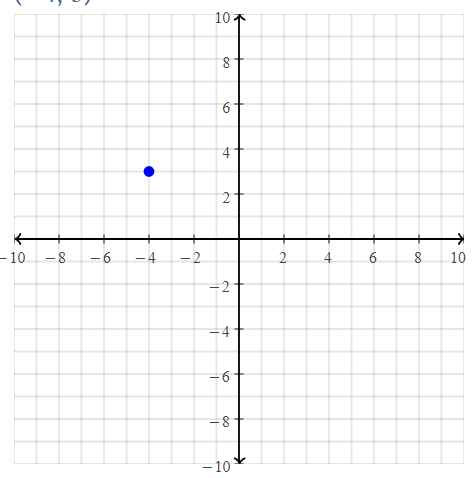
Question 16.
D(5, -2)
Answer:
The given point is: D (5, -2)
Hence,
The representation of the given point in the coordinate plane is:
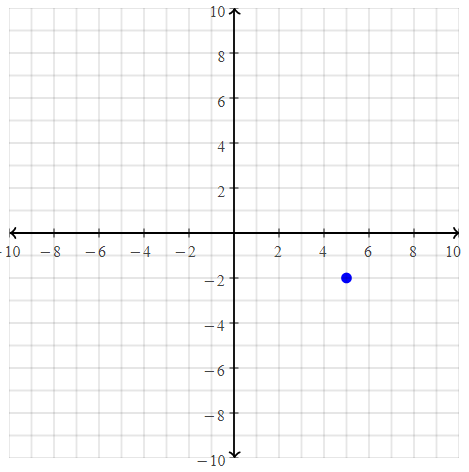
Question 17.
E(-2.5, 1.5)
Answer:
The given point is: E (-2.5, 1.5)
Hence,
The representation of the given point in the coordinate plane is:
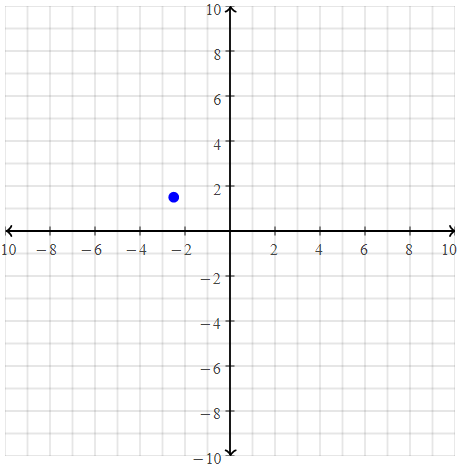
Question 18.
F(2, 1.5)
Answer:
The given point is: F (2, 1.5)
Hence,
The representation of the given point in the coordinate plane is:
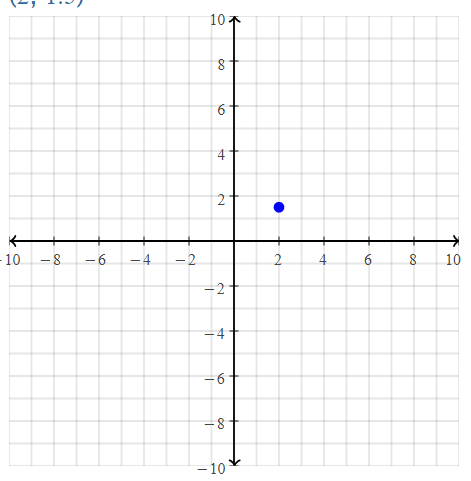
Question 19.
G(-2, -1\(\frac{1}{2}\))
Answer:
The given point is: G (-2, -1\(\frac{1}{2}\))
Hence,
The representation of the given point in the coordinate plane is:
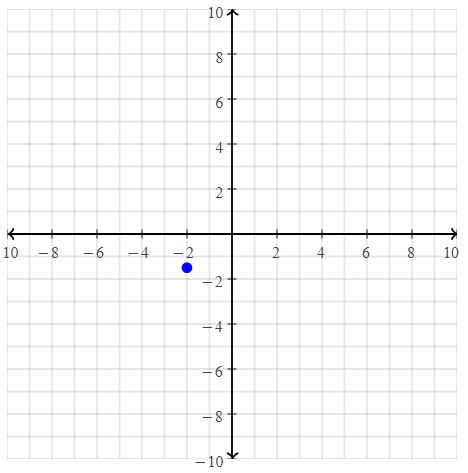
Question 20.
H(1\(\frac{1}{2}\), -1)
Answer:
The given point is: H (1\(\frac{1}{2}\), -1)
Hence,
The representation of the given point in the coordinate plane is:
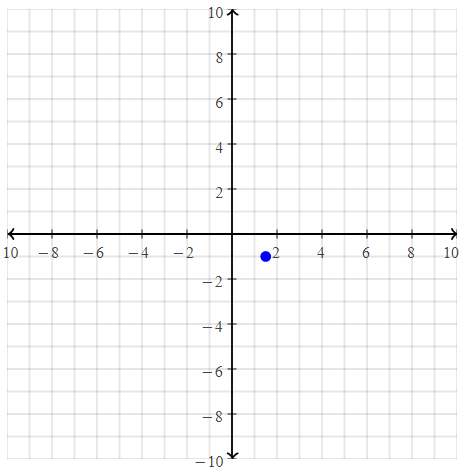
In 21-26, write the ordered pair for each point.
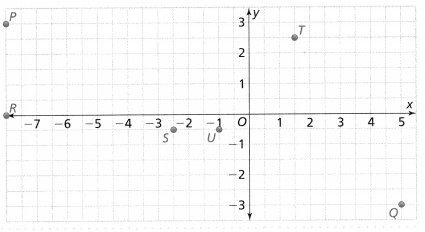
Question 21.
P
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point P from the given coordinate plane is: P (0, -8)
Hence, from the above,
We can conclude that
The coordinates of point P from the given coordinate plane is: P (0, -8)
Question 22.
Q
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point Q from the given coordinate plane is: Q (5, -3)
Hence, from the above,
We can conclude that
The coordinates of point Q from the given coordinate plane is: Q (5, -3)
Question 23.
R
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point R from the given coordinate plane is: R (-8, 0)
Hence, from the above,
We can conclude that
The coordinates of point R from the given coordinate plane is: R (-8, 0)
Question 24.
S
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point S from the given coordinate plane is: S (-2.5, -0.5)
Hence, from the above,
We can conclude that
The coordinates of point S from the given coordinate plane is: S (-2.5, -0.5)
Question 25.
T
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point T from the given coordinate plane is: T (1.5, 2.5)
Hence, from the above,
We can conclude that
The coordinates of point T from the given coordinate plane is: T (1.5, 2.5)
Question 26.
U
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point U from the given coordinate plane is: U (-1, -0.5)
Hence, from the above,
We can conclude that
The coordinates of point U from the given coordinate plane is: U (-1, -0.5)
In 27-30, use the map at the right.

Question 27.
Which building is located in Quadrant III?
Answer:
The given map is:

Now,
We know that,
a. If both x and y are positive, then the point lies in the “First quadrant”
b. If x is negative and y is positive, then the point lies in the “Second quadrant”
c. If both x and y are negative, then the point lies in the “Third quadrant”
d. If x is positive and y is negative, then the point lies in the “Fourth quadrant”
So,
From the given map,
We can observe that
The building that is located in Quadrant III is: Fire House
Hence, from the above,
We can conclude that
The building that is located in Quadrant III is: Fire House
Question 28.
Which two places have the same x-coordinate?
Answer:
The given map is:

Now,
We know that,
a. If both x and y are positive, then the point lies in the “First quadrant”
b. If x is negative and y is positive, then the point lies in the “Second quadrant”
c. If both x and y are negative, then the point lies in the “Third quadrant”
d. If x is positive and y is negative, then the point lies in the “Fourth quadrant”
So,
From the given map,
We can observe that
The two buildings that have the same x-coordinate are: Swimming pool and clubhouse
Hence, from the above,
We can conclude that
The two buildings that have the same x-coordinate are: Swimming pool and clubhouse
Question 29.
Use Structure The city council wants the location of the entrance to a new city park to be determined by the reflection of the school entrance across the y-axis. What are the coordinates of the entrance to the new city park on this map?

Answer:
It is given that
The city council wants the location of the entrance to a new city park to be determined by the reflection of the school entrance across the y-axis
Now,
The given map is:

Now,
From the given map,
We can observe that
The coordinates of the school entrance are: (4, 6)
Now,
We know that,
The reflection of (x, y) across the y-axis is: (-x, y)
So,
The coordinates of the entrance to a new city park are: (-4, 6)
Hence, from the above,
We can conclude that
The coordinates of the entrance to a new city park are: (-4, 6)
Question 30.
Higher-Order Thinking You are at the market square (0, 0) and want to get to the doctor’s office. Following the gridlines, what is the shortest route?

Answer:
It is given that
You are at the market square (0, 0) and want to get to the doctor’s office.
Now,
The given map is:

Now,
The representation of the distance of the Market and doctor’s office in the map are:

Now,
From the given map,
We can observe that
The shortest route can be determined by using the Pythagoras Theorem since a right triangle is formed
So,
The shortest route between the market and doctor’s office = \(\sqrt{4² + 2²}\)
= \(\sqrt{20}\)
= 4.47 units
Hence, from the above,
We can conclude that
The shortest route between the market and the doctor’s office is: 4.47 units
In 31-36, use the coordinate plane at the right.
Question 31.
What is located at (-0.7,-0.2)?
Answer:
The given point is: (-0.7, -0.2)
Now,
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that the landmark that is located at (-0.7, -0.2) is: Pond
Hence, from the above,
We can conclude that
The pond is located at (-0.7, -0.2)
Question 32.
What is located at (\(\frac{3}{10}\), –\(\frac{1}{5}\))?
Answer:
The given point is: (\(\frac{3}{10}\), –\(\frac{1}{5}\))
Now,
The given coordinate plane is:

Now,
The representation of the given point in the form of a decimal number is: (0.3, -0.2)
Now,
From the given coordinate plane,
We can observe that the landmark that is located at (\(\frac{3}{10}\), –\(\frac{1}{5}\)) is: Start of Hiking Trail
Hence, from the above,
We can conclude that
The start of Hiking Trail is located at (\(\frac{3}{10}\), –\(\frac{1}{5}\))
Question 33.
Be Precise Write the ordered pair to locate the end of the hiking trail in two different ways.
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates to locate the end of the hiking trail is: (0.2, -0.8)
Hence, from the above,
We can conclude that
The coordinates to locate the end of the hiking trail is: (0.2, -0.8)
Question 34.
What are the coordinates of the information center? Explain.
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of the Information center are: (-0.2, 0.7)
Hence, from the above,
We can conclude that
The coordinates of the Information center are: (-0.2, 0.7)
Question 35.
What are the coordinates of the point that is a reflection across the x-axis of the pond?
Answer:
From Question 31,
We can observe that,
The location of the pond in the coordinate plane is: (-0.7, -0.2)
Now,
The given coordinate plane is:

Now,
We know that,
The reflection of (x, y) across the x-axis is: (x, -y)
So,
The coordinates of the point that is a reflection across the x-axis of the pond are: (-0.7, 0.2)
Hence, from the above,
We can conclude that
The coordinates of the point that is a reflection across the x-axis of the pond are: (-0.7, 0.2)
Question 36.
Use Structure Which picnic areas are located at points that are reflections of each other across one of the axes of the coordinate plane?
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of Picnic area 1 are: (-0.8, 0.6)
The coordinates of Picnic area 2 are: (0.6, 0.9)
The coordinates of Picnic area 3 are: (0.6, 0.3)
The coordinates of Picnic area 4 are: (-0.8, -0.6)
Now,
We know that,
The reflection of (x, y) across the x-axis is: (x, -y)
The reflection of (x, y) across the y-axis is: (-x, y)
Hence, from the above,
We can conclude that
Picnic area 4 is the reflection of Picnic area 1 across the x-axis
Assessment Practice
Question 37.
Graph and label each point on the coordinate plane at the right.
A. (\(\frac{3}{4}\), -1\(\frac{1}{2}\))
B. (-2.75, -2.25)
C. (0, 2\(\frac{1}{4}\))
D. (-1.75, 2)
Answer:
The given points are:
A. (\(\frac{3}{4}\), -1\(\frac{1}{2}\))
B. (-2.75, -2.25)
C. (0, 2\(\frac{1}{4}\))
D. (-1.75, 2)
Hence,
The representation of the given points in the coordinate plane are:
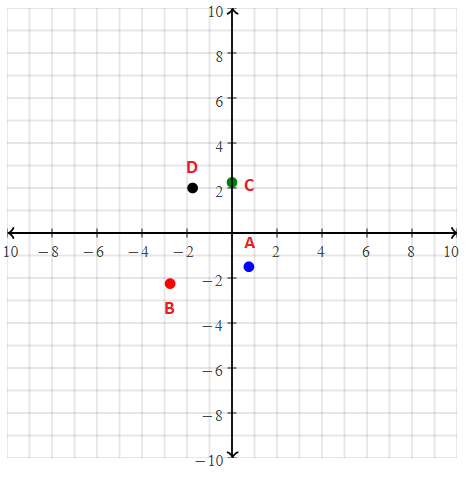
3-Act Mathematical Modeling: The Ultimate Throw
3-ACT MATH
The ULTIMATE THROW
ACT 1
Question 1.
After watching the video, what is the first question that comes to mind?
Answer:
Question 2.
Write the Main Question you will answer.
Answer:
Question 3.
Make a prediction to answer this Main Question.
The person who threw the flying disc farther is ![]()
Answer:
Question 4.
Construct Arguments Explain how you arrived at your prediction.

Answer:
ACT 2
Question 5.
What information in this situation would be helpful to know? How would you use that information?
Answer:
Question 6.
Use Appropriate Tools What tools can you use to solve the problem? Explain how you would use them strategically.
Answer:
Question 7.
A Model with Math
Represent the situation using mathematics. Use your representation to answer the Main Question.
Answer:
Question 8.
What is your answer to the Main Question? Does it differ from your prediction? Explain.
Answer:
АСТ 3
Question 9.
Write the answer you saw in the video.
Answer:
Question 10.
Reasoning Does your answer match the answer in the video? If not, what are some reasons that would explain the difference?

Answer:
Question 11.
Make Sense and Persevere Would you change your model now that you know the answer? Explain.
Answer:
Reflect
Question 12.
Model with Math
Explain how you used a mathematical model to represent the situation. How did the model help you answer the Main Question?
Answer:
Question 13.
Make Sense and Persevere When did you struggle most while solving the problem? How did you overcome that obstacle?

Answer:
SEQUEL
Question 14.
Reasoning Suppose each person walks to the other person’s disc. They throw each other’s discs toward the starting point. Where do you think each disc will land?

Answer:
Lesson 2.5 Find Distances on the Coordinate Plane
Solve & Discuss It!
Graph the points on the coordinate plane below. What picture do you make when you connect the points in order?
(3, 3), (0, 0), (-4,-4), (-9,0), (-4, 4), (0, 0), (3, -3), (3, 3)
Name a pair of points that are the same distance from the x-axis. Explain your choice.
Answer:
The given points are:
(3, 3), (0, 0), (-4,-4), (-9,0), (-4, 4), (0, 0), (3, -3), (3, 3)
Now,
Represent the given points in the coordinate plane and connect the points in the given order
So,
The representation of the given points in the coordinate plane is:
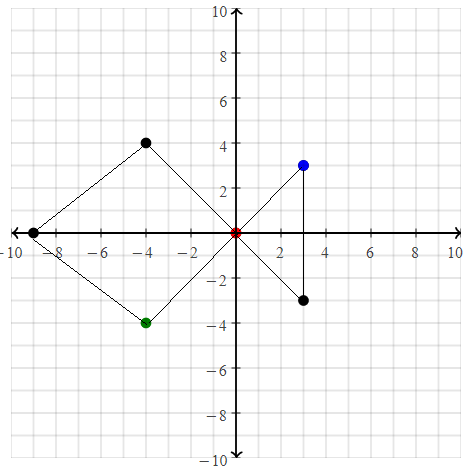
Now,
From the given coordinate plane,
We can observe that
When we connect the given points in order,
The picture you made looks like a composite figure of a rhombus and a triangle
Now,
The pair of points that are the same distance from the x-axis is:
(3, 3), (3, -3); and (-4, 4), (-4, -4)
Hence, from the above,
We can conclude that
a. When we connect the given points in order,
The picture you made looks like a composite figure of a rhombus and a triangle
b. The pair of points that are the same distance from the x-axis is:
(3, 3), (3, -3); and (-4, 4), (-4, -4)
Use Structure How can you use the structure of the grid to find a pair of points that are the same distance from the x-axis?
Answer:
Derived from the Pythagorean Theorem, the distance formula is used to find the distance between two points in the plane. The Pythagorean Theorem, a²+b²=c² is based on a right triangle where a and b are the lengths of the legs adjacent to the right angle, and c is the length of the hypotenuse.
Focus on math practices
Use Structure How can you use the coordinate plane to find the total length of the picture you graphed?
Answer:
We know that,
The “Linear distance” between the two points is the square root of the sum of the squared values of the x-axis distance and the y-axis distance
Ex:
The distance between (3,2) and (7,8) is \(\sqrt{52}\), or approximately 7.21 units.

? Essential Question How can you find the distance between two points on a coordinate plane?
Answer:
We know that,
The distance between two points by using the distance formula, which is an application of the Pythagorean theorem. We can rewrite the Pythagorean theorem as
d=√(x2-x1)²+(y2-y1)²
to find the distance between any two points.
Try It!
What is the distance from the school to the playground? Explain how you used absolute values to find the distance?
Answer:
The given map is:

Now,
From the given coordinate plane,
We can observe that
The coordinates at which the school is located are: (-4, 2)
The coordinates at which the playground is located are: (-4, 5)
Now,
Compare the given points with (x, a), and (x, b) respectively
We know that,
Let (x, a), and (y, b) are the two points
Now,
The absolute distance of (x, a) = | x + a|
The absolute distance of (y, b) = | y + b|
So,
The absolute distance between (x, a), and (y, b) = |x + a| + |y + b|
So,
The absolute distance between (-4, 2), and (-4, 5) = | -4 + 2| + |-4 +5|
= |-2| + |1|
= 2 + 1
= 3 units
Hence, from the above,
We can conclude that
The distance from the school to the playground is: 3 units
Convince Me! To find the distance from the school to the playground, do you add or subtract the absolute values of the y-coordinates? Explain.
Answer:
Let (x, a), and (y, b) are the two points
Now,
The absolute distance of (x, a) = | x + a|
The absolute distance of (y, b) = | y + b|
So,
The absolute distance between (x, a), and (y, b) = |x + a| + |y + b|
Hence, from the above,
We can conclude that
To find the distance from the school to the playground, we added the absolute values of the y-coordinates
Try It!
What is the total distance of the Coulters’ return trip after their day at the water park?
![]()
Answer:
The given figure is:

Now,
From the given figure,
we can observe that
The total distance of the Coulters’ return trip after their day at the water park = (The absolute distance of Water park) + (The absolute distance of Coulters’ home)
Now,
We know that,
Let (x, a), and (y, b) are the two points
Now,
The absolute distance of (x, a) = | x + a|
The absolute distance of (y, b) = | y + b|
So,
The absolute distance between (x, a), and (y, b) = |x + a| + |y + b|
Now,
From the given points,
We can observe that the x-coordinates are the same for the Water park and the Coulters’ home
So,
![]()
Hence, from the above,
We can conclude that
The total distance of the Coulters’ return trip after their day at the Water Park is: 151 miles
Try It!
Point D is in Quadrant IV and is the same distance from point B as point A. What are the coordinates of point D?

Answer:
KEY CONCEPT
You can use absolute values to find distances between points on a coordinate plane.
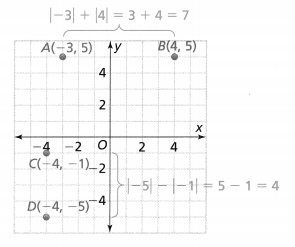
Do You Understand?
Question 1.
?Essential Question How can you find the distance between two points on a coordinate plane?
Answer:
We know that,
The distance between two points by using the distance formula, which is an application of the Pythagorean theorem. We can rewrite the Pythagorean theorem as
d=√(x2-x1)²+(y2-y1)²
to find the distance between any two points.
Question 2.
Look for Relationships To find the distance between two points using their coordinates, when do you add their absolute values and when do you subtract them?
Answer:
Case 1:
Let the coordinates of points be (x, y), and (a, b)
So,
The absolute value of (x, y) is: |x + y|
The absolute value of (a, b) is: |a + b|
Hence, from the above,
We can conclude that
We will add the absolute values when both the coordinates of the given points are positive
Case 2:
Let the coordinates of points be (x, -y), and (-a, b)
So,
The absolute value of (x, -y) is: |x – y|
The absolute value of (-a, b) is: |b – a|
Hence, from the above,
We can conclude that
We will subtract the absolute values when any one of the coordinates of the given points are negative
Question 3.
Reasoning Can you use absolute value to find the distance between Li’s house and Tammy’s house in
Example 1? Explain.

Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The coordinates at which Li’s House is located = (-4, -3)
The coordinates at which Tammy’s house is located = (2, 0)
Now,
We know that,
The absolute distance between two points is: |x + a| + |y + b|
Hence, from the above,
We can conclude that
You can use absolute value to find the distance between Li’s house and Tammy’s house that is present in Example 1
Do You Know How?
In 4-9, find the distance between each pair of points.
Question 4.
(-5, 2) and (-5, 6)
Answer:
The given points are: (-5, 2) , and (-5, 6)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The absolute distance between two points = |x + a| + |y + b|
So,
The distance between (-5, 2), and (-5, 6) = |-5 + 2| + |-5 + 6|
= 3 + 1
= 4 units
Hence, from the above,
We can conclude that
The distance between the given pair of points is: 4 units
Question 5.
(4.5, -3.3) and (4.5, 5.5)
Answer:
The given points are: (4.5, -3.3), and (4.5, 5.5)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The absolute distance between two points = |x + a| – |y + b|
So,
The distance between (4.5, -3.3), and (4.5, 5.5) = |4.5 – 3.3| – |4.5 + 5.5|
= |1.2 – 10|
= 8.8 units
Hence, from the above,
We can conclude that
The distance between the given pair of points is: 11.2 units
Question 6.
(5\(\frac{1}{2}\), -7\(\frac{1}{2}\)) and (5\(\frac{1}{2}\), -1\(\frac{1}{2}\))
Answer:
The given points are: (5\(\frac{1}{2}\), -7\(\frac{1}{2}\)) and (5\(\frac{1}{2}\), -1\(\frac{1}{2}\))
Now,
Convert the coordinates of the given points into decimal numbers
So,
The given points are: (5.5, -3.5), and (5.5, -1.5)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The absolute distance between two points = |x + a| – |y + b|
So,
The distance between (5.5, -3.5), and (5.5, -1.5) = |5.5 – 3.5| – |5.5 – 1.5|
= |2 – 4|
= 2 units
Hence, from the above,
We can conclude that
The distance between the given pair of points is: 2 units
Question 7.
(-2\(\frac{1}{4}\), -8 ) and (7\(\frac{3}{4}\), -8)
Answer:
The given points are: (-2\(\frac{1}{4}\), -8 ) and (7\(\frac{3}{4}\), -8)
Now,
Convert the coordinates of the given points into a decimal number
So,
The given points are: (-2.25, -8), and (7.75, -8)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The absolute distance between two points = |x + a| – |y + b|
So,
The distance between (-2.25, -8), and (7.75, -8) = |-2.25 – 8| – |7.75 – 8|
= |10.25 – 0.25|
= 10 units
Hence, from the above,
We can conclude that
The distance between the given pair of points is: 10 units
Question 8.
(5\(\frac{1}{4}\), -3\(\frac{1}{4}\)) and (5\(\frac{1}{4}\), -6\(\frac{1}{4}\))
Answer:
The given points are: (5\(\frac{1}{4}\), -3\(\frac{1}{4}\)) and (5\(\frac{1}{4}\), -6\(\frac{1}{4}\))
Now,
Convert the coordinates of the given points into a decimal number
So,
The given points are: (5.25, -3.25), and (5.25, -6.25)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The absolute distance between two points = |x + a| + |y + b|
So,
The distance between (5.25, -3.25), and (5.25, -6.25) = |5.25 – 3.25| + |5.25 – 6.25|
= 2 + 1
= 3 units
Hence, from the above,
We can conclude that
The distance between the given pair of points is: 3 units
Question 9.
(-1\(\frac{1}{2}\), –6\(\frac{1}{2}\)) and (-2\(\frac{1}{2}\), -6\(\frac{1}{2}\))
Answer:
The given points are: (-1\(\frac{1}{2}\), –6\(\frac{1}{2}\)) and (-2\(\frac{1}{2}\), -6\(\frac{1}{2}\))
Now,
Convert the coordinates of the given points into a decimal number
So,
The given points are: (-1.5, -6.5), and (-2.5, -6.5)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The absolute distance between two points = |x + a| + |y + b|
So,
The distance between (-1.5, -6.5), and (-2.5, -6.5) = |-1.5 – 6.5| – |-2.5 – 6.5|
= |8 – 9|
= 1 units
Hence, from the above,
We can conclude that
The distance between the given pair of points is: 1 units
Practice & Problem Solving
Scan for Multimedia
Leveled Practice In 10-15, find the distance between each pair of points.
Question 10.
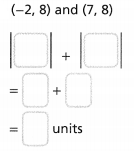
Answer:
The given points are: (-2, 8), and (7, 8)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between two points = |x + a| + |y + b|
So,
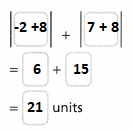
Hence, from the above,
We can conclude that
The distance between the given points is: 21 units
Question 11.
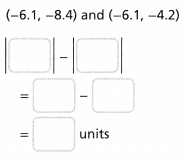
Answer:
The given points are: (-6.1, -8.4), and (-6.1, -4.2)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between two points = |x + a| – |y + b|
Now,
Since the x-coordinates are the same, subtract the y-coordinates to find the distance between the given points
So,
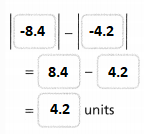
Hence, from the above,
We can conclude that
The distance between the given points is: 4.2 units
Question 12.
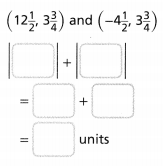
Answer:
The given points are: (12\(\frac{1}{2}\), 3\(\frac{3}{4}\)), and (-4\(\frac{1}{2}\), 3\(\frac{3}{4}\))
Now,
Convert the coordinates of the given points into a decimal number
So,
The given points are: (12.5, 3.75), and (-4.5, 3.75)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between two points = |x + a| + |y + b|
Now,
Since y-coordinates are the same, add the x-coordinates to find the distance between the given points
So,
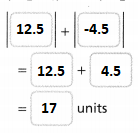
Hence, from the above,
We can conclude that
The distance between the given points is: 17 units
Question 13.
(-5, -3) and (-5, -6)
Answer:
The given points are: (-5, -3) , and (-5, -6)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The absolute distance between two points = |x + a| – |y + b|
So,
The distance between (-5, -3), and (-5, -6) = |-5 – 3| – |-5 – 6|
= |8 – 11|
= 3 units
Hence, from the above,
We can conclude that
The distance between the given pair of points is: 3 units
Question 14.
(-5.4, 4.7) and (0.6, 4.7)
Answer:
The given points are: (-5.4, 4.7), and (0.6, 4.7)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The absolute distance between two points = |x + a| – |y + b|
So,
The distance between (-5.4, 4.7), and (0.6, 4.7) = |-5.4 + 4.7| – |0.6 + 4.7|
= |-0.7 – 5.3|
= 6 units
Hence, from the above,
We can conclude that
The distance between the given pair of points is: 6 units
Question 15.
(7\(\frac{1}{2}\), -5\(\frac{3}{4}\)) and (7\(\frac{1}{2}\), -1\(\frac{1}{4}\))
Answer:
The given points are: (7\(\frac{1}{2}\), -5\(\frac{3}{4}\)) and (7\(\frac{1}{2}\), -1\(\frac{1}{4}\))
Now,
Convert the coordinates of the given points into a decimal number
So,
The given points are: (7.5, -5.75), and (7.5, -1.25)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The absolute distance between two points = |x + a| – |y + b|
So,
The distance between (7.5, -5.75), and (7.5, -1.25) = |7.5 – 5.75| – |7.5 – 1.25|
= |1.75 – 6.25|
= 4.5 units
Hence, from the above,
We can conclude that
The distance between the given pair of points is: 4.5 units
In 16-19, use the map at the right.
Question 16.
Find the distance from roller coaster 1 to the swings.
Answer:
The given map is:

Now,
From the given map,
We can observe that
The coordinates of roller coaster 1 are: (-6, 7)
The coordinates of the swings are: (1, 7)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between the two points = |x + a| – |y – b|
So,
The distance from roller coaster 1 to the swings = |-6 + 7| – |1 + 7|
= |1 – 8|
= 7 units
Hence, from the above,
We can conclude that
The distance from roller coaster 1 to the swings is: 7 units
Question 17.
Find the distance from the Ferris wheel to the roller coaster 3.
Answer:
The given map is:

Now,
From the given map,
We can observe that
The coordinates of the Ferris Wheel are: (-6, 2)
The coordinates of roller coaster 3 are: (-6, -8)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between the two points = |x + a| + |y – b|
So,
The distance from Ferris Wheel to the roller coaster 3 = |-6 + 2| – |-6 – 8|
= |-4 + 14|
= 10 units
Hence, from the above,
We can conclude that
The distance from Ferris Wheel to the roller coaster 3 is: 10 units
Question 18.
Find the total distance from roller coaster 2 to roller coaster 3 and then to the water slide.
Answer:
The given map is:

Now,
From the given map,
We can observe that
The coordinates of roller coaster 2 are: (-6, -3)
The coordinates of roller coaster 3 are: (-6, -8)
The coordinates of the Water slide are: (8, -8)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between the two points = |x + a| + |y – b|
So,
The distance from Ferris Wheel to the roller coaster 3 = |-6 + 2| – |-6 – 8|
= |-4 + 14|
= 10 units
Hence, from the above,
We can conclude that
The distance from Ferris Wheel to the roller coaster 3 is: 10 units
Question 19.
Higher Order Thinking Is the distance from the merry-go-round to the water slide the same as the distance from the water slide to the merry-go-round? Explain.
Answer:
The given map is:

Now,
From the given map,
We can observe that
The coordinates of merry-go-round are: (8, 2)
The coordinates of the Water slide are: (8, -8)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between the two points = |x + a| + |y – b|
So,
The distance from merry-go-round to the Water slide = |8 + 2| – |8 – 8|
= |0 + 10|
= 10 units
So,
The distance from the Water slide to merry-go-round = |8 – 8| – |8 + 2|
= |0 – 10|
= 10 units
Hence, from the above,
We can conclude that
The distance from merry-go-round to the Water slide and the distance from the Water slide to merry-go-round are the same
In 20 and 21, use the coordinate plane at the right.
The graph shows the locations of point G and point H. Point J is graphed at (n, -3). The distance from point H to point J is equal to the distance from point H to point G.

Question 20.
What is the distance from point H to point J?
Answer:
It is given that
The graph shows the locations of point G and point H. Point J is graphed at (n, -3). The distance from point H to point J is equal to the distance from point H to point G.
Now,
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of G are: (0, -y)
It is given that
The coordinates of point J are: (n, -3)
Now,
Compare points H and J with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = | x + a| – |y + b|
So,
The distance between points H and J = |n – 6| – |n – 3|
= |n – 6 – n + 3|
= 3 units
Hence, from the above,
We can conclude that
The distance from point G to point H is: 3 units
Question 21.
What is the value of n?
Answer:
It is given that
The graph shows the locations of point G and point H. Point J is graphed at (n, -3). The distance from point H to point J is equal to the distance from point H to point G.
Now,
The given coordinate plane is:

Now,
From Exercise 20,
We know that,
The distance from point G to point H is: 3 units
Now,
|n – 6 + n – 3| = 3
|2n – 9| = 3
2n = 3 + 9
2n = 12
n = \(\frac{12}{2}\)
n = 6 units
Hence, from the above,
We can conclude that
The value of n is: 6 units
Question 22.
Use Structure Suppose a, b, and c are all negative numbers. How do you find the distance between points (a, b) and (a, c)?
Answer:
It is given that
a, b, and c are all negative numbers.
Now,
The given points are: (a, b), and (a, c)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| – |y + b|
So,
The distance between the given points = |-a + (-b)| – |-a + (-c)|
= |-a – b| – |-a – c|
= |-a – b + a + c|
= |c – b| units
Hence, from the above,
We can conclude that
The distance between points (a, b), and (a, c) is: |c – b| units
Question 23.
A scientist graphed the locations of the epicenter of an earthquake and all of the places where people reported feeling the earthquake. She positioned the epicenter at (-1, 8) and the farthest location reported to have felt the quake was positioned at (85, 8). If each unit on the graph represents 1 mile, how far from its epicenter was the earthquake felt?
Answer:
It is given that
A scientist graphed the locations of the epicenter of an earthquake and all of the places where people reported feeling the earthquake. She positioned the epicenter at (-1, 8) and the farthest location reported to have felt the quake was positioned at (85, 8) and each unit on the graph represents 1 mile
Now,
The given points are: (-1, 8), (85, 8)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| – |y + b|
So,
The distance between the given points = |-1 + 8| – |85 + 8|
= |7 – 93|
= 86 miles
Hence, from the above,
We can conclude that
The earthquake felt 86 miles away from its epiccenter
Question 24.
The rectangle ABCD shown on the coordinate plane represents an overhead view of a piece of land. Each unit represents 1,000 feet. What are the dimensions of the rectangular piece of land, in feet?
Answer:
It is given that
The rectangle ABCD shown on the coordinate plane represents an overhead view of a piece of land. Each unit represents 1,000 feet
Now,
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The dimensions of the rectangle present in the given coordinate plane are:
A (0, 0), B (0, 4), C (5, 5), and D (5, 0)
So,
The dimensions of the rectangular piece of land, in feet are:
A (0, 0), B (0, 4,000), C (5,000, 5,000), and D (5,000, 0)
Hence, from the above,
We can conclude that
The dimensions of the rectangular piece of land, in feet are:
A (0, 0), B (0, 4,000), C (5,000, 5,000), and D (5,000, 0)
Assessment Practice
Question 25.
You are given the following ordered pairs.
(3.5, -1) (-1.5, 3) (-3, 3) (3.5, 2.5) (-1.5, -1.5)
PART A
Graph the ordered pairs on the coordinate plane.
Answer:
The given ordered pairs are:
(3.5, -1), (-1.5, 3), (-3, 3), (3.5, 2.5), (-1.5, -1.5)
Hence,
The representation of the given ordered pairs in the coordinate plane is:

PART B
Find the two ordered pairs on the coordinate plane that are 4.5 units apart.
Answer:
The given ordered pairs are:
A (3.5, -1), B(-1.5, 3), C(-3, 3), D(3.5, 2.5), E(-1.5, -1.5)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x – a| + |y + b|
So,
The distance of AB = 6.41 units
The distance of AC = 7.63 units
The dsitance of AD = 3.5 units
The distance of AE = 5.02 units
The distance of BC = 4.5 units
The distance of BD = 5.02 units
The distance of BE = 4.5 units
Hence, from the above,
We can conclude that
The two ordered pairs on the coordinate plane that are 4.5 units apart is:
B(-1.5, 3), and C (-3, 3); B(-1.5, 3), and E (-1.5, -1.5)
Lesson 2.6 Represent Polygons on the Coordinate Plane
Solve & Discuss It!
ACTIVITY
Draw a polygon with vertices at A(-1, 6), B(-7, 6), C(-7, -3), and D(-1, -3). Then find the perimeter of the polygon.
Answer:
The vertices of a given polygon are:
A(-1, 6), B(-7, 6), C(-7, -3), and D(-1, -3)
So,
The representtaion of the given vertices of a polygon in the coordinate plane are:
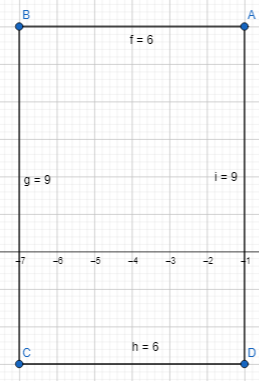
Now,
We know that,
The “Perimeter” of a figure is the sum of all of the side lengths of a given figure
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance betwee 2points = |x + a| + |y + b|
So,
The distace of AB = |-1 + 6| + |-7 + 6|
= |5 + 1|
= 6 units
The distance of BC = |-7 + 6| + |-7 – 3|
= |1 – 10|
= 9 units
The distace of CD = |-7 – 3| + |-1 – 3|
= |10 – 4|
= 6 units
The distace of DA = |-1 – 3| + |-1 + 6|
= |5 + 4|
= 9 units
So,
The perimeter of the given polygon = 6 + 6 + 9 + 9
= 30 units
Hence, from the above,
We can conclude that
The perimeter of the given polygon is: 30 units
Use Structure How can you use the coordinate plane to draw the polygon and find its perimeter?
Answer:
You can use ordered pairs to represent vertices of polygons. To draw a polygon in a coordinate plane, plot and connect the ordered pairs
To find the perimeter of a regular polygon, we take the length of each side, , and multiply it by the number of sides
Focus on math practices
Construct Arguments What type of polygon did you draw? Use a definition to justify your answer.
Answer:
The representation of the vertices of the given polyon is:

Now,
From the given coordinate plane,
We can observe that
The opposite side lengths are equal and all the angle measures are 90°
Now,
We know that,
The polygon that has the same opposite side lengths is called as “Rectangle”
Hence, from the above,
We can conclude that
The type of polyon did you draw is: Rectangle
Visual Learning
? Essential Question How is distance used to solve problems about polygons in a coordinate plane?
Answer:
To find the distance between two points with the same x-coordinates, subtract their y-coordinates. To find the distance between two points with the same y-coordinates, subtract their x-coordinates
To find the distance between the different x and y-coordinates, subtract the x-coordinates of the 2 points and y-coordinates of the 2 points and add both the values
Try It!
The archaeologist later decides to extend the roped-off area so that the new perimeter goes from A to B to the food tent to the working tent and then back to A. How much rope does she need now?

Answer:
It is given that
The archaeologist later decides to extend the roped-off area so that the new perimeter goes from A to B to the food tent to the working tent and then back to A
Now,
The given figure is:
Now,
From the given figure,
We can observe that
The coordinates of A are: (-4, 6)
The coordinates of B are: (2, 6)
The coordinates of Food Tent are: (2, -2)
The coordinates of Working Tent are: (-4, -2)
Now,
Compare the given points with (x, a), and (y, b)
So,

Hence, from the above,
We can concldue that
The length of rope the archaeologist needs now is: 28 meters
Convince Me! How could you use the formula for the perimeter of a rectangle to find the perimeter of the larger rectangle using two of the distances?
Answer:
We know that,
The perimeter of a rectangle = 2(l + w)
Now,
If the perimeter and the length of a rectangle are known, then
Width = P/2 – l,
where,
l = length, w = width, and P = perimeter of the rectangle.
Now,
If the perimeter and the width are known, then
Length(L) = P/2 – w.
Try It!
The rancher needs to replace the fence for the holding pen for the horses. How much fencing does he need?
The rancher needs ![]() yards of fencing.
yards of fencing.
Answer:
It is given that
The rancher needs to replace the fence for the holding pen for the horses
Now,
The given figure is:

Now,
From the given figure,
The coordinates of the fence that is used for the holding pen for the houses is:
A (4.5, 14), B (15, 14), C (15, 8), D (10, 8), E (10, 3), F (15, 3), G (15, -2.25), and H (4.5, -2.25)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
Now,
The distance of AB = |4.5 – 15| = 11.5 units
The distance of BC = |14 – 8| = 6 units
The distance of CD = |15 – 10| = 5 units
The distance of DE = |8 – 3| = 5 units
The distance of EF = |10 – 15| = 5 units
The distance of FG = | 3 + 2.25| = 5.25 units
The distance of GH = |15 – 4.5| = 11.5 units
The distance of HA = |14 + 2.25| = 16.25 units
Now,
We know that,
To find the length of fencing, we have to find the perimeter of the given polyon
So,
The length of the fencing that Rancher needed = 11.5 + 6 + 5 + 5 + 5 + 5.25 + 11.5 + 16.25
= 65.5 yards
Hence, from the above,
We can conclude that
The rancher needs 65.5 yards of fencing
Try It!
Joaquin says that quadrilateral ADEF is a square. Is he correct? Explain.
Answer:
It is given that
Joaquin says that quadrilateral ADEF is a square
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The coordinates of A are: (-5, 2)
The coordinates of D are: (7, 2)
The coordinates of E are: (7, -8)
The coordinates of F are: (-5, -8)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
Now,
The distance of AD = |-5 + 2| + |7 + 2|
= 12 units
The distance of DE = |7 + 2| + |7 – 8|
= 10 units
The distance of EF = |7 – 8| + |-5 – 8|
= 12 units
The disatnce of FD = |-5 – 8| – |-5 + 2|
= 10 units
Now,
From the given side lengths,
We can observe that
The opposite side lengths are equal
Now,
we know that,
The rectangle has the opposite side lengths
Hence, from the above,
We can conclude that
Joaquin is not correct
KEY CONCEPT
You can represent polygons on a coordinate plane and solve problems by using absolute values to find side lengths.
Add or subtract absolute values to find the length of each side.
AB: |-3| + |2| = 3 + 2 = 5 units
BC: |4| – |2| = 4 – 2 = 2 units
CD: |-3| + |2| = 3 + 2 = 5 units
DA: |4| – |2| = 4 – 2 = 2 units
Do You Understand?
Question 1.
?Essential Question How is distance used to solve problems about polygons in a coordinate plane?
Answer:
To find the distance between two points with the same x-coordinates, subtract their y-coordinates. To find the distance between two points with the same y-coordinates, subtract their x-coordinates
To find the distance between the different x and y-coordinates, subtract the x-coordinates of the 2 points and y-coordinates of the 2 points and add both the values
Question 2.
Reasoning In Example 1, why do you add absolute values to find the distance from A to B but subtract absolute values to find the distance from B to C?
Answer:
From Example 1,
We know that,
The coordinates of A, B, and C are:
A (-4, 6), B (2, 6), and C (2, 1)
Now,
We know that,
The absolute distance between given points = |x + a| + |y + b|
Now,
When the y-coordinates are the same,
The absolute distance between 2 points = |x + y|
So,
The absolute distance from A and B is positive because the x-coordinates move from left to right (or) vice-versa
When the x-coordinates are the same,
The absolute distance between 2 points = |a – b|
So,
The absolute distance from B and C is negative because the y-coordinates move from top to bottom (or) vice-versa
Question 3.
Construct Arguments Could you add or subtract the absolute values of coordinates to find the length of the diagonal AC of rectangle ABCD in Example 1? Explain.
Answer:
From Example 1,
We know that,
A (-4, 6), B (2, 6), C (2, 1), and D (-4, 1)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
So,
The distance of the diagonal AC of rectangle ABCD is solved by the addition of the absolute values of the coordinates of A and C
Hence, from the above,
We can conclude that
We add the absolute values of coordinates to find the length of the diagonal AC of rectangle ABCD in Example 1
Do You Know How?
Question 4.
Find the perimeter of rectangle MNOP with vertices M(-2,5), N(-2, -4), 0(3,-4), and P(3, 5).
Answer:
The given vertices of rectangle MNOP are:
M(-2,5), N(-2, -4), 0(3,-4), and P(3, 5)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
Now,
The disatnce of MN = |-2 + 5| + |-2 – 4|
= |3 + 6|
= 9 units
The distance of NO = |-2 – 4| + |3 – 4|
= |6 – 1|
= 5 units
The distance of OP = |3 – 4| + |3 + 5|
= |1 + 8|
= 9 units
The distance of PM = |3 + 5| + |-2 + 5|
= |8 – 3|
= 5 units
Now,
The perimeter of the rectangle MNOP = MN + NO + OP + PM
= 9 + 5 + 9 + 5
= 28 units
Hence, from the above,
We can conclude that
The perimeter of the given rectangle MNOP is: 28 units
Question 5.
Jen draws a polygon with vertices E(-2, 3.5), F(3, 3.5), G(3, -1.5), and H(-2, -1.5). Is EFGH a square? Justify your answer.
Answer:
It is given that
Jen draws a polygon with vertices E(-2, 3.5), F(3, 3.5), G(3, -1.5), and H(-2, -1.5)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
Now,
The distance of EF = |3 + 2|
= 5 units
The distance of FG = |3.5 + 1.5|
= 5 units
The distance of GH = |3 + 2|
= 5 units
The distance of HE = |3.5 + 1.5|
= 5 units
Now,
We know that,
The “Square” has all the same side lengths
Hence, from the above,
We can conclude that
EFGH is a square
Question 6.
Square ABCD has vertices A(-4.5, 4), B(3.5, 4), C(3.5, -4), and D(-4.5, -4). What is the area of square ABCD?
Answer:
It is given that
Square ABCD has vertices A(-4.5, 4), B(3.5, 4), C(3.5, -4), and D(-4.5, -4)
Now,
We know that,
The square has the same side lengths
So,
The distance between any 2 points is sufficient to find the area of square ABCD
Now,
We know that,
The area of a square = Side²
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
Now,
The distance of AB =|3.5 + 4.5|
= 8 units
So,
The area of square ABCD = Side²
= 8²
= 64 units²
Hence, from the above,
We can conclude that
The area of square ABCD is: 64 units²
Practice & Problem Solving
Scan for Multimedia
Leveled Practice
In 7 and 8, find the perimeter of each rectangle.
Question 7.
Rectangle JKLM: J(-3, 8), K(-3,-1), L(4, -1), M(4,8)
JK = |8| + |-1| = ![]()
KL = |–3| + |4| = ![]()
Perimeter = ![]() units
units
Answer:
The given vertices of Rectangle JKLM are: J(-3, 8), K(-3,-1), L(4, -1), M(4,8)
Now,
We know that,
The side lengths of the parallel sides are the same
So,
In Rectangle JKLM,
JK = LM and KL = MJ
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
Now,

Hence, from the above,
We can conclude that
The perimeter of Rectangle JKLM is: 16 units
Question 8.
Rectangle WXYZ: W(-3, -2), X(4, -2), Y(4, -5), Z(-3, -5)
WX = |-3| + |4| = ![]()
XY = |–5| – |-2| = ![]()
Perimeter = ![]() units
units
Answer:
The given vertices of Rectangle WXYZ are: W(-3, -2), X(4, -2), Y(4, -5), Z(-3, -5)
Now,
We know that,
The side lengths of the parallel sides are the same
So,
In Rectangle WXYZ,
WX = YZ and XY = ZW
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
Now,
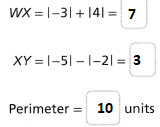
Hence, from the above,
We can conclude that
The perimeter of Rectangle JKLM is: 10 units
Question 9.
Triangle JKL has vertices J(0, 0), K(5, 0), and L(0, -3). Is triangle JKL equilateral? Justify your answer.
Answer:
It is given that
Triangle JKL has vertices J(0, 0), K(5, 0), and L(0, -3)
Now,
We know that,
The “Equilateral Triangle” is a triangle that has the same side lengths
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
So,
The distance of JK = |0 + 0| + |5 + 0|
= 5 units
The distance of KL = |5 + 0| + |0 – 3|
= 8 units
The distance of LJ = |0 – 3| + |0 + 0|
= 3 units
So,
From the given side lengths,
JK ≠ L ≠ LJ
Hence, from the above,
Hence, from the above,
We can conclude that
Triangle JKL is not an equilateral triangle
Question 10.
Polygon WXYZ has vertices W(-1.5, 1.5), X(6, 1.5), Y(6, -4.5), and Z(-1.5, -4.5). Is WXYZ a rectangle? Justify your answer.
Answer:
It is given that
Polygon WXYZ has vertices W(-1.5, 1.5), X(6, 1.5), Y(6, -4.5), and Z(-1.5, -4.5)
Now,
The representation of the given polygon WXYZ with its side lengths is:
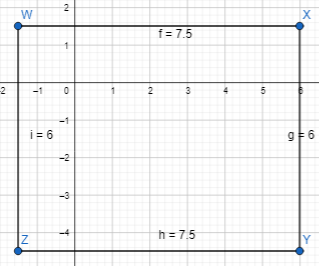
Now,
From the above figure,
We can observe that
The side lengths of the opposite sides are equal
Now,
We know that,
A “Rectangle” has the same opposite side lengths
Hence, from the above,
We can conclude that
Polygon WXYZ is a rectangle
Question 11.
What are the perimeter and area of rectangle ABCD?
Answer:
The given figure is:

Now,
From the given figure,
We can observe that
The coordinates of the rectangle ABCD are:
A (-3, -7), B (4, -7), C (4, 6), and D (-3, 6)
Now,
We know that,
In a Rectangle,
The side lengths of the opposite sides are the same
So,
AB = CD and BC = DA
Now,
We know that,
The perimeter of a rectangle = 2 (l + w)
The area of a rectangle = l × w
Now,
The distance of AB = |-3 – 7| + |4 – 7|
= |-10 + 3|
= 7 units
The disatnce of BC = |4 – 3| + |6 + 6|
= |1 + 12|
=13 units
So,
The perimeter of Rectangle ABCD = 2 (AB + BC)
= 2 (7 + 13)
= 2 (20)
= 40 units
The area of Rectangle ABCD = AB × CD
= 7 × 13
= 91 units²
Hence, from the above,
We can conclude that
The perimeter of Rectangle BACD is: 40 units
The area of Rectangle BACD is: 91 units²
Question 12.
Mike used a coordinate plane to design the patio shown at the right. Each unit on the grid represents 1 yard. To buy materials to build the patio, Mike needs to know its perimeter. What is the perimeter of the patio?
Answer:
It is given that
Mike used a coordinate plane to design the patio shown at the right. Each unit on the grid represents 1 yard.
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The coordinates of the given patio are:
A (3, 2), B (3, 4), C (7, 4), D (7, 7), E (9, 7), and F (9, 2)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
Now,
The distance of AB = |4 – 2| = 2 units
The disatnce of BC = |7 – 3| = 4 units
The distance of CD = |7 – 4| = 3 units
The distance of DE = |9 – 7| = 2 units
The distance of EF = |7 – 2| = 5 units
The distance of FA = |9 – 3| = 6 units
Now,
The perimeter of the patio = 2 + 4 + 3 + 2 + 5 + 6
= 22 units
Hence, from the above,
We can conclude that
The perimeter of the patio is: 22 units
Question 13.
Jordan started at her home at point H. She ran to the bank (B), the library (1), the post office (P), the café (C), her school (S), and then back to her home, as shown. The coordinates represent the position, in miles, of each of these locations with respect to the center of town, which is located at the origin. What is the total distance that Jordan ran?
Answer:
It is given that
Jordan started at her home at point H. She ran to the bank (B), the library (1), the post office (P), the café (C), her school (S), and then back to her home, as shown. The coordinates represent the position, in miles, of each of these locations with respect to the center of town, which is located at the origin
Now,
The given figure is:

Now,
From the given figure,
We can observe that
The coordinates are:
H (\(\frac{-3}{4}\), \(\frac{1}{2}\)), B (1, \(\frac{1}{2}\)), L (1, –\(\frac{1}{4}\)), P (\(\frac{1}{2}\), –\(\frac{1}{4}\)), C (\(\frac{1}{2}\), –\(\frac{3}{4}\)), S (-\(\frac{3}{4}\), –\(\frac{3}{4}\))
Now,
The representation of the given coordinates with its side lengths is:
So,
The total distance that Jordan ran = 1.75 + 0.75 + 0.70 + 1.25 + 1.25
= 5.7 miles
Hence, from the above,
We can conclude that
The total distance that Jordan ran is: 5.7 miles
Question 14.
Use Structure Ana drew a plan for a rectangular piece of material that she will use for a quilt. The vertices are (-1.2, -3.5), (-1.2, 4.4), and (5.5, 4.4). What are the coordinates of the fourth vertex?
Answer:
It is given that
Ana drew a plan for a rectangular piece of material that she will use for a quilt. The vertices are (-1.2, -3.5), (-1.2, 4.4), and (5.5, 4.4)
Now,
Let the vertices be A (-1.2, -3.5), B (-1.2, 4.4), C (5.5, 4.4), and D (x, y)
Now,
We know that,
In a Rectangle,
The opposite side lengths are the same
So,
For the given quilt,
AB = CD and BC = DA
Now,
If you observe carefully the vertices given, you will see that there are two vertex with same coordinates in x axis: (-1.2, -3.5), and (-1.2, 4.4),
And one vertex has other coordinate in x axis, it is: (5.5, 4.4)
So,
To form a rectangle, you need a fourth vertex that will have same coordinate in x than (5.5, 4.4) and same coordinate in y axis as (-1.2, -3.5),
So,
The fourth vertex coordinate is (5.5, -3.5)
Hence, from the above,
We can conclude that
The coordinates of the fourth vertex are: (5.5, -3.5)
Question 15.
Mr. Janas is building a pool in his backyard. He sketches the rectangular pool on a coordinate plane. The vertices of the pool are A(-5, 7), B(1,7), C(1, -1), and D(-5, -1). If each unit represents 1 yard, how much area of the backyard is needed for the pool?
Answer:
It is given that
Mr. Janas is building a pool in his backyard. He sketches the rectangular pool on a coordinate plane. The vertices of the pool are A(-5, 7), B(1,7), C(1, -1), and D(-5, -1)
Now,
The representation of the given vertices of a rectangular pool and its side lengths in the coordinate plane is:

Now,
We know that,
In a Rectangle,
The opposite side lengths have the same value
Now,
We know that,
The area of a Rectangle = Length × Width
So,
The area of the rectangular swimming pool = AB × BC
= 6 × 8
= 48 yard²
Hence, from the above,
We can conclude that
The area of the given rectangular swimming pool is: 48 yard²
Question 16.
Vocabulary Why is absolute value used to find distances on a coordinate plane?
Answer:
We know that the absolute value of a point on the number line (or the absolute value of the coordinate of a tree in your backyard) tells you the distance between that point (or tree) and the number zero at origin of your coordinate system
Question 17.
Higher Order Thinking A square on a coordinate plane has one vertex at (-0.5, -2) and a perimeter of 10 units. If all of the vertices are located in Quadrant III, what are the coordinates of the other three vertices?
Answer:
It is given that
A square on a coordinate plane has one vertex at (-0.5, -2) and a perimeter of 10 units and all of the vertices are located in Quadrant III
Now,
We know that,
The perimeter of square is:
where,
b is the length side of the square
Now,
According to the given information,
Now,
Divide the above equation by 4 both sides
So,
Now,
A (-0.5, -2) —> The given coordinates of one vertex
Now,
we know that
All of the vertices are located in Quadrant III
So,
The other three vertices are located at the left and down of vertex A
Now,
The coordinate of vertex B located at 2.5 units at left of vertex A
The coordinate of vertex C located at 2.5 units at left and 2.5 units down of vertex A
The coordinate of vertex D located at 2.5 units down of vertex A
So,
B(-0.5-2.5,-2) —–> B(-3, -2)
C(-0.5-2.5,-2-2.5) —–> C(-3, -4.5)
D(-0.5,-2-2.5) —–> D(-0.5, -4.5)
Hence, from the above,
We can conclude that
The coordinates of the other three vertices are:
B (-3, -2), C (-3, -4.5), and D (-0.5, -4.5)
Assessment Practice
Question 18.
You are given the following points on a coordinate plane: A(-1\(\frac{1}{2}\), –\(\frac{1}{2}\)), B(-1\(\frac{1}{2}\), -3), and C (4, -3).
PART A
Using absolute value, find the distance (number of units) between points A and B.
Answer:
The given points are:
A(-1\(\frac{1}{2}\), –\(\frac{1}{2}\)), B(-1\(\frac{1}{2}\), -3), and C (4, -3)
Now,
The representation of the given coordinates along with its side lengths in the coordinate plane is:
So,
From the above figure,
We can observe that
The distance between points A and B is: 2.5 units
Hence, from the above,
We can conclude that
The distance between points A and B is: 2.5 units
PART B
Select all the coordinates that are 8 units from point C.
![]() (12, -3)
(12, -3)
![]() (12, -11)
(12, -11)
![]() (4, -3)
(4, -3)
![]() (-4, -3)
(-4, -3)
![]() (4,-11)
(4,-11)
Answer:
It is given that
The coordinates of Point C are: C (4, -3)
Now,
When the coordiantes of point C moves 8 units towards right,
C (4 + 8, -3) = C (12, -3)
When the coordiantes of point C moves 8 units towards left,
C (4 – 8, -3) = C (-4, -3)
Hence, from the above,
We can conclude that
All the coordinates that are 8 units from point C are:

Topic 2 REVIEW
? Topic Essential Question
What are integers and rational numbers? How are points graphed on a coordinate plane?
Answer:
An “Integer” can be written as a fraction by giving it a denominator of one. So, any integer is a rational number
“Rational numbers” are those numbers that are integers and can be expressed in the form of \(\frac{x}{y}\) where both numerator and denominator are integers
To graph or plot points, we use two perpendicular lines called the x-axis and the y-axis. The horizontal number line is the x-axis and the vertical line is the y-axis. Every point in the coordinate plane is represented by an ordered pair of x and y coordinates.
Vocabulary Review
Complete each definition and then provide an example of each vocabulary word.
Vocabulary
absolute value
opposite
ordered pair
rational number

Answer:

Use Vocabulary in Writing
Explain how the points A(9, –\(\frac{2}{5}\)) and B(9, \(\frac{2}{5}\)) are related. Use vocabulary words in your explanation.
Answer:
The given points are:
A(9, –\(\frac{2}{5}\)) and B(9, \(\frac{2}{5}\))
Now,
Compare the given points with (x, a), and (y, b)
Now,
From the given points,
We can observe that
a. The x-coordinates are the same
b. The y-coordinates are opposite to each other
c. The y-coordinates and x-coordinates are rational numbers since they can be written in the form of \(\frac{x}{y}\)
Concepts and Skills Review
LESSON 2.1 Understand Integers
Quick Review
Integers are all of the counting numbers, their opposites, and 0. Opposites are integers located on opposite sides of 0 and the same distance from 0 on a number line.
Example
For each point on the number line, write the integer and its opposite.

A: 4,-4 B: 0,0 C: -6,6
The opposite of the opposite of a number is the number itself.
Practice
For each point on the number line, write the integer and its opposite.

Question 1.
A
Answer:
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the given number line represents 1 unit
Now,
We know that,
The opposite value of a is: -a
The opposite value of -a is: a
Hence, from the above,
We can conclude that
The value of A from the given number line is: 3
The opposite value of A is: -3
Question 2.
B
Answer:
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the given number line represents 1 unit
Now,
We know that,
The opposite value of a is: -a
The opposite value of -a is: a
Hence, from the above,
We can conclude that
The value of B from the given number line is: -1
The opposite value of B is: 1
Question 3.
C
Answer:
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the given number line represents 1 unit
Now,
We know that,
The opposite value of a is: -a
The opposite value of -a is: a
Hence, from the above,
We can conclude that
The value of C from the given number line is: 6
The opposite value of C is: -6
Question 4.
D
Answer:
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the given number line represents 1 unit
Now,
We know that,
The opposite value of a is: -a
The opposite value of -a is: a
Hence, from the above,
We can conclude that
The value of D from the given number line is: -7
The opposite value of D is: 7
Question 5.
E
Answer:
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the given number line represents 1 unit
Now,
We know that,
The opposite value of a is: -a
The opposite value of -a is: a
Hence, from the above,
We can conclude that
The value of E from the given number line is: -5
The opposite value of E is: 5
Question 6.
F
Answer:
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the given number line represents 1 unit
Now,
We know that,
The opposite value of a is: -a
The opposite value of -a is: a
Hence, from the above,
We can conclude that
The value of F from the given number line is: 1
The opposite value of F is: -1
LESSON 2.2 Represent Rational Numbers on the Number Line
Quick Review
Rational numbers are numbers that can be written as a quotient \(\frac{a}{b}\), where a and b are integers and b does not equal 0. You can use number lines to represent, compare, and order rational numbers.
Example
Compare and order -0.1, 0.75, and –\(\frac{1}{4}\) from least to greatest.
Plot the numbers on a number line.
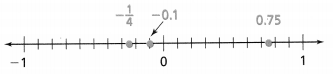
so –\(\frac{1}{4}\) < -0.1 < 0.75, and their order from least to greatest is –\(\frac{1}{4}\), -0.1, 0.75.
Practice
In 1-3, plot each rational number on the number line.

Question 1.
\(\frac{3}{4}\)
Answer:
The given point is: \(\frac{3}{4}\)
Now,
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the given number line represents 0.1 unit
Now,
The representation of \(\frac{3}{4}\) in the decimal form is: 0.75
Hence,
The representation of the given point on the given number line is:
![]()
Question 2.
–\(\frac{2}{5}\)
Answer:
The given point is: –\(\frac{2}{5}\)
Now,
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the given number line represents 0.1 unit
Now,
The representation of –\(\frac{2}{5}\) in the decimal form is: -0.4
Hence,
The representation of the given point on the given number line is:
![]()
Question 3.
0.5
Answer:
The given point is: 0.5
Now,
The given number line is:

Now,
From the given number line,
We can observe that
Each line in the given number line represents 0.1 unit
Hence,
The representation of the given point on the given number line is:
![]()
In 4-7, use <, >, or = to compare.
Question 4.
0.25 ![]() \(\frac{1}{4}\)
\(\frac{1}{4}\)
Answer:
The given numbers are: 0.25 and \(\frac{1}{4}\)
Now,
The conversion of \(\frac{1}{4}\) into a decimal number is: 0.25
Hence, from the above,
We can conclude that
![]()
Question 5.
1\(\frac{5}{8}\) ![]() 1.6
1.6
Answer:
The given numbers are: 1\(\frac{5}{8}\) and 1.6
Now,
The conversion of 1\(\frac{5}{8}\) into a decimal number is: 1.625
Hence, from the above,
We can conclude that
![]()
Question 6.
3.65 ![]() 3\(\frac{3}{4}\)
3\(\frac{3}{4}\)
Answer:
The given numbers are: 3.65 and 3\(\frac{3}{4}\)
Now,
The conversion of 3\(\frac{3}{4}\) into a decimal number is: 3.75
Hence, from the above,
We can conclude that
![]()
Question 7.
–\(\frac{2}{3}\) ![]() \(\frac{3}{4}\)
\(\frac{3}{4}\)
Answer:
The given numbers are: –\(\frac{2}{3}\) and \(\frac{3}{4}\)
Now,
The conversion of \(\frac{3}{4}\) into a decimal number is: 0.75
The conversion of –\(\frac{2}{3}\) into a decimal number is: -0.66
Hence, from the above,
We can conclude that
![]()
LESSON 2.3 Absolute Values of Rational Numbers
Quick Review
The absolute value of a number is its distance from 0 on the number line. Distance is always positive. Absolute values are never negative.
Example
Find the absolute values and order |3|, |4|, |-2|, |–5| from least to greatest.

Practice
In 1-4, find each value.
Question 1.
|-9|
Answer:
The given absolute number is: |-9|
Now,
We know that,
The absolute value of any number is positive
Hence, from the above,
We can conclude that
The value of |-9| is: 9
Question 2.
|-2|
Answer:
The given absolute number is: |-2|
Now,
We know that,
The absolute value of any number is positive
Hence, from the above,
We can conclude that
The value of |-2| is: 2
Question 3.
|4|
Answer:
The given absolute number is: |4|
Now,
We know that,
The absolute value of any number is positive
Hence, from the above,
We can conclude that
The value of |4| is: 4
Question 4.
-|-10|
Answer:
The given absolute number is: -|-10|
Now,
We know that,
The absolute value of any number is positive
Hence, from the above,
We can conclude that
The value of -|-10| is: -10
In 5-8, order the values from least to greatest.
Question 5.
|-3|, |-2|, |10|
Answer:
The given absolute numbers are: |-3|, |-2|, and |10|
Now,
We know that,
The absolute value of any number is positive
So,
The values of the given absolute numbers are: 3, 2, and 10
So,
The order of the given absolute numbers from the least to the greatest is: 2, 3, and 10
Hence, from the above,
We can conclude that
The order of the given absolute numbers from the least to the greatest is: 2, 3, and 10
Question 6.
|-7|, |0|, |-5|
Answer:
The given absolute numbers are: |-7|, |0|, and |-5|
Now,
We know that,
The absolute value of any number is positive
So,
The values of the given absolute numbers are: 7, 0, and 5
So,
The order of the given absolute numbers from the least to the greatest is: 0, 5, and 7
Hence, from the above,
We can conclude that
The order of the given absolute numbers from the least to the greatest is: 0, 5, and 7
Question 7.
|-18.5|, |18|, |-12.5|
Answer:
The given absolute numbers are: |-18.5|, |18|, and |-12.5|
Now,
We know that,
The absolute value of any number is positive
So,
The values of the given absolute numbers are: 18.5, 18, and 12.5
So,
The order of the given absolute numbers from the least to the greatest is: 12.5, 18, and 18.5
Hence, from the above,
We can conclude that
The order of the given absolute numbers from the least to the greatest is: 12.5, 18, and 18.5
Question 8.
|26|, |-20|, |-24.5|
Answer:
The given absolute numbers are: |26|, |-20|, and |-24.5|
Now,
We know that,
The absolute value of any number is positive
So,
The values of the given absolute numbers are: 26, 20, and 24.5
So,
The order of the given absolute numbers from the least to the greatest is: 20, 24.5, and 26
Hence, from the above,
We can conclude that
The order of the given absolute numbers from the least to the greatest is: 20, 24.5, and 26
LESSON 2.4 Represent Rational Numbers on the Coordinate Plane
Quick Review
An ordered pair (x, y) of numbers gives the coordinates that locate a point on a coordinate plane. Coordinates can be whole numbers, fractions, mixed numbers, or decimals.
Example
Explain how to plot any point with coordinates (x, y).
• Start at the origin, (0, 0).
• Use the x-coordinate to move right (if positive) or left (if negative) along the x-axis.
• Then use the y-coordinate of the point to move up (if positive) or down (if negative) following the y-axis.
• Draw and label the point on the coordinate plane. Explain how to name the location of a point on a coordinate plane. Follow the grid line from the point to the x-axis to name the x-coordinate, and follow the grid line from the point to the y-axis to name the y-coordinate.
Practice
In 1-6, give the ordered pair for each point.
Question 1.
U
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point U are: (0, 2.5)
Hence, from the above,
We can conclude that
The ordered pair for point U is: (0, 2.5)
Question 2.
V
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point V are: (-2, 1.5)
Hence, from the above,
We can conclude that
The ordered pair for point V is: (-2, 1.5)
Question 3.
W
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point W are: (-4, -1)
Hence, from the above,
We can conclude that
The ordered pair for point W is: (-4, -1)
Question 4.
X
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point X are: (2.5, 0)
Hence, from the above,
We can conclude that
The ordered pair for point X is: (2.5, 0)
Question 5.
Y
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point Y are: (2, -1.5)
Hence, from the above,
We can conclude that
The ordered pair for point Y is: (2, -1.5)
Question 6.
Z
Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The coordinates of point Z are: (-1.5, -3)
Hence, from the above,
We can conclude that
The ordered pair for point Z is: (-1.5, -3)
LESSONS 2.5 AND 2.6 Find Distances and Represent Polygons on the Coordinate Plane
Quick Review
You can use absolute value to find the distance between two points that share the same X- or y-coordinate. When the y-coordinates are the same, use the x-coordinates to find the distance. When the x-coordinates are the same, use the y-coordinates. If the points are in different quadrants, add their absolute values. If the points are in the same quadrant, subtract their absolute values.
You can use what you know about finding the distance between two points to find the lengths of the sides of a polygon on a coordinate plane.
Example
Find the length of side AB.
The ordered pairs for points A and B are A(-3, 2) and B(-1, 2). The points are in the same quadrant, so subtract the absolute values of the x-coordinates.
|-3| – |-1| = 3 – 1 = 2 units
The length of side AB is 2 units.
Practice
In 1-6, find the remaining side lengths of polygon ABCDEF. Then find the polygon’s perimeter.

Answer:
The given coordinate plane is:

Now,
From the given coordinate plane,
The coordinates of the vertices are:
A (-3, 2) B (-1, 2), C (-1, 1), D (1, 1), E (1, -2), F (-3, -2)
Question 1.
Length of BC
Answer:
The given coordinates of points B and C are: B (-1, 2), and C (-1, 1)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
So,
The length of BC = |2 – 1|
= 1 unit
Hence, from the above,
We can conclude that
The length of BC is: 1 unit
Question 2.
Length of CD
Answer:
The given coordinates of points C and D are: C (-1, 1), and D (1, 1)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
So,
The length of CD = |1 + 1|
= 2 units
Hence, from the above,
We can conclude that
The length of CD is: 2 units
Question 3.
Length of DE
Answer:
The given coordinates of points D and E are: D (1, 1), and E (1, -2)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
So,
The length of DE = |2 + 1|
= 3 units
Hence, from the above,
We can conclude that
The length of DE is: 3 units
Question 4.
Length of EF
Answer:
The given coordinates of points E and F are: E (1, -2), and F (-3, -2)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
So,
The length of EF = |3 + 1|
= 4 units
Hence, from the above,
We can conclude that
The length of EF is: 4 units
Question 5.
Length of FA
Answer:
The given coordinates of points F and A are: F (-3, -2), and A (-3, 2)
Now,
Compare the given points with (x, a), and (y, b)
Now,
We know that,
The distance between 2 points = |x + a| + |y + b|
So,
The length of FA = |2 + 2|
= 4 units
Hence, from the above,
We can conclude that
The length of FA is: 4 units
Question 6.
Perimeter of ABCDEF
Answer:
We know that,
The perimeter of any polygon is the sum of its side lengths
So,
The perimeter of polygon ABCDEF = AB + BC + CD+ DE+ EF+ FA
= 2 + 1 + 2 + 3 + 4 + 4
= 16 units
Hence, from the above,
We can conclude that
The perimeter of the given polygon ABCDEF is: 16 units
In 7 and 8, polygon QRST has vertices Q(-4, -1), R(-4,5), S(2,5), and T(2, -1).
Question 7.
Draw and label polygon QRST on the coordinate plane.
Answer:
The given vertices of the polygon QRST are:
Q (-4, -1), R (-4,5), S (2,5), and T (2, -1)
Hence,
The representation of the given vertices along with its side lengths in the given coordinate plane is:
Question 8.
Construct an argument to justify whether or not polygon QRST is a square.
Answer:
From Exercise 7,
The representation of polygon QRST along with its side lengths in the given coordinate plane is:

Now,
From the given coordinate plane,
We can observe that
The sidelengths of all the sides are the same
Now,
We know that,
A “Square” has the same side lengths on all the four sides
Hence, from the above,
We can conclude that
Polygon QRST is a square
Topic 2 Fluency Practice
Hidden Clue
For each ordered pair, simplify the two coordinates. Then locate and label the corresponding point on the graph. Draw line segments to connect the points in alphabetical order. Use the completed picture to help answer the riddle below.