Engage NY Eureka Math 6th Grade Module 2 Lesson 16 Answer Key
Eureka Math Grade 6 Module 2 Lesson 16 Opening Exercise Answer Key
a. What is an even number?
Answer:
Possible student responses:
An integer that can be evenly divided by 2
A number whose unit digit is 0, 2, 4, 6, or 8
All the multiples of 2
b. List some examples of even numbers.
Answer:
Answers will vary.
c. What is an odd number?
Answer:
Possible student responses:
An integer that CANNOT be evenly divided by 2
A number whose unit digit is 1, 3, 5, 7, or 9
All the numbers that are NOT multiples of 2
d. List some examples of odd numbers.
Answer:
Answers will vary.
What happens when we add two even numbers? Do we always get an even number?
Answer:
Before holding a discussion about the process to answer the following questions, have students write or share their predictions.
Eureka Math Grade 6 Module 2 Lesson 16 Exercise Answer Key
Exercise 1.
Why is the sum of two even numbers even?
a. Think of the problem 12 + 14. Draw dots to represent each number.
Answer:
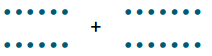
b. Circle pairs of dots to determine if any of the dots are left over.
Answer:
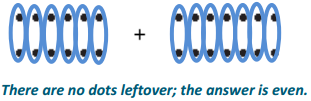
c. Is this true every time two even numbers are added together? Why or why not?
Answer:
Since 12 is represented by 6 sets of two dots, and 14 is represented by 7 sets of two dots, the sum is 13 sets of two dots. This is true every time two even numbers are added together because even numbers never have dots left over when we are circling pairs. Therefore, the answer is always even.
Exercise 2.
Why is the sum of two odd numbers even?
a. Think of the problem 11 + 15. Draw dots to represent each number.
Answer:
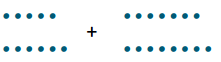
b. Circle pairs of dots to determine if any of the dots are left over.
Answer:
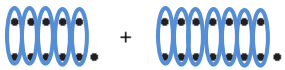
When we circle groups of two dots, there is one dot remaining in each representation because each addend is an odd number. When we look at the sum, however, the two remaining dots can form a pair, leaving us with a sum that is represented by groups of two dots. The sum is, therefore, even. Since each addend is odd, there is one dot for each addend that does not have a pair. However, these two dots can be paired together, which means there are no dots without a pair, making the sum an even number.
c. Is this true every time two odd numbers are added together? Why or why not?
Answer:
This is true every time two odd numbers are added together because every odd number has one dot remaining when we circle pairs of dots. Since each number has one dot remaining, these dots can be combined to make another pair. Therefore, no dots remain, resulting in an even sum.
Exercise 3.
Why is the sum of an even number and an odd number odd?
a. Think of the problem 14 + 11. Draw dots to represent each number.
Answer:
Students draw dots to represent each number. After circling pairs of dots, there is one dot left for the number 11, and the number 14 has no dots remaining. Since there is one dot left over, the sum is odd because not every dot has a pair.
b. Circle pairs of dots to determine if any of the dots are left over.
Answer:
Students draw dots to represent each number. After circling pairs of dots, there is one dot left for the number 11, and the number 14 has no dots remaining. Since there is one dot left over, the sum is odd because not every dot has a pair.
C. Is this true every time an even number and an odd number are added together? Why or why not?
Answer:
This is always true when an even number and an odd number are added together because only the odd number will have a dot remaining after we circle pairs of dots. Since this dot does not have a pair, the sum is odd.
d. What if the first addend is odd and the second is even? Is the sum still odd? Why or why not? For example, If we had 11 + 14, would the sum be odd?
Answer:
The sum is still odd for two reasons. First, the commutative property states that changing the order of an addition problem does not change the answer. Because an even number plus an odd number is odd, then an odd number plus an even number is also odd. Second, it does not matter which addend is odd; there is still one dot remaining, making the sum odd.
Let’s sum it up:
Answer:
→ “Even” + “even” = “even”
→ “Odd” + “odd” = “even”
→ “Odd” + “even” = “odd”
Exploratory Challenge/Exercises 4-6
Exercise 4.
The product of two even numbers is even.
Answer:
Answers will vary, but one example answer is provided.
Using the problem 6 × 14, students know that this is equivalent to six groups of fourteen, or
14 + 14 + 14 + 14 + 14 + 14. Students also know that the sum of two even numbers is even; therefore, when adding the addends two at a time, the sum is always even. This means the sum of six even numbers is even, making the product even since It is equivalent to the sum.
Using the problem 6 × 14, students can use the dots from previous examples.
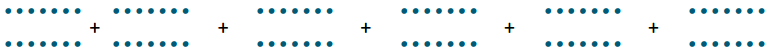
From here, students can circle dots and see that there are no dots remaining, so the answer must be even.
Exercise 5.
The product of two odd numbers is odd.
Answer:
Answers will vary, but an example answer is provided.
Using the problem 5 × 15, students know that this is equivalent to five groups of fifteen, or
15 + 15 + 15 + 15 + 15. Students also know that the sum of two odd numbers is even, and the sum of an odd and even number is odd. When adding two of the addends together at a time, the answer rotates between even and odd. When the final two numbers are added together, one is even and the other odd. Therefore, the sum is odd, which makes the product odd since it is equivalent to the sum.
Using the problem 5 × 15, students may also use the dot method.

After students circle the pairs of dots, one dot from each set of 15 remains, for a total of 5 dots. Students can group these together and circle more pairs, as shown below.
![]()
Since there is still one dot remaining, the product of two odd numbers is odd.
Exercise 6.
The product of an even number and an odd number is even.
Answer:
Answers will vary, but one example is provided.
Using the problem 6 × 7, students know that this is equivalent to the sum of six sevens, or 7 + 7 + 7 + 7 + 7 + 7.
Students also know that the sum of two odd numbers is even, and the sum of two even numbers is even. Therefore, when adding two addends at a time, the result is an even number. The sum of these even numbers is also even, which means the total sum is even. This also Implies the product is even since the sum and product are equivalent.
Using the problem 6 × 7, students may also use the dot method.
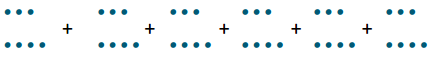
After students circle the pairs of dots, one dot from each set of 7 remains, for a total of 6 dots. Students can group these together and circle more pairs, as shown below.
![]()
Since there are no dots remaining, the product of an even number and an odd number is even.
Eureka Math Grade 6 Module 2 Lesson 16 Problem Set Answer Key
Without solving, tell whether each sum or product Is even or odd. Explain your reasoning.
Question 1.
346 + 721
Answer:
The sum is odd because the sum of an even and an odd number is odd.
Question 2.
4,690 × 141
Answer:
The product is even because the product of an even and an odd number is even.
Question 3.
1,462,891 × 745,629
Answer:
The product is odd because the product of two odd numbers is odd.
Question 4.
425,922 + 32,481,064
Answer:
The sum is even because the sum of two even numbers is even.
Question 5.
32 + 45 + 67 + 91 + 34 + 56
Answer:
The first two addends are odd because an even and an odd is odd.
Odd number +67 is even because the sum of two odd numbers is even.
Even number +91 is odd because the sum of an even and an odd number is odd.
Odd number +34 is odd because the sum of an odd and an even number is odd.
Odd number +56 is odd because the sum of an odd andan even number is odd.
Therefore, the final sum is odd.
Eureka Math Grade 6 Module 2 Lesson 16 Exit Ticket Answer Key
Determine whether each sum or product is even or odd. Explain your reasoning.
Question 1.
56,426+17,895
Answer:
The sum is odd because the sum of an even number and an odd number is odd.
Question 2.
317,362 × 129,324
Answer:
The product is even because the product of two even numbers is even.
Question 3.
104,81 + 4,569
Answer:
The sum is even because the sum of two odd numbers is even.
Question 4.
32,457 × 12,781
Answer:
The product is odd because the product of two odd numbers is odd.
Question 5.
Show or explain why 12 + 13 + 14 + 15 + 16 results in an even sum.
Answer:
12 + 13 is odd because even + odd is odd.
Odd number +14 is odd because odd + even is odd.
Odd number +15 is even because odd + odd is even.
Even number +16 is even because even + even is even.
OR
Students may group even numbers together, 12 + 14 + 16, which results in an even number. Then, when students combine the two odd numbers, 13 + 15, the result is another even number. We know that the sum of two evens results in another even number.