Engage NY Eureka Math 6th Grade Module 2 Lesson 17 Answer Key
Eureka Math Grade 6 Module 2 Lesson 17 Opening Exercise Answer Key
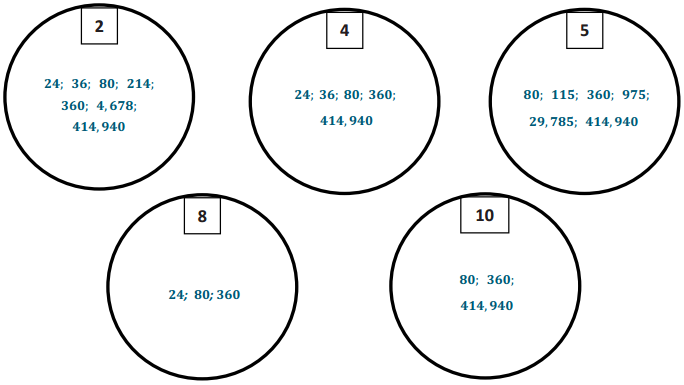
Below is a list of 10 numbers. Place each number in the circle(s) that is a factor of the number. Some numbers can be placed in more than one circle. For example, if 32 were on the list, it would be placed in the circles with 2, 4, and 8 because they are all factors of 32.
24; 36; 80; 115; 214; 360; 975; 4,678; 29,785; 414, 940
Answer:
Discussion:
Divisibility rule for 2: If and only if its unit digit is 0, 2, 4, 6, or 8
Divisibility rule for 4: If and only if its last two digits are a number divisible by 4
Divisibility rule for 5: If and only if its unit digit is 0 or 5
Divisibility rule for 8: If and only if its last three digits are a number divisible by 8
Divisibility rule for 10: If and only if its unit digit is 0
Decimal numbers with fraction parts do not follow the divisibility tests:
Students learn two new divisibility rules today. The rules are used to determine if numbers are divisible by 3 or 9. Start with students who already know the factors of 3 and 9, so they can see that the rule works.
→ What do the numbers 12, 18, 30, 66, and 93 all have in common?
Each is divisible by 3.
→ Calculate the sum of the digits for each given number. For example, the sum of the digits in the number 12 is 3 because 1 + 2 = 3.
Give students time to find the sums. Record the sums on the board.
→ What do these sums have in common?
They are divisible by 3.
→ When the sum of a number’s digits is divisible by 3, the entire number is divisible by 3. Now let’s examine a different set of numbers: 27, 36, 54, 72, and 99. What do these numbers have in common?
They are divisible by 9.
→ Calculate the sum of the digits for each given number.
Provide time for students to find the sums. Record the sums on the board.
→ What do all the sums have in common?
They are divisible by 9.
→ When the sum of the digits is divisible by 3 and 9, the entire number is divisible by 9. Let’s use this knowledge to determine if a large number is divisible by 3, 9, or both. The number 765 is divisible by both 3 and 9.
→ We can use what we know about the distributive property to prove that 765 is divisible by 3 and by 9.
→ Let’s begin by expanding 765.
Display the following progression.
→ We can represent 765 as:
7 × 100 + 6 × 10 + 5 × 1
→ We can further decompose the numbers that are easily seen as divisible by 3 and 9.
→ Let’s decompose 100 to 99 + 1. Why would we do this?
Because we already know that 99 is divisible by 3 and 9.
7(99 + 1) + 6 × 10 + 5
→ We can also decompose 10 to 9 + 1. Why would we do this?
Because we already know that 9 is divisible by 3 and 9.
7(99 + 1) + 6(9+ 1) + 5
→ Let’s use the distributive property further to distribute the factor 7 in the expression. We can represent 7
times the quantity (99 + 1) as 7(99) + 7 × 1, or 7(99) + 7.
7(99) + 7+ 6(9 + 1) + 5
→ We can distribute the factor 6 in the same fashion. How can we distribute the factor 6 in the expression?
We can represent 6 times the quantity (9 + 1) as 6(9) + 6 × 1, or 6(9) + 6.
7(99) + 7 + 6(9) + 6 + 5
→ Since we know that 9 is divisible by both 3 and 9, let’s factor the 9 out of the expression. We can use the commutative and associative properties to easily see this.
7(99) + 7 + 6(9) + 6 + 5
7(9 × 11) + 6(9 × 1) + 7 + 6 + 5
9(7 × 11 + 6) + 7 + 6 + 5
→ Let’s investigate our current expression. Obviously the product of 9(7 × 11 + 6) is divisible by 9 since the 9 is already factored out.
→ What about the sum of 7 + 6 + 5? What is the sum? Is this sum divisible by 3 and 9?
7 + 6 + 5 = 18.
This sum is divisible by 3 and 9.
→ Are 3 and 9 both factors of 18?
Yes
→ What do you notice about the addends 7 + 6 + 5?
They are the digits of our original number 765.
Let’s look once more at the expression:
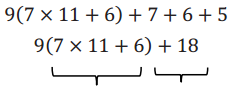
→ Since the first term is divisible by 3 and 9, the number 765 is divisible by 3 and 9 if and only if 7 + 6 + 5 is also divisible by 3 and 9.
→ This process can be used for any decimal whole number!
Introduce the divisibility rules for 3 and 9. Have students record the rules in their student materials.
Divisibility rule for 3: If the sum of the digits is divisible by 3, then the number is divisible by 3.
Divisibility rule for 9: If the sum of the digits is divisible by 9, then the number is divisible by 9.
Eureka Math Grade 6 Module 2 Lesson 17 Example Answer Key
Example 1.
This example shows how to apply the two new divisibility rules we just discussed.
Explain why 378 is divisible by 3 and 9.
a. Expand 378.
Answer:
300 + 70 + 8
3 × 100 + 7 × 1o + 8
b. Decompose the expression to factor by 9.
Answer:
3(99 + 1) + 7(9 + 1) + 8
3(99) + 3 + 7(9) + 7 + 8
c. Factor the 9.
Answer:
3(9 × 11) + 3 + 7(9 × 1) + 7 + 8
9(3 × 11 + 7) + 3 + 7 + 8
d. What is the sum of the three digits?
Answer:
3 + 7 + 8 = 18; the sum of the three digits is 18.
e. Is 18 divisible by 9?
Answer:
Yes
f. Is the entire number 378 divisible by 9? Why or why not?
Answer:
The number 378 is divisible by 9 because the sum of the digits is divisible by 9.
g. Is the number 378 divisible by 3? Why or why not?
Answer:
Three is a factor of 378 because if 9 is a factor of 378, then 3 will also be a factor. OR
The number 378 is divisible by 3 because the sum of the digits is divisible by 3.
Example 2.
Is 3,822 divisible by 3 or 9? Why or why not?
Answer:
The number 3,822 is divisible by 3 but not by 9 because the sum of the digits is 3 + 8 + 2 + 2 = 15, and 15 is divisible by 3 but not by 9.
Eureka Math Grade 6 Module 2 Lesson 17 Exercise Answer Key
Circle ALL the numbers that are factors of the given number. Complete any necessary work in the space provided.
Exercise 1.
2,838 is divisible by
![]()
Answer:
Explain your reasoning for your choice(s).
Answer:
The number 2,838 is divisible by 3 because 3 is a factor of 2,838. I know this because the sum of the digits is 21, which is divisible by 3. The number 2,838 is not divisible by 9 because 21 is not divisible by 9, and 2,838 is not divisible by 4 because the last two digits (38) are not divisible by 4.
Exercise 2.
34,515 is divisible by
![]()
Answer:
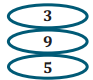
Explain your reasoning for your choice (s).
Answer:
The number 34,515 is divisible by 3 and 9 because both 3 and 9 are factors of 34,515. I know this because the sum of the digits is 18, and 18 is divisible by both 3 and 9. The number 34,515 is also divisible by 5 because the unit digit is a 5.
Exercise 3.
10,534,341 is divisible by
![]()
Answer:
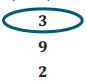
Explain your reasoning for your choice(s).
Answer:
The number 10,534,341 is divisible by 3 but not 9 because 3 is afactor of 10,534,341, but 9 is not. I know this because the sum of the digits is 21, which is divisible by 3 but not 9. The number 10, 534, 341 is not divisible by 2 because it does not end with 0, 2, 4, 6, or 8.
Exercise 4.
4,320 is divisible by
![]()
Answer:
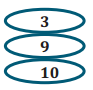
Explain your reasoning for your choice(s).
Answer:
The number 4,320 is divisible by 3 and 9 because 3 and 9 are factors of 4,320. I know this because the sum of the digits is 9, which is divisible by 3 and 9. The number 4,320 is also divisible by 10 because 10 is a factor of 4,320. I know this because the unit digit is 0.
Exercise 5.
6,240 is divisible by
![]()
Answer:
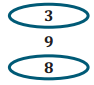
Explain your reasoning for your choice(s).
Answer:
The number 6,240 is divisible by 3 but not divisible by 9 because 3 is a factor of 6,240, but 9 is not. I know this because the sum of the digits is 12, which is divisible by 3 but not divisible by 9. The number 6,240 is divisible by 8 because the last three digits (240) is divisible by 8.
Eureka Math Grade 6 Module 2 Lesson 17 Problem Set Answer Key
Question 1.
Is 32, 643 divisible by both 3 and 9? Why or why not?
Answer:
The number 32,643 is divisible by both 3 and 9 because the sum of the digits is 18, which is divisible by 3 and 9.
Question 2.
Circle all the factors of 424,380 from the list below.
Answer:
![]()
Question 3.
Circle all the factors of 322,875 from the list below.
Answer:
![]()
Question 4.
Write a 3-digit number that ¡s divisible by both 3 and 4. Explain how you know this number is divisible by 3 and 4.
Answer:
Answers will vary. Possible student response: The sum of the digits is divisible by 3, and that’s how I know the number is divisible by 3. The last 2 digits are divisible by 4, so the entire number is divisible by 4.
Question 5.
Write a 4-digit number that Is divisible by both 5 and 9. Explain how you know this number Is divisible by 5 and 9.
Answer:
Answers will vary. Possible student response: The number ends with a 5 or 0, so the entire number is divisible by 5. The sum of the digits is divisible by 9, so the entire number is divisible by 9.
Eureka Math Grade 6 Module 2 Lesson 17 Exit Ticket Answer Key
Question 1.
Is 26, 341 divisible by 3? If it is, write the number as the product of 3 and another factor. If not, explain.
Answer:
The number 26,341 is not divisible by 3 because the sum of the digits is 16, which is not divisible by 3.
Question 2.
Is 8,397 divisible by 9? If it is, write the number as the product of 9 and another factor. If not, explain.
Answer:
The number 8,397 is divisible by 9 because the sum of the digits is 27, which is divisible by 9. Nine is a factor of 8,397 because 9 × 933 = 8,397.
Question 3.
Explain why 186,426 is divisible by both 3 and 9.
Answer:
The number 186, 426 is divisible by both 3 and 9 because the sum of the digits is 27, which is divisible by both 3 and 9.