Eureka Math Grade 6 Module 2 Lesson 3 Answer Key

Engage NY Eureka Math 6th Grade Module 2 Lesson 3 Answer Key

Eureka Math Grade 6 Module 2 Lesson 3 Example Answer Key

Example 1.
\(\frac{8}{9} \div \frac{2}{9}\)
Write the expression in unit form, and then draw a model to solve.
Answer:

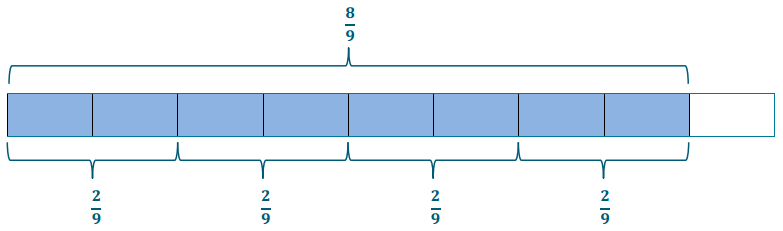
Here we have 4 groups of \(\frac{2}{9}\). Therefore, the quotient is 4.

Example 2.
\(\frac{9}{12} \div \frac{3}{12}\)
Write the expression in unit form, and then draw a model to solve.
Answer:

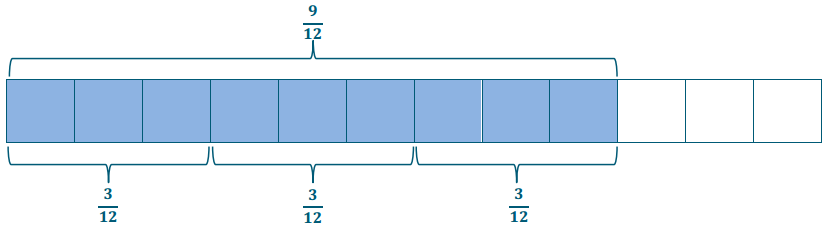
9 twelfths ÷ 3 twelfths = 9 ÷ 3 = 3

Example 3.
\(\frac{7}{9} \div \frac{3}{9}\)
Answer:

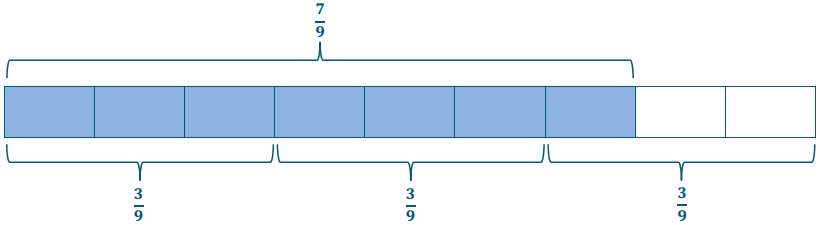
→ Look at your model. How many units of \(\frac{3}{9}\) can you see in \(\frac{3}{9}\)?
→2 complete units and then part of another

→ How can we name the part of the incomplete unit?
→There is one out of the three needed pieces to make another whole. So, it is \(\frac{1}{3}\)
→This means that \(\frac{7}{9} \div \frac{3}{9}\) = 2\(\frac{1}{3}\).
→This is the same as 7 ÷ 3.

→Do we get the same result solving \(\frac{7}{9} \div \frac{3}{9}\) as we do when solving \(\frac{7}{9} \times \frac{9}{3}\) ?

Eureka Math Grade 6 Module 2 Lesson 3 Exercise Answer Key

Write an expression to represent each problem. Then, draw a model to solve.

Exercise 1.
How many fourths are In 3 fourths?
Answer:
I need to divide three fourths by one fourth, which is 3.
\(\frac{3}{4} \div \frac{1}{4}\) = 3 fourth = 3 ÷ 1

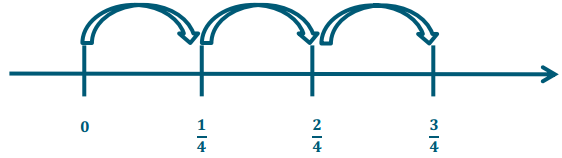
There are 3 one-fourths in three-fourths.

Exercise 2.
\(\frac{4}{5} \div \frac{2}{5}\)
Answer:

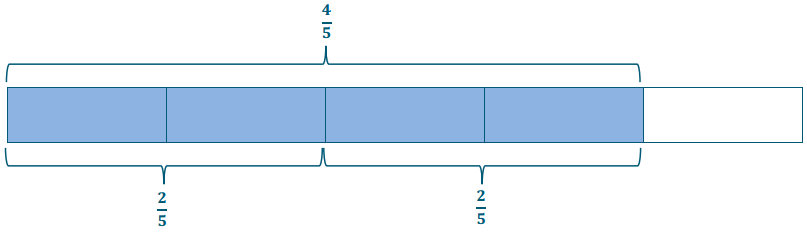
This is really 4 fifths ÷ 2 fifths, which is 2.

Exercise 3.
\(\frac{9}{4} \div \frac{3}{4}\)
Answer:

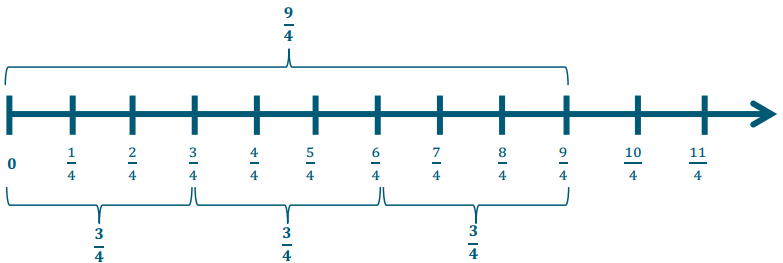
This is really 9 fourths ÷ 3 fourths, which is 3.

Exercise 4.
\(\frac{7}{8} \div \frac{2}{8}\)
Answer:

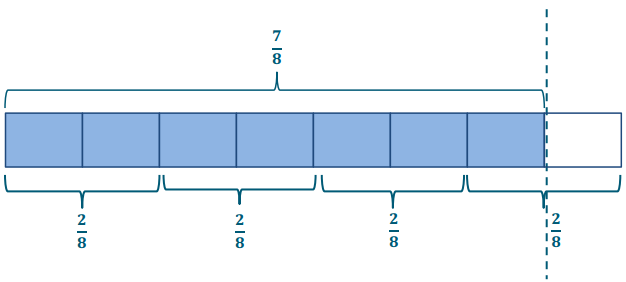
This is really 7 eighths ÷ 2 eighths, which is \(\frac{7}{8}\) or 3\(\frac{1}{2}\)

Exercise 5.
\(\frac{13}{10} \div \frac{2}{10}\)
Answer:

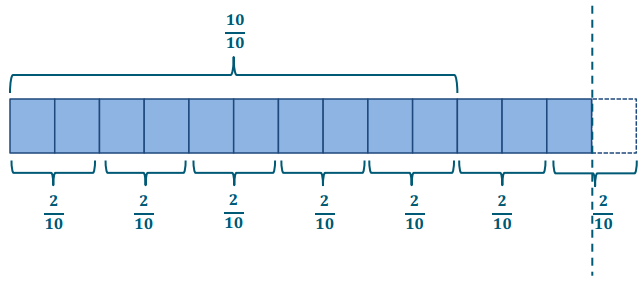
This is really 13 tenths ÷ 2 tenths, which is \(\frac{13}{2}\) or 6\(\frac{1}{2}\)

Exercise 6.
\(\frac{11}{9} \div \frac{3}{9}\)
Answer:

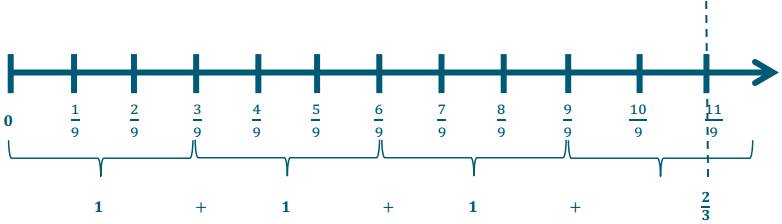
This is really 11 ninths ÷ 3 ninths, which is \(\frac{11}{3}\) or 3\(\frac{2}{3}\).

Eureka Math Grade 6 Module 2 Lesson 3 Problem Set Answer Key

For the following exercises, rewrite the division expression in unit form. Then, find the quotient. Draw a model to support your answer.

Question 1.
\(\frac{4}{5} \div \frac{1}{5}\)
Answer:
4 fifths ÷ 1 fifth = 4

Question 2.
\(\frac{8}{9} \div \frac{4}{9}\)
Answer:
8 ninths ÷ 4 ninths = 2

Question 3.
\(\frac{15}{4} \div \frac{3}{4}\)
Answer:
15 fourths ÷ 3 fourths = 5

Question 4.
\(\frac{13}{5} \div \frac{4}{5}\)
Answer:
13 fifths ÷ 4fifths = ÷=3

Rewrite the expression In unit form, and find the quotient.

Question 5.
\(\frac{10}{3} \div \frac{2}{3}\)
Answer:
10 thirds ÷ 2 thirds = 5

Question 6.
\(\frac{8}{5} \div \frac{3}{5}\)
Answer:
8 fifths ÷ 3 fifths = = 2

Question 7.
\(\frac{12}{7} \div \frac{12}{7}\)
Answer:
12 sevenths ÷ 12 sevenths = 1

Represent the division expression using unit form. Find the quotient. Show all necessary work.

Question 8.
A runner is \(\) mile from the finish line. If she can travel \(\) mile per minute, how long will it take her to finish the race?
Answer:
7 eighths ÷ 3 eighths = \(\frac{7}{3}=2 \frac{1}{3}\)
It will take her 2\(\frac{1}{3}\) minutes to finish the race.

Question 9.
An electrician has 4. 1 meters of wire.
a. How many strips m long can he cut?
Answer:
41 tenths ÷ 7 tenths = \(\frac{41}{7}\) = 5\(\frac{6}{7}\)
He can cut 5 complete strips.

b. How much wire will he have left over?
Answer:
He will have \(\frac{6}{10}\)m left over.

Question 10.
Saeed bought 21\(\frac{1}{2}\) lb. of ground beef. He used \(\frac{1}{4}\) of the beef to make tacos and \(\frac{2}{3}\) of the remainder to make quarter-pound burgers. How many burgers did he make?
Answer:
\(\frac{1}{2}\) of 21\(\frac{1}{2}\) = 10\(\frac{3}{4}\) → 10\(\frac{3}{4}\) Ib. of beef is used for burgers.
43 fourths ÷ 1 fourth = 43
Saeed made 43 burgers.

Question 11.
A baker bought some flour. He used \(\frac{2}{5}\) of the flour to make bread and used the rest to make batches of muffins. If he used 16 lb. of flour making bread and \(\frac{2}{3}\) lb. for each batch of muffins, how many batches of muffins did he make?
Answer:
16 is \(\frac{2}{5}\) group of what size?
2 units = 16
1 unit = 16 ÷ 2 = 8
3 units = 3 × 8 = 24
The baker used 24 ib. of flour for muffins.

24 ÷ \(\frac{2}{3}\)
72 thirds ÷ 2 thirds = 36
The baker made 36 batches of muffins.

Eureka Math Grade 6 Module 2 Lesson 3 Exit Ticket Answer Key

Find the quotient. Draw a model to support your solution.

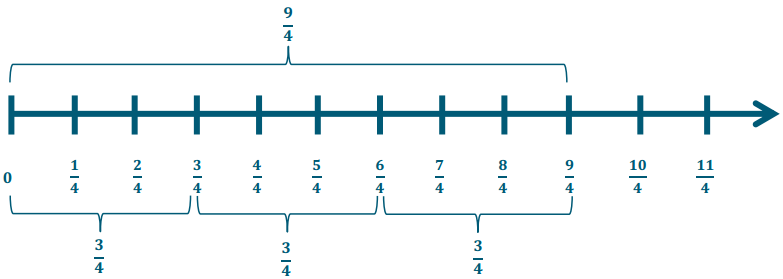
Question 1.
\(\frac{9}{4} \div \frac{3}{4}\)
This is really 9 fourths ÷ 3 fourths, which is 3.
Answer:

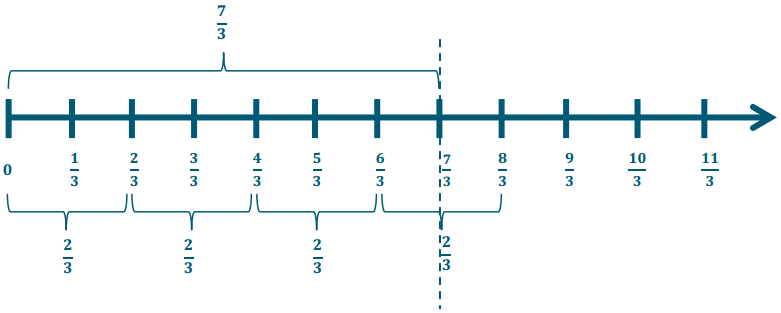
Question 2.
\(\frac{7}{3} \div \frac{2}{3}\)
Answer:
This is really 7 thirds ÷ 2 thirds, which is \(\frac{7}{2}\) or 3\(\frac{1}{2}\).

Eureka Math Grade 6 Module 2 Lesson 3 Opening Exercise Answer Key

Question 1.
Draw a model to represent 12 ÷ 3.
Answer:
There are two interpretations:
Partitive Division

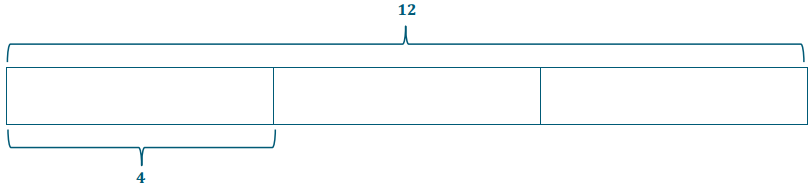
Measurement Division

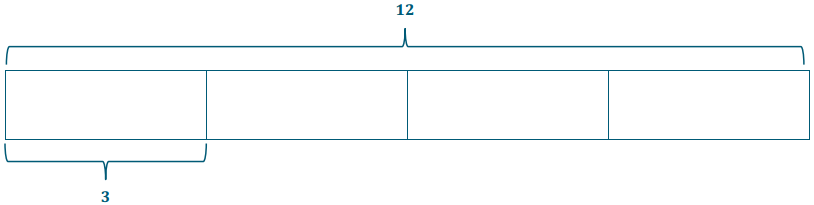
Question 2.
Create a question or word problem that matches your model.
Answer:
Answers will vary.
Sample Solutions for Partitive Division Model:
12 cards are shared with 3 people. How many cards does each person get?
12 is 3 of what number?

Sample Solutions for Measurement Division Model:
12 balls are put in groups of 3. How many groups are made?
How many 3’s are in 12?