Engage NY Eureka Math 6th Grade Module 2 Lesson 6 Answer Key
Eureka Math Grade 6 Module 2 Lesson 6 Example Answer Key
Example 1.
Divide 50 ÷ \(\frac{2}{3}\).
Answer:
Step 1: Decide on an Interpretation.
Today, we use the partitive interpretation and Interpret the divisor, 2 thirds, to be the number of groups. I’m asking myself, “50 is 2 thirds group of what size?”
Step 2: Draw a model.
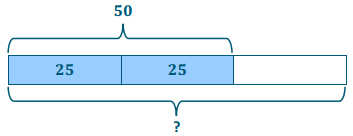
Step 3: Find the answer.
2 units = 50
1 unit = 50 ÷ 2 = 25
3 units = 3 × 25 = 75
Step 4: Choose a unit.
Answers will vary, but dollars will be used throughout the discussion below.
Step 5: Set up a situation based upon the model.
Answers will vary, but there is a story problem provided in the discussion.
Example 2.
Divide \(\frac{1}{2} \div \frac{3}{4}\)
Answer:
Step 1: Decide on an interpretation.
Today, we use the partitive interpretation and Interpret the divisor, 3 fourths, to be the number of groups. I’m asking myself, “1 half is 3 fourths of what number?”
Step 2: Draw a model.
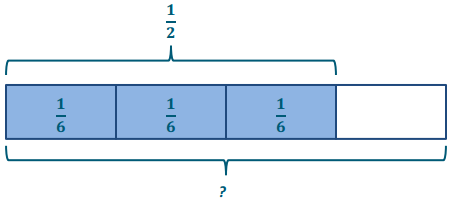
Step 3: Find the answer.
3 units = \(\frac{1}{2}\)
1 unit = \(\frac{1}{2}\) ÷ 3 = \(\frac{1}{3}\) of \(\frac{1}{2}\) = \(\frac{1}{6}\)
4 units = 4 × 1 sixth = 4 sixths = \(\frac{4}{6}\)
Step 4: Choose a unit.
Answers will vary.
Step 5: Set up a situation based upon the model.
Answers will vary.
Eureka Math Grade 6 Module 2 Lesson 6 Exercise Answer Key
Exercise 1.
Using the same dividend and divisor, work with a partner to create your own story problem. You may use the same unit, dollars, but your situation must be unique. You could try another unit, such as miles, If you prefer.
Answer:
Possible story problems:
1. Ronaldo has ridden 50 miles during his bicycle race and is \(\frac{2}{3}\) of the way to the finish line. How long is the race?
2. Samantha used 50 tickets (\(\frac{2}{3}\) of her total) to trade for a kewpie doll at the fair. How many tickets did she start with?
Exercise 2.
Using the same dividend and divisor, work with a partner to create your own story problem. Try a different unit.
Answer:
Possible story problems:
1. Daryl completed 3 fourths of his homework in a half hour. How long does it take Daryl to complete all of his homework?
2. A snail saw food sitting a distance away. After traveling for a half foot, a snail had covered \(\frac{3}{4}\) the distance. How far away was the food?
Eureka Math Grade 6 Module 2 Lesson 6 Problem Set Answer Key
Question 1.
\(\frac{15}{16}\) is 1 sixteenth groups of what size?
Answer:
15 sixteenths ÷ 1 sixteenth = 15. The size of the group is 15.
Question 2.
\(\frac{7}{8}\) teaspoons is \(\frac{1}{4}\) groups of what size?
Answer:
7 eighths ÷ 2 eighths = \(\frac{7}{2}\) = 3\(\frac{1}{2}\). The size of the group is 3\(\frac{1}{2}\).
Question 3.
A 4-cup container of food is \(\frac{2}{3}\) groups of what size?
Answer:
12 thirds ÷ 2 thirds = 6. The size of the group is 6.
Question 4.
Write a partitive division story problem for 6 ÷ \(\frac{3}{4}\).
Answer:
Answers will vary.
Question 5.
Write a partitive division story problem for \(\frac{5}{12}\) ÷ \(\frac{1}{6}\)
Answer:
Answers will vary.
Question 6.
Fill In the blank to complete the equation. Then, find the quotient, and draw a model to support your solution.
a.
![]()
Answer:
\(\frac{1}{4} \div 7=\frac{1}{7} \text { of } \frac{1}{4}=\frac{1}{28}\)
b.
![]()
Answer:
\(\frac{5}{6} \div 4=\frac{1}{4} \text { of } \frac{5}{6}=\frac{5}{24}\)
Question 7.
There is \(\frac{3}{5}\) of a pie left. If 4 friends wanted to share the pie equally, how much would each friend receive?
Answer:
\(\frac{3}{5} \div 4=\frac{3}{5} \times \frac{1}{4}=\frac{3}{20}\)
Each friend would receive \(\frac{3}{20}\) of the pie.
Question 8.
In two hours, Holden completed \(\frac{3}{4}\) of his race. How long will it take Holden to complete the entire race?
Answer:
2 ÷ \(\frac{3}{4}\) = 8 fourths = \(\frac{8}{3}\) = 2\(\frac{2}{3}\)
It will take Holden 2\(\frac{2}{3}\) hews to complete the race.
Question 9.
Sam cleaned \(\frac{1}{3}\) of his house in 50 minutes. How many hours will it take him to clean his entire house?
Answer:
50 minutes = \(\frac{1}{60} \frac{\text { hour }}{\text { minutes }}\) = \(\frac{5}{6}\) hours
\(\frac{5}{6} \div \frac{1}{3}\) = 5 sixths ÷ 2 sixths = \(\frac{5}{2}\) = 2\(\frac{1}{2}\)
It will take Sam 2\(\frac{1}{2}\) hours to clean his entire house.
Question 10.
It took Mario 10 months to beat \(\frac{5}{8}\) of the levels on his new video game. How many years will it take for Mario to beat all the levels?
Answer:
10 months = \(\frac{1}{12} \frac{\text { year }}{\text { month } s}\) = \(\frac{10}{12}\) years = \(\frac{5}{6}\) years
\(\frac{5}{6} \div \frac{5}{8}=\frac{20}{24} \div \frac{15}{24}=\frac{20}{15}=1 \frac{1}{3}\)
Mario will need 1\(\frac{1}{3}\) years to beat all the levels.
Question 11.
A recipe calls for 1\(\frac{1}{2}\) cups of sugar. Marley only has measuring cups that measure \(\frac{1}{4}\) cup. How many times will Marley have to fill the measuring cup?
Answer:
\(1 \frac{1}{2} \div \frac{1}{4}=\frac{3}{2} \div \frac{1}{4}=\frac{6}{4} \div \frac{1}{4}=6\)
Marley will have to use the measuring cup 6 times.
Eureka Math Grade 6 Module 2 Lesson 6 Exit Ticket Answer Key
Question 1.
Write a story problem using the partitive Interpretation of division for the following: 25 ÷ \(\frac{5}{8}\) = 40.
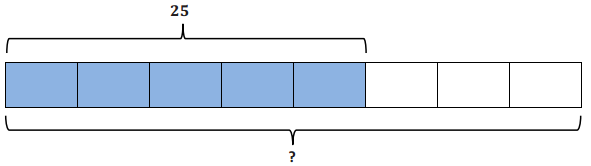
Answer:
Zolanda spent \(\frac{5}{8}\) of her class period, or 25 minutes, taking notes. How long was the class period? (Accept any other reasonable story problem showing 25 ÷ \(\frac{5}{8}\) = 40.)