Engage NY Eureka Math Grade 6 Module 6 Lesson 6 Answer Key
Eureka Math Grade 6 Module 6 Lesson 6 Example Answer Key
Recall that in Lesson 3, Robert, a sixth-grader at Roosevelt Middle School, investigated the number of hours of sleep sixth-grade students get on school nights. Today, he is to make a short report to the class on his investigation. Here is his report.
“I took a survey of twenty-nine sixth-graders, asking them, ‘How many hours of sleep per night do you usually get when you have school the next day?’ The first thing I had to do was to organize the data. I did this by drawing a dot plot. Looking at the dot plot, I would say that a typical amount of sleep is 8 or 9 hours.”
Dot plot of number of hours of sleep

Michelle is Robert’s classmate. She liked his report but has a really different thought about determining the center of the number of hours of sleep. Her idea is to even out the data in order to determine a typical or center value.
Exercises 1 – 6:
Suppose that Michelle asks ten of her classmates for the number of hours they usually sleep when there is school the next day. Suppose they responded (in hours): 8 10 8 8 11 11 9 8 10 7.
Exercise 1.
How do you think Robert would organize this new data? What do you think Robert would say is the center of these ten data points? Why?
Answer:
Robert would use a dot plot to organize his data and would say the center is around 8 hours because it is the most common value.
Exercise 2.
Do you think his value is a good measure to use for the center of Michelle’s data set? Why or why not?
Answer:
Answers will vary. For example, students might say it is a good measure, as most of the values are around 8 hours, or they might say it is not a good measure because half of the values are greater than 8 hours.
The measure of center that Michelle is proposing is called the mean. She finds the total number of hours of sleep for the ten students. That is 90 hours. She has 90 Unifix cubes (Snap cubes). She gives each of the ten students the number of cubes that equals the number of hours of sleep each had reported.
She then asks each of the ten students to connect their cubes in a stack and put their stacks on a table to compare them. She then has them share their cubes with each other until they all have the same number of cubes in their stacks when they are done sharing.
Exercise 3.
Make ten stacks of cubes representing the number of hours of sleep for each of the ten students. Using Michelle’s method, how many cubes are in each of the ten stacks when they are done sharing?
Answer:
There are 9 cubes in each of the 10 stocks.
Exercise 4.
Noting that each cube represents one hour of sleep, interpret your answer to Exercise 3 in terms of number of hours of sleep. What does this number of cubes in each stack represent? What is this value called?
Answer:
If all ten students slept the same number of hours, it would be 9 hours. The 9 cubes for each stack represent the 9 hours of sleep for each student if this was a fair share. This value is called the mean.
Exercise 5.
Suppose that the student who told Michelle he slept 7 hours changes his data value to 8 hours. What does Michelle’s procedure now produce for her center of the new set of data? What did you have to do with that extra cube to make Michelle’s procedure work?
Answer:
The extra cube must be split into 10 equal parts. The mean is now 9\(\frac{1}{10}\).
Exercise 6.
Interpret Michelle’s fair share procedure by developing a mathematical formula that results in finding the fair share value without actually using cubes. Be sure that you can explain clearly how the fair share procedure and the mathematical formula relate to each other.
Answer:
Answers may vary. The fair share procedure is the same as adding all of the data values and dividing by the total number of data values.
Example 2:
Suppose that Robert asked five sixth graders how many pets each had. Their responses were 2, 6, 2, 4, 1. Robert showed the data with cubes as follows:
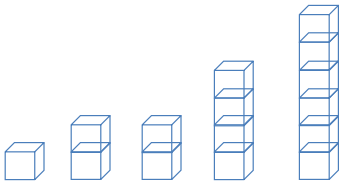
Note that one student has one pet, two students have two pets each, one student has four pets, and one student has six pets. Robert also represented the data set in the following dot plot.

Robert wants to illustrate Michelle’s fair share method by using dot plots. He drew the following dot plot and said that it represents the result of the student with six pets sharing one of her pets with the student who has one pet.

Robert also represented the dot plot above with cubes. His representation is shown below.
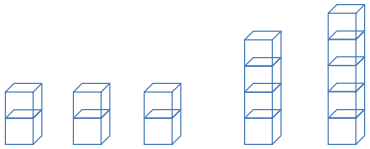
Exercises 7 – 10:
Now, continue distributing the pets based on the following steps.
Exercise 7.
Robert does a fair share step by having the student with five pets share one of her pets with one of the students with two pets.
a. Draw the cubes representation that shows the result of this fair share step.
Answer:
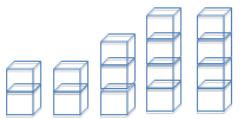
b. Draw the plot that shows the result of this fair share step.
Answer:
![]()
Exercise 8.
Robert does another fair share step by having one of the students who has four pets share one pet with one of the students who has two pets.
a.
Draw the cubes representation that shows the result of this fair share step.
Answer:
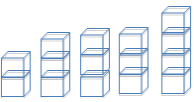
b.
Draw the dot plot that shows the result of this fair share step.
Answer:

Exercise 9.
Robert does a final fair share step by having the student who has four pets share one pet with the student who has
two pets.
a. Draw the cubes representation that shows the resuft of this final fair share step.
Answer:
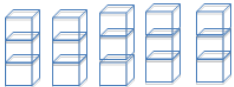
b. Draw the dot plot representation that shows the result of this final fair share step.
Answer:

Exercise 10.
Explain in your own words why the final representations using cubes and a dot plot show that the mean number of pets owned by the five students is 3 pets.
Answer:
The shoring method produces 3 pets for each of the fwe students. The cubes representation shows that after sharing, each student has a fair share of three pets. The dot plot representation should have all of the data points at the same point on the number line, the mean. In this problem, the mean number of pets is 3 for these five students, so there should be five dots above 3 on the horizontal scale.
Eureka Math Grade 6 Module 6 Lesson 6 Problem Set Answer Key
Question 1.
A game was played where ten tennis balls are tossed into a basket from a certain distance. The numbers of successful tosses for six students were 4, 1, 3, 2, 1, 7.
a. Draw a representation of the data using cubes where one cube represents one successful toss of a tennis ball into the basket.
Answer:
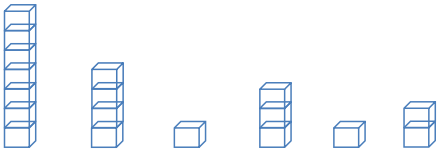
b. Represent the original data set using a dot plot.
Answer:

Question 2.
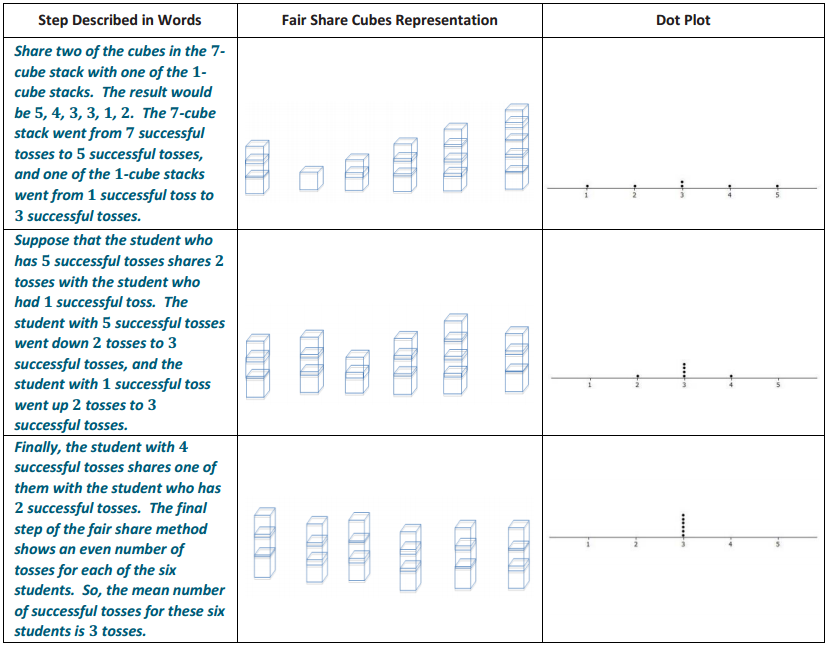
Find the mean number of successful tosses for this data set using the fair share method. For each step, show the cubes representation and the corresponding dot plot. Explain each step in words in the context of the problem. You may move more than one successful toss in a step, but be sure that your explanation is clear. You must show two or more steps.
Answer:
Clearly, there are several ways of getting to the final fair share cubes representation where each of the six stacks contains three cubes. Ideally, students move one cube at a time since, for many students, the leveling is seen more easily in that way. If a student shortcuts the process by moving several cubes at once, that is okay, as long as the graphic representations are correctly done and the explanation is dear. The table below provides one possible representation.
Question 3.
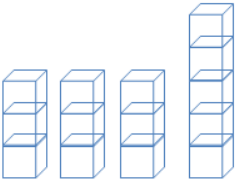
The numbers of pockets in the clothes worn by four students to school today are 4, 1, 3, and 6. Paige produces the following cubes representation as she does the fair share process. Help her decide how to finish the process now that she has stacks of 3, 3, 3, and 5 cubes.
Answer:
It should be dear to students that there are two extra cubes in the stack of five cubes. Those two extra cubes need to be distributed among the four students. That requires that each of the extra cubes needs to be split in half to produce four halves. Each of the four students gets half of a pocket to have a fair shore mean of three and one half pockets.
Question 4.
Suppose that the mean number of chocolate chips in 30 cookies is 14 chocolate chips.
a. Interpret the mean number of chocolate chips in terms of fair share.
Answer:
Answers will vary. 1f each of the 30 cookies were to have the same number of chocolate chips, each would have 14 chocolate chips.
b. Describe the dot plot representation of the fair share mean of 14 chocolate chips in 30 cookies.
Answer:
Answers will vary. There should be 30 different dots on the dot plot, all of them stacked up at 14.
Question 5.
Suppose that the following are lengths (in millimeters) of radish seedlings grown ¡n identical conditions for three days: 12 11 12 14 13 9 13 11 13 10 10 14 16 13 11
a. Find the mean length for these 15 radish seedlings.
Answer:
The mean length is 12\(\frac{2}{15}\) mm.
b. Interpret the value from part (a) in terms of the fair share mean length.
Answer:
If each of the 15 radish seedlings were to have the same length, each would have a length of 12\(\frac{2}{15}\) mm.
Note:
Students should realize what the cubes representation for these data would look like but also realize that it may be a little cumbersome to move cubes around in the fair share process. Ideally, they would set up the initial cubes representation and then use the mathematical approach of summing the lengths to be 182 mm, which by division (distributed evenly to 15 plant) would yield 12\(\frac{2}{15}\) mm as the fair share mean length.
Eureka Math Grade 6 Module 6 Lesson 6 Exit Ticket Answer Key
Question 1.
If a class of 27 students had a mean of 72 on a test, interpret the mean of 72 In the sense of a fair share measure of the center of the test scores.
Answer:
Answers will vary. 72 would be the test score that all 27 students would have if all 27 students had the same score.
Question 2.
Suppose that your school’s soccer team has scored a mean of 2 goals in each of 5 games.
a. Draw a representation using cubes that display that your school’s soccer team has scored a mean of 2 goals in each of 5 games. Let 1 cube stand for 1 goal.
Answer:
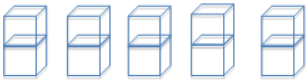
Answers will vary. There should be 10 total cubes that are placed in no more than 5 different stacks. One possibility is the one shown here, where each of the 5 stacks contains 2 cubes. However, any set of stacks where 10 cubes are divided into 5 or fewer (assuming that a “missing stack” represents a game in which 0 goals were scored) stacks would have o fair shore (mean) of 2 and would be an acceptable representation.
b. Draw a dot plot that displays that your school’s soccer team has scored a mean of 2 goals in each of 5 games.
Answer:

Answers will vary. One possibility ¡s the one shown here where all five dots are at 2. However, any dot plot that has exactly 5 dots and for which the sum of the values represented by the dot Is 10 would be an acceptable representation of a data set that has a mean of 2.