Engage NY Eureka Math 7th Grade Module 1 Lesson 4 Answer Key
Eureka Math Grade 7 Module 1 Lesson 4 Example Answer Key
Which Team Will Win the Race?
You have decided to walk in a long-distance race. There are two teams that you can join. Team A walks at a constant rate of 2.5 miles per hour. Team B walks 4 miles the first hour and then 2 miles per hour after that.
Task: Create a table for each team showing the distances that would be walked for times of 1, 2, 3, 4, 5, and 6 hours. Using your tables, answer the questions that follow.
Answer:
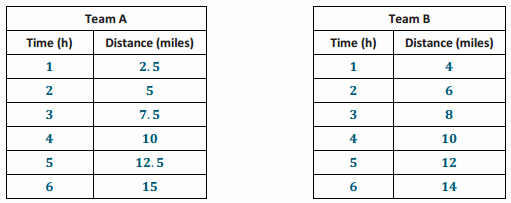
a. For which team is distance proportional to time? Explain your reasoning.
Answer:
Distance is proportional to time for Team A since all the ratios comparing distance to time are equivalent. The value of each ratio is 2.5. Every measure of time can be multiplied by 2.5 to give the corresponding measures of distance.
b. Explain how you know the distance for the other team is not proportional to time.
Answer:
For Team B, the ratios are not equivalent. The values of the ratios are 4, 3, \(\frac{8}{3}\), \(\frac{5}{2}\), \(\frac{12}{5}\), and \(\frac{7}{3}\). Therefore, every measure of time cannot be multiplied by a constant to give each corresponding measure of distance.
c. At what distance in the race would it be better to be on Team B than Team A? Explain.
Answer:
If the race were fewer than 10 miles, Team B is faster because more distance would be covered in less time.
d. If the members on each team walked for 10 hours, how far would each member walk on each team?
Answer:
Team A = 25 miles
Team B = 22 miles
e. Will there always be a winning team, no matter what the length of the course? Why or why not?
Answer:
No, there would be a tie (both teams win) if the race were 10 miles long. It would take each team 4 hours to complete a 10-mile race.
f. If the race were 12 miles long, which team should you choose to be on if you wish to win? Why would you choose this team?
Answer:
I should choose Team A because they would finish in 4.8 hours compared to Team B finishing in 5 hours.
g. How much sooner would you finish on that team compared to the other team?
Answer:
\(\frac{2}{10}\) of an hour or \(\frac{2}{10}\)(60) = 12 minutes
Eureka Math Grade 7 Module 1 Lesson 4 Exercise Answer Key
Bella types at a constant rate of 42 words per minute. Is the number of words she can type proportional to the number of minutes she types? Create a table to determine the relationship.

Answer:

This relationship is proportional because I can multiply the number of minutes by the constant to get the corresponding number of words. The value of the ratio is 42. The constant is also 42.
Question 2.
Mark recently moved to a new state. During the first month, he visited five state parks. Each month after, he visited two more. Complete the table below, and use the results to determine if the number of parks visited is proportional to the number of months
Answer:
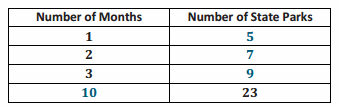
This relationship is not proportional. There is no constant value that can be multiplied by the number of months to get the corresponding number of parks visited.
Question 3.
The table below shows the relationship between the side length of a square and the area. Complete the table. Then, determine if the length of the sides is proportional to the area.
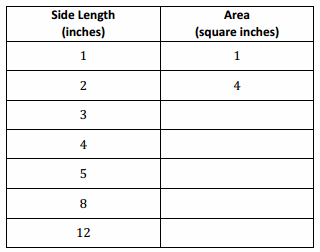
Answer:
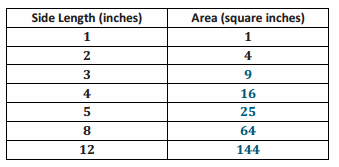
This relationship is not proportional. There is no constant value that can be multiplied by the side length to get the corresponding area.
Eureka Math Grade 7 Module 1 Lesson 4 Exit Ticket Answer Key
The table below shows the relationship between the side lengths of a regular octagon and its perimeter.
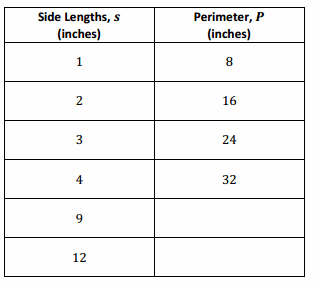
Complete the table.
If Gabby wants to make a regular octagon with a side length of 20 inches using wire, how much wire does she need? Justify your reasoning with an explanation of whether perimeter is proportional to the side length.
Answer:
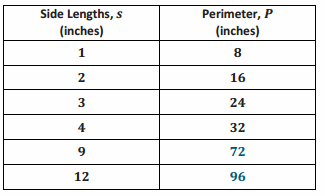
20(8)=160
Gabby would need 160 inches of wire to make a regular octagon with a side length of 20 inches. This table shows that the perimeter is proportional to the side length because the constant is 8, and when all side lengths are multiplied by the constant, the corresponding perimeter is obtained. Since the perimeter is found by adding all 8 side lengths together (or multiplying the length of 1 side by 8), the two numbers must always be proportional.
Eureka Math Grade 7 Module 1 Lesson 4 Problem Set Answer Key
Question 1.
Joseph earns $15 for every lawn he mows. Is the amount of money he earns proportional to the number of lawns he mows? Make a table to help you identify the type of relationship.

Answer:

The table shows that the earnings are proportional to the number of lawns mowed. The value of each ratio is 15. The constant is 15.
Question 2.
At the end of the summer, Caitlin had saved $120 from her summer job. This was her initial deposit into a new savings account at the bank. As the school year starts, Caitlin is going to deposit another $5 each week from her allowance. Is her account balance proportional to the number of weeks of deposits? Use the table below. Explain your reasoning.

Answer:
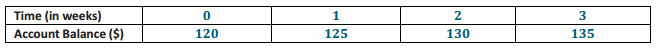
Caitlin’s account balance is not proportional to the number of weeks because there is no constant such that any time in weeks can be multiplied to get the corresponding balance. In addition, the ratio of the balance to the time in weeks is different for each column in the table.
120:0 is not the same as 125:1.
Question 3.
Lucas and Brianna read three books each last month. The table shows the number of pages in each book and the length of time it took to read the entire book.
![]()
a. Which of the tables, if any, represent a proportional relationship?
Answer:
The table shows Lucas’s number of pages read to be proportional to the time because when the constant of 26 is multiplied by each measure of time, it gives the corresponding values for the number of pages read.
b. Both Lucas and Brianna had specific reading goals they needed to accomplish. What different strategies did each person employ in reaching those goals?
Answer:
Lucas read at a constant rate throughout the summer, 26 pages per hour, whereas Brianna’s reading rate was not the same throughout the summer.