Engage NY Eureka Math 7th Grade Module 3 Lesson 7 Answer Key
Eureka Math Grade 7 Module 3 Lesson 7 Example Answer Key
Example
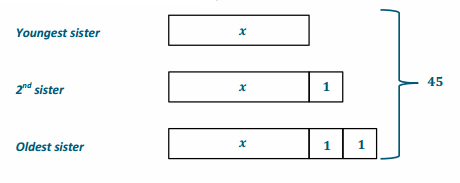
The ages of three sisters are consecutive integers. The sum of their ages is 45. Calculate their ages.
a. Use a tape diagram to find their ages.
Answer:
45-3=42
42÷3=14
Youngest sister: 14 years old
2nd sister: 15 years old
Oldest sister: 16 years old
b. If the youngest sister is x years old, describe the ages of the other two sisters in terms of x, write an expression for the sum of their ages in terms of x, and use that expression to write an equation that can be used to find their ages.
Answer:
Youngest sister: x years old
2nd sister: (x+1) years old
Oldest sister: (x+2) years old
Sum of their ages: x+(x+1)+(x+2)
Equation: x+(x+1)+(x+2)=45
c. Determine if your answer from part (a) is a solution to the equation you wrote in part (b).
Answer:
x+(x+1)+(x+2)=45
14+(14+1)+(14+2)=45
45=45
True
→ Let x be an integer; write an algebraic expression that represents one more than that integer.
→ x+1
→ Write an algebraic expression that represents two more than that integer.
→ x+2
Discuss how the unknown unit in a tape diagram represents the unknown integer, represented by x. Consecutive integers begin with the unknown unit; then, every consecutive integer thereafter increases by 1 unit.
Eureka Math Grade 7 Module 3 Lesson 7 Opening Exercise Answer Key
Your brother is going away to college, so you no longer have to share a bedroom. You decide to redecorate a wall by hanging two new posters on the wall. The wall is 14 feet wide, and each poster is four feet wide. You want to place the posters on the wall so that the distance from the edge of each poster to the nearest edge of the wall is the same as the distance between the posters, as shown in the diagram below. Determine that distance.
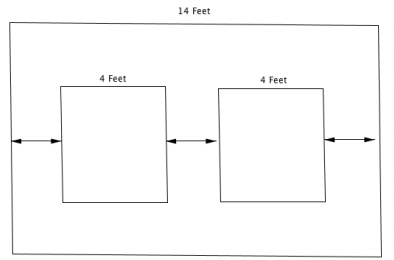
Answer:
14-4-4=6
6÷3=2
The distance is 2 feet
Your parents are redecorating the dining room and want to place two rectangular wall sconce lights that are 25 inches wide along a 10 \(\frac{2}{3}\)-foot wall so that the distance between the lights and the distances from each light to the nearest edge of the wall are all the same. Design the wall and determine the distance.
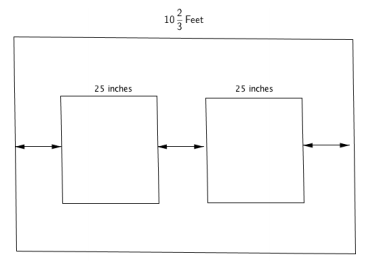
Answer:
25 in. = \(\frac{25}{12}\) ft. = 2 \(\frac{1}{12}\) ft.
(10 \(\frac{2}{3}\) ft. – 2 \(\frac{1}{12}\) ft. – 2 \(\frac{1}{12}\) ft.) ÷ 3
(10 \(\frac{8}{12}\) ft. – 2 \(\frac{1}{12}\) ft. – 2 \(\frac{1}{12}\) ft.) ÷ 3
(6 \(\frac{6}{12}\) ft.) ÷ 3
6 \(\frac{1}{2}\) ft. ÷ 3
\(\frac{13}{2}\) ft. ÷ 3
\(\frac{13}{2}\) ft. × \(\frac{1}{3}\)
\(\frac{13}{6}\) ft.
2 \(\frac{1}{6}\) ft.
OR
10 \(\frac{2}{3}\) ft.
10 ft.×12 \(\frac{in}{ft.}\) + \(\frac{2}{3}\) ft. × 12 \(\frac{in}{ft}\)
120 in. + 8 in.
128 in.
(128 in. – 25 in. – 25 in.) ÷ 3
78 in. ÷ 3
26 in.
Let the distance between a light and the nearest edge of a wall be x ft. Write an expression in terms of x for the total length of the wall. Then, use the expression and the length of the wall given in the problem to write an equation that can be used to find that distance.
Answer:
3x+2 \(\frac{1}{12}\)+2 \(\frac{1}{12}\)
3x+2 \(\frac{1}{12}\)+2 \(\frac{1}{12}\)=10 \(\frac{2}{3}\)
Now write an equation where y stands for the number of inches: Let the distance between a light and the nearest edge of a wall be y inches. Write an expression in terms of y for the total length of the wall. Then, use the expression and the length of the wall to write an equation that can be used to find that distance (in inches).
Answer:
2 \(\frac{1}{12}\) feet =25 inches; therefore, the expression is 3y+25+25.
10 \(\frac{2}{3}\) feet =128 inches; therefore, the equation is 3y+25+25=128.
What value(s) of y makes the second equation true: 24, 25, or 26?
Answer:
y=24
3y+25+25=128
3(24)+25+25=128
72+25+25=128
122=128
False
y=25
3y+25+25=128
3(25)+25+25=128
75+25+25=128
125=128
False
y=26
3y+25+25=128
3(26)+25+25=128
78+25+25=128
128=128
True
Since substituting 26 for y results in a true equation, the distance between the light and the nearest edge of the wall should be 26 in.
Eureka Math Grade 7 Module 3 Lesson 7 Exercise Answer Key
Sophia pays a $19.99 membership fee for an online music store.
a. If she also buys two songs from a new album at a price of $0.99 each, what is the total cost?
Answer:
$21.97
b. If Sophia purchases n songs for $0.99 each, write an expression for the total cost.
Answer:
0.99n+19.99
c. Sophia’s friend has saved $118 but is not sure how many songs she can afford if she buys the membership and some songs. Use the expression in part (b) to write an equation that can be used to determine how many songs Sophia’s friend can buy.
Answer:
0.99n+19.99=118
d. Using the equation written in part (c), can Sophia’s friend buy 101, 100, or 99 songs?
Answer:
n=99
0.99n+19.99=118
0.99(99)+19.99=118
98.01+19.99=118
118=118
True
n=100
0.99n+19.99=118
0.99(100)+19.99=118
99+19.99=118
118.99=118
False
n=101
0.99n+19.99=118
0.99(101)+19.99=118
99.99+19.99=118
119.98=118
False
Eureka Math Grade 7 Module 3 Lesson 7 Problem Set Answer Key
Question 1.
Check whether the given value is a solution to the equation.
a. 4n-3=-2n+9 n=2
Answer:
4(2)-3=-2(2)+9
8-3=-4+9
5=5
True
b. 9m-19=3m+1 m=\(\frac{10}{3}\)
Answer:
9(\(\frac{10}{3}\))-19=3(\(\frac{10}{3}\))+1
\(\frac{90}{3}\)-19=30/3+1
30-19=10+1
11=11
True
c. 3(y+8)=2y-6 y=30
Answer:
3(30+8)=2(30)-6
3(38)=60-6
114=54
False
Question 2.
Tell whether each number is a solution to the problem modeled by the following equation.
Mystery Number: Five more than -8 times a number is 29. What is the number?
Let the mystery number be represented by n.
The equation is 5+(-8)n=29.
a. Is 3 a solution to the equation? Why or why not?
Answer:
No, because 5-24≠29.
b. Is -4 a solution to the equation? Why or why not?
Answer:
No, because 5+32≠29.
c. Is -3 a solution to the equation? Why or why not?
Answer:
Yes, because 5+24=29.
d. What is the mystery number?
Andrew:
-3 because 5 more than -8 times -3 is 29.
Question 3.
The sum of three consecutive integers is 36.
a. Find the smallest integer using a tape diagram.
Answer:
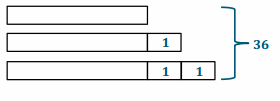
36-3=33
33÷3=11
The smallest integer is 11.
b. Let n represent the smallest integer. Write an equation that can be used to find the smallest integer.
Answer:
Smallest integer: n
2nd integer: (n+1)
3rd integer: (n+2)
Sum of the three consecutive integers: n+(n+1)+(n+2)
Equation: n+(n+1)+(n+2)=36.
c. Determine if each value of n below is a solution to the equation in part (b).
n=12.5
Answer:
No, it is not an integer and does not make a true equation.
n=12
Answer:
No, it does not make a true equation.
n=11
Answer:
Yes, it makes a true equation.
Question 4.
Andrew is trying to create a number puzzle for his younger sister to solve. He challenges his sister to find the mystery number. “When 4 is subtracted from half of a number, the result is 5.” The equation to represent the mystery number is \(\frac{1}{2}\) m-4=5. Andrew’s sister tries to guess the mystery number.
a. Her first guess is 30. Is she correct? Why or why not?
Answer:
No, it does not make a true equation.
\(\frac{1}{2}\) (30)-4=5
15-4=5
11=5
False
b. Her second guess is 2. Is she correct? Why or why not?
Answer:
No, it does not make a true equation.
\(\frac{1}{2}\) (2)-4=5
1-4=5
-3=5
False
c. Her final guess is 4 \(\frac{1}{2}\). Is she correct? Why or why not?
Answer:
No, it does not make a true equation.
\(\frac{1}{2}\) (4 \(\frac{1}{2}\))-4=5
2 \(\frac{1}{4}\)-4=5
-1 \(\frac{3}{4}\)=5
False
Eureka Math Grade 7 Module 3 Lesson 7 Exit Ticket Answer Key
Question 1.
Check whether the given value of x is a solution to the equation. Justify your answer.
a. \(\frac{1}{3}\) (x+4)=20 x=48
Answer:
(\(\frac{1}{3}\) (48+4)=20
\(\frac{1}{3}\) (52)=20
False, 48 is NOT a solution to \(\frac{1}{3}\) (x+4)=20.
17 \(\frac{1}{3}\)=20
b. 3x-1=5x+10 x=-5 \(\frac{1}{2}\)
(3(-5 \(\frac{1}{2}\))-1=5(-5 \(\frac{1}{2}\))+10
–\(\frac{33}{2}\)-1=-\(\frac{55}{2}\)+10
True, -5 \(\frac{1}{2}\) is a solution to 3x-1=5x+10.
–\(\frac{35}{2}\)=-\(\frac{35}{2}\)
Question 2.
The total cost of four pens and seven mechanical pencils is $13.25. The cost of each pencil is 75 cents.
a. Using an arithmetic approach, find the cost of a pen.
Answer:
(13.25-7(0.75))÷4
(13.25-5.25)÷4
8÷4
2
The cost of a pen is $2.
b. Let the cost of a pen be p dollars. Write an expression for the total cost of four pens and seven mechanical pencils in terms of p.
Answer:
4p+7(0.75) or 4p+5.25
c. Write an equation that could be used to find the cost of a pen.
Answer:
4p+7(0.75)=13.25 or 4p+5.25=13.25
d. Determine a value for p for which the equation you wrote in part (b) is true.
Answer:
4p+5.25=13.25
4(2)+5.25=13.25
8+5.25=13.25
True, when p=2, the equation is true.
13.25=13.25
e. Determine a value for p for which the equation you wrote in part (b) is false.
Answer:
Any value other than 2 will make the equation false.