Engage NY Eureka Math 7th Grade Module 3 Lesson 8 Answer Key
Eureka Math Grade 7 Module 3 Lesson 8 Example Answer Key
Example 1.
Julia, Keller, and Israel are volunteer firefighters. On Saturday, the volunteer fire department held its annual coin drop fundraiser at a streetlight. After one hour, Keller had collected $42.50 more than Julia, and Israel had collected $15 less than Keller. The three firefighters collected $125.95 in total. How much did each person collect?
Find the solution using a tape diagram.
Answer:
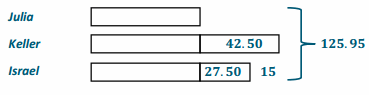
3 units + 42.50+27.50=125.95
3 units + 70=125.95
3 units =55.95
1 unit =18.65
42.50+27.50=70
125.95-70=55.95
55.95÷3=18.65
Julia collected $18.65. Keller collected $61.15. Israel collected $46.15.
What were the operations we used to get our answer?
Answer:
First, we added 42.50 and 27.50 to get 70. Next, we subtracted 70 from 125.95. Finally, we divided 55.95 by 3 to get 18.65.
The amount of money Julia collected is j dollars. Write an expression to represent the amount of money Keller collected in dollars.
Answer:
j+42.50
Using the expressions for Julia and Keller, write an expression to represent the amount of money Israel collected in dollars.
Answer:
j+42.50-15
or
j+27.50
Using the expressions written above, write an equation in terms of j that can be used to find the amount each person collected.
Answer:
j+(j+42.50)+(j+27.50)=125.95
Solve the equation written above to determine the amount of money each person collected, and describe any if-then moves used.
Answer:
j+(j+42.50)+(j+27.50)=125.95
3j+70=125.95 Any order, any grouping
(3j+70)-70=125.95-70 If-then move: Subtract 70 from both sides (to make a 0).
3j+0=55.95 Any grouping, additive inverse
3j=55.95 Additive identity
(\(\frac{1}{3}\))(3j)=(55.95)(\(\frac{1}{3}\)) If-then move: Multiply both sides by \(\frac{1}{3}\) (to make a 1).
(\(\frac{1}{3}\)∙3)j=18.65 Associative property
1∙j=18.65 Multiplicative inverse
j=18.65 Multiplicative identity
If Julia collected $18.65, then Keller collected $18.65+$42.50=$61.15, and Israel collected
$61.15-$15=$46.15.
Example 2.
You are designing a rectangular pet pen for your new baby puppy. You have 30 feet of fence barrier. You decide that you would like the length to be 6\(\frac{1}{3}\) feet longer than the width.
Draw and label a diagram to represent the pet pen. Write expressions to represent the width and length of the pet pen.
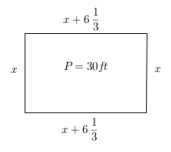
Answer:
Width of the pet pen: x ft.
Then, (x+6 \(\frac{1}{3}\)) ft. represents the length of the pet pen.
Find the dimensions of the pet pen.
Answer:
Arithmetic
(30-6\(\frac{1}{3}\)-6 \(\frac{1}{3}\))÷4
17 \(\frac{1}{3}\)÷4
4 \(\frac{1}{3}\)
The width is 4 \(\frac{1}{3}\) ft.
The length is 4 \(\frac{1}{3}\) ft.+6 \(\frac{1}{3}\) ft.=10 \(\frac{2}{3}\) ft.
Algebraic
x+(x+6 \(\frac{1}{3}\))+x+(x+6 \(\frac{1}{3}\))=30
4x+12 \(\frac{2}{3}\)=30
4x+12 \(\frac{2}{3}\)-12 \(\frac{2}{3}\)=30-12 \(\frac{2}{3}\)
If-then move: Subtract 12 \(\frac{2}{3}\) from both sides.
4x=17 \(\frac{1}{3}\)
(\(\frac{1}{4}\))(4x)=(17 \(\frac{1}{3}\))(\(\frac{1}{4}\))
If-then move: Multiply both sides by \(\frac{1}{4}\)
x=4 \(\frac{1}{3}\)
If the perimeter of the pet pen is 30 ft. and the length of the pet pen is 6 \(\frac{1}{3}\) ft. longer than the width, then the width would be 4 \(\frac{1}{3}\) ft., and the length would be 4 \(\frac{1}{3}\) ft.+6 \(\frac{1}{3}\) ft.=10 \(\frac{2}{3}\) ft.
Example 3.
Nancy’s morning routine involves getting dressed, eating breakfast, making her bed, and driving to work. Nancy spends \(\frac{1}{3}\) of the total time in the morning getting dressed, 10 minutes eating breakfast, 5 minutes making her bed, and the remaining time driving to work. If Nancy spends 35 \(\frac{1}{2}\) minutes getting dressed, eating breakfast, and making her bed, how long is her drive to work?
Write and solve this problem using an equation. Identify the if-then moves used when solving the equation.
Answer:
Total time of routine: x minutes
\(\frac{1}{3}\) x+10+5=35 \(\frac{1}{2}\)
\(\frac{1}{3}\) x+15=35 \(\frac{1}{2}\)
\(\frac{1}{3}\) x+15-15=35 \(\frac{1}{2}\)-15
If-then move: Subtract 15 from both sides.
\(\frac{1}{3}\) x+0=20 \(\frac{1}{2}\)
3(\(\frac{1}{3}\) x)=3(20 \(\frac{1}{2}\))
If-then move: Multiply both sides by 3.
x=61 \(\frac{1}{2}\)
If-then move: Subtract 15 from both sides.
61 \(\frac{1}{2}\)-35 \(\frac{1}{2}\)=26
It takes Nancy 26 minutes to drive to work.
Is your answer reasonable? Explain.
Answer:
Yes, the answer is reasonable because some of the morning activities take 35 \(\frac{1}{2}\) minutes, so the total amount of time for everything will be more than 35 \(\frac{1}{2}\) minutes. Also, when checking the total time for all of the morning routine, the total sum is equal to total time found. However, to find the time for driving to work, a specific activity in the morning, it is necessary to find the difference from the total time and all the other activities.
Example 4.
The total number of participants who went on the seventh-grade field trip to the Natural Science Museum consisted of all of the seventh-grade students and 7 adult chaperones. Two-thirds of the total participants rode a large bus, and the rest rode a smaller bus. If 54 students rode the large bus, how many students went on the field trip?
Answer:
Arithmetic Approach:
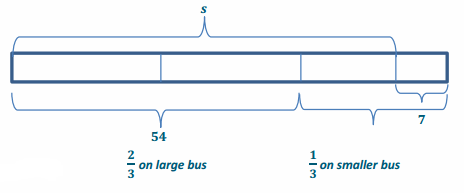
Total on both buses: (54÷2)×3=81
Total number of students: 81-7=74; 74 students went on the field trip.
Algebraic Approach: Challenge students to build the equation and solve it on their own first. Then, go through the steps with them, pointing out how we are “making zeros” and “making ones.” Point out that, in this problem, it is advantageous to make a 1 first. (This example is an equation of the form p(x+q)=r.)
Number of students: s
Total number of participants: s+7
\(\frac{2}{3}\) (s+7)=54
\(\frac{3}{2}\) (\(\frac{2}{3}\) (s+7))=\(\frac{3}{2}\) (54)
If-then move: Multiply both sides by \(\frac{3}{2}\) (to make a 1).
(\(\frac{3}{2}\)∙\(\frac{2}{3}\))(s+7)=81
If-then move: Subtract 7 from both sides (to make a 0).
1(s+7)=81
s+7=81
(s+7)-7=81-7
s+0=74
s=74
74 students went on the field trip.
Eureka Math Grade 7 Module 3 Lesson 8 Opening Exercise Answer Key
Recall and summarize the if-then moves.
Answer:
If a number is added or subtracted to both sides of a true equation, then the resulting equation is also true:
If a=b, then a+c=b+c.
If a=b, then a-c=b-c.
If a number is multiplied or divided to each side of a true equation, then the resulting equation is also true:
If a=b, then ac=bc.
If a=b and c≠0, then a÷c=b÷c.
Write 3+5=8 in as many true equations as you can using the if-then moves. Identify which if-then move you used.
Answer:
Answers will vary, but some examples are as follows:
If 3+5=8, then 3+5+4=8+4. Add 4 to both sides.
If 3+5=8, then 3+5-4=8-4. Subtract 4 from both sides.
If 3+5=8, then 4(3+5)=4(8). Multiply both sides by 4.
If 3+5=8, then (3+5)÷4=8÷4. Divide both sides by 4.
Eureka Math Grade 7 Module 3 Lesson 8 Problem Set Answer Key
Write and solve an equation for each problem.
Question 1.
The perimeter of a rectangle is 30 inches. If its length is three times its width, find the dimensions.
Answer:
The width of the rectangle: w inches
The length of the rectangle: 3w inches
Perimeter=2(length+width)
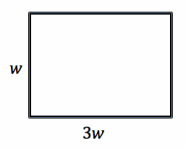
2(w+3w)=30
2(4w)=30
8w=30
(\(\frac{1}{8}\))(8w)=(\(\frac{1}{8}\))(30)
w=3 \(\frac{3}{4}\)
OR
2(w+3w)=30
(w+3w)=15
4w=15
w=3 \(\frac{3}{4}\)
The width is 3 \(\frac{3}{4}\) inches.
The length is (3)(3\(\frac{3}{4}\) in.)=(3)(\(\frac{15}{4}\) in.)=11 \(\frac{1}{4}\) in.
Question 2.
A cell phone company has a basic monthly plan of $40 plus $0.45 for any minutes used over 700. Before receiving his statement, John saw he was charged a total of $48.10. Write and solve an equation to determine how many minutes he must have used during the month. Write an equation without decimals.
Answer:
The number of minutes over 700: m minutes
40+0.45m=48.10
0.45m+40-40=48.10-40
0.45m=8.10
(\(\frac{1}{0.45}\))(0.45m)=8.10(\(\frac{1}{0.45}\))
m=18
4000+45m=4810
45m+4000-4000=4810-4000
45m=810
(\(\frac{1}{45}\))(45m)=810(\(\frac{1}{45}\))
m=18
John used 18 minutes over 700 for the month. He used a total of 718 minutes.
Question 3.
A volleyball coach plans her daily practices to include 10 minutes of stretching, \(\frac{2}{3}\) of the entire practice scrimmaging, and the remaining practice time working on drills of specific skills. On Wednesday, the coach planned 100 minutes of stretching and scrimmaging. How long, in hours, is the entire practice?
Answer:
The duration of the entire practice: x hours
\(\frac{2}{3}\) x+\(\frac{10}{60}\)=\(\frac{100}{60}\)
\(\frac{2}{3}\) x+\(\frac{1}{6}\)=\(\frac{5}{3}\)
\(\frac{2}{3}\) x+\(\frac{1}{6}\)–\(\frac{1}{6}\)=\(\frac{5}{3}\)–\(\frac{1}{6}\)
\(\frac{2}{3}\) x=\(\frac{9}{6}\)
(\(\frac{3}{2}\))(\(\frac{2}{3}\) x)=\(\frac{3}{2}\) (\(\frac{9}{6}\))
x=\(\frac{27}{12}\)=2 \(\frac{1}{4}\)
The entire practice is a length of 2\(\frac{1}{4}\) hours, or 2.25 hours.
Question 4.
The sum of two consecutive even numbers is 54. Find the numbers.
Answer:
First consecutive even integer: x
Second consecutive even integer: x+2
x+(x+2)=54
2x+2=54
2x+2-2=54-2
2x+0=52
(\(\frac{1}{2}\))(2x)=(\(\frac{1}{2}\))(52)
x=26
The consecutive even integers are 26 and 28.
Question 5.
Justin has $7.50 more than Eva, and Emma has $12 less than Justin. Together, they have a total of $63.00. How much money does each person have?
Answer:
The amount of money Eva has: x dollars
The amount of money Justin has: (x+7.50) dollars
The amount of money Emma has: ((x+7.50)-12) dollars, or (x-4.50) dollars
x+(x+7.50)+(x-4.50)=63
3x+3=63
3x+3-3=63-3
3x+0=60
(\(\frac{1}{3}\))3x=(\(\frac{1}{3}\))60
x=20
If the total amount of money all three people have is $63, then Eva has $20, Justin has $27.50, and Emma has $15.50.
Question 6.
Barry’s mountain bike weighs 6 pounds more than Andy’s. If their bikes weigh 42 pounds altogether, how much does Barry’s bike weigh? Identify the if-then moves in your solution.
Answer:
If we let a represent the weight in pounds of Andy’s bike, then a+6 represents the weight in pounds of Barry’s bike.
a+(a+6)=42
(a+a)+6=42
2a+6=42
2a+6-6=42-6
If 2a+6=42, then 2a+6-6=42-6.
2a+0=36
2a=36
\(\frac{1}{2}\)∙2a=\(\frac{1}{2}\)∙36
If 2a = 36, then \(\frac{1}{2}\)∙2a = \(\frac{1}{2}\)∙36.
1∙a=18
a=18
Barry’s Bike: a+6
(18)+6=24
Barry’s bike weighs 24 pounds.
Question 7.
Trevor and Marissa together have 26 T-shirts to sell. If Marissa has 6 fewer T-shirts than Trevor, find how many T-shirts Trevor has. Identify the if-then moves in your solution.
Answer:
Let t represent the number of T-shirts that Trevor has, and let t-6 represent the number of T-shirts that Marissa has.
t+(t-6)=26
(t+t)+(-6)=26
2t+(-6)=26
2t+(-6)+6=26+6
If-then move: Addition property of equality
2t+0=32
2t=32
\(\frac{1}{2}\)∙2t=\(\frac{1}{2}\)∙32
If-then move: Multiplication property of equality
1∙t=16
t=16
Trevor has 16 T-shirts to sell, and Marissa has 10 T-shirts to sell.
Question 8.
A number is 1\(\frac{1}{7}\) of another number. The difference of the numbers is 18. (Assume that you are subtracting the smaller number from the larger number.) Find the numbers.
Answer:
If we let n represent a number, then 1\(\frac{1}{7}\) n represents the other number.
n-(1\(\frac{1}{7}\) n)=18
7\(\frac{1}{7}\) n-1\(\frac{1}{7}\) n=18
6\(\frac{1}{7}\) n=18
\(\frac{7}{6}\)∙6\(\frac{1}{7}\) n=\(\frac{7}{6}\)∙18
1n=7∙3
n=21
The numbers are 21 and 3.
Question 9.
A number is 6 greater than \(\frac{1}{2}\) another number. If the sum of the numbers is 21, find the numbers.
Answer:
If we let n represent a number, then \(\frac{1}{2}\) n+6 represents the first number.
n+(\(\frac{1}{2}\) n+6)=21
(n+\(\frac{1}{2}\) n)+6=21
(\(\frac{2}{2}\) n+\(\frac{1}{2}\) n)+6=21
\(\frac{3}{2}\) n+6=21
\(\frac{3}{2}\) n+6-6=21-6
\(\frac{3}{2}\) n+0=15
\(\frac{3}{2}\) n=15
\(\frac{2}{3}\)∙\(\frac{3}{2}\) n=\(\frac{2}{3}\)∙15
1n=2∙5
n=10
Since the numbers sum to 21, they are 10 and 11.
Question 10.
Kevin is currently twice as old as his brother. If Kevin was 8 years old 2 years ago, how old is Kevin’s brother now?
Answer:
If we let b represent Kevin’s brother’s age in years, then Kevin’s age in years is 2b.
2b-2=8
2b-2+2=8+2
2b=10
(\(\frac{1}{2}\))(2b)=(\(\frac{1}{2}\))(10)
b=5
Kevin’s brother is currently 5 years old.
Question 11.
The sum of two consecutive odd numbers is 156. What are the numbers?
Answer:
If we let n represent one odd number, then n+2 represents the next consecutive odd number.
n+(n+2)=156
2n+2-2=156-2
2n=154
(\(\frac{1}{2}\))(2n)=(\(\frac{1}{2}\))(154)
n=77
The two numbers are 77 and 79.
Question 12.
If n represents an odd integer, write expressions in terms of n that represent the next three consecutive odd integers. If the four consecutive odd integers have a sum of 56, find the numbers.
Answer:
If we let n represent an odd integer, then n+2, n+4, and n+6 represent the next three consecutive odd integers.
n+(n+2)+(n+4)+(n+6)=56
4n+12=56
4n+12-12=56-12
4n=44
n=11
The numbers are 11, 13, 15, and 17.
Question 13.
The cost of admission to a history museum is $3.25 per person over the age of 3; kids 3 and under get in for free. If the total cost of admission for the Warrick family, including their two 6-month old twins, is $19.50, find how many family members are over 3 years old.
Answer:
If we let w represent the number of Warrick family members, then w-2 represents the number of family members over the age of 3 years.
3.25(w-2)=19.5
3.25w-6.5=19.5
3.25w-6.5+6.5=19.5+6.5
3.25w=26
w=8
w-2=6
There are 6 members of the Warrick family over the age of 3 years.
Question 14.
Six times the sum of three consecutive odd integers is -18. Find the integers.
Answer:
If we let n represent the first odd integer, then n+2 and n+4 represent the next two consecutive odd integers.
6(n+(n+2)+(n+4))=-18
6(3n+6)=-18
18n+36=-18
18n+36-36=-18-36
18n=-54
n=-3
n+2=-1
n+4=1
The integers are -3, -1, and 1.
Question 15.
I am thinking of a number. If you multiply my number by 4, add -4 to the product, and then take \(\frac{1}{3}\) of the sum, the result is -6. Find my number.
Answer:
Let n represent the given number.
\(\frac{1}{3}\) (4n+(-4))=-6
\(\frac{4}{3}\) n-\(\frac{4}{3}\)=-6
\(\frac{4}{3}\) n-\(\frac{4}{3}\)+\(\frac{4}{3}\)=-6+\(\frac{4}{3}\)
\(\frac{4}{3}\) n=\(\frac{-14}{3}\)
n=-3 \(\frac{1}{2}\)
Question 16.
A vending machine has twice as many quarters in it as dollar bills. If the quarters and dollar bills have a combined value of $96.00, how many quarters are in the machine?
Answer:
If we let d represent the number of dollar bills in the machine, then 2d represents the number of quarters in the machine.
2d∙(\(\frac{1}{4}\))+1d∙(1)=96
\(\frac{1}{2}\) d+1d=96
1 \(\frac{1}{2}\) d=96
\(\frac{3}{2}\) d=96
\(\frac{2}{3}\) (\(\frac{3}{2}\) d)=\(\frac{2}{3}\) (96)
d=64
2d=128
There are 128 quarters in the machine.
Eureka Math Grade 7 Module 3 Lesson 8 Exit Ticket Answer Key
Mrs. Canale’s class is selling frozen pizzas to earn money for a field trip. For every pizza sold, the class makes $5.35. They have already earned $182.90, but they need $750. How many more pizzas must they sell to earn $750? Solve this problem first by using an arithmetic approach, then by using an algebraic approach. Compare the calculations you made using each approach.
Answer:
Arithmetic Approach:
Amount of money needed: 750-182.90=567.10
Number of pizzas needed: 567.10÷5.35=106
If the class wants to earn a total of $750, then they must sell 106 more pizzas.
Algebraic Approach:
Let x represent the number of additional pizzas they need to sell.
5.35x+182.90=750
5.35x+182.90-182.90=750-182.90
5.35x+0=567.10
(\(\frac{1}{5.35}\))(5.35x)=(\(\frac{1}{5.35}\))(567.10)
x=106
OR
5.35x+182.90=750
100(5.35x+182.90)=100(750)
535x+18290=75000
535x+18290-18290=75000-18290
(\(\frac{1}{5.35}\))(535x)=(\(\frac{1}{5.35}\))(56710)
x=106
If the class wants to earn $750, then they must sell 106 more pizzas.
Both approaches subtract 182.90 from 750 to get 567.10. Dividing by 5.35 is the same as multiplying by \(\frac{1}{5.35}\). Both result in 106 more pizzas that the class needs to sell.