Engage NY Eureka Math 7th Grade Module 5 Lesson 8 Answer Key
Eureka Math Grade 7 Module 5 Lesson 8 Example Answer Key
Coins were discussed in previous lessons of this module. What is special about a coin? In most cases, a coin has two different sides: a head side (heads) and a tail side (tails). The sample space for tossing a coin is {heads, tails}. If each outcome has an equal chance of occurring when the coin is tossed, then the probability of getting heads is \(\frac{1}{2}\), or 0.5. The probability of getting tails is also 0.5. Note that the sum of these probabilities is 1.
The probabilities formed using the sample space and what we know about coins are called the theoretical probabilities. Using observed relative frequencies is another method to estimate the probabilities of heads or tails. A relative frequency is the proportion derived from the number of the observed outcomes of an event divided by the total number of outcomes. Recall from earlier lessons that a relative frequency can be expressed as a fraction, a decimal, or a percent. Is the estimate of a probability from this method close to the theoretical probability? The following example investigates how relative frequencies can be used to estimate probabilities.
Beth tosses a coin 10 times and records her results. Here are the results from the 10 tosses:

The total number of heads divided by the total number of tosses is the relative frequency of heads. It is the proportion of the time that heads occurred on these tosses. The total number of tails divided by the total number of tosses is the relative frequency of tails.
a. Beth started to complete the following table as a way to investigate the relative frequencies. For each outcome, the total number of tosses increased. The total number of heads or tails observed so far depends on the outcome of the current toss. Complete this table for the 10 tosses recorded in the previous table.
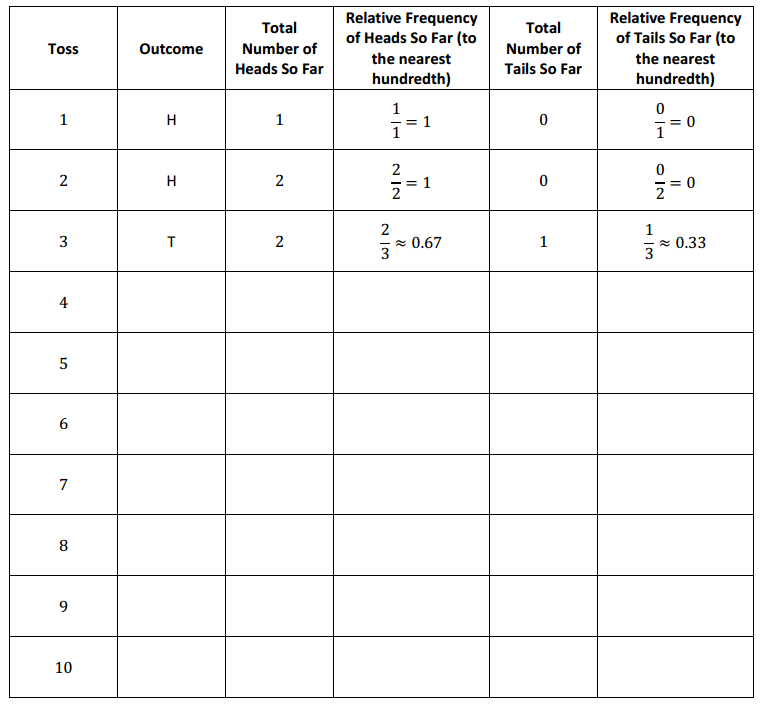
b. What is the sum of the relative frequency of heads and the relative frequency of tails for each row of the table?
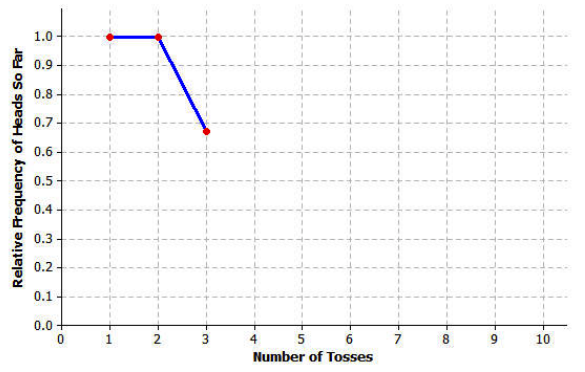
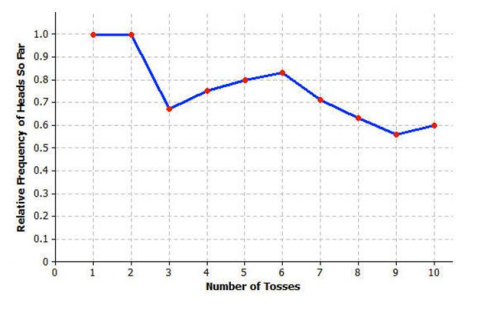
c. Beth’s results can also be displayed using a graph. Use the values of the relative frequency of heads so far from the table in part (a) to complete the graph below.
d. Beth continued tossing the coin and recording the results for a total of 40 tosses. Here are the results of the next 30 tosses:
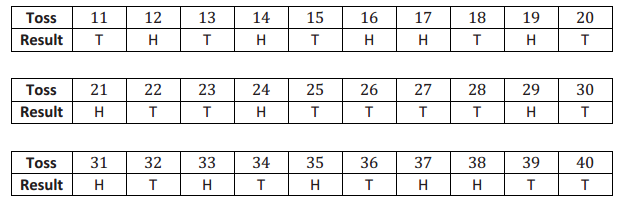
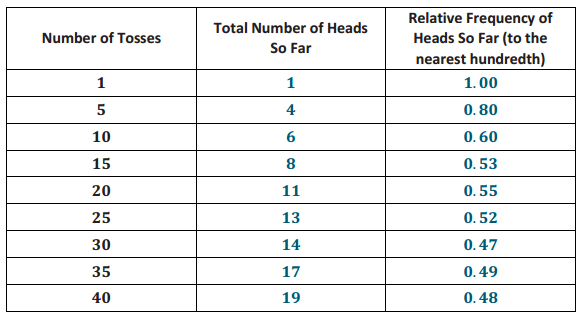
As the number of tosses increases, the relative frequency of heads changes. Complete the following table for the 40 coin tosses:
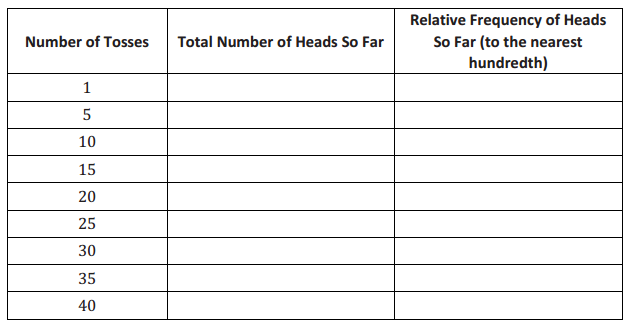
e. Use the relative frequency of heads so far from the table in part (d) to complete the graph below for the total number of tosses of 1, 5, 10, 15, 20, 25, 30, 35, and 40.
f. What do you notice about the changes in the relative frequency of the number of heads so far as the number of tosses increases?
g. If you tossed the coin 100 times, what do you think the relative frequency of heads would be? Explain your answer.
h. Based on the graph and the relative frequencies, what would you estimate the probability of getting heads to be? Explain your answer.
i. How close is your estimate in part (h) to the theoretical probability of 0.5? Would the estimate of this probability have been as good if Beth had only tossed the coin a few times instead of 40?
The value you gave in part (h) is an estimate of the theoretical probability and is called an experimental or estimated probability.
Answer:
a.
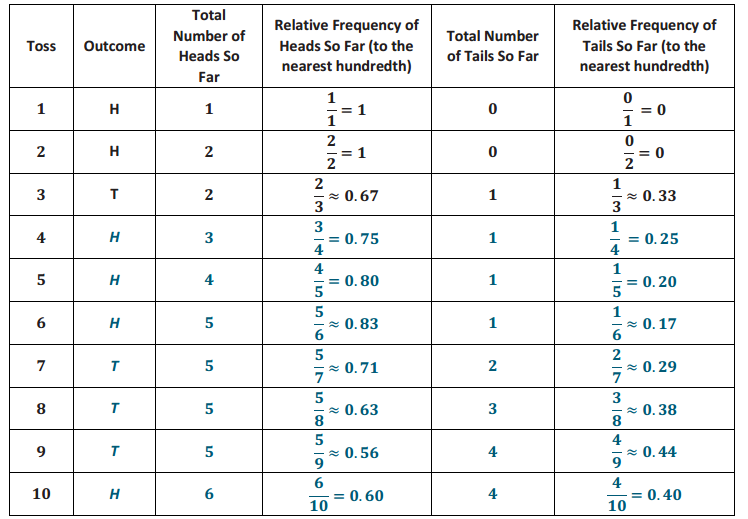
b. The sum of the relative frequency of heads and the relative frequency of tails for each row is 1.00.
c.
d.
e.
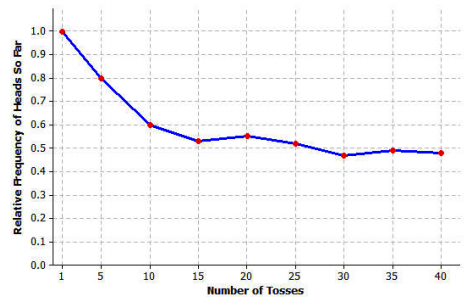
f. The relative frequencies seem to change less as the number of tosses increases. The line drawn to connect the relative frequencies seems to be leveling off.
g. Answers will vary. Anticipate most students will indicate 50 heads result in 100 tosses, for a relative frequency of 0.50. This is a good time to indicate that the value of 0.50 is where the graph of the relative frequencies seems to be approaching. However, the relative frequencies will vary. For example, if the relative frequency for 100 tosses was 0.50 (and it could be), what would the relative frequency for 101 tosses be? Point out to students that no matter the outcome on the 101st toss, the relative frequency of heads would not be exactly 0.50.
h. Answers will vary. Anticipate that students will estimate the probability to be 0.50, as that is what they determined in the opening discussion, and that is the value that the relative frequencies appear to be approaching. Some students may estimate the probability as 0.48, as that was the last relative frequency obtained after 40 tosses. That estimate is also a good estimate of the probability.
i. In the beginning, the relative frequencies jump around. The estimated probabilities and the theoretical probabilities should be nearly the same as the number of observations increases. The estimated probabilities would likely not be as good after just a few coin tosses.
Eureka Math Grade 7 Module 5 Lesson 8 Exercise Answer Key
Exercises 1–8
Beth received nine more pennies. She securely taped them together to form a small stack. The top penny of her stack showed heads, and the bottom penny showed tails. If Beth tosses the stack, what outcomes could she observe?
Answer:
She could observe heads, tails, and on the side.
Exercise 1.
Beth wanted to determine the probability of getting heads when she tosses the stack. Do you think this probability is the same as the probability of getting heads with just one coin? Explain your answer.
Answer:
The outcomes when tossing this stack would be {heads, tails, side}. This changes the probability of getting heads, as there are three outcomes.
Exercise 2.
Make a sturdy stack of 10 pennies in which one end of the stack has a penny showing heads and the other end tails. Make sure the pennies are taped securely, or you may have a mess when you toss the stack. Toss the stack to observe possible outcomes. What is the sample space for tossing a stack of 10 pennies taped together? Do you think the probability of each outcome of the sample space is equal? Explain your answer.
Answer:
The sample space is {heads, tails, side}. A couple of tosses should clearly indicate to students that the stack often lands on its side. As a result, the probabilities of heads, tails, and on the side do not appear to be the same.
Exercise 3.
Record the results of 10 tosses. Complete the following table of the relative frequencies of heads for your 10 tosses:
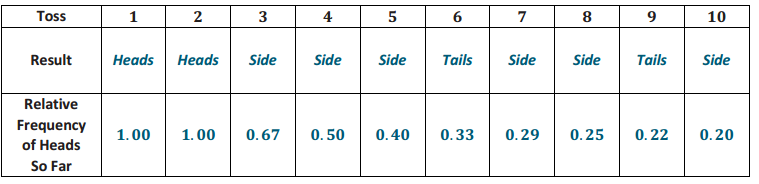
Answer:
Answers will vary; the results of an actual toss are shown below.
Exercise 4.
Based on the value of the relative frequencies of heads so far, what would you estimate the probability of getting heads to be?
Answer:
If students had a sample similar to the above, they would estimate the probability of tossing a heads as 0.20 (or something close to that last relative frequency).
Exercise 5.
Toss the stack of 10 pennies another 20 times. Complete the following table:
Answer:
Answers will vary; student data will be different.

Exercise 6.
Summarize the relative frequency of heads so far by completing the following table:
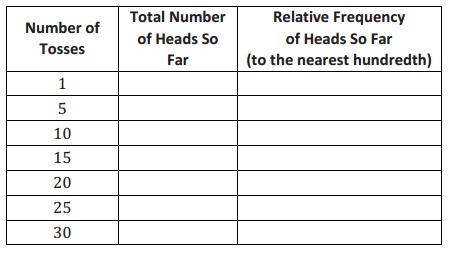
Answer:
A sample table is provided using data from Exercises 3 and 5.
Exercise 7.
Based on the relative frequencies for the 30 tosses, what is your estimate of the probability of getting heads? Can you compare this estimate to a theoretical probability like you did in the first example? Explain your answer.
Answer:
Answers will vary. Students are anticipated to indicate an estimated probability equal or close to the last value in the relative frequency column. For this example, that would be 0.27. An estimate of 0.25 for this sample would have also been a good estimate. Students would indicate that they could not compare this to a theoretical probability because the theoretical probability is not known for this example. Allow for a range of estimated probabilities. Factors that might affect the results for the long-run frequencies include how much tape is used to create the stack and how sturdy the stack is. Discussing these points with students is a good summary of this lesson.
Exercise 8.
Create another stack of pennies. Consider creating a stack using 5 pennies, 15 pennies, or 20 pennies taped together in the same way you taped the pennies to form a stack of 10 pennies. Again, make sure the pennies are taped securely, or you might have a mess!
Toss the stack you made 30 times. Record the outcome for each toss:
Answer:
The Problem Set involves another example of obtaining results from a stack of pennies. Suggestions include stacks of 5, 15, and 20 (or a chosen number). The Problem Set includes questions based on the results from tossing one of these stacks. Provide students in small groups one of these stacks. Each group should collect data for 30 tosses to use for the Problem Set.
Eureka Math Grade 7 Module 5 Lesson 8 Problem Set Answer Key
Question 1.
If you created a stack of 15 pennies taped together, do you think the probability of getting a heads on a toss of the stack would be different than for a stack of 10 pennies? Explain your answer.
Answer:
The estimated probability of getting a heads for a stack of 15 pennies would be different than for a stack of 10 pennies. A few tosses indicate that it is very unlikely that the outcome of heads or tails would result, as the stack almost always lands on its side. (The possibility of a heads or a tails is noted, but it has a small probability of being observed.)
Question 2.
If you created a stack of 20 pennies taped together, what do you think the probability of getting a heads on a toss of the stack would be? Explain your answer.
Answer:
The estimated probability of getting a heads for a stack of 20 pennies is very small. The toss of a stack of this number of pennies almost always lands on its side.
Question 3.
Based on your work in this lesson, complete the following table of the relative frequencies of heads for the stack you created:

Answer:
Answers will vary based on the outcomes of tossing the stack. Anticipate results of 0 for a stack of 20 pennies. Samples involving 15 pennies have a very small probability of showing heads.
Question 4.
What is your estimate of the probability that your stack of pennies will land heads up when tossed? Explain your answer.
Answer:
Answers will vary based on the relative frequencies.
Question 5.
Is there a theoretical probability you could use to compare to the estimated probability? Explain your answer.
Answer:
There is no theoretical probability that could be calculated to compare to the estimated probability.
Eureka Math Grade 7 Module 5 Lesson 8 Exit Ticket Answer Key
Question 1.
Which of the following graphs would not represent the relative frequencies of heads when tossing 1 penny? Explain your answer.
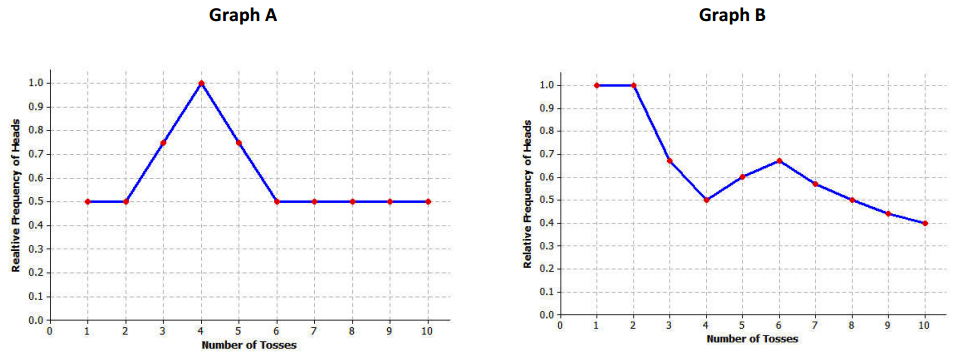
Answer:
Graph A would not represent a possible graph of the relative frequencies. The first problem is the way Graph A starts. After the first toss, the probability would either be a 0 or a 1. Also, it seems to settle exactly to the theoretical probability without showing the slight changes from toss to toss.
Question 2.
Jerry indicated that after tossing a penny 30 times, the relative frequency of heads was 0.47 (to the nearest hundredth). He indicated that after 31 times, the relative frequency of heads was 0.55. Are Jerry’s summaries correct? Why or why not?
Answer:
Jerry’s summaries have errors. If he tossed the penny 30 times and the relative frequency of heads was 0.47, then he had 14 heads. If his next toss was heads, then the relative frequency would be \(\frac{15}{31}\), or 0.48 (to the nearest hundredth). If his next toss was tails, then the relative frequency would be \(\frac{14}{31}\), or 0.45 (to the nearest hundredth).
Question 3.
Jerry observed 5 heads in 100 tosses of his coin. Do you think this was a fair coin? Why or why not?
Answer:
Students should indicate Jerry’s coin is probably not a fair coin. The relative frequency of heads for a rather large number of tosses should be close to the theoretical probability. For this problem, the relative frequency of 0.05 is quite different from 0.5 and probably indicates that the coin is not fair.