Engage NY Eureka Math 7th Grade Module 6 Lesson 27 Answer Key
Eureka Math Grade 7 Module 6 Lesson 27 Example Answer Key
Example 1.
A swimming pool holds 10,000 ft3 of water when filled. Jon and Anne want to fill the pool with a garden hose. The garden hose can fill a five – gallon bucket in 30 seconds. If each cubic foot is about 7.5 gallons, find the flow rate of the garden hose in gallons per minute and in cubic feet per minute. About how long will it take to fill the pool with a garden hose? If the hose is turned on Monday morning at 8:00 a.m., approximately when will the pool be filled?
Answer:
→ If the hose fills a 5 – gallon bucket in 30 seconds, how much would it fill in 1 minute? Find the flow rate in gallons per minute.
→ It would fill 10 gallons in 1 minute; therefore, the flow rate is 10 \(\frac{\mathrm{gal}}{\mathrm{min}}\).
→ Find the flow rate in cubic feet per minute.
Convert gallons to cubic feet: (10 gal.) \(\frac{1}{7.5} \frac{\mathrm{ft}^{3}}{\mathrm{gal}}\) = 1 \(\frac{1}{3}\)ft3
Therefore, the flow rate of the garden hose in cubic feet per minute is 1 \(\frac{1}{3} \frac{\mathrm{ft}^{3}}{\mathrm{~min}}\)
→ How many minutes would it take to fill the 10,000 ft3 pool?
\(\frac{10,000 \mathrm{ft}^{3}}{1 \frac{1}{3}\left(\frac{\mathrm{ft}^{3}}{1 \mathrm{~min}}\right)}\) = 7,500 min.
→ How many days and hours is 7,500 minutes?
(7,500 min.) \(\frac{1 \mathrm{~h}}{60 \mathrm{~min}}\) = 125 h, or 5 days and 5 hours
→ At what time will the pool be filled?
The pool begins to fill at 8:00 a.m. on Monday, so 5 days and 5 hours later on Saturday at 1:00 p.m., the pool will be filled.
Example 2.
A square pipe (a rectangular prism – shaped pipe) with inside dimensions of 2 in.×2 in. has water flowing through it at a flow speed of 3 \(\frac{\mathrm{ft}}{\mathrm{s}}\). The water flows into a pool in the shape of a right triangular prism, with a base in the shape of a right isosceles triangle and with legs that are each 5 feet in length. How long will it take for the water to reach a depth of
4 feet?
Answer:
→ This problem is slightly different than the previous example. In this example, we are given a flow speed (also known as linear flow speed) instead of a flow rate.
→ What do you think the term flow speed means based on what you know about flow rate and what you know about the units of each?
Flow speed in this problem is measured in feet per second. Flow rate in Example 1 is measured in gallons per minute (or cubic feet per minute).
Flow speed is the distance that the liquid moves in one unit of time.
→ Now, let’s go back to our example. The water is traveling at a flow speed of 3 \(\frac{\mathrm{ft}}{\mathrm{s}}\). This means that for each second that the water is flowing out of the pipe, the water travels a distance of 3 ft. Now, we need to determine the volume of water that passes per second; in other words, we need to find the flow rate.
→ Each second, the water in a cross – section of the pipe will travel 3 ft. This is the same as the volume of a right rectangular prism with dimensions 2 in.×2 in.×3 ft.
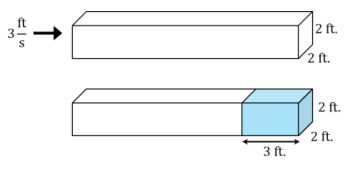
→ The volume of this prism in cubic feet is \(\frac{1}{6}\) ft.×\(\frac{1}{6}\) ft.×3 ft. = \(\frac{1}{12}\) ft3, and the volume of water flowing out of the pipe every second is \(\frac{1}{12}\) ft3. So, the flow rate is \(\frac{1}{12}\) \(\frac{\mathrm{ft}^{3}}{\mathrm{~s}}\).
→ Seconds is a very small unit of time when we think about filling up a pool. What is the flow rate in cubic feet per minute?
\(\frac{\frac{1}{12} \mathrm{ft}^{3}}{1 \mathrm{~s}} \cdot \frac{60 \mathrm{~s}}{1 \mathrm{~min}}\) = 5 \(\frac{\mathrm{ft}^{3}}{\min }\)
→ What is the volume of water that will be in the pool once the water reaches a depth of 4 ft.?
The volume of water in the pool will be \(\frac{1}{2}\)(5 ft.)(5 ft.)(4 ft.) = 50 ft3.
→ Now that we know our flow rate and the total volume of water in the pool, how long will it take for the pool to fill to a depth of 4 ft.?
\(\frac{50 \mathrm{ft}^{3}}{5 \frac{\mathrm{ft}^{3}}{\mathrm{~min}}}\) = 10 min.
It will take 10 minutes to fill the pool to a depth of 4 ft
Eureka Math Grade 7 Module 6 Lesson 27 Exercise Answer Key
Exercise 1.
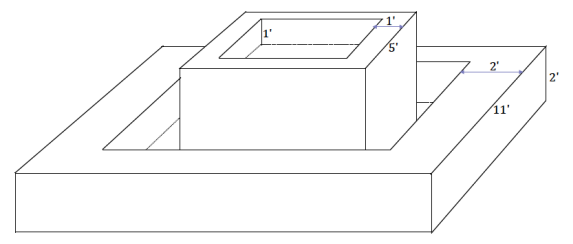
A park fountain is about to be turned on in the spring after having been off all winter long. The fountain flows out of the top level and into the bottom level until both are full, at which point the water is just recycled from top to bottom through an internal pipe. The outer wall of the top level, a right square prism, is five feet in length; the thickness of the stone between outer and inner wall is 1 ft.; and the depth is 1 ft. The bottom level, also a right square prism, has an outer wall that is 11 ft. long with a 2 ft. thickness between the outer and inner wall and a depth of 2 ft. Water flows through a 3 in.×3 in. square pipe into the top level of the fountain at a flow speed of 4 \(\frac{\mathrm{ft}}{\mathrm{s}}\). Approximately how long will it take for both levels of the fountain to fill completely?
Answer:
Volume of top:
3 ft.×3 ft.×1 ft. = 9 ft3
Volume of bottom:
(7 ft.×7 ft.×2 ft.) – (5 ft.×5 ft.×2 ft.) = 48 ft3
Combined volume of both levels:
9 ft3 + 48 ft3 = 57 ft3
With a flow speed of 4 \(\frac{\mathrm{ft}}{\mathrm{s}}\) through a 3 in.×3 in. square pipe, the volume of water moving through the pipe in one second is equivalent to the volume of a right rectangular prism with dimensions 3 in.×3 in.×4 ft. The volume in feet is
\(\frac{1}{4}\) ft.×\(\frac{1}{4}\) ft.×4 ft. = \(\frac{1}{4}\) ft3. Therefore, the flow rate is \(\frac{1}{2}\) because \(\frac{1}{4}\) ft3 of water flows every second.
Volume of water that will flow in one minute:
\(\frac{\frac{1}{4} \mathrm{ft}^{3}}{1 \mathrm{~s}} \cdot \frac{60 \mathrm{~s}}{1 \mathrm{~min}}\) = 15 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\)
Time needed to fill both fountain levels: \(\frac{57 \mathrm{ft}^{3}}{15 \frac{\mathrm{ft}^{3}}{\min }}\) = 3.8 min.; it will take 3.8 minutes to fill both fountain levels.
Exercise 2.
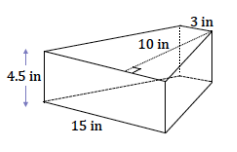
A decorative bathroom faucet has a 3 in.×3 in. square pipe that flows into a basin in the shape of an isosceles trapezoid prism like the one shown in the diagram. If it takes one minute and twenty seconds to fill the basin completely, what is the approximate speed of water flowing from the faucet in feet per second?
Answer:
Volume of the basin in cubic inches:
\(\frac{1}{2}\) (3 in. + 15 in.)(10 in.)×4.5 in. = 405 in3
Approximate volume of the basin in cubic feet:
(405 in3 )(\(\frac{1 \mathrm{ft}^{3}}{1.728 \mathrm{in}^{3}}\)) = 0.234375 ft3
Based on the rate of water flowing out the faucet, the volume of water can also be calculated as follows:
Let s represent the distance that the water is traveling in 1 second.
3 in. ∙ 3 in. ∙ s = \(\frac{1}{4}\) ft. ∙ \(\frac{1}{4}\) ft. ∙ s ft. = 0.234375 ft3
Therefore, the speed of the water flowing from the faucet is 3.75 \(\frac{\mathrm{ft}}{\mathrm{s}}\).
Eureka Math Grade 7 Module 6 Lesson 27 Problem Set Answer Key
Question 1.
Harvey puts a container in the shape of a right rectangular prism under a spot in the roof that is leaking. Rainwater is dripping into the container at an average rate of 12 drops a minute. The container Harvey places under the leak has a length and width of 5 cm and a height of 10 cm. Assuming each raindrop is roughly 1 cm3, approximately how long does Harvey have before the container overflows?
Answer:
Volume of the container in cubic centimeters:
5 cm×5 cm×10 cm = 250 cm3
Number of minutes until the container is filled with rainwater:
(250 cm3)(\(\frac{1 \mathrm{~min}}{12 \mathrm{~cm}^{3}}\))≈20.8 min.
Question 2.
A large square pipe has inside dimensions 3 in.×3 in., and a small square pipe has inside dimensions 1 in.×1 in. Water travels through each of the pipes at the same constant flow speed. If the large pipe can fill a pool in 2 hours, how long will it take the small pipe to fill the same pool?
Answer:
If s is the length that the water travels in one minute, then in one minute the large pipe provides \(\frac{1}{4}\) ft. ∙ \(\frac{1}{4}\) ft. ∙ s ft. of water. In one minute, the small pipe provides one – ninth as much, \(\frac{1}{12}\) ft. ∙ \(\frac{1}{12}\) ft. ∙ s ft. of water. Therefore, it will take the small pipe nine times as long. It will take the small pipe 18 hours to fill the pool.
Question 3.
A pool contains 12,000 ft3 of water and needs to be drained. At 8:00 a.m., a pump is turned on that drains water at a flow rate of 10 ft3 per minute. Two hours later, at 10:00 a.m., a second pump is activated that drains water at a flow rate of 8 ft3 per minute. At what time will the pool be empty?
Answer:
Water drained in the first two hours: \(\frac{10 \mathrm{ft}^{3}}{1 \mathrm{~min}}\) ∙ 120 min. = 1,200 ft3
Volume of water that still needs to be drained: 12,000 ft3 – 1,200 ft3 = 10,800 ft3
Amount of time needed to drain remaining water with both pumps working:
10,800 ft3 (\(\frac{1 \mathrm{~min}}{10 \mathrm{ft}^{3}} + \frac{1 \mathrm{~min}}{8 \mathrm{ft}^{3}}\)) = 600 min., or 10 h.
The total time needed to drain the pool is 12 hours, so the pool will drain completely at 8:00 p.m.
Question 4.
In the previous problem, if water starts flowing into the pool at noon at a flow rate of 3 ft3 per minute, how much longer will it take to drain the pool?
Answer:
At noon, the first pump will have been on for four hours, and the second pump will have been on for two hours. The cubic feet of water drained by the two pumps together at noon is
240 min.(\(\frac{10 \mathrm{ft}^{3}}{1 \mathrm{~min}}\)) + 120 min.(\(\frac{8 \mathrm{ft}^{3}}{1 \mathrm{~min}}\)) = 3,360 ft3
Volume of water that still needs to be drained:
12,000 ft3 – 3,360 ft3 = 8,640 ft2
If water is entering the pool at 3 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\) but leaving it at 18 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\), the net effect is that water is leaving the pool at 15 \(\frac{\mathrm{ft}^{3}}{\mathrm{~min}}\)
8,640 ft3 (\(\frac{1 \mathrm{~min}}{15 \mathrm{ft}^{3}}\)) = 576 min., or 9 h. and 36 min.
The pool will finish draining at 9:36 p.m. the same day. It will take an additional 1 hour and 36 minutes to drain the pool.
Question 5.
A pool contains 6,000 ft3 of water. Pump A can drain the pool in 15 hours, Pump B can drain it in 12 hours, and Pump C can drain it in 10 hours. How long will it take all three pumps working together to drain the pool?
Answer:
Rate at which Pump A drains the pool: \(\frac{1}{15}\) pool per hour
Rate at which Pump B drains the pool: \(\frac{1}{12}\) pool per hour
Rate at which Pump C drains the pool: \(\frac{1}{10}\) pool per hour
Together, the pumps drain the pool at (\(\frac{1}{15}\) + \(\frac{1}{12}\) + \(\frac{1}{10}\)) pool per hour, or \(\frac{1}{4}\) pool per hour. Therefore, it will take
4 hours to drain the pool when all three pumps are working together.
Question 6.
A 2,000 – gallon fish aquarium can be filled by water flowing at a constant rate in 10 hours. When a decorative rock is placed in the aquarium, it can be filled in 9.5 hours. Find the volume of the rock in cubic feet (1 ft3 = 7.5 gal.)
Answer:
Rate of water flow into aquarium:
\(\frac{2,000 \text { gal }}{10 \mathrm{~h}} = \frac{200 \mathrm{gal}}{1 \mathrm{~h}}\)
Since it takes half an hour less time to fill the aquarium with the rock inside, the volume of the rock is
\(\frac{200 \text { gal }}{1 \mathrm{~h}}\) = 100 gal.
Volume of the rock:
100 gal.(\(\frac{1 \mathrm{ft}^{3}}{7.5 \mathrm{gal}}\))≈13.3 ft3; the volume of the rock is approximately 13.3 ft3.
Eureka Math Grade 7 Module 6 Lesson 27 Exit Ticket Answer Key
Question 1.
Jim wants to know how much his family spends on water for showers. Water costs $1.50 for 1,000 gallons. His family averages 4 showers per day. The average length of a shower is 10 minutes. He places a bucket in his shower and turns on the water. After one minute, the bucket has 2.5 gallons of water. About how much money does his family spend on water for showers in a 30 – day month?
Answer:
Number of gallons of water in one day of showering (four ten – minute showers): 4(10 min.)(\(\frac{2.5 \mathrm{gal}}{1 \mathrm{~min}}\)) = 100 gal.
Number of gallons of water in 30 days: (30 days)(\(\frac{100 \mathrm{gal}}{1 \mathrm{~min}}\)) = 3,000 gal.
Cost of showering for 30 days: (3,000 gal.)(\(\frac{\$ 1.50}{1,000 \mathrm{gal}}\)) = $4.50
The family spends $4.50 in a 30 – day month on water for showers.