Engage NY Eureka Math 7th Grade Module 6 Lesson 3 Answer Key
Eureka Math Grade 7 Module 6 Lesson 3 Example Answer Key
Example 1.
Set up and solve an equation to find the value of x.
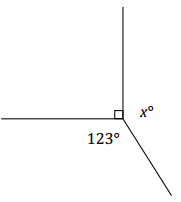
Answer:
x + 90 + 123 = 360 ∠s at a point
x + 213 = 360
x + 213 – 213 = 360 – 213
x = 147
Answer:
Example 2
Four rays meet at a common endpoint. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of x. Find the measurements of ∠BAC and ∠DAE.
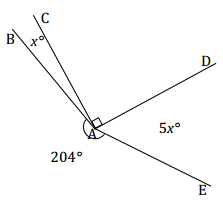
Answer:
The sum of the degree measurements of ∠BAC, ∠CAD, ∠DAE and the arc that measures 204° is 360°.
x + 90 + 5x + 204 = 360
6x + 294 = 360
6x + 294 – 294 = 360 – 294
6x = 66
(\(\frac{1}{6}\))6x = (\(\frac{1}{6}\)) 66
x = 11 ∠s at a point
The measurement of ∠BAC: 11°
The measurement of ∠DAE: 5(11)° = 55°
Example 3.
Two lines meet at a point that is also the endpoint of two rays. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of x. Find the measurements of ∠BAC and ∠BAH.
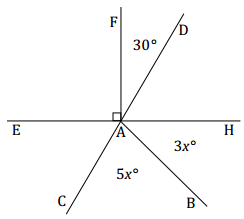
Answer:
∠DAE is formed by adjacent angles ∠EAF and ∠FAD; the measurement of ∠DAE is equal to the sum of the measurements of the adjacent angles. This is also true for the measurement of ∠CAH, formed by adjacent angles ∠CAB and ∠BAH. ∠CAH is vertically opposite from and equal in measurement to ∠DAE.
90 + 30 = 120 ∠DAE, ∠s add
5x + 3x = 8x ∠CAH, ∠s add
8x = 120 Vert.∠s
(\(\frac{1}{8}\))8x = (\(\frac{1}{8}\))120
x = 15
The measurement of ∠BAC: 5(15)° = 75°
The measurement of ∠BAH: 3(15)° = 45°
Example 4.
Two lines meet at a point. Set up and solve an equation to find the value of x. Find the measurement of one of the vertical angles.
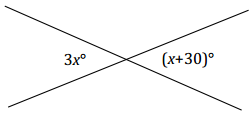
Answer:
Students use information in the figure and a protractor to solve for x.
i) Students measure a 30° angle as shown; the remaining portion of the angle must be x° (∠s add).
ii) Students can use their protractor to find the measurement of x° and use this measurement to partition the other angle in the vertical pair.
As a check, students should substitute the measured x value into each expression and evaluate; each angle of the vertical pair should equal the other. Students can also use their protractor to measure each angle of the vertical angle pair.
With a modified figure, students can write an algebraic equation that they have the skills to solve.
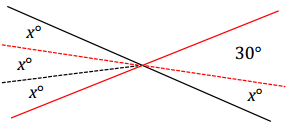
2x = 30 Vert.∠s
(\(\frac{1}{2}\))2x = (\(\frac{1}{2}\))30
x = 15
Measurement of each angle in the vertical pair: 3(15)° = 45°
Extension: The algebra steps above are particularly helpful as a stepping – stone in demonstrating how to solve the equation that takes care of the problem in one step as follows:
3x = x + 30 Vert.∠s
3x – x = x – x + 30
2x = 30
(\(\frac{1}{2}\))2x = (\(\frac{1}{2}\))30
x = 15
Measurement of each angle in the vertical pair: 3(15)° = 45°
Students understand the first line of this solution because of their knowledge of vertical angles. In fact, the only line they are not familiar with is the second line of the solution, which is a skill that they learn in Grade 8. Showing students this solution is simply a preview.
Eureka Math Grade 7 Module 6 Lesson 4 Exercise Answer Key
Exercise 1.
Five rays meet at a common endpoint. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of a.
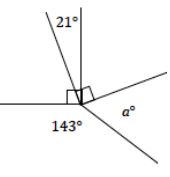
Answer:
The sum of angles at a point is 360°.
90 + (90 – 21) + a + 143 = 360
302 + a = 360
302 – 302 + a = 360 – 302
a = 58 ∠s at a point
Exercise 2.
Four rays meet at a common endpoint. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of x. Find the measurement of ∠CAD.
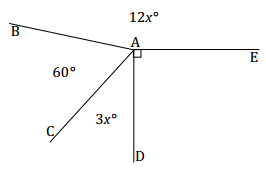
Answer:
∠BAC, ∠CAD, ∠DAE, and ∠EAB are angles at a point and sum to 360°.
3x + 60 + 12x + 90 = 360
15x + 150 = 360
15x + 150 – 150 = 360 – 150
15x = 210
(\(\frac{1}{15}\))15x = (\(\frac{1}{15}\))210
x = 14 ∠s at a point
The measurement of ∠CAD: 3(14)° = 42°
Exercise 3.
Lines AB and EF meet at a point which is also the endpoint of two rays. In a complete sentence, describe the relevant angle relationships in the diagram. Set up and solve an equation to find the value of x. Find the measurements of ∠DHF and ∠AHD.
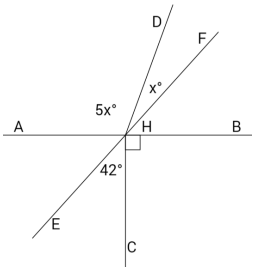
Answer:
The measurement of ∠AHF, formed by adjacent angles ∠AHD and ∠DHF, is equal to the sum of the measurements of the adjacent angles. This is also true for the measurement of ∠EHB, which is formed by adjacent angles ∠EHC and ∠CHB. ∠AHF is vertically opposite from and equal in measurement to ∠EHB.
5x + x = 6x ∠AHF, ∠s add
42 + 90 = 132 ∠EHB, ∠s add
6x = 132 Vert.∠s
(\(\frac{1}{6}\))6x = (\(\frac{1}{6}\))132
x = 22
The measurement of ∠DHF: 22°
The measurement of ∠AHD: 5(22)° = 110°
Exercise 4.
Set up and solve an equation to find the value of x. Find the measurement of one of the vertical angles.
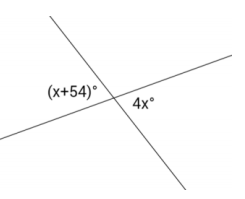
Answer:
Students use information in the figure and a protractor to solve for x.
i) Students measure a 54° angle as shown; the remaining portion of the angle must be x (∠s add).
ii) Students can use their protractors to find the measurement of x and use this measurement to partition the other angle in the vertical pair.
Students should perform a check as in Example 4 before solving an equation that matches the modified figure.
54 = 3x Vert.∠s
(\(\frac{1}{3}\))54 = (\(\frac{1}{3}\))3x
x = 18
Measurement of each vertical angle: 4(18)° = 72°
Extension:
x + 54 = 4x Vert.∠s
x – x + 54 = 4x – x
54 = 3x
(\(\frac{1}{3}\))54 = (\(\frac{1}{3}\))3x
x = 18
Eureka Math Grade 7 Module 6 Lesson 3 Problem Set Answer Key
Question 1.
Two lines meet at a point. Set up and solve an equation to find the value of x.
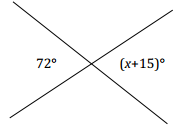
Answer:
x + 15 = 72 Vert.∠s
x + 15 – 15 = 72 – 15
x = 57
Question 2.
Three lines meet at a point. Set up and solve an equation to find the value of a. Is your answer reasonable? Explain how you know.
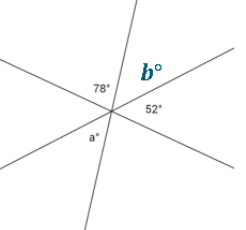
Answer:
Let b = a. Vert.∠s
78 + b + 52 = 180 ∠s on a line
b + 130 = 180
b + 130 – 130 = 180 – 130
b = 50
Since b = a, a = 50.
The answer seems reasonable since it is similar in magnitude to the 52° angle.
Question 3.
Two lines meet at a point that is also the endpoint of two rays. Set up and solve an equation to find the values of a and b.
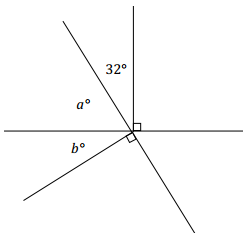
Answer:
a + 32 + 90 = 180 ∠s on a line
a + 122 = 180
a + 122 – 122 = 180 – 122
a = 58
a + b + 90 = 180 ∠s on a line
58 + b + 90 = 180
b + 148 = 180
b + 148 – 148 = 180 – 148
b = 32
Scaffolded solutions:
a. Use the equation above.
b. The angle marked a°, the angle with measurement 32°, and the right angle are angles on a line. Their measurements sum to 180°.
c. The answers seem reasonable because once the values of a and b are substituted, it appears that the two angles (a° and b°) form a right angle. We know those two angles should form a right angle because the angle adjacent to it is a right angle.
Question 4.
Three lines meet at a point that is also the endpoint of a ray. Set up and solve an equation to find the values of x and y.
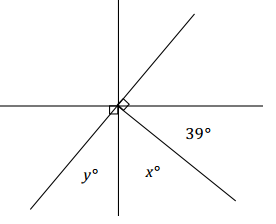
Answer:
x + 39 + 90 = 180 ∠s on a line
x + 129 = 180
x + 129 – 129 = 180 – 129
x = 51
y + x + 90 = 180 ∠s on a line
y + 51 + 90 = 180
y + 141 = 180
y + 141 – 141 = 180 – 141
y = 39
Question 5.
Two lines meet at a point. Find the measurement of one of the vertical angles. Is your answer reasonable? Explain how you know.
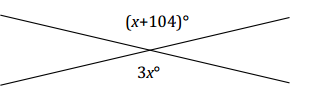
Answer:
2x = 104 vert.∠s
(\(\frac{1}{2}\))2x = (\(\frac{1}{2}\))104
x = 52
Measurement of each vertical angle: 3(52)° = 156°
The answer seems reasonable because a rounded value of 50 would make the numeric value of each expression 150 and 154, which are reasonably close for a check.
A solution can include a modified diagram, as shown, and the supporting algebra work.
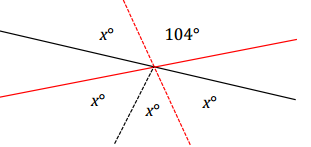
Solutions may also include the full equation and solution:
3x = x + 104 Vert.∠s
3x – x = x – x + 104
2x = 104
(1/2)2x = (1/2)104
x = 52
Question 6.
Three lines meet at a point that is also the endpoint of a ray. Set up and solve an equation to find the value of y.
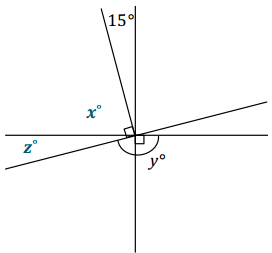
Answer:
Let x° and z° be the measurements of the indicated angles.
x + 15 = 90 Vert. ∠s
x + 15 – 15 = 90 – 15
x = 75
x + z = 90 Complementary ∠s
75 + z = 90
75 – 75 + z = 90 – 75
z = 15
z + y = 180 ∠s on a line
15 + y = 180
15 – 15 + y = 180 – 15
y = 165
Question 7.
Three adjacent angles are at a point. The second angle is 20° more than the first, and the third angle is 20° more than the second angle.
a. Find the measurements of all three angles.
b. Compare the expressions you used for the three angles and their combined expression. Explain how they are equal and how they reveal different information about this situation.
Answer:
a. x + (x + 20) + (x + 20 + 20) = 360 ∠s at a point
3x + 60 = 360
3x + 60 – 60 = 360 – 60
3x = 300
(\(\frac{1}{3}\))3x = (\(\frac{1}{3}\))300
x = 100
Angle 1: 100°
Angle 2: 100° + 20° = 120°
Angle 3: 100° + 20° + 20° = 140°
b. By the commutative and associative laws, x + (x + 20) + (x + 20 + 20) is equal to (x + x + x) + (20 + 20 + 20), which is equal to 3x + 60. The first expression, x + (x + 20) + (x + 20 + 20), shows the sum of three unknown numbers, where the second is 20 more than the first, and the third is 20 more than the second. The expression 3x + 60 shows the sum of three times an unknown number with 60.
Question 8.
Four adjacent angles are on a line. The measurements of the four angles are four consecutive even numbers. Determine the measurements of all four angles.
Answer:
x + (x + 2) + (x + 4) + (x + 6) = 180 ∠s on a line
4x + 12 = 180
4x + 12 – 12 = 180 – 12
4x = 168
(\(\frac{1}{4}\))4x = (\(\frac{1}{4}\))168
x = 42
The four angle measures are 42°, 44°, 46°, and 48°.
Question 9.
Three adjacent angles are at a point. The ratio of the measurement of the second angle to the measurement of the first angle is 4:3. The ratio of the measurement of the third angle to the measurement of the second angle is 5:4. Determine the measurements of all three angles.
Answer:
Let the smallest measure of the three angles be 3x°. Then, the measure of the second angle is 4x°, and the measure of the third angle is 5x°.
3x + 4x + 5x = 360 ∠s at a point
12x = 360
(1\(\frac{1}{12}\))12x = (\(\frac{1}{12}\))360
x = 30
Angle 1: 3(30)° = 90°
Angle 2: 4(30)° = 120°
Angle 3: 5(30)° = 150°
Question 10.
Four lines meet at a point. Solve for x and y in the following diagram.
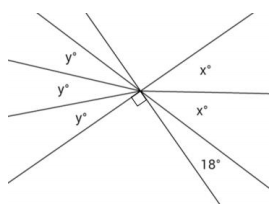
Answer:
2x + 18 + 90 = 180 ∠s on a line
2x + 108 = 180
2x + 108 – 108 = 180 – 108
2x = 72
(\(\frac{1}{2}\))2x = (\(\frac{1}{2}\))72
x = 36
2x = 3y Vert. ∠s
2(36) = 3y
72 = 3y
(\(\frac{1}{3}\))72 = (\(\frac{1}{3}\))3y
y = 24
Eureka Math Grade 7 Module 6 Lesson 3 Exit Ticket Answer Key
Question 1.
Two rays have a common endpoint on a line. Set up and solve an equation to find the value of z. Find the measurements of ∠AYC and ∠DYB.
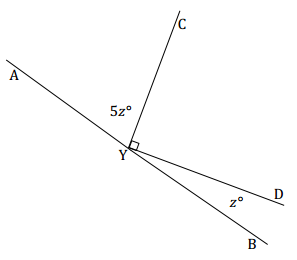
Answer:
5z + 90 + z = 180 ∠s on a line
6z + 90 = 180
6z + 90 – 90 = 180 – 90
6z = 90
(\(\frac{1}{6}\))6z = (\(\frac{1}{6}\))90
z = 15
The measurement of ∠AYC: 5(15)° = 75°
The measurement of ∠DYB: 15°
Scaffolded solutions:
a. Use the equation above.
b. The angle marked z°, the right angle, and the angle with measurement 5z° are angles on a line. Their measurements sum to 180°.
c. The answers seem reasonable because once 15 is substituted in for z, the measurement of ∠AYC is 75°, which is slightly smaller than a right angle, and the measurement of ∠DYB is 15°, which is an acute angle.
Question 2.
Two lines meet at a point that is also the vertex of an angle. Set up and solve an equation to find the value of x. Find the measurements of ∠CAH and ∠EAG.
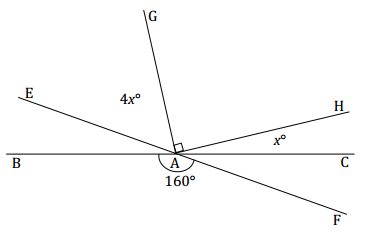
Answer:
4x + 90 + x = 160 vert.∠s
5x + 90 = 160
5x + 90 – 90 = 160 – 90
5x = 70
(\(\frac{1}{5}\))5x = (\(\frac{1}{5}\))70
x = 14
The measurement of ∠CAH: 14°
The measurement of ∠EAG: 4(14)° = 56°