Engage NY Eureka Math 7th Grade Module 6 Lesson 1 Answer Key
Eureka Math Grade 7 Module 6 Lesson 1 Example Answer Key
Example 1.
The measures of two supplementary angles are in the ratio of 2:3. Find the measurements of the two angles.
Answer:
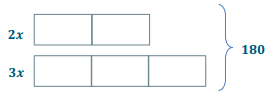
2x + 3x = 180
5x = 180
(\(\frac{1}{5}\))5x = (\(\frac{1}{5}\))180
x = 36
Angle 1 = 2(36)° = 72°
Angle 2 = 3(36)° = 108°
Example 2.
Two lines meet at a point that is also the vertex of an angle. Set up and solve an appropriate equation for x and y.
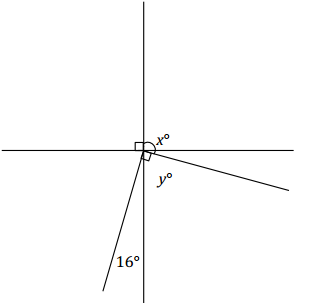
Answer:
16 + y = 90 Complementary angles
16 – 16 + y = 90-16
y = 74
x + (74) = 180 Supplementary angles
x + 74 – 74 = 180 – 74
x = 106
Eureka Math Grade 7 Module 6 Lesson 1 Exercise Answer Key
Exercise 1.
In a complete sentence, describe the relevant angle relationships in the diagram. Write an equation for the angle relationship shown in the figure and solve for x. Confirm your answers by measuring the angle with a protractor.
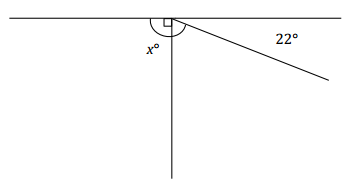
Answer:
The angles x° and 22° are supplementary and sum to 180°.
x + 22 = 180
x + 22 – 22 = 180 – 22
x = 158
The measure of the angle is 158°.
Exercise 2.
In a pair of complementary angles, the measurement of the larger angle is three times that of the smaller angle. Find the measurements of the two angles.
Answer:
x + 3x = 90
4x = 90
(\(\frac{1}{4}\))4x = (\(\frac{1}{4}\))90
x = 22.5
Angle 1 = 22.5°
Angle 2 = 3(22.5)° = 67.5°
Exercise 3.
The measure of a supplement of an angle is 6° more than twice the measure of the angle. Find the measurement of the two angles.
Answer:
x + (2x + 6) = 180
3x + 6 = 180
3x + 6 – 6 = 180 – 6
3x = 174
(\(\frac{1}{3}\))3x = (\(\frac{1}{3}\))174
x = 58
Angle 1 = 58°
Angle 2 = 2(58)° + 6° = 122°
Exercise 4.
The measure of a complement of an angle is 32° more than three times the angle. Find the measurement of the two angles.
Answer:
x + (3x + 32) = 90
4x + 32 – 32 = 90 – 32
4x = 58
(\(\frac{1}{4}\))4x = (\(\frac{1}{4}\))58
x = 14.5
Angle 1 = 14.5°
Angle 2 = 3(14.5)° + 32° = 75.5°
Scaffolding solutions:
a. The x° angle and the 22° angle are supplementary and sum to 180°.
b. x + 22 = 180
c. The equation shows that an unknown value, x (which is the unknown angle in the diagram) plus 22 is equal to 180. The 22 represents the angle that we know, which is 22 degrees.
d.
x + 22 = 180
x + 22 – 22 = 180 – 22
x = 158
x = 158 means that in the diagram, the missing angle measures 158°.
The answer of 158° is correct. If we substitute 158 for x, we get 158 + 22 = 180, which is a true number sentence. This is reasonable because when we look at the diagram, we would expect the angle to be obtuse.
Eureka Math Grade 7 Module 6 Lesson 1 Problem Set Answer Key
Question 1.
Two lines meet at a point that is also the endpoint of a ray. Set up and solve the appropriate equations to determine x and y.
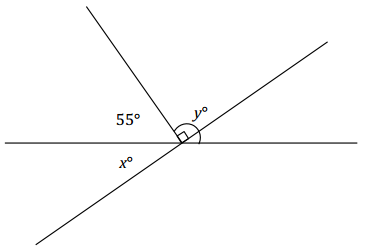
Answer:
x + 55 = 90 Complementary angles
x + 55 – 55 = 90 – 55
x = 35
55 + y = 180 Supplementary angles
55 – 55 + y = 180 – 55
y = 125
Question 2.
Two lines meet at a point that is also the vertex of an angle. Set up and solve the appropriate equations to determine x and y.
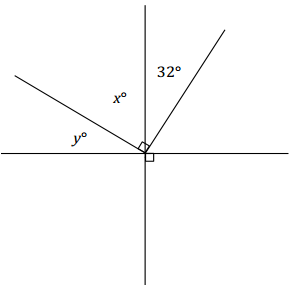
Answer:
y + x = 90 Complementary angles
x + 32 = 90 Complementary angles
x + 32 – 32 = 90 – 32
x = 58
y + (58) = 90 Complementary angles
y + 58 – 58 = 90 – 58
y = 32
Question 3.
Two lines meet at a point that is also the vertex of an angle. Set up and solve an appropriate equation for x and y.
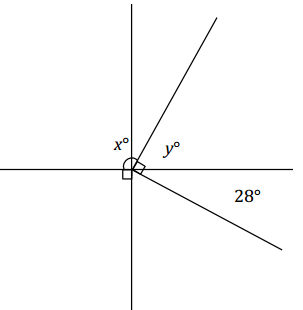
Answer:
x + y = 180 Supplementary angles
28 + y = 90 Complementary angles
28 – 28 + y = 90 – 28
y = 62
x + (62) = 180 Supplementary angles
x + 62-62 = 180 – 62
x = 118
Question 4.
Set up and solve the appropriate equations for s and t.
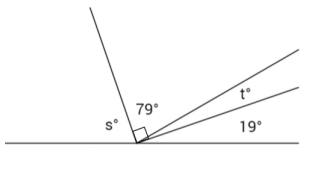
Answer:
79 + t = 90 Complementary angles
79 – 79 + t = 90 – 79
t = 11
19 + (11) + 79 + s = 180 Angles on a line
109 + s = 180
109 – 109 + s = 180 – 109
s = 71
Question 5.
Two lines meet at a point that is also the endpoint of two rays. Set up and solve the appropriate equations for m and n.
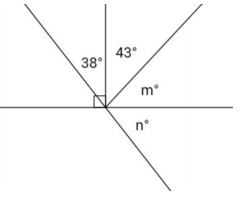
Answer:
43 + m = 90 Complementary angles
43-43 + m = 90-43
m = 47
38 + 43 + (47) + n = 180 Angles on a line
128 + n = 180
128-128 + n = 180-128
n = 52
Question 6.
The supplement of the measurement of an angle is 16° less than three times the angle. Find the measurement of the angle and its supplement.
Answer:
x + (3x-16) = 180
4x-16 + 16 = 180 + 16
4x = 196
(\(\frac{1}{4}\))4x = (\(\frac{1}{4}\))196
x = 49
Angle = 49°
Supplement = 3(49)°-16° = 131°
Question 7.
The measurement of the complement of an angle exceeds the measure of the angle by 25%. Find the measurement of the angle and its complement.
Answer:
x + (x + \(\frac{1}{4}\) x) = 90
x + \(\frac{5}{4}\) x = 90
\(\frac{9}{4}\)x = 90
(\(\frac{4}{9}\)) \(\frac{9}{4}\)x = (\(\frac{4}{9}\))90
x = 40
Angle = 40°
Complement = \(\frac{5}{4}\)(40)° = 50°
Question 8.
The ratio of the measurement of an angle to its complement is 1:2. Find the measurement of the angle and its complement.
Answer:
x + 2x = 90
3x = 90
(\(\frac{1}{3}\))3x = (\(\frac{1}{3}\))90
x = 30
Angle = 30°
Complement = 2(30)° = 60°
Question 9.
The ratio of the measurement of an angle to its supplement is 3:5. Find the measurement of the angle and its supplement.
Answer:
3x + 5x = 180
8x = 180
(\(\frac{1}{8}\))8x = (\(\frac{1}{8}\))180
x = 22.5
Angle = 3(22.5)° = 67.5°
Supplement = 5(22.5)° = 112.5°
Question 10.
Let x represent the measurement of an acute angle in degrees. The ratio of the complement of x to the supplement of x is 2:5. Guess and check to determine the value of x. Explain why your answer is correct.
Answer:
Solutions will vary; x = 30°.
The complement of 30° is 60°. The supplement of 30° is 150°. The ratio of 60 to 150 is equivalent to 2:5.
Eureka Math Grade 7 Module 6 Lesson 1 Exit Ticket Answer Key
Question 1.
Set up and solve an equation for the value of x. Use the value of x and a relevant angle relationship in the diagram to determine the measurement of ∠EAF.
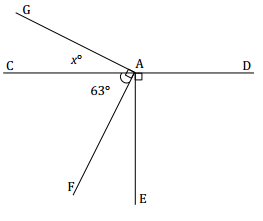
Answer:
x + 63 = 90
x + 63 – 63 = 90 – 63
x = 27
∠CAG and ∠EAF are the complements of 63°. The measurement of ∠CAG is 27°; therefore, the measurement of ∠EAF is also 27°.
Question 2.
The measurement of the supplement of an angle is 39° more than half the angle. Find the measurement of the angle and its supplement.
Answer:
x + (\(\frac{1}{2}\)x + 39) = 180
1.5x + 39 = 180
1.5x + 39 – 39 = 180 – 39
1.5x = 141
1.5x ÷ 1.5 = 141 ÷ 1.5
x = 94
The measurement of the angle is 94°.
The measurement of the supplement is \(\frac{1}{2}\)(94)° + 39° = 86°.
OR
x + (\(\frac{1}{2}\)x + 39) = 180
\(\frac{3}{2}\)x + 39 = 180
\(\frac{3}{2}\)x + 39 – 39 = 180 – 39
\(\frac{3}{2}\)x = 141
(\(\frac{2}{3}\))(\(\frac{3}{2}\)x) = (\(\frac{2}{3}\))141
x = 94
The measurement of the angle is 94°.
The measurement of the supplement is \(\frac{1}{2}\)(94)° + 39° = 86°.