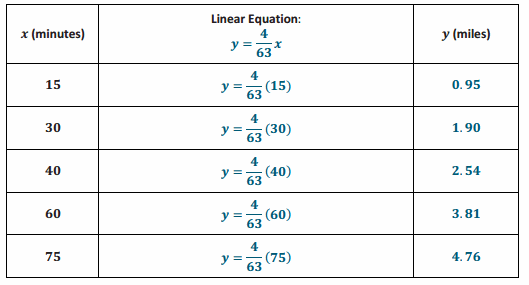Engage NY Eureka Math 8th Grade Module 4 Lesson 10 Answer Key
Eureka Math Grade 8 Module 4 Lesson 10 Example Answer Key
Example 1.
Consider the word problem below. We can do several things to answer this problem, but let’s begin to organize our work using a table for time and distance:
Example 1.
Paul walks 2 miles in 25 minutes. How many miles can Paul walk in 137.5 minutes?
Answer:
As students answer the questions below, fill in the table.
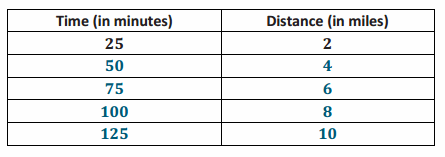
→ How many miles would Paul be able to walk in 50 minutes? Explain.
→ Paul could walk 4 miles in 50 minutes because 50 minutes is twice the time we were given, so we can calculate twice the distance, which is 4.
→ How many miles would Paul be able to walk in 75 minutes? Explain.
→ Paul could walk 6 miles in 75 minutes because 75 minutes is three times the number of minutes we were given, so we can calculate three times the distance, which is 6.
→ How many miles would Paul be able to walk in 100 minutes?
→ He could walk 8 miles.
→ How many miles would he walk in 125 minutes?
→ He could walk 10 miles.
→ How could we determine the number of miles Paul could walk in 137.5 minutes?
Provide students time to think about the answer to this question. They may likely say that they can write a proportion to figure it out. Allow them to share and demonstrate their solutions. Then, proceed with the discussion below, if necessary.
→ Since the relationship between the distance Paul walks and the time it takes him to walk that distance is proportional, we let y represent the distance Paul walks in 137.5 minutes and write the following:
Answer:
\(\frac{25}{2}\)=\(\frac{13.75}{y}\)
25y=137.5(2)
25y=275
y=11
Therefore, Paul can walk 11 miles in 137.5 minutes.
→ How many miles, y, can Paul walk in x minutes?
Provide students time to think about the answer to this question. Allow them to share their ideas, and then proceed with the discussion below, if necessary.
→ We know for a fact that Paul can walk 2 miles in 25 minutes, so we can write the ratio \(\frac{25}{2}\) as we did with the proportion. We can write another ratio for the number of miles, y, Paul walks in x minutes. It is \(\frac{x}{y}\). For the same reason we could write the proportion before, we can write one now with these two ratios:
\(\frac{25}{2}\)=\(\frac{x}{y}\).
Does this remind you of something we have done recently? Explain.
→ This is a linear equation in disguise. All we need to do is multiply each numerator by the other fraction’s denominator, and then we will have a linear equation.
25y=2x
→ Recall our original question: How many miles, y, can Paul walk in x minutes? We need to solve this equation for y.
25y=2x
y=\(\frac{2}{25}\) x
y=0.08x
Paul can walk 0.08x miles in x minutes. This equation will allow us to answer all kinds of questions about Paul with respect to any given number of minutes or miles.
→ Let’s go back to the table and look for y=0.08x or its equivalent y=\(\frac{2}{25}\) x. What do you notice?
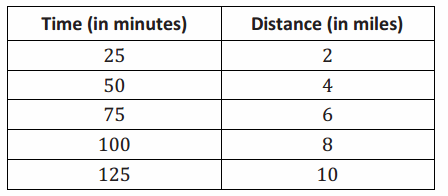
→ The fraction \(\frac{2}{25}\) came from the first row in the table. It is the distance traveled divided by the time it took to travel that distance. It is also in between each row of the table. For example, the difference between 4 miles and 2 miles is 2, and the difference between the associated times 50 and 25 is 25. The pattern repeats throughout the table.
Show on the table the +2 between each distance interval and the +25 between each time interval. Remind students that they have done work like this before, specifically finding a unit rate for a proportional relationship. Make clear that the unit rate found in the table was exactly the same as the unit rate found using the proportion and that the unit rate is the rate at which Paul walks.
→ Let’s look at another problem where only a table is provided.
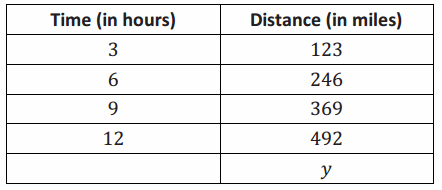
We want to know how many miles, y, can be traveled in any number of hours x. Using our previous work, what should we do?
→ We can write and solve a proportion that contains both x and y or use the table to help us determine the unit rate.
→ How many miles, y, can be traveled in any number of hours x?
→ Student work:
\(\frac{123}{3}\)=\(\frac{y}{x}\)
123x=3y
\(\frac{123}{3}\) x=y
41x=y
→ What does the equation y=41x mean?
→ It means that the distance traveled, y, is equal to the rate of 41 multiplied by the number of hours x traveled at that rate.
Example 2.
The point of this problem is to make clear to students that constant rate must be assumed in order to write linear equations in two variables and to use those equations to answer questions about distance, time, and rate.
→ Consider the following word problem: Alexxa walked from Grand Central Station (GCS) on 42nd Street to Penn Station on 7th Avenue. The total distance traveled was 1.1 miles. It took Alexxa 25 minutes to make the walk. How many miles did she walk in the first 10 minutes?
→ Give students a minute to think and/or work on the problem. Expect them to write a proportion and solve the problem. The next part of the discussion gets them to think about what is meant by “constant” speed or, rather, lack of it.
→ She walked 0.44 miles. (Assuming students used a proportion to solve.)
→ Are you sure about your answer? How often do you walk at a constant speed? Notice the problem did not even mention that she was walking at the same rate throughout the entire 1.1 miles. What if you have more information about her walk: Alexxa walked from GCS along 42nd Street to an ATM 0.3 miles away in 8 minutes. It took her 2 minutes to get some money out of the machine. Do you think your answer is still correct?
→ Probably not since we now know that she had to stop at the ATM.
→ Let’s continue with Alexxa’s walk: She reached the 7th Avenue junction 13 minutes after she left GCS, a distance of 0.6 miles. There, she met her friend Karen with whom she talked for 2 minutes. After leaving her friend, she finally got to Penn Station 25 minutes after her walk began.
→ Is this a more realistic situation than believing that she walked the exact same speed throughout the entire trip? What other events typically occur during walks in the city?
→ Stoplights at crosswalks, traffic, maybe a trip/fall, or running an errand
→ This is precisely the reason we need to take a critical look at what we call proportional relationships and constant speed, in general.
→ The following table shows an accurate picture of Alexxa’s walk:
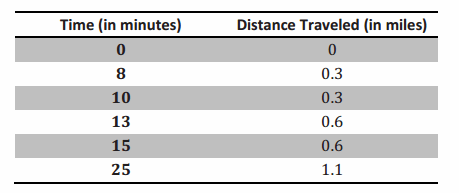
With this information, we can answer the question. Alexxa walked exactly 0.3 miles in 10 minutes.
→ Now that we have an idea of what could go wrong when we assume a person walks at a constant rate or that a proportion can give us the correct answer all of the time, let’s define what is called average speed.
→ Suppose a person walks a distance of d (miles) in a given time interval t (minutes). Then, the average speed in the given time interval is \(\frac{d}{t}\) in miles per minute.
→ With this definition, we can calculate Alexxa’s average speed: The distance that Alexxa traveled divided by the time interval she walked is \(\frac{1.1}{25}\) miles per minute.
→ If we assume that someone can actually walk at the same average speed over any time interval, then we say that the person is walking at a constant speed.
Suppose the average speed of a person is the same constant C for any given time interval. Then, we say that the person is walking at a constant speed C.
→ If the original problem included information specifying constant speed, then we could write the following:
Alexxa’s average speed for 25 minutes is \(\frac{1.1}{25}\).
Let y represent the distance Alexxa walked in 10 minutes. Then, her average speed for 10 minutes is \(\frac{y}{10}\).
Since Alexxa is walking at a constant speed of C miles per minute, then we know that
\(\frac{1.1}{25}\)=C, and \(\frac{y}{10}\)=C.
Since both fractions are equal to C, then we can write
\(\frac{1.1}{25}\) = \(\frac{y}{10}\)
With the assumption of constant speed, we now have a proportional relationship, which would make the answer you came up with in the beginning correct.
We can go one step further and write a statement in general. If Alexxa walks y miles in x minutes, then
\(\)=C, and \(\)=\(\).
To find how many miles y Alexxa walks in x miles, we solve the equation for y:
\(\frac{1.1}{25}\)=\(\frac{y}{x}\)
25y=1.1x
\(\frac{25}{2}\)5 y=\(\frac{1.1}{25}\) x
y=\(\frac{1.1}{25}\) x,
where the last equation is an example of a linear equation in two variables x and y. With this general equation, we can find the distance y Alexxa walks in any given time x. Since we have more information about Alexxa’s walk, where and when she stopped, we know that the equation cannot accurately predict the distance she walks after a certain number of minutes. To do so requires us to assume that she walks at a constant rate. This is an assumption we generally take for granted when solving problems about rate.
Eureka Math Grade 8 Module 4 Lesson 10 Exercise Answer Key
Question 1.
Wesley walks at a constant speed from his house to school 1.5 miles away. It took him 25 minutes to get to school.
a. What fraction represents his constant speed, C?
Answer:
\(\frac{1.5}{25}\)=C
b. You want to know how many miles he has walked after 15 minutes. Let y represent the distance he traveled after 15 minutes of walking at the given constant speed. Write a fraction that represents the constant speed, C, in terms of y.
Answer:
\(\frac{y}{15}\)=C
c. Write the fractions from parts (a) and (b) as a proportion, and solve to find how many miles Wesley walked after 15 minutes.
Answer:
\(\frac{1.5}{25}\)=\(\frac{y}{15}\)
25y=22.5
\(\frac{25}{25}\) y=\(\frac{22.5}{25}\)
y=0.9
Wesley walks 0.9 miles in 15 minutes.
d. Let y be the distance in miles that Wesley traveled after x minutes. Write a linear equation in two variables that represents how many miles Wesley walked after x minutes.
Answer:
\(\frac{1.5}{25}\)=\(\frac{y}{x}\)
25y=1.5x
\(\frac{25}{25}\)y=\(\frac{1.5}{25}\) x
y=\(\frac{1.5}{25}\) x
Question 2.
Stefanie drove at a constant speed from her apartment to her friend’s house 20 miles away. It took her 45 minutes to reach her destination.
a. What fraction represents her constant speed, C?
Answer:
\(\frac{20}{45}\)=C
b. What fraction represents constant speed, C, if it takes her x number of minutes to get halfway to her friend’s house?
Answer:
\(\frac{10}{x}\)=C
c. Write and solve a proportion using the fractions from parts (a) and (b) to determine how many minutes it takes her to get to the halfway point.
Answer:
\(\frac{20}{45}\)=\(\frac{10}{x}\)
20x=450
\(\frac{20}{20}\) x=\(\frac{450}{20}\)
x=22.5
Stefanie gets halfway to her friend’s house, 10 miles away, after 22.5 minutes.
d. Write a two-variable equation to represent how many miles Stefanie can drive over any time interval.
Answer:
Let y represent the distance traveled over any time interval x. Then,
\(\frac{20}{45}\)=\(\frac{y}{x}\)
20x=45y
\(\frac{20}{45}\) x=\(\frac{45}{45}\) y
\(\frac{4}{9}\) x=y.
Exercise 3.
The equation that represents how many miles, y, Dave travels after x hours is y=50x+15. Use the equation to complete the table below.

Answer:
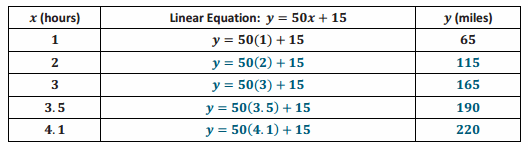
Eureka Math Grade 8 Module 4 Lesson 10 Exit Ticket Answer Key
Alex skateboards at a constant speed from his house to school 3.8 miles away. It takes him 18 minutes.
a. What fraction represents his constant speed, C?
Answer:
\(\frac{3.8}{18}\)=C
b. After school, Alex skateboards at the same constant speed to his friend’s house. It takes him 10 minutes. Write the fraction that represents constant speed, C, if he travels a distance of y.
Answer:
\(\frac{y}{10}\)=C
c. Write the fractions from parts (a) and (b) as a proportion, and solve to find out how many miles Alex’s friend’s house is from school. Round your answer to the tenths place.
\(\frac{3.8}{18}\)=\(\frac{y}{10}\)
3.8(10)=18y
38=18y
\(\frac{38}{18}\)=y
2.1≈y
Alex’s friend lives about 2.1 miles from school.
Eureka Math Grade 8 Module 4 Lesson 10 Problem Set Answer Key
Students practice writing and solving proportions to solve constant speed problems. Students write two variable equations to represent situations, generally.
Question 1.
Eman walks from the store to her friend’s house, 2 miles away. It takes her 35 minutes.
a. What fraction represents her constant speed, C?
Answer:
\(\frac{2}{35}\)=C
b. Write the fraction that represents her constant speed, C, if she walks y miles in 10 minutes.
Answer:
\(\frac{y}{10}\)=C
c. Write and solve a proportion using the fractions from parts (a) and (b) to determine how many miles she walks after 10 minutes. Round your answer to the hundredths place.
Answer:
\(\frac{2}{35}\)=\(\frac{y}{10}\)
35y=20
\(\frac{35}{35}\) y=\(\frac{20}{35}\)
y=0.57142…
Eman walks about 0.57 miles after 10 minutes.
d. Write a two-variable equation to represent how many miles Eman can walk over any time interval.
Answer:
Let y represent the distance Eman walks in x minutes.
\(\frac{2}{35}\)=\(\frac{y}{x}\)
35y=2x
\(\frac{35}{35}\) y=\(\frac{2}{35}\) x
y=\(\frac{2}{35}\) x
Question 2.
Erika drives from school to soccer practice 1.3 miles away. It takes her 7 minutes.
a. What fraction represents her constant speed, C?
Answer:
\(\frac{1.3}{7}\)=C
b. What fraction represents her constant speed, C, if it takes her x minutes to drive exactly 1 mile?
Answer:
\(\frac{1}{x}\)=C
c. Write and solve a proportion using the fractions from parts (a) and (b) to determine how much time it takes her to drive exactly 1 mile. Round your answer to the tenths place.
Answer:
\(\frac{1.3}{7}\)=\(\frac{1}{x}\)
1.3x=7
\(\frac{1.3}{1.3}\) x=7/(1.3)
x=5.38461…
It takes Erika about 5.4 minutes to drive exactly 1 mile.
d. Write a two-variable equation to represent how many miles Erika can drive over any time interval.
Answer:
Let y be the number of miles Erika travels in x minutes.
\(\frac{1.3}{7}\)=\(\frac{y}{x}\)
7y=1.3x
\(\frac{7}{7}\) y=\(\frac{1.3}{7}\) x
y=\(\frac{1.3}{7}\) x
Question 3.
Darla drives at a constant speed of 45 miles per hour.
a. If she drives for y miles and it takes her x hours, write the two-variable equation to represent the number of miles Darla can drive in x hours.
Answer;
\(\frac{y}{x}\)=45
y=45x
b. Darla plans to drive to the market 14 miles from her house, then to the post office 3 miles from the market, and then return home, which is 15 miles from the post office. Assuming she drives at a constant speed the entire time, how long will it take her to run her errands and get back home? Round your answer to the hundredths place.
Answer:
Altogether, Darla plans to drive 32 miles because 14+3+15=32.
32=45x
\(\frac{32}{45}\)=\(\frac{45}{45}\) x
0.71111…=x
It will take Darla about 0.71 hours to run her errands and get back home.
Question 4.
Aaron walks from his sister’s house to his cousin’s house, a distance of 4 miles, in 80 minutes. How far does he walk in 30 minutes?
Answer:
I cannot say for sure how far Aaron walks in 30 minutes because I do not know if he is walking at a constant speed. Maybe he stopped at his friend’s house for 20 minutes.
Question 5.
Carlos walks 4 miles every night for exercise. It takes him exactly 63 minutes to finish his walk.
a. Assuming he walks at a constant rate, write an equation that represents how many miles, y, Carlos can walk in x minutes.
Answer:
Since \(\frac{4}{63}\)=C and \(\frac{y}{x}\)=C, then
\(\frac{4}{63}\)=\(\frac{y}{x}\)
63y=4x
\(\frac{63}{63}\)y=\(\frac{4}{63}\) x
y=\(\frac{4}{63}\) x”.”
b. Use your equation from part (a) to complete the table below. Use a calculator, and round all values to the hundredths place.
Answer: