Engage NY Eureka Math 8th Grade Module 4 Lesson 11 Answer Key
Eureka Math Grade 8 Module 4 Lesson 11 Example Answer Key
Example 1.
Pauline mows a lawn at a constant rate. Suppose she mows a 35-square-foot lawn in 2.5 minutes. What area, in square feet, can she mow in 10 minutes? t minutes?
→ What is Pauline’s average rate in 2.5 minutes?
→ Pauline’s average rate in 2.5 minutes is \(\frac{35}{2.5}\) square feet per minute.
→ What is Pauline’s average rate in 10 minutes?
→ Let A represent the square feet of the area mowed in 10 minutes. Pauline’s average rate in 10 minutes is \(\frac{A}{10}\) square feet per mintute.
→ Let C be Pauline’s constant rate in square feet per minute; then, \(\frac{35}{2.5}\)=C, and \(\frac{A}{10}\)=C. Therefore,
Answer;
\(\frac{35}{2.5}\)=\(\frac{A}{10}\)
350=2.5A
\(\frac{350}{2.5}\)=\(\frac{2.5}{2.5}\) A
140=A
Pauline mows 140 square feet of lawn in 10 minutes.
→ If we let y represent the number of square feet Pauline can mow in t minutes, then Pauline’s average rate in t minutes is \(\frac{y}{t}\) square feet per minute.
→ Write the two-variable equation that represents the area of lawn, y, Pauline can mow in t minutes.
Answer:
\(\frac{35}{2.5}\)=\(\frac{y}{t}\)
2.5y=35t
\(\frac{2.5}{2.5}\) y=\(\frac{35}{2.5}\) t
y=\(\frac{35}{2.5}\) t
→ What is the meaning of \(\frac{35}{2.5}\) in the equation y=\(\frac{35}{2.5}\) t?
→ The number \(\frac{35}{2.5}\) represents the constant rate at which Pauline can mow a lawn.
→ We can organize the information in a table.
Answer:
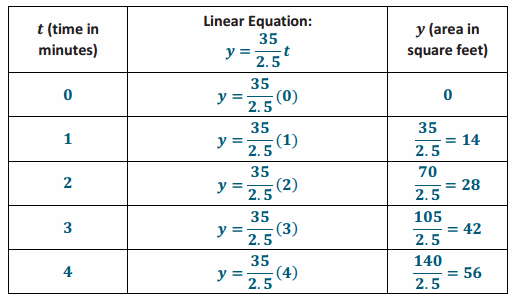
→ On a coordinate plane, we will let the x-axis represent time t, in minutes, and the y-axis represent the area of mowed lawn in square feet. Then we have the following graph.
Answer:
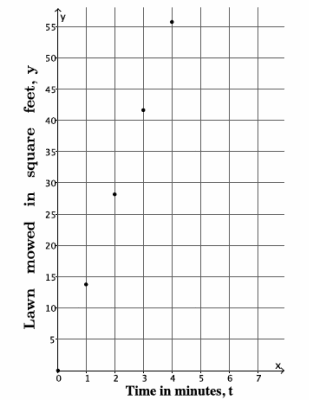
→ Because Pauline mows at a constant rate, we would expect the square feet of mowed lawn to continue to rise as the time, in minutes, increases.
Example 2.
Water flows at a constant rate out of a faucet. Suppose the volume of water that comes out in three minutes is 10.5 gallons. How many gallons of water come out of the faucet in t minutes?
→ Write the linear equation that represents the volume of water, V, that comes out in t minutes.
Answer:
Let C represent the constant rate of water flow.
\(\frac{10.5}{3}\)=C, and \(\frac{V}{t}\)=C; then, \(\frac{10.5}{3}\)=\(\frac{V}{t}\).
\(\frac{10.5}{3}\)=\(\frac{V}{t}\)
3V=10.5t
\(\frac{3}{3}\) V=\(\frac{10.5}{3}\) t
V=\(\frac{10.5}{3}\) t
→ What is the meaning of the number \(\frac{10.5}{3}\) in the equation V=\(\frac{10.5}{3}\) t?
→ The number \(\frac{10.5}{3}\) represents the constant rate at which water flows from a faucet.
→ Using the linear equation V=\(\frac{10.5}{3}\) t, complete the table.
Answer:
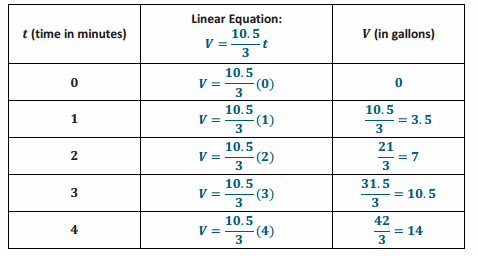
→ On a coordinate plane, we will let the x-axis represent time t in minutes and the y-axis represent the volume of water. Graph the data from the table.
Answer:
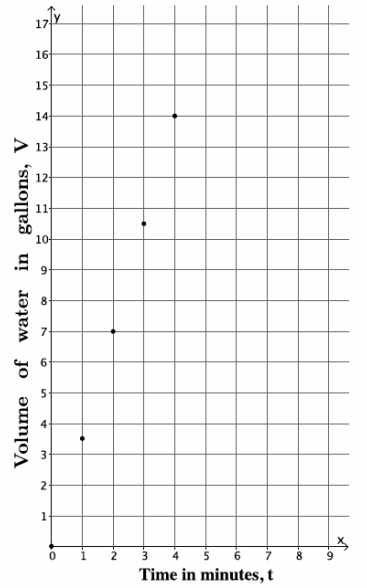
→ Using the graph, about how many gallons of water do you think would flow after 1 \(\frac{1}{2}\) minutes? Explain.
→ After 1 \(\frac{1}{2}\) minutes, between 3 \(\frac{1}{2}\) and 7 gallons of water will flow. Since the water is flowing at a constant rate, we can expect the volume of water to rise between 1 and 2 minutes. The number of gallons that flow after 1 \(\frac{1}{2}\) minutes then would have to be between the number of gallons that flow out after 1 minute and 2 minutes.
→ Using the graph, about how long would it take for 15 gallons of water to flow out of the faucet? Explain.
→ It would take between 4 and 5 minutes for 15 gallons of water to flow out of the faucet. It takes 4 minutes for 14 gallons to flow; therefore, it must take more than 4 minutes for 15 gallons to come out. It must take less than 5 minutes because 3 \(\frac{1}{2}\) gallons flow out every minute.
→ Graphing proportional relationships like these last two constant rate problems provides us more information than simply solving an equation and calculating one value. The graph provides information that is not so obvious in an equation.
Eureka Math Grade 8 Module 4 Lesson 11 Exercise Answer Key
Exercise 1.
Juan types at a constant rate. He can type a full page of text in 3 \(\frac{1}{2}\) minutes. We want to know how many pages, p, Juan can type after t minutes.
a. Write the linear equation in two variables that represents the number of pages Juan types in any given time interval.
Let C represent the constant rate that Juan types in pages per minute. Then,
Answer:
\(\frac{1}{3.5}\)=C, and \(\frac{p}{t}\)=C; therefore, \(\frac{1}{3.5}\)=\(\frac{p}{t}\).
\(\frac{1}{3.5}\)=\(\frac{p}{t}\)
3.5p=t
\(\frac{3.5}{3.5}\) p=\(\frac{1}{3.5}\) t
p=\(\frac{1}{3.5}\) t
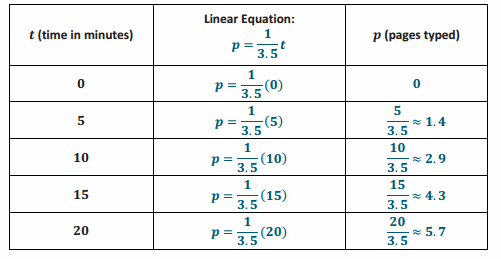
b. Complete the table below. Use a calculator, and round your answers to the tenths place.
Answer:
c. Graph the data on a coordinate plane.
Answer:
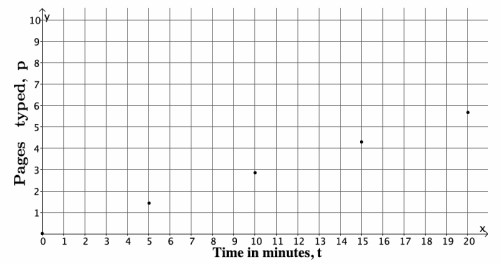
d. About how long would it take Juan to type a 5-page paper? Explain.
Answer;
It would take him between 15 and 20 minutes. After 15 minutes, he will have typed 4.3 pages. In 20 minutes, he can type 5.7 pages. Since 5 pages is between 4.3 and 5.7, then it will take him between 15 and 20 minutes.
Question 2.
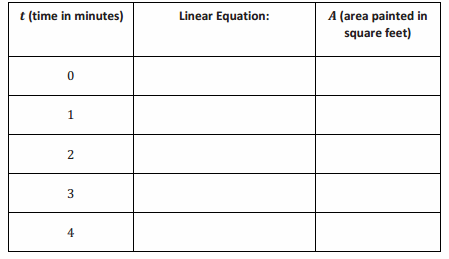
Emily paints at a constant rate. She can paint 32 square feet in 5 minutes. What area, A, in square feet, can she paint in t minutes?
a. Write the linear equation in two variables that represents the number of square feet Emily can paint in any given time interval.
Answer:
Let C be the constant rate that Emily paints in square feet per minute. Then,
\(\frac{32}{5}\)=C, and \(\frac{A}{t}\)=C; therefore, \(\frac{32}{5}\)=\(\frac{A}{t}\).
\(\frac{32}{5}\)=\(\frac{A}{t}\)
5A=32t
\(\frac{5}{5}\) A=\(\frac{32}{5}\) t
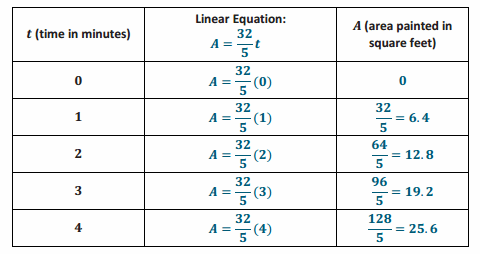
A=\(\frac{32}{5}\) t
b. Complete the table below. Use a calculator, and round answers to the tenths place.
Answer:
c. Graph the data on a coordinate plane.
Answer:
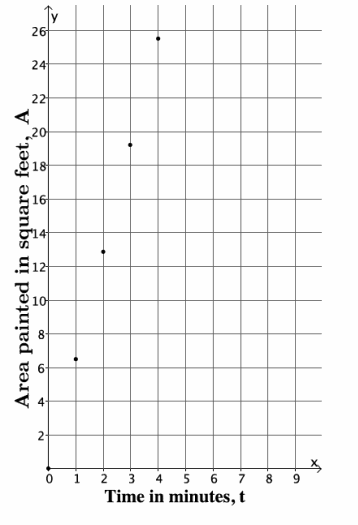
d. About how many square feet can Emily paint in 2 \(\frac{1}{2}\) minutes? Explain.
Answer:
Emily can paint between 12.8 and 19.2 square feet in 2 \(\frac{1}{2}\) minutes. After 2 minutes, she paints 12.8 square feet, and after 3 minutes, she will have painted 19.2 square feet.
Question 3.
Joseph walks at a constant speed. He walked to a store that is one-half mile away in 6 minutes. How many miles, m, can he walk in t minutes?
a. Write the linear equation in two variables that represents the number of miles Joseph can walk in any given time interval, t.
Answer:
Let C be the constant rate that Joseph walks in miles per minute. Then,
\(\frac{0.5}{6}\)=C, and \(\frac{m}{t}\)=C; therefore, \(\frac{0.5}{6}\)=\(\frac{m}{t}\).
\(\frac{0.5}{6}\)=\(\frac{m}{t}\)
6m=0.5t
\(\frac{6}{6}\) m=\(\frac{0.5}{6}\) t
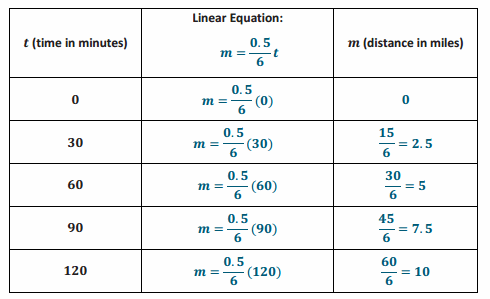
m=\(\frac{0.5}{6}\) t
b. Complete the table below. Use a calculator, and round answers to the tenths place.
Answer:
c. Graph the data on a coordinate plane.
Answer:
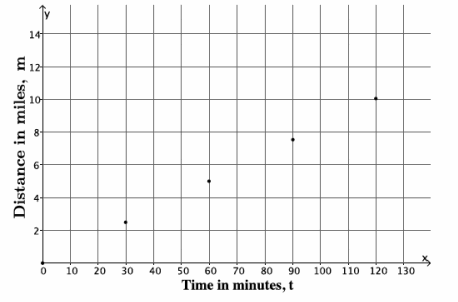
d. Joseph’s friend lives 4 miles away from him. About how long would it take Joseph to walk to his friend’s house? Explain.
Answer:
It will take Joseph a little less than an hour to walk to his friend’s house. Since it takes 30 minutes for him to walk 2.5 miles and 60 minutes to walk 5 miles, and 4 is closer to 5 than 2.5, it will take Joseph less than an hour to walk the 4 miles.
Eureka Math Grade 8 Module 4 Lesson 11 Exit Ticket Answer Key
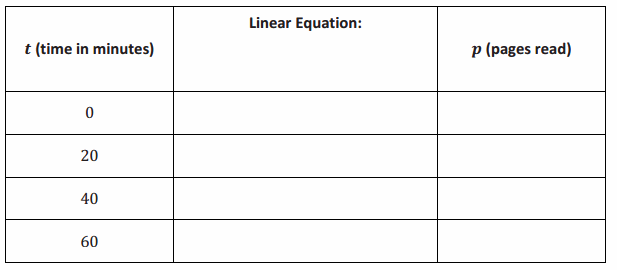
Vicky reads at a constant rate. She can read 5 pages in 9 minutes. We want to know how many pages, p, Vicky can read after t minutes.
a. Write a linear equation in two variables that represents the number of pages Vicky reads in any given time interval.
Answer:
Let C represent the constant rate that Vicky reads in pages per minute. Then,
\(\frac{5}{9}\)=C, and \(\frac{p}{t}\)=C; therefore, \(\frac{5}{9}\)=\(\frac{p}{t}\).
\(\frac{5}{9}\)=\(\frac{p}{t}\)
9p=5t
\(\frac{9}{9}\) p=\(\frac{5}{9}\) t
p=\(\frac{5}{9}\) t
b. Complete the table below. Use a calculator, and round answers to the tenths place.
Answer:
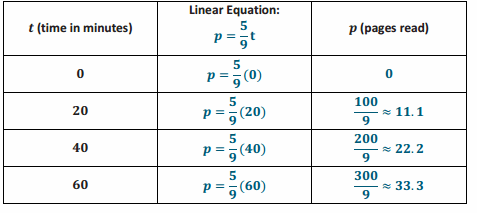
c. About how long would it take Vicky to read 25 pages? Explain.
Answer:
It would take her a little over 40 minutes. After 40 minutes, she can read about 22.2 pages, and after 1 hour, she can read about 33.3 pages. Since 25 pages is between 22.2 and 33.3, it will take her between 40 and 60 minutes to read 25 pages.
Eureka Math Grade 8 Module 4 Lesson 11 Problem Set Answer Key
Students practice writing two-variable equations that represent a constant rate.
Question 1.
A train travels at a constant rate of 45 miles per hour.
a. What is the distance, d, in miles, that the train travels in t hours?
Answer:
Let C be the constant rate the train travels. Then, \(\frac{45}{1}\)=C, and \(\frac{d}{t}\)=C; therefore, \(\frac{45}{1}\)=\(\frac{d}{t}\).
\(\frac{45}{1}\)=\(\frac{d}{t}\)
d=45t
b. How many miles will it travel in 2.5 hours?
Answer:
d=45(2.5)
=112.5
The train will travel 112.5 miles in 2.5 hours.
Question 2.
Water is leaking from a faucet at a constant rate of \(\frac{1}{3}\) gallons per minute.
a. What is the amount of water, w, in gallons per minute, that is leaked from the faucet after t minutes?
Answer:
Let C be the constant rate the water leaks from the faucet in gallons per minute. Then,
\(\frac{\frac{1}{3}}{1}\)=C, and \(\frac{w}{t}\)=C; therefore, \(\frac{\frac{1}{3}}{1}\) = \(\frac{w}{t}\).
\(\frac{\frac{1}{3}}{1}\)=\(\frac{w}{t}\)
w=\(\frac{1}{3}\) t
b. How much water is leaked after an hour?
Answer:
w=\(\frac{1}{3}\) t
=\(\frac{1}{3}\) (60)
=20
The faucet will leak 20 gallons in one hour.
Question 3.
A car can be assembled on an assembly line in 6 hours. Assume that the cars are assembled at a constant rate.
a. How many cars, y, can be assembled in t hours?
Answer:
Let C be the constant rate the cars are assembled in cars per hour. Then,
\(\frac{1}{6}\)=C, and \(\frac{y}{t}\)=C; therefore, \(\frac{1}{6}\)=\(\frac{y}{t}\).
\(\frac{1}{6}\)=\(\frac{y}{t}\)
6y=t
\(\frac{6}{6}\) y=\(\frac{1}{6}\)t
y=\(\frac{1}{6}\) t
b. How many cars can be assembled in a week?
Answer:
A week is 24×7=168 hours. So, y=\(\frac{1}{6}\) (168)=28. Twenty-eight cars can be assembled in a week.
Question 4.
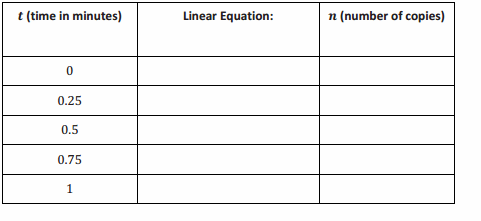
A copy machine makes copies at a constant rate. The machine can make 80 copies in 2 \(\frac{1}{2}\) minutes.
a. Write an equation to represent the number of copies, n, that can be made over any time interval in minutes, t.
Answer:
Let C be the constant rate that copies can be made in copies per minute. Then,
\(\frac{80}{2 \frac{1}{2}}\))=C, and \(\frac{n}{t}\)=C; therefore, \(\frac{80}{2 \frac{1}{2}}\)= \(\frac{n}{t}\).
\(\frac{80}{2 \frac{1}{2}}\)=\(\frac{n}{t}\)
2 \(\frac{1}{2}\) n=80t
\(\frac{5}{2}\) n=80t
\(\frac{2}{5}\)∙\(\frac{5}{2}\) n=\(\frac{2}{5}\)∙80t
n=32t
b. Complete the table below.
Answer:
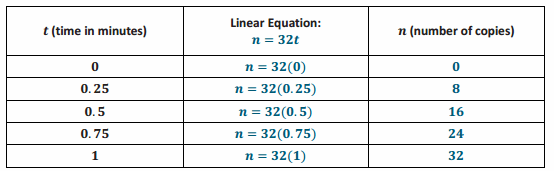
c. Graph the data on a coordinate plane.
Answer:
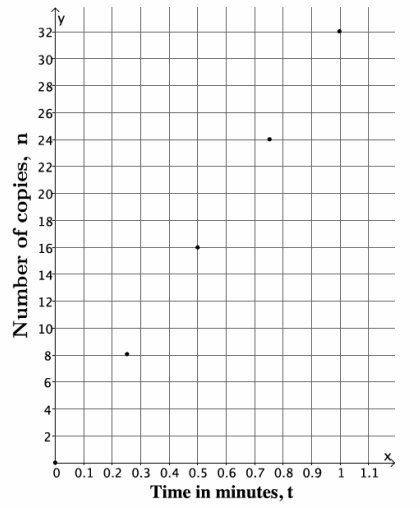
d. The copy machine runs for 20 seconds and then jams. About how many copies were made before the jam occurred? Explain.
Answer:
Since 20 seconds is approximately 0.3 of a minute, then the number of copies made will be between 8 and 16 because 0.3 is between 0.25 and 0.5.
Question 5.
Connor runs at a constant rate. It takes him 34 minutes to run 4 miles.
a. Write the linear equation in two variables that represents the number of miles Connor can run in any given time interval in minutes, t.
Answer:
Let C be the constant rate that Connor runs in miles per minute, and let m represent the number of miles he ran in t minutes. Then,
\(\frac{4}{34}\)=C, and \(\frac{m}{t}\)=C; therefore, \(\frac{4}{34}\)=\(\frac{m}{t}\).
\(\frac{4}{34}\)=\(\frac{m}{t}\)
34m=4t
\(\frac{34}{34}\) m=\(\frac{4}{34}\) t
m=\(\frac{4}{34}\) t
m=\(\frac{2}{17}\) t
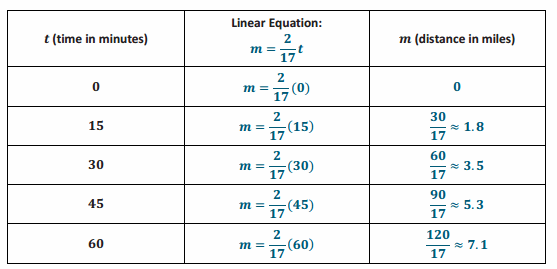
b. Complete the table below. Use a calculator, and round answers to the tenths place.
Answer:
c. Graph the data on a coordinate plane.
Answer:
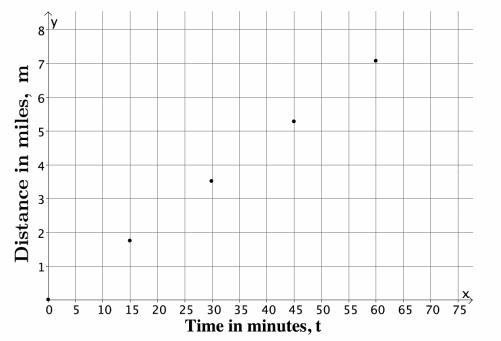
d. Connor ran for 40 minutes before tripping and spraining his ankle. About how many miles did he run before he had to stop? Explain.
Answer:
Since Connor ran for 40 minutes, he ran more than 3.5 miles but less than 5.3 miles. Since 40 is between 30 and 45, then we can use those reference points to make an estimate of how many miles he ran in 40 minutes, probably about 5 miles.