Engage NY Eureka Math 8th Grade Module 4 Lesson 25 Answer Key
Eureka Math Grade 8 Module 4 Lesson 25 Exercise Answer Key
Exploratory Challenge/Exercises 1–5
Exercise 1.
Sketch the graphs of the linear system on a coordinate plane: 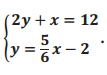
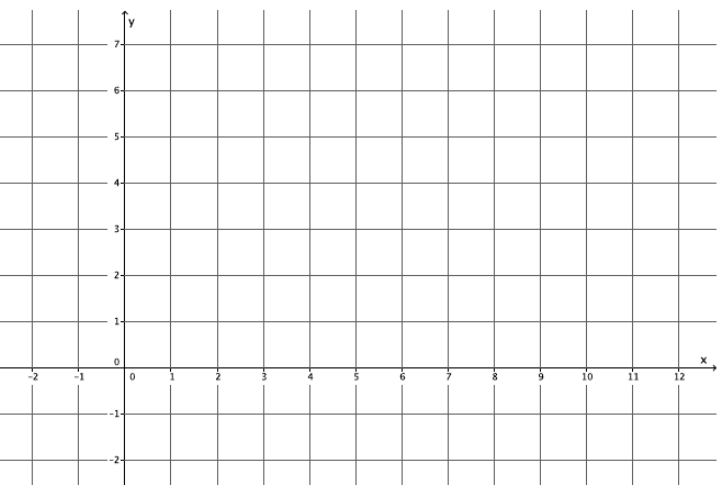
Answer:
For the equation 2y + x = 12:
2y + 0 = 12
2y = 12
y = 6
The y – intercept point is (0, 6).
2(0) + x = 12
x = 12
The x – intercept point is (12, 0).
For the equation y = \(\frac{5}{6}\) x – 2:
The slope is \(\frac{5}{6}\), and the y – intercept point is (0, – 2).
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(6, 3)
b. Verify that the ordered pair named in part (a) is a solution to 2y + x = 12.
Answer:
2(3) + 6 = 12
6 + 6 = 12
12 = 12
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to y = \(\frac{5}{6}\) x – 2.
Answer:
3 = \(\frac{5}{6}\) (6) – 2
3 = 5 – 2
3 = 3
The left and right sides of the equation are equal.
d. Could the point (4, 4) be a solution to the system of linear equations? That is, would (4, 4) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point (4, 4) is a solution to the equation 2y + x = 12 because it is on the graph of that equation. However, the point (4, 4) is not on the graph of the equation y = \(\frac{5}{6}\) x – 2. Therefore, (4, 4) cannot be a solution to the system of equations.
Exercise 2.
Sketch the graphs of the linear system on a coordinate plane:
x + y = – 2
y = 4x + 3
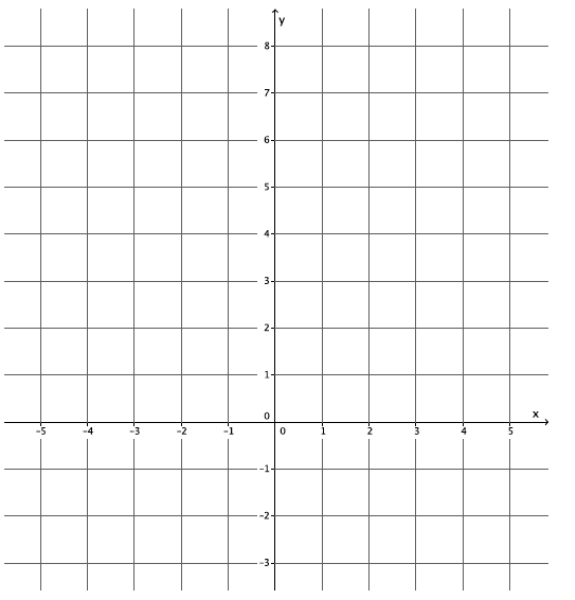
Answer:
For the equation x + y = – 2:
0 + y = – 2
y = – 2
The y – intercept point is (0, – 2).
x + 0 = – 2
x = – 2
The x – intercept point is ( – 2, 0).
For the equation y = 4x + 3:
The slope is \(\frac{4}{1}\), and the y – intercept point is (0, 3).
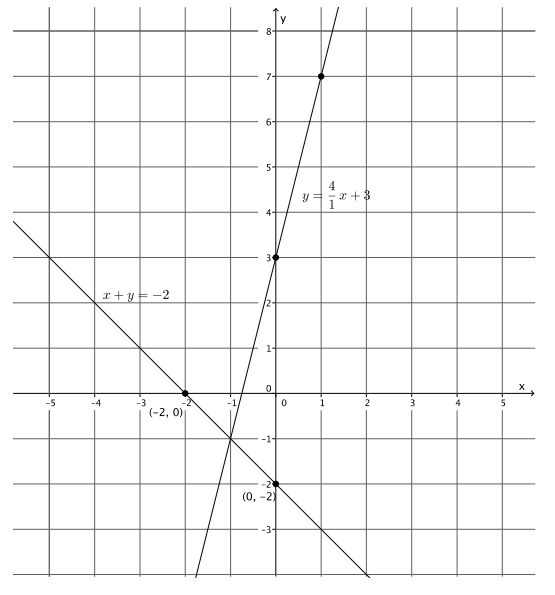
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 1, – 1)
b. Verify that the ordered pair named in part (a) is a solution to x + y = – 2.
Answer:
– 1 + ( – 1) = – 2
– 2 = – 2
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to y = 4x + 3.
Answer:
– 1 = 4( – 1) + 3
– 1 = – 4 + 3
– 1 = – 1
The left and right sides of the equation are equal.
d. Could the point ( – 4, 2) be a solution to the system of linear equations? That is, would ( – 4, 2) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point ( – 4, 2) is a solution to the equation x + y = – 2 because it is on the graph of that equation. However, the point ( – 4, 2) is not on the graph of the equation y = 4x + 3. Therefore, ( – 4, 2) cannot be a solution to the system of equations.
Exercise 3.
Sketch the graphs of the linear system on a coordinate plane:
3x + y = – 3
– 2x + y = 2
Answer:
For the equation 3x + y = – 3:
3(0) + y = – 3
y = – 3
The y – intercept point is (0, – 3).
3x + 0 = – 3
3x = – 3
x = – 1
The x – intercept point is ( – 1, 0).
For the equation – 2x + y = 2:
– 2(0) + y = 2
y = 2
The y – intercept point is (0, 2).
– 2x + 0 = 2
– 2x = 2
x = – 1
The x – intercept point is ( – 1, 0).
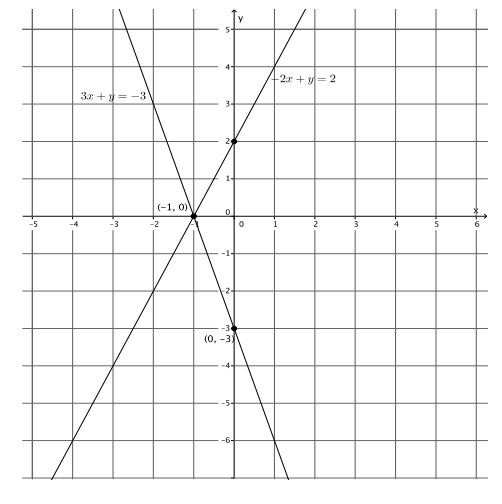
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 1, 0)
b. Verify that the ordered pair named in part (a) is a solution to 3x + y = – 3.
Answer:
3( – 1) + 0 = – 3
– 3 = – 3
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to – 2x + y = 2.
Answer:
– 2( – 1) + 0 = 2
2 = 2
The left and right sides of the equation are equal.
d. Could the point (1, 4) be a solution to the system of linear equations? That is, would (1, 4) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point (1, 4) is a solution to the equation – 2x + y = 2 because it is on the graph of that equation. However, the point (1, 4) is not on the graph of the equation 3x + y = – 3. Therefore, (1, 4) cannot be a solution to the system of equations.
Exercise 4.
Sketch the graphs of the linear system on a coordinate plane:
2x – 3y = 18
2x + y = 2
Answer:
For the equation 2x – 3y = 18:
2(0) – 3y = 18
– 3y = 18
y = – 6
The y – intercept point is (0, – 6).
2x – 3(0) = 18
2x = 18
x = 9
The x – intercept point is (9, 0).
For the equation 2x + y = 2:
2(0) + y = 2
y = 2
The y – intercept point is (0, 2).
2x + 0 = 2
2x = 2
x = 1
The x – intercept point is (1, 0).
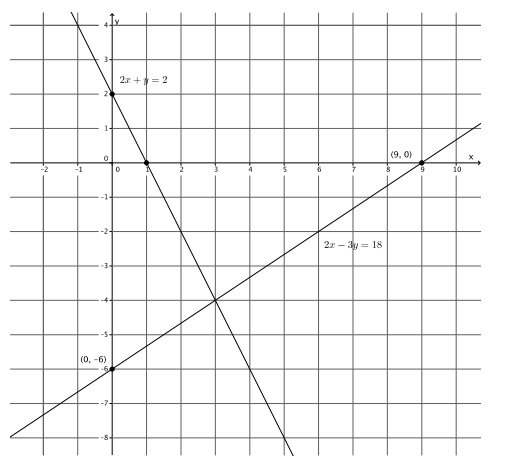
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(3, – 4)
b. Verify that the ordered pair named in part (a) is a solution to 2x – 3y = 18.
Answer:
2(3) – 3( – 4) = 18
6 + 12 = 18
18 = 18
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to 2x + y = 2.
Answer:
2(3) + ( – 4) = 2
6 – 4 = 2
2 = 2
The left and right sides of the equation are equal.
d. Could the point (3, – 1) be a solution to the system of linear equations? That is, would (3, – 1) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point (3, – 1) is not on the graph of either line; therefore, it is not a solution to the system of linear equations.
Exercise 5.
Sketch the graphs of the linear system on a coordinate plane:
y – x = 3
y = – 4x – 2
Answer:
For the equation y – x = 3:
y – 0 = 3
y = 3
The y – intercept point is (0, 3).
0 – x = 3
– x = 3
x = – 3
The x – intercept point is ( – 3, 0).
For the equation y = – 4x – 2:
The slope is – \(\frac{4}{1}\), and the y – intercept point is (0, – 2).
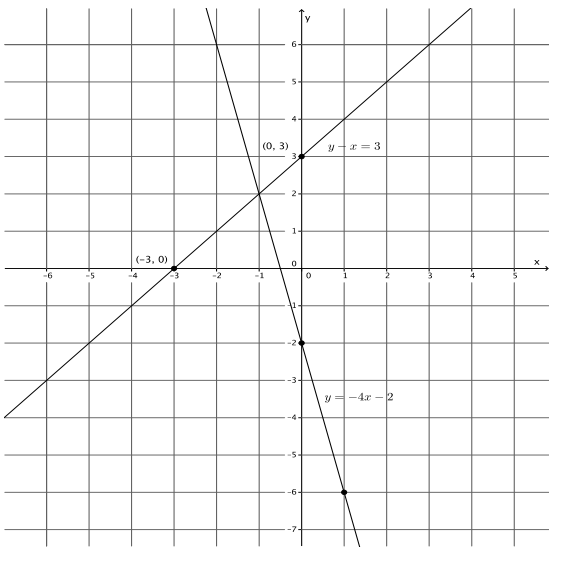
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 1, 2)
b. Verify that the ordered pair named in part (a) is a solution to y – x = 3.
Answer:
2 – ( – 1) = 3
3 = 3
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to y = – 4x – 2.
Answer:
2 = – 4( – 1) – 2
2 = 4 – 2
2 = 2
The left and right sides of the equation are equal.
d. Could the point ( – 2, 6) be a solution to the system of linear equations? That is, would ( – 2, 6) make both equations true? Why or why not?
Answer:
No. The graphs of the equations represent all of the possible solutions to the given equations. The point ( – 2, 6) is a solution to the equation y = – 4x – 2 because it is on the graph of that equation. However, the point ( – 2, 6) is not on the graph of the equation y – x = 3. Therefore, ( – 2, 6) cannot be a solution to the system of equations.
Exercise 6.
Write two different systems of equations with (1, – 2) as the solution.
Answer:
Answers will vary. Two sample solutions are provided:
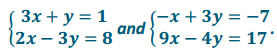
Eureka Math Grade 8 Module 4 Lesson 25 Problem Set Answer Key
Question 1.
Sketch the graphs of the linear system on a coordinate plane:
y = \(\frac{1}{3}\) x + 1
y = – 3x + 11
Answer:
For the equation y = \(\frac{1}{3}\) x + 1:
The slope is \(\frac{1}{3}\), and the y – intercept point is (0, 1).
For the equation y = – 3x + 11:
The slope is – \(\frac{3}{1}\), and the y – intercept point is (0, 11).
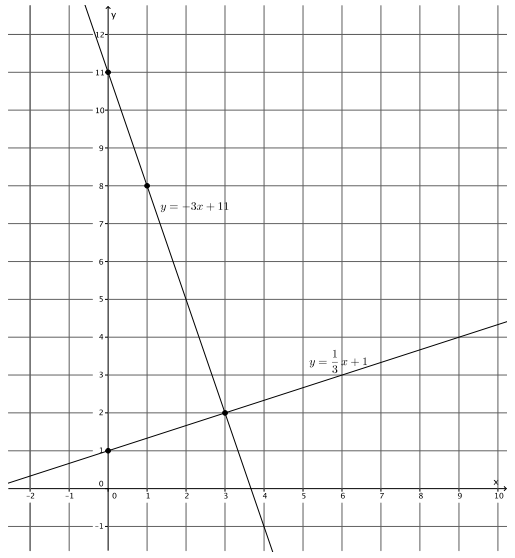
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(3, 2)
b. Verify that the ordered pair named in part (a) is a solution to y = \(\frac{3}{1}\) x + 1.
Answer:
2 = \(\frac{3}{1}\) (3) + 1
2 = 1 + 1
2 = 2
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to y = – 3x + 11.
Answer:
2 = – 3(3) + 11
2 = – 9 + 11
2 = 2
The left and right sides of the equation are equal.
Question 2.
Sketch the graphs of the linear system on a coordinate plane:
y = \(\frac{1}{2}\) x + 4
x + 4y = 4
Answer:
For the equation y = \(\frac{1}{2}\) x + 4:
The slope is \(\frac{1}{2}\), and the y – intercept point is(0, 4).
For the equation x + 4y = 4:
0 + 4y = 4
4y = 4
y = 1
The y – intercept point is (0, 1).
x + 4(0) = 4
x = 4
The x – intercept point is (4, 0).
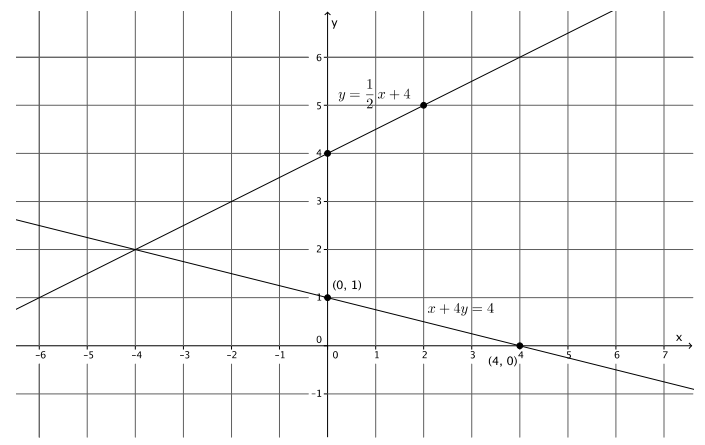
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 4, 2)
b. Verify that the ordered pair named in part (a) is a solution to y = \(\frac{1}{2}\) x + 4.
Answer:
2 = \(\frac{1}{2}\) ( – 4) + 4
2 = – 2 + 4
2 = 2
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to x + 4y = 4.
Answer:
– 4 + 4(2) = 4
– 4 + 8 = 4
4 = 4
The left and right sides of the equation are equal.
Question 3.
Sketch the graphs of the linear system on a coordinate plane:
y = 2
x + 2y = 10
Answer:
For the equation x + 2y = 10:
0 + 2y = 10
2y = 10
y = 5
The y – intercept point is (0, 5).
x + 2(0) = 10
x = 10
The x – intercept point is (10, 0).
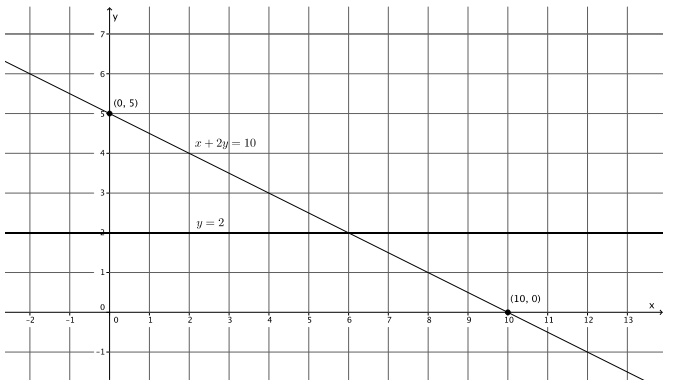
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(6, 2)
b. Verify that the ordered pair named in part (a) is a solution to y = 2.
Answer:
2 = 2
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to x + 2y = 10.
Answer:
6 + 2(2) = 10
6 + 4 = 10
10 = 10
The left and right sides of the equation are equal.
Question 4.
Sketch the graphs of the linear system on a coordinate plane:
– 2x + 3y = 18
2x + 3y = 6
Answer:
For the equation – 2x + 3y = 18:
– 2(0) + 3y = 18
3y = 18
y = 6
The y – intercept point is (0, 6).
– 2x + 3(0) = 18
– 2x = 18
x = – 9
The x – intercept point is ( – 9, 0).
For the equation 2x + 3y = 6:
2(0) + 3y = 6
3y = 6
y = 2
The y – intercept point is (0, 2).
2x + 3(0) = 6
2x = 6
x = 3
The x – intercept point is (3, 0).
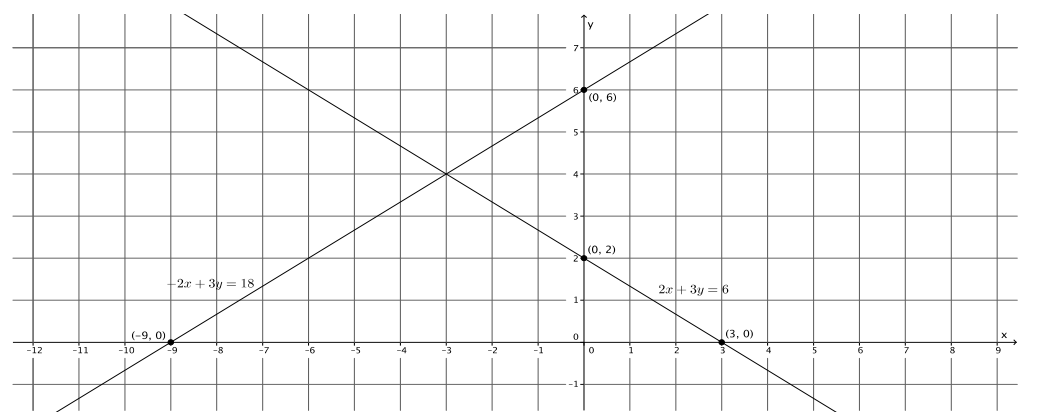
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
( – 3, 4)
b. Verify that the ordered pair named in part (a) is a solution to – 2x + 3y = 18.
Answer:
– 2( – 3) + 3(4) = 18
6 + 12 = 18
18 = 18
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to 2x + 3y = 6.
Answer:
2( – 3) + 3(4) = 6
– 6 + 12 = 6
6 = 6
The left and right sides of the equation are equal.
Question 5.
Sketch the graphs of the linear system on a coordinate plane:
x + 2y = 2
y = \(\frac{2}{3}\) x – 6
Answer:
For the equation x + 2y = 2:
0 + 2y = 2
2y = 2
y = 1
The y – intercept point is (0, 1).
x + 2(0) = 2
x = 2
The x – intercept point is (2, 0).
For the equation y = \(\frac{2}{3}\) x – 6:
The slope is \(\frac{2}{3}\), and the y – intercept point is (0, – 6).
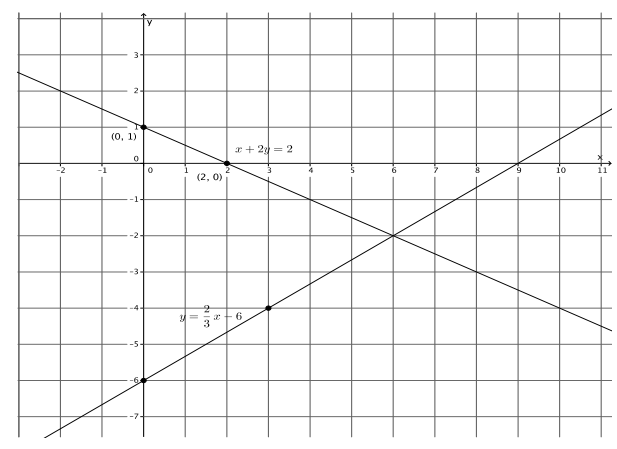
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(6, – 2)
b. Verify that the ordered pair named in part (a) is a solution to x + 2y = 2.
Answer:
6 + 2( – 2) = 2
6 – 4 = 2
2 = 2
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to y = \(\frac{2}{3}\) x – 6.
Answer:
– 2 = \(\frac{2}{3}\) (6) – 6
– 2 = 4 – 6
– 2 = – 2
The left and right sides of the equation are equal.
Question 6.
Without sketching the graph, name the ordered pair where the graphs of the two linear equations intersect.
x = 2
y = – 3
Answer:
(2, – 3)
Eureka Math Grade 8 Module 4 Lesson 25 Exit Ticket Answer Key
Question 1.
Sketch the graphs of the linear system on a coordinate plane:
2x – y = – 1
y = 5x – 5
Answer:
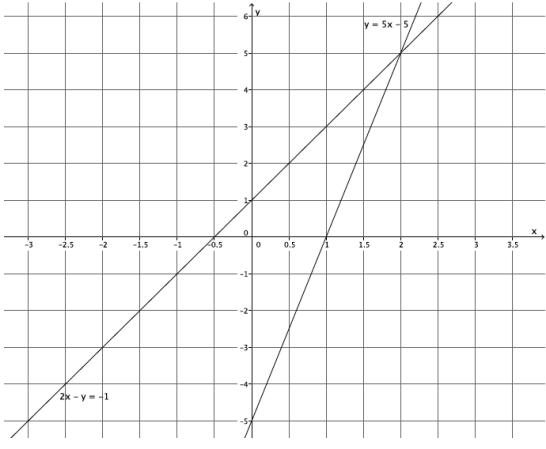
a. Name the ordered pair where the graphs of the two linear equations intersect.
Answer:
(2, 5)
b. Verify that the ordered pair named in part (a) is a solution to 2x – y = – 1.
Answer:
2(2) – 5 = – 1
4 – 5 = – 1
– 1 = – 1
The left and right sides of the equation are equal.
c. Verify that the ordered pair named in part (a) is a solution to y = 5x – 5.
Answer:
5 = 5(2) – 5
5 = 10 – 5
5 = 5
The left and right sides of the equation are equal.