Engage NY Eureka Math 8th Grade Module 4 Lesson 23 Answer Key
Eureka Math Grade 8 Module 4 Lesson 23 Exercise Answer Key
Exploratory Challenge/Exercises 1–3
Exercise 1.
Sketch the graph of the equation 9x + 3y = 18 using intercepts. Then, answer parts (a)–(f) that follow.
Answer:
9(0) + 3y = 18
3y = 18
y = 6
The y – intercept point is (0,6).
9x + 3(0) = 18
9x = 18
x = 2
The x – intercept point is (2,0).
a. Sketch the graph of the equation y = – 3x + 6 on the same coordinate plane.
Answer:
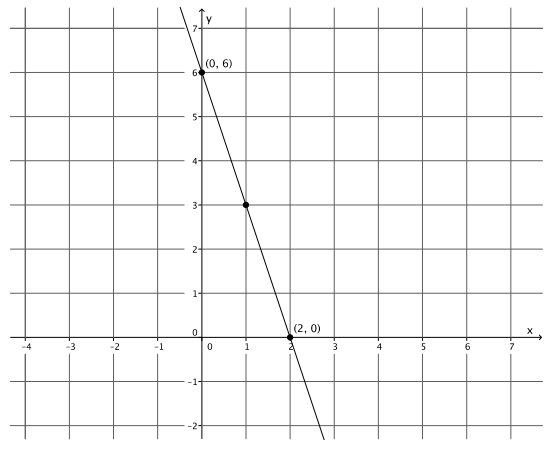
b. What do you notice about the graphs of 9x + 3y = 18 and y = – 3x + 6? Why do you think this is so?
Answer:
The graphs of the equations produce the same line. Both equations go through the same two points, so they are the same line.
c. Rewrite y = – 3x + 6 in standard form.
Answer:
y = – 3x + 6
3x + y = 6
d. Identify the constants a, b, and c of the equation in standard form from part (c).
Answer:
a = 3, b = 1, and c = 6
e. Identify the constants of the equation 9x + 3y = 18. Note them as a’, b’, and c’.
Answer:
a’ = 9, b’ = 3, and c’ = 18
f. What do you notice about \(\frac{a^{\prime}}{a}\), \(\frac{b^{\prime}}{b}\), and \(\frac{c^{\prime}}{c}\)?
Answer:
\(\frac{a^{\prime}}{a}\) = \(\frac{9}{3}\) = 3, \(\frac{b^{\prime}}{b}\) = \(\frac{3}{1}\) = 3, and \(\frac{c^{\prime}}{c}\) = \(\frac{18}{6}\) = 3
Each fraction is equal to the number 3.
Exercise 2.
Sketch the graph of the equation y = \(\frac{1}{2}\) x + 3 using the 𝒚y – intercept point and the slope. Then, answer parts (a)–(f) that follow.
a. Sketch the graph of the equation 4x – 8y = – 24 using intercepts on the same coordinate plane.
Answer:
4(0) – 8y = – 24
– 8y = – 24
y = 3
The y – intercept point is (0,3).
4x – 8(0) = – 24
4x = – 24
x = – 6
The x – intercept point is ( – 6,0).
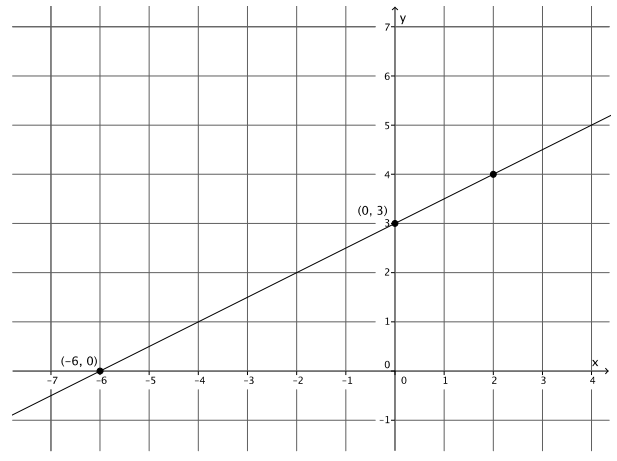
b. What do you notice about the graphs of y = \(\frac{1}{2}\) x + 3 and 4x – 8y = – 24? Why do you think this is so?
Answer:
The graphs of the equations produce the same line. Both equations go through the same two points, so they are the same line.
c. Rewrite y = \(\frac{1}{2}\) x + 3 in standard form.
Answer:
y = \(\frac{1}{2}\) x + 3
(y = \(\frac{1}{2}\) x + 3)2
2y = x + 6
– x + 2y = 6
– 1( – x + 2y = 6)
x – 2y = – 6
d. Identify the constants a, b, and c of the equation in standard form from part (c).
Answer:
a = 1, b = – 2, and c = – 6
e. Identify the constants of the equation 4x – 8y = – 24. Note them as a’, b’, and c’.
Answer:
a’ = 4, b’ = – 8, and c’ = – 24
f. What do you notice about \(\frac{a^{\prime}}{a}\), \(\frac{b^{\prime}}{b}\), and \(\frac{c^{\prime}}{c}\)?
Answer:
\(\frac{a^{\prime}}{a}\) = \(\frac{4}{1}\) = 4, \(\frac{b^{\prime}}{b}\) = \(\frac{ – 8}{ – 2}\) = 4, and \(\frac{c^{\prime}}{c}\) = \(\frac{ – 24}{ – 6}\) = 4
Each fraction is equal to the number 4.
Exercise 3.
The graphs of the equations y = \(\frac{2}{3}\) x – 4 and 6x – 9y = 36 are the same line.
a. Rewrite y = \(\frac{2}{3}\) x – 4 in standard form.
Answer:
y = \(\frac{2}{3}\) x – 4
(y = \(\frac{2}{3}\) x – 4)3
3y = 2x – 12
– 2x + 3y = – 12
– 1( – 2x + 3y = – 12)
2x – 3y = 12
b. Identify the constants a, b, and c of the equation in standard form from part (a).
Answer:
a = 2, b = – 3, and c = 12
c. Identify the constants of the equation 6x – 9y = 36. Note them as a’, b’, and c’.
Answer:
a’ = 6, b’ = – 9, and c’ = 36
d. What do you notice about \(\frac{a^{\prime}}{a}\), \(\frac{b^{\prime}}{b}\), and \(\frac{c^{\prime}}{c}\)?
Answer:
\(\frac{a^{\prime}}{a}\) = \(\frac{6}{2}\) = 3, \(\frac{b^{\prime}}{b}\) = \(\frac{ – 9}{ – 3}\) = 3, and \(\frac{c^{\prime}}{c}\) = \(\frac{36}{12}\) = 3
Each fraction is equal to the number 3.
e. You should have noticed that each fraction was equal to the same constant. Multiply that constant by the standard form of the equation from part (a). What do you notice?
Answer:
2x – 3y = 12
3(2x – 3y = 12)
6x – 9y = 36
After multiplying the equation from part (a) by 3, I noticed that it is the exact same equation that was given.
Exercises 4–8
Exercise 4.
Write three equations whose graphs are the same line as the equation 3x + 2y = 7.
Answer:
Answers will vary. Verify that students have multiplied a, b, and c by the same constant when they write the new equation.
Exercise 5.
Write three equations whose graphs are the same line as the equation x – 9y = \(\frac{3}{4}\).
Answer:
Answers will vary. Verify that students have multiplied a, b, and c by the same constant when they write the new equation.
Exercise 6.
Write three equations whose graphs are the same line as the equation – 9x + 5y = – 4.
Answer:
Answers will vary. Verify that students have multiplied a, b, and c by the same constant when they write the new equation.
Exercise 7.
Write at least two equations in the form ax + by = c whose graphs are the line shown below.
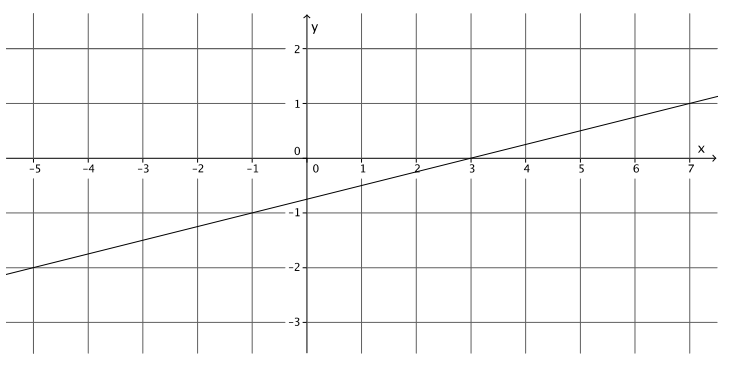
Answer:
Answers will vary. Verify that students have the equation – x + 4y = – 3 in some form.
Exercise 8.
Write at least two equations in the form ax + by = c whose graphs are the line shown below.
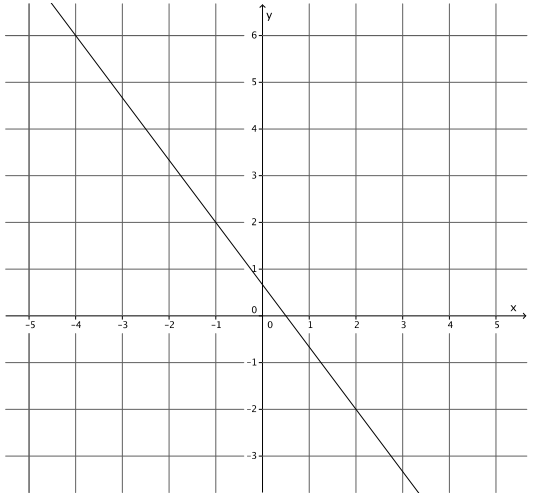
Answer:
Answers will vary. Verify that students have the equation 4x + 3y = 2 in some form.
Eureka Math Grade 8 Module 4 Lesson 23 Problem Set Answer Key
Question 1.
Do the equations x + y = – 2 and 3x + 3y = – 6 define the same line? Explain.
Yes, these equations define the same line. When you compare the constants from each equation, you get
Answer:
\(\frac{a^{\prime}}{a}\) = \(\frac{3}{1}\) = 3, \(\frac{b^{\prime}}{b}\) = \(\frac{3}{1}\) = 3, and \(\frac{c^{\prime}}{c}\) = \(\frac{ – 6}{ – 2}\) = 3
When I multiply the first equation by 3, I get the second equation.
(x + y = – 2)3
3x + 3y = – 6
Therefore, these equations define the same line.
Question 2.
Do the equations y = – \(\frac{5}{4}\) x + 2 and 10x + 8y = 16 define the same line? Explain.
Answer:
Yes, these equations define the same line. When you rewrite the first equation in standard form, you get
y = – \(\frac{5}{4}\) x + 2
(y = – \(\frac{5}{4}\) x + 2)4
4y = – 5x + 8
5x + 4y = 8″.”
When you compare the constants from each equation, you get
\(\frac{a^{\prime}}{a}\) = \(\frac{10}{5}\) = 2, \(\frac{b^{\prime}}{b}\) = \(\frac{8}{4}\) = 2, and \(\frac{c^{\prime}}{c}\) = \(\frac{16}{8}\) = 2.
When I multiply the first equation by 2, I get the second equation.
(5x + 4y = 8)2
10x + 8y = 16
Therefore, these equations define the same line.
Question 3.
Write an equation that would define the same line as 7x – 2y = 5.
Answer:
Answers will vary. Verify that students have written an equation that defines the same line by showing that the fractions \(\frac{a^{\prime}}{a}\) = \(\frac{b^{\prime}}{b}\) = \(\frac{c^{\prime}}{c}\) = s, where s is some constant.
Question 4.
Challenge: Show that if the two lines given by ax + by = c and a’x + b’y = c’ are the same when b = 0 (vertical lines), then there exists a nonzero number s so that a’ = sa, b’ = sb, and c’ = sc.
Answer:
When b = 0, then the equations are ax = c and a’x = c’. We can rewrite the equations as x = \(\frac{c}{a}\) and x = \(\frac{c^{\prime}}{a^{\prime}}\). Because the equations graph as the same line, then we know that
\(\frac{c}{a} = \frac{c^{\prime}}{a^{\prime}}\)
and we can rewrite those fractions as
\(\frac{a^{\prime}}{a} = \frac{c^{\prime}}{c}\)
These fractions are equal to the same number. Let that number be s. Then \(\frac{a^{\prime}}{a}\) = s and \(\frac{c^{\prime}}{c}\) = s. Therefore, a’ = sa and c’ = sc.
Question 5.
Challenge: Show that if the two lines given by ax + by = c and a’x + b’y = c’ are the same when a = 0 (horizontal lines), then there exists a nonzero number s so that a’ = sa, b’ = sb, and c’ = sc.
Answer:
When a = 0, then the equations are by = c and b’y = c’. We can rewrite the equations as y = \(\frac{c}{b}\) and y = \(\frac{c^{\prime}}{b^{\prime}}\). Because the equations graph as the same line, then we know that their slopes are the same.
\(\frac{c}{b} = \frac{c^{\prime}}{b^{\prime}}\)
We can rewrite the proportion.
\(\frac{b^{\prime}}{b} = \frac{c^{\prime}}{c}\)
These fractions are equal to the same number. Let that number be s. Then \(\frac{b^{\prime}}{b}\) = s and \(\frac{c^{\prime}}{c}\) = s. Therefore, b’ = sb and c’ = sc.
Eureka Math Grade 8 Module 4 Lesson 23 Exit Ticket Answer Key
Question 1.
Do the graphs of the equations – 16x + 12y = 33 and – 4x + 3y = 8 graph as the same line? Why or why not?
Answer:
No. In the first equation, a = – 16, b = 12, and c = 33, and in the second equation, a’ = – 4, b’ = 3, and c’ = 8. Then,
\(\frac{a^{\prime}}{a}\) = \(\frac{ – 4}{ – 16}\) = \(\frac{1}{4}\), \(\frac{b^{\prime}}{b}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\), and \(\frac{c^{\prime}}{c}\) = \(\frac{8}{33}\) = \(\frac{8}{33}\)
Since each fraction does not equal the same number, then they do not have the same graph.
Question 2.
Given the equation 3x – y = 11, write another equation that will have the same graph. Explain why.
Answer:
Answers will vary. Verify that students have written an equation that defines the same line by showing that the fractions \(\frac{a^{\prime}}{a}\) = \(\frac{b^{\prime}}{b}\) = \(\frac{c^{\prime}}{c}\) = s, where s is some constant.