Hello Kids!!! What you are waiting for? Here is the Answer Key for Go Math HMH Grade 4 Chapter 7? Just make use of these Go Math Grade 4 Answer Key Homework Practice FL Chapter 7 Add and Subtract Fractions and practice well. Students who are preparing for the grade 4 maths exam can get this Go Math Grade 4 Answer Key Homework Practice FL Chapter 7 Add and Subtract Fractions pdf from here to access and download for free.
Go Math Grade 4 Answer Key Homework Practice FL Chapter 7 Add and Subtract Fractions
Download Go Math Grade 4 Solution Key Homework Practice FL Chapter 7 Add and Subtract Fractions in pdf format and aid your preparation. First of all, begin your practice session with textbook solutions and then jump into this Go Math Grade 4 Answer Key Homework Practice FL Chapter 7 Add and Subtract Fractions for gaining better subject knowledge. These solutions are written by subject experts in a comprehend manner. So, you all can easily understand and practice more concepts.
Lesson: 1 – Add and Subtract Parts of a Whole
- Common Core – Add and Subtract Fractions – Page No. 133
- Common Core – Add and Subtract Fractions – Page No. 134
Lesson: 2 – Write Fractions as Sums
- Common Core – Add and Subtract Fractions – Page No. 135
- Common Core – Add and Subtract Fractions – Page No. 136
Lesson: 3 – Add Fractions Using Models
- Common Core – Add and Subtract Fractions – Page No. 137
- Common Core – Add and Subtract Fractions – Page No. 138
Lesson: 4 – Subtract Fractions Using Models
- Common Core – Add and Subtract Fractions – Page No. 139
- Common Core – Add and Subtract Fractions – Page No. 140
Lesson: 5 – Add and Subtract Fractions
- Common Core – Add and Subtract Fractions – Page No. 141
- Common Core – Add and Subtract Fractions – Page No. 142
Lesson: 6 – Rename Fractions and Mixed Numbers
- Common Core – Add and Subtract Fractions – Page No. 143
- Common Core – Add and Subtract Fractions – Page No. 144
Lesson: 7 – Add and Subtract Mixed Numbers
- Common Core – Add and Subtract Fractions – Page No. 145
- Common Core – Add and Subtract Fractions – Page No. 146
Lesson: 8 – Record Subtraction with
- Common Core – Add and Subtract Fractions – Page No. 147
- Common Core – Add and Subtract Fractions – Page No. 148
Lesson: 9 – Fractions and Properties of Addition
- Common Core – Add and Subtract Fractions – Page No. 149
- Common Core – Add and Subtract Fractions – Page No. 150
Lesson: 10 – Read each problem and solve.
- Common Core – Add and Subtract Fractions – Page No. 151
- Common Core – Add and Subtract Fractions – Page No. 152
Lesson 7.1
- Common Core – Add and Subtract Fractions – Page No. 153
- Common Core – Add and Subtract Fractions – Page No. 154
Common Core – Add and Subtract Fractions – Page No. 133
Add and Subtract Parts of a Whole
Use the model to write an equation.
Question 1.
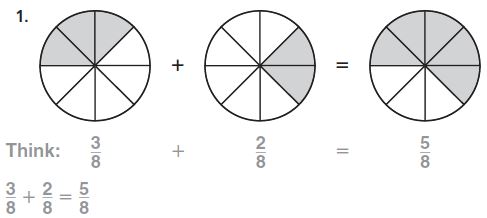
Explanation:
By seeing the above 3 figures we can say that the fraction of the shaded part of the first circle is 3/8, the fraction of the second figure is 2/8
By adding the 2 fractions we get the fraction of the third circle.
3/8 + 2/8 = 5/8
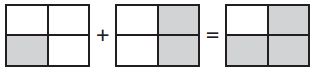
Question 2.
Type below:
_________
Answer: 4/5 – 3/5 = 1/5
Explanation:
The fraction of the shaded part for the above rectangle is 4/5
The fraction of the box is 3/5
The equation for the above figure is 4/5 – 3/5 = 1/5
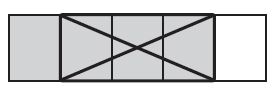
Question 3.
Type below:
_________
Answer: 1/4 + 2/4 = 3/4
Explanation:
The name of the fraction for the shaded part of first figure is 1/4
The name of the fraction for the shaded part of second figure is 1/4
The name of the fraction for the shaded part of third figure is 3/4
So, The equation for the above figure is 1/4 + 2/4 = 3/4
Use the model to solve the equation.
Question 4.
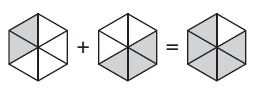
\(\frac{2}{6}+\frac{3}{6}\) = \(\frac{□}{□}\)
Answer: \(\frac { 2 }{ 6 } +\frac { 3 }{ 6 } =\frac { 5 }{ 6 } \)
Explanation:
The name of the fraction for the shaded part of first figure is 2/6
The name of the fraction for the shaded part of second figure is 3/6
The name of the fraction for the shaded part of third figure is 5/6
So, The equation for the above figure is \(\frac { 2 }{ 6 } +\frac { 3 }{ 6 } =\frac { 5 }{ 6 } \)
Question 5.
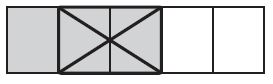
\(\frac{3}{5}-\frac{2}{5}\) = \(\frac{□}{□}\)
Answer: \(\frac { 3 }{ 5 } -\frac { 2 }{ 5 } =\frac { 1 }{ 5 } \)
Explanation:
The name of the fraction for the shaded part of figure is 3/5
The name of the fraction for the shaded part of closed box is 2/5
So, The equation for the above figure is \(\frac { 3 }{ 5 } -\frac { 2 }{ 5 } =\frac { 1 }{ 5 } \)
Problem Solving
Question 6.
Jake ate \(\frac{4}{8}\) of a pizza. Millie ate \(\frac{3}{8}\) of the same pizza. How much of the pizza was eaten by Jake and Millie?
\(\frac{□}{□}\)
Answer: 7/8 of pizza
Explanation:
Given that,
Jake ate \(\frac { 4 }{ 8 } \) of a pizza.
Millie ate \(\frac { 3}{ 8 } \) of the same pizza.
To find how much of the pizza was eaten by Jake and Millie
We have to add both the fractions
\(\frac { 4 }{ 8 } \) + \(\frac { 3 }{ 8 } \) = \(\frac { 7 }{ 8 } \)
Thus the fraction of the pizza eaten by Jake and Millie is \(\frac { 7 }{ 8 } \)
Question 7.
Kate ate \(\frac{1}{4}\) of her orange. Ben ate \(\frac{2}{4}\) of his banana. Did Kate and Ben eat \(\frac{1}{4}+\frac{2}{4}=\frac{3}{4}\) of their fruit?
Explain.
Type below:
__________
Answer: No, one whole refers to orange and the other whole to a banana.
Common Core – Add and Subtract Fractions – Page No. 134
Lesson Check
Question 1.
A whole pie is cut into 8 equal slices. Three of the slices are served. How much of the pie is left?
Options:
a. \(\frac{1}{8}\)
b. \(\frac{3}{8}\)
c. \(\frac{5}{8}\)
d. \(\frac{7}{8}\)
Answer: \(\frac { 5 }{ 8} \)
Explanation:
Given,
A whole pie is cut into 8 equal slices. Three of the slices are served.
The fraction of 8 slices is 8/8.
Out of which 3/8 are served.
8/8 – 3/8 = 5/8
Therefore \(\frac { 5 }{ 8} \) of the pie is left.
Thus the correct answer is option c.
Question 2.
An orange is divided into 6 equal wedges. Jody eats 1 wedge. Then she eats 3 more wedges. How much of the orange did Jody eat?
Options:
a. \(\frac{1}{6}\)
b. \(\frac{4}{6}\)
c. \(\frac{5}{6}\)
d. \(\frac{6}{6}\)
Answer: \(\frac { 4}{ 6 } \)
Explanation:
Given,
An orange is divided into 6 equal wedges.
Jody eats 1 wedge.
Then she eats 3 more wedges.
The fraction of orange that Jody eat is \(\frac { 4}{ 6 } \).
Thus the correct answer is option b.
Spiral Review
Question 3.
Which list of distances is in order from least to greatest?
Options:
a. \(\frac{1}{8} mile, \frac{3}{16} mile, \frac{3}{4} mile\)
b. \(\frac{3}{4} mile, \frac{1}{8} mile, \frac{3}{16} mile\)
c. \(\frac{1}{8} mile, \frac{3}{4} mile, \frac{3}{16} mile\)
d. \(\frac{3}{16} mile, \frac{1}{8} mile, \frac{3}{4} mile\)
Answer: \(\frac { 1 }{ 8 } \) Mile, \(\frac { 3 }{ 16 } \) Mile, \(\frac { 3 }{ 4 } \) Mile
Explantion:
Compare the three fractions 1/8, 3/4 and 3/16
Make the common denominators.
1/8 × 2/2 = 2/16
3/4 × 4/4 = 12/16
The fractions are 2/16, 12/16 and 3/16
The numerator with the highest number will be the greatest.
The fractions from least to greatest is \(\frac { 1 }{ 8 } \) Mile, \(\frac { 3 }{ 16 } \) Mile, \(\frac { 3 }{ 4 } \) Mile.
Thus the correct answer is option d.
Question 4.
Jeremy walked \(\frac{6}{8}\) of the way to school and ran the rest of the way. What fraction, in simplest form, shows the part of the way that Jeremy walked?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{3}{8}\)
c. \(\frac{1}{2}\)
d. \(\frac{3}{4}\)
Answer: \(\frac { 3 }{ 4 } \)
Explanation:
Given,
Jeremy walked 6/8 of the way to school and ran the rest of the way.
The simplest form of 6/8 is 3/8.
The simplest form of part of the way that Jeremy walked is 3/8.
Thus the correct answer is option b.
Question 5.
An elevator starts on the 100th floor of a building. It descends 4 floors every 10 seconds. At what floor will the elevator be 60 seconds after it starts?
Options:
a. 60th floor
b. 66th floor
c. 72nd floor
d. 76th floor
Answer: 76th floor
Explanation:
Given,
An elevator starts on the 100th floor of a building.
It descends 4 floors every 10 seconds.
4 floors – 10 seconds
? – 60 seconds
60 × 4/10 = 240/10 = 24 floors
100 – 24 = 76th floor
Thus the correct answer is option d.
Question 6.
For a school play, the teacher asked the class to set up chairs in 20 rows with 25 chairs in each row. After setting up all the chairs, they were 5 chairs short. How many chairs did the class set up?
Options:
a. 400
b. 450
c. 495
d. 500
Answer: 495
Explanation:
Given,
For a school play, the teacher asked the class to set up chairs in 20 rows with 25 chairs in each row.
After setting up all the chairs, they were 5 chairs short.
20 × 25 = 500
500 – 5 = 495
Therefore the class set up 495 chairs.
Thus the correct answer is c.
Common Core – Add and Subtract Fractions – Page No. 135
Write Fractions as Sums
Write the fraction as a sum of unit fractions.
Question 1.
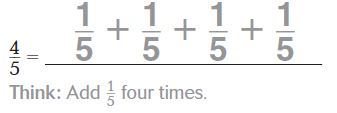
Answer: 1/5 + 1/5 + 1/5 + 1/5
Explanation:
The sum of the unit fractions for 4/5 is 1/5 + 1/5 + 1/5 + 1/5.
Question 2.
\(\frac{3}{8}\) =
Type below:
__________
Answer: 1/8 + 1/8 + 1/8
Explanation:
The sum of the unit fractions for 3/8 is 1/8 + 1/8 + 1/8
Question 3.
\(\frac{6}{12}\) =
Type below:
__________
Answer: 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12
Explanation:
The sum of the unit fractions for 6/12 is 1/12 + 1/12 + 1/12 + 1/12 + 1/12 + 1/12
Question 4.
\(\frac{4}{4}\) =
Type below:
__________
Answer: 1/4 + 1/4 + 1/4 + 1/4
Explanation:
The sum of the unit fractions for 4/4 is 1/4 + 1/4 + 1/4 + 1/4
Write the fraction as a sum of fractions three different ways.
Question 5.
\(\frac{7}{10}\)
Type below:
__________
Answer: 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10
Explanation:
The sum of the unit fractions for 7/10 is 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10 + 1/10
Question 6.
\(\frac{6}{6}\)
Type below:
__________
Answer: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6
Explanation:
The sum of the unit fractions for 6/6 is 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6
Problem Solving
Question 7.
Miguel’s teacher asks him to color \(\frac{4}{8}\) of his grid. He must use 3 colors: red, blue, and green. There must be more green sections than red sections. How can Miguel color the sections of his grid to follow all the rules?
Type below:
__________
Answer: 1/8 red, 1/8 blue, and 2/8 green
Explanation:
If there are 8 tiles, coloring \(\frac { 4 }{ 8 }\) means coloring 4 tiles. Using those three colors, we could use each 1 time with 1 leftover. Since we must have more green, we would use it twice; this would give us 2 green, 1 red and 1 blue.
Since the grid is not necessarily 8 squares, we must account for this by saying 2/8 green, 1/8 red, and 1/8 blue
Question 8.
Petra is asked to color \(\frac{6}{6}\) of her grid. She must use 3 colors: blue, red, and pink. There must be more blue sections than red sections or pink sections. What are the different ways Petra can color the sections of her grid and follow all the rules?
Type below:
__________
Answer: 3/6 blue, 2/6 red, 1/6 pink
Explanation:
1. 3 blues, 2 red, 1 pink.
2. 3 blues, 2 pink, 1 red.
3. 4 blues, 1 red, 1 pink
The different ways in which Petra can color the sections of her grid and follow the rules are;
1. 3 blues, 2 red, 1 pink.
2. 3 blues, 2 pink, 1 red.
3. 4 blues, 1 red, 1 pink
All these three ways follows the rules that; there must be three colors an also Blue sections are more than red sections or pink sections.
Common Core – Add and Subtract Fractions – Page No. 136
Lesson Check
Question 1.
Jorge wants to write \(\frac{4}{5}\) as a sum of unit fractions. Which of the following should he write?
Options:
a. \(\frac{3}{5}+\frac{1}{5}\)
b. \(\frac{2}{5}+\frac{2}{5}\)
c. \(\frac{1}{5}+\frac{1}{5}+\frac{2}{5}\)
d. \(\frac{1}{5}+\frac{1}{5}+\frac{1}{5}+\frac{1}{5}\)
Answer: \(\frac { 1 }{ 5 } +\frac { 1 }{ 5 } +\frac { 1 }{ 5 } +\frac { 1 }{ 5 } \)
Explanation:
Given,
Jorge wants to write \(\frac { 4 }{ 5 } \) as a sum of unit fractions.
The sum of the unit fraction for \(\frac { 4 }{ 5 } \) is \(\frac { 1 }{ 5 } +\frac { 1 }{ 5 } +\frac { 1 }{ 5 } +\frac { 1 }{ 5 } \)
Thus the correct answer is option d.
Question 2.
Which expression is equivalent to \(\frac{7}{8}\)?
Options:
a. \(\frac{5}{8}+\frac{2}{8}+\frac{1}{8}\)
b. \(\frac{3}{8}+\frac{3}{8}+\frac{1}{8}+\frac{1}{8}\)
c. \(\frac{4}{8}+\frac{2}{8}+\frac{1}{8}\)
d. \(\frac{4}{8}+\frac{2}{8}+\frac{2}{8}\)
Answer: \(\frac { 4 }{ 8 } +\frac { 2 }{ 8 }+\frac { 1 }{ 8 } \)
Explanation:
The fraction equivalent to \(\frac { 7 }{ 8 } \) is \(\frac { 4 }{ 8 } +\frac { 2 }{ 8 }+\frac { 1 }{ 8 } \).
Thus the correct answer is option c.
Spiral Review
Question 3.
An apple is cut into 6 equal slices. Nancy eats 2 of the slices. What fraction of the apple is left?
Options:
a. \(\frac{1}{6}\)
b. \(\frac{2}{6}\)
c. \(\frac{3}{6}\)
d. \(\frac{4}{6}\)
Answer: \(\frac { 4 }{ 6 } \)
Explanation:
Given,
An apple is cut into 6 equal slices. Nancy eats 2 of the slices.
6 – 2 = 4
\(\frac { 6 }{ 6 } \) – \(\frac { 2 }{ 6 } \) = \(\frac { 4 }{ 6 } \)
Thus the correct answer is option d.
Question 4.
Which of the following numbers is a prime number?
Options:
a. 1
b. 11
c. 21
d. 51
Answer: 11
Explanation:
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers.
11 is a multiple of 1 and itself.
Thus the correct answer is option b.
Question 5.
A teacher has a bag of 100 unit cubes. She gives an equal number of cubes to each of the 7 groups in her class. She gives each group as many cubes as she
can. How many unit cubes are left over?
Options:
a. 1
b. 2
c. 3
d. 6
Answer: 2
Explanation:
Given,
A teacher has a bag of 100 unit cubes. She gives an equal number of cubes to each of the 7 groups in her class.
She gives each group as many cubes as she can.
100 divided by 7 is 14 r 2, so there are 2 leftover.
Thus the correct answer is option b.
Question 6.
Jessie sorted the coins in her bank. She made 7 stacks of 6 dimes and 8 stacks of 5 nickels. She then found 1 dime and 1 nickel. How many dimes and nickels does Jessie have in all?
Options:
a. 84
b. 82
c. 80
d. 28
Answer: 84
Explanation:
Given,
Jessie sorted the coins in her bank. She made 7 stacks of 6 dimes and 8 stacks of 5 nickels.
She then found 1 dime and 1 nickel.
43 dimes and 41 nickles
43 + 41 = 84
Jessie has 84 dimes and nickels in all.
Thus the correct answer is option a.
Common Core – Add and Subtract Fractions – Page No. 137
Add Fractions Using Models
Find the sum. Use fraction strips to help.
Question 1.
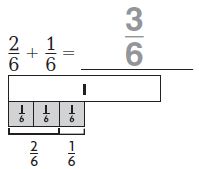
Answer: 3/6
Question 2.
\(\frac{4}{10}+\frac{5}{10}\) = \(\frac{□}{□}\)
Answer: 9/10
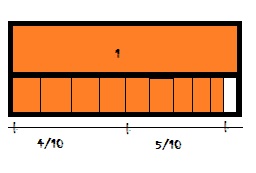
Question 3.
\(\frac{1}{3}+\frac{2}{3}\) = \(\frac{□}{□}\)
Answer: 3/3
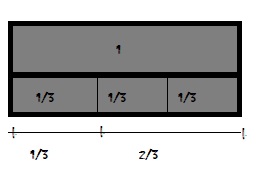
Question 4.
\(\frac{2}{4}+\frac{1}{4}\) = \(\frac{□}{□}\)
Answer: 3/4
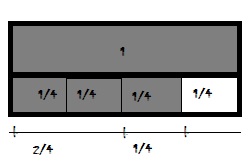
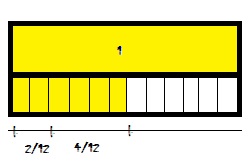
Question 5.
\(\frac{2}{12}+\frac{4}{12}\) = \(\frac{□}{□}\)
Answer: 6/12
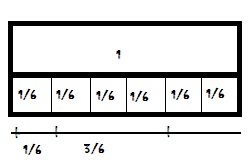
Question 6.
\(\frac{1}{6}+\frac{2}{6}\) = \(\frac{□}{□}\)
Answer: 3/6
Question 7.
\(\frac{3}{12}+\frac{9}{12}\) = \(\frac{□}{□}\)
Answer: 12/12
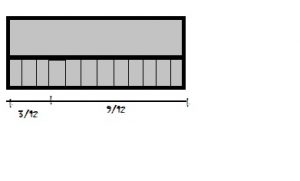
Question 8.
\(\frac{3}{8}+\frac{4}{8}\) = \(\frac{□}{□}\)
Answer: 7/8
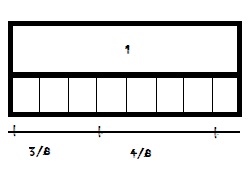
Question 9.
\(\frac{3}{4}+\frac{1}{4}\) = \(\frac{□}{□}\)
Answer: 4/4
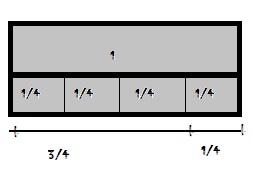
Question 10.
\(\frac{1}{5}+\frac{2}{5}\) = \(\frac{□}{□}\)
Answer: 3/5
Explanation:
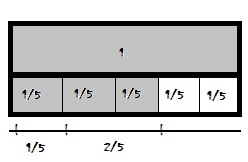
Problem Solving
Question 11.
Lola walks \(\frac{4}{10}\) mile to her friend’s house. Then she walks \(\frac{5}{10}\) mile to the store. How far does she walk in all?
\(\frac{□}{□}\) mile
Answer: \(\frac { 9 }{ 10 } \) mile
Explanation:
Given,
Lola walks \(\frac { 4 }{ 10} \) mile to her friend’s house.
Then she walks \(\frac { 5 }{ 10 } \) mile to the store.
\(\frac { 4 }{ 10} \) + \(\frac { 5 }{ 10 } \) = \(\frac { 9 }{ 10 } \)
Therefore she walked \(\frac { 9 }{ 10 } \) mile in all.
Question 12.
Evan eats \(\frac{1}{8}\) of a pan of lasagna and his brother eats \(\frac{2}{8}\) of it. What fraction of the pan of lasagna do they eat in all?
\(\frac{□}{□}\)
Answer: \(\frac { 3 }{ 8 } \) of the pan
Explanation:
Given,
Evan eats \(\frac { 1 }{ 8 } \) of a pan of lasagna and his brother eats \(\frac { 2 }{ 8 } \) of it.
\(\frac { 1 }{ 8 } \) + \(\frac { 2 }{ 8 } \)
= \(\frac { 3 }{ 8 } \)
Question 13.
Jacqueline buys \(\frac{2}{4}\) yard of green ribbon and \(\frac{1}{4}\) yard of pink ribbon. How many yards of ribbon does she buy in all?
\(\frac{□}{□}\) yard
Answer: \(\frac { 3 }{ 4 } \) yard
Explanation:
Given,
Jacqueline buys \(\frac { 2 }{ 4 } \) yard of green ribbon and \(\frac { 1 }{ 4 } \) yard of pink ribbon.
\(\frac { 2 }{ 4 } \) + \(\frac { 1 }{ 4 } \)
= \(\frac { 3 }{ 4 } \)
Thus Jacqueline bought \(\frac { 3 }{ 4 } \) yards of ribbon in all.
Question 14.
Shu mixes \(\frac{2}{3}\) pound of peanuts with \(\frac{1}{3}\) pound of almonds. How many pounds of nuts does Shu mix in all?
\(\frac{□}{□}\) pound
Answer: 3/3 pound
Explanation:
Given,
Shu mixes \(\frac { 2 }{ 3 } \) pound of peanuts with \(\frac { 1 }{ 3 } \) pound of almonds.
\(\frac { 2 }{ 3 } \) + \(\frac { 1 }{ 3 } \)
= \(\frac { 3 }{ 3 } \)
Therefore Shu mix \(\frac { 3 }{ 3 } \) pounds of nuts in all.
Common Core – Add and Subtract Fractions – Page No. 138
Lesson Check
Question 1.
Mary Jane has \(\frac{3}{8}\) of a medium pizza left. Hector has \(\frac{2}{8}\) of another medium pizza left. How much pizza do they have altogether?
Options:
a. \(\frac{1}{8}\)
b. \(\frac{4}{8}\)
c. \(\frac{5}{8}\)
d. \(\frac{6}{8}\)
Answer: \(\frac { 5 }{ 8 } \)
Explanation:
Given,
Mary Jane has \(\frac { 3 }{ 8 } \) of a medium pizza left.
Hector has \(\frac { 2 }{ 8 } \) of another medium pizza left.
To find how much pizza do they have altogether we have to add both the fractions.
\(\frac { 3 }{ 8 } \) + \(\frac { 2 }{ 8 } \) = \(\frac { 5 }{ 8 } \)
Therefore Mary Jane and Hector has \(\frac { 5 }{ 8 } \) pizza altogether.
Thus the correct answer is option c.
Question 2.
Jeannie ate \(\frac{1}{4}\) of an apple. Kelly ate \(\frac{2}{4}\) of the apple. How much did they eat in all?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{2}{8}\)
c. \(\frac{3}{8}\)
d. \(\frac{3}{4}\)
Answer: \(\frac { 3 }{ 4 } \)
Explanation:
Given,
Jeannie ate \(\frac { 1 }{ 4 } \) of an apple.
Kelly ate \(\frac { 2 }{ 4 } \) of the apple.
\(\frac { 1 }{ 4 } \) + \(\frac { 2 }{ 4 } \) = \(\frac { 3 }{ 4 } \)
Thus the correct answer is option d.
Spiral Review
Question 3.
Karen is making 14 different kinds of greeting cards. She is making 12 of each kind. How many greeting cards is she making?
Options:
a. 120
b. 132
c. 156
d. 168
Answer: 168
Explanation:
Given,
Karen is making 14 different kinds of greeting cards.
She is making 12 of each kind.
To find how many greeting cards she is making we have to multiply 14 and 12.
14 × 12 = 168.
Thus the correct answer is option d.
Question 4.
Jefferson works part time and earns $1,520 in four weeks. How much does he earn each week?
Options:
a. $305
b. $350
c. $380
d. $385
Answer: $380
Explanation:
Jefferson works part-time and earns $1,520 in four weeks.
1520 – 4 weeks
? – 1 week
1520/4 = $380
Thus the correct answer is option c
Question 5.
By installing efficient water fixtures, the average American can reduce water use to about 45 gallons of water per day. Using such water fixtures, about how many gallons of water would the average American use in December?
Options:
a. about 1,200 gallons
b. about 1,500 gallons
c. about 1,600 gallons
d. about 2,000 gallons
Answer: about 1,500 gallons
Explanation:
Given,
By installing efficient water fixtures, the average American can reduce water use to about 45 gallons of water per day.
1 day – 45 gallons
31 days – ?
45 × 31 = 1395 gallons
The number near to 1395 is 1500 gallons.
Thus the correct answer is option b.
Question 6.
Collin is making a bulletin board and note center. He is using square cork tiles and square dry-erase tiles. One of every 3 squares will be a cork square. If he uses 12 squares for the center, how many will be cork squares?
Options:
a. 3
b. 4
c. 6
d. 8
Answer: 4
Explanation:
Given that,
Collin is making a bulletin board and note center.
He is using square cork tiles and square dry-erase tiles.
One of every 3 squares will be a cork square.
12/3 = 4
Thus the correct answer is option b.
Common Core – Add and Subtract Fractions – Page No. 139
Subtract Fractions Using Models
Subtract. Use fraction strips to help.
Question 1.
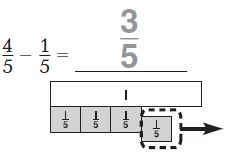
Answer: 3/5
Explanation:
Given the fraction, 4/5 and 1/5
The denominators of both the fractions are the same so subtract the numerators.
4/5 – 1/5 = 3/5
Question 2.
\(\frac{3}{4}-\frac{1}{4}\) = \(\frac{□}{□}\)
Answer: 2/4
Explanation:
Given the fractions \(\frac { 3}{ 4 } \) and [/latex] \frac { 1}{ 4 } [/latex]
The denominators of both the fractions are the same so subtract the numerators.
\(\frac { 3}{ 4 } – \frac { 1}{ 4 } = \frac { 2 }{ 4 } \)
Question 3.
\(\frac{5}{6}-\frac{1}{6}\) = \(\frac{□}{□}\)
Answer: 4/6
Explanation:
Given the fractions \(\frac { 5 }{ 6 } \) and [/latex] \frac { 1 }{ 6 } [/latex]
The denominators of both the fractions are the same so subtract the numerators.
\(\frac { 5}{ 6 } – \frac { 1}{ 6 } = \frac { 4 }{ 6 } \)
Question 4.
\(\frac{7}{8}-\frac{1}{8}\) = \(\frac{□}{□}\)
Answer: 6/8
Explanation:
Given the fractions \(\frac { 7 }{ 8 } \) and [/latex] \frac { 1 }{ 8 } [/latex]
The denominators of both the fractions are the same so subtract the numerators.
\(\frac { 7}{ 8 } – \frac { 1}{ 8 } = \frac { 6 }{ 8 } \)
Question 5.
1 – \(\frac{2}{3}\) = \(\frac{□}{□}\)
Answer: 1/3
Explanation:
Given the fractions \(\frac { 1 }{ 3 } \) and [/latex] \frac { 2 }{ 3 } [/latex]
The denominators of both the fractions are the same so subtract the numerators.
\(\frac { 1}{ 3 } – \frac { 2}{ 3 } = \frac { 1}{ 3 } \)
Question 6.
\(\frac{8}{10}-\frac{2}{10}\) = \(\frac{□}{□}\)
Answer: 6/10
Explanation:
Given the fractions \(\frac { 8 }{ 10 } \) and [/latex] \frac { 2 }{ 10 } [/latex]
The denominators of both the fractions are the same so subtract the numerators.
\(\frac { 8}{ 10 } – \frac { 2}{ 10 } = \frac { 6 }{ 10 } \)
Question 7.
\(\frac{3}{4}-\frac{1}{4}\) = \(\frac{□}{□}\)
Answer: 2/4
Explanation:
Given the fractions \(\frac { 3 }{ 4 } \) and [/latex] \frac { 1 }{ 4 } [/latex]
The denominators of both the fractions are the same so subtract the numerators.
\(\frac { 3}{ 4 } – \frac { 1}{ 4 } = \frac { 2 }{ 4 } \)
Question 8.
\(\frac{7}{6}-\frac{5}{6}\) = \(\frac{□}{□}\)
Answer: 2/6
Explanation:
Given the fractions \(\frac { 7 }{ 6 } \) and [/latex] \frac { 5 }{ 6 } [/latex]
The denominators of both the fractions are the same so subtract the numerators.
\(\frac { 7}{ 6 } – \frac {5}{ 6 } = \frac { 2 }{ 6 } \)
Problem Solving
Use the table for 9 and 10.
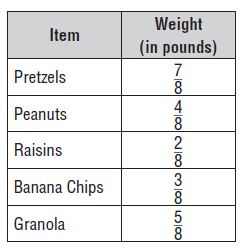
Question 9.
Ena is making trail mix. She buys the items shown in the table. How many more pounds of pretzels than raisins does she buy?
\(\frac{□}{□}\)
Answer: 5/8 pound
Explanation:
Given that,
Ena is making trail mix.
pretzels = 7/8
Raisins = 2/8
To find the number of more pounds of pretzels than raisins she buy
we have to subtract both the fractions.
7/8 – 2/8 = 5/8
Question 10.
How many more pounds of granola than banana chips does she buy?
\(\frac{□}{□}\)
Answer: 2/8 pound
Explanation:
Granola = 5/8
Banana Chips = 3/8
To find How many more pounds of granola than banana chips does she buy we have to subtract both the fractions.
5/8 – 3/8 = 2/8 pounds
Common Core – Add and Subtract Fractions – Page No. 140
Lesson Check
Question 1.
Lee reads for \(\frac{3}{4}\) hour in the morning and \(\frac{2}{4}\) hour in the afternoon. How much longer does Lee read in the morning than in the afternoon?
Options:
a. 5 hours
b. \(\frac{5}{4}\) hours
c. \(\frac{4}{4}\) hour
d. \(\frac{1}{4}\) hour
Answer: \(\frac { 1}{ 4} \)
Explanation:
Given,
Lee reads for \(\frac { 3}{ 4} \) hour in the morning and \(\frac {2}{ 4} \) hour in the afternoon.
\(\frac { 3}{ 4} \) – \(\frac {2}{ 4} \) = \(\frac { 1}{ 4} \)
Lee read \(\frac { 1}{ 4} \) hour in the morning than in the afternoon.
Thus the correct answer is option d.
Question 2.
Which equation does the model below represent?
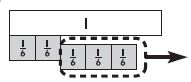
Options:
a. \(\frac{3}{6}-\frac{2}{6}=\frac{1}{6}\)
b. \(\frac{2}{6}-\frac{1}{6}=\frac{1}{6}\)
c. \(\frac{5}{6}-\frac{3}{6}=\frac{2}{6}\)
d. 1 – \(\frac{3}{6}\) = \(\frac{3}{6}\)
Answer: \(\frac { 5}{ 6} – \frac { 3}{ 6} = \frac { 2}{ 6} \)
Explanation:
From the above figure we can say that \(\frac { 5}{ 6} – \frac { 3}{ 6} = \frac { 2}{ 6} \)
Thus the correct answer is option c.
Spiral Review
Question 3.
A city received 2 inches of rain each day for 3 days. The meteorologist said that if the rain had been snow, each inch of rain would have been 10 inches of snow. How much snow would that city have received in the 3 days?
Options:
a. 20 inches
b. 30 inches
c. 50 inches
d. 60 inches
Answer: 60 inches
Explanation:
Given,
A city received 2 inches of rain each day for 3 days.
2 × 3 inches = 6 inches
The meteorologist said that if the rain had been snow, each inch of rain would have been 10 inches of snow.
6 × 10 inches = 60 inches
Therefore the city has received 60 inches of snow in 3 days.
Thus the correct answer is option d.
Question 4.
At a party there were four large submarine sandwiches, all the same size. During the party, \(\frac{2}{3}\) of the chicken sandwich, \(\frac{3}{4}\) of the tuna sandwich, \(\frac{7}{12}\) of the roast beef sandwich, and \(\frac{5}{6}\) of the veggie sandwich were eaten. Which sandwich had the least amount left?
Options:
a. chicken
b. tuna
c. roast beef
d. veggie
Answer: veggie
Explanation:
Given,
At a party there were four large submarine sandwiches, all the same size. During the party, \(\frac { 2}{ 3} \) of the chicken sandwich, \(\frac { 3}{ 4} \) of the tuna sandwich, \(\frac { 7}{ 12} \) of the roast beef sandwich, and \(\frac { 5}{ 6} \) of the veggie sandwich were eaten.
Compare the fractions \(\frac { 2}{ 3} \), \(\frac { 3}{ 4} \) , \(\frac { 7}{ 12} \) and \(\frac { 5}{ 6} \).
Among all the fractions veggie has the least fraction.
Thus the correct answer is option d.
Question 5.
Deena uses \(\frac{3}{8}\) cup milk and \(\frac{2}{8}\) cup oil in a recipe. How much liquid does she use in all?
Options:
a. \(\frac{1}{8}\) cup
b. \(\frac{5}{8}\) cup
c. \(\frac{6}{8}\) cup
d. 5 cups
Answer: \(\frac {5}{ 8} \) cup
Explanation:
Given,
Deena uses \(\frac { 3}{ 8} \) cup milk and \(\frac { 2}{ 8} \) cup oil in a recipe.
\(\frac { 3}{ 8} \) + \(\frac { 2}{ 8} \) = \(\frac {5}{ 8} \) cup
Therefore she used \(\frac {5}{ 8} \) cup of milk in all.
Thus the correct answer is option b.
Question 6.
In the car lot, \(\frac{4}{12}\) of the cars are white and \(\frac{3}{12}\) of the cars are blue. What fraction of the cars in the lot are either white or blue?
Options:
a. \(\frac{1}{12}\)
b. \(\frac{7}{24}\)
c. \(\frac{7}{12}\)
d. 7
Answer: \(\frac { 7}{ 12} \)
Explanation:
Given,
In the car lot, \(\frac { 4}{ 12} \) of the cars are white and \(\frac { 3}{ 12} \) of the cars are blue.
\(\frac { 4}{ 12} \) + \(\frac { 3}{ 12} \) = \(\frac { 7}{ 12} \)
Thus the correct answer is option c.
Common Core – Add and Subtract Fractions – Page No. 141
Add and Subtract Fractions
Find the sum or difference.
Question 1.
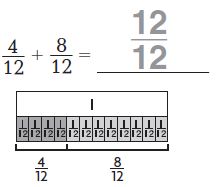
Answer: 12/12
Explanation:
The denominators of both the fractions are the same so add the numerators.
\(\frac{4}{12}\) + \(\frac{8}{12}\)
= \(\frac{12}{12}\)
Question 2.
\(\frac{3}{6}-\frac{1}{6}\) = \(\frac{□}{□}\)
Answer: 2/6
Explanation:
The denominators of both the fractions are the same so Subtract the numerators.
\(\frac{3}{6}\) – \(\frac{1}{6}\)
= \(\frac{2}{6}\)
Question 3.
\(\frac{4}{5}-\frac{3}{5}\) = \(\frac{□}{□}\)
Answer: 1/5
Explanation:
The denominators of both the fractions are the same so Subtract the numerators.
\(\frac{4}{5}\) – \(\frac{3}{5}\)
= \(\frac{1}{5}\)
Question 4.
\(\frac{6}{10}+\frac{3}{10}\) = \(\frac{□}{□}\)
Answer: 9/10
Explanation:
The denominators of both the fractions are the same so add the numerators.
\(\frac{6}{10}+\frac{3}{10}\) = \(\frac{9}{10}\)
Question 5.
1 – \(\frac{3}{8}\) = \(\frac{□}{□}\)
Answer: 5/8
Explanation:
The denominators of both the fractions are the same so Subtract the numerators.
1 – \(\frac{3}{8}\)
= \(\frac{8}{8}\) – \(\frac{3}{8}\)
= \(\frac{5}{8}\)
Question 6.
\(\frac{1}{4}+\frac{2}{4}\) = \(\frac{□}{□}\)
Answer: 3/4
Explanation:
The denominators of both the fractions are the same so add the numerators.
\(\frac{1}{4}+\frac{2}{4}\) = \(\frac{3}{4}\)
Question 7.
\(\frac{9}{12}-\frac{5}{12}\) = \(\frac{□}{□}\)
Answer: 4/12
Explanation:
The denominators of both the fractions are the same so Subtract the numerators.
\(\frac{9}{12}-\frac{5}{12}\) = \(\frac{4}{12}\)
Question 8.
\(\frac{5}{6}-\frac{2}{6}\) = \(\frac{□}{□}\)
Answer: 3/6
Explanation:
The denominators of both the fractions are the same so Subtract the numerators.
\(\frac{5}{6}-\frac{2}{6}\) = \(\frac{3}{6}\)
Question 9.
\(\frac{2}{3}+\frac{1}{3}\) = \(\frac{□}{□}\)
Answer: 3/3 = 1
Explanation:
The denominators of both the fractions are the same so add the numerators.
\(\frac{2}{3}+\frac{1}{3}\) = \(\frac{3}{3}\) = 1
Problem Solving
Use the table for 10 and 11. 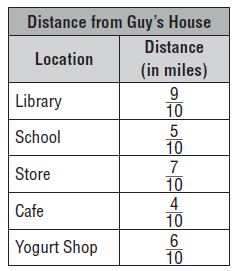
Question 10.
Guy finds how far his house is from several locations and makes the table shown. How much farther away from Guy’s house is the library than the cafe?
\(\frac{□}{□}\)
Answer: \(\frac{5}{10}\) mile
Explanation:
The distance from Guy’s house to the library is \(\frac{9}{10}\) mile
The distance from Guy’s house to the cafe is \(\frac{4}{10}\) mile
To find how much farther away from Guy’s house is the library than the cafe subtract both the fractions.
\(\frac{9}{10}\) – \(\frac{4}{10}\) = \(\frac{5}{10}\) mile
Question 11.
If Guy walks from his house to school and back, how far does he walk?
\(\frac{□}{□}\)
Answer: 10/10 mile
Explanation:
The distance from Guy’s house to school = \(\frac{5}{10}\) mile
From school to house \(\frac{5}{10}\) mile
\(\frac{5}{10}\) + \(\frac{5}{10}\) = \(\frac{10}{10}\) mile
Common Core – Add and Subtract Fractions – Page No. 142
Lesson Check
Question 1.
Mr. Angulo buys \(\frac{5}{8}\) pound of red grapes and \(\frac{3}{8}\) pound of green grapes. How many pounds of grapes did Mr. Angulo buy in all?
Options:
a. \(\frac{1}{8}\) pound
b. \(\frac{2}{8}\) pound
c. 1 pound
d. 2 pounds
Answer: 1 pound
Explanation:
Given that,
Mr. Angulo buys \(\frac{5}{8}\) pound of red grapes and \(\frac{3}{8}\)pound of green grapes.
\(\frac{5}{8}\) + \(\frac{3}{8}\)
= \(\frac{8}{8}\)
= 1
Thus the correct answer is option c.
Question 2.
Which equation does the model below represent?
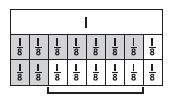
Options:
a. \(\frac{7}{8}+\frac{2}{8}=\frac{9}{8}\)
b. \(\frac{5}{8}-\frac{2}{8}=\frac{3}{8}\)
c. \(\frac{8}{8}-\frac{5}{8}=\frac{3}{8}\)
d. \(\frac{7}{8}-\frac{2}{8}=\frac{5}{8}\)
Answer: \(\frac{7}{8}\) – \(\frac{2}{8}\) = \(\frac{5}{8}\)
Explanation:
By seeing the above figure we can say that, the equation of the model is
\(\frac{7}{8}\) – \(\frac{2}{8}\) = \(\frac{5}{8}\)
Thus the correct answer is option d.
Spiral Review
Question 3.
There are 6 muffins in a package. How many packages will be needed to feed 48 people if each person has 2 muffins?
Options:
a. 4
b. 8
c. 16
d. 24
Answer: 16
Explanation:
There are 6 muffins in a package.
Number of people = 48
48/6 = 8
Also given that each person gets 2 muffins.
8 × 2 = 16
Thus the correct answer is option c.
Question 4.
Camp Oaks gets 32 boxes of orange juice and 56 boxes of apple juice. Each shelf in the cupboard can hold 8 boxes of juice. What is the least number of shelves
needed for all the juice boxes?
Options:
a. 4
b. 7
c. 11
d. 88
Answer: 11
Explanation:
Given,
Camp Oaks gets 32 boxes of orange juice and 56 boxes of apple juice.
Each shelf in the cupboard can hold 8 boxes of juice.
First, add the boxes of orange juice and apple juice.
32 + 56 = 88 boxes of juice
Now divide 88 by 8
88/8 = 11
Thus the correct answer is option c.
Question 5.
A machine makes 18 parts each hour. If the machine operates 24 hours a day, how many parts can it make in one day
Options:
a. 302
b. 332
c. 362
d. 432
Answer: 432
Explanation:
Given,
A machine makes 18 parts each hour.
Multiply the number of parts with the number of hours.
18 × 24 = 432 parts in a day.
Thus the correct answer is option d.
Question 6.
Which equation does the model below represent?
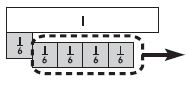
Options:
a. \(\frac{5}{6}-\frac{4}{6}=\frac{1}{6}\)
b. \(\frac{4}{5}-\frac{1}{5}=\frac{3}{5}\)
c. \(\frac{5}{5}-\frac{4}{5}=\frac{1}{5}\)
d. \(\frac{6}{6}-\frac{4}{6}=\frac{2}{6}\)
Answer: \(\frac{5}{6}\) – \(\frac{4}{6}\) = \(\frac{1}{6}\)
Explanation:
By observing the figure we can say that the equation is \(\frac{5}{6}\) – \(\frac{4}{6}\) = \(\frac{1}{6}\).
Thus the correct answer is option a.
Common Core – Add and Subtract Fractions – Page No. 143
Rename Fractions and Mixed Numbers
Write the mixed number as a fraction.
Question 1.
2 \(\frac{3}{5}\)
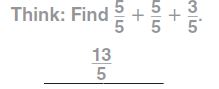
Question 2.
4 \(\frac{1}{3}\)
\(\frac{□}{□}\)
Answer: \(\frac{13}{3}\)
Explanation:
\(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{1}{3}\) = \(\frac{13}{3}\)
Question 3.
1 \(\frac{2}{5}\)
\(\frac{□}{□}\)
Answer: \(\frac{7}{5}\)
Explanation:
\(\frac{5}{5}\) + \(\frac{2}{5}\) = \(\frac{7}{5}\)
Question 4.
3 \(\frac{3}{2}\)
\(\frac{□}{□}\)
Answer: \(\frac{9}{2}\)
Explanation:
\(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{1}{2}\) = \(\frac{9}{2}\)
Question 5.
4 \(\frac{1}{8}\)
\(\frac{□}{□}\)
Answer: \(\frac{33}{8}\)
Explanation:
\(\frac{8}{8}\) + \(\frac{8}{8}\) + \(\frac{8}{8}\) + \(\frac{8}{8}\) + \(\frac{1}{8}\) = \(\frac{33}{8}\)
Question 6.
1 \(\frac{7}{10}\)
\(\frac{□}{□}\)
Answer: \(\frac{17}{10}\)
Explanation:
\(\frac{10}{10}\) + \(\frac{7}{10}\) = \(\frac{17}{10}\)
Question 7.
5 \(\frac{1}{2}\)
\(\frac{□}{□}\)
Answer: \(\frac{11}{2}\)
Explanation:
\(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{1}{2}\) = \(\frac{11}{2}\)
Question 8.
2 \(\frac{3}{8}\)
\(\frac{□}{□}\)
Answer: \(\frac{19}{8}\)
Explanation:
\(\frac{8}{8}\) + \(\frac{8}{8}\) + \(\frac{3}{8}\)
Write the fraction as a mixed number.
Question 9.
\(\frac{31}{6}\)
______ \(\frac{□}{□}\)
Answer: 5 \(\frac{1}{6}\)
Explanation:
\(\frac{6}{6}\) + \(\frac{6}{6}\) + \(\frac{6}{6}\) + \(\frac{6}{6}\) + \(\frac{6}{6}\) + \(\frac{1}{6}\)
1 + 1 + 1 + 1 + 1 + \(\frac{1}{6}\) = 5 \(\frac{1}{6}\)
Question 10.
\(\frac{20}{10}\)
______ \(\frac{□}{□}\)
Answer: 2
Explanation:
\(\frac{10}{10}\) + \(\frac{10}{10}\) = 1 + 1 = 2
Question 11.
\(\frac{15}{8}\)
______ \(\frac{□}{□}\)
Answer: 1 \(\frac{7}{8}\)
Explanation:
\(\frac{8}{8}\) + \(\frac{7}{8}\)
1 + \(\frac{7}{8}\) = 1 \(\frac{7}{8}\)
Question 12.
\(\frac{13}{6}\)
______ \(\frac{□}{□}\)
Answer: 2 \(\frac{1}{6}\)
Explanation:
\(\frac{6}{6}\) + \(\frac{6}{6}\) + \(\frac{1}{6}\)
= 1 + 1 + \(\frac{1}{6}\) = 2 \(\frac{1}{6}\)
Question 13.
\(\frac{23}{10}\)
______ \(\frac{□}{□}\)
Answer: 2 \(\frac{3}{10}\)
Explanation:
\(\frac{10}{10}\) + \(\frac{10}{10}\) + \(\frac{3}{10}\)
1 + 1 + \(\frac{3}{10}\) = 2 \(\frac{3}{10}\)
Question 14.
\(\frac{19}{5}\)
______ \(\frac{□}{□}\)
Answer: 3 \(\frac{4}{5}\)
Explanation:
\(\frac{5}{5}\) + \(\frac{5}{5}\) + \(\frac{5}{5}\) + \(\frac{4}{5}\)
1 + 1 + 1 + \(\frac{4}{5}\) = 3 \(\frac{4}{5}\)
Question 15.
\(\frac{11}{3}\)
______ \(\frac{□}{□}\)
Answer: 3 \(\frac{2}{3}\)
Explanation:
\(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{2}{3}\)
= 1 + 1 + 1 \(\frac{2}{3}\)
= 3 \(\frac{2}{3}\)
Question 16.
\(\frac{9}{2}\)
______ \(\frac{□}{□}\)
Answer: 4 \(\frac{1}{2}\)
Explanation:
\(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{1}{2}\)
= 1 + 1 + 1 + 1 + \(\frac{1}{2}\)
= 4 \(\frac{1}{2}\)
Question 17.
A recipe calls for 2 \(\frac{2}{4}\) cups of raisins, but Julie only has a \(\frac{1}{4}\) -cup measuring cup. How many \(\frac{1}{4}\) cups does Julie need to measure out 2 \(\frac{2}{4}\) cups of raisins?
She needs ______ \(\frac{1}{4}\) cups
Answer: 10 \(\frac{1}{4}\) cups
Explanation:
Given,
A recipe calls for 2 \(\frac{2}{4}\) cups of raisins, but Julie only has a \(\frac{1}{4}\) -cup measuring cup.
\(\frac{4}{4}\) + \(\frac{4}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
= 10 \(\frac{1}{4}\) cups
Question 18.
If Julie needs 3 \(\frac{1}{4}\) cups of oatmeal, how many 14 cups of oatmeal will she use?
She will use ______ \(\frac{1}{4}\) cups of oatmeal
Answer: 13 \(\frac{1}{4}\) cups of oatmeal
Explanation:
\(\frac{4}{4}\) + \(\frac{4}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{1}{4}\)
= 13 \(\frac{1}{4}\)
Therefore Julie needs 13 \(\frac{1}{4}\) cups of oatmeal.
Common Core – Add and Subtract Fractions – Page No. 144
Lesson Check
Question 1.
Which of the following is equivalent to \(\frac{16}{3}\)?
Options:
a. 3 \(\frac{1}{5}\)
b. 3 \(\frac{2}{5}\)
c. 5 \(\frac{1}{3}\)
d. 5 \(\frac{6}{3}\)
Answer: 5 \(\frac{1}{3}\)
Explanation:
Convert from improper fraction to the mixed fraction.
\(\frac{16}{3}\) = \(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{3}{3}\) + \(\frac{1}{3}\)
= 5 \(\frac{1}{3}\)
Thus the correct answer is option c.
Question 2.
Stacey filled her \(\frac{1}{2}\) cup measuring cup seven times to have enough flour for a cake recipe. How much flour does the cake recipe call for?
Options:
a. 3 cups
b. 3 \(\frac{1}{2}\) cups
c. 4 cups
d. 4 \(\frac{1}{2}\) cups
Answer: 3 \(\frac{1}{2}\) cups
Explanation:
Given,
Stacey filled her \(\frac{1}{2}\)cup measuring cup seven times to have enough flour for a cake recipe.
\(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{2}{2}\) + \(\frac{1}{2}\)
1 + 1 + 1 + \(\frac{1}{2}\)
= 3 \(\frac{1}{2}\) cups
Thus the correct answer is option b.
Spiral Review
Question 3.
Becki put some stamps into her stamp collection book. She put 14 stamps on each page. If she completely filled 16 pages, how many stamps did she put in the book?
Options:
a. 224
b. 240
c. 272
d. 275
Answer: 224
Explanation:
Becki put some stamps into her stamp collection book.
She put 14 stamps on each page.
If she completely filled 16 pages
Multiply 14 with 16 pages.
14 × 16 = 224 pages
Thus the correct answer is option a.
Question 4.
Brian is driving 324 miles to visit some friends. He wants to get there in 6 hours. How many miles does he need to drive each hour?
Options:
a. 48 miles
b. 50 miles
c. 52 miles
d. 54 miles
Answer: 54 miles
Explanation:
Brian is driving 324 miles to visit some friends. He wants to get there in 6 hours.
Divide the number of miles by hours.
324/6 = 54 miles
Thus the correct answer is option d.
Question 5.
During a bike challenge, riders have to collect various colored ribbons. Each \(\frac{1}{2}\) mile they collect a red ribbon, each \(\frac{1}{8}\) mile they collect a green ribbon, and each \(\frac{1}{4}\) mile they collect a blue ribbon. Which colors of ribbons will be collected at the \(\frac{3}{4}\) mile marker?
Options:
a. red and green
b. red and blue
c. green and blue
d. red, green, and blue
Answer: green and blue
Explanation:
Given,
During a bike challenge, riders have to collect various colored ribbons.
Each \(\frac{1}{2}\) mile they collect a red ribbon, each \(\frac{1}{8}\) mile they collect a green ribbon, and each \(\frac{1}{4}\) mile they collect a blue ribbon.
Green and Blue colors of ribbons will be collected at the \(\frac{3}{4}\) mile marker.
Thus the correct answer is option c.
Question 6.
Stephanie had \(\frac{7}{8}\) pound of bird seed. She used \(\frac{3}{8}\) pound to fill a bird feeder. How much bird seed does Stephanie have left?
Options:
a. \(\frac{3}{8}\) pound
b. \(\frac{4}{8}\) pound
c. 1 pound
d. \(\frac{10}{8}\) pound
Answer: \(\frac{4}{8}\) pound
Explanation:
Given,
Stephanie had \(\frac{7}{8}\) pound of bird seed.
She used \(\frac{3}{8}\) pound to fill a bird feeder.
\(\frac{7}{8}\) – \(\frac{3}{8}\) = \(\frac{4}{8}\) pound
Thus the correct answer is option b.
Common Core – Add and Subtract Fractions – Page No. 145
Add and Subtract Mixed Numbers
Find the sum. Write the sum as a mixed number, so the fractional part is less than 1.
Question 1.
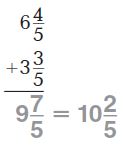
Question 2.
4 \(\frac{1}{2}\)
+ 2 \(\frac{1}{2}\)
_______ \(\frac{□}{□}\)
Answer: 7
4 \(\frac{1}{2}\)
+2 \(\frac{1}{2}\)
6 \(\frac{2}{2}\) = 6 + 1 = 7
Question 3.
2 \(\frac{2}{3}\)
+ 3 \(\frac{2}{3}\)
_______ \(\frac{□}{□}\)
Answer: 6 \(\frac{1}{3}\)
Explanation:
2 \(\frac{2}{3}\)
+3 \(\frac{2}{3}\)
5 \(\frac{4}{3}\)
= 5 + 1 \(\frac{1}{3}\)
= 6 \(\frac{1}{3}\)
Question 4.
6 \(\frac{4}{5}\)
+ 7 \(\frac{4}{5}\)
_______ \(\frac{□}{□}\)
Answer: 14 \(\frac{3}{5}\)
Explanation:
6 \(\frac{4}{5}\)
+7 \(\frac{4}{5}\)
13 \(\frac{8}{5}\)
13 + 1 \(\frac{3}{5}\)
= 14 \(\frac{3}{5}\)
Question 5.
9 \(\frac{3}{6}\)
+ 2 \(\frac{2}{6}\)
_______ \(\frac{□}{□}\)
Answer: 11 \(\frac{5}{6}\)
Explanation:
9 \(\frac{3}{6}\)
+2 \(\frac{2}{6}\)
11 \(\frac{5}{6}\)
Question 6.
8 \(\frac{4}{12}\)
+ 3 \(\frac{6}{12}\)
_______ \(\frac{□}{□}\)
Answer: 11 \(\frac{10}{12}\)
Explanation:
8 \(\frac{4}{12}\)
+3 \(\frac{6}{12}\)
11 \(\frac{10}{12}\)
Question 7.
4 \(\frac{3}{8}\)
+ 1 \(\frac{5}{8}\)
_______ \(\frac{□}{□}\)
Answer: 6
Explanation:
4 \(\frac{3}{8}\)
+1 \(\frac{5}{8}\)
5 \(\frac{8}{8}\)
= 5 + 1 = 6
Question 8.
9 \(\frac{5}{10}\)
+ 6 \(\frac{3}{10}\)
_______ \(\frac{□}{□}\)
Answer: 15 \(\frac{8}{10}\)
Explanation:
9 \(\frac{5}{10}\)
+6 \(\frac{3}{10}\)
15 \(\frac{8}{10}\)
Find the difference.
Question 9.
6 \(\frac{7}{8}\)
– 4 \(\frac{3}{8}\)
_______ \(\frac{□}{□}\)
Answer: 2 \(\frac{4}{8}\)
Explanation:
6 \(\frac{7}{8}\)
-4 \(\frac{3}{8}\)
2 \(\frac{4}{8}\)
Question 10.
4 \(\frac{2}{3}\)
– 3 \(\frac{1}{3}\)
_______ \(\frac{□}{□}\)
Answer: 1 \(\frac{1}{3}\)
Explanation:
4 \(\frac{2}{3}\)
-3 \(\frac{1}{3}\)
1 \(\frac{1}{3}\)
Question 11.
6 \(\frac{4}{5}\)
– 3 \(\frac{3}{5}\)
_______ \(\frac{□}{□}\)
Answer: 3 \(\frac{1}{5}\)
Explanation:
6 \(\frac{4}{5}\)
-3 \(\frac{3}{5}\)
3 \(\frac{1}{5}\)
Question 12.
7 \(\frac{3}{4}\)
– 2 \(\frac{1}{4}\)
_______ \(\frac{□}{□}\)
Answer: 5 \(\frac{1}{2}\)
Explanation:
7 \(\frac{3}{4}\)
-2 \(\frac{1}{4}\)
5 \(\frac{2}{4}\) = 5 \(\frac{1}{2}\)
Problem Solving
Question 13.
James wants to send two gifts by mail. One package weighs 2 \(\frac{3}{4}\) pounds. The other package weighs 1 \(\frac{3}{4}\) pounds. What is the total weight of the packages?
_______ \(\frac{□}{□}\)
Answer: 4 \(\frac{1}{2}\)
Explanation:
2 \(\frac{3}{4}\)
+ 1 \(\frac{3}{4}\)
4 \(\frac{1}{2}\)
Question 14.
Tierra bought 4 \(\frac{3}{8}\) yards blue ribbon and 2 \(\frac{1}{8}\) yards yellow ribbon for a craft project. How much more blue ribbon than yellow ribbon did Tierra buy?
_______ \(\frac{□}{□}\)
Answer: 2 \(\frac{1}{4}\)
Explanation:
Given,
4 \(\frac{3}{8}\)
-2 \(\frac{1}{8}\)
2 \(\frac{1}{4}\)
Common Core – Add and Subtract Fractions – Page No. 146
Lesson Check
Question 1.
Brad has two lengths of copper pipe to fit together. One has a length of 2 \(\frac{5}{12}\) feet and the other has a length of 3 \(\frac{7}{12}\) feet. How many feet of pipe does he have in all?
Options:
a. 5 feet
b. 5 \(\frac{6}{12}\) feet
c. 5 \(\frac{10}{12}\)
d. 6 feet
Answer: 5 feet
Explanation:
Given,
Brad has two lengths of copper pipe to fit together. One has a length of 2 \(\frac{5}{12}\) feet and the other has a length of 3 \(\frac{7}{12}\) feet.
Add both the lengths
2 \(\frac{5}{12}\) + 3 \(\frac{7}{12}\)
= 5 \(\frac{12}{12}\) = 5 feet
Thus the correct answer is option a.
Question 2.
A pattern calls for 2 \(\frac{1}{4}\)yards of material and 1 \(\frac{1}{4}\)yards of lining. How much total fabric is needed?
Options:
a. 2 \(\frac{2}{4}\) yards
b. 3 yards
c. 3 \(\frac{1}{4}\) yards
d. 3 \(\frac{2}{4}\) yards
Answer: 3 \(\frac{2}{4}\) yards
Explanation:
Given,
A pattern calls for 2 \(\frac{1}{4}\) yards of material and 1 \(\frac{1}{4}\) yards of lining.
2 \(\frac{1}{4}\) + 1 \(\frac{1}{4}\)
= 3 + \(\frac{1}{4}\) + \(\frac{1}{4}\)
= 3 \(\frac{2}{4}\) yards
Thus the correct answer is option d.
Spiral Review
Question 3.
Shanice has 23 baseball trading cards of star players. She agrees to sell them for $16 each. How much will she get for the cards?
Options:
a. $258
b. $358
c. $368
d. $468
Answer: $368
Explanation:
Given,
Shanice has 23 baseball trading cards of star players. She agrees to sell them for $16 each.
To find how much will she get for the cards
23 × 16 = 368
Therefore she will get $368 for the cards.
Thus the correct answer is option c.
Question 4.
Nanci is volunteering at the animal shelter. She wants to spend an equal amount of time playing with each dog. She has 145 minutes to play with all 7 dogs. About how much time can she spend with each dog?
Options:
a. about 10 minutes
b. about 20 minutes
c. about 25 minutes
d. about 26 minutes
Answer: about 20 minutes
Explanation:
Given,
Nanci is volunteering at the animal shelter. She wants to spend an equal amount of time playing with each dog. She has 145 minutes to play with all 7 dogs.
145/7 = 20.7
Therefore she can spend about 20 minutes with each dog.
Thus the correct answer is option b.
Question 5.
Frieda has 12 red apples and 15 green apples. She is going to share the apples equally among 8 people and keep any extra apples for herself. How many apples
will Frieda keep for herself?
Options:
a. 3
b. 4
c. 6
d. 7
Answer: 3
Explanation:
Given,
Frieda has 12 red apples and 15 green apples.
She is going to share the apples equally among 8 people and keep any extra apples for herself.
12 + 15 = 27
27/8
27 – 24 = 3
Thus Frieda keep for herself 3 apples.
Thus the correct answer is option a.
Question 6.
The Lynch family bought a house for $75,300. A few years later, they sold the house for $80,250. How much greater was the selling price than the purchase price?
Options:
a. $4,950
b. $5,050
c. $5,150
d. $5,950
Answer: $4,950
Explanation:
Given,
The Lynch family bought a house for $75,300.
A few years later, they sold the house for $80,250.
$80,250 – $75,300 = $4,950
Thus the correct answer is option a.
Common Core – Add and Subtract Fractions – Page No. 147
Record Subtraction with
Find the difference.
Question 1.

Question 2.
6
– 3 \(\frac{2}{5}\)
_______ \(\frac{□}{□}\)
Answer: 2 \(\frac{3}{5}\)
Explanation:
First subtract the whole numbers
6 – 3 = 3
Next subtract the fractions,
3 – \(\frac{2}{5}\) = 2 \(\frac{3}{5}\)
Question 3.
5 \(\frac{1}{4}\)
– 2 \(\frac{3}{4}\)
_______ \(\frac{□}{□}\)
Answer: 2 \(\frac{1}{2}\)
Explanation:
First subtract the whole numbers
5 – 2 = 3
Next subtract the fractions,
\(\frac{1}{4}\) – \(\frac{3}{4}\) = – \(\frac{1}{2}\)
3 – \(\frac{1}{2}\)
= 2 \(\frac{1}{2}\)
Question 4.
9 \(\frac{3}{8}\)
– 8 \(\frac{7}{8}\)
_______ \(\frac{□}{□}\)
Answer: \(\frac{1}{2}\)
Explanation:
First subtract the whole numbers
9 – 8 = 1
Next subtract the fractions,
\(\frac{3}{8}\) – \(\frac{7}{8}\)
= – \(\frac{4}{8}\)
= – \(\frac{1}{2}\)
= 1 – \(\frac{1}{2}\)
= \(\frac{1}{2}\)
Question 5.
12 \(\frac{3}{10}\)
– 7 \(\frac{7}{10}\)
_______ \(\frac{□}{□}\)
Answer: 4 \(\frac{3}{5}\)
Explanation:
First subtract the whole numbers
12 – 7 = 5
Next subtract the fractions,
\(\frac{3}{10}\) – \(\frac{7}{10}\) = – \(\frac{4}{10}\)
5 – \(\frac{4}{10}\)
5 – \(\frac{2}{5}\) = 4 \(\frac{3}{5}\)
Question 6.
8 \(\frac{1}{6}\)
– 3 \(\frac{5}{6}\)
_______ \(\frac{□}{□}\)
Answer: 4 \(\frac{1}{3}\)
Explanation:
First subtract the whole numbers
8 – 3 = 5
Next subtract the fractions,
\(\frac{1}{6}\) – \(\frac{5}{6}\) = – \(\frac{2}{3}\)
5 – \(\frac{2}{3}\) = 4 \(\frac{1}{3}\)
Question 7.
7 \(\frac{3}{5}\)
– 4 \(\frac{4}{5}\)
_______ \(\frac{□}{□}\)
Answer: 2 \(\frac{4}{5}\)
Explanation:
First subtract the whole numbers
7 – 4 = 3
Next subtract the fractions,
\(\frac{3}{5}\) – \(\frac{4}{5}\) = – \(\frac{1}{5}\)
3 – \(\frac{1}{5}\) = 2 \(\frac{4}{5}\)
Question 8.
10 \(\frac{1}{2}\)
– 8 \(\frac{1}{2}\)
_______ \(\frac{□}{□}\)
Answer: 2
Explanation:
First subtract the whole numbers
10 – 8 = 2
\(\frac{1}{2}\) – \(\frac{1}{2}\) = 0
Question 9.
7 \(\frac{1}{6}\)
– 2 \(\frac{5}{6}\)
_______ \(\frac{□}{□}\)
Answer: 4 \(\frac{1}{3}\)
Explanation:
First subtract the whole numbers
7 – 2 = 5
Next subtract the fractions,
\(\frac{1}{6}\) – \(\frac{5}{6}\) = – \(\frac{4}{6}\)
5 – \(\frac{4}{6}\) = 4 \(\frac{1}{3}\)
Question 10.
9 \(\frac{3}{12}\)
– 4 \(\frac{7}{12}\)
_______ \(\frac{□}{□}\)
Answer: 2 \(\frac{2}{3}\)
Explanation:
First subtract the whole numbers
9 – 4 = 5
Next subtract the fractions,
\(\frac{3}{12}\) – \(\frac{7}{12}\) = – \(\frac{4}{12}\) = – \(\frac{1}{3}\)
5 – \(\frac{1}{3}\) = 2 \(\frac{2}{3}\)
Question 11.
9 \(\frac{1}{10}\)
– 8 \(\frac{7}{10}\)
_______ \(\frac{□}{□}\)
Answer: \(\frac{2}{5}\)
Explanation:
First subtract the whole numbers
9 – 8 = 1
Next subtract the fractions,
\(\frac{1}{10}\) – \(\frac{7}{10}\) = – \(\frac{6}{10}\)
1 – \(\frac{3}{5}\) = \(\frac{2}{5}\)
Question 12.
9 \(\frac{1}{3}\)
– \(\frac{2}{3}\)
_______ \(\frac{□}{□}\)
Answer: 8 \(\frac{2}{3}\)
Explanation:
9 \(\frac{1}{3}\)
– \(\frac{2}{3}\)
8 \(\frac{2}{3}\)
Question 13.
3 \(\frac{1}{4}\)
– 1 \(\frac{3}{4}\)
_______ \(\frac{□}{□}\)
Answer: 1 \(\frac{1}{2}\)
3 \(\frac{1}{4}\)
– 1 \(\frac{3}{4}\)
1 \(\frac{1}{2}\)
Question 14.
4 \(\frac{5}{8}\)
– 1 \(\frac{7}{8}\)
_______ \(\frac{□}{□}\)
Answer: 2 \(\frac{3}{4}\)
Explanation:
First subtract the whole numbers
4 – 1 = 3
Next subtract the fractions,
\(\frac{5}{8}\) – \(\frac{7}{8}\) = – \(\frac{1}{4}\)
3 – \(\frac{1}{4}\) = 2 \(\frac{3}{4}\)
Question 15.
5 \(\frac{1}{12}\)
– 3 \(\frac{8}{12}\)
_______ \(\frac{□}{□}\)
Answer: 1 \(\frac{5}{12}\)
Explanation:
First subtract the whole numbers
5 – 3 = 2
Next subtract the fractions,
\(\frac{1}{12}\) – \(\frac{8}{12}\) = – \(\frac{7}{12}\)
2 – \(\frac{7}{12}\) = 1 \(\frac{5}{12}\)
Question 16.
7
– 1 \(\frac{3}{5}\)
_______ \(\frac{□}{□}\)
Answer: 5 \(\frac{2}{5}\)
Explanation:
7
– 1 \(\frac{3}{5}\)
5 \(\frac{2}{5}\)
Problem Solving
Question 17.
Alicia buys a 5-pound bag of rocks for a fish tank. She uses 1 \(\frac{1}{8}\) pounds for a small fish bowl. How much is left?
_______ \(\frac{□}{□}\)
Answer: 3 \(\frac{7}{8}\)
Explanation:
Given,
Alicia buys a 5-pound bag of rocks for a fish tank. She uses 1 \(\frac{1}{8}\) pounds for a small fish bowl.
First subtract the whole numbers
5 – 1 = 4
4 – 1 \(\frac{1}{8}\)
= 3 \(\frac{7}{8}\)
Question 18.
Xavier made 25 pounds of roasted almonds for a fair. He has 3 \(\frac{1}{2}\) pounds left at the end of the fair. How many pounds of roasted almonds did he sell at the fair?
_______ \(\frac{□}{□}\)
Answer: 21 \(\frac{1}{2}\)
Explanation:
Given,
Xavier made 25 pounds of roasted almonds for a fair.
He has 3 \(\frac{1}{2}\) pounds left at the end of the fair.
First subtract the whole numbers
25 – 3 = 22
22 – \(\frac{1}{2}\) = 21 \(\frac{1}{2}\)
Common Core – Add and Subtract Fractions – Page No. 148
Lesson Check
Question 1.
Reggie is making a double-layer cake. The recipe for the first layer calls for 2 \(\frac{1}{4}\) cups sugar. The recipe for the second layer calls for 1 \(\frac{1}{4}\) cups sugar. Reggie has 5 cups of sugar. How much will he have left after making both recipes?
Options:
a. 1 \(\frac{1}{4}\) cups
b. 1 \(\frac{2}{4}\) cups
c. 2 \(\frac{1}{4}\) cups
d. 2 \(\frac{2}{4}\) cups
Answer: 1 \(\frac{2}{4}\) cups
Explanation:
Given,
Reggie is making a double-layer cake. The recipe for the first layer calls for 2 \(\frac{1}{4}\) cups sugar.
The recipe for the second layer calls for 1 \(\frac{1}{4}\) cups sugar.
Reggie has 5 cups of sugar.
2 \(\frac{1}{4}\) + 1 \(\frac{1}{4}\) = 3 \(\frac{1}{2}\)
5 – 3 \(\frac{1}{2}\) = 1 \(\frac{2}{4}\) cups
Thus the correct answer is option b.
Question 2.
Kate has 4 \(\frac{3}{8}\) yards of fabric and needs 2 \(\frac{7}{8}\) yards to make a skirt. How much extra fabric will she have left after making the skirt?
Options:
a. 2 \(\frac{4}{8}\) yards
b. 2 \(\frac{2}{8}\) yards
c. 1 \(\frac{4}{8}\) yards
d. 1 \(\frac{2}{8}\) yards
Answer: 1 \(\frac{4}{8}\) yards
Explanation:
Given,
Kate has 4 \(\frac{3}{8}\) yards of fabric and needs 2 \(\frac{7}{8}\) yards to make a skirt.
First, subtract the whole numbers
4 – 2 = 2
Next, subtract the fractions,
\(\frac{3}{8}\) – \(\frac{7}{8}\) = – \(\frac{4}{8}\)
2 – \(\frac{4}{8}\) = 1 \(\frac{4}{8}\) yards
Thus the correct answer is option c.
Spiral Review
Question 3.
Paulo has 128 glass beads to use to decorate picture frames. He wants to use the same number of beads on each frame. If he decorates 8 picture frames, how many beads will he put on each frame?
Options:
a. 6
b. 7
c. 14
d. 16
Answer: 16
Explanation:
Given,
Paulo has 128 glass beads to use to decorate picture frames. He wants to use the same number of beads on each frame
128/8 = 16
Thus the correct answer is option d.
Question 4.
Madison is making party favors. She wants to make enough favors so each guest gets the same number of favors. She knows there will be 6 or 8 guests at the party. What is the least number of party favors Madison should make?
Options:
a. 18
b. 24
c. 30
d. 32
Answer: 24
Explanation:
Given,
Madison is making party favors. She wants to make enough favors so each guest gets the same number of favors.
She knows there will be 6 or 8 guests at the party.
To find the least number of party favors, we have to consider the number of guests.
In this case, there are two possibilities—6 or 8.
For 6: 6, 12, 18, 24 (Add 6 to each number)
For 8: 8, 16, 24 (Add 8 to each number)
Now in both series, the least number (that is in common) is 24. Hence, Madison should make at least 24 party favors.
Thus the correct answer is option b.
Question 5.
A shuttle bus makes 4 round-trips between two shopping centers each day. The bus holds 24 people. If the bus is full on each one-way trip, how many passengers are carried by the bus each day?
Options:
a. 96
b. 162
c. 182
d. 192
Answer: 96
Explanation:
Given,
A shuttle bus makes 4 round-trips between two shopping centers each day. The bus holds 24 people.
4 × 24 = 96
Thus the correct answer is option a.
Question 6.
To make a fruit salad, Marvin mixes 1 \(\frac{3}{4}\) cups of diced peaches with 2 \(\frac{1}{4}\) cups of diced pears. How many cups of peaches and pears are in the fruit salad?
Options:
a. 4 cups
b. 3 \(\frac{2}{4}\) cups
c. 3 \(\frac{1}{4}\) cups
d. 3 cups
Answer: 4 cups
Explanation:
Given,
To make a fruit salad, Marvin mixes 1 \(\frac{3}{4}\) cups of diced peaches with 2 \(\frac{1}{4}\) cups of diced pears.
1 \(\frac{3}{4}\) + 2 \(\frac{1}{4}\)
= 4 cups
Thus the correct answer is option a.
Common Core – Add and Subtract Fractions – Page No. 149
Fractions and Properties of Addition
Use the properties and mental math to find the sum.
Question 1.
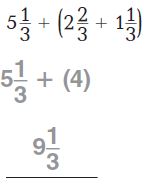
Question 2.
\(10 \frac{1}{8}+\left(3 \frac{5}{8}+2 \frac{7}{8}\right)\)
_______ \(\frac{□}{□}\)
Answer: 16 \(\frac{5}{8}\)
Explanation:
Given,
\(10 \frac{1}{8}+\left(3 \frac{5}{8}+2 \frac{7}{8}\right)\)
First add the whole numbers in the bracket.
3 + 2 = 5
10 \(\frac{1}{8}\) + 5 + \(\frac{5}{8}\) + \(\frac{7}{8}\)
10 \(\frac{1}{8}\) + 5 + \(\frac{12}{8}\)
10 + 5 = 15
15 + \(\frac{1}{8}\) + \(\frac{12}{8}\)
15 + \(\frac{13}{8}\)
16 \(\frac{5}{8}\)
\(10 \frac{1}{8}+\left(3 \frac{5}{8}+2 \frac{7}{8}\right)\) = 16 \(\frac{5}{8}\)
Question 3.
\(8 \frac{1}{5}+\left(3 \frac{2}{5}+5 \frac{4}{5}\right)\)
_______ \(\frac{□}{□}\)
Answer: 17 \(\frac{2}{5}\)
Explanation:
\(8 \frac{1}{5}+\left(3 \frac{2}{5}+5 \frac{4}{5}\right)\)
8 \(\frac{1}{5}\) + 3 \(\frac{2}{5}\) + 5 \(\frac{4}{5}\)
3 + 5 = 8
8 \(\frac{1}{5}\) + 8 + \(\frac{2}{5}\) + \(\frac{4}{5}\)
8 \(\frac{1}{5}\) + 8 + \(\frac{6}{5}\)
8 + 8 = 16
16 + \(\frac{1}{5}\) + \(\frac{6}{5}\)
16 + \(\frac{7}{5}\)
17 \(\frac{2}{5}\)
\(8 \frac{1}{5}+\left(3 \frac{2}{5}+5 \frac{4}{5}\right)\) = 17 \(\frac{2}{5}\)
Question 4.
\(6 \frac{3}{4}+\left(4 \frac{2}{4}+5 \frac{1}{4}\right)\)
_______ \(\frac{□}{□}\)
Answer: 16 \(\frac{1}{2}\)
Explanation:
\(6 \frac{3}{4}+\left(4 \frac{2}{4}+5 \frac{1}{4}\right)\)
First add the whole numbers in the bracket.
6 \(\frac{3}{4}\) + 4 \(\frac{2}{4}\) + 5 \(\frac{1}{4}\)
4 + 5 = 9
6 \(\frac{3}{4}\) + 9 \(\frac{3}{4}\)
6 + 9 = 15
15 + \(\frac{3}{4}\) + \(\frac{3}{4}\)
16 \(\frac{1}{2}\)
\(6 \frac{3}{4}+\left(4 \frac{2}{4}+5 \frac{1}{4}\right)\) = 16 \(\frac{1}{2}\)
Question 5.
\(\left(6 \frac{3}{6}+10 \frac{4}{6}\right)+9 \frac{2}{6}\)
_______ \(\frac{□}{□}\)
Answer: 26 \(\frac{3}{6}\)
Explanation:
\(\left(6 \frac{3}{6}+10 \frac{4}{6}\right)+9 \frac{2}{6}\)
6 \(\frac{3}{6}\) + 10 \(\frac{4}{6}\) + 9 \(\frac{2}{6}\)
First add the whole numbers in the bracket.
6 + 10 = 16
16 + \(\frac{3}{6}\) + \(\frac{4}{6}\) + 9 \(\frac{2}{6}\)
16 + \(\frac{7}{6}\) + 9 \(\frac{2}{6}\)
16 + 9 = 25
25 + \(\frac{7}{6}\) + \(\frac{2}{6}\)
25 + \(\frac{9}{6}\)
= 26 \(\frac{3}{6}\)
\(\left(6 \frac{3}{6}+10 \frac{4}{6}\right)+9 \frac{2}{6}\) = 26 \(\frac{3}{6}\)
Question 6.
\(\left(6 \frac{2}{5}+1 \frac{4}{5}\right)+3 \frac{1}{5}\)
_______ \(\frac{□}{□}\)
Answer: 11 \(\frac{2}{5}\)
Explanation:
\(\left(6 \frac{2}{5}+1 \frac{4}{5}\right)+3 \frac{1}{5}\)
6 \(\frac{2}{5}\) + 1 \(\frac{4}{5}\) + 3 \(\frac{1}{5}\)
First add the whole numbers in the bracket.
6 + 1 = 7
7 \(\frac{2}{5}\) + \(\frac{4}{5}\) + 3 \(\frac{1}{5}\)
7 + \(\frac{6}{5}\) + 3 \(\frac{1}{5}\)
7 + 3 = 10
10 + \(\frac{6}{5}\) + \(\frac{1}{5}\)
10 + \(\frac{7}{5}\) = 11 \(\frac{2}{5}\)
Therefore \(\left(6 \frac{2}{5}+1 \frac{4}{5}\right)+3 \frac{1}{5}\) = 11 \(\frac{2}{5}\)
Question 7.
\(7 \frac{7}{8}+\left(3 \frac{1}{8}+1 \frac{1}{8}\right)\)
_______ \(\frac{□}{□}\)
Answer: 12 \(\frac{1}{8}\)
Explanation:
\(7 \frac{7}{8}+\left(3 \frac{1}{8}+1 \frac{1}{8}\right)\)
7 \(\frac{7}{8}\) + 3 \(\frac{1}{8}\) + 1 \(\frac{1}{8}\)
First add the whole numbers in the bracket.
3 + 1 = 4
7 \(\frac{7}{8}\) + 4 + \(\frac{1}{8}\) + \(\frac{1}{8}\)
7 \(\frac{7}{8}\) + 4 +\(\frac{2}{8}\)
7 + 4 = 11
11 + \(\frac{7}{8}\) + \(\frac{2}{8}\)
11 + \(\frac{9}{8}\) = 12 \(\frac{1}{8}\)
Thus \(7 \frac{7}{8}+\left(3 \frac{1}{8}+1 \frac{1}{8}\right)\) = 12 \(\frac{1}{8}\)
Question 8.
\(14 \frac{1}{10}+\left(20 \frac{2}{10}+15 \frac{7}{10}\right)\)
_______ \(\frac{□}{□}\)
Answer: 50
Explanation:
\(14 \frac{1}{10}+\left(20 \frac{2}{10}+15 \frac{7}{10}\right)\)
First add the whole numbers in the bracket.
14 \(\frac{1}{10}\) + 20 \(\frac{2}{10}\) + 15 \(\frac{7}{10}\)
20 + 15 = 35
14 \(\frac{1}{10}\) + 35 + \(\frac{2}{10}\) + \(\frac{7}{10}\)
14 \(\frac{1}{10}\) + 35 \(\frac{9}{10}\)
49 \(\frac{1}{10}\) + \(\frac{9}{10}\)
49 + 1 = 50
Thus \(14 \frac{1}{10}+\left(20 \frac{2}{10}+15 \frac{7}{10}\right)\) = 50
Question 9.
\(\left(13 \frac{2}{12}+8 \frac{7}{12}\right)+9 \frac{5}{12}\)
_______ \(\frac{□}{□}\)
Answer: 31 \(\frac{2}{12}\)
Explanation:
\(\left(13 \frac{2}{12}+8 \frac{7}{12}\right)+9 \frac{5}{12}\)
13 \(\frac{2}{12}\) + 8 \(\frac{7}{12}\) + 9 \(\frac{5}{12}\)
First add the whole numbers in the bracket.
13 + 8 = 21
21 + \(\frac{2}{12}\) + \(\frac{7}{12}\) + 9 \(\frac{5}{12}\)
21 + \(\frac{9}{12}\) + 9 \(\frac{5}{12}\)
30 + \(\frac{9}{12}\) + \(\frac{5}{12}\) = 31 \(\frac{2}{12}\)
Thus \(\left(13 \frac{2}{12}+8 \frac{7}{12}\right)+9 \frac{5}{12}\) = 31 \(\frac{2}{12}\)
Problem Solving
Question 10.
Nate’s classroom has three tables of different lengths. One has a length of 4 \(\frac{1}{2}\) feet, another has a length of 4 feet, and a third has a length of 2 \(\frac{1}{2}\) feet. What is the length of all three tables when pushed end to end?
_______ \(\frac{□}{□}\)
Answer: 11
Explanation:
Given,
Nate’s classroom has three tables of different lengths. One has a length of 4 \(\frac{1}{2}\) feet, another has a length of 4 feet, and a third has a length of 2 \(\frac{1}{2}\) feet.
4 \(\frac{1}{2}\) + 4 + 2 \(\frac{1}{2}\)
4 + 4 + 2 = 10
\(\frac{1}{2}\) + \(\frac{1}{2}\) = 1
10 + 1 = 11
Therefore the length of all three tables when pushed end to end is 11 feet.
Question 11.
Mr. Warren uses 2 \(\frac{1}{4}\) bags of mulch for his garden and another 4 \(\frac{1}{4}\) bags for his front yard. He also uses \(\frac{3}{4}\) bag around a fountain. How many total bags of mulch does Mr. Warren use?
_______ \(\frac{□}{□}\)
Answer: 7 \(\frac{1}{4}\)
Explanation:
Given,
Mr. Warren uses 2 \(\frac{1}{4}\) bags of mulch for his garden and another 4 \(\frac{1}{4}\) bags for his front yard.
He also uses \(\frac{3}{4}\) bag around a fountain.
2 \(\frac{1}{4}\) + 4 \(\frac{1}{4}\) + \(\frac{3}{4}\)
2 + 4 = 6
6 + \(\frac{1}{4}\) + \(\frac{1}{4}\) + \(\frac{3}{4}\)
= 7 \(\frac{1}{4}\)
Common Core – Add and Subtract Fractions – Page No. 150
Lesson Check
Question 1.
A carpenter cut a board into three pieces. One piece was 2 \(\frac{5}{6}\) feet long. The second piece was 3 \(\frac{1}{6}\) feet long. The third piece was 1 \(\frac{5}{6}\) feet long. How long was the board?
Options:
a. 6 \(\frac{5}{6}\) feet
b. 7 \(\frac{1}{6}\) feet
c. 7 \(\frac{5}{6}\) feet
d. 8 \(\frac{1}{6}\) feet
Answer: c. 7 \(\frac{5}{6}\) feet
Explanation:
Given,
A carpenter cut a board into three pieces. One piece was 2 \(\frac{5}{6}\) feet long. The second piece was 3 \(\frac{1}{6}\) feet long.
The third piece was 1 \(\frac{5}{6}\) feet long.
Add three pieces.
2 \(\frac{5}{6}\) + 3 \(\frac{1}{6}\)
= 5 + \(\frac{6}{6}\)
= 5 + 1 = 6
6 + 1 \(\frac{5}{6}\)
= 7 \(\frac{5}{6}\) feet
Thus the correct answer is option c.
Question 2.
Harry works at an apple orchard. He picked 45 \(\frac{7}{8}\) pounds of apples on Monday. He picked 42 \(\frac{3}{8}\) pounds of apples on Wednesday. He picked 54 \(\frac{1}{8}\) pounds of apples on Friday. How many pounds of apples did Harry pick those three days?
Options:
a. 132 \(\frac{3}{8}\) pounds
b. 141 \(\frac{3}{8}\) pounds
c. 142 \(\frac{1}{8}\) pounds
d. 142 \(\frac{3}{8}\) pounds
Answer: 142 \(\frac{3}{8}\) pounds
Explanation:
Given,
Harry works at an apple orchard. He picked 45 \(\frac{7}{8}\) pounds of apples on Monday.
He picked 42 \(\frac{3}{8}\) pounds of apples on Wednesday.
He picked 54 \(\frac{1}{8}\) pounds of apples on Friday.
45 \(\frac{7}{8}\) + 42 \(\frac{3}{8}\) + 54 \(\frac{1}{8}\)
Add the whole numbers first
45 + 42 + 54 = 141
141 + \(\frac{7}{8}\) + \(\frac{3}{8}\) + \(\frac{1}{8}\)
141 + 1 \(\frac{3}{8}\)
= 142 \(\frac{3}{8}\) pounds
Thus the correct answer is option d.
Spiral Review
Question 3.
There were 6 oranges in the refrigerator. Joey and his friends ate 3 \(\frac{2}{3}\) oranges. How many oranges were left?
Options:
a. 2 \(\frac{1}{3}\) oranges
b. 2 \(\frac{2}{3}\) oranges
c. 3 \(\frac{1}{3}\) oranges
d. 9 \(\frac{2}{3}\) oranges
Answer: 9 \(\frac{2}{3}\) oranges
Explanation:
Given,
There were 6 oranges in the refrigerator.
Joey and his friends ate 3 \(\frac{2}{3}\) oranges.
6 + 3 \(\frac{2}{3}\)
= 9 \(\frac{2}{3}\) oranges
Thus the correct answer is option d.
Question 4.
Darlene was asked to identify which of the following numbers is prime. Which number should she choose?
Options:
a. 2
b. 12
c. 21
d. 39
Answer: 2
Explanation:
A prime number is an integer, or whole number, that has only two factors 1 and itself.
In the above options, all are composite numbers except 2.
Therefore 2 is a prime number.
Thus the correct answer is option a.
Question 5.
A teacher has 100 chairs to arrange for an assembly. Which of the following is NOT a way the teacher could arrange the chairs?
Options:
a. 10 rows of 10 chairs
b. 8 rows of 15 chairs
c. 5 rows of 20 chairs
d. 4 rows of 25 chairs
Answer: 8 rows of 15 chairs
Explanation:
A teacher has 100 chairs to arrange for an assembly.
15 × 8 = 120
So, 8 rows of 15 chairs are not the way to arrange the chairs.
Thus the correct answer is option b.
Question 6.
Nic bought 28 folding chairs for $16 each. How much money did Nic spend on chairs?
Options:
a. $196
b. $348
c. $448
d. $600
Answer: c. $448
Explanation:
Given,
Nic bought 28 folding chairs for $16 each.
28 × 16 = 448
Thus the correct answer is option c.
Common Core – Add and Subtract Fractions – Page No. 151
Read each problem and solve.
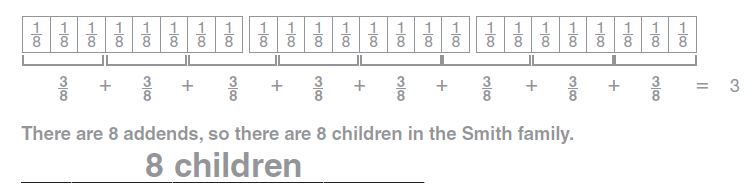
Question 1.
Each child in the Smith family was given an orange cut into 8 equal sections. Each child ate \(\frac{5}{8}\) of the orange. After combining the leftover sections, Mrs. Smith noted that there were exactly 3 full oranges left. How many children are in the Smith family?
Question 2.
Val walks 2 \(\frac{3}{5}\) miles each day. Bill runs 10 miles once every 4 days. In 4 days, who covers the greater distance?
_________
Answer: Val
Explanation:
Given,
Val walks 2 \(\frac{3}{5}\) miles each day. Bill runs 10 miles once every 4 days.
2 \(\frac{3}{5}\) × 4
Convert from mixed fraction to the improper fraction.
2 \(\frac{3}{5}\) = \(\frac{13}{5}\) × 4 = 10.4
10.4 > 10
Thus Val covers the greater distance.
Question 3.
Chad buys peanuts in 2-pound bags. He repackages them into bags that hold \(\frac{5}{6}\) pound of peanuts. How many 2-pound bags of peanuts should Chad buy so that he can fill the \(\frac{5}{6}\) -pound bags without having any peanuts left over?
_________ 2-pound bags
Answer: 5
Explanation:
Given,
Chad buys peanuts in 2-pound bags. He repackages them into bags that hold \(\frac{5}{6}\) pound of peanuts.
\(\frac{5}{6}\) + \(\frac{5}{6}\) + \(\frac{5}{6}\) + \(\frac{5}{6}\) + \(\frac{5}{6}\)
Thus 5 2-pound bags of peanuts are left.
Question 4.
A carpenter has several boards of equal length. He cuts \(\frac{3}{5}\) of each board. After cutting the boards, the carpenter notices that he has enough pieces left over to make up the same length as 4 of the original boards. How many boards did the carpenter start with?
_________
Answer: 10
Explanation:
Given,
A carpenter has several boards of equal length. He cuts \(\frac{3}{5}\) of each board. After cutting the boards, the carpenter notices that he has enough pieces left over to make up the same length as 4 of the original boards.
4 of the original boards have a summed length of 20 units. 5 x 4 = 20.
Since 2/5 is left from each board, you simply add them until the 2’s add to 20.
So, 2 x 10 = 20. Hence, there are 10 2/5 boards.
That’s just 4 of the boards that the 2/5 make up, but that should also mean that there are 10 3/5 boards as well.
30/5 + 20/5 = 50/5 = 10
Common Core – Add and Subtract Fractions – Page No. 152
Lesson Check
Question 1.
Karyn cuts a length of ribbon into 4 equal pieces, each 1 \(\frac{1}{4}\) feet long. How long was the ribbon?
Options:
a. 4 feet
b. 4 \(\frac{1}{4}\) feet
c. 5 feet
d. 5 \(\frac{1}{4}\) feet
Answer: 5 feet
Explanation:
Given,
Karyn cuts a length of ribbon into 4 equal pieces, each 1 \(\frac{1}{4}\) feet long.
1 \(\frac{1}{4}\) × 4
Convert from the mixed fraction to the improper fraction.
1 \(\frac{1}{4}\) = \(\frac{5}{4}\)
\(\frac{5}{4}\) × 4 = 5 feet
Thus the correct answer is option c.
Question 2.
Several friends each had \(\frac{2}{5}\) of a bag of peanuts left over from the baseball game. They realized that they could have bought 2 fewer bags of peanuts between them. How many friends went to the game?
Options:
a. 6
b. 5
c. 4
d. 2
Answer: 5
Explanation:
Given,
Several friends each had \(\frac{2}{5}\) of a bag of peanuts left over from the baseball game.
They realized that they could have bought 2 fewer bags of peanuts between them
2 ÷ \(\frac{2}{5}\) = 5
Thus the correct answer is option b.
Spiral Review
Question 3.
A frog made three jumps. The first was 12 \(\frac{5}{6}\) inches. The second jump was 8 \(\frac{3}{6}\) inches. The third jump was 15 \(\frac{1}{6}\) inches. What was the total distance the frog jumped?
Options:
a. 35 \(\frac{3}{6}\) inches
b. 36 \(\frac{1}{6}\) inches
c. 36 \(\frac{3}{6}\) inches
d. 38 \(\frac{1}{6}\) inches
Answer: 36 \(\frac{3}{6}\) inches
Explanation:
Given,
A frog made three jumps. The first was 12 \(\frac{5}{6}\) inches. The second jump was 8 \(\frac{3}{6}\) inches. The third jump was 15 \(\frac{1}{6}\) inches.
First add the whole numbers
12 + 8 + 15 = 35
Next add the fractions,
\(\frac{5}{6}\) + \(\frac{3}{6}\) + \(\frac{1}{6}\) = 1 \(\frac{3}{6}\)
35 + \(\frac{3}{6}\) = 36 \(\frac{3}{6}\) inches
Thus the correct answer is option c.
Question 4.
LaDanian wants to write the fraction \(\frac{4}{6}\) as a sum of unit fractions. Which expression should he write?
Options:
a. \(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\)
b. \(\frac{2}{6}+\frac{2}{6}\)
c. \(\frac{3}{6}+\frac{1}{6}\)
d. \(\frac{1}{6}+\frac{1}{6}+\frac{2}{6}\)
Answer: \(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\)
Explanation:
Given,
LaDanian wants to write the fraction \(\frac{4}{6}\) as a sum of unit fractions.
The unit fraction for \(\frac{4}{6}\) is \(\frac{1}{6}+\frac{1}{6}+\frac{1}{6}+\frac{1}{6}\)
Thus the correct answer is option a.
Question 5.
Greta made a design with squares. She colored 8 out of the 12 squares blue. What fraction of the squares did she color blue?
Options:
a. \(\frac{1}{4}\)
b. \(\frac{1}{3}\)
c. \(\frac{2}{3}\)
d. \(\frac{3}{4}latex]
Answer: [latex]\frac{2}{3}\)
Explanation:
Given,
Greta made a design with squares. She colored 8 out of the 12 squares blue.
\(\frac{8}{12}\)
= \(\frac{2}{3}\)
Thus the correct answer is option c.
Question 6.
The teacher gave this pattern to the class: the first term is 5 and the rule is add 4, subtract 1. Each student says one number. The first student says 5. Victor is tenth in line. What number should Victor say?
Options:
a. 17
b. 19
c. 20
d. 21
Answer:
given
a=5
d=4-1=3
to find t10
tn=a + (n-1) d
t10=5 + (10-1) 3
t10=5 + 27
t10 = 32
victor is tenth in line,therefore he should say the number 32
Common Core – Add and Subtract Fractions – Page No. 153
Lesson 7.1
Use the model to write an equation.
Question 1.
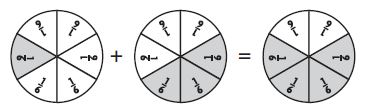
Type below:
_________
Answer: 1/6 + 3/6 = 4/6
Explanation:
From the figure, we can see that the shaded fraction of the first circle is 1/6.
The shaded fraction of the second circle is 3/6
The shaded fraction of the third circle is 4/6.
Question 2.
Type below:
_________
Answer: 5/8
Explanation:
From the above figure, we can say that the fraction of the shaded part is 5/8.
Use the model to solve the equation.
Question 3.
\(\frac{3}{10}+\frac{5}{10}\) =
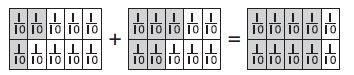
\(\frac{□}{□}\)
Answer: \(\frac{8}{10}\)
Explanation:
The shaded part of the first figure is 3/10
The shaded part of the second figure is 5/10
\(\frac{3}{10}+\frac{5}{10}\) = \(\frac{8}{10}\)
Question 4.
\(\frac{7}{12}-\frac{6}{12}\) =
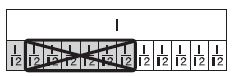
\(\frac{□}{□}\)
Answer: \(\frac{1}{12}\)
Explanation:
The shaded part of the above figure is 7/12. Out of which 6/12 are subtracted.
\(\frac{7}{12}-\frac{6}{12}\) = \(\frac{1}{12}\)
Lesson 7.2
Write the fraction as a sum of unit fractions.
Question 5.
\(\frac{2}{3}\) =
Type below:
_________
Answer: The unit fraction of \(\frac{2}{3}\) is \(\frac{1}{3}\) + \(\frac{1}{3}\)
Question 6.
\(\frac{3}{10}\) =
Type below:
_________
Answer: The unit fraction of \(\frac{3}{10}\) is \(\frac{1}{10}\) + \(\frac{1}{10}\) + \(\frac{1}{10}\)
Question 7.
\(\frac{4}{6}\) =
Type below:
_________
Answer: The unit fraction of \(\frac{4}{6}\) is \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\)
Question 8.
\(\frac{5}{12}\) =
Type below:
_________
Answer: The unit fraction of \(\frac{5}{12}\) is \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\) + \(\frac{1}{12}\)
Lessons 7.3–7.5
Find the sum or difference. Use fraction strips to help.
Question 9.
\(\frac{3}{8}+\frac{2}{8}\) =
\(\frac{□}{□}\)
Answer: \(\frac{5}{8}\)
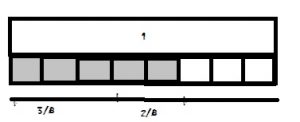
Question 10.
\(\frac{4}{5}+\frac{1}{5}\) =
\(\frac{□}{□}\)
Answer: 1
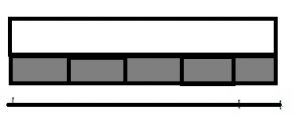
Question 11.
\(\frac{6}{10}+\frac{1}{10}\) =
\(\frac{□}{□}\)
Answer: \(\frac{7}{10}\)
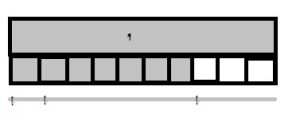
Question 12.
\(\frac{5}{6}-\frac{4}{6}\) =
\(\frac{□}{□}\)
Answer: \(\frac{1}{6}\)
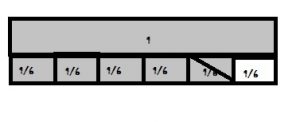
Question 13.
\(\frac{3}{4}-\frac{1}{4}\) =
\(\frac{□}{□}\)
Answer: \(\frac{1}{2}\)
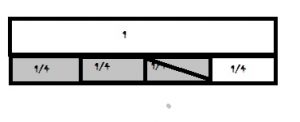
Question 14.
1 – \(\frac{7}{12}\) =
\(\frac{□}{□}\)
Answer: \(\frac{5}{12}\)
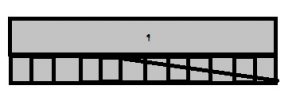
Question 15.
\(\frac{7}{10}-\frac{3}{10}\) =
\(\frac{□}{□}\)
Answer: \(\frac{4}{10}\)
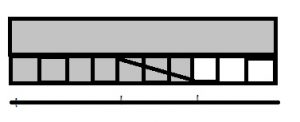
Question 16.
\(\frac{2}{6}+\frac{4}{6}\) =
\(\frac{□}{□}\)
Answer: 1
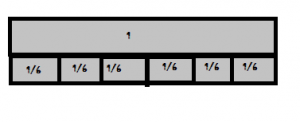
Question 17.
\(\frac{5}{8}-\frac{4}{8}\) =
\(\frac{□}{□}\)
Answer: \(\frac{1}{8}\)
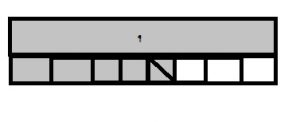
Common Core – Add and Subtract Fractions – Page No. 154
Lesson 7.6
Write each mixed number as a fraction and each fraction as a mixed number.
Question 1.
4 \(\frac{2}{3}\) =
\(\frac{□}{□}\)
Answer: \(\frac{14}{3}\)
Explanation:
First multiply 4 and 3
4 × 3 = 12
And then add 2 to 12
12 + 2 = 14
Thus the fraction of the mixed fraction is \(\frac{14}{3}\).
Question 2.
6 \(\frac{1}{4}\) =
\(\frac{□}{□}\)
Answer: \(\frac{25}{4}\)
Explanation:
First multiply 6 and 4
6 × 4 = 24
And then add 1 to 24
24 + 1 = 25
Thus the fraction of the mixed fraction is \(\frac{25}{4}\)
Question 3.
\(\frac{11}{3}\) =
_______ \(\frac{□}{□}\)
Answer: 3 \(\frac{2}{3}\)
Explanation:
Convert from improper fraction to the mixed fraction.
3 × 3 = 9
9 + 2 = 11
\(\frac{11}{3}\) = 3 \(\frac{2}{3}\)
Question 4.
\(\frac{16}{15}\) =
_______ \(\frac{□}{□}\)
Answer: 1 \(\frac{1}{15}\)
Explanation:
Given,
Convert from improper fraction to the mixed fraction.
15 × 1 = 15
15 + 1 = 16
\(\frac{16}{15}\) = 1 \(\frac{1}{15}\)
Lessons 7.7–7.8
Find the sum or difference.
Question 5.
\(3 \frac{1}{4}+2 \frac{3}{4}\) =
_______ \(\frac{□}{□}\)
Answer: 6
Explanation:
Given,
\(3 \frac{1}{4}+2 \frac{3}{4}\)
First add the whole numbers
3 + 2 = 5
\(\frac{1}{4}\) + \(\frac{3}{4}\) = 1
5 + 1 = 6
\(3 \frac{1}{4}+2 \frac{3}{4}\) = 6
Question 6.
\(1 \frac{5}{12}+2 \frac{1}{12}\) =
_______ \(\frac{□}{□}\)
Answer: 3 \(\frac{6}{12}\)
Explanation:
Given,
\(1 \frac{5}{12}+2 \frac{1}{12}\)
First add the whole numbers
1 + 2 = 3
3 \(\frac{5}{12}\) + \(\frac{1}{12}\) = 3 \(\frac{6}{12}\)
Question 7.
\(9 \frac{5}{6}-7 \frac{1}{6}\) =
_______ \(\frac{□}{□}\)
Answer: 2 \(\frac{4}{6}\)
Explanation:
Given,
\(9 \frac{5}{6}-7 \frac{1}{6}\)
First subtract the whole numbers
9 – 7 = 2
5/6 – 1/6 = \(\frac{4}{6}\)
2 + \(\frac{4}{6}\) = 2 \(\frac{4}{6}\)
Thus \(9 \frac{5}{6}-7 \frac{1}{6}\) = 2 \(\frac{4}{6}\)
Question 8.
\(9 \frac{3}{10}-1 \frac{7}{10}\) =
_______ \(\frac{□}{□}\)
Answer: 7 \(\frac{6}{10}\)
Explanation:
Given,
\(9 \frac{3}{10}-1 \frac{7}{10}\)
First subtract the whole numbers
9 – 1 = 8
3/10 – 7/10 = – 4/10
8 – 4/10 = 7 \(\frac{6}{10}\)
Lesson 7.9
Use the properties and mental math to find the sum.
Question 9.
\(\left(1 \frac{1}{4}+4\right)+2 \frac{3}{4}\)
_______ \(\frac{□}{□}\)
Answer: 8
Explanation:
Given,
\(\left(1 \frac{1}{4}+4\right)+2 \frac{3}{4}\)
1 \(\frac{1}{4}\) + 4 + 2 \(\frac{3}{4}\)
Add the whole numbers
1 + 4 = 5
5 \(\frac{1}{4}\) + 2 \(\frac{3}{4}\)
5 + 2 = 7
\(\frac{1}{4}\) + \(\frac{3}{4}\) = 1
7 + 1 = 8
Question 10.
\(\frac{3}{5}+\left(90 \frac{2}{5}+10\right)\)
_______ \(\frac{□}{□}\)
Answer: 101
Explanation:
Given,
\(\frac{3}{5}+\left(90 \frac{2}{5}+10\right)\)
Add the whole numbers
90 + 10 = 100
3/5 + 2/5 = 5/5 = 1
100 + 1 = 101
Question 11.
\(3 \frac{2}{6}+\left(2 \frac{1}{6}+\frac{4}{6}\right)\)
_______ \(\frac{□}{□}\)
Answer: 6 \(\frac{1}{6}\)
Explanation:
Given,
\(3 \frac{2}{6}+\left(2 \frac{1}{6}+\frac{4}{6}\right)\)
1/6 + 4/6 = 5/6
3 \(\frac{2}{6}\) + 2 \(\frac{5}{6}\) = 6 \(\frac{1}{6}\)
Question 12.
\(\left(\frac{5}{8}+2 \frac{3}{8}\right)+1 \frac{3}{8}\)
_______ \(\frac{□}{□}\)
Answer: 4 \(\frac{3}{8}\)
Explanation:
Given,
\(\left(\frac{5}{8}+2 \frac{3}{8}\right)+1 \frac{3}{8}\)
5/8 + 3/8 = 8/8 = 1
2 + 1 = 3
3 + 1 3/8 = 4 \(\frac{3}{8}\)
Lesson 7.10
Question 13.
Adrian jogs \(\frac{3}{4}\) mile each morning. How many days will it take him to jog 3 miles?
____ days
Answer: 4 days
Explanation:
Given,
Adrian jogs \(\frac{3}{4}\) mile each morning.
\(\frac{3}{4}\)/3 = 4
Thus it will take 4 days for him to jog 3 miles.
Question 14.
Trail mix is sold in 1-pound bags. Mary will buy some trail mix and re-package it so that each of the 15 members of her hiking club gets one \(\frac{2}{5}\) -pound bag. How many 1-pound bags of trail mix should Mary buy to have enough trail mix without leftovers?
____ 1-pound bags
Answer: 6 1-pound bags
Explanation:
Given,
Trail mix is sold in 1-pound bags. Mary will buy some trail mix and re-package it so that each of the 15 members of her hiking club gets one \(\frac{2}{5}\) -pound bag.
15 × \(\frac{2}{5}\) = 6
Therefore Mary should buy 6 1-pound bags to have enough trail mix without leftovers.
Conclusion:
I believe the questuins and solutions shed in Go Math Grade 4 Answer Key Homework Practice FL Chapter 7 Add and Subtract Fractions pdf will show some light on you while practicing. Identify your preparation level by answering the problems involved in HMH Go Math Grade 4 Answer Key Chapter 7 Add and Subtract Fractions. Keep visiting our site ccssmathanswers.com to find the pdfs of chapterwise Go Math Grade 4 Answer Key.
