Go Math Grade 8 Answer Key Chapter 8 Volume contains all the topics which help the students to score better marks in the exams. The main aim of providing the Go Math 8th Grade Answer Key for Chapter 13 Volume is to make the students understand the concepts in a simple way. Download Go Math Grade 8 Answer Key Chapter 13 Volume pdf. So, the students who are preparing for 3rd standard exams can check HMH Go Math Solution Key Grade 8 Chapter 13 Volume. Be the first to grab your HMH Go Math Grade 8 Answer Key and read all the questions of maths.
Download Go Math Grade 8 Chapter 13 Volume Answer Key Pdf
The topics covered in Go Math Grade 8 Answer Key Chapter 13 Volume are volume of cone, cylinders, and spheres. Get the clear cut explanations for all the questions here. Refer to Go Math Grade 8 Answer Key Chapter 13 Volume to get the highest marks in the exam. Learn and practice the maths in the best way using Go Math Grade 8 Answer Key Chapter 13 Volume. Check the topics before you start your preparation from the below sections.
Lesson 1: Volume of Cylinders
Lesson 2: Volume of Cones
Lesson 3: Volume of Spheres
Model Quiz :
Review :
Guided Practice – Volume of Cylinders – Page No. 402
Question 1.
Vocabulary Describe the bases of a cylinder.
Type below:
____________
Answer:
The ends of a cylinder are the bases of the cylinder of the two flat surfaces.
Question 2.
Figure 1 shows a view from above of inch cubes on the bottom of a cylinder. Figure 2 shows the highest stack of cubes that will fit inside the cylinder. Estimate the volume of the cylinder. Explain your reasoning.
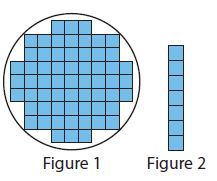
________ in3
Answer:
427in³
Explanation:
Number of inch cubes that fit in the base of the cylinder = 61
Number of inch cubes that fit in the length of the cylinder = 7
Volume of cylinder = basearea x height
V= 61 x 7
V = 427 cubic units.
Volume of each cube = 1 in³
Volume of cylinder = 427in³
Question 3.
Find the volume of the cylinder to the nearest tenth. Use 3.14 for π.
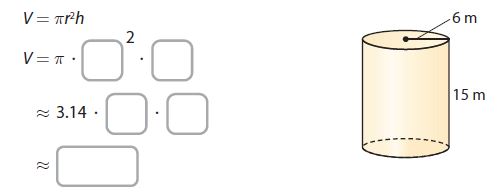
The volume of the cylinder is approximately _____ m3.
________ m3
Answer:
The volume of the cylinder is approximately 1695.6 m3.
1695.6m³
Explanation:
V = πr²h
V = π . 6² . 15
V = 3.14 × 36 × 15
V = 1695.6m³
Question 4.
A Japanese odaiko is a very large drum that is made by hollowing out a section of a tree trunk. A museum in Takayama City has three odaikos of similar size carved from a single tree trunk. The largest measures about 2.7 meters in both diameter and length, and weighs about 4.5 metric tons. Using the volume formula for a cylinder, approximate the volume of the drum to the nearest tenth.
The radius of the drum is about _____ m.
The volume of the drum is about _____ m3.
The radius of the drum is about ___________ m
The volume of the drum is about ___________ m3
Answer:
The radius of the drum is about 1.35 m.
The volume of the drum is about 15.5 m3.
Explanation:
Diameter of base of drum = 2.7 m
The radius of the base of the drum = 2.7/2
R = 1.35 m
The volume of cylinder = πr²h
Height (h) = 2.7 m
Radius (R) = 1.35 m
Volume = 3.14 × (1.35) × 2.7
V = 15.4511 m³
V = 15.5 m³
ESSENTIAL QUESTION CHECK-IN
Question 5.
How do you find the volume of a cylinder? Describe which measurements of a cylinder you need to know.
Type below:
____________
Answer:
The volume of the cylinder is = πr²h
Explanation:
We need to find the radius of the base, r, and the height of the cylinder, h.
The volume of the cylinder is = πr²h
13.1 Independent Practice – Volume of Cylinders – Page No. 403
Find the volume of each figure. Round your answers to the nearest tenth if necessary. Use 3.14 for π.
Question 6.

_________ cm3
Answer:
569.9 cm³
Explanation:
Radius of base = 11 cm
Height of cylinder = 1.5 cm
The volume of cylinder = πr²h
V = 3.14 × (11)² × 1.5
V = 569.91
V = 569.9 cm³
Question 7.
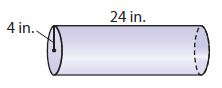
_________ in3
Answer:
1205.8 in³
Explanation:
Radius of base = 4 in
Height of cylinder = 24 in
The volume of cylinder = πr²h
V = 3.14 × (4)² × 24
V = 1205.76
V = 1205.8 in³
Question 8.
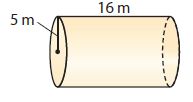
_________ m3
Answer:
1256 m³
Explanation:
Radius of base = 5 m
Height of cylinder = 16 m
The volume of cylinder = πr²h
V = 3.14 × (5)² × 16
V = 1256
V = 1256 m³
Question 9.
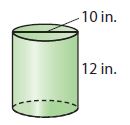
_________ in3
Answer:
942 in³
Explanation:
Diameter of base = 10 in
Radius of base = 5 in
Height of cylinder = 12 in
The volume of cylinder = πr²h
V = 3.14 × (5)² × 12
V = 942 in³
Question 10.
A cylinder has a radius of 4 centimeters and a height of 40 centimeters.
_________ cm3
Answer:
2009.6 cm³
Explanation:
Radius of base = 4 cm
Height of cylinder = 40 cm
The volume of cylinder = πr²h
V = 3.14 × (4)² × 40
V = 2009.6 cm³
Question 11.
A cylinder has a radius of 8 meters and a height of 4 meters.
_________ m3
Answer:
803.8 m³
Explanation:
The radius of base = 8 m
Height of cylinder = 4 m
The volume of cylinder = πr²h
V = 3.14 × (8)² × 4
V = 803.84 m³
V = 803.8 m³
Round your answer to the nearest tenth, if necessary. Use 3.14 for π.
Question 12.
The cylindrical Giant Ocean Tank at the New England Aquarium in Boston is 24 feet deep and has a radius of 18.8 feet. Find the volume of the tank.
_________ ft3
Answer:
26635.2 ft³
Explanation:
Base radius of the tank = 18.8 ft
Depth of the tank in the ocean = 24 ft
The volume of cylinder = πr²h
V = 3.14 × (18.8)² × 24
V = 3.14 × 354.44 × 24
V = 26635.2384 ft³
V = 26635.2 ft³
Question 13.
A standard-size bass drum has a diameter of 22 inches and is 18 inches deep. Find the volume of this drum.
_________ in3
Answer:
6838.9 in³
Explanation:
Base diameter of drum = 22 in
Base radius of the drum = 22/2 = 11 in
Depth of the bass drum = 18 in
Volume of the bass drum = πr²h
V = 3.14 × (11)² × 18
V = 3.14 × 121 × 18
V = 6838.92 in³
V = 6838.9 in³
Question 14.
Grain is stored in cylindrical structures called silos. Find the volume of a silo with a diameter of 11.1 feet and a height of 20 feet.
_________ ft3
Answer:
1934.4 ft³
Explanation:
Base diameter of silo = 11.1 ft
Base radius of the silo = 11.1/2 = 5.55 ft
Depth of the silo = 20 ft
Volume of the silo = πr²h
V = 3.14 × (5.55)² × 18
V = 3.14 × 30.8025 × 18
V = 1934.397 ft³
V = 1934.4 ft³
Question 15.
The Frank Erwin Center, or “The Drum,” at the University of Texas in Austin can be approximated by a cylinder that is 120 meters in diameter and 30 meters in height. Find its volume.
_________ m3
Answer:
339120 m³
Explanation:
Base diameter of the drum = 120 m
Base radius of the drum = 120/2 = 60 m
Height of the drum = 30 m
Volume of the drum = πr²h
V = 3.14 × (60)² × 30
V = 3.14 × 3600 × 30
V = 339120 m³
Volume of Cylinders – Page No. 404
Question 16.
A barrel of crude oil contains about 5.61 cubic feet of oil. How many barrels of oil are contained in 1 mile (5280 feet) of a pipeline that has an inside diameter of 6 inches and is completely filled with oil? How much is “1 mile” of oil in this pipeline worth at a price of $100 per barrel?
__________ barrels
$ __________
Answer:
184.7 barrels
$18470
Explanation:
Volume of barrel = 5.61 cubic feet
Length of the pipe = 1 mile = 5280 feet
Diameter of the pipe = 6 inches = 0.5 feet
Radius of the pipe = 6/2 inches = 3 inches = 0.25 feet
Volume of oil in the pipe = πr²h = 3.14 × (0.25)² × 5280 = 1036.2 cubic feet
Number of barrels in the pipe = 1036.2/5.61 = 184.7 barrels
Cost of one barrel = $100
Cost of 184.7 barrels =184.7 × $100 = $18470
Question 17.
A pan for baking French bread is shaped like half a cylinder. It is 12 inches long and 3.5 inches in diameter. What is the volume of uncooked dough that would fill this pan?
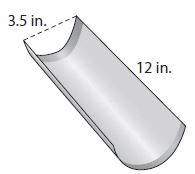
_________ in3
Answer:
57.697 in³
Explanation:
The length of the pan = 12 in
The diameter of the pan = 3.5 in
Radius = 3.5/2 = 1.75 in
The volume of uncooked dough = Half the volume of the full cylinder of the above dimensions.
= (πr²h)/2 = (3.14 × (1.75)² × 12)/2 = 115.395/2 = 57.697 in³
FOCUS ON HIGHER ORDER THINKING
Question 18.
Explain the Error A student said the volume of a cylinder with a 3-inch diameter is two times the volume of a cylinder with the same height and a 1.5-inch radius. What is the error?
Type below:
_______________
Answer:
The volume of the cylinder of 3 in is four times the volume of the new cylinder of radius 1.5 in
Explanation:
The volume of a cylinder is directly proportional to the square of the radius of the cylinder. The volume does not depend on the radius linearly.
Volume = πr²h
V1 = π(3)²h
V2 = π(1.5)²h
V1/V2 = (π(3)²h)/(π(1.5)²h)
V1/V2 = 4
V1 = 4V2
Question 19.
Communicate Mathematical Ideas Explain how you can find the height of a cylinder if you know the diameter and the volume. Include an example with your explanation.
Type below:
_______________
Answer:
Let the diameter be D.
Radius r = D/2
Volume = πr²h
Volume = π(D/2)²h
V = π((D)²/4)h
h = 4V/π(D)²
To find the height of a cylinder with diameter D = 2 m
Let the volume be 10 m³
h = 4V/π(D)²
h = (4 × 10)/(3.14 × 2²)
h = 3.18 m³
Question 20.
Analyze Relationships Cylinder A has a radius of 6 centimeters. Cylinder B has the same height and a radius half as long as cylinder A. What fraction of the volume of cylinder A is the volume of cylinder B? Explain.
Fraction: \(\frac{□}{□}\)
Answer:
\(\frac{VA}{4}\)
Explanation:
rA = 6 cm
rB = half of the radius of cylinder A = 3 cm
hA = hB
VA = πrA²h
VB = πrB²h
VA/VB = (πrA²h)/(πrB²h)
VA/VB = 6²/3² = 36/9 = 4
Thus VB = VA/4
Guided Practice – Volume of Cones – Page No. 408
Question 1.
The area of the base of a cylinder is 45 square inches and its height is 10 inches. A cone has the same area for its base and the same height. What is the volume of the cone?
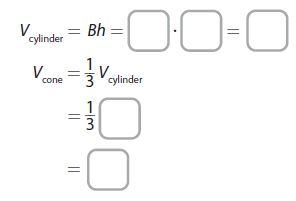
The volume of the cone is _____ in3.
_________ in3
Answer:
150 in³
Explanation:
In the question, the area of the base of the cylinder, B = 45 in²
Height of the cylinder, h = 10 inch
Volume of the cylinder, V cylinder = B × h = 45 × 10 = 450 inch³
Volume of the cone, V Cone = 1/3 V cylinder
=1/3(450 inch) = 150 inch³
So, the volume of the cone is
Vcone = 150 in³
Question 2.
A cone and a cylinder have congruent height and bases. The volume of the cone is 18 m3.What is the volume of the cylinder? Explain.
_________ m3
Answer:
54 m3
Explanation:
The volume of the cone is 18 m3.
Vcone = 1/3 Vcylinder
Vcylinder = 3Vcone
Vcylinder = 3.18
Vcylinder = 54 m3
Find the volume of each cone. Round your answer to the nearest tenth if necessary. Use 3.14 for π.
Question 3.
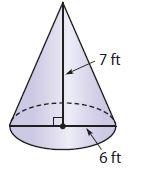
_________ ft3
Answer:
65.94 ft³
Explanation:
the diameter of the cone is 6ft.
so, the radius of the cone is 3ft.
the height of the cone is 7ft.
the volume of the cone = 1/3 × πr²h = 1/3 × 3.14 × 3² × 7 = 65.94 ft³
Question 4.
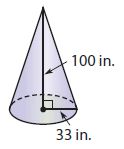
_________ in3
Answer:
113982in³
Explanation:
The radius is 33inch and the height is 100 inch
Volume of the cone = 1/3 × πr²h = 1/3 × π(33)²100 = 113982in³
Question 5.
Gretchen made a paper cone to hold a gift for a friend. The paper cone was 15 inches high and had a radius of 3 inches. Find the volume of the paper cone to the nearest tenth. Use 3.14 for π.
_________ in3
Answer:
141.3in³
Explanation:
the radius of the cone is 3inch and the height of the cone is 15inch.
Volume of the cone = 1/3 × πr²h = 1/3 × π(3)² × 15 = 141.3in³
Question 6.
A cone-shaped building is commonly used to store sand. What would be the volume of a cone-shaped building with a diameter of 50 meters and a height of 20 meters? Round your answer to the nearest tenth. Use 3.14 for π.
_________ m3
Answer:
13083.33 m³
Explanation:
The diameter of the cone is 50 meters. So, the radius of the cone is 25 meters. The height of the cone is 20 meters.
Volume of the cone = 1/3 × πr²h = 1/3 × π(25)² × 20 = 13083.33 m³
ESSENTIAL QUESTION CHECK-IN
Question 7.
How do you find the volume of a cone?
Type below:
____________
Answer:
V cone = 1/3 V cylinder
V cone = 1/3 πr²h
13.2 Independent Practice – Volume of Cones – Page No. 409
Find the volume of each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for π.
Question 8.
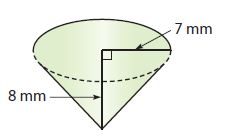
_________ mm3
Answer:
410.3 mm³
Explanation:
Radius r = 7 mm
height = 8 mm
Volume of cone = 1/3 πr²h
Volume = 1/3(3.14)(7)²(8)
Volume = 410.29 mm³
Volume = 410.3 mm³
Question 9.
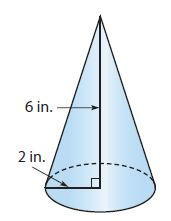
_________ in3
Answer:
25.1 in3
Explanation:
Radius r = 2 in
Height = 6 in
Volume of cone = 1/3 πr²h
Volume = 1/3(3.14)(2)²(6)
Volume = 25.12 in3
Volume = 25.1 in3
Question 10.
A cone has a diameter of 6 centimeters and a height of 11.5 centimeters.
_________ cm3
Answer:
108.3 cm3
Explanation:
Diameter of base = 6 cm
Radius = 6/2 cm = 3 cm
Height = 11.5 cm
Volume of cone = 1/3 πr²h
Volume = 1/3(3.14)(3)² (11.5)
Volume = 108.33 cm3
Volume = 108.3 cm3
Question 11.
A cone has a radius of 3 meters and a height of 10 meters.
_________ m3
Answer:
94.2 m3
Explanation:
Radius r = 3 m
Height = 10 m
Volume of cone = 1/3 πr²h
Volume = 1/3(3.14)(3)²(10)
Volume = 94.2 m3
Round your answers to the nearest tenth if necessary. Use 3.14 for π.
Question 12.
Antonio is making mini waffle cones. Each waffle cone is 3 inches high and has a radius of \(\frac{3}{4}\) inch. What is the volume of a waffle cone?
_________ in3
Answer:
1.8 in3
Explanation:
Radius = 3/4 in
Radius r = 0.75 in
Height = 3 in
Volume of each waffle cone = 1/3 πr²h
Volume = 1/3 (3.14) (0.75)² (3)
Volume = 1.76625 in3
Volume = 1.8 in3
Question 13.
A snack bar sells popcorn in cone-shaped containers. One container has a diameter of 8 inches and a height of 10 inches. How many cubic inches of popcorn does the container hold?
_________ in3
Answer:
167.5 in3
Explanation:
Diameter of base = 8 in
Radius = 8/2 in = 4 in
Height = 10 in
Volume of cone = 1/3 πr²h
Volume = 1/3 (3.14) (4)² (10)
Volume = 167.466 in3
Volume = 167.5 in3
Question 14.
A volcanic cone has a diameter of 300 meters and a height of 150 meters. What is the volume of the cone?
_________ m3
Answer:
3534291.7 m3
Explanation:
Diameter of base = 300 m
Radius = 300/2 m = 150 m
Height = 150 m
Volume of cone = 1/3 πr²h
Volume = 1/3 (3.14) (150)² (150)
Volume = 3534291.735 m3
Volume = 3534291.7 m3
Question 15.
Multistep Orange traffic cones come in a variety of sizes. Approximate the volume, in cubic inches, of a traffic cone that has a height of 2 feet and a diameter of 10 inches. Use 3.14 for π.
_________ in3
Answer:
628 in³
Explanation:
The radius of the cone is Diameter/2 = 10/2 = 5
The height of the cone is 2 ft = 2 . 12 = 24 in
Vcone = 1/3 πr²h
Vcone = 1/3 (3.14) (5)² (24)
Vcone = 628 in³
Find the missing measure for each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for π.
Question 16.
radius = _______
height = 6 in.
volume = 100.48 in3
_________ in.
Answer:
radius = 4 in.
4 in.
Explanation:
Let radius be R.
Height = 6 in
Volume = 100.4 in
Volume of cone = 1/3 πr²h
√(3v/hπ) = R
√((3 × 100.48)/(18.84)) = R
√(301.44/18.84) = R
R = √(16)
R = 4 in
Question 17.
diameter = 6 cm
height = _______
volume = 56.52 cm3
_______ cm
Answer:
height = 6 cm
h = 6 cm
Explanation:
Let height be h
Diameter = 6 cm
Radius = 6/2 = 3 cm
Volume = 56.52 cm
Volume of cone = 1/3 πr²h
(3V/r²h) = h
(3 × 56.52)/(3² × 3.14) = h
169.56/28.26 = h
h = 6 cm
Question 18.
The diameter of a cone-shaped container is 4 inches, and its height is 6 inches. How much greater is the volume of a cylinder-shaped container with the same diameter and height? Round your answer to the nearest hundredth. Use 3.14 for π.
Type below:
____________
Answer:
The volume of the cylinder is 50.24 in³ greater than the volume of the cone.
Explanation:
The diameter of a cone, d = 4 inch
radius of a cone, r = d/2 = 4/2 = 2 inches
height of a cone, h = 6 inches.
So, volume of a cone, V cone = 1/3 πr²h
= 1/3 (3.14) (2)² (6)
= 25.12 in³
And volume of a cylinder with same diameter and height,
V cylinder = πr²h = (3.14) (2)² (6) = 75.36 in³
The volume of the cylinder is 50.24 in³ greater than the volume of the cone.
FOCUS ON HIGHER ORDER THINKING – Volume of Cones – Page No. 410
Question 19.
Alex wants to know the volume of sand in an hourglass. When all the sand is in the bottom, he stands a ruler up beside the hourglass and estimates the height of the cone of sand.
a. What else does he need to measure to find the volume of sand?
____________
Answer:
To find the volume of the sand, he needs to measure the radius of the base of the hourglass.
Question 19.
b. Make a Conjecture If the volume of sand is increasing at a constant rate, is the height increasing at a constant rate? Explain.
____________
Answer:
The volume of the cone is linearly proportional to the height of the cone. Therefore, if the volume is increasing at a constant rate, the height is also increasing at a constant rate.
Question 20.
Problem Solving The diameter of a cone is x cm, the height is 18 cm, and the volume is 301.44 cm3. What is x? Use 3.14 for π.
________ cm
Answer:
8 cm
Explanation:
V cone = 1/3 πr²h
301.44 = 1/3 . 3.14 . r² . 18
r² = 904.32/56.52
r² = 16
r = 4 cm
The diameter of the circle is twice its radius, therefore
x = 2 . r
x = 2 . 4
x = 8 cm
Question 21.
Analyze Relationships A cone has a radius of 1 foot and a height of 2 feet. How many cones of liquid would it take to fill a cylinder with a diameter of 2 feet and a height of 2 feet? Explain.
________ cones
Answer:
3 cones
Explanation:
The diameter of the base of the cylinder is 2 feet, which means that its radius is 1 foot. Its height is 2 feet. The volume of this cylinder is
V cylinder = πr²h
V cylinder = (3.14) (1)² (2)
V cylinder = 6.28
The radius of the cone is 1 foot and the height of the cone is 2 feet. The volume of the cone is:
V cone = 1/3 πr²h
V cone = 1/3 (3.14) (1)² (2)
V cone = 1/3 × 6.28
V cone = 1/3 . V cylinder
V cone = 2.09
It would take 3 cones of liquid to fill the cylinder.
Question 22.
Critique Reasoning Herb knows that the volume of a cone is one third that of a cylinder with the same base and height. He reasons that a cone with the same height as a given cylinder but 3 times the radius should therefore have the same volume as the cylinder, since \(\frac{1}{3}\) ⋅ 3 = 1. Is Herb correct? Explain.
____________
Answer:
The volume of the given cylinder is V cylinder = πr²h
The volume of the cone with the same height h as a given cylinder but 3 times the radius r is
V cone = 1/3 π(3r)²h
V cone = 3 πr²h
V cone = 3 V cylinder
As we can see, Herb is not correct. The volume of the cone is not equal to the volume of the cylinder. But it is three times the volume of the cylinder.
Guided Practice – Volume of Spheres – Page No. 414
Question 1.
Vocabulary A sphere is a three-dimensional figure with all points _____ from the center.
Type below:
____________
Answer:
A sphere is a three-dimensional figure with all points at equal distance from the center.
Question 2.
Vocabulary The _____ is the distance from the center of a sphere to a point on the sphere.
Type below:
____________
Answer:
radius
Explanation:
The radius is the distance from the center f the sphere to a point on the sphere
Find the volume of each sphere. Round your answers to the nearest tenth if necessary. Use 3.14 for π.
Question 3.
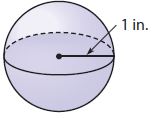
_______ in3
Answer:
4.12 in3
Explanation:
V = 4/3πr³
V = 4/3 (3.14) (1)³
V = 4.12 in3
Question 4.
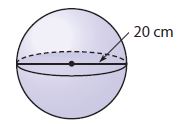
_______ cm3
Answer:
4186.7 cm³
Explanation:
Diameter = 20 cm
Radius r = 20/2 = 10 cm
Volume of sphere = 4/3πr³
Volume = 4/3 (3.14) (10)³
Volume = 4186.66 cm³
Volume = 4186.7 cm³
Question 5.
A sphere has a radius of 1.5 feet.
_______ ft3
Answer:
14.1 ft³
Explanation:
Radius r = 1.5 ft
The volume of sphere = 4/3πr³
Volume = 4/3 (3.14) (1.5)³
Volume = 14.13 ft³
Volume = 14.1 ft³
Question 6.
A sphere has a diameter of 2 yards.
_______ yd3
Answer:
4.2 yd³
Explanation:
Diameter = 2 yards
Radius r = 2/2 yards
Radius r = 1 yd
Volume of sphere = 4/3πr³
Volume = 4/3 (3.14) (1)³
Volume = 4.1866 yd³
Volume = 4.2 yd³
Question 7.
A baseball has a diameter of 2.9 inches. Find the volume of the baseball. Round your answer to the nearest tenth if necessary. Use 3.14 for π.
_______ in3
Answer:
12.8 in³
Explanation:
Diameter of baseball = 2.9 in
Radius r = 2.9/2 in
Radius of baseball = 1.45 in
The volume of sphere = 4/3πr³
Volume = 4/3 (3.14) (1.45)³
Volume = 12.763 in³
Volume = 12.8 in³
Question 8.
A basketball has a radius of 4.7 inches. What is its volume to the nearest cubic inch. Use 3.14 for π.
_______ in3
Answer:
1304 in³
Explanation:
Radius of baseball = 4.7 in
The volume of sphere = 4/3πr³
Volume = 4/3 (3.14) (4.7)³
Volume = 1304.0168 in³
Volume = 1304 in³
Question 9.
A company is deciding whether to package a ball in a cubic box or a cylindrical box. In either case, the ball will touch the bottom, top, and sides.
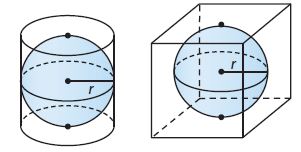
a. What portion of the space inside the cylindrical box is empty? Explain.
Type below:
_______________
Answer:
The volume of the cylinder is V cylinder = πr²h
Since the ball touches the bottom, top, and sides, then the height of the cylinder will be equal to 2r.
V cylinder = πr²(2r) = 2πr³
On the other hand, the volume of the sphere is
V sphere = 4/3 πr³
The volume of the empty space inside the cylindrical box is found by subtracting the volume of the sphere from the volume of the cylinder
V cylinder – V sphere = 2πr³ – 4/3 πr³
= (2 – 4/3)πr³
= 2/3πr³
Question 9.
b. Find an expression for the volume of the cubic box.
Type below:
_______________
Answer:
The volume of a cube with side a is V cube = a³
Since the ball touches the bottom, top, and sides, then the side of the cube will be equal to 2r.
V cube = (2r)³
V cube = 8r³
Question 9.
c. About what portion of the space inside the cubic box is empty? Explain
Type below:
_______________
Answer:
The volume of the empty space inside the cubical box is found by subtracting the volume of the sphere from the volume of the cube:
V cube – V sphere = 8r³ – 4/3 πr³
= (8 – 4/3π)r³
= (8 – 4.2)r³
= 3.8r³
ESSENTIAL QUESTION CHECK-IN
Question 10.
Explain the steps you use to find the volume of a sphere.
Type below:
_______________
Answer:
Step 1: The radius of the sphere is found out.
Step 2: The volume of the sphere is 4/3 πr³; where R is the radius.
Step 3: Put the value of radius in the equation of volume.
Step 4: Calculate the volume.
13.3 Independent Practice – Volume of Spheres – Page No. 415
Find the volume of each sphere. Round your answers to the nearest tenth if necessary. Use 3.14 for π.
Question 11.
radius of 3.1 meters
_______ m3
Answer:
124.7 m³
Explanation:
The volume of the sphere with a radius of 3.1 meter is 4/3 πr³
V = 4/3 . (3.14) . (3.1)³
V = 124.7 m³
Question 12.
diameter of 18 inches
_______ in3
Answer:
3052.1 in³
Explanation:
The diameter of the sphere is 18 inches, which means that its radius is 9 inches. The volume of the sphere is
V = 4/3 πr³
V = 4/3 . (3.14) . (9)³
V = 3052.08 in³
V = 3052.1 in³
Question 13.
r = 6 in.
_______ in3
Answer:
904.3 in³
Explanation:
The volume of the sphere with a radius of 6 inches is
V = 4/3 πr³
V = 4/3 (3.14) (6)³
V = 904.32
V = 904.3 in³
Question 14.
d = 36 m
_______ m3
Answer:
24416.6 m³
Explanation:
d = 36 m
radius r = 36/2 = 18 m
Volume = 4/3 πr³
= 4/3 (3.14) (18)³
= 24416.64
Volume = 24416.6 m³
Question 15.
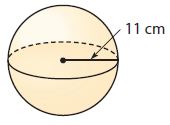
_______ cm3
Answer:
5572.5 cm³
Explanation:
The volume of the sphere with a radius of 11 centimeters is
V = 4/3 πr³
V = 4/3 (3.14) (11)³
V = 5572.5 cm³
Question 16.
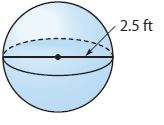
_______ ft3
Answer:
8.2 feet³
Explanation:
The diameter of the sphere is 2.5 feet, which means that its radius is 1.25 feet. The volume of the sphere is
V = 4/3 πr³
V = 4/3 . (3.14) . (1.25)³
V = 8.2 feet³
The eggs of birds and other animals come in many different shapes and sizes. Eggs often have a shape that is nearly spherical. When this is true, you can use the formula for a sphere to find their volume.
Question 17.
The green turtle lays eggs that are approximately spherical with an average diameter of 4.5 centimeters. Each turtle lays an average of 113 eggs at one time. Find the total volume of these eggs, to the nearest cubic centimeter.
_______ cm3
Answer:
5389 cm³
Explanation:
The diameter of an egg (sphere) is 4.5 centimeters, which means that its radius is 2.25 centimeters. The volume of a single egg is
V = 4/3 πr³
V = 4/3 (3.14) (2.25)³
V = 47.68875 cm³
Therefore, the total volume of 113 eggs is
113 . V = 113(47.68875)
= 5388.82875
= 5389 cm³
Question 18.
Hummingbirds lay eggs that are nearly spherical and about 1 centimeter in diameter. Find the volume of an egg. Round your answer to the nearest tenth.
_______ cm3
Answer:
0.5 cm³
Explanation:
The diameter of an egg (sphere) is 1 centimeter, which means that its radius is 0.5 centimeters. The volume of a single egg is
V = 4/3 πr³
V = 4/3 (3.14) (0.5)³
V = 0.5 cm³
Question 19.
Fossilized spherical eggs of dinosaurs called titanosaurid sauropods were found in Patagonia. These eggs were 15 centimeters in diameter. Find the volume of an egg. Round your answer to the nearest tenth.
_______ cm3
Answer:
1766.25 cm³
Explanation:
Diameter of an egg = 15 cm
Its radius = 15/2 = 7.5 cm
Volume = 4/3 πr³
V = 4/3 (3.14) (7.5)³
V = 1766.25 cm³
Question 20.
Persevere in Problem Solving An ostrich egg has about the same volume as a sphere with a diameter of 5 inches. If the eggshell is about \(\frac{1}{12}\) inch thick, find the volume of just the shell, not including the interior of the egg. Round your answer to the nearest tenth.
_______ in3
Answer:
6.8 in³
Explanation:
Diameter including the eggshell
= 5 + (2 . 1/2)
= (5 + 1/6) in
= 5.166 in
Radius including egg shell = 5.166/2 = 2.5833 in
Volume = 4/3 πr³
Volume = 4/3 (3.14) (2.5833)³
=72.176 in³
Volume with shell = 72.2 in³
Radius excluding shell = 5/2 = 2.5 in
Volume = 4/3 (3.14) (2.5)³
= 65.416 in³
Volume (without shell) = 65.4 in³
Volume of shell = Total volume – Inner Volume
= 72.2 – 65.4
= 6.8 in³
Question 21.
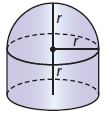
Multistep Write the steps you would use to find a formula for the volume of the figure at right. Then write the formula.
Type below:
_____________
Answer:
5/3πr³
Explanation:
The radius of hemisphere = r
Radius of cylinder = r
Height of cylinder = r
Step 1: Find the formula for the volume of a hemisphere
The volume of hemisphere = 4/3 π/2 r³
= 2/3πr³
Step 2: Find the formula for the volume of a cylinder
The volume of cylinder = πr²h
=πr³
Step 3: Add both the volume expressions:
Total volume = 2/3πr³ + πr³
= 5/3πr³
Volume of Spheres – Page No. 416
Question 22.
Critical Thinking Explain what happens to the volume of a sphere if you double the radius.
Type below:
_____________
Answer:
Let Radius = r
Volume V1 = 4/3πr³
Radius = 2r
Volume V2 = 4/3π(2r)³
= 8 . 4/3πr³
= 8 V1
= 8(initial volume)
By doubling the radius of sphere we make the voulme 8 times the intial value.
Question 23.
Multistep A cylindrical can of tennis balls holds a stack of three balls so that they touch the can at the top, bottom, and sides. The radius of each ball is 1.25 inches. Find the volume inside the can that is not taken up by the three tennis balls.

_______ in3
Answer:
12.3 in³
Explanation:
Radius of the ball = 1.25 inch
Height of the cylinder = (2 × 1.25) × 3
= (2.5) × 3
= 7.5 in
radius of base of cylinder = 1.25 in.
Volume of cylinder = πr²h
= (3.14) (1.25)² (7.5)
= 36.7968
= 36.8 in³
Volume of a ball (all three) = 3 × 4/3πr³
= 4 (3.14) (1.25)³
= 24.53125 in³
= 24.5 in³
Volume of empty space = Volume of cylinder – Volume of ball
= 36.8 – 24.5 = 12.3 in³
FOCUS ON HIGHER ORDER THINKING
Question 24.
Critique Reasoning A sphere has a radius of 4 inches, and a cube-shaped box has an edge length of 7.5 inches. J.D. says the box has a greater volume, so the sphere will fit in the box. Is he correct? Explain.
_____________
Answer:
The volume of sphere = 4/3πr³
= 4/3 (3.14) (4)³
= 267.9466
= 268
The volume of cube = (7.5)³
= 421.875
=421.9
The volume of cube > Volume of a sphere
But the base of the cube has an area of (7.5 × 7.5) = 56.25 while the cross-action area of the sphere.
πr² = (3.14) (4)² = 50.24
The cross-section area of the cube is less than that of a sphere. thus J.D. is wrong and the ball (sphere) will not fit in the cube.
Question 25.
Critical Thinking Which would hold the most water: a bowl in the shape of a hemisphere with radius r, a cylindrical glass with radius r and height r, or a cone-shaped drinking cup with radius r and height r? Explain.
_____________
Answer:
The volume of a sphere with radius r is
V sphere = 4/3πr³
Therefore, the volume of a hemisphere is
V hemisphere = V sphere/2
V hemisphere = 2/3πr³
The volume of a cylinder with radius r and height r is
V cylinder = πr²h
V cylinder = πr³
The volume of a cone with radius r and height r is
V cone = 1/3πr²h
V cone = 1/3πr³
V cone < V hemisphere < V cylinder
Therefore, the cylindrical glass with radius r and height r will hold the most water.
Question 26.
Analyze Relationships Hari has models of a sphere, a cylinder, and a cone. The sphere’s diameter and the cylinder’s height are the same, 2r. The cylinder has radius r. The cone has diameter 2r and height 2r. Compare the volumes of the cone and the sphere to the volume of the cylinder.
Type below:
_____________
Answer:
Radius of sphere = 2r/2 = r
Volume of sphere = 4/3πr³
Radius of cylinder = r
Height of cylinder = 2r
volume of cylinder = πr²(2r)
V cylinder = 2πr³
Radius of cone = 2r/2 = r
Height of cone = 2r
Volume of cone = 1/3 πr²(2r)
V cone = 2/3πr³
Volume of cylinder > Volume of sphere > Volume of cone
2πr³ > 4/3πr³ > 2/3πr³
Question 27.
A spherical helium balloon that is 8 feet in diameter can lift about 17 pounds. What does the diameter of a balloon need to be to lift a person who weighs 136 pounds? Explain.
_______ feet
Answer:
Diameter of ballon = 8 ft
Weight it could lift = 17 pound
Volume = 4/3 π(8/2)³
= 4³(4π/3)
4³/x(4π/3) = 17/36
1/x = 1/8 × 3/4π × 1/48
x = 4π/3 . 4³ . 2³
x = 4/3. π . 8³
The volume of ballon which can lift 136 pounds is equal to 4/3. π . 8³
The radius of that ballon = 8ft
Diameter = 8 . 2 = 16 ft
Ready to Go On ? – Model Quiz – Page No. 417
13.1 Volume of Cylinders
Find the volume of each cylinder. Round your answers to the nearest tenth if necessary. Use 3.14 for π.
Question 1.
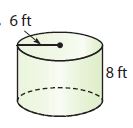
_______ ft3
Answer:
904.8 ft³
Explanation:
Radius of base = 6 ft
Height of cylinder = 8 ft
The volume of cylinder = πr²h
Volume = (3.14) (6)² (8)
Volume = 904.77 ft³
Volume = 904.8 ft³
Question 2.
A can of juice has a radius of 4 inches and a height of 7 inches. What is the volume of the can?
_______ in3
Answer:
351.7 in³
Explanation:
Radius if cylindrical can = 4 in
Height of cylindrical can = 7 in
The volume of cylinder = πr²h
Volume = (3.14) (4)² (7)
Volume = 351.68 in³
Volume = 351.7 in³
13.2 Volume of Cones
Find the volume of each cone. Round your answers to the nearest tenth if necessary. Use 3.14 for π.
Question 3.
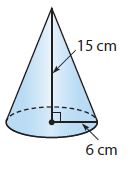
_______ cm3
Answer:
565.2 cm³
Explanation:
Radius of base of cone = 6 cm
Height of cone = 15 cm
Volume of cone = 1/3πr²h
Volume = 1/3 (3.14) (4)² (7)
Volume = 565.2 cm³
Question 4.
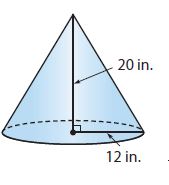
_______ in3
Answer:
3014.4 in³
Explanation:
The radius of the base of cone = 12 in
Height of cone = 20 in
The volume of cone = 1/3πr²h
Volume = 1/3 (3.14) (12)² (20)
Volume = 3014.4 in³
13.3 Volume of Spheres
Find the volume of each sphere. Round your answers to the nearest tenth if necessary. Use 3.14 for π.
Question 5.
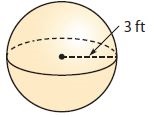
_______ in3
Answer:
113 in³
Explanation:
Radius of sphere = 3 ft
Volume of sphere = 4/3πr³
Volume = 4/3 (3.14) (3)³
Volume = 113.04 ft³
Volume = 113 in³
Question 6.
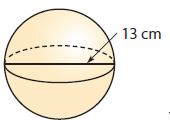
_______ cm3
Answer:
1149.8 cm³
Explanation:
Diameter = 13 cm
Radius = 13/2 cm = 6.5 cm
Volume of sphere = 4/3πr³
Volume = 4/3 (3.14) (6.5)³
Volume = 1149.7633 cm³
Volume = 1149.8 cm³
ESSENTIAL QUESTION
Question 7.
What measurements do you need to know to find the volume of a cylinder? a cone? a sphere?
Type below:
___________
Answer:
Sphere: To find the volume of the sphere, the radius is to be measured.
Cylinder: To measure the volume of the cylinder, we need to find out the base radius of the base of the cylinder along with the height of the cylinder.
Cone: To calculate the volume of the cone, we need to calculate the base radius of the base of the cone along with the height of the cone.
Explanation:
The volume of sphere = 4/3 πr³
Sphere: For finding the volume of the sphere, the radius is to be measured
The volume of Cylinder = πr²h
Cylinder: To calculate the volume of the cylinder, we need to find out the base radius of the base of the cylinder along with the height of the cylinder
The volume of Cone = 1/3 πr²h
Cone: To calculate the volume of the cone, we need to measure the base radius of the base of the cone along with the height of the cone
Selected Response – Mixed Review – Page No. 418
Question 1.
The bed of a pickup truck measures 4 feet by 8 feet. To the nearest inch, what is the length of the longest thin metal bar that will lie flat in the bed?
Options:
a. 11 ft 3 in.
b. 10 ft 0 in.
c. 8 ft 11 in.
d. 8 ft 9 in.
Answer:
d. 8 ft 9 in.
Explanation:
The length of the longest thin metal bar that will lie flat in the bed’s equal to the length of the bed’s hypotenuse. Let a = 4 and b = 8. Using the Pythagorean Theorem
a² + b² = c²
4² + 8² = c²
16 + 64 = c²
80 = c²
Rounding the length of the hypotenuse to the nearest tenth of a foot
c = 8.9 ft
Therefore, the length of the longest thin metal bar that will lie flat in the bed is 8 ft. 9 in.
Question 2.
Using 3.14 for π, what is the volume of the cylinder below to the nearest tenth?
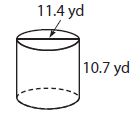
OPtions:
a. 102 cubic yards
b. 347.6 cubic yards
c. 1,091.6 cubic yards
d. 4,366.4 cubic yards
Answer:
c. 1,091.6 cubic yards
Explanation:
Diameter of the base of the cylinder = 11.4 yd
Radius = 11.4/2 yd = 5.7 yd
Height = 10.7 ys
Volume of cylinder = πr²h
Volume = (3.14) (5.7)² (10.7)
Volume = 1091.599 yd³
Volume = 1091.6 yd³
Question 3.
Rhett made mini waffle cones for a birthday party. Each waffle cone was 3.5 inches high and had a radius of 0.8 inches. What is the volume of each cone to the nearest hundredth?
Options:
a. 1.70 cubic inches
b. 2.24 cubic inches
c. 2.34 cubic inches
d. 8.79 cubic inches
Answer:
c. 2.34 cubic inches
Explanation:
Height of each waffle cone = 3.5 in
Radius of base = 0.8 in
Volume of cone = 1/3 πr²h
Volume = 1/3 (3.14) (0.8)² (3.5)
Volume = 2.344533 in³
Volume = 2.34 in³
Question 4.
What is the volume of a cone that has a height of 17 meters and a base with a radius of 6 meters? Use 3.14 for π and round to the nearest tenth.
Options:
a. 204 cubic meters
b. 640.6 cubic meters
c. 2,562.2 cubic meters
d. 10,249 cubic meters
Answer:
b. 640.6 cubic meters
Explanation:
Height of the cone = 17 m
Radius of base = 6 m
Volume of cone = 1/3 πr²h
Volume = 1/3 (3.14) (6)² (17)
Volume = 640.56 m³
Volume = 640.6 m³
Question 5.
Using 3.14 for π, what is the volume of the sphere to the nearest tenth?
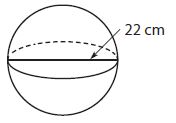
Options:
a. 4,180 cubic centimeters
b. 5,572.5 cubic centimeters
c. 33,434.7 cubic centimeters
d. 44,579.6 cubic centimeters
Answer:
b. 5,572.5 cubic centimeters
Explanation:
Diameter of the base of the sphere = 22 cm
Radius = 22/2 yd = 11 cm
Volume of sphere = 4/3 πr³
Volume = 4/3 (3.14) (11)³
Volume = 5572.4533 cm³
Volume = 5572.5 cm³
Mini-Task
Question 6.
A diagram of a deodorant container is shown. It is made up of a cylinder and half of a sphere.
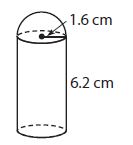
Use 3.14 for π and round answers to the nearest tenth.
a. What is the volume of the half sphere?
_______ cm3
Answer:
8.574 cm³
Explanation:
The radius of the cylinder as well as the hemisphere = 1.6 cm
Height = 6.2 cm
the volume of the hemisphere = 2/3 πr³
the volume of the hemisphere = 2/3 (3.14) (1.6)³
the volume of the hemisphere = 8.574 cm³
Question 6.
b. What is the volume of the cylinder?
_______ cm3
Answer:
49.838 cm³
Explanation:
The volume of cylinder = πr²h
= (3.14) (1.6)² (6.2)
= 49.838 cm³
Question 6.
c. What is the volume of the whole figure?
_______ cm3
Answer:
58.4 cm³
Explanation:
Total volume = Volume of cylinder + volume of a hemisphere
Total volume = 8.574 cm³ + 49.838 cm³
Total volume = 58.4 cm³
Conclusion:
I wish the detail provided in Go Math Grade 8 Solution Key Chapter 13 Volume is helpful for you guys. In addition to the exercise problems, you can also get the explanation with answers to the review test. Check out the solutions after your practice from our Go Math 8th Grade Chapter 13 Volume. Hence Download HMH 8th Grade Go Math Answer Key Chapter 13 Volume pdf for free. Learn the concept of volume from here and compare them with real life. This will help you to improve your skills and also score good marks in the exams.
