Properties of a Rectangle Rhombus and Square is always a confusing concept for students. Learning every individual topic is important to score good marks in the exam. So, we have explained every individual topic clearly in a detailed manner in this article. Therefore, those who wish to learn the concepts of Parallelogram and its properties, problems, can completely learn the Parallelogram concepts on our website.
Rectangle
A rectangle is said to be a parallelogram when it has all 4 angles having equal measure.
Properties of Rectangle
- The Opposite sides of a rectangle are parallel.
- Also, the Opposite sides of a rectangle are equal in length.
- Diagonals are equal in length.
- The interior angles are 90 degrees each.
- Diagonals bisect each other.
- It has horizontal and vertical lines of symmetry.
- Each of the diagonal bisects the rectangle into 2 congruent triangles.
- If you combine the 4 sides of a rectangle, then the mid-points of it form a rhombus.
Rectangle Formulas
If l is the length of the rectangle and b is the breadth of the rectangle, then
Area = lb square units
Perimeter = 2 (l+b) units.
Diagonal Properties of a Rectangle
Prove that the diagonals of a rectangle are equal and bisect each other.
Proof:
Let PQRS be a rectangle that has diagonals PQ and QS intersect at the point O.
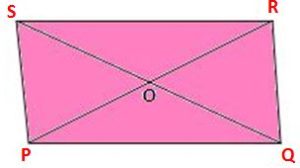
From ∆ PQR and ∆ QPS,
PQ = QP (common)
∠PQR = ∠QPS (each equal to 90º)
QR = PS (opposite sides of a rectangle).
Therefore, ∆ PQR ≅ ∆ QPS (by SAS congruence)
⇒ PR = QS.
Hence, the diagonals of a rectangle are equal.
From ∆ OPQ and ∆ ORS,
∠OPQ = ∠ORS (alternate angles)
∠OQP = ∠OSR (alternate angles)
PQ = RS (opposite sides of a rectangle)
Therefore, ∆OPQ ≅ ∆ ORS. (by ASA congruence)
⇒ OP = OR and OQ = OS.
This shows that the diagonals of a rectangle bisect each other.
Hence, the diagonals of a rectangle are equal and bisect each other.
Rhombus
The rhombus is a quadrilateral that consists of four sides with equal lengths.
Properties of Rhombus
- The Rhombus consists of parallel and equal opposite sides. As it consists of parallel and equal opposite sides, it is said to be a parallelogram.
- All available sides (4 sides) are equal.
- Also, opposite angles in a rhombus are equal.
- Diagonals bisect each other.
- Diagonals of a rhombus intersect each other at right angles.
- Furthermore, Diagonals bisect opposite vertex angles.
- Every diagonal divides the rhombus into 2 congruent triangles.
Rhombus Formula
If b is the side, a and b are the two diagonals of the rhombus, then
Area = ab/2 Square units.
Perimeter = 4b units
Diagonal Properties of a Rhombus
Prove that the diagonals of a rhombus bisect each other at right angles.
Proof:
Let PQRS be a rhombus whose diagonals AC and BD intersect at point O.
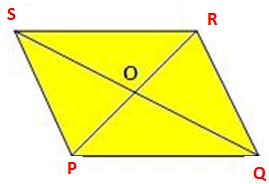
The diagonals of a parallelogram bisect each other. Also, we know that every rhombus is a parallelogram.
So, the diagonals of a rhombus bisect each other.
Therefore, OP = OR and OQ = OS
From ∆ ROQ and ∆ ROS,
RQ = RS (sides of a rhombus)
RO = RO (common).
OQ = OS (proved)
Therefore, ∆ ROQ ≅ ∆ ROS (by SSS congruence)
⇒ ∠ROQ = ∠ROS
But, ∠ROQ + ∠ROS = 2 right angles (linear pair)
Therefore, ∠ROQ = ∠ROS = 1 right angle.
Hence, the diagonals of a rhombus bisect each other at right angles.
Square
A square is a rectangle that has all equal sides.
Properties of Square
- The opposite sides of a square are parallel.
- All 4 sides are equal in length.
- Diagonals are equal in length.
- Diagonals bisect opposite vertex angles.
- The interior angles of a square measure 90 degrees each.
- Diagonals bisect each other at right angles.
- It has 4 lines of symmetry – a horizontal, a vertical, and 2 diagonals.
- Each diagonal bisects the square into 2 congruent triangles.
Square Formula
If b is the side of the square, then
Area = b² square units
Perimeter = 4b units.
Diagonal Properties of a Square
Prove that the diagonals of a square are equal and bisect each other at right angles.
Proof:
We know that the diagonals of a rectangle are equal.
Also, every square is a rectangle.
Therefore, the diagonals of a square are equal.
Again, the diagonals of a rhombus bisect each other at right angles. But, every square is a rhombus.
So, the diagonals of a square bisect each other at right angles.
Hence, the diagonals of a square are equal and also bisect each other at right angles.
Note 1: If the diagonals of a quadrilateral are equal but it is not necessary to be a rectangle.
Note 2: If the diagonals of a quadrilateral interest at a point with right angles then also it is not necessary to become a rhombus.