A set is a collection of well-defined objects. The best examples are set of even numbers between 2 and 20, set of whole numbers. The change in writing the order of elements in a set does not make any change. And if anyone or more elements of a set are repeated, then also the set remains the same. Check out the detailed information on the properties of set operations in the following sections along with the formulas.
Properties of Sets
If two or more sets are combined together to form another set under the provided constraints, then operations on the sets are carried out. the six important properties of set operations are along the lines.
1. Commutative Property
2. Associative Property
3. Distributive Property
4. Identity Property
5. Complement Property
6. Idempotent Property
What are the Basic Properties of Set Operations?
Here, we will discuss the six important set operations using the Venn diagrams.
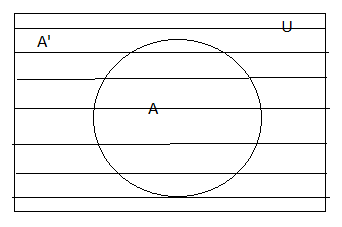
To understand the following properties, let us take A, B, and C are three sets and U be the universal set.
Property 1: Commutative Property
Intersection and union of sets satisfy the commutative property.
(i) A U B = B U A
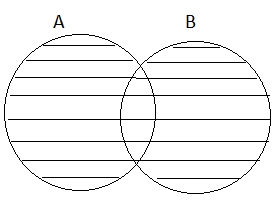 =
= 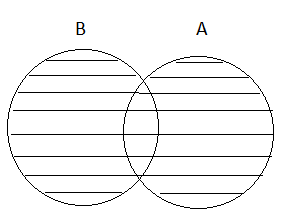
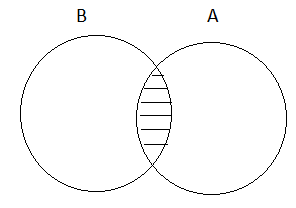
(ii) A ∩ B = B ∩ A
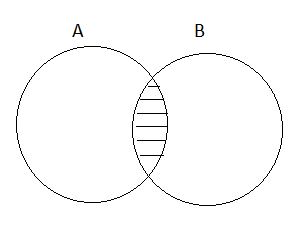 =
= 
Property 2: Associative Property
Intersection and union of sets satisfy the associative property.
(i) (A⋂B)⋂C = A⋂(B⋂C)
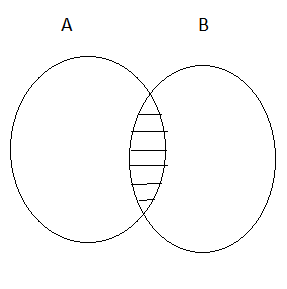
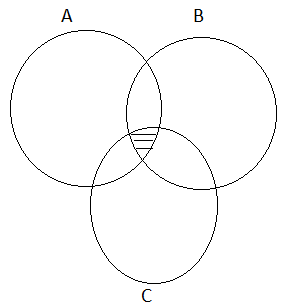
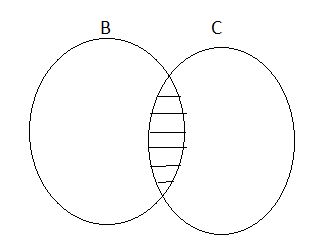

(ii) (A⋃B)⋃C = A⋃(B⋃C)
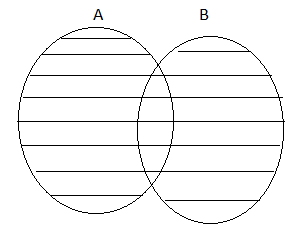
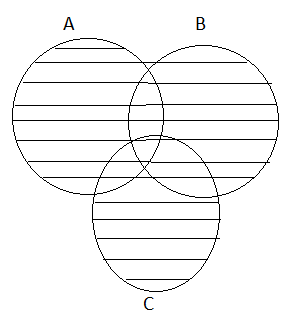
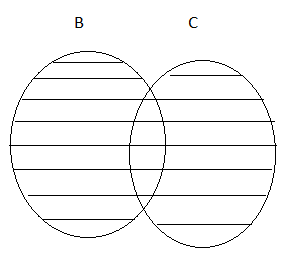

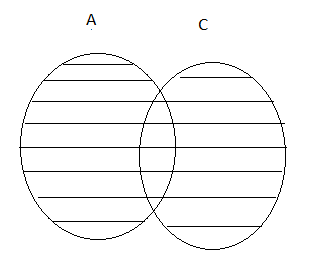
Property 3: Distributive Property
(i) A⋃(B⋂C) = (A⋃B)⋂(A⋃C)

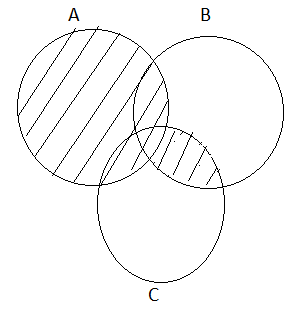

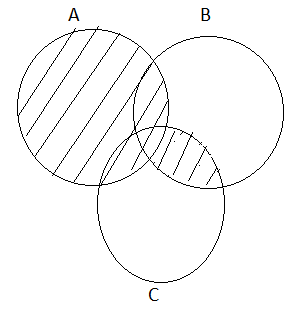
(ii) A⋂(B⋃C) = (A⋂B)⋃(A⋂C)

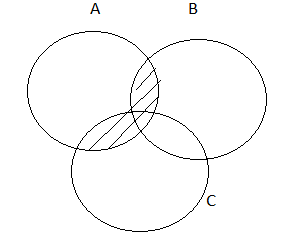


Property 4: Identity Property
(i) A⋃∅ = A
(ii) A⋂U = A
Property 5: Complement Property
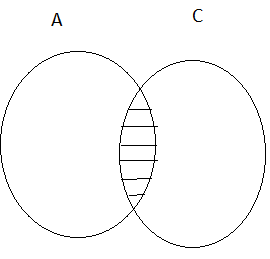
(i) A⋃Ac = U
(ii) A⋂Ac = ∅
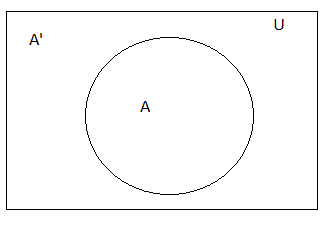
Property 6: Idempotent Property
(i) A⋂A = A
(ii) A⋃A = A
Solved Examples on Properties of Sets
Example 1:
If A = {1, 4, 6}, U = {1, 2, 3, 4, 5, 6} prove the complement property.
Solution:
Given that,
A = {1, 4, 6}, U = {1, 2, 3, 4, 5, 6}
A’ = {2, 3, 5}
To prove that A⋃A’ = U
L.H.S = AUA’
= {1, 4, 6} U {2, 3, 5}
= {1, 4, 6, 2, 3, 5}
= R.H.S
To prove A⋂A’ = ∅
L.H.S = {1, 4, 6} ⋂ {2, 3, 5}
= { }
= R.H.S
Hence, proved.
Example 2:
If A = {4, 10, 25}, B = {1, 5, 8}, C = {2, 16, 18}, prove that A⋃(B⋂C) = (A⋃B)⋂(A⋃C).
Solution:
Given that,
A = {4, 10, 25}, B = {1, 4, 5, 8}, C = {5, 2, 4, 16, 18}
L.H.S = A⋃(B⋂C)
= {4, 10, 25} U ({1, 4, 5, 8} ⋂ {2, 5, 16, 4, 18})
= {4, 10, 25} U {4, 5}
= {4, 5, 10, 25}
R.H.S = (A⋃B)⋂(A⋃C)
= ({4, 10, 25} U {1, 4, 5, 8}) ⋂ ({4, 10, 25} ⋃ {5, 2, 4, 16, 18})
= {1, 4, 5, 8, 10, 25} ⋂ {2, 4, 5, 10, 16, 18, 25}
= {4, 5, 10, 25}
Therefore, L.H.S = R.H.S
Example 3:
If A = {2, 4, 6, 8}, B = {1, 3, 5, 7}, C = {1, 2, 5, 8}, then show that (A⋃B)⋃C = A⋃(B⋃C)
Solution:
Given that,
A = {2, 4, 6, 8}, B = {1, 3, 5, 7}, C = {1, 2, 5, 8}
L.H.S = (A⋃B)⋃C
= ({2, 4, 6, 8} U {1, 3, 5, 7}) U {1, 2, 5, 8}
= {1, 2, 3, 4, 5, 6, 7, 8} U {1, 2, 5, 8}
= {1, 2, 3, 4, 5, 6, 7, 8
R.H.S = A⋃(B⋃C)
= {2, 4, 6, 8} U ({1, 3, 5, 7} U {1, 2, 5, 8})
= {2, 4, 6, 8} U {1, 2, 3, 5, 7}
= {1, 2, 3, 4, 5, 6, 7, 8}
Hence, shown.
Also, Read
