Learn Regular and Irregular Polygon Concepts and properties along with examples. Know the difference between Regular Polygons and Irregular Polygons and find out the given shape is a regular or irregular polygon. Check out the step-by-step process to find the given shape is a polygon or not? Also, we have given clear details about Regular and Irregular Polygons. Go through the Solved Examples on Regular and Irregular Polygons and learn how to solve problems on them quickly and easily.
Regular Polygon – Definition
A polygon that consists of equal sides with equal length and also by having equal angles called a regular polygon.
Examples of a Regular Polygon
Let us have a look at the different Examples of a Regular Polygon below.
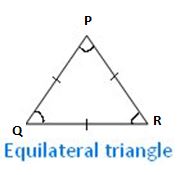
Equilateral Triangle:
An equilateral triangle is a triangle in which all three sides have the same length and all angles are equal.
In the below figure of an equilateral triangle PQR there are three sides i.e., PQ, QR, and RP are equal and there are three angles i.e., ∠PQR, ∠QRP, and ∠RPQ are equal.
Therefore, an equilateral triangle is a regular polygon.
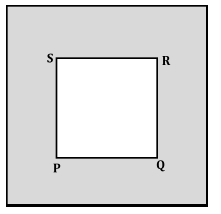
Square:
A Square is a quadrilateral that has four equal sides and four equal angles.
In the below figure of a square PQRS there are four sides i.e., PQ, QR, RS and SP are equal and there are four angles i.e., ∠PQR, ∠QRS, ∠RSP, and ∠SPQ are equal.
Therefore, a square is a regular polygon.
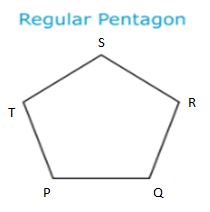
Regular Pentagon:
A polygon is regular when all angles are equal and all sides are equal.
In the below figure of a regular pentagon PQRST there are five sides i.e., PQ, QR, RS, ST, and TP are equal and there are five angles i.e., ∠PQR, ∠QRS, ∠RST, ∠STP, and ∠TPQ are equal.
Therefore, a regular pentagon is a regular polygon.
Irregular Polygon – Definition
A polygon that consists of unequal sides with unequal lengths and also having unequal angles called an irregular polygon.
Examples of Irregular Polygon
Let us have a look at the different Examples of a Regular Polygon below.
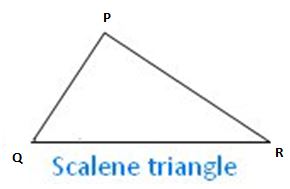
Scalene Triangle:
A scalene triangle is a triangle that has all three sides are in different lengths, and all three angles are of different measures.
In the adjoining figure of a scalene triangle PQR there are three sides i.e., PQ, QR, and RS are unequal and there are three angles i.e., ∠PQR, ∠RSP, and ∠SPQ are unequal.
Therefore, a scalene triangle is an irregular polygon.
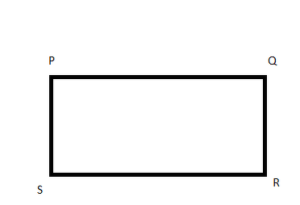
Rectangle:
A Rectangle is a four sided-polygon, having all the internal angles equal to 90 degrees. Each angle is at right angles. The opposite sides of the rectangle are equal in length which makes it different from a square.
In the adjoining figure of a rectangle PQRS there are four sides i.e., PQ, QR, RS, and SP where the opposite sides are equal i.e., PQ = RS, and QR = PS. So, all the sides are not equal to each other.
Similarly, among the four angles i.e., ∠PQR, ∠QRS, ∠RSP, and ∠SPQ where the opposite angles are equal i.e., ∠PQR = ∠RSP and ∠QRS = ∠SPQ. So, all the angles are not equal to each other.
Therefore, a rectangle is an irregular polygon.
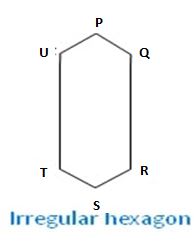
Irregular Hexagon:
An irregular hexagon is a six-sided shape whose sides are not equal.
In the adjoining figure of an irregular hexagon PQRSTU there are six sides i.e., PQ, QR, RS, ST, TU, and UP are equal and there are six angles i.e., ∠PQR, ∠QRS, ∠RST, ∠STU, ∠TUP, and ∠UPQ are equal.
Therefore, an irregular hexagon is an irregular polygon.