Supplementary angles are the angles that are added up to 180 degrees. If one angle is 120 degrees then the other angle is 60 degrees in supplementary angles because by adding 120 and 60, we get 180 degrees. By adding two supplementary angles, they form a straight line and a straight angle. One important thing in supplementary angles is the two angles need not be next to each other.
The important geometry concepts Lines and Angles are explained on our website with detailed explanations and solved examples. Learn all the concepts and improve your preparation level easily.
Supplementary Angle Definition
Supplementary Angle form 180º by adding two angles.
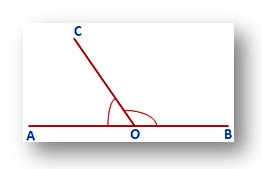
From the given figure, Angle AOC is one angle and angle BOC is another angle. By adding the two angles AOC and BOC, we get 180º. ∠AOC and ∠BOC are Supplementary Angles.
∠AOC + ∠BOC = 180°
Properties of Supplementary Angles
Have a look at the important properties of supplementary angles explained in the below modules. They are as such
- The two angles are said to be supplementary angles when they add up to form 180°.
- The two supplementary angles together make a straight line, but the angles need not be together.
- Two acute angles cannot be a supplement by each other.
- “S” of supplementary angles stands for the “Straight” line. This means they form 180°.
- The two right angles are always supplementary.
Adjacent and Non-Adjacent Supplementary Angles
The supplementary angles may be classified as either adjacent or non-adjacent. The adjacent supplementary angles have the common line segment or arm with each other. Also, the non-adjacent supplementary angles do not have the line segment or arm.

Supplementary Angles Theorem
The supplementary angle theorem states that if two angles are supplementary to the same angle, then the two angles are said to be congruent.
Proof:
If ∠a and ∠b are two different angles that are supplementary to a third angle ∠c, such that,
∠a + ∠c = 180 ……. (1)
∠b + ∠c = 180 ……. (2)
Then, from the above two equations, we can say,
∠a = ∠b
Hence proved.
Supplementary Angles Examples
1. Verify if 125°, 55° are a pair of supplementary angles?
Solution:
Add the given two angles and check if the resultant angle is 180° or not.
125° + 55° = 180°
The resultant angle is 180°. Hence, they are a pair of supplementary angles.
2. Find the supplement of the angle (30 + x)°.
Solution:
To find the supplement of (30 + x)°, subtract it from 180°
Supplement of the angle (30 + x)° = 180° – (30 + x)°
= 180° – 30° – x°
= (150 – x) °
3. If angles of measures (y – 2)° and (3y + 7)° are a pair of supplementary angles. Find the measures.
Solution:
Since (y – 2)° and (3y + 7)° represent a pair of supplementary angles, then their sum must be equal to 180°.
Therefore, (y – 2) + (3y + 7) = 180
y – 2 + 3y + 7 = 180
y + 3y – 2 + 7 = 180
4y + 5 = 180
Subtract 5 from both sides
4y + 5 – 5 = 180 – 5
4y = 180 – 5
4y = 175
y = 175/4
y = 43.75°
Therefore, we know the value of y = 43.75°, put the value in place of y
y – 2
= 43.75 – 2
= 41.75°
And again, 3y + 7
= 3 × 43.75° + 7
= 118 + 5
= 138.25°
Therefore, the two supplementary angles are 41.75° and 138.25°.
4. Two supplementary angles are in the ratio 5 : 4. Find the measure of the angles.
Solution:
Let the common ratio be m.
If one angle is 5m, then the other angle is 4m.
Therefore, 5m + 4m = 180
9m = 180
m = 180/9
m = 20
Put the value of m = 20
One angle is 5m
= 5 × 20
= 100°
And the other angle is 4m
= 4 × 20
= 80°
Therefore, the two supplementary angles are 100° and 80°.
5. In the given figure find the measure of the unknown angle.
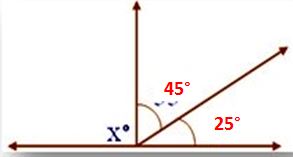
Solution:
x + 45° + 25° = 180°
The sum of angles at a point on a line on one side of it is 180°
Therefore, x + 70° = 180°
Subtract 70° from both sides
x + 70° – 70° = 180° – 70°
x = 110°