Get better practice by referring to the Worksheet on Functions or Mapping. Students who are interested in learning the complete concept of Functions or Mapping can learn it from Functions Mapping Worksheets. These Worksheets help you to have better practice for exams. We have included different problems along with solutions and explanations for your better preparation.
Easily improve your preparation level with the help of or Functions Worksheet. Check out the step-by-step solution and get complete knowledge of the concept. Mainly domain, co-domain, and range of functions are covered in the Worksheet on Mapping or Functions.
Do Read: Worksheet on Math Relation
Functions or Mapping Worksheet with Solutions
1. Which of the following represents a mapping?
(a) {(5, 3); (6, 4); (8, 6); (10, 8)}
(b) {(3, 9); (4, 13); (5, 17)}
(c) {(4, 8); (4, 12); (5, 10); (6, 12)}
(d) {(2, 3); (3, 4); (4, 5); (5, 6)}
(e) {(3, 2); (4, 2); (6, 2); (8, 2)}
(f) {(2, 4); (2, 6); (3, 6)}
Solution:
(a) Given that {(5, 3); (6, 4); (8, 6); (10, 8)}
Let the two sets are P and Q.
The required diagram is
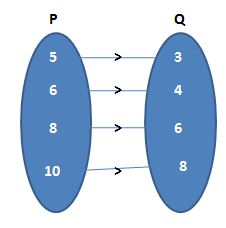
Different elements of P can have the same image in Q. Adjoining figure represents a mapping.
(b) Given that {(3, 9); (4, 13); (5, 17)}
Let the two sets are P and Q.
The required diagram is
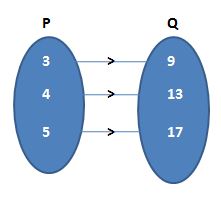
Different elements of P can have the same image in Q. Adjoining figure represents a mapping.
(c) Given that {(4, 8); (4, 12); (5, 10); (6, 12)}
Let the two sets are P and Q.
The required diagram is
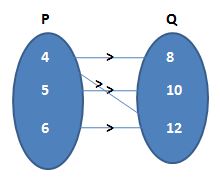
No element of P must have more than one image. The adjoining figure does not represent a mapping since element 4 in set P is associated with two elements 8, 12 of set Q.
(d) Given that {(2, 3); (3, 4); (4, 5); (5, 6)}
Let the two sets are P and Q.
The required diagram is
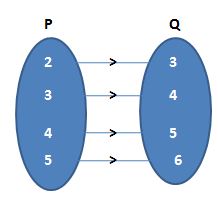
Different elements of P can have the same image in Q. Adjoining figure represents a mapping.
(e) Given that {(3, 2); (4, 2); (6, 2); (8, 2)}
Let the two sets are P and Q.
The required diagram is
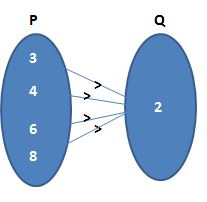
Different elements of P can have the same image in Q. Adjoining figure represents a mapping.
(f) Given that {(2, 4); (2, 6); (3, 6)}
Let the two sets are P and Q.
The required diagram is
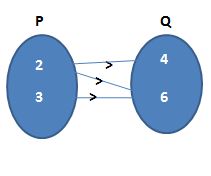
No element of P must have more than one image. The adjoining figure does not represent a mapping since element 2 in set P is associated with two elements 4, 6 of set Q.
Therefore, (a), (b), (d), (e) represents a mapping.
2. Which of the following arrow diagrams represents a mapping?
(a) 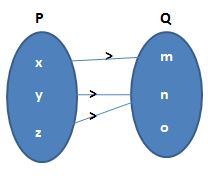
(b) 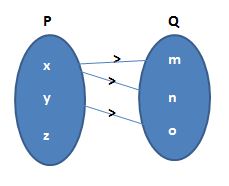
(c) 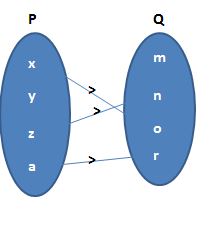
(d) 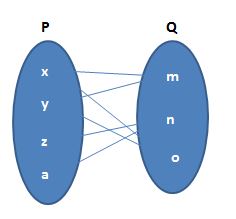
Solution:
(a) Different elements of P can have the same image in Q. Adjoining figure represents a mapping.
(b) Every element of P must have an image in Q. Adjoining figure does not represent a mapping since the element z in set P is not associated with any element of set Q.
No element of P must have more than one image. The adjoining figure does not represent a mapping since element x in set P is associated with two elements m, n of set Q.
(c) Every element of P must have an image in Q. Adjoining figure does not represent a mapping since the element y in set P is not associated with any element of set Q.
(d) No element of P must have more than one image. The adjoining figure does not represent a mapping since element x in set P is associated with two elements m, o of set Q.
Therefore, (a) represents a mapping.
3. A function f is defined by f(x) = 3x – 5. Write the values of
(a) f(0)
(b) f(-3)
(c) f(4)
(d) f(-2)
Solution:
Given that a function f is defined by f(x) = 3x – 5.
(a) f(0)
To find the f(0), substitute 0 in the place of the x.
The given equation is f(x) = 3x – 5
f(0) = 3 (0) – 5 = 0 – 5 = -5
f(0) = -5
Therefore, the answer is f(0) = -5
(b) f(-3)
To find the f(-3), substitute -3 in the place of the x.
The given equation is f(x) = 3x – 5
f(-3) = 3 (-3) – 5 = -9 – 5 = -14
f(-3) = -14
Therefore, the answer is f(-3) = -14
(c) f(4)
To find the f(4), substitute 4 in the place of the x.
The given equation is f(x) = 3x – 5
f(4) = 3 (4) – 5 = 12 – 5 = 7
f(4) = 7
Therefore, the answer is f(4) = 7
(d) f(-2)
To find the f(-2), substitute -2 in the place of the x.
The given equation is f(x) = 3x – 5
f(-2) = 3 (-2) – 5 = -6 – 5 = -11
f(-2) = -11
Therefore, f(0) = -5; f(-3) = -14; f(4) = 7; f(-2) = -11
4. Find the range of each of the following functions.
(a) f(x) = 7 – x, x ∈ N, x > 0
(b) f(x) = x² + 4, x ∈ R
Solution:
(a) Given that f(x) = 7 – x, x ∈ N, x > 0
x > 0
Multiply -1 on both sides.
– x < 0
Add 7 on both sides
7 – x < 0 + 7
7 – x < 7
We know that f(x) = 7 – x
f(x) < 7
We know that value of f(x) is less than 7
Hence, Range = (-∞, 7)
(b) Given that f(x) = x² + 4, x ∈ R
x² ≥ 0
Add 4 on both sides.
x² + 4 ≥ 0 + 4
x² + 4 ≥ 4
We know that f(x) = x² + 4
f(x) ≥ 4
Hence, Range of f(x) = (4, ∞)
5. Let M = {2, 4, 8, 7} and N = {5, 9, 17, 18, 19}
Consider the rule f(x) = x + 3, where x ∈ A.
Represent the mapping in the roster form.
Also, find the domain and range of the mapping.
Solution:
Given that M = {2, 4, 7, 8} and N = {5, 9, 17, 18, 19}
Consider the rule f(x) = x + 3, where x ∈ A.
For the required Relation we have to find the ordered pairs where x co-ordinate is from set M which is mapped to the y co-ordinate from set N.
If f(2) = 2 + 3 = 5
f(4) = 4 + 3 = 7
f(7) = 7 + 3 = 10
f(8) = 8 + 3 = 11
A set of ordered pairs r = {(2, 5); (4, 7); (7, 10); (8, 11)}
Domain = Set of all first elements in a relation = {2, 4, 7, 8}
Range = Set of all second elements in a relation = {5, 7, 10, 11}
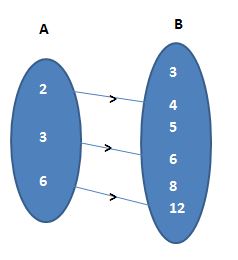
6. Let A = {2, 3, 6} B = {3, 4, 5, 6, 8, 12}
Draw the arrow diagram to represent the rule f(x) = 2x from A to B.
Solution:
Given that A = {2, 3, 6} B = {3, 4, 5, 6, 8, 12}
Consider the rule f(x) = 2x from A to B
For the required Relation we have to find the ordered pairs where x co-ordinate is from set A which is mapped to the y co-ordinate from set B.
If f(2) = 2 (2) = 4
f(3) = 2 (3) = 6
f(6) = 2 (6) = 12
A set of ordered pairs r = {(2, 4); (3, 6); (6, 12)}
7. Let A = {4, 9, 12} and B = {2, 3, 4}
(a) Show that the relation R = {(4, 2), (9, 3)} is not a mapping from A to B.
(b) Show that the relation R = {(4, 2); (4, 4); (9, 3); (12, 2); (12, 4)} from A to B is not a mapping from A to B.
Solution:
Given that A = {4, 9, 12} and B = {2, 3, 4}
(a) R = {(4, 2), (9, 3)} is not a mapping from A to B.
Every element of A must have an image in B. From the given information, set A element 12 is not associated with any element of set B.
Therefore, R = {(4, 2), (9, 3)} is not a mapping from A to B.
(b) R = {(4, 2); (4, 4); (9, 3); (12, 2); (12, 4)} from A to B
No element of A must have more than one image. From the given information, set A elements 4 and 12 are associated with two elements of set B. Element 4 of Set A associated with 2 and 4. Also, the 12 of Set A associated with 2 and 4.
Therefore, R = {(4, 2); (4, 4); (9, 3); (12, 2); (12, 4)} from A to B is not a mapping from A to B.
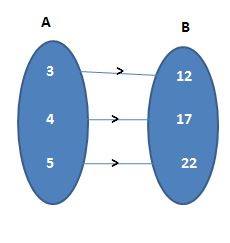
8. Let A = {3, 4, 5} and B = {12, 17, 22}
Consider the rule f(x) = 5x – 3, where x ∈ A
(a) Show that f is a mapping from A to B.
(b) Find the domain and range of the mapping.
(c) Represent the mapping in the roster form.
(d) Draw the arrow diagram to represent the mapping.
Solution:
Given that A = {3, 4, 5} and B = {12, 17, 22}
(a) If f(x) = 5x – 3, where x ∈ A
Substitute elements of A in f(x)
f(3) = 5 (3) – 3 = 12
f(4) = 5 (4) – 3 = 17
f(5) = 5 (5) – 3 = 22
Different elements of A can have the same image in B. Adjoining figure represents a mapping.
Therefore, f is a mapping from A to B.
(b) Domain = Set of all first elements in a relation = {3, 4, 5}
Range = Set of all second elements in a relation = {12, 17, 22}
(c) The mapping in the roster form r = {(3, 12); (4, 17); (5, 22)}
(d)