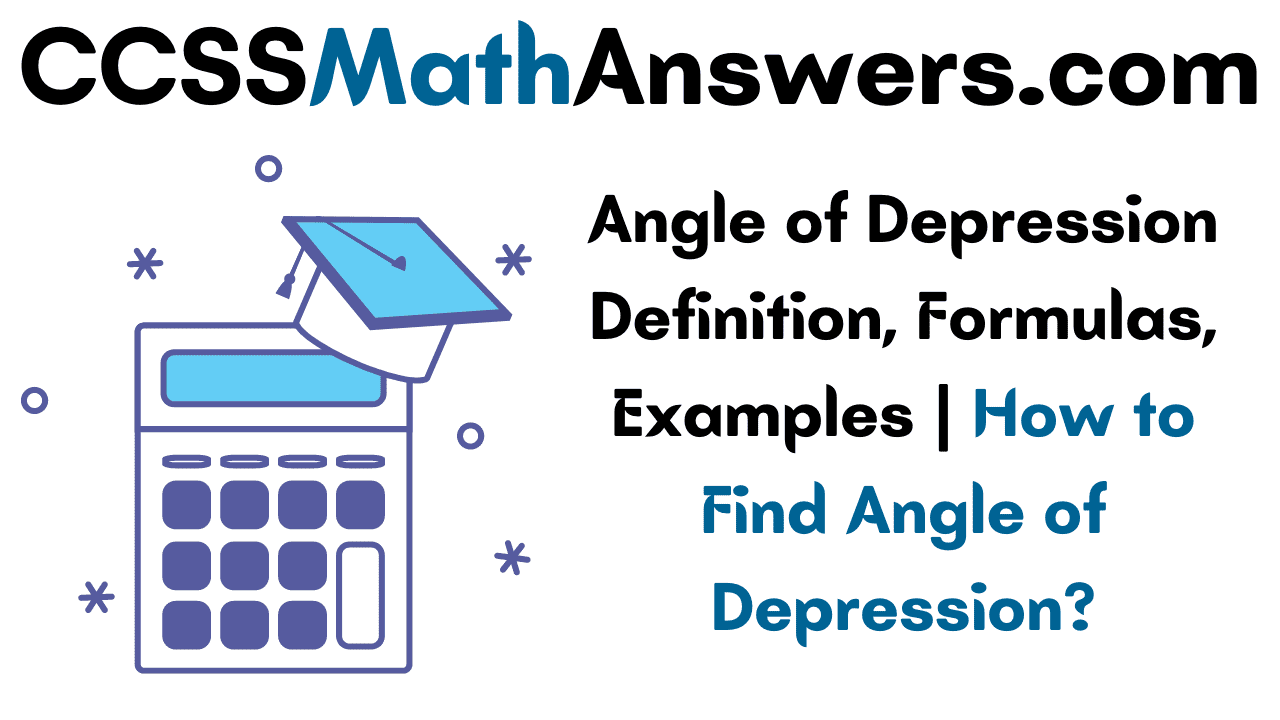The angle of depression is created when the observer is higher than the object he is looking at. If a person looks at an object that is located at a distance lower than the person, the angle is formed below the horizontal line drawn with the level of the eye of the person and line joining object with the person’s eye. This angle is calculated by using the concept of trigonometry. Get the definition, formulas, and example questions with answers in the below sections.
Angle of Depression – Definition
The angle of depression is the angle formed between the horizontal line and the observation of the object from the horizontal line. This angle of depression is used to find the distance between the two objects when the angles, object’s distance from the ground are known parameters. It is also defined as the angle that is constructed with the horizontal line if the line of sight is downward from the horizontal line.
If the object observed by the observer is below the level of the observer, then the angle created between the horizontal line and the observer’s line of sight is called the angle of depression. In the above figure, θ is the angle of depression.
Angle of Depression Formulas
With the angle of elevation, if you know two sides of the right triangle are known, then the formula of the angle of depression is
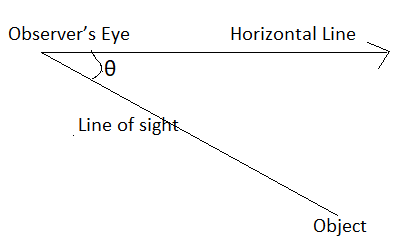
tan θ = \(\frac { Opposite Side }{ Adjacent Side } \)
θ = tan-1 (\(\frac { Opposite Side }{ Adjacent Side } \))
Also, check
Angle of Elevation and Angle of Depression
The angle of elevation and angle of depression are opposite to each other. The elevation angle is formed when it is between the line of sight and the horizontal line. And if the line of sight is above the horizontal line, then the angle is called the angle of elevation. In the angle of depression, the line of sight is downwards to the horizontal line.
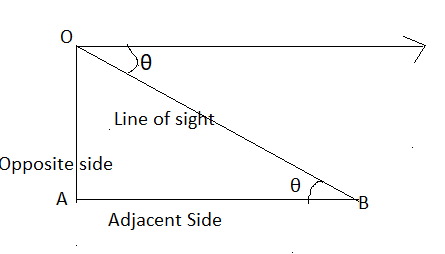
∠ABO = ∠O = θ
Angle of Depression Problems
Example 1:
The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 60° and 30° respectively. Find (i) The height of the lamp post. (ii) The difference between the height of the lamp post and the apartment. (iii) The distance between the lamp post and the apartment.
Solution:
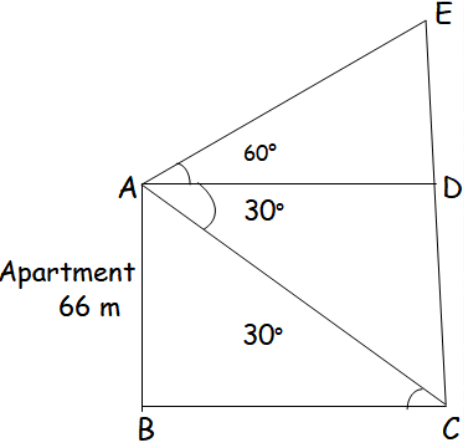
Triangle AED forms a right triangle
So, tan 60° = \(\frac { ED }{ AD } \)
√3 = \(\frac { ED }{ AD } \)
AD = \(\frac { ED }{ √3 } \) —- (i)
In trinagle ABC,
tan 30° = \(\frac { AB }{ BC } \)
\(\frac { 1 }{ √3 } \) = \(\frac { 66 }{ BC }\)
BC = 66√3 —- (ii)
Equating both equations
\(\frac { ED }{ √3 } \) = 66√3
ED = 66√3 (√3 )
ED = 66(3)
ED = 198
(i) Height of lamp post = ED + DC
= 198 + 66
= 264 m
(ii) The difference between height of the lamp post and the apartment
= 364 – 66
= 198 m
(iii) The distance between the lamp post and the apartment
BC = 66√3
= 66(1.732)
= 114.31 m
Example 2:
An airplane is flying at a height of 2 miles above level ground. The angle of depression from the plane to the foot of the tree is 15°. What is the distance the plane must fly to be directly above the tree?
Solution:
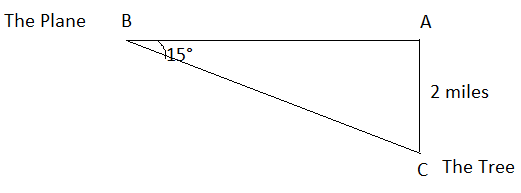
To find the distance BA use the tangent function
tan 15° = \(\frac { 2 }{ BA } \)
0.26794919243 = \(\frac { 2 }{ BA } \)
BA = \(\frac { 2 }{ 0.26794919243 } \)
BA = 7.464
So, the plane must fly 7.464 ft horizontally to be directly over the tree.
Example 3:
A buoy in the ocean is observed from the top of a 40-meter-high oil rig. The angle of depression from the top of the tower to the buoy is 6°. How far is the buoy from the base of the oil rig?
Solution:
Given that,
The angle of depression from the top of the tower to the buoy = 6°
A buoy in the ocean is observed from the top of a 40-meter-high oil rig.
Tan 6° = \(\frac { 40 }{ h } \)
h = \(\frac { 40 }{ tan 6° } \)
h = \(\frac { 40 }{ 0.105104 } \)
h = 380.6
It is approximately 380.6 m from the buoy to the base of the oil rig.
Example 4:
A lift in a building of height 90 feet with transparent glass walls is descending from the top of the building. At the top of the building, the angle of depression to a fountain in the garden is 60°. Two minutes later, the angle of depression reduces to 30°. If the fountain is 30√3 feet from the entrance of the lift, find the speed of the lift which is descending.
Solution:
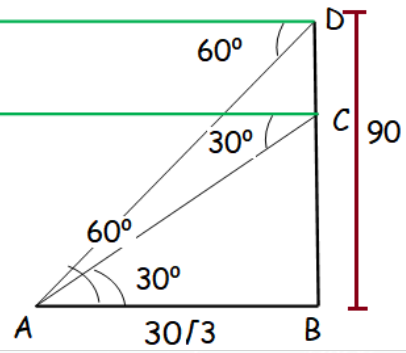
In the diagram above, in the right triangle ABC,
tan 30° = \(\frac { Opposite side }{ adjacent side } \)
\(\frac { 1 }{ √3 } \) = \(\frac { BC }{ 30√3 } \)
1 x 30√3 = √3 x BC
BC = 30
DC = DB – CB
DC = 90 – 30
DC = 60 feet
So, the left has descended 60 ft in 2 minutes.
Speed = \(\frac { Distance }{ Time } \)
Speed = \(\frac { 60 }{ 2 } \)
Speed = 30 ft/min
Speed = \(\frac { 30 ft }{ 60 sec } \)
Speed = 0.5 ft/sec
So, the speed of the lift which is descending is 0.5 ft/sec.