Prasanna

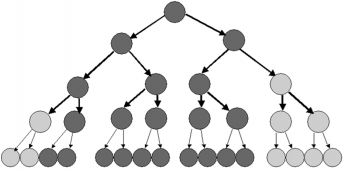
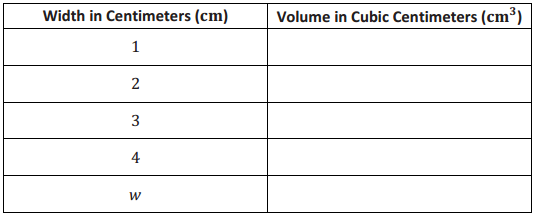
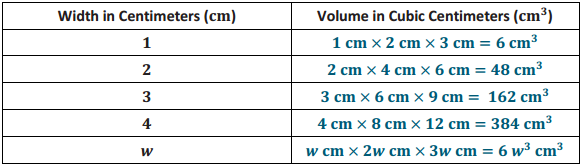
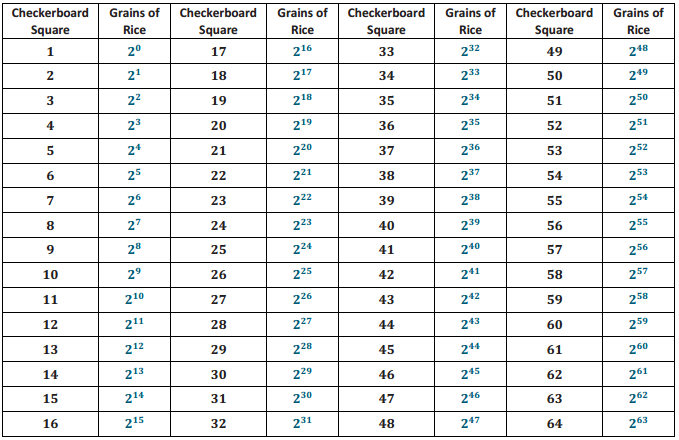
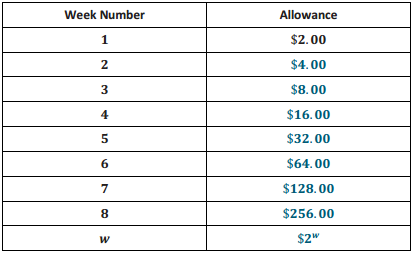
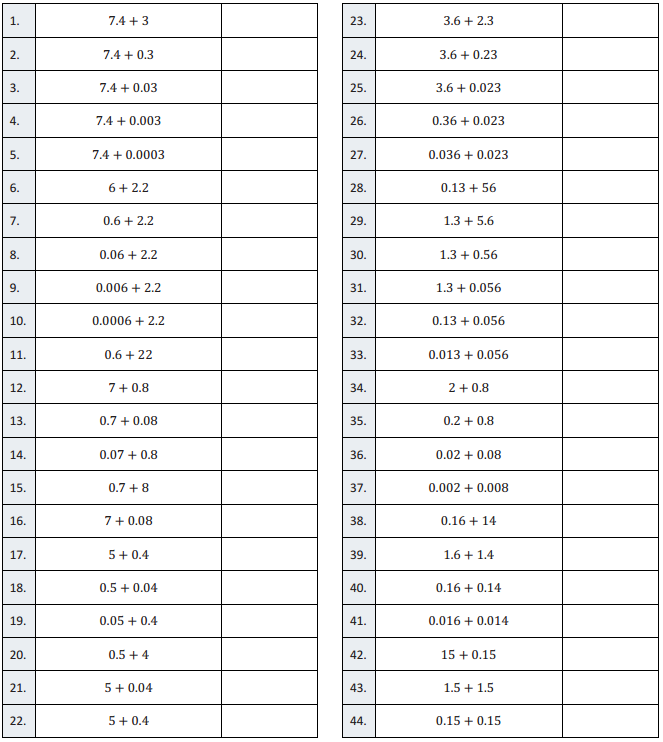
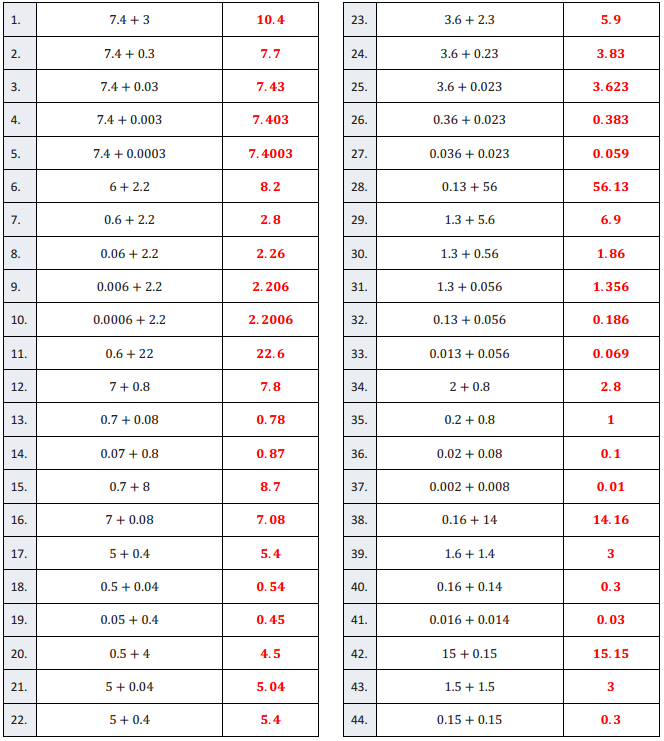
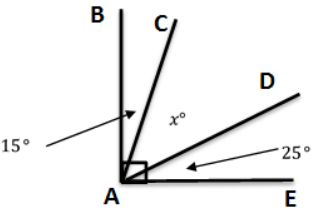
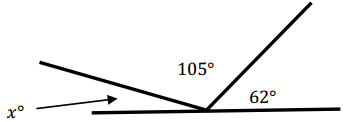
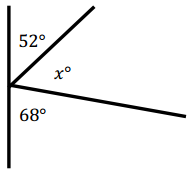
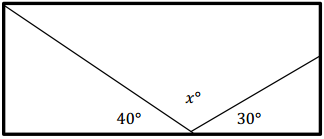
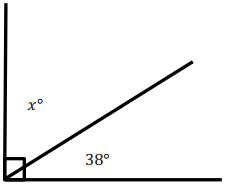
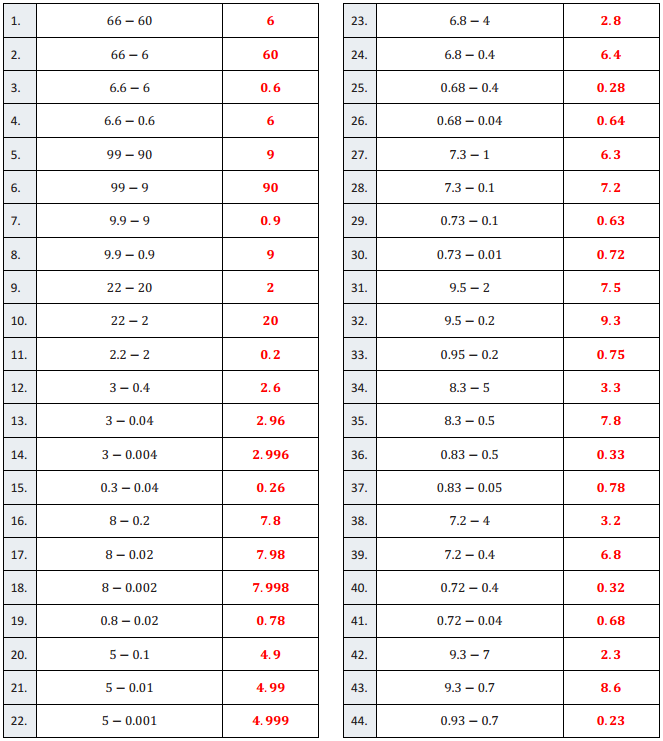
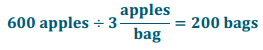Engage NY Eureka Math Grade 6 Module 4 Lesson 25 Answer Key

Eureka Math Grade 6 Module 4 Lesson 25 Opening Exercise Answer Key

Opening Exercise:

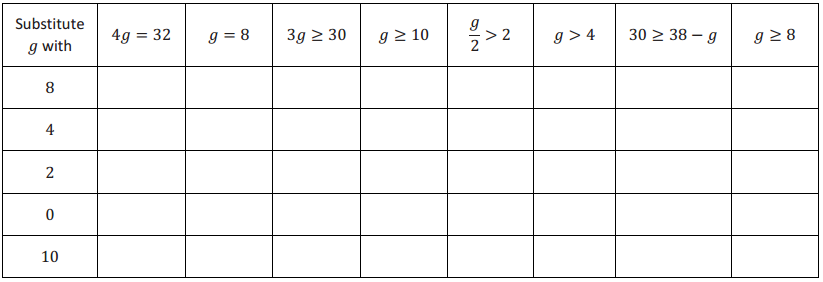
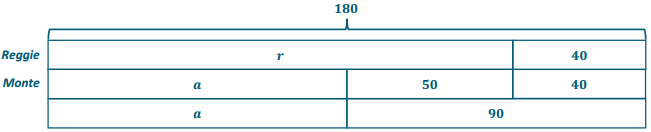
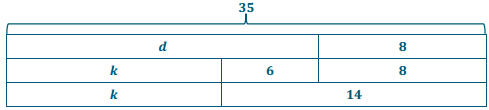
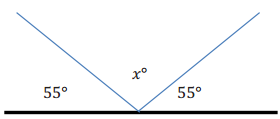
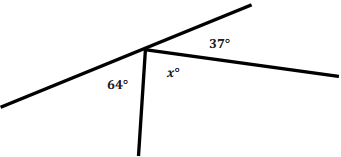
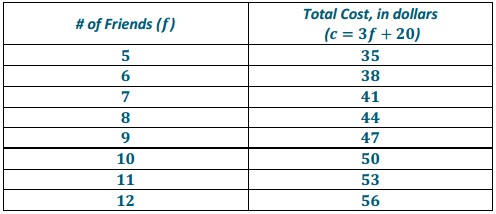
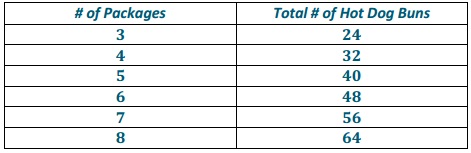
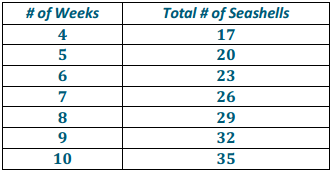
Identify a value for the variable that would make each equation or inequality into a true number sentence. Is this the only possible answer? State when the equation or inequality is true using equality and inequality symbols.

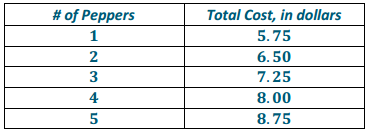
a. 3 + g = 15
Answer:
12 is the only value of g that will make the equation true. The equation is true when g = 12.

b. 30 > 2d
Answer:
Answers will vary. There is more than one value of d that will make the inequality true. The inequality is true when d < 15.

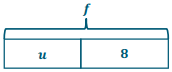
c. \(\frac{15}{f}\) < 5
Answer:
Answers will vary. There is more than one value off that will make the inequality true. The inequality is true when f > 3.

d. 42 ≤ 50 – m
Answer:
Answers will vary. There is more than one value of m that will make the inequality true. The inequality is true when m ≤ 8.

Eureka Math Grade 6 Module 4 Lesson 25 Example Answer Key

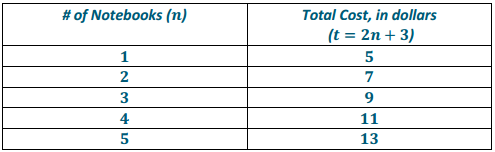
Example:

Each of the following numbers, if substituted for the variable, makes one of the equations below into a true number sentence. Match the number to that equation: 3, 6, 15, 16, 44.

a. n + 26 = 32
Answer:
6

b. n – 12 = 32
Answer:
44

c. 17n = 51
Answer:
3

d. 4² = n
Answer:
16

e. \(\frac{n}{3}\) = 5
Answer:
15

Eureka Math Grade 6 Module 4 Lesson 25 Problem Set Answer Key

Find the solution to each equation.

Question 1.
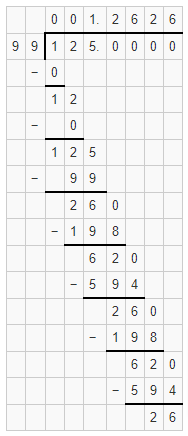
43 = y
Answer:
y = 64

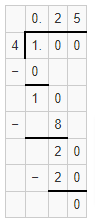
Question 2.
8a = 24
Answer:
a = 3

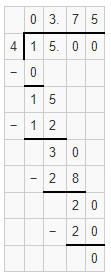
Question 3.
32 = g – 4
Answer:
g = 36

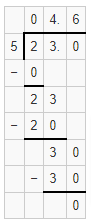
Question 4.
56 = j + 29
Answer:
j = 27

Question 5.
\(\frac{48}{r}\) = 12
Answer:
r = 4

Question 6.
k = 15 – 9
k = 6

Question 7.
x . \(\frac{1}{5}\) = 60
Answer:
x = 300

Question 8.
m + 3 . 45 = 12 . 8
Answer:
m = 9 . 35

Question 9.
a = 1⁵
Answer:
a = 1

Eureka Math Grade 6 Module 4 Lesson 25 Exit Ticket Answer Key

Find the solution to each equation.

Question 1.
7f = 49
Answer:
f = 7

Question 2.
1 = \(\frac{r}{12}\)
Answer:
r = 12

Question 3.
1.5 = d + 0.8
Answer:
d = 0.7

Question 4.
9² = h
Answer:
h = 81

Question 5.
q = 45 – 19
Answer:
q = 26

Question 6.
40 = \(\frac{1}{2}\)p
Answer:
p = 80

Eureka Math Grade 6 Module 4 Lesson 25 Division of Fractions Answer Key

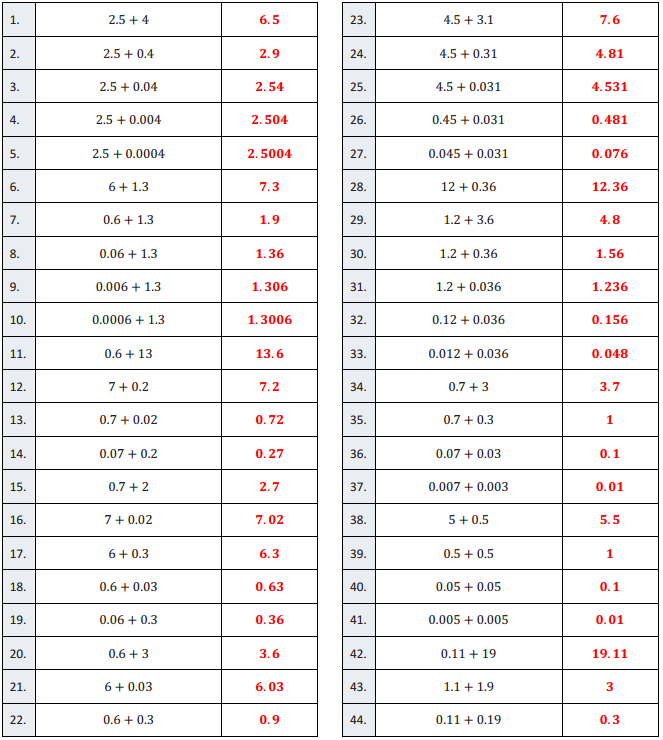
Division of Fractions – Round 1:

Directions: Evaluate each expression and simplify:

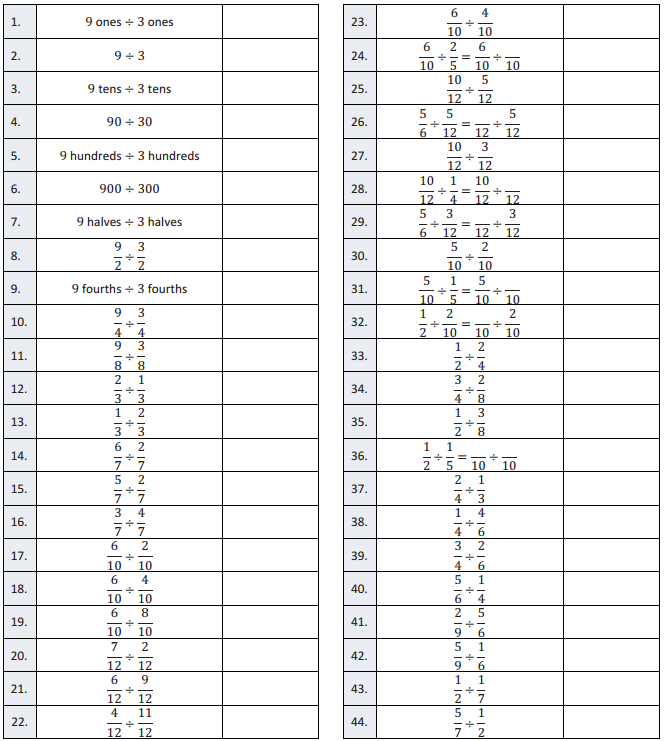
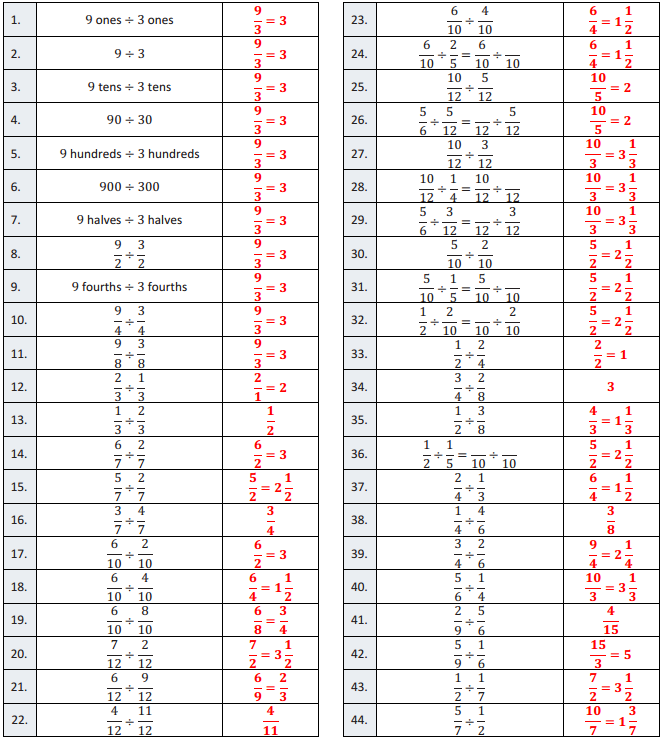
Question 1.
9 ones ÷ 3ones
Answer:
\(\frac{9}{3}\) = 3

Question 2.
9 ÷ 3
Answer:
\(\frac{9}{3}\) = 3

Question 3.
9tens ÷ 3tens
Answer:
\(\frac{9}{3}\) = 3

Question 4.
90 ÷ 30
Answer:
\(\frac{9}{3}\) = 3

Question 5.
9 hundreds ÷ 3 hundreds
Answer:
\(\frac{9}{3}\) = 3

Question 6.
900 ÷ 300
Answer:
\(\frac{9}{3}\) = 3

Question 7.
9 halves ÷ 3 halves
Answer:
\(\frac{9}{3}\) = 3

Question 8.
\(\frac{9}{2}\) ÷ \(\frac{9}{2}\)
Answer:
\(\frac{9}{3}\) = 3

Question 9.
9 fourths ÷ 9 fourths
Answer:
\(\frac{9}{3}\) = 3

Question 10.
\(\frac{9}{4}\) \(\frac{3}{4}\)
Answer:
\(\frac{9}{3}\) = 3

Question 11.
\(\frac{9}{8}\) ÷ \(\frac{3}{8}\)
Answer:
\(\frac{9}{3}\) =3

Question 12.
\(\frac{2}{3}\) ÷ \(\frac{1}{3}\)
Answer:
\(\frac{2}{1}\) = 2

Question 13.
\(\frac{1}{3}\) ÷ \(\frac{2}{3}\)
Answer:
\(\frac{1}{2}\)

Question 14.
\(\frac{6}{7}\) ÷ \(\frac{2}{7}\)
Answer:
\(\frac{6}{2}\) = 3

Question 15.
\(\frac{5}{7}\) ÷ \(\frac{2}{7}\)
Answer:
\(\frac{5}{2}\) = 2\(\frac{1}{2}\)

Question 16.
\(\frac{3}{7}\) ÷ \(\frac{4}{7}\)
Answer:
\(\frac{3}{4}\)

Question 17.
\(\frac{6}{10}\) ÷ \(\frac{2}{10}\)
Answer:
\(\frac{6}{2}\) = 3

Question 18.
\(\frac{6}{10}\) ÷ \(\frac{4}{10}\)
Answer:
\(\frac{6}{4}\) = 1\(\frac{1}{2}\)

Question 19.
\(\frac{6}{10}\) ÷ \(\frac{8}{10}\)
Answer:
\(\frac{6}{8}\) = \(\frac{3}{4}\)

Question 20.
\(\frac{7}{12}\) \(\frac{2}{12}\)
Answer:
\(\frac{7}{2}\) = 3\(\frac{1}{2}\)

Question 21.
\(\frac{6}{12}\) ÷ \(\frac{9}{12}\)
Answer:
\(\frac{6}{9}\) = \(\frac{2}{3}\)

Question 22.
\(\frac{4}{12}\) ÷ \(\frac{11}{12}\)
Answer:
\(\frac{4}{11}\)

Question 23.
\(\frac{6}{10}\) \(\frac{4}{10}\)
Answer:
\(\frac{6}{4}\) = 1\(\frac{1}{2}\)

Question 24.
\(\frac{9}{3}\) ÷ \(\frac{9}{3}\) = \(\frac{9}{3}\) ÷ \(\overline{10}\)
Answer:
\(\frac{6}{4}\) = 1\(\frac{1}{2}\)

Question 25.
\(\frac{10}{12}\) \(\frac{5}{12}\)
Answer:
\(\frac{10}{5}\) = 2

Question 26.
\(\frac{6}{4}\) ÷ \(\frac{6}{4}\) = \(\frac{6}{4}\) ÷ \(\overline{10}\)
Answer:
\(\frac{10}{5}\) = 2

Question 27.
\(\frac{10}{12}\) ÷ \(\frac{3}{12}\)
Answer:
\(\frac{10}{3}\) = 3\(\frac{1}{3}\)

Question 28.
\(\frac{10}{12}\) ÷ \(\frac{1}{4}\) = \(\frac{10}{12}\) ÷ \(\overline{10}\)
Answer:
\(\frac{10}{3}\) = 3\(\frac{1}{3}\)

Question 29.
\(\frac{5}{6}\) ÷ \(\frac{3}{12}\) = \(\overline{10}\) ÷ \(\frac{3}{12}\)
Answer:
\(\frac{10}{3}\) = 3\(\frac{1}{3}\)

Question 30.
\(\frac{5}{10}\) \(\frac{2}{10}\)
Answer:
\(\frac{5}{2}\) = 2\(\frac{1}{2}\)

Question 31.
\(\frac{5}{10}\) ÷ \(\frac{1}{5}\) = \(\frac{5}{10}\) ÷ \(\overline{10}\)
Answer:
\(\frac{5}{2}\) = 2\(\frac{1}{2}\)

Question 32.
\(\frac{1}{2}\) ÷ \(\frac{2}{10}\) = \(\overline{10}\) ÷ \(\frac{2}{10}\)
Answer:
\(\frac{5}{2}\) = 2\(\frac{1}{2}\)

Question 33.
\(\frac{1}{2}\) ÷ \(\frac{2}{4}\)
Answer:
\(\frac{1}{2}\) = 1

Question 34.
\(\frac{3}{4}\) ÷ \(\frac{2}{8}\)
Answer:
3

Question 35.
\(\frac{1}{2}\) ÷ \(\frac{3}{8}\)
Answer:
\(\frac{4}{3}\) = 1\(\frac{1}{3}\)

Question 36.
\(\frac{1}{2}\) ÷ \(\frac{1}{5}\) = \(\overline{10}\) ÷ \(\overline{10}\)
Answer:
\(\frac{5}{2}\) = 2\(\frac{1}{2}\)

Question 37.
\(\frac{2}{4}\) ÷ \(\frac{1}{3}\)
Answer:
\(\frac{6}{4}\) = 1\(\frac{1}{2}\)

Question 38.
\(\frac{1}{4}\) ÷ \(\frac{4}{6}\)
Answer:
\(\frac{3}{8}\)

Question 39.
\(\frac{3}{4}\) ÷ \(\frac{2}{6}\)
Answer:
\(\frac{9}{4}\) = 2\(\frac{1}{2}\)

Question 40.
\(\frac{5}{6}\) ÷ \(\frac{1}{4}\)
Answer:
\(\frac{10}{3}\) = 3\(\frac{1}{3}\)

Question 41.
\(\frac{2}{9}\) ÷ \(\frac{5}{6}\)
Answer:
\(\frac{4}{15}\)

Question 42.
\(\frac{5}{9}\) ÷ \(\frac{1}{6}\)
Answer:
\(\frac{15}{3}\) = 5

Question 43.
\(\frac{1}{2}\) ÷ \(\frac{1}{7}\)
Answer:
\(\frac{7}{2}\) = 3\(\frac{1}{2}\)

Question 44.
\(\frac{5}{7}\) ÷ \(\frac{1}{2}\)
Answer:
\(\frac{10}{7}\) = 1\(\frac{3}{7}\)

Division of Fractions – Round 2:

Directions: Evaluate each expression:

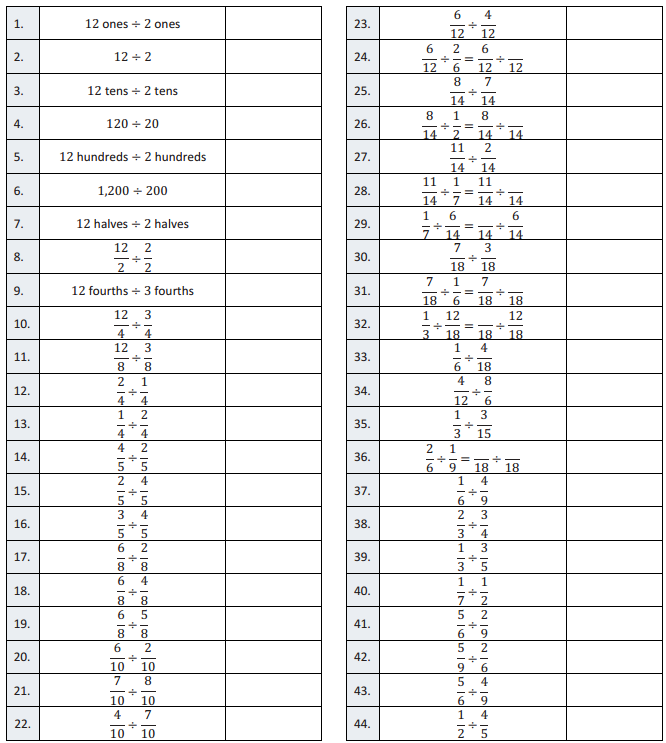
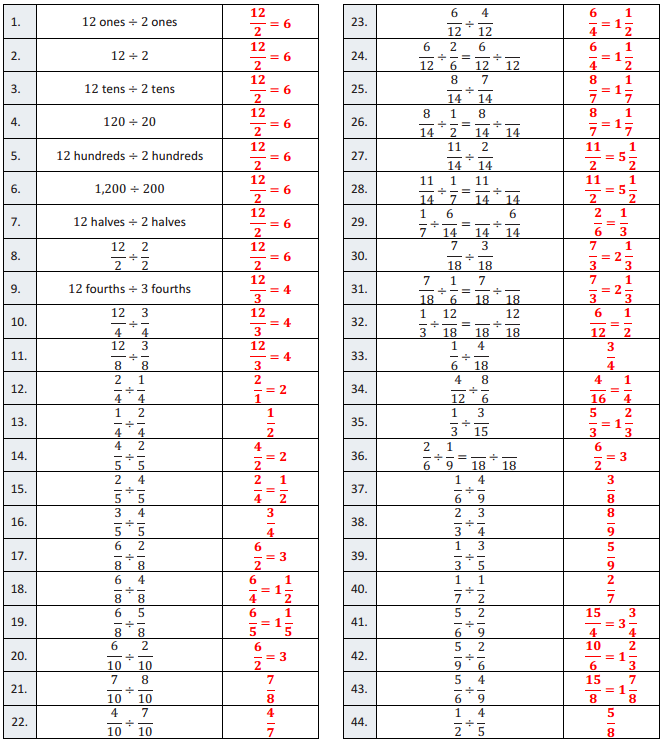
Question 1.
12ones ÷ 2ones
Answer:
\(\frac{12}{2}\) = 6

Question 2.
12 ÷ 2
Answer:
\(\frac{12}{2}\) = 6

Question 3.
12tens ÷ 2tens
Answer:
\(\frac{12}{2}\) = 6

Question 4.
120 ÷ 20
Answer:
\(\frac{12}{2}\) = 6

Question 5.
12 hundreds ÷ 2 hundreds
Answer:
\(\frac{12}{2}\) = 6

Question 6.
1,200 ÷ 200
Answer:
\(\frac{12}{2}\) = 6

Question 7.
12 halves ÷ 2 halves
Answer:
\(\frac{12}{2}\) = 6

Question 8.
\(\frac{12}{2}\) ÷ \(\frac{2}{2}\)
Answer:
\(\frac{12}{2}\) = 6

Question 9.
12 fourths ÷ 3 fourths
Answer:
\(\frac{12}{3}\) = 4

Question 10.
\(\frac{12}{4}\) ÷ \(\frac{12}{2}\)
Answer:
\(\frac{12}{3}\) = 4

Question 11.
\(\frac{12}{8}\) ÷ \(\frac{3}{8}\)
Answer:
\(\frac{12}{2}\) = 4

Question 12.
\(\frac{2}{4}\) ÷ \(\frac{1}{4}\)
Answer:
\(\frac{2}{1}\) = 2

Question 13.
\(\frac{1}{4}\) ÷ \(\frac{2}{4}\)
Answer:
\(\frac{1}{2}\)

Question 14.
\(\frac{4}{5}\) ÷ \(\frac{2}{5}\)
Answer:
\(\frac{4}{2}\) = 2

Question 15.
\(\frac{2}{5}\) ÷ \(\frac{4}{5}\)
Answer:
\(\frac{2}{4}\) = \(\frac{1}{2}\)

Question 16.
\(\frac{3}{5}\) ÷ \(\frac{4}{5}\)
Answer:
\(\frac{3}{4}\)

Question 17.
\(\frac{6}{8}\) ÷ \(\frac{2}{8}\)
Answer:
\(\frac{6}{2}\) = 3

Question 18.
\(\frac{6}{8}\) ÷ \(\frac{4}{8}\)
Answer:
\(\frac{6}{4}\) = 1\(\frac{1}{2}\)

Question 19.
\(\frac{6}{8}\) ÷ \(\frac{5}{8}\)
Answer:
\(\frac{6}{5}\) = 1\(\frac{1}{5}\)

Question 20.
\(\frac{6}{10}\) ÷ \(\frac{2}{10}\)
Answer:
\(\frac{6}{2}\) = 3

Question 21.
\(\frac{7}{10}\) ÷ \(\frac{8}{10}\)
Answer:
\(\frac{7}{8}\)

Question 22.
\(\frac{4}{10}\) ÷ \(\frac{7}{10}\)
Answer:
\(\frac{4}{7}\)

Question 23.
\(\frac{6}{12}\) ÷ \(\frac{4}{12}\)
Answer:
\(\frac{6}{4}\) = 1\(\frac{1}{2}\)

Question 24.
\(\frac{6}{12}\) ÷ \(\frac{2}{6}\) = \(\frac{6}{12}\) ÷ \(\overline{12}\)
Answer:
\(\frac{6}{4}\) = 1\(\frac{1}{2}\)

Question 25.
\(\frac{8}{14}\) ÷ \(\frac{7}{14}\)
Answer:
\(\frac{8}{7}\) = 1\(\frac{1}{7}\)

Question 26.
\(\frac{8}{14}\) ÷ \(\frac{1}{2}\) = \(\frac{8}{14}\) ÷ \(\overline{14}\)
Answer:
\(\frac{8}{7}\) = 1\(\frac{1}{7}\)

Question 27.
\(\frac{11}{14}\) = \(\frac{2}{14}\)
Answer:
\(\frac{11}{2}\) = 5\(\frac{1}{2}\)

Question 28.
\(\frac{11}{14}\) ÷ \(\frac{1}{7}\) = \(\frac{11}{14}\) ÷ \(\overline{14}\)
Answer:
\(\frac{11}{2}\) = 5\(\frac{1}{2}\)

Question 29.
\(\frac{1}{7}\) ÷ \(\frac{6}{14}\) = \(\overline{14}\) ÷ \(\frac{6}{14}\)
Answer:
\(\frac{2}{6}\) = \(\frac{1}{3}\)

Question 30.
\(\frac{7}{18}\) ÷ \(\frac{3}{18}\)
Answer:
\(\frac{7}{3}\) = 2\(\frac{1}{3}\)

Question 31.
\(\frac{7}{18}\) ÷ \(\frac{1}{6}\) = \(\frac{7}{18}\) ÷ \(\overline{18}\)
Answer:
\(\frac{7}{3}\) = 2\(\frac{1}{3}\)

Question 32.
\(\frac{1}{3}\) ÷ \(\frac{12}{18}\) = \(\overline{18}\) ÷ \(\frac{12}{18}\)
Answer:
\(\frac{6}{12}\) = \(\frac{1}{2}\)

Question 33.
\(\frac{1}{6}\) ÷ \(\frac{4}{18}\)
Answer:
\(\frac{3}{4}\)

Question 34.
\(\frac{4}{12}\) ÷ \(\frac{8}{6}\)
Answer:
\(\frac{4}{16}\) = \(\frac{1}{4}\)

Question 35.
\(\frac{1}{3}\) ÷ \(\frac{3}{15}\)
Answer:
\(\frac{5}{3}\) = 1\(\frac{2}{3}\)

Question 36.
\(\frac{2}{6}\) ÷ \(\frac{1}{9}\) = \(\overline{18}\) ÷ \(\overline{18}\)
Answer:
\(\frac{6}{2}\) = 3

Question 37.
\(\frac{1}{6}\) ÷ \(\frac{4}{9}\)
Answer:
\(\frac{3}{8}\)

Question 38.
\(\frac{2}{3}\) ÷ \(\frac{3}{4}\)
Answer:
\(\frac{8}{9}\)

Question 39.
\(\frac{1}{3}\) ÷ \(\frac{3}{5}\)
Answer:
\(\frac{5}{9}\)

Question 40.
\(\frac{1}{7}\) ÷ \(\frac{1}{2}\)
Answer:
\(\frac{2}{7}\)

Question 41.
\(\frac{5}{6}\) ÷ \(\frac{2}{9}\)
Answer:
\(\frac{15}{4}\) = 3\(\frac{3}{4}\)

Question 42.
\(\frac{5}{9}\) ÷ \(\frac{2}{6}\)
Answer:
\(\frac{10}{6}\) = 1\(\frac{2}{3}\)

Question 43.
\(\frac{5}{6}\) ÷ \(\frac{4}{9}\)
Answer:
\(\frac{15}{8}\) = 1\(\frac{7}{8}\)

Question 44.
\(\frac{1}{2}\) ÷ \(\frac{4}{5}\)
Answer:
\(\frac{5}{8}\)

Engage NY Eureka Math Grade 6 Module 4 Lesson 24 Answer Key

Eureka Math Grade 6 Module 4 Lesson 24 Opening Exercise Answer Key

Opening Exercise:

State whether each number sentence is true or false. If the number sentence is false, explain why.

a. 4 + 5 > 9
Answer:
False. 4 + 5 is not greater than 9.

b. 36 = 18
Answer:
True

c. 32 > \(\frac{64}{4}\)
Answer:
True

d. 78 – 15 < 68
Answer:
True

e. 22 ≥ 11 + 12
Answer:
False. 22 is not greater than or equal to 23.

Eureka Math Grade 6 Module 4 Lesson 24 Example Answer Key

Example 1:

Write true or false if the number substituted for g results in a true or false number sentence.

Answer:

Example 2:

State when the following equations/inequalities will be true and when they will be false.

a. r + 15 = 25
Answer:
→ Can you think of a number that will make this equation true?
Yes. Substituting 10 for r will make a true number sentence.

→ Is 10 the only number that results in a true number sentence? Why or why not?
Yes. There is only one value that, if substituted, will result in a true number sentence. There is only one number that can be added to 15 to get exactly 25.

→ What will make the number sentence false?
Any number that is not 10 will result in a false number sentence.

→ If we look back to the original questions, how can we state when the equation will be true? False?
The equation is true when the value substituted for r is 10 and false when the value of r is any other number.

b. 6 – d > 0
Answer:
→ If we wanted 6 – d to equal 0, what would the value of d have to be? Why?
The value of d would have to be 6 because 6 – 6 = 0.

→ Will substituting 6 for d result in a true number sentence? Why or why not?
If d has a value of 6, then the resulting number sentence would not be true because the left side has to be greater than 0, not equal to 0.

→ How about substituting 5 for d? 4? 3? 2?
Yes. Substituting any of these numbers for d into the inequality results in true number sentences.

→ What values can we substitute for d in order for the resulting number sentence to be true?
The inequality is true for any value of d that is less than 6.

→ What values for d would make the resulting number sentence false?
The inequality is false for any value of d that is greater than or equal to 6.

→ Let’s take a look at a number line and see why these statements make sense.

Display a number line on the board. Label the number line as shown below.

→ Let’s begin at 6. If I were to subtract 1 from 6, where would that place be on the number line?
5

→ So, if we substitute 1 for d, then 6 – 1 = 5, and the resulting number sentence is true. How about if I subtracted 2 from 6? Would our number sentence be true for the value 2?
Yes

→ What if I subtracted 6 from the 6 on the number line? Where would that be on the number line?
0

→ So, if we substitute 6 for d, will the resulting number sentence be true or false?
False

→ Let’s try one more. We have already determined that any number greater than or equal to 6 will result in a false number sentence. Let’s try a number greater than 6. Let’s try the number 7.

→ Start with the 6 on the number line. If we were to subtract 7, in which direction on the number line would we
move?
To the left

→ And how many times will we move to the left?
7

→ Model beginning at 6 on the number line, and move a finger, or draw the unit skips, while continually moving to the left on the number line 7 times.

→ So, it seems we have ended up at a place to the left of O. What number is represented by this position?
-1

c. \(\frac{1}{2}\)f = 15
Answer:
The equation is true when the value substituted for fis 30 (f = 30) and false when the value off is any other number (f ≠ 30).

d. \(\frac{y}{3}\) < 10
Answer:
The inequality is true for any value of y that is less than 30 (y < 30) and false when the value of y is greater than or equal to 30 (y ≥ 30).

e. 7g ≥ 42
Answer:
The inequality is true for any value of g that is greater than or equal to 6 (g ≥ 6) and false when the value of g is less than (g < 6).

f. a – 8 ≤ 15
Answer:
The inequality is true for any value of a that is less than or equal to 23 (a ≤ 23) and false when the value of a is greater than 23 (a > 23).

Eureka Math Grade 6 Module 4 Lesson 24 Exercise Answer Key

Exercises:

Complete the following problems in pairs. State when the following equations and inequalities will be true and when they will be fake.

Exercise 1.
15c > 45
Answer:
The inequality is true for any value of c that is greater than 3 (c > 3) and false when the value of c is less than or equal to (c ≤ 3).

Exercise 2.
25 = d – 10
Answer:
The equation is true when the value of d is 35 (d = 35) and false when the value of d is any other number (d ≠ 35).

Exercise 3.
56 ≥ 2e
Answer:
The inequality is true for any value of e that is less than or equal to 28 (e ≤ 28) and false when the value of e is greater than 8 (e > 28).

Exercise 4.
\(\frac{h}{5}\) ≥ 12
Answer:
The inequality is true for any value of h that is greater than or equal to 60 (h ≥ 60) and false when the value of h is less than (h < 60).

Exercise 5.
45 > h + 29
Answer:
The inequality is true for any value of h that is less than 16 (h < 16) and false when the value of h is greater than or
equal to 16 (h ≥ 16).

Exercise 6.
4a ≤ 16
Answer:
The inequality is true for any value of a that is less than or equal to 4 (a ≤ 4) and false when the value of a is greater than (a > 4).

Exercise 7.
3x = 24
Answer:
The equation is true when the value of x is 8 (x = 8) and false when the value of x is any other number (x ≠ 8).

Identify all equality and inequality signs that can be placed into the blank to make a true number sentence.

Exercise 8.
15 + 9 ___ 24
Answer:
= or ≥ or ≤

Exercise 9.
8.7 ___ 50
Answer:
> or ≥

Exercise 10.
\(\frac{15}{2}\) ___ 10
Answer:
< or ≤

Exercise 11.
34 ___ 17 . 2
Answer:
= or ≥ or ≤

Exercise 12.
18 ___ 24.5 – 6
Answer:
< or ≤

Eureka Math Grade 6 Module 4 Lesson 24 Problem Set Answer Key

State when the following equations and inequalities will be true and when they will be false.

Question 1.
36 = 9k
Answer:
The equation is true when the value of k is 4 and false when the value of k is any number other than 4.
OR
The equation is true when k = 4 and false when k ≠ 4.

Question 2.
67 > f – 15
Answer:
The inequality is true for any value off that is less than 82 and false when the value of f is greater than or equal to 82.
OR
The inequality is true when f < 82 and false when f ≥ 82.

Question 3.
\(\frac{v}{9}\) = 3
Answer:
The equation is true when the value of v is 27 and false when the value of v is any number other than 27.
OR
The equation is true when v = 27 and false when v ≠ 27.

Question 4.
10 + b > 42
Answer:
The inequality is true for any value of b that is greater than 32 and false when the value of b is less than or equal to 32.
OR
The inequality is true when b > 32 and false when b ≤ 32.

Question 5.
d – 8 ≥ 35
Answer:
The inequality is true for any value of d that is greater than or equal to 43 and false when the value of d is less than 43
OR
The inequality is true when d ≥ 43 and false when d <43.

Question 6.
32f < 64
Answer:
The inequality is true for any value of f that is less than 2 and false when the value off is greater than or equal to 2.
OR
The inequality is true when f < 2 and false when f ≥ 2.

Question 7.
10 – h ≤ 7
Answer:
The inequality is true for any value of h that is greater than or equal to 3 and false when the value of h is less than 3.
OR
The inequality is true when h ≥ 3 and false when h < 3.

Question 8.
42 + 8 ≥ g
Answer:
The inequality is true for any value of g that is less than or equal to 50 and false when the value of g is greater than 50.
OR
The inequality is true when g < 50 and false when g > 50.

Question 9.
\(\frac{m}{3}\) = 14
Answer:
The equation is true when the value of m is 42 and false when the value of m is any number other than 42.
OR
The equation is true when m = 42 and false when m ≠ 42.

Eureka Math Grade 6 Module 4 Lesson 24 Exit Ticket Answer Key

State when the following equations and inequalities will be true and when they will be false.

Question 1.
5g > 45
Answer:
The inequality is true for any value of g that is greater than 9 and false when the value of g is less than or equal to 9.
OR
The inequality is true when g > 9 and false when g ≤ 9.

Question 2.
14 = 5 + k
Answer:
The equation is true when the value of k is 9 and false when the value of k is any other number.
OR
The equation is true when k = 9 and false when k ≠ 9.

Question 3.
26 – w < 12
Answer:
The inequality is true for any value of w that is greater than 14 and false when the value of w is less than or equal to 14.
OR
The inequality is true when w > 14 and false when w < 14.

Question 4.
32 ≤ a + 8
Answer:
The inequality is true for any value of a that is greater than or equal to 24 and false when the value of a is less than 24.
OR
The inequality is true when a ≥ 24 and false when a < 24.

Question 5.
2 . h ≤ 16
Answer:
The inequality is true for any value of h that is less than or equal to 8 and false when the value of h is greater than 8.
OR
The inequality is true when h < 8 and false when h > 8.

Engage NY Eureka Math Grade 6 Module 4 Lesson 23 Answer Key

Eureka Math Grade 6 Module 4 Lesson 23 Opening Exercise Answer Key

Opening Exercise:

Determine what each symbol stands for, and provide an example.

Answer:

→ What is another example of a number sentence that includes an equal symbol?
Answers will vary. Ask more than one student.

The student’s height is the height marked by the tape on the wall. Have students stand next to the marked height. Discuss how their heights compare to the height of the tape. Are there other students in the room who have the same height?

Use the student’s height measurement in the example (the example uses a student 4\(\frac{7}{8}\) ft. in height).

→ What is another example of a number sentence that includes a greater than symbol?
Answers will vary. Ask more than one student.

Have students taller than the tape on the wall stand near the tape. Discuss how more than one student has a height that is greater than the tape, so there could be more than one number inserted into the inequality: > 4\(\frac{7}{8}\).

→ What is another example of a number sentence that includes a less than symbol?
Answers will vary. Ask more than one student.

Have students shorter than the tape on the wall stand near the tape. Discuss how more than one student has a height that is less than the tape, so there could be more than one number inserted into the inequality: < 4\(\frac{7}{8}\).

→ What is another example of a number sentence that includes a less than or equal to symbol?
Answers will vary. Ask more than one student.

Ask students who are the exact height as the tape and students who are shorter than the tape to stand near the tape. Discuss how this symbol is different from the previous symbol.

→ What is another example of a number sentence that includes a greater than or equal to symbol?
Answers will vary. Ask more than one student.

→ Which students would stand near the tape to demonstrate this symbol?
Students who are the same height as or taller than the tape

Eureka Math Grade 6 Module 4 Lesson 23 Example Answer Key

For each equation or inequality your teacher displays, write the equation or inequality and then substitute 3 for every x. Determine if the equation or inequality results in a true number sentence or a false number sentence.
Answer:
Display 5 + x = 8.
→ Substitute 3 for x and evaluate. Does this result in a true number sentence or a false number sentence?
True

→ Why is the number sentence a true number sentence?
Each expression on either side of the equal sign evaluates to 8. 8 = 8

Display 5x = 8.
→ Substitute 3 for x and evaluate. Does this result in a true number sentence or a false number sentence?
False

→ Why is the number sentence a false number sentence?
Five times three equals fifteen. Fifteen does not equal eight, so the number sentence 5(3) = 8 is false.

Display 5 + x > 8.
→ Substitute 3 for x and evaluate. Does this result in a true number sentence or a false number sentence?
False

→ Why is the number sentence a false number sentence?
Each expression on either side of the in equality sign evaluates to 8. However, the inequality sign states that eight is greater than eight, which is not true. We have already shown that 8 = 8.

Display 5x > 8.
→ Substitute 3 for x and evaluate. Does this result in a true number sentence or a false number sentence?
True

→ Why is the number sentence a true number sentence?
When three is substituted, the left side of the inequality evaluates to fifteen. Fifteen is greater than eight, so the number sentence is true.

Display 5 + x ≥ 8.
→ Substitute 3 for x and evaluate. Does this result in a true number sentence or a false number sentence?
True

→ Why is the number sentence a true number sentence?
Each expression on either side of the inequality sign evaluates to 8. Because the inequality sign states that the expression on the left side can be greater than or equal to the expression on the right side, the number sentence is true because we have already shown that 8 = 8.

→ Can you find a number other than three that we can substitute for x that will result in a false number sentence?
Answers will vary, but any number less than three will result in a false number sentence.

Eureka Math Grade 6 Module 4 Lesson 23 Exercise Answer Key

Exercises:

Substitute the indicated value into the variable, and state (in a complete sentence) whether the resulting number sentence is true or false. If true, find a value that would result in a false number sentence. If false, find a value that would result in a true number sentence.

Exercise 1.
4 + x = 12. Substitute 8 for x.
Answer:
When 8 is substituted for x, the number sentence is true.
Answers will vary on values to make the sentence false; any number other than 8 will make the sentence false.

Exercise 2.
3g > 15. Substitute 4\(\frac{1}{2}\) for g.
Answer:
When 4\(\frac{1}{2}\) is substituted for g, the number sentence is false.
Answers will vary on values that make the sentence true; any number greater than 5 will make the sentence true.

Exercise 3.
\(\frac{f}{4}\) < 2. Substitute 8 for f.
Answer:
When 8 is substituted for f, the number sentence is false.
Answers will vary on values to make the sentence true; any number less than 8 will make the sentence true.

Exercise 4.
14.2 ≤ h – 10.3. Substitute 25.8 for h.
Answer:
When 25.8 is substituted for h, the number sentence is true.
Answers will vary on values to make the sentence false; any number less than 24.5 will make the sentence false.

Exercise 5.
4 = \(\frac{8}{h}\). Substitute 6 for h.
Answer:
When 6 is substituted for h, the number sentence is false.
2 is the only value that will make the sentence true.

Exercise 6.
3 > k + \(\frac{1}{4}\). Substitute 1\(\frac{1}{2}\) for k.
Answer:
When 1\(\frac{1}{2}\) is substituted for k, the number sentence is true.
Answers will vary on values to make the sentence false; the number 2\(\frac{3}{4}\) or any number greater than 2\(\frac{3}{4}\) will make the sentence false.

Exercise 7.
4.5 – d > 2.5. Substitute 2.5 for d.
Answer:
When 2.5 is substituted for d, the number sentence is false.
Answers will vary on values to make the sentence true; any number less than 2 will make the number sentence true.

Exercise 8.
8 ≥ 32p. Substitute for \(\frac{1}{2}\)p.
Answer:
When \(\frac{1}{2}\) is substituted for p, the number sentence is false.
Answers will vary on values to make the sentence true; the number \(\frac{1}{4}\) or any number less than \(\frac{1}{4}\) will make the sentence true.

Exercise 9.
\(\frac{w}{2}\) < 32. Substitute 16 for w.
Answer:
When 16 is substituted for p, the number sentence is true.
Answers will vary on values to make the sentence false; the number 64 or any other number greater than 64 will make the sentence false.

Exercise 10.
18 ≤ 32 – b. Substitute 14 for b.
Answer:
When 14 is substituted for b, the number sentence is true.
Answers will vary on values to make the sentence false; any number greater than 14 will make the sentence false.

Eureka Math Grade 6 Module 4 Lesson 23 Problem Set Answer Key

Substitute the value for the variable, and state (in a complete sentence) whether the resulting number sentence is true or false. If true, find a value that would result in a false number sentence. If false, find a value that would result in a true number sentence.

Question 1.
3\(\frac{5}{6}\) = 1-+h. Substitute 2\(\frac{1}{6}\) for h.
Answer:
When 2\(\frac{1}{6}\) is substituted in for h, the number sentence is true. Answers will vary, but any value for h other than 2\(\frac{1}{6}\) will result in a false number sentence.

Question 2.
39 > 156g. Substitute \(\frac{1}{4}\) for g.
Answer:
When \(\frac{1}{4}\) is substituted in for g, the number sentence is false. Answers will vary, but any value for g less than \(\frac{1}{4}\) will result in a true number sentence.

Question 3.
\(\frac{f}{4}\) ≤ 3. Substitute 12 for f.
Answer:
When 12 is substituted in for f, the number sentence is true. Answers will vary, but any value for f greater than 12 will result in a false number sentence.

Question 4.
121 – 98 ≥ r. Substitute 23 for r.
Answer:
When 23 is substituted in for r, the number sentence is true. Answers will vary, but any value for r greater than 23 will result in a false number sentence.

Question 5.
\(\frac{54}{q}\) = 6. Substitute 10 for q.
Answer:
When 10 is substituted in for q, the number sentence is false. The number 9 is the only value for q that will result in a true number sentence.

Create a number sentence using the given variable and symbol. The number sentence you write must be true for the given value of the variable

Question 6.
Variable: d Symbol: ≥ The sentence is true when 5 is substituted for d.
Answer:

Question 7.
Variable: y Symbol: ≠ The sentence is true when 10 is substituted for y.
Answer:

Question 8.
Variable: k Symbol: < The sentence Is true when 8 is substituted for k.
Answer:

Question 9.
Variable: a Symbol: < The sentence is true when 9 is substituted for a.
Answer:

Answers will vary for Problems 6 – 9.

Eureka Math Grade 6 Module 4 Lesson 23 Exit Ticket Answer Key

Substitute the value for the variable, and state in a complete sentence whether the resulting number sentence is true or false. If true, find a value that would result in a false number sentence. If false, find a value that would result in a true number sentence.

Question 1.
15a ≥ 75. Substitute 5 for a.
Answer:
When 5 is substituted in for a, the number sentence is true. Answers will vary, but any value for a less than 5 will result in a false number sentence.

Question 2.
23 + b = 30. Substitute 10 for b.
Answer:
When 10 is substituted in for b, the number sentence is false. The only value for b that will result in a true number sentence is 7.

Question 3.
20 > 86 – h. Substitute 46 for h.
Answer:
When 46 is substituted in for h, the number sentence will be false. Answers will vary, but any value for h greater than 66 will result in a true number sentence.

Question 4.
32 > 8m. Substitute 5 for m.
Answer:
When 5 is substituted in for m, the number sentence is false. Answers will vary, but the value of 4 and any value less than 4 for m will result in a true number sentence.

Engage NY Eureka Math Grade 6 Module 4 Lesson 22 Answer Key

Eureka Math Grade 6 Module 4 Lesson 22 Example Answer Key

Example 1: Folding Paper

Exercises:

Exercise 1.
Predict how many times you can fold a piece of paper in half.
My prediction: _____
Answer:

Exercise 2.
Before any folding (zero folds), there is only one layer of paper. This is recorded in the first row of the table. Fold your paper in half. Record the number of layers of paper that result. Continue as long as possible.

Answer:

a. Are you able to continue folding the paper indefinitely? Why or why not?
Answer:
No. The stack got too thick on one corner because it kept doubling each time.

b. How could you use a calculator to find the next number in the series?
Answer:
I could multiply the number by 2 to find the number of layers after another fold.

c. What is the relationship between the number of folds and the number of layers?
Answer:
As the number of folds increases by one, the number of layers doubles.

d. How is this relationship represented in the exponential form of the numerical expression?
Answer:
I could use 2 as a base and the number of folds as the exponent.

e. If you fold paper f times, write an expression to show the number of paper layers.
Answer:
There would be 2^f layers of paper.

Exercise 3.
If the paper were to be cut instead of folded, the height of the stack would double at each successive stage, and it would be possible to continue.

a. Write an expression that describes how many layers of paper result from 16 cuts.
Answer:
2¹⁶

b. Evaluate this expression by writing it in standard form.
Answer:
2¹⁶ = 65,536

Example 2: Bacterial Infection

Bacteria are microscopic single-celled organisms that reproduce in a couple of different ways, one of which is called binary fission. In binary fission, a bacterium increases its size until it is large enough to split into two parts that are identical. These two grow until they are both large enough to split into two individual bacteria. This continues as long as growing conditions are favorable.

a. Record the number of bacteria that result from each generation.

Answer:

b. How many generations would it take until there were over one million bacteria present?
Answer:
20 generations will produce more than one million bacteria. 2²⁰ = 1,048,576

c. Under the right growing conditions, many bacteria can reproduce every 15 minutes. Under these conditions, how long would It take for one bacterium to reproduce itself into more than one million bacteria?
Answer:
It would take 20 fifteen-minute periods, or 5 hours.

d. Write an expression for how many bacteria would be present after g generations.
Answer:
There will be 2^g bacteria present after g generations.

Example 3: Volume of a Rectangular Solid

This box has a width, w. The height of the box, h, is twice the width. The length of the box, l, is three times the width. That is, the width, height, and length of a rectangular prism are in the ratio of 1: 2: 3.

For rectangular solids like this, the volume is calculated by multiplying length times width times height.
V = l . w . h
V = 3w . w . 2w
V = 3 .2 . w . w . w
V = 6w³

Follow the above example to calculate the volume of these rectangular solids, given the width, w.

Answer:

Eureka Math Grade 6 Module 4 Lesson 22 Problem Set Answer Key

Question 1.
A checkerboard has 64 squares on it.

a. If one grain of rice is put on the first square, 2 grains of rice on the second square, 4 grains of rice on the third square, 8 grains of rice on the fourth square, and so on (doubling each time), complete the table to show how many grains of rice are on each square. Write your answers in exponential form on the table below.

Answer:

b. How many grains of rice would be on the last square? Represent your answer in exponential form and standard form. Use the table above to help solve the problem.
Answer:
There would be 2⁶³ 0r 9,223, 372, 036, 854, 775, 808 grains of rice.

c. Would It have been easier to write your answer to part (b) in exponential form or a standard form?
Answer:
Answers will vary. Exponential form is more concise: 2⁶³. Standard form is longer and more complicated to calculate: 9,223, 372, 036, 854, 775, 808. (In word form: nine quintillions, two hundred twenty-three quadrillion, three hundred seventy-two trillion, thirty-six billion, eight hundred fifty-four million, seven hundred seventy-five thousand, eight hundred eight.)

Question 2.
If an amount of money is invested at an annual interest rate of 6%, it doubles every 12 years. If Alejandra invests $500, how long will it take for her investment to reach $2, 000 (assuming she does not contribute any additional funds)?
Answer:
It will take for 24 years. After 12 years, Alejandra will have doubled her money and will have $1,000. If she waits an additional 12 years, she will have $2,000.

Question 3.
The athletics director at Peter’s school has created a phone tree that is used to notify team players in the event a game has to be canceled or rescheduled. The phone tree is initiated when the director calls two captains. During the second stage of the phone tree, the captains each call two players. During the third stage of the phone tree, these players each call two other players. The phone tree continues until all players have been notified. If there are 50 players on the teams, how many stages will it take to notify all of the players?
Answer:
It will take five stages. After the first stage, two players have been called, and 48 will not have been called. After the second stage, four more players will have been called, for a total of six; 44 players will remain uncalled. After the third stage, players (eight) more will have been called, totaling 14; 36 remain uncalled. After the fourth stage, 2 more players (16) will have gotten a call, for a total of 30 players notified. Twenty remain uncalled at this stage. The fifth round of calls will cover all of them because 2⁵ includes 32 more players.

Eureka Math Grade 6 Module 4 Lesson 22 Exit Ticket Answer Key

Question 1.
Naomi’s allowance is $2.00 per week. If she convinces her parents to double her allowance each week for two months, what will her weekly allowance be at the end of the second month (week 8)?

Answer:

Question 2.
Write the expression that describes Naomi’s allowance during week w in dollars.
Answer:
$2^w

Eureka Math Grade 6 Module 4 Lesson 22 Multiplication of Decimals Answer Key

Question 1.
0.5 × 0.5 =
Answer:
0.25

Question 2.
0.6 × 0.6=
Answer:
0.36

Question 3.
0.7 × 0.7=
Answer:
0.49

Question 4.
0.5 × 0.6=
Answer:
0.3

Question 5.
1.5 × 1.5=
Answer:
2.25

Question 6.
2.5 × 2.5=
Answer:
6.25

Question 7.
0.25 × 0.25 =
Answer:
0. 0625

Question 8.
0.1 × 0.1=
Answer:
0.01

Question 9.
0.1 × 123.4 =
Answer:
12.34

Question 10.
0.01 × 123.4 =
Answer:
1.234

Engage NY Eureka Math 6th Grade Module 4 Lesson 20 Answer Key

Eureka Math Grade 6 Module 4 Lesson 20 Example Answer Key

Example 1.
The farmers’ market is selling bags of apples. In every bag, there are 3 apples.
a. Complete the table

Answer:

b. What if the market had 25 bags of apples to sell? How many apples is that in all?
Answer:
If B = 25, then 3B = 3 25 = 75. The market had 75 apples to sell.

c. If a truck arrived that had some number, a, more apples on it, then how many bags would the clerks use to bag up the apples?
Answer:
a ÷ 3 bags are needed. If there are 1 or 2 apples left over, an extra bag will be needed (although not full).

d. If a truck arrived that had 600 apples on It, how many bags would the clerks use to bag up the apples?
apples
Answer:

e. How is part (d) different from part (b)?
Answer:
Part (d) gives the number of apples and asks for the number of bags. Therefore, we needed to divide the number of apples by 3. Part (b) gives the number of bags and asks for the number of apples. Therefore, we needed to multiply the number of bags by 3.

Eureka Math Grade 6 Module 4 Lesson 20 Exercise Answer Key

Exercise 1.
In New York State, there is a five-cent deposit on all carbonated beverage cans and bottles. When you return the empty can or bottle, you get the five cents back.
a. Complete the table.

Answer:

b. If we let C represent the number of cans, what is the expression that shows how much money is returned?
Answer:
0.05c

c. Use the expression to find out how much money Brett would receive if he returned 222 cans.
Answer:
if c = 222, then 0. 05C = 0.05 ? 222 = 11.10. Brett would receive $11. 10 if he returned 222 cans.

d. If Gavin needs to earn $4. 50 for returning cans, how many cans does he need to collect and return?
Answer:
4.50 ÷ 0.05 = 90. Gavin needs to collect and return 90 cans.

e. How is part (d) different from part (c)?
Answer:
Part (d) gives the amount of money and asks for the number of cans. Therefore, we needed to divide the amount of money by 0.05. Part (c) gives the number of cans and asks for the amount of money. Therefore, we needed to multiply the number of cans by 0.05.

Exercise 2.
The fare for a subway or a local bus ride is $2. 50.
a. Complete the table.

Answer:

b. If we let R represent the number of rides, what is the expression that shows the cost of the rides?
Answer:
2.50R or 2. 5R

c. Use the expression to find out how much money 60 rides would cost.
Answer:
If R = 60, then 2.50R = 2.50 ∙ 60 = 150.00. Sixty rides would cost $150.00.

d. If a commuter spends $175.00 on subway or bus rides, how many trips did the commuter take?
Answer:
175.00 ÷ 2.50 = 70. The commuter took 70 trips.

e. How is part (d) different from part (c)?
Answer:
Part (d) gives the amount of money and asks for the number of rides. Therefore, we needed to divide the
amount of money by the cost of each ride ($2. 50). Part (c) gives the number of rides and asks for the amount of money. Therefore, we needed to multiply the number of rides by $2. 50.

Challenge Problem

Exercise 3.
A pendulum swings though a certain number of cycles in a given time. Owen made a pendulum that swings 12 times every 15 seconds.
a. Construct a table showing the number of cycles through which a pendulum swings. Include data for up to one minute. Use the last row for C cycles, and write an expression for the time it takes for the pendulum to make C cycles.

Answer:

b. Owen and his pendulum team set their pendulum in motion and counted 16 cycles. What was the elapsed time?
Answer:
C = 16; \(\frac{15 \cdot 16}{12}\) = 20. The elapsed time is 20 seconds.

c. Write an expression for the number of cycles a pendulum swings in S seconds.
Answer:
\(\frac{12}{15}\)S or \(\frac{4}{5}\)S or 0.8 ∙ S

d. In a different experiment, Owen and his pendulum team counted the cycles of the pendulum for iS seconds. How many cycles did they count?
Answer:
S = 35; 0.8 ∙ 35 = 28. They counted 28 cycles.

Eureka Math Grade 6 Module 4 Lesson 20 Problem Set Answer Key

Question 1.
A radio station plays 12 songs each hour. They never stop for commercials, news, weather, or traffic reports.
a. Write an expression describing how many songs are played by the radio station in H hours.
Answer:
12H

b. How many songs will be played ¡n an entire day (24 hours)?
Answer:
12 ∙ 24 = 288. There will be 288 songs played.

c. How long does it take the radio station to play 60 consecutive songs?
Answer:

Question 2.
A ski area has a high-speed lift that can move 2,400 skiers to the top of the mountain each hour.
a. Write an expression describing how many skiers can be lifted in H hours.
Answer:
2,400H

b. How many skiers can be moved to the top of the mountain in 14 hours?
Answer:
14 ∙ 2,400 = 33,600. 33,600 skiers can be moved.

c. How long will it take to move 3,600 skiers to the top of the mountain?
Answer:
3,600 ÷ 2,400 = 1.5. It will take an hour and a half to move 3,600 skiers to the top of the mountain.

Question 3.
Polly writes a magazine column, for which she earns $35 per hour. Create a table of values that shows the relationship between the number of hours that Polly works, H, and the amount of money Polly earns in dollars, E.

Answer:
Answers will vary. Sample answers are shown.

a. If you know how many hours Polly works, can you determine how much money she earned? Write the
corresponding expression.
Answer:
Multiplying the number of hours that Polly works by her rate ($35 per hour) will calculate her pay. 35H ¡s the expression for her pay in dollars.

b. Use your expression to determine how much Polly earned after working for 3\(\frac { 1 }{ 2 }\) hours.
Answer:
35H = 35 ∙ 3.5 = 122.5. Polly makes $122. 50 for working 3\(\frac{1}{2}\) hours.

c. If you know how much money Polly earned, can you determine how long she worked? Write the corresponding expression.
Answer:
Dividing Polly’s pay by 35 will calculate the number of hours she worked. E ÷ 35 ¡s the expression for the
number of hours she worked.

d. Use your expression to determine how long Polly worked if she earned $52. 50.
Answer:
52.50 – 35 = 1.5; Polly worked on hour and a half for $52.50.

Question 4.
Mitchell delivers newspapers after school, for which he earns $0.09 per paper. Create a table of values that shows the relationship between the number of papers that Mitchell delivers, P, and the amount of money Mitchell earns in dollars, E.

Answer:
Answers will vary. Sample answers are shown.

a. If you know how many papers Mitchell delivered, can you determine how much money he earned? Write the corresponding expression.
Answer:
Multiplying the number of papers that Mitchell delivers by his rate ($0.09 per paper) will calculate his pay. 0. 09P is the expression for his pay in dollars.

b. Use your expression to determine how much Mitchell earned by delivering 300 newspapers.
Answer:
0. 09P = 0. 09 ∙ 300 = 27. Mitchell earned $27. 00 for delivering 300 newspapers.

c. If you know how much money Mitchell earned, can you determine how many papers he delivered? Write the corresponding expression.
Answer:
Dividing Mitchell’s pay by $0.09 will calculate the number of papers he delivered. E ÷ 0.09 Is the expression for the number of papers he delivered.

d. Use your expression to determine how many papers Mitchell delivered if he earned $58. 50 last week.
Answer:
58.50 ÷ 0.09 = 650; therefore, Mitchell delivered 650 newspapers last week.

Question 5.
Randy is an art dealer who sells reproductions of famous paintings. Copies of the Mona Lisa sell for $475.
a. Last year Randy sold $9, 975 worth of Mona Lisa reproductions. How many did he sell?
Answer:
9,975 ÷ 475 = 21. He sold 21 copies of the painting.

b. If Randy wants to increase his sales to at least $15,000 this year, how many copies will he need to sell (without changing the price per painting)?
Answer:
15,000 ÷ 475 is about 31.6. He will have to sell 32 paintings in order to increase his sales to at least $15,000.

Eureka Math Grade 6 Module 4 Lesson 20 Exit Ticket Answer Key

Anna charges $8. 50 per hour to babysit. Complete the table, and answer the questions below.

Answer:

a. Write an expression describing her earnings for working H hours.
Answer:
8.50H or 8.5H

b How much will she earn if she works for 3 hours?
Answer:
If H = 3.5, then 8.5H = 8.5 ∙ 3.5 = 29.75. She will earn $29.75.

c. How long will it take Anna to earn $51.00?
Answer:
51 ÷ 8.5 = 6. It will take Anna 6 hours to earn $51.00.

Engage NY Eureka Math 6th Grade Module 4 Lesson 21 Answer Key

Eureka Math Grade 6 Module 4 Lesson 21 Example Answer Key

Look at Example 1 with your group. Determine the cost for various numbers of pizzas, and also determine the expression that describes the cost of having P pizzas delivered.

a. Pizza Queen has a special offer on lunch pizzas: $4.00 each. They charge $2.00 to deliver, regardless of how many pizzas are ordered. Determine the cost for various numbers of pizzas, and also determine the expression that describes the cost of having P pizzas delivered.

Answer:

What mathematical operations did you need to perform to find the total cost?
Answer:
Multiplication and addition. We multiplied the number of pizzas by $4 and then added the $2 delivery fee.

Suppose our principal wanted to buy a pizza for everyone in our class. Determine how much this would cost.
Answer:
Answers will vary depending on the number of students in your class.

b. If the booster club had $400 to spend on pizza, what is the greatest number of pizzas they could order?
Answer:
The greatest number of pizzas they could order would be 99. The pizzas themselves would cost 99 × $4 = $396, and then add $2.00 for delivery. The total bill is $398.

c. If the pizza price was raised to $5. 00 and the delivery price was raised to $3. 00, create a table that shows the total cost (pizza plus delivery) of 1, 2, 3, 4, and 5 pIzzas. Include the expression that describes the new cost of ordering P pizzas.

Answer:

Eureka Math Grade 6 Module 4 Lesson 21 Mathematical Modeling Exercise Answer Key

Mathematical Modeling Exercise
The Italian Villa Restaurant has square tables that the servers can push together to accommodate the customers. Only one chair fits along the side of the square table. Make a model of each situation to determine how many seats will fit around various rectangular tables.

Answer:

Are there any other ways to think about solutions to this problem?
Answer:
Regardless of the number of tables, there is one chair on each end, and each table has two chairs opposite one another.

It is impractical to make a model of pushing 50 tables together to make a long rectangle. If we did have a rectangle that long, how many chairs would fit on the long sides of the table?
Answer:
50 on each side, for a total of 100

How many chairs fit on the ends of the long table?
Answer:
2 chairs, one on each end

How many chairs fit in all? Record it on your table.
Answer:
102 chairs in all

Work with your group to determine how many chairs would fit around a very long rectangular table If 200 square tables were pushed together.
Answer:
200 chairs on each side, totaling 400, plus one on each end; grand total 402

If we let T represent the number of square tables that make one long rectangular table, what is the expression for the number of chairs that will fit around it?
Answer:
2T + 2

Eureka Math Grade 6 Module 4 Lesson 21 Problem Set Answer Key

Question 1.
Compact discs (CDs) cost $12 each at the Music Emporium. The company charges $4. 50 for shipping and handling, regardless of how many compact discs are purchased.
a. Create a table of values that shows the relationship between the number of compact discs that Mickey buys, D, and the amount of money Mickey spends, C, in dollars.

Answer:

b. If you know how many CDs Mickey orders, can you determine how much money he spends? Write the corresponding expression.
Answer:
12D + 4.5

c. Use your expression to determine how much Mickey spent buying 8 CDs.
Answer:
8(12) + 4. 50 = 100. 50. Mickey spent $100. 50.

Question 2.
Mr. Gee’s class orders paperback books from a book club. The books cost $2.95 each. Shipping charges are set at $4. 00, regardless of the number of books purchased.
a. Create a table of values that shows the relationship between the number of books that Mr. Gee’s class buys, B, and the amount of money they spend, C, in dollars.

Answer:

b. If you know how many books Mr. Gee’s class orders, can you determine how much money they spend? Write the corresponding expression.
Answer:
2.95B + 4

c. Use your expression to determine how much Mr. Gee’s class spent buying 24 books.
Answer:
24(2.95) + 4 = 74. Mr. Gee’s class spent $74.80.

Question 3.
Sarah is saving money to take a trip to Oregon. She received $450 in graduation gifts and saves $120 per week working.
a. Write an expression that shows how much money Sarah has after working W weeks.
Answer:
450 + 120W

b. Create a table that shows the relationship between the amount of money Sarah has (M) and the number of weeks she works (W).

Answer:

c. The trip will cost $1, 200. How many weeks will Sarah have to work to earn enough for the trip?
Answer:
Sarah will have to work 7 weeks to earn enough for the trip.

Question 4.
Mr. Gee’s language arts class keeps track of how many words per minute are read aloud by each of the students. They collect this oral reading fluency data each month. Below is the data they collected for one student in the first four months of school.
a. Assume this increase in oral reading fluency continues throughout the rest of the school year. Complete the table to project the reading rate for this student for the rest of the year.

Answer:

b. If this increase in oral reading fluency continues throughout the rest of the school year, when would this student achieve the goal of reading 165 words per minute?
Answer:
The student will meet the goal in May.

c. The expression for this student’s oral reading fluency is 121 + 5m, where m represents the number of
months during the school year. Use this expression to determine how many words per minute the student would read after 12 months of instruction.
Answer:
The student would read 181 words per minute: 121 + 5 × 12.

Question 5.
When corn seeds germinate, they tend to grow 5 inches in the first week and then 3 inches per week for the remainder of the season. The relationship between the height (H) and the number of weeks since germination (W) is shown below.
a. Complete the missing values in the table.

Answer:

b. The expression for this height is 2 + 3W. How tall will the corn plant be after 15 weeks of growth?
Answer:
2 + 3(15) = 47. The plant will be 47 inches tall.

Question 6.
The Honeymoon Charter Fishing Boat Company only allows newlywed couples on their sunrise trips. There is a captain, a first mate, and a deck hand manning the boat on these trips.
a. Write an expression that shows the number of people on the boat when there are C couples booked for the trip.
Answer:
3 + 2C

b. If the boat can hold a maximum of 20 people, how many couples can go on the sunrise fishing trip?
Answer:
Eight couples (16 passengers) can fit along with the 3 crew members, totaling 19 people on the boat. A ninth couple would overload the boat.

Eureka Math Grade 6 Module 4 Lesson 21 Exit Ticket Answer Key

Krystal Klear Cell Phone Company charges $5.00 per month for service. The company also charges $0. 10 for each text message sent.
a. Complete the table below to calculate the monthly charges for various numbers of text messages sent.

Answer:

b. If Suzannah’s budget limit is $10 per month, how many text messages can she send in one month?
Answer:
Suzannah can send 50 text messages in one month for $10.

Engage NY Eureka Math Grade 6 Module 4 Lesson 28 Answer Key

Eureka Math Grade 6 Module 4 Lesson 28 Mathematical Modeling Exercise Answer Key

Mathematical Modeling Exercise:

Question 1.
Juan has gained 20 lb. since last year. He now weighs 120 lb. Rashod is 15 Ib. heavier than Diego. If Rashod and Juan weighed the same amount last year, how much does Diego weigh? Let j represent Juan’s weight last year in pounds, and let d represent Diego’s weight in pounds.

Draw a tape diagram to represent Juan’s weight.
Answer:

Draw a tape diagram to represent Rashod’s weight.
Answer:

Draw a tape diagram to represent Diego’s weight.
Answer:

What would combining all three tape diagrams look like?
Answer:

Write an equation to represent Juan’s tape diagram.
Answer:
j + 20 = 120

Write an equation to represent Rashod’s tape diagram.
Answer:
d + 15 + 20 – 120

How can we use the final tape diagram or the equations above to answer the question presented?
Answer:
By combining 15 and 20 from Rashod’s equation, we can use our knowledge of addition identities to determine Diego’s weight.
The final tape diagram can be used to write a third equation d + 35 = 120. We con use our knowledge of addition identities to determine Diego’s weight
Calculate Diego’s weight.
d + 35 – 35 – 120 – 35
d = 85
We can use identities to defend our thought that d + 35 – 35 = d.

Does your answer make sense?
Answer:
Yes. If Diego weighs 85 lb., and Rashod weighs 15 lb. more than Diego, then Rashod weighs 100 lb., which is what Juan weighed before he gained 20 lb.

Eureka Math Grade 6 Module 4 Lesson 28 Example Answer Key

Example 1:

Marissa has twice as much money as Frank. Christina has $20 more than Marissa. If Christina has $100, how much money does Frank have? Let f represent the amount of money Frank has in dollars and m represents the amount of money Marissa has in dollars.

Draw a tape diagram to represent the amount of money Frank has.
Answer:

Draw a tape diagram to represent the amount of money Marissa has.
Answer:

Draw a tape diagram to represent the amount of money Christina has.
Answer:

Which tape diagram provides enough information to determine the value of the variable m?
Answer:
The tape diagram represents the amount of money Christina has.

Write and solve the equation.
Answer:
m + 20 = 100
m + 20 – 20 = 100 – 20
m = 80
The identities we have discussed throughout the module solidify that m + 20 – 20 = m

What does the 80 represent?
Answer:
80 is the amount of money, in dollars, that Morissa has.

Now that we know Marissa has $80, how can we use this information to find out how much money Frank has?
Answer:
We can write an equation to represent Marissa’s tape diagram since we now know the length is 80.

Write an equation.
Answer:
2f = 80

Solve the equation.
Answer:
2f ÷ 2 = 80 – 2
f = 40
Once again, the identities we have used throughout the module can solidify that 2f ÷ 2 = f.

What does the 40 represent?
Answer:
The 40 represents the amount of money Frank has in dollars.

Does 40 make sense in the problem?
Answer:
Yes, because if Frank has $40, then Marissa has twice this, which is $80. Then, Christina has $100 because she has $20 more than Marissa, which is what the problem stated.

Eureka Math Grade 6 Module 4 Lesson 28 Exercise Answer Key

Station One: Use tape diagrams to solve the problem:

Raeana is twice as old as Madeline, and Laura is 10 years older than Raeana. If Laura is 50 years old, how old is Madeline? Let m represent Madeline’s age in years, and let r represent Raeana’s age in years.

Raeano’s Tape Diagram:

Madeline’s Tape Diagram:

Laura’s Tape Diagram:

Equation for Laura’s Tape Diagram:
r ÷ 10 = 50
r + 10 – 10 = 50 – 10
r = 40
We now know that Raeana is 40 years old, and we can use this and Raeana’s tape diagram to determine the age of
Madeline.
2m = 40
2m – 2 = 40 ÷ 2
m = 20
There are, Madeline is 20 years old.

Station Two: Use tape diagrams to solve the problem.

Cadi has 90 apps on her phone. Braylen has half the amount of apps as Thees. If Cadi has three times the amount of apps as Theiss how many apps does Braylen have? Let b represent the number of Braylen’s apps and t represent the number of Theiss’s apps.
Answer:
Theiss’s Tape Diagram:

Broylen’s Tape Diagram:

Carli’s Tape Diagram:

Equation for Corll’s Tape Dio gram:
3t = 90
3t ÷ 3 = 90 + 3
t = 30
We now know that fleas has 30 opps on his phone. We can use this information to write an equation for Braylen’s tape diagram and determine how many opps ore on Bra ykn’s phone.
2h = 30
2b ÷ 2 = 30 + 2
b = 15

Therefore, Broylen has 15 apps on his phone.

Station Three: Use tape diagrams to solve the problem.

Reggie ran for 180 yards during the last football game, which is 40 more yards than his previous personal best Monte ran 50 more yards than Adrian during the same game. If Monte ran the same amount of yards Reggie ran in one game for his previous personal best, how many yards did Adrian run? Let r represent the number of yards Reggie ran during his previous personal best and a represents the number of yards Adrian ran.
Answer:
Reggie’s Tape Diagram:

Monte’s Tape Diagram:

Adrian Tape Diagram:

Combining all 3 tape diagrams:

Equation for Reggie’s Tape Diagram:
r + 40 = 180

Equation for Monte’s Tape Diagram:
a + 50 + 40 = 180
a + 90 = 180
a + 90 – 90 = 180 – 90
a = 90
Therefore, Adrian ran 90 yards during the football game.

Station Four: Use tape diagrams to solve the problem.

Lance rides his bike downhill at a pace of 60 miles per hour. When Lance is riding uphill, he rides 8 miles per hour slower than on flat roads. If Lance’s downhill speed is 4 times faster than his flat-road speed, how fast does he travel uphill? Let f represent Lance’s pace on flat roads in miles per hour and u represent Lance’s pace uphill in miles per hour.
Answer:
Tape Diagram for Uphill Pace:

Tape Diagram for Downhill Pace:

Equation for Downhill Pace:
4f = 60
4f ÷ 4 = 60 ÷4
f = 15

Equation for Uphill Pace:
u + 8 = 15
u + 8 – 8 = 15 – 8
u = 7
Therefore, Lance travels at a pace of 7 miles per hour uphill.

Eureka Math Grade 6 Module 4 Lesson 28 Problem Set Answer Key

Use tape diagrams to solve each problem.

Question 1.
Dwayne scored SS points in the last basketball game, which is 10 points more than his previous personal best. Lebron scored 15 points more than Chris in the same game. Lebron scored the same number of points as Dwayne’s previous personal best. Let d represent the number of points Dwayne scored during his previous personal best and c represent the number of Chris’s points.

a. How many points did Chris score during the game?
Answer:

Equation for Dwayne’s Tape Diagram: d + 10 = 55
Equation for Lebrons Tape Diagram:
c + 15 + 10 = 55
c + 25 = 55
c + 25 – 25 = 55 – 25
c = 30
Therefore, Chris scored 30 points in the game.

b. If these are the only three players who scored, what was the team’s total number of points at the end of the game?
Answer:
Dwayne scored 55 points. Chris scored 30 points. Lebron scored 45 points (answer to Dwayre’s equation). Therefore, the total number of points scored is 55 + 30 + 45 = 130.

Question 2.
The number of customers at Yummy Smoothies varies throughout the day. During the lunch rush on Saturday, there were 120 customers at Yummy Smoothies. rhe number of customers at Yummy Smoothies during dinner time was 10 customers fewer than the number during breakfast. The number of customers at Yummy Smoothies during lunch was 3 times more than during breakfast. How many people were at Yummy Smoothies during breakfast? How many people were at Yummy Smoothies during dinner? Let d represent the number of customers at Yummy Smoothies during dinner and b represent the number of customers at Yummy Smoothies during breakfast.
Answer:
Tape Diagram for Lunch:

Tape Diagram for Dinner:

Equation for Lunchs Tape Diagram:
3b = 120
3b ÷ 3 = 120 ÷ 3
b = 40

Now that we know 40 customers were at Yummy Smoothies for breakfast, we can use this information and the tape diagram for dinner to determine how many customers were at Yummy Smoot hies during dinner.
d + 10 = 40
d + 10 – 10 = 40 – 10
d = 30
Therefore, 30 customers were at Yummy Smoothies during dinner and 40 customers during breakfast.

Question 3.
Karter has 24 T-shirts. Karter has 8 fewer pairs of shoes than pairs of pants. If the number of T-shirts Karter has is double the number of pants he has, how many pairs of shoes does Karter have? Let p represent the number of pants Karter has and s represent the number of pairs of shoes he has.
Answer:
Tape Diagram for T-shirts:

Tape Diagram for Shoes:

Equation for T-Shirts Tape Diagram:
2p = 24
2p ÷ 2 = 24 ÷ 2
p = 12

Equation for Shoes Tape Diagram:
s + 8 = 12
s + 8 – 8 = 12 – 8
s = 4
Karter has 4 pairs of shoes.

Question 4.
Darnell completed 35 push-ups in one minute, which is 8 more than his previous personal best. Mia completed 6 more push-ups than Katie. If Mia completed the same amount of push-ups as Darnell completed during his previous personal best, how many push-ups did Katie complete? Let d represent the number of push-ups Darnell completed during his previous personal best and k represent the number of push-ups Katie completed.
Answer:

d + 8 = 35
k + 6 + 8 = 35
k + 14 = 35
k + 14 – 14 = 35 – 14
k = 21
Katie completed 21 push-ups.

Question 5.
Justine swims freestyle at a pace of 150 laps per hour, Justine swims breaststroke 20 laps per hour slower than she swims butterfly. If Justine’s freestyle speed is three times faster than her butterfly speed, how fast does she swim breaststroke? Let b represent Justine’s butterfly sped in laps per hour and r represent Justine’s breaststroke sped in laps per hour.
Answer:
Tape Diagram for breaststroke:

Tape Diagram for Freestyle:

3b = 150
3b ÷ 3 = 150 ÷ 3
b = 50
Therefore, Justine swims butterfly at apace of 50 laps per hour.
r + 20 = 50
r + 20 – 20 = 50 – 20
r = 30
Therefore, Justine swims breaststroke at a pace of 30 laps per hour.

Eureka Math Grade 6 Module 4 Lesson 28 Exit Ticket Answer Key

Use tape diagrams and equations to solve the problem with visual models and algebraic methods.

Question 1.
Alyssa is twice as old as Brittany, and Jazmyn is 15 years older than Alyssa. If Jazmyn is 35 years old, how old is Brittany? Let a represent Alyssa’s age in years and b represent Brittany’s age in years.
Answer:
Brittany’s Tape Diagram:

Alyssa’s Tape Diagram:

Jazmyn’s Tape Diagram:

Equation for jazmyn’s Tape Diagram:
a + 15 = 35
a + 15 – 15 = 35 – 15
a = 20

Now that we know Alyssa is 20 years old, we can use this information and Alyssa’s tape diagram to determine Brittany’s age.
2b = 20
2b ÷ 2 = 20 ÷ 2
b = 10
Therefore, Brittany is 10 years old.

Eureka Math Grade 6 Module 4 Lesson 28 Addition of Decimals II Answer Key

Addition of Decimals II – Round 1:

Directions: Evaluate each expression:

Question 1.
2.5 + 4
Answer:
6.5

Question 2.
2.5 + 0.4
Answer:
2.9

Question 3.
2.5 + 0.04
Answer:
2.54

Question 4.
2.5 + 0.004
Answer:
2.504

Question 5.
2.5 + 0.0004
Answer:
2.5004

Question 6.
6 + 1.3
Answer:
7.3

Question 7.
0.6 + 1.3
Answer:
1.9

Question 8.
0.06 + 1.3
Answer:
1.36

Question 9.
0.006 + 1.3
Answer:
1.306

Question 10.
0.0006 + 1.3
Answer:
1.3006

Question 11.
0.6 + 13
Answer:
13.6

Question 12.
7 + 0.2
Answer:
7.2

Question 13.
0.7 + 0.02
Answer:
0.72

Question 14.
0.07 + 0.2
Answer:
0.27

Question 15.
0.7 + 2
Answer:
2.7

Question 16.
7 + 0.02
Answer:
7.02

Question 17.
6 + 0.3
Answer:
6.3

Question 18.
0.6 + 0.03
Answer:
0.63

Question 19.
0.06 + 0.3
Answer:
0.36

Question 20.
0.6 + 3
Answer:
3.6

Question 21.
6 + 0.03
Answer:
6.03

Question 22.
0.6 + 0.3
Answer:
0.9

Question 23.
4.5 + 3.1
Answer:
7.6

Question 24.
4.5 + 0.31
Answer:
4.81

Question 25.
4.5 + 0.031
Answer:
4.531

Question 26.
0.45 + 0.031
Answer:
0.481

Question 27.
0.045 + 0.03 1
Answer:
0.076

Question 28.
12 +0.36
Answer:
12.36

Question 29.
1.2 + 3.6
Answer:
4.8

Question 30.
1.2 + 0.36
Answer:
1.56

Question 31.
1.2 + 0.036
Answer:
1.236

Question 32.
0.12 + 0.036
Answer:
0.156

Question 33.
0.012 + 0.036
Answer:
0.048

Question 34.
0.7 + 3
Answer:
3.7

Question 35.
0.7 + 0.3
Answer:
1

Question 36.
0.07 + 0.03
Answer:
0.1

Question 37.
0.007 + 0.003
Answer:
0.01

Question 38.
5 + 0.5
Answer:
5.5

Question 39.
0.5 + 0.5
Answer:
1

Question 40.
0.05 + 0.05
Answer:
0.1

Question 41.
0.005 + 0.005
Answer:
0.01

Question 42.
0.11+ 19
Answer:
19.11

Question 43.
1.1 + 1.9
Answer:
3

Question 44.
0.11+0.19
Answer:
0.3

Addition of Decimals II – Round 2:

Directions: Evaluate each expression:

Question 1.
7.4 + 3
Answer:
10.4

Question 2.
7.4 + 0.3
Answer:
7.7

Question 3.
7.4 + 0.03
Answer:
7.43

Question 4.
7.4 + 0.003
Answer:
7.403

Question 5.
7.4 + 0.0003
Answer:
7.4003

Question 6.
6 + 2.2
Answer:
8.2

Question 7.
0.6 + 2.2
Answer:
2.8

Question 8.
0.06 + 2.2
Answer:
2.26

Question 9.
0.006 + 2.2
Answer:
2.206

Question 10.
0.0006 + 2.2
Answer:
2.2006

Question 11.
0.6 + 22
Answer:
22.6

Question 12.
7 + 0.8
Answer:
7.8

Question 13.
0.7 + 0.08
Answer:
0.78

Question 14.
0.07 + 0.8
Answer:
0.87

Question 15.
0.7 + 8
Answer:
8.7

Question 16.
7 + 0.08
Answer:
7.08

Question 17.
5 + 0.4
Answer:
5.4

Question 18.
0.5 + 0.04
Answer:
0.54

Question 19.
0.05 + 0.4
Answer:
0.45

Question 20.
0.5 + 4
Answer:
4.5

Question 21.
5 + 0.04
Answer:
5.04

Question 22.
5 + 0.4
Answer:
5.4

Question 23.
3.6 + 2.3
Answer:
5.9

Question 24.
3.6 + 0.23
Answer:
3.83

Question 25.
3.6 + 0.023
Answer:
3.623

Question 26.
0.36 + 0.023
Answer:
0.383

Question 27.
0.036 + 0.023
Answer:
0.059

Question 28.
0.13 + 56
Answer:
56.13

Question 29.
1.3 + 5.6
Answer:
6.9

Question 30.
1.3 + 0.56
Answer:
1.86

Question 31.
1.3 + 0.056
Answer:
1.356

Question 32.
0.13 + 0.056
Answer:
0.186

Question 33.
0.013 + 0.056
Answer:
0.069

Question 34.
2 + 0.8
Answer:
2.8

Question 35.
0.2 + 0.8
Answer:
1

Question 36.
0.02 + 0.08
Answer:
0.1

Question 37.
0.002 + 0.008
Answer:
0.01

Question 38.
0.16 + 14
Answer:
14.16

Question 39.
1.6 + 1.4
Answer:
3

Question 40.
0.16 + 0.14
Answer:
0.3

Question 41.
0.016+0.014
Answer:
0.03

Question 42.
15 + 0.15
Answer:
15.15

Question 43.
1.5 + 1.5
Answer:
3

Question 44.
0.15 + 0.15
Answer:
0.3

Engage NY Eureka Math Grade 6 Module 4 Lesson 29 Answer Key

Eureka Math Grade 6 Module 4 Lesson 29 Example Answer Key

Example:

The school librarian, Mr. Marker, knows the library has 1,400 books but wants to reorganize how the books are displayed on the shelves. Mr. Marker needs to know how many fiction, nonfiction, and resource books are in the library. He knows that the library has four times as many fiction books as resource books and half as many nonfiction books as fiction books. If these are the only types of books in the library, how many of each type of boo are in the library?

Draw a tape diagram to represent the total number of books in the library.
Answer:

Draw two more tape diagrams, one to represent the number of fiction books in the library and one to represent the number of resource books in the library.
Answer:

What variable should we use throughout the problem?
Answer:
We should user to represent the number of resource books in the library because it represents the fewest amount of books. Choosing the variable to represent a different type of book would create fractions throughout the problem.

Write the relationship between resource books and fiction books algebraically.
Answer:
If we let r represent the number resource books, then 4r represents the number of fiction books.

Draw a tape diagram to represent the number of nonfiction books.
Answer:

How did you decide how many sections this tape diagram would have?
Answer:
There are half as many nonfiction books as fiction books. Since the fiction book tape diagram has four sections, the nonfiction book tape diagram should have two sections.

Represent the number of nonfiction books in the library algebraically.
Answer:
2r because that is half as many as fiction books.

Use the tape diagrams we drew to solve the problem.
Answer:
We know that combining the tape diagrams for each type of book will leave us with 1,400 total books.

Write an equation that represents the tape diagram.
Answer:
4r + 2r + r = 1,400

Determine the value of r.
Answer:
We can gather like terms and then solve the equation.
7r = 1,400
7r + 7 = 1,400 + 7
r = 200

→ What does this 200 mean?
There are 200 resource books in the library because r represented the number of resource books.

How many fiction books are in the library?
Answer:
There are 800 fiction books in the library because 4(200) = 800.

How many nonfiction books are in the library?
Answer:
There are 400 nonfiction books in the library because 2(200) = 400.

→ We can use a different math tool to solve the problem as well. If we were to make a table, how many columns would we need?
4

→ Why do we need four columns?
We need to keep track of the number of fiction, nonfiction, and resource books that are in the library, but we also need to keep track of the total number of books.

Set up a table with four columns, and label each column.
Answer:

→ Highlight the important information from the word problem that will help us fill out the second row in our table.

The school librarian, Mr. Marker, knows the library has 1,400 books but wants to reorganize how the books are displayed on the shelves. Mr. Marker needs to know how many fiction, nonfiction, and resource books are in the library. He knows that the library has four times as many fiction books as resource books and half as many nonfiction books as fiction books. If these are the only types of books in the library, how many of each type of book are in the library?

→ Fill out the second row of the table using the algebraic representations.

→ If r = 1, how many of each type of book would be in the library?

→ How can we fill out another row of the table?
Substitute different values in for r.

→ Substitute 5 in for r. How many of each type of book would be in the library then?

→ Does the library have four times as many fiction books as resource books?
Yes, because 5 . 4 = 20.

→ Does the library have half as many nonfiction books as fiction books?
Yes, because half of 20 is 10.

→ How do we determine how many of each type of book is in the library when there are 1,400 books in the library?
Continue to multiply the rows by the same value, until the total column has 1400 books.

At this point, allow students to work individually to determine how many fiction, nonfiction, and resource books are in the library if there are 1,400 total books. Each table may look different because students may choose different values to multiply by. A sample answer is shown below.

How many fiction books are in the library?
Answer:
800

How many nonfiction books are in the library?
Answer:
400

How many resource books are in the library?
Answer:
200

Does the library have four times as many fiction books as resource books?
Answer:
Yes, because 200 . 4 = 800.

Does the library have half as many nonfiction books as fiction books?
Answer:
Yes, because half of 800 is 400.

Does the library have 1,400 books?
Answer:
Yes, because 800 + 400 + 200 = 1400.

Eureka Math Grade 6 Module 4 Lesson 29 Exercise Answer Key

Exercises:

Solve each problem below using tables and algebraic methods. Then, check your answers with the word problems.

Exercise 1.
Indiana Ridge Middle School wanted to add a new school sport, so they surveyed the students to determine which sport is most popular. Students were able to choose among soccer, football, lacrosse, or swimming. The same number of students chose lacrosse and swimming. The number of students who chose soccer was double the number of students who chose lacrosse. The number of students who chose football was triple the number of students who chose swimming. If 434 students completed the survey, how many students chose each sport?
Answer:

The rest of the table will vary.

124 students chose soccer, 186 students chose football, 62 students chose lacrosse, and 62 students chose swimming.

We can confirm that these numbers satisfy the conditions of the word problem because lacrosse and swimming were chosen by the same number of students. 124 is double 62, so soccer was chosen by double the number of students as lacrosse, and 186 is triple 62, so football was chosen by 3 times as many students as swimming. Also,
124 + 186 + 62 + 62 = 434.

Algebraically: Let s represent the number of students who chose swimming. Then, 2s is the number of students who chose soccer, 3s is the number of students who chose football, and s is the number of students who chose lacrosse.
2s + 3s + s + s = 434
7s = 434
7s ÷ 7 = 434 ÷ 7
s = 62

Therefore, 62 students chose swimming, and 62 students chose lacrosse. 124 students chose soccer because 2(62) = 124, and 186 students chose football because 3(62) = 186.

Exercise 2.
At Prairie Elementary School, students are asked to pick their lunch ahead of time so the kitchen staff will know what to prepare. On Monday, 6 times as many students chose hamburgers as chose salads. The number of students who chose lasagna was one third the number of students who chose hamburgers. If 225 students ordered lunch, how many students chose each option if hamburger, salad, and lasagna were the only three options?
Answer:

The rest of the table will vary.

150 students chose a hamburger for lunch, 25 students chose a salad, and 50 students chose lasagna.

We can confirm that these numbers satisfy the conditions of the word problem because 25 . 6 = 150, so hamburgers were chosen by 6 times more students than salads. Also, \(\frac{1}{3}\) . 150 = 50, which means lasagna was chosen by one third of the number of students who chose hamburgers. Finally, 150 + 25 + 50 = 225, which means 225 students completed the survey.

Algebraically: Let s represent the number of students who chose a salad. Then, 6s represents the number of students who chose hamburgers, and 2s represents the number of students who chose lasagna.
6s + s + 2s = 225
9s = 225
9s ÷ 9 = 225 ÷ 9s
s = 25
This means that 25 students chose salad, 150 students chose hamburgers because 6(25) = 150, and 50 students chose lasagna because 2(25) = 50.

Exercise 3.
The art teacher, Mr. Gonzalez, is preparing for a project. In order for students to have the correct supplies, Mr. Gonzalez needs 10 times more markers than pieces of construction paper. He needs the same number of bottles of glue as pieces of construction paper. The number of scissors required for the project is half the number of pieces of construction paper. If Mr. Gonzalez collected 400 items for the project, how many of each supp’y did he collect?
Answer:

The rest of the table will vary.

Mr. Gonzalez collected 320 markers, 32 pieces of construction paper, 32 glue bottles, and 16 scissors for the project.

We can confirm that these numbers satisfy the conditions of the word problem because Mr. Gonzalez collected the same number of pieces of construction paper and glue bottles. Also, 32 . 10 = 320, so Mr. Gonzalez collected 10 times more markers than pieces of construction paper and glue bottles. Mr. Gonzalez only collected 16 pairs of scissors, which is half of the number of pieces of construction paper. The supplies collected add up to 400 supplies, which is the number of supplies indicated in the word problem.

Algebraically: Let s represent the number of scissors needed for the project, which means 20s represents the number of markers needed, 2s represents the number of pieces of construction paper needed, and 2s represents the number of glue bottles needed.

20s + 2s + 2s + s = 400
25s = 400
\(\frac{25 s}{25}=\frac{400}{25}\)
s = 16
This means that 16 pairs of scissors, 320 markers, 32 pieces of construction paper, and 32 glue bottles are required
for the project.

Exercise 4.
The math teacher, Ms. Zentz, is buying appropriate math tools to use throughout the year. She is planning on buying twice as many rulers as protractors. The number of calculators Ms. Zentz Is planning on buying is one quarter of the number of protractors. If Ms. Zentz buys 65 Items, how many protractors does Ms. Zentz buy?
Answer:

The rest of the table will vary.

Ms. Zentz will buy 20 protractors.

We can confirm that this number satisfies the conditions of the word problem because the number of protractors is half of the number of rulers, and the number of calculators is one fourth of the number of protractors. Also, 40 + 20 + 5 = 65, so the total matches the total supplies that Ms. Zentz bought.

Algebraically: Let c represent the number of calculators Ms. Zentz needs for the year. Then, 8c represents the number of rulers, and 4c represents the number of protractors Ms. Zentz will need throughout the year.
8c + 4c + c = 65
13c = 65
\(\frac{13 c}{13}=\frac{65}{13}\)
c = 5
Therefore, Ms. Zentz will need 5 calculators, 40 rulers, and 20 protractors throughout the year.

Eureka Math Grade 6 Module 4 Lesson 29 Problem Set Answer Key

Create tables to solve the problems, and then check your answers with the word problems.

Question 1.
On average, a baby uses three times the number of large diapers as small diapers and double the number of medium diapers as small diapers.

a. If the average baby uses 2,940 diapers, size large and small, how many of each size would be used?
Answer:

An average baby would use 490 small diapers, 980 medium diapers, and 1,470 large diapers.
The answer makes sense because the number of large diapers is 3 times more than small diapers. The number of medium diapers is double the number of small diapers, and the total number of diapers is 2, 940.

b. Support your answer with equations.
Answer:
Let s represent the number of small diapers a baby needs. Therefore, 2s represents the number of medium diapers, and 3s represents the amount of large diapers a baby needs.
s + 2s + 3s = 2,940
6s = 2,940
\(\frac{6 s}{6}=\frac{2,940}{6}\)
s = 490
Therefore, a baby requires 490 small diapers, 980 medium diapers (because 2(490) = 980), and 1,470 large diapers (because 3(490) = 1470), which matches the answer in part (a).

Question 2.
Tom has three times as many pencils as pens but has a total of 100 writing utensils.

a. How many pencils does Tom have?
Answer:

b. How many more pencils than pens does Tom have?
Answer:
75 – 25 = 50. Tom has 50 more pencils than pens.

Question 3.
Serena’s mom is planning her birthday party. She bought balloons, plates, and cups. Serena’s mom bought twice as many plates as cups. The number of balloons Serena’s mom bought was half the number of cups.

a. If Serena’s mom bought 84 items, how many of each item did she buy?
Answer:

Serena’s mom bought 12 balloons, 48 plates, and 24 cups.

b. Tammy brought 12 balloons to the party. How many total balloons were at Serena’s birthday party?
Answer:
12 + 12 = 24. There were 24 total balloons at the party.

c. If half the plates and all but four cups were used during the party, how many plates and cups were used?
Answer:
\(\frac{1}{2}\) . 48 = 24. Twenty-four plates were used during the party.
24 – 4 = 20. Twenty cups were used during the party.

Question 4.
Elizabeth has a lot of jewelry. She has four times as many earrings as watches but half the number of necklaces as earrings. Elizabeth has the same number of necklaces as bracelets.

a. If Elizabeth has 117 pieces of jewelry, how many earrings does she have?
Answer:

Elizabeth has 52 earrings, 13 watches, 26 necklaces, and 26 bracelets.

b. Support your answer with an equation.
Answer:
Let w represent the number of watches Elizabeth has. Therefore, 4w represents the number of earrings Elizabeth has, and 2w represents both the number of necklaces and bracelets she has.

4w + w + 2w + 2w = 117
9w = 117
\(\frac{9 w}{9}=\frac{117}{9}\)
w = 13
Therefore, Elizabeth has 13 watches, 52 earrings because 4(13) = 52, and 26 necklaces and bracelets each because 2(13) = 26.

Question 5.
Claudia was cooking breakfast for her entire family. She made double the amount of chocolate chip pancakes as she did regular pancakes. She only made half as many blueberry pancakes as she did regular pancakes. Claudia also knows her family loves sausage, so she made triple the amount of sausage as blueberry pancakes.

a. How many of each breakfast item did Claudia make If she cooked 90 Items in total?
Answer:

Claudia cooked 36 chocolate chip pancakes, 18 regular pancakes, 9 blueberry pancakes, and 27 pieces of sausage.

b. After everyone ate breakfast, there were 4 chocolate chip pancakes, 5 regular pancakes, 1 blueberry pancake, and no sausage left. How many of each item did the family eat?
Answer:
The family ate 32 chocolate chip pancakes, 13 regular pancakes, 8 blueberry pancakes, and 27 pieces of sausage during breakfast.

Question 6.
During a basketball game, Jeremy scored triple the number of points as Donovan. Kolby scored double the number of points as Donovan.

a. If the three boys scored 36 points, how many points did each boy score?
Answer:
Jeremy scored 18 points, Donovan scored 6 points, and Kolby scored 12 points.

b. Support your answer with an equation.
Answer:
Let d represent the number of points Donovan scored, which means 3d represents the number of points Jeremy scored, and 2d represents the number of points Kolby scored.
3d + d + 2d = 36
6d = 36
\(\frac{6 d}{6}=\frac{36}{6}\)
d = 6
Therefore, Donovan scored 6 points, Jeremy scored 18 points because 3(6) = 18, and Kolby scored 12 points because 2(6) = 12

Eureka Math Grade 6 Module 4 Lesson 29 Exit Ticket Answer Key

Solve the problem using tables and equations, and then check your answer with the word problem. Try to find the answer only using two rows of numbers on your table.

Question 1.
A pet store owner, Byron, needs to determine how much food he needs to feed the animals. Byron knows that he needs to order the same amount of bird food as hamster food. He needs four times as much dog food as bird food and needs half the amount of cat food as dog food. If Byron orders 600 packages of animal food, how much dog food does he buy? Let b represent the number of packages of bird food Byron purchased for the pet store.
Answer:

The rest of the table will vary (unless they follow suggestions from the Closing).

Byron would need to order 300 packages of dog food.

The answer makes sense because Byron ordered the same amount of bird food and hamster food. The table also shows that Byron ordered four times as much dog food as bird food, and the amount of cat food he ordered Is half the amount of dog food. The total amount of pet food Byron ordered was 600 packages, which matches the word problem.

Algebraically: Let b represent the number of packages of bird food Byron purchased for the pet store. Therefore, b also represents the amount of hamster food, 4b represents the amount of dog food, and 2b represents the amount of cat food required by the pet store.

b + b + 4b + 2b = 600
8b = 600
8b ÷ 8 = 600 ÷ 8
b = 75
Therefore, Byron will order 75 pounds of bird food, which results in 300 pounds of dog food because 4(75) = 300.

Engage NY Eureka Math Grade 6 Module 4 Lesson 30 Answer Key

Eureka Math Grade 6 Module 4 Lesson 30 Opening Exercise Answer Key

Opening Exercise:

Draw an example of each term, and write a brief description.

Acute:
Answer:
Less than 90°

Obtuse
Answer:
Between 90° and 180°

Right
Answer:
Exactly 90°

Straight
Answer:
Exactly 180°

Reflex
Answer:
Between 180° and 360°

Eureka Math Grade 6 Module 4 Lesson 30 Example Answer Key

Example 1:

∠ABC measures 90°. The angle has been separated into two angles. If one angle measures 57°, what is the measure of the other angle?

Answer:
In this lesson, we will be using algebra to help us determine unknown measures of angles.

How are these two angles related?
Answer:
x° + 57° = 90°

What equation could we use to solve for x?
Answer:
Now, let’s solve.
x° + 57° – 57° = 90° – 57°
x° = 33°
The measure of the unknown angle is 33°.

Example 2:

Michelle is designing a parking lot. She has determined that one of the angles should be 115°. What is the measure of angle x and angle y?

How is angle x related to the 115° angle?
Answer:
The two angles form o straight line. Therefore, they should add up to 180°.

What equation would we use to show this?
Answer:
x° + 115° = 180°

How would you solve this equation?
Answer:
115° was added to angle x, so I will take away 115° to get back to angle X.
x° + 115° – 115° = 180° – 115°
x° = 65°
The angle next to 115°, labeled with an x, is equal to 65°.

How is angle y related to the angle that measures 115°?
Answer:
These two angles also form a straight line and must add up to 180°.
Therefore, angles x and y must both be equal to 65°.

Example 3:

A beam of light is reflected off a mirror. Below is a diagram of the reflected beam. Determine the missing angle measure.

How are the angles in this question-related?
Answer:
There are three angles that, when all placed together, form a straight line. This means that the three angles have a sum of 180°.

What equation could we write to represent the situation?
Answer:
55° + x + 55° = 180°

How would you solve an equation like this?
Answer:
We can combine the two angles that we do know.
55° + 550 + x° = 180°
110° + x° = 180°
110° – 110° + x° = 180° – 110°
x° = 70°
The angle of the bounce is 70°.

Example 4:

∠ABC measures 90°. It has been split into two angles, ∠ABD and ∠DBC. The measure of ∠ABD and ∠DBC is in a ratio of 4: 1. What are the measures of each angle? Use a tape diagram to represent the ratio 4: 1.

What is the measure of each angle?
5 units = 90°
1 unit = 18°
4 units = 72°
∠ABD is 72°. ∠DBC is 18°

How can we represent this situation with an equation?
Answer:
4x° + x° = 90°

Solve the equation to determine the measure of each angle.
4x° + x° = 90°
5x° = 90°
5x° ÷ 5 = 90° ÷ 5
x° = 18°
4x° = 4(18°) = 72°
The measure of ∠DBC is 18° and the measure of ∠ABD is 72°.

Eureka Math Grade 6 Module 4 Lesson 30 Exercise Answer Key

Exercises:

Write and solve an equation in each of the problems.

Exercise 1.
∠ABC measures 900. It has been split into two angles, ∠ABD and ∠DBC. The measure of the two angles is in a ratio of 2: 1. What are the measures of each angle?

Answer:
x° + 2x° = 90°
3x° = 90°
\(\frac{3 x^{\circ}}{3}=\frac{90^{\circ}}{3}\)
x° = 30°
One of the angles measures 30°, and the other measures 60°.

Exercise 2.
Solve for x.

Answer:
x° + 64° + 37° = 180°
x° + 101° = 180°
x° + 101° – 101° = 180° – 101°
x° = 79°

Exercise 3.
Candice is building a rectangular piece of a fence according to the plans her boss gave her. One of the angles is not labeled. Write an equation, and use it to determine the measure of the unknown angle.

Answer:
x° + 49° = 90°
x° + 49° – 49° = 90° – 49°
x° = 41°

Exercise 4.
Rashid hit a hockey puck against the wall at a 38° angle. The puck hit the wall and traveled in a new direction. Determine the missing angle in the diagram.

Answer:
38° + x° + 38° = 180°
76° + x° = 180°
76° – 76° + x° = 180° – 76°
x° = 104°
The measure of the missing angle is 104°.

Exercise 5.
Jaxon is creating a mosaic design on a rectangular table. He has added two pieces to one of the corners. The first piece has an angle measuring 38° and is placed in the corner. A second piece has an angle measuring 27° and is also placed in the comer. Draw a diagram to model the situation. Then, write an equation, and use it to determine the measure of the unknown angle in a third piece that could be added to the corner of the table.
Answer:

x° + 38° + 27° = 90°
x° + 65° = 90°
x° + 65° – 65° = 90° – 65°
x° = 25°
The measure of the unknown angle is 25°.

Eureka Math Grade 6 Module 4 Lesson 30 Problem Set Answer Key

Write and solve an equation for each problem.

Question 1.
Solve for x.

Answer:
x° + 52° = 90°
x° + 52° – 52° = 90° – 52°
x° = 38°
The measure of the missing angle is 38°

Question 2.
∠BAE measures 90°. Solve for x.

Answer:
15° + x + 25° = 90°
15° + 25° + x = 90
40° + x = 90°
40° – 40° + x = 90°
x° = 50°

Question 3.
Thomas is putting in a tile floor. He needs to determine the angles that should be cut in the tiles to fit in the comer. The angle in the comer measures 90°. One piece of the tile will have a measure of 24°. Write an equation, and use it to determine the measure of the unknown angle.
Answer:
x° + 24° = 90°
x° + 24° – 24° = 90° – 24°
x° = 66°
The measure of the unknown angle is 66°.

Question 4.
Solve for x°.

Answer:
x° + 105° + 62° = 180°
x° + 167° = 180°
x° + 167° – 167° = 180° – 167°
x° = 13°
The measure of the missing angle is 13°.

Question 5.
Aram has been studying the mathematics behind pinball machines. He made the following diagram of one of his

Answer:
52° + x° + 68° = 180°
120° + x° = 180°
120° + x° – 120° = 180° – 120°
x° = 60°
The measure of the missing angle is 60°.

Question 6.
The measures of two angles have a sum of 90°. The measures of the angles are in a ratio of 2: 1. Determine the measures of both angles.
Answer:
2x° + x° = 90°
3x° = 90°
\(\frac{3 x^{\circ}}{3}=\frac{90^{\circ}}{3}\)
x° = 30°
The angles measure 30° and 60°.

Question 7.
The measures of two angles have a sum of 1800. The measures of the angles are in a ratio of 5: 1. Determine the measures of both angles.
Answer:
5x° + x° = 180°
6x° = 180°
\(\frac{6 x^{\circ}}{6}=\frac{180}{6}\)
x° = 30°
The angles measure 30° and 150°.

Eureka Math Grade 6 Module 4 Lesson 30 Exit Ticket Answer Key

Write an equation, and solve for the missing angle in each question.

Question 1.
Alejandro is repairing a stained glass window. He needs to take ft apart to repair ft. Before taking ft apart, he makes a sketch with angle measures to put ft back together. Write an equation, and use ft to determine the measure of the unknown angle.

Answer:
40° + x° + 30° = 180°
x° + 40° + 30° = 180°
x° + 70° = 180°
x° + 70° – 70° = 180° – 70°
x° = 110°
The missing angle measures 110°.

Question 2.
Hannah is putting in a tile floor. She needs to determine the angles that should be cut in the tiles to fit in the corner. The angle in the comer measures 90°. One piece of the tile will have a measure of 38°. Wrfte an equation, and use it to determine the measure of the unknown angle.

Answer:
x° + 38° = 90°
38° – 38° = 90° – 38°
x° = 52°
The measure of the unknown angle is 52°.

Eureka Math Grade 6 Module 4 Lesson 30 Subtraction of Decimals Answer Key

Subtraction of Decimals – Round 1:

Directions: Evaluate each expression.

Question 1.
55 – 50
Answer:
5

Question 2.
55 – 5
Answer:
50

Question 3.
5.5 – 5
Answer:
0.5

Question 4.
5.5 – 0.5
Answer:
5.0

Question 5.
88 – 80
Answer:
8

Question 6.
88 – 8
Answer:
80

Question 7.
8.8 – 8
Answer:
0.8

Question 8.
8.8 – 0.8
Answer:
8

Question 9.
33 – 30
Answer:
3

Question 10.
33 – 3
Answer:
30

Question 11.
3.3 – 3
Answer:
0.3

Question 12.
1 – 0.3
Answer:
0.7

Question 13.
1 – 0.03
Answer:
0.97

Question 14.
1 – 0.003
Answer:
0.997

Question 15.
0.1 – 0.03
Answer:
0.07

Question 16.
4 – 0.8
Answer:
3.2

Question 17.
4 – 0.08
Answer:
3.92

Question 18.
4 – 0.008
Answer:
3.992

Question 19.
0.4 – 0.08
Answer:
0.32

Question 20.
9 – 0.4
Answer:
8.6

Question 21.
9 – 0.04
Answer:
8.96

Question 22.
9 – 0.004
Answer:
8.996

Question 23.
9.9 – 5
Answer:
4.9

Question 24.
9.9 – 0.5
Answer:
9.4

Question 25.
0.99 – 0.5
Answer:
0.49

Question 26.
0.99 – 0.05
Answer:
0.94

Question 27.
4.7-2
Answer:

Question 28.
4.7 – 0.2
Answer:
4.5

Question 29.
0.47 – 0.2
Answer:
0.27

Question 30.
0.47 – 0.02
Answer:
0.45

Question 31.
8.4 – 1
Answer:
7.4

Question 32.
8.4 – 0.1
Answer:
8.3

Question 33.
0.84 – 0.1
Answer:
0.83

Question 34.
7.2 – 5
Answer:
5.2

Question 35.
7.2 – 0.5
Answer:
6.7

Question 36.
0.72 – 0.5
Answer:
0.22

Question 37.
0.72 – 0.05
Answer:
0.67

Question 38.
8.6 – 7
Answer:
1.6

Question 39.
8.6 – 0.7
Answer:
7.9

Question 40.
0.86 – 0.7
Answer:
0.16

Question 41.
0.86 – 0.07
Answer:
0.79

Question 42.
5.1 – 4
Answer:
1.1

Question 43.
5.1 – 4.7
0.4
Answer:

Question 44.
0.51 – 0.4
Answer:
0.11

Subtraction of Decimals-Round 2:

Directions: Evaluate each expression:

Question 1.
66 – 60
Answer:
6

Question 2.
66 – 6
Answer:
60

Question 3.
6.6 – 6
Answer:
0.6

Question 4.
6.6 – 0.6
Answer:
6

Question 5.
99 – 90
Answer:
9

Question 6.
99 – 9
Answer:
90

Question 7.
9.9 – 9
Answer:
0.9

Question 8.
9.9 – 0.9
Answer:
9

Question 9.
22 – 20
Answer:
2

Question 10.
22 – 2
Answer:
20

Question 11.
2.2 – 2
Answer:
0.2

Question 12.
3 – 0.4
Answer:
2.6

Question 13.
3 – 0.04
Answer:
2.96

Question 14.
3 – 0.004
Answer:
2.996

Question 15.
0.3 – 0.04
Answer:
0.26

Question 16.
8 – 0.2
Answer:
7.8

Question 17.
8 – 0.02
Answer:
7.98

Question 18.
8 – 0.002
Answer:
7.998

Question 19.
0.8 – 0.02
Answer:
0.78

Question 20.
5 – 0.1
Answer:
4.9

Question 21.
5 – 0.01
Answer:
4.99

Question 22.
5 – 0.001
Answer:
4.999

Question 23.
6.8 – 4
Answer:
2.8

Question 24.
6.8 – 0.4
Answer:
6.4

Question 25.
0.68 – 0.4
Answer:
0.28

Question 26.
0.68 – 0.04
Answer:
0.64

Question 27.
7.3 – 1
Answer:
6.3

Question 28.
7.3 – 0.1
Answer:
7.2

Question 29.
0.73 – 0.1
Answer:
0.63

Question 30.
0.73 – 0.01
Answer:
0.72

Question 31.
9.5 – 2
Answer:
7.5

Question 32.
9.5 – 0.2
Answer:
9.3

Question 33.
0.95 – 0.2
Answer:
0.75

Question 34.
8.3 – 5
Answer:
3.3

Question 35.
8.3 – 0.5
Answer:
7.8

Question 36.
0.83 – 0.5
Answer:
0.33

Question 37.
0.83 – 0.05
Answer:
0.78

Question 38.
7.2 – 4
Answer:
3.2

Question 39.
7.2 – 0.4
Answer:
6.8

Question 40.
0.72 – 0.4
Answer:
0.32

Question 41.
0.72 – 0.04
Answer:
0.68

Question 42.
9.3 – 7
Answer:
2.3

Question 43.
9.3 – 0.7
Answer:
8.6

Question 44.
0.93 – 0.7
Answer:
0.23

Engage NY Eureka Math Grade 6 Module 4 Lesson 31 Answer Key

Eureka Math Grade 6 Module 4 Lesson 31 Example Answer Key

Example 1:

Marcus reads for 30 minutes each night. He wants to determine the total number of minutes he will read over the course of a month. He wrote the equation t = 30d to represent the total amount of time that he has spent reading, where t represents the total number of minutes read and d represents the number of days that he read during the month. Determine which variable is independent and which is dependent. Then, create a table to show how many minutes he has read in the first seven days.
Independent Variable: ________
Dependent Variable: _________

Answer:
Independent Variable: Number of days
Dependent Variable: Total minutes read

Example 2:

Kira designs websites. She can create three different websites each week. Kira wants to create an equation that will give her the total number of websites she can design given the number of weeks she works. Determine the independent and dependent variables. Create a table to show the number of websites she can design over the first 5 weeks. Finally, write an equation to represent the number of websites she can design when given any number of weeks.
Independent Variable: ________
Dependent Variable: _________
Equation: _______

Answer:
Independent variable: # of weeks worked Worked (w)
Dependent variable: # of websites designed

Equation d = 3w, where w is the number of weeks worked and d is the number of websites designed.

Example 3:

Priya streams movies through a company that charges her a $5 monthly fee plus $1. 50 per movie. Determine the independent and dependent variables, write an equation to model the situation, and create a table to show the total cost per month given that she might stream between 4 and 10 movies in a month.
Independent Variable: ________
Dependent Variable: _________
Equation: _______

Answer:
Independent variable: # of movies watched per month
Dependent variable: Total cost per month, in dollars
Equation: c = 1.5m + 5 or c = 1.50m + 5

Eureka Math Grade 6 Module 4 Lesson 31 Exercise Answer Key

Exercises:

Exercise 1.
Sarah is purchasing pencils to share. Each package has 12 pencils. The equation n = 12p, where n is the total number of pencils and p is the number of packages, can be used to determine the total number of pencils Sarah purchased. Determine which variable is dependent and which is independent. Then, make a table showing the number of pencils purchased for 3 – 7 packages.

Answer:
The number of packages, p, is the independent variable.
The total number of pencils, n, is the dependent variable.

Exercise 2.
Charlotte reads 4 books each week. Let b be the number of books she reads each week, and let w be the number of weeks that she reads. Determine which variable is dependent and which is independent. Then, write an equation to model the situation, and make a table that shows the number of books read in under 6 weeks.

Answer:
The number of weeks, w, is the independent variable.
The number of books, b, is the dependent variable.
b = 4w

Exercise 3.
A miniature golf course has a special group rate. You can pay $20 plus $3 per person when you have a group of 5 or more friends. Let f be the number of friends and c be the total cost. Determine which variable is independent and which is dependent, and write an equation that models the situation. Then, make a table to show the cost for 5 to 12 friends.

Answer:
The number of friends, f, is the independent variable.
The total cost in dollars, c, is the dependent variable.
c = 3f +20

Exercise 4.
Carlos is shopping for school supplies. He bought a pencil box for $3, and he also needs to buy notebooks. Each notebook is $2. Let t represent the total cost of the supplies and n be the number of notebooks Carlos buys. Determine which variable is independent and which is dependent, and write an equation that models the situation. Then, make a table to show the cost for 1 to 5 notebooks.

Answer:
The total number of notebooks, n, is the independent variable.
The total cost in dollars, t, is the dependent variable.
t = 2n + 3

Eureka Math Grade 6 Module 4 Lesson 31 Problem Set Answer Key

Question 1.
Jazlyah sells 3 houses each month. To determine the number of houses she can sell in any given number of months, she uses the equation t = 3m, where t is the total number of houses sold and m is the number of months. Name the independent and dependent variables. Then, create a table to show how many houses she sells in fewer than 6 months.

Answer:
The independent variable is the number of months. The dependent variable is the total number of houses sold.

Question 2.
Joshua spends 25 minutes of each day reading. Let d be the number of days that he reads, and let m represent the total minutes of reading. Determine which variable is independent and which is dependent. Then, write an equation that models the situation. Make a table showing the number of minutes spent reading over 7 days.

Answer:
The number of days, d, is the independent variable.
The total number of minutes of reading, m, is the dependent variable.
m = 25d

Question 3.
Each package of hot dog buns contains 8 buns. Let p be the number of packages of hot dog buns and b be the total number of buns. Determine which variable is independent and which is dependent. Then, write an equation that models the situation, and make a table showing the number of hot dog buns in 3 to 8 packages.

Answer:
The number of packages, p, is the independent variable.
The total number of hot dog buns, b, is the dependent variable.
b = 8p

Question 4.
Emma was given 5 seashells. Each week she collected 3 more. Let w be the number of weeks Emma collects seashells and s be the number of seashells she has total. Which variable is independent, and which is dependent? Write an equation to model the relationship, and make a table to show how many seashells she has from week 4 to week 10.

Answer:
The number of weeks, w, is the independent variable.
The total number of seashells, s, is the dependent variable.
s = 3w + 5

Question 5.
Emilia is shopping for fresh produce at a farmers market. She bought a watermelon for $5, and she also wants to buy peppers. Each pepper is $0. 75. Let t represent the total cost of the produce and n be the number of peppers bought. Determine which variable Is independent and which is dependent, and write an equation that models the situation. Then, make a table to show the cost for 1 to 5 peppers.

Answer:
The number of peppers, n, is the independent variable.
The total cost in dollars, t, is the dependent variable.
t = 0.75n + 5

Question 6.
A taxicab service charges a flat fee of $7 plus an additional $1.25 per mile driven. Show the relationship between the total cost and the number of miles driven. Which variable is independent, and which is dependent? Write an equation to model the relationship, and make a table to show the cost of 4 to 10 miles.

Answer:
The number of miles driven, m, is the independent variable.
The total cost in dollars, c, is the dependent variable.
c = 125m + 7

Eureka Math Grade 6 Module 4 Lesson 31 Exit Ticket Answer Key

For each problem, determine the independent and dependent variables, write an equation to represent the situation, and then make a table with at least 5 values that models the situation.

Question 1.
Kyla spends 60 minutes of each day exercising. Let d be the number of days that Kyla exercises, and let m represent the total minutes of exercise in a given time frame. Show the relationship between the number of days that Kyla exercises and the total minutes that she exercises.
Independent variable: _______
Dependent variable: ________
Equation: _______

Answer:
Tables may vary.
Independent variable: Number of Days
Dependent variable: Total Number of Minutes
Equation: m = 60d

Question 2.
A taxicab service charges a flat fee of $8 plus an additional $1.50 per mile. Show the relationship between the total cost and the number of miles driven.
Independent variable: _______
Dependent variable: ________
Equation: _______

Answer:
Tables may vary.
Independent variable: Number of miles
Dependent variable: Total cost, in dollars
Equation: c = 1.50m + 8