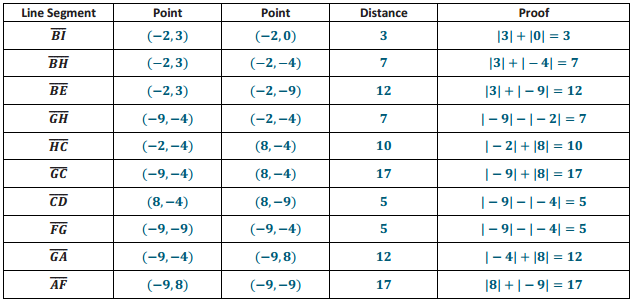
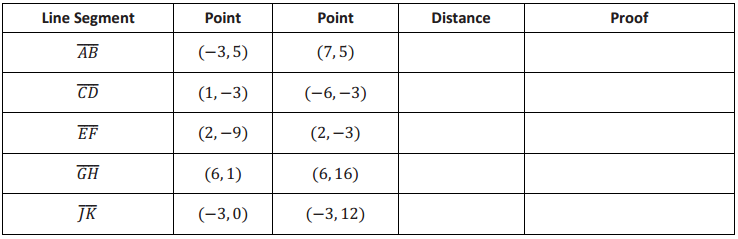
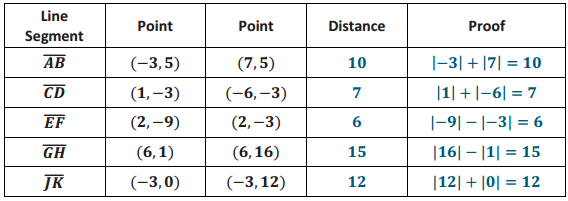
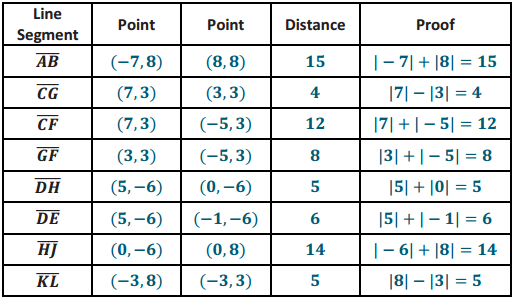
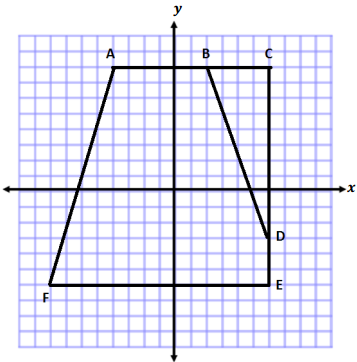
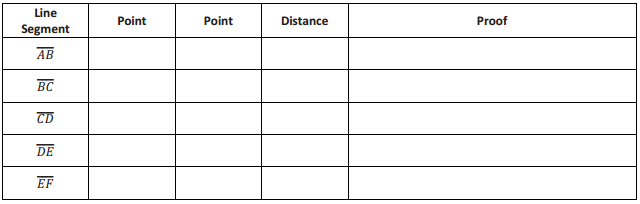
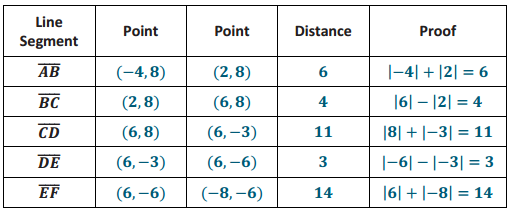
Engage NY Eureka Math 5th Grade Module 6 Lesson 29 Answer Key
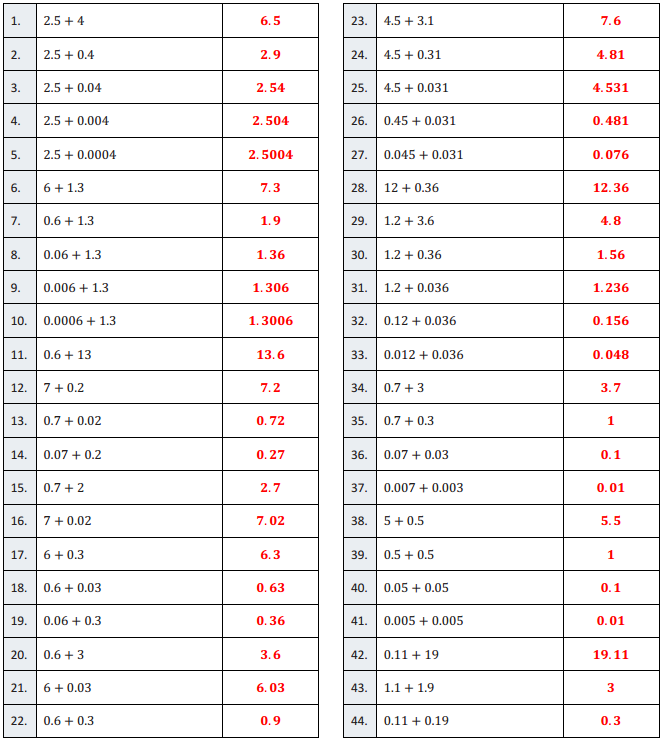
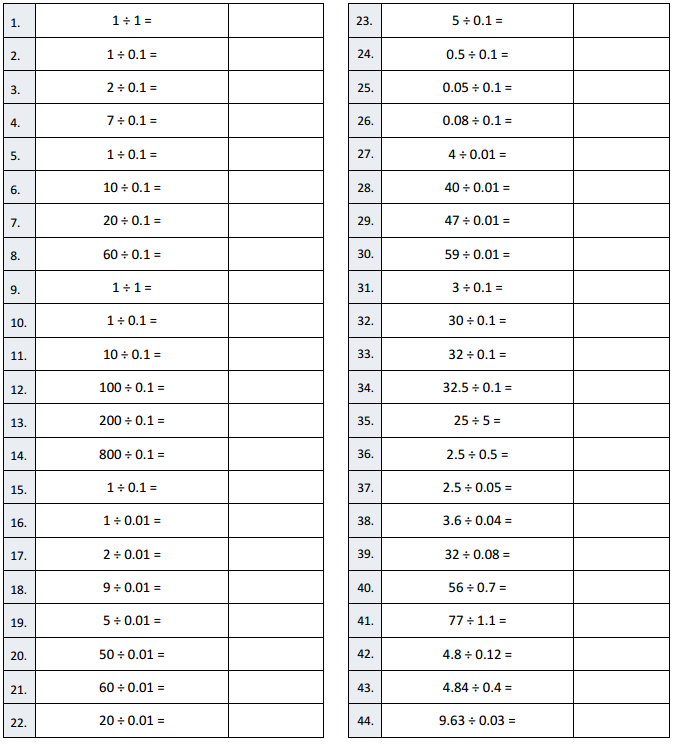
Eureka Math Grade 5 Module 6 Lesson 29 Sprint Answer Key
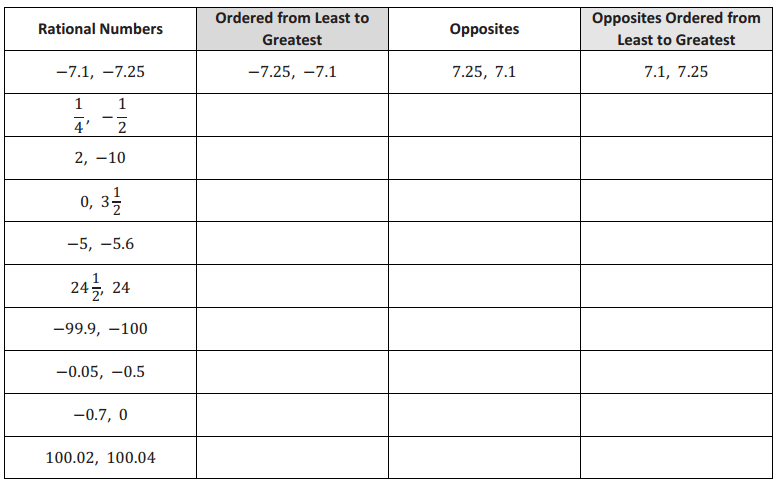
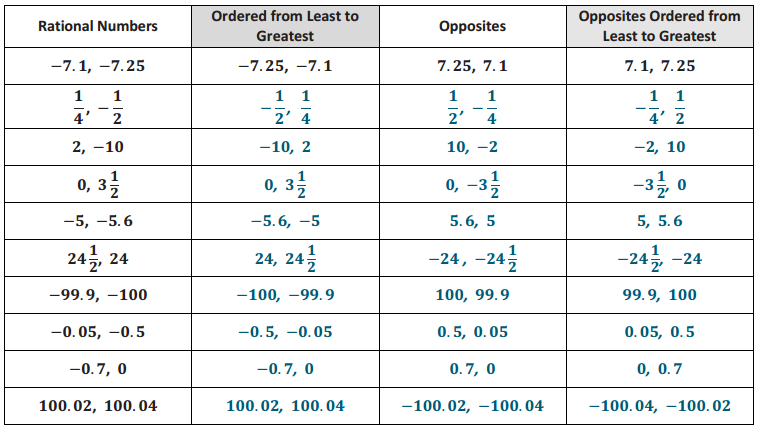
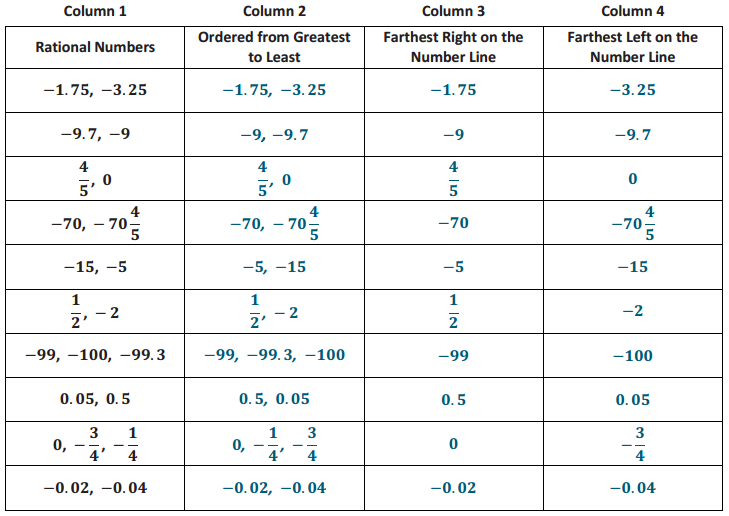
A
Multiply Decimals
Question 1.
3 × 2 =
Answer:
3 × 2 = 6
Question 2.
3 × 0.2 =
Answer:
3 × 0.2 = 0.6
Explanation :
Equation : 3 × 0.2
Multiply without decimals = 3 × 2 = 6
0.2 have 1 decimal places, So, the answer = 0.6
Question 3.
3 × 0.02 =
Answer:
3 × 0.02 = 0.06
Explanation :
Equation : 3 × 0.02
Multiply without decimals = 3 × 2 = 6
0.02 have 2 decimal places, So, the answer = 0.06
Question 4.
3 × 3 =
Answer:
3 × 3 = 9
Question 5.
3 × 0.3 =
Answer:
3 × 0.3 = 0.9
Explanation :
Equation : 3 × 0.3
Multiply without decimals = 3 × 3 = 9
0.3 have 1 decimal places, So, the answer = 0.9
Question 6.
3 × 0.03 =
Answer:
3 × 0.03 = 0.09
Explanation :
Equation : 3 × 0.03
Multiply without decimals = 3 × 3 = 9
0.03 have 2 decimal places, So, the answer = 0.09
Question 7.
2 × 4 =
Answer:
2 × 4 = 8
Question 8.
2 × 0.4 =
Answer:
2 × 0.4 = 0.8
Explanation :
Equation : 2 × 0.4
Multiply without decimals = 2 × 4 = 8
0.4 have 1 decimal places, So, the answer = 0.8
Question 9.
2 × 0.04 =
Answer:
2 × 0.04 = 0.08
Explanation :
Equation : 2 × 0.04
Multiply without decimals = 2 × 4 = 8
0.04 have 2 decimal places, So, the answer = 0.08
Question 10.
5 × 3 =
Answer:
5 × 3 = 15
Question 11.
5 × 0.3 =
Answer:
5 × 0.3 = 1.5
Explanation :
Equation : 5 × 0.3
Multiply without decimals = 5 × 3 = 15
15 have 1 decimal places, So, the answer = 1.5
Question 12.
5 × 0.03 =
Answer:
5 × 0.03 =0.15
Explanation :
Equation : 5 × 0.03
Multiply without decimals = 5 × 3 = 15
15have 2 decimal places, So, the answer = 0.15
Question 13.
7 × 2 =
Answer:
7 × 2 = 14
Question 14.
7 × 0.2 =
Answer:
7 × 0.2 = 1.4
Explanation :
Equation : 7 × 0.2
Multiply without decimals = 7 × 2 = 14
0.2 have 1 decimal places, So, the answer = 1.4
Question 15.
7 × 0.02 =
Answer:
7 × 0.02 = 0.14
Explanation :
Equation : 7 × 0.02
Multiply without decimals = 7 × 2 = 14
0.02 have 2 decimal places, So, the answer = 0.14
Question 16.
4 × 3 =
Answer:
4 × 3 = 12
Question 17.
4 × 0.3 =
Answer:
4 × 0.3 = 1.2
Explanation :
Equation : 4 × 0.3
Multiply without decimals = 4 × 3 = 12
0.3 have 1 decimal places, So, the answer = 1.2
Question 18.
0.4 × 3 =
Answer:
0.4 × 3 = 1.2
Question 19.
0.4 × 0.3 =
Answer:
0.4 × 0.3 = 0.12
Explanation :
Equation : 0.4 × 0.3 =
Multiply without decimals = 4 × 3 = 12
0.4 have 1 decimal places and 0.3 have 1 decimal places So, the answer have 2 decimal place= 0.12
Question 20.
0.4 × 0.03 =
Answer:
0.4 × 0.03 = 0.012
Explanation :
Equation : 0.4 × 0.03
Multiply without decimals = 4 × 3 = 12
0.4 have 1 decimal places and 0.03 have 2 decimal places So, the answer have 3 decimal place= 0.012
Question 21.
0.3 × 0.04 =
Answer:
0.3 × 0.04 =0.012
Explanation :
Equation : 0.3 × 0.04
Multiply without decimals = 3 × 4 = 12
0.3 have 1 decimal places and 0.04 have 2 decimal places, So, the answer will have 3 decimal places = 0.012
Question 22.
6 × 2 =
Answer:
6 × 2 = 12
Question 23.
0.6 × 2 =
Answer:
0.6 × 2 = 1.2
Explanation :
Equation : 0.6 × 2
Multiply without decimals = 6 × 2 = 12
0.6 have 1 decimal places, So, the answer will have 1 decimal point = 1.2
Question 24.
0.6 × 0.2 =
Answer:
0.6 × 0.2 = 0.12
Explanation :
Equation : 0.6 × 0.2
Multiply without decimals = 6 × 2 = 12
0.6 have 1 decimal places and 0.2 have 1 decimal places, So, the answer will have 2 decimal points = 0.12
Question 25.
0.6 × 0.02 =
Answer:
0.6 × 0.02 = 0.012
Explanation :
Equation : 0.6 × 0.02
Multiply without decimals = 6 × 2 = 12
0.6 have 1 decimal places and 0.02 have 2 decimal places, So, the answer will have 3 decimal points = 0.012
Question 26.
0.2 × 0.06 =
Answer:
0.2 × 0.06 = 0.012
Explanation :
Equation : 0.2 × 0.06
Multiply without decimals = 2 × 6 = 12
0.2 have 1 decimal places and 0.06 have 2 decimal places, So, the answer will have 3 decimal points = 0.012
Question 27.
5 × 7 =
Answer:
5 × 7 = 35
Question 28.
0.5 × 7 =
Answer:
0.5 × 7 = 3.5
Explanation :
Equation : 0.5 × 7
Multiply without decimals = 5 × 7 = 35
0.5 have 1 decimal place , So, the answer will have 1 decimal place = 3.5
Question 29.
0.5 × 0.7 =
Answer:
0.5 × 0.7 = 0.35
Explanation :
Equation : 0.5 × 0.7
Multiply without decimals = 5 × 7 = 35
0.5 have 1 decimal place and 0.7 have 1 decimal place , So, the answer will have 2 decimal places = 0.35
Question 30.
0.5 × 0.07 =
Answer:
0.5 × 0.07 = 0.035
Explanation :
Equation : 0.5 × 0.07
Multiply without decimals = 5 × 7 = 35
0.5 have 1 decimal place and 0.07 have 2 decimal place , So, the answer will have 3 decimal places = 0.035
Question 31.
0.7 × 0.05 =
Answer:
0.7 × 0.05 = 0.035
Explanation :
Equation : 0.7 × 0.05
Multiply without decimals = 7 × 5 = 35
0.7 have 1 decimal place and 0.05 have 2 decimal place , So, the answer will have 3 decimal places = 0.035
Question 32.
2 × 8 =
Answer:
2 × 8 = 16
Question 33.
9 × 0.2 =
Answer:
9 × 0.2 = 1.8
Explanation :
Equation : 9 × 0.2
Multiply without decimals = 9 × 2 = 18
0.2 have 1 decimal places, So, the answer will have 1 decimal place =1.8
Question 34.
3 × 7 =
Answer:
3 × 7 = 21
Question 35.
8 × 0.03 =
Answer:
8 × 0.03 = 0.24
Explanation :
Equation : 8 × 0.03
Multiply without decimals = 8 × 3 = 24
0.03 have 2 decimal places, So, the answer will have 2 decimal places = 0.24
Question 36.
4 × 6 =
Answer:
4 × 6 = 24
Question 37.
0.6 × 7 =
Answer:
0.6 × 7 = 4.2
Explanation :
Equation : 0.6 × 7
Multiply without decimals = 6 × 7 = 42
0.6 have 1 decimal place, So, the answer will have 1 decimal place= 4.2
Question 38.
0.7 × 0.7 =
Answer:
0.7 × 0.7 = 0.49
Explanation :
Equation : 0.7 × 0.7
Multiply without decimals = 7 × 7 = 49
0.7 have 1 decimal place and another 0.7 have 1 decimal place So, the answer will have 2 decimal place = 0.49
Question 39.
0.8 × 0.06 =
Answer:
0.8 × 0.06 = 0.048
Explanation :
Equation : 0.8 × 0.06
Multiply without decimals = 8 × 6 = 48
0.8 will have 1 decimal place and 0.06 have 2 decimal places, So, the answer will have 3 decimal places = 0.048
Question 40.
0.09 × 0.6 =
Answer:
0.09 × 0.6 = 0.054
Explanation :
Equation : 0.09 × 0.6
Multiply without decimals = 9 × 6 = 54
0.09 have 2 decimal places and 0.6 will have 1 decimal place So, the answer will have 3 decimal places = 0.054
Question 41.
6 × 0.8 =
Answer:
6 × 0.8 = 4.8
Explanation :
Equation : 6 × 0.8
Multiply without decimals = 6 × 8 = 48
0.8 have 1 decimal place, So, the answer will have 1 decimal place = 4.8
Question 42.
0.7 × 0.9 =
Answer:
0.7 × 0.9 = 0.63
Explanation :
Equation : 0.7 × 0.9
Multiply without decimals = 7 × 9 = 63
0.7 have 1 decimal place and 0.9 have 1 decimal place, So, the answer will have 2 decimal places = 0.63
Question 43.
0.08 × 0.8 =
Answer:
0.08 × 0.8 = 0.064
Explanation :
Equation : 0.08 × 0.8
Multiply without decimals = 8 × 8 = 64
0.08 have 2 decimal place and 0.8 have 1 decimal place , So, the answer will have 3 decimal places = 0.064
Question 44.
0.9 × 0.08 =
Answer:
0.9 × 0.08 = 0.072
Explanation :
Equation : 0.9 × 0.08
Multiply without decimals = 9 × 8 = 72
0.9 have 1 decimal place and 0.08 have 2 decimal places, So, the answer will have 3 decimal places = 0.072
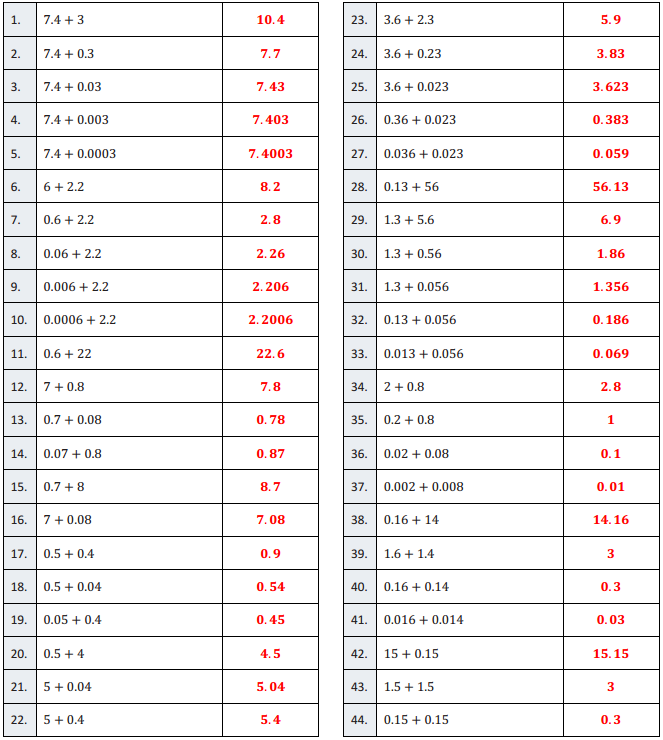
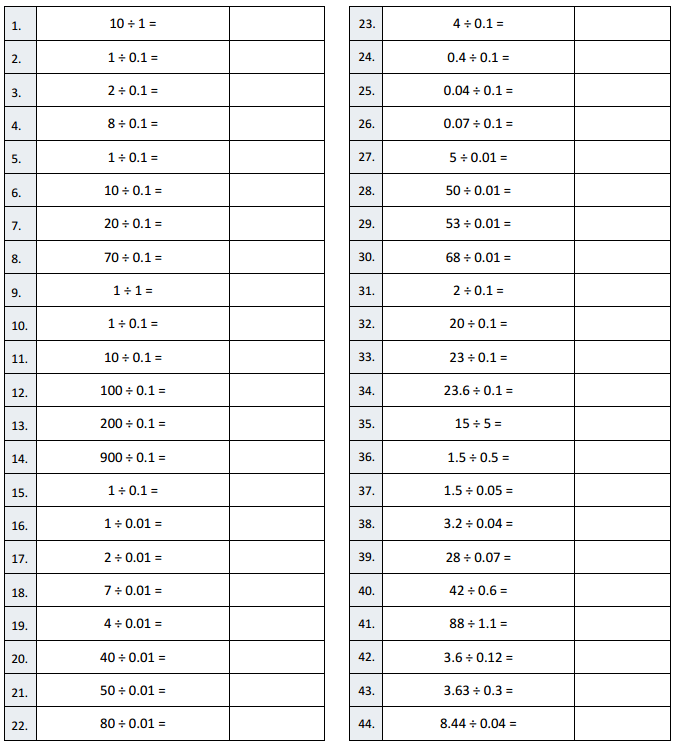
B
Multiply Decimals
Question 1.
4 × 2 =
Answer:
4 × 2 = 8
Question 2.
4 × 0.2 =
Answer:
4 × 0.2 = 0.8
Explanation :
Equation : 4 × 0.2
Multiply without decimals = 4× 2 = 8
0.2 have 1 decimal places, So, the answer will have 1 decimal place =0.8
Question 3.
4 × 0.02 =
Answer:
4 × 0.02 = 0.08
Explanation :
Equation : 4 × 0.02
Multiply without decimals = 4 × 2 = 8
0.02 have 2 decimal places, So, the answer will have 2 decimal places = 0.08
Question 4.
2 × 3 =
Answer:
2 × 3 = 6
Question 5.
2 × 0.3 =
Answer:
2 × 0.3 = 0.6
Explanation :
Equation : 2 × 0.3
Multiply without decimals = 2 × 3 = 6
0.3 have 1 decimal places, So, the answer will have 1 decimal place =0.6
Question 6.
2 × 0.03 =
Answer:
2 × 0.03 = 0.06
Explanation :
Equation : 2 × 0.03
Multiply without decimals = 2 × 3 = 6
0.03 have 2 decimal places, So, the answer will have 2 decimal places = 0.06
Question 7.
3 × 3 =
Answer:
3 × 3 = 9
Question 8.
3 × 0.3 =
Answer:
3 × 0.3 = 0.9
Explanation :
Equation : 3 × 0.3
Multiply without decimals = 3 × 3 = 9
0.3 have 1 decimal places, So, the answer will have 1 decimal place =0.9
Question 9.
3 × 0.03 =
Answer:
3 × 0.03 = 0.09
Explanation :
Equation : 3 × 0.03
Multiply without decimals = 3 × 3 = 9
0.03 have 2 decimal places, So, the answer will have 2 decimal places = 0.09
Question 10.
4 × 3 =
Answer:
4 × 3 = 12
Question 11.
4 × 0.3 =
Answer:
4 × 0.3 = 1.2
Explanation :
Equation : 4 × 0.3
Multiply without decimals = 4 × 3 = 12
0.3 have 1 decimal places, So, the answer will have 1 decimal place =1.2
Question 12.
4 × 0.03 =
Answer:
4 × 0.03 = 0.012
Explanation :
Equation : 4 × 0.03
Multiply without decimals = 4 × 3 = 12
0.03 have 2 decimal places, So, the answer will have 2 decimal places = 0.12
Question 13.
9 × 2 =
Answer:
9 × 2 = 18
Question 14.
9 × 0.2 =
Answer:
9 × 0.2 = 1.8
Explanation :
Equation : 9 × 0.2
Multiply without decimals = 9 × 2 = 18
0.2 have 1 decimal places, So, the answer will have 1 decimal place =1.8
Question 15.
9 × 0.02 =
Answer:
9 × 0.02 = 0.18
Explanation :
Equation : 9 × 0.02
Multiply without decimals = 9 × 2 = 18
0.02 have 2 decimal places, So, the answer will have 2 decimal places = 0.18
Question 16.
5 × 3 =
Answer:
5 × 3 = 15
Question 17.
5 × 0.3 =
Answer:
5 × 0.3 = 1.5
Explanation :
Equation : 5 × 0.3
Multiply without decimals = 5 × 3 = 15
0.3 have 1 decimal places, So, the answer will have 1 decimal place =1.5
Question 18.
0.5 × 3 =
Answer:
0.5 × 3 = 0.15
Explanation :
Equation : 0.5 × 3
Multiply without decimals = 5 × 3 = 15
0.5 have 1 decimal places, So, the answer will have 1 decimal place =0.15
Question 19.
0.5 × 0.3 =
Answer:
0.5 × 0.3 = 0.15
Explanation :
Equation : 0.5 × 0.3
Multiply without decimals = 5 × 3 = 15
0.5 have 1 decimal place and 0.3 have 1 decimal place, So, the answer will have 2 decimal places = 0.15
Question 20.
0.5 × 0.03 =
Answer:
0.5 × 0.03 = 0.015
Explanation :
Equation : 0.5 × 0.03
Multiply without decimals = 5 × 3 = 15
0.03 have 2 decimal place and 0.5 have 1 decimal place , So, the answer will have 3 decimal places = 0.015
Question 21.
0.3 × 0.05 =
Answer:
0.3 × 0.05 = 0.015
Explanation :
Equation : 0.3 × 0.05
Multiply without decimals = 5 × 3 = 15
0.05 have 2 decimal place and 0.3 have 1 decimal place , So, the answer will have 3 decimal places = 0.015
Question 22.
8 × 2 =
Answer:
8 × 2 = 16
Question 23.
0.8 × 2 =
Answer:
0.8 × 2 = 1.6
Explanation :
Equation : 0.8 × 2
Multiply without decimals = 8 × 2 = 16
0.8 have 1 decimal places, So, the answer will have 1 decimal place =1.6
Question 24.
0.8 × 0.2 =
Answer:
0.8 × 0.2 = 0.16
Explanation :
Equation : 0.8 × 0.2
Multiply without decimals = 8 × 2 = 16
0.8 have 1 decimal place and 0.2 have 1 decimal place, So, the answer will have 2 decimal places = 0.16
Question 25.
0.8 × 0.02 =
Answer:
0.8 × 0.02 = 0.016
Explanation :
Equation : 0.8 × 0.02
Multiply without decimals = 8 × 2 = 16
0.02 have 2 decimal place and 0.8 have 1 decimal place , So, the answer will have 3 decimal places = 0.016
Question 26.
0.2 × 0.08 =
Answer:
0.2 × 0.08 = 0.016
Explanation :
Equation : 0.2 × 0.08
Multiply without decimals = 2 × 8 = 16
0.08 have 2 decimal place and 0.2 have 1 decimal place , So, the answer will have 3 decimal places = 0.016
Question 27.
5 × 9 =
Answer:
5 × 9 = 45
Question 28.
0.5 × 9 =
Answer:
0.5 × 9 = 4.5
Explanation :
Equation : 0.5 × 9
Multiply without decimals = 5 × 9 = 45
0.5 have 1 decimal places, So, the answer will have 1 decimal place =4.5
Question 29.
0.5 × 0.9 =
Answer:
0.5 × 0.9 = 0.45
Explanation :
Equation : 0.5 × 0.9
Multiply without decimals = 5 × 9 = 45
0.5 have 1 decimal place and 0.9 have 1 decimal place, So, the answer will have 2 decimal places = 0.45
Question 30.
0.5 × 0.09 =
Answer:
0.5 × 0.09 = 0.045
Explanation :
Equation : 0.5 × 0.09
Multiply without decimals = 5 × 9 = 45
0.09 have 2 decimal place and 0.5 have 1 decimal place , So, the answer will have 3 decimal places = 0.045
Question 31.
0.9 × 0.05 =
Answer:
0.9 × 0.05 = 0.045
Explanation :
Equation : 0.9 × 0.05
Multiply without decimals = 9 × 5 = 0.045
0.05 have 2 decimal place and 0.9 have 1 decimal place , So, the answer will have 3 decimal places = 0.045
Question 32.
2 × 6 =
Answer:
2 × 6 = 12
Question 33.
7 × 0.2 =
Answer:
7 × 0.2 = 1.4
Explanation :
Equation : 7 × 0.2
Multiply without decimals = 7 × 2 = 14
0.2 have 1 decimal places, So, the answer will have 1 decimal place =1.4
Question 34.
3 × 8 =
Answer:
3 × 8 = 24
Question 35.
9 × 0.03 =
Answer:
9 × 0.03 = 0.27
Explanation :
Equation : 9 × 0.03
Multiply without decimals = 9 × 3 = 27
0.03 have 2 decimal places, So, the answer will have 2 decimal places = 0.27
Question 36.
4 × 8 =
Answer:
4 × 8 = 32
Question 37.
0.7 × 6 =
Answer:
0.7 × 6 = 4.2
Explanation :
Equation : 0.7 × 6
Multiply without decimals = 7 × 6 = 42
0.7 have 1 decimal places, So, the answer will have 1 decimal place =4.2
Question 38.
0.6 × 0.6 =
Answer:
0.6 × 0.6 = 0.36
Explanation :
Equation : 0.6 × 0.6
Multiply without decimals = 6 × 6 = 36
0.6 have 1 decimal place and another 0.6 have 1 decimal place, So, the answer will have 2 decimal places = 0.36
Question 39.
0.6 × 0.08 =
Answer:
0.6 × 0.08 = 0.048
Explanation :
Equation : 0.6 × 0.08
Multiply without decimals = 6 × 8 = 48
0.08 have 2 decimal place and 0.6 have 1 decimal place , So, the answer will have 3 decimal places = 0.048
Question 40.
0.06 × 0.9 =
Answer:
0.06 × 0.9 = 0.054
Explanation :
Equation : 00.06 × 0.9
Multiply without decimals = 6 × 9 = 54
0.06 have 2 decimal place and 0.8 have 1 decimal place , So, the answer will have 3 decimal places = 0.054
Question 41.
8 × 0.6 =
Answer:
8 × 0.6 = 4.8
Explanation :
Equation : 8 × 0.6
Multiply without decimals = 8 × 6 = 42
0.6 have 1 decimal places, So, the answer will have 1 decimal place =4.2
Question 42.
0.9 × 0.7 =
Answer:
0.9 × 0.7 = 0.63
Explanation :
Equation : 0.9 × 0.7
Multiply without decimals = 9 × 7 = 63
0.7 have 1 decimal place and 0.9 have 1 decimal place, So, the answer will have 2 decimal places = 0.63
Question 43.
0.07 × 0.7 =
Answer:
0.07 × 0.7 = 0.049
Explanation :
Equation : 0.07 × 0.7
Multiply without decimals = 7 × 7 = 49
0.07 have 2 decimal place and 0.7 have 1 decimal place , So, the answer will have 3 decimal places = 0.049
Question 44.
0.8 × 0.09 =
Answer:
0.8 × 0.09 = 0.072
Explanation :
Equation : 0.8 × 0.09
Multiply without decimals = 8 × 9 = 72
0.09 have 2 decimal place and 0.8 have 1 decimal place , So, the answer will have 3 decimal places = 0.072
Eureka Math Grade 5 Module 6 Lesson 29 Reflection Answer Key
It is said that the true measure of knowing something is being able to teach it to someone else. Who can you teach these terms to this summer? How will you teach these terms to your summer student?
Answer:
Eureka Math Grade 5 Module 6 Lesson 29 Homework Answer Key
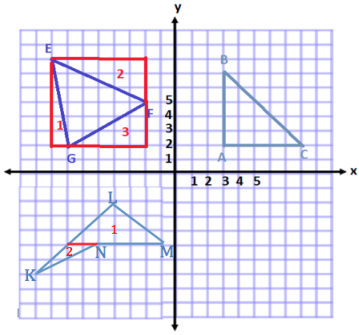
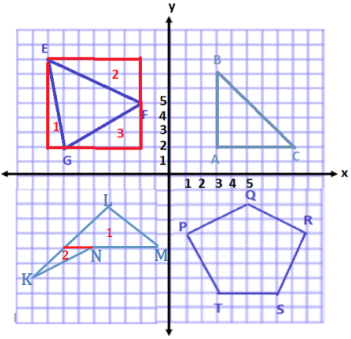
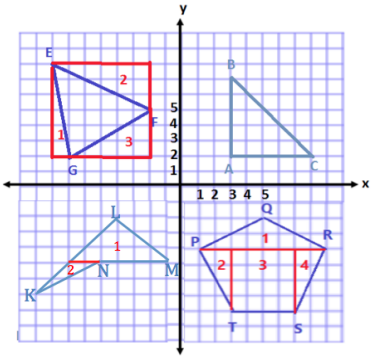
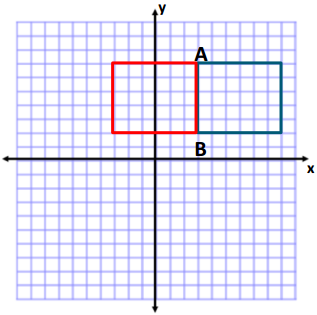
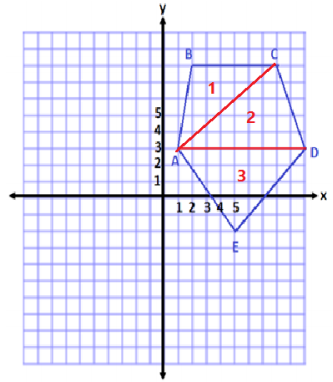
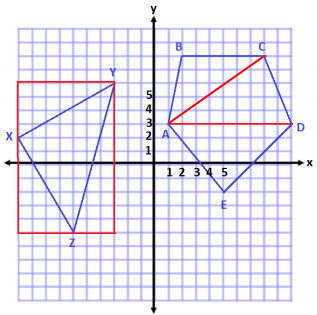
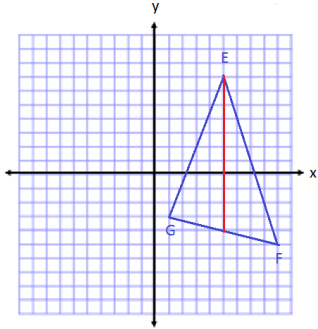
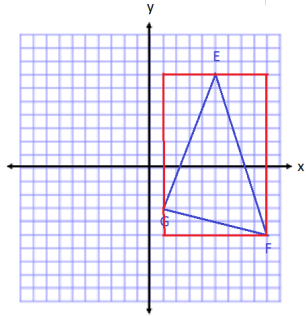
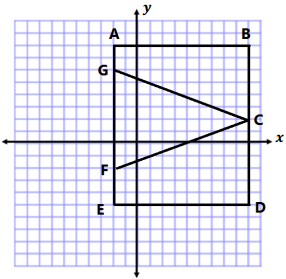
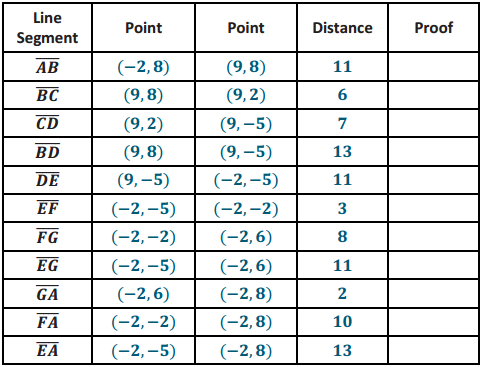
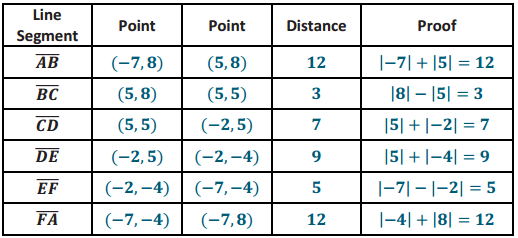
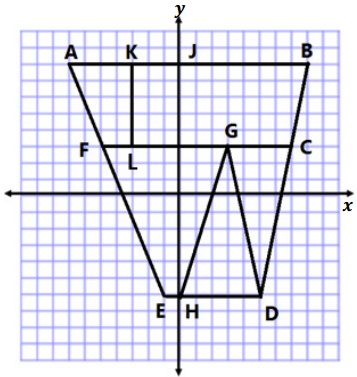
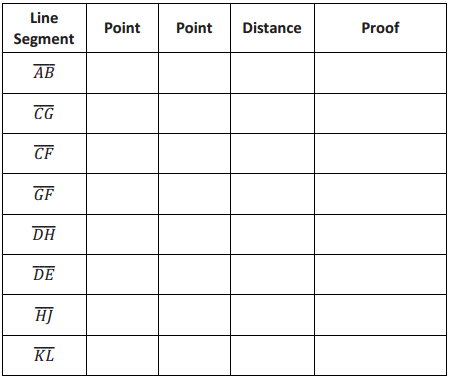
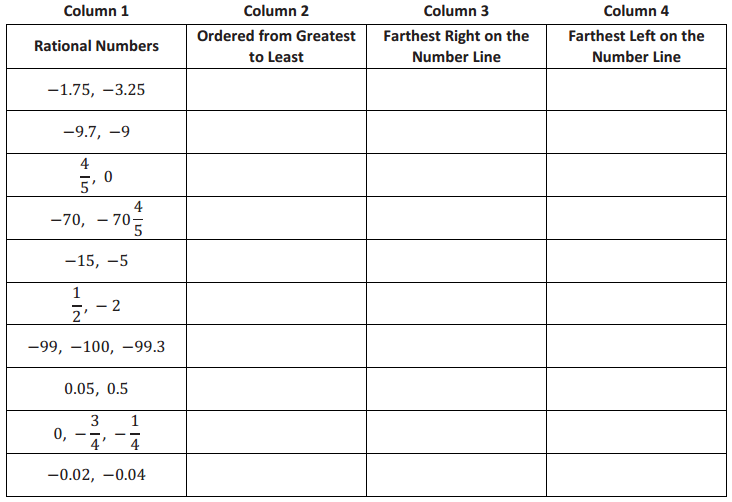
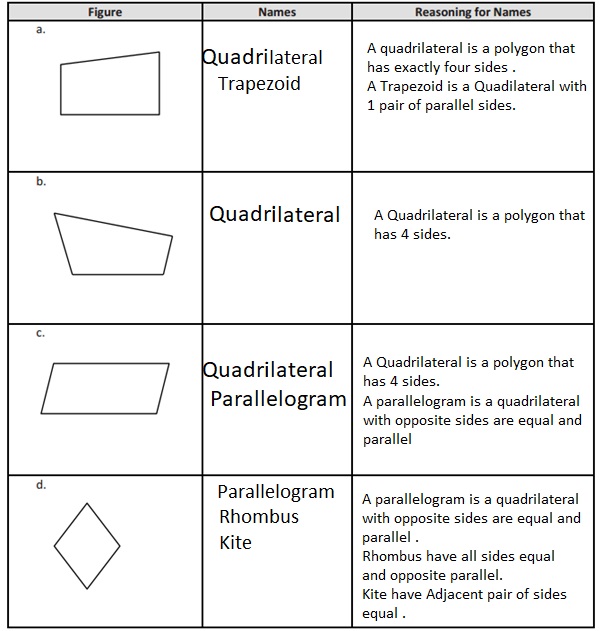
Question 1.
Use your ruler, protractor, and set square to help you give as many names as possible for each figure below. Then, explain your reasoning for how you named each figure.

Answer:
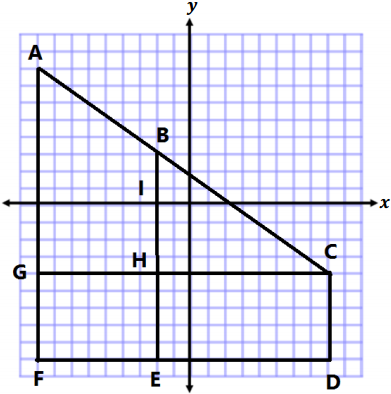
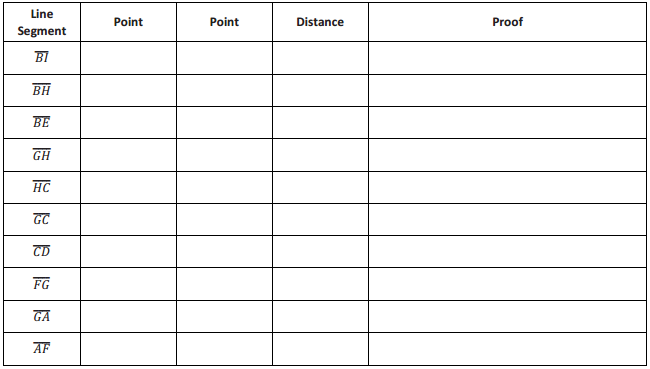
Question 2.
Mark draws a figure that has the following characteristics:
- Exactly 4 sides that are each 7 centimeters long.
- Two sets of parallel lines.
- Exactly 4 angles that measure 35 degrees, 145 degrees, 35 degrees, and 145 degrees.
a. Draw and label Mark’s figure below.
b. Give as many names of quadrilaterals as possible for Mark’s figure. Explain your reasoning for the names of Mark’s figure.
c. List the names of Mark’s figure in Problem 2(b) in order from least specific to most specific. Explain your thinking.
Answer:
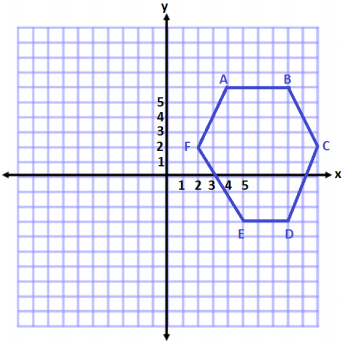
a. The Quadrilateral ABCD is drawn in which opposite angles are equal and all sides are equal .
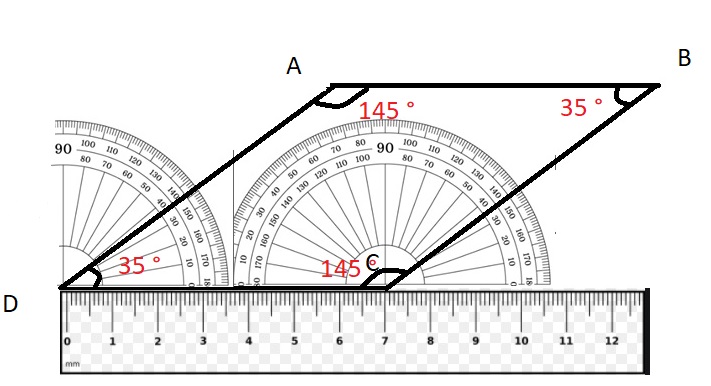
b.
The different names for Above Quadrilateral are ABCD.
It is a parallelogram because A parallelogram is a quadrilateral with opposite sides are equal and parallel
It is a Rhombus because Rhombus have all sides equal and opposite are parallel.
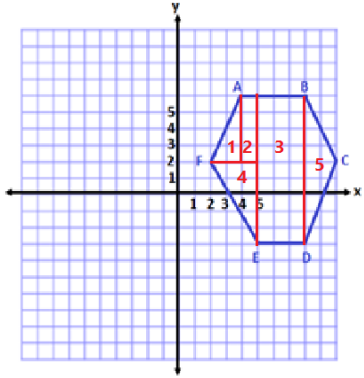
c.
Parallelogram have opposite sides equal and parallel . It also contains opposite angles equal .
It is a Rhombus because rhombus have all sides equal and opposite angles are equal.
Rhombus is more specific because all the properties given are same as rhombus .