Prasanna

Engage NY Eureka Math 4th Grade Module 3 Lesson 10 Answer Key

Eureka Math Grade 4 Module 3 Lesson 10 Problem Set Answer Key

Question 1.
Solve using the standard algorithm.
a. 3 × 42
Answer:
42
X 3
126
3 X 42 = 126,

Explanation:
In standard algorithm we add same time of multiplying as
42
X 3
126 ,here 3 X 2 ones = 6 ones then 3 X 4 tens = 12 tens
we write 2 at tens place and write 1 at hundred place,
So 3 X 42 = 126 as shown above.

b. 6 × 42
Answer:
1
42
X 6
252
6 X 42 = 252,

Explanation:
In standard algorithm we add same time of multiplying as
1
42
X 6
252 ,here 6 X 2 ones = 12 ones we write 2 at ones place and
1 at tens places then 6 x 4 tens = 24 tens, 24 tens +1 ten =
25 tens we write 5 at tens place and write 2 at hundred place,
So 6 X 42 = 252 as shown above.

c. 6 × 431
Answer:
1
431
X 6
2,586
6 X 42 = 2,586,

Explanation:
In standard algorithm we add same time of multiplying as
1
431
X 6
2,586 ,here 6 X 1 ones = 6 ones then 6 X 3 tens = 18 tens,
we write 8 at tens place and write 1 at hundreds place,
6 X 4 hundreds = 24 hundreds, 24 hundreds + 1 hundred =
25 hundreds we write 25 hundreds as 5 at hundreds place and
2 at thousands place, So 6 X 431 = 2,586 as shown above.

d. 3 × 431
Answer:
431
X 3
1,293
3 X 431 = 1,293,

Explanation:
In standard algorithm we add same time of multiplying as
431
X 3
1,293 ,here 3 X 1 ones = 3 ones then 3 X 3 tens = 9 tens,
we write 9 at tens place and 3 X 4 hundreds = 12 hundreds,
we write 12 hundreds as 2 at hundreds place and 1 at
thousands place, So 3 X 431 = 1,293 as shown above.

e. 3 × 6,212
Answer:
6,212
X 3
18,636
3 X 6,212 = 18,636,

Explanation:
In standard algorithm we add same time of multiplying as
6,212
X 3
18,636 ,here 3 X 2 ones = 6 ones then 3 X 1 ten = 3 tens,
we write 3 at tens place, 3 X 2 hundreds = 6 hundreds,
3 X 6 thousands = 18 thousands we write 18 thousands as
8 at thousands place and 1 at ten thousands place,
So 3 X 6,212 = 18,636 as shown above.

f. 3 × 3,106
Answer:
1
3,106
X 3
9,318
3 X 3,106 = 9,318,

Explanation:
In standard algorithm we add same time of multiplying as
1
3,106
X 3   
9,318 ,
here 3 X 6 ones = 18 ones we write 8 at ones place and
1 at tens places then 3 X 0 tens = 0 tens, 0 tens + 1 ten = 1 ten
at ten place, 3 X 1 hundred = 3 hundreds
we write 3 at hundreds place and 3 X 3 thousands =
9 thousands we write 9 at thousands place,
So 3 X 3,106 = 9,318 as shown above.

g. 4 × 4,309
Answer:
1,3
4,309
X 4
17,236
4 X 4,309 = 17,236,

Explanation:
In standard algorithm we add same time of multiplying as
1,3
4,309
X 4   
17,236 ,here 4 X 9 ones = 36 ones we write 6 at ones place and
3 at tens places then 4 X 0 tens = 0 tens, 0 tens + 3 tens = 3 tens
at ten place, 4 X 3 hundreds = 12 hundreds
we write 12 hundreds as 2 at hundreds place and 1 at
thousands place, 4 X 4 thousands = 16 thousands,
16 thousands + 1 thousand = 17 thousands we write 7 at
thousands place and 1 at ten thousands place,
So 4 X 4,309 = 17,236 as shown above.

h. 4 × 8,618
Answer:
2,3
8,618
X 4
34,472
4 X 8,618 = 34,472,

Explanation:
In standard algorithm we add same time of multiplying as
2,3
8,618
X 4   
34,472 ,here 4 X 8 ones = 32 ones we write 2 at ones place and
3 at tens places then 4 X 1 ten = 4 tens, 4 tens + 3 tens = 7 tens
at ten place, 4 X 6 hundreds = 24 hundreds
we write 24 hundreds as 4 at hundreds place and 2 at
thousands place, 4 X 8 thousands = 32 thousands,
32 thousands + 2 thousands = 34 thousands we write 4 at
thousands place and 3 at ten thousands place,
So 4 X 8,618 = 34,472 as shown above.

Question 2.
There are 365 days in a common year. How many days
are in 3 common years?
Answer:
There are 1,095 days in 3 common years,

Explanation:
Given there are 365 days in a common year.
So number of days in 3 common years are 3 X 365 days =
1
365
X 3
1,095
here 3 X 5 ones = 15 ones we write 1 at ones place and
5 at tens places then 3 X 6 tens = 18 tens,
we write 8 at ten place and 1 at hundreds place and
3 X 3 hundreds = 9 hundreds, 9 hundreds + 1 hundered =
10 hundereds we write 10 hundreds as 0 at hundreds place and
1 at thousands place, So 3 X 365 = 1,095.
therefore, there are 1,095 days in 3 common years.

Question 3.
The length of one side of a square city block is 462 meters.
What is the perimeter of the block?
Answer:
The perimeter of the block is 1,848 meters,

Explanation:
Given the length of one side of a square city block is 462 meters,
So the perimeter of the block is as we know perimeter of the
square is 4 X length, So 4 X 462 meters =
2
462
X 4
1,848
here first we write 4 X 2 ones = 8 ones, 4 X 6 tens = 24 tens we
write 4 at tens place and 2 at hundreds place and
4 X 4 hundreds = 16 hundreds, 16 hundreds + 2 hundreds =
18 hundreds we write 8 at hundreds place and 1 at thousands
place so 4 X 462 = 1,848. Therefore the perimeter of
the square block is 1,848 meters.

Question 4.
Jake ran 2 miles. Jesse ran 4 times as far. There are 5,280 feet
in a mile. How many feet did Jesse run?
Answer:
Jesse ran 42,240 feet,

Explanation:
Given Jake ran 2 miles. Jesse ran 4 times as far.
There are 5,280 feet in a mile. So Jesse ran 4 X 2 = 8 miles,
8 miles X 5,280 feet =
  2,6
5,280
X 8
42,240
here 8 X 0 ones = 0 ones we write 0 at ones place
then 8 X 8 tens = 64 tens, 4 at ten place, 6 at hundreds
place, 8 X 2 hundreds = 16 hundreds, 16 hundreds + 6 hundreds =
22 hundreds we write 22 hundreds as 2 at hundreds place and
2 at thousands place, 8 X 5 thousands = 40 thousands,
40 thousands + 2 thousands = 42 thousands we write 2 at
thousands place and 4 at ten thousands place, So 8 X 5,280 =
42,240, therefore Jesse ran 42,240 feet.

Eureka Math Grade 4 Module 3 Lesson 10 Exit Ticket Answer Key

Question 1.
Solve using the standard algorithm.
a. 2,348 × 6
Answer:
2,2,4
2,348
X 6
14,088
6 X 2,348 = 14,088,

Explanation:
In standard algorithm we add same time of multiplying as
2,2,4
2,348
X 6   
14,088 ,here 6 X 8 ones = 48 ones we write 8 at ones place and
4 at tens places then 6 X 4 tens = 24 tens, 24 tens + 4 tens = 28 tens,
8 at tens place and 2 at hundreds place, 6 X 3 hundreds =
18 hundreds, 18 hundreds + 2 hundreds = 20 hundreds,
we write 20 hundreds as 0 at hundreds place and 2 at
thousands place, 6 X 2 thousands = 12 thousands,
12 thousands + 2 thousands = 14 thousands we write 4 at
thousands place and 1 at ten thousands place,
So 6 X 2,348 = 14,088 as shown above.

b. 1,679 × 7
Answer:
4,5,6
1,679
X 7
11,753
1,679 X 7 = 11,753,

Explanation:
In standard algorithm we add same time of multiplying as
4,5,6
1,679
X 7   
11,753 ,here 7 X 9 ones = 63 ones we write 3 at ones place and
6 at tens places then 7 X 7 tens = 49 tens, 49 tens + 6 tens = 55 tens,
5 at tens place and 5 at hundreds place, 7 X 6 hundreds =
42 hundreds, 42 hundreds + 5 hundreds = 47 hundreds,
we write 47 hundreds as 7 at hundreds place and 4 at
thousands place, 7 X 1 thousands = 7 thousands,
7 thousands + 4 thousands = 11 thousands we write 1 at
thousands place and 1 at ten thousands place,
So 7 X 1,679 = 11,753 as shown above.

Question 2.
A farmer planted 4 rows of sunflowers. There were 1,205 plants
in each row. How many sunflowers did he plant?
Answer:
Number of sunflowers planted are 4,820,

Explanation:
Given a farmer planted 4 rows of sunflowers.
There were 1,205 plants in each row. So number of
sunflowers did he planted are 4 X 1,205 =
     2
1,205
X 4
4,820
here 5 X 4 ones = 20 ones we write 0 at ones place and
2 at tens places then 4 X 0 tens = 0 tens, 0 tens + 2 tens = 2 tens,
2 at tens place, 4 X 2 hundreds = 8 hundreds,
we write 8 hundreds at hundreds place and
4 X 1 thousands = 4 thousands, 4 at thousands place,
So 4 X 1,205 = 4,820, therefore number of sunflowers
planted are 4,820.

Eureka Math Grade 4 Module 3 Lesson 10 Homework Answer Key

Question 1.
Solve using the standard algorithm.
a. 3 × 41
Answer:
41
X 3
123
3 X 41 = 123,

Explanation:
In standard algorithm we add same time of multiplying as
41
X 3
123 ,here 3 X 1 one = 3 ones then 3 X 4 tens = 12 tens
we write 2 at tens place and write 1 at hundred place,
So 3 X 41 = 123 as shown above.

b. 9 × 41
Answer:
41
X 9
369
9 X 41 = 369,

Explanation:
In standard algorithm we add same time of multiplying as
41
X 9
369 ,here 9 X 1 one = 9 ones we write 9 at ones place
then 9 x 4 tens = 36 tens, we write 6 at tens place and
write 3 at hundred place,
So 9 X 41 = 369 as shown above.

c. 7 × 143
Answer:
3,2
143
X 7
1,001
7 X 143 = 1,001,

Explanation:
In standard algorithm we add same time of multiplying as
3,2
143
X 7
1,001 ,here 7 X 3 ones = 21 ones we write 1 at ones place and
2 at tens places then 7 x 4 tens = 28 tens, 28 tens +2 tens =
30 tens we write 0 at tens place and write 3 at hundreds place,
Now 7 X 1 hundred = 7 hundreds, 7 hundreds + 3 hundreds =
10 hundreds we write 0 at hundreds place and 1 at
thousands places, So 7 X 143 = 1,001 as shown above.

d. 7 × 286
Answer:
6,4
286
X 7
2,002
7 X 286 = 2,002,

Explanation:
In standard algorithm we add same time of multiplying as
6,4
286
X 7
2,002 ,here 7 X 6 ones = 42 ones we write 2 at ones place and
4 at tens places then 7 x 8 tens = 56 tens, 56 tens +4 tens =
60 tens we write 0 at tens place and write 6 at hundreds place,
Now 7 X 2 hundreds = 14 hundreds, 14 hundreds + 6 hundreds =
20 hundreds we write 0 at hundreds place and 2 at
thousands places, So 7 X 286 = 2,002 as shown above.

e. 4 × 2,048
Answer:
1,3
2,048
X 4
8,192
4 X 2,048 = 8,192,

Explanation:
In standard algorithm we add same time of multiplying as
1,3
2,048
X 4
8,192 ,here 4 X 8 ones = 32 ones, we write 2 at ones place,
3 at tens place then 4 X 4 tens = 16 tens, 16 tens + 3 tens =
19 tens we write 9 at tens place, 1 at hundreds place,
4 X 0 hundreds = 0 hundreds, 0 hundreds +1 hundred =
1 hundred, 4 X 2 thousands = 8 thousands we write 8 at
thousands place, So 4 X 2,048 = 8,192 as shown above.

f. 4 × 4,096
Answer:
3,2
4,096
X 4
16,384
4 X 4,096 = 16,384,

Explanation:
In standard algorithm we add same time of multiplying as
3,2
4,096
X 4
16,384 ,here 4 X 6 ones = 24 ones, we write 4 at ones place,
2 at tens place then 4 X 9 tens = 36 tens, 36 tens + 2 tens =
38 tens we write 8 at tens place, 3 at hundreds place,
4 X 0 hundreds = 0 hundreds, 0 hundreds +3 hundreds =
3 hundreds at hundreds place, 4 X 4 thousands =
16 thousands we write 6 at thousands place and
1 at ten thousands place,
So 4 X 4,096 = 16,384 as shown above.

g. 8 × 4,096
Answer:
7,4
4,096
X 8
32,768
8 X 4,096 = 32,768,

Explanation:
In standard algorithm we add same time of multiplying as
7,4
4,096
X 8
32,768 ,here 8 X 6 ones = 48 ones, we write 8 at ones place,
4 at tens place then 8 X 9 tens = 72 tens, 72 tens + 4 tens =
76 tens we write 6 at tens place, 7 at hundreds place,
8 X 0 hundreds = 0 hundreds, 0 hundreds +7 hundreds =
7 hundreds at hundreds place, 8 X 4 thousands =
32 thousands we write 2 at thousands place and
3 at ten thousands place,
So 8 X 4,096 = 32,768 as shown above.

h. 4 × 8,192
Answer:
3
8,192
X   4
32,768
4 X 8,192 = 32,768,

Explanation:
In standard algorithm we add same time of multiplying as
3
8,192
X 4
32,768 ,here 4 X 2 ones = 8 ones, we write 8 at ones place
then 4 X 9 tens = 36 tens we write 6 at tens place,
3 at hundreds place, 4 X 1 hundred = 4 hundreds,
4 hundreds +3 hundreds = 7 hundreds at hundreds place,
4 X 8 thousands = 32 thousands we write 2 at thousands place and
3 at ten thousands place, So 4 X 8,192 = 32,768 as shown above.

Question 2.
Robert’s family brings six gallons of water for
the players on the football team. If one gallon of
water contains 128 fluid ounces,
how many fluid ounces are in six gallons?
Answer:
There are 768 fluid ounces in six gallons,

Explanation:
Given Robert’s family brings six gallons of water for
the players on the football team. If one gallon of
water contains 128 fluid ounces, Number of fluid ounces
are in six gallons are 6 X 128 fluid ounces =
1,4
128
X 6
768 , here 6 X 8 ones = 48 ones we write 8 at ones place,
4 at tens place then 6 x 2 tens = 12 tens, 12 tens + 4 tens =
16 tens we write 6 at tens place and write 1 at hundreds place,
6 X 1 hundred = 6 hundreds, 6 hundreds + 1 hundred =
7 hundreds, So 6 X 128 = 768,
therefore there are 768 fluid ounces in six gallons.

Question 3.
It takes 687 Earth days for the planet Mars to revolve
around the sun once. How many Earth days does it take
Mars to revolve around the sun four times?
Answer:
It will take 2,748 Earth daysfor Mars to revolve
around the sun four times,

Explanation:
Given It takes 687 Earth days for the planet Mars to revolve
around the sun once. So Earth days does it take
Mars to revolve around the sun four times is
4 X 687 Earth days =
3,2
687
X 4
2,748
here 4 X 7 ones = 28 ones, we write 8 at ones place,
2 at tens place then 4 X 8 tens = 32 tens, 32 tens + 2 tens =
34 tens we write 4 at tens place, 3 at hundreds place,
4 X 6 hundreds = 24 hundreds, 24 hundreds +3 hundreds =
27 hundreds, 7 at hundreds place, 2 at thousands place
So 4 X 687 = 2,748 as shown above, therefore, it will take
2,748 Earth daysfor Mars to revolve around the sun four times.

Question 4.
Tammy buys a 4-gigabyte memory card for her camera.
Dijonea buys a memory card with twice as much storage as Tammy’s.
One gigabyte is 1,024 megabytes. How many megabytes
of storage does Dijonea have on her memory card?
Answer:
8,192 megabytes of storage does Dijonea
have on her memory card,

Explanation:
Given Tammy buys a 4-gigabyte memory card for her camera.
Dijonea buys a memory card with twice as much storage as Tammy’s.
One gigabyte is 1,024 megabytes. Dijonea has storage of
2 X 4 – gigabyte = 8 gigabyte memory card now Dijonea has
number of megabytes of storage is 8 X 1,024 megabytes =
1,3
1,024
X 8
8,192
here 8 X 4 ones = 32 ones, we write 2 at ones place,
3 at tens place then 8 X 2 tens = 16 tens, 16 tens + 3 tens =
19 tens we write 9 at tens place, 1 at hundreds place,
8 X 0 hundreds = 0 hundreds, 0 hundreds + 1 hundred =
1 hundred, 1 at hundreds place, 8 X 1 thousand =
8 thousand, 8 at thousands place, So 8 X 1,024 =
8,192 as shown above, therefore, 8,192 megabytes of
storage does Dijonea have on her memory card.

Engage NY Eureka Math 4th Grade Module 3 Lesson 8 Answer Key

Eureka Math Grade 4 Module 3 Lesson 8 Problem Set Answer Key

Question 1.
Represent the following expressions with disks,
regrouping as necessary, writing a matching expression, and
recording the partial products vertically as shown below.
a. 1 × 213

1 × _2__ hundreds + 1 × _1__ ten + 1 × _3__ ones

Answer:

Explanation:
Represented the following expression 1 X 213 with disks,
regrouped as necessary. Wrote a matching expression 1 X 213 = 213
and recorded the partial products vertically as shown above.

b. 2 × 213

Answer:

Explanation:
Represented the following expression 2 X 213 with disks,
regrouped as necessary. Wrote a matching expression 2 X 213 = 426
and recorded the partial products vertically as shown above.

c. 3 × 214

Answer:

Explanation:
Represented the following expression 3 X 214 with disks,
regrouped as necessary. Wrote a matching expression 3 X 214 = 642
and recorded the partial products vertically as shown above.

d. 3 × 1,254

Answer:

Explanation:
Represented the following expression 3 X 1,254 with disks,
regrouped as necessary. Wrote a matching expression 3 X 1,254 = 3,762
and recorded the partial products vertically as shown above.

Question 2.
Represent the following expressions with disks,
using either method shown during class, regrouping as necessary.
To the right, record the partial products vertically.
a. 3 × 212
Answer:

Explanation:
Represented the following expression 3 X 212 with disks,
regrouped as necessary and recorded the partial products
vertically as shown above.

b. 2 × 4,036
Answer:

Explanation:
Represented the following expression 2 X 4,036 = 8,072 with disks,
regrouped as necessary and recorded the partial products
vertically as shown above.

c. 3 × 2,546
Answer:

Explanation:
Represented the following expression 3 X 2,546 = 7,638 with disks,
regrouped as necessary and recorded the partial products
vertically as shown above.

d. 3 × 1,407
Answer:
Explanation:
Represented the following expression 3 X 1,407 = 4,221 with disks,
regrouped as necessary and recorded the partial products
vertically as shown above.

Question 3.
Every day at the bagel factory, Cyndi makes 5 different
kinds of bagels. If she makes 144 of each kind,
what is the total number of bagels that she makes?
Answer:
Total number of bagels Cyndi makes are 720 every day,

Explanation:
Given every day at the bagel factory, Cyndi makes 5 different
kinds of bagels. If she makes 144 of each kind,
The total number of bagels Cyndi makes are
5 X 144 = 720 every day.

Eureka Math Grade 4 Module 3 Lesson 8 Exit Ticket Answer Key

Represent the following expressions with disks, regrouping as necessary. To the right, record the partial products vertically.

Question 1.
4 × 513
Answer:

Explanation:
Represented the following expression 4 X 513 = 2,052 with disks,
regrouped as necessary and recorded the partial products
vertically as shown above.

Question 2.
3 × 1,054
Answer:

Explanation:
Represented the following expression 3 X 1,054 = 3,162 with disks,
regrouped as necessary and recorded the partial products
vertically as shown above.

Eureka Math Grade 4 Module 3 Lesson 8 Homework Answer Key

Question 1.
Represent the following expressions with disks, regrouping as necessary, writing a matching expression, and recording the partial products vertically as shown below.
a. 2 × 424

2 × ___ ________ + 2 × ___ _____ + 2 × ___ ones

Answer:

Explanation:
Represented the following expression 2 X 424 with disks,
regrouped as necessary. Wrote a matching expression 2 X 424 = 848
and recorded the partial products vertically as shown above.

b. 3 × 424

Answer:

Explanation:
Represented the following expression 3 X 424 with disks,
regrouped as necessary. Wrote a matching expression 3 X 424 = 1,272
and recorded the partial products vertically as shown above.

c. 4 × 1,424
Answer:

Explanation:
Represented the following expression 4 X 1,424 with disks,
regrouped as necessary. Wrote a matching expression 4 X 1,424 = 5,696
and recorded the partial products vertically as shown above.

Question 2.
Represent the following expressions with disks, using either
method shown in class, regrouping as necessary.
To the right, record the partial products vertically.
a. 2 × 617
Answer:

Explanation:
Represented the following expression 2 X 617 with disks,
regrouped as necessary. Wrote a matching expression 2 X 617 = 1,234
and recorded the partial products vertically as shown above.

b. 5 × 642
Answer:

Explanation:
Represented the following expression 5 X 642 with disks,
regrouped as necessary. Wrote a matching expression 5 X 642 = 3,210
and recorded the partial products vertically as shown above.

c. 3 × 3,034
Answer:

Explanation:
Represented the following expression 3 X 3,034 with disks,
regrouped as necessary. Wrote a matching expression 3 X 3,034 = 9,102
and recorded the partial products vertically as shown above.

Question 3.
Every day, Penelope jogs three laps around the playground
to keep in shape. The playground is rectangular with a
width of 163 m and a length of 320 m.
a. Find the total amount of meters in one lap.
Answer:
The total amount of meters in one lap is 52,160 square meters,

Explanation:
Given the playground is rectangular with a
width of 163 m and a length of 320 m, So the
total area of the playground is 163 m X 320 m =
52,160 square meters.Therefore the total amount of meters
in one lap is 52,160 square meters penelope jogs.

b. Determine how many meters Penelope jogs in three laps.
Answer:
Penelope jogs 1,56,480 square meters in three laps,

Explanation:
Given every day, Penelope jogs three laps around the
playground to keep in shape. The playground is rectangular
with a width of 163 m and a length of 320 m, so total area
of the rectangular playground is 163 m X 320 m =
52,160 square meters, Now for 3 laps it is 3 X 52,160 sq mt =
1,56,480 square meters.

Engage NY Eureka Math 4th Grade Module 3 Lesson 9 Answer Key

Eureka Math Grade 4 Module 3 Lesson 9 Problem Set Answer Key

Question 1.
Solve using each method.

Answer:

Explanation:
Given expression as 4 X 34 =
Partial Products
34
X 4
  16
+120
136 , Here we first write multiplication of 4 X 4 ones, then
4 X 3 tens then add as shown above 16 + 120 = 136,
In standard algorithm we add same time of multiplying as
1
34
X 4
136 ,here 4 X 4 ones= 16 ones we write 6 at ones place and take 1
at tens place then 4 x 3 at tens place = 12 tens
add 1 ten to 12 tens we get 13 tens so 4 X 34 = 136.

Answer:

Explanation:
Given expression as 3 X 224 =
Partial Products
224
X 3
  12
60
+600
672 , Here we first write multiplication of 3 X 4 ones, then
3 X 2 tens and 3 X 2 hundreds then add as shown above
12 + 60 + 600 = 672,
In standard algorithm we add same time of multiplying as
1
224
X 3
672 ,here 3 X 4 ones = 12 ones we write 2 at ones place and
take 1 at tens place then 3 x 2 tens = 6 tens add 1 ten to 6 tens
we get 7 tens and 3 X 2 hundreds = 6 hundreds,  so 4 X 244 = 672.

Question 2.
Solve. Use the standard algorithm.
a.

Answer:

   7     5     3      

Explanation:
In standard algorithm we add same time of multiplying as
1
251
X 3
753 ,here 3 X 1 ones = 3 ones then 3 x 5 tens = 15 tens
we write 5 at tens place and take 1 to hundred place and
3 X 2 hundreds = 6 hundreds, now adding 1 hundred to
6 hundreds we get 7 hundreds , so 3 X 251 = 753.

b.

Answer:

  8      1      0

Explanation:
In standard algorithm we add same time of multiplying as
1, 3
135
X 6
810 ,here 6 X 5 ones = 30 ones, we write 0 at ones place and
take 3 to tens places then 6 x 3 tens = 18 tens + 3 tens = 21 tens,
we write 1 at tens place and take 2 to hundred place and
6 X 1 hundred = 6 hundreds, now adding 2 hundreds to
6 hundreds we get 8 hundreds , so 6 X 135 = 810.

c.

Answer:

2,   7   3   6

Explanation:
In standard algorithm we add same time of multiplying as
 3
304
X 9
2,736 ,here 9 X 4 ones = 36 ones, we write 6 at ones place and
take 3 to tens places then 9 x 0 ten = 0 ten + 3 tens = 3 tens,
9 X 3 hundreds = 27 hundreds, now we write 7 at hundreds place
and 2 at thousands place as shown above, So 9 X 304 = 2,736.    

d.

Answer:

1,  6    2   0

Explanation:
In standard algorithm we add same time of multiplying as
2
405
X 4
1,620 ,here 4 X 5 ones = 20 ones, we write 0 at ones place and
take 2 to tens places then 4 x 0 ten = 0 ten + 2 tens = 2 tens,
4 X 4 hundreds = 16 hundreds, now we write 6 at hundreds place
and 1 at thousand place as shown above, So 4 X 405 = 1,620.

e.

Answer:

1,  5    8   0

Explanation:
In standard algorithm we add same time of multiplying as
3
316
X 5
1,580 ,here 5 X 6 ones = 30 ones, we write 0 at ones place and
take 3 to tens places then 5 x 1 ten = 5 tens + 3 tens = 8 tens,
5 X 3 hundreds = 15 hundreds, now we write 5 at hundreds place
and 1 at thousand place as shown above, So 5 X 316 = 1,580.

f.

Answer:

2,  3   5    2

Explanation:
In standard algorithm we add same time of multiplying as
5,1
392
X 6
2,352 ,here 6 X 2 ones = 12 ones, we write 2 at ones place and
take 1 to tens places then 6 x 9 tens = 54 tens + 1 tens = 55 tens,
we write 5 at tens place and take another 5 to hundreds place,
6 X 3 hundreds = 18 hundreds,18 hundreds + 5 hundreds =
23 hundreds now we write 3 at hundreds place
and 2 at thousands place as shown above, So 6 X 392 = 2,352.

Question 3.
The product of 7 and 86 is ________.
Answer:
The product of 7 and 86 is 602,

Explanation:
Give to find the product of 7 and 86 is
4
86
X 7
602
first we multiply 7 with 6 ones = 42 ones we write 2 at ones
place and take 4 to tens place now 7 X 8 = 56 tens adding
4 tens we get 60 tens, So 7 X 86 = 602.

Question 4.
9 times as many as 457 is _________.
Answer:
9 times as many as 457 is 4,113,

Explanation:
Given to find 9 times as many as 457 is
6
457
X 9
4,113 ,here 9 X 7 ones = 63 ones, we write 3 at ones place and
take 6 to tens places then 9 x 5 tens = 45 tens + 6 tens = 51 tens,
we write 1 at tens place and take 5 to hundreds place,
9 X 4 hundreds = 36 hundreds, 36 hundreds + 5 hundreds =
41 hundreds now we write 1 at hundred place
and 4 at thousands place as shown above, So 9 X 457 = 4,113.

Question 5.
Jashawn wants to make 5 airplane propellers. He needs
18 centimeters of wood for each propeller. How many
centimeters of wood will he use?

Answer:
Jashawn needs 90 centimeters of wood to make
5 airplane propellers,

Explanation:
Given Jashawn wants to make 5 airplane propellers.
He needs 18 centimeters of wood for each propeller.
So number of centimeters of wood will he use is 5 X 18 cms =
4
18
X 5
90
here first we multiply 5 X 8 ones = 40 ones, we write 0
at ones place and take 4 to tens place then 5 X 1 ten =
5 tens+ 4 tens = 9 tens, So 5 X 18 = 90 centimeters,
therefore, Jashawn needs 90 centimeters of wood to make
5 airplane propellers.

Question 6.
One game system costs $238. How much will 4 game
systems cost?
Answer:
4 game systems will cost $952,

Explanation:
Given one game system costs $238. So for 4 game
systems it will cost 4 X $238 =
 1, 3
$238
X  4
952
here first we multiply 4 X 8 ones = 32 ones,
we write 2 at ones place and take 3 to tens places
then 4 x 3 tens = 12 tens + 3 tens = 15 tens,
we write 5 at tens place and take 1 to hundred place,
4 X 2 hundreds = 8 hundreds, now 8 hundreds + 1 hundred =
9 hundreds, So 5 X $238 = 952, therefore 4 game systems will cost $952.

Question 7.
A small bag of chips weighs 48 grams. A large bag of
chips weighs three times as much as the small bag.
How much will 7 large bags of chips weigh?

Answer:
7 large bags of chips weigh 1,008 grams,

Explanation:
Given a small bag of chips weighs 48 grams.
A large bag of chips weighs three times as much as
the small bag means 3 X 48 grams=
2
48
X 3
144
here first we multiply 3 X 8 ones = 24 ones, we write 4
at ones place and take 2 to tens place then 3 X 4 ten =
12 tens+ 2 tens = 14 tens, we write 14 tens as 4 at tens place
and 1 at hundreds place, So 3 X 48 grams = 144 grams,
Now 7 large bags of chips weigh 7 X 144 grams =
 3,2
144
X 7
1,008
here first we multiply 7 X 4 ones = 28 ones, we write 8
at ones place and take 2 to tens place then 7 X 4 ten =
28 tens+ 2 tens = 30 tens, we write 30 tens as 0 at tens place
and other 3 at hundreds place,now 7 X 1 hundred = 7 hundred,
7 hundred + 3 hundreds = 10 hundreds we write 0 at
hundreds place at 1 at thousands place, So 7 X 144 = 1,008 grams,
therefore, 7 large bags of chips weigh 1,008 grams.

Eureka Math Grade 4 Module 3 Lesson 9 Exit Ticket Answer Key

Question 1.
Solve using the standard algorithm.
a.

Answer:

5,  4     7   2
Explanation:
In standard algorithm we add same time of multiplying as
7
608
X 9
5,472 ,here 9 X 8 ones = 72 ones, we write 2 at ones place and
take 7 to tens places then 9 x 0 tens = 0 tens + 7 tens = 7 tens,
we write 7 at tens place and 9 X 6 hundreds = 54 hundreds,
now we write 4 at hundreds place and 5 at thousands place as shown above, So 9 X 608 = 5,472.

b.

Answer:

4, 0 1 8
Explanation:
In standard algorithm we add same time of multiplying as
2
574
X 7
4,018 ,here 7 X 4 ones = 28 ones, we write 8 at ones place and
take 2 to tens places then 7 x 7 tens = 49 tens + 2 tens = 51 tens,
we write 1 at tens place and 5 at hundreds place and
7 X 5 hundreds = 35 hundreds, 35 hundreds + 5 hundreds =
40 hundreds,now we write 0 at hundreds place and 4
at thousands place as shown above, So 7 X 574 = 4,018.

Question 2.
Morgan is 23 years old. Her grandfather is 4 times as old.
How old is her grandfather?
Answer:
Morgan’s grandfather is 92 years old,

Explanation:
Given Morgan is 23 years old and her grandfather is 4 times
as old. So Morgan’s grandfather’s is 4 X 23 years =
1
23
X 4
92, here 4 X 3 ones = 12 ones, we write 2 at ones place and
take 1 to tens places then 4 x 2 tens = 8 tens, 8 tens + 1 ten =
9 tens, So Morgan’s grandfather is 92 years old.

Eureka Math Grade 4 Module 3 Lesson 9 Homework Answer Key

Question 1.
Solve using each method.

Answer:

Explanation:
Given expression as 2 X 46 =
Partial Products
46
X 2
  12
+80
92 , Here we first write multiplication of 2 X 6 ones, then
2 X 4 tens then add as shown above 12 + 80 = 92,
In standard algorithm we add same time of multiplying as
1
46
X 2
92 ,here 2 X 6 ones= 12 ones we write 2 at ones place and take 1
at tens place then 2 x 4 at tens place = 8 tens
add 1 ten to 8 tens we get 9 tens so 2 X 46 = 92.

Answer:

Explanation:
Given expression as 4 X 315 =
Partial Products
315
X 4
 20
40
+1200
1,260 , Here we first write multiplication of 4 X 5 ones, then
4 X 1 ten and 4 X 3 hundreds then add as shown above
20 + 40 + 1,200 = 1,260,
In standard algorithm we add same time of multiplying as
2
315
X 4
1,260 ,here 4 X 5 ones = 20 ones we write 0 at ones place and
take 2 at tens place then 4 x 1 tens = 4 tens add 2 tens to 4 tens
we get 6 tens and 4 X 3 hundreds = 12 hundreds, we write 2 at
hundreds and 1 at thousands places,  so 4 X 315 = 1,260.

Question 2.
Solve using the standard algorithm.
a.

Answer:

  9         2       8  

Explanation:
In standard algorithm we add same time of multiplying as
1
232
X 4
928 ,here 4 X 2 ones = 8 ones then 4 x 3 tens = 12 tens
we write 2 at tens place and take 1 to hundred place and
4 X 2 hundreds = 8 hundreds, now adding 1 hundred to
8 hundreds we get 9 hundreds , so 4 X 232 = 928.

b.

Answer:

     8      5       2
Explanation:
In standard algorithm we add same time of multiplying as
2, 1
142
X 6
852 ,here 6 X 2 ones = 12 ones, we write 2 at ones place and
take 1 to tens places then 6 x 4 tens = 24 tens + 1 tens = 25 tens,
we write 5 at tens place and take 2 to hundred place and
6 X 1 hundred = 6 hundreds, now adding 2 hundreds to
6 hundreds we get 8 hundreds , so 6 X 142 = 852.

c.

Answer:

 2,      1      9    8
Explanation:
In standard algorithm we add same time of multiplying as
 2
314
X 7
2,198 ,here 7 X 4 ones = 28 ones, we write 8 at ones place and
take 2 to tens places then 7 x 1 ten = 7 tens + 2 tens = 9 tens,
7 X 3 hundreds = 21 hundreds, now we write 1 at hundreds place
and 2 at thousands place as shown above, So 7 X 314 = 2,198.    

d.

Answer:

1,   3     2     0

Explanation:
In standard algorithm we add same time of multiplying as
1
440
X 3
1,320 ,here 3 X 0 ones = 0 ones, we write 0 at ones place,
3 x 4 tens = 12 tens we write 2 at tens place and take 1
at hundreds place, 3 X 4 hundreds = 12 hundreds,
12 hundreds + 1 hundred = 13 hundreds ,now we write 3
at hundreds place and 1 at thousand place as shown above,
So 3 X 440 = 1,320.

e.

Answer:

4,    0     5     6
Explanation:
In standard algorithm we add same time of multiplying as
5
507
X 8
4,056 ,here 8 X 7 ones = 56 ones, we write 6 at ones place and
take 5 to tens places then 8 x 0 tens = 0 tens + 5 tens = 5 tens,
we write 5 at tens place, 8 X 5 hundreds = 40 hundreds,now we write
0 at hundreds place and 4 at thousands place as shown above,
So 8 X 507 = 4,056.

f.

Answer:

3,    4      5      6
Explanation:
In standard algorithm we add same time of multiplying as
7, 3
384
X 9
3,456 ,here 9 X 4 ones = 36 ones, we write 6 at ones place and
take 3 to tens places then 9 x 8 tens = 72 tens + 3 tens = 75 tens,
we write 5 at tens places 7 at hundreds place and
9 X 3 hundreds = 27 hundreds, 27 hundreds + 7 hundreds =
34 hundreds now we write 4 at hundreds place and
3 at thousands place as shown above,
So 9 X 384 = 3,456.

Question 3.
What is the product of 8 and 54?
Answer:
The product of 8 and 54 is 432,

Explanation:
Give to find the product of 8 and 54 is
3
54
X 8
432
first we multiply 8 with 4 ones = 32 ones we write 2 at ones
place and take 3 to tens place now 8 X 5 = 40 tens adding
3 tens we get 43 tens, So 8 X 54 = 432.

Question 4.
Isabel earned 350 points while she was playing Blasting Robot.
Isabel’s mom earned 3 times as many points as Isabel.
How many points did Isabel’s mom earn?
Answer:
Isabel’s mom earn 1050 points,

Explanation:
Given Isabel earned 350 points while she was
playing Blasting Robot. Isabel’s mom earned 3 times
as many points as Isabel. So  points did Isabel’s mom earn
is 3 X 350 =
1
350
X 3
1050,
first we multiply 3 with 0 ones = 0 ones ,
3 X 5 = 15 tens we write 15 tens as 5 at tens place and
1 at hundreds place and 3 X 3 = 9 hundreds + 1 hundred =
10 hundreds we write 10 hundreds as 0 at hundreds place and
1 at thousands place, So 3 X 350 = 1050.
Therefore, Isabel’s mom earn 1050 points.

Question 5.
To get enough money to go on a field trip, every student
in a club has to raise $53 by selling chocolate bars.
There are 9 students in the club. How much money does
the club need to raise to go on the field trip?
Answer:
The club needs to raise $477 to go on the field trip,

Explanation:
Given to get enough money to go on a field trip, every student
in a club has to raise $53 by selling chocolate bars.
There are 9 students in the club. So money does
the club need to raise to go on the field trip is 9 X $53 =
2
$53
X 9
$477
first we multiply 9 with 3 ones = 27 ones , we write 7 at
ones place and 2 at tens place, 9 X 5 tens= 45 tens,
45 tens + 2 tens = 47 tens we write 47 tens as
7 at tens place and 4 at hundreds place so 9 X $53 = $477,
therefore,the club needs to raise $477 to go on the field trip.

Question 6.
Mr. Meyers wants to order 4 tablets for his classroom.
Each tablet costs $329. How much will all four tablets cost?
Answer:
Total cost for all four tablets are $1,316,

Explanation:
Given Mr. Meyers wants to order 4 tablets for his classroom.
Each tablet costs $329. So total cost for four tablets are
4 X $329 =
1,3
$329
X 4
$ 1,316
first we multiply 4 with 9 ones = 36 ones , we write 6 at
ones place and 3 at tens place, 4 X 2 tens= 8 tens,
8 tens + 3 tens = 11 tens we write 11 tens as
1 at tens place and 1 at hundreds place, Now 4 X 3 hundreds =
12 hundreds, 12 hundreds + 1 hundred = 13 hundreds, we write
3 at hundreds place and 1 at thousands place, So 4 X $329 = $1,316.

Question 7.
Amaya read 64 pages last week. Amaya’s older brother,
Rogelio, read twice as many pages in the same amount of time.
Their big sister, Elianna, is in high school and read 4 times as
many pages as Rogelio did. How many pages did
Elianna read last week?
Answer:
Elianna read 512 pages last week,

Explanation:
Given Amaya read 64 pages last week. Amaya’s older brother,
Rogelio, read twice as many pages in the same amount of time.
So Rogelio reads 2 X 64 pages =
64
X 2
128
2 X 4 ones = 8  and 2 X 6 tens= 120, So 2 X 64 = 8 + 120 = 128,
So Rogelio reads 128 pages,
Their big sister, Elianna, is in high school and read 4 times as
many pages as Rogelio did. So number of pages did
Elianna read last week are 4 X 128 pages=
1, 3
128
x 4
512
here we first we multiply 4 with 8 ones = 32 ones ,
we write 2 at ones place and 3 at tens place, 4 X 2 tens= 8 tens,
8 tens + 3 tens = 11 tens we write 11 tens as
1 at tens place and 1 at hundreds place and 4 X 1 hundred =
4 hundreds, 4 hundreds +1 hundred = 5 hundreds, So
4 X 128 pages = 512 pages,
therefore, Elianna read 512 pages last week.

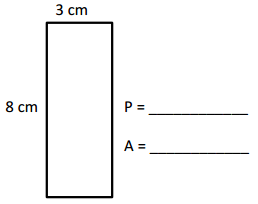
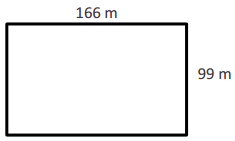
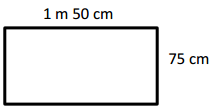
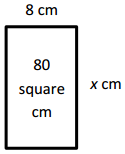
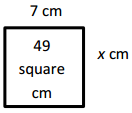
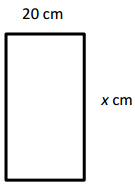
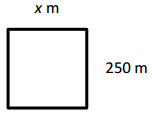
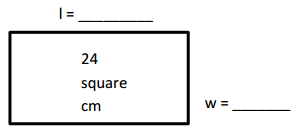
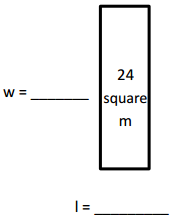
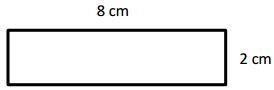
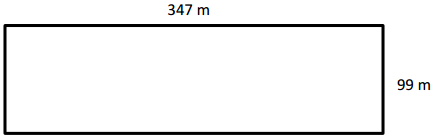
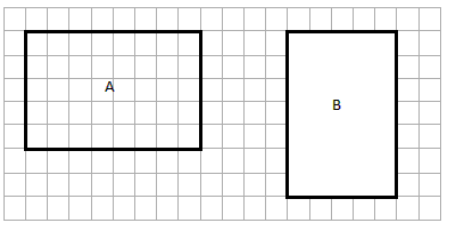
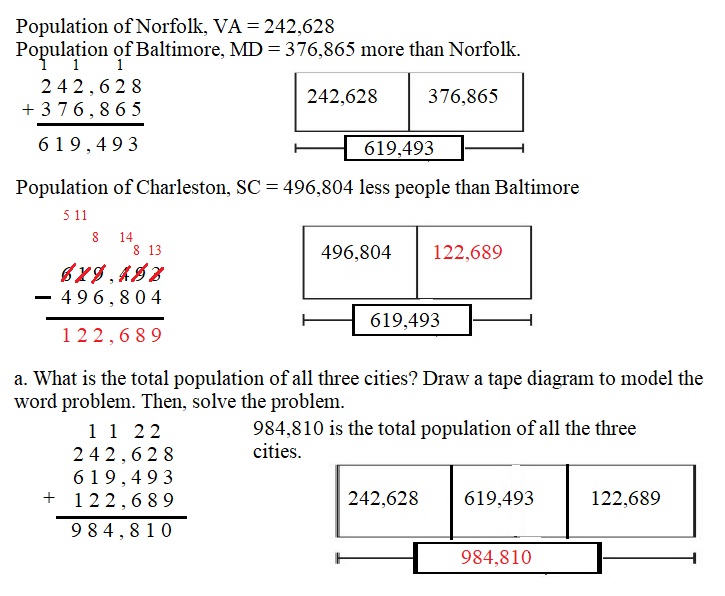
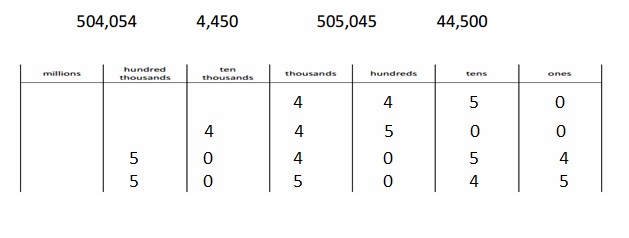
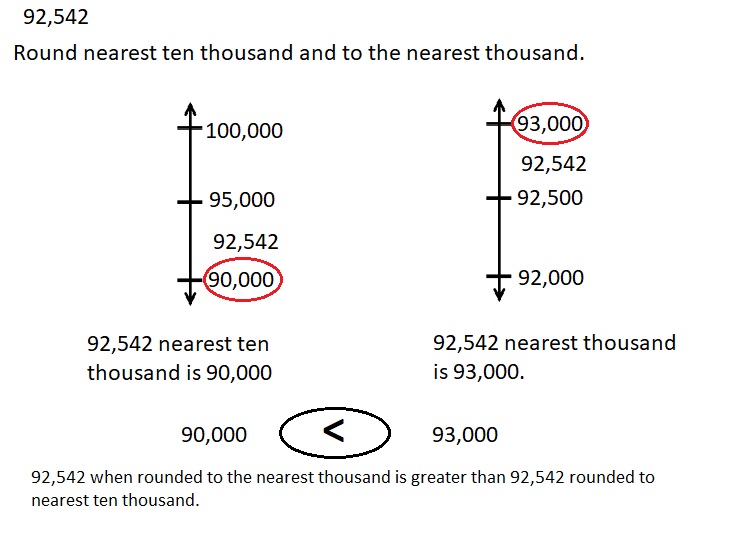
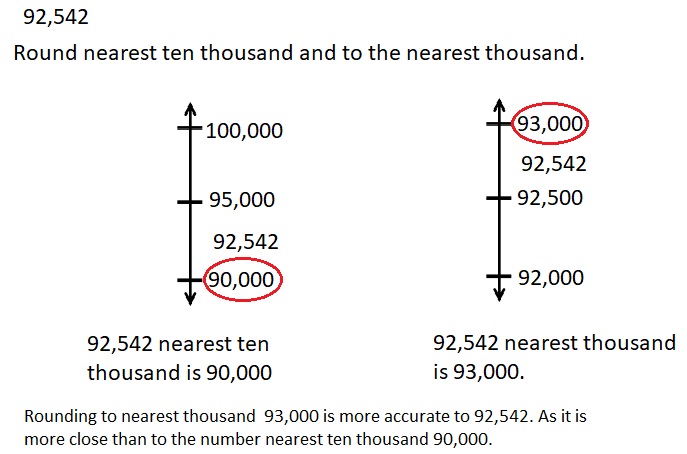
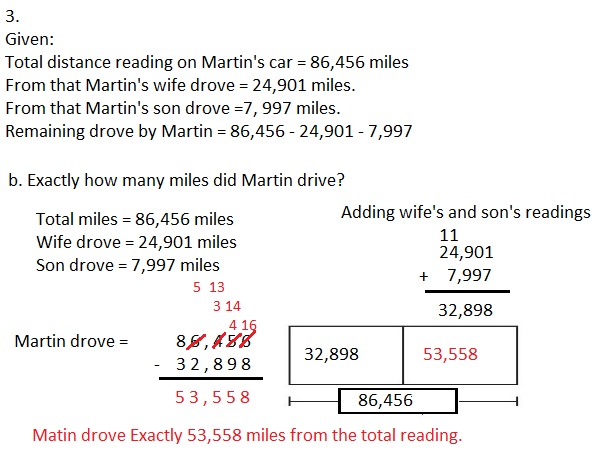
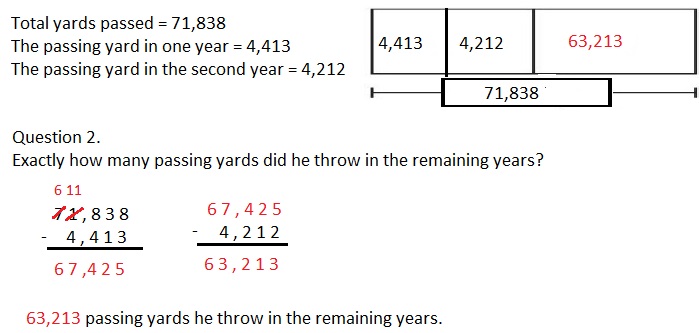
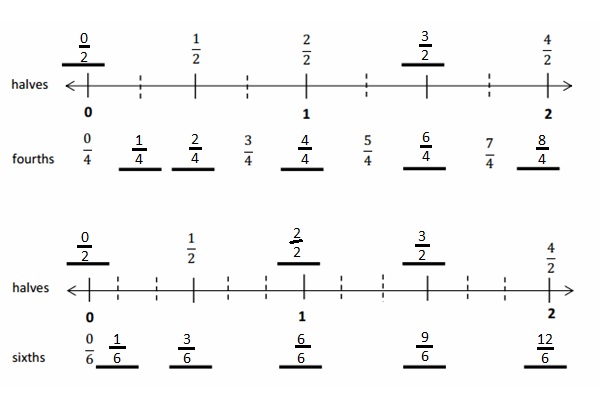
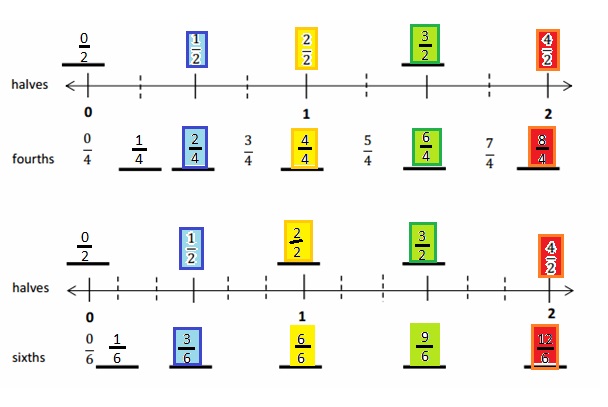
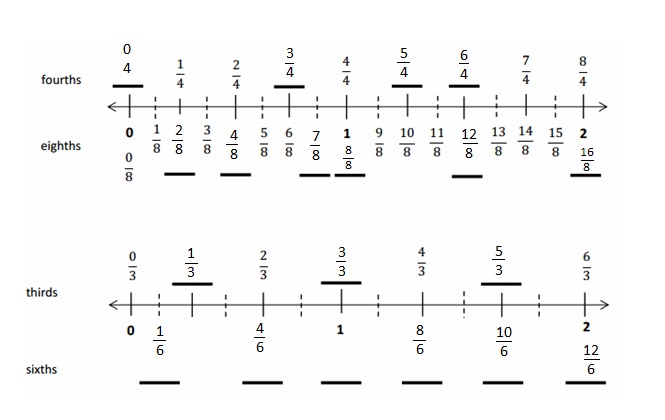
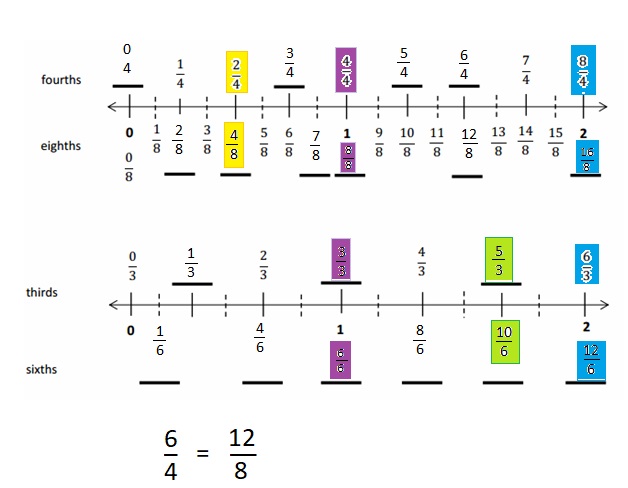
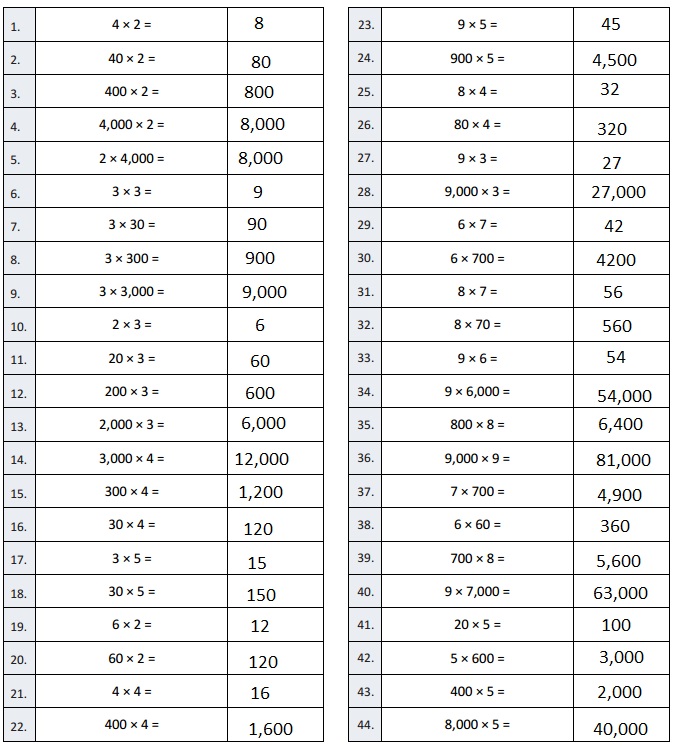
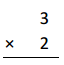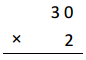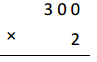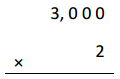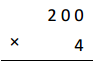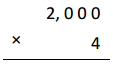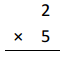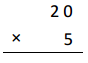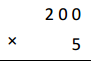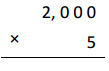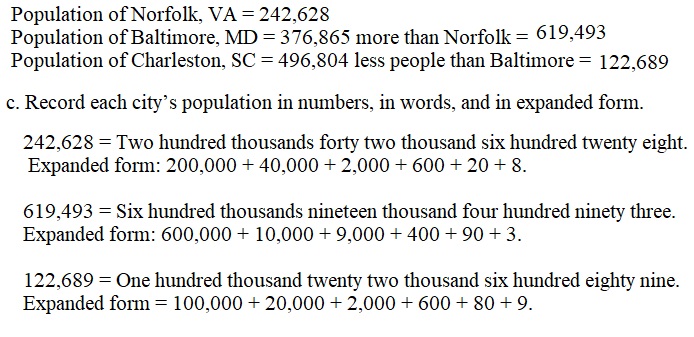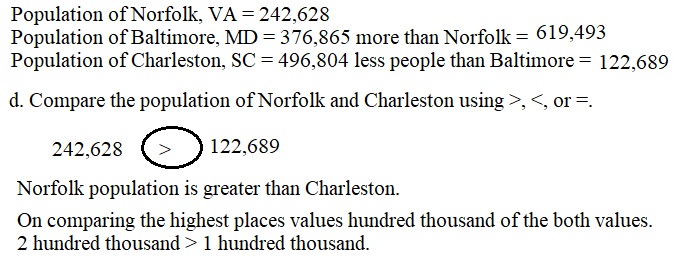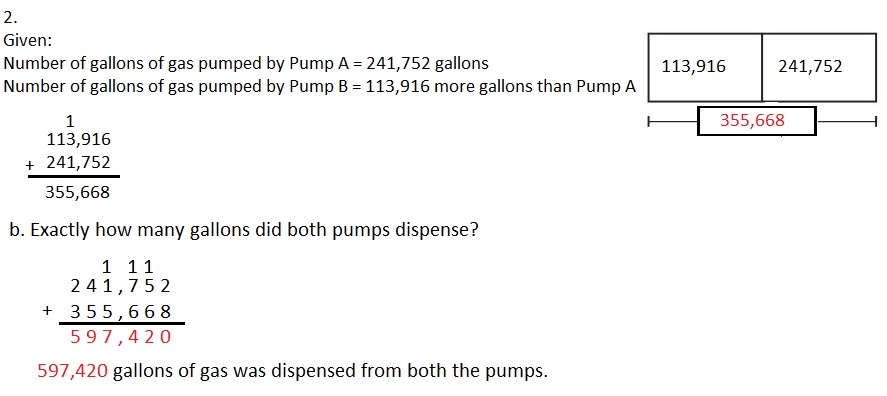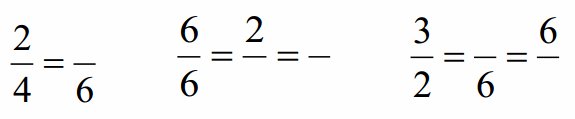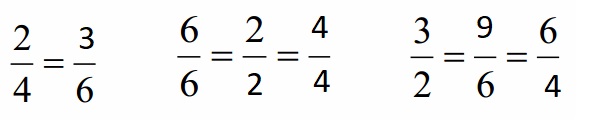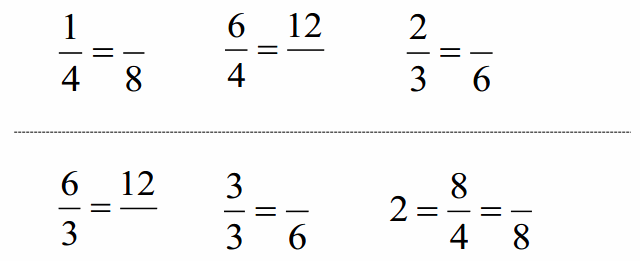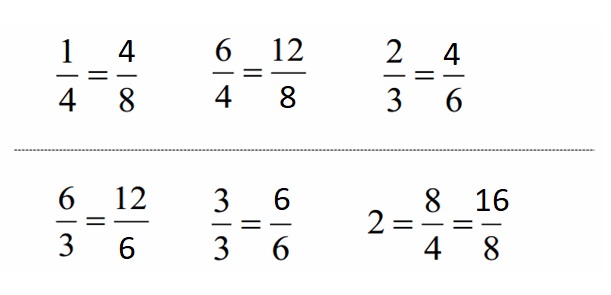Engage NY Eureka Math 4th Grade Module 3 Lesson 7 Answer Key

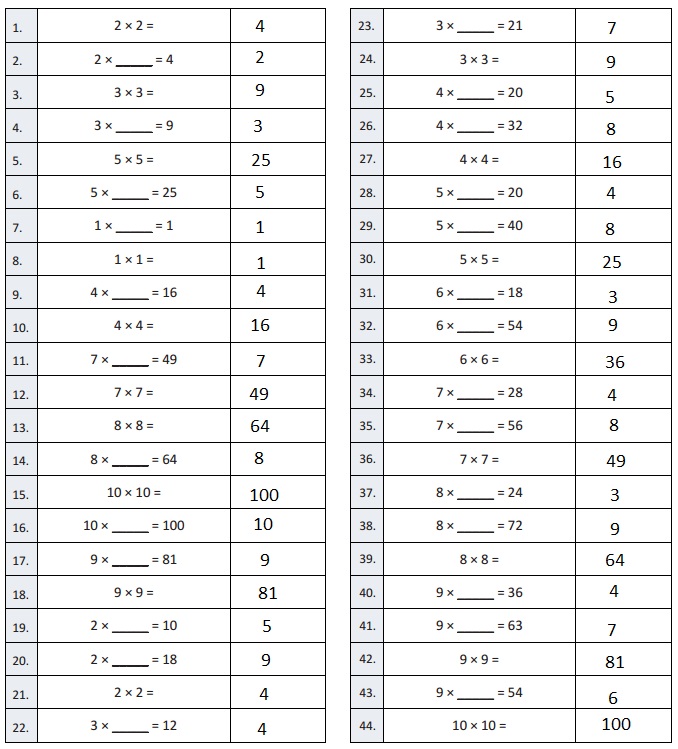
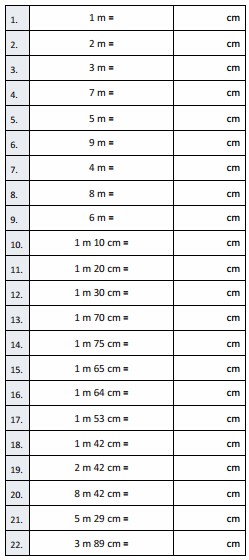
Eureka Math Grade 4 Module 3 Lesson 7 Sprint Answer Key

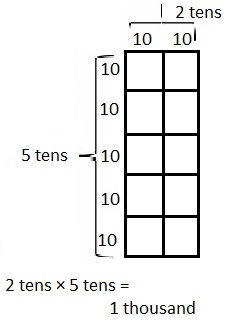
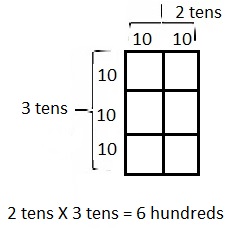
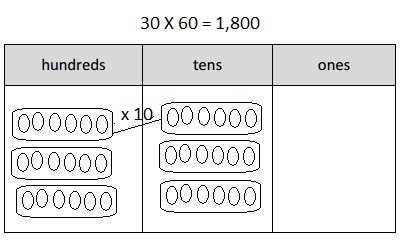
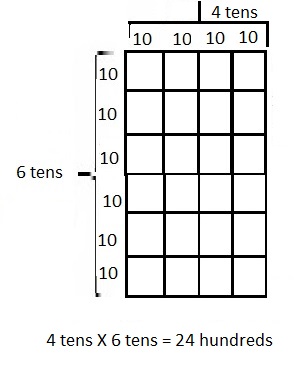
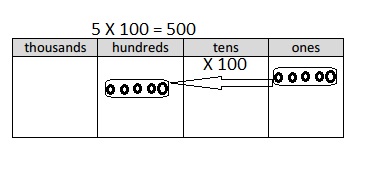
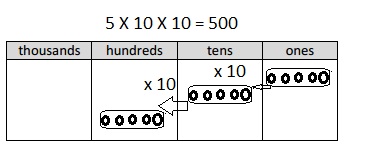
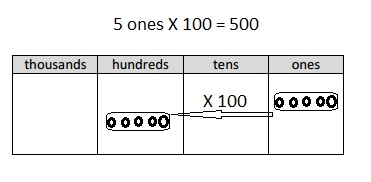
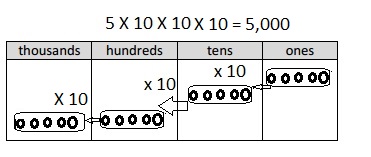
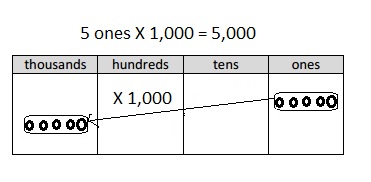
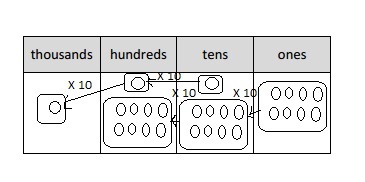
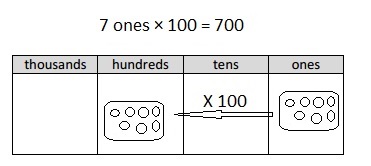
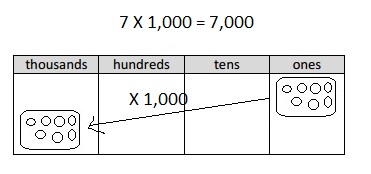
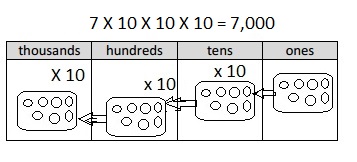
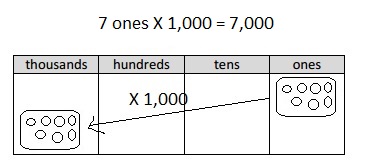
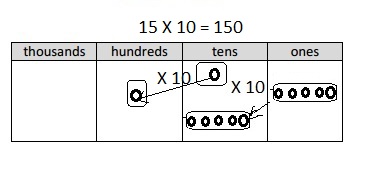
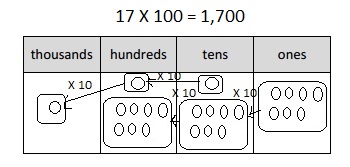
Multiply Multiples of 10, 100, and 1,000

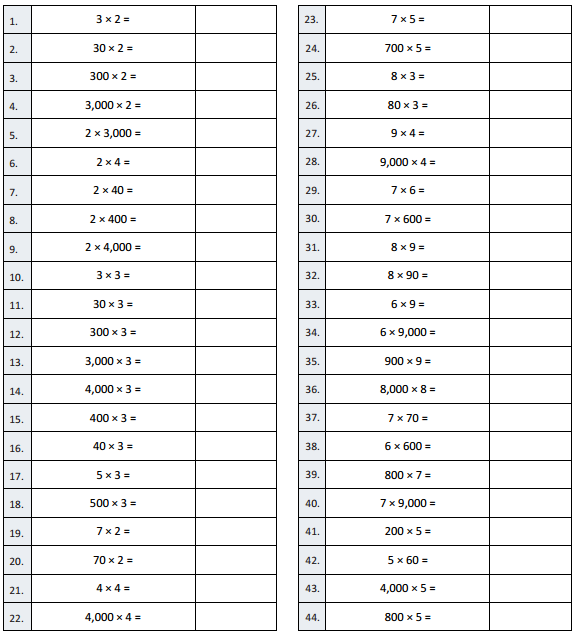
Question 1.
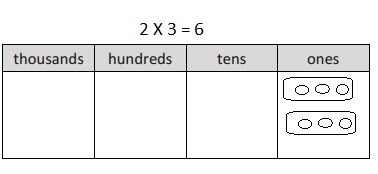
3 × 2 =
Answer:
3 X 2 = 6,

Explanation:
Given 3 X 2 = multiplying 3 with 2 we get 6,
3 X 2 = 6.

Question 2.
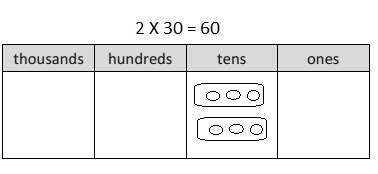
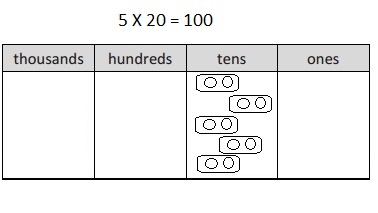
30 × 2 =
Answer:
30 X 2 =
3 X 10 X 2 = 60,

Explanation:
Given 30 X 2 = writing 30 as 3 X 10 and multiplying with 2
as  3 X 10 X 2 we get 60, So 30 X 2 = 60.

Question 3.
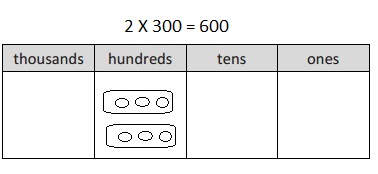
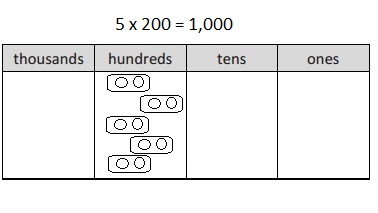
300 × 2 =
Answer:
300 X 2 =
3 X 100 X 2 = 600,

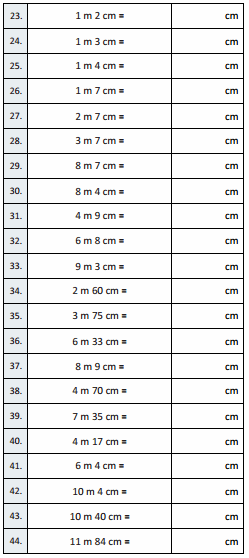
Explanation:
Given 300 X 2 = writing 300 as 3 X 100 and multiplying 2 we get 600,
3 X 100 X 2 = 600, so 300 X 2 = 600.

Question 4.
3,000 × 2 =
Answer:
3,000 X 2 =
3 X 1,000 X 2 = 6,000,

Explanation:
Given 3,000 X 2 = writing 3,000 as 3 X 1,000 and multiplying with 2
we get 6,000 as 3 X 1,000 X 2 = 6,000, So 3,000 X 2 = 6,000.

Question 5.
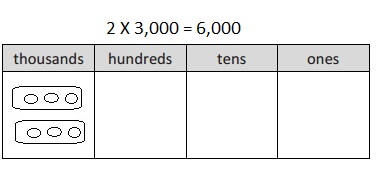
2 × 3,000 =
Answer:
2 X 3,000 =
2 X 3 X 1,000 = 6,000,

Explanation:
Given 2 X 3,000 = writing 3,000 as 3 X 1,000 and multiplying with
2 we get 6,000,2 X 3 X 1,000 = 6,000, So 2 X 3,000 = 6,000.

Question 6.
2 × 4 =
Answer:
2 X 4 = 8,

Explanation:
Given 2 X 4 = multiplying 2 with 4 we get 8,
2 X 4 = 8.

Question 7.
2 × 40 =
Answer:
2 X 40 =

2 X 4 X 10 = 80,

Explanation:
Given 2 X 40 = writing 40 as 4 X 10 and multiplying with 2 we get 80,
as 2 X 4 x 10 = 80, So 2 X 40 = 80.

Question 8.
2 × 400 =
Answer:
2 X 400 =
2 X 4 X 100 = 800,

Explanation:
Given 2 X 400 = writing 400 as 4 X 100 and multiplying with 2
we get 800 as 2 X 4 X 100 = 800, So 2 X 400 = 800.

Question 9.
2 × 4,000 =
Answer:
2 X 4,000 =
2 X 4 X 1,000 = 8,000,

Explanation:
Given 2 X 4,000 = writing 4,000 as 4 X 1,000 and multiplying with 2,
we get 8,000, as 2 X 4 X 1,000 = 8,000, So 2 X 4,000 = 8,000.

Question 10.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3 = multiplying 3 with 3 we get 9,
3 X 3 = 9.

Question 11.
30 × 3 =
Answer:
30 X 3 =
3 X 10 X 3 = 90,

Explanation:
Given 30 X 3 = writing 30 as 3 X 10 and multiplying with 3 we get 90
as 3 X 10 X 3 = 90, So 30 X 3 = 90.

Question 12.
300 × 3 =
Answer:
300 X 3 =
3 X 100 X 3 = 900,

Explanation:
Given 300 X 3 = writing 300 as 3 X 100 and multiplying with 3
we get 900 as 3 X 100 X 3 = 900, So 300 X 3 = 900.

Question 13.
3,000 × 3 =
Answer:
3,000 X 3 =
3 X 1,000 X 3 = 9,000,

Explanation:
Given 3,000 X 3 = writing 3,000 as 3 X 1,000 and multiplying with 3 we get 9,000 as 3 X 1,000 X 3 = 9,000, So 3,000 X 3 = 9,000.

Question 14.
4,000 × 3 =
Answer:
4,000 X 3 =
4 X 1,000 X 3 = 12,000,

Explanation:
Given 4,000 X 3 = writing 4,000 as 4 X 1,000 and multiplying
with 3 we get 12,000 so 4 X 1,000 X 3 = 12,000, So 4,000 X 3 = 12,000.

Question 15.
400 × 3 =
Answer:
400 X 3 =
4 X 100 X 3 = 1,200,

Explanation:
Given 400 X 3 = writing 400 as 4 X 100 and multiplying
with 3 we get 1,200 as 4 X 100 X 3 = 1,200, So 400 X 3 = 1,200.

Question 16.
40 × 3 =
Answer:
40 X 3 =
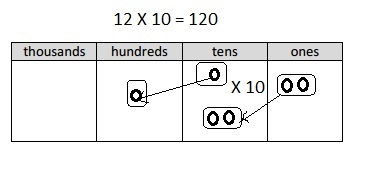
4 X 10 X 3 = 120,

Explanation:
Given 40 X 3 = writing 40 as 4 X 10 multiplying with 3 we get 120
as 4 X 10 X 3 = 120, So 40 X 3 = 120.

Question 17.
5 × 3 =
Answer:
5 X 3 = 15,

Explanation:
Given 5 X 3 = multiplying 5 with 3 we get 15,
5 X 3 = 15.

Question 18.
500 × 3 =
Answer:
500 X 3 =
5 X 100 X 3 = 1,500,

Explanation:
Given 500 X 3 = writing 500 as 5 X 100 and multiplying with 3 we get 1,500 as 5 x 100 X 3 = 1,500, So 500 X 3 = 1,500.

Question 19.
7 × 2 =
Answer:
7 X 2 = 14,

Explanation:
Given 7 X 2 = multiplying 7 with 2 we get 14,
7 X 2 = 14.

Question 20.
70 × 2 =
Answer:
70 X 2 =
7 X 10 X 2 = 140,

Explanation:
Given 70 X 2 = writing 70 as 7 X 10 and multiplying with 2
we get 140 as 7 X 10 X 2 = 140, So 70 X 2 = 140.

Question 21.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = multiplying 4 with 4 we get 16,
4 X 4 = 16.

Question 22.
4,000 × 4 =
Answer:
4,000 X 4 =
4 X 1,000 X 4 = 1,600,

Explanation:
Given 4,000 X 4 = writing 4,000 as 4 X 1,000 and multiplying
with 4 we get 1,600 as 4 X 1,000 X 4 = 1,600, So 4,000 X 4 = 1,600.

Question 23.
7 × 5 =
Answer:
7 X 5 = 35,

Explanation:
Given 7 X 5 = multiplying 7 with 5 we get 35,
7 X 5 = 35.

Question 24.
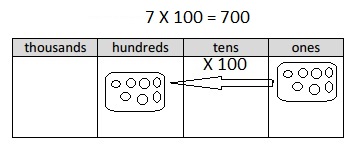
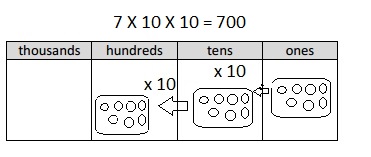
700 × 5 =
Answer:
700 X 5 =
7 x 100 X 5 = 3,500,

Explanation:
Given 700 X 5 = writing 700 as 7 X 100 and multiplying
with 5 we get 3,500 as 7 X 100 X 5 = 700, So 700 X 5 = 3,500.

Question 25.
8 × 3 =
Answer:
8 X 3 = 24,

Explanation:
Given 8 X 3 = multiplying 8 with 3 we get 24,
8 X 3 = 24.

Question 26.
80 × 3 =
Answer:
80 X 3 =
8 X 10 X 3 = 240,

Explanation:
Given 80 X 3 = writing 80 as 8 X 10 and multiplying
with 3 we get 240 as 8 X 10 X 3 = 240, So 80 X 3 = 240.

Question 27.
9 × 4 =
Answer:
9 X 4 = 36,

Explanation:
Given 9 X 4 = multiplying 9 with 4 we get 36,
9 X 4 = 36.

Question 28.
9,000 × 4 =
Answer:
9,000 x 4 =
9 X 1,000 X 4 = 36,000,

Explanation:
Given 9,000 X 4 = writing 9,000 as 9 X 1,000 and multiplying
with 4 we get 36,000 as 9 X 1,000 X 4 = 36,000,
So 9,000 X 4 = 36,000.

Question 29.
7 × 6 =
Answer:
7 X 6 = 42,

Explanation:
Given 7 X 6 = multiplying 7 with 6 we get 42,
7 X 6 = 42.

Question 30.
7 × 600 =
Answer:
7 X 600 =
7 X 6 X 100 = 4,200,

Explanation:
Given 7 X 600 = writing 600 as 6 X 100 and multiplying
with 7 we get 4,200 as 7 X 6 X 100 = 4,200 or 7 X 600 = 4,200.

Question 31.
8 × 9 =
Answer:
8 X 9 = 72,

Explanation:
Given 8 X 9 = multiplying 8 with 9 we get 72,
8 X 9 = 72.

Question 32.
8 × 90 =
Answer:
8 X 90 =
8 X 9 X 10 = 720,

Explanation:
Given 8 X 90 = writing 90 as 9 X 10 and multiplying
with 8 we get 720 as 8 x 9 X 10 = 720, So 8 X 90 = 720.

Question 33.
6 × 9 =
Answer:
6 X 9 = 54,

Explanation:
Given 6 X 9 = multiplying 6 with 9 we get 54,
6 X 9 = 54.

Question 34.
6 × 9,000 =
Answer:
6 X 9,000 =
6 X 9 X 1,000 = 54,000,

Explanation:
Given 6 X 9,000 = writing 9,000 as 9 X 1,000 and multiplying
with 6 we get 54,000 as 6 x 9 X 1,000 = 54,000, So 6 X 9,000 = 54,000.

Question 35.
900 × 9 =
Answer:
900 X 9 =
9 X 100 X 9 = 8,100,

Explanation:
Given 900 X 9 = writing 900 as 9 X 100 and multiplying
with 9 we get 8,100 as 9 X 100 X 9 = 8,100, So 900 X 9 = 8,100.

Question 36.
8,000 × 8 =
Answer:
8,000 X 8 =
8 X 1,000 X 8 = 64,000,

Explanation:
Given 8,000 X 8 = writing 8,000 as 8 X 1,000 and multiplying
with 8 we get 64,000 as 8 X 1,000 X 8 = 64,000, So 8,000 X 8 = 64,000.

Question 37.
7 × 70 =
Answer:
7 X 70 =
7 X 7 X 10 = 490,

Explanation:
Given 7 X 70 = writing 70 as 7 X 10 and multiplying
with 7 we get 490 as 7 X 7 X 10 = 490, So 7 X 70 = 490.

Question 38.
6 × 600 =
Answer:
6 X 600 =
6 X 6 X 100 = 3,600,

Explanation:
Given 6 X 600 = writing 600 as 6 X 100 and multiplying
with 6 we get 3,600 as 6 x 6 X 100 = 3,600, So 6 X 600 = 3,600.

Question 39.
800 × 7 =
Answer:
800 X 7 =
8 X 100 X 7 = 5,600,

Explanation:
Given 800 X 7 = writing 800 as 8 x 100 and multiplying
with 7 we get 5,600 as 8 X 100 X 7 = 5,600, So 800 X 7 = 5,600.

Question 40.
7 × 9,000 =
Answer:
7 X 9,000 =
7 X 9 X 1,000 = 63,000,

Explanation:
Given 7 X 9,000 = writing 9,000 as 9 X 1,000 and multiplying
with 7 we get 63,000 as 7 X 9 X 1,000 = 63,000, So 7 X 9,000 = 63,000.

Question 41.
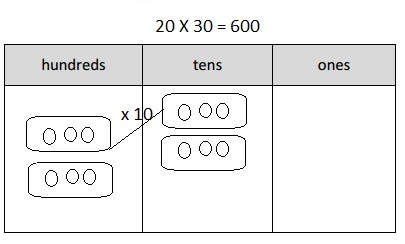
200 × 5 =
Answer:
200 X 5 =
2 X 100 X 5 = 1,000,

Explanation:
Given 200 X 5 = writing 200 as 2 X 100 and multiplying
with 5 we get 1,000 as 2 X 100 X 5 = 1,000, So 200 X 5 = 1,000.

Question 42.
5 × 60 =
Answer:
5 X 60 =
5 X 6 X 10 =300,

Explanation:
Given 5 X 60 = writing 60 as 6 X 10 and multiplying
with 5 we get 300 as 5 X 6 X 10 = 300, So 5 X 60 = 300.

Question 43.
4,000 × 5 =
Answer:
4,000 X 5 =
4 X 1,000 X 5 = 20,000,

Explanation:
Given 4,000 X 5 = writing 4,000 as 4 X 1,000 and multiplying
with 5 we get 20,000 as 4 x 1,000 X 5 = 20,000, So 4,000 X 5 = 20,000.

Question 44.
800 × 5 =
Answer:
800 X 5 = 4,000,
8 X 100 X 5 = 4,000,

Explanation:
Given 800 X 5 = writing 800 as 8 X 100 and multiplying
with 5 we get 4,000 as 8 X 100 X 5 = 4,000, So 800 X 5 = 4,000.

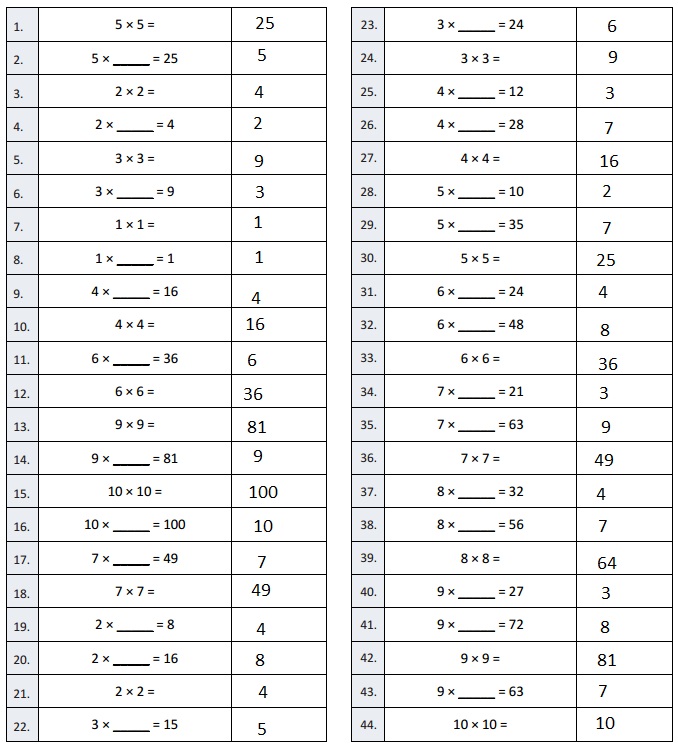
Multiply Multiples of 10, 100, and 1,000

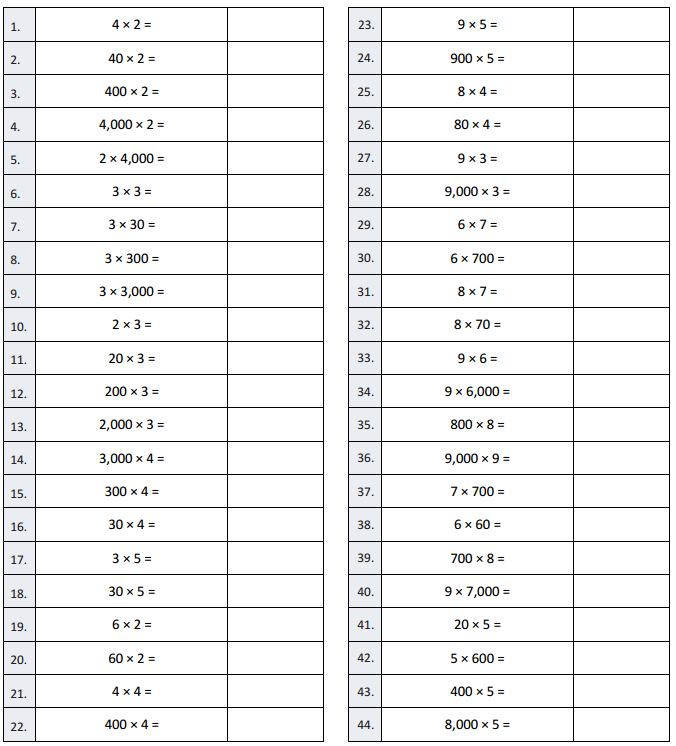
Question 1.
4 × 2 =
Answer:
4 X 2 = 8,

Explanation:
Given 4 X 2 = multiplying 4 with 2 we get 8,
4 X 2 = 8.

Question 2.
40 × 2 =
Answer:
40 X 2 =
4 X 10 X 2 = 80,

Explanation:
Given 40 X 2 = writing 40 as 4 X 10 and multiplying
with 2 we get 80 as 4 X 10 X 2 = 80, So 40 X 2 = 80.

Question 3.
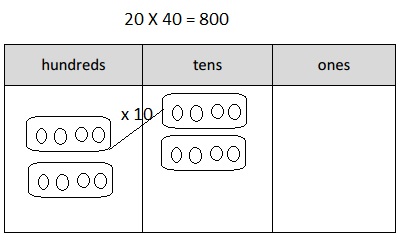
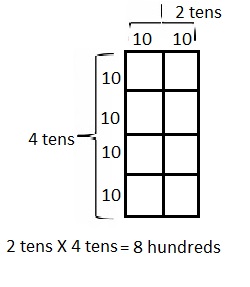
400 × 2 =
Answer:
400 X 2 =
4 X 100 X 2 = 800,

Explanation:
Given 400 X 2 = writing 400 as 4 X 100 and multiplying
with 2 we get 800 as 4 X 100 X 2 = 800, So 400 X 2 = 800.

Question 4.
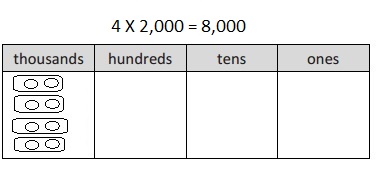
4,000 × 2 =
Answer:
4,000 X 2 =
4 X 1,000 X 2 = 8,000,

Explanation:
Given 4,000 X 2 = writing 4,000 as 4 X 1,000 and multiplying with 2,
we get 8,000, as 4 X 1,000 X 2 = 8,000, So 4,000 X 2 = 8,000.

Question 5.
2 × 4,000 =
Answer:
2 X 4,000 =
2 X 4 X 1,000 = 8,000,

Explanation:
Given 2 X 4,000 = writing 4,000 as 4 X 1,000 and multiplying with 2,
we get 8,000, as 2 X 4 X 1,000 = 8,000, So 2 X 4,000 = 8,000.

Question 6.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3 = multiplying 3 with 3 we get 9,
3 X 3 = 9.

Question 7.
3 × 30 =
Answer:
3 X 30 =
3 X 3 X 10 = 90,

Explanation:
Given 3 X 30 = writing 30 as 3 X 10 and multiplying with 3 we get 90
as 3 X 3 X 10 = 90, So 3 X 30 = 90.

Question 8.
3 × 300 =
Answer:
3 X 300 =
3 X 3 X 100 = 900,

Explanation:
Given 3 X 300 = writing 300 as 3 X 100 and multiplying with 3
we get 900 as 3 X 3 X 100 = 900, So 3 X 300 = 900.

Question 9.
3 × 3,000 =
Answer:
3 X 3,000 =
3 X 3 X 1,000 = 9,000,

Explanation:
Given 3 X 3,000 = writing 3,000 as 3 X 1,000 and multiplying with 3 we get 9,000 as 3 X 3 X 1,000 = 9,000, So 3 X 3,000 = 9,000.

Question 10.
2 × 3 =
Answer:
2 X 3 = 6,

Explanation:
Given 2 X 3 = multiplying 2 with 3 we get 6,
2 X 3 = 6.

Question 11.
20 × 3 =
Answer:
20 X 3 =
2 x 10 X 3 = 60,

Explanation:
Given 20 X 3 = writing 20 as 2 X 10 and multiplying with 3 we get 60
as 2 X 10 X 3 = 60, So 20 X 3 = 60.

Question 12.
200 × 3 =
Answer:
200 X 3 =
2 X 100 X 3 = 600,

Explanation:
Given 200 X 3 = writing 200 as 2 X 100 and multiplying
with 3 we get 600 as 2 X 100 X 3 = 600, So 200 X 3 = 600.

Question 13.
2,000 × 3 =
Answer:
2,000 X 3 =
2 X 1,000 X 3 = 6,000,

Explanation:
Given 2,000 X 3 = writing 2,000 as 2 X 1,000 and
multiplying with 3 we get 6,000 as 2 X 1,000 X 3 = 6,000,
So 2,000 X 3 = 6,000.

Question 14.
3,000 × 4 =
Answer:
3,000 X 4 =
3 X 1,000 X 4 = 12,000,

Explanation:
Given 3,000 X 4 = writing 3,000 as 3 X 1,000 and
multiplying with 4 we get 12,000 as 3 X 1,000 X 4 = 12,000,
So 3,000 X 4 = 12,000.

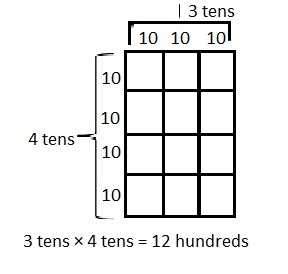
Question 15.
300 × 4 =
Answer:
300 X 4 =
3 X 100 X 4 = 1,200,

Explanation:
Given 300 X 4 = writing 300 as 3 X 100 and multiplying
with 4 we get 1,200 as 3 X 100 X 4 = 1,200, So 300 X 4 = 1,200.

Question 16.
30 × 4 =
Answer:
30 X 4 =
3 X 10 X 4 = 120,

Explanation:
Given 30 X 4 = writing 30 as 3 X 10 and multiplying
with 4 we get 120 as 3 X 10 X 4 = 120, So 30 X 4 = 120.

Question 17.
3 × 5 =
Answer:
3 X 5 = 15,

Explanation:
Given 3 X 5 = multiplying 3 with 5 we get 15
as 3 X 5 = 15, So 3 X 5 = 15.

Question 18.
30 × 5 =
Answer:
30 X 5 =
3 X 10 X 5 = 150,

Explanation:
Given 30 X 5 = writing 30 as 3 X 10 and multiplying
with 5 we get 150 as 3 X 10 X 5 = 150, So 30 X 5 = 150.

Question 19.
6 × 2 =
Answer:
6 X 2 = 12,

Explanation:
Given 6 X 2 = multiplying 6 with 2 we get 12
as 6 X 2 = 12, So 6 X 2 = 12.

Question 20.
60 × 2 =
Answer:
60 X 2 =
6 X 10 X 2 = 120,

Explanation:
Given 60 X 2 = writing 60 as 6 X 10 and multiplying
with 2 we get 120 as 6 X 10 X 2 = 120, So 60 X 2 = 120.

Question 21.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = multiplying 4 with 4 we get 16
as 4 X 4 = 16, So 4 X 4 = 16.

Question 22.
400 × 4 =
Answer:
400 X 4 =
4 X 100 X 4 = 1,600,

Explanation:
Given 400 X 4 = writing 400 as 4 X 100 and multiplying
with 4 we get 1,600 as 4 X 100 X 4 = 1,600, So 400 X 4 = 1,600.

Question 23.
9 × 5 =
Answer:
9 X 5 = 45,

Explanation:
Given 9 X 5 = multiplying 9 with 5 we get 45 as
9 X 5 = 45.

Question 24.
900 × 5 =
9 X 100 X 5 = 4,500,

Explanation:
Given 900 X 5 = writing 900 as 9 X 100 and multiplying
with 5 we get 4,500 as 9 X 100 X 5 = 4,500, So 900 X 5 = 4,500.

Question 25.
8 × 4 =
Answer:
8 X 4 = 32,

Explanation:
Given 8 X 4 = multiplying 8 with 4 we get 32 as
8 X 4 = 32.

Question 26.
80 × 4 =
Answer:
80 X 4 =
8 X 10 X 4 = 320,

Explanation:
Given 80 X 4 = writing 80 as 8 X 10 and multiplying
with 4 we get 320 as 8 X 10 X 4 = 320, So 80 X 4 = 320.

Question 27.
9 × 3 =
Answer:
9 X 3 = 27,

Explanation:
Given 9 X 3 = multiplying 9 with 3 we get 27 as
9 X 3 = 27.

Question 28.
9,000 × 3 =
Answer:
9,000 X 3 =
9 X 1,000 X 3 = 27,000,

Explanation:
Given 9,000 X 3 = writing 9,000 as 9 X 1,000 and
multiplying with 3 we get 27,000 as 9 X 1,000 X 3 = 27,000,
So 9,000 X 3 = 27,000.

Question 29.
6 × 7 =
Answer:
6 X 7 = 42,

Explanation:
Given 6 X 7 = multiplying 6 with 7 we get 42 as
6 X 7 = 42.

Question 30.
6 × 700 =
Answer:
6 X 700 =
6 X 7 X 100 = 4,200,

Explanation:
Given 6 X 700 = writing 700 as 7 X 100 and multiplying
with 6 we get 4,200 as 6 X 7 X 100 = 4,200, So 6 X 700 = 4,200.

Question 31.
8 × 7 =
Answer:
8 X 7 = 56,

Explanation:
Given 8 X 7 = multiplying 8 with 7 we get 56 as
8 X 7 = 56.

Question 32.
8 × 70 =
Answer:
8 X 70 =
8 X 7 X 10 = 560,

Explanation:
Given 8 X 70 = writing 70 as 7 X 10 and multiplying
with 8 we get 560 as 8 x 7 X 10 = 560, So 8 X 70 = 560.

Question 33.
9 × 6 =
Answer:
9 X 6 = 54,

Explanation:
Given 9 X 6 = multiplying 9 with 6 we get 54 as
9 X 6 = 54.

Question 34.
9 × 6,000 =
Answer:
9 X 6,000 =
9 X 6 X 1,000 = 54,000,

Explanation:
Given 9 X 6,000 = writing 6,000 as 6 X 1,000 and multiplying with 9,
we get 54,000, as 9 X 6 X 1,000 = 54,000, So 9 X 6,000 = 54,000.

Question 35.
800 × 8 =
Answer:
800 X 8 =
8 X 100 X 8 = 6,400,

Explanation:
Given 800 X 8 = writing 800 as 8 X 100 and multiplying
with 8 we get 6,400 as 8 X 100 X 8 = 6,400, So 800 X 8 = 6,400.

Question 36.
9,000 × 9 =
Answer:
9,000 x 9 =
9 X 1,000 X 9 = 81,000,

Explanation:
Given 9,000 X 9 = writing 9,000 as 9 X 1,000 and multiplying
with 9 we get 81,000 as 9 X 1,000 X 9 = 81,000,
So 9,000 X 9 = 81,000.

Question 37.
7 × 700 =
Answer:
7 X 700 =
7 X 7 X 100 = 4,900,

Explanation:
Given 7 X 700 = writing 700 as 7 X 100 and multiplying
with 7 we get 4,900 as 7 X 7 X 100 = 4,900, So 7 X 700 = 4,900.

Question 38.
6 × 60 =
Answer:
6 X 60 =
6 X 6 X 10 = 360,

Explanation:
Given 6 X 60 = writing 60 as 6 X 10 and multiplying
with 6 we get 360 as 6 x 6 X 10 = 360, So 6 X 60 = 360.

Question 39.
700 × 8 =
Answer:
700 X 8 =
7 X 100 X 8 = 5,600,

Explanation:
Given 700 X 8 = writing 700 as 7 X 100 and multiplying
with 8 we get 5,600 as 7 X 100 X 8 = 5,600, So 700 X 8 = 5,600.

Question 40.
9 × 7,000 =
Answer:
9 X 7000 =
9 X 7 X 1,000 = 63,000,

Explanation:
Given 9 X 7,000 = writing 7,000 as 7 X 1,000 and multiplying with 9,
we get 63,000, as 9 X 7 X 1,000 = 63,000, So 9 X 7,000 = 63,000.

Question 41.
20 × 5 =
Answer:
20 X 5 =
2 X 10 X 5 = 100,

Explanation:
Given 20 X 5 = writing 20 as 2 X 10 and multiplying
with 5 we get 100 as 2 X 10 X 5 = 100, So 20 X 5 = 100.

Question 42.
5 × 600 =
Answer:
5 X 600 =
5 X 6 X 100 = 3,000,

Explanation:
Given 5 X 600 = writing 600 as 6 X 100 and multiplying
with 5 we get 3,000 as 5 X 6 X 100 = 3,000, So 5 X 600 = 3,000.

Question 43.
400 × 5 =
Answer:
400 X 5 =
4 X 100 X 5 = 2,000,

Explanation:
Given 400 X 5 = writing 400 as 4 X 100 and multiplying
with 5 we get 2,000 as 4 X 100 X 5 = 2,000, So 400 X 5 = 2,000.

Question 44.
8,000 × 5 =
Answer:
8,000 x 5 =
8 X 1,000 X 5 = 40,000,

Explanation:
Given 8,000 X 5 = writing 8,000 as 8 X 1,000 and multiplying
with 5 we get 40,000 as 8 X 1,000 X 5 = 40,000,
So 8,000 X 5 = 40,000.

Eureka Math Grade 4 Module 3 Lesson 7 Problem Set Answer Key

Question 1.
Represent the following expressions with disks, regrouping as necessary, writing a matching expression, and recording the partial products vertically as shown below.
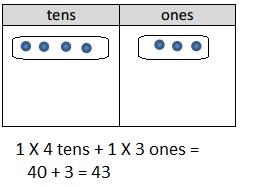
a. 1 × 43


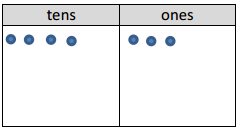
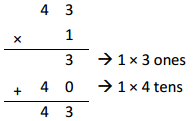
Answer:

43
X1
    3—-1 X 3 ones
+40—-1 X 4 tens
43

Explanation:
Represented the following expression 1 X43 with disks,
regrouped as necessary, wrote a matching expression, and
recorded the partial products vertically as shown above 1 X 43 = 43.

b. 2 × 43

Answer:

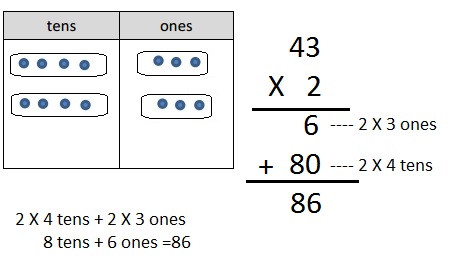
Explanation:
Represented the following expression 2 X 43 with disks,
regrouped as necessary, wrote a matching expression, and
recorded the partial products vertically as shown above 2 X 43 = 86.

c. 3 × 43

Answer:

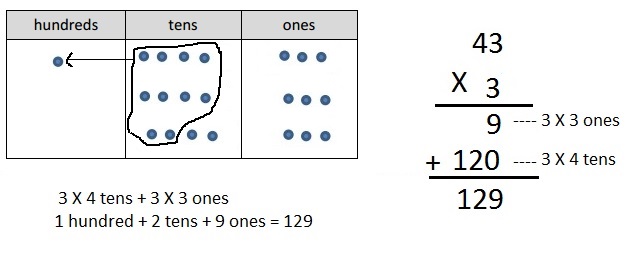
Explanation:
Represented the following expression 3 X 43 with disks,
regrouped as necessary, wrote a matching expression, and
recorded the partial products vertically as shown above 3 X 43 = 129.

d. 4 × 43

Answer:

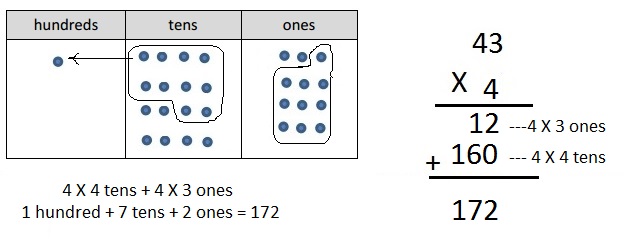
Explanation:
Represented the following expression 4 X 43 with disks,
regrouped as necessary, wrote a matching expression, and
recorded the partial products vertically as shown above 4 X 43 = 172.

Question 2.
Represent the following expressions with disks,
regrouping as necessary. To the right, record the partial
products vertically.
a. 2 × 36

Answer:

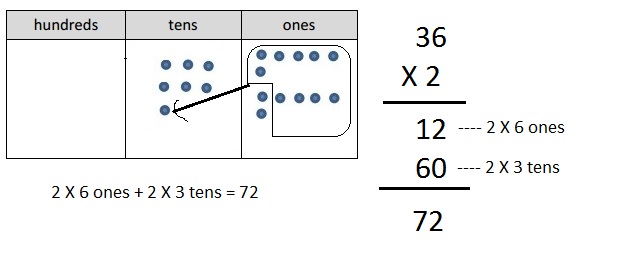
Explanation:
Represented the following expression 2 X 36 with disks,
regrouped as necessary. To the right, record the partial
products vertically as 2 X 36 = 72 as shown above.

b. 3 × 61

Answer:

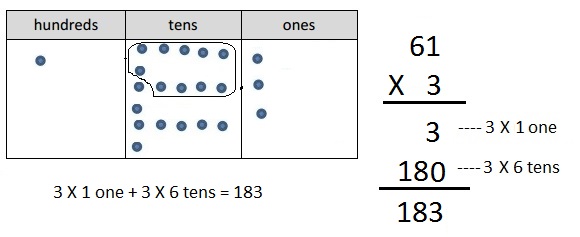
Explanation:
Represented the following expression 3 X 61 with disks,
regrouped as necessary. To the right, recorded the partial
products vertically as 3 X 61 = 183 as shown above.

c. 4 × 84

Answer:

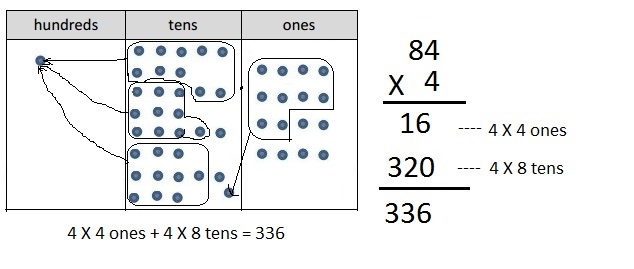
Explanation:
Represented the following expression 4 X 84 with disks,
regrouped as necessary. To the right, recorded the partial
products vertically as 4 X 84 = 336 as shown above.

Eureka Math Grade 4 Module 3 Lesson 7 Exit Ticket Answer Key

Represent the following expressions with disks, regrouping as necessary. To the right, record the partial products vertically.

Question 1.
6 × 41

Answer:

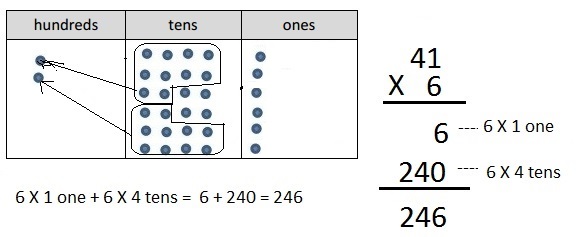
Explanation:
Represented the following expression 6 X 41 with disks,
regrouped as necessary. To the right, recorded the partial
products vertically as 6 X 41 = 246 as shown above.

Question 2.
7 × 31

Answer:

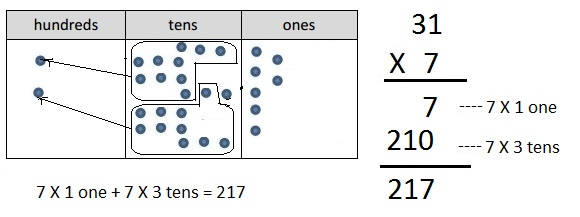
Explanation:
Represented the following expression 7 X 31 with disks,
regrouped as necessary. To the right, recorded the partial
products vertically as 7 X 31 = 217 as shown above.

Eureka Math Grade 4 Module 3 Lesson 7 Homework Answer Key

Question 1.
Represent the following expressions with disks, regrouping as necessary, writing a matching expression, and recording the partial products vertically.
a. 3 × 24

Answer:

Explanation:
Represented the following expression 3 X 24 with disks,
regrouped as necessary. To the right, recorded the partial
products vertically as 3 X 24 = 72 as shown above.

b. 3 × 42

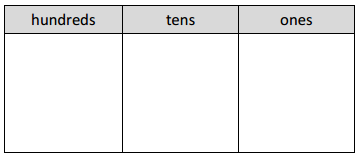
Answer:

Explanation:
Represented the following expression 3 X 42 with disks,
regrouped as necessary. To the right, recorded the partial
products vertically as 3 X 42 = 126 as shown above.

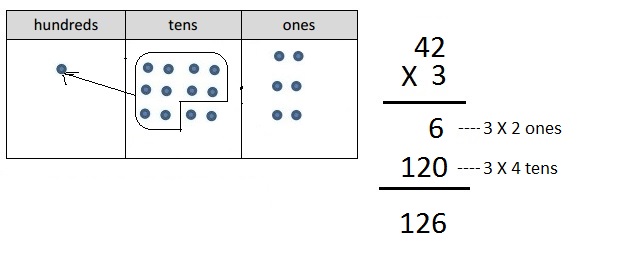
c. 4 × 34

Answer:

Explanation:
Represented the following expression 4 X 34 with disks,
regrouped as necessary. To the right, recorded the partial
products vertically as 4 X 34 = 136 as shown above.

Question 2.
Represent the following expressions with disks, regrouping as necessary. To the right, record the partial products vertically.
a. 4 × 27

Answer:

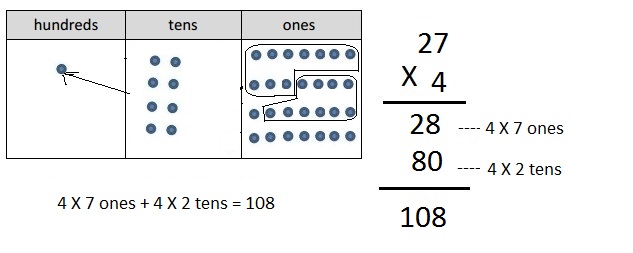
Explanation:
Represented the following expression 4 X 27 with disks,
regrouped as necessary. To the right, recorded the partial
products vertically as 4 X 27 = 108 as shown above.

b. 5 × 42

Answer:

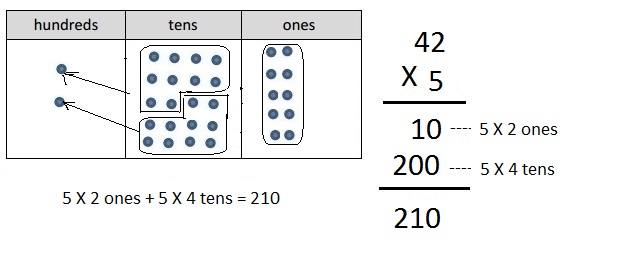
Explanation:
Represented the following expression 5 X 42 with disks,
regrouped as necessary. To the right, recorded the partial
products vertically as 5 X 42 = 210 as shown above.

Question 3.
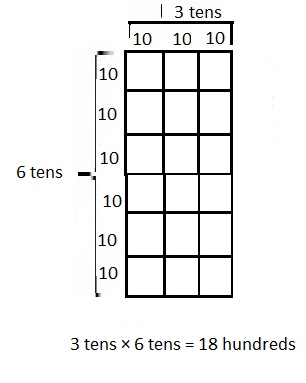
Cindy says she found a shortcut for doing multiplication problems.
When she multiplies 3 × 24, she says, “3 × 4 is 12 ones,
or 1 ten and 2 ones. Then, there’s just 2 tens left in 24,
so add it up, and you get 3 tens and 2 ones.”
Do you think Cindy’s shortcut works?
Explain your thinking in words, and justify your
response using a model or partial products.
Answer:
No, Cindy’s shortcut will not work,

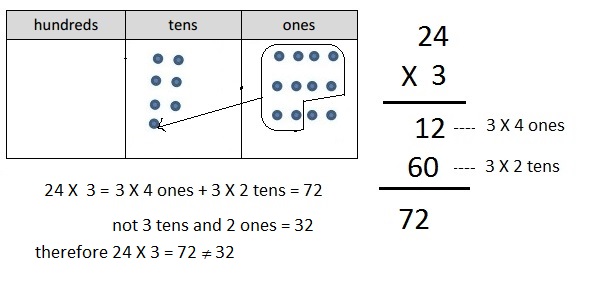
Explanation:
Given Cindy says she found a shortcut for doing multiplication problems.
When she multiplies 3 × 24, she says, “3 × 4 is 12 ones,
or 1 ten and 2 ones. Then, there’s just 2 tens left in 24,
so add it up, and you get 3 tens and 2 ones.”
No I don’t think Cindy’s shortcut works,
because 3 X 24 = 72 not 32,
Explained my thinking in words, and justified
using a model or partial products as show above.

Eureka Math Grade 4 Module 3 Lesson 7 Template Answer Key

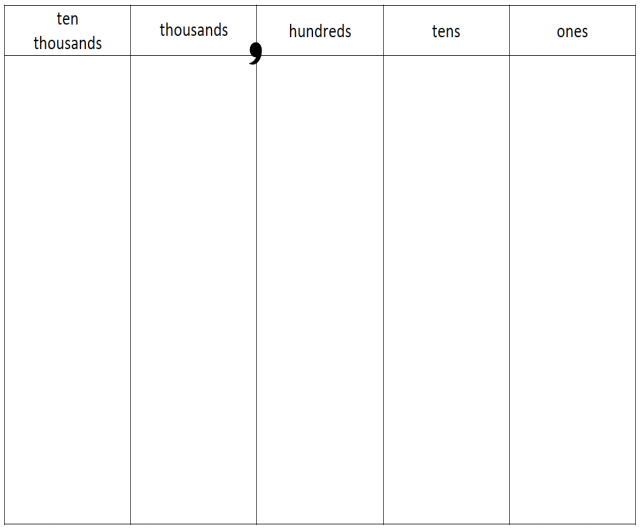
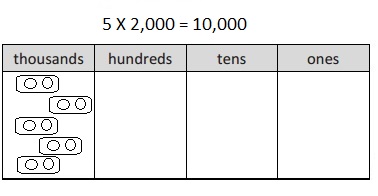
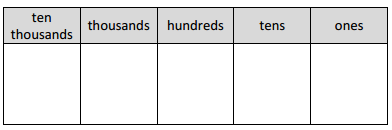
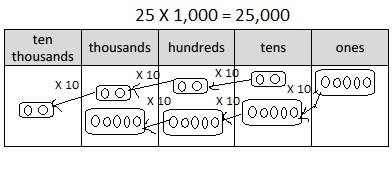
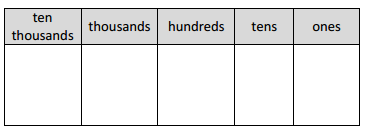
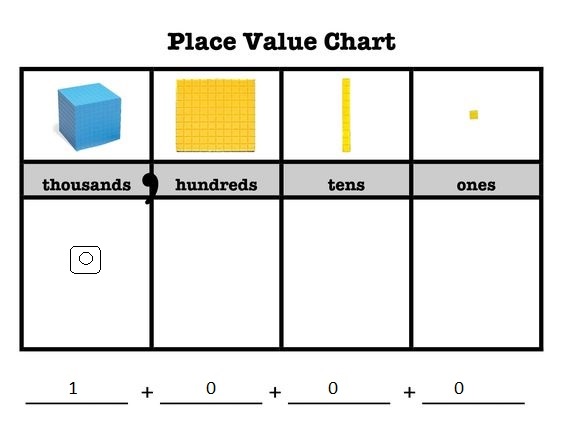
_10,000____________
ten thousand value chart
Answer:

Explanation:
A place value chart is diagram that helps us to find and
compare the place value of the digits in numbers through
millions. The place value of a digit in the place value chart
increases by ten times as we shift to the left and decreases
by ten times as we shift to the right.
For example for ten thousand place value chart where we write
10,000 as 10 in thousands place, 0 in hundreds place, 0 in tens place
and 0 in ones place as shown above.

Engage NY Eureka Math 4th Grade Module 3 Lesson 6 Answer Key

Eureka Math Grade 4 Module 3 Lesson 6 Problem Set Answer Key

Represent the following problem by drawing disks in the place value chart.

Question 1.
To solve 20 × 40, think
(2 tens × 4) × 10 = __800___
20 × (4 × 10) = ___800_____
20 × 40 = _____800__

Answer:

20 X 40 = 800,
(2 tens × 4) × 10 = 8 hundreds,
20 × (4 × 10) = 800,
20 × 40 = 800,

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 20 X 40 = 800,
(2 tens × 4) × 10 =8 hundreds, 20 × (4 × 10) = 800 and
20 × 40 = 800.

Question 2.
Draw an area model to represent 20 × 40.
2 tens × 4 tens = _____ __8 hundreds__________
Answer:

Explanation:
Drawn an area model to represent 20 × 40,
as shown above 2 tens X 4 tens = 8 hundreds.

Question 3.
Draw an area model to represent 30 × 40.
3 tens × 4 tens = _____ twelve hundreds_____________
30 × 40 = __12,00____
Answer:

Explanation:
Drawn an area model to represent 30 × 40,
as shown above 3 tens X 4 tens = 12 hundreds.

Question 4.
Draw an area model to represent 20 × 50.
2 tens × 5 tens = _____ ___1 thousand__________
20 × 50 = __1,000_____
Answer:

Explanation:
Drawn an area model to represent 20 × 50,
as shown above 2 tens X 5 tens = 1 thousand.

Rewrite each equation in unit form and solve.

Question 5.
20 × 20 = __400______
2 tens × 2 tens = ___4__ hundreds
Answer:
20 X 20 = 400,
2 tens × 2 tens = 4 hundreds,

Explanation:
Given equation is 20 X 20, Rewrote in unit form as
2 tens X 2 tens = 4 hundreds, So 20 X 20 = 40.

Question 6.
60 × 20 = ___1,200____
6 tens × 2 __tens___ = __12__ hundreds
Answer:
60 X 20 = 1,200,
6 tens × 2 tens = 12 hundreds,

Explanation:
Given equation is 60 X 20 = 1,200,  Rewrote in unit form as
6 tens X 2 tens = 12 hundreds, So 60 X 20 = 1,200.

Question 7.
70 × 20 = __1,400_____
__7___ tens × __2___ tens = 1,400__
Answer:
70 X 20 = 1,400,
7 tens X 2 tens = 1,400,

Explanation:
Given equation is 70 X 20 = 1,400, Rewrote in unit form as
7 tens X 2 tens = 14 hundreds, So 70 X 20 = 1,400.

Question 8.
70 × 30 = ___2,100____
__7__ __tens_____ × __3__ _tens______ = __21__ hundreds
Answer:
70 X 30 = 2,100,
7 tens X 3 tens = 21 hundreds,

Explanation:
Given equation is 70 X 30 = 2,100, Rewrote in unit form as
7 tens X 3 tens = 21 hundreds, So 70 X 30 = 2,100.

Question 9.
If there are 40 seats per row, how many seats are in 90 rows?
Answer:
There are 3,600 seats in 90 rows,

Explanation:
Given there are 40 seats per row, So number of seats in 90 rows are
40 seats X 90 = 3,600 seats, therefore there are 3,600 seats in 90 rows.

Question 10.
One ticket to the symphony costs $50. How much
money is collected if 80 tickets are sold?
Answer:
$4,000 amount money is collected if 80 tickets are sold,

Explanation:
Given one ticket to the symphony costs $50. So
money collected if 80 tickets are sold are $50 X 80 = $4,000.
Therefore, $4,000 amount money is collected if 80 tickets are sold.

Eureka Math Grade 4 Module 3 Lesson 6 Exit Ticket Answer Key

Represent the following problem by drawing disks in the place value chart.
Question 1.
To solve 20 × 30, think
(2 tens × 3) × 10 = ____600____
20 × (3 × 10) = ____600____
20 × 30 = ___600____

Answer:

20 X 30 = 600,
(2 tens × 3) × 10 =6 hundreds,
20 × (3 × 10) = 600,
20 × 30 = 600,

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 20 X 30 = 600,
(2 tens × 3) × 10 =3 hundreds, 20 × (3 × 10) = 600 and
20 × 30 = 600.

Question 2.
Draw an area model to represent 20 × 30.
2 tens × 3 tens = _____ _6 hundreds___________
Answer:

Explanation:
Drawn an area model to represent 20 × 30,
as shown above 2 tens X 3 tens = 6 hundreds.

Question 3.
Every night, Eloise reads 40 pages. How many total pages
does she read at night during the 30 days of November?
Answer:
1,200 pages she read at night during the 30 days
of November,

Explanation:
Given every night, Eloise reads 40 pages, Total number of
pages she read at night during the 30 days of November are
40 pages X 30 = 1,200 pages, So Eloise 1,200 pages she read at
night during the 30 days of November.

Eureka Math Grade 4 Module 3 Lesson 6 Homework Answer Key

Represent the following problem by drawing disks in the place value chart.

Question 1.
To solve 30 × 60, think
(3 tens × 6) × 10 = ___1,800_____
30 × (6 × 10) = __1,800______
30 × 60 = __1,800_____

Answer:

30 X 60 = 1,800,
(3 tens × 6) × 10 =18 hundreds,
30 × (6 × 10) = 1,800,
30 × 60 = 1,800,

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 30 X 60 = 1,800,
(3 tens × 6) × 10 =18 hundreds, 30 × (6 × 10) = 1,800 and
30 × 60 = 1,800.

Question 2.
Draw an area model to represent 30 × 60.
3 tens × 6 tens = _____18 hundreds_____________
Answer:

Explanation:
Drawn an area model to represent 30 × 60,
as shown above 3 tens X 6 tens = 18 hundreds.

Question 3.
Draw an area model to represent 20 × 20.
2 tens × 2 tens = _____ 4 hundreds_____________
20 × 20 = __400____
Answer:

Explanation:
Drawn an area model to represent 20 × 20,
as shown above 2 tens X 2 tens = 4 hundreds.

Question 4.
Draw an area model to represent 40 × 60.
4 tens × 6 tens = __24___ _hundreds____________
40 × 60 = ___240____
Answer:

Explanation:
Drawn an area model to represent 40 × 60,
as shown above 4 tens X 6 tens = 24 hundreds.

Rewrite each equation in unit form and solve.

Question 5.
50 × 20 = ___1,000_____
5 tens × 2 tens = _10____ hundreds
Answer:
50 X 20 = 1,000,
5 tens X 2 tens = 10 hundreds,

Explanation:
Given equation is 50 X 20 = 1,000, Rewrote in unit form as
5 tens X 2 tens = 10 hundreds, So 50 X 20 = 1,000.

Question 6.
30 × 50 = _1,500____
3 tens × 5 _tens___ = _15___ hundreds
Answer:
30 X 50 = 1,500,
3 tes X 5 tens = 15 hundreds,

Explanation:
Given equation is 30 X 50 = 1,500, Rewrote in unit form as
3 tens X 5 tens = 15 hundreds, So 30 X 50 = 1,500.

Question 7.
60 × 20 = __1,200______
__6___ tens × __2___ tens = 12 __hundreds_______
Answer:
60 X 20 = 1,200,
6 tens X 2 tens = 12 hundreds,

Explanation:
Given equation is 60 X 20 = 1,200, Rewrote in unit form as
6 tens X 2 tens = 12 hundreds, So 60 X 20 = 1,200.

Question 8.
40 × 70 = __2,800______
_4___ ___tens____ × _7___ __tens_____ = __28___ hundreds
Answer:
40 X 70 = 2,800,
4 tens X 7 tens = 28 hundreds,

Explanation:
Given equation is 40 X 70 = 2,800, Rewrote in unit form as
4 tens X 7 tens = 28 hundreds, So 40 X 70 = 2,800.

Question 9.
There are 60 seconds in a minute and 60 minutes in an hour.
How many seconds are in one hour?
Answer:
There are 3,600 seconds in one hour,

Explanation:
There are 60 seconds in a minute and 60 minutes in an hour.
Number of seconds are there in one hour is 60 seconds X 60 =
3,600 seconds,therefore, there are 3,600 seconds in one hour.

Question 10.
To print a comic book, 50 pieces of paper are needed.
How many pieces of paper are needed to print 40 comic books?
Answer:
Number of pieces of paper needed to print 40 comic books are
2,000 pieces,

Explanation:
Given to print a comic book, 50 pieces of paper are needed.
So number of pieces of paper are needed to print 40 comic books
are 50 pieces X 40 = 2,000 pieces.

Engage NY Eureka Math 4th Grade Module 3 Lesson 5 Answer Key

Eureka Math Grade 4 Module 3 Lesson 5 Problem Set Answer Key

Draw place value disks to represent the value of the following expressions.

Question 1.
2 × 3 = __6____
2 times __3___ ones is __6___ ones.


Answer:

2 X 3 = 6,
2 times 3 ones is 6 ones,
3
X 2
6__

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 2 X 3 = 6.

Question 2.
2 × 30 = ___60___
2 times __3___ tens is __6 tens_______ .


Answer:

2 X 30 = 60,
2 times 3 tens is 6 tens,
30
X 2
60_

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 2 X 30 = 60.

Question 3.
2 × 300 = ___600___
2 times ___hundreds ___ is _____6 hundreds________.


Answer:

2 X 300 = 600,
2 times 3 hundreds is 6 hundreds,
300
X 2
600_

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 2 X 300 = 600.

Question 4.
2 × 3,000 = __6,000____
__2__ times ___3 thousands___ is ____6 thousands____ .


Answer:

2 X 3,000 = 6,000,
2 times 3 thousands is 6 thousands,
3,000
X   2
6,000_

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 2 X 3,000 = 6,000.

Question 5.
Find the product

Answer:

Explanation:
Given a. 20 X 7 = 140, multiplying 20 with 7 we get 140,

b. 3 X 60 = 180, multiplying 3 with 60 we get 180,

c. 3 X 400 = 1,200, multiplying 3 with 400 we get 1,200,

d. 2 X 800 = 1,600, multiplying 2 with 800 we get 1,600,

e. 7 X 30 = 210, multiplying 7 with 30 we get 210,

f. 60 X 6 = 360, multiplying 60 with 6 we get 360,

g. 400 X 4 = 1,600, multiplying 400 with 4 we get 1,600,

h. 4 X 8,000 = 32,000, multiplying 4 with 8,000 we get 32,000,

i. 5 X 30 = 150, multiplying 5 with 30 we get 150,

j. 5 X 60 = 300, multiplying 5 with 60 we get 300,

k. 5 X 400 = 2,000, multiplying 5 with 400 we get 2,000,

l. 8,000 X 5 = 40,000, multiplying 8,000 with 5 we get 40,000.

Question 6.
Brianna buys 3 packs of balloons for a party.
Each pack has 60 balloons. How many balloons does Brianna have?
Answer:
Brianna have 180 balloons in all,

Explanation:
Given Brianna buys 3 packs of balloons for a party,
Each pack has 60 balloons. So number of balloons
does Brianna have are 3 X 60 balloons = 180 balloons.

Question 7.
Jordan has twenty times as many baseball cards as his brother.
His brother has 9 cards. How many cards does Jordan have?
Answer:
Jordan have 180 cards in total,

Explanation:
Given Jordan has twenty times as many baseball cards
as his brother. His brother has 9 cards. So number of
cards does Jordan have are 20 X 9 cards = 180 cards.

Question 8.
The aquarium has 30 times as many fish in one tank
as Jacob has. The aquarium has 90 fish.
How many fish does Jacob have?
Answer:
Jacob has 3 fishes in all,

Explanation:
Given the aquarium has 30 times as many fish in one tank
as Jacob has. The aquarium has 90 fish.
Number of fishes does Jacob have are 90 fish ÷ 30 = 3 fishes,
(3 X 30 = 90), Therefore, Jacob has 3 fishes in all.

Eureka Math Grade 4 Module 3 Lesson 5 Exit Ticket Answer Key

Draw place value disks to represent the value of the following expressions.

Question 1.
4 × 200 = ___800___
4 times ____2 hundreds_________ is _______800_________.


Answer:

4 X 200 = 800,
4 times 2 hundreds is 800,
200
X 4
800_

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 4 X 200 = 800.

Question 2.
4 × 2,000 = _8,000_____
___4___ times ____2 thousands_______ is __8 thousands_______.


Answer:

4 X 2,000 = 8,000,
4 times 2 thousands is 8 thousands,
2,000
X   4
8,000

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 4 X 2,000 = 8,000.

Question 3.
Find the product.

Answer:

Explanation:
Given a. 30 X 3 = 90, multiplying 30 with 3 we get 90,

b. 8 X 20 = 160, multiplying 8 with 20 we get 160,

c. 6 X 400 = 2,400, multiplying 6 with 400 we get 2,400,

d. 2 X 900 = 1,800, multiplying 2 with 900 we get 1,800,

e. 8 X 80 = 640, multiplying 8 with 80 we get 640,

f. 30 X 4 = 120, multiplying 30 with 4 we get 120,

g. 500 X 6 = 3,000, multiplying 500 with 6 we get 3,000,

h. 8 X 5,000 = 40,000, multiplying 8 with 5,000 we get 40,000.

Question 4.
Bonnie worked for 7 hours each day for 30 days.
How many hours did she work altogether?
Answer:
Bonnie has worked for 210 hours altogether in 30 days,

Explanation:
Given Bonnie worked for 7 hours each day for 30 days.
So number of hours did she work altogether is 7 hours X 30 =
210 hours, Therefore, Bonnie has worked for 210 hours
altogether in 30 days.

Eureka Math Grade 4 Module 3 Lesson 5 Homework Answer Key

Question 1.
5 × 2 = __10____
5 times __2__ ones is __10___ ones.


Answer:

5 X 2 = 10,
5 times 2 ones is 10 ones,
2
X 5
10__

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 5 X 2 = 10.

Question 2.
5 × 20 = _100_____
5 times ____2______ tens is _____10 tens________________.


Answer:

5 X 20 = 100,
5 times 2 tens is 10 tens,
20
X 5
100_

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 5 X 20 = 100.

Question 3.
5 × 200 = __1,000____
5 times ____2 hundreds______ is ____10 hundreds_____.


Answer:

5 X 200 = 1,000,
5 times 2 hundreds is 10 hundreds,
200
X 5
1,000_

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 5 X 200 = 1,000.

Question 4.
5 × 2,000 = _10,000_____
__5__ times _______2 thousands____ is ___10 thousands________ .


Answer:

5 X 2,000 = 10,000,
5 times 2 thousands is 10 thousands,
2,000
X    5
10,000_

Explanation:
Drawn place value disks to represent the value of the
following expression as shown above as 5 X 2,000 = 10,000.

Question 5.
Find the product.

Answer:

Explanation:
Given a. 20 X 9 = 180, multiplying 20 with 9 we get 180,

b. 6 X 70 = 420, multiplying 6 with 70 we get 420,

c. 7 X 700 = 4,900, multiplying 7 with 700 we get 4,900,

d. 3 X 900 = 2,700, multiplying 3 with 900 we get 2,700,

e. 9 X 90 = 810, multiplying 9 with 90 we get 810,

f. 40 X 7 = 280, multiplying 40 with 7 we get 280,

g. 600 X 6 = 3,600, multiplying 600 with 6 we get 3,600,

h. 8 X 6,000 = 48,000, multiplying 8 with 6,000 we get 48,000.

i. 5 X 70 = 350, multiplying 5 with 70 we get 350,

j. 5 X 80 = 400, multiplying 5 with 80 we get 400,

k. 5 X 200 = 1,000, multiplying 5 with 200 we get 1,000,

l. 6,000 X 5 = 30,000, multiplying 6,000 with 5 we get 30,000.

Question 6.
At the school cafeteria, each student who orders
lunch gets 6 chicken nuggets. The cafeteria staff prepares
enough for 300 kids. How many chicken nuggets does the
cafeteria staff prepare altogether?
Answer:
1,800 chicken nuggets the cafeteria staff prepare altogether,

Explanation:
Given at the school cafeteria, each student who orders
lunch gets 6 chicken nuggets. The cafeteria staff prepares
enough for 300 kids. Number of chicken nuggets does the
cafeteria staff prepare altogether is 6 chicken nuggets X 300 = 1,800,
therefore, 1,800 chicken nuggets the cafeteria staff prepare altogether.

Engage NY Eureka Math 4th Grade Module 3 Lesson 4 Answer Key

Eureka Math Grade 4 Module 3 Lesson 4 Problem Set Answer Key

Draw place value disks and arrows as shown to represent each product.

Question 1.
5 × 100 = ___500___
5 × 10 × 10 = ___500___
5 ones × 100 = ___500____

Answer:
5 x 100 = 500,

5 X 10 X 10 = 500,

5 ones × 100 = 500,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the products as 5 x 100 = 500, 5 X 10 X 10 = 500
and 5 ones X 100 = 500.

Question 2.
5 × 1,000 = ____5,000______
5 × 10 × 10 × 10 = __5,000_____
5 ones × 1,000 = ____ _5,000____

Answer:
5 X 1,000 = 5,000,

5 X 10 X 10 X 10 = 5,000,

5 ones × 1,000 = 5,000,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the product as 5 x 1,000 = 5,000,
5 X 10 X 10 X 10 = 5,000 and 5 ones X 1,000 = 5,000.

Question 3.
Fill in the blanks in the following equations.
a. 6 × 10 = ____60____
Answer:
6 x 10 = 60,

Explanation:
Given 6 X 10 multiplying 6 with 10 we get 60,
so 6 X 10 = 60.

b. __100____ × 6 = 600
Answer:
100 X 6 = 600,

Explanation:
Given ____ × 6 = 600, so we get unknown factor as
600 ÷ 6 = 100, so 100 X 6 = 600.

c. 6,000 = ______ × 1,000
Answer:
6,000 = 6 X 1,000,

Explanation:
Given 6,000 = ______ × 1,000, so we get unknown factor as
6,000 ÷ 1,000 = 6, so 6,000 = 6 X 1,000.

d. 10 × 4 = ______
Answer:
10 X 4 = 40,

Explanation:
Given 10 X 4 = ____,multiplying 10 with 4 we get 40,
so 10 X 4 = 40.

e. 4 × ______ = 400
Answer:
4 X 100 = 400,

Explanation:
Given 4 x ____  = 400, so we get unknown factor as
400 ÷ 4 = 100, so 4 X 100 = 400.

f. ______ × 4 = 4,000
Answer:
1,000 X 4 = 4,000,

Explanation:
Given ______ × 1,000 = 4,000 so we get unknown factor as
4,000 ÷ 4 = 1,000, so 1,000 X 4 = 4,000.

g. 1,000 × 9 = ______
Answer:
1,000 X 9 = 9,000,

Explanation:
Given 1,000 X 9 =___ ,multiplying 1,000 with 9 we get 9,000,
so 1,000 X 9 = 9,000.

h. ______ = 10 × 9
Answer:
90 = 10 X 9,
Explanation:
Given _____ = 10 X 9 multiplying 10 with 9 we get 90,
so 90 = 10 X 9.

i. 900 = ______ × 100
Answer:
900 = 9 X 100,

Explanation:
Given 900 = ______ × 100 so we get unknown factor as
900 ÷ 100 = 9, so 900 = 9 X 100.

Draw place value disks and arrows to represent each product.

Question 4.
12 × 10 = ____120______
(1 ten 2 ones) × 10 = ______120_________

Answer:
12 x 10 = 120,
(1 ten 2 ones) × 10 = 120,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the products as 12 x 10 = 120 and (1 ten 2 ones) = 120.

Question 5.
18 × 100 = ___18,00_______
18 × 10 × 10 = __18,00________
(1 ten 8 ones) × 100 = ____18,00________

Answer:
18 × 100 =18,00,
18 × 10 × 10 = 18,00,
(1 ten 8 ones) × 100 = 18,00,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the products as 18 x 100 = 18,00 ,
18 X 10 X 10 = 18,00 and (1 ten 8 ones) × 100 = 18,00.

Question 6.
25 × 1,000 = ____25,000______
25 × 10 × 10 × 10 = ____25,000______
(2 tens 5 ones) × 1,000 = ______25,000__________

Answer:
25 × 1,000 = 25,000,
25 × 10 × 10 × 10 = 25,000,
(2 tens 5 ones) × 1,000 = 25,000,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the products as 25 × 1,000 = 25,000,
25 × 10 × 10 × 10 = 25,000 and (2 tens 5 ones) × 1,000 = 25,000.

Decompose each multiple of 10, 100, or 1,000 before multiplying.

Question 7.
3 × 40 = 3 × 4 × __10___
= 12 × __10____
= ___120_______
Answer:

3 X 40 = 3 X 4 X 10
= 12 X 10
= 120,

Explanation:
Given 3 X 40 decomposing into 10 before multiplying
first we write 40 as 4 X 10,
then we multiply with 3, as 3 X 4 X 10,
Now we multiply 3 and 4 then 10
we get 12 X 10 = 120,
So 3 X 40 = 120.

Question 8.
3 × 200 = 3 × ___2__ × __100____
= ___6___ × ___100___
= ____600____
Answer:
3 X 200 = 3 X 2 X 100
= 6 X 100
= 600,

Explanation:
Given 3 X 200 decomposing into 100 before multiplying
first we write 200 as 2 X 100,
then we multiply with 3 as 3 X 2 X 100,
Now we multiply 3 and 2 then 100
we get 6 X 100 = 6,00,
So 3 X 200 = 600.

Question 9.
4 × 4,000 = __4___ × __4___× __1,000_______
= ___16___ × __1,000_______
= ____16,000_____
Answer:
4 × 4,000 = 4 X 4 X 1,000,
=16 X 1,000
= 16,000,

Explanation:
Given 4 X 4,000 decomposing into 1,000 before multiplying
first we write 4,000 as 4 X 1,000,
then we multiply with 4 as 4 X 4 X 1,000,
Now we multiply 4 and 4 then 1,000
we get 16 X 1,000 = 16,000,
So 4 X 4,000 = 16,000.

Question 10.
5 × 4,000 = __5___ × __4___ × ___1,000______
= ___20___ × __1,000______
= __20,000______
Answer:
5 X 4,000 = 5 X 4 X 1,000,
= 20 X 1,000,
= 20,000,

Explanation:
Given 5 X 4,000 decomposing into 1,000 before multiplying
first we write 4,000 as 4 X 1,000,
then we multiply with 5 as 5 X 4 X 1,000,
Now we multiply 5 and 4 then 1,000
we get 20 X 1,000 = 20,000,
So 5 X 4,000 = 20,000.

Eureka Math Grade 4 Module 3 Lesson 4 Exit Ticket Answer Key

Fill in the blanks in the following equations.

a. 5 × 10 = ___50_____
Answer:
5 X 10 = 50,

Explanation:
Given 5 X 10 multiplying 5 with 10 we get 50,
so 5 X 10 = 50.

b. ______ × 5 = 500
Answer:
100 X 5 = 500,

Explanation:
Given  ____  X 5 = 500 so we get unknown factor as
500 ÷ 5 = 100, so 100 X 5 = 500.

c. 5,000 = ______ × 1000
Answer:
5,000 = 5 x 1,000,

Explanation:
Given 5,000 = _______ X 1,000, now we get unknown factor as
5,000 ÷ 1,000 = 5, so 5,000 = 5 X 1,000.

d. 10 × 2 = ______
Answer:
10 X 2 = 20,

Explanation:
Given 10 X 2 multiplying 10 with 2 we get 20,
so 10 X 2 = 20.

e. ______ × 20 = 2,000
Answer:
100 X 20 = 2,000,

Explanation:
Given_______ X 20 = 2,000, now we get unknown factor as
2,000 ÷ 20 = 100, so 100 X 20 = 2,000.

f. 2,000 = 10 × ______
Answer:
2,000 = 10 X 200,

Explanation:
Given 2,000 = 10 X _________, now we get unknown factor as
2,000 ÷ 10 = 200, so 2,000 = 10 X 200.

g. 100 × 18 = ______
Answer:
100 X 18 = 1,800,

Explanation:
Given 100 X 18 multiplying 100 with 18 we get 1,800
so 100 X 18 = 1,800.

h. ______ = 10 × 32
Answer:
320 = 10 X 32,

Explanation:
Given_______  = 10 X 32, multiplying 10 with 32 we get 320,
so 320 = 10 X 32.

i. 4,800 = ______ × 100
Answer:
4,800 = 48 X 100,

Explanation:
Given 4,800 = _______ X 100, now we get unknown factor as
4,800 ÷ 100 = 48, so 4,800 = 48 X 100.

j. 60 × 4 = ______
Answer:
60 × 4 = 240,

Explanation:
Given 60 X 4, multiplying 60 with 4 we get 240,
so 60 X 4 = 240.

k. 5 × 600 = ______
Answer:
5 X 600 = 3,000,

Explanation:
Given 5 X 600 = _________,multiplying 5 with 600 we get 3,000,
so 5 X 600 = 3,000.

l. 8,000 × 5 = ______,
Answer:
8,000 X 5 = 40,000,

Explanation:
Given 8,000 X 5 = _______, multiplying 8,000 with 5 we get 40,000,
so 8,000 X 5 = 40,000.

Eureka Math Grade 4 Module 3 Lesson 4 Homework Answer Key

Question 1.
7 × 100 = ___700_______
7 × 10 × 10 = __700________
7 ones × 100 = ____700_______

Answer:
7 X 100 = 700,

7 × 10 × 10 = 700,

7 ones × 100 = 700,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the products as 7 x 100 = 700, 7 X 10 X 10 = 700
and 7 ones X 100 = 700.

Question 2.
7 × 1,000 = ____7,000______
7 × 10 × 10 × 10 = __7,000________
7 ones × 1,000 = ____7,000_____________

Answer:
7 × 1,000 = 7,000,

7 × 10 × 10 × 10 = 7,000,

7 ones × 1,000 = 7,000,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the products as 7 x 1,000 = 7,000, 7 X 10 X 10 X 10 = 7,000
and 7 ones X 1,000 = 7,000.

Question 3.
Fill in the blanks in the following equations.
a. 8 × 10 = ________
Answer:
8 X 10 = 80,

Explanation:
Given 8 X 10 = ________, multiplying 8 with 10 we get 80,
so 8 X 10 = 80.

b. ______ × 8 = 800
Answer:
100 X 8 = 800,

Explanation:
Given ______ X 8 = 800, now we get unknown factor as
800 ÷ 8 = 100, so 100 X 8 = 800.

c. 8,000 = ______ × 1,000
Answer:
8,000 = 8 X 1,000,

Explanation:
Given 8,000 = 8 X 1,000, now we get unknown factor as
8,000 ÷ 1,000 = 8, so 8,000 = 8 X 1,000.

d. 10 × 3 = ______
Answer:
10 X 3 = 30,

Explanation:
Given 10 X 3 = ________, multiplying 10 with 3 we get 30,
so 10 X 3 = 30.

e. 3 × ______ = 3,000
Answer:
3 X 1,000 = 3,000,

Explanation:
Given 3 X ______ = 3,000, now we get unknown factor as
3,000 ÷ 3 = 1,000, so 3 X 1,000 = 3,000.

f. ______ × 3 = 300
Answer:
100 X 3= 300,

Explanation:
Given ______ X 3 = 300, now we get unknown factor as
300 ÷ 3 = 100, so 100 X 3 = 300.

g. 1,000 × 4 = ______
Answer:
1,000 X 4 = 4,000,

Explanation:
Given 1,000 X 4 = ________, multiplying 1,000 with 4 we get 4,000,
so 1,000 X 4 = 4,000.

h. ______ = 10 × 4
Answer:
40 = 10 X 4,

Explanation:
Given ______ = 10 X 4, multiplying 10 with 4 we get 40,
so 40 = 10 X 4.

i. 400 = ______ × 100
Answer:
400 = 4 X 100,

Explanation:
Given 400 = 4 X 100, now we get unknown factor as
400 ÷ 100 = 4, so 400 = 4 X 100.

Draw place value disks and arrows to represent each product.

Question 4.
15 × 10 = ___150_______
(1 ten 5 ones) × 10 = _____150________

Answer:
15 X 10 = 150,
(1 ten 5 ones) × 10 = 150,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the products as 15 x 10 = 150 and (1 ten 5 ones) = 150.

Question 5.
17 × 100 = ___1,700_______
17 × 10 × 10 = ___1,700_______
(1 ten 7 ones) × 100 = _______1,700___________

Answer:
17 × 100 = 1,700,
17 × 10 × 10 = 17,00,
(1 ten 7 ones) × 100 = 17,00,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the products as 17 x 100 = 17,00 ,
17 X 10 X 10 = 17,00 and (1 ten 7 ones) × 100 = 17,00.

Question 6.
36 × 1,000 = __________
36 × 10 × 10 × 10 = __________
(3 tens 6 ones) × 1,000 = ____________

Answer:
36 × 1,000 = 36,000,
36 × 10 × 10 × 10 = 36,000,
(3 tens 6 ones) × 1,000 = 36,000,

Explanation:
Drawn and  placed value disks and arrow as shown above
to represent the products as 36 × 1,000 = 36,000,
36 × 10 × 10 × 10 = 36,000 and (3 tens 6 ones) × 1,000 = 36,000.

Decompose each multiple of 10, 100, or 1000 before multiplying.

Question 7.
2 × 80 = 2 × 8 × __16___
= 16 × _10_____
= ___160_______
Answer:
2 X 80 = 2 X 8 X 10,
= 16 X 10,
= 160,

Explanation:
Given 2 X 80 decomposing into 10 before multiplying
first we write 80 as 8 X 10,
then we multiply with 2, as 2 X 8 X 10,
Now we multiply 2 and 8 then 10
we get 16 X 10 = 160,
So 2 X 80 = 160.

Question 8.
2 × 400 = 2 × _4___ × __100____
= ___8___ × __100____
= ___800_____
Answer:
2 X 400 = 2 X 4 X 100
= 8 X 100
= 800,

Explanation:
Given 3 X 200 decomposing into 100 before multiplying
first we write 200 as 2 X 100,
then we multiply with 3 as 3 X 2 X 100,
Now we multiply 3 and 2 then 100
we get 6 X 100 = 6,00,
So 3 X 200 = 600.

Question 9.
5 × 5,000 = _____ × _____ × _________
= ______ × _________
= _________
Answer:
5 × 5,000 = 5 X 5 X 1,000,
=25 X 1,000
= 25,000,

Explanation:
Given 5 X 5,000 decomposing into 1,000 before multiplying
first we write 5,000 as 5 X 1,000,
then we multiply with 5 as 5 X 5 X 1,000,
Now we multiply 5 and 5 then 1,000
we get 25 X 1,000 = 25,000,
So 5 X 5,000 = 25,000.

Question 10.
7 × 6,000 = _____ × _____ × _________
= ________ × ________
= ________
Answer:
7 X 6,000 = 7 X 6 X 1,000,
= 42 X 1,000,
= 42,000,

Explanation:
Given 7 X 6,000 decomposing into 1,000 before multiplying
first we write 6,000 as 6 X 1,000,
then we multiply with 7 as 7 X 6 X 1,000,
Now we multiply 7 and 6 then 1,000
we get 42 X 1,000 = 42,000,
So 7 X 6,000 = 42,000.

Eureka Math Grade 4 Module 3 Lesson 4 Template Answer Key

______1,000___________
thousands place value chart
Answer:

Explanation:
A place value chart is diagram that helps us to find and
compare the place value of the digits in numbers through
millions. The place value of a digit in the place value chart
increases by ten times as we shift to the left and decreases
by ten times as we shift to the right.
For example for one thousand place value chart where we write
1,000 as 1 in thousands place, 0 in hundreds place, 0 in tens place
and 0 in ones place as shown above.

Engage NY Eureka Math 4th Grade Module 3 Lesson 3 Answer Key

Eureka Math Grade 4 Module 3 Lesson 3 Sprint Answer Key

Squares and Unknown Factors

Question 1.
2 × 2 =
Answer:
2 X 2 = 4,

Explanation:
Given 2 X 2 = the squares of 2 is 4 and
2 X 2 = 4.

Question 2.
2 × _____ = 4
Answer:
2 X 2 = 4,

Explanation:
Given 2 × _____ = 4, the unknown factor is
4 ÷ 2 = 2, So 2 X 2 = 4.

Question 3.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3 = the squares of 3 is 9 and
3 X 3 = 9.

Question 4.
3 × _____ = 9
Answer:
3 X 3 = 9,

Explanation:
Given 3 × _____ = 9, the unknown factor is
9 ÷ 3 = 2, So 3 X 3 = 9.

Question 5.
5 × 5 =
Answer:
5 X 5 = 25,

Explanation:
Given 5 X 5 = the squares of 5 is 25 and
5 X 5 = 25.

Question 6.
5 × _____ = 25
Answer:
5 X 5 = 25,

Explanation:
Given 5 × _____ = 25, the unknown factor is
25 ÷ 5 = 5, So 5 X 5 = 25.

Question 7.
1 × _____ = 1
Answer:
1 x 1 = 1,

Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.

Question 8.
1 × 1 =
Answer:
1 X 1 = 1,

Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.

Question 9.
4 × _____ = 16
Answer:
4 X 4 = 16,

Explanation:
Given 4 × _____ = 16, the unknown factor is
16 ÷ 4 = 1, So 4 X 4 = 16.

Question 10.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.

Question 11.
7 × _____ = 49
Answer:
7 X 7 = 49,

Explanation:
Given 7 × _____ = 49, the unknown factor is
49 ÷ 7 = 7, So 7 X 7 = 49.

Question 12.
7 × 7 =
Answer:
7 X 7 = 49,

Explanation:
Given 7 X 7 = the squares of 7 is 49 and
7 X 7 = 49.

Question 13.
8 × 8 =
Answer:
8 X 8 = 64,

Explanation:
Given 8 X 8 = the squares of 8 is 64 and
8 X 8 = 64.

Question 14.
8 × _____ = 64
Answer:
8 X 8 = 64,

Explanation:
Given 8 × _____ = 64, the unknown factor is
64 ÷ 8 = 8, So 8 X 8 = 64.

Question 15.
10 × 10 =
Answer:
10 X 10 = 100,

Explanation:
Given 10 X 10 = the squares of 10 is 100 and
10 X 10 = 100.

Question 16.
10 × _____ = 100
Answer:
10 X 10 = 100,

Explanation:
Given 10 × _____ = 100, the unknown factor is
100 ÷ 10 = 10, So 10 X 10 = 100.

Question 17.
9 × _____ = 81
Answer:
9 X 9 = 81,

Explanation:
Given 9 × _____ = 81, the unknown factor is
81 ÷ 9 = 9, So 9 X 9 = 81.

Question 18.
9 × 9 =
Answer:
9 x 9 = 81,

Explanation:
Given 9 X 9 = the squares of 9 is 81 and
9 X 9 = 81.

Question 19.
2 × _____ = 10
Answer:
2 X 5 = 10,

Explanation:
Given 2 × _____ = 10, the unknown factor is
10 ÷ 2 = 5, So 2 X 5 = 10.

Question 20.
2 × _____ = 18
Answer:
2 X 9 = 18,

Explanation:
Given 2 × _____ = 18, the unknown factor is
18 ÷ 2 = 9, So 2 X 9 = 18.

Question 21.
2 × 2 =
Answer:
2 x 2 = 4,

Explanation:
Given 2 X 2 = the squares of 2 is 4 and
2 X 2 = 4.

Question 22.
3 × _____ = 12
Answer:
3 X 4 = 12,

Explanation:
Given 3 × _____ = 12, the unknown factor is
12 ÷ 3 = 4, So 3 X 4 = 12.

Question 23.
3 × _____ = 21
Answer:
3 X 7 = 21,

Explanation:
Given 3 × _____ = 21, the unknown factor is
21 ÷ 3 = 7, So 3 X 7 = 21.

Question 24.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3 = the squares of 3 is 9 and
3 X 3 = 9.

Question 25.
4 × _____ = 20
Answer:
4 X 5 = 20,

Explanation:
Given 4 × _____ = 20, the unknown factor is
20 ÷ 4 = 5, So 4 X 5 = 20.

Question 26.
4 × _____ = 32
Answer:
4 X 8 = 32,

Explanation:
Given 4 × _____ = 32, the unknown factor is
32 ÷ 4 = 8, So 4 X 8 = 32.

Question 27.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.

Question 28.
5 × _____ = 20
Answer:
5 X 4 = 20,

Explanation:
Given 5 × _____ = 20, the unknown factor is
20 ÷ 5 = 4, So 5 X 4 = 20.

Question 29.
5 × _____ = 40
Answer:
5 X 8 = 40,

Explanation:
Given 5 × _____ = 40, the unknown factor is
40 ÷ 5 = 8, So 5 X 8 = 40.

Question 30.
5 × 5 =
Answer:
5 X 5 = 25,

Explanation:
Given 5 X 5 = the squares of 5 is 25 and
5 X 5 = 25.

Question 31.
6 × _____ = 18
Answer:
6 X 3 = 18,

Explanation:
Given 6 × _____ = 18, the unknown factor is
18 ÷ 6 = 3, So 6 X 3 = 18.

Question 32.
6 × _____ = 54
Answer:
6 X 9 = 54,

Explanation:
Given 6 × _____ = 18, the unknown factor is
54 ÷ 6 = 9, So 6 X 9 = 54.

Question 33.
6 × 6 =
Answer:
6 X 6 = 36,

Explanation:
Given 6 X 6 = the squares of 6 is 36 and
6 X 6 = 36.

Question 34.
7 × _____ = 28
Answer:
7 X 4 = 28,

Explanation:
Given 7 × _____ = 28, the unknown factor is
28 ÷ 4 = 7, So 7 X 4 = 28.

Question 35.
7 × _____ = 56
Answer:
7 X 8 = 56,

Explanation:
Given 7 × _____ = 56, the unknown factor is
56 ÷ 7 = 8, So 7 X 8 = 56.

Question 36.
7 × 7 =
Answer:
7 X 7 = 49,

Explanation:
Given 7 X 7 = 49 the squares of 7 is 49 and
7 X 7 = 49.

Question 37.
8 × _____ = 24
Answer:
8 X 3 = 24,

Explanation:
Given 8 × _____ = 24, the unknown factor is
24 ÷ 8 = 3, So 8 X 3 = 24.

Question 38.
8 × _____ = 72
Answer:
8 X 9 = 72,

Explanation:
Given 8 × _____ = 72, the unknown factor is
72 ÷ 8 = 9, So 8 X 9 = 72.

Question 39.
8 × 8 =
Answer:
8 X 8 = 64,

Explanation:
Given 8 X 8= 64 the squares of 8 is 64 and
8 X 8 = 64.

Question 40.
9 × _____ = 36
Answer:
9 X 4 = 36,

Explanation:
Given 9 × _____ = 36, the unknown factor is
36 ÷ 9 = 4, So 9 X 4 = 36.

Question 41.
9 × _____ = 63
Answer:
9 X 7 = 63,

Explanation:
Given 9 × _____ = 63, the unknown factor is
63 ÷ 9 = 7, So 9 X 7 = 63.

Question 42.
9 × 9 =
Answer:
9 x 9 = 81,

Explanation:
Given 9 X 9= 81 the squares of 9 is 81 and
9 X 9 = 81.

Question 43.
9 × _____ = 54
Answer:
9 X 6 = 54,

Explanation:
Given 9 × _____ = 54, the unknown factor is
54 ÷ 9 = 6, So 9 X 6 = 54.

Question 44.
10 × 10 =
Answer:
10 X 10 = 100,

Explanation:
Given 10 X 10= 100 the squares of 10 is 100 and
10 X 10 = 100.

Squares and Unknown Factors

Question 1.
5 × 5 =
Answer:
5 X 5 = 25,

Explanation:
Given 5 X 5= 25 the squares of 5 is 25 and
5 X 5 = 25.

Question 2.
5 × _____ = 25
Answer:
5 X 5 = 25,

Explanation:
Given 5 × _____ = 25, the unknown factor is
25 ÷ 5 = 5, So 5 X 5 = 25.

Question 3.
2 × 2 =
Answer:
2 X 2 = 4,

Explanation:
Given 2 X 2= 4 the squares of 2 is 4 and
2 X 2 = 4.

Question 4.
2 × _____ = 4
Answer:
2 X 2 = 4,

Explanation:
Given 2 × _____ = 4, the unknown factor is
4 ÷ 2 = 2, So 2 X 2 = 4.

Question 5.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3= 9 the squares of 3 is 9 and
3 X 3 = 9.

Question 6.
3 × _____ = 9
Answer:
3 x 3 = 9,

Explanation:
Given 3 × _____ = 9, the unknown factor is
9 ÷ 3 = 3, So 3 X 3 = 9.

Question 7.
1 × 1 =
Answer:
1 X 1 = 1,

Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.

Question 8.
1 × _____ = 1
Answer:
1 x 1 = 1,

Explanation:
Given 1 × _____ = 1, the unknown factor is
1 ÷ 1 = 1, So 1 X 1 = 1.

Question 9.
4 × _____ = 16
Answer:
4 X 4 = 16,

Explanation:
Given 4 × _____ = 16, the unknown factor is
16 ÷ 4 = 1, So 4 X 4 = 16.

Question 10.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.

Question 11.
6 × _____ = 36
Answer:
6 X 6 = 36,

Explanation:
Given 6 × _____ = 36, the unknown factor is
36 ÷ 6 = 6, So 6 X 6 = 36.

Question 12.
6 × 6 =
Answer:
6 X 6 = 36,

Explanation:
Given 6 X 6 = the squares of 6 is 36 and
6 X 6 = 36.

Question 13.
9 × 9 =
Answer:
9 x 9 = 81,

Explanation:
Given 9 X 9 = the squares of 9 is 81 and
9 X 9 = 81.

Question 14.
9 × _____ = 81
Answer:
9 X 9 = 81,

Explanation:
Given 9 × _____ = 81, the unknown factor is
81 ÷ 9 = 9, So 9 X 9 = 81.

Question 15.
10 × 10 =
Answer:
10 X 10 = 100,

Explanation:
Given 10 X 10 = the squares of 10 is 100 and
10 X 10 = 100.

Question 16.
10 × _____ = 100
Answer:
10 X 10 = 100,

Explanation:
Given 10 × _____ = 100, the unknown factor is
100 ÷ 10 = 10, So 10 X 10 = 100.

Question 17.
7 × _____ = 49
Answer:
7 X 7 = 49,

Explanation:
Given 7 × _____ = 49, the unknown factor is
49 ÷ 7 = 7, So 7 X 7 = 49.

Question 18.
7 × 7 =
Answer:
7 X 7 = 49,

Explanation:
Given 7 X 7 = the squares of 7 is 49 and
7 X 7 = 49.

Question 19.
2 × _____ = 8
Answer:
2 X 4 = 8,

Explanation:
Given 2 × _____ = 8, the unknown factor is
8 ÷ 2 = 4, So 2 X 4 = 8.

Question 20.
2 × _____ = 16
Answer:
2 X 8 = 16,

Explanation:
Given 2 × _____ = 16, the unknown factor is
16 ÷ 2 = 8, So 2 X 8 = 16.

Question 21.
2 × 2 =
Answer:
2 X 2 = 4,

Explanation:
Given 2 X 2 = the squares of 2 is 4 and
2 X 2 = 4.

Question 22.
3 × _____ = 15
Answer:
3 X 5 = 15,

Explanation:
Given 3 × _____ = 15, the unknown factor is
15 ÷ 3 = 5, So 3 X 5 = 15.

Question 23.
3 × _____ = 24
Answer:
3 X 8 = 24,

Explanation:
Given 3 × _____ = 24, the unknown factor is
24 ÷ 3 = 8, So 3 X 8 = 24.

Question 24.
3 × 3 =
Answer:
3 X 3 = 9,

Explanation:
Given 3 X 3 = the squares of 3 is 9 and
3 X 3 = 9.

Question 25.
4 × _____ = 12
Answer:

Explanation:
Given 4 × _____ = 12, the unknown factor is
12 ÷ 4 = 3, So 4 X 3 = 12.

Question 26.
4 × _____ = 28
Answer:
4 X 7 = 28,

Explanation:
Given 4 × _____ = 28, the unknown factor is
28 ÷ 4 = 7, So 4 X 7 = 28.

Question 27.
4 × 4 =
Answer:
4 X 4 = 16,

Explanation:
Given 4 X 4 = the squares of 4 is 16 and
4 X 4 = 16.

Question 28.
5 × _____ = 10,
Answer:
5 X 2 = 10,

Explanation:
Given 5 × _____ = 10, the unknown factor is
10 ÷ 5 = 2, So 5 X 2 = 10.

Question 29.
5 × _____ = 35,
Answer:
5 X 7 = 35,

Explanation:
Given 5 × _____ = 10, the unknown factor is
35 ÷ 5 = 7, So 5 X 7 = 35.

Question 30.
5 × 5 =
Answer:
5 X 5 = 25,

Explanation:
Given 5 X 5 = the squares of 5 is 25 and
5 X 5 = 25.

Question 31.
6 × _____ = 24
Answer:
6 X 4 = 24,

Explanation:
Given 6 × _____ = 24, the unknown factor is
24 ÷ 6 = 4, So 6 X 4 = 24.

Question 32.
6 × _____ = 48
Answer:
6 X 8 = 48,

Explanation:
Given 6 × _____ = 48, the unknown factor is
48 ÷ 6 = 8, So 6 X 8 = 48.

Question 33.
6 × 6 =
Answer:
6 X 6 = 36,

Explanation:
Given 6 × _____ = 36, the unknown factor is
36 ÷ 6 = 6, So 6 X 6 = 36.

Question 34.
7 × _____ = 21
Answer:
7 X 3 = 21,

Explanation:
Given 7 × _____ = 21, the unknown factor is
21 ÷ 7 = 3, So 7 X 3 = 21.

Question 35.
7 × _____ = 63
Answer:
7 X 9 = 63,

Explanation:
Given 7 × _____ = 63, the unknown factor is
63 ÷ 7 = 9, So 7 X 9 = 63.

Question 36.
7 × 7 =
Answer:
7 X 7 = 49,

Explanation:
Given 7 X 7 = the squares of 7 is 49 and
7 X 7 = 49.

Question 37.
8 × _____ = 32
Answer:
8 X 4 = 32,

Explanation:
Given 8 × _____ = 32, the unknown factor is
32 ÷ 8 = 4, So 8 X 4 = 32.

Question 38.
8 × _____ = 56
Answer:
8 X 7 = 56,

Explanation:
Given 8 × _____ = 56, the unknown factor is
56 ÷ 8 = 7, So 8 X 7 = 56.

Question 39.
8 × 8 =
Answer:
8 X 8 = 64,

Explanation:
Given 8 X 8 = the squares of 8 is 64 and
8 X 8 = 64.

Question 40.
9 × _____ = 27
Answer:
9 X 3 = 27,

Explanation:
Given 9 × _____ = 27, the unknown factor is
27 ÷ 9 = 3, So 9 X 3 = 27.

Question 41.
9 × _____ = 72
Answer:
9 X 8 = 72,

Explanation:
Given 9 × _____ = 72, the unknown factor is
72 ÷ 9 = 8, So 9 X 8 = 72.

Question 42.
9 × 9 =
Answer:
9 X 9 = 81,

Explanation:
Given 9 X 9 = the squares of 8 is 64 and
9 X 9 = 81.

Question 43.
9 × _____ = 63
Answer:
9 X 7 = 63,

Explanation:
Given 9 × _____ = 63, the unknown factor is
63 ÷ 9 = 7, So 9 X 7 = 63.

Question 44.
10 × 10 =
Answer:
10 X 10 = 100,

Explanation:
Given 10 X 10 = the squares of 10 is 100 and
10 X 10 = 100.

Eureka Math Grade 4 Module 3 Lesson 3 Problem Set Answer Key

Solve the following problems. Use pictures, numbers, or words to show your work.

Question 1.
The rectangular projection screen in the school auditorium
is 5 times as long and 5 times as wide as the rectangular
screen in the library. The screen in the library is 4 feet long
with a perimeter of 14 feet. What is the perimeter of the
screen in the auditorium?
Answer:
The perimeter of the screen in the auditorium is 70 feet,

Explanation:
Given the rectangular projection screen in the school auditorium
is 5 times as long and 5 times as wide as the rectangular
screen in the library. The screen in the library is 4 feet long
with a perimeter of 14 feet. Let wide of of screen in library be w feet,
so 14 feet = 2 X (4 feet + w feet),
14 feet = 8 feet + 2 X w feet,
2 X w feet = 14 feet – 8 feet = 6 feet,
So wide = 6 feet ÷ 2 = 3 feet,
Now the rectangular projection screen in the school auditorium
is 5 X 4 feet = 20 feet long and wide is 5 X 3 feet = 15 feet wide,
So the perimeter of the screen in the auditorium is
2 X (20 feet + 15 feet) = 2 X 35 feet = 70 feet.

Question 2.
The width of David’s rectangular tent is 5 feet. The length is
twice the width. David’s rectangular air mattress measures
3 feet by 6 feet. If David puts the air mattress in the tent,
how many square feet of floor space will be available for
the rest of his things?
Answer:
32 square feet of floor space will be available for
the rest of his things,

Explanation:
Given the width of David’s rectangular tent is 5 feet. The length is
twice the width. David’s rectangular air mattress measures
3 feet by 6 feet. Area of the rectangular tent is
5 feet X ( 2 X 5 feet) = 5 feet X 10 feet = 50 square feet,
now David’s rectangular air mattress area is 3 feet x 6 feet =
18 square feet, If David puts the air mattress in the tent,
number of square feet of floor space will be available for
the rest of his things is 50 square feet – 18 square feet =
32 square feet.

Question 3.
Jackson’s rectangular bedroom has an area of 90 square feet.
The area of his bedroom is 9 times that of his rectangular closet.
If the closet is 2 feet wide, what is its length?
Answer:
The closet length is 5 feet,

Explanation:
Given Jackson’s rectangular bedroom has an area of 90 square feet.
The area of his bedroom is 9 times that of his rectangular closet.
So closet area is 90 X feet X feet ÷ 9 = 10 square feet,
As given closet is 2 feet wide, the length will be
10 feet X feet = 2 feet X length of the closet,
length of the closet = 10 feet x feet ÷ 2 feet = 5 feet.
therefore the length of the closer is 5 feet.

Question 4.
The length of a rectangular deck is 4 times its width.
If the deck’s perimeter is 30 feet, what is the deck’s area?
Answer:
The area of the deck is 36 square feet,

Explanation:
Given the length of a rectangular deck is 4 times its width.
If the deck’s perimeter is 30 feet, then
30 feet = 2 X (4 X width + width) ,
30 feet ÷ 2 = 5 X width,
15 feet = 5 width
therefore width = 15 feet ÷ 5 = 3 feet and
length = 4 X 3 feet = 12 feet,
Now the area of the deck is 12 feet X 3 feet = 36 square feet.

Eureka Math Grade 4 Module 3 Lesson 3 Exit Ticket Answer Key

Solve the following problem. Use pictures, numbers, or
words to show your work.

A rectangular poster is 3 times as long as it is wide.
A rectangular banner is 5 times as long as it is wide.
Both the banner and the poster have perimeters of 24 inches.
What are the lengths and widths of the poster and the banner?
Answer:
The rectangular poster is 9 inches long and 3 inches wide,
The rectangular banner is 10 inches long and 2 inches wide,

Explanation:
Given a rectangular poster is 3 times as long as it is wide.
A rectangular banner is 5 times as long as it is wide.
Both the banner and the poster have perimeters of 24 inches.
First rectangular poster, So 24 inches = 2 X (3 X wide + wide),
24 inches ÷ 2 = 4 wide,
12 inches = 4 wide
therefore wide = 12 inches ÷ 4 = 3 inches and
long =3 X 3 inches = 9 inches,
Now rectangular banner, 24 inches = 2 X (5 X wide + wide),
24 inches ÷ 2 = 6 wide,
12 inches = 6 wide,
wide = 12 inches ÷ 6 = 2 inches, and long = 5 X 2 inches = 10 inches,
Shown the work above in the picture,
Therefore, The rectangular poster is 9 inches long and 3 inches wide,
The rectangular banner is 10 inches long and 2 inches wide.

Eureka Math Grade 4 Module 3 Lesson 3 Homework Answer Key

Solve the following problems. Use pictures, numbers, or words to show your work.

Question 1.
Katie cut out a rectangular piece of wrapping paper that was
2 times as long and 3 times as wide as the box that she
was wrapping. The box was 5 inches long and 4 inches wide.
What is the perimeter of the wrapping paper that Katie cut?
Answer:
The perimeter of the wrapping paper that Katie cut is 44 inches,

Explanation:
Given Katie cut out a rectangular piece of wrapping paper that was
2 times as long and 3 times as wide as the box that she
as wrapping. The box was 5 inches long and 4 inches wide.
So the wrapping paper length is 2 X 5 inches = 10 inches and
width is 3 X 4 inches = 12 inches, Now the perimeter of the
wrapping paper that Katie cut is 2 X (10 inches + 12 inches) =
2 X 22 inches = 44 inches. Shown the work above in the picture,
therefore, the perimeter of the wrapping paper that Katie cut is 44 inches.

Question 2.
Alexis has a rectangular piece of red paper that is
4 centimeters wide. Its length is twice its width.
She glues a rectangular piece of blue paper on top
of the red piece measuring 3 centimeters by 7 centimeters.
How many square centimeters of red paper will be visible on top?
Answer:
11 square centimeters of red paper will be visible on top,

Explanation:
Given Alexis has a rectangular piece of red paper that is
4 centimeters wide. Its length is twice its width.
She glues a rectangular piece of blue paper on top
of the red piece measuring 3 centimeters by 7 centimeters.
Area of rectangular piece of red paper = 4 cm X ( 2 X 4 cm) =
4 cm X 8 cm = 32 square cm, Now area of rectangular piece
of blue paper on top of the red piece is 3 cm X 7 cm = 21 square cm,
So number of square centimeters of red paper will be visible on top
is 32 sq cm – 21 sq cm = 11 sq cm. Shown the work above in the picture,
Therefore, 11 square centimeters of red paper will be visible on top.

Question 3.
Brinn’s rectangular kitchen has an area of 81 square feet.
The kitchen is 9 times as many square feet as Brinn’s pantry.
If the rectangular pantry is 3 feet wide,
what is the length of the pantry?
Answer:
The length of the pantry is 3 feet,

Explanation:
Given Brinn’s rectangular kitchen has an area of 81 square feet.
The kitchen is 9 times as many square feet as Brinn’s pantry.
So area of Brinn’s pantry is 81 sq feet ÷ 9 = 9 sq feet,
Given the rectangular pantry is 3 feet wide so
length of the pantry is 9 sq feet ÷ 3 feet = 3 feet,
Shown the work above in the picture, therefore
the length of the pantry is 3 feet.

Question 4.
The length of Marshall’s rectangular poster is 2 times its width.
If the perimeter is 24 inches, what is the area of the poster?
Answer:
The area of the Marshall’s poster is 32 square inches,

Explanation:
Given the length Marshall’s rectangular poster is 2 times its width
and the perimeter is 24 inches, so 24 inches = 2 X (2 X width + width),
24 inches ÷ 2 = 3 X width,
12 inches =  3 X width
So width = 12 inches ÷ 3 = 4 inches, length = 2 X 4 inches = 8 inches,
now area of the poster is 8 inches X 4 inches = 32 square inches,
Shown the work above in the picture, therefore
The area of the poster is 32 square inches.

Engage NY Eureka Math 4th Grade Module 3 Lesson 2 Answer Key

Eureka Math Grade 4 Module 3 Lesson 2 Problem Set Answer Key

Question 1.
A rectangular porch is 4 feet wide. It is 3 times as long as it is wide.
a. Label the diagram with the dimensions of the porch.

Answer:

Explanation:
Given a rectangular porch is 4 feet wide.
It is 3 times as long as it is wide.
Labeled the diagram with the dimensions of the porch as
shown above, width= 4 feet and long = 3 X 4 feet = 12 feet
or 4 feet + 4 feet + 4 feet = 12 feet respectively.

b. Find the perimeter of the porch.
Answer:
Perimeter of the porch is 32 feet,

Explanation:
Given width = 4 feet and long is 12 feet, so perimeter
of rectangular porch is 2 X ( 12 feet + 4 feet) =
2 X (16 feet) = 32 feet.

Question 2.
A narrow rectangular banner is 5 inches wide.
It is 6 times as long as it is wide.
a. Draw a diagram of the banner, and label its dimensions.
Answer:

Explanation:
Drawn a diagram of the banner, and labeled its dimensions
as shown above wide 5 inches and long is 6 x 5 inches =
30 inches.

b. Find the perimeter and area of the banner.
Answer:
Perimeter of the banner : 70 inches,
Area of the banner : 150 inches²,

Explanation:
Given a narrow rectangular banner is 5 inches wide.
It is 6 times as long as it is wide. So wide = 5 inches,
long = 6 X 5 inches = 30 inches,
Perimeter of the banner = 2 X (l + w) = 2 X (30 inches + 5 inches) =
2 X ( 35 inches) = 70 inches and area of the banner = l X w =
30 inches X 5 inches = 150 square inches.

Question 3.
The area of a rectangle is 42 square centimeters.
Its length is 7 centimeters.
a. What is the width of the rectangle?
Answer:
The width of the rectangle is 6 centimeters,

Explanation:
Given The area of a rectangle is 42 square centimeters.
Its length is 7 centimeters. So let us take width as x cm,
so 42 sq cm = 7 cm X x cm, x cm = 42 sq cm X cm ÷ 7 cm = 6 cm,
therefore, the width of the rectangle is 6 centimeters.

b. Charlie wants to draw a second rectangle that is the
same length but is 3 times as wide. Draw and label
Charlie’s second rectangle.
Answer:

Explanation:
Given Charlie wants to draw a second rectangle that is the
same length but is 3 times as wide means length is 7 cm and
wide is 3 X 7 cm = 21 cm, Drawn and labeled Charlie’s
second rectangle as shown above.

c. What is the perimeter of Charlie’s second rectangle?
Answer:
Perimeter of Charlie’s second rectangle is 56 centimeters,

Explanation:
Given Charlie’s second rectangle has length 7 cm and
width as 21 cm so perimeter is 2 X ( 7 cm + 21 cm) =
2 X (28 cm) = 56 cm, therefore perimeter of Charlie’s
second rectangle is 56 centimeters.

Question 4.
The area of Betsy’s rectangular sandbox is 20 square feet.
The longer side measures 5 feet. The sandbox at the park is
twice as long and twice as wide as Betsy’s.
a. Draw and label a diagram of Betsy’s sandbox.
What is its perimeter?
Answer:
Perimeter of Betsy’s sandbox is 18 feet,

Explanation:
Given the area of Betsy’s rectangular sandbox is 20 square feet.
The longer side measures 5 feet. Drawn and labeled a diagram
of Betsy’s sandbox as shown above and the its perimeter is as
area = 20 square feet, lets take width as x feet so
x feet = 20 feet X feet ÷ 5 feet = 4 feet, now perimeter =
2 X ( 5 feet + 4 feet) = 2 X 9 feet = 18 feet,
therefore, Perimeter of Betsy’s sandbox is 18 feet.

b. Draw and label a diagram of the sandbox at the park.
What is its perimeter?
Answer:
The perimeter of the sand box at park is 36 feet,

Explanation:
Given the sandbox at the park is twice as long
and twice as wide as Betsy’s means long is
5 feet + 5 feet = 10 feet and wide is 4 feet + 4 feet = 8 feet,
Now draw and labeled a diagram of the sandbox at the park.
Perimeter of sandbox at park is 2 X (10 feet + 8 feet) =
2 X 18 feet = 36 feet.

c. What is the relationship between the two perimeters?
Answer:
Perimeter of sandbox at park is twice the perimeter of Betsy’s sandbox,

Explanation:
As both length and width of sandbox at park is twice of
Betsy’s sandbox, so their perimeter of sandbox at park is twice
the perimeter of Betsy’s sandbox.

d. Find the area of the park’s sandbox using the formula A = l × w.
Answer:
Area of the park’s sandbox is 80 square feet,

Explanation:
As sandbox at park has 10 feet long and 8 feet wide so
area of sandbox at park is 10 feet X 8 feet = 80 square feet.

e. The sandbox at the park has an area that is how many
times that of Betsy’s sandbox?
Answer:
The sandbox at the park has an area that is four
times that of Betsy’s sandbox,

Explanation:
Given area of Betsy’s rectangular sandbox is 20 square feet
and area of the park’s sandbox is 80 square feet,
so number of times more is 80 square feet ÷ 20 square feet = 4,
therefore the sandbox at the park has an area that is four
times that of Betsy’s sandbox.

f. Compare how the perimeter changed with how the area changed between the two sandboxes. Explain what you notice using words,
pictures, or numbers.
Answer:
Sand box at park has twice perimeter and area has became
four times that of Betsy’s sandbox,

Explanation:
As we know Perimeter of Betsy’s sandbox is 18 feet and
perimeter of the sand box at park is 36 feet,
Area of Betsy’s rectangular sandbox is 20 square feet and
area of the park’s sandbox is 80 square feet, Now on comparing
Sand box at park has twice perimeter and area has became
four times to that of Betsy’s sandbox.

Eureka Math Grade 4 Module 3 Lesson 2 Exit Ticket Answer Key

Question 1.
A table is 2 feet wide. It is 6 times as long as it is wide.
a. Label the diagram with the dimensions of the table.

Answer:

Explanation:
Labeled the diagram with the dimensions of the table as
shown above, wide= 2 feet and long is  6 X 2 feet = 12 feet.

b. Find the perimeter of the table.
Answer:
Perimeter of the table is 28 feet,

Explanation:
Given wide is 2 ffet and long is 12 feet,
So Perimeter of the table is 2 X ( 12 feet + 2 feet) =
2 X 14 feet = 28 feet.

Question 2.
A blanket is 4 feet wide. It is 3 times as long as it is wide.
a. Draw a diagram of the blanket, and label its dimensions.
Answer:

Explanation:
Labeled the diagram of the blanket with the dimensions as
shown above, wide= 4 feet and long is  3 X 4 feet = 12 feet.

b. Find the perimeter and area of the blanket.
Answer:
Perimeter is 32 feet and area of the blanket is 48 square feet,

Explanation:
Given wide as 4 feet and long is 12 feet, So perimeter of the
blanket is 2 X (12 feet + 4 feet) = 2 X (16 feet) = 32 feet and
area is 12 feet X 4 feet = 48 square feet.

Eureka Math Grade 4 Module 3 Lesson 2 Homework Answer Key

Question 1.
A rectangular pool is 7 feet wide. It is 3 times as long as it is wide.
a. Label the diagram with the dimensions of the pool.

Answer:

Explanation:
Labeled the diagram of the rectangular pool with
the dimensions as shown above, wide= 7 feet and
long is  3 X 7 feet = 21 feet.

b. Find the perimeter of the pool.
Answer:
Perimeter of the rectangular pool is 56 feet,

Explanation:
Given rectangular pool is 7 feet wide and 21 feet long,
So perimeter is 2 X (21 feet + 7 feet) = 2 X 28 feet = 56 feet.

Question 2.
A poster is 3 inches long. It is 4 times as wide as it is long.
a. Draw a diagram of the poster, and label its dimensions.
Answer:

Explanation:
Labeled the diagram of the poster with
the dimensions as shown above, long = 3 inches,
and wide is  4 X 3 inches = 12 inches.

b. Find the perimeter and area of the poster.
Answer:
Perimeter of the poster is 30 inches and
area of the poster is 36 square inches,

Explanation:
Given poster as 3 inches long and 4 X 3 inches = 12 inches wide,
So perimeter of the poster is 2 X ( 3 inches + 12 inches) =
2 X 15 inches = 30 inches and area of the poster is
3 inches X 12 inches = 36 square inches.

Question 3.
The area of a rectangle is 36 square centimeters, and
its length is 9 centimeters.
a. What is the width of the rectangle?
Answer:
The width of the rectangle is 4 centimeters,

Explanation:
Given the area of a rectangle is 36 square centimeters
and its length is 9 centimeters so width of the rectangle is
36 sq cm = 9 cm X width , width = 36 cm X cm ÷ 9 cm = 4 cm,
therefore the width of the rectangle is 4 centimeters.

b. Elsa wants to draw a second rectangle that is the
same length but is 3 times as wide. Draw and label
Elsa’s second rectangle.
Answer:

Explanation:
Given Elsa wants to draw a second rectangle that is the
same length but is 3 times as wide. Drawn and labeled
Elsa’s second rectangle with length as 9 centimeters and
wide as 3 X 9 cm = 27 centimeters.

c. What is the perimeter of Elsa’s second rectangle?
Answer:
Perimeter of Elsa’s second rectangle is 72 centimeters,

Explanation:
Given Elsa’s second rectangle is with length 9 cm and
wide is 27 cm, So perimeter is 2 X (9 cm + 27 cm) =
2 X (36 cm) = 72 centimeters.
therefore, Perimeter of Elsa’s second rectangle is 72 centimeters.

Question 4.
The area of Nathan’s bedroom rug is 15 square feet.
The longer side measures 5 feet. His living room rug is
twice as long and twice as wide as the bedroom rug.
a. Draw and label a diagram of Nathan’s bedroom rug.
What is its perimeter?
Answer:

Perimeter of Nathan’s bedroom rug is 16 feet,

Explanation:
Given the area of Nathan’s bedroom rug is 15 square feet.
The longer side measures 5 feet so width is
15 feet X feet ÷ 5 feet = 3 feet, now preimeter of
Nathan’s bedroom rug is 2 X (5 feet + 3 feet) =
2 X 8 feet = 16 feet, Drawn and labeled a diagram of
Nathan’s bedroom rug as shown above.

b. Draw and label a diagram of Nathan’s living room rug.
What is its perimeter?
Answer:

Perimeter of Nathan’s living room rug is 32 feet,

Explanation:
Drawn and labeled a diagram of Nathan’s living room rug
as shown above with long as 2 X 5 feet = 10 feet and
width as 2 X 3 feet = 6 feet. Perimeter of Nathan’s
living room rug is2 X (10 feet + 6 feet) 2 X 16 feet = 32 feet.

c. What is the relationship between the two perimeters?
Answer:
The perimeter of Nathan’s living room rug is twice the
perimeter of Nathan’s bedroom rug,

Explanation:
As perimeter of Nathan’s bedroom rug is 16 feet and
perimeter of Nathan’s living room rug is 32 feet and
as both length and width of Nathan’s living room rug is
twice of Nathan’s bedroom rug.

d. Find the area of the living room rug using the formula A = l × w.
Answer:
The area of the living room rug is 60 square feet,

Explanation:
Given living room rug has long 10 feet and width 6 feet,
So area of the living room rug is 10 feet X 6 feet = 60 square feet.

e. The living room rug has an area that is how many
times that of the bedroom rug?
Answer:
The living room rug has an area that is four
times that of the bedroom rug,

Explanation:
The area of the living room rug is 60 square feet and
the area of Nathan’s bedroom rug is 15 square feet.
So number of times the area of the living room rug to
the area of Nathan’s bedroom rug is
60 sq feet ÷ 15 square feet = 4,
Therefore, the living room rug has an area that is four
times that of the bedroom rug.

f. Compare how the perimeter changed with how
the area changed between the two rugs.
Explain what you notice using words, pictures, or numbers.
Answer:
Nathan’s living room has twice perimeter and area has became
four times that of Nathan’s bedroom rug,

Explanation:
As we know Perimeter of  is Nathan’s bedroom rug 16 feet and
perimeter of Nathan’s living room is 32 feet,
Area of Nathan’s bedroom rug is 15 square feet and
area of Nathan’s living room is 60 square feet, Now on comparing
Nathan’s living room has twice perimeter and area has became
four times to that of Nathan’s bedroom rug.

Engage NY Eureka Math 4th Grade Module 3 Lesson 1 Answer Key

Eureka Math Grade 4 Module 3 Lesson 1 Problem Set Answer Key

Question 1.
Determine the perimeter and area of rectangles A and B.

a. A = _____63 cm²__________     A = ______54 cm²_________

b. P = ______32 cm_________     P = ______30 cm_________
Answer:

a. A = 63 cm² , A = 54 cm²,

Explanation:
As shown in figure A length = 9 cm , breadth = 7 cm,
Area of rectangle is = l X b = 9 cm X 7 cm = 63 square cm,
and in figure B length = 6 cm , breadth = 9 cm,
Area of rectangle is = l X b = 6 cm X 9 cm = 54 square cm.

b. P = 32 cm,  P = 30 cm,

Explanation:
As shown in figure A length = 9 cm , breadth = 7 cm,
Perimeter of rectangle is =2 X (l + b) = 2(9 cm + 7 cm) =
2 X (16 cm) = 32 cm,
and in figure B length = 6 cm , breadth = 9 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (6 cm + 9 cm) =
2 X (15 cm) = 30 cm.

Question 2.
Determine the perimeter and area of each rectangle.
a.

P = _____22 cm_______
A = _____30 cm²_______
Answer:
Perimeter = 22 cm,
Area = 30 cm²,

Explanation:
Given length = 5 cm and breadth = 6 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (5 cm + 6 cm) =
2 X (11 cm) = 22 cm,
Area of rectangle is = l X b = 5 cm X 6 cm = 30 square cm.

b.

P = ____22 cm_______
A = ____ 24 cm²________
Answer:
Perimeter = 22 cm,
Area = 24 cm²,

Explanation:
Given length = 8 cm and breadth = 3 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (8 cm + 3 cm) =
2 X (11 cm) = 22 cm,
Area of rectangle is = l X b = 8 cm X 3 cm = 24 square cm.

Question 3.
Determine the perimeter of each rectangle.
a.

P = ____530 m________
Answer:
Perimeter = 530 m,

Explanation:
Given length = 99 m and breadth = 166 m,
Perimeter of rectangle is =2 X (l + b) = 2 X (99 m + 166 m) =
2 X ( 265 m) = 530 m.

b.

P = ____450 cm________
Answer:
Perimeter =  450 cm,

Explanation:
Given length = 75 cm and breadth = 1 m 50 cm,
we know 1 m = 100 cm ,
so breadth =  1 X 100 cm + 50 cm =150 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (75 cm + 150 cm) =
2 X (225 cm) = 450 cm.

Question 4.
Given the rectangle’s area, find the unknown side length.
a.

x = ____10 cm________
Answer:
Unknown side length = 10 cm,

Explanation:
Given width of rectangle as 8 cm and area as 80 square cm,
and unknow side length is x cm, we know area of rectangle is
length X breadth, So 80 sq cm = 8 cm X x cm,
So x cm = 80 sq cm ÷ 8 cm = 10 cm,
therefore unknown side length = 10 cm.

b.

x = ____7 cm________
Answer:
Unknown side length = 7 cm,

Explanation:
Given width of rectangle as 7 cm and area as 49 square cm,
and unknow side length is x cm, we know area of rectangle is
length X breadth, So 49 sq cm = 7 cm X x cm,
So x cm = 49 sq cm ÷ 7 cm = 7 cm,
therefore unknown side length = 7 cm.

Question 5.
Given the rectangle’s perimeter, find the unknown side length.
a. P = 120 cm

Answer:
Unknown side length = 40 cm,

Explanation:
Given width of rectangle as 20 cm and perimeter as 120 cm,
and unknow side length is x cm, we know perimeter of
rectangle is 2 X (length + breadth),
So 120 cm = 2 X (x cm + 20 cm),
120 cm ÷ 2 = (x cm + 20 cm),
60 cm = (x cm + 20 cm),
So x cm = 60 cm – 20 cm = 40 cm,
therefore unknown side length = 40 cm.

b. p = 1000 m

Answer:
Unknown side width = 250 m,

Explanation:
Given length of rectangle as 250 m and perimeter as 1000 m,
and unknow side width is x m, we know perimeter of
rectangle is 2 X (length + breadth),
So 1000 m = 2 X (250 m + x m),
1000 m ÷ 2 = (250 m + x m ),
500 m = 250 m + x m ,
So x m = 500 m – 250 m = 250 m,
therefore unknown side length = 250 m.

Question 6.
Each of the following rectangles has whole number side lengths.
Given the area and perimeter, find the length and width.
a. P = 20 cm

Answer:
The whole number side lengths are
If length of rectangle is 4 cm then width is 6 cm or
length of rectangle is 6 cm then width is 4 cm,

Explanation:
Given area = 24 square cm and perimeter = 20 cm of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 24 sq cm = l X w and
perimeter = 2 X (length + width) ,
20 cm = 2 X ( l + w), l + w = 20 cm ÷ 2 =10 cm,
so l = 10 cm – w, now 24 = (10 – w) X w,
we get w²– 10 w + 24 = 0,
So w²– 6 w – 4 w + 24 = 0,
w(w – 6) – 4(w – 6) = 0, therefore w = 6 cm or w = 4 cm,
So l = 10 cm – 6 cm = 4 cm or l = 10 cm  – 4 cm = 6 cm,
Therfore, If length of rectangle is 4 cm then width is 6 cm or
length of rectangle is 6 cm then width is 4 cm.

b. P = 28 m

Answer:
The whole number side lengths are
If length of rectangle is 2 m then width is 12 m or
length of rectangle is 12 m then width is 2 m.

Explanation:
Given area = 24 square m and perimeter = 28 m of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 24 sq m = l X w and
perimeter = 2 X (length + width) ,
28 m = 2 X ( l + w), l + w = 28 m ÷ 2 =14 m,
so l = 14 m – w, now 24 = (14 – w) X w,
we get w²– 14 w + 24 = 0,
So w²– 12 w – 2 w + 24 = 0,
w(w – 12) – 2(w – 12) = 0, therefore w = 12 m or w = 2 m,
So l = 14 m – 12 m = 2 m or l = 14 m – 2 m = 12 m,
Therfore, If length of rectangle is 2 m then width is 12 m or
length of rectangle is 12 m then width is 2 m.

Eureka Math Grade 4 Module 3 Lesson 1 Exit Ticket Answer Key

Question 1.
Determine the area and perimeter of the rectangle.

Answer:
Area = 16 cm²,
Perimeter = 20 cm,

Explanation:
Given length = 8 cm and breadth = 2 cm,
Area of rectangle is = l X b = 8 cm X 2 cm = 16 square cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (8 cm + 2 cm) =
2 X (10 cm) = 20 cm.

Question 2.
Determine the perimeter of the rectangle.

Answer:
Perimeter = 892 m,

Explanation:
Given length = 347 m and breadth = 99 m,
Perimeter of rectangle is =2 X (l + b) = 2 X (347 m + 99 m) =
2 X (446 m) = 892 m.

Eureka Math Grade 4 Module 3 Lesson 1 Homework Answer Key

Question 1.
Determine the perimeter and area of rectangles A and B.

a. A = _____40 cm²__________    A = ______35 cm²_________

b. P = ______26 cm_________    P = _______24 cm________
Answer:

a. A = 40 cm² , A = 35 cm²,

Explanation:
As shown in figure A length = 8 cm , breadth = 5 cm,
Area of rectangle is = l X b = 8 cm X 5 cm = 40 square cm,
and in figure B length = 5 cm , breadth = 7 cm,
Area of rectangle is = l X b = 5 cm X 7 cm = 35 square cm,

b. P = 26 cm,  P = 24 cm,

Explanation:
As shown in figure A length = 8 cm , breadth = 5 cm,
Perimeter of rectangle is =2 X (l + b) = 2(8 cm + 5 cm) =
2 X (13 cm) = 26 cm,
and in figure B length = 5 cm , breadth = 7 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (5 cm + 7 cm) =
2 X (12 cm) = 24 cm.

Question 2.
Determine the perimeter and area of each rectangle.
a.

P = ____20 cm________
A = ___ 21 cm²____
Answer:
Perimeter = 20 cm,
Area = 21 cm²,

Explanation:
Given length = 7 cm and breadth = 3 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (7 cm + 3 cm) =
2 X (10 cm) = 20 cm,
Area of rectangle is = l X b = 7 cm X 3 cm = 21 square cm,

b.

P = ___26 cm_________
A = ______36 cm²______
Answer:
Perimeter = 26 cm,
Area = 36 cm²,

Explanation:
Given length = 9 cm and breadth = 4 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (9 cm + 4 cm) =
2 X (13 cm) = 26 cm,
Area of rectangle is = l X b = 9 cm X 4 cm = 36 square cm,

Question 3.
Determine the perimeter of each rectangle.
a.

P = _____850 m_______
Answer:
Perimeter = 850 m,

Explanation:
Given length = 76 m and breadth = 149 m,
Perimeter of rectangle is =2 X (l + b) = 2 X (76 m + 149 cm) =
2 X ( 425 m) = 850 m.

b.

P = ____510 cm________
Answer:
Perimeter =  510 cm,

Explanation:
Given length = 45 cm and breadth = 2 m 10 cm,
we know 1 m = 100 cm ,
so breadth =  2 X 100 cm + 10 cm = 200 cm + 10 cm = 210 cm,
Perimeter of rectangle is =2 X (l + b) = 2 X (45 cm + 210 cm) =
2 X (255 cm) = 510 cm.

Question 4.
Given the rectangle’s area, find the unknown side length.
a.

x = _____10 cm_______
Answer:
Unknown side length = 10 cm,

Explanation:
Given width of rectangle as 6 cm and area as 60 square cm,
and unknow side length is x cm, we know area of rectangle is
length X breadth, So 60 sq cm = 6 cm X x cm,
So x cm = 60 sq cm ÷ 6 cm = 10 cm,
therefore unknown side length = 10 cm.

b.

x = _____5 m_______
Answer:
Unknown side length = 5 m,

Explanation:
Given width of rectangle as 5 m and area as 25 square m,
and unknow side length is x m, we know area of rectangle is
length X breadth, So 25 sq m = 5 m X x m,
So x m = 25 sq m ÷ 5 m = 5 m,
therefore unknown side length = 5 m.

Question 5.
Given the rectangle’s perimeter, find the unknown side length.
a. P = 180 cm

x = ____40 cm________
Answer:
Unknown side length = 40 cm,

Explanation:
Given width of rectangle as 40 cm and perimeter as 180 cm,
and unknow side length is x cm, we know perimeter of
rectangle is 2 X (length + breadth),
So 180 cm = 2 X (x cm + 40 cm),
180 cm ÷ 2 = (x cm + 40 cm),
90 cm = (x cm + 40 cm),
So x cm = 90 cm – 40 cm = 50 cm,
therefore unknown side length = 50 cm.

b. P = 1,000 m

x = ____350 m________
Answer:
Unknown side width = 350 m,

Explanation:
Given length of rectangle as 150 m and perimeter as 1000 m,
and unknow side width is x m, we know perimeter of
rectangle is 2 X (length + breadth),
So 1000 m = 2 X (150 m + x m),
1000 m ÷ 2 = (150 m + x m ),
500 m = 150 m + x m ,
So x m = 500 m – 150 m = 350 m,
therefore unknown side length = 350 m.

Question 6.
Each of the following rectangles has whole number side lengths. Given the area and perimeter, find the length and width.
a. A = 32 square cm
P = 24 cm

Answer:
The whole number side lengths are
If length of recatangle is 4 cm then width is 8 cm or
length of rectangle is 8 cm then width is 4 cm,

Explanation:
Given area = 32 square cm and perimeter = 24 cm of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 32 sq cm = l X w and
perimeter = 2 X (length + width) ,
24 cm = 2 X ( l + w), l + w = 24 cm ÷ 2 =12 cm,
so l = 12 cm – w, now 32 = (12 – w) X w,
we get w²– 12 w + 32 = 0,
So w²– 8 w – 4 w + 32 = 0,
w(w – 8) – 4(w – 8) = 0, therefore w = 8 cm or w = 4 cm,
So l = 12 cm – 8 cm = 4 cm or l = 12 cm  – 4 cm = 8 cm,
Therfore, If length of recatangle is 4 cm then width is 8 cm or
length of rectangle is 8 cm then width is 4 cm.

b. A = 36 square m
P = 30 m

Answer:
The whole number side lengths are
If length of rectangle is 3 m then width is 12 m or
length of rectangle is 12 m then width is 3 m.

Explanation:
Given area = 36 square m and perimeter = 30 m of rectangles,
lets take length as l and width as w and we know
area of rectangle = length X width , 36 sq m = l X w and
perimeter = 2 X (length + width) ,
30 m = 2 X ( l + w), l + w = 30 m ÷ 2 =15 m,
so l = 15 m – w, now 36 = (15 – w) X w,
we get w²– 15 w + 36 = 0,
So w²– 12 w – 3 w + 24 = 0,
w(w – 12) – 3(w – 12) = 0, therefore w = 12 m or w = 3 m,
So l = 15 m – 12 m = 3 m or l = 15 m – 3 m = 12 m,
Therfore, If length of rectangle is 3 m then width is 12 m or
length of rectangle is 12 m then width is 3 m.

Engage NY Eureka Math 4th Grade Module 1 End of Module Assessment Answer Key

Question 1.
Compare the values of each 7 in the number 771,548. Use a picture, numbers, or words to explain.
Answer:
In the given number 771,548 the two 7 represent 7 hundred thousand and 7 ten thousand.
7 hundred thousand > 7 ten thousand.
7 hundred thousand is ten times greater than 7 ten thousand.
Explanation:
expanded form of 771,548
700,000 + 70,000 + 1,000 + 500 + 40 + 8

Question 2.
Compare using >, <, or =. Write your answer inside the circle.
a. 234 thousands + 7 ten thousands  241,000
Answer:
234 thousands + 7 ten thousands  >  241,000
Explanation:

3 hundred thousands is greater than 2 hundred thousands.

b. 4 hundred thousands – 2 thousands 200,000
Answer:
4 hundred thousands – 2 thousands  > 200,000
Explanation:

c. 1 million 4 hundred thousands + 6 hundred thousands
Answer:
1 million = 4 hundred thousands + 6 hundred thousands
Explanation:

d. 709 thousands – 1 hundred thousand 708 thousands
Answer:
709 thousands – 1 hundred thousand < 708 thousands
Explanation:

Question 3.
Norfolk, VA, has a population of 242,628 people. Baltimore, MD, has 376,865 more people than Norfolk. Charleston, SC, has 496,804 less people than Baltimore.
Given:
Population of Norfolk, VA = 242,628
Population of Baltimore, MD = 376,865 more than Norfolk.
Population of Charleston, SC = 496,804 less people than Baltimore
a. What is the total population of all three cities? Draw a tape diagram to model the word problem. Then, solve the problem.
Answer:

b. Round to the nearest hundred thousand to check the reasonableness of your answer for the population of Charleston, SC.
Answer:

c. Record each city’s population in numbers, in words, and in expanded form.
Answer:

d. Compare the population of Norfolk and Charleston using >, <, or =.
Answer:

e. Eddie lives in Fredericksburg, VA, which has a population of 24,286. He says that Norfolk’s population is about 10 times as large as Fredericksburg’s population. Explain Eddie’s thinking.
Answer:
Population of Fredericksburg,VA, = 24,286
Population of Norfolk = 242,628
Norfolk population is almost 10 times as large as Fredericksburg’s population.
Highest place value of Fredericksburg is 2 ten thousand and Highest place value of Norfolk is 2 hundred thousand
2 ten thousand × 10 = 2 hundred thousand.
Eddie’s thinking is reasonable.

Engage NY Eureka Math 4th Grade Module 1 Mid Module Assessment Answer Key

Question 1.
a. Arrange the following numbers in order from least to greatest:

Answer:
4,450       44,500     504,054           505,045
Explanation:
The following numbers are arranged from least to greatest
place value chart

b. Use the words ten times to tell how you ordered the two smallest numbers using words, pictures, or numbers.
Answer:
4,450 and 44,500 are the smallest numbers
44,500 is ten times more than 4,450.
Explanation:
ten times more of thousand is ten thousand

Question 2.
Compare using >, <, or =. Write your answer inside the circle.
a. 1 hundred thousand  10,000
b. 200 thousands 4 hundreds  204,000
c. 7 hundreds + 4 thousands + 27 ones  6 thousands + 4 hundreds
d. 1,000,000  10 hundred thousands
Answer:

Explanation:
a . 1 hundred thousand is represented as 100,000. which is ten times more than 10,000. So, 100,000 > 10,000.
b. 200 thousands 4 hundreds = 200,400 . 204,00 is 200 thousands 4 thousand.
4 thousand is 10 times more than 4 hundred. So, 204,000 is greater than 200,400.
c. 7 hundreds + 4 thousands + 27 ones  6 thousands + 4 hundreds
                     700 + 4,000 + 27 = 4,727  <   6,000  + 400 = 6,400
So on comparing 6 thousand is more than 4 thousand.
d. 1,000,000 is represented as 1 million or 10 hundred thousands  and the other number is 10 hundred thousands. So,  both are same .

Question 3.
The football stadium at Louisiana State University (LSU) has a seating capacity of 92,542.
a. According to the 2010 census, the population of San Jose, CA, was approximately ten times the amount of people that LSU’s stadium can seat. What was the population of San Jose in 2010?
Answer:
The seating capacity of Louisiana state university = 92,542
The population of San Jose in 2010 = 925,420 population.
Explanation:
given :
seating capacity of LSU = 92,542. the highest place value of the value is ten thousand. ten times the highest place value is hundred thousand. Ten times 92,542 is 925,420.
b. Write the seating capacity of the LSU stadium in words and in expanded form.
Answer:
92,542 in words = ninety two thousand five hundred forty two.
expanded form = 90,000 + 2,000 + 500 + 40 + 2.
c. Draw two separate number lines to round the LSU stadium’s seating capacity to the nearest ten thousand and to the nearest thousand.
Answer:

d. Compare the stadium’s seating rounded to the nearest ten thousand and the seating rounded to the nearest thousand using >, <, or =.
Answer:

e. Which estimate (rounding to the nearest ten thousand or nearest thousand) is more accurate? Use words and numbers to explain.
Answer:

Engage NY Eureka Math 4th Grade Module 1 Lesson 17 Answer Key

Eureka Math Grade 4 Module 1 Lesson 17 Problem Set Answer Key

Draw a tape diagram to represent each problem. Use numbers to solve, and write your answer as a statement.

Question 1.
Sean’s school raised $32,587. Leslie’s school raised $18,749. How much more money did Sean’s school raise?
Answer:
Sean’s school raised =$32,587
Leslie’s school raised = $18,749
The amount of more money raised by Sean’s school than Leslie’s school = 32,587 – 18,749

Question 2.
At a parade, 97,853 people sat in bleachers, and 388,547 people stood along the street. How many fewer people were in the bleachers than standing on the street?
Answer:
Number of people sat in bleachers = 97,853
Number of people stood along the street = 388,547
Number of fewer people in the bleachers than standing on the streets. = 388,547 – 97,853

Question 3.
A pair of hippos weighs 5,201 kilograms together. The female weighs 2,038 kilograms. How much more does the male weigh than the female?
Answer:
Weight of a pair hippos  together =5,201 kilograms.
Weight of a female hippo = 2,038 kilograms.
weight of the male hippo = 5,201 – 2,038

Question 4.
A copper wire was 240 meters long. After 60 meters was cut off, it was double the length of a steel wire. How much longer was the copper wire than the steel wire at first?
Answer:
Total length of a copper wire = 240 m
Number of meters used = 60 m.
After using 60 m the length of copper wire is double the steel wire =240 – 60 = 180 m = 180 ÷ 2 = 90 m
The length of the steel wire is 90 m.

Eureka Math Grade 4 Module 1 Lesson 17 Exit Ticket Answer Key

Draw a tape diagram to represent each problem. Use numbers to solve, and write your answer as a statement.

A mixture of 2 chemicals measures 1,034 milliliters. It contains some of Chemical A and 755 milliliters of Chemical B. How much less of Chemical A than Chemical B is in the mixture?
Answer:
Mixture of 2 chemicals measures =1,034 milliliters.
Chemical B measures = 755 milliliters.
Chemical A measures = X milliliters.

Eureka Math Grade 4 Module 1 Lesson 17 Homework Answer Key

Draw a tape diagram to represent each problem. Use numbers to solve, and write your answer as a statement.

Question 1.
Gavin has 1,094 toy building blocks. Avery only has 816 toy building blocks. How many more building blocks does Gavin have?
Answer:
Total building blocks Gavin has = 1,094 blocks
Total building blocks Avery has = 816 blocks.

Question 2.
Container B holds 2,391 liters of water. Together, Container A and Container B hold 11,875 liters of water. How many more liters of water does Container A hold than Container B?
Answer:
Total liters of water Container B holds = 2,391 liters
Together both Container A and Container B holds = 11,875 liters.

Question 3.
A piece of yellow yarn was 230 inches long. After 90 inches had been cut from it, the piece of yellow yarn was twice as long as a piece of blue yarn. At first, how much longer was the yellow yarn than the blue yarn?
Answer:
The length of a yellow yarn = 230 inch
After cutting 90 inch of yellow yarn = Twice as long as a piece of blue yarn.