Prasanna

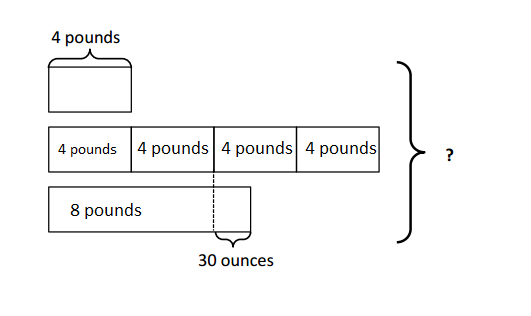
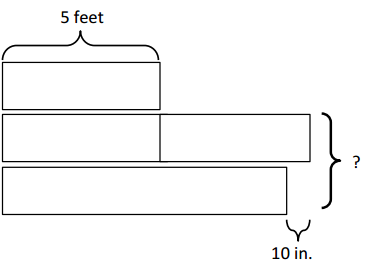
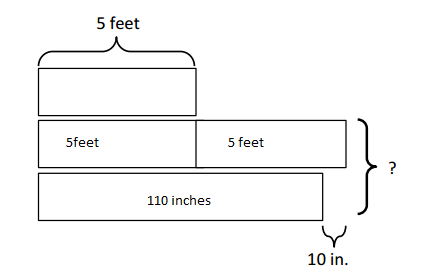
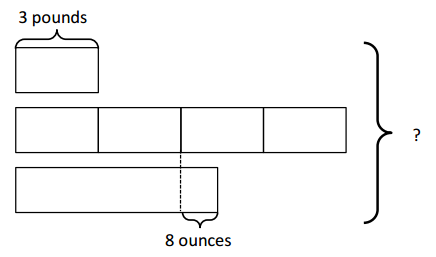
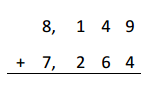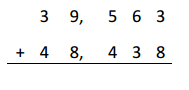Engage NY Eureka Math 4th Grade Module 7 Lesson 10 Answer Key

Eureka Math Grade 4 Module 7 Lesson 10 Problem Set Answer Key

Use RDW to solve the following problems.
Question 1.
Paula’s time swimming in the Ironman Triathlon was 1 hour 25 minutes. Her time biking was 5 hours longer than her swimming time. She ran for 4 hours 50 minutes. How long did it take her to complete all three parts of the race?
Answer:

Given that,

The time taken for swimming in the Iron man Triathlon = 1 hour 25 minutes

The time required for biking is 5 hours longer than her swimming

Which means,

1 hour + 5 hours = 6 hours 25 minutes

The time required for running = 4 hours 50 minutes

Total : 1 hour 25 minutes + 6 hours 25 minutes  + 4 hours 50 minutes

= 12 hours 40 minutes

Therefore, Paula took 12 hours 40 minutes to complete her three parts of race.

Question 2.
Nolan put 7 gallons 3 quarts of gas into his car on Monday and twice as much on Saturday. What was the total amount of gas put into the car on both days?
Answer:

We know that, 1 gallon = 4 quarts

The amount of gas kept into the car on Monday = 7 gallons 3 quarts

Also, given on Saturday Nolan put twice more than Monday

Which means

3 x( 7 gallons 3 quarts )

= 21 gallons 9 quarts

It is also written as

23 gallons 1 quart

Therefore, the total amount of gas Nolan put in his car on both the days = 23 gallons 1 quart.

Question 3.
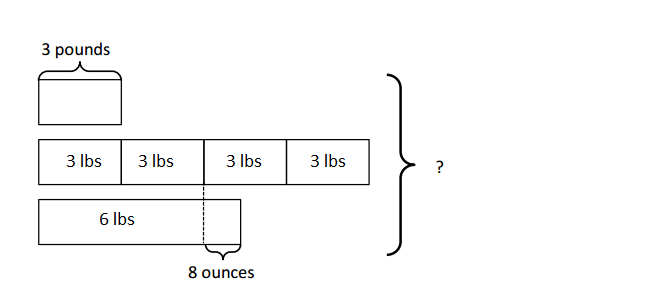
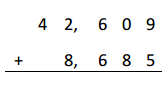
One pumpkin weighs 7 pounds 12 ounces. A second pumpkin weighs 10 pounds 4 ounces. A third pumpkin weighs 2 pounds 9 ounces more than the second pumpkin. What is the total weight of all three pumpkins?
Answer:

1 pound = 16 ounces

The weight of first pumpkin = 7 pounds 12 ounces

The weight of second pumpkin = 10 pounds 4 ounces

Given, the third one is 2 pounds 9 ounces more than the second pumpkin

Which means, 10 pounds 4 ounces + 2 pounds 9 ounces = 12 pounds 13 ounces

Total weight = 7 pounds 12 ounces + 10 pounds 4 ounces  +12 pounds 13 ounces

= 29 pounds 29 ounces

It is also written as 30 pounds 13 ounces

Therefore, the total weight of 3 pumpkins = 30 pounds 13 ounces.

Question 4.
Mr. Lane is 6 feet 4 inches tall. His daughter, Mary, is 3 feet 8 inches shorter than her father. His son is 9 inches taller than Mary. How many inches taller is Mr. Lane than his son?
Answer:

Given that,

The height of Mr. lane = 6 feet 4 inches

The height of Mary is 3 feet 8 inches shorter than her father

Which means,

6 feet 4 inches – 3 feet 8 inches

= 2 feet 8 inches

Also given, his son 9 inches taller than Mary

2 feet 8 inches + 9 inches = 3 feet 5 inches

Now, 6 feet 4 inches – 3 feet 5 inches

= 2 feet 11 inches

2 feet = 24 inches

24 inches + 11 inches = 35 inches

Therefore, Mr. lane is 35 inches taller than his son.

Eureka Math Grade 4 Module 7 Lesson 10 Exit Ticket Answer Key

Use RDW to solve the following problem.
Hadley spent 1 hour and 20 minutes completing her math homework, 45 minutes completing her social studies homework, and 30 minutes studying her spelling words. How much time did Hadley spend on homework and studying?
Answer:

Given that,

The time taken to complete math homework = 1 hour 20 minutes

The time taken to complete her social studies = 45 minutes

The time taken to study her spelling words = 30 minutes

Total time = 1 hour 20 minutes + 45 minutes + 30 minutes

= 1 hour 95 minutes

It is also written as 2 hours 35 minutes

Therefore, Hadley spent 2 hours 35 minutes to complete his homework and studying.

Eureka Math Grade 4 Module 7 Lesson 10 Homework Answer Key

Use RDW to solve the following problems.
Question 1.
On Saturday, Jeff used 2 quarts 1 cup of water from a full gallon to replace some water that leaked from his fish tank. On Sunday, he used 3 pints of water from the same gallon. How much water was left in the gallon after Sunday?
Answer:

The amount of water Jeff used from a full gallon to replace some water that leaked from fish tank = 2 quarts 1 cup

The amount of water he use on Saturday from same gallon = 3 pints which means 6 cups

Total : 2 quarts 1 cup + 6 cups = 2 quarts 7 cups ( W e know that 4 cups = 1 quart)

It is also written as 3 quarts 3 cups

Now,

1 gallon – 3 quarts 3 cups = 1 cup

Therefore, the leftover amount of water = 1 cup.

Question 2.
To make punch, Julia poured 1 quart 3 cups of ginger ale into a bowl and then added twice as much fruit juice. How much punch did she make in all?
Answer:

Given that,

The amount of ginger Julia poured into a bowl =1 quart 3 cups

Also given the amount of fruit juice is twice

Which means, 2 quart 6 cups

Total : 1 quart 3 cups + 2 quart 6 cups = 3 quart 9 cups

9 cups = 2 quarts 1 cup

= 5 quart 1 cup

We know that 4 quart = 1 gallon

So, 1 gallon 1 quart 1 cup

Therefore, the amount of punch she made = 1 gallon 1 quart and 1 cup

Question 3.

Patti went swimming for 1 hour 15 minutes on Monday. On Tuesday, she swam twice as long as she swam on Monday. On Wednesday, she swam 50 minutes less than the time she swam on Tuesday. How much time did she spend swimming during that three-day period?
Answer:

Given,

The amount of time Patti swims on Monday = 1 hour 15 minutes

The amount of time She swims on Tuesday is twice as long as on Monday

Which means, 1 hour 15 minutes + 1 hour 15 minutes = 2 hours 30 minutes

The amount of time she swims on Wednesdays is 50 minutes less than the time she swim on Tuesday

Which means, 2 hours 30 minutes – 50 minutes = 1 hour 40 minutes

The total time she spend swimming during three day period =

1 hour 15 minutes + 2 hours 30 minutes +  1 hour 40 minutes

= 4 hours 85 minutes

It is also written as 5 hours 25 minutes

Therefore, she swam 5 hours 25 minutes

Question 4.
Myah is 4 feet 2 inches tall. Her sister, Ally, is 10 inches taller. Their little brother is half as tall as Ally. How tall is their little brother in feet and inches?
Answer:

Given Myah’s height is 4 feet 2 inches

Also, given Ally is 10 inches taller

So, 4 feet 2 inches + 10 = 5 feet

Their little brother is half as tall as Ally

Now,

5 feet / 2

Which means, 2 feet 6 inches

Therefore, the height of his little brother = 2 feet 6 inches

Question 5.
Rick and Laurie have three dogs. Diesel weighs 89 pounds 12 ounces. Ebony weighs 33 pounds 14 ounces less than Diesel. Luna is the smallest at 10 pounds 2 ounces. What is the combined weight of the three dogs in pounds and ounces?
Answer:

The weight of Diesel = 89 pounds 12 ounces

Also given, Ebony weighs 33 pounds 14 ounces less than diesel

89 pounds 12 ounces – 33 pounds 14 ounces

= 55 pounds 14 ounces

The weight of Luna is 10 pounds 2 ounces

Total weight = 89 pounds 12 ounces + 55 pounds 14 ounces + 10 pounds 2 ounces

= 155 pounds 12 ounces

Therefore, The combined weight = 155 pounds 12 ounces.

Engage NY Eureka Math 4th Grade Module 7 Lesson 9 Answer Key

Eureka Math Grade 4 Module 7 Lesson 9 Problem Set Answer Key

Question 1.
Determine the following sums and differences. Show your work.
a. 23 min + 37 min = _______ hr
b. 1 hr 11 min + 49 min = _______ hr
c. 1 hr – 12 min = _______ min
d. 4 hr – 12 min = _______ hr _______ min
e. 22 sec + 38 sec = _______ min
f. 3 min – 45 sec = _______ min _______ sec
Answer:

a. 23 min + 37 min = 1 hr
b. 1 hr 11 min + 49 min = 2  hr
c. 1 hr – 12 min = 48 min
d. 4 hr – 12 min = 3 hr 48 min
e. 22 sec + 38 sec = 1 min
f. 3 min – 45 sec = 2 min 15 sec

Question 2.
Find the following sums and differences. Show your work.
a. 3 hr 45 min + 25 min = _____ hr _____ min
b. 2 hr 45 min + 6 hr 25 min = _____ hr _____ min
c. 3 hr 7 min – 42 min = _____ hr _____ min
d. 5 hr 7 min – 2 hr 13 min = _____ hr _____ min
e. 5 min 40 sec + 27 sec = ______ min _____ sec
f. 22 min 48 sec – 5 min 58 sec = ________ min ____ sec
Answer:

a. 3 hr 45 min + 25 min = 4 hr 10 min
b. 2 hr 45 min + 6 hr 25 min = 9 hr 10 min
c. 3 hr 7 min – 42 min = 2 hr 25  min
d. 5 hr 7 min – 2 hr 13 min = 2 hr 54 min
e. 5 min 40 sec + 27 sec = 6 min 7 sec
f. 22 min 48 sec – 5 min 58 sec = 16 min 50 sec

Question 3.
At the cup-stacking competition, the first place finishing time was 1 minute 52 seconds. That was 31 seconds faster than the second place finisher. What was the second place time?
Answer:

Given that,

The first place finishing time = 1 minute 52 seconds

Also given, The first place finishing time is 31 seconds faster than second place finisher

Now,

1 minute 52 seconds + 31 seconds = 2 minutes 23 seconds

Therefore, the second place time is 2 minutes 23 seconds.

Question 4.
Jackeline and Raychel have 5 hours to watch three movies that last 1 hour 22 minutes, 2 hours 12 minutes, and 1 hour 57 minutes, respectively.
a. Do the girls have enough time to watch all three movies? Explain why or why not.
b. If Jackeline and Raychel decide to watch only the two longest movies and take a 30-minute break in between, how much of their 5 hours will they have left over?
Answer:

a.

Given that, the total time = 5 hours

The time required to watch three movies respectively, :

1 hour 22 minutes + 2 hours 12 minutes + 1 hour 57 minutes

= 5 hours 31 minutes

Therefore, they do not have enough time to watch all the three movies.

They need 31 minutes more to complete all movies.

b.

The time required to watch long movies with 30 minutes break in between =

2 hours 12 minutes + 1 hour 57 minutes + 30 minutes

= 4 hours 39 minutes

Now,

5 hours – 4 hours 39 minutes

= 21 minutes

They will have 21 minutes left over.

Eureka Math Grade 4 Module 7 Lesson 9 Exit Ticket Answer Key

Find the following sums and differences. Show your work.
Question 1.
2 hr 25 min + 25 min = ______ hr ______ min
Answer:

2 hr 25 min + 25 min = 2 hr 50 min

Question 2.
4 hr 45 min + 2 hr 35 min = ______ hr _____ min
Answer:

4 hr 45 min + 2 hr 35 min = 7 hr 20 min

Question 3.
11 hr 6 min – 32 min = _______ hr _______ min
Answer:

11 hr 6 min – 32 min = 10 hr 34 min

Question 4.
8 hr 9 min – 6 hr 42 min = ______ hr_____ min
Answer:

8 hr 9 min – 6 hr 42 min = 1 hr 27 min

Eureka Math Grade 4 Module 7 Lesson 9 Homework Answer Key

Question 1.
Determine the following sums and differences. Show your work.
a. 41 min + 19 min = _______ hr
b. 2 hr 21 min + 39 min = _______ hr
c. 1 hr – 33 min = _______ min
d. 3 hr – 33 min = _______ hr _______ min
e. 31 sec + 29 sec = _______ min
f. 5 min – 15 sec = _______ min ________ sec
Answer:

a. 41 min + 19 min = 1 hr
b. 2 hr 21 min + 39 min = 3 hr
c. 1 hr – 33 min = 27 min
d. 3 hr – 33 min = 2 hr 27 min
e. 31 sec + 29 sec = 1 min
f. 5 min – 15 sec = 4 min 45 sec

Question 2.
Find the following sums and differences. Show your work.
a. 5 hr 30 min + 35 min = ______ hr ______ min
b. 3 hr 15 min + 5 hr 55 min = ______ hr_____ min
c. 4 hr 4 min – 38 min = _______ hr ______ min
d. 7 hr 3 min – 4 hr 25 min = ______ hr _____ min
e. 3 min 20 sec + 49 sec = ______ min ______ sec
f. 22 min 37 sec – 5 min 58 sec = ____ min ____ sec
Answer:

a. 5 hr 30 min + 35 min = 6 hr 5 min
b. 3 hr 15 min + 5 hr 55 min = 9 hr 10 min
c. 4 hr 4 min – 38 min = 3 hr 26 min
d. 7 hr 3 min – 4 hr 25 min = 2 hr 38 min
e. 3 min 20 sec + 49 sec = 4 min 9 sec
f. 22 min 37 sec – 5 min 58 sec =  16 min 39 sec

Question 3.
It took 5 minutes 34 seconds for Melissa’s oven to preheat to 350 degrees. That was 27 seconds slower than it took Ryan’s oven to preheat to the same temperature. How long did it take Ryan’s oven to preheat?
Answer:

Given that, the time taken for Melissa to preheat to 350 degrees = 5 minutes 34 seconds

Also given,

The time is 27 seconds slower than Ryan’s oven to preheat the same temperature.

Now, 5 minutes 34 seconds – 27 seconds

= 5 minutes 7 seconds

Therefore, Ryan took 5 minutes 7 seconds to preheat the oven

Question 4.
Joanna read three books. Her goal was to finish all three books in a total of 7 hours. She completed them, respectively, in 2 hours 37 minutes, 3 hours 9 minutes, and 1 hour 51 minutes.
a. Did Joanna meet her goal? Write a statement to explain why or why not.
b. Joanna completed the two shortest books in one evening. How long did she spend reading that evening? How long, with her goal in mind, did that leave her to read the third book?
Answer:

The total time to  finish three books according to Joanna’s goal = 7 hours

The total she completed reading :

2 hours 37 minutes + 3 hours 9 minutes + 1 hour 51 minutes

= 7 hours 37 minutes

So, She did not reach her goal

She took 37 minutes more than her goal.

b.

The time required to read shortest book =

2 hours 37 min + 1 hour 51 minutes = 4 hours 28 minutes

Now,

7 hours – 4 hours 28 minutes = 2 hours 32 minutes

Therefore, Joanna is left with 2 hours 32 minutes to complete the third book.

Engage NY Eureka Math 4th Grade Module 7 Lesson 8 Answer Key

Eureka Math Grade 4 Module 7 Lesson 8 Problem Set Answer Key

Question 1.
Determine the following sums and differences. Show your work.
a. 7 oz + 9 oz = ________ lb
b. 1 lb 5 oz + 11 oz = ________ lb
c. 1 lb – 13 oz = ________ oz
d. 12 lb – 4 oz = ________ lb ________ oz
e. 3 lb 9 oz + 9 oz = ________ lb ________ oz
f. 30 lb 9 oz + 9 lb 9 oz = ________ lb ________ oz
g. 25 lb 2 oz – 14 oz = ________ lb ________ oz
h. 125 lb 2 oz – 12 lb 3 oz = ________ lb ________ oz
Answer:

a. 7 oz + 9 oz = 1 lb
b. 1 lb 5 oz + 11 oz = 2 lb
c. 1 lb – 13 oz = 3 oz
d. 12 lb – 4 oz = 11 lb 12 oz
e. 3 lb 9 oz + 9 oz = 4 lb 2 oz
f. 30 lb 9 oz + 9 lb 9 oz = 40 lb 2 oz
g. 25 lb 2 oz – 14 oz =  24 lb 4 oz
h. 125 lb 2 oz – 12 lb 3 oz = 112 lb 15 oz

Question 2.
The total weight of Sarah and Amanda’s full backpacks is 27 pounds. Sarah’s backpack weighs 15 pounds 9 ounces. How much does Amanda’s backpack weigh?
Answer:

Given that, the weight of the both backpacks = 27 pounds

Also given, the weight of Sarah’s bag = 15 pounds 9 ounces

Now,

27 – 15 lb 9  oz = 11 lb 7 oz

Therefore, the weight of Amanda’s backpack = 11 pounds 7 ounces

Question 3.
In Emma’s supply box, a pencil weighs 3 ounces. Her scissors weigh 3 ounces more than the pencil, and a bottle of glue weighs three times as much as the scissors. How much does the bottle of glue weigh in pounds and ounces?
Answer:

Given that,

The weight of pencil = 3 ounces

Also given the weight of scissors is 3 ounces more than the pencil

= 3 oz x 6

= 18 oz

1 pound = 16 ounces

So, 1 pound 2 ounces

Therefore, the bottle of glue weighs 1 pound 2 ounces.

Question 4.
Use the information in the chart about Jodi’s school supplies to answer the following questions:

a. On Mondays, Jodi packs only her laptop and supply case into her backpack. How much does her full backpack weigh?
b. On Tuesdays, Jodi brings her laptop, supply case, two notebooks, and two textbooks in her backpack. On Fridays, Jodi only packs her binder and supply case. How much less does Jodi’s full backpack weigh on Friday than it does on Tuesday?
Answer:

a.

The weight of backpack = 2 lb 14 oz

The weight of laptop = 5 lb 12 oz

The weight of supply case = 1 lb

Total weight = 2 lb 14 oz + 5 lb 12 oz + 1 lb

= 8 lb 26 oz

It is also written as 9 pounds 10 ounces

Therefore, the weight of  Emma’s backpack = 9 pounds 10 ounces.

b.

On Tuesdays :

The weight of laptop, supply case, two notebooks, and two textbooks

5 lb 12 oz + 1 lb + 11 lb + 11 lb + 3 lb 8 oz + 3 lb 8 oz

= 12 lb 50 oz

It is also written as 15 lb 2 oz.

On Fridays ;

Binder and supply case

2 lb 5 oz + 1 lb = 3 lb 5 oz

Now,

15 lb 2 oz – 3 lb 5 oz =

11 lb 13 oz

Therefore, Jodi’s backpack weight is 11 pounds 13 ounces less on Friday than on Tuesdays

Eureka Math Grade 4 Module 7 Lesson 8 Exit Ticket Answer Key

Determine the following sums and differences. Show your work.
Question 1.
4 lb 6 oz + 10 oz = ________ lb ________ oz
Answer:

4 lb 6 oz + 10 oz = 5 lb 0 oz

Question 2.
12 lb 4 oz + 3 lb 14 oz = ________ lb ________ oz
Answer:

12 lb 4 oz + 3 lb 14 oz = 16 lb 2 oz

Question 3.
5 lb 4 oz – 12 oz = ________ lb ________ oz
Answer:

5 lb 4 oz – 12 oz = 4 lb 8 oz

Question 4.
20 lb 5 oz – 13 lb 7 oz = ________ lb ________oz
Answer:

20 lb 5 oz – 13 lb 7 oz = 6 lb 14 oz

Eureka Math Grade 4 Module 7 Lesson 8 Homework Answer Key

Question 1.
Determine the following sums and differences. Show your work.
a. 11 oz + 5 oz = ________ lb
b. 1 lb 7 oz + 9 oz = ________lb
c. 1 lb – 11 oz = ________ oz
d. 12 lb – 8 oz = ________ lb ________ oz
e. 5 lb 8 oz + 9 oz = ________ lb ________ oz
f. 21 lb 8 oz + 6 lb 9 oz = ________ lb ________ oz
g. 23 lb 1 oz – 15 oz = ________ lb ________ oz
h. 89 lb 2 oz – 16 lb 4 oz = ________ lb ________ oz
Answer:

a. 11 oz + 5 oz = 1 lb
b. 1 lb 7 oz + 9 oz = 2 lb
c. 1 lb – 11 oz = 5 oz
d. 12 lb – 8 oz = 11 lb 8 oz
e. 5 lb 8 oz + 9 oz = 6 lb 1 oz
f. 21 lb 8 oz + 6 lb 9 oz = 28 lb 1 oz
g. 23 lb 1 oz – 15 oz = 22 lb 2 oz
h. 89 lb 2 oz – 16 lb 4 oz = 72 lb 14 oz

Question 2.
When David took his dog, Rocky, to the vet in December, Rocky weighed 29 pounds 9 ounces. When he took Rocky back to the vet in March, Rocky weighed 34 pounds 4 ounces. How much weight did Rocky gain?
Answer:

The weight of David’s dog Rocky in December = 29 pounds 9 ounces

The weight of dog in March = 34 pounds 4 ounces

It is also written as 33 pounds 20 ounces

Now,

33 pounds 20 ounces – 29 pounds 9 ounces

= 4 pounds 11 ounces

Therefore, Rocky gained : 4 pounds 11 ounces.

Question 3.
Bianca had 6 identical jars of bubble bath. She put them all in a bag that weighed 2 ounces. The total weight of the bag filled with the six jars was 1 pound 4 ounces. How much did each jar weigh?
Answer:

1 pound 4 oz = 20 oz

The weight of bag = 2 oz

Now, 20 oz – 2 oz = 18 oz

18 / 6 = 3

Therefore, Each jar weighs 3 ounces.

Question 4.
Use the information in the chart about Melissa’s school supplies to answer the following questions:

a. On Wednesdays, Melissa packs only two notebooks and a binder into her backpack. How much does her full backpack weigh on Wednesdays?
b. On Thursdays, Melissa puts her laptop, supply case, two textbooks, and a notebook in her backpack. How much does her full backpack weigh on Thursdays?
c. How much more does the backpack weigh with 3 textbooks and a notebook than it does with just 1 textbook and the supply case?
Answer:

a.

On Wednesdays,

The weight of two notebooks and a binder in backpack :

11 oz +11 oz +2 lb 5 oz + 2 lb 14 oz

= 4 lb 41 oz

It is also written as 6 lb 9 oz

Therefore, the weight of backpack on Wednesdays = 6 pounds and 9 ounces.

b.

On Thursdays,

The weight of laptop, supply case, Two textbooks and a note book in her backpack :

5 lb 12 oz + 1 lb + 3 lb 8 oz + 3 lb 8 oz + 11 oz + 2 lb 14 oz

= 17 lb 5 oz

Therefore, the weight of backpack on Wednesdays = 17 lb 5 oz

c.

The weight of three textbooks and a notebook =

3 lb 8 oz + 3 lb 8 oz + 3 lb + 8 oz + 11 oz = 11 lb 3 oz

The weight of  1 textbook and supply case =

3 lb 8 oz + 1 lb = 4 lb 8 oz

Now , 11 oz 3 oz – 4 lb 8 oz = 6 lb 11 oz

Therefore, the bag weighs 6 lb 11 oz more.

Engage NY Eureka Math 4th Grade Module 7 Lesson 7 Answer Key

Eureka Math Grade 4 Module 7 Lesson 7 Problem Set Answer Key

Question 1.
Determine the following sums and differences. Show your work.
a. 1 ft + 2 ft = _______ yd
b. 3 yd 1 ft + 2 ft = _______ yd
c. 1 yd – 1 ft = _______ ft
d. 8 yd – 1 ft = _______ yd _______ ft
e. 3 in + 9 in = _______ ft
f. 6 in + 9 in = _______ ft _______ in
g. 1 ft – 8 in = _______ in
h. 5 ft – 8 in = _______ ft _______ in
Answer:

a. 1 ft + 2 ft = 1  yd
b. 3 yd 1 ft + 2 ft = 4 yd
c. 1 yd – 1 ft = 2 ft
d. 8 yd – 1 ft =7 yd 2 ft
e. 3 in + 9 in = 1 ft
f. 6 in + 9 in = 1 ft 3 in
g. 1 ft – 8 in = 4 in
h. 5 ft – 8 in = 4 ft 4 in

Question 2.
Find the following sums and differences. Show your work.
a. 5 yd 2 ft + 2 ft = _______ yd _______ ft
b. 7 yd 2 ft + 2 yd 2 ft = _______ yd _______ ft
c. 4 yd 1 ft – 2 ft = _______ yd _______ ft
d. 6 yd 1 ft – 2 yd 2 ft =_______ yd _______ ft
e. 6 ft 9 in + 4 in = _______ ft _______ in
f. 4 ft 4 in + 3 ft 11 in =_______ ft _______ in
g. 34 ft 4 in – 8 in = _______ ft _______ in
h. 7 ft 1 in – 5 ft 10 in = _______ ft _______ in
Answer:

a. 5 yd 2 ft + 2 ft = 6 yd 1 ft
b. 7 yd 2 ft + 2 yd 2 ft = 10 yd 1 ft
c. 4 yd 1 ft – 2 ft = 3 yd 2 ft
d. 6 yd 1 ft – 2 yd 2 ft =3 yd 2 ft
e. 6 ft 9 in + 4 in = 7 ft 1 in
f. 4 ft 4 in + 3 ft 11 in = 8 ft 3 in
g. 34 ft 4 in – 8 in = 33 ft 8 in
h. 7 ft 1 in – 5 ft 10 in = 1 ft 3 in

Question 3.
Matthew is 6 feet 2 inches tall. His little cousin Emma is 3 feet 6 inches tall. How much taller is Matthew than Emma?
Answer:

The height of Matthew = 6 feet 2 inches Which means, 74 inches

The height of his little cousin Emma = 3 feet 6 inches Which means, 42 inches

Now, the age difference = 6 ft 2 in – 3 ft 6 in = 2 ft 8 in

Therefore, the Mathew is 2 feet 8 inches than Emma.

Question 4.
In gym class, Jared climbed 10 feet 4 inches up a rope. Then, he continued to climb up another 3 feet 9 inches. How high did Jared climb?
Answer:

Given that,

Firstly,Jared climbed 10 feet 4 inches

The length he continued climbing = 3 feet 9 inches

Total length = 10 feet 4  inches + 3 feet 9 inches = 13 feet and 13 inches

Also written as 14 feet 1 inch

Therefore, the total length Jared climbed = 14 feet 1 inch.

Question 5.
A quadrilateral has a perimeter of 18 feet 2 inches. The sum of three of the sides is 12 feet 4 inches.
a. What is the length of the fourth side?
b. An equilateral triangle has a side length equal to the fourth side of the quadrilateral. What is the perimeter of the triangle?
Answer:

a.

Given , the parameter of quadrilateral = 18 feet 2 inches or 17 feet 14 inches

The sum of three of the sides = 12 feet 4 inches

The length of fourth side = 18 ft 2 in – 12 ft 4 in = 5 ft 10 in

Therefore, the length of forth side = 5 ft 10 in

b.

The perimeter of triangle =

3 x (5 ft 10 in)

15 ft 30 inches

30 inches can also be written as 24 inches 6 inches

24 inches = 2 ft

Total = 17 ft 6 in

Therefore, the perimeter of triangle = 17 ft 6 in.

Eureka Math Grade 4 Module 7 Lesson 7 Exit Ticket Answer Key

Determine the following sums and differences. Show your work.
Question 1.
4 yd 1 ft + 2 ft ________ yd
Answer:

4 yd 1 ft + 2 ft = 5 yd

Question 2.
6 yd – 1 ft = ________ yd ________ ft
Answer:

6 yd – 1 ft = 5 yd 2 ft

Question 3.
4 yd 1 ft + 3 yd 2 ft = ________ yd
Answer:

4 yd 1 ft + 3 yd 2 ft = 8 yd

Question 4.
8 yd 1 ft – 3 yd 2 ft =________ yd ________ ft
Answer:

8 yd 1 ft – 3 yd 2 ft = 4 yd 2 ft

Eureka Math Grade 4 Module 7 Lesson 7 Homework Answer Key

Question 1.
Determine the following sums and differences. Show your work.
a. 2 yd 2 ft + 1 ft = ________ yd
b. 2 yd – 1 ft = ________ yd ________ ft
c. 2 ft + 2 ft = ________ yd ________ ft
d. 5 yd – 1 ft = ________ yd ________ft
e. 7 in + 5 in = ________ ft
f. 7 in + 7 in =________ ft ________ in
g. 1 ft – 2 in = ________ in
h. 2 ft – 6 in = ________ ft ________ in
Answer:

a. 2 yd 2 ft + 1 ft = 3 yd
b. 2 yd – 1 ft = 1 yd 2 ft
c. 2 ft + 2 ft = 1 yd 1 ft
d. 5 yd – 1 ft = 4 yd 2 ft
e. 7 in + 5 in = 1 ft
f. 7 in + 7 in = 1 ft 2 in
g. 1 ft – 2 in = 10 in
h. 2 ft – 6 in = 1 ft 6 in

Question 2.
Find the following sums and differences. Show your work.
a. 4 yd 2 ft + 2 ft = ________ yd ________ ft
b. 6 yd 2 ft + 1 yd 1 ft = ________ yd ________ ft
c. 5 yd 1 ft – 2 ft = ________ yd ________ ft
d. 7 yd 1 ft – 5 yd 2 ft = ________ yd ________ ft
e. 7 ft 8 in + 5 in = ________ ft ________ in
f. 6 ft 5 in + 5 ft 9 in = ________ ft ________ in
g. 32 ft 3 in – 7 in = ________ ft ________ in
h. 8 ft 2 in – 3 ft 11 in = ________ ft ________ in
Answer:

a. 4 yd 2 ft + 2 ft = 5 yd 1 ft
b. 6 yd 2 ft + 1 yd 1 ft = 8 yd 0 ft
c. 5 yd 1 ft – 2 ft = 4 yd 2 ft
d. 7 yd 1 ft – 5 yd 2 ft = 1 yd 2 ft
e. 7 ft 8 in + 5 in = 8 ft 1 in
f. 6 ft 5 in + 5 ft 9 in = 12 ft 2 in
g. 32 ft 3 in – 7 in = 31 ft 8 in
h. 8 ft 2 in – 3 ft 11 in =  4 ft 3 in

Question 3.
Laurie bought 9 feet 5 inches of blue ribbon. She also bought 6 feet 4 inches of green ribbon. How much ribbon did she buy altogether?
Answer:

Given that,

The length of blue ribbon Laurie bought = 9 feet 5 inches

The length of green ribbon Laurie bought = 6 feet 4 inches

Total length : 9 ft 5 in + 6 ft 4 in

= 15 ft 9 in

Therefore, the total length of ribbons Laurie bought altogether = 15 feet 9 inches.

Question 4.
The length of the room is 11 feet 6 inches. The width of the room is 2 feet 9 inches shorter than the length. What is the width of the room?
Answer:

11 feet 6 inches can also be written as 10 feet 18 inches

Given that the width of the room is 2 feet 9 inches smaller than the length

Now, 10 feet 18 inches – 2 feet 9 inches

= 8 feet 9 inches

Therefore, the width of the room = 8 feet 9 inches.

Question 5.
Tim’s bedroom is 12 feet 6 inches wide. The perimeter of the rectangular-shaped bedroom is 50 feet.
a. What is the length of Tim’s bedroom?
b. How much longer is the length of Tim’s room than the width?
Answer:

a.

12 feet 6 inches + 12 feet 6 inches = 50

25 ft = 50

= 12 ft 6 in

Therefore, the length of Tim’s room is 12 feet 6 inches.

b.

The length and width are the same .

Engage NY Eureka Math 4th Grade Module 7 Lesson 6 Answer Key

Eureka Math Grade 4 Module 7 Lesson 6 Problem Set Answer Key

Question 1.
Determine the following sums and differences. Show your work.
a. 3 qt + 1 qt = _______ gal
b. 2 gal 1 qt + 3 qt = _______ gal
c. 1 gal – 1 qt = _______ qt
d. 5 gal – 1 qt = _______ gal _______ qt
e. 2 c + 2 c = _______ qt
f. 1 qt 1 pt + 3 pt = _______ qt
g. 2 qt – 3 pt = _______ pt
h. 5 qt – 3 c _______ qt _______ c
Answer:

a. 3 qt + 1 qt = 1 gal
b. 2 gal 1 qt + 3 qt = 3 gal
c. 1 gal – 1 qt = 3 qt
d. 5 gal – 1 qt = 4 gal 3 qt
e. 2 c + 2 c = 1 qt
f. 1 qt 1 pt + 3 pt = 2 qt
g. 2 qt – 3 pt = 1 pt
h. 5 qt – 3 c = 4 qt 1 c

Question 2.
Find the following sums and differences. Show your work.
a. 6 gal 3 qt + 3 qt = _______ gal _______ qt
b. 10 gal 3 qt + 3 gal 3 qt = _______ gal _______ qt
c. 9 gal 1 pt – 2 pt = _______ gal _______ pt
d. 7 gal 1 pt – 2 gal 7 pt = _______ gal _______ pt
e. 16 qt 2 c + 4 c = _______ qt _______ c
6 gal 5 pt + 3 gal 3 pt = _______ gal _______ pt
Answer:

a. 6 gal 3 qt + 3 qt = 7 gal 2 qt
b. 10 gal 3 qt + 3 gal 3 qt = 14 gal 2 qt
c. 9 gal 1 pt – 2 pt = 8 gal 7 pt
d. 7 gal 1 pt – 2 gal 7 pt = 4 gal 2 pt
e. 16 qt 2 c + 4 c = 17 qt 2 c
6 gal 5 pt + 3 gal 3 pt = 10 gal 0 pt

Question 3.
The capacity of a pitcher is 3 quarts. Right now, it contains 1 quart 3 cups of liquid. How much more liquid can the pitcher hold?
Answer:

Given that,

The capacity of a pitcher = 3 quarts

Which means, 2 qt+4 cup

Also given, the pitcher contains 1 quart 3 cups of liquid

Now, 3 qt – 1 quart 3 cups =

1 qt 1 c

Therefore, the pitcher can hold 1 quart 1 cup more liquid.

Question 4.
Dorothy follows the recipe in the table to make her grandma’s cherry lemonade.
a. How much lemonade does the recipe make?

Answer:

Give, 5 pints of lemon juice

2 cups = 2 pints of sugar syrup

1 gallon 1 quart = 10 pints of water

3 quarts = 6 pints of cherry juice

Total : 5 + 2 +10 +6 = 22

Therefore,the recipe makes 22 pints or 2 gallons 3 quarts of lemonade.

b. How many more cups of water could Dorothy add to the recipe to make an exact number of gallons of lemonade?
Answer:

The number of pints lemonade make = 22 pints or 2 gallons 3 quarts

1 qt = 4 cups

2 gallons 3 quarts + 1 qt = 3 gal

Therefore, Dorothy need to add 4 cups to make an exact number of gallons of lemonade.

Eureka Math Grade 4 Module 7 Lesson 6 Exit Ticket Answer Key

Question 1.
Find the following sums and differences. Show your work.
a. 7 gal 2 qt + 3 gal 3 qt = _______ gal _______ qt
b. 9 gal 1 qt – 5 gal 3 qt = _______ gal _______ qt
Answer:

a. 7 gal 2 qt + 3 gal 3 qt = 11 gal 1 qt
b. 9 gal 1 qt – 5 gal 3 qt = 3 gal 2 qt

Question 2.
Jason poured 1 gallon 1 quart of water into an empty 2-gallon bucket. How much more water can be added to reach the bucket’s 2-gallon capacity?
Answer:

Given that, 1 gallon 1 quart water is poured into 2 gallon bucket

2 gal – 1 gal 1 quart

= 1 gal 1 qt

We , know that, 1 gal = 4 qt

So, 4 qt – 1 qt = 3 qt

Therefore, Jason need to add 3 quarts more water to reach the bucket’s 2 gallon capacity.

Eureka Math Grade 4 Module 7 Lesson 6 Homework Answer Key

Question 1.
Determine the following sums and differences. Show your work.
a. 5 qt + 3 qt = _______ gal
b. 1 gal 2 qt + 2 qt = _______ gal
c. 1 gal – 3 qt =_______ qt
d. 3 gal – 2 qt = _______ gal _______ qt
e. 1 c + 3 c =_______ qt
f. 2 qt 3 c + 5 c = _______ qt
g. 1 qt – 1 pt = _______ pt
h. 6 qt – 5 pt = _______ qt _______ pt
Answer:

a. 5 qt + 3 qt = 2 gal
b. 1 gal 2 qt + 2 qt = 2 gal
c. 1 gal – 3 qt = 1 qt
d. 3 gal – 2 qt = 2 gal 2 qt
e. 1 c + 3 c = 1 qt
f. 2 qt 3 c + 5 c = 4 qt
g. 1 qt – 1 pt = 1 pt
h. 6 qt – 5 pt = 3 qt 1 pt

Question 2.
Find the following sums and differences. Show your work.
a. 4 gal 2 qt + 3 qt = _______ gal _______ qt
b. 12 gal 2 qt + 5 gal 3 qt = _______ gal _______ qt
c. 7 gal 2 pt – 3 pt = _______ gal _______ pt
d. 11 gal 3 pt – 4 gal 6 pt = _______ gal _______ pt
e. 12 qt 5 c + 6 c = _______ qt _______ c
f. 8 gal 6 pt + 5 gal 4 pt = _______ gal _______ pt
Answer:

a. 4 gal 2 qt + 3 qt = 5 gal 1 qt
b. 12 gal 2 qt + 5 gal 3 qt = 18 gal 1 qt
c. 7 gal 2 pt – 3 pt = 6 gal 7 pt
d. 11 gal 3 pt – 4 gal 6 pt = 6 gal 5 pt
e. 12 qt 5 c + 6 c = 14 qt 3 c
f. 8 gal 6 pt + 5 gal 4 pt = 14 gal 2 pt

Question 3.
The capacity of a bucket is 5 gallons. Right now, it contains 3 gallons 2 quarts of liquid. How much more liquid can the bucket hold?
Answer:

Given that ,

The quantity of the bucket = 5 gallons

The the quantity of water the bucket contains now = 3 gallons 2 quarts

3 gal 2 quarts + 2 qt = 4 gallons

4 gal + 1 gal = 5 gallons

Therefore, the bucket can holds 1 gal 2 qt of more water.

Question 4.
Grace and Joyce follow the recipe in the table to make a homemade bubble solution.
a. How much solution does the recipe make?

Answer:

Given

2 gallons 3 pints of water

2 quarts 1 cup of dish soap and

2 cups of corn syrup

Total :

2 gal 3 pt + 2 qt 1 c + 2 c = 3 gallons 1 cup

Therefore, the recipe make 3 gal 1 cup of solution.

b. How many more cups of solution would they need to fill a 4-gallon container?
Answer:

The quantity of the recipe = 3 gal 1 cup

We know that, 1 gal = 4 qt

and 1 qt = 2 pt which means, 4 x 2 = 8 pt

1 pt = 2 cups which means, 8 x 2 = 16

Therefore, 3 gal 1 cup + 15 more cups can make 4 gallons of the recipe.

Engage NY Eureka Math 4th Grade Module 7 Lesson 5 Answer Key

Eureka Math Grade 4 Module 7 Lesson 5 Sprint Answer Key

A
Convert Length Units

Question 1.
1 km =
Answer:
1000 m

Question 2.
2 km =
Answer:
2000 m

Question 3.
3 km =
Answer:
3000 m

Question 4.
7 km =
Answer:
7000 m

Question 5.
5 km =
Answer:
5000 m

Question 6.
1 m =
Answer:
100 cm

Question 7.
2 m =
Answer:
200 cm

Question 8.
3 m =
Answer:
300 cm

Question 9.
9 m =
Answer:
900 cm

Question 10.
6 m =
Answer:
600 cm

Question 11.
1 yd =
Answer:
3 ft

Question 12.
2 yd =
Answer:
6 ft

Question 13.
3 yd =
Answer:
9 ft

Question 14.
10 yd =
Answer:

30 ft

Question 15.
5 yd =
Answer:
15 ft

Question 16.
1 ft =
Answer:
12 in

Question 17.
2 ft =
Answer:
24 in

Question 18.
3 ft =
Answer:
36 in

Question 19.
10 ft =
Answer:
120 in

Question 20.
4 ft =
Answer:
48 in

Question 21.
9 km =
Answer:
9000 m

Question 22.
4 km =
Answer:
4000 m

Question 23.
6 km =
Answer:
6000 m

Question 24.
5 m =
Answer:
500 cm

Question 25.
7 m =
Answer:
700 cm

Question 26.
4 m =
Answer:
400 cm

Question 27.
8 m =
Answer:
800 cm

Question 28.
4 yd =
Answer:
12 ft

Question 29.
8 yd =
Answer:
24 ft

Question 30.
6 yd =
Answer:
18 ft

Question 31.
9 yd =
Answer:
27 ft

Question 32.
5 ft =
Answer:
60 in

Question 33.
6 ft =
Answer:
72 in

Question 34.
1,000 m =
Answer:
1 km

Question 35.
8,000 m =
Answer:
8 km

Question 36.
100 cm =
Answer:
1 m

Question 37.
600 cm =
Answer:
6 m

Question 38.
3 ft =
Answer:
1 yd

Question 39.
24 ft =
Answer:
8 yd

Question 40.
12 in =
Answer:
1 ft

Question 41.
72 in =
Answer:
6 ft

Question 42.
8 ft =
Answer:
96 in

Question 43.
84 in =
Answer:
7 ft

Question 44.
9 ft =
Answer:
108 in

B
Convert Length Units

Question 1.
1 m =
Answer:
100 cm

Question 2.
2 m =
Answer:
200 cm

Question 3.
3 m =
Answer:
300 cm

Question 4.
7 m =
Answer:
700 cm

Question 5.
5 m =
Answer:
500 cm

Question 6.
1 km =
Answer:
1000 m

Question 7.
2 km =
Answer:
2000 m

Question 8.
3 km =
Answer:
3000 m

Question 9.
9 km =
Answer:
9000 m

Question 10.
6 km =
Answer:
6000 m

Question 11.
1 yd =
Answer:
3 ft

Question 12.
2 yd =
Answer:
6 ft

Question 13.
3 yd =
Answer:
9 ft

Question 14.
5 yd =
Answer:
15 ft

Question 15.
10 yd =
Answer:
30 ft

Question 16.
1 ft =
Answer:
12 in

Question 17.
2 ft =
Answer:
24 in

Question 18.
3 ft =
Answer:
36 in

Question 19.
10 ft =
Answer:
120 in

Question 20.
4 ft =
Answer:
48 in

Question 21.
9 m =
Answer:
900 cm

Question 22.
4 m =
Answer:
400 cm

Question 23.
6 m =
Answer:
600 cm

Question 24.
5 km =
Answer:
5000 m

Question 25.
7 km =
Answer:
7000 m

Question 26.
4 km =
Answer:
4000 m

Question 27.
8 km =
Answer:
8000 m

Question 28.
6 yd =
Answer:
18 ft

Question 29.
9 yd =
Answer:
27 ft

Question 30.
4 yd =
Answer:
12 ft

Question 31.
8 yd =
Answer:
24 ft

Question 32.
5 ft =
Answer:
60 in

Question 33.
6 ft =
Answer:
72 in

Question 34.
100 cm =
Answer:
1 m

Question 35.
800 cm =
Answer:
8 m

Question 36.
1000 m =
Answer:
1 km

Question 37.
6000 m =
Answer:
6 km

Question 38.
3 ft =
Answer:
1 yd

Question 39.
27 ft =
Answer:
9 yd

Question 40.
12 in =
Answer:
1 ft

Question 41.
84 in =
Answer:
7 ft

Question 42.
9 ft =
Answer:
108 in

Question 43.
72 in =
Answer:
6 ft

Question 44.
8 ft =
Answer:
96 in

Eureka Math Grade 4 Module 7 Lesson 5 Problem Set Answer Key

Question 1.
a. Label the rest of the tape diagram below. Solve for the unknown.

3 feet + 3 feet = 6 feet

1 feet = 12 inches

6 feet = 6 x 12 = 72 inches

72 inches – 5 inches = 67 inches

b. Write a problem of your own that could be solved using the diagram above.
Answer:

Maria, knitted a cloth of length 3 feet. Mark knitted a cloth as twice as long as Maria. Jacob knitted a cloth which is 5 inches shorter than Mark. Calculate the length of Mark and Jacob altogether

Question 2.
Create a problem of your own using the diagram below, and solve for the unknown.

Answer:

Harry have 3 dogs. First dog weighs 4 pounds. Second dog weighs 4 times more than the first dog and the third dog weighs 30 ounces more than the half of second dog. Calculate the total weight of three dogs.

4 pounds x 7 = 28 pounds

30 ounces = 1 pound 14 ounces

Total : 28 pounds + 1 pound 14 ounces

= 29 pounds 14 ounces

Eureka Math Grade 4 Module 7 Lesson 5 Exit Ticket Answer Key

Caitlin ran 1,680 feet on Monday and 2,340 feet on Tuesday. How many yards did she run in those two days?
Answer:

The total distance Caitlin ran on Monday = 1680

The total distance she ran on Tuesday = 2, 340

Total : 1680 + 2340

= 4,020

We know that, 1 yard = 3 feet

Now, 4020 / 3 = 1340

Therefore, Caitlin ran 1340 yards in two days.

Eureka Math Grade 4 Module 7 Lesson 5 Homework Answer Key

Draw a tape diagram to solve the following problems.
Question 1.
Timmy drank 2 quarts of water yesterday. He drank twice as much water today as he drank yesterday. How many cups of water did Timmy drink in the two days?
Answer:

The amount of water he drank today = 2 quarts

1 quart = 4 cups

So, 2 quarts = 2 x 4 = 8 cups

Also given, he drank twice as much water today as he drank yesterday

Now, 4 quarts = 4 x 4 = 16

Total : 8 cups + 16 cups = 24 cups

Therefore, Timmy drank 24 cups of water in two days altogether.

Question 2.
Lisa recorded a 2-hour television show. When she watched it, she skipped the commercials. It took her 84 minutes to watch the show. How many minutes did she save by skipping the commercials?
Answer:

The time period of television show = 2 hours

We know that, 1 hour = 60 minutes

2 hours = 2 x 60 = 120 minutes

The time period of commercials Lisa skipped= 84 minutes

Now, 120 minutes – 84 minutes = 36 minutes

Therefore, Lisa saved 36 minutes.

Question 3.
Jason bought 2 pounds of cashews. Sarah ate 9 ounces. David ate 2 ounces more than Sarah. How many ounces were left in Jason’s bag of cashews?
Answer:

The amount of cashews Jason bought = 2 pounds

2 pounds = 2 x 16 = 32 ounces

The amount of cashews Sarah ate = 9

The amount of cashews David ate is 2 ounces more than Sarah

That is 9 + 2 = 11

Total cashews they ate all together = 9 + 11 = 20

Now,

32 – 20 = 12

Therefore, 12 ounces of cashews were left in Jason bag

Question 4.
a. Label the rest of the tape diagram below. Solve for the unknown.

5 feet + 5 feet = 10 feet

1 feet = 12 inches

10 feet = 10 x 12 = 120 inches

Now, 120 – 10 = 110 inches.

b. Write a problem of your own that could be solved using the diagram above.
Answer:

Harry, Henry and Ron each throw a stone. Harry stone flies 5 feet. Henry’s stone flies twice as far as Harry’s stone. Ron’s stone flies 10 inches shorter than Henry. Calculate the total distance flown by Henry and Ron?

Question 5.
Create a problem of your own using the diagram below, and solve for the unknown.

Answer:

Leo weight = 3 pounds

Bailey weight = 4 x 3 = 12 pounds

Rio weight = 6 pounds 8 ounces

Total :

3 pounds + 12 pounds + 6 pounds 8 ounces

= 21 pounds 8 ounces .

I have 3 cats. Leo weighs 3 pounds. Bailey weighs 4 times as much as Leo. Rio weighs 10 ounces more than the half of Bailey. Calculate the total weight of the three cats.

Engage NY Eureka Math 4th Grade Module 7 Lesson 4 Answer Key

Eureka Math Grade 4 Module 7 Lesson 4 Problem Set Answer Key

Use RDW to solve the following problems.
Question 1.
Beth is allowed 2 hours of TV time each week. Her sister is allowed 2 times as much. How many minutes of TV can Beth’s sister watch?
Answer: 240 minutes

Explanation :

1 hour= 60 minutes

Number of minutes = Number of hours x 60

2 x 60 = 120 minutes

Given, Beth’s sister is allowed 2 as much =

120 x 2 = 240 minutes

Therefore, Beth’s sister can watch TV for 240 minutes i.e, 4 hours

Question 2.
Clay weighs 9 times as much as his baby sister. Clay weighs 63 pounds. How much does his baby sister weigh in ounces?
Answer: 112 ounces

Explanation :

1 pound = 16 ounces

Which means, 63 pounds = 63 x 16 = 1008 ounces

Given that, Clay weighs 9 times as much as his baby sister

1008 / 9 = 112

Therefore, His baby sister weight 112 ounces.

Question 3.
Helen has 4 yards of rope. Daniel has 4 times as much rope as Helen. How many more feet of rope does Daniel have compared to Helen?
Answer: 36 feet

Explanation :

1 yard = 3 feet

Which means, 4 x 3 = 12

Given that, Daniel has 4 times as much rope as Helen

12 x 4 = 48 feet

Now, 48 – 12 = 36

Therefore, Daniel has 36 feet more than Helen.

Question 4.
A dishwasher uses 11 liters of water for each cycle. A washing machine uses 5 times as much water as a dishwasher uses for each load. Combined, how many millilitres of water are used for 1 cycle of each machine?
Answer: 66,000

Explanation:

1 litre = 1000 millilitres

11 litres = 1000 x 11 = 11,000

Given that, a washing machine uses 5 times as much water as a dishwasher

11,000 x 5 = 55,000

Combined, The number of millilitres of water both the machines used for 1 cycle

11,000 + 55,000 = 66,000 millilitres.

Question 5.
Joyce bought 2 pounds of apples. She bought 3 times as many pounds of potatoes as pounds of apples. The melons she bought were 10 ounces lighter than the total weight of the potatoes. How many ounces did the melons weigh?
Answer: 86 ounces

Explanation :

1 pound = 16 ounces

Which means, 2 pounds of apples = 2 x 16 =32 ounces

Given that,

She bought 3 times as many of potatoes as pounds of apples

3 x 32 ounces = 96 ounces

Also given,

The melons she bought were 10 ounces lighter than the total weight of potatoes

So, 96 – 10 = 86 ounces

Therefore, The weight of melons = 86 ounces

Eureka Math Grade 4 Module 7 Lesson 4 Exit Ticket Answer Key

Use RDW to solve the following problem.
Brian has a melon that weighs 3 pounds. He cut it into six equal pieces. How many ounces did each piece weigh?
Answer: 8 ounces

Explanation:

1 pound = 16 ounces

Which means, 3 pounds = 16+16+16 = 48 ounces

Given that, melon is cut into 6 equal parts

So, 48 divided by 6

48 / 6 = 8

Therefore, each piece weighs 8 ounces.

Eureka Math Grade 4 Module 7 Lesson 4 Homework Answer Key

Use RDW to solve the following problems.
Question 1.
Sandy took the train to New York City. The trip took 3 hours. Jackie took the bus, which took twice as long. How many minutes did Jackie’s trip take?
Answer: 360 hours

Explanation :

1 hour = 60 minutes

Given that, The time took for sandy’s trip by train = 3 hours

Number of minutes= number of hours x 60

3 x 60 = 180

Also given, By bus,Jackie’s trip time is twice than Sandy’s trip

180 x 2 = 360

Therefore, the time taken for Jackie’s trip = 360 minutes.

Question 2.
Coleton’s puppy weighed 3 pounds 8 ounces at birth. The vet weighed the puppy again at 6 months, and the puppy weighed 7 pounds. How many ounces did the puppy gain?
Answer: 56 ounces

Explanation :

Initial weight of the puppy = 3 pounds 8 ounces

1 pound = 16 ounces

3 pounds = 16+16+16 = 48 ounces

Total initial weight : 48 + 8 = 56

Given that, The weight of the puppy after 6 months = 7 pounds

Which means, 7 x 16 = 112

The weight gained by puppy =

112 – 56 = 56

Therefore, the puppy gained 56 ounces.

Question 3.
Jessie bought a 2-liter bottle of juice. Her sister drank 650 millilitres. How many millilitres were left in the bottle?
Answer:

1 litre = 1000 millilitres

Which means, 2 litres = 1000+1000 = 2000 millilitres

Given that her sister drank 650 millilitres

Now, the quantity of leftover water =

2000 – 650 = 1350

Therefore, The number of millilitres were left in bottle = 1350 millilitres.

Question 4.
Hudson has a chain that is 1 yard in length. Myah’s chain is 3 times as long. How many feet of chain do they have in all?
Answer: 12 feet

Explanation :

1 yard = 3 feet

Given that, Myah’s chain is 3 times long than Hudson

So, 1 x 3 = 3 yards

3 yards = 3+ 3+ 3 = 9  feet

The length of the chain they have in both :  3 + 9 = 12

Therefore,  12 feet of chain they have in all.

Question 5.
A box weighs 8 ounces. A shipment of boxes weighs 7 pounds. How many boxes are in the shipment?
Answer: 14

Given that,

Each box weighs 8 ounces

The total weight of shipment of boxes = 7 pounds

1 pound = 16 ounces

Which means, 7 pounds = 7 x 16 = 112 ounces

Now, the number of boxes in shipment : 112 / 8 =14

Therefore, total number of boxes in the shipment = 14

Question 6.
Tracy’s rain barrel has a capacity of 27 quarts of water. Beth’s rain barrel has a capacity of twice the amount of water as Tracy’s rain barrel. Trevor’s rain barrel can hold 9 quarts of water less than Beth’s barrel.
a. What is the capacity of Trevor’s rain barrel?
b. If Tracy, Beth, and Trevor’s rain barrels were filled to capacity, and they poured all of the water into a 30-gallon bucket, would there be enough room? Explain.
Answer:

Given,

The capacity of Tracy’s barrel = 27 quarts

The capacity of Beth’s rain barrel is twice the amount of Tracy

Which means, 27 + 27 = 54 quarts

a.

The capacity of Trevor’s rain barrel is 9 quarts less than Beth’s barrel

Which means, 54 – 9 = 45 quarts

Therefore, the capacity of Trevor’s rain barrel is 54 quarts.

b.

Total capacity of Tracy, Beth and Trevor is 27 + 54 + 45 = 126 quarts

According to given condition, if they are poured into 30 gallon bucket

Now, 1 gallon = 4 quarts

30 gallons = 30 x 4 = 120 quarts

Therefore, there is no enough room in the 30 gallons bucket because there will be a shortage of 6 quarts.

Engage NY Eureka Math 4th Grade Module 7 Lesson 3 Answer Key

Eureka Math Grade 4 Module 7 Lesson 3 Practice Sheet Answer Key

a.

The rule for converting minutes to seconds is ______________

Number of minutes x 60 = Number of seconds

b.

The rule for converting hours to minutes is ____________

Number of hours x 60 = Number of minutes.

c.

The rule for converting days to hours is ______________
Answer:

Number of days x 24 = Number of hours.

Eureka Math Grade 4 Module 7 Lesson 3 Problem Set Answer Key

Use RDW to solve Problems 1–2.
Question 1.
Courtney needs to leave the house by 8:00 a.m. If she wakes up at 6:00 a.m., how many minutes does she have to get ready? Use the number line to show your work.

Answer: 120 minutes

Explanation :

8 – 6 = 2 hours

1 hour = 60 minutes

2 hours = 2 x 60 = 120

So, Courtney have 120 minutes to get ready

Question 2.
Giuliana’s goal was to run a marathon in under 6 hours. What was her goal in minutes?
Answer: 360 minutes.

Explanation :

Number of minutes = Number of hours x 60

Number of hours = 6

So, 6 x 60 = 360

Therefore, Giuliana’s goal to rum a marathon in under 360 minutes.

Question 3.
Complete the following conversion tables and write the rule under each table.
a.

The rule for converting hours to minutes and minutes to seconds is ___________

To calculate number of minutes,

Number of hours x 60 = Number of minutes

b.

The rule for converting days to hours is ____________
Answer:

To calculate number of hours,

Number of days x 24 = Number of hours.

Question 4.
Solve.
a. 9 hours 30 minutes = __________ minutes
b. 7 minutes 45 seconds = _______ seconds
c. 9 days 20 hours = __________ hours
d. 22 minutes 27 seconds = ______ seconds
e. 13 days 19 hours = __________ hours
f. 23 hours 5 minutes = _______ minutes
Answer:

a. 9 hours 30 minutes = 570 minutes
b. 7 minutes 45 seconds = 465 seconds
c. 9 days 20 hours = 236 hours
d. 22 minutes 27 seconds = 1,347 seconds
e. 13 days 19 hours = 331 hours
f. 23 hours 5 minutes = 1,385 minutes

Question 5.
Explain how you solved Problem 4(f).
Answer:

Given, 23 hours 5 minutes.

1 hour = 60 minutes

Number of minutes = Number of hours x 60

So, 23 x 60 = 1380

and 1380 + 5 = 1385

Therefore, 23 hours 5 minutes = 1350 minutes.

Question 6.
How many seconds are in 14 minutes 43 seconds?
Answer:

Given,

14 minutes 43 seconds

1 minutes = 60 seconds

Number of seconds = Number of minutes x 60

14 x 60 = 840 seconds

And 840 + 43 = 883 seconds

Therefore, 14 minutes 43 seconds = 883 seconds.

Question 7.
How many hours are there in 4 weeks 3 days?
Answer:

Given,

4 weeks 3 days

1 week = 7 days

So, 7 x 4 = 28 days

So, 28 + 3 = 31 days

1 day = 24 hours

Number of hours = Number of days x 24

31 x 24 = 744 hours

Therefore, 4 weeks 3 days = 744 hours

Eureka Math Grade 4 Module 7 Lesson 3 Exit Ticket Answer Key

The astronauts from Apollo 17 completed 3 spacewalks while on the moon for a total duration of 22 hours 4 minutes. How many minutes did the astronauts walk in space?
Answer:

Given,

22 hours 4 minutes is the total duration

1 hour = 60 minutes

Number of minutes = Number of hours x 60

So, 22 x 60 = 1,320

1320 + 4 = 1324

Therefore, 22 hours 4 minutes = 1324 minutes

So, The time duration required for astronaut to walk in space = 1324 minutes.

Eureka Math Grade 4 Module 7 Lesson 3 Homework Answer Key

Use RDW to solve Problems 1–2.
Question 1.
Jeffrey practiced his drums from 4:00 p.m. until 7:00 p.m. How many minutes did he practice? Use the number line to show your work.

Answer: 180

Explanation :

7 – 4 = 3

1 hour = 60 minutes

Number of minutes = Number of hours x 60

3 x 60 = 180 minutes

Therefore, Jeffrey practiced his drums for 180 minutes.

Question 2.
Isla used her computer for 5 hours over the weekend. How many minutes did she spend on the computer?
Answer: 300 minutes

Explanation :

1 hour = 60 minutes

Number of minutes = Number of hours x 60

5 x 60 = 300

Therefore, Isla used her computer for 300 minutes

5 hours = 300 minutes.

Question 3.
Complete the following conversion tables and write the rule under each table.
a.

The rule for converting hours to minutes is ________________

Number of minutes = Number of hours x 60

b.

The rule for converting days to hours is _________________
Answer:

Number of hours = number of days  x  24

Question 4.
Solve.
a. 10 hours 30 minutes = ________ minutes
b. 6 minutes 15 seconds = ________ seconds
c. 4 days 20 hours = ________ hours
d. 3 minutes 45 seconds = ________ seconds
e. 23 days 21 hours = ________ hours
f. 17 hours 5 minutes = ________ minutes
Answer:

a. 10 hours 30 minutes = 630 minutes
b. 6 minutes 15 seconds = 375 seconds
c. 4 days 20 hours = 116 hours
d. 3 minutes 45 seconds = 225 seconds
e. 23 days 21 hours = 573 hours
f. 17 hours 5 minutes = 1,025 minutes

Question 5.
Explain how you solved Problem 4(f).
Answer:

17 hours 5 minutes

1 hour = 60 minutes

Number of minutes = Number of hours x 60

17 x 60 = 1020

So, 1020 + 5 = 1025

Therefore, 17 hours 5 minutes = 1025 minutes

Question 6.
It took a space shuttle 8 minutes 36 seconds to launch and reach outer space. How many seconds did it take?
Answer:

Given, 8 minutes 36 seconds

1 minute = 60 seconds

Number of seconds = Number of minutes x 60

8 x 60 = 480 seconds

So, 480 + 8 = 488 seconds

8 minutes 36 seconds = 488 seconds.

Question 7.
Apollo 16’s mission lasted just over 1 week 4 days. How many hours are there in 1 week 4 days?
Answer:

Given,

1 week 4 days

1 week = 7 days

So, 7 + 4 = 11

1 day = 24 hours

Number of hours = number of days x 24

So, 11 x 24 = 264 hours

Therefore, 1 week 4 days = 264 hours.

Engage NY Eureka Math 4th Grade Module 7 Lesson 2 Answer Key

Eureka Math Grade 4 Module 7 Lesson 2 Core Fluency Practice Set A Answer Key

Practice Set A Part 1: Multi-Digit Addition Fluency
Question 1.

Answer:

Question 2.

Answer:

42,609 + 8685

=  51,294

Question 3.

Answer:

39,563 +

48, 438

= 88, 001

Question 4.

Answer:

658,199

+ 25675

= 683, 874

Question 5.

Answer:

445, 976

+  37, 415

= 483, 391

Question 6.

Answer:

438 , 617

+493, 859

= 932, 476

Practice Set A Part 2: Multi-Digit Addition Fluency
Question 1.

Answer:

9202

+ 6211

= 15413

Question 2.

Answer:

42, 774

+8, 520

= 51,294

Question 3.

Answer:

53,545

+34,456

= 88,001

Question 4.

Answer:

604, 754

+  79,120

= 683,874

Question 5.

Answer:

454, 315

+   29, 076

=  483,391

Question 6.

Answer:

110, 728

+ 821, 748

= 932, 476

Eureka Math Grade 4 Module 7 Lesson 2 Core Fluency Practice Set B Answer Key

Practice Set B Part 1: Multi-Digit Subtraction Fluency
Question 1.

Answer:

7,739

– 5, 546

= 2193

Question 2.

Answer:

23, 145

–  5, 129

= 18,016

Question 3.

Answer:

71, 378

– 61,876

=

Question 4.

Answer:

479,541

–  78,856

= 400,685

Practice Set B Part 2: Multi-Digit Subtraction Fluency
Question 1.

Answer:

7699

– 5506

= 2193

Question 2.

Answer:

19,145

–   1, 129

=12,016

Question 3.

Answer:

71, 878

+62, 376

= 9, 502

Question 4.

Answer:

479, 497

– 78, 812

= 400, 685

Eureka Math Grade 4 Module 7 Lesson 2 Core Fluency Practice Set C Answer Key

Practice Set C Part 1: Multi-Digit Subtraction with Zeros Fluency
Question 1.

Answer:

7890

-5472

=2418

Question 2.

Answer:

28,001

–   5, 853

= 22,148

Question 3.

Answer:

60, 407

– 35, 344

= 25,063

Question 4.

Answer:

400, 069

–   24,362

= 375, 707

Practice Set C Part 2: Multi-Digit Subtraction with Zeros Fluency
Question 1.

Answer:

7890

-5472

= 2418

Question 2.

Answer:

28, 609

–   6461

= 22,148

Question 3.

Answer:

60, 497

– 35,434

= 25,063

Question 4.

Answer:

400, 869

–    25162

= 375,707

Eureka Math Grade 4 Module 7 Lesson 2 Core Fluency Practice Set D Answer Key

Practice Set D Part 1: Multi-Digit Addition and Subtraction Fluency
Question 1.

Answer:

9327

+ 9664

= 18991

Question 2.

Answer:

39,463

– 38938

= 00,525

Question 3.

Answer:

758, 194

+ 35,478

=793,672

Question 4.

Answer:

839,014

–  27075

= 811, 939

Question 5.

Answer:

438, 615

+ 193,979

= 632,594

Question 6.

Answer:

960, 043

-368,972

= 591,071

Practice Set D Part 2: Multi-Digit Addition and Subtraction Fluency
Question 1.

Answer:

9630

+ 9361

=18,991

Question 2.

Answer:

34, 478

– 33, 953

= 00,525

Question 3.

Answer:

754 , 454

+  39, 218

= 793, 672

Question 4.

Answer:

839, 099

–  27, 160

= 811,939

Question 5.

Answer:

108,215

– 524,379

= 632,584

Question 6.

Answer:

959 , 943

– 368, 872

= 591,071

Eureka Math Grade 4 Module 7 Lesson 2 Practice Sheet Answer Key

a.

The rule for converting gallons to quarts is ______________

To convert gallons into quarts,

The number of gallons x 4 = number of quarts

b.

The rule for converting quarts to pints is ________________

To convert, quarts into pints,

The number of quarts x 2 = number of pints

c.

The rule for converting pints to cups is ________________

To convert pints into cups

Number of pints x 2 = number of cups.

d.
1 gallon = ________ pints
1 quart = ________ cups
1 gallon = ________ cups

Answer :

1 gallon = 8 pints

1 quart =  4 cups
1 gallon = 16 cups

Eureka Math Grade 4 Module 7 Lesson 2 Problem Set Answer Key

Use RDW to solve Problems 1–3.

Question 1.
Susie has 3 quarts of milk. How many pints does she have?
Answer:

1 quarts = 2 pints

So, 3 quarts = 3 x 2 = 6

Therefore, Susie has 3 pints

Question 2.
Kristin has 3 gallons 2 quarts of water. Alana needs the same amount of water but only has 8 quarts. How many more quarts of water does Alana need?
Answer:

Given that, Kristin has 3 gallon 2 quarts of water

1 gallon = 4 quarts

3 gallons 2 quarts = 14 quarts

Also given, Alana needs same amount of water but only has 8 quarts

So, 14 quarts – 8 quarts = 6 quarts

Therefore, Alana needs 6 more quarts.

Question 3.
Leonard bought 4 liters of orange juice. How many milliliters of juice does he have?
Answer:

1 litre = 1,000 millilitres

4 litres = 4 x 1000 = 4000 millilitres

Therefore, Leonard has 4000 millilitres of juice.

Question 4.
Complete the following conversion tables and write the rule under each table.
a.

The rule for converting gallons to quarts is ___________

To convert, gallons x quarts

Number of gallons x 4 = number of quarts

b.

The rule for converting quarts to pints is ___________
Answer:

To convert quarts into pints ,

Number of quarts x 2 = number of pints

Question 5.
Solve.
a. 8 gallons 2 quarts = __________ quarts
b. 15 gallons 2 quarts = __________ quarts
c. 8 quarts 2 pints = __________ pints
d. 12 quarts 3 pints = __________ cups
e. 26 gallons 3 quarts = __________ pints
f. 32 gallons 2 quarts = __________ cups
Answer:

a. 8 gallons 2 quarts =34  quarts
b. 15 gallons 2 quarts = 62 quarts
c. 8 quarts 2 pints = 18 pints
d. 12 quarts 3 pints = 54 cups
e. 26 gallons 3 quarts = 214 pints
f. 32 gallons 2 quarts = 520 cups

Question 6.
Answer true or false for the following statements. If your answer is false, make the statement true.
a. 1 gallon > 4 quarts _________
b. 5 liters = 5,000 milliliters ________
c. 15 pints < 1 gallon 1 cup _________
Answer:

a.

1 gallon > 4 quarts

False, 1 gallon = 4 quarts

b. 5 liters = 5,000 milliliters ________

True

c. 15 pints < 1 gallon 1 cup _________

False

15 pints > 1 gallon 1 cup.

Question 7.
Russell has 5 liters of a certain medicine. If it takes 2 milliliters to make 1 dose, how many doses can he make? Answer:

Total number of litres = 5 litres

1 litre = 1,000 millilitres

5 litres = 1000 x 5 = 5000

Given, 2 millilitres will make 1 dose

5000 / 2 = 2500 ml

Therefore, Russel can make 2500 doses

Question 8.
Each month, the Moore family drinks 16 gallons of milk and the Siler family goes through 44 quarts of milk. Which family drinks more milk each month?
Answer:

1 gallon = 4 quarts

Given, Moore family drink 16 gallons of milk

So, 16 gallons = 64 quarts

Siler family drinks 44 quarts of milk

Now, 64 – 44 = 20

Therefore, Moore family drinks more milk than Siler family.

Moore family drinks 20 quarts more than Siler.

Question 9.
Keith’s lemonade stand served lemonade in glasses with a capacity of 1 cup. If he had 9 gallons of lemonade, how many cups could he sell?
Answer:

1 gallon = 16 cups

Now, 9 gallons =

16 x 9 = 144 cups

Therefore, Keith can sold 144 cups of lemonade.

Eureka Math Grade 4 Module 7 Lesson 2 Exit Ticket Answer Key

Question 1.
Complete the table.

Answer:

Question 2.
Bonnie’s doctor recommended that she drink 2 cups of milk per day. If she buys 3 quarts of milk, will it be enough milk to last 1 week? Explain how you know.
Answer:

Given, Bonnie’s is recommended to drink 2 cups of milk

The amount of milk she bought = 3 quarts

1 quart = 4 cups

So, 3 quarts = 3 x 4 = 12 cups

1 week = 7 days

7 days x 2 cups = 14 cups

14 cups – 12 cups = 2 cups

Therefore,  Bonnie do not have mil to drink for 1 week . there is a shortage of 2 cups.

Eureka Math Grade 4 Module 7 Lesson 2 Homework Answer Key

Use the RDW process to solve Problems 1–3.
Question 1.
Dawn needs to pour 3 gallons of water into her fish tank. She only has a 1-cup measuring cup. How many cups of water should she put in the tank?
Answer:

Total quantity of water Dawn needs to pour in fish tank = 3 gallons

We know that,

1 gallon = 16 cups

3 gallons = 16 x 3 = 48

Therefore, Dawn should put 48 cups of water in to the tank.

Question 2.
Julia has 4 gallons 2 quarts of water. Ally needs the same amount of water but only has 12 quarts. How much more water does Ally need?
Answer:

Given that,

The amount of water Julia has = 4 gallons 2 quarts

The amount of water Ally have = 12 quarts

12 quarts = 3 gallons

Now, 3 gallons – 4 gallons 2 quarts = 1 gallon  2 quarts

Therefore, Ally needs 1 gallon 2 quarts.

Question 3.
Sean drank 2 liters of water today, which was 280 milliliters more than he drank yesterday. How much water did he drink yesterday?
Answer:

Given,

The amount of water Sean drink today = 2 litres

1 litre = 1000 millilitres

2 litres = 1000 x 2 = 2000 millilitres

Also given, she drank 280 millilitres more than yesterday

Now, 2000 – 280 = 1720

Therefore, the amount of water she drank yesterday = 1720 millilitres.

Question 4.
Complete the tables.
a.

b.

Answer:

Question 5.
Solve.
a. 6 gallons 3 quarts = __________ quarts
b. 12 gallons 2 quarts = __________ quarts
c. 5 quarts 1 pint = __________ pints
d. 13 quarts 3 pints = __________ cups
e. 17 gallons 2 quarts = __________ pints
f. 27 gallons 3 quarts = __________ cups
Answer:

a. 6 gallons 3 quarts = 27 quarts
b. 12 gallons 2 quarts = 50 quarts
c. 5 quarts 1 pint = 11 pints
d. 13 quarts 3 pints = 58 cups
e. 17 gallons 2 quarts = 140 pints
f. 27 gallons 3 quarts = 444 cups

Question 6.
Explain how you solved Problem 5(f).
Answer:

27 gallons 3 quarts = 444 cups

1 gallon = 4 quarts

27 gallons = 27 x 4 = 108 quarts

108 + 3 = 111

1 quart = 4 cups

111 cups = 111 x 4 = 444

Therefore, 27 gallons 3 quarts = 444 Cups.

Question 7.
Answer true or false for the following statements. If your answer is false, make the statement true by correcting the right side of the comparison.
a. 2 quarts > 10 pints __________
b. 6 liters = 6,000 milliliters __________
c. 16 cups < 4 quarts 1 cup ___________
Answer:

a. 2 quarts > 10 pints __________

False, 1 quart = 2 pints

So, 2 quarts = 4 pints

Therefore, 2 quarts < 10 pints
b. 6 liters = 6,000 milliliters __________

True.
c. 16 cups < 4 quarts 1 cup ___________

False,

1 quart = 4 cups

4 quarts = 4 x 4 = 16 cups

Therefore, 16 cups = 4 quarts.

Question 8.
Joey needs to buy 3 quarts of chocolate milk. The store only sells it in pint containers. How many pints of chocolate milk should he buy? Explain how you know.
Answer:

We know that,

1 quart = 2 pints

Now, the amount of chocolate milk Joey needs to buy = 3 quarts

3 quarts = 3 x 2 = 6 pints

Therefore, Joey should buy 6 pints of chocolate milk.

Question 9.
Granny Smith made punch. She used 2 pints of ginger ale, 3 pints of fruit punch, and 1 pint of orange juice. She served the punch in glasses that had a capacity of 1 cup. How many cups can she fill?
Answer:

We know that,

1 pint = 2 cups

The amount of ginger ale granny used = 2 pints

The amount of fruit punch she used = 3

The amount of orange juice she used = 1 pint

Total : 2+3+1 = 6  pints

Now, 6 pints x 2 = 12 cups

Therefore, she can fill 12 cups.

Engage NY Eureka Math 4th Grade Module 7 Lesson 1 Answer Key

Eureka Math Grade 4 Module 7 Lesson 1 Sprint Answer Key

A
Convert to Dollars

Question 1.
1 cent =
Answer:
$ 0.01

Question 2.
2 cents =
Answer:

$0.02

Question 3.
3 cents =
Answer:

$0.03

Question 4.
8 cents =
Answer:

$0.08

Question 5.
80 cents =
Answer:

$0.8

Question 6.
70 cents =
Answer:

$0.7

Question 7.
60 cents =
Answer:

$0.6

Question 8.
20 cents =
Answer:

$0.2

Question 9.
1 penny =
Answer:

1 penny = 1 cent

$0.01

Question 10.
1 dime =
Answer:

1 dime = 10 cents

$0.1

Question 11.
2 pennies =
Answer:

2 pennies = 2 cents

$0.02

Question 12.
2 dimes =
Answer:

2 dimes = 10 +10 = 20 cents

$0.2

Question 13.
3 pennies =
Answer:

3 pennies = 3 cents

$0.03

Question 14.
3 dimes =
Answer:

3 dimes = 10+10+10+ = 30 cents

$0.3

Question 15.
9 dimes =
Answer:

9 dimes = 10+10+10+10+10+10+10+10+10+ = 90 cents

$0.9

Question 16.
7 pennies =
Answer:

7 pennies = 7 cents

$ 0.07

Question 17.
8 dimes =
Answer:

8 dimes = 10+10+10+10+10+10+10+10 = 80

$0.8

Question 18.
4 pennies =
Answer:

4 pennies = 4 cents

$0.04

Question 19.
6 dimes =
Answer:

6 dimes = 10+10+10+10+10+10 = 60

$0.6

Question 20.
8 pennies =
Answer:

8 pennies = 8 cents

$0.08

Question 21.
7 dimes =
Answer:

7 dimes = 10+10+10+10+10+10+10 = 70 cents

$0.7

Question 22.
9 pennies =
Answer:

9 pennies = 9 cents

$0.09

Question 23.
6 pennies =
Answer:

6 pennies = 6 cents

$0.06

Question 24.
5 dimes =
Answer:

5 dimes = 10+10+10+10+10 = 50 cents

$0.5

Question 25.
5 pennies =
Answer:

5 pennies = 5 cents

$0.05

Question 26.
1 dime 1 penny =
Answer:

1 dime = 10 cents

1 penny = 1 cents

Total : 10 +1 = 11

$0.11

Question 27.
1 dime 2 pennies =
Answer:

1 dime = 10 cents

2 pennies = 2 cents

Total : 10+2 = 12

$0.12

Question 28.
1 dime 7 pennies =
Answer:

1 dime = 10 cents

7 pennies = 7 cents

Total : 10+7 = 17

$0.17

Question 29.
4 dimes 5 pennies =
Answer:

4 dimes = 10+10+10+10 = 40 cents

5 pennies = 5 cents

Total : 40+5 = 45

$0.45

Question 30.
6 dimes 3 pennies =
Answer:

6 dimes = 10+10+10+10+10+10 = 60

3 pennies = 3 cents

Total : 60 + 3 = 63

$0.63

Question 31.
3 pennies 6 dimes =
Answer:

3 pennies = 3 cents

6 dimes = 10+10+10+10+10+10 = 60

Total : 3 + 60 = 63

$0.63

Question 32.
7 pennies 9 dimes =
Answer:

7 pennies = 7 cents

9 dimes = 10+10+10+10+10+10+10+10+10 = 90

Total : 7 + 90 = 97

$0.97

Question 33.
1 quarter =
Answer:

1 quarter = 25 cents

$0.25

Question 34.
2 quarters =
Answer:

2 quarters = 25 + 25 = 50 cents

$0.50

Question 35.
3 quarters =
Answer:

3 quarters = 25+ 25+ 25 = 75 cents

$0.75

Question 36.
2 quarters 3 pennies =
Answer:

2 quarters = 25+ 25 = 50 cents

3 pennies = 3 cents

Total : 50 + 3 = 53

$0.53

Question 37.
1 quarter 3 pennies =
Answer:

1 quarters = 25 cents

3 pennies = 3 cents

Total : 25 + 3 = 28

$0.28

Question 38.
3 quarters 3 pennies =
Answer:

3 quarters = 25 + 25+ 25 = 75 cents

3 pennies = 3 cents

Total : 75 + 3 = 78

$0.78

Question 39.
2 quarters 2 dimes =
Answer:

2 quarters = 25+25 = 50 cents

2 dimes = 10 + 10 = 20 cents

Total : 50+ 20 = 70

$0.70

Question 40.
1 quarter 1 dime =
Answer:

1 quarter = 25 cents

1 dime = 10 cents

Total : 25 + 10 = 35 cents

$0.35

Question 41.
3 quarters 1 dime =
Answer:

3 quarters = 25+25+25 = 75 cents

1 dime = 10 cents

Total : 75 + 10 = 85

$0.85

Question 42.
1 quarter 4 dimes =
Answer:

1 quarter = 25 cents

4 dimes = 10+10+10+10 = 40 cents

Total : 25+40 =65

$0.65

Question 43.
3 quarters 2 dimes =
Answer:

3 quarters = 25+25+25 = 75 cents

2 dimes = 10+10 = 20

Total : 75 + 20 = 95

$0.95

Question 44.
3 quarters 18 pennies =
Answer:

3 quarters = 25+25+25 = 75 cents

18 pennies = 18 cents

Total : 75 + 18 = 93

$0.93

B
Convert to Dollars

Question 1.
2 cent =
Answer:
$ 0.2

Question 2.
3 cents =
Answer:

$0.03

Question 3.
4 cents =
Answer:

$0.04

Question 4.
9 cents =
Answer:

$0.09

Question 5.
90 cents =
Answer:

$0.90

Question 6.
80 cents =
Answer:

$0.80

Question 7.
70 cents =
Answer:

$0.70

Question 8.
30 cents =
Answer:

$0.30

Question 9.
1 penny =
Answer:

$0.01

Question 10.
1 dime =
Answer:

1 dime = 10 cents

$0.10

Question 11.
2 pennies =
Answer:

2 pennies = 2 cents

$0.02

Question 12.
2 dimes =
Answer:

2 dimes = 10 + 10 = 20

$0.20

Question 13.
3 pennies =
Answer:

3 pennies = 3 cents

$0.03

Question 14.
3 dimes =
Answer:

3 dimes = 10+10+10 =30

$0.30

Question 15.
8 dimes =
Answer:

8 dimes = 10+10+10+10+10+10+10+10 = 80

$0.80

Question 16.
6 pennies =
Answer:

6 pennies = 6 cents

$0.06

Question 17.
7 dimes =
Answer:

7 dimes = 10+10+10+10+10+10+10 = 70 cents

$0.70

Question 18.
9 pennies =
Answer:

9 pennies = 9 cents

$0.09

Question 19.
5 dimes =
Answer:

5 dimes = 10+10+10+10+10 =50 cents

$0.50

Question 20.
7 pennies =
Answer:

7 pennies = 7 cents

$0.07

Question 21.
9 dimes =
Answer:

9 dimes = 10+10+10+10+10+10+10+10+10 = 90 cents

$0.90

Question 22.
8 pennies =
Answer:

8 pennies = 8 cents

$0.08

Question 23.
5 pennies =
Answer:

5 pennies = 5 cents

$0.05

Question 24.
6 dimes =
Answer:

6 dimes = 10+10+10+10+10+10 = 60

$0.60

Question 25.
4 pennies =
Answer:

4 pennies = 4 cents

$0.04

Question 26.
1 dime 1 penny =
Answer:

1 dime = 10 cents

1 penny = 1 cent

Total : 10 + 1 = 11

$0.11

Question 27.
1 dime 2 pennies =
Answer:

1 dime = 10 cents

2 pennies = 2 cents

Total : 10 + 2 = 12

$0.12

Question 28.
1 dime 8 pennies =
Answer:

1 dime = 10 cents

8 pennies = 8 cents

Total : 10+8= 18

$0.18

Question 29.
5 dimes 4 pennies =
Answer:

5 dimes = 10+10+10+10+10 = 50 cents

4 pennies = 4 cents

Total : 50 + 4 = 54

$0.54

Question 30.
7 dimes 4 pennies =
Answer:

7 dimes = 10+10+10+10+10+10+10 = 70

4 pennies = 4 cents

Total : 70 + 4 = 74

$0.74

Question 31.
4 pennies 7 dimes =
Answer:

4 pennies = 4 cents

7 dimes = 10+10+10+10+10+10+10 = 70 cents

Total ; 4 + 70 = 74

$0.74

Question 32.
6 pennies 8 dimes =
Answer:

6 pennies = 6 cents

8 dimes = 10+10+10+10+10+10+10+10 = 80

Total : 6 + 80 = 86

$0.86

Question 33.
1 quarter =
Answer:

1 quarter = 25 cents

$0.25

Question 34.
2 quarters =
Answer:

2 quarters = 25+ 25 = 50

$0.50

Question 35.
3 quarters =
Answer:

3 quarters = 25+25+25 = 75

$0.75

Question 36.
2 quarters 4 pennies =
Answer:

2 quarters = 25+25=50

4 pennies = 4 cents

Total : 50+4 = 54

$0.54

Question 37.
1 quarter 4 pennies =
Answer:

1 quarter = 25 cents

4 pennies = 4 cents

Total : 25 + 4 = 29

$0.29

Question 38.
3 quarters 4 pennies =
Answer:

3 quarters = 25+ 25+ 25 = 75

4 pennies = 4 cents

Total : 75 + 4 = 79

$0.79

Question 39.
2 quarters 3 dimes =
Answer:

2 quarters = 25+25 = 50 cents

3 dimes = 10+10 + 10 = 30 cents

Total : 50+ 30 = 80

$0.80

Question 40.
1 quarter 2 dime =
Answer:

1 quarter = 25 cents

2 dimes = 10+10 = 20 cents

Total : 25 +20 = 45

$0.45

Question 41.
3 quarters 2 dime =
Answer:

3 quarters = 25+25+25 = 75 cents

2 dimes = 10+10 = 20

Total : 75 + 20 = 95

$0.95

Question 42.
1 quarter 5 dimes =
Answer:

1 quarter = 25 cents

5 dimes = 10+10+10+10+10 = 50

Total : 25+50 = 75

$0.75

Question 43.
3 quarters 1 dimes =
Answer:

3 quarters = 25 + 25 + 25 = 75

1 dime = 10 cents

Total : 75 + 10 = 85

$0.85

Question 44.
3 quarters 19 pennies =
Answer:

3 quarters = 25+ 25 + 25 = 75

19 pennies = 19 cents

Total : 75 + 19 = 94

$0.94

Eureka Math Grade 4 Module 7 Lesson 1 Practice Sheet Answer Key

a.

The rule for converting pounds to ounces is _______ .

To convert pounds into ounces, multiply pounds value by 16

b.

The rule for converting yards to feet is ________.

To convert yards into feet, multiply yards value by 3

c.

The rule for converting feet to inches is __________.

To convert feet to inches, multiply feet value by 12

Eureka Math Grade 4 Module 7 Lesson 1 Problem Set Answer Key

Use RDW to solve Problems 1–3.

Question 1.
Evan put a 2-pound weight on one side of the scale. How many 1-ounce weights will he need to put on the other side of the scale to make them equal?
Answer:

1 pound = 16 ounces

Which means , 2 pounds = 16 + 16 = 32

Therefore, Evan need 32 weight on other side to make them equal.

Question 2.
Julius put a 3-pound weight on one side of the scale. Abel put 35 1-ounce weights on the other side. How many more 1-ounce weights does Abel need to balance the scale?
Answer:

1 lb = 16 oz

Which means, 3 lb = 48 oz

48 – 35 = 13

Therefore, Able needs 13 more 1- ounce weights to balance the scale.

Question 3.
Mrs. Upton’s baby weighs 5 pounds and 4 ounces. How many total ounces does the baby weigh?
Answer:

1 pound = 16 ounces

Which means, 5 pounds = 5 x 16 = 80 oz

So, 80 + 4 = 84 oz

Therefore, Mrs. Upton’s baby weigh 84 ounces.

Question 4.
Complete the following conversion tables, and write the rule under each table.
a.

The rule for converting pounds to ounces is __________

To convert pounds to ounces, multiply pounds value by 16

b.

The rule for converting feet to inches is __________

To convert Feet into inches, multiply feet value by 12.

c.

The rule for converting yards to feet is ___________
Answer:

To convert yard to feet, multiply yard value by 3.

Question 5.
Solve.
a. 3 feet 1 inch = _______ inches
b. 11 feet 10 inches = _______ inches
c. 5 yards 1 foot = _______ feet
d. 12 yards 2 feet = _______ feet
e. 27 pounds 10 ounces = _______ ounces
f. 18 yards 9 feet = _______ feet
g. 14 pounds 5 ounces = _______ ounces
h. 5 yards 2 feet = _______ inches
Answer:

a. 3 feet 1 inch = 37 inches
b. 11 feet 10 inches  142 inches
c. 5 yards 1 foot = 16 feet
d. 12 yards 2 feet =  38 feet
e. 27 pounds 10 ounces = 442 ounces
f. 18 yards 9 feet =63 feet
g. 14 pounds 5 ounces = 229 ounces
h. 5 yards 2 feet = 17 inches

Question 6.
Answer true or false for the following statements. If the statement is false, change the right side of the comparison to make it true.
a. 2 kilograms > 2,600 grams ___________
b. 12 feet < 140 inches ___________
c. 10 kilometres = 10,000 meters ___________
Answer:

a. False , 2 kg = 2000 grams

So, 2 kilograms < 2,600 grams

b. False, 12 feet = 144 inches

So, 12 feet > 140 inches

c. True

Eureka Math Grade 4 Module 7 Lesson 1 Exit Ticket Answer Key

Question 1.
Solve.
a. 8 feet = _________ inches
b. 4 yards 2 feet = _________ feet
c. 14 pounds 7 ounces = ________ ounces
Answer:

a. 8 feet = 96 inches
b. 4 yards 2 feet = 14 feet
c. 14 pounds 7 ounces = 231 ounces

Question 2.
Answer true or false for the following statements. If the statement is false, change the right side of the comparison to make it true.
a. 3 pounds > 60 ounces __________
b. 12 yards < 40 feet _________
Answer:

a. False , 3 pounds = 48 ounces

so, 3 pounds < 60 ounces

b. True

Eureka Math Grade 4 Module 7 Lesson 1 Homework Answer Key

Question 1.
Complete the tables.
a.

b.

c.

Answer:

Question 2.
a. 2 yards 2 inches = ________ inches
b. 9 yards 10 inches = ________ inches
c. 4 yards 2 feet = ________ feet
d. 13 yards 1 foot = ________ feet
e. 17 feet 2 inches = ________ inches
f. 11 yards 1 foot = ________ feet
g. 15 yards 2 feet = ________ feet
h. 5 yards 2 feet = ________ inches
Answer:

a. 2 yards 2 inches = 74 inches
b. 9 yards 10 inches =  334 inches
c. 4 yards 2 feet =  14 feet
d. 13 yards 1 foot = 40 feet
e. 17 feet 2 inches = 206 inches
f. 11 yards 1 foot = 34 feet
g. 15 yards 2 feet = 47 feet
h. 5 yards 2 feet = 17 inches

Question 3.
Ally has a piece of string that is 6 yards 2 feet long. How many inches of string does she have?
Answer:

6 yards = 36+36+36+36+36+36 = 216 inches

2 feet =  12+12 = 24 inches

Total :  216 + 24 = 240

Therefore, she have 240 inches of string

Question 4.
Complete the table.

Answer:

Question 5.
Renee’s baby sister weighs 7 pounds 2 ounces. How many ounces does her sister weigh?
Answer:

7 pounds = 16+16+16+16+16+16+16 = 112 ounces

and 2 ounces

Total : 112 + 2 = 114

Therefore, Renee’s baby sister weighs 114 ounces

Question 6.
Answer true or false for the following statements. If the statement is false, change the right side of the comparison to make it true.
a. 4 kilograms < 4,100 grams ________
b. 10 yards < 360 inches ________
c. 10 liters = 100,000 millilitres ________
Answer:

a. True

b. False , 10 yards = 360 inches

c. False , 10 litres = 10000 millilitres.