Prasanna

Engage NY Eureka Math 7th Grade Module 4 Lesson 14 Answer Key

Eureka Math Grade 7 Module 4 Lesson 14 Example Answer Key

Example 1.
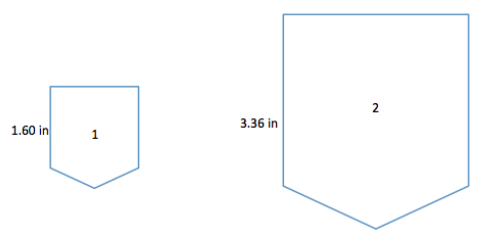
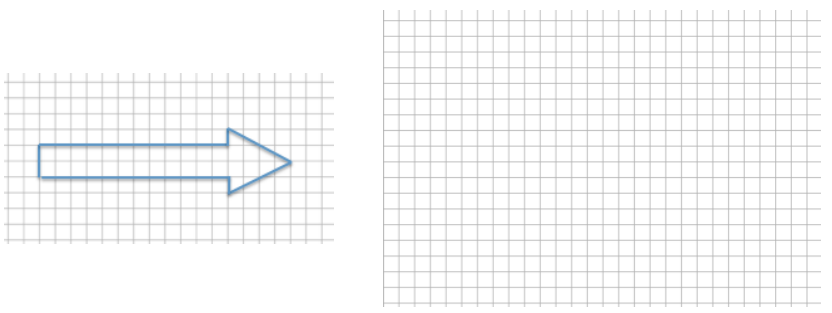
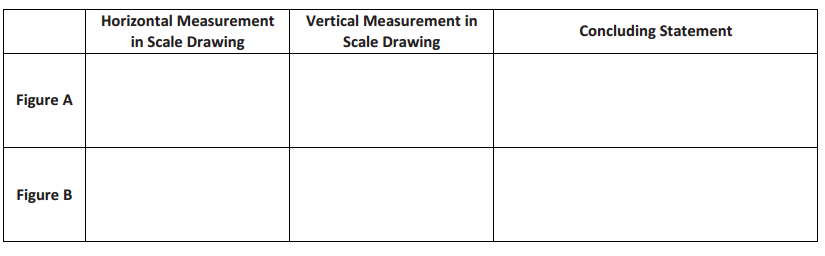
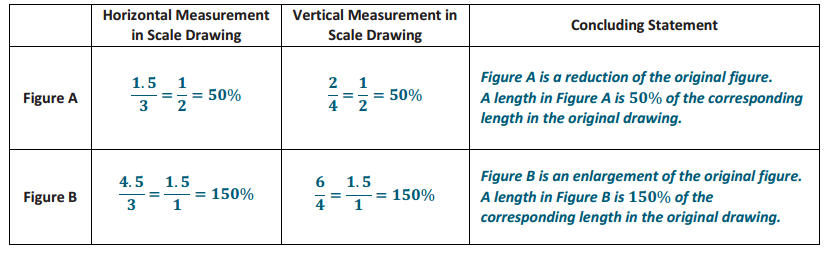
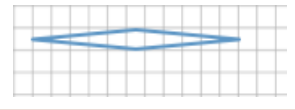
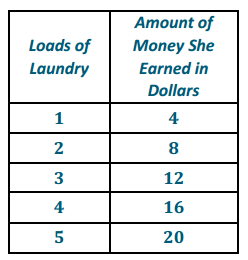
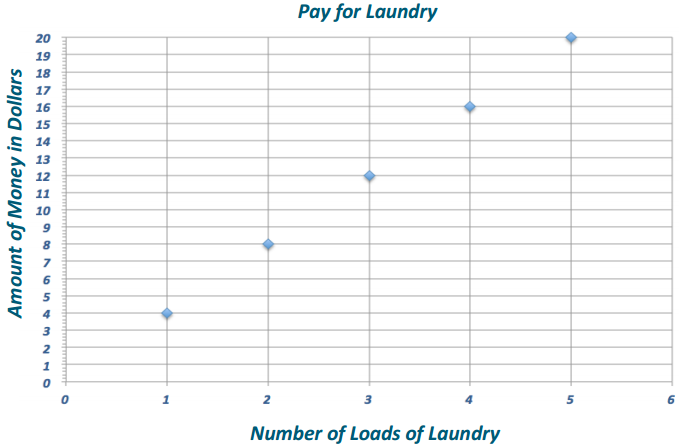
The distance around the entire small boat is 28.4 units. The larger figure is a scale drawing of the smaller drawing of the boat. State the scale factor as a percent, and then use the scale factor to find the distance around the scale drawing.

Answer:
Scale factor:
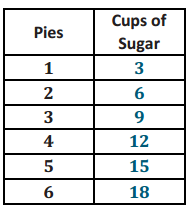
Horizontal distance of the smaller boat: 8 units Vertical sail distance of smaller boat: 6 units
Horizontal distance of the larger boat: 22 units Vertical sail distance of larger boat: 16.5 units
Scale factor: Quantity = Percent × Whole
Smaller boat is the whole.
Total Distance:
Distance around smaller boat = 28.4 units
Distance around larger boat = 28.4(275%) = 28.4(2.75) = 78.1
The distance around the larger boat is 78.1 units.
Length in larger = Percent × Length in smaller
22 = P × 8
\(\frac{22}{8}\) = 2.75 = 275%

Length in larger = Percent × Length in smaller
16.5 = P × 6
\(\frac{16.5}{6}\) = 2.75 = 275%

Example 2: Time to Garden

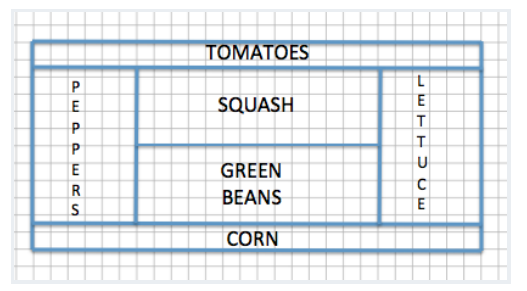
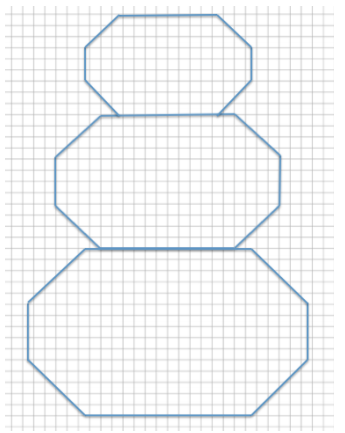
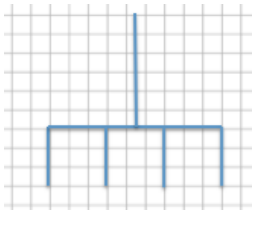
Sherry designed her garden as shown in the diagram above. The distance between any two consecutive vertical grid lines is 1 foot, and the distance between any two consecutive horizontal grid lines is also 1 foot. Therefore, each grid square has an area of one square foot. After designing the garden, Sherry decided to actually build the garden 75% of the size represented in the diagram.
a. What are the outside dimensions shown in the blueprint?
Answer:
Blueprint dimensions: Length: 26 boxes = 26 ft.
Width: 12 boxes = 12 ft.

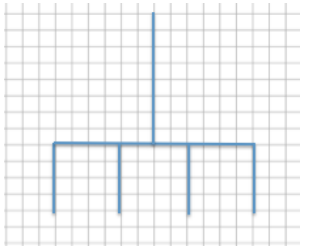
b. What will the overall dimensions be in the actual garden? Write an equation to find the dimensions. How does the problem relate to the scale factor?
Answer:
Actual garden dimensions (75% of blueprint): 19.5 ft. × 9 ft.
Length: (26 ft.)(0.75) = 19.5 ft.
Width: (12 ft.)(0.75) = 9 ft.
Since the scale factor was given as 75%, each dimension of the actual garden should be 75% of the original corresponding dimension. The actual length of the garden,19.5 ft., is 75% of 26 ft., and the actual width of the garden, 9 ft., is 75% of 12 ft.

c. If Sherry plans to use a wire fence to divide each section of the garden, how much fence does she need?
Answer:
Dimensions of the blueprint:

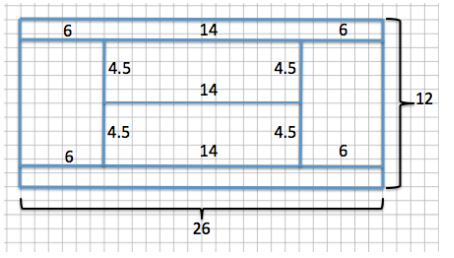
Total amount of wire needed for the blueprint:
26(4)+12(2)+4.5(4)+14 = 160
The amount of wire needed is 160 ft.
New dimensions of actual garden:
Length: 19.5 ft. (from part (b))
Width: 9 ft. (from part (b))
Inside borders: 4.5(0.75) = 3.375; 3.375 ft.
14(0.75) = 10.5; 10.5 ft.
The dimensions of the inside borders are 3.375 ft. by 10.5 ft.

Total wire with new dimensions:
19.5(4)+9(2)+3.375(4)+10.5 = 120
OR
160(0.75) = 120
Total wire with new dimensions is 120 ft.
Simpler way: 75% of 160 ft. is 120 ft.

d. If the fence costs $3.25 per foot plus 7% sales tax, how much would the fence cost in total?
Answer:
3.25(120) = 390
390(1.07) = 417.30
The total cost is $417.30.

Example 3.
Race Car #2 is a scale drawing of Race Car #1. The measurement from the front of Race Car #1 to the back of Race Car #1 is 12 feet, while the measurement from the front of Race Car #2 to the back of Race Car #2 is 39 feet. If the height of Race Car #1 is 4 feet, find the scale factor, and write an equation to find the height of Race Car #2. Explain what each part of the equation represents in the situation.

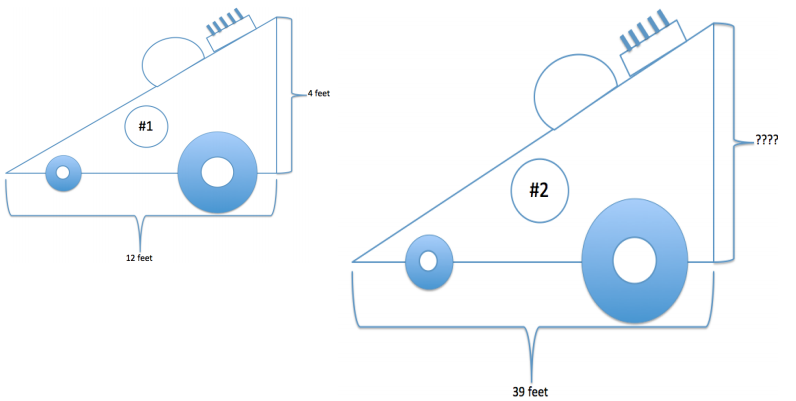
Answer:
Scale Factor: The larger race car is a scale drawing of the smaller. Therefore, the smaller race car is the whole in the relationship.
Quantity = Percent × Whole
Larger = Percent × Smaller
39 = Percent × 12
\(\frac{39}{12}\) = 3.25 = 325%
Height: 4(3.25) = 13
The height of Race Car #2 is 13 ft.
The equation shows that the smaller height, 4 ft., multiplied by the scale factor of 3.25, equals the larger height, 13 ft.

Eureka Math Grade 7 Module 4 Lesson 14 Exercise Answer Key

Exercise 1.
The length of the longer path is 32.4 units. The shorter path is a scale drawing of the longer path. Find the length of the shorter path, and explain how you arrived at your answer.

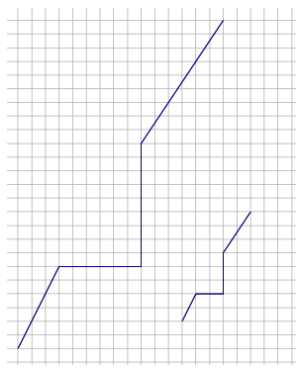
Answer:
First, determine the scale factor. Since the smaller path is a reduction of the original drawing, the scale factor should be less than 100%. Since the smaller path is a scale drawing of the larger, the larger path is the whole in the relationship.
Quantity = Percent × Whole
To determine the scale factor, compare the horizontal segments of the smaller path to the larger path.
Smaller = Percent × Larger
2 = Percent × 6
\(\frac{2}{6}\) = \(\frac{1}{3}\) = 33 \(\frac{1}{3}\)%
To determine the length of the smaller path, multiply the length of the larger path by the scale factor.
32.4(\(\frac{1}{3}\)) = 10.8
The length of the shorter path is 10.8 units.

Exercise 2.
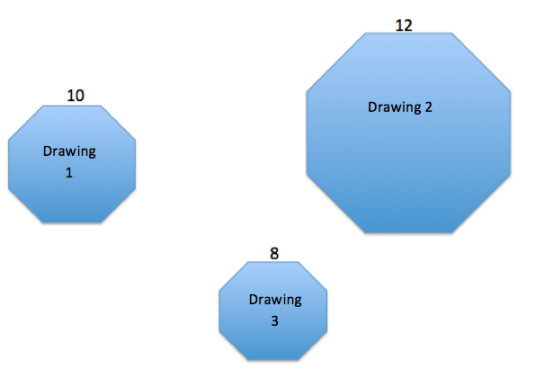
Determine the scale factor, and write an equation that relates the height of side A in Drawing 1 and the height of side B in Drawing 2 to the scale factor. The height of side A is 1.1 cm. Explain how the equation illustrates the relationship.

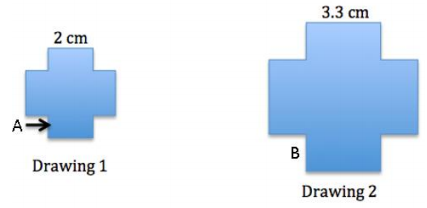
Answer:
Equation: 1.1(scale factor) = height of side B in Drawing 2
First find the scale factor:
Quantity = Percent × Whole
Drawing 2 = Percent × Drawing 1
3.3 = Percent × 2
\(\frac{3.3}{2}\) = 1.65 = 165%
Equation: (1.1)(1.65) = 1.815
The height of side B in Drawing 2 is 1.815 cm.
Once we determine the scale factor, we can write an equation to find the unknown height of side B in Drawing 2 by multiplying the scale factor by the corresponding height in the original drawing.

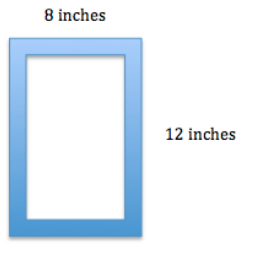
Exercise 3.
The length of a rectangular picture is 8 inches, and the picture is to be reduced to be 45 \(\frac{1}{2}\)% of the original picture. Write an equation that relates the lengths of each picture. Explain how the equation illustrates the relationship.
Answer:
8(0.455) = 3.64
The length of the reduced picture is 3.64 in. The equation shows that the length of the reduced picture, 3.64, is equal to the original length, 8, multiplied by the scale factor, 0.455.

Eureka Math Grade 7 Module 4 Lesson 14 Problem Set Answer Key

Question 1.
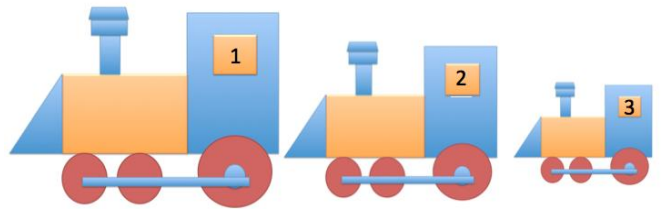
The smaller train is a scale drawing of the larger train. If the length of the tire rod connecting the three tires of the larger train, as shown below, is 36 inches, write an equation to find the length of the tire rod of the smaller train. Interpret your solution in the context of the problem.

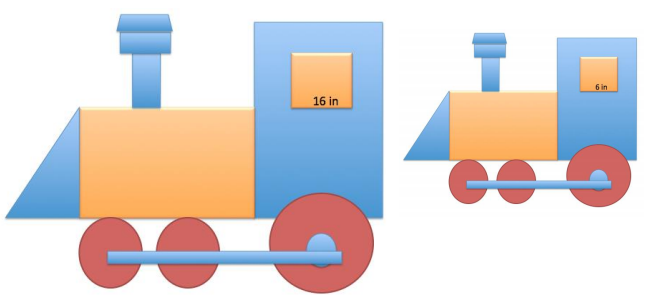
Answer:
Scale factor:
Smaller = Percent × Larger
6 = Percent × 16
\(\frac{6}{16}\) = 0.375 = 37.5%
Tire rod of smaller train: (36)(0.375) = 13.5
The length of the tire rod of the smaller train is 13.5 in.
Since the scale drawing is smaller than the original, the corresponding tire rod is the same percent smaller as the windows. Therefore, finding the scale factor using the windows of the trains allows us to then use the scale factor to find all other corresponding lengths.

Question 2.
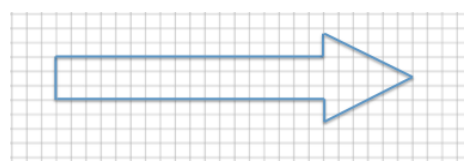
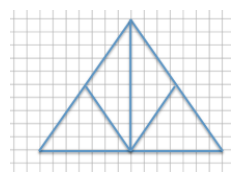
The larger arrow is a scale drawing of the smaller arrow. If the distance around the smaller arrow is 25.66 units. What is the distance around the larger arrow? Use an equation to find the distance and interpret your solution in the context of the problem.

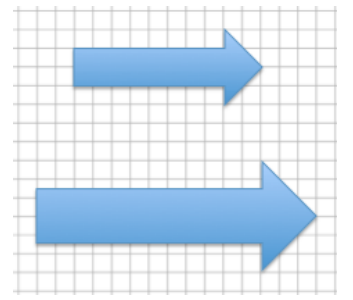
Answer:
Horizontal distance of smaller arrow: 8 units
Horizontal distance of larger arrow: 12 units
Scale factor:
Larger = Percent × Smaller
12 = Percent × 8
\(\frac{12}{8}\) = 1.5 = 150%
Distance around larger arrow:
(25.66)(1.5) = 38.49
The distance around the larger arrow is 38.49 units.
An equation where the distance of the smaller arrow is multiplied by the scale factor results in the distance around the larger arrow.

Question 3.
The smaller drawing below is a scale drawing of the larger. The distance around the larger drawing is 39.4 units. Using an equation, find the distance around the smaller drawing.

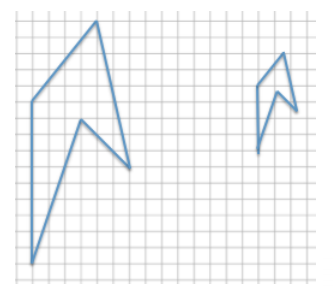
Answer:
Vertical distance of larger drawing: 10 units
Vertical distance of smaller drawing: 4 units
Scale factor:
Smaller = Percent × Larger
4 = Percent × 10
\(\frac{4}{10}\) = 0.4 = 40%
Total distance:
(39.4)(0.4) = 15.76
The total distance around the smaller drawing is 15.76 units.

Question 4.
The figure is a diagram of a model rocket and is a two-dimensional scale drawing of an actual rocket. The length of a model rocket is 2.5 feet, and the wing span is 1.25 feet. If the length of an actual rocket is 184 feet, use an equation to find the wing span of the actual rocket.

Answer:
Length of actual rocket: 184 ft.
Length of model rocket: 2.5 ft.
Scale Factor:
Actual = Percent × Model
184 = Percent × 2.5
\(\frac{184}{2.5}\) = 73.60 = 7,360%

Wing span:
Model rocket wing span: 1.25 ft.
Actual rocket wing span : (1.25)(73.60) = 92
The wing span of the actual rocket is 92 ft.

Eureka Math Grade 7 Module 4 Lesson 14 Exit Ticket Answer Key

Question 1.
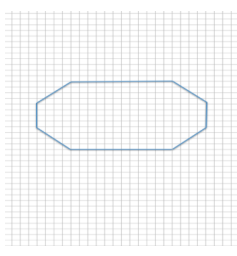
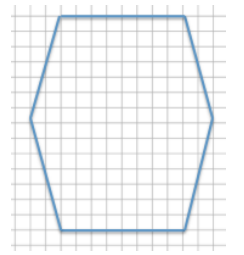
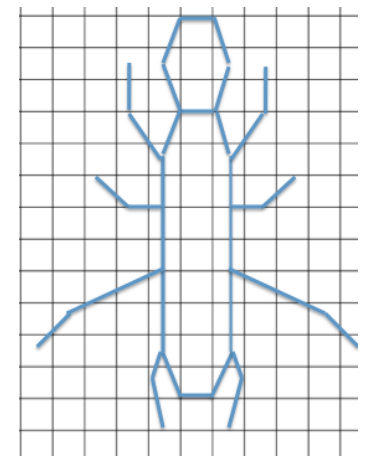
Each of the designs shown below is to be displayed in a window using strands of white lights. The smaller design requires 225 feet of lights. How many feet of lights does the enlarged design require? Support your answer by showing all work and stating the scale factor used in your solution.

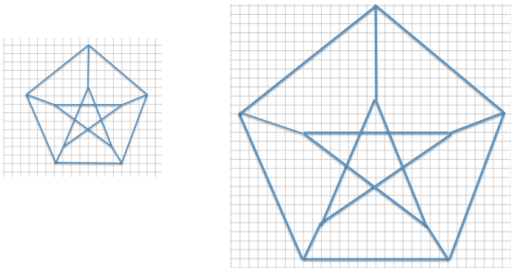
Answer:
Scale Factor:
Bottom horizontal distance of the smaller design: 8
Bottom horizontal distance of the larger design: 16
The smaller design represents the whole since we are going from the smaller to the larger.
Quantity = Percent × Whole
Larger = Percent × Smaller
16 = Percent × 8
\(\frac{16}{8}\) = 2 = 200%
Number of feet of lights needed for the larger design:
225 ft.(200%) = 225 ft.(2) = 450 ft.

Engage NY Eureka Math 7th Grade Module 4 Lesson 13 Answer Key

Eureka Math Grade 7 Module 4 Lesson 13 Example Answer Key

Example 1.
The scale factor from Drawing 1 to Drawing 2 is 60%. Find the scale factor from Drawing 2 to Drawing 1. Explain your reasoning.

Answer:
The scale drawing from Drawing 2 to Drawing 1 is an enlargement. Drawing 1 is represented by 100%, and Drawing 2, a reduction of Drawing 1, is represented by 60%. A length in Drawing 2 is the whole, so the scale factor from Drawing 2 to 1 is length in Drawing 1 = percent × length in Drawing 2.
100% = percent × 60%
\(\frac{100 \%}{60 \%}\) = \(\frac{1}{0.60}\) = \(\frac{1}{\frac{3}{5}}\) = \(\frac{5}{3}\) = 166 \(\frac{2}{3}\)%

Example 2.
A regular octagon is an eight-sided polygon with side lengths that are all equal. All three octagons are scale drawings of each other. Use the chart and the side lengths to compute each scale factor as a percent. How can we check our answers?



Answer:


To check our answers, we can start with 10 (the length of the original Drawing 1) and multiply by the scale factors we found to see whether we get the corresponding lengths in Drawings 2 and 3.
Drawing 1 to 2: 10(1.20) = 12
Drawing 2 to 3: 12(\(\frac{2}{3}\)) = 8

Example 3.
The scale factor from Drawing 1 to Drawing 2 is 112%, and the scale factor from Drawing 1 to Drawing 3 is 84%. Drawing 2 is also a scale drawing of Drawing 3. Is Drawing 2 a reduction or an enlargement of Drawing 3? Justify your answer using the scale factor. The drawing is not necessarily drawn to scale.

Answer:
First, I needed to find the scale factor of Drawing 3 to Drawing 2 by using the relationship
Quantity = Percent × Whole.
Drawing 3 is the whole. Therefore,
Drawing 2 = Percent × Drawing 3
112% = Percent × 84%
\(\frac{1.12}{0.84}\) = \(\frac{112}{84}\) = \(\frac{4}{3}\) = 133 \(\frac{1}{3}\)%
Since the scale factor is greater than 100%, Drawing 2 is an enlargement of Drawing 3.

Explain how you could use the scale factors from Drawing 1 to Drawing 2 (112%) and from Drawing 2 to Drawing 3 (75%) to show that the scale factor from Drawing 1 to Drawing 3 is 84%.
Answer:
The scale factor from Drawing 1 to Drawing 2 is 112%, and the scale factor from Drawing 2 to Drawing 3 is 75%; therefore, I must find 75% of 112% to get from Drawing 2 to Drawing 3. (0.75)(1.12) = 0.84. Comparing this answer to the original problem, the resulting scale factor is indeed what was given as the scale factor from Drawing 1 to
Drawing 3.

Eureka Math Grade 7 Module 4 Lesson 13 Exercise Answer Key

Opening Exercise
Scale factor: \(\frac{\text { length in SCALE drawing }}{\text { Corresponding length in ORIGINAL drawing }}\)
Describe, using percentages, the difference between a reduction and an enlargement.
Answer:
A scale drawing is a reduction of the original drawing when the lengths of the scale drawing are smaller than the lengths in the original drawing. The scale factor is less than 100%.
A scale drawing is an enlargement of the original drawing when the lengths of the scale drawing are greater than the lengths in the original drawing. The scale factor is greater than 100%.

Use the two drawings below to complete the chart. Calculate the first row (Drawing 1 to Drawing 2) only.


Answer:

Compare Drawing 2 to Drawing 1. Using the completed work in the first row, make a conjecture (statement) about what the second row of the chart will be. Justify your conjecture without computing the second row.
Answer:
Drawing 1 will be a reduction of Drawing 2. I know this because the corresponding lengths in Drawing 1 are smaller than the corresponding lengths in Drawing 2. Therefore, the scale factor from Drawing 2 to Drawing 1 would be less than 100%.

Compute the second row of the chart. Was your conjecture proven true? Explain how you know.
Answer:
The conjecture was true because the calculated scale factor from Drawing 2 to Drawing 1 was 62.5%. Since the scale factor is less than 100%, the scale drawing is indeed a reduction.

Eureka Math Grade 7 Module 4 Lesson 13 Problem Set Answer Key

Question 1.
The scale factor from Drawing 1 to Drawing 2 is 41 \(\frac{2}{3}\)%. Justify why Drawing 1 is a scale drawing of Drawing 2 and why it is an enlargement of Drawing 2. Include the scale factor in your justification.

Answer:
Quantity = Percent × Whole
Length in Drawing 1 = Percent × Length in Drawing 2
100% = Percent × 41 \(\frac{2}{3}\)%
\(\frac{100 \%}{41 \frac{2}{3} \%}\) = \(\frac{100 \cdot 3}{41 \frac{2}{3} \cdot 3}\) = \(\frac{300}{125}\) = \(\frac{12}{5}\) = 2.40 = 240%
Drawing 1 is a scale drawing of Drawing 2 because the lengths of Drawing 1 would be larger than the corresponding lengths of Drawing 2.
Since the scale factor is greater than 100%, the scale drawing is an enlargement of the original drawing.

Question 2.
The scale factor from Drawing 1 to Drawing 2 is 40%, and the scale factor from Drawing 2 to Drawing 3 is 37.5%. What is the scale factor from Drawing 1 to Drawing 3? Explain your reasoning, and check your answer using an example.

Answer:
To find the scale factor from Drawing 1 to 3, I needed to find 37.5% of 40%, so (0.375)(0.40) = 0.15. The scale factor from Drawing 1 to Drawing 3 would be 15%.
Check: Assume the length of Drawing 1 is 10. Then, using the scale factor for Drawing 2, the corresponding length of Drawing 2 would be 4. Then, applying the scale factor to Drawing 3, Drawing 3 would be 4(0.375) = 1.5. To go directly from Drawing 1 to Drawing 3, which was found to have a scale factor of 15%, then 10(0.15) = 1.5.

Question 3.
Traci took a photograph and printed it to be a size of 4 units by 4 units as indicated in the diagram. She wanted to enlarge the original photograph to a size of 5 units by 5 units and 10 units by 10 units.
a. Sketch the different sizes of photographs.

Answer:

b. What was the scale factor from the original photo to the photo that is 5 units by 5 units?
Answer:
The scale factor from the original to the 5 by 5 enlargement is \(\frac{5}{4}\) = 1.25 = 125%.

c. What was the scale factor from the original photo to the photo that is 10 units by 10 units?
Answer:
The scale factor from the original to the 10 by 10 photo is \(\frac{10}{4}\) = 2.5 = 250%.

d. What was the scale factor from the 5 × 5 photo to the 10 × 10 photo?
The scale factor from the 5 × 5 photo to the 10 × 10 photo is \(\frac{10}{5}\) = 2 = 200%.

e. Write an equation to verify how the scale factor from the original photo to the enlarged 10 × 10 photo can be calculated using the scale factors from the original to the 5 × 5 and then from the 5 × 5 to the 10 × 10.
Answer:
Scale factor original to 5 × 5: (125%)
Scale factor 5 × 5 to 10 × 10: (200%)
4(1.25) = 5
5(2.00) = 10
Original to 10 × 10, scale factor = 250%
4(2.50) = 10
The true equation 4(1.25)(2.00) = 4(2.50) verifies that a single scale factor of 250% is equivalent to a scale factor of 125% followed by a scale factor of 200%.

Question 4.
The scale factor from Drawing 1 to Drawing 2 is 30%, and the scale factor from Drawing 1 to Drawing 3 is 175%. What are the scale factors of each given relationship? Then, answer the question that follows. Drawings are not to scale.

a. Drawing 2 to Drawing 3
Answer:
The scale factor from Drawing 2 to Drawing 3 is
\(\frac{175 \%}{30 \%}\) = \(\frac{1.75}{0.30}\) = \(\frac{175}{30}\) = \(\frac{35}{6}\) = 5 \(\frac{5}{6}\) = 583 \(\frac{1}{3}\)%.

b. Drawing 3 to Drawing 1
Answer:
The scale factor from Drawing 3 to Drawing 1 is
\(\frac{1}{1.75}\) = \(\frac{100}{175}\) = \(\frac{4}{7}\) ≈ 57.14%.

c. Drawing 3 to Drawing 2
Answer:
The scale factor from Drawing 3 to Drawing 2 is
\(\frac{0.3}{1.75}\) = \(\frac{30}{175}\) = \(\frac{6}{35}\) ≈ 17.14%.

d. How can you check your answers?
Answer:
To check my answers, I can work backwards and multiply the scale factor from Drawing 1 to Drawing 3 of 175% to the scale factor from Drawing 3 to Drawing 2, and I should get the scale factor from Drawing 1 to Drawing 2.
(1.75)(0.1714) ≈ 0.29995 ≈ 0.30 = 30%

Eureka Math Grade 7 Module 4 Lesson 13 Exit Ticket Answer Key

Question 1.
Compute the scale factor, as a percent, for each given relationship. When necessary, round your answer to the nearest tenth of a percent.

a. Drawing 1 to Drawing 2
Answer:
Drawing 2 = Percent × Drawing 1
3.36 = Percent × 1.60
\(\frac{3.36}{1.60}\) = 2.10 = 210%

b. Drawing 2 to Drawing 1
Answer:
Drawing 1 = Percent × Drawing 2
1.60 = Percent × 3.36
\(\frac{1.60}{3.36}\) = \(\frac{1}{2.10}\) ≈ 0.476190476 ≈ 47.6%

c. Write two different equations that illustrate how each scale factor relates to the lengths in the diagram.
Answer:
Drawing 1 to Drawing 2:
1.60(2.10) = 3.36
Drawing 2 to Drawing 1:
3.36(0.476) = 1.60

Question 2.
Drawings 2 and 3 are scale drawings of Drawing 1. The scale factor from Drawing 1 to Drawing 2 is 75%, and the scale factor from Drawing 2 to Drawing 3 is 50%. Find the scale factor from Drawing 1 to Drawing 3.

Answer:
Drawing 1 to 2 is 75%. Drawing 2 to 3 is 50%. Therefore, Drawing 3 is 50% of 75%, so
(0.50)(0.75) = 0.375. To determine the scale factor from Drawing 1 to Drawing 3, we went from 100% to 37.5%. Therefore, the scale factor is 37.5%. Using the relationship:
Drawing 3 = Percent × Drawing 1
37.5% = Percent × 100%
0.375 = Percent
= 37.5%

Engage NY Eureka Math 7th Grade Module 4 Lesson 12 Answer Key

Eureka Math Grade 7 Module 4 Lesson 12 Example Answer Key

Example 1.
Create a snowman on the accompanying grid. Use the octagon given as the middle of the snowman with the following conditions:

a. Calculate the width, neck, and height, in units, for the figure to the right.
Answer:
Width: 20
Neck: 12
Height: 12

b. To create the head of the snowman, make a scale drawing of the middle of the snowman with a scale factor of 75%. Calculate the new lengths, in units, for the width, neck, and height.
Answer:
Width: 75%(20) = (0.75)(20) = 15
Neck: 75%(12) = (0.75)(12) = 9
Height : 75%(12) = (0.75)(12) = 9

c. To create the bottom of the snowman, make a scale drawing of the middle of the snowman with a scale factor of 125%. Calculate the new lengths, in units, for the width, waist, and height.
Answer:
Width: 125%(20) = (1.25)(20) = 25
Waist: 125%(12) = (1.25)(12) = 15
Height: 125%(12) = (1.25)(12) = 15

d. Is the head a reduction or an enlargement of the middle?
Answer:
The head is a reduction of the middle since the lengths of the sides are smaller than the lengths in the original drawing and the scale factor is less than 100% (75%).

e. Is the bottom a reduction or an enlargement of the middle?
Answer:
The bottom is an enlargement of the middle since the lengths of the scale drawing are larger than the lengths in the original drawing, and the scale factor is greater than 100% (125%).

f. What is the significance of the scale factor as it relates to 100%? What happens when such scale factors are applied?
Answer:
A scale factor of 100% would create a drawing that is the same size as the original drawing; therefore, it would be neither an enlargement nor reduction. A scale factor of less than 100% results in a scale drawing that is a reduction of the original drawing. A scale factor of greater than 100% results in a scale drawing that is an enlargement of the original drawing.

g. Use the dimensions you calculated in parts (b) and (c) to draw the complete snowman.
Answer:

Example 2.
Create a scale drawing of the arrow below using a scale factor of 150%.

Answer:

Example 3: Scale Drawings Where the Horizontal and Vertical Scale Factors Are Different
Sometimes it is helpful to make a scale drawing where the horizontal and vertical scale factors are different, such as when creating diagrams in the field of engineering. Having differing scale factors may distort some drawings.

For example, when you are working with a very large horizontal scale, you sometimes must exaggerate the vertical scale in order to make it readable. This can be accomplished by creating a drawing with two scales. Unlike the scale drawings with just one scale factor, these types of scale drawings may look distorted. Next to the drawing below is a scale drawing with a horizontal scale factor of 50% and vertical scale factor of 25% (given in two steps). Explain how each drawing is created.

Answer:
Each horizontal distance in the scale drawing is 50%
(or half) of the corresponding length in the original drawing. Each vertical distance in the scale drawing is 25% (or one-fourth) of the corresponding length in the original drawing.
Horizontal distance of house: 8(0.50) = 8(\(\frac{1}{2}\)) = 4
Vertical distance of house: 8(0.25) = 8(\(\frac{1}{4}\)) = 2
Vertical distance of top of house:
4(0.25) = 4(\(\frac{1}{4}\)) = 1

Eureka Math Grade 7 Module 4 Lesson 12 Exercise Answer Key

Opening Exercise:

Compare the corresponding lengths of Figure A to the original octagon in the middle. This is an example of a particular type of scale drawing called a _________. Explain why it is called that.
Answer:
reduction
A scale drawing is a reduction of the original drawing when the side lengths of the scale drawing are smaller than the corresponding side lengths of the original figure or drawing.

Compare the corresponding lengths of Figure B to the original octagon in the middle. This is an example of a particular type of scale drawing called an __________. Explain why it is called that.
Answer:
enlargement
A scale drawing is an enlargement of the original drawing when the side lengths of the scale drawing are larger than the corresponding side lengths of the original figure or drawing.

The scale factor is the quotient of any length in the scale drawing and its corresponding length in the original drawing.
Use what you recall from Module 1 to determine the scale factors between the original figure and Figure A and the original figure and Figure B.
Answer:
Scale factor between original and Figure A: \(\frac{1.5}{3}\) = \(\frac{1}{2}\) or \(\frac{2}{4}\) = \(\frac{1}{2}\)
Scale factor between original and Figure B: \(\frac{4.5}{3}\) = \(\frac{3}{2}\) or \(\frac{6}{4}\) = \(\frac{3}{2}\)

Use the diagram to complete the chart below to determine the horizontal and vertical scale factors. Write answers as a percent and as a concluding statement using the previously learned reduction and enlargement vocabulary.

Answer:

Exercise 1.
Create a scale drawing of the following drawing using a horizontal scale factor of 183 \(\frac{1}{3}\)% and a vertical scale factor of 25%.

Answer:

Horizontal scale factor: \(\frac{183 \frac{1}{3} \cdot 3}{100 \cdot 3}\) = \(\frac{550}{300}\) = \(\frac{11}{6}\)
Horizontal distance: 6(\(\frac{11}{6}\)) = 11
Vertical scale factor: \(\frac{25}{100}\) = \(\frac{1}{4}\)
Vertical distance: 4(\(\frac{1}{4}\)) = 1
New sketch:

Exercise 2.
Chris is building a rectangular pen for his dog. The dimensions are 12 units long and 5 units wide.

Chris is building a second pen that is 60% the length of the original and 125% the width of the original. Write equations to determine the length and width of the second pen.
Answer:
Length: 12 × 0.60 = 7.2
The length of the second pen is 7.2 units.
Width: 5 × 1.25 = 6.25
The width of the second pen is 6.25 units.

Eureka Math Grade 7 Module 4 Lesson 12 Problem Set Answer Key

Question 1.
Use the diagram below to create a scale drawing using a scale factor of 133 \(\frac{1}{3}\)%. Write numerical equations to find the horizontal and vertical distances in the scale drawing.

Answer:
Scale factor: 133 \(\frac{133 \frac{1}{3} \cdot 3}{100 \cdot 3}\) = \(\frac{400}{300}\) = \(\frac{4}{3}\)
Horizontal distance: 9(\(\frac{4}{3}\)) = 12
Vertical distance forks: 3(\(\frac{4}{3}\)) = 4
Vertical distance handle: 6(\(\frac{4}{3}\)) = 8
Scale drawing:

Question 2.
Create a scale drawing of the original drawing given below using a horizontal scale factor of 80% and a vertical scale factor of 175%. Write numerical equations to find the horizontal and vertical distances.

Answer:
Horizontal scale factor: 80% = \(\frac{80}{100}\) = \(\frac{4}{5}\)
Horizontal segment lengths: 10(0.80) = 8 or 10(\(\frac{4}{5}\)) = 8
Horizontal distance: 15(\(\frac{4}{5}\)) = 12
Vertical scale factor: 175% = \(\frac{175}{100}\) = \(\frac{7}{4}\)
Vertical distance: 8(\(\frac{7}{4}\)) = 14
Scale drawing:

Question 3.
The accompanying diagram shows that the length of a pencil from its eraser to its tip is 7 units and that the eraser is 1.5 units wide. The picture was placed on a photocopy machine and reduced to 66 2/3%. Find the new size of the pencil, and sketch a drawing. Write numerical equations to find the new dimensions.

Answer:
Scale factor: 66 \(\frac{2}{3}\)% = \(\frac{66 \frac{2}{3} \cdot 3}{100 \cdot 3}\) = \(\frac{200}{300}\) = \(\frac{2}{3}\)
Pencil length: 7(\(\frac{2}{3}\)) = 4 \(\frac{2}{3}\)
Eraser: (1 \(\frac{1}{2}\))(\(\frac{2}{3}\)) = (\(\frac{3}{2}\))(\(\frac{2}{3}\)) = 1

Question 4.
Use the diagram to answer each question.
a. What are the corresponding horizontal and vertical distances in a scale drawing if the scale factor is 25%? Use numerical equations to find your answers.

Answer:
Horizontal distance on original drawing: 14
Vertical distance on original drawing: 10
Scale drawing:
Scale factor: 25%
\(\frac{25}{100}\) = \(\frac{1}{4}\)
Horizontal distance: 14(\(\frac{1}{4}\)) = 3.5
Vertical distance: 10(\(\frac{1}{4}\)) = 2.5

b. What are the corresponding horizontal and vertical distances in a scale drawing if the scale factor is 160%? Use a numerical equation to find your answers.
Answer:
Horizontal distance on original drawing: 14
Vertical distance on original drawing: 10
Scale drawing:
Scale factor: 160%
\(\frac{160}{100}\) = \(\frac{8}{5}\)
Horizontal distance: 14(\(\frac{8}{5}\)) = 22.4
Vertical distance: 10(\(\frac{8}{5}\)) = 16

Question 5.
Create a scale drawing of the original drawing below using a horizontal scale factor of 200% and a vertical scale factor of 250%.

Answer:

Question 6.
Using the diagram below, on grid paper sketch the same drawing using a horizontal scale factor of 50% and a vertical scale factor of 150%.

Answer:

Eureka Math Grade 7 Module 4 Lesson 12 Exit Ticket Answer Key

Question 1.
Create a scale drawing of the picture below using a scale factor of 60%. Write three equations that show how you determined the lengths of three different parts of the resulting picture.

Answer:
Scale factor: 60% = \(\frac{60}{100}\) = \(\frac{3}{5}\)
Horizontal distances: 10(\(\frac{3}{5}\)) = 6
5(\(\frac{3}{5}\)) = 3
Vertical distances: 5(\(\frac{3}{5}\)) = 3
7 \(\frac{1}{2}\) (\(\frac{3}{5}\)) = \(\frac{15}{2}\) (\(\frac{3}{5}\)) = \(\frac{9}{2}\) = 4.5
Scale drawing:

Equations:
Left vertical distance: 5 × 0.60 = 3
Right vertical distance: 7.5 × 0.60 = 4.5
Top horizontal distance: 5 × 0.60 = 3
Bottom horizontal distance: 10 × 0.60 = 6

Question 2.
Sue wants to make two picture frames with lengths and widths that are proportional to the ones given below.
Note: The illustration shown below is not drawn to scale.

a. Sketch a scale drawing using a horizontal scale factor of 50% and a vertical scale factor of 75%. Determine the dimensions of the new picture frame.
Answer:

Horizontal measurement: 8(0.50) = 4
Vertical measurement: 12(0.75) = 9
4 in. by 9 in.

b. Sketch a scale drawing using a horizontal scale factor of 125% and a vertical scale factor of 140%. Determine the dimensions of the new picture frame.
Answer:

Horizontal measurement: 8(1.25) = 10
Vertical measurement: 12(1.40) = 16.8
10 in. by 16.8 in.

Engage NY Eureka Math 6th Grade Module 1 Lesson 14 Answer Key

Eureka Math Grade 6 Module 1 Lesson 14 Example Answer Key

Example 1.
Dinner service starts once the train is 250 miles away from Yonkers. What is the minimum time the players will have to wait before they can have their meal?

Answer:


The minimum time is 5 hours.

Eureka Math Grade 6 Module 1 Lesson 14 Exercise Answer Key

Exercise 1.
Create a table to show the time it will take Kelli and her team to travel from Yonkers to each town listed in the
schedule assuming that the ratio of the amount of time traveled to the distance traveled is the same for each city.
Then, extend the table to include the cumulative time it will take to reach each destination on the ride home.

Answer:

Exercise 2.
Create a double number line diagram to show the time It will take Kelli and her team to travel from Yonkers to each town listed in the schedule. Then, extend the double number line diagram to include the cumulative time it will take to reach each destination on the ride home. Represent the ratio of the distance traveled on the round trip to the amount of time taken with an equation.

Answer:

Using the information from the double number line diagram, how many miles would be traveled in one hour?
Answer:
50

How do you know?
Answer:
If the train is moving at a constant speed, half of 2 hours is 1 hour, and half of 100 miles is 50 miles.

Eureka Math Grade 6 Module 1 Lesson 14 Problem Set Answer Key

Question 1.
Complete the table of values to find the following:
Find the number of cups of sugar needed if for each pie Karrie makes, she has to use 3 cups of sugar.

Answer:

Use a graph to represent the relationship

Answer:

Create a double number line diagram to show the relationship.

Answer:

Question 2.
Write a story context that would be represented by the ratio 1: 4.
Answer:
Answers will vary. Example: Kendra’s mom pays her four dollars for every load of laundry she washes and dries.

Complete a table of values for this equation and graph.

Answer:

Answer:

Eureka Math Grade 6 Module 1 Lesson 14 Exit Ticket Answer Key

Dominic works on the weekends and on vacations from school mowing lawns in his neighborhood. For every lawn he mows, he charges $12. Complete the table. Then determine ordered pairs, and create a labeled graph.

Answer:

Question 1.
How many lawns wIll Dominic need to mow In order to make $240?
Answer:
20 lawns

Question 2.
How much money wIll Dominic make If he mows 9 lawns?
Answer:
$108

Engage NY Eureka Math 6th Grade Module 1 Lesson 13 Answer Key

Eureka Math Grade 6 Module 1 Lesson 13 Exercise Answer Key

Exercise 1
Jorge is mixing a special shade of orange paint. He mixed 1 gallon of red paint with 3 gallons of yellow paint. Based on this ratio, which of the following statements are true?

→ \(\frac{3}{4}\) of a 4 gallon mix would be yellow paint.
Answer:
True

→ Every 1 gallon of yellow paint requires \(\frac{1}{3}\) gallon of red paint. .
Answer:
True

→ Every 1 gallon of red paint requires 3 gallons of yellow paint.
Answer:
True

→ There is 1 gallon of red paint in a 4-gallon mix of orange paint,
Answer:
True

→ There are 2 gallons of yellow paint in an 8-gallon mix of orange paint.
Answer:
False

Use the space below to determine If each statement is true or false.

Answer:
Allow students to discuss each question with a partner or group. When the class comes back together as a whole group, each group is responsible for explaining to the class one of the statements and whether the group feels the statement is true or false and why. (The first four statements are true while the fifth statement is false. To be made true, the fifth statement should read “There are 6 gallons of yellow paint in an 8 galIon mix of orange paint.”)

Exercise 2.
Based on the information on red and yellow paint given in Exercise 1, complete the table below.

Answer:

Exercise 3
a. Jorge now plans to mix red paint and blue paint to create purple paint. The color of purple he has decided to make combines red paint and blue paint in the ratio 4: 1. If Jorge can only purchase paint in one gallon containers, construct a ratio table for all possible combinations for red and blue paint that will give Jorge no more than 25 gallons of purple paint.

Answer:

Write an equation that will let Jorge calculate the amount of red paint he will need for any given amount of blue paint.
Answer:
R = 4B

Write an equation that will let Jorge calculate the amount of blue paint he will need for any given amount o
red paint.
Answer:
B = \(\frac{1}{4}\)R

If Jorge has 24 gallons of red paint, how much blue paint will he have to use to create the desired color of purple?
Answer:
Jorge will have to use 6 gallons of blue paint.

If Jorge has 24 gallons of blue paint, how much red paint will he have to use to create the desired color of purple?
Answer:
Jorge will have to use 96 gallons of red paint.

b. Using the same relationship of red to blue from above, create a table that models the relationship of the three colors blue, red, and purple (total) paint. Let B represent the number of gallons of blue paint, let R represent the number of gallons of red paint, and let T represent the total number of gallons of (purple) paint. Then write an equation that models the relationship between the blue paint and the total amount of paint, and answer the questions.

Answer:

Equation:
Answer:
T = 5B

Value of the ratio of total paint to blue paint:
Answer:
\(\frac{5}{1}\)

How is the value of the ratio related to the equation?
Answer:
The value of the ratio is used to determine the total paint value by multiplying it with the blue paint value.

Exercise 4.
During a particular U.S. Air Force training exercise, the ratio of the number of men to the number of women was 6: 1. Use the ratio table provided below to create at least two equations that model the relationship between the number of men and the number of women participating in this training exercise.

Answer:

Equations:
Answer:
M = 6w
W = \(\left(\frac{1}{6}\right)\)M
\(\frac{M}{W}\) = 6
\(\frac{W}{M}\) = \(\frac{1}{6}\)

If 200 women participated in the training exercise, use one of your equations to calculate the number of men who participated.
Answer:
I can substitute 200 for the value of women and multiply by 6, the value of the ratio, to get the number of men. There would be 1,200 men participating in the training exercise.

Exercise 5.
Malia is on a road trip. During the first five minutes of Malia’s trip, she sees 18 cars and 6 trucks. Assuming this ratio of cars to trucks remains constant over the duration of the trip, complete the ratio table using this comparison. Let T represent the number of trucks she sees, and let C represent the number of cars she sees.

Answer:

What is the value of the ratio of the number of cars to the number of trucks?
Answer:
\(\frac{3}{1}\)

What equation would model the relationship between cars and trucks?
Answer:
C = 3T and T = \(\left(\frac{1}{3}\right)\)C

At the end of the trip, Malla had counted 1, 254 trucks. How many cars did she see?
Answer:
C = 1,254.3; C = 3, 762 cars

Exercise 6
Kevin is training to run a half-marathon. His training program recommends that he run for 5 minutes and walk for 1 minute. Let R represent the number of minutes running, and let W represent the number of minutes walking.

Answer:

What is the value of the ratio of the number of minutes walking to the number of minutes running?
Answer:
\(\frac{1}{5}\)

What equation could you use to calculate the minutes spent walking if you know the minutes spent running?
Answer:
W = \(\frac{1}{5}\)R; Answers will vary.

Eureka Math Grade 6 Module 1 Lesson 13 Problem Set Answer Key

A cookie recipe calls for 1 cup of white sugar and 3 cups of brown sugar.
Make a table showing the comparison of the amount of white sugar to the amount of brown sugar.

Answer:

Question 1.
Write the value of the ratio of the amount of white sugar to the amount of brown sugar.
Answer:
\(\frac{1}{3}\)

Question 2.
Write an equation that shows the relationship of the amount of white sugar to the amount of brown sugar.
Answer:
B = 3W or W = \(\frac{1}{3}\) B

Question 3.
Explain how the value of the ratio can be seen In the table.
Answer:
The values in the first row show the values in the ratio. The ratio of the amount of brown sugar to the amount of white sugar is 3: 1. The value of the ratio is \(\frac{3}{1}\).

Question 4.
Explain how the value of the ratio can be seen in the equation.
Answer:
The amount of brown sugar is represented as B in the equation. The amount of white sugar is represented as W. The value is represented because the amount of brown sugar is three times as much as the amount of white sugar, or B = 3W.

Using the same recipe, compare the amount of white sugar to the amount of total sugars used in the recipe.
Make a table showing the comparison of the amount of white sugar to the amount of total sugar.

Answer:

Question 5.
Write the value of the ratio of the amount of total sugar to the amount of white sugar.
Answer:
\(\frac{4}{1}\)

Question 6.
Write an equation that shows the relationship of total sugar to white sugar.
Answer:
T = 4W

Eureka Math Grade 6 Module 1 Lesson 13 Exit Ticket Answer Key

Question 1.
A carpenter uses four nails to install each shelf. Complete the table to represent the relationship between the number of nails (N) and the number of shelves (S). Write the ratio that describes the number of nails per number of shelves. Write as many different equations as you can that describe the relationship between the two quantities.

Answer:

\(\left(\frac{N}{S}\right)=\left(\frac{4}{1}\right)\)
Equations:
N = 4s
S = \(\left(\frac{1}{4}\right)\)N

Engage NY Eureka Math 6th Grade Module 1 Lesson 12 Answer Key

Eureka Math Grade 6 Module 1 Lesson 12 Exercise Answer Key

Exercise 2.
The amount of sugary beverages Americans consume is a leading health concern. For a given brand of cola, a 12 oz. serving of cola contains about 40 g of sugar. Complete the ratio table, using the given ratio to find equivalent ratios.

Answer:
Answers may vary but are found by either multiplying or dividing both 12 and 40 by the same number.

Exercise 3.
A 1 L bottle of cola contains approximately 34 fluid ounces. How many grams of sugar would be in a 1 L bottle of the cola? Explain and show how to arrive at the solution.
Answer:

Exercise 4.
A school cafeteria has a restriction on the amount of sugary drinks available to students. Drinks may not have more than 25 g of sugar. Based on this restriction, what is the largest size cola (in ounces) the cafeteria can offer to students?
Answer:

My estimate is between 6 and 12 oz. but closer to 6 ounces. I need to find \(\frac{1}{4}\) of 6 and add it to 6.
\(\frac{1}{4} \times \frac{6}{1}=\frac{6}{4}=1 \frac{1}{2}\)
6 + 1\(\frac{1}{2}\) = 7\(\frac{1}{2}\)
As 7\(\frac{1}{2}\) oz. cola is the largest size that the school cafeteria can offer to students.

Exercise 5.
Shontelle solves three math problems in four minutes.
a. Use this information to complete the table below.

Answer:

b. Shontelle has soccer practice on Thursday evening. She has a half hour before practice to work on her math homework and to talk to her friends. She has 20 math skill-work questions for homework, and she wants to complete them before talking with her friends. How many minutes will Shontelle have left after completing her math homework to talk to her friends?
Use a double number line diagram to support your answer, and show all work.
Answer:

Step 1: \(\frac{2}{3} \times 4=\frac{8}{3}=2 \frac{2}{3}\)
Step 2: \(24+2 \frac{2}{3}=26 \frac{2}{3}\)
Step 3: \(30-26 \frac{2}{3}=3 \frac{1}{3}\)
Shontelle can talk to her friends for 3\(\frac{1}{3}\) minutes.

Eureka Math Grade 6 Module 1 Lesson 12 Problem Set Answer Key

Question 1.
While shopping, Kyla found a dress that she would like to purchase, but it costs $52.25 more than she has. Kyla charges $5.50 an hour for babysitting. She wants to figure out how many hours she must babysit to earn $52.25 to buy the dress. Use a double number line to support your answer.
Answer:
9.5 hours

Question 2.
Frank has been driving at a constant speed for 3 hours, during which time he traveled 195 miles. Frank would like to know how long it will take him to complete the remaining 455 miles, assuming he maintains the same constant speed. Help Frank determine how long the remainder of the trip will take. Include a table or diagram to support your answer.
Answer:
7 hours

Eureka Math Grade 6 Module 1 Lesson 12 Exit Ticket Answer Key

Question 1.
Kyra is participating in a fundraiser walk-a-thon. She walks 2 miles in 30 minutes. If she continues to walk at the same rate, determine how many minutes it will take her to walk 7 miles. Use a double number line diagram to support your answer.
Answer:

It will take kyra 105 minutes to walk 7 miles.