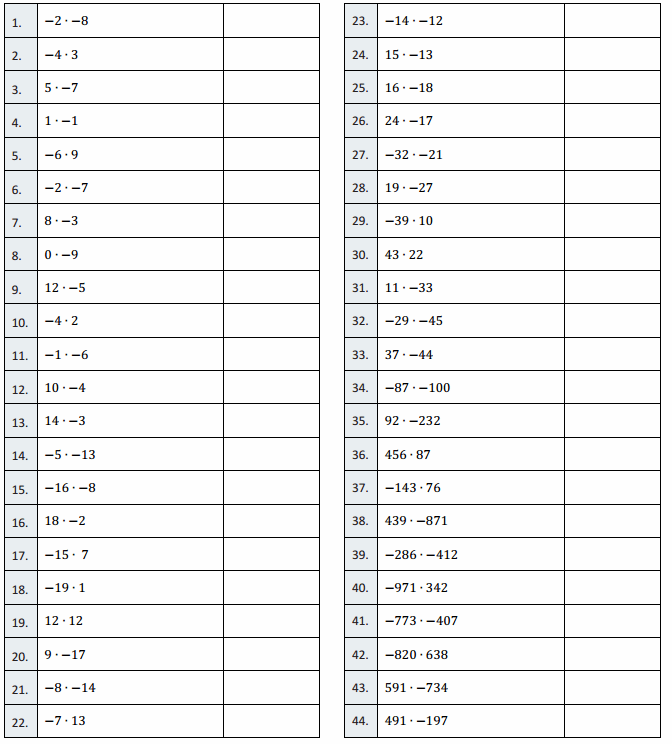
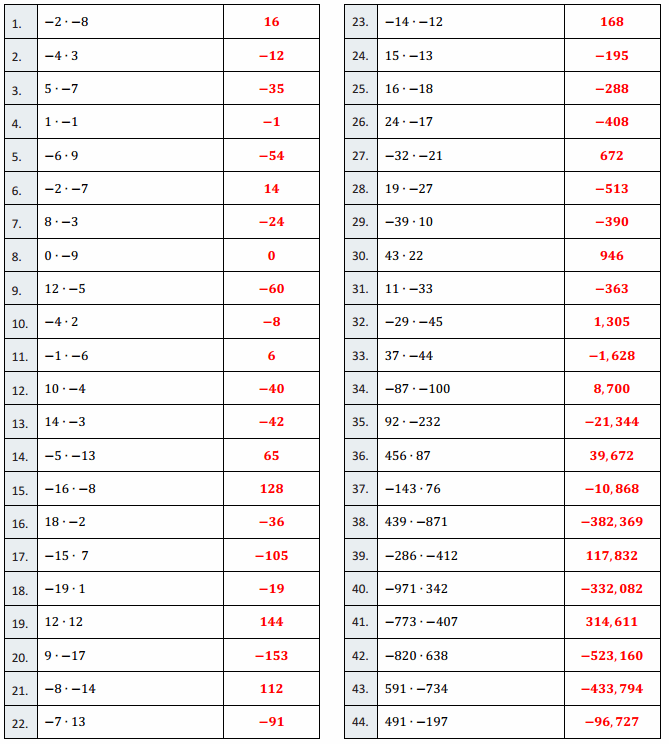
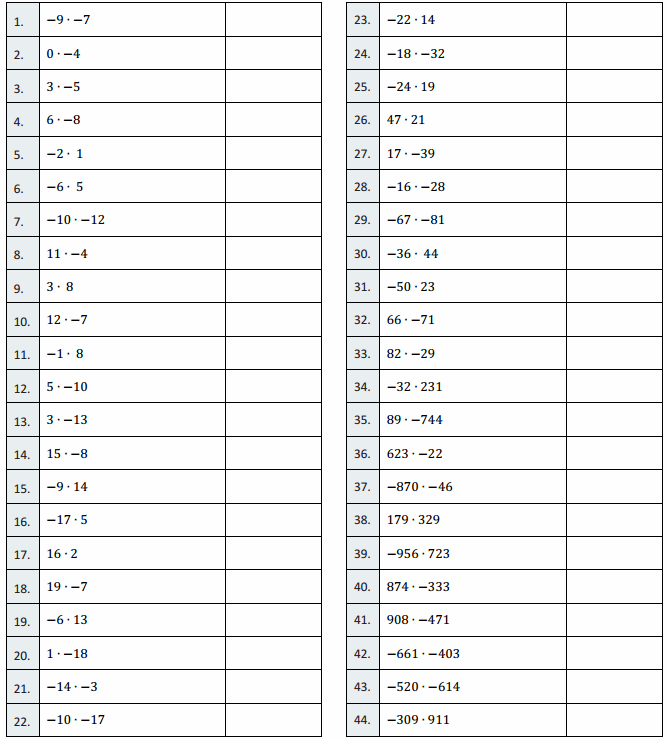
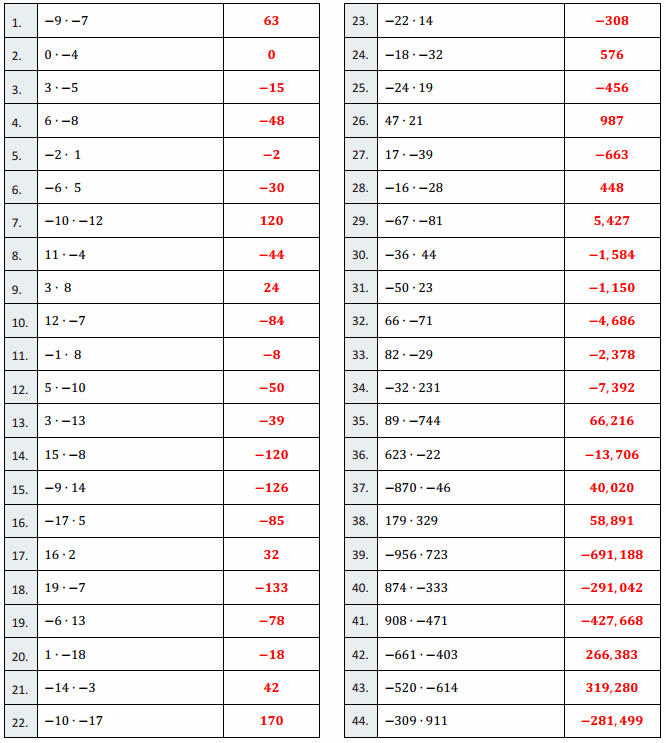
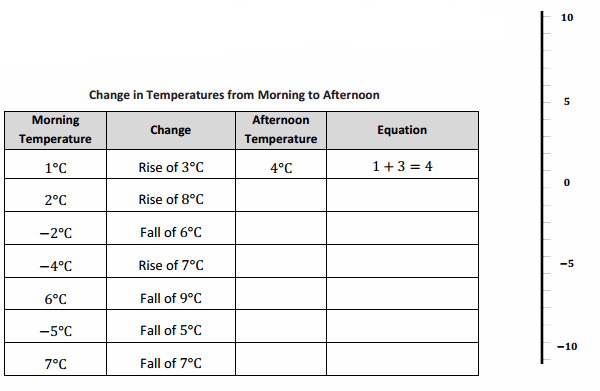
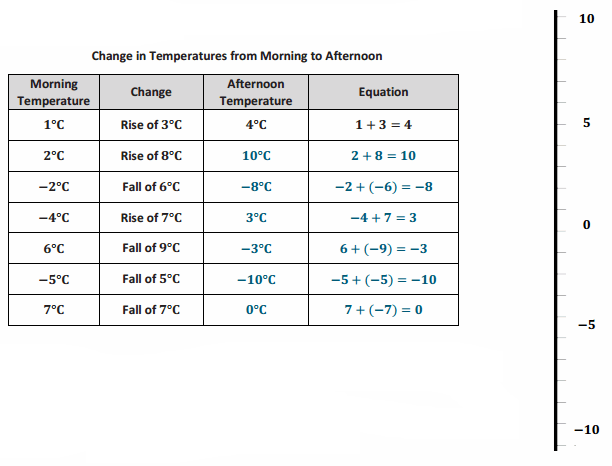
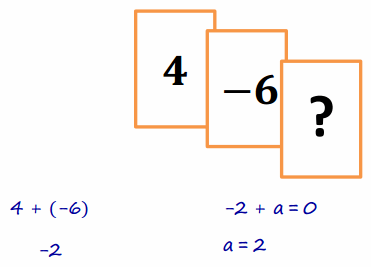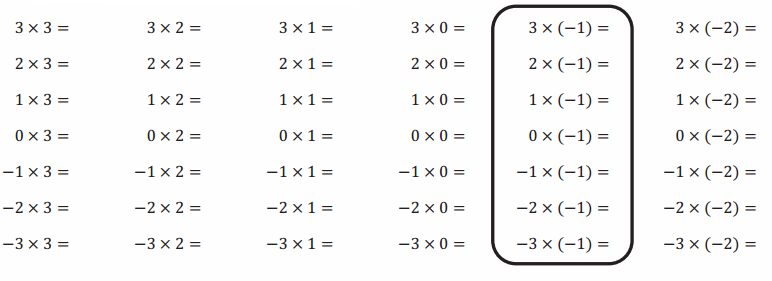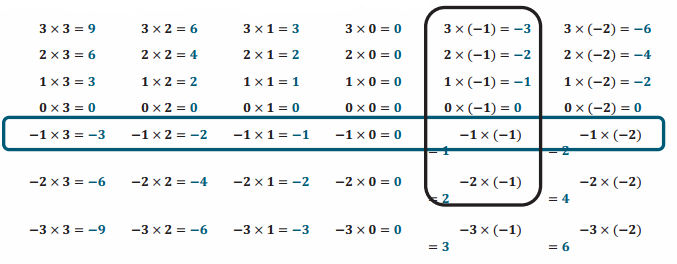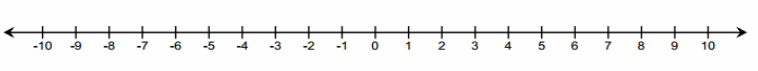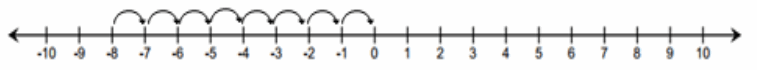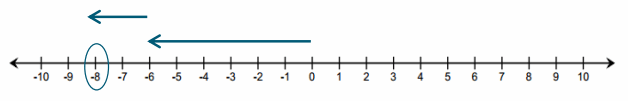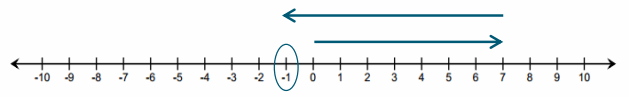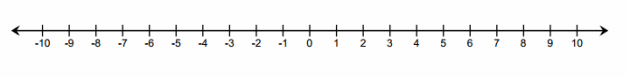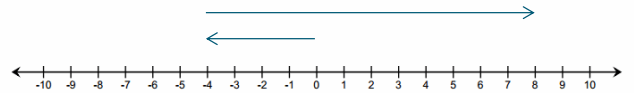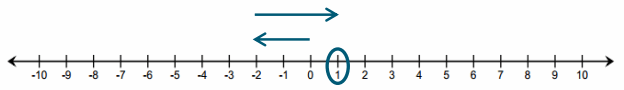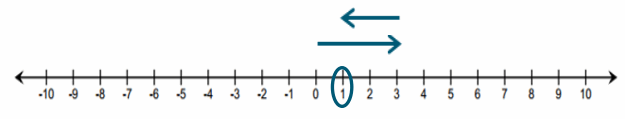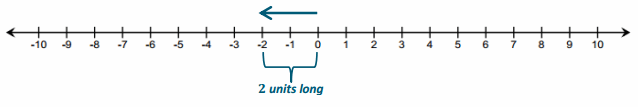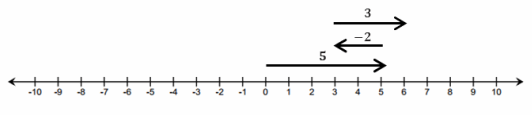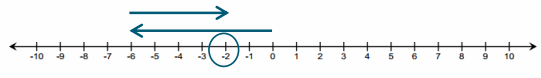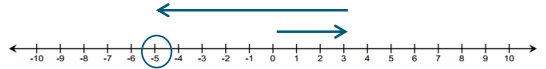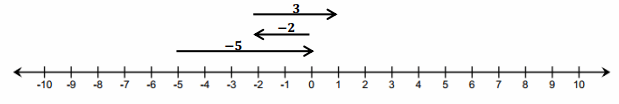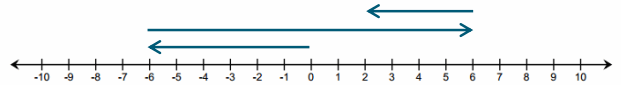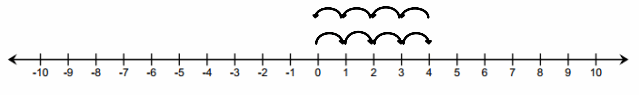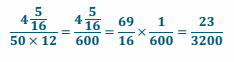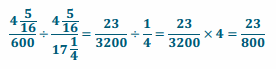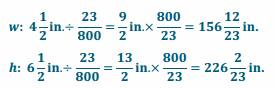Engage NY Eureka Math 7th Grade Module 2 Lesson 5 Answer Key
Eureka Math Grade 7 Module 2 Lesson 5 Example Answer Key
Example 1.
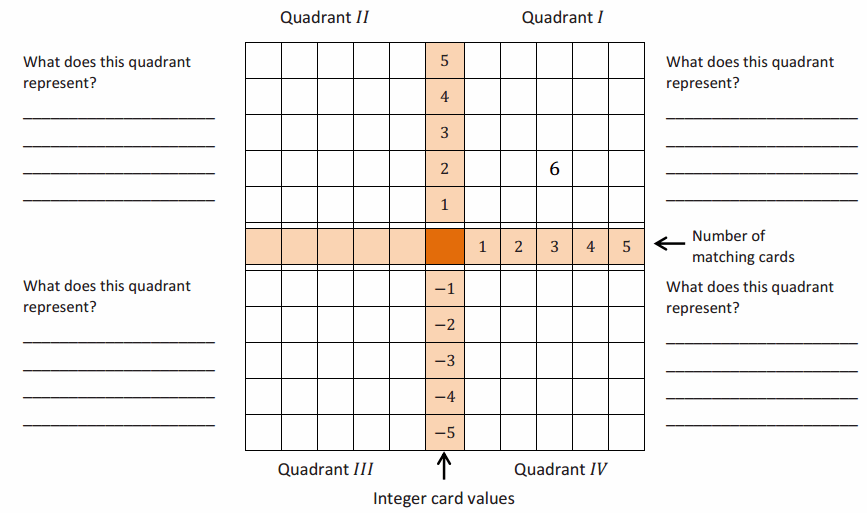
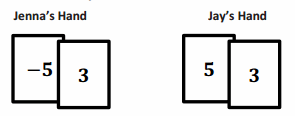
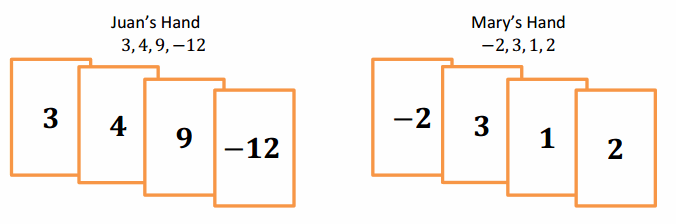
Exploring Subtraction with the Integer Game
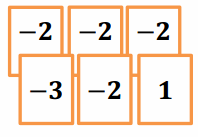
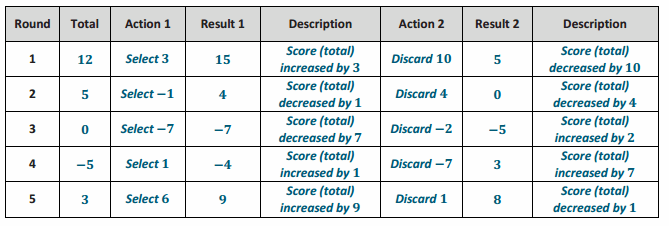
Play the Integer Game in your group. Start Round 1 by selecting four cards. Follow the steps for each round of play.
Write the value of your hand in the Total column.
Then, record what card values you select in the Action 1 column and discard from your hand in the Action 2 column.
After each action, calculate your new total, and record it under the appropriate Results column.
Based on the results, describe what happens to the value of your hand under the appropriate Descriptions column. For example, “Score increased by 3.”
Answer:
sample student work
Discussion: Making Connections to Integer Subtraction
Question 1.
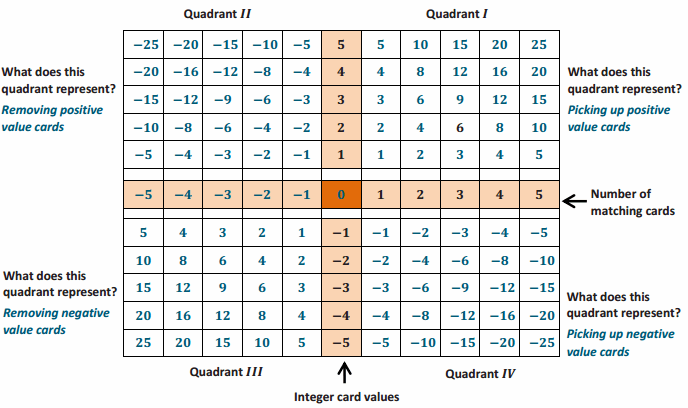
How did selecting positive value cards change the value of your hand?
Answer:
It increased my score by the value of the card.
Question 2.
How did selecting negative value cards change the value of your hand?
Answer:
It decreased my score by the absolute value of the card.
Question 3.
How did discarding positive value cards change the value of your hand?
Answer:
It decreased my score by the value of the card.
Question 4.
How did discarding negative value cards change the value of your hand?
Answer:
It increased my score by the absolute value of the card.
Question 5.
What operation reflects selecting a card?
Answer:
Addition
Question 6.
What operation reflects discarding or removing a card?
Answer:
Subtraction
Question 7.
Based on the game, can you make a prediction about what happens to the result when
a. Subtracting a positive integer?
Answer:
The result of the hand will decrease by the value of the integer.
b. Subtracting a negative integer?
Answer:
The result of the hand will increase by the absolute value of the negative integer.
At the end of the lesson, the class reviews its predictions.
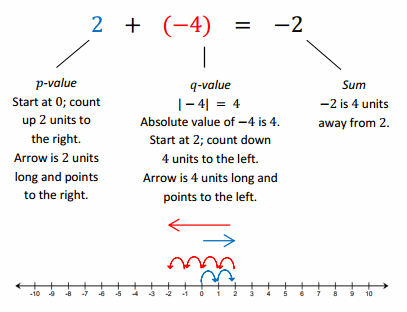
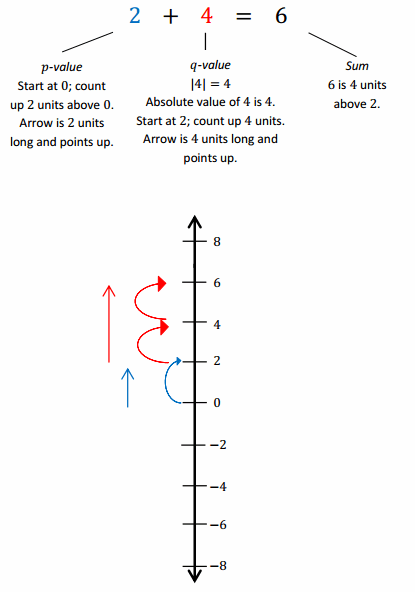
Example 2:
Subtracting a Positive Number
Follow along with your teacher to complete the diagrams below.
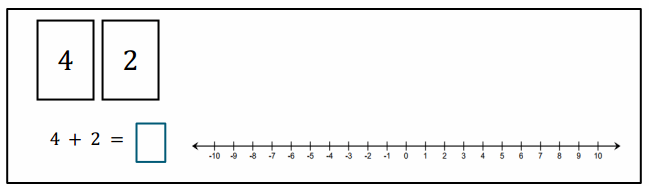
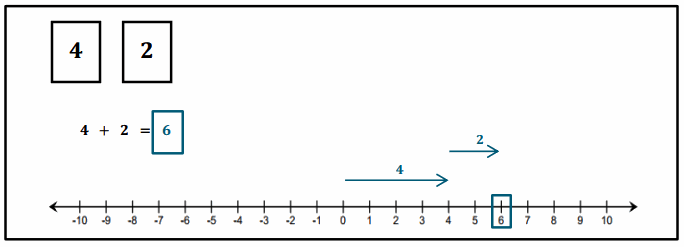
Answer:
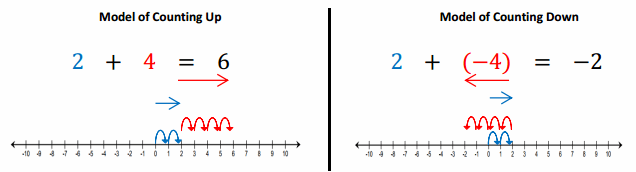
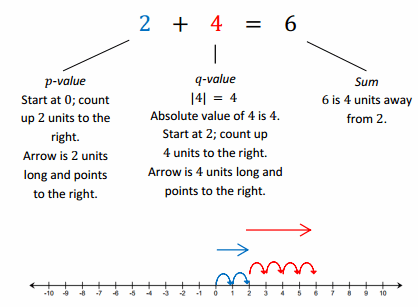
If I had these two cards, the sum would be 6.
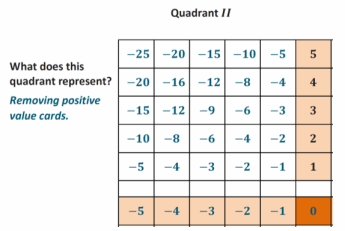
Show that discarding (subtracting) a positive card, which is the same as subtracting a positive number, decreases the value of the hand.
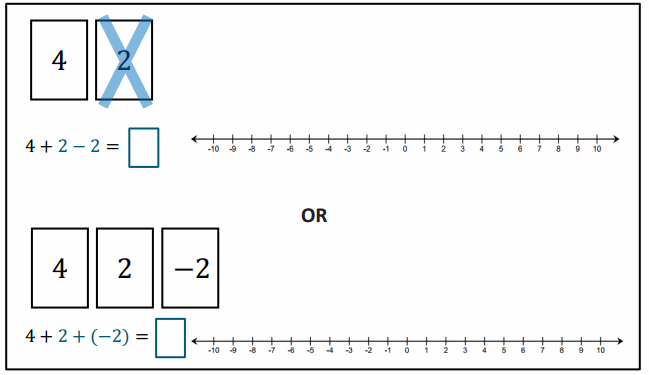
Answer:
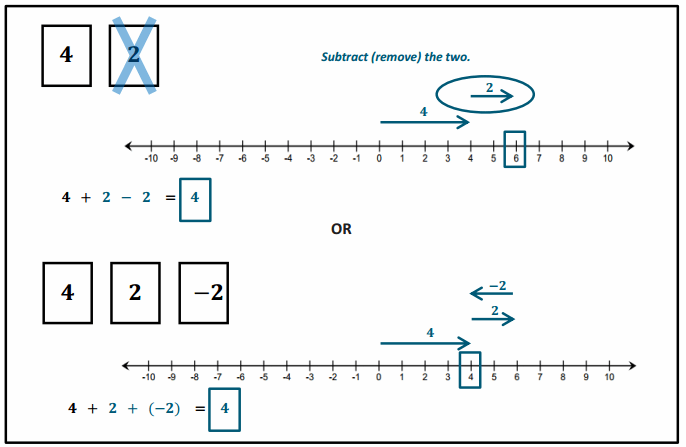
If I discarded or removed the 2, my score would decrease by 2 because I would still have a 4 left in my hand.
4 + 2 – 2 = 4. Taking away, or subtracting, 2 causes my score to decrease by 2.
Removing ___ a positive card changes the score in the same way as ___ adding a card whose value is the ___ ___ (or opposite). In this case, adding the corresponding ____
Answer:
Removing (subtracting) a positive card changes the score in the same way as adding a card whose value is the
additive inverse (or opposite). In this case, adding the corresponding negative such that 4 – 2 = 4 + (-2).
Subtracting a positive q-value is represented on the number line as moving to the left on a number line.
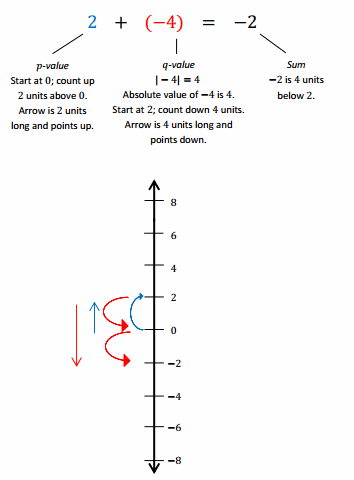
Example 3.
Subtracting a Negative Number
Follow along with your teacher to complete the diagrams below.
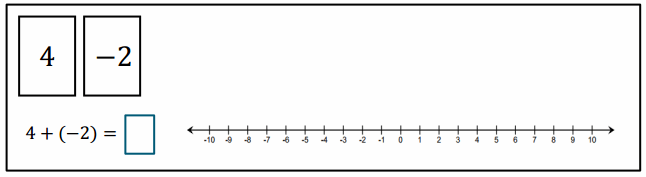
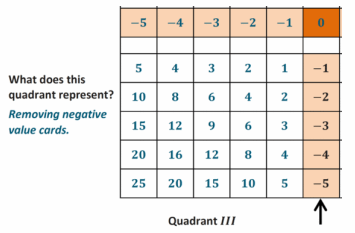
How does removing a negative card change the score, or value, of the hand?
Answer:
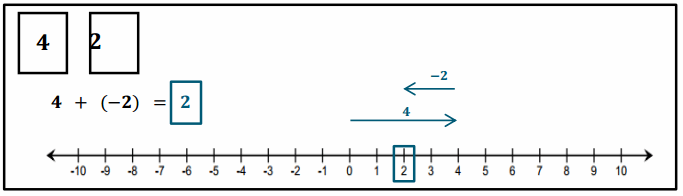
If I discarded, or removed, the -2, my score would increase by 2 because I would still have a 4 left in my hand.
4 + (-2) – (-2) = 4. Taking away, or subtracting, -2 causes my score to increase by 2.
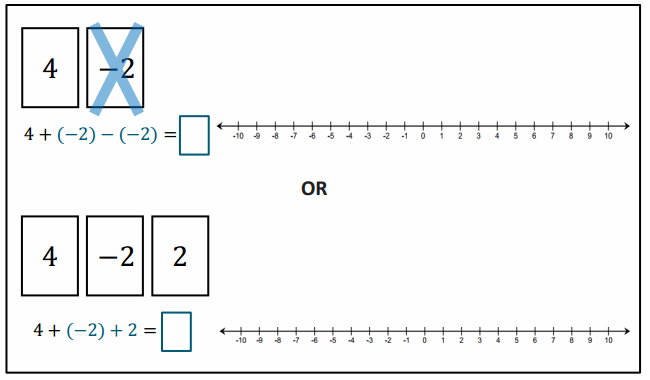
Answer:
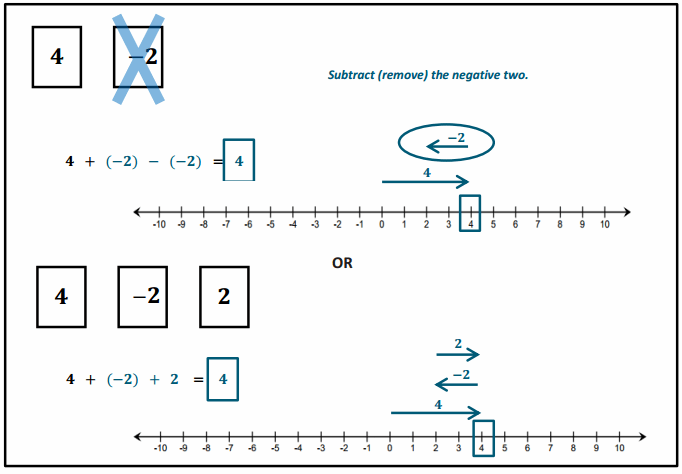
Removing (___) a negative card changes the score in the same way as ___ a card whose value is the ___ (or opposite). In this case, adding the corresponding ____
Answer:
Removing (subtracting) a negative card changes the score in the same way as adding a card whose value is the
additive inverse (or opposite). In this case, adding the corresponding positive such that 4 – (-2) = 4 + 2.
Subtracting a negative q-value is represented on the number line as moving to the right on a number line because it is the opposite of subtracting a positive q-value (move to the left).
THE RULE OF SUBTRACTION: Subtracting a number is the same as adding its additive inverse (or opposite).
Eureka Math Grade 7 Module 2 Lesson 5 Exercise Answer Key
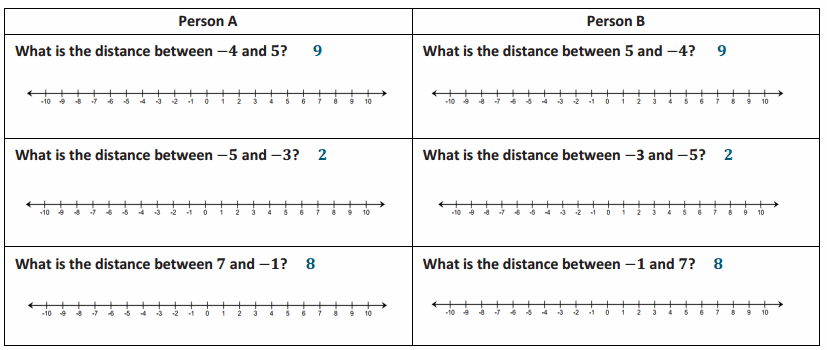
Question 1.
Using the rule of subtraction, rewrite the following subtraction sentences as addition sentences and solve. Use the number line below if needed.
a. 8 – 2
Answer:
![]()
b. 4 – 9
Answer:
![]()
c. -3 – 7
Answer:
-3 + (-7) = -10
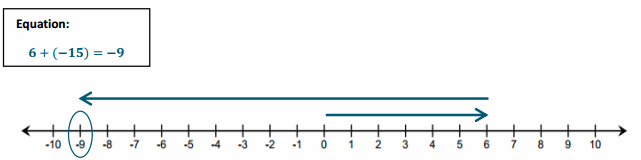
d. – 9 – (-2)
Answer:
![]()
Exercise 2.
Find the differences.
a. -2 – (-5)
Answer:
![]()
b. 11 – (-8)
Answer:
11 + 8 = 19
c. -10 – (-4)
Answer:
![]()
Question 3.
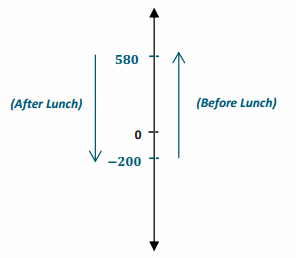
Write two equivalent expressions that represent the situation. What is the difference in their elevations? An airplane flies at an altitude of 25,000 feet. A submarine dives to a depth of 600 feet below sea level.
Answer:
25,000 – (-600) and 25,000 + 600
The difference in their elevation is 25,600 feet.
Eureka Math Grade 7 Module 2 Lesson 5 Problem Set Answer Key
Question 1.
On a number line, find the difference of each number and 4. Complete the table to support your answers. The first example is provided.

Answer:

Question 2.
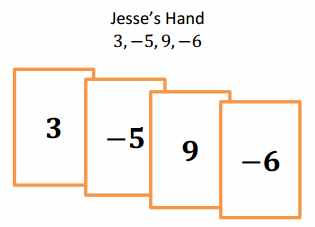
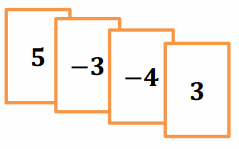
You and your partner were playing the Integer Game in class. Here are the cards in both hands.
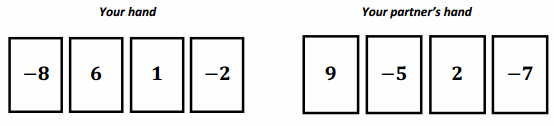
a. Find the value of each hand. Who would win based on the current scores? (The score closest to 0 wins.)
Answer:
My hand: -8 + 6 + 1 + (-2) = -3
Partner’s hand: 9 + (-5) + 2 + (-7) = -1
My partner would win because -1 is closer to 0. It is 1 unit to the left of 0.
b. Find the value of each hand if you discarded the -2 and selected a 5, and your partner discarded the -5 and selected a 5. Show your work to support your answer.
Answer:
My hand: Discard the -2, -3 – (-2) = -1; Select a 5: -1 + 5 = 4.
Partner’s hand: Discard the -5, -1 – (-5) = 4; Select a 5: 4 + 5 = 9.
c. Use your score values from part (b) to determine who would win the game now.
Answer:
I would win now because 4 is closer to zero.
Question 3.
Write the following expressions as a single integer.
a. -2+16
Answer:
14
b. -2 – (-16)
Answer:
14
c. 18 – 26
Answer:
-8
d. -14 – 23
Answer:
-37
e. 30 – (-45)
Answer:
75
Question 4.
Explain what is meant by the following, and illustrate with an example:
“For any real numbers, p and q, p – q = p + (-q).”
Answer:
Subtracting a number is the same as adding its additive inverse. Examples will vary. A sample response is shown below.
p = 4, q = 6, 4 – 6 is the same as 4 + (-6) because -6 is the opposite of 6.
4 – 6 = -2
4 + (-6) = -2
So, 4 – 6 = 4 + (-6) because they both equal -2.
Question 5.
Choose an integer between -1 and -5 on the number line, and label it point P. Locate and label the following points on the number line. Show your work.
Answer:
Answers will vary. A sample response is shown below given that the student chose -3 for P.
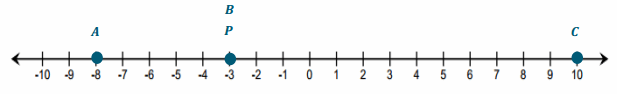
a. Point A: P – 5
Answer:
Point A: -3 – 5 = -8
b. Point B: (P-4)+4
Answer:
Point B: (-3 – 4) + 4 = -3 (same as P)
c. Point C: -P-(-7)
Answer:
Point C: -(-3) – (-7) = 3 + 7 = 10
Eureka Math Grade 7 Module 2 Lesson 5 Exit Ticket Answer Key
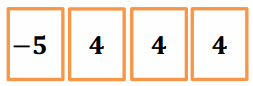
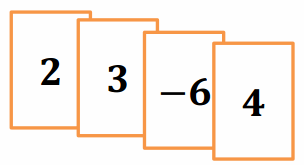
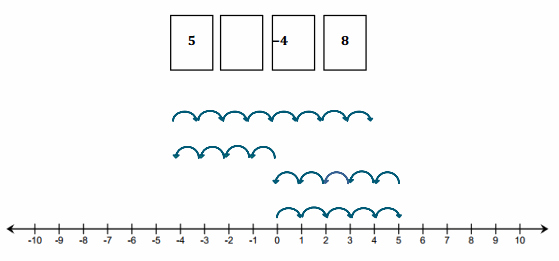
Question 1.
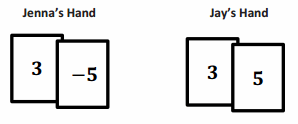
If a player had the following cards, what is the value of his hand?
Answer:
The current value of the hand is -2. 1 + (-7) + 4 = -2.
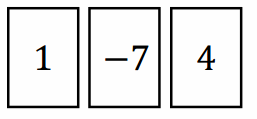
a. Identify two different ways the player could get to a score of 5 by adding or removing only one card. Explain.
Answer:
He could remove the -7 or add 7. If he removes the -7, the value of the hand will be 5, which is 7 larger than -2. He could also get a sum of 5 by adding 7 to the hand. Therefore, removing the -7 gives him the same result as adding 7.
b. Write two equations for part (a), one for each of the methods you came up with for arriving at a score of 5.
Answer:
-2 – (-7) = 5 and -2 + 7 = 5
Question 2.
Using the rule of subtraction, rewrite the following subtraction expressions as addition expressions, and find the sums.
a. 5 – 9
Answer:
5 + (-9) = -4
b. -14 – (-2)
Answer:
-14 + 2 = -12
Eureka Math Grade 7 Module 2 Lesson 5 Challenge Problem Answer Key
Question 6.
Write two equivalent expressions that represent the situation. What is the difference in their elevations?
An airplane flies at an altitude of 26,000 feet. A submarine dives to a depth of 700 feet below sea level.
Answer:
Two equivalent expressions are 26,000 – (-700) and 26,000 + 700. The difference in their elevations is 26,700 feet.