Prasanna

Basically, Standard Form in Maths can be represented for numbers like decimal numbers, rational numbers, fractions, polynomials, equations, linear equations, etc. As we all know that the simplified form of the fractions called decimal numbers. Eventually, we can say that standard form is the representation of large numbers in small numbers irrespective of any form of numbers. In this article, we have explained what is the standard form of numbers, decimals, equations, etc. How to do it, Rules, and solved Standard form examples.

So, Let’s dive into it!

What is Standard Form?

A Standard Form is a process of formulating a given mathematical concept such as number, equation, polynomial, etc. in the standard form by following certain basic rules.

Standard Form of a Number

The definition of the standard form of a number is representing the very large expanded number in a small number. Here, we will see how to write a numerical in standard form with an example.

Now, we are taking a large number in the expanded form and convert the number into standard form.

Example: 

Write the given expanded form into standard form.

10,00,00,000 + 5,00,00,000 + 4,00,000 + 80,000 + 2,000 + 60 + 9.

Solution:

With the help of this below table, we will write the given expanded form of number into the standard form of a number.

Expanded Form                                                                                                   Standard Form

10,00,00,000 + 5,00,00,000 + 4,00,000 + 80,000 + 2,000 + 60 + 9       =             150482069

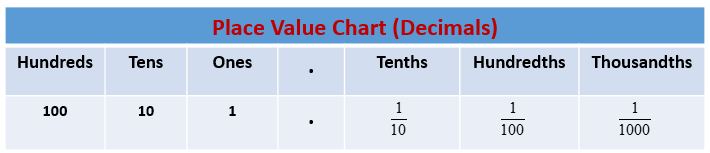
Standard Form of a Decimal Number

In Britain, the Scientific Notation’s other name is the Standard Form. And in other countries, it means not in the form of the large expanded number. We all know that it’s tough to read numbers such as 0.000000002345678 or 12345678900000. In order to help you all while reading these large numbers, we convert them into standard form.

Any number which we will address as a decimal number, among 1.0 and 10.0, multiplied by a power of 10, is stated to be in standard form. For example, 0.67X10¹³ is in the standard form.

Example:

Write down the standard form of the given decimal number 5326.6?

Solution:

The given decimal number 5326.6 can be written in this way in a scientific notation:

Because 5326.6 = 53266 X 1000 =  5.3266 × 10^3.

Standard Form of a Linear Equation

The “Standard Form” for writing down a Linear Equation is Ax + By = C

A shouldn’t be negative, A and B shouldn’t both be zero, and A, B, and C should be integers.

Example:

Put this y = 7x + 4 in linear equation standard form?

Solution:

Given equation is Y= 7x + 4

Now, you have to change 7x from right to left like this, −7x + y = 4

Multiply all by −1:

7x − y = −4

Note: A = 7, B = −1, C = −4.

Standard Form of a Quadratic Equation

The Standard Form for writing down a Quadratic Equation is ax^2 + bx + c = 0, a is not equal to 0.

Example: 

Put this equation x(x−1) = 4 in the standard form?

Solution:

Given equation is x(x−1) = 4

In the first step, you have to expand x(x−1):

x(x−1) = x² − x

x² − x = 4

Next step is to move the 4 numerical to left side,

x² − x − 4 = 0.

Where A=1, B= -1, C= -4

The standard form of a quadratic equation x(x−1) = 4 is x² − x − 4 = 0. 

FAQs on Standard Form Rules in Maths

1. What is the standard form of an Equation?

An Equation in Standard Form looks like (some expression) = 0 ie., x + y = 0, where the left side of an equation are x and y terms and the Zero is on the right side.

2. What is meant by the standard form of a circle?

The graph of a circle is fully defined by its center and radius. The standard form for the equation of a circle is (x−h)²+(y−k)²=r². The center is (h,k) and the radius measures r units.

3. How to write 81 900 000 000 000 in standard form?

Steps on how to find or write the standard form of a given number ie., 81 900 000 000 000:

• In step-1, write the first digit 8
• Now, add a point then it becomes 8.
• Count the remaining digits after the digit 8 and write the count in the power of 10.
• For this example, there are 13 digits. So, the standard form of 81 900 000 000 000 is 8.19 × 10¹³.

According to Demorgan’s Law Complement of Union of Two Sets is the Intersection of their Complements and the Complement of Intersection of Two Sets is the Union of Complements. The Law can be expressed as such ( A ∪ B) ‘ = A ‘ ∩ B ‘. By referring to the further modules you can find Demorgan’s Law Statement, Proof along with examples.

For any two finite sets A and B, we have

(i) (A U B)’ = A’ ∩ B’ (which is a De Morgan’s law of union).

(ii) (A ∩ B)’ = A’ U B’ (which is a De Morgan’s law of intersection).

De Morgan’s Laws Statement and Proof

A Set is a well-defined collection of objects or elements. You can perform various operations on sets such as Complement, Union, and Intersection. These Operations and usage can be further simplified by a set of simple laws called Demorgan’s Laws.

Any Set that includes all the elements related to a particular context is called a universal set. Let us assume a Universal Set U such that A and B are Subsets of it.

De Morgan’s Law Proof: (A∪B)’= A’∩ B’   

As per Demorgan’s First Law, the Complement of Union of Two Sets A and B is equal to the Intersection of Complements of Sets A and B.

(A∪B)’= A’∩ B’

Let P = (A U B)’ and Q = A’ ∩ B’

Consider x to be an arbitrary element of P then x ∈ P ⇒ x ∈ (A U B)’

⇒ x ∉ (A U B)

⇒ x ∉ A and x ∉ B

⇒ x ∈ A’ and x ∈ B’

⇒ x ∈ A’ ∩ B’

⇒ x ∈ Q

Therefore, P ⊂ Q …………….. (i)

Let us consider y to be an arbitrary element of Q then y ∈ Q ⇒ y ∈ A’ ∩ B’

⇒ y ∈ A’ and y ∈ B’

⇒ y ∉ A and y ∉ B

⇒ y ∉ (A U B)

⇒ y ∈ (A U B)’

⇒ y ∈ P

Therefore, Q ⊂ P …………….. (ii)

Combining (i) and (ii) we get; P = Q i.e. (A U B)’ = A’ ∩ B’

De Morgan’s Law Proof: (A ∩ B)’ = A’ U B’

Let us consider Sets M = (A ∩ B)’ and N = A’ U B’

Let x be an arbitrary element of M then x ∈ M ⇒ x ∈ (A ∩ B)’

⇒ x ∉ (A ∩ B)

⇒ x ∉ A or x ∉ B

⇒ x ∈ A’ or x ∈ B’

⇒ x ∈ A’ U B’

⇒ x ∈ N

Thus, M ⊂ N …………….. (i)

Again, let y be an arbitrary element of N then y ∈ N ⇒ y ∈ A’ U B’

⇒ y ∈ A’ or y ∈ B’

⇒ y ∉ A or y ∉ B

⇒ y ∉ (A ∩ B)

⇒ y ∈ (A ∩ B)’

⇒ y ∈ M

Thus, N ⊂ M …………….. (ii)

Combining (i) and (ii) we get; M = N i.e. (A ∩ B)’ = A’ U B’

Examples of De Morgan’s Law

1. If U = {a,b,c, d, e}, X = {b, c, d} and Y = {b, d, e}. Prove that De Morgan’s law: (X ∩ Y)’ = X’ U Y’?

Solution:

Given Sets are U = {a,b,c, d, e}, X = {b, c, d} and Y = {b, d, e}

Firstly find the (X ∩ Y) = {b, c, d} ∩ {b, d, e}

= { b,d}

(X ∩ Y)’ = U – (X ∩ Y)

= {a,b,c, d, e} – { b,d}

= {a,c,e}

X’ =  U – X

= {a,b,c, d, e} – {b, c, d}

= {a,e}

Y’ = U – Y

= {a,b,c, d, e} – {b, d, e}

= {a,c}

X’ U Y’ = {a,e} U {a,c}

= {a,c,e}

Hence Prooved (X ∩ Y)’ = X’ U Y’

2. Let U = {1, 2, 3, 4, 5, 6, 7, 8}, A = {2, 3, 4} and B = {5, 6, 8}. Show that (A ∪ B)’ = A’ ∩ B’?

Solution:

Given Sets are U = {1, 2, 3, 4, 5, 6, 7, 8}, A = {4, 5, 6} and B = {5, 6, 8}
(A ∪ B) = {4, 5, 6} ∪ {5, 6, 8}

= {4, ,5, 6, 8}

(A ∪ B)’ = U – (A ∪ B)

= {1, 2, 3, 4, 5, 6, 7, 8} – {4, ,5, 6, 8}

= {1, 2, 3,7}

A’ = U – A

= {1, 2, 3, 4, 5, 6, 7, 8} – {4, 5, 6}

= {1, 2, 3, 7, 8}

B’ = U – B

= {1, 2, 3, 4, 5, 6, 7, 8} – {5, 6, 8}

= {1, 2, 3, 4, 7}

A’ ∩ B’ = {1, 2, 3, 7, 8} ∩ {1, 2, 3, 4, 7}

= {1, 2, 3, 7}

Hence Prooved (A ∪ B)’ = A’ ∩ B’

Binary Subtraction is one among the four binary operations in which we perform subtraction of binary numbers i.e. 0 or 1. It is similar to the Basic Arithmetic Operation of Decimals. When we subtract 1 from 0 we need to borrow 1 from the next digit to reduce the digit by 1 and the remainder left here is 1. Go through the entire article to know about Binary Subtraction Rules, Subtraction Table, Tricks and Procedure on How to Subtract Binary Numbers, etc.

What is meant by Binary Subtraction?

Binary Numbers Subtraction is similar to Subtraction of Decimals or Base 10 Numbers. For instance, 1+1+1 is 3 in base 10 whereas in a binary number system 1+1+1 is 11. While Performing Addition and Subtraction in Binary Numbers be careful with borrowing as you might need to do them quite often.

While performing subtraction of several columns of binary digits you need to consider the borrowing. If you subtract 1 from 0 the result will be 1 where 1 is borrowed from the next highest order digit.

Binary Subtraction Table

On Adding Two Binary Numbers 1 and 1 we get the result 10 in which we consider 0 and carry forward 1 to the next higher-order bit. On Subtracting 1 from 1, the result is 0 and nothing will be carry forwarded.

While subtracting 1 from 0 in the case of decimal numbers we borrow 1 from the preceding higher-order number and make it 10 and after subtracting result becomes 9. However, in the case of Binary Subtraction, the result is 0.

Rules for Binary Subtraction

Binary Subtraction is quite simple compared to Decimal Subtraction if you remember the following tips and tricks.

0 – 0 = 0
0 – 1 = 1 ( with a borrow of 1)
1 – 0 = 1
1 – 1 = 0

You can look at the binary subtraction examples provided below for better understanding.

How to Subtract Binary Numbers?

Follow the below-listed steps to perform Binary Subtraction. You will find the Subtraction of Binary Numbers much easier after going through the below steps. They are as follows

• Align the numbers similar to an ordinary subtraction problem. Write the larger number up and the smaller number below it. If the Smaller Digit has few digits align them towards the right same as in decimal subtraction.
• Begin from the right column and perform the subtraction operation of binary numbers. While doing so keep the binary subtraction rules in mind and do accordingly.
• Solve column by column moving from right to left.

Binary Subtraction Examples

1. Find the Value of 1010011 – 001110?

Solution:

Write the given numbers as if you subtracting decimal numbers. Align them to the right and fill them with leading zeros so that both the numbers have the same digits.

1011011

(-)0001010

——————

1010001

Binary Notation

Decimal Notation

The decimal Equivalent of given numbers is

1011011 = 91

001010 = 10

91-10 = 81

2. Find the value of 1100010 – 001000?

Solution:

Write the given numbers as if you subtracting decimal numbers. Align them to the right and fill them with leading zeros so that both the numbers have the same digits.

1100010

(-)0001000

——————

1,011,010

Decimal Notation

The decimal Equivalent of given numbers is

1100010 = 98

1000 = 8

98-8 = 90

Binary Subtraction using 1’s Complement

Go through the below procedure and perform the Binary Subtraction easily. They are as follows

• Firstly, write the 1’s complement of the subtrahend.
• And then add the 1’s complement subtrahend with the minuend.
• If the result has a carryover add the carryover in the least significant bit.
• If it has no carryover take the 1’s complement of resultant and it is negative.

Questions on Binary Subtraction using 1’s Complement

1. (11001)₂  – (1010)₂

Solution:

(11001)₂  = 25

(1010)₂  = 10 – subtrahend

Fill with leading zeros till you have the same number of digits in both the numbers. Firstly, take the 1’s complement of subtrahend i.e. (01010)₂.

1’s complement of the subtrahend is 10101. Add 1 to the 1’s complement of the second number

10101
+   1
↓
10110

Now instead of subtracting add the 1’s complement of the second number to the first one

11001
+ 10110

——————
101111

Remove the leading 1 to obtain the result.

Then, remove the leading zeros as it will not alter the result and you can write the final result of subtraction as such

11001
– 1010

——————

1111

FAQs on Binary Subtraction

1. What are the Rules of Binary Subtraction?

Rules of Binary Subtraction are as follows

0 – 0 = 0
0 – 1 = 1 ( with a borrow of 1)
1 – 0 = 1
1 – 1 = 0

2. How many basic binary subtraction combinations are possible?

There are four possible binary subtraction combinations when subtracting binary digits.

3. What signs does the binary digit 0 and 1 represent?

0 represents the positive sign and 1 represents the negative sign.

Mathematics is the study of numbers, shapes, and patterns. It includes various complex and simple arithmetic topics that help people in their daily life routine. In Maths, Numbers play a major role and they can be of different types like Real Numbers, Whole Numbers, Natural Numbers, Decimal Numbers, Rational Numbers, etc. Today, we are going to discuss one of the main topics of Decimal Numbers. In Decimals, identifying the Decimal Place Values is a fundamental topic and everyone should know the techniques clearly. So, here we will be discussing elaborately the topic of Decimal Place Values Chart.

Let’s get into it.

What is the Place Value of Decimals?

Place value is a positional notation system where the position of a digit in a number, determines its value. The place value for decimal numbers is arranged exactly the identical form of treating whole numbers, but in this case, it is reverse. On the basis of the preceding exponential of 10, the place value in decimals can be decided.

Decimal Place Value Chart

On the place value chart, the numbers on the left of the decimal point are multiplied with increasing positive powers of 10, whereas the digits on the right of the decimal point are multiplied with increasing negative powers of 10 from left to right.

• The first digit after the decimal represents the tenths place.
• The second digit after the decimal represents the hundredths place.
• The third digit after the decimal represents the thousands place.
• The rest of the digits proceed to fill in the place values until there are no digits left.

How to write the place value of decimals for the number 132.76?

• The place of 6 in the decimal 132.76 is 6/100
• The place of 7 in the decimal 132.76 is 7/10
• The place of 2 in the decimal 132.76 is 2
• The place of 3 in the decimal 132.76 is 30
• The place of 1 in the decimal 132.76 is 100.

Examples:

1.  Write the place value of digit 7 in the following decimal number: 5.47?

The number 7 is in the place of hundredths, and its place value is 7 x 10 ^-2 = 7/100 = 0.07.

2. Identify the place value of the 6 in the given number: 689.87?

Given number is 689.87

The place of 6 in the decimal 689.87 is 600 or 6 hundreds. 

3. Write the following numbers in the decimal place value chart.

(i) 4532.079

(ii) 490.7042

Solutions: 

(i) 4532.079

4532.079 in the decimal place value chart.

(ii) 490.7042

490.7042 in the decimal place value chart.

In your day-to-day life, you might need to convert from one unit to another. To Perform the Required Calculations you might need to learn about Mathematical Conversions. Thus, it is necessary to learn about Unit Conversions to change from one unit to another unit.  Before understanding the Units of Measurement you need to be aware of the relationship between them.

Go through the entire article to learn about units of length conversion chart, unit of mass and weight conversion chart, unit of time conversion chart, units of capacity and volume conversion chart, unit of a temperature conversion chart, etc. Math Conversion Charts are quite important and interesting to learn.

What is Conversion of Units?

Depending on the Situation each unit differs. For instance, the area of the room is expressed in Meters whereas the thickness of the pencil is expressed in mm. Thus, it is necessary to convert from one unit to another.

Importance of Mathematical Conversions

In Order to have accuracy and avoid confusion in measurement, we need to change from one unit to another. For example, we will measure the length of the pencil in cm but no in km. Likewise, we need to convert from one unit to another. While converting from one unit to another of the same quantity we use multiplicative conversion factors. Let’s see how to convert different units of length and mass in the later modules.

Length Conversion Chart

Mass Conversion Chart

Unit Conversion Table

Length Conversion Table

Mass Conversion Table

Capacity Conversion Table

Points to remember:

• To convert bigger units to smaller units multiply
• To convert smaller units to bigger units divide

Solved Examples on Conversion of Units

1. Convert 4 cm to km?

Solution:

Step 1:

Draw a line or box as below

Step 2:

Put 1 at the larger unit to be converted.

Here we want to convert cm to km,

Since km is the larger unit, thus put 1 under the corresponding column (km).

Step 3:

Now place 0 till the smaller unit

Since the conversion is from a smaller unit to larger we need to divide the given length by 100000 i.e. 10⁵

4 cm = 4/10⁵

= 0.00004 km

2. Convert 7 gms to milligrams?

Solution:

We need to convert grams to milligrams

We know 1 gram = 1000 mg

Thus 7 g = 7*1000

= 7000 mg

In Geometry Topics, the most commonly solved topic is Rotations. A Rotation is a circular motion of any figure or object around an axis or a center. If we talk about the real-life examples, then the known example of rotation for every person is the Earth, it rotates on its own axis. However, Rotations can work in both directions ie., Clockwise and Anticlockwise or Counterclockwise. 90° and 180° are the most common rotation angles whereas 270° turns about the origin occasionally.

Here, in this article, we are going to discuss the 90 Degree Clockwise Rotation like definition, rule, how it works, and some solved examples. So, Let’s get into this article!

90 Degree Clockwise Rotation

If a point is rotating 90 degrees clockwise about the origin our point M(x,y) becomes M'(y,-x). In short, switch x and y and make x negative.

Rule of 90 Degree Rotation about the Origin

• When the object is rotating towards 90° clockwise then the given point will change from (x,y) to (y,-x).
• When the object is rotating towards 90° anticlockwise then the given point will change from (x,y) to (-y,x).

Solved Examples:

Example 1:

Solve the given coordinates of the points obtained on rotating the point through a 90° clockwise direction?

(i) A (4, 7)

(ii) B (-8, -9)

(iii) C (-2, 8)

Solution:

When the point rotated through 90º about the origin in the clockwise direction, then the new place of the above coordinates are as follows:

(i) The current position of point A (4, 7) will change into A’ (7, -4)

(ii) The current position of point B (-8, -9) will change into B’ (-9, 8)

(iii) The current position of point C (-2, 8) will change into C’ (8, 2)

Example 2: 

Let P (-6, 3), Q (9, 6), R (2, 7) S (3, 8) be the vertices of a closed figure. If this figure is rotated 90° about the origin in a clockwise direction, find the vertices of the rotated figure.

Solution:

Given vertices are P (-6, 3), Q (9, 6), R (2, 7) S (3, 8)

Now, we will solve this closed figure when it rotates in a 90° clockwise direction,

In step 1, we have to apply the rule of 90 Degree Clockwise Rotation about the Origin

(x, y) → (-y, x)

Next, find the new position of the points of the rotated figure by using the rule in step 1.

(x, y) → (y, -x)

P (-6, 3) → P'(3, 6)

Q (9, 6) → Q’ (6, -9)

R (2, 7) → R'(7, -2)

S (3, 8) → S'(8, -3)

Finally, the Vertices of the rotated figure are P'(3, 6), Q’ (6, -9), R'(7, -2), S'(8, -3).

Example 3:

Find the new position of the given coordinates A(-5,6), B(3,7), and C(2,1) after rotating 90 degrees clockwise about the origin?

Solution:

Given Coordinates are A(-5,6), B(3,7), and C(2,1)

The rule/formula for 90 degree clockwise rotation is (x, y) —> (y, -x). 

After applying this rule for all coordinates, it changes into new coordinates and the result is as follows:

A(-5,6) –> A'(6,5)

B(3,7) –> B'(7,-3)

C(2,1) –> C'(1,-2)

I believe that the above graph clears all your doubts regarding the 90 degrees rotation about the origin in a clockwise direction. At last, the result of the coordinates is A'(6,5), B'(7,-3), C'(1,-2). 

FAQs on 90 Degree Clockwise Rotation

1. Is a 90 Degree rotation clockwise or counterclockwise?

Considering that the rotation is 90 Degree, you should rotate the point in a clockwise direction.

2. What are the types of rotation?

You can see the rotation in two ways ie., clockwise or counterclockwise. In case, there is an object which is rotating that can rotate in different ways as shown below:

• 90 degrees counterclockwise
• 90 degrees clockwise
• 180 degrees counterclockwise
• 180 degrees clockwise

3. What is the rule of Rotation by 90° about the origin?

The rule for a rotation by 90° Counterclockwise about the origin is (x,y)→(−y,x)

The rule for a rotation by 90° Clockwise about the origin is (x,y)→(y,−x)

Solving the Profit and Loss Questions can give you an idea of how to solve related problems. Know different methods and formulae involved to calculate the Profit and Loss. Try to solve the Profit and Loss Questions on your own and then verify your solution with ours to know where you went wrong. By solving them regularly you can increase your speed and accuracy thereby attempt the exam well and score better grades in the exam.

Question 1:

If the manufacturer gains 15%, the wholesale dealer gets 20% and the retailer gets 30%, then find the cost of production of a blackboard, the retail price of which is $ 1360?

Solution:

Cost of production of blackboard be ‘X’

115% of 120% of 130% of cost price is

i.e. \(\frac { 115 }{ 120 } \)*\(\frac { 120 }{ 100 } \)*\(\frac { 130}{ 100} \)*1360

Cost of production of a blackboard $ 758.08

Question 2:

A man bought a dog and a kennel for $ 4500. He sold the dog at a gain of 25% and the carriage at a loss of 15%, thereby gaining 3% on the whole. Find the cost of the dog.

Solution:

Cost price (C.P.) of dog ‘X’

Cost price (C.P.) of kennel ‘4500 – X’

25% of x – 15% of (4500 – X) = 3% of 4500

Cost of a dog is $ 1373.68.

Question 3:

Profit earned by selling television for $ 6000 is 25% more than the loss incurred by selling the article for $ 4500. At what price should the article be sold to earn 25% profit?

Solution:

let cost price (C.P.) be ‘X’

By equalizing,

(6000 – X) = \(\frac { 125 }{ 100 } \)*(X-4500)

Desired selling price of the television is $ 6458.3.

Question 4:

A manufacturer undertakes to supply 2200 pieces of a particular component at $ 30 per piece. According to his estimates, even if 6% fail to pass the quality tests, then he will make a profit of 30%. However, as it turned out, 60% of the components were rejected. What is the loss to the manufacturer?

Solution:

Incurred cost = $(\(\frac { 100 }{ 130 } \)*30*(94% of 2200))

Loss = C.P. – S.P.

The loss to the manufacturer is $ 8123.07.

Question 5:

John bought a lorry for a certain sum of money. He spent 15% of the cost on repairs and sold the lorry for a profit of $ 1600. How did he spend on repairs if he made a profit of 30%?

Solution:

Let the Cost price (C.P.) of the lorry be ‘X’

Profit (P) = $16,00

Profit (%) = 30

Profit (%) = \(\frac { 100 }{ CP } \)*P

30 = \(\frac { 100 }{ CP} \)*1600

CP = \(\frac { 100 }{ CP} \)*1600

CP = \(\frac { 100 }{ 30} \)*1600

= $5333.3

The C.P Includes both original price and repairs cost

C.P +0.15C.P = $5333.3

1.15 C.P = $5333.3

C.P = $4637.68

Repairs Cost = Total Cost Price – Cost Price for which john bought the lorry

= $5333.3 – $4637.68

= $ 695.61

Expenditure spend on repairs = $ 695.61.

Question 6:

A boy bought 25 litres of milk at the rate of $ 12 per litre. He got it churned after spending $ 15 and 7kg of cream and 25 lit of toned milk were obtained. If he sold the cream at $ 40 per kg and toned milk at $ 6 per lit, what is his profit % in the transaction?

Solution:

Cost price (C.P.) = $ ((25*12) + 15)

Selling price (S.P.) = $ ((7*40) + (25*6))

Gained profit % on the above transaction is 36.50%.

Question 7:

Arun purchased 150 reams of paper at $ 90 per ream. He spent $ 300 on transportation, paid local tax at the rate of 50 paise per ream, and paid $ 76 to coolie. If he wants to have a gain of 10%, what must be the selling price per ream?

Solution:

Total investment = $ (((150*90) + 300) + ((50/100 * 150) + 76))

Find selling price per ream

Selling price per ream = $ 102.3

Question 8:

A retailer mixes three varieties of dal costing $ 50, $ 25, and $ 30 per kg in the ratio 3: 5: 2 in terms of weight, and sells the mixture at $ 35 per kg. What percentage of profit does he make?

Solution:

Cost price (C.P.) of dal for 10 kgs = $ ((3*50) + (5*25) + (2*30))

Selling price for 10 kgs = $ (10*35)

Profit percentage on transactions is 4.74%.

Question 9:

A man buys chocolates at 3 for $ 2 and an equal number at 5 for $ 3 and sells the whole at 6 for $ 4. His gain or loss percent is?

Solution:

Suppose he buys 7 eggs of each kind

Find C.P. and S.P. for 14 eggs

C.P. = $ ((\(\frac { 2 }{ 3 } \) * 7) + (\(\frac { 3 }{ 5 } \) * 7)) = $ 8.86

Similarly, find S.P.

The gain % obtain is 5.34%.

Question 10:

The manufacturer of a certain item can sell all he can produce at the selling price of $ 65 each. It costs him $ 45 in material and labor to produce each item and he has overhead expenses of $ 3500 per week in order to operate the plant. The number of units he should produce and sell in order to make a profit of at least $ 1200 per week is?

Solution:

Consider he produces ‘x’ items

Cost price (C.P.) = $ (45x + 3500)

Selling price (S.P.) = $ 65x

The number of units produced per week to gain profit is 235.

Get the complete practice test questions and worksheet here. Follow the step by step procedure to solve examples on the division of integers all the problems. Know the shortcuts, tricks, and steps involved in solving Division of Integers problems. Also, find the definitions, formulae before going to start the practice sessions. Go through the below sections to know the detailed information regarding formulas, definitions, and problems.

Integers Division Rules

Rule 1: The quotient value of a positive integer number and a negative integer number is negative.

Rule 2: The quotient value of two positive integer numbers is a positive number.

Rule 3: The quotient value of two negative integer numbers is a positive number.

Division of Integers Rules and Examples

Question 1: Find the value of ||-17|+17| / ||-25|-42|

Solution:

||-17|+17| / ||-25|-42|

= |17+17| / |25–42|

= |34| / |-17|

= 34 / 17

= 2

Question 2: Simplify: {36 / (-9)} / {(-24) / 6}

Solution:

{36 / (-9)} / {(-24) / 6}

= {36/-9} / {-24/6}

= – (36/9) / – (24/6)

= -4/-4

= 4/4

=1

Question 3: Find the value of [32 + 2 x 17 + (-6)] ÷ 15

Solution:

[32+2 x 17+(-6)] / 15

= [32+34+(-6)] / 15

= (66-6) / 15

= 60 / 15

= 4

Question 4: Divide the absolute values of the two given integers?

Solution:

The quotient of the absolute value of integer +24 and the absolute value of integer -8

From the rules given above, dividing the integers with different signs gives the final result as negative.

When positive(+) 24 is divided by negative(-) 8 results negative(-) 3, which can be defined as +24/(-8) = -3

Question 5: Prove that [((-8) / (-4)] ≠ =-8 / [(-4) / (-2)]

Solution:

From the given question

[((-8)/(-4)]/(-2)] ≠ -8/[(-4)/(-2)]

First of all, we will consider the LHS part i.e., [((-8) / (-4)] / (-2)]

To solve the equation, first, we divide 8 by 4, we get the result as 2

As both numbers have a negative sign, it will be positive.

Then we divide the result (2) by -2, then the final result will be -1.

Therefore, the result of the LHS part is -1.

Now, we consider the RHS part i.e., -8 / [(-4) / (-2)]

First of all, we divide -4 by -2, the result will be 2.

As both the numbers have a negative sign, the result will be positive.

Now, divide -8 by the above result 2.

Hence, the result will be -4.

Therefore, the result of RHS is -4.

Hence, LHS ≠ RHS

The above given equation [((-8) / (-4)] / (-2)] ≠ -8 / [(-4) / (-2)] is thus satisfied.

Question 6: In a maths test containing 10 questions, 2 marks are given for every correct answer and (-1) marks are given for every wrong answer. Rohith attempts all the questions and 8 questions answers are correct. What is Rohith’s total score?

Solution:

From the given question,

The marks given for every correct answer = 2 marks

Marks given for 8 correct answers = 2 * 8= 16 marks

Marks given for 1 incorrect answer = -1 marks

Marks given for 2 incorrect answers = -1 * 2 = -2 marks

Rohit’s total score = 16-2 = 14 marks

Therefore, the answer is 14 marks.

Question 7: Priya sells 20 pens and some pencils losing 2 Rs in all. If Priya gains 2 Rs on each pen and loses 1 Rs on each pencil. How many pencils does Priya sell?

Solution:

Suppose that Priya sells x pencils.

Total gain on pens = 2*20 = 40 Rs

Total loss on pencils = 1x = x

Total loss on selling pens and pencils = (-2)

40-x = (-2)

40+2 = x

x = 42

Therefore, Priya sells 42 pencils.

Thus, the answer is 42 pencils.

Question 8: To make ice cream, the room temperature must be decreased from 45degree C at the rate of 5 degrees C per hour. What will be the room temperature 12 hours after the freezing point of the icecream?

Solution:

As given in the question,

Temperature after 12 hours = 12*5 = 60degree C

Room temperature = 45degree C

Hence, the room temperature after freezing process of 12 hours = (45-60)degree C

= -15degree C

Question 9:

A car runs at a rate of 50km/hr. If the car starts at 5 km above the starting point, how long will it take to reach 2505km?

Solution:

As per the question,

Total distance covered by car = (2505-5) km = 2500 km

Rate of car = 50km/hr

From the above values, Distance = 2500 km, speed = 50 km/hr

Therefore, the time required by the car = distance/speed

=2500/50 = 50 hours

Therefore, the car will take 50 hours to travel 2505 km.

Hence, The final solution is 50 hours.

Question 10: Jason borrowed $5 a day to buy launch. She now owes $65 dollars. How many days did Jane borrow $5?

Solution:

As per the question,

Jason borrowed a launch at =  $5

Now she owes = $65

No of days = (-65) / (-5)

= 13 days

Therefore, Jane borrows $5 for 13 days.

Hence, The final solution is 13 days.

Division of Integers Word Problems

Question 11: Allen’s score in a video game was changed by -120 points because he missed some target points. He got -15 points for each of the missed targets. How many targets did he miss?

Solution: 

As per the given question,

Allen scored points in a video game = -120

He got points for missed targets = -15

No of targets he missed = -120/-15 = 8 targets.

Therefore, he missed 8 targets.

Question 12: Karthik made five of his truck payments late and was fined five late fees. The total change in his savings of late fees was -$30. What integer represents the one late fee?

Solution:

As given in the question, Karthik has made five of his truck payments. Therefore, it is positive.

He was fined -$30 as the late fees.

To find one late fee, we have to divide the fine by no of payments he did.

Therefore, One Late fee = -$30/5

=-$6

Thus, He paid $6 for each payment as late fees.

Hence, the final answer is -$6.

Do you find it difficult to understand the Integers Multiplication? Here is the best solution for you all. We are providing Examples on Multiplication of Integers here. Integers Multiplication is an important concept which helps you to score more marks in the exam. Questions on Multiplication of Integers with Answers are available so that you can practice them regularly. Learn How to Multiply Integers by referring to the further modules.

Worked out Multiplication of Integers Problems

Before going to solve the Integers Multiplication problems, know all the definitions, rules, formulae etc. In the upcoming sections, you will find all the details and also problem-solving techniques and tips. To be more precise, you can only solve the problems if you know all the details regarding integers.  Know various properties of integers beforehand and how they work while multiplying the integers.

Key Points to Remember on Properties of Integers Multiplication

• The Closure Integer Property of multiplication defines that the product value of two or three integer numbers will be an integer number.
• The commutative Integer Multiplication property defines that swapping two or three integers will not differ the value of the final result.
• The associative Integer Multiplication property defines that the grouping of integer values together will not affect the final result.
• The distributive Integer property of multiplication defines that the distribution concept of 1 operation value on other mathematical integer values within the given braces.
• Multiplication by zero defines the product value of any negative or positive integer number by zero
• Multiplicative Integer defines the final result as 1 when any integer number is multiplied with 1.

Integer Multiplication Rules on Problems

Question 1:

The temperature in an area drops by 4 degrees for 4 hours. How much is the total drop in the temperature?

Solution:

As given in the question, the temperature drops by 4 degrees. Therefore, the temperature is a negative factor.

Also. given that it decreases for 4 hours.

The total drop in temperature is (-4) * (4) = -16

Therefore, the total drop in temperature is 16 degrees C

Thus, the final result is -16 degree C

Question 2:

Jason borrowed $2 a day to buy a launch. She now owes $60. How many days did Jason borrow $2?

Solution:

As given in the question, Jason borrowed to buy a launch = $2

After buying she owes $60

No of days Jason borrowed money = 60/2 = 30

Therefore, the total days = 30 days

Thus, the final result is 30 days.

Question 3: A football team 12 yards on each of the four consecutive plays. What was the team’s total change in position for four plays?

Solution: 

As given in the question, A football team lost yards = -12 yards

No of plays = 4

Team total change in position for 4 plays = (-12) * (4) = 48

Therefore, the total change = -48 yards

Thus, the final answer is -48 yards.

Question 4: On a certain day, the temperature changed at a rate of -2 degrees F per hour. If this happened for continuous 5 days. For how many days there was a change in temperature?

Solution:

As per the given question, The temperature changed at the rate = -2 degree F

The change happened for days = 5 days

No of days there was a change = (-2)*5 = -10

Therefore, there was a change for days = 10 days

Thus, the final solution is 10 days.

Question 5: Flora made 6 deposits $ 7 each from her bank account. What was the overall change in her account?

Solution:

As per the given question,

Flora made no of deposits = 6

Amount of deposited money = $7

The overall change in the account = 6 * ($7) = 42

Therefore, the change in money = 42

Thus, the final solution is $42

Questions on Multiplication of Integers

Question 6: A winter coat was priced at $200. Each month for three months, the price was reduced by $15. How much was the coat reduced in price?

Solution:

As per the given question,

The price of the winter coat is reduced by $15, Therefore it is negative = -$15

No of times it is reduced = 3

The absolute values of |3| and |-15| are 3 and 15

The coat reduced in price = 3*15 = 45

Therefore, the total change in price = $45

Thus the final answer = -$45

Question 7:

Netflix charges $9 per month for their streaming plan to watch movies. If they automatically bill a customer for 6 months, How much will be deducted from the customer’s bank account?

Solution:

As per the given question,

Netflix charges $9 per month. Therefore, it is negative.

Given, the bill will be deducted automatically for months = 6

The absolute values of |6| and |9| are 6 and 9.

The amount of money deducted from customers bank account = 6*9 = 54

Therefore, the total amount after determining the signs = -$54

Hence, the final solution is -$54

Question 8: Lisa decided her hair was too long. In June and again in July. she cut 3 inches off. Then, in August, September, and October she cut off 2 inches. Write an equation to represent the change in the length of her hair?

Solution:

As given in the question,

In 2 months, she cut 3 inches off her hair. Cutting her hair made the length shorter, therefore it is negative.

In 3 months, she cut 2 inches off her hair. This is also negative.

For the month of June and July, the length of the hair she cut = 2 * (-3) = -6

For the months August, September, and October, the length of the hair she cut = 3 * (-2) = -6

Therefore, the total length = (-6) + (-6) = -12 inches

Thus. the complete length she cut = 12 inches

Hence, the final solution is -12 inches

Question 9: The depth of the water in a pool decreases an average of two inches each week during the summer. What will be the change in the depth of water of four weeks?

Solution:

As given in the question,

The depth of the water in a pool decreases each week = 2 inches

As the water level decreases, it will be negative.

The decrease in water for weeks = 4

The change in depth of water = (-2)*4 = -8

Therefore, the water level decreases by 8 inches.

Thus, the final solution is -8 inches

Question 10:

For every 1000 feet, you gain in elevation, the temperature drops by 3 degrees. If you increase your elevation by 5000 feet, How would the temperature change?

Solution:

As per the given question,

The temperature drops by 3 degrees. Therefore, it will be negative.

Also given for every 1000 feet it is 3 degrees. Thus for every 5000 feet, it is 5 degrees.

The temperature change = (-3)*5 = -15

Thus, for every 5000 feet, the temperature changes by -15 degrees.

Hence, the final solution is -15 degrees.

Wanna start your preparation from basics? Then here is the most basic and important concept. Learn all the Fundamental Operations and their usage in day to day life. Solve all the important problems involved in fundamental algebra operations. Know the definitions, rules, strategies, tips, tricks, and problems. Refer to the upcoming sections to get more information regarding mathematical expressions and operations.

Fundamental Operations – Introduction

Fundamental Operations are the basic concept to solve any type of problem. We perform the operations at one time and generally, it starts from the left towards the right. If the expression contains more than 1 fundamental operation, then you can’t perform them in the order they appear in the question. There are certain rules to follow to perform various operations when more than 1 fundamental value is available. The precedence order has to be followed to solve the Fundamental Operation. The precedence order will be shown in the below sections.

Order of Expression – DMAS Rule

The fundamental operations are expressed in an order. Generally, the order will be in the format of “DMAS” where “D” stands for “Division”, “M” stands for “Multiplication”, “A” stands for “Addition”, “S” stands for “Subtraction”. This order is considered and sequentially performed from left to right.

As there are fundamental operations in arithmetic, there are in a wat that three pairs of arithmetic operations, and for each pair of operations is the reversal of co-operation within the pairs. As addition and subtraction are reverse operations of each other. It is similar for other operations too. In regard to Algebra, everyone must understand that it is a set of rules based on fundamental operations which helps for faster calculations and an easy approach for variable problem-solving.

Basic Fundamental Operations to Simplify Mathematical Expressions

Addition

The addition is defined by the operator (+). It is the fundamental operation of the arithmetic operators. It implies the combination of distinct quantities or sets. It involves counting numbers from one to one by incrementing the values. The result value after adding all the numbers is called the “sum”. The numbers and the initial number are called addends.

The addition of natural numbers involves 2 important properties i.e., associativity and commutativity.

Addition Operation on Positive and Negative Integers

Positive (+) + Positive (+) = Positive (+)
Negative (-) + Positive (+) = Negative (-)
Positive (+) + Negative (-) = Sign of the largest Number
Negative (-) + Positive (+) = Sign of the largest number

Examples:
5+4 = 9
(-5) + (-4) = -9
(-5) + 4 = -1
4 + (-5) = -1
(-4) + 5 = -1
5 + (-4) = 1

Example Problem:

An empty water tank of 8 feet high is available. A monkey is sitting at the bottom of that tank. The monkey tried jumping to the top of the tank. While jumping it jumps 3 ft up and slides down to 2 ft. How many jumps will the monkey take to reach the top of the water tank?

Solution:

As per the given question,

Monkey’s first jump = 3 ft up and 2 ft down

= (+3)-2=1

2nd Jump of the Monkey = 3 ft up and 2 ft down = (1+3) = 4

= (+4)-2=2

Therefore, the monkey covers 2 ft after the 2nd jump

3rd Jump of the Monkey = 3 ft up and 2 ft down = (2+3) = 5

=(+5)-2 = 3

Therefore, the monkey covers 3 ft after the 3rd jump

4th Jump of the Monkey = 3 ft up and 2 ft down = (3+3) = 6

=(+6)-2 = 4

Hence, the monkey covers 4 ft after the 4th jump

5th Jump of the Monkey = 3 ft up and 2 ft down = (4+3)=7

=(+7)-2 = 5

Therefore, the monkey covers 5 ft after the 5th jump.

6th Jump of the Monkey = 3 ft up = (5+3) = 8

As the water tank is 8 feet high, the monkey will reach the top of the water tank in the 6th jump.

Subtraction

The subtraction is defined by the operator (-). Subtraction is the inverse property of addition. It means that removing one quantity from another quantity. It involves incrementing down from the given number. The result value after subtracting all the numbers is called the “difference”. The number from which other number is subtracted is called subtrahend. The subtracted number is called minuend.

Subtraction Operation on Positive and Negative Integers

Negative (-) – Positive (+) = Negative (-)
Positive (+) – Negative (-) = Positive (+)
Negative (-) – Negative (-) = Sign of the largest Number
Negative (-) + Positive (+) = Sign of the largest number

Examples:

(-5)-4 = (-5) + (-4) =- 9
5 – (-4) = 5 +4 = 9
(-5) – (-4) = (-5) + 4 = -1
(-4) – (-5) = (-4) + 5 = 1

Example Problem:

At a height of 3000 feet above sea level, a plane is flying. At some time, there is a submarine that is exactly above and floating 700 feet below sea level. Calculate the vertical distance using the concept of subtraction of integers?

Solution:

Height of the plane that is flying = 3000 feet

Depth of the submarine = -700 feet ( It is negative, as it is below the sea level).

To calculate the vertical distance, we use the subtraction of integers operation.

3000-(-700) = 3000 + 700 = 3700 feet

Therefore, the vertical distance is 3700 feet.

Multiplication

The multiplication is defined by the operator (“x” o “*”). Multiplication is the repeated property of addition. It means that a particular number is being repeatedly added to itself several times. It involves adding the number with the same number. The result value after multiplying all the numbers is called the “product”. The number to which another number is multiplied is called multiplicand. The multiplied number is called a multiplier.

Multiplication Operation on Positive and Negative Integers

Negative (-) x Positive (+) = Negative (-)
Positive (+) x Negative (-) = Negative (-)
Negative (-) x Negative (-) = Negative (-)
Positive (+) + Positive (+) = Positive (+)

Examples:

5×4 = 12

(-3) x (-4) = 12

(-3) x 4 = – 12

3 x (-4) = -12

Example Problems:

The submarine descends 40 feet per minute from sea level. Find the relation of the submarine with the sea level 5 minutes after it starts descending?

Solution:

The submarine below sea level =40 feet

As it is below sea level, it is negative. Therefore, it is -40.

After 5 minutes, the submarine is at = -40 x 5 = -200 feet

Therefore, the final solution is -200 feet.

Division

The division is defined by the operator (÷). The division is the inverse property of multiplication. It means that a particular number or quantity is split into equal or the same parts. It involves the splitting of numbers in the same proportions. The result value after dividing the numbers is called the “quotient”. The original number is called “dividend”. The number which is used for dividing into groups is called “divisor”. The final result is “quotient”.

Division Operation on Positive and Negative Integers

Negative (-) ÷ Positive (+) = Negative (-)

Positive (+) ÷ Negative (-) = Negative (-)

Negative (-) ÷ Negative (-) = Positive (+)

Positive (+) ÷ Positive (+) = Positive (+)

Examples:

20÷4 = 5

(-20)÷(-4) = 5

(-20) ÷ 4 = -5

20÷(-4) = -5

Example Problem:

In a living room, there are 120 books in total and they are placed on 6 shelves. Consider that each shelf has an equal number of books, Calculate the number of books on each shelf?

Solution:

As per the given question,

The total no of books = 120

No of seats placed on shelves = 6

To determine the number of books on each shelf = 120/6 =20

Therefore, the number of books on each shelf = 20 books.

Thus the final solution is 20 books.

Practice Test on Parallelogram will help you to test your knowledge. Answer on your own for every question given below. Before you take the practice test, make sure you have read the concept completely and solved all problems. It becomes easy if you have a perfect grip on the entire concept. Also, it will avoid you to confuse while choosing the answers. Complete concept and Objective Questions on Parallelogram are given on our website for free of cost.

Tick (✔) the correct answer in each of the following

1. From the given options, which parallelogram two diagonals are not necessarily equal ………………..

(a) square
(b) rectangle
(c) isosceles trapezium
(d) rhombus

2. A rhombus has diagonals of 16 cm and 12 cm. Find the length of each side?

(a) 8cm
(b) 12cm
(c) 10cm
(d) 9cm

3. Two adjacent angles of a parallelogram are (4b + 15)° and (2b – 10)°. The value of b is ………………. .

(a) 29.16
(b) 32
(c) 42
(d) 36

4. From the given options, which parallelogram two diagonals do not necessarily intersect at right angles ………………..

(a) rhombus
(b) rectangle
(c) kite
(d) parallelogram

5. The length and breadth of a rectangle are in the ratio 8 : 6. If the diagonal measures 50 cm. Find the perimeter of a rectangle?

(a) 800 cm
(b) 700 cm
(c) 600 cm
(d) 560 cm

6. The bisectors of any two adjacent angles of a parallelogram intersect at ………………..

(a) 90°
(b) 30°
(c) 60°
(d) 45°

7. If an angle of a parallelogram is 2/3 of its adjacent angle find the angle of a parallelogram.

(a) 72°
(b) 54°
(c) 108°
(d) 81°

8. The diagonals do not necessarily bisect the interior angles at the vertices in a ………………..

(a) square
(b) rectangle
(c) rhombus
(d) all of these

9. In a square PQRS, PQ = (3a + 5) cm and RS = (2a – 2) cm. Find the value of a?

(a) 4
(b) 5
(c) 7
(d) 8

10. If one angle if a parallelogram is 24º less than twice the smallest angle then the largest angle if parallelogram is?

(a) 68°
(b) 112°
(c) 102°
(d) 176°

Uses of Brackets are given here. Find the various uses and types of brackets. Before knowing the complete details regarding the brackets, know the fundamental operations like addition, subtraction, multiplication, and division. Know the history, rules, and precedence order of brackets. Go through the below sections to know the complete details regarding the usage of brackets.

History of Brackets

The word bracket is derived from the French word “Braguette” which the “piece around”. Anything that is written in brackets is defined as the piece of that bracket. Most brackets are used to enclose notes, references, explanations, etc. which are called crotchets as per the typographical brackets. Later, brackets were used as the group bracketed together for equal standing in some of the graded systems which are mostly used for sports brackets.

Brackets Usage

Mathematical brackets are known as symbols and parentheses which are most often used to create groups or that which clarify the order in which operations are to be done in the given algebraic expression.

Brackets symbol             Name

            ( )                         Parentheses or common brackets

            { }                        Braces or Curly brackets

            [ ]                         Brackets or square brackets or box brackets

             _                          Vinculum

The Left Part of the Bracket indicates the start of the bracket and the right part indicates the end of the bracket.

While Writing mathematical expressions having more than one bracket, parenthesis is used in the innermost part followed by braces, and these two are covered by square brackets. You need to know about the Uses of brackets to perform a  set of operations prior to the others.

Types of Brackets, Braces, Paranthesis in Math

Mathematical brackets are used for grouping. These brackets can include:

• ( )
• [ ]
• { }

In the grouping of numbers, brackets come in pairs. There will be a pair of sets i.e., the opening bracket and a closing bracket. Brackets are generally used to give clarity in the order of operations.

Suppose that there is an expression: 3+5*7-2. You cannot understand which operation to perform at the beginning. Therefore, we include brackets to understand the precedence of operations. If the problem is given as (3+5)*(7-2) = 8*5 = 40.

In the above problem, the parentheses will tell you the usual order of operations and will give you visual clarity.

“( ) Brackets”

The symbols “(” “)” are known as parentheses. These are called Brackets or Round Brackets. They are called Round Brackets as they are not curly or square braces. The input of the function is enclosed in parentheses. Parenthesis means “to put beside” in Geek language. Things like additional information, asides, clarifications, citations are defined by Paranteseis. Any type of information written in parentheses can be as short as a word or number or a few sentences. If something is given in parenthesis, then that sentence must have the capability of standing on its own.

Example: The little puppy (Rocky) skipped across the garden to her mother.

“Square Brackets [ ]”

The square brackets are denoted inside the parentheses to define something to the sub-ordinate clause. Square brackets are defined by the symbol “[ ]”. The main purpose of using square brackets is writing in the conjunction or to insert a name or word for clarification.

Square brackets are needed to add clarifications.

Example: She [Rosy] hit the policeman

They are also used to add additional information

Example: Two teams in the FIFA football final match were from South America [ Argentina and Uruguay]

Missing words can also be added with the help of square brackets.

Example: It is [a] good answer.

Authorial Comments or editorial can also be added using square brackets.

Example: There are not present [my emphasis]

Square brackets are also used to modify the direct quotation.

Example: The direct quotation is “I love traveling” which can be modified as ” He love[s] traveling”.

These can also be used for nesting.

Example: (We use square brackets [in this way] inside the round brackets).

“Curly Brackets { }”

Mostly curly brackets are not used for general purposes. They are mostly used in programming or math concepts. They are mainly used to hold terms or terms and hold a list of items.

Example:

3{2+[5(3+1)+4]}

This is the example of lists

Example of programming languages:

$value=0;

do{

$value++;

if ($value >=20)

{

Print(“Value is equal to or greater than 10. Ending.”);

exit;

}

}

until ($value >=200);

Curly brackets can also be used in sets in mathematics.

Grouping of numbers resembles Sets.

Example: {1,2,4,6,9}

Difference between ( ) and [ ] in math

Square brackets [ ] are used for commands whereas parenthesis or round brackets represent braces and to describe some special words.

Multiple Level of Grouping

If you planning for an equation, then grouping within other grouping is a little bit confusing. To avoid that confusion, we use various brackets and group the numbers with order precedence. If we are using the brackets, then we can define the level of operations within the equation.

Example:

2 + {1+[2+3*(5+4)]}

In the above example, first, we go for the inner calculations.

Therefore, first, we have to go for the grouping of (5+4) = 9

Then, we go for the multiplication of 3 and 9 i.e., 18

For the next order, we go for the addition of 3 with 18, the result will be 21.

The next precedence will be the addition of 1 and 21, the result will be 22.

Then, we go for the last grouping of 2 and 22, Therefore, the result of the addition is 24.

With the above example, it is clear that finding a way of solving the equation will be easy.

Questions on How to Use Brackets

Problem 1:

Simplify the expression : [(3*2) + (4*5)]/(7-3)

Solution:

Start solving the problem by simplifying the equation that is inside the parentheses i.e., 4 *5 = 20

Then, solve the equation of other parentheses, i.e., 3 * 2 = 6

Then simplify the equation within the square brackets i.e., [6 + 20]= 26

Now, solve the equation outside the parenthesis i.e., 7-3 = 4

Now finish the division of the two values = 26/4 = 6.5

Therefore, the final solution is 6.5

Problem 2:

Simplify the equation, [(3+2)*4 – (5*6)]/[1-(3+4)*2]

Solution:

Start solving the problem by simplifying the equation inside the parenthesis i.e., 5 *6 = 30

Then, solve the equation (3+2)*4 = %*4 = 20

Then, go for the next equation of 3+4 = 7, 7*4 = 28

Now, go for the other equation in the brackets i.e., 5*6=30

The second part of the equation is 3 + -7, then 7*2 = 14

Now, solve the equation of 1-14 = -13

Finally, divide the values -10/-13 = 0.769

Therefore, the final solution is -0.769

Thus, the three types of brackets are helpful for solving various equations. Check all the uses and importance of using the brackets and also know the preceding order.

Depending upon the length and angles, quadrilaterals are classifieds in different ways. Let us check Different Types of Quadrilaterals and their definition, properties along with their diagrams. A quadrilateral can be explained using the below properties

• The sum of the interior angles is 360 degrees in a quadrilateral.
• A quadrilateral consists of 4 sides and 4 vertices, and also 4 angles.
• The sum of the interior angle from the formula of the polygon using (n – 2) × 180 where n is equal to the number of sides of the polygon.

The main types in a quadrilateral are squares and rectangles, etc., with the same angles and sides.

Various Types of Quadrilaterals

Mainly quadrilaterals are classified into six types. They are

1. Parallelogram
2. Rhombus
3. Rectangle
4. Square
5. Trapezium
6. Kite

Parallelogram

A quadrilateral is said to be a parallelogram when it has two pairs of parallel sides and opposite sides are parallel and equal in length. Also, the opposite angles are equal in a parallelogram. Let us take a parallelogram PQRS, then the side PQ is parallel to the side RS. Also, the side PS is parallel to a side QR.

Two diagonals are present in the parallelogram and they intersect each other at a midpoint. From the figure, PR and QS are two diagonals. Also, the diagonals are equal in length from the midpoint.

PQ ∥ RS and PS ∥ QR.

Rhombus

Rhombus is a quadrilateral when all the four sides of a quadrilateral having equal lengths. In a rhombus, opposite sides are parallel and opposite angles are equal.

From the above figure, PQRS is a rhombus in which PQ ∥ RS, PS ∥ QR, and PQ = QR = RS = SP.

Rectangle

A quadrilateral is considered as a rectangle when all 4 angles of it are equal and each angle is 90 degrees. Also, both pairs of opposite sides of a rectangle are parallel and have equal lengths.

From the above figure, PQRS is a quadrilateral in which PQ ∥ RS, PS ∥ QR and ∠P = ∠Q = ∠R = ∠S = 90°.

So, PQRS is a rectangle.

Square

A square is a quadrilateral consists all the sides and angles are equal. Also, every angle of a square is 90 degrees. The pairs of opposite sides of a square are parallel to each other.

From the above figure, PQRS is a quadrilateral in which PQ ∥ RS, PS ∥ QR, PQ = QR = RS = SP and ∠P = ∠Q = ∠R = ∠S = 90°.

So, PQRS is a square.

Trapezium

A quadrilateral is called a trapezium when it has one pair of opposite parallel sides.

From the above figure, PQRS is a quadrilateral in which PQ ∥ RS. So, PQRS is a trapezium. A trapezium its non-parallel sides are equal is called an isosceles trapezium.

Kite

A quadrilateral is said to be a kite that has two pairs of equal-length sides and the sides are adjacent to each other.

From the above figure, PQRS is a quadrilateral. PQ = PS, QR = RS, PS ≠ QR, and PQ ≠ RS.

So, PQRS is a kite.

Important Points to Remember for Quadrilaterals

Look at some of the important points need to remember about a quadrilateral.

• A square is a rectangle and also it becomes a rhombus.
• The rectangle and rhombus do not become a square.
• A parallelogram is a trapezium.
• Square, rectangle, and rhombus are types of parallelograms.
• A trapezium is not a parallelogram.
• Kite is not a parallelogram.

Problems on Parallelogram are given in this article along with an explanation. It is easy to learn and understand the entire concept of a Parallelogram by solving every problem over here. There are various types of problems included according to the new updated syllabus. Get a good score in the exam and improve your preparation level immediately by working on your difficult topics.

1. Prove that any two adjacent angles of a parallelogram are supplementary?

Solution:
Let us take a parallelogram PQRS.

Then, PS ∥ QR and PQ is a transversal.
The sum of the interior angles on the same side of the transversal is 180°
Therefore, P + Q = 180°
Similarly, ∠R + ∠S = 180°, ∠Q + ∠R = 180°, and ∠S + ∠P = 180°.
Thus, the sum of any two adjacent angles of a parallelogram is 180°.

Hence, any two adjacent angles of a parallelogram are supplementary.

2. Two adjacent angles of a parallelogram PQRS are as 2 : 3. Find the measure of each of its angles?

Solution:
Let us take a parallelogram PQRS.

Then, ∠P and ∠Q are its adjacent angles.
Let ∠P = (2a)° and ∠Q = (3a)°.
The sum of adjacent angles of a parallelogram is 180°
Then, ∠P + ∠Q = 180°
⇒ 2a + 3a = 180
⇒ 5a = 180
⇒ a = 36.
Therefore, ∠P = (2 × 36)° = 72° and ∠Q = (3 × 36°) = 108°.
∠Q and ∠R are adjacent angles. By adding them, we get 180°
Also, ∠Q + ∠R = 180°
= 108° + ∠R = 180° [Since, ∠Q = 108°]
∠R = (180° – 108°) = 72°.
∠R and ∠S are adjacent angles and add up to 180°.
Also, ∠R + ∠S = 180°
⇒ 72° + ∠S = 180°
⇒ ∠S = (180° – 72°) 108°.

Therefore, ∠P = 72°, ∠Q = 108°, ∠R = 72°and ∠S = 108°.

3. In the adjoining figure, PQRS is a parallelogram in which ∠P = 75°. Find the measure of each of the angles ∠Q, ∠R, and ∠S.

Solution:
It is given that PQRS is a parallelogram in which ∠P = 75°.

Since the sum of any two adjacent angles of a parallelogram is 180°,
∠P + ∠Q = 180°
⇒ 75° + ∠Q = 180°
⇒∠Q = (180° – 75°) = 105°
∠Q and ∠R are adjacent angles and add up to 180º.
Also, ∠Q + ∠R = 180°
⇒ 105° + ∠R = 180°
⇒ ∠R = (180° – 105°) = 75°.
∠R and ∠S are adjacent angles
Further, ∠R + ∠S = 180°
⇒ 75° + ∠S = 180°
⇒ ∠S = (180° – 75°) = 105°.

Therefore, ∠Q = 105°, ∠R = 75° and ∠S = 105°.

4. In the adjoining figure, PQRS is a parallelogram in which ∠QPS = 75° and ∠SQR = 60°. Calculate:
(i) ∠RSQ and (ii) ∠PSQ.

Solution:
Let us draw a parallelogram PQRS.

We know that the opposite angles of a parallelogram are equal.
Therefore, ∠QRS = ∠QPS = 75°.
(i) Now, in ∆ QRS, we have
The sum of the angles of a triangle is 180°
∠RSQ + ∠SQR + ∠QRS = 180°
⇒ ∠RSQ + 60° + 75° = 180°
⇒ ∠RSQ + 135° = 180°
⇒ ∠RSQ = (180° – 135°) = 45°.
(ii) PS ∥ QR and QS are the transversals.
Therefore, ∠PSQ = ∠SQR = 60° [alternate interior angles]

Hence, ∠PSQ = 60°.

5. In the adjoining figure, PQRS is a parallelogram in which ∠RPS = 40°, ∠QPR = 35°, and ∠ROS = 65°.
Calculate: (i) ∠PQS (ii) ∠QSR (iii) ∠PRQ (iv) ∠RQS.

Solution:
(i) ∠POQ = ∠ROS = 65° (vertically opposite angles)
Now, from ∆OPQ, we can write as:
The sum of the angles of a triangle is 180°
∠OPQ + ∠PQO + ∠POQ =180°
⇒ 35°+ ∠PQO + 65° = 180°
⇒ ∠PQO + 100° = 180°
⇒ ∠PQO = (180° – 100°) = 80°
⇒ ∠PQS = ∠PQO = 80°.
(ii) PQ ∥ SR and QS is a transversal.
Therefore, ∠QSR = ∠PQS = 80° [alternate interior angles]
Hence, ∠QSR = 80°.
(iii) PS ∥ QR and PR is a transversal.
Therefore, ∠PRQ = ∠RPS = 40° [alternate interior angles]
Hence, ∠PRQ = 40°.
(iv) ∠QRS = ∠QPS = (35° + 40°) = 75° [opposite angles of a parallelogram]
Now, in ∆RQS, we have
The sum of the angles of a triangle is 180°.
∠QSR + ∠QRS + ∠RQS = 180°
⇒ 80° + 75° + ∠RQS = 180°
⇒ 155° + ∠RQS = 180°
⇒ ∠RQS = (180° – 155°) = 25°.
Hence, ∠RQS = 25°.

6. In the adjoining figure, PQRS is a parallelogram, PO and QO are the bisectors of ∠P and ∠Q respectively. Prove that ∠POQ = 90°.

Solution:
We know that the sum of two adjacent angles of a parallelogram is 180°
Therefore, ∠P + ∠Q = 180° ……………. (i)
Since PO and QO are the bisectors of ∠P and ∠Q, respectively, we have
∠OPQ = 1/2∠P and ∠PQO = 1/2∠Q.
From ∆OPQ, we have
The sum of the angles of a triangle is 180°
∠OPQ + ∠POQ + ∠PQO = 180°
⇒ ¹/₂∠P + ∠PQO + ¹/₂∠Q = 180°
⇒ ¹/₂(∠P + ∠Q) + ∠POQ = 180°
⇒ (¹/₂ × 180°) + ∠POQ = 180° [from equation (i)]
⇒ 90° + ∠POQ = 180°
⇒ ∠POQ = (180° – 90°) = 90°.

Hence, ∠POQ = 90°.

7. The ratio of two sides of a parallelogram is 5: 4. If its perimeter is 54 cm, find the lengths of its sides?

Solution:
Let the lengths of two sides of the parallelogram be 5a cm and 4a cm respectively.
Find the perimeter using given values.
Then, its perimeter = 2(5a + 4a) cm = 2 (9a) cm = 18a cm.
Therefore, 18a = 54 ⇔ a = 54/18 = 3.

Therefore, one side = (5 × 3) cm = 15 cm and other side = (4 × 3) cm = 12 cm.

8. The length of a rectangle is 16 cm and each of its diagonals measures 20 cm. Find its breadth?

Solution:
Let PQRS be the given rectangle in which length PQ = 16 cm and diagonal PR = 20 cm.

Since each angle of a rectangle is a right angle, we have
∠PQR = 90°.
From the right ∆PQR, we have
PQ² + QR² = PR² [From Pythagoras’ Theorem]
⇒ QR² = (PR² – PQ²) = {(20)² – (16)²} = (400 – 256) = 144

⇒ QR = √144 = 12 cm.

Hence, breadth = 12 cm.

9. In the below figure, PQRS is a rhombus whose diagonals PR and QS intersect at a point O. If side PQ = 20 cm and diagonal QS = 32 cm, find the length of diagonal PR.

Solution:
We know that the diagonals of a rhombus bisect each other at right angles.
Therefore, QO = ¹/₂QS = (¹/₂ × 32) cm = 16 cm, PQ = 20 cm and ∠POQ = 90°.
From right ∆OPQ, we have PQ² = PO² + QO²
⇒ PO² = (PQ² – QO²) = {(20) ² – (16)²} cm²
= (400 – 256) cm²
= 144 cm²
⇒ PO = √144 cm = 12 cm.

Therefore, PR = 2 × PO = (2 × 12) cm = 24 cm.

The quadrilateral is a figure formed by adding the four-line segments. It consists of 4 sides, 4 vertices, and two diagonals. By going through this entire article you will get a complete idea of Quadrilateral like Types, Sides, Angles, Vertices, Diagonals of it, its Properties etc. If P, Q, R, S are four points and where no three points are collinear and also the line segments PQ, QR, RS, and SP do not intersect at their endpoints. Check the below figure that is the quadrilateral PQRS.

In a quadrilateral PQRS
(i) The vertices in a quadrilateral are P, Q, R, S.
(ii) The sides of a quadrilateral are PQ, QR, RS, and SP.
(iii) Also, the angles of quadrilateral are ∠SPQ, ∠PQR, ∠QRS and ∠RSP.
(iv) The line segments are PQ and QS.

Convex Quadrilaterals and Concave Quadrilaterals

If each angle of a quadrilateral is less than 180°, then it is called a convex quadrilateral. Also, if one angle of the quadrilateral is more than 180°, then it is called a concave quadrilateral. A quadrilateral is not a simple closed figure.

Sides, Angles, Vertices, Diagonals of the Quadrilateral

Have a look at the complete details of a Quadrilateral below.

Adjacent Sides of a Quadrilateral

Adjacent Sides of a Quadrilateral are nothing but the sides that have a common endpoint. If PQRS is a Quadrilateral, then (PQ, QR), (QR, RS), (RS, SP), and (SP, PQ) are four pairs of adjacent sides of quadrilateral PQRS.

Opposite Sides of a Quadrilateral

In a given quadrilateral, the two sides are said to be opposite sides when they do not have a common endpoint. If PQRS is a quadrilateral, then (PQ, SR) and (PS, QR) are two pairs of opposite sides of quadrilateral PQRS.

Adjacent Angles of a Quadrilateral

An angle is formed when two rays meeting at a common endpoint. Two angles of a quadrilateral are said to be adjacent when they have a common arm. From the given figure, (∠P, ∠Q), (∠Q, ∠R), (∠R, ∠S), and (∠S, ∠P) are four pairs of adjacent angles of quadrilateral PQRS.

Opposite Angles of a Quadrilateral

Opposite Angles of a Quadrilateral are not adjacent angles. If you consider a quadrilateral PQRS, then (∠P, ∠R) and (∠Q, ∠S) are two pairs of opposite angles of quadrilateral PQRS.

Adjacent Vertices of a Quadrilateral

In a Quadrilateral, if two vertices have a common side are known as adjacent vertices. From the figure, the pairs of adjacent vertices are (P, Q); (Q, R); (R, S), and (S, P).

Opposite Vertices of a Quadrilateral

Opposite Vertices of a Quadrilateral are vertices that do not have a common side. From the figure, the pairs of opposite vertices are (P, R) and (Q, S).

Diagonal of a Quadrilateral

When a line segment of the opposite vertices of a quadrilateral is joined, then the diagonal of the quadrilateral is formed. From the given figure, the two diagonals are PR and QS.