Eureka Math

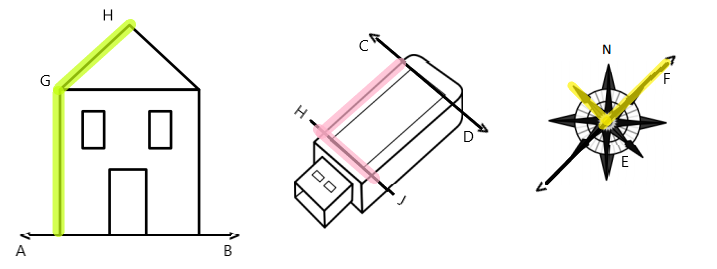
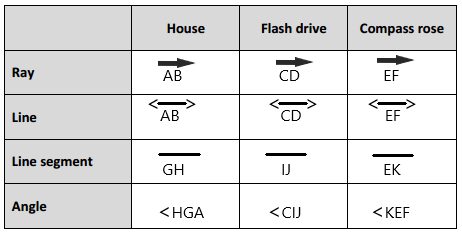
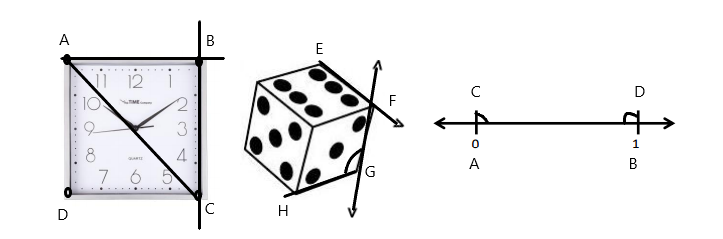
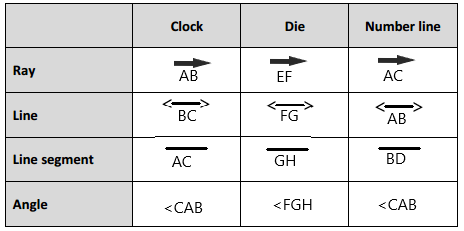
Engage NY Eureka Math 4th Grade Module 4 Lesson 6 Answer Key

Eureka Math Grade 4 Module 4 Lesson 6 Practice Sheet Answer Key

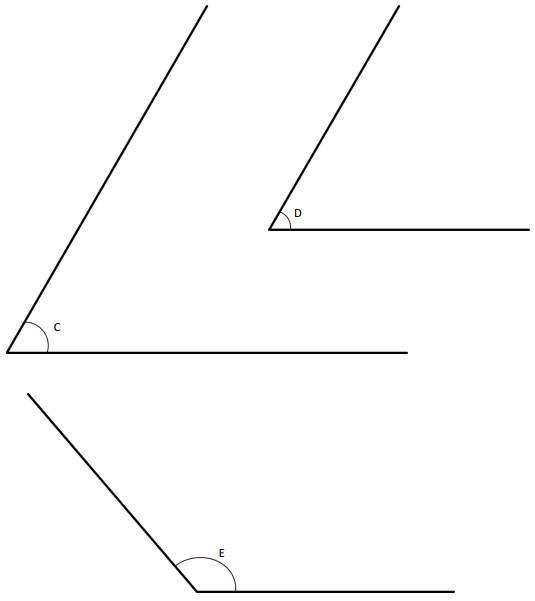
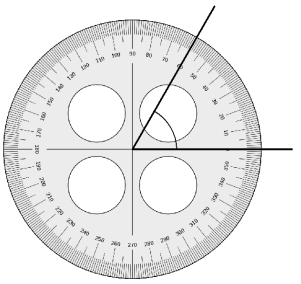
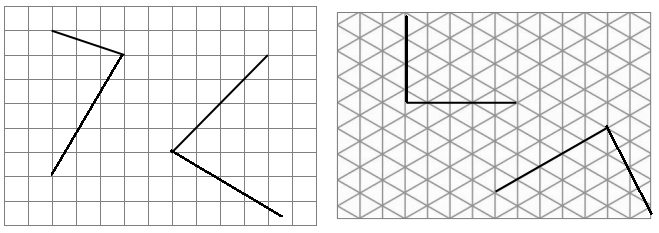
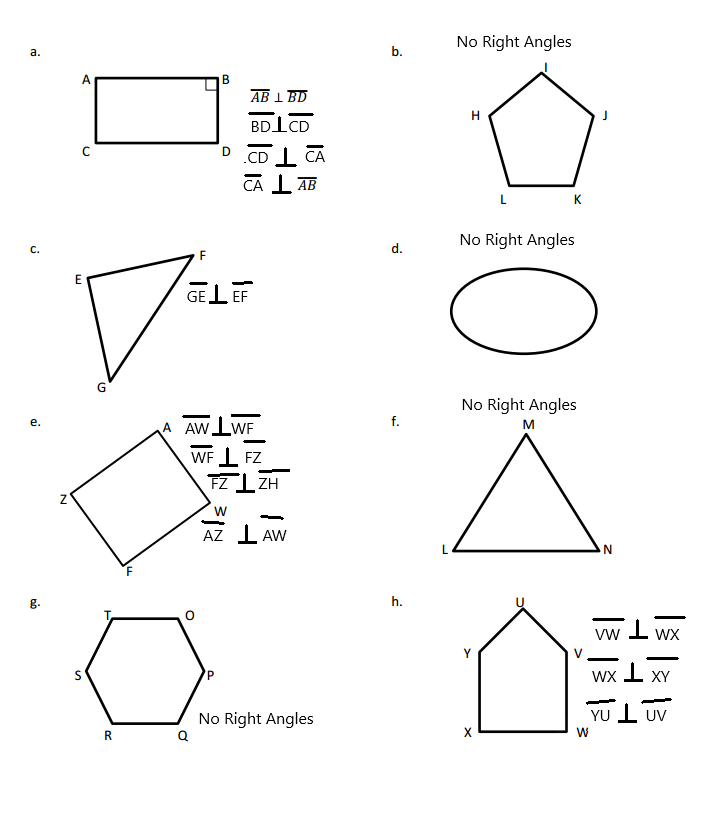
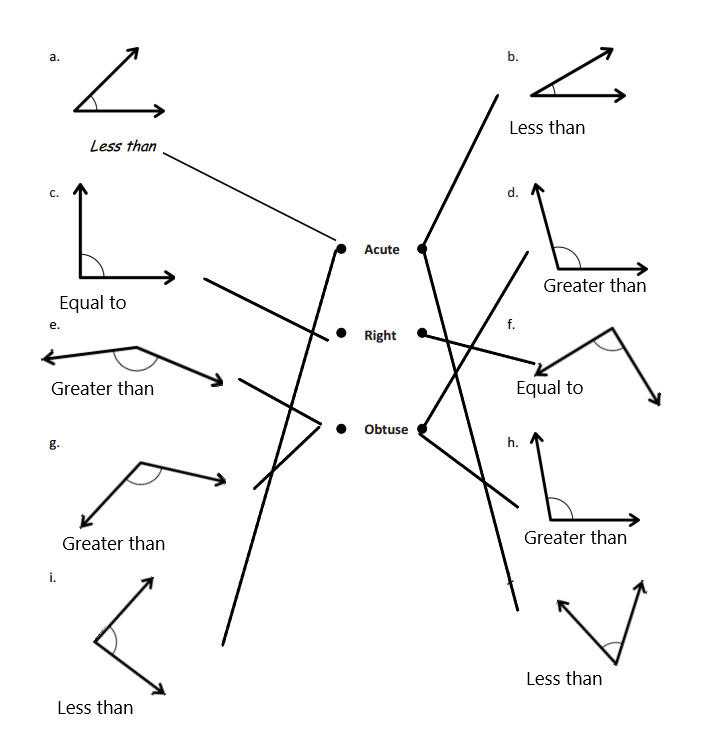
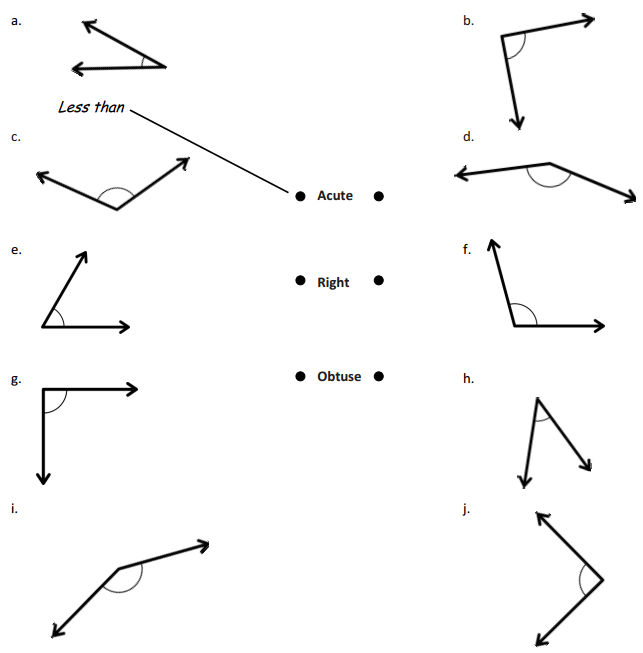
Answer:
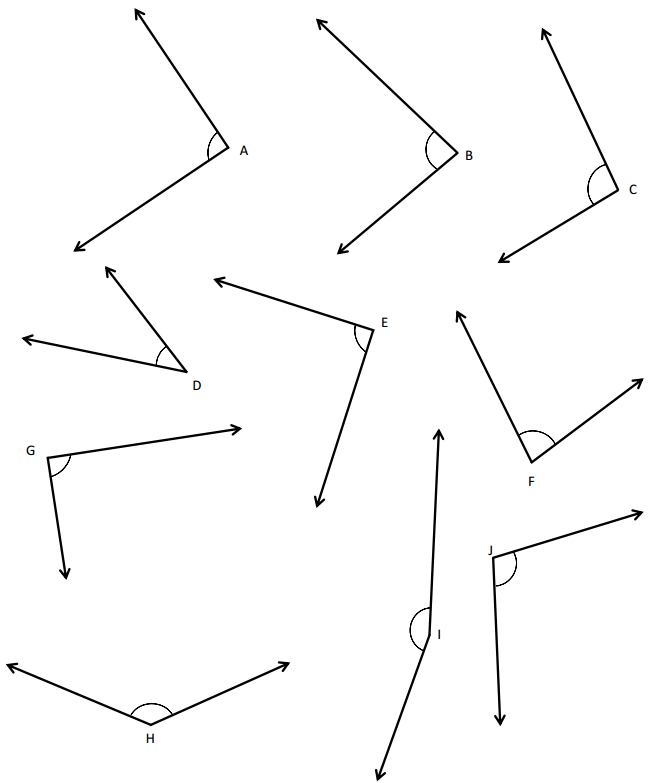
The angle C is an acute angle.
The angle D is an acute angle.
The angle E is an obtuse angle.

Explanation:
In the above image, we can see that the angle D is less than 90°. So the angle D will be the acute angle. And we can see that angle C is less than 90°. So the angle D will be the acute angle. And we can see that angle E is greater than 90°, so the angle is an obtuse angle.

Eureka Math Grade 4 Module 4 Lesson 6 Problem Set Answer Key

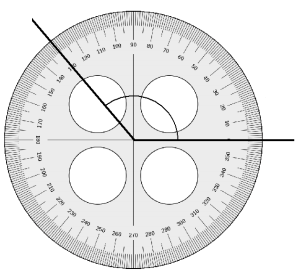
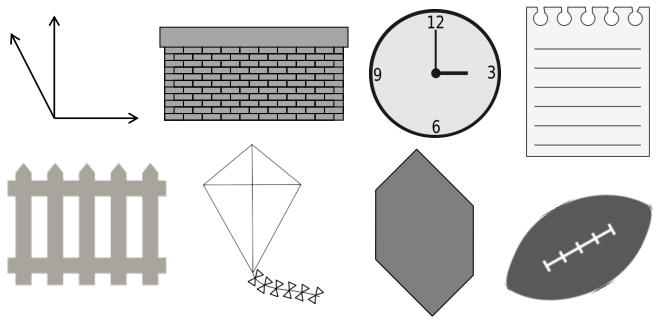
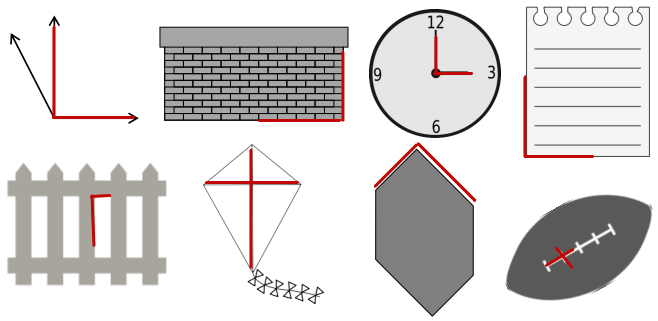
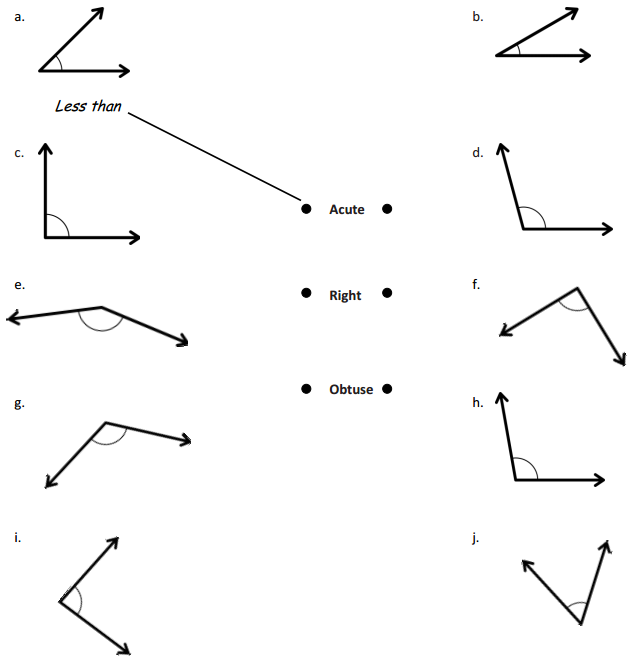
Question 1.
Use a protractor to measure the angles, and then record the measurements in degrees.
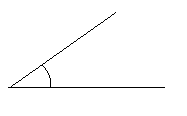
a.

Answer:
The above angle is 36°.

Explanation:
By measuring the angle with protractor we will get the angle as 36° and it is an acute angle as the angle is less than 90°.

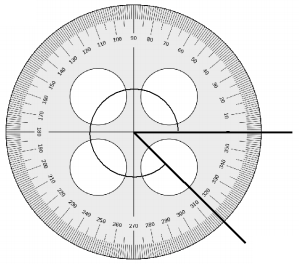
b.

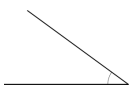
Answer:
The above angle is 36°.

Explanation:
By measuring the angle with protractor we will get the angle as 36° and it is an acute angle as the angle is less than 90°.

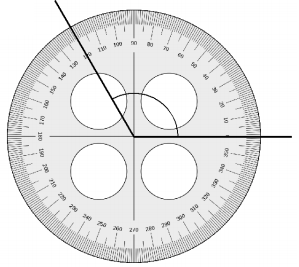
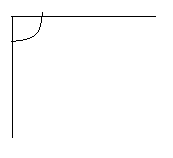
c.

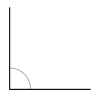
Answer:
The above angle is 90°.

Explanation:
By measuring the angle with protractor we will get the angle as 90° and it is a right angle as the angle is  90°.

d.

Answer:
The above angle is 90°.

Explanation:
By measuring the angle with protractor we will get the angle as 90° and it is a right angle as the angle is  90°.

e.

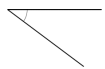
Answer:
The above angle is 36°.

Explanation:
By measuring the angle with protractor we will get the angle as 36° and it is an acute angle as the angle is less than 90°.

f.

Answer:
The above angle is 155°.

Explanation:
By measuring the angle with protractor we will get the angle as 155° and it is an obtuse angle as the angle is greater than 90°.

g.

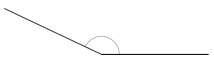
Answer:
The above angle is 155°.

Explanation:
By measuring the angle with protractor we will get the angle as 155° and it is an obtuse angle as the angle is greater than 90°.

h.

Answer:
The above angle is 90°.

Explanation:
By measuring the angle with protractor we will get the angle as 90° and it is a right angle as the angle is  90°.

i.

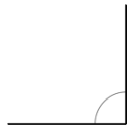
Answer:
The above angle is 90°.

Explanation:
By measuring the angle with protractor we will get the angle as 90° and it is a right angle as the angle is  90°.

j.

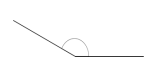
Answer:
The above angle is 150°.

Explanation:
By measuring the angle with protractor we will get the angle as 150° and it is an obtuse angle as the angle is greater than 90°.

Question 2.
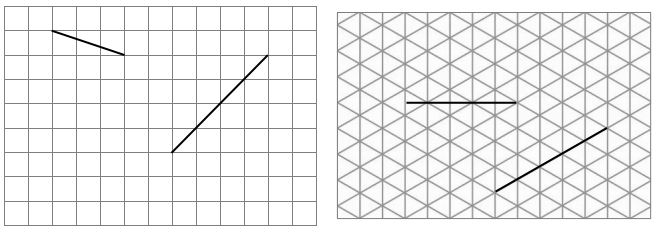
a. Use three different-size protractors to measure the angle. Extend the lines as needed using a straightedge.
Protractor #1: ________°
Protractor #2: ________°
Protractor #3: ________°

Answer:
Protractor #1: 29°
Protractor #2: 29°
Protractor #3: 29°

Explanation:
By using three different protractors we have got the same angle measurement, which is 29°.

b. What do you notice about the measurement of the above angle using each of the protractors?
Answer:
We have noticed that the measure of the angle is the same using each of the protractors.

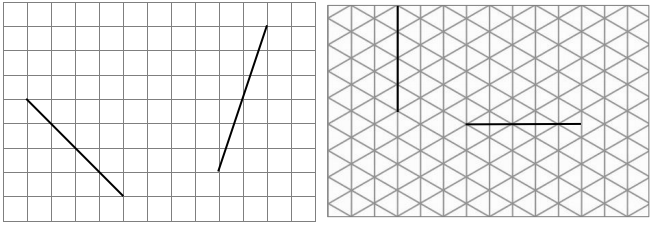
Question 3.
Use a protractor to measure each angle. Extend the length of the segments as needed. When you extend the segments, does the angle measure stay the same? Explain how you know.
a.

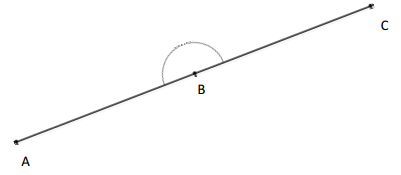
Answer:
Here, the angle measurement remains the same, we came to know that by measuring with a small protractor. Then we extended the length of the segments and then we have to measure with a large protractor. So by measuring with a small protractor and large protractor there is no change in measuring the angles. And the measurement of the angle is 180°.

b.

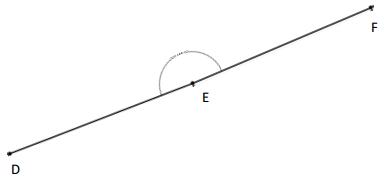
Answer:
Here, the angle measurement remains the same, we came to know that by measuring with a small protractor. Then we extended the length of the segments and then we have to measure with a large protractor. So by measuring with a small protractor and large protractor there is no change in measuring the angles. And the measurement of the angle is 178°.

Eureka Math Grade 4 Module 4 Lesson 6 Exit Ticket Answer Key

Use any protractor to measure the angles, and then record the measurements in degrees.

Question 1.

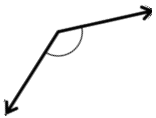
Answer:
The above angle is 105°.

Explanation:
By measuring the angle with protractor we will get the angle as 105° and it is an obtuse angle as the angle is greater than 90°.

Question 2.

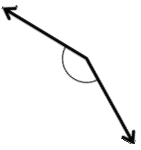
Answer:
The above angle is 150°.

Explanation:
By measuring the angle with protractor we will get the angle as 150° and it is an obtuse angle as the angle is greater than 90°.

Question 3.

Answer:
The above angle is 36°.

Explanation:
By measuring the angle with protractor we will get the angle as 36° and it is an acute angle as the angle is less than 90°.

Question 4.

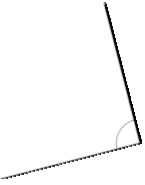
Answer:
The above angle is 90°.

Explanation:
By measuring the angle with protractor we will get the angle as 90° and it is a right angle as the angle is  90°.

Eureka Math Grade 4 Module 4 Lesson 6 Homework Answer Key

Question 1.
Use a protractor to measure the angles, and then record the measurements in degrees.
a.

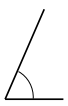
Answer:
The angle would be 60° or above but less 90° and the angle is called as acute angle.

Explanation:
In the above image, we can see that the angle is less than 90°. So the angle would be 60° or above but less 90° and the angle is called as acute angle.

b.

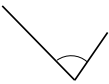
Answer:
The angle would be 60° or above but less 90° and the angle is called as acute angle.

Explanation:
In the above image, we can see that the angle is less than 90°. So the angle would be 60° or above but less 90° and the angle is called as acute angle.

c.

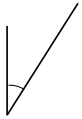
Answer:
The angle would be 60° or above but less 90° and the angle is called as acute angle.

Explanation:
In the above image, we can see that the angle is less than 90°. So the angle would be 60° or above but less 90° and the angle is called as acute angle.

d.

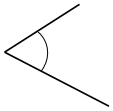
Answer:
The angle would be 60° or above but less 90° and the angle is called as acute angle.

Explanation:
In the above image, we can see that the angle is less than 90°. So the angle would be 60° or above but less 90° and the angle is called as acute angle.

e.

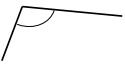
Answer:
The angle would be above 90° but less 180° and the angle is called as obtuse angle.

Explanation:
In the above image, we can see that the angle is greater than 90°. So the angle would be above 90° and the angle is called as obtuse angle.

f.

Answer:
The angle would be above 90° but less 180° and the angle is called as obtuse angle.

Explanation:
In the above image, we can see that the angle is greater than 90°. So the angle would be above 90° and the angle is called as obtuse angle.

g.

Answer:
The angle would be above 90° but less 180° and the angle is called as obtuse angle.

Explanation:
In the above image, we can see that the angle is greater than 90°. So the angle would be above 90° and the angle is called as obtuse angle.

h.

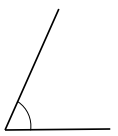
Answer:
The angle would be 60° or above but less 90° and the angle is called as acute angle.

Explanation:
In the above image, we can see that the angle is less than 90°. So the angle would be 60° or above but less 90° and the angle is called as acute angle.

i.

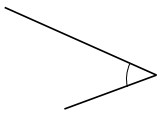
Answer:
The angle would be 60° or above but less 90° and the angle is called as acute angle.

Explanation:
In the above image, we can see that the angle is less than 90°. So the angle would be 60° or above but less 90° and the angle is called as acute angle.

j.

Answer:
The angle would be above 90° but less 180° and the angle is called as obtuse angle.

Explanation:
In the above image, we can see that the angle is greater than 90°. So the angle would be above 90° and the angle is called as obtuse angle.

Question 2.
Using the green and red circle cutouts from today’s lesson, explain to someone at home how the cutouts can be used to show that the angle measures are the same even though the circles are different sizes. Write words to explain what you told him or her.

Answer:
Here, if we center the smaller circle on the larger circle and the diameters lines up. So the angles are in the same measurement and the arcs are different.

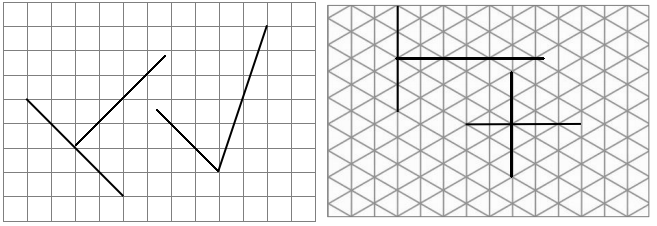
Question 3.
Use a protractor to measure each angle. Extend the length of the segments as needed. When you extend the segments, does the angle measure stay the same? Explain how you know.
a.

Answer:
Here, the angle measurement remains the same, we came to know that by measuring with a small protractor. Then we extended the length of the segments and then we have to measure with a large protractor. So by measuring with a small protractor and large protractor there is no change in measuring the angles. And the measurement of the angle is 178°.

b.

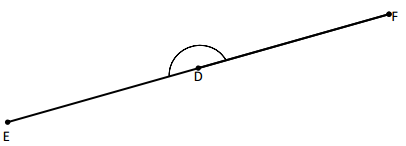
Answer:
Here, the angle measurement remains the same, we came to know that by measuring with a small protractor. Then we extended the length of the segments and then we have to measure with a large protractor. So by measuring with a small protractor and large protractor there is no change in measuring the angles. And the measurement of the angle is 180°.

Engage NY Eureka Math 4th Grade Module 4 Lesson 5 Answer Key

Eureka Math Grade 4 Module 4 Lesson 5 Problem Set Answer Key

Question 1.
Make a list of the measures of the benchmark angles you drew, starting with Set A.
Round each angle measure to the nearest 5° Both sets have been started for you.
a. Set A: 45°, 90°,
Answer:
The angles that are nearest to 5° will be 90°, 180°, 270°, 360°.

Explanation:
Here, the list of the angles in Set A is 45°, 90°, 135°, 180°, 225°, 270°, 315°, 360°, so here we need to round off the each angle which is nearest to 5° and the angles will be 90°, 180°, 270°, 360° are the angles which are nearest to 5°.

b. Set B: 30°,60°,
Answer:
The angles that are nearest to 5° will be 90°, 180°, 270°, 360°.

Explanation:
Here, the list of the angles in Set A is 30°, 60°, 90°, 120°, 150°, 180°, 210°, 240°,  so here we need to round off the each angle which is nearest to 5° and the angles will be 90°, 180°, 270°, 360° are the angles which are nearest to 5°.

Question 2.
Circle any angle measures that appear on both lists. What do you notice about them?
Answer:
We have noticed that they all are right angles and they all are quarter turns.

Explanation:
The angles that are cricled are 90°, 180°, 270°, 360°, and we have noticed that they all are right angles and they all are quarter turns.

Question 3.
List the angle measures from Problem 1 that are acute. Trace each angle with your finger as you say its measurement.
Answer:
The angles are 30°, 45°, and 60°.

Explanation:
The angles that measures from problem 1 that are acute which we have traced is 30°, 45°, and 60°.

Question 4.
List the angle measures from Problem 1 that are obtuse. Trace each angle with your finger as you say its measurement.
Answer:
The angles are 120°, 135°, and 150°.

Explanation:
The angles that measures from problem 1 that are acute which we have traced is 120°, 135°, and 150°.

Question 5.
We found out today that 1° is \(\frac{1}{360}\) of a whole turn. It is 1 out of 360°. That means a 2° angle is \(\frac{2}{360}\) of a whole turn. What fraction of a whole turn is each of the benchmark angles you listed in Problem 1?
Answer:
The angles in the set A are \(\frac{45}{360}\),\(\frac{90}{360}\), \(\frac{135}{360}\),\(\frac{180}{360}\),\(\frac{225}{360}\),\(\frac{270}{360}\), \(\frac{315}{360}\), \(\frac{360}{360}\).
The angles in the set A are \(\frac{30}{360}\),\(\frac{60}{360}\), \(\frac{90}{360}\),\(\frac{120}{360}\),\(\frac{150}{360}\),\(\frac{180}{360}\), \(\frac{210}{360}\), \(\frac{240}{360}\), \(\frac{270}{360}\), \(\frac{240}{360}\), \(\frac{300}{360}\), \(\frac{330}{360}\), \(\frac{360}{360}\).

Explanation:
The fraction of a whole turn is each of the benchmark angles that are listed in problem 1 set A is \(\frac{45}{360}\),\(\frac{90}{360}\), \(\frac{135}{360}\),\(\frac{180}{360}\),\(\frac{225}{360}\),\(\frac{270}{360}\), \(\frac{315}{360}\), \(\frac{360}{360}\).
The fraction of a whole turn is each of the benchmark angles that are listed in problem 1 set B is \(\frac{30}{360}\),\(\frac{60}{360}\), \(\frac{90}{360}\),\(\frac{120}{360}\),\(\frac{150}{360}\),\(\frac{180}{360}\), \(\frac{210}{360}\), \(\frac{240}{360}\), \(\frac{270}{360}\), \(\frac{240}{360}\), \(\frac{300}{360}\), \(\frac{330}{360}\), \(\frac{360}{360}\).

Question 6.
How many 45° angles does it take to make a full turn?
Answer:
It takes eight 45° angles to make a full turn.

Explanation:
As the circle has 360° for full turn and for 45° It takes eight 45° angles to make a full turn.

Question 7.
How many 30° angles does it take to make a full turn?
Answer:
It takes twelve 45° angles to make a full turn.

Explanation:
As the circle has 360° for full turn and for 45° It takes twelve 45° angles to make a full turn.

Question 8.
If you didn’t have a protractor, how could you reconstruct a quarter of it from 0° to 90°?
Answer:
Here, we could use two 45° angles or three 30° angles and we will put them together and we can make a right angle template.

Eureka Math Grade 4 Module 4 Lesson 5 Exit Ticket Answer Key

Question 1.
How many right angles make a full turn?
Answer:
It takes four right angles to make a full turn.

Explanation:
As the circle has 360° for full turn and four right angles It takes four right angles to make a full turn.

Question 2.
What is the measurement of a right angle?
Answer:
The measurement of a right angle is 90° as the set of two lines intersect each other at 90° and they form a right angle. So the measurement of right angle is 90°.

Question 3.
What fraction of a full turn is 1°
Answer:
As a full turn is 360°, so 1° of 360° written in the fraction as \(\frac{1}{360}\).

Question 4.
Name at least four benchmark angle measurements.
Answer:
The four benchmark angle measurements are 30°, 45°, 60°, 90°.

Explanation:
Here the benchmarks are defined as the standard or reference point against which something can be measured or compared. And benchmark numbers are the numbers against which other numbers or qualities can be estimated or compared. Here the four benchmark angle measurements are 30°, 45°, 60°, 90°.

Eureka Math Grade 4 Module 4 Lesson 5 Homework Answer Key

Question 1.
Identify the measures of the following angles.
a.

Answer:
The above angle is measured as 60°.

Explanation:
In the above image, we can see that the angle is 60° and is known as acute angle. As the angle measures less than 90°, so the above angle is measured as 60°.

b.

Answer:
The above angle is measured as 130°.

Explanation:
In the above image, we can see that the angle is 130° and is known as obtuse angle. As the angle measures greater than 90°. So the above angle is measured as 130°.

c.

Answer:
The above angle is measured as 315°.

Explanation:
In the above image, we can see that the angle is 315° and is known as reflex angle. As the angle measures greater than 180°. So the above angle is measured as 315°.

d.

Answer:
The above angle is measured as 120°.

Explanation:
In the above image, we can see that the angle is 120° and is known as obtuse angle. As the angle measures greater than 90°. So the above angle is measured as 90°.

Question 2.
If you didn’t have a protractor, how could you construct one? Use words, pictures, or numbers to explain in the space below.
Answer:
Here, we will take a rectangular sheet of paper and we will fold the top side against aside. And next we will remove the bookmark which is at the bottom. Now we will unfold the square which we had made earlier, now we will fold with + shape and then X shape. So now we can measure the angles in 45° increments.

Eureka Math Grade 4 Module 4 Lesson 5 Template Answer Key

_________________
circular protractor
Answer:
A protractor is a measuring instrument which will be transparent made with a plastic or a glass. A circular protractor is a protractor which has two sets of measurements, here one set is marked with 180° and the opposite direction is marked with 360°.

Engage NY Eureka Math 4th Grade Module 4 Lesson 3 Answer Key

Eureka Math Grade 4 Module 4 Lesson 3 Problem Set Answer Key

Question 1.
On each object, trace at least one pair of lines that appear to be perpendicular.

Answer:
When two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines.

Explanation:

When two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. In the above images, we have traced out the perpendicular lines and the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect.

Question 2.
How do you know if two lines are perpendicular?
Answer:
When two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect.

Question 3.
In the square and triangular grids below, use the given segments in each grid to draw a segment that is perpendicular using a straightedge.

Answer:
As two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect.

Explanation:

In the above image, we have constructed the perpendicular lines, as two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect.

Question 4.
Use the right angle template that you created in class to determine which of the following figures have a right angle. Mark each right angle with a small square. For each right angle, you find, name the corresponding pair of perpendicular sides. (Problem 4(a) has been started for you.)

Answer:
The perpendicular angles in the image a are <AB and <BD, <BD and <CD, <CD and <CA, <CA and <AB.
There are no perpendicular angles in image b as there are no right angles.
The perpendicular angles in the image c are <GE and <EF
There are no perpendicular angles in the image d as there are no right angles.
The perpendicular angles in the image e are <AW and <WF, <WF and <FZ, <FZ and <ZH, <AZ and <AW
There are no perpendicular angles in the image f as there are no right angles.
There are no perpendicular angles in the image g as there are no right angles.
The perpendicular angles in the image h are <VW and <WX, <WX and <XY, <YU, and <UV.

Explanation:

As two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect. As in the above image a is a square the perpendicular angles are <AB and <BD, <BD and <CD, <CD and <CA, <CA and <AB. And in image b we can see that the image is polygon so there will be No Right Angles. In image c we can see some angles, so the perpendicular angles are <GE and <EF. In image d there will be No Right Angles as there as it is in oval shape and no angles in that image. In image e, there are some angles, so the perpendicular angles are <AW and <WF, <WF and <FZ, <FZ and <ZH, <AZ and <AW. In image f, there are no angles, so there will be no perpendicular angles as there are No Right Angles. In image g there are no angles, so there will be no perpendicular angles as there are No Right Angles. In image e, there are some angles, so the perpendicular angles are <VW and <WX, <WX and <XY, <YU, and <UV.

Question 5.
Mark each right angle on the following figure with a small square. (Note: A right angle does not have to be inside the figure.) How many pairs of perpendicular sides does this figure have?

Answer:
There are 12 pairs of perpendicular sides.

Explanation:

As two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect. So in the above image, we can see that there are 12 pairs of perpendicular sides.

Question 6.
True or false? Shapes that have at least one right angle also have at least one pair of perpendicular sides. Explain your thinking.
Answer:
Yes, it is true. As the right angles are created by sides that are perpendicular, so if a figure has a right angle it must have perpendicular sides.

Eureka Math Grade 4 Module 4 Lesson 3 Exit Ticket Answer Key

Use a right angle template to measure the angles in the following figures. Mark each right angle with a small square. Then, name all pairs of perpendicular sides.

Question 1.

Answer:
In the above image a is a square the perpendicular angles are <BC and <CD, <ED and <DC, <AE and <AB.

Explanation:
As two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect. As in the above image a is a square the perpendicular angles are <BC and <CD, <ED and <DC, <AE and <AB.

Question 2.

Answer:
In the above image a is a square the perpendicular angles are <MN and <MP.

Explanation:
As two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect. As in the above image a is a square the perpendicular angles are <MN and <MP.

Eureka Math Grade 4 Module 4 Lesson 3 Homework Answer Key

Question 1.
On each object, trace at least one pair of lines that appear to be perpendicular.

Answer:
Refer below to check the perpendicular angles which are traced for the images.

Explanation:

As two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect. In the above image, we have traced the perpendicular angles of the images.

Question 2.
How do you know if two lines are perpendicular?
Answer:
When two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect. By that, we will get to know that two lines are perpendicular.

Question 3.
In the square and triangular grids below, use the given segments in each grid to draw a segment that is perpendicular. Use a straightedge.

Answer:
As two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect.

Explanation:

In the above image, we have constructed the perpendicular lines, as two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect.

Question 4.
Use the right angle template that you created in class to determine which of the following figures have a right angle. Mark each right angle with a small square. For each right angle you find, name the corresponding pair of perpendicular sides. (Problem 4(a) has been started for you.)

Answer:
The perpendicular angles in the image a are <CA and <AB, <AB and <BD, <BD and <CD, <CD and <AC.
There are no perpendicular angles in image b as there are no right angles.
The perpendicular angles in the image c are <DO and <GO.
There are no perpendicular angles in the image d as there are no right angles.
There are no perpendicular angles in image e as there are no right angles.
The perpendicular angles in the image f are <ON and <NM, <ON and <OP, <PM and <OP, <PM and <MN.
There are no perpendicular angles in the image g as there are no right angles.
The perpendicular angles in the image h are <UV and <VW, <US and <SZ, <WY and <XY, <SZ and <ZY, <XY and <YZ.

Explanation:

As two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect. As in the above image a is a square the perpendicular angles are <CA and <AB, <AB and <BD, <BD and <CD, <CD and <AC. And in image b we can see that the image is polygon so there will be No Right Angles. In image c we can see some angles, so the perpendicular angles are <DO and <GO. In image d there will be No Right Angles as there as it is in oval shape and no angles in that image. In image e, there are no angles, so there will be no perpendicular angles as there are No Right Angles. In image f, there are some angles, so the perpendicular angles are <ON and <NM, <ON and <OP, <PM and <OP, <PM and <MN. In image g, there are no angles, so there will be no perpendicular angles as there are No Right Angles. In image h, there are some angles, so the perpendicular angles are <UV and <VW, <US and <SZ, <WY and <XY, <SZ and <ZY, <XY and <YZ.

Question 5.
Use your right angle template as a guide, and mark each right angle in the following figure with a small square. (Note: A right angle does not have to be inside the figure.) How many pairs of perpendicular sides does this figure have?

Answer:
In the above image, we can see that there are 9 pairs of perpendicular sides.

Explanation:

As two distinct lines intersect each other at 90 degrees those lines are called perpendicular lines. A right angle is also known as perpendicular lines. And the properties of perpendicular lines are these lines should always intersect at right angles. So if the two lines are perpendicular to the same line then those lines will be parallel to each other and will never intersect. So in the above image, we can see that there are 9 pairs of perpendicular sides.

Question 6.
True or false? Shapes that have no right angles also have no perpendicular segments. Draw some figures to help explain your thinking.
Answer:
Yes, it is true. As the shapes without right angles have no perpendicular segments because perpendicular lines meet at right angles. So the rhombus has equal sides but no right angles and no perpendicular segments.

Engage NY Eureka Math 4th Grade Module 4 Lesson 2 Answer Key

Eureka Math Grade 4 Module 4 Lesson 2 Problem Set Answer Key

Question 1.
Use the right angle template that you made in class to determine if each of the following angles is greater than, less than, or equal to a right angle. Label each as greater than, less than, or equal to, and then connect each angle to the correct label of acute, right, or obtuse. The first one has been completed for you.

Answer:
In the above image, the acute angles will be a,b, i, and j.
In the above image, the right angles will be c and f.
In the above image, the obtuse angles will be d,e,g,h.

Explanation:

Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle. So in the above image, the acute angles will be a, b, i, and j.
Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle. So in the above image, the right angles will be c and f.
Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle. So in the above image, the obtuse angles will be d, e, g, h.

Question 2.
Use your right angle template to identify acute, obtuse, and right angles within Picasso’s painting Factory, Horta de Ebbo. Trace at least two of each, label with points, and then name them in the table below the painting.


Answer:
In the above image the acute angles will be <GHI, <JKL.
In the above image the right angles will be <MKN, <PQR.
In the above image the obtuse angles will be <ABC, <DEF.

Explanation:


Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle. So in the above image, the acute angles will be <GHI, <JKL.
Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle. So in the above image, the right angles will be <MKN, <PQR.
Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle. So in the above image, the obtuse angles will be <ABC, <DEF.

Question 3.
Construct each of the following using a straightedge and the right angle template that you created. Explain the characteristics of each by comparing the angle to a right angle. Use the words greater than, less than, or equal to in your explanations.
a. Acute angle
Answer:
Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle.

Explanation:
Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle.

b. Right angle
Answer:
Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle.

Explanation:
Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle.

c. Obtuse angle
Answer:
Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle.

Explanation:
Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle.

Eureka Math Grade 4 Module 4 Lesson 2 Exit Ticket Answer Key

Question 1.
Fill in the blanks to make true statements using one of the following words: acute, obtuse, right, straight.
a. In class, we made a __________________ angle when we folded paper twice.
Answer:
In class, we made a right angle when we folded the paper twice.

Explanation:
By folding paper twice we will get a right angle triangle. As the right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle.

b. An __________________ angle is smaller than a right angle.
Answer:
An acute angle is smaller than a right angle.

Explanation:
An acute angle is smaller than a right angle. As the acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle.

c. An __________________ angle is larger than a right angle, but smaller than a straight angle.
Answer:
An obtuse angle is larger than a right angle but smaller than a straight angle.

Explanation:
An obtuse angle is larger than a right angle but smaller than a straight angle. As the obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called the Obtuse angle.

Question 2.
Use a right angle template to identify the angles below.

a. Which angles are right angles? ____________________________________________________
Answer:
In the above image, the right angles are <C and <G.

Explanation:
Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle. So in the above image, the right angles are <C and <G.

b. Which angles are obtuse angles? __________________________________________________
Answer:
In the above image, the obtuse angles are <B and <E.

Explanation:
Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle. So in the above image, the obtuse angles are <B and <E.

c. Which angles are acute angles? ___________________________________________________
Answer:
In the above image, the obtuse angles are <A and <D.

Explanation:
Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle. So in the above image, the obtuse angles are <A and <D.

d. Which angles are straight angles? _________________________________________________
Answer:
In the above image, the obtuse angles are <F and <H.

Explanation:
A straight line is a line that cannot be curved or bent and a line is an object in geometry that is characterized under the zero-width object that extends on both sides. The straight line is a line that extends to both sides to infinity and has no curves. So in the above image, the obtuse angles are <F and <H.

Eureka Math Grade 4 Module 4 Lesson 2 Homework Answer Key

Question 1.
Use the right angle template that you made in class to determine if each of the following angles is greater than, less than, or equal to a right angle. Label each as greater than, less than, or equal to, and then connect each angle to the correct label of acute, right, or obtuse. The first one has been completed for you.

Answer:
In the above image, the acute angles will be a, e, h.
In the above image, the right angles will be g, j, b.
In the above image, the obtuse angles will be c, i, d, f.

Explanation:

Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle. So in the above image, the acute angles will be a, e, h.
Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle. So in the above image, the right angles will be g, j, b.
Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle. So in the above image, the obtuse angles will be c, i, d, f.

Question 2.
Use your right angle template to identify acute, obtuse, and right angles within this painting.
Trace at least two of each, label with points, and then name them in the table below the painting.


Answer:
In the above image, the acute angles will be <ABC, <DEF.
In the above image, the right angles will be <MNO, <PQR.
In the above image, the obtuse angles will be <GHI, <JKL.

Explanation:

Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle. So in the above image, the acute angles will be <ABC, <DEF.
Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle. So in the above image, the right angles will be <MNO, <PQR.
Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle. So in the above image, the obtuse angles will be <GHI, <JKL.

Question 3.
Construct each of the following using a straightedge and the right angle template that you created. Explain the characteristics of each by comparing the angle to a right angle. Use the words greater than, less than, or equal to in your explanations.
a. Acute angle
Answer:
Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle.

Explanation:

Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle.

b. Right angle
Answer:
Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle.

Explanation:

Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle.

c. Obtuse angle
Answer:
Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle.

Explanation:

Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle.

Eureka Math Grade 4 Module 4 Lesson 2 Template Answer Key

_______________________________
Answer:
In the above image, the acute angles will be <D, <F.
In the above image, the right angles will be <A, <B, <E, <G.
In the above image, the obtuse angles will be <C, <H, <I, <J.

Explanation:
Acute angle: An acute angle is an angle that measures less than 90 degrees. In other words, we can say that the angle which is smaller than the right angle is also known as the Acute angle. So in the above image, the acute angles will be <D, <F.
Right angle: A right angle is an angle that has straight lines that intersect each other at 90 degrees which are perpendicular to each other at the intersection so that we will form a right angle. So in the above image, the right angles will be <A, <B, <E, <G.
Obtuse angle: An obtuse angle is an angle that measures greater than 90 degrees and less than 180 degrees, so the angles that are longer than a right angle and smaller than a straight angle are called Obtuse angle. So in the above image, the obtuse angles will be <C, <H, <I, <J.

Engage NY Eureka Math 4th Grade Module 4 Lesson 1 Answer Key

Eureka Math Grade 4 Module 4 Lesson 1 Problem Set Answer Key

Question 1.
Use the following directions to draw a figure in the box to the right.
a. Draw two points: A and B.
b. Use a straightedge to draw \(\overline{A B}\).
c. Draw a new point that is not on \(\overline{A B}\). Label it C.
d. Draw \(\overline{A C}\).
e. Draw a point not on \(\overline{A B}\) or \(\overline{A C}\). Call it D.
f. Construct
g. Use the points you’ve already labeled to name one angle. ____________

Answer:
The labeled angle is <ACD/<BAC.

Explanation:
Here, we have to draw two points and then labeled them as A and B.
And used a straightedge to draw \(\overline{A B}\).
Then we have to draw a new point that is not on \(\overline{A B}\). And we will label it as C.
Then we will draw \(\overline{A C}\).
Then we will draw a point not on \(\overline{A B}\) or \(\overline{A C}\). And we will label it as D.
And then we will construct
We will use these points and we will label with one angle as <ACD/<BAC.

Question 2.
Use the following directions to draw a figure in the box to the right.
a. Draw two points: A and B.
b. Use a straightedge to draw \(\overline{A B}\).
c. Draw a new point that is not on \(\overline{A B}\). Label it C.
d. Draw \(\overline{B C}\).
e. Draw a new point that is not on \(\overline{A B}\) or \(\overline{A C}\)
Label it D.
f. Construct .
g. Identify ∠DAB by drawing an arc to indicate the position of the angle.
h. Identify another angle by referencing points that you have already drawn. _____________

Answer:
The labeled angle is <ABC.

Explanation:
Here, we have to draw two points and label them as A and B.
And use a straightedge to draw \(\overline{A B}\).
Then we have to draw a new point that is not on \(\overline{A B}\). Label it C.
Then we will draw \(\overline{B C}\).
And we will draw a new point that is not on \(\overline{A B}\) or \(\overline{A C}\)
Label it D.
So we will construct  .

Then we have identified ∠DAB by drawing an arc to indicate the position of the angle.
And we have Identified another angle by referencing points that we have already drawn.

Question 3.
a. Observe the familiar figures below. Label some points on each figure.
b. Use those points to label and name representations of each of the following in the table below: ray, line, line segment, and angle. Extend segments to show lines and rays.


Extension: Draw a familiar figure. Label it with points, and then identify rays, lines, line segments, and angles as applicable.
Answer:
The ray of the house is marked as AB,
The ray of the flash drive is marked as CD,
The ray of the direction compass is marked as EF.
The Line of the house is marked as AB,
The Line of the flash drive is marked as CD,
The Line of the direction compass is marked as EF.
The Line segment of the house is marked as GH,
The Line segment of the flash drive is marked as IJ,
The Line segment of the direction compass is marked as EK.
The Angle of the house is marked as <HGA,
The Angle of the flash drive is marked as <CIJ,
The Angle of the direction compass is marked as <KEF.

Explanation:

Ray: A Ray can be defined as a part of the line which has a fixed starting point but does not have any endpoint and it can be extended infinitely in one direction and a ray may pass through more than one point.
The ray of the house is marked as AB,
The ray of the flash drive is marked as CD,
The ray of the direction compass is marked as EF.
Line: A line can be defined as a long, straight and continuous path which is represented using arrowheads at both directions and the lines that do not have a fixed point it can be extended in two directions.
The Line of the house is marked as AB,
The Line of the flash drive is marked as CD,
The Line of the compass rose is marked as EF.
Line segment: A line segment is a straight line that passes through the two points and has fixed point and it can not be extended.
The Line segment of the house is marked as GH,
The Line segment of the flash drive is marked as IJ,
The Line segment of the compass rose is marked as EK.
Angle: A figure which is formed by two rays or lines that shares a common endpoint and is called an angle.
So in the above, we can see the house, flash drive, and a compass rose.
The Angle of the house is marked as <HGA,
The Angle of the flash drive is marked as <CIJ,
The Angle of the compass rose is marked as <KEF.

Eureka Math Grade 4 Module 4 Lesson 1 Exit Ticket Answer Key

Question 1.
Draw a line segment to connect the word to its picture.

Answer:
Ray: A Ray can be defined as a part of the line which has a fixed starting point but does not have any endpoint and it can be extended infinitely in one direction and a ray may pass through more than one point.
Line: A line can be defined as a long, straight and continuous path which is represented using arrowheads at both directions and the lines that do not have a fixed point it can be extended in two directions.
Line segment: A line segment is a straight line that passes through the two points and has fixed point and it can not be extended.
Point: A point is an exact location and it has no point only position and point can usually be named often with letters like A, B, etc.
Angle: A figure which is formed by two rays or lines that shares a common endpoint and is called an angle.

Explanation:

Ray: A Ray can be defined as a part of the line which has a fixed starting point but does not have any endpoint and it can be extended infinitely in one direction and a ray may pass through more than one point.
Line: A line can be defined as a long, straight and continuous path which is represented using arrowheads at both directions and the lines that do not have a fixed point it can be extended in two directions.
Line segment: A line segment is a straight line that passes through the two points and has fixed point and it can not be extended.
Point: A point is an exact location and it has no point only position and a point can usually be named often with letters like A, B, etc.
Angle: A figure which is formed by two rays or lines that shares a common endpoint and is called an angle.

Question 2.
How is a line different from a line segment?
Answer:
A line can be defined as a long, straight and continuous path which is represented using arrowheads in both directions and the lines do not have a fixed point it can be extended in two directions, but the line segment is a straight line that passes through the two points and have a fixed point and it can not be extended.

Eureka Math Grade 4 Module 4 Lesson 1 Homework Answer Key

Question 1.
Use the following directions to draw a figure in the box to the right.
a. Draw two points: W and X.
b. Use a straightedge to draw \(\overline{W X}\).
c. Draw a new point that is not on \(\overline{W X}\). Label it Y.
d. Draw \(\overline{W Y}\).
e. Draw a point not on \(\overline{W X}\) or \(\overline{W Y}\). Call it Z.
f. Construct
g. Use the points you’ve already labeled to name one angle. ____________

Answer:
The labeled angle is <XWY.

Explanation:
Here, we will draw two points which are represented with W and X.
And we will use a straightedge to draw \(\overline{W X}\).
And then we will draw a new point that is not on \(\overline{W X}\). And we will label it as Y.
Then we will draw \(\overline{W X}\).
Next we will draw a point not on \(\overline{W X}\) or \(\overline{W Y}\). And we will call it Z.
And then we will construct 
Then we will use these points which were already labeled and name the angle as <XWY.

Question 2.
Use the following directions to draw a figure in the box to the right.
a. Draw two points: W and X.
b. Use a straightedge to draw \(\overline{W X}\).
c. Draw a new point that is not on \(\overline{W X}\). Label it Y.
d. Draw \(\overline{W Y}\).
e. Draw a new point that is not on \(\overline{W Y}\) or on the line containing \(\overline{W X}\). Label it Z.
f. Construct .
g. Identify ∠ZWX by drawing an arc to indicate the position of the angle.
h. Identify another angle by referencing points that you have already drawn. _____________

Answer:
The identified angle is <XW.

Explanation:
Here, we will draw two points and will label them as W and X.
And we will use a straightedge to draw \(\overline{W X}\).
Now we need to draw a new point that is not on \(\overline{W X}\). Label it Y.
Then we will draw \(\overline{W Y}\).
Next, we will draw a new point that is not on \(\overline{W Y}\) or on the line containing \(\overline{W X}\) and Label it as Z.
Then we need to Construct  .
And then we will identify the angle ∠ZWX by drawing an arc to indicate the position of the angle.
So we will Identify another angle by referencing points that we have already drawn and label the angle as <XW.

Question 3.
a. Observe the familiar figures below. Label some points on each figure.
b. Use those points to label and name representations of each of the following in the table below: ray, line, line segment, and angle. Extend segments to show lines and rays.


Extension: Draw a familiar figure. Label it with points, and then identify rays, lines, line segments, and angles as applicable.
Answer:
The ray of the clock is marked as AB,
The ray of the die is marked as EF,
The ray of the number line is marked as AC.
The Line of the clock is marked as BC,
The Line of the die is marked as FG,
The Line of the number line is marked as AB.
The Line segment of the clock is marked as AC,
The Line segment of the die is marked as GH,
The Line segment of the number line is marked as BD.
The Angle of the clock is marked as <CAB,
The Angle of the die is marked as <FGH
The Angle of the number line is marked as <CAB.

Explanation:

Ray: A Ray can be defined as a part of the line which has a fixed starting point but does not have any endpoint and it can be extended infinitely in one direction and a ray may pass through more than one point.
The ray of the clock is marked as AB,
The ray of the die is marked as EF,
The ray of the number line is marked as AC.
Line: A line can be defined as a long, straight and continuous path which is represented using arrowheads at both directions and the lines that do not have fixed points it can be extended in two directions.
The Line of the clock is marked as BC,
The Line of the die is marked as FG,
The Line of the number line is marked as AB.
Line segment: A line segment is a straight line that passes through the two points and has fixed point and it can not be extended.
The Line segment of the clock is marked as AC,
The Line segment of the die is marked as GH,
The Line segment of the number line is marked as BD.
Angle: A figure which is formed by two rays or lines that shares a common endpoint and is called an angle.
So in the above, we can see the clock, die, and a number line.
The Angle of the clock is marked as <CAB,
The Angle of the die is marked as <FGH
The Angle of the number line is marked as <CAB.

Engage NY Eureka Math Grade 6 Module 5 Lesson 17 Answer Key

Eureka Math Grade 6 Module 5 Lesson 17 Opening Exercise Answer Key

Opening Exercise:

a. Write a numerical equation for the area of the figure below. Explain and identify different parts of the figure.

i.
Answer:
A = \(\frac{1}{2}\) (14 cm)(12 cm) = 84cm²
14 cm represents the bose of the figure because 5 cm + 9 cm = 14 cm, and 12 cm represents the altitude of the figure because it forms a right angle with the base.

ii. How would you write an equation that shows the area of a triangle with base b and height h?
Answer:
A = \(\frac{1}{2}\) bh

b. Write a numerical equation for the area of the figure below. Explain and identify different parts of the figure.

Answer:
A = (28 ft.)(18 ft) = 504 ft²
28 ft. represents the base of the rectangle, 18 ft. and 18 ft. represents the height of the rectangle.

ii. How would you write an equation that shows the area of a rectangle with base b and height h?
Answer:
A = bh.

Eureka Math Grade 6 Module 5 Lesson 17 Example Answer Key

Example 1:

Use the net to calculate the surface area of the figure. (Note: all measurements are in centimeters.)

Answer:
→ When you are calculating the area of a figure, what are you finding?
The area of a figure is the amount of space inside a two-dimensional figure.

→ The surface area is similar to the area, but the surface area is used to describe three-dimensional figures. What do you think is meant by the surface area of a solid?
The surface area of a three-dimensional figure is the area of each face added together.

→ What type of figure does the net create? How do you know?
It creates a rectangular prism because there are six rectangular faces.

If the boxes on the grid paper represent a 1 cm × 1 cm box, label the dimensions of the net.

→ The surface area of a figure is the sum of the areas of all faces. Calculate the area of each face, and record this value inside the corresponding rectangle.

→ In order to calculate the surface area, we have to find the sum of the areas we calculated since they represent the area of each face. There are two faces that have an area of 4 cm² and four faces that have an area of 2 cm². How can we use these areas to write a numerical expression to show how to calculate the surface area of the net?
The numerical expression to calculate the surface area of the net would be
(1 cm × 2 cm) + (1 cm × 2 cm) + (1 cm × 2 cm) + (1 cm × 2 cm) + (2 cm × 2 cm)+ (2 cm × 2 cm).

→ Write the expression more compactly, and explain what each part represents on the net.
4(1 cm × 2 cm) + 2(2 cm × 2 cm)
The expression means there are 4 rectangles that have dimensions 1 cm × 2 cm on the net and 2 rectangles that have dimensions 2 cm × 2 cm on the net.

→ What is the surface area of the net?
The surface area of the net is 16 cm².

Example 2:

Use the net to write an expression for surface area. (Note: all measurements are in square feet.)

Answer:
→ What type of figure does the net create? How do you know?
It creates a square pyramid because one face is a square and the other four faces are triangles.

→ If the boxes on the grid paper represent a 1 ft. × 1 ft. square, label the dimensions of the net.

→ How many faces does the rectangular pyramid have?
5

→ Knowing the figure has 5 faces, use the knowledge you gained in Example ito calculate the surface area of the rectangular pyramid.
Area of Base: 3 ft. × 3 ft. = 9 ft²
Area of Triangles: \(\frac{1}{2}\) × 3 ft. × 2 ft. = 3 ft²
Surface Area: 9 ft² + 3 ft² + 3 ft² + 3 ft² + 3 ft² = 21 ft²

Eureka Math Grade 6 Module 5 Lesson 17 Exercise Answer Key

Exercises:

Name the solid the net would create, and then write an expression for the surface area. Use the expression to determine the surface area. Assume that each box on the grid paper represents a 1 cm × 1 cm square. Explain how the expression represents the figure.

Exercise 1.

Answer:
Name of Shape: Rectangular Pyramid, but more specifically a Square Pyramid
Surface Area: 4 cm × 4 cm + 4(\(\frac{1}{2}\) × 4 cm × 3 cm)
Work: 16 cm² + 4(6 cm²) = 40 cm²
The surface area is 40 cm². The figure is made up of a square base that measures 4 cm × 4 cm and four triangles, each with a base of 4 cm and a height of 3 cm.

Exercise 2.

Answer:
Name of Shape: Rectangular Prism
Surface Area: 2(5 cm × 5 cm) + 4(5 cm × 2 cm)
Work: 2(25 cm² ) + 4(10 cm²) = 90 cm²
The surface area is 90 cm². The figure has 2 square faces, each of which measures 5 cm × 5 cm, and 4 rectangular faces, each of which measures 5 cm × 2 cm.

Exercise 3.

Answer:
Name of Shape: Rectangular Pyramid
SurfaceArea: 3 cm × 4 cm + 2(\(\frac{1}{2}\) × 4 cm × 4 cm)+ 2(\(\frac{1}{2}\) × 4 cm × 3 cm)
Work: 12 cm² + 2(8 cm²) + 2(6 cm²) = 40 cm²
The surface area is 40 cm². The figure has 1 rectangular base that measures 3 cm × 4 cm, 2 triangular faces, each with a bose of 4 cm and a height of 4 cm, and 2 other triangular faces, each with a base of 3 cm and a height of 4 cm.

Exercise 4.

Answer:
Name of Shape: Rectangular Prism
Surface Area: 2(6 cm × 5 cm) + 2(5 cm × 1 cm) + 2(6 cm × 1 cm)
Work: 2(30 cm²) + 2(5 cm²) + 2(6 cm²) = 82 cm²
The surface area is 82 cm². The figure has two 6 cm × 5 cm rectangular faces, two 5 cm × 1 cm rectangular faces, and two 6 cm × 1 cm rectangular faces.

Eureka Math Grade 6 Module 5 Lesson 17 Problem Set Answer Key

Name the shape, and write an expression for surface area. Calculate the surface area of the figure. Assume each box on the grid paper represents a 1 ft. × 1 ft. square.

Question 1.

Answer:
Name of Shape: Rectangular Prism
SurfaceArea: (2 ft. × 4 ft.) + (2 ft. × 4 ft.)+ (4 ft. × 7 ft.) + (4 ft. × 7 ft.) + (7 ft. × 2 ft.)+ (7 ft. × 2 ft.)
Work: 2(2 ft. × 4 ft.) + 2(4 ft. × 7 ft.) + 2(7 ft. × 2 ft.)
= 16 ft² + 56 ft² + 28 ft²
= 100 ft²

Question 2.

Answer:
Name of Shape: Rectangular Pyramid
SurfaceArea: (2 ft. × 5 ft.) + (\(\frac{1}{2}\) × 2ft. × 4ft.)+ (\(\frac{1}{2}\) × 2 ft. × 4ft.) + (\(\frac{1}{2}\) × 5 ft. × 4ft.) + \(\frac{1}{2}\) × 5ft. × 4 ft.)
Work: 2 ft. × 5 ft. + 2(\(\frac{1}{2}\) × 2 ft. × 4 ft.) + 2(\(\frac{1}{2}\) × 5 ft. × 4ft.)
= 10 ft² + 8 ft² + 20 ft² = 38 ft²

Explain the error in each problem below. Assume each box on the grid paper represents a 1 m × 1 m square.

Question 3.

Name of Shape: Rectangular Pyramid, but more specifically a Square Pyramid
Area of Base: 3m × 3m = 9m²
Area of Triangles: 3 m × 4m = 12 m²
SurfaceArea: 9m² + 12m² + 12m² + 12m² + 12m² = 57m²
Answer:
The error in the solution is the area of the triangles. In order to calculate the correct area of the triangles, you must use the correct formula A = \(\frac{1}{2}\)bh. Therefore, the area of each triangle would be 6 m² and not 12 m².

Question 4.

Name of Shape: Rectangular Prism or, more specifically. a Cube
Area of Faces: 3m × 3m = 9m²
Surface Area: 9 m² + 9 m² + 9 m² + 9 m² + 9 m² = 45m²
Answer:
The surface area is incorrect because the student did not find the sum of all 6 faces. The solution is shown above only calculates the sum of 5 faces. Therefore, the correct surface area should be 9 m² + 9 m² + 9 m² + 9 m² + 9 m² + 9m² = 54m² and not 45m².

Question 5.
Sofia and Ella are both writing expressions to calculate the surface area of a rectangular prism. However, they wrote different expressions.

a. Examine the expressions below, and determine if they represent the same value. Explain why or why not. Sofia’s Expression:
(3 cm × 4 cm) + (3 cm × 4 cm) + (3 cm × 5 cm) + (3 cm × 5 cm) + (4 cm × 5 cm) + (4 cm × 5 cm)

Ella’s Expression:
2(3 cm × 4 cm) + 2(3 cm × 5 cm) + 2(4 cm × 5 cm)
Answer:
Sofia’s and Ella’s expressions are the same, but Ella used the distributive property to make her expression more compact than Sofia’s.

b. What fact about the surface area of a rectangular prism does Ella’s expression show more clearly than Sofia’s?
Answer:
A rectangular prism is composed of three pairs of sides with identical areas.

Eureka Math Grade 6 Module 5 Lesson 17 Exit Ticket Answer Key

Question 1.
Name the shape, and then calculate the surface area of the figure. Assume each box on the grid paper represents a 1 in. × 1 in. square.

Answer:
Name of Shape: Rectangular Pyramid
Area of Base: 5 in. × 4 in. = 20 in²
Area of Triangles: \(\frac{1}{2}\) × 4 in. × 4 in. = 8 in², \(\frac{1}{2}\) × 5 in. × 4 in. = 10 in²
SurfaceArea: 20 in² +8 in² + 8in² + 10 in² + 10 in² = 56 in²

Eureka Math Grade 6 Module 5 Lesson 17 Addition and Subtraction Equations Answer Key

Addition and Subtraction Equations – Round 1:

Directions: Find the value of m in each equation.

Question 1.
m + 4 = 11
Answer:
m = 7

Question 2.
m + 2 = 5
Answer:
m = 3

Question 3.
m + 5 = 8
Answer:
m = 3

Question 4.
m – 7 = 10
Answer:
m = 17

Question 5.
m – 8 = 1
Answer:
m = 9

Question 6.
m – 4 = 2
Answer:
m = 6

Question 7.
m + 12 = 34
Answer:
m = 22

Question 8.
m + 25 = 45
Answer:
m = 20

Question 9.
m + 43 = 89
Answer:
m = 46

Question 10.
m – 20 = 31
Answer:
m = 51

Question 11.
m – 13 = 34
Answer:
m = 47

Question 12.
m – 45 = 68
Answer:
m = 113

Question 13.
m + 34 = 41
Answer:
m = 7

Question 14.
m + 29 = 52
Answer:
m = 23

Question 15.
m + 37 = 61
Answer:
m = 24

Question 16.
m – 43 = 63
Answer:
m = 106

Question 17.
m – 21 = 40
valuem = 61

Question 18.
m – 54 = 37
Answer:
m = 91

Question 19.
4 + m = 9
Answer:
m = 5

Question 20.
6 + m = 13
Answer:
m = 7

Question 21.
2 + m = 31
Answer:
m = 29

Question 22.
15 = m + 11
Answer:
m = 4

Question 23.
24 = m + 13
Answer:
m = 11

Question 24.
32 = m + 28
Answer:
m = 4

Question 25.
4 = m – 7
Answer:
m = 11

Question 26.
3 = m – 5
Answer:
m = 8

Question 27.
12 = m – 14
Answer:
m = 26

Question 28.
23.6 = m – 7.1
Answer:
m = 30.7

Question 29.
14.2 = m – 33.8
Answer:
m = 48

Question 30.
2.5 = m -41.8
Answer:
m = 44.3

Question 31.
64.9 = m + 23.4
Answer:
m = 41.5

Question 32.
72.2 = m + 38.7
Answer:
m = 33.5

Question 33.
1.81 = m – 15.13
Answer:
m = 16.94

Question 34.
24.68 = m – 56.82
Answer:
m = 81.5

Addition and Subtraction Equations – Round 2:

Directions: Find the value of m in each equation.

Question 1.
m + 2 = 7
Answer:
m = 5

Question 2.
m + 4 = 10
Answer:
m = 6

Question 3.
m + 8 = 15
Answer:
m = 7

Question 4.
m + 7 = 23
Answer:
m = 16

Question 5.
m + 12 = 16
Answer:
m = 4

Question 6.
m – 5 = 2
Answer:
m = 7

Question 7.
m – 3 = 8
Answer:
m = 11

Question 8.
m – 4 = 12
Answer:
m = 16

Question 9.
m – 14 = 45
Answer:
m = 59

Question 10.
m + 23 = 40
Answer:
m = 17

Question 11.
m + 13 = 31
Answer:
m = 18

Question 12.
m – 23 = 48
Answer:
m = 25

Question 13.
m + 38 = 52
Answer:
m = 14

Question 14.
m – 14 = 27
Answer:
m = 41

Question 15.
m – 23 = 35
Answer:
m = 58

Question 16.
m – 17 = 18
Answer:
m = 35

Question 17.
m – 64 = 1
Answer:
m = 65

Question 18.
6 = m + 3
Answer:
m = 3

Question 19.
12 = m + 7
Answer:
m = 5

Question 20.
24 = m + 16
Answer:
m = 8

Question 21.
13 = m + 9
Answer:
m = 4

Question 22.
32 = m – 3
Answer:
m = 35

Question 23.
22 = m – 12
Answer:
m = 34

Question 24.
34 = m – 10
Answer:
m = 44

Question 25.
48 = m + 29
Answer:
m = 19

Question 26.
21 = m + 17
Answer:
m = 4

Question 27.
52 = m + 37
Answer:
m = 15

Question 28.
\(\frac{6}{7}\) + m = \(\frac{4}{7}\)
Answer:
m = \(\frac{2}{7}\)

Question 29.
\(\frac{2}{3}\) = m – \(\frac{5}{3}\)
Answer:
m = \(\frac{7}{3}\)

Question 30.
\(\frac{1}{4}\) – m = \(\frac{8}{3}\)
Answer:
m = \(\frac{35}{12}\)

Question 31.
\(\frac{5}{6}\) = m – \(\frac{7}{12}\)
Answer:
m = \(\frac{17}{12}\)

Question 32.
\(\frac{7}{8}\) = m – \(\frac{5}{12}\)
Answer:
m = \(\frac{31}{24}\)

Question 33.
\(\frac{7}{6}\) + m = \(\frac{16}{3}\)
Answer:
m = \(\frac{25}{6}\)

Question 34.
\(\frac{1}{3}\) + m = \(\frac{13}{15}\)
Answer:
m = \(\frac{8}{15}\)

Engage NY Eureka Math 6th Grade Module 3 Lesson 19 Answer Key

Eureka Math Grade 6 Module 3 Lesson 19 Exercise Answer Key

Exploratory Challenge

The Length of a Line Segment is the Distance Between its End Points

Exercise 1.
Locate and label (4, 5) and (4, – 3). Draw the line segment between the end points given on the coordinate plane. How long is the line segment that you drew? Explain.

Answer:
The length of the line segment is also 8 units. I found that the distance between (4, – 3) and (4, 5) is 8 units. Because the end points are on opposite sides of zero, I added the absolute values of the second coordinates together, so the distance from end to end is 8 units.

Exercise 2.
Draw a horizontal line segment starting at (4, – 3) that has a length of 9 units. What are the possible coordinates of the other end point of the line segment? (There is more than one answer.)
Answer:
(- 5, – 3) or (13, – 3)

Which point did you choose to be the other end point of the horizontal line segment? Explain how and why you chose that point. Locate and label the point on the coordinate grid.
Answer:
The other end point of the horizontal line segment is (- 5, – 3). I chose this point because the other option, (13, – 3), is located off of the given coordinate grid.
Note: Students may choose the end point (13, – 3), but they must change the number scale of the x-axis to do so.

Exercise 3.
Extending Lengths of Line Segments to Sides of Geometric Figures
The two line segments that you have just drawn could be seen as two sides of a rectangle. Given this, the end points of the two line segments would be three of the vertices of this rectangle.
a. Find the coordinates of the fourth vertex of the rectangle. Explain how you find the coordinates of the fourth vertex using absolute value.
Answer:
The fourth vertex is (- 5, 5). The opposite sides of a rectangle are the same length, so the length of the vertical side starting at (- 5, – 3) has to be 8 units long. Also, the side from (- 5, – 3) to the remaining vertex is a vertical line, so the end points must have the same first coordinate. |- 3| = 3, and 8 – 3 = 5, so the remaining vertex must be five units above the x-axis.
Note: Students can use a similar argument using the length of the horizontal side starting at (4, 5), knowing it has to be 9 units long.

b. How does the fourth vertex that you found relate to each of the consecutive vertices in either direction?
Explain.
The fourth vertex has the same first coordinate as (- 5, – 3) because they are the end points of a vertical line segment. The fourth vertex has the same second coordinate as (4, 5) since they are the end points of a horizontal line segment.

c. Draw the remaining sides of the rectangle.
Answer:

Using Lengths of Sides of Geometric Figures to Solve Problems

Exercise 4.
Using the vertices that you have found and the lengths of the line segments between them, find the perimeter of the rectangle.
Answer:
8 + 9 + 8 + 9 = 34; the perimeter of the rectangle is 34 units.

Exercise 5.
Find the area of the rectangle.
Answer:
9 × 8 = 72; the area of the rectangle is 72 units².

Exercise 6.
Draw a diagonal line segment through the rectangle with opposite vertices for end points. What geometric figures are formed by this line segment? What are the areas of each of these figures? Explain.
Answer:
The diagonal line segment cuts the rectangle into two right triangles. The areas of the triangles are 36 units² each because the triangles each make up half of the rectangle, and half of 72 is 36.

Extension (If time allows): Line the edge of a piece of paper up to the diagonal in the rectangle. Mark the length of the diagonal on the edge of the paper. Align your marks horizontally or vertically on the grid, and estimate the length of the diagonal to the nearest integer. Use that estimation to now estimate the perimeter of the triangles.
Answer:
The length of the diagonal is approximately 12 units, and the perimeter of each triangle is approximately 29 units.

Exercise 7
Construct a rectangle on the coordinate plane that satisfies each of the criteria listed below. Identify the coordinate of each of its vertices.
→ Each of the vertices lies in a different quadrant.
→ Its sides are either vertical or horizontal.
→ The perimeter of the rectangle is 28 units.
Answers will vary. The example to the right shows a rectangle with side lengths 10 and 4 units. The coordinates of the rectangle’s vertices are (- 6,3), (4, 3), (4, – 1), and (- 6, – 1).

Using absolute value, show how the lengths of the sides of your rectangle provide a perimeter of 28 units.
Answer:
|- 6| = 6, |4| = 4, and 6 + 4 = 10, so the width of my rectangle is 10 units.
|3| = 3, |-1| = 1, and 3 + 1 = 4, so the height of my rectangle is 4 units.
10 + 4 + 10 + 4 = 28, so the perimeter of my rectangle is 28 units.

Eureka Math Grade 6 Module 3 Lesson 19 Problem Set Answer Key

Question 1.
One end point of a line segment is (-3, -6). The length of the line segment is 7 units. Find four points that could serve as the other end point of the given line segment.
Answer:
(- 10, – 6); (4, – 6); (- 3, 1); (- 3, – 13)

Question 2.
Two of the vertices of a rectangle are (1, – 6) and (- 8, – 6). If the rectangle has a perimeter of 26 units, what are the coordinates of its other two vertices?
Answer:
(1, – 2) and (- 8, – 2), or (1, – 10) and (- 8, – 10)

Question 3.
A rectangle has a perimeter of 28 units, an area of 48 square units, and sides that are either horizontal or vertical. If one vertex is the point (- 5, – 7) and the origin is In the interior of the rectangle, find the vertex of the rectangle that is opposite (- 5, – 7).
Answer:
(1, 1)

Eureka Math Grade 6 Module 3 Lesson 19 Exit Ticket Answer Key

Question 1.
The coordinates of one end point of a line segment are (- 2, – 7). The line segment is 12 units long. Give three
possible coordinates of the line segment’s other end point.
Answer:
(10, – 7); (- 14, – 7); (- 2, 5); (- 2, – 19)

Question 2.
Graph a rectangle with an area of 12 units² such that its vertices lie in at least two of the four quadrants in the coordinate plane. State the lengths of each of the sides, and use absolute value to show how you determined the lengths of the sides.
Answer:
Answers will vary. The rectangle can have side lengths of 6 and 2 or 3 and 4. A sample is provided on the grid on the right. 6 × 2 = 12

Eureka Math Grade 6 Module 3 Lesson 19 Opening Exercise Answer Key

Question 1.
In the coordinate plane, find the distance between the points using absolute value.

Answer:
The distance between the points is 8 units. The points have the same first coordinates and, therefore, lie on the same vertical line. |- 3| = 3, and |5| = 5, and the numbers lie on opposite sides of 0, so their absolute values are added together; 3 + 5 = 8. We can check our answer by just counting the number of units between the two points.

Engage NY Eureka Math 6th Grade Module 4 Lesson 1 Answer Key

Eureka Math Grade 6 Module 4 Lesson 1 Exercise Answer Key

Exercise 1.
Predict what will happen when a tape diagram has a large number of squares, some squares are removed, and then the same amount of squares are added back on.
Answer:
Possible answer: When some squares are removed from a tape diagram, and then the same amount of squares are added back on, the tape diagram will end up with the same amount of squares that it started with.

Exercise 2.
Build a tape diagram with 10 squares.
a. Remove six squares. Write an expression to represent the tape diagram.
Answer:
10 – 6

b. Add six squares onto the tape diagram. Alter the original expression to represent the current tape diagram.
Answer:
10 – 6 + 6

c. Evaluate the expression.
Answer:
10

Exercise 3.
Write an equation, using variables, to represent the identities we demonstrated with tape diagrams.
Answer:
Possible answer: w – x + x = w

Exercise 4.
Using your knowledge of identities, fill In each of the blanks.
a. 4 + 5 – ______ = 4
Answer:
5

b. 25 – _____ + 10 = 25
Answer:
10

C. ______ + 16 – 16 = 45
Answer:
45

d. 56 – 20 + 20 = ______
Answer:
56

Exercise 5.
Using your knowledge of identities, fill In each of the blanks.
a. a + b – ______ = a
Answer:
b

b. c – d + d = ______
Answer:
C

c. e + _______ – f = e
Answer:
f

d. ________ – h + h = g
Answer:
g

Eureka Math Grade 6 Module 4 Lesson 1 Problem Set Answer Key

Question 1.
Fill in each blank.
a. ____ +15 – 15 = 21
21

b. 450 – 230 + 230 = ____
Answer:
450

c. 1289 – ______ + 856 = 1289
Answer:
856

Question 2.
Why are the equations w – x + x = w and w + x – x = w called identities?
Answer:
Possible answer: These equations are called identities because the variables can be replaced with any numbers, and after completing the operations, I returned to the original value.

Eureka Math Grade 6 Module 4 Lesson 1 Exit Ticket Answer Key

Question 1.
Draw a series of tape diagrams to represent the following number sentences.
a. 3 + 5 – 5 = 3
Answer:

b. 8 – 2 + 2 = 8
Answer:

Question 2.
Fill in each blank.
a. 65+ _____ – 15 = 65
Answer:
15

b. ______ + g – g = k
Answer:
k

c. a + b – _______ = a
Answer:
b

d. 367 – 93 + 93 = _________
Answer:
367

Eureka Math Grade 6 Module 4 Lesson 1 Opening Exercise Answer Key

a. Draw a tape diagram to represent the following expression: 5 + 4.
Answer:

b. Write an expression for each tape diagram.
i.

Answer:

ii.

Answer:

Eureka Math Grade 6 Module 4 Lesson 1 Multiplication of Decimals Answer Key

Progression of Exercises

Question 1.
0.5 × 0.5 =
Answer:
0.25

Question 2.
0.6 × 0.6 =
Answer:
0.36

Question 3.
0.7 × 0.7 =
Answer:
0.49

Question 4.
0.5 × 0.6 =
Answer:
0.3

Question 5.
1.5 × 1.5 =
Answer:
2.25

Question 6.
2.5 × 2.5 =
Answer:
6.25

Question 7.
0.25 × 0.25 =
Answer:
0. 0625

Question 8.
0.1 × 0.1 =
Answer:
0.01

Question 9.
0.1 × 123.4 =
Answer:
12.34

Question 10.
0.01 × 123.4 =
Answer:
1.234

Engage NY Eureka Math 6th Grade Module 3 End of Module Assessment Answer Key

Eureka Math Grade 6 Module 3 End of Module Assessment Answer Key

Question 1.
Mr. Kindle invested some money in the stock market. He tracks his gains and losses using a computer program. Mr. Kindle receives a daily email that updates him on all his transactions from the previous day. This morning, his email read as follows:
Good morning, Mr. Kindle,
Yesterday’s investment activity included a loss of $800, a gain of $960, and another gain of $230. Log in now to see your current balance.

a. Write an integer to represent each gain and loss.

Answer:

b. Mr. Kindle noticed that an error had been made on his account. The “loss of $800” should have been a “gain of $800.” Locate and label both points that represent “a loss of $800” and “a gain of $800” on the number line below. Describe the relationship of these two numbers when zero represents no change (gain or loss).

Answer:

– 800 and 800 are opposites.

c. Mr. Kindle wanted to correct the error, so he entered – (- $800) into the program. He made a note that read, “The opposite of the opposite of $800 is $800.” Is his reasoning correct? Explain.
Answer:
Yes, he is correct. The opposite of 800 is – 800, and the opposite of that is 800.

Question 2.
At 6:00 a.m., Buffalo, NY, had a temperature of 10°F. At noon, the temperature was – 10°F, and at midnight, it was – 20°F.
a. Write a statement comparing – 10°F and – 20°F.

Answer:
– 10°F is warmer than – 20°F.

b. Write an inequality statement that shows the relationship between the three recorded temperatures. Which temperature is the warmest?
Answer:
– 20 < – 10 < 10
10°F is the warmest temperature.

c. Explain how to use absolute value to find the number of degrees below zero the temperature was at noon.
Answer:
|- 10| = 10
The temperature at noon was 10° below zero.

d. In Peekskill, NY, the temperature at 6:00 a.m. was – 12°F. At noon, the temperature was the exact opposite of Buffalo’s temperature at 6:00 a.m. At midnight, a meteorologist recorded the temperature as – 6°F in Peekskill. He concluded that “For temperatures below zero, as the temperature increases, the absolute value of the temperature decreases.” Is his conclusion valid? Explain and use a vertical number line to support your answer.
Answer:

|- 12| = 12
|- 10| = 10
|- 6| = 6
The absolute values are decreasing.

Yes, his conclusion is valid. Absolute value is a number’s distance from zero. As the temperature increases from – 12 to – 10 to – 6 they get closer to zero, So their distance from zero is decreasing.

Question 3.
Choose an integer between 0 and – 5 on a number line, and label the point P. Locate and label each of the following points and their values on the number line.

Answer:

a. Label point A: the opposite of point P.
Answer:
3

b. Label point B: a number less than point P.
Answer:
– 5

c. Label point C: a number greater than point P.
Answer:
0

d. Label point D: a number halfway between point P and the integer to the right of point P.
Answer:
– 2.5

Question 4.
Julia is learning about elevation in math class. She decided to research some facts about New York State to better understand the concept. Here are some facts that she found.

• Mount Marcy is the highest point in New York State. It is 5,343 feet above sea level.
• Lake Erie is 210 feet below sea level.
• The elevation of Niagara Falls, NY, is 614 feet above sea level.
• The lobby of the Empire State Building is 50 feet above sea level.
• New York State borders the Atlantic Coast, which is at sea level.
• The lowest point of Cayuga Lake is 435 feet below sea level.

a. Write an integer that represents each location in relationship to sea level.

Answer:

b. Explain what negative and positive numbers tell Julia about elevation.
Answer:
A  negative number means the elevation is below sea level. A positive number means the elevation is above sea level.

c. Order the elevations from least to greatest, and then state their absolute values. Use the chart below to record your work.

Answer:

d. Circle the row in the table that represents sea level. Describe how the order of the elevations below sea level compares to the order of their absolute values. Describe how the order of the elevations above sea level compares to the order of their absolute values.
Answer:
The elevations below sea level have absolute values that are their opposites, so the order is opposite. – 435 < – 210  but 435 > 210. The elevations above sea level are the same as their absolute values, so the order is the same.
50 < 614 < 5,343

Question 5.
For centuries, a mysterious sea serpent has been rumored to live at the bottom of Mysterious Lake. A team of historians used a computer program to plot the last five positions of the sightings.

a. Locate and label the locations of the last four sightings: A (- 9\(\frac{1}{2}\), 0), B(- 3, – 4.75), C(9, 2), and D(8, – 2.5).
Answer:

b. Over time, most of the sightings occurred in Quadrant Ill. Write the coordinates of a point that lies in Quadrant III.
Answer:
(- 6, – 3)

c. What is the distance between point A and the point (9\(\frac{1}{2}\), 0)? Show your work to support your answer.
Answer:

d. What are the coordinates of point E on the coordinate plane?
Answer:
(5, 2)

e. Point F is related to point E. Its x-coordinate is the same as point E’s, but its y-coordinate is the opposite of point E’s. Locate and label point F. What are the coordinates? How far apart are points E and F? Explain how you arrived at your answer.
Answer:
The coordinates of F are (5, -2). Points E and F are 4 units apart. Since their x-coordinates are the same, I just counted the number of units from 2 to – 2 (between their y- Coordinates), and that is 4.

Engage NY Eureka Math 6th Grade Module 3 Mid Module Assessment Answer Key

Eureka Math Grade 6 Module 3 Mid Module Assessment Answer Key

Question 1.
The picture below is a flood gauge that is used to measure how far (in feet) a river’s water level is above or below its normal level.
a. Explain what the number 0 on the gauge represents, and explain what the numbers above and below 0 represent.
Answer:
The number 0 represents the normal average water level in the river. The numbers below 0 indicate low water and the numbers above 0 indicate high water level.

b. Describe what the picture indicates about the river’s current water level.

Answer:
The river’s water level is about 2 feet below normal.

c. What number represents the opposite of the water level shown in the picture, and where is it located on the gauge? What would it mean if the river water was at that level?
Answer:
The water level is currently at approximately – 2.0 feet. The opposite of – 2 is 2. 2 is on the opposite side of 0, or above zero. If the river was at 2, the water level would be higher than normal.

d. If heavy rain is in the forecast for the area for the next 24 hours, what reading might you expect to see on this gauge tomorrow? Explain your reasoning.
Answer:
I would expect to see the water level closer to 0 or even higher. Heavy rain should cause the amount of water in the river to increase, So its level would move up the number line.

Question 2.
Isaac made a mistake in his checkbook. He wrote a check for $8.98 to rent a video game but mistakenly recorded it in his checkbook as an $8.98 deposit.
a. Represent each transaction with a rational number, and explain the difference between the transactions.
Answer:
A check will decrease his account balance
So it can be represented by – 8.98
A deposit will increase his account balance
So it can be represented by 8.98.

b. On the number line below, locate and label the points that represent the rational numbers listed in part (a). Describe the relationship between these two numbers. Zero on the number line represents Isaac’s balance before the mistake was made.

Answer:

The numbers that represent the two transactions are opposites.

c. Use absolute value to explain how a debit of $8.98 and a credit of $8.98 are similar.
Answer:
The check and deposit have the same absolute value (8.98) So they will change his account balance by the same amount of money, but they change the balance in opposite directions.

Question 3.
A local park’s programs committee is raising money by holding mountain bike races on a course through the park. During each race, a computer tracks the competitors’ locations on the course using GPS tracking. The table shows how far each competitor is from a checkpoint.

a. The checkpoint is represented by 0 on the number line. Locate and label points on the number line
for the positions of each listed participant. Label the points using rational numbers.

Answer:

b. Which of the competitors is closest to the checkpoint? Explain.
Answer:
Florence is closest to the checkpoint because her distance to the checkpoint is 0.1 miles which is less than any of the other girls distances.

c. Two competitors are the same distance from the checkpoint. Are they in the same location? Explain.
Answer:
Rebecca and Lita are both of 0.5 miles from the checkpoint, they are just on opposite sides of the check point.

d. Who is closer to finishing the race, Nancy or Florence? Support your answer.
Answer:
Florence is closer to finishing the race because the number representing her position (- 0.1) is to the right of (-\(\frac{2}{10}\)) on the number line which is Nancy’s position.

Question 4.
Andrea and Marta are testing three different coolers to see which keeps the coldest temperature. They placed a bag of ice in each cooler, closed the coolers, and then measured the air temperature inside each after 90 minutes. The temperatures are recorded in the table below:

Marta wrote the following inequality statement about the temperatures:
– 4.3 < – 2.91 < 5.7.
Andrea claims that Marta made a mistake in her statement and that the inequality statement should be written as
– 2.91 < – 4.3 < 5.7.
a. Is either student correct? Explain.
Answer:
Marta is correct because the order of the numbers in her inequality is the same as the order of the numbers on the number line moving from left to right (or from down to up).

b. The students want to find a cooler that keeps the temperature inside the cooler more than 3 degrees below the freezing point of water (0°C) after 90 minutes. Indicate which of the tested coolers meets this goal, and explain why.
Answer:
More than 3 degrees below 0°C means less than – 3°C. The only cooler to keep the temperature less than – 3°C is Cooler c. Cooler c held a temperature of – 4.3°C which is to the left of – 3°C on the number line.

Question 5.
Mary manages a company that has been hired to flatten a plot of land. She took several elevation samples from the land and recorded those elevations below:

a. The landowner wants the land flat and at the same level as the road that passes in front of it. The road’s elevation is 830 feet above sea level. Describe in words how elevation samples B, C, and E compare to the elevation of the road.
Answer:
Samples B and C are higher than 830 feet and so higher than the road. sample E is lower than 830 feet and so lower than the road.

b. The table below shows how some other elevation samples compare to the level of the road:

Write the values in the table in order from least to greatest.
_________< _________< _________< _________< _________< _________
Answer:
– 4.5    <   – 0.9    <   – 0.5    <   1.3    <   2.2    <   3.1 

c. Indicate which of the values from the table in part (b) is farthest from the elevation of the road. Use absolute value to explain your answer.
Answer:
– 4.5 (sample k) is furthest from the elevation of the road because its absolute value (4.5) is greater than the absolute values of the other sample in the table.

Engage NY Eureka Math 8th Grade Module 4 Lesson 4 Answer Key

Eureka Math Grade 8 Module 4 Lesson 4 Exercise Answer Key

For each problem, show your work, and check that your solution is correct.

Exercise 1.
Solve the linear equation x+x+2+x+4+x+6=-28. State the property that justifies your first step and why you chose it.
Answer:
The left side of the equation can be transformed from x+x+2+x+4+x+6 to 4x+12 using the commutative and distributive properties. Using these properties decreases the number of terms of the equation. Now we have the equation:
4x+12=-28
4x+12-12=-28-12
4x=-40
\(\frac{1}{4}\)∙4x=-40∙\(\frac{1}{4}\)
x=-10.
The left side of the equation is equal to (-10)+(-10)+2+(-10)+4+(-10)+6, which is -28. Since the left side is equal to the right side, then x=-10 is the solution to the equation.
Note: Students could use the division property in the last step to get the answer.

Exercise 2.
Solve the linear equation 2(3x+2)=2x-1+x. State the property that justifies your first step and why you chose it.
Answer:
Both sides of equation can be rewritten using the distributive property. I have to use it on the left side to expand the expression. I have to use it on the right side to collect like terms.
The left side is
2(3x+2)=6x+4.
The right side is
2x-1+x=2x+x-1
=3x-1.
The equation is
6x+4=3x-1
6x+4-4=3x-1-4
6x=3x-5
6x-3x=3x-3x-5
(6-3)x=(3-3)x-5
3x=-5
\(\frac{1}{3}\)∙3x=\(\frac{1}{3}\)∙(-5)
x=-\(\frac{5}{3}\).
The left side of the equation is 2(3x+2). Replacing x with –\(\frac{5}{3}\) gives 2(3(-\(\frac{5}{3}\))+2)=2(-5+2)=2(-3)=-6. The right side of the equation is 2x-1+x. Replacing x with –\(\frac{5}{3}\) gives 2(-\(\frac{5}{3}\))-1+(-\(\frac{5}{3}\))=-\(\frac{10}{3}\)-1-\(\frac{5}{3}\)=-6. Since both sides are equal to -6, then x=-\(\frac{5}{3}\) is a solution to 2(3x+2)=2x-1+x.
Note: Students could use the division property in the last step to get the answer.

Exercise 3.
Solve the linear equation x-9=\(\frac{3}{5}\) x. State the property that justifies your first step and why you chose it.
Answer;
I chose to use the subtraction property of equality to get all terms with an x on one side of the equal sign.
x-9=\(\frac{3}{5}\) x
x-x-9=\(\frac{3}{5}\) x-x
(1-1)x-9=(\(\frac{3}{5}\)-1)x
-9=-\(\frac{2}{5}\) x
–\(\frac{5}{2}\)∙(-9)=-\(\frac{5}{2}\)∙-\(\frac{2}{5}\) x
4\(\frac{5}{2}\)=x
The left side of the equation is 4\(\frac{5}{2}\)– \(\frac{18}{2}\)=\(\frac{27}{2}\). The right side is \(\frac{3}{5}\)∙4\(\frac{5}{2}\)=\(\frac{3}{1}\)∙\(\frac{9}{2}\)=\(\frac{27}{2}\). Since both sides are equal to the same number, then x=4\(\frac{5}{2}\) is a solution to x-9=\(\frac{3}{5}\) x.

Exercise 4.
Solve the linear equation 29-3x=5x+5. State the property that justifies your first step and why you chose it.
Answer:
I chose to use the addition property of equality to get all terms with an x on one side of the equal sign.
29-3x=5x+5
29-3x+3x=5x+3x+5
29=8x+5
29-5=8x+5-5
24=8x
\(\frac{1}{8}\)∙24=\(\frac{1}{8}\)∙8x
3=x
The left side of the equal sign is 29-3(3)=29-9=20. The right side is equal to 5(3)+5=15+5=20. Since both sides are equal, x=3 is a solution to 29-3x=5x+5.
Note: Students could use the division property in the last step to get the answer.

Exercise 5.
Solve the linear equation \(\frac{1}{3}\) x-5+171=x. State the property that justifies your first step and why you chose it.
Answer:
I chose to combine the constants -5 and 171. Then, I used the subtraction property of equality to get all terms with an x on one side of the equal sign.
\(\frac{1}{3}\) x-5+171=x
\(\frac{1}{3}\) x+166=x
\(\frac{1}{3}\) x-\(\frac{1}{3}\) x+166=x-\(\frac{1}{3}\) x
166=\(\frac{2}{3}\) x
166∙\(\frac{3}{2}\)=\(\frac{3}{2}\)∙\(\frac{2}{3}\) x
83∙3=x
249=x
The left side of the equation is \(\frac{1}{3}\)∙249-5+171=83-5+171=78+171=249, which is exactly equal to the right side. Therefore, x=249 is a solution to \(\frac{1}{3}\) x-5+171=x.

Eureka Math Grade 8 Module 4 Lesson 4 Exit Ticket Answer Key

Question 6.
Guess a number for x that would make the equation true. Check your solution.
5x-2=8
Answer:
When x=2, the left side of the equation is 8, which is the same as the right side. Therefore, x=2 is the solution to the equation.

Question 7.
Use the properties of equality to solve the equation 7x-4+x=12. State which property justifies your first step and why you chose it. Check your solution.
Answer:
I used the commutative and distributive properties on the left side of the equal sign to simplify the expression to fewer terms.
7x-4+x=12
7x+x-4=12
(7+1)x-4=12
8x-4=12
8x-4+4=12+4
8x=16
\(\frac{8}{8}\)x=\(\frac{16}{8}\)
x=2
The left side of the equation is 7(2)-4+2=14-4+2=12. The right side is also 12. Since the left side equals the right side, x=2 is the solution to the equation.

Question 8.
Use the properties of equality to solve the equation 3x+2-x=11x+9. State which property justifies your first step and why you chose it. Check your solution.
Answer:
I used the commutative and distributive properties on the left side of the equal sign to simplify the expression to fewer terms.
3x+2-x=11x+9
3x-x+2=11x+9
(3-1)x+2=11x+9
2x+2=11x+9
2x-2x+2=11x-2x+9
(2-2)x+2=(11-2)x+9
2=9x+9
2-9=9x+9-9
-7=9x
–\(\frac{7}{9}\)=\(\frac{9}{9}\) x
–\(\frac{7}{9}\)=x
The left side of the equation is 3(\(\frac{-7}{9}\))+2-\(\frac{-7}{9}\)=-\(\frac{21}{9}\)+\(\frac{18}{9}\)+\(\frac{7}{9}\)=\(\frac{4}{9}\). The right side is 11(-\(\frac{7}{9}\))+9=\(\frac{-77}{9}\)+\(\frac{81}{9}\)=\(\frac{4}{9}\). Since the left side equals the right side, x=-\(\frac{7}{9}\) is the solution to the equation.

Eureka Math Grade 8 Module 4 Lesson 4 Problem Set Answer Key

Students solve equations using properties of equality.

For each problem, show your work, and check that your solution is correct.

Question 1.
Solve the linear equation x+4+3x=72. State the property that justifies your first step and why you chose it.
Answer:
I used the commutative and distributive properties on the left side of the equal sign to simplify the expression to fewer terms.
x+4+3x=72
x+3x+4=72
(1+3)x+4=72
4x+4=72
4x+4-4=72-4
4x=68
\(\frac{4}{4}\) x=\(\frac{68}{4}\)
x=17
The left side is equal to 17+4+3(17)=21+51=72, which is equal to the right side. Therefore, x=17 is a solution to the equation x+4+3x=72.

Question 2.
Solve the linear equation x+3+x-8+x=55. State the property that justifies your first step and why you chose it.
Answer:
I used the commutative and distributive properties on the left side of the equal sign to simplify the expression to fewer terms.
x+3+x-8+x=55
x+x+x+3-8=55
(1+1+1)x+3-8=55
3x-5=55
3x-5+5=55+5
3x=60
\(\frac{3}{3}\) x=\(\frac{60}{3}\)
x=20
The left side is equal to 20+3+20-8+20=43-8+20=35+20=55, which is equal to the right side. Therefore, x=20 is a solution to x+3+x-8+x=55.

Question 3.
Solve the linear equation \(\frac{1}{2}\) x+10=\(\frac{1}{4}\) x+54. State the property that justifies your first step and why you chose it.
Answer;
I chose to use the subtraction property of equality to get all of the constants on one side of the equal sign.
\(\frac{1}{2}\) x+10=\(\frac{1}{4}\) x+54
\(\frac{1}{2}\) x+10-10=\(\frac{1}{4}\) x+54-10
\(\frac{1}{2}\) x=\(\frac{1}{4}\) x+44
\(\frac{1}{2}\) x-\(\frac{1}{4}\) x=\(\frac{1}{4}\) x-\(\frac{1}{4}\) x+44
\(\frac{1}{4}\) x=44
4∙\(\frac{1}{4}\) x=4∙44
x=176
The left side of the equation is \(\frac{1}{2}\) (176)+10=88+10=98. The right side of the equation is
\(\frac{1}{4}\) (176)+54=44+54=98. Since both sides equal 98, x=176 is a solution to the equation
\(\frac{1}{2}\) x+10=\(\frac{1}{4}\) x+54.

Question 4.
Solve the linear equation \(\frac{1}{4}\) x+18=x. State the property that justifies your first step and why you chose it.
I chose to use the subtraction property of equality to get all terms with an x on one side of the equal sign.
\(\frac{1}{4}\) x+18=x
\(\frac{1}{4}\) x-\(\frac{1}{4}\) x+18=x-\(\frac{1}{4}\) x
18=\(\frac{3}{4}\) x
\(\frac{4}{3}\)∙18=\(\frac{4}{3}\)∙\(\frac{3}{4}\) x
24=x
The left side of the equation is \(\frac{1}{4}\) (24)+18=6+18=24, which is what the right side is equal to. Therefore, x=24 is a solution to \(\frac{1}{4}\) x+18=x.

Question 5.
Solve the linear equation 17-x=\(\frac{1}{3}\)∙15+6. State the property that justifies your first step and why you chose it.
Answer:
The right side of the equation can be simplified to 11. Then, the equation is
17-x=11,
and x=6. Both sides of the equation equal 11; therefore, x=6 is a solution to the equation 17-x=\(\frac{1}{3}\)∙15+6. I was able to solve the equation mentally without using the properties of equality.

Question 6.
Solve the linear equation \(\frac{x+x+2}{4}\)=189.5. State the property that justifies your first step and why you chose it.
Answer:
I chose to use the multiplication property of equality to get all terms with an x on one side of the equal sign.
\(\frac{x+x+2}{4}\)=189.5
x+x+2=4(189.5)
2x+2=758
2x+2-2=758-2
2x=756
\(\frac{2}{2}\) x=\(\frac{756}{2}\)
x=378
The left side of the equation is \(\frac{378+378+2}{4}\)=\(\frac{758}{4}\)=189.5, which is equal to the right side of the equation. Therefore, x=378 is a solution to \(\frac{x+x+2}{4}\)=189.5.

Question 7.
Alysha solved the linear equation 2x-3-8x=14+2x-1. Her work is shown below. When she checked her answer, the left side of the equation did not equal the right side. Find and explain Alysha’s error, and then solve the equation correctly.
2x-3-8x=14+2x-1
-6x-3=13+2x
-6x-3+3=13+3+2x
-6x=16+2x
-6x+2x=16
-4x=16
\(\frac{-4}{-4}\) x=\(\frac{16}{-4}\)
x=-4
Answer:
Alysha made a mistake on the fifth line. She added 2x to the left side of the equal sign and subtracted 2x on the right side of the equal sign. To use the property correctly, she should have subtracted 2x on both sides of the equal sign, making the equation at that point:
-6x-2x=16+2x-2x
-8x=16
\(\frac{-8}{-8}\) x=\(\frac{16}{-8}\)
x=-2.

Engage NY Eureka Math 8th Grade Module 4 Lesson 3 Answer Key

Eureka Math Grade 8 Module 4 Lesson 3 Exercise Answer Key

Exercise 1.
Is the equation a true statement when x=-3? In other words, is -3 a solution to the equation 6x+5=5x+8+2x? Explain.
Answer:
If we replace x with the number -3, then the left side of the equation is
6∙(-3)+5=-18+5
=-13″,”
and the right side of the equation is
5∙(-3)+8+2∙(-3)=-15+8-6
=-7-6
=-13.
Since -13=-13, then x=-3 is a solution to the equation 6x+5=5x+8+2x.
Note: Some students may have transformed the equation.

Exercise 2.
Does x=12 satisfy the equation 16-\(\frac{1}{2}\) x=\(\frac{3}{4}\) x+1? Explain.
Answer:
If we replace x with the number 12, then the left side of the equation is
16-\(\frac{1}{2}\) x=16-\(\frac{1}{2}\)∙(12)
=16-6
=10,
and the right side of the equation is
\(\frac{3}{4}\) x+1=\(\frac{3}{4}\)∙(12)+1
=9+1
=10.
Since 10=10, then x=12 is a solution to the equation 16-\(\frac{1}{2}\) x=\(\frac{3}{4}\) x+1.

Exercise 3.
Chad solved the equation 24x+4+2x=3(10x-1) and is claiming that x=2 makes the equation true. Is Chad correct? Explain.
Answer:
If we replace x with the number 2, then the left side of the equation is
24x+4+2x=24∙2+4+2∙2
=48+4+4
=56,
and the right side of the equation is
3(10x-1)=3(10∙2-1)
=3(20-1)
=3(19)
=57.
Since 56≠57, then x=2 is not a solution to the equation 24x+4+2x=3(10x-1), and Chad is not correct.

Exercise 4.
Lisa solved the equation x+6=8+7x and claimed that the solution is x=-\(\frac{1}{3}\). Is she correct? Explain.
Answer:
If we replace x with the number –\(\frac{1}{3}\), then the left side of the equation is
x+6=-\(\frac{1}{3}\)+6
=5 \(\frac{2}{3}\),
and the right side of the equation is
8+7x=8+7∙(-\(\frac{1}{3}\))
=8-\(\frac{7}{3}\)
=\(\frac{24}{3}\)–\(\frac{7}{3}\)
=\(\frac{17}{3}\).
Since 5 \(\frac{2}{3}\)=\(\frac{17}{3}\), then x=-\(\frac{1}{3}\) is a solution to the equation x+6=8+7x, and Lisa is correct.

Exercise 5.
Angel transformed the following equation from 6x+4-x=2(x+1) to 10=2(x+1). He then stated that the solution to the equation is x=4. Is he correct? Explain.
Answer:
No, Angel is not correct. He did not transform the equation correctly. The expression on the left side of the equation 6x+4-x=2(x+1) would transform to
6x+4-x=6x-x+4
=(6-1)x+4
=5x+4.
If we replace x with the number 4, then the left side of the equation is
5x+4=5∙4+4
=20+4
=24,
and the right side of the equation is
2(x+1)=2(4+1)
=2(5)
=10.
Since 24≠10, then x=4 is not a solution to the equation 6x+4-x=2(x+1), and Angel is not correct.

Exercise 6.
Claire was able to verify that x=3 was a solution to her teacher’s linear equation, but the equation got erased from the board. What might the equation have been? Identify as many equations as you can with a solution of x=3.
Answer;
Answers will vary. Ask students to share their equations and justifications as to how they knew x=3 would make a true number sentence.

Exercise 7.
Does an equation always have a solution? Could you come up with an equation that does not have a solution?
Answer:
Answers will vary. Expect students to write equations that are false. Ask students to share their equations and justifications as to how they knew the equation they wrote did not have a solution. The concept of “no solution” is introduced in Lesson 6 and solidified in Lesson 7.

Eureka Math Grade 8 Module 4 Lesson 3 Problem Set Answer Key

Students practice determining whether or not a given number is a solution to the linear equation.

Question 1.
Given that 2x+7=27 and 3x+1=28, does 2x+7=3x+1? Explain.
Answer:
No, because a linear equation is a statement about equality. We are given that 2x+7=27, but 3x+1=28. Since each linear expression is equal to a different number, 2x+7≠3x+1.

Question 2.
Is -5 a solution to the equation 6x+5=5x+8+2x? Explain.
Answer:
If we replace x with the number -5, then the left side of the equation is
6∙(-5)+5=-30+5
=-25,
and the right side of the equation is
5∙(-5)+8+2∙(-5)=-25+8-10
=-17-10
=-27.
Since -25≠-27, then -5 is not a solution of the equation 6x+5=5x+8+2x.
Note: Some students may have transformed the equation.

Question 3.
Does x=1.6 satisfy the equation 6-4x=-\(\frac{x}{4}\)? Explain.
Answer:
If we replace x with the number 1.6, then the left side of the equation is
6-4∙1.6=6-6.4
=-0.4,
and the right side of the equation is
–\(\frac{-1.6}{4}\)=-0.4.
Since -0.4=-0.4, then x=1.6 is a solution of the equation 6-4x=-\(\frac{x}{4}\).

Question 4.
Use the linear equation 3(x+1)=3x+3 to answer parts (a)–(d).
a. Does x=5 satisfy the equation above? Explain.
Answer:
If we replace x with the number 5, then the left side of the equation is
3(5+1)=3(6)
=18,
and the right side of the equation is
3x+3=3∙5+3
=15+3
=18.
Since 18=18, then x=5 is a solution of the equation 3(x+1)=3x+3.

b. Is x=-8 a solution of the equation above? Explain.
Answer:
If we replace x with the number -8, then the left side of the equation is
3(-8+1)=3(-7)
=-21,
and the right side of the equation is
3x+3=3∙(-8)+3
=-24+3
=-21.
Since -21=-21, then x=-8 is a solution of the equation 3(x+1)=3x+3.

c. Is x=\(\frac{1}{2}\) a solution of the equation above? Explain.
Answer:
If we replace x with the number \(\frac{1}{2}\), then the left side of the equation is
3(\(\frac{1}{2}\)+1)=3(\(\frac{1}{2}\)+\(\frac{2}{2}\))
=3(\(\frac{3}{2}\))
=\(\frac{9}{2}\),
and the right side of the equation is
3x+3=3∙(\(\frac{1}{2}\))+3
= \(\frac{3}{2}\)+3
=\(\frac{3}{2}\)+\(\frac{6}{2}\)
=\(\frac{9}{2}\).
Since \(\frac{9}{2}\)=\(\frac{9}{2}\), then x=\(\frac{1}{2}\) is a solution of the equation 3(x+1)=3x+3.

d. What interesting fact about the equation 3(x+1)=3x+3 is illuminated by the answers to parts (a), (b), and (c)? Why do you think this is true?
Answer:
Note to teacher: Ideally, students will notice that the equation 3(x+1)=3x+3 is an identity under the distributive law. The purpose of this problem is to prepare students for the idea that linear equations can have more than one solution, which is a topic of Lesson 7.

Eureka Math Grade 8 Module 4 Lesson 3 Exit Ticket Answer Key

Question 1.
Is 8 a solution to \(\frac{1}{2}\) x+9=13? Explain.
Answer:
If we replace x with the number 8, then the left side is \(\frac{1}{2}\) (8)+9=4+9=13, and the right side is 13. Since 13=13, then x=8 is a solution.

Question 2.
Write three different equations that have x=5 as a solution.
Answer:
Answers will vary. Accept equations where x=5 makes a true number sentence.

Question 3.
Is -3 a solution to the equation 3x-5=4+2x? Explain.
Answer:
If we replace x with the number -3, then the left side is 3(-3)-5=-9-5=-14. The right side is 4+2(-3)=4-6=-2. Since -14≠-2, then -3 is not a solution of the equation.

Engage NY Eureka Math 8th Grade Module 4 Lesson 7 Answer Key

Eureka Math Grade 8 Module 4 Lesson 7 Exercise Answer Key

Exercises
Solve each of the following equations for x.

Exercise 1.
7x-3=5x+5
Answer:
7x-3=5x+5
7x-3+3=5x+5+3
7x=5x+8
7x-5x=5x-5x+8
2x=8
x=4

Exercise 2.
7x-3=7x+5
Answer:
7x-3=7x+5
7x-7x-3=7x-7x+5
-3≠5
This equation has no solution.

Exercise 3.
7x-3=-3+7x
Answer:
7x-3=-3+7x
7x-3+3=-3+3+7x
7x=7x
OR
7x-3=-3+7x
7x-7x-3=-3+7x-7x
-3=-3

Exercises 4–10

Give a brief explanation as to what kind of solution(s) you expect the following linear equations to have. Transform the equations into a simpler form if necessary.

Exercise 4.
11x-2x+15=8+7+9x
Answer:
If I use the distributive property on the left side, I notice that the coefficients of the x are the same, specifically 9, and when I simplify the constants on the right side, I notice that they are the same. Therefore, this equation has infinitely many solutions.

Exercise 5.
3(x-14)+1=-4x+5
Answer:
If I use the distributive property on the left side, I notice that the coefficients of x are different. Therefore, the equation has one solution.

Exercise 6.
-3x+32-7x=-2(5x+10)
Answer:
If I use the distributive property on the each side of the equation, I notice that the coefficients of x are the same, but the constants are different. Therefore, this equation has no solutions.

Exercise 7.
\(\frac{1}{2}\) (8x+26)=13+4x
Answer:
If I use the distributive property on the left side, I notice that the coefficients of x are the same, specifically 4, and the constants are also the same, 13. Therefore, this equation has infinitely many solutions.

Exercise 8.
Write two equations that have no solutions.
Answer:
Answers will vary. Verify that students have written equations where the coefficients of x on each side of the equal sign are the same and that the constants on each side are unique.

Exercise 9.
Write two equations that have one unique solution each.
Answer:
Answers will vary. Accept equations where the coefficients of x on each side of the equal sign are unique.

Exercise 10.
Write two equations that have infinitely many solutions.
Answer:
Answers will vary. Accept equations where the coefficients of x and the constants on each side of the equal sign are the same.

Eureka Math Grade 8 Module 4 Lesson 7 Problem Set Answer Key

Students apply their knowledge of solutions to linear equations by writing equations with unique solutions, no solutions, and infinitely many solutions.

Question 1.
Give a brief explanation as to what kind of solution(s) you expect for the linear equation 18x+\(\frac{1}{2}\) =6(3x+25). Transform the equation into a simpler form if necessary.
Answer:
If I use the distributive property on the right side of the equation, I notice that the coefficients of x are the same, but the constants are different. Therefore, this equation has no solutions.

Question 2.
Give a brief explanation as to what kind of solution(s) you expect for the linear equation 8-9x=15x+7+3x. Transform the equation into a simpler form if necessary.
Answer:
If I collect the like terms on the right side of the equation, then I notice that the coefficients of x are different, and so are the constants. Therefore, this equation will have a unique solution.

Question 3.
Give a brief explanation as to what kind of solution(s) you expect for the linear equation 5(x+9)=5x+45. Transform the equation into a simpler form if necessary.
Answer:
This is an identity under the distributive property. Therefore, this equation will have infinitely many solutions.

Question 4.
Give three examples of equations where the solution will be unique; that is, only one solution is possible.
Answer:
Accept equations where the coefficients of x on each side of the equal sign are unique.

Question 5.
Solve one of the equations you wrote in Problem 4, and explain why it is the only solution.
Answer:
Verify that students solved one of the equations. They should have an explanation that includes the statement that there is only one possible number that could make the equation true. They may have referenced one of the simpler forms of their transformed equation to make their case.

Question 6.
Give three examples of equations where there will be no solution.
Answer:
Accept equations where the coefficients of x on each side of the equal sign are the same, and the constants on each side are unique.

Question 7.
Attempt to solve one of the equations you wrote in Problem 6, and explain why it has no solution.
Answer:
Verify that students have solved one of the equations. They should have an explanation that includes the statement about getting a false equation (e.g., 6≠10).

Question 8.
Give three examples of equations where there will be infinitely many solutions.
Answer:
Accept equations where the coefficients of x and constants on each side of the equal sign are the same.

Question 9.
Attempt to solve one of the equations you wrote in Problem 8, and explain why it has infinitely many solutions.
Answer:
Verify that students have solved one of the equations. They should have an explanation that includes the statement about the linear expressions being exactly the same, an identity; therefore, any rational number x would make the equation true.

Eureka Math Grade 8 Module 4 Lesson 7 Exit Ticket Answer Key

Give a brief explanation as to what kind of solution(s) you expect the following linear equations to have. Transform the equations into a simpler form if necessary.

Question 1.
3(6x+8)=24+18x
Answer:
If I use the distributive property on the left side, I notice that the coefficients of x are the same, and the constants are the same. Therefore, this equation has infinitely many solutions.

Question 2.
12(x+8)=11x-5
Answer:
If I use the distributive property on the left side, I notice that the coefficients of x are different, and the constants are different. Therefore, this equation has a unique solution.

Question 3.
5x-8=11-7x+12x
Answer:
If I collect the like terms on the right side, I notice that the coefficients of x are the same, but the constants are different. Therefore, this equation has no solution.

Engage NY Eureka Math 8th Grade Module 4 Lesson 6 Answer Key

Eureka Math Grade 8 Module 4 Lesson 6 Exercise Answer Key

Exercises
Find the value of x that makes the equation true.

Exercise 1.
17-5(2x-9)=-(-6x+10)+4
Answer:
17-5(2x-9)=-(-6x+10)+4
17-10x+45=6x-10+4
62-10x=6x-6
62-10x+10x=6x+10x-6
62=16x-6
62+6=16x-6+6
68=16x
\(\frac{68}{16}\)=\(\frac{16}{16}\) x
\(\frac{68}{16}\) =x
\(\frac{17}{4}\) =x

Exercise 2.
-(x-7)+\(\frac{5}{3}\) =2(x+9)
Answer;
-(x-7)+\(\frac{5}{3}\) =2(x+9)
-x+7+\(\frac{5}{3}\) =2x+18
-x+\(\frac{26}{3}\) =2x+18
-x+x+\(\frac{26}{3}\) =2x+x+18
\(\frac{26}{3}\) =3x+18
\(\frac{26}{3}\) -18=3x+18-18
–\(\frac{28}{3}\) =3x
\(\frac{1}{3}\)∙\(\frac{-28}{3}\) =\(\frac{1}{3}\)∙3x
–\(\frac{28}{9}\) =x

Question 3.
\(\frac{4}{9}\) +4(x-1)=\(\frac{28}{9}\) -(x-7x)+1
Answer;
\(\frac{4}{9}\) +4(x-1)=\(\frac{28}{9}\) -(x-7x)+1
\(\frac{4}{9}\) –\(\frac{4}{9}\) +4(x-1)=\(\frac{28}{9}\) –\(\frac{4}{9}\) -(x-7x)+1
4x-4=2\(\frac{4}{9}\) -x+7x+1
4x-4=\(\frac{33}{9}\) +6x
4x-4+4=\(\frac{33}{9}\) +36/9+6x
4x=\(\frac{69}{9}\) +6x
4x-6x=\(\frac{69}{9}\) +6x-6x
-2x=\(\frac{23}{3}\)
\(\frac{1}{-2}\) ∙-2x=\(\frac{1}{-2}\)∙\(\frac{23}{3}\)
x=-\(\frac{23}{6}\)

Question 4.
5(3x+4)-2x=7x-3(-2x+11)
Answer:
5(3x+4)-2x=7x-3(-2x+11)
15x+20-2x=7x+6x-33
13x+20=13x-33
13x-13x+20=13x-13x-33
20≠-33
This equation has no solution.

Question 5.
7x-(3x+5)-8=\(\frac{1}{2}\) (8x+20)-7x+5
Answer:
7x-(3x+5)-8=\(\frac{1}{2}\) (8x+20)-7x+5
7x-3x-5-8=4x+10-7x+5
4x-13=-3x+15
4x-13+13=-3x+15+13
4x=-3x+28
4x+3x=-3x+3x+28
7x=28
x=4

Question 6.
Write at least three equations that have no solution.
Answer:
Answers will vary. Verify that the equations written have no solution.

Eureka Math Grade 8 Module 4 Lesson 6 Problem Set Answer Key

Students practice using the distributive property to transform equations and solve.

Transform the equation if necessary, and then solve it to find the value of x that makes the equation true.

Question 1.
x-(9x-10)+11=12x+3(-2x+\(\frac{1}{3}\))
x-(9x-10)+11=12x+3(-2x+\(\frac{1}{3}\))
x-9x+10+11=12x-6x+1
-8x+21=6x+1
-8x+8x+21=6x+8x+1
21=14x+1
21-1=14x+1-1
20=14x
\(\frac{20}{14}\)=\(\frac{14}{14}\)
\(\frac{10}{7}\)=x

Question 2.
7x+8(x+\(\frac{1}{4}\) )=3(6x-9)-8
Answer:
7x+8(x+\(\frac{1}{4}\) )=3(6x-9)-8
7x+8x+2=18x-27-8
15x+2=18x-35
15x-15x+2=18x-15x-35
2=3x-35
2+35=3x-35+35
37=3x
\(\frac{37}{3}\) =\(\frac{3}{3}\) x
\(\frac{37}{3}\) =x

Question 3.
-4x-2(8x+1)=-(-2x-10)
Answer:
-4x-2(8x+1)=-(-2x-10)
-4x-16x-2=2x+10
-20x-2=2x+10
-20x+20x-2=2x+20x+10
-2=22x+10
-2-10=22x+10-10
-12=22x
–\(\frac{12}{22}\) =\(\frac{22}{22}\) x
–\(\frac{6}{11}\) =x

Question 4.
11(x+10)=132
Answer:
11(x+10)=132
(\(\frac{1}{11}\) )11(x+10)=(\(\frac{1}{11}\) )132
x+10=12
x+10-10=12-10
x=2

Question 5.
37x+\(\frac{1}{2}\) -(x+\(\frac{1}{4}\) )=9(4x-7)+5
Answer:
37x+\(\frac{1}{2}\) -(x+\(\frac{1}{4}\) )=9(4x-7)+5
37x+\(\frac{1}{2}\) -x-\(\frac{1}{4}\) =36x-63+5
36x+\(\frac{1}{4}\) =36x-58
36x-36x+\(\frac{1}{4}\) =36x-36x-58
\(\frac{1}{4}\) ≠-58
This equation has no solution.

Question 6.
3(2x-14)+x=15-(-9x-5)
Answer:
3(2x-14)+x=15-(-9x-5)
6x-42+x=15+9x+5
7x-42=20+9x
7x-7x-42=20+9x-7x
-42=20+2x
-42-20=20-20+2x
-62=2x
-31=x

Question 7.
8(2x+9)=56
Answer:
8(2x+9)=56
(\(\frac{1}{8}\) )8(2x+9)=(\(\frac{1}{8}\) )56
2x+9=7
2x+9-9=7-9
2x=-2
(\(\frac{1}{2}\) )2x=(\(\frac{1}{2}\) )-2
x=-1

Eureka Math Grade 8 Module 4 Lesson 6 Exit Ticket Answer Key

Transform the equation if necessary, and then solve to find the value of x that makes the equation true.

Question 1.
5x-(x+3)=\(\frac{1}{3}\) (9x+18)-5
Answer:
5x-(x+3)=\(\frac{1}{3}\) (9x+18)-5
5x-x-3=3x+6-5
4x-3=3x+1
4x-3x-3=3x-3x+1
x-3=1
x-3+3=1+3
x=4

Question 2.
5(3x+9)-2x=15x-2(x-5)
Answer:
5(3x+9)-2x=15x-2(x-5)
15x+45-2x=15x-2x+10
13x+45=13x+10
13x-13x+45=13x-13x+10
45≠10
Since 45≠10, the equation has no solution.

Engage NY Eureka Math 8th Grade Module 4 Lesson 5 Answer Key

Eureka Math Grade 8 Module 4 Lesson 5 Example Answer Key

Example 1.
One angle is five degrees less than three times the measure of another angle. Together, the angle measures have a sum of 143°. What is the measure of each angle?

Provide students with time to make sense of the problem and persevere in solving it. They could begin their work by guessing and checking, drawing a diagram, or other methods as appropriate. Then, move to the algebraic method shown below.
→ What do we need to do first to solve this problem?
→ First, we need to define our variable (symbol). Let x be the measure of the first angle in degrees.
→ If x is the measure of the first angle, how do you represent the measure of the second angle?
→ The second angle is 3x-5.
→ What is the equation that represents this situation?
→ The equation is x+3x-5=143.
→ The equation that represents this situation is x+3x-5=143. Solve for x, and then determine the measure of each angle.

As students share their solutions for this and subsequent problems, ask them a variety of questions to reinforce the concepts of the last few lessons. For example, ask students to discuss whether or not this is a linear equation and how they know, to justify their steps and explain why they chose their particular first step, to explain what the solution means, or to justify how they know their answer is correct.
Answer:
x+3x-5=143
(1+3)x-5=143
4x-5=143
4x-5+5=143+5
4x=148
x=37
The measure of the first angle is 37°. The second angle is 3(37°)-5°=111°-5°=106°.

Example 2.
Given a right triangle, find the degree measure of the angles if one angle is ten degrees more than four times the degree measure of the other angle and the third angle is the right angle.

Give students time to work. As they work, walk around and identify students who are writing and solving the problem in different ways. The instructional goal of this example is to make clear that there are different ways to solve a linear equation as opposed to one “right way.” Select students to share their work with the class. If students do not come up with different ways of solving the equation, talk them through the following student work samples.
Again, as students share their solutions, ask them a variety of questions to reinforce the concepts of the last few lessons. For example, ask students to discuss whether or not this is a linear equation and how they know, to justify their steps and explain why they chose their particular first step, to explain what the solution means, or to justify how they know their answer is correct.
Answer:
Solution One
Let x be the measure of the first angle. Then, the second angle is 4x+10. The sum of the measures for the angles for this right triangle is x+4x+10+90=180.
x+4x+10+90=180
(1+4)x+100=180
5x+100=180
5x+100-100=180-100
5x=80
x=16
The measure of the first angle is 16°, the measure of the second angle is 4(16°)+10°=64°+10°=74°, and the measure of the third angle is 90°.

Solution Two
Let x be the measure of the first angle. Then, the second angle is 4x+10. Since we have a right triangle, we already know that one angle is 90°, which means that the sum of the other two angles is 90: x+4x+10=90.
x+4x+10=90
(1+4)x+10=90
5x+10=90
5x+10-10=90-10
5x=80
x=16
The measure of the first angle is 16°, the measure of the second angle is 4(16°)+10°=64°+10°=74°, and the measure of the third angle is 90°.

Solution Three
Let x be the measure of the second angle. Then, the first angle is \(\frac{x-10}{4}\). Since we have a right triangle, we already know that one angle is 90°, which means that the sum of the other two angles is 90: x+\(\frac{x-10}{4}\)=90.
x+\(\frac{x-10}{4}\)=90
4(x+\(\frac{x-10}{4}\)=90)
4x+x-10=360
(4+1)x-10=360
5x-10=360
5x-10+10=360+10
5x=370
x=74
The measure of the second angle is 74°, the measure of the first angle is \(\frac{74^{\circ}-10^{\circ}}{4}\)=\(\frac{64^{\circ}}{4}\)=16°, and the measure of the third angle is 90°.

Solution Four
Let x be the measure of the second angle. Then, the first angle is \(\frac{x-10}{4}\). The sum of the three angles is
x+\(\frac{x-10}{4}\)+90=180.
x+\(\frac{x-10}{4}\)+90=180
x+\(\frac{x-10}{4}\)+90-90=180-90
x+\(\frac{x-10}{4}\)=90
\(\frac{4 x}{4}\)+\(\frac{x-10}{4}\)=90
\(\frac{4 x+x-10}{4}\)=90
4x+x-10=360
5x-10+10=360+10
5x=370
x=74
The measure of the second angle is 74°, the measure of the first angle is \(\frac{74^{\circ}-10^{\circ}}{4}\)=\(\frac{64^{\circ}}{4}\)=16°, and the measure of the third angle is 90°.

Make sure students see at least four different methods of solving the problem. Conclude this example with the statements below.
→ Each method is slightly different either in terms of how the variable is defined or how the properties of equality are used to solve the equation. The way you find the answer may be different from your classmates’ or your teacher’s.
→ As long as you are accurate and do what is mathematically correct, you will find the correct answer.

Eureka Math Grade 8 Module 4 Lesson 5 Exercise Answer Key

Exercises
For each of the following problems, write an equation and solve.

Exercise 1.
A pair of congruent angles are described as follows: The degree measure of one angle is three more than twice a number, and the other angle’s degree measure is 54.5 less than three times the number. Determine the measure of the angles in degrees.
Answer;
Let x be the number. Then, the measure of one angle is 3+2x, and the measure of the other angle is 3x-54.5. Because the angles are congruent, their measures are equal. Therefore,
3+2x=3x-54.5
3+2x-2x=3x-2x-54.5
3=x-54.5
3+54.5=x-54.5+54.5
57.5=x
Replacing x with 57.5 in 3+2x gives 3+2(57.5)=3+115=118; therefore the measure of the angles is 118°.

Exercise 2.
The measure of one angle is described as twelve more than four times a number. Its supplement is twice as large. Find the measure of each angle in degrees.
Answer;
Let x be the number. Then, the measure of one angle is 4x+12. The other angle is 2(4x+12)=8x+24. Since the angles are supplementary, their sum must be 180°.
4x+12+8x+24=180
12x+36=180
12x+36-36=180-36
12x=144
x=12
Replacing x with 12 in 4x+12 gives 4(12)+12=48+12=60. Replacing x with 12 in 2(4x+12) gives 2(4(12)+12)=2(48+12)=2(60)=120. Therefore, the measures of the angles are 60° and 120°.

Exercise 3.
A triangle has angles described as follows: The measure of the first angle is four more than seven times a number, the measure of the second angle is four less than the first, and the measure of the third angle is twice as large as the first. What is the measure of each angle in degrees?
Answer:
Let x be the number. The measure of the first angle is 7x+4. The measure of the second angle is 7x+4-4=7x. The measure of the third angle is 2(7x+4)=14x+8. The sum of the angles of a triangle must be 180°.
7x+4+7x+14x+8=180
28x+12=180
28x+12-12=180-12
28x=168
x=6
Replacing x with 6 in 7x+4 gives 7(6)+4=42+4=46. Replacing x with 6 in 7x gives 7(6)=42. Replacing x with 6 in 14x+8 gives 14(6)+8=84+8=92. Therefore, the measures of the angles are 46°, 42°, and 92°.

Exercise 4.
One angle measures nine more than six times a number. A sequence of rigid motions maps the angle onto another angle that is described as being thirty less than nine times the number. What is the measure of the angle in degrees?
Answer:
Let x be the number. Then, the measure of one angle is 6x+9. The measure of the other angle is 9x-30. Since rigid motions preserve the measures of angles, then the measure of these angles is equal.
6x+9=9x-30
6x+9-9=9x-30-9
6x=9x-39
6x-9x=9x-9x-39
-3x=-39
x=13
Replacing x with 13 in 6x+9 gives 6(13)+9=78+9=87. Therefore, the angle measure is 87°.

Exercise 5.
A right triangle is described as having an angle of measure six less than negative two times a number, another angle measure that is three less than negative one-fourth the number, and a right angle. What are the measures of the angles in degrees?
Answer;
Let x be a number. Then, the measure of one angle is -2x-6. The measure of the other angle is –\(\frac{x}{4}\)-3. The sum of the two angles must be 90°.
-2x-6+(-\(\frac{x}{4}\))-3=90
(-\(\frac{8x}{4}\))+(-\(\frac{x}{4}\))-9=90
(-\(\frac{9x}{4}\))-9+9=90+9
–\(\frac{9x}{4}\)=99
-9x=396
x=-44
Replacing x with -44 gives -2x-6 gives -2(-44)-6=88-6=82. Replacing x with -44 in –\(\frac{x}{4}\)-3 gives 90-82=8. Therefore, the angle measures are 82° and 8°.

Exercise 6.
One angle is one less than six times the measure of another. The two angles are complementary angles. Find the measure of each angle in degrees.
Answer:
Let x be the measure of the first angle. Then, the measure of the second angle is 6x-1. The sum of the measures will be 90 because the angles are complementary.
x+6x-1=90
7x-1=90
7x-1+1=90+1
7x=91
x=13
The first angle is x and therefore measures 13°. Replacing x with 13 in 6x-1 gives 6(13)-1=78-1=77. Therefore, the second angle measure is 77°.

Eureka Math Grade 8 Module 4 Lesson 5 Problem Set Answer Key

Students practice writing and solving linear equations.

For each of the following problems, write an equation and solve.

Question 1.
The measure of one angle is thirteen less than five times the measure of another angle. The sum of the measures of the two angles is 140°. Determine the measure of each angle in degrees.
Answer:
Let x be the measure of the one angle. Then, the measure of the other angle is 5x-13.
x+5x-13=140
6x-13=140
6x-13+13=140+13
6x=153
x=25.5
Since one angle measure is x, it is 25.5°. Replacing x with 25.5 in 5x-13 gives
5(25.5)-13=140-25.5=114.5. Therefore, the other angle measures 114.5°.

Question 2.
An angle measures seventeen more than three times a number. Its supplement is three more than seven times the number. What is the measure of each angle in degrees?
Answer:
Let x be the number. Then, the measure of one angle is 3x+17. The measure of the other angle is 7x+3. Since the angles are supplementary, the sum of their measures will be 180.
3x+17+7x+3=180
10x+20=180
10x+20-20=180-20
10x=160
x=16
Replacing x with 16 in 3x+17 gives 3(16)+17=65. Replacing x with 16 in 7x+3 gives (16)+3= 112+3=115. Therefore, the angle measures are 65° and 115°.

Question 3.
The angles of a triangle are described as follows: ∠A is the largest angle; its measure is twice the measure of ∠B. The measure of ∠C is 2 less than half the measure of ∠B. Find the measures of the three angles in degrees.
Answer:
Let x be the measure of ∠B. Then, the measure of ∠A is 2x, and the measure of ∠C is \(\frac{x}{2}\)-2. The sum of the measures of the angles must be 180°.
x+2x+\(\frac{x}{2}\) -2=180
3x+\(\frac{x}{2}\) -2+2=180+2
3x+\(\frac{x}{2}\) =182
6\(\frac{x}{2}\) +\(\frac{x}{2}\) =182
7\(\frac{x}{2}\) =182
7x=364
x=52
Since x is the measure of ∠B, then ∠B is 52°. Replacing x with 52 in 2x gives 2(52)=104. Therefore, the measure of ∠A is 104°. Replacing x with 52 in \(\frac{x}{2}\) -2 gives \(\frac{52}{2}\)-2=26-2=24. Therefore, the measure of ∠C is 24°.

Question 4.
A pair of corresponding angles are described as follows: The measure of one angle is five less than seven times a number, and the measure of the other angle is eight more than seven times the number. Are the angles congruent? Why or why not?
Answer:
Let x be the number. Then, the measure of one angle is 7x-5, and the measure of the other angle is 7x+8. Assume they are congruent, which means their measures are equal.
7x-5=7x+8
7x-7x-5=7x-7x+8
-5≠8
Since -5≠8, the angles are not congruent.

Question 5.
The measure of one angle is eleven more than four times a number. Another angle is twice the first angle’s measure. The sum of the measures of the angles is 195°. What is the measure of each angle in degrees?
Answer:
Let x be the number. The measure of one angle can be represented with 4x+11, and the other angle’s measure can be represented as 2(4x+11)=8x+22.
4x+11+8x+22=195
12x+33=195
12x+33-33=195-33
12x=162
x=13.5
Replacing x with 13.5 in 4x+11 gives 4(13.5)+11=54+11=65. Replacing x with 13.5 in 2(4x+11) gives 2(4(13.5)+11)=2(54+11)=2(65)=130. Therefore, the measures of the angles are 65° and 130°.

Question 6.
Three angles are described as follows: ∠B is half the size of ∠A. The measure of ∠C is equal to one less than two times the measure of ∠B. The sum of ∠A and ∠B is 114°. Can the three angles form a triangle? Why or why not?
Answer:
Let x represent the measure of ∠A. Then, the measure of ∠B is \(\frac{x}{2}\) , and the measure of ∠C is 2(\(\frac{x}{2}\) )-1=x-1.
The sum of the measures of ∠A and ∠B is 114.
x+\(\frac{x}{2}\) =114
\(\frac{3x}{2}\) =114
3x=228
x=76
Since x is the measure of ∠A, then ∠A is 76°. Replacing x with 76 in \(\frac{x}{2}\) gives \(\frac{76}{2}\)=38; therefore, the measure of ∠B is 38°. Replacing x with 76 in x-1 gives 76-1=75, therefore the measure of ∠C is 75°. The sum of the three angle measures is 76°+38°+75°=189°. Since the sum of the measures of the interior angles of a triangle must equal 180°, these angles do not form a triangle. The sum is too large.

Eureka Math Grade 8 Module 4 Lesson 5 Exit Ticket Answer Key

For each of the following problems, write an equation and solve.

Question 1.
Given a right triangle, find the measures of all of the angles, in degrees, if one angle is a right angle and the measure of the second angle is six less than seven times the measure of the third angle.
Answer:
Let x represent the measure of the third angle. Then, 7x-6 can represent the measure of the second angle. The sum of the two angles in the right triangle will be 90°.
7x-6+x=90
8x-6=90
8x-6+6=90+6
8x=96
\(\frac{8}{8}\) x=\(\frac{96}{8}\)
x=12
The third angle is x and therefore measures 12°. Replacing x with 12 in 7x-6 gives 7(12)-6=84-6=78. Therefore, the measure of the second angle is 78°. The measure of the third angle is 90°.

Question 2.
In a triangle, the measure of the first angle is six times a number. The measure of the second angle is nine less than the first angle. The measure of the third angle is three times the number more than the measure of the first angle. Determine the measure of each angle in degrees.
Answer:
Let x be the number. Then, the measure of the first angle is 6x, the measure of the second angle is 6x-9, and the measure of the third angle is 3x+6x. The sum of the measures of the angles in a triangle is 180°.
6x+6x-9+3x+6x=180
21x-9=180
21x-9+9=180+9
21x=189
\(\frac{21}{21}\) x=\(\frac{189}{21}\)
x=9
Replacing x with 9 in 6x gives 6(9)=54. Replacing x with 9 in 6x-9 gives 6(9)-9=54-9=45. Replacing x with 9 in 3x+6x gives 54+3(9)=54+27=81. Therefore, the angle measures are 54°, 45°, and 81°.