Engage NY Eureka Math 8th Grade Module 3 Lesson 6 Answer Key
Eureka Math Grade 8 Module 3 Lesson 6 Example Answer Key
Example 1.
Students learn the multiplicative effect of scale factor on a point. Note that this effect holds when the center of dilation is the origin. In this lesson, the center of any dilation used is always assumed to be (0,0).
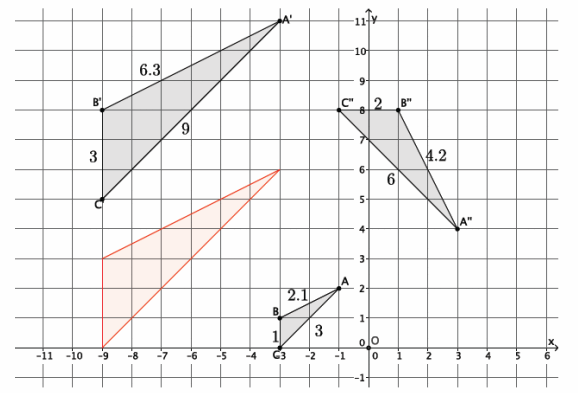
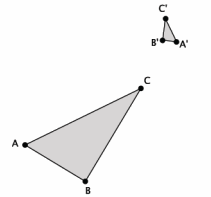
Show the diagram below, and ask students to look at and write or share a claim about the effect that dilation has on the coordinates of dilated points.
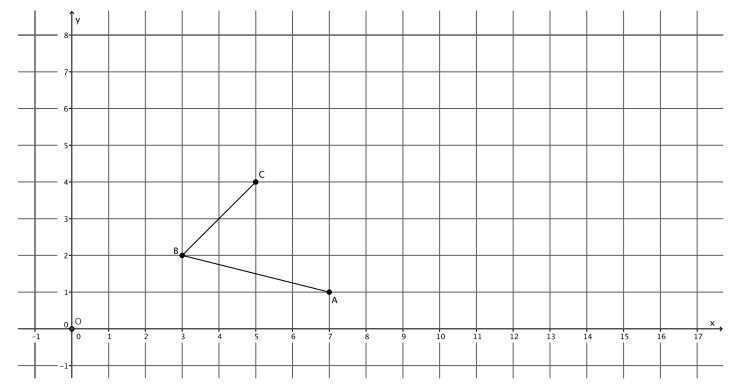
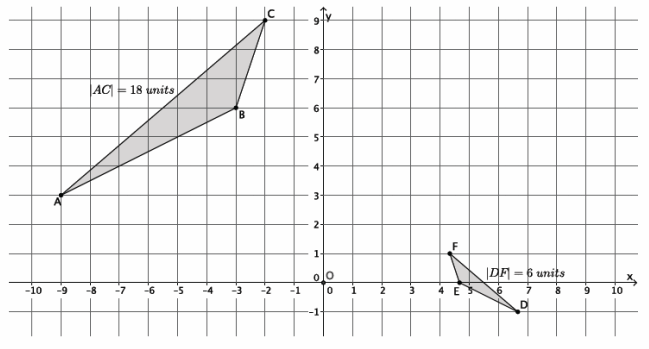
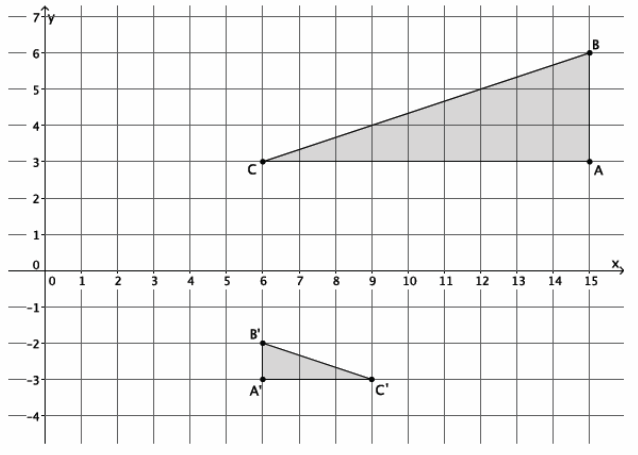
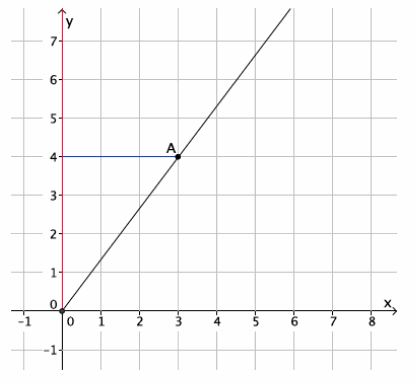
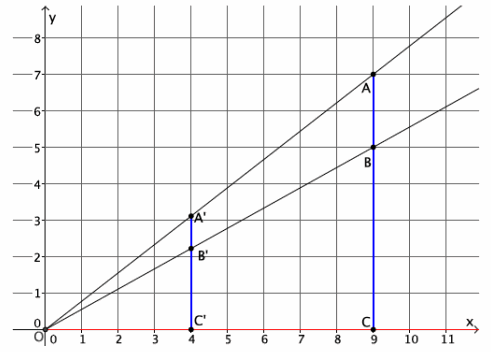
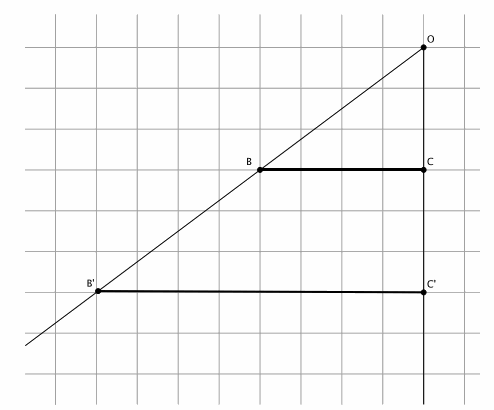
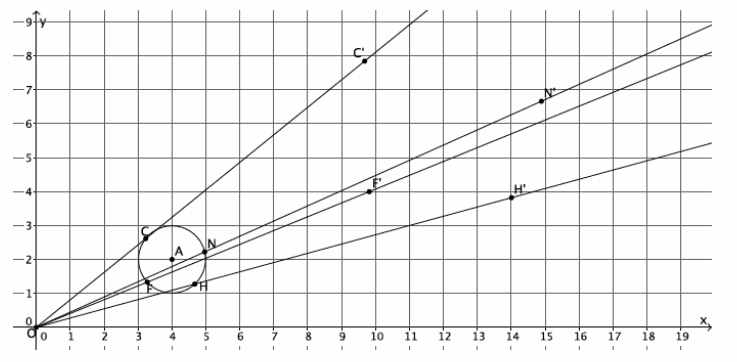
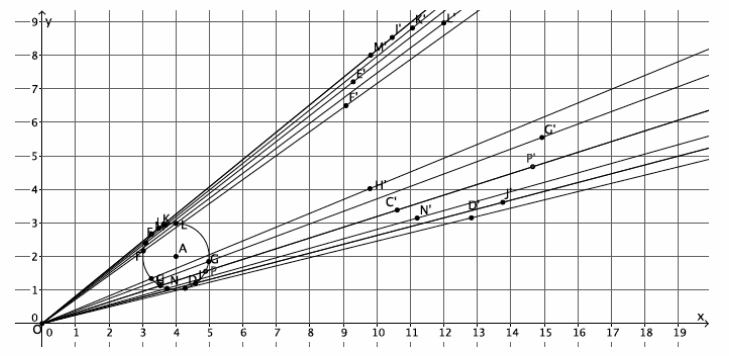
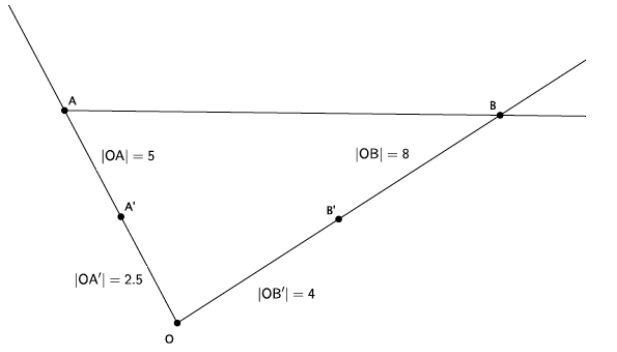
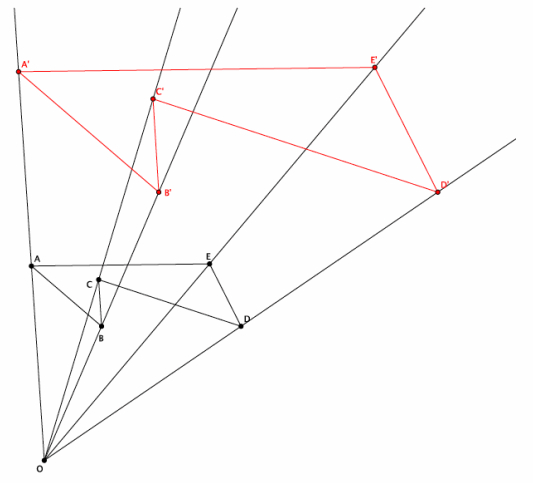
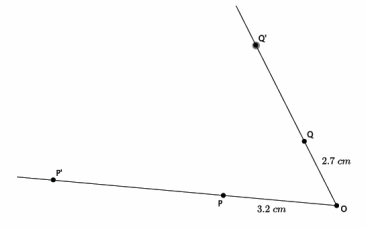
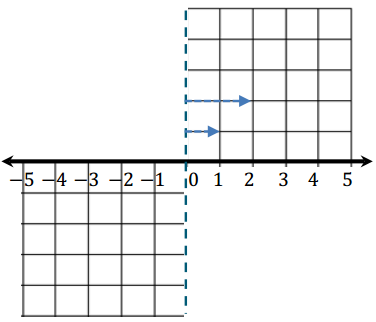
→ The graph below represents a dilation from center (0,0) by scale factor r=2.
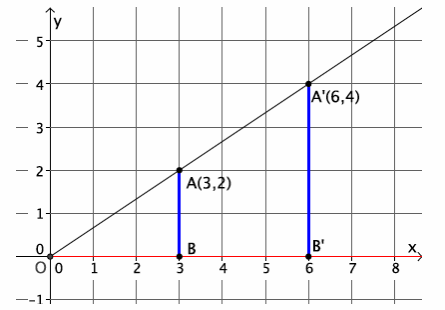
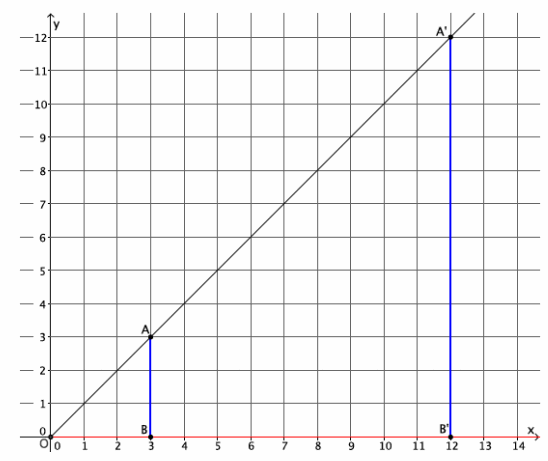
Show students the second diagram below so they can check if their claims were correct. Give students time to verify the claims that they made about the above graph with the one below. Then, have them share their claims with the class. Use the discussion that follows to crystallize what students observed.
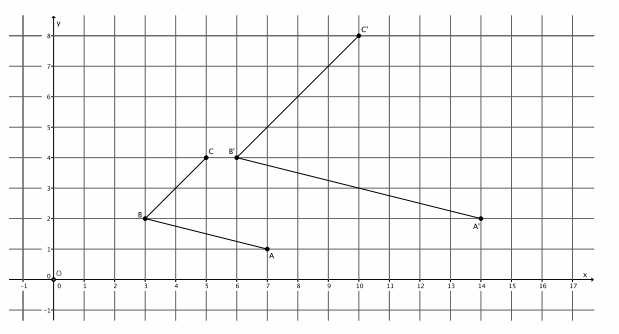
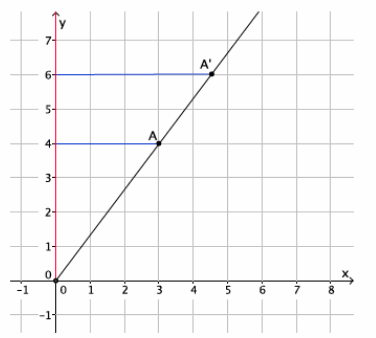
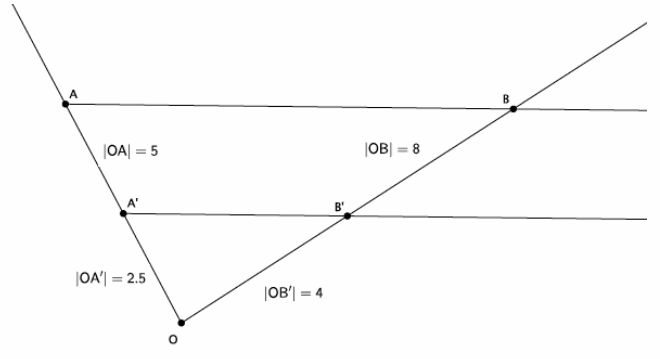
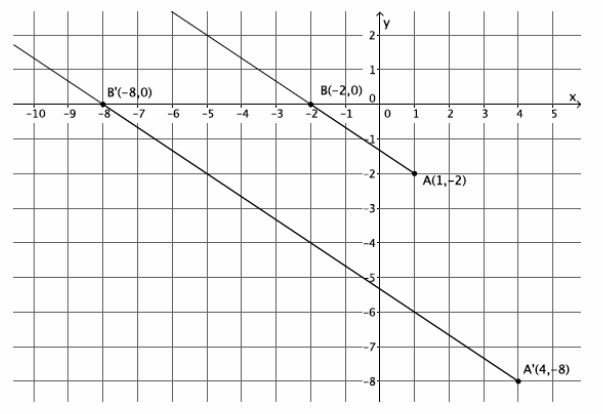
→ The graph below represents a dilation from center (0,0) by scale factor r=4.
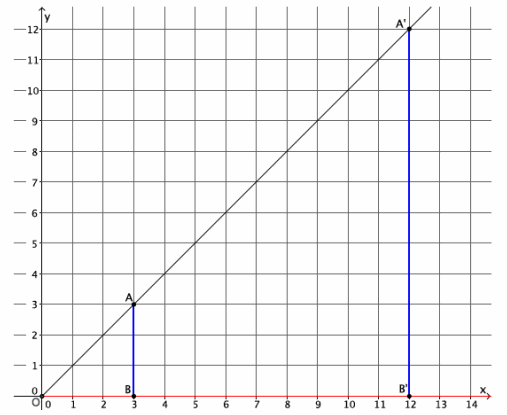
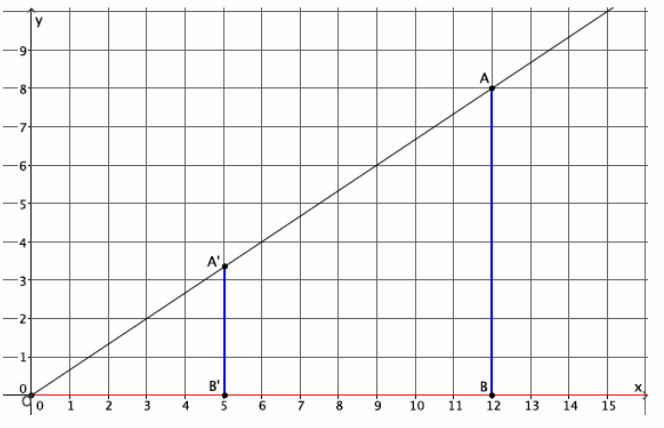
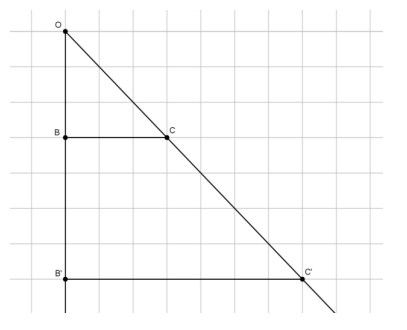
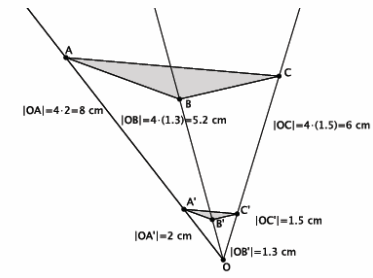
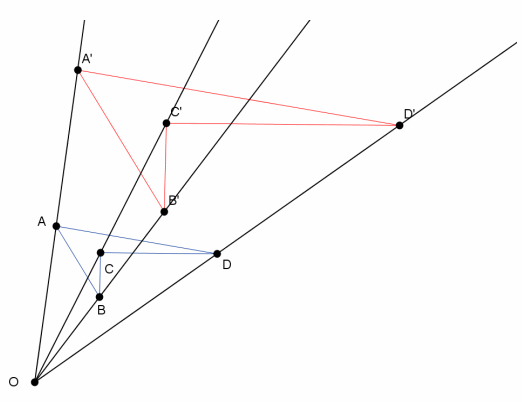
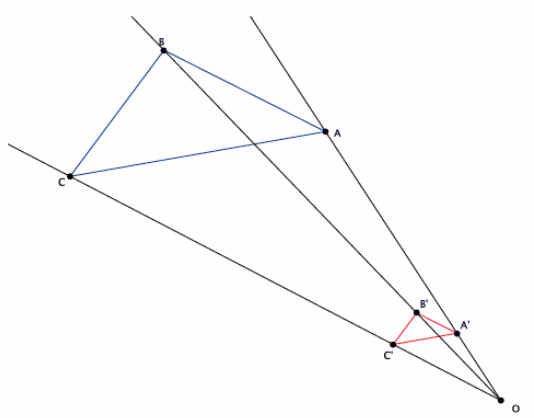
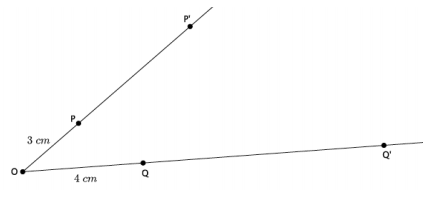
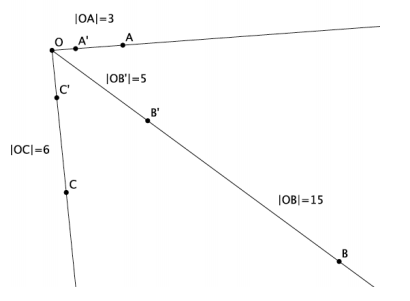
→ In Lesson 5, we found the location of a dilated point by using the knowledge of dilation and scale factor, as well as the lines of the coordinate plane to ensure equal angles, to find the coordinates of the dilated point. For example, we were given the point A(5,2) and told the scale factor of dilation was r=2. Remember that the center of this dilation is (0,0). We created the following picture and determined the location of A’to be (10,4).
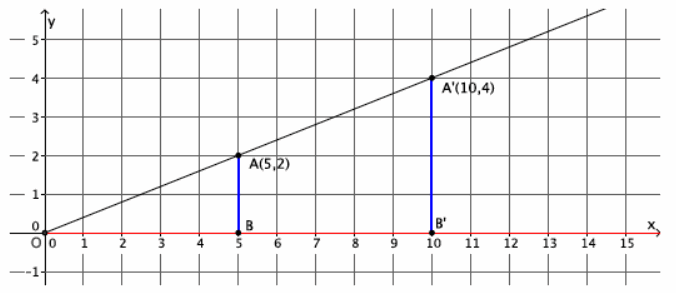
→ We can use this information and the observations we made at the beginning of class to develop a shortcut for finding the coordinates of dilated points when the center of dilation is the origin.
→ Notice that the horizontal distance from the y-axis to point A was multiplied by a scale factor of 2. That is, the x-coordinate of point A was multiplied by a scale factor of 2. Similarly, the vertical distance from the x-axis to point A was multiplied by a scale factor of 2.
→ Here are the coordinates of point A(5,2) and the dilated point A'(10,4). Since the scale factor was 2, we can more easily see what happened to the coordinates of A after the dilation if we write the coordinates of A’as (2∙5,2∙2), that is, the scale factor of 2 multiplied by each of the coordinates of A to get A’.
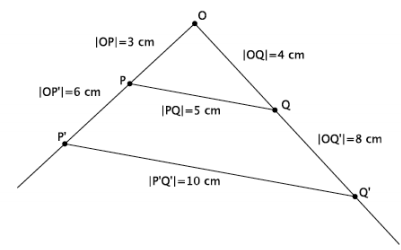
→ The reasoning goes back to our understanding of dilation. The length r|OB|=|OB’|, by the definition of dilation, and the length r|AB|=|A’B’|; therefore,
r=\(\frac{\left|O B^{\prime}\right|}{|O B|}\) =\(\frac{\left|A^{\prime} B^{\prime}\right|}{|A B|}\),
where the length of the segment OB’is the x-coordinate of the dilated point (i.e., 10), and the length of the segment A’B’is the y-coordinate of the dilated point (i.e., 4).
In other words, based on what we know about the lengths of dilated segments, when the center of dilation is the origin, we can determine the coordinates of a dilated point by multiplying each of the coordinates in the original point by the scale factor.
Example 2.
Students learn the multiplicative effect of scale factor on a point.
→ Let’s look at another example from Lesson 5. We were given the point A(7,6) and asked to find the location of the dilated point A’when r=\(\frac{11}{7}\). Our work on this problem led us to coordinates of approximately (11,9.4) for point A’. Verify that we would get the same result if we multiply each of the coordinates of point A by the scale factor.
A'(\(\frac{11}{7}\)∙7,\(\frac{11}{7}\)∙6)
\(\frac{11}{7}\)∙7=11
and
\(\frac{11}{7}\)∙6=\(\frac{66}{7}\)≈9.4
Therefore, multiplying each coordinate by the scale factor produced the desired result.
Example 3.
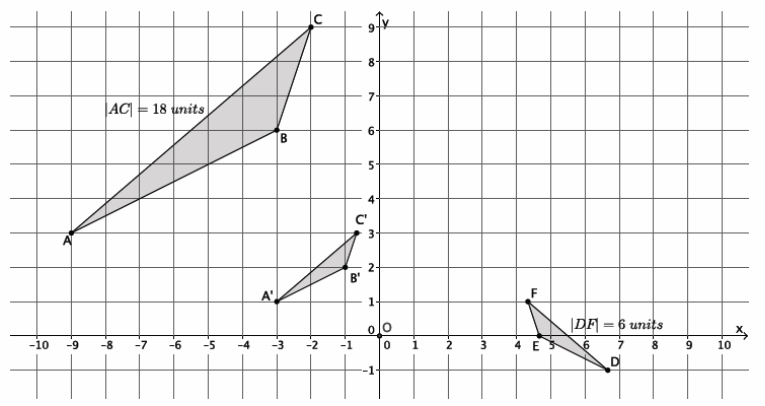
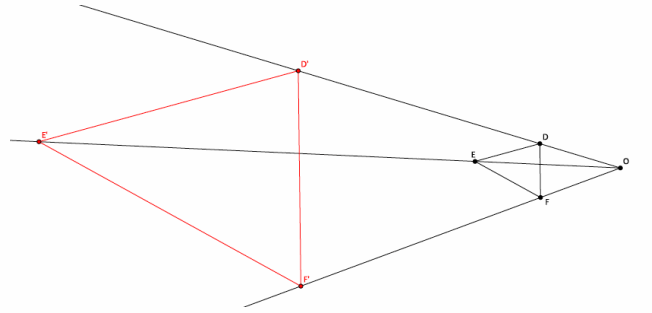
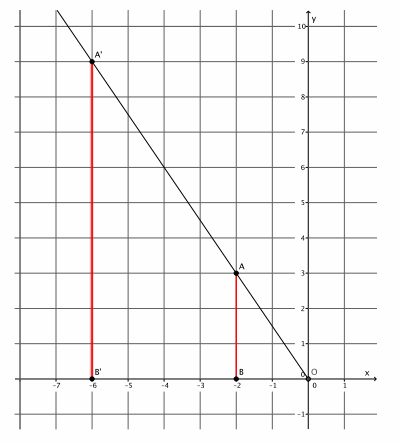
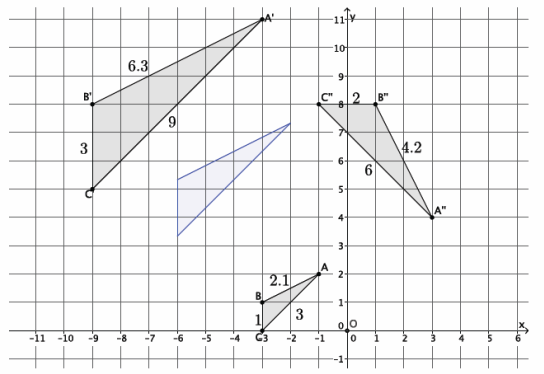
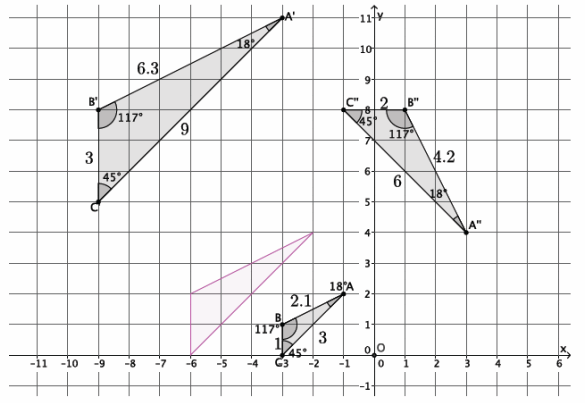
→ The coordinates in other quadrants of the graph are affected in the same manner as we have just seen. Based on what we have learned so far, given point A(-2,3), predict the location of A’when A is dilated from a center at the origin, (0,0), by scale factor r=3.
Provide students time to predict, justify, and possibly verify, in pairs, that A'(3∙(-2),3∙3)=(-6,9). Verify the fact on the coordinate plane, or have students share their verifications with the class.
→ As before, mark a point B on the x-axis. Then, |OB’|=3|OB|. Where is point B’located?
→ Since the length of |OB|=2, then |OB’|=3∙2=6. But we are looking at a distance to the left of zero; therefore, the location of B’is (-6,0).
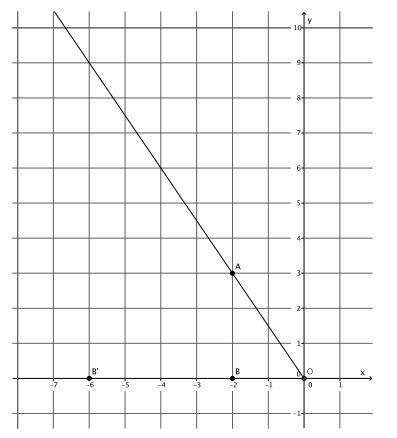
→ Now that we know where B’is, we can easily find the location of A’. It is on the ray \(\overrightarrow{O A}\), but at what location?
→ The location of A'(-6,9), as desired
Example 4.
Students learn the multiplicative effect of scale factor on a two-dimensional figure.
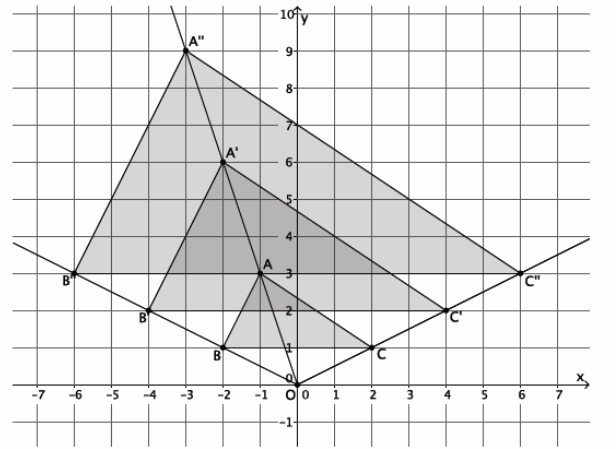
→ Now that we know the multiplicative relationship between a point and its dilated location (i.e., if point P(p1,p2) is dilated from the origin by scale factor r, then P'(rp1,rp2 )), we can quickly find the coordinates of any point, including those that comprise a two-dimensional figure, under a dilation of any scale factor.
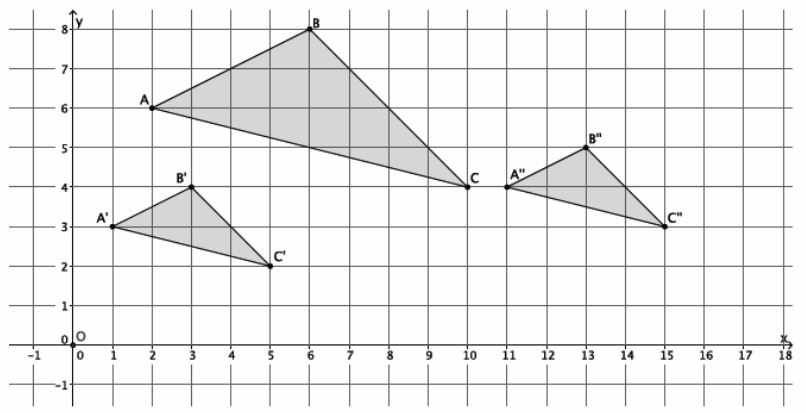
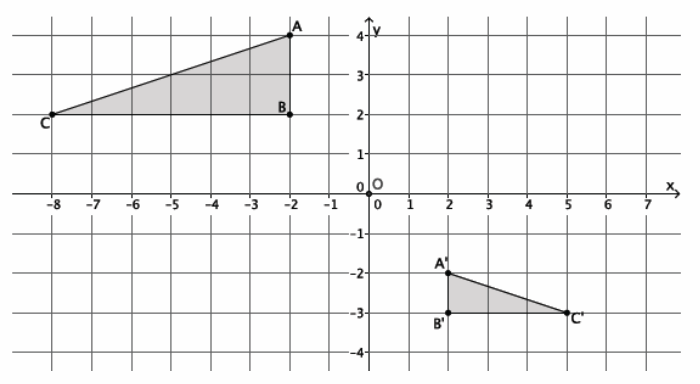
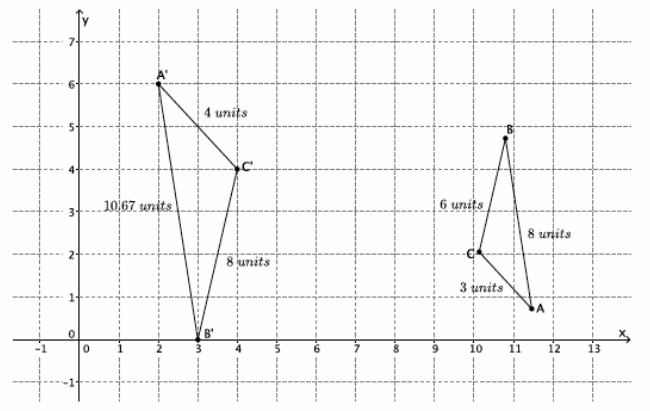
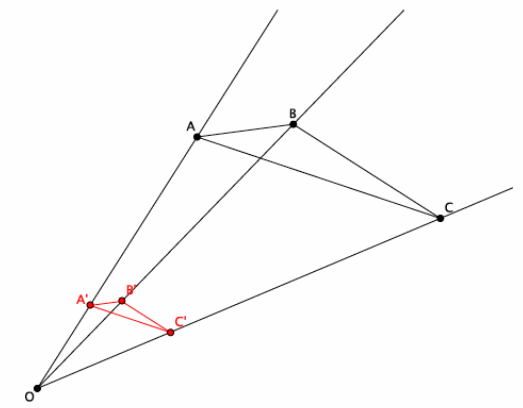
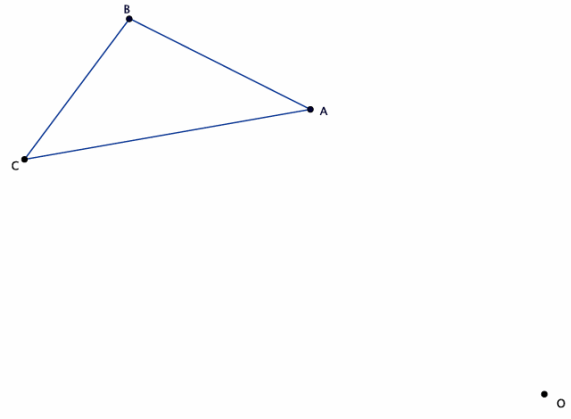
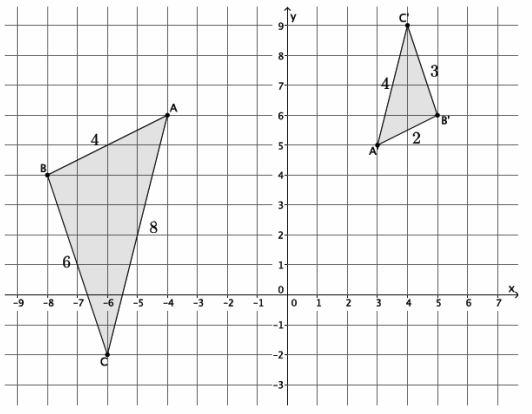
→ For example, triangle ABC has coordinates A(2,3), B(-3,4), and C(5,7). The triangle is being dilated from the origin with scale factor r=4. What are the coordinates of triangle A’B’C’?
→ First, find the coordinates of A’.
→ A'(4⋅2,4⋅3)=A'(8,12)
→ Next, locate the coordinates of B’.
→ B'(4⋅(-3),4⋅4)=B'(-12,16)
→ Finally, locate the coordinates of C’.
→ C'(4∙5,4∙7)=C'(20,28)
→ Therefore, the vertices of triangle A’B’C’have coordinates of (8,12), (-12,16), and (20,28), respectively.
Example 5.
→ Students learn the multiplicative effect of scale factor on a two-dimensional figure.
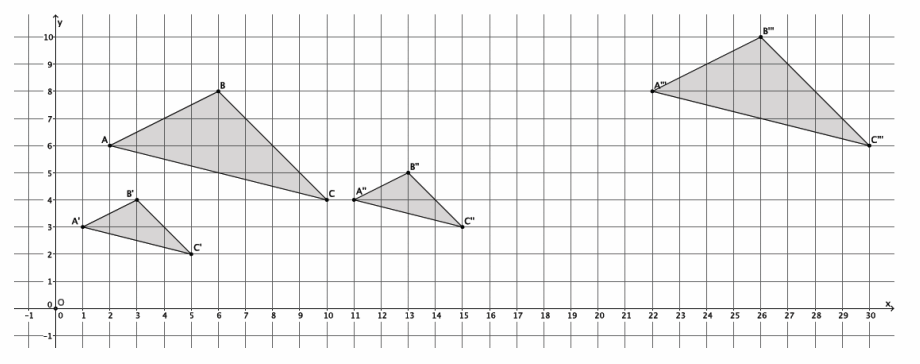
→ Parallelogram ABCD has coordinates of (-2,4), (4,4), (2,-1), and (-4,-1), respectively. Find the coordinates of parallelogram A’B’C’D’after a dilation from the origin with a scale factor r=\(\frac{1}{2}\).
→ A'(\(\frac{1}{2}\)∙(-2),\(\frac{1}{2}\)∙4)=A'(-1,2)
→ B'(\(\frac{1}{2}\)∙4,\(\frac{1}{2}\)∙4)=B'(2,2)
→ C'(\(\frac{1}{2}\)∙2,\(\frac{1}{2}\)∙(-1))=C'(1,-\(\frac{1}{2}\))
→ D'(\(\frac{1}{2}\)∙(-4),\(\frac{1}{2}\)∙(-1))=D'(-2,-\(\frac{1}{2}\))
Therefore, the vertices of parallelogram A’B’C’D’have coordinates of (-1,2), (2,2), (1,-\(\frac{1}{2}\)), and (-2,-\(\frac{1}{2}\)), respectively.
Eureka Math Grade 8 Module 3 Lesson 6 Exercise Answer Key
Exercises 1–5.
Point A(7,9) is dilated from the origin by scale factor r=6. What are the coordinates of point A’?
Answer:
A'(6∙7,6∙9)=A'(42,54)
Exercise 2.
Point B(-8,5) is dilated from the origin by scale factor r=\(\frac{1}{2}\). What are the coordinates of point B’?
Answer:
B'(\(\frac{1}{2}\)∙(-8),\(\frac{1}{2}\)∙5)=B'(-4,\(\frac{5}{2}\))
Exercise 3.
Point C(6,-2) is dilated from the origin by scale factor r=\(\frac{3}{4}\). What are the coordinates of point C’?
Answer:
C'(\(\frac{3}{4}\)∙6,\(\frac{3}{4}\)∙(-2))=C'(\(\frac{9}{2}\),-\(\frac{3}{2}\))
Exercise 4.
Point D(0,11) is dilated from the origin by scale factor r=4. What are the coordinates of point D’?
Answer:
D'(4∙0,4∙11)=D'(0,44)
Exercise 5.
Point E(-2,-5) is dilated from the origin by scale factor r=\(\frac{3}{2}\). What are the coordinates of point E’?
Answer:
E'(\(\frac{3}{2}\)∙(-2),\(\frac{3}{2}\)∙(-5))=E'(-3,-\(\frac{15}{2}\))
Exercises 6–8.
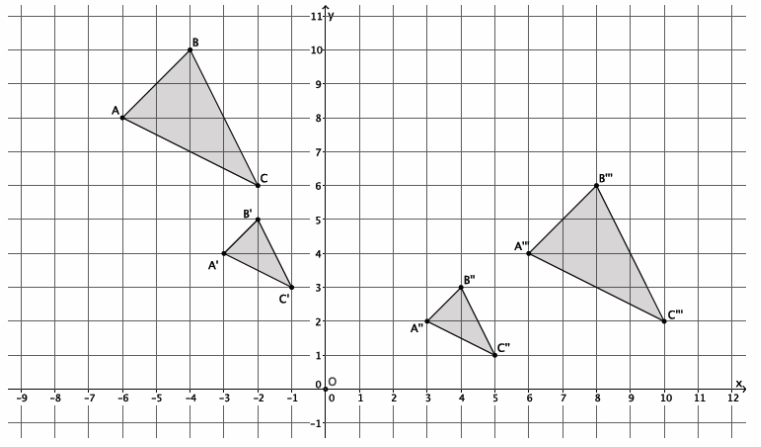
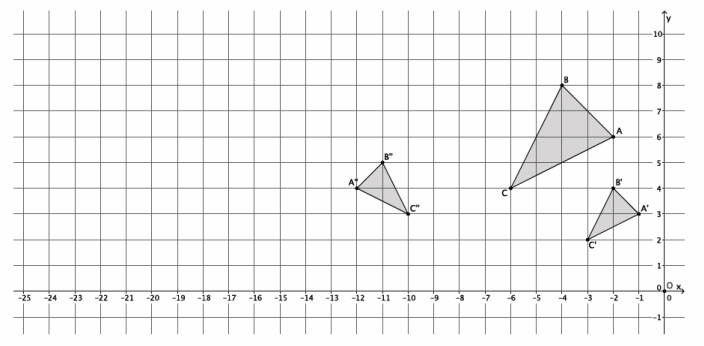
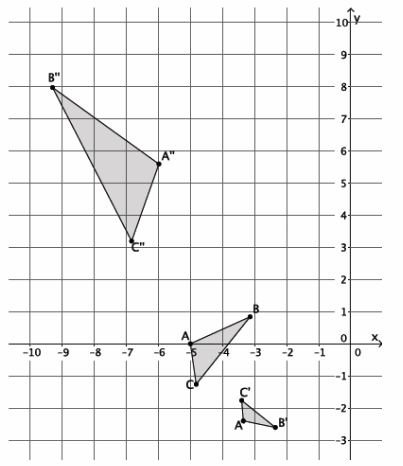
Exercise 6.
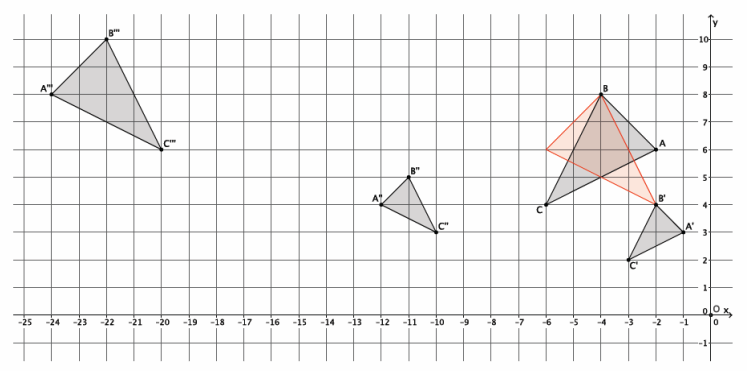
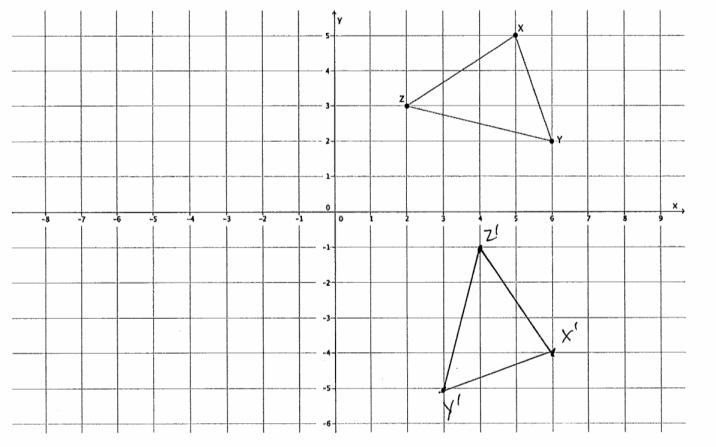
The coordinates of triangle ABC are shown on the coordinate plane below. The triangle is dilated from the origin by scale factor r=12. Identify the coordinates of the dilated triangle A’B’C’.
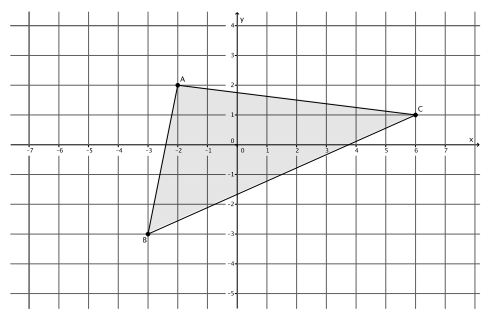
Point A(-2,2), so A'(12∙(-2),12∙2)=A'(-24,24).
Point B(-3,-3), so B'(12∙(-3),12∙(-3))=B'(-36,-36).
Point C(6,1), so C'(12∙6,12∙1)=C'(72,12).
The coordinates of the vertices of triangle A’B’C’are (-24,24), (-36,-36), and (72,12), respectively.
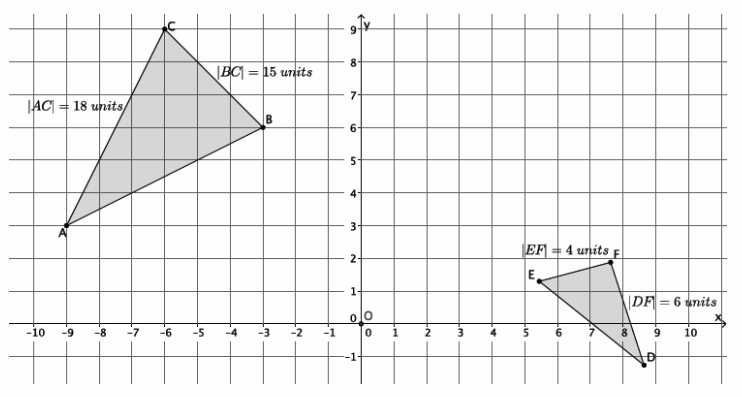
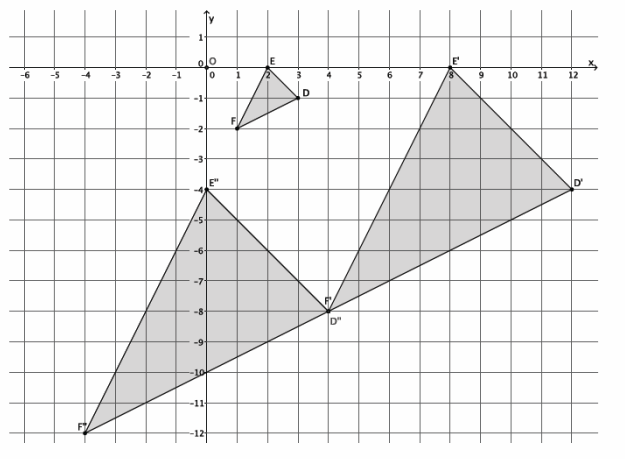
Exercise 7.
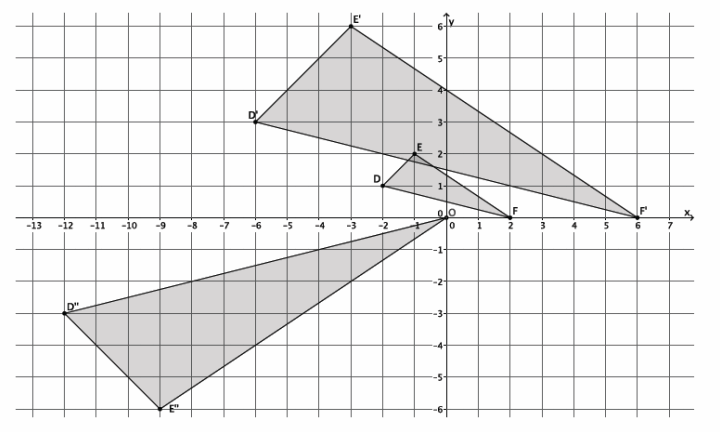
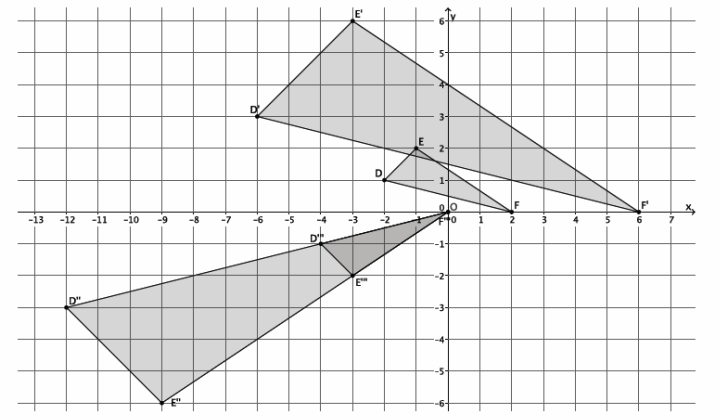
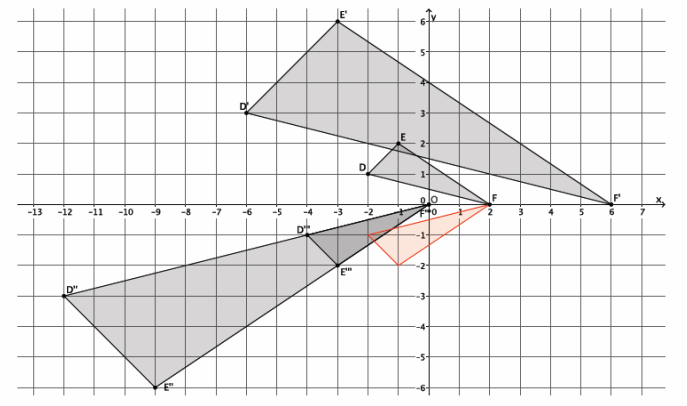
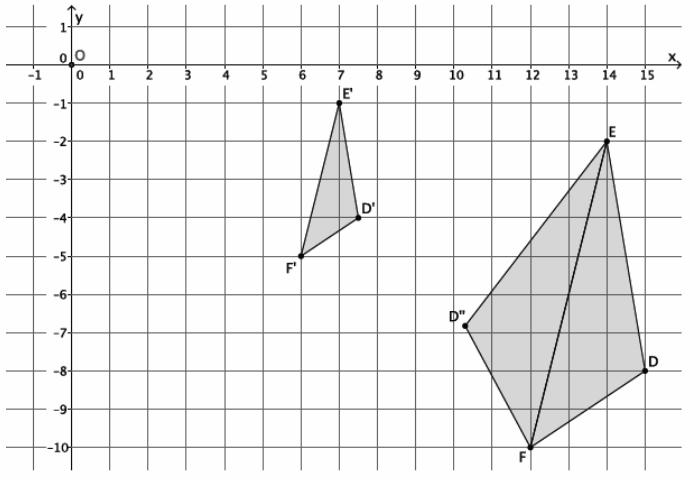
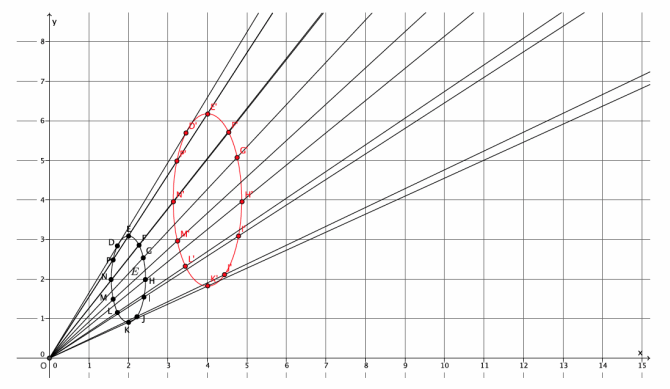
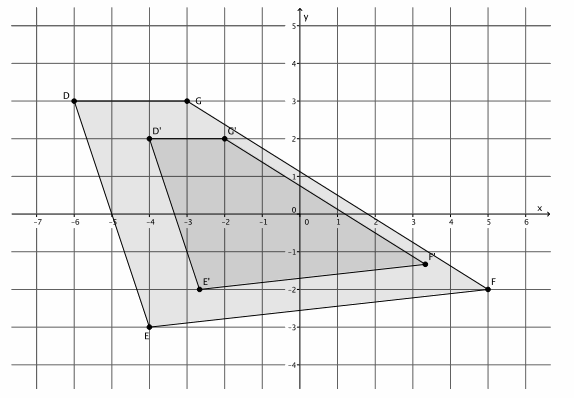
Figure DEFG is shown on the coordinate plane below. The figure is dilated from the origin by scale factor r=\(\frac{2}{3}\). Identify the coordinates of the dilated figure D’E’F’G’, and then draw and label figure D’E’F’G’ on the coordinate plane.
Answer:
Point D(-6,3), so D'(\(\frac{2}{3}\)∙(-6),\(\frac{2}{3}\)∙3)=D'(-4,2).
Point E(-4,-3), so E'(\(\frac{2}{3}\)∙(-4),\(\frac{2}{3}\)∙(-3))=E'(-\(\frac{8}{3}\),-2).
Point F(5,-2), so F'(\(\frac{2}{3}\)∙5,\(\frac{2}{3}\)∙(-2))=F'(\(\frac{10}{3}\),-\(\frac{4}{3}\) ). –
Point G(-3,3), so G'(\(\frac{2}{3}\)∙(-3),\(\frac{2}{3}\)∙3)=G'(-2,2).
The coordinates of the vertices of figure D’E’F’G’are (-4,2), (-\(\frac{8}{3}\),-2), (\(\frac{10}{3}\),-\(\frac{4}{3}\)), and (-2,2), respectively.
Exercise 8.
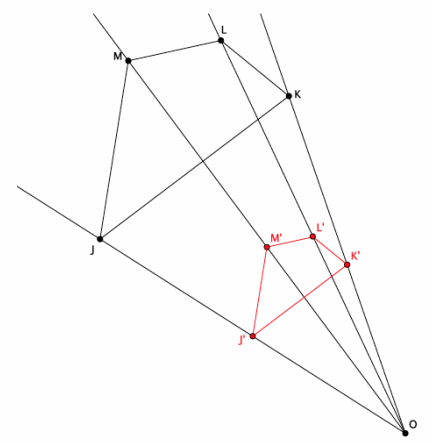
The triangle ABC has coordinates A(3,2), B(12,3), and C(9,12). Draw and label triangle ABC on the coordinate plane. The triangle is dilated from the origin by scale factor r=\(\frac{1}{3}\). Identify the coordinates of the dilated triangle
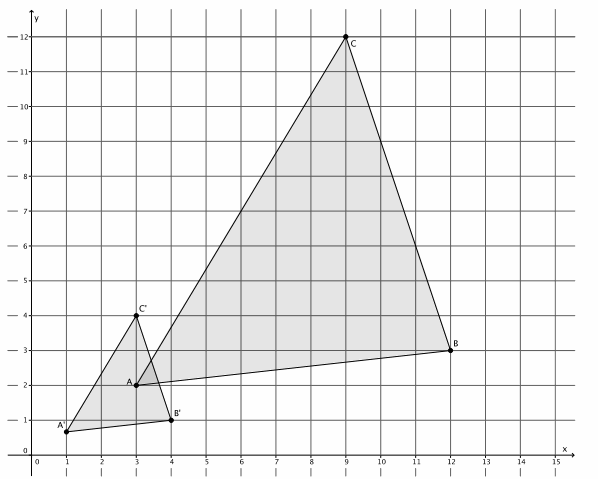
A’B’C’, and then draw and label triangle A’B’C’on the \(\frac{1}{3}\) coordinate plane.
Answer:
Point A(3,2), then A'(\(\frac{1}{3}\)∙3,\(\frac{1}{3}\)∙2)=A'(1,\(\frac{2}{3}\)).
Point B(12,3), so B'(\(\frac{1}{3}\)∙12,\(\frac{1}{3}\)∙3)=B'(4,1).
Point C(9,12), so C'(\(\frac{1}{3}\)∙9,\(\frac{1}{3}\)∙12)=C'(3,4).
The coordinates of triangle A’B’C’are (1,\(\frac{2}{3}\)), (4,1), and (3,4), respectively.
Eureka Math Grade 8 Module 3 Lesson 6 Problem Set Answer Key
Students practice finding the coordinates of dilated points of two-dimensional figures.
Question 1.
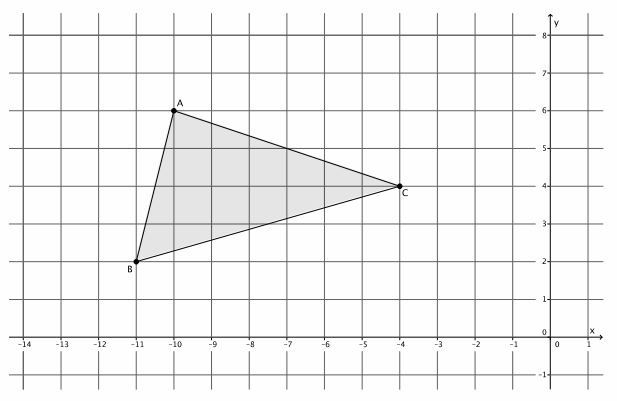
Triangle ABC is shown on the coordinate plane below. The triangle is dilated from the origin by scale factor r=4. Identify the coordinates of the dilated triangle A’B’C’.
Answer:
Point A(-10,6), so A'(4∙(-10),4∙6)=A'(-40,24).
Point B(-11,2), so B'(4∙(-11),4∙2)=B'(-44,8).
Point C(-4,4), so C'(4∙(-4),4∙4)=C'(-16,16).
The coordinates of the vertices of triangle A’B’C’are (-40,24), (-44,8), and (-16,16), respectively.
Question 2.
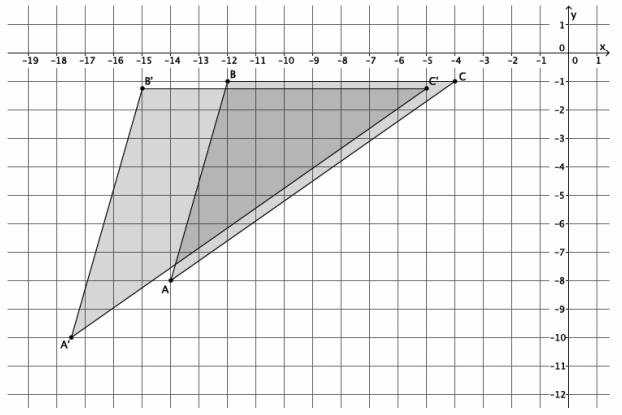
Triangle ABC is shown on the coordinate plane below. The triangle is dilated from the origin by scale factor r=\(\frac{5}{4}\). Identify the coordinates of the dilated triangle A’B’C’.
Answer:
Point A(-14,-8), so A'(\(\frac{5}{4}\)∙(-14),\(\frac{5}{4}\)∙(-8))=A'(-\(\frac{35}{2}\),-10).
Point B(-12,-1), so B'(\(\frac{5}{4}\)∙(-12),\(\frac{5}{4}\)∙(-1))=B'(-15,-\(\frac{5}{4}\)).
Point C(-4,-1), so C'(\(\frac{5}{4}\)∙(-4),\(\frac{5}{4}\)∙(-1))=B'(-5,-\(\frac{5}{4}\)).
The coordinates of the vertices of triangle A’B’C’are (-\(\frac{35}{2}\),-10), (-15,-\(\frac{5}{4}\)), and (-5,-\(\frac{5}{4}\)), respectively.
Question 3.
The triangle ABC has coordinates A(6,1), B(12,4), and C(-6,2). The triangle is dilated from the origin by a scale factor r=\(\frac{1}{2}\). Identify the coordinates of the dilated triangle A’B’C’.
Answer:
Point A(6,1), so A'(\(\frac{1}{2}\)∙6,\(\frac{1}{2}\)∙1)=A'(3,\(\frac{1}{2}\)).
Point B(12,4), so B'(\(\frac{1}{2}\)∙12,\(\frac{1}{2}\)∙4)=B'(6,2).
Point C(-6,2), so C'(\(\frac{1}{2}\)∙(-6),\(\frac{1}{2}\)∙2)=C'(-3,1).
The coordinates of the vertices of triangle A’B’C’are (3,\(\frac{1}{2}\)), (6,2), and (-3,1), respectively.
Question 4.
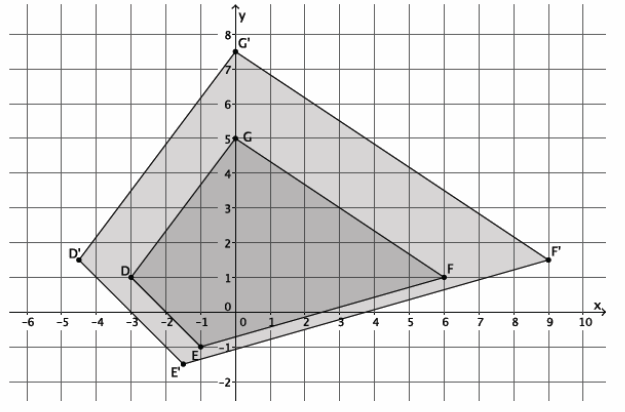
Figure DEFG is shown on the coordinate plane below. The figure is dilated from the origin by scale factor r=\(\frac{3}{2}\). Identify the coordinates of the dilated figure D’E’F’G’, and then draw and label figure D’E’F’G’ on the coordinate plane.
Answer:
Point D(-3,1), so D'(\(\frac{3}{2}\)∙(-3),\(\frac{3}{2}\)∙1)=D'(-\(\frac{9}{2}\),\(\frac{3}{2}\)).
Point E(-1,-1), so E'(\(\frac{3}{2}\)∙(-1),\(\frac{3}{2}\)∙(-1))=E'(-\(\frac{3}{2}\),-\(\frac{3}{2}\)).
Point F(6,1), so F'(\(\frac{3}{2}\)∙6,\(\frac{3}{2}\)∙1)=F'(9,\(\frac{3}{2}\)).
Point G(0,5), so G'(\(\frac{3}{2}\)∙0,\(\frac{3}{2}\)∙5)=G'(0,\(\frac{15}{2}\)).
The coordinates of the vertices of figure D’E’F’G’are (-\(\frac{9}{2}\),\(\frac{3}{2}\)), (-\(\frac{3}{2}\),-\(\frac{3}{2}\)), (9,\(\frac{3}{2}\)), and (0,\(\frac{15}{2}\)), respectively.
Question 5.
Figure DEFG has coordinates D(1,1), E(7,3), F(5,-4), and G(-1,-4). The figure is dilated from the origin by scale factor r=7. Identify the coordinates of the dilated figure D’E’F’G’.
Answer:
Point D(1,1), so D'(7∙1,7∙1)=D'(7,7).
Point E(7,3), so E'(7∙7,7∙3)=E'(49,21).
Point F(5,-4), so F'(7∙5,7∙(-4))=F'(35,-28).
Point G(-1,-4), so G'(7∙(-1),7∙(-4))=G'(-7,-28).
The coordinates of the vertices of figure D’E’F’G’are (7,7), (49,21),(35,-28), and (-7,-28), respectively.
Eureka Math Grade 8 Module 3 Lesson 6 Exit Ticket Answer Key
Question 1.
The point A(7,4) is dilated from the origin by a scale factor r=3. What are the coordinates of point A’?
Answer:
Since point A(7,4), then A'(3∙7,3∙4)=A'(21,12).
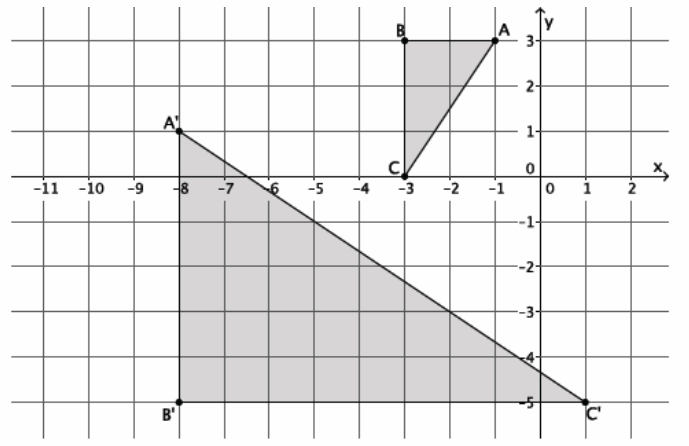
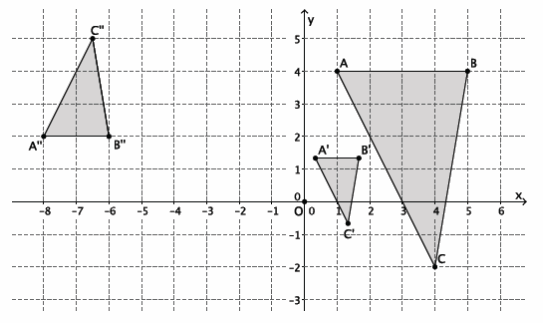
Question 2.
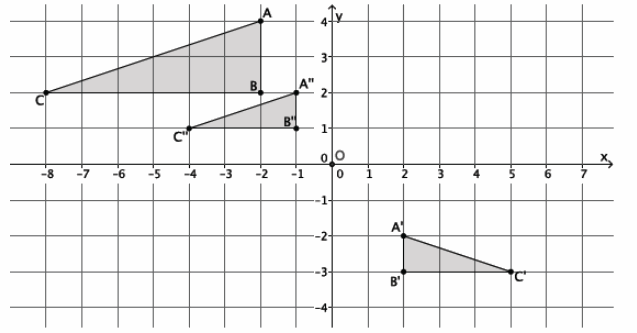
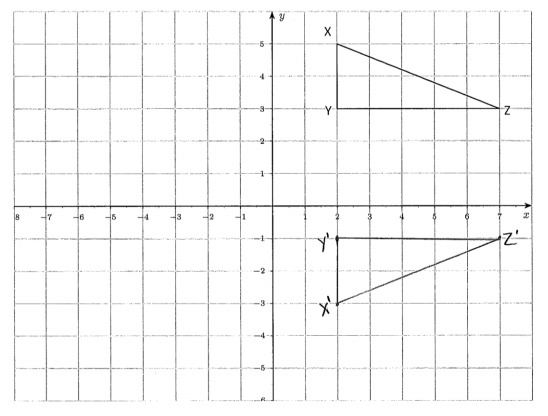
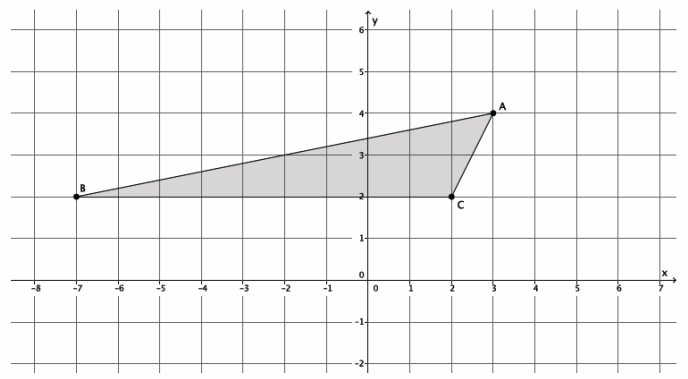
The triangle ABC, shown on the coordinate plane below, is dilated from the origin by scale factor r=\(\frac{1}{2}\). What is the location of triangle A’B’C’? Draw and label it on the coordinate plane.
Answer:
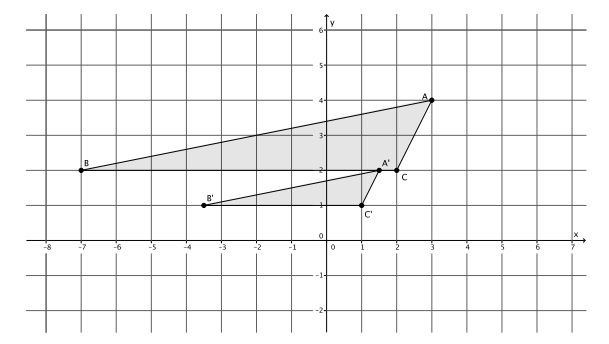
Point A(3,4), so A'(\(\frac{1}{2}\)∙3,\(\frac{1}{2}\)∙4)=A'(\(\frac{3}{2}\),2).
Point B(-7,2), so B'(\(\frac{1}{2}\)∙(-7),\(\frac{1}{2}\)∙2)=B'(-\(\frac{7}{2}\),1).
Point C(2,2), so C'(\(\frac{1}{2}\)∙2,\(\frac{1}{2}\)∙2)=C'(1,1).
The coordinates of the vertices of triangle A’B’C’are (\(\frac{3}{2}\),2), (-\(\frac{7}{2}\),1), and (1,1), respectively.



















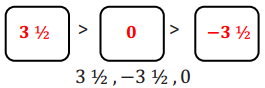
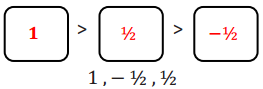




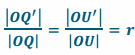 and that line QU is parallel to line Q’U’. Since U is a point on line PQ, then we also know that line PQ is parallel to line Q’U’. But we already know that
and that line QU is parallel to line Q’U’. Since U is a point on line PQ, then we also know that line PQ is parallel to line Q’U’. But we already know that