Eureka Math

Engage NY Eureka Math 8th Grade Module 2 End of Module Assessment Answer Key

Eureka Math Grade 8 Module 2 End of Module Assessment Task Answer Key

Question 1.
△ABC≅ △A’B’C’. Use the picture to answer the question below.

Describe a sequence of rigid motions that would prove a congruence between △ABC and △A’B’C’.
Answer:
Let T be the Translation AWNG \(\overrightarrow{A^{\prime} A}\) so that t(A’) = A. Let R be the rotation around A, d degrees so that R(A’B’) = AB. By hypothesis |AB| = |A’B’|. Let |∠A| = |∠A|, |∠B| = |∠B|, so the composition ʌ.R.T will map ∆A’B’C’ to ∆A’B’C’ to ∆ABC, i.e., ʌ(R(T(△A’B’C’))) = △ABC

Question 2.
Use the diagram to answer the question below.

k || l

Answer:

Line k is parallel to line l. m∠EDC=41° and m∠ABC=32°. Find the m∠BCD. Explain in detail how you know you are correct. Add additional lines and points as needed for your explanation.
Answer:
Let F be a point on line or so that ∠DCF is a straight angle. Then because r || l, ∠EDC ≅ ∠CFA and have equal measure. ∠ABC and ∠CFA are the remote interior angles of △BCF which means ∠BCD = ∠ABC + CFA. Therefore ∠BCD = 32 + 41 = 73°.

Question 3.
Use the diagram below to answer the questions that follow. Lines L₁ and L₂ are parallel, L₁ || L₂. Point N is the midpoint of segment GH.

a. If the measure of ∠IHM is 125°, what is the measure of ∠IHJ? ∠JHN? ∠NHM?
Answer:
∠IHJ = 55°
∠JHN = 125°
∠NHM = 55°

b. What can you say about the relationship between ∠4 and ∠6? Explain using a basic rigid motion. Name another pair of angles with this same relationship.
Answer:
∠4 & ∠6 are alternate interior angles that are equal because L₁ || L₂. Let R be a rotation of 180° around point N. Then R(N) = N, R(L₃) = L₃ and R(L₁) = L₂. Rotations are degree preserving so (∠4) = ∠6
∠3 & ∠5 are also alternate interior angles that are equal.

c. What can you say about the relationship between ∠1 and ∠5? Explain using a basic rigid motion. Name another pair of angles with this same relationship.
Answer:
∠1 & ∠5 are corresponding angles that are equal because L₁ || L₂. Let T be the Translation along vector \(\overrightarrow{G H}\). Then T(L₂) = L₁ and T(∠5) = ∠1.
∠3 & ∠7 are also corresponding angles that are equal.

Engage NY Eureka Math 8th Grade Module 4 Lesson 2 Answer Key

Eureka Math Grade 8 Module 4 Lesson 2 Exercise Answer Key

Write each of the following statements in Exercises 1–12 as a mathematical expression. State whether or not the expression is linear or nonlinear. If it is nonlinear, then explain why.

Exercise 1.
The sum of a number and four times the number
Answer:
Let x be a number; then, x+4x is a linear expression.

Exercise 2.
The product of five and a number
Answer:
Let x be a number; then, 5x is a linear expression.

Exercise 3.
Multiply six and the reciprocal of the quotient of a number and seven.
Answer:
Let x be a number; then, 6∙\(\frac{7}{x}\) is a nonlinear expression. The expression is nonlinear because the number
\(\frac{7}{x}\)=7∙\(\frac{1}{x}\)=7∙x^-1. The exponent of the x is the reason it is not a linear expression.

Exercise 4.
Twice a number subtracted from four times a number, added to 15
Answer:
Let x be a number; then, 15+(4x-2x) is a linear expression.

Exercise 5.
The square of the sum of six and a number
Answer:
Let x be a number; then,(x+6)² is a nonlinear expression. When you multiply(x+6)², you get x²+12x+36. The x² is the reason it is not a linear expression.

Exercise 6.
The cube of a positive number divided by the square of the same positive number
Answer:
Let x be a number; then, \(\frac{x^{3}}{x^{2}}\) is a nonlinear expression. However, if you simplify the expression to x, then it is linear.

Exercise 7.
The sum of four consecutive numbers
Answer:
Let x be the first number; then, x+(x+1)+(x+2)+(x+3) is a linear expression.

Exercise 8.
Four subtracted from the reciprocal of a number
Answer:
Let x be a number; then, \(\frac{1}{x}\)-4 is a nonlinear expression. The term \(\frac{1}{x}\) is the same as x^-1, which is why this expression is not linear. It is possible that a student may let x be the reciprocal of a number, \(\frac{1}{x}\), which would make the expression linear.

Exercise 9.
Half of the product of a number multiplied by itself three times
Answer:
Let x be a number; then, \(\frac{1}{2}\)∙x∙x∙x is a nonlinear expression. The term \(\frac{1}{2}\)∙x∙x∙x is the same as\(\frac{1}{2}\) x³, which is why this expression is not linear.

Exercise 10.
The sum that shows how many pages Maria read if she read 45 pages of a book yesterday and \(\frac{2}{3}\) of the remaining pages today
Answer:
Let x be the number of remaining pages of the book; then, 45+\(\frac{2}{3}\) x is a linear expression.

Exercise 11.
An admission fee of $10 plus an additional $2 per game
Answer:
Let x be the number of games; then, 10+2x is a linear expression.

Exercise 12.
Five more than four times a number and then twice that sum
Answer:
Let x be the number; then, 2(4x+5) is a linear expression.

Eureka Math Grade 8 Module 4 Lesson 2 Problem Set Answer Key

Students practice writing expressions and identifying them as linear or nonlinear.

Write each of the following statements as a mathematical expression. State whether the expression is linear or nonlinear. If it is nonlinear, then explain why.

Question 1.
A number decreased by three squared
Answer:
Let x be a number; then, x-3² is a linear expression.

Question 2.
The quotient of two and a number, subtracted from seventeen
Answer:
Let x be a number; then, 17-\(\frac{2}{x}\) is a nonlinear expression. The term \(\frac{2}{x}\) is the same as 2∙\(\frac{1}{x}\) and \(\frac{1}{x}\)=x^-1, which is why it is not linear.

Question 3.
The sum of thirteen and twice a number
Answer:
Let x be a number; then, 13+2x is a linear expression.

Question 4.
5.2 more than the product of seven and a number
Answer:
Let x be a number; then, 5.2+7x is a linear expression.

Question 5.
The sum that represents the number of tickets sold if 35 tickets were sold Monday, half of the remaining tickets were sold on Tuesday, and 14 tickets were sold on Wednesday
Answer:
Let x be the remaining number of tickets; then, 35+\(\frac{1}{2}\) x+14 is a linear expression.

Question 6.
The product of 19 and a number, subtracted from the reciprocal of the number cubed
Answer:
Let x be a number; then, \(\frac{1}{x^{3}}\) -19x is a nonlinear expression. The term \(\frac{1}{x^{3}}\) is the same as x^-3, which is why it is not linear.

Question 7.
The product of 15 and a number, and then the product multiplied by itself four times
Answer:
Let x be a number; then,(15x)⁴ is a nonlinear expression. The expression can be written as 15⁴∙x⁴. The exponent of 4 with a base of x is the reason it is not linear.

Question 8.
A number increased by five and then divided by two
Answer:
Let x be a number; then, \(\frac{x+5}{2}\) is a linear expression.

Question 9.
Eight times the result of subtracting three from a number
Answer:
Let x be a number; then, 8(x-3) is a linear expression.

Question 10.
The sum of twice a number and four times a number subtracted from the number squared
Answer:
Let x be a number; then, x²-(2x+4x) is a nonlinear expression. The term x² is the reason it is not linear.

Question 11.
One-third of the result of three times a number that is increased by 12
Answer:
Let x be a number; then, \(\frac{1}{3}\) (3x+12) is a linear expression.

Question 12.
Five times the sum of one-half and a number
Answer:
Let x be a number; then, 5(\(\frac{1}{2}\)+x) is a linear expression.

Question 13.
Three-fourths of a number multiplied by seven
Answer:
Let x be a number; then, \(\frac{3}{4}\)x∙7 is a linear expression.

Question 14.
The sum of a number and negative three, multiplied by the number
Answer:
Let x be a number; then, (x+(-3))x is a nonlinear expression because (x+(-3))x=x²-3x after using the distributive property. It is nonlinear because the power of x in the term x² is greater than 1.

Question 15.
The square of the difference between a number and 10
Answer:
Let x be a number; then, (x-10)² is a nonlinear expression because (x-10)²=x²-20x+100. The term x² is a positive power of x>1; therefore, this is not a linear expression.

Eureka Math Grade 8 Module 4 Lesson 2 Exit Ticket Answer Key

Write each of the following statements as a mathematical expression. State whether the expression is a linear or nonlinear expression in x.

Question 1.
Seven subtracted from five times a number, and then the difference added to nine times a number
Answer:
Let x be a number; then, (5x-7)+9x. The expression is a linear expression.

Question 2.
Three times a number subtracted from the product of fifteen and the reciprocal of a number
Answer:
Let x be a number; then, 15∙\(\frac{1}{x}\)-3x. The expression is a nonlinear expression.

Question 3.
Half of the sum of two and a number multiplied by itself three times
Answer:
Let x be a number; then, \(\frac{1}{2}\) (2+x³). The expression is a nonlinear expression.

Engage NY Eureka Math 8th Grade Module 4 Lesson 1 Answer Key

Eureka Math Grade 8 Module 4 Lesson 1 Exercise Answer Key

Write each of the following statements using symbolic language.

Exercise 1.
The sum of four consecutive even integers is -28.
Answer:
Let x be the first even integer. Then, x+x+2+x+4+x+6=-28.

Exercise 2.
A number is four times larger than the square of half the number.
Answer:
Let x be the number. Then, x=4(\(\frac{x}{2}\))².

Exercise 3.
Steven has some money. If he spends $9.00, then he will have \(\frac{3}{5}\) of the amount he started with.
Answer:
Let x be the amount of money (in dollars) Steven started with. Then, x-9=\(\frac{3}{5}\) x.

Exercise 4.
The sum of a number squared and three less than twice the number is 129.
Answer:
Let x be the number. Then, x²+2x-3=129.

Exercise 5.
Miriam read a book with an unknown number of pages. The first week, she read five less than \(\frac{1}{3}\) of the pages. The second week, she read 171 more pages and finished the book. Write an equation that represents the total number of pages in the book.
Answer:
Let x be the total number of pages in the book. Then, \(\frac{1}{3}\) x-5+171=x.

Eureka Math Grade 8 Module 4 Lesson 1 Problem Set Answer Key

Students practice transcribing written statements into symbolic language.

Write each of the following statements using symbolic language.

Question 1.
Bruce bought two books. One book costs $4.00 more than three times the other. Together, the two books cost him $72.
Answer:
Let x be the cost of the less expensive book. Then, x+4+3x=72.

Question 2.
Janet is three years older than her sister Julie. Janet’s brother is eight years younger than their sister Julie. The sum of all of their ages is 55 years.
Answer:
Let x be Julie’s age. Then, (x+3)+(x-8)+x=55.

Question 3.
The sum of three consecutive integers is 1,623.
Answer:
Let x be the first integer. Then, x+(x+1)+(x+2)=1623.

Question 4.
One number is six more than another number. The sum of their squares is 90.
Answer:
Let x be the smaller number. Then, x²+(x+6)²=90.

Question 5.
When you add 18 to \(\frac{1}{4}\) of a number, you get the number itself.
Answer:
Let x be the number. Then, \(\frac{1}{4}\) x+18=x.

Question 6.
When a fraction of 17 is taken away from 17, what remains exceeds one-third of seventeen by six.
Answer:
Let x be the fraction of 17. Then, 17-x=\(\frac{1}{3}\)∙17+6.

Question 7.
The sum of two consecutive even integers divided by four is 189.5.
Answer:
Let x be the first even integer. Then, \(\frac{x+(x+2)}{4}\)=189.5.

Question 8.
Subtract seven more than twice a number from the square of one-third of the number to get zero.
Answer:
Let x be the number. Then, (\(\frac{1}{3}\) x)²-(2x+7)=0.

Question 9.
The sum of three consecutive integers is 42. Let x be the middle of the three integers. Transcribe the statement accordingly.
Answer:
(x-1)+x+(x+1)=42

Eureka Math Grade 8 Module 4 Lesson 1 Exit Ticket Answer Key

Write each of the following statements using symbolic language.

Question 1.
When you square five times a number, you get three more than the number.
Answer:
Let x be the number. Then, (5x)²=x+3.

Question 2.
Monica had some cookies. She gave seven to her sister. Then, she divided the remainder into two halves, and she still had five cookies left.
Answer:
Let x be the original amount of cookies. Then, \(\frac{1}{2}\) (x-7)=5.

Engage NY Eureka Math 8th Grade Module 3 Mid Module Assessment Answer Key

Eureka Math Grade 8 Module 3 Mid Module Assessment Task Answer Key

Question 1.
Use the figure below to complete parts (a) and (b).

Answer:

a. Use a compass and ruler to produce an image of the figure with center O and scale factor r=2.

b. Use a ruler to produce an image of the figure with center O and scale factor r=\(\frac{1}{2}\).

Question 2.
Use the diagram below to answer the questions that follow.

Let D be the dilation with center O and scale factor r>0 so that Dilation(P)=P’ and Dilation(Q)=Q’.

a. Use lengths |OQ|=10 units and |OQ’ |=15 units to determine the scale factor r of dilation D. Describe how to determine the coordinates of P’ using the coordinates of P.
Answer:
|OQ|r= |OQ’|

r = \(\frac{15}{10}\)
r = \(\frac{3}{2}\)
The same factor is r = \(\frac{3}{2}\)
Since the coordinates of P = (-4, -3) the coordinates of the dilated point P’ will be the same factor times the coordinates of P. Therefore P’ = (\(\frac{3}{2}\) × (-4), \(\frac{3}{2}\) × (-3)) = (-6, -45)

b. If |OQ|=10 units, |OQ’|=15 units, and |P’Q’|=11.2 units, determine |PQ|. Round your answer to the tenths place, if necessary.
Answer:
\(\frac{15}{10}\) = \(\frac{11.2}{|PQ|}\)
15(|PQ|) = 112
|PQ| = \(\frac{112}{15}\) ≈ 7.5
The length of \(\overline{P Q}\) is about 7.5 units.

Question 3.
Use a ruler and compass, as needed, to answer parts (a) and (b).

a. Is there a dilation D with center O that would map figure PQRS to figure P’Q’R’S’? Explain in terms of scale factor, center, and coordinates of corresponding points.

Answer:

P = (3, -2)
P’ = (9, -6)
Q = (3, -1)
Q’ = (9, -3)
R = (4, 1)
R’ = (12, 3)
S = (0, 2)
S’ = (0, 6)
Yes, there is a dilation D with Genter O, that maps PQS to P’Q’R’S’. The scale factor is 3. The image of each point is 3 times the coordinates of the original image. For example, P = (3, -2) and P’ = (3 × 3, 3 × (-2)) = (9, -6)

b. Is there a dilation D with center O that would map figure PQRS to figure P’Q’R’S’? Explain in terms of scale factor, center, and coordinates of corresponding points.

Answer:

No, there is not a dilation D that will map PQRS to P’Q’R’S’. A dilation will move A point, S, to its image S’ on the ray \(\overrightarrow{O S}\). In the picture above O, S, S’ are not on the same ray. A similar statement can be made for points P, Q and R, Therefore, there is no dilation that maps PQRS to P’Q’R’S’.

c. Triangle ABC is located at points A(-4,3), B(3,3), and C(2,-1) and has been dilated from the origin by a scale factor of 3. Draw and label the vertices of triangle ABC. Determine the coordinates of the dilated triangle A’B’C’, and draw and label it on the coordinate plane.

Answer:

A= (-4, 3)
A’ = (-4×3, 3×3) = (-12, 9)
B =(3, 3)
B’ = (3×3, 3×3) = (9, 9)
C = (2, -1)
C’ = (2×3, -1×3) = (6, -3)

Engage NY Eureka Math 8th Grade Module 3 End of Module Assessment Answer Key

Eureka Math Grade 8 Module 3 End of Module Assessment Task Answer Key

Question 1.
Use the diagram below to answer the questions that follow.

Answer:

a. Dilate △OPQ from center O and scale factor r=\(\frac{4}{9}\). Label the image △OP’Q’.

b. Find the coordinates of points P’ and Q’.
Answer:
P’ = (6, 2)
Q’ = (6, \(\frac{38}{9}\))
\(\frac{\left(P^{\prime} Q^{\prime}\right)}{|P Q|}\) = \(\frac{4}{9}\)
\(\frac{\left|P^{\prime} Q^{\prime}\right|}{5}\) = \(\frac{4}{9}\)
|P’Q’| = \(\frac{20}{9}\)
\(\frac{20}{9}\) + 2 = \(\frac{20}{9}\) + \(\frac{18}{9}\)
= \(\frac{38}{9}\)

c. Are ∠OQP and ∠OQ’P’ equal in measure? Explain.
Answer:
Yes ∠OQP = ∠OQ’P’ Since D(△OQP) = △OQ’P’ and dilations are degree preserving, then ∠OQP = ∠OQ’P’.
∠OQP & ∠OQ’P’ are corresponding angles of parallel lines PQ & P’Q’, therefore ∠OQR = ∠OQ’P’

d. What is the relationship between segments PQ and P’Q’? Explain in terms of similar triangles.
Answer:
The lines that contain \(\overline{\text { PQ }}\) and \(\overline{p^{\prime} Q^{\prime}}\) are parallel. ∆OPQ ~ ∆OP’Q’ by the AA criterion (∠D = ∠D, ∠OP’Q’ = ∠OPQ), Therefore by the fundamental theorem of similarity \(\overline{P Q}\) || \(\overline{P^{\prime} Q^{\prime}}\)

e. If the length of segment OQ is 9.8 units, what is the length of segment OQ’? Explain in terms of similar triangles.
Answer:
Since ∆OPQ ~ ∆OP’Q’, then the ratios of lengths of corresponding sides will be equal to the scale factor then
\(\frac{\left|O P^{\prime}\right|}{|O P|}\) = \(\frac{\left|O Q^{\prime}\right|}{|O Q|}\) = \(\frac{4}{9}\)
\(\frac{4}{9}\) = \(\frac{\left|O Q^{\prime}\right|}{|9.0|}\)
39.2 = 9(|OQ’|)
4.36 = |OQ’|
|OQ’| is approximately 4.4 units.

Question 2.
Use the diagram below to answer the questions that follow. The length of each segment is as follows: segment OX is 5 units, segment OY is 7 units, segment XY is 3 units, and segment X’Y’ is 12.6 units.

a. Suppose segment XY is parallel to segment X’Y’. Is △OXY similar to △OX’Y’? Explain.
Answer:
Yes, ∆OXY ~ ∆OX’Y’. Since \(\overline{X Y}\) || \(X^{\prime} Y^{\prime}\) and ∠OYX = ∠OY’X’. Because corresponding angles of parallel lines are equal in measure, by AA ∆OXY ~ ∆OX’Y’.

b. What is the length of segment OX’? Show your work.
Answer:
\(\frac{12.6}{3}\) = \(\frac{\left|O X^{\prime}\right|}{|5|}\)
5(12.6) = 3(|OX’|)
63 = 3(|OX’|)
21 = |OX’|
|OX’| is 21 units.

c. What is the length of segment OY’? Show your work.
Answer:
\(\frac{12.6}{3}\) = \(\frac{\left|OY^{\prime}\right|}{|7|}\)
12.6(7) = (3|OY’|)
88.2 = 3(|OY’|)
29.4 = |OY’|
|OY’| is 29.4 units.

Question 3.
Given △ABC ~△A^’ B^’ C’ and △ABC ~△A”B”C” in the diagram below, answer parts (a)–(c).

a. Describe the sequence that shows the similarity for △ABC and △A’ B’ C’.
Answer:
\(\frac{B^{\prime} C^{\prime}}{B C}\) = \(\frac{2}{1}\) = 2 = r
Le D be the dilation from center O and scale factor r=2. Let there be a reflection across the Y-axis. Then the dilation followed by the reflection maps △ABC onto △A’B’C’.

b. Describe the sequence that shows the similarity for △ABC and △A”B”C”.
Answer:
Let D be the dilation from center O and scale factor. 0<r<1. Let there be a rotation of 180° around center O. Then the dilation followed by the rotation maps △ABC onto △A”B”C”.

c. Is △A’B’C’ similar to △A”B”C”? How do you know?
Answer:
Yes △A’B’C’ ~ △A”B”C”. Dilations preserve angle measures and since △ABC ~ △A’B’C and △ABC ~ △A”B”C”, we know ∠A= ∠A’ = ∠A”, ∠B = ∠B’=∠B”, by AA Criterion for similarity △A’B’C’ ~ △ A”B”C”. Also, similarity is Transitive.

Engage NY Eureka Math 8th Grade Module 3 Lesson 14 Answer Key

Eureka Math Grade 8 Module 3 Lesson 14 Example Answer Key

Example 1.
To maintain the focus of the lesson, allow the use of calculators in order to check the validity of the right angle using the Pythagorean theorem.
→ The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle?

→ To find out, we need to put these numbers into the Pythagorean theorem. Recall that side c is always the longest side. Since 610 is the largest number, it is representing the c in the Pythagorean theorem. To determine if this triangle is a right triangle, then we need to verify the computation.

→ Find the value of the left side of the equation: 272²+546²=372 100. Then, find the value of the right side of the equation: 610²=372 100. Since the left side of the equation is equal to the right side of the equation, we have a true statement, that is, 272²+546²=610². What does that mean about the triangle?
→ It means that the triangle with side lengths of 272, 546, and 610 is a right triangle.

Example 2.
→ The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle?

→ What do we need to do to find out if this is a right triangle?
→ We need to see if it makes a true statement when we replace a, b, and c with the numbers using the Pythagorean theorem.
→ Which number is c? How do you know?
→ The longest side is 12; therefore, c=12.
→ Use your calculator to see if it makes a true statement. (Give students a minute to calculate.) Is it a right triangle? Explain.
→ No, it is not a right triangle. If it were a right triangle, the equation 7²+9²=12² would be true. But the left side of the equation is equal to 130, and the right side of the equation is equal to 144. Since 130≠144, then these lengths do not form a right triangle.

Eureka Math Grade 8 Module 3 Lesson 14 Exercise Answer Key

Exercise 1.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 9²+12²=15² is a true statement. The left side of the equation is equal to 225. The right side of the equation is equal to 225. That means 9²+12²=15² is true, and the triangle shown is a right triangle by the converse of the Pythagorean theorem.

Exercise 2.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 3.5²+4.2²=4.5² is a true statement. The left side of the equation is equal to 29.89. The right side of the equation is equal to 20.25. That means 3.5²+4.2²=4.5² is not true, and the triangle shown is not a right triangle.

Exercise 3.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 72²+154²=170² is a true statement. The left side of the equation is equal to 28,900. The right side of the equation is equal to 28,900. That means 72²+154²=170² is true, and the triangle shown is a right triangle by the converse of the Pythagorean theorem.

Exercise 4.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 9²+40²=41² is a true statement. The left side of the equation is equal to 1,681. The right side of the equation is equal to 1,681. That means 9²+40²=41² is true, and the triangle shown is a right triangle by the converse of the Pythagorean theorem.

Exercise 5.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 10²+34²=36² is a true statement. The left side of the equation is equal to 1,256. The right side of the equation is equal to 1,296. That means 10²+34²=36² is not true, and the triangle shown is not a right triangle.

Exercise 6.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 2²+5²=7² is a true statement. The left side of the equation is equal to 29. The right side of the equation is equal to 49. That means 2²+5²=7² is not true, and the triangle shown is not a right triangle.

Exercise 7.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 2.5²+6²=6.5² is a true statement. The left side of the equation is equal to 42.25. The right side of the equation is equal to 42.25. That means 2.5²+6²=6.5² is true, and the triangle shown is a right triangle by the converse of the Pythagorean theorem.

Eureka Math Grade 8 Module 3 Lesson 14 Exit Ticket Answer Key

Question 1.
The numbers in the diagram below indicate the lengths of the sides of the triangle. Bernadette drew the following triangle and claims it is a right triangle. How can she be sure?

Answer:
Since 37 is the longest side, if this triangle was a right triangle, 37 would have to be the hypotenuse (or c). Now she needs to check to see if 12²+35²=37² is a true statement. The left side is 1,369, and the right side is 1,369. That means 12²+35²=37² is true, and this is a right triangle.

Question 2.
Do the lengths 5, 9, and 14 form a right triangle? Explain.
Answer:
No, the lengths of 5, 9, and 14 do not form a right triangle. If they did, then the equation 5²+9²=14² would be a true statement. However, the left side equals 106, and the right side equals 196. Therefore, these lengths do not form a right triangle.

Eureka Math Grade 8 Module 3 Lesson 14 Problem Set Answer Key

Students practice using the converse of the Pythagorean theorem and identifying common errors in computations.

Question 1.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 12²+16²=20² is a true statement. The left side of the equation is equal to 400. The right side of the equation is equal to 400. That means 12²+16²=20² is true, and the triangle shown is a right triangle.

Question 2.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 47²+24²=53² is a true statement. The left side of the equation is equal to 2,785. The right side of the equation is equal to 2,809. That means 47²+24²=53² is not true, and the triangle shown is not a right triangle.

Question 3.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 51²+68²=85² is a true statement. The left side of the equation is equal to 7,225. The right side of the equation is equal to 7,225. That means 51²+68²=85² is true, and the triangle shown is a right triangle.

Question 4.
The numbers in the diagram below indicate the units of length of each side of the triangle. Sam said that the following triangle is a right triangle because 9+32=40. Explain to Sam what he did wrong to reach this conclusion and what the correct solution is.

Answer:
Sam added incorrectly, but more importantly forgot to square each of the side lengths. In other words, he said 9+32=40, which is not a true statement. However, to show that a triangle is a right triangle, you have to use the Pythagorean theorem, which is a²+b²=c². Using the Pythagorean theorem, the left side of the equation is equal to 1,105, and the right side is equal to 1,600. Since 1,105≠1,600, the triangle is not a right triangle.

Question 5.
The numbers in the diagram below indicate the units of length of each side of the triangle. Is the triangle shown below a right triangle? Show your work, and answer in a complete sentence.

Answer:
We need to check if 24²+7²=25² is a true statement. The left side of the equation is equal to 625. The right side of the equation is equal to 625. That means 24²+7²=25² is true, and the triangle shown is a right triangle.

Question 6.
Jocelyn said that the triangle below is not a right triangle. Her work is shown below. Explain what she did wrong, and show Jocelyn the correct solution.

We need to check if 27²+45²=36² is a true statement. The left side of the equation is equal to 2,754. The right side of the equation is equal to 1,296. That means 27²+45²=36² is not true, and the triangle shown is not a right triangle.
Answer:
Jocelyn made the mistake of not putting the longest side of the triangle in place of c in the Pythagorean theorem, a²+b²=c². Specifically, she should have used 45 for c, but instead she used 36 for c. If she had done that part correctly, she would have seen that, in fact, 27²+36²=45² is a true statement because both sides of the equation equal 2,025. That means that the triangle is a right triangle.

Engage NY Eureka Math 8th Grade Module 3 Lesson 12 Answer Key

Eureka Math Grade 8 Module 3 Lesson 12 Example Answer Key

Example.
Not all flagpoles are perfectly upright (i.e., perpendicular to the ground). Some are oblique (i.e., neither parallel nor at a right angle, slanted). Imagine an oblique flagpole in front of an abandoned building. The question is, can we use sunlight and shadows to determine the length of the flagpole?

Assume that we know the following information: The length of the shadow of the flagpole is 15 feet. There is a mark on the flagpole 3 feet from its base. The length of the shadow of this three-foot portion of the flagpole is 1.7 feet.
Answer:
Students may say that they would like to directly measure the length of the pole. Remind them a direct measurement may not always be possible.

→ Where would the shadow of the flagpole be?
→ On the ground, some distance from the base of the flagpole

→ In the picture below, OA is the length of the flagpole. OB is the length of the shadow cast by the flagpole. (OC) ̅ represents the segment from the base to the 3-foot mark up the flagpole, and OD is the length of the shadow cast by the length of (OC) ̅ that is 1.7 feet in length. (Note: The picture is not drawn to scale.)

→ If we assume that all sunbeams are parallel to each other (i.e., \(\overline{C D}\)||\(\overline{A B}\)̅), do we have a pair of similar triangles? Explain.
→ If \(\overline{C D}\) || \(\overline{A B}\), then △COD~△AOB, by the AA criterion. Corresponding angles of parallel lines are equal, so we know that ∠CDO=∠ABO, and ∠COD is equal to itself.

→ Now that we know △COD~△AOB, how can we find the length of the flagpole?
→ Since the triangles are similar, then we know that the ratios of their corresponding sides must be equal. Therefore, if we let x represent the length of the flagpole (i.e., OA), then
\(\frac{x}{3}\)=\(\frac{15}{1.7}\)

→ We are looking for the value of x that makes the fractions equivalent.
→ Therefore, 1.7x=45, and x≈26.47. The length of the flagpole is approximately 26.47 feet.

Eureka Math Grade 8 Module 3 Lesson 12 Exercise Answer Key

Mathematical Modeling Exercises 1–3

Exercise 1.
You want to determine the approximate height of one of the tallest buildings in the city. You are told that if you place a mirror some distance from yourself so that you can see the top of the building in the mirror, then you can indirectly measure the height using similar triangles. Let point O be the location of the mirror so that the person shown can see the top of the building.

a. Explain why △ABO~△STO.
Answer:
The triangles are similar by the AA criterion. The angle that is formed by the figure standing is 90° with the ground. The building also makes a 90° angle with the ground. The measure of the angle formed with the mirror at ∠AOB is equal to the measure of ∠SOT. Since there are two pairs of corresponding angles that are equal in measure, then △ABO~△STO.

b. Label the diagram with the following information: The distance from eye level straight down to the ground is 5.3 feet. The distance from the person to the mirror is 7.2 feet. The distance from the person to the base of the building is 1,750 feet. The height of the building is represented by x.

c. What is the distance from the mirror to the building?
Answer:
1750 ft.-7.2 ft.=1742.8 ft.

d. Do you have enough information to determine the approximate height of the building? If yes, determine the approximate height of the building. If not, what additional information is needed?
Answer:
Yes, there is enough information about the similar triangles to determine the height of the building.
Since x represents the height of the building, then
\(\frac{x}{5.3}\) = \(\frac{1,742.8}{7.2}\)
We are looking for the value of x that makes the fractions equivalent. Then, 7.2x=9236.84, and
x≈1282.9. The height of the building is approximately 1,282.9 feet.

Exercise 2.
A geologist wants to determine the distance across the widest part of a nearby lake. The geologist marked off specific points around the lake so that the line containing \(\overline{D E}\) would be parallel to the line containing \(\overline{B C}\). The segment BC is selected specifically because it is the widest part of the lake. The segment DE is selected specifically because it is a short enough distance to easily measure. The geologist sketched the situation as shown below.

a. Has the geologist done enough work so far to use similar triangles to help measure the widest part of the lake? Explain.
Answer:
Yes, based on the sketch, the geologist found a center of dilation at point A. The geologist marked points around the lake that, when connected, would make parallel lines. So, the triangles are similar by the AA criterion. Corresponding angles of parallel lines are equal in measure, and the measure of ∠DAE is equal to itself. Since there are two pairs of corresponding angles that are equal, then △DAE~△BAC.

b. The geologist has made the following measurements: |DE|=5 feet, |AE|=7 feet, and |EC|=15 feet. Does she have enough information to complete the task? If so, determine the length across the widest part of the lake. If not, state what additional information is needed.
Answer:
Yes, there is enough information about the similar triangles to determine the distance across the widest part of the lake.
Let x represent the length of segment BC; then
\(\frac{x}{5}\)=\(\frac{22}{7}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 7x=110, and x≈15.7. The distance across the widest part of the lake is approximately 15.7 feet.

c. Assume the geologist could only measure a maximum distance of 12 feet. Could she still find the distance across the widest part of the lake? What would need to be done differently?
Answer:
The geologist could still find the distance across the widest part of the lake. However, she would have to select different points D and E at least 3 feet closer to points B and C, respectively. That would decrease the length of \(\overline{\boldsymbol{E C}}\) to, at most, 12 feet. Then \(\overline{\boldsymbol{D E}}\), in its new position, would still have to be contained within a line that was parallel to the line containing \(\overline{\boldsymbol{B C}}\) in order to calculate the desired distance.

Exercise 3.
A tree is planted in the backyard of a house with the hope that one day it is tall enough to provide shade to cool the house. A sketch of the house, tree, and sun is shown below.

a. What information is needed to determine how tall the tree must be to provide the desired shade?
Answer:
We need to ensure that we have similar triangles. For that reason, we need to know the height of the house and the length of the shadow that the house casts. We also need to know how far away the tree was planted from that point (i.e., the center). Assuming the tree grows perpendicular to the ground, the height of the tree and the height of the house would be parallel, and by the AA criterion, we would have similar triangles.

b. Assume that the sun casts a shadow 32 feet long from a point on top of the house to a point in front of the house. The distance from the end of the house’s shadow to the base of the tree is 53 feet. If the house is 16 feet tall, how tall must the tree get to provide shade for the house?
Answer:
If we let x represent the height the tree must be, then
\(\frac{16}{x}\)=\(\frac{32}{53}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 32x=848, and x=26.5. The tree must grow to a height of 26.5 feet to provide the desired shade for the house.

c. Assume that the tree grows at a rate of 2.5 feet per year. If the tree is now 7 feet tall, about how many years will it take for the tree to reach the desired height?
Answer:
The tree needs to grow an additional 19.5 feet to reach the desired height. If the tree grows 2.5 feet per year, then it will take the tree 7.8 years or about 8 years to reach a height of 26.5 feet.

Eureka Math Grade 8 Module 3 Lesson 12 Problem Set Answer Key

Students practice solving real-world problems using properties of similar triangles.

Question 1.
The world’s tallest living tree is a redwood in California. It’s about 370 feet tall. In a local park, there is a very tall tree. You want to find out if the tree in the local park is anywhere near the height of the famous redwood.

a. Describe the triangles in the diagram, and explain how you know they are similar or not.
Answer:
There are two triangles in the diagram, one formed by the tree and the shadow it casts, △ESO, and another formed by the person and his shadow, △DRO. The triangles are similar if the height of the tree is measured at a 90° angle with the ground and if the person standing forms a 90° angle with the ground. We know that ∠DOR is an angle common to both triangles. If ∠ESO=∠DRO=90°, then △ESO~△DRO by the AA criterion.

b. Assume △ESO~△DRO. A friend stands in the shadow of the tree. He is exactly 5.5 feet tall and casts a shadow of 12 feet. Is there enough information to determine the height of the tree? If so, determine the height. If not, state what additional information is needed.
Answer:
No, there is not enough information to determine the height of the tree. I need either the total length of the shadow that the tree casts or the distance between the base of the tree and the friend.

c. Your friend stands exactly 477 feet from the base of the tree. Given this new information, determine about how many feet taller the world’s tallest tree is compared to the one in the local park.
Let x represent the height of the tree; then
\(\frac{x}{5.5}\)=\(\frac{489}{12}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 12x=2689.5, and x=224.125. The world’s tallest tree is about 146 feet taller than the tree in the park.

d. Assume that your friend stands in the shadow of the world’s tallest redwood, and the length of his shadow is just 8 feet long. How long is the shadow cast by the tree?
Answer:
Let x represent the length of the shadow cast by the tree; then
\(\frac{x}{8}\)=\(\frac{370}{5.5}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 5.5x=2960, and
x≈538.2. The shadow cast by the world’s tallest tree is about 538 feet in length.

Question 2.
A reasonable skateboard ramp makes a 25° angle with the ground. A two-foot-tall ramp requires about 4.3 feet of wood along the base and about 4.7 feet of wood from the ground to the top of the two-foot height to make the ramp.
a. Sketch a diagram to represent the situation.
Answer:
A sample student drawing is shown below.

b. Your friend is a daredevil and has decided to build a ramp that is 5 feet tall. What length of wood is needed to make the base of the ramp? Explain your answer using properties of similar triangles.
Answer:
Sample student drawing and work are shown below.

△EDA~△CBA by the AA criterion because ∠A is common to both triangles, and ∠EDA=∠CBA=90°.
If we let x represent the base of the 5-foot ramp, then
\(\frac{4.3}{x}\)=\(\frac{2}{5}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 2x=21.5, and x=10.75. The base of the 5-foot ramp must be 10.75 feet in length.

c. What length of wood is required to go from the ground to the top of the 5-foot height to make the ramp? Explain your answer using properties of similar triangles.
Answer:
If we let y represent the length of the wood needed to make the ramp, then
\(\frac{4.7}{y}\)=\(\frac{2}{5}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 2y=23.5, and
y=11.75. The length of wood needed to make the ramp is 11.75 feet.

Eureka Math Grade 8 Module 3 Lesson 12 Exit Ticket Answer Key

Henry thinks he can figure out how high his kite is while flying it in the park. First, he lets out 150 feet of string and ties the string to a rock on the ground. Then, he moves from the rock until the string touches the top of his head. He stands up straight, forming a right angle with the ground. He wants to find out the distance from the ground to his kite. He draws the following diagram to illustrate what he has done.

a. Has Henry done enough work so far to use similar triangles to help measure the height of the kite? Explain.
Answer:
Yes Based on the sketch, Henry found a center of dilation, point A. Henry has marked points so that, when connected, would make parallel lines. So, the triangles are similar by the AA criterion. Corresponding angles of parallel lines are equal in measure, and the measure of ∠BAC is equal to itself. Since there are two pairs of corresponding angles that are equal, then △BAC~△DAE.

b. Henry knows he is 5\(\frac{1}{2}\) feet tall. Henry measures the string from the rock to his head and finds it to be 8 feet. Does he have enough information to determine the height of the kite? If so, find the height of the kite. If not, state what other information would be needed.
Answer:
Yes, there is enough information. Let x represent the height DE. Then,
\(\frac{8}{150}\)=\(\frac{5.5}{x}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 8x=825, and x=103.125 feet. The height of the kite is approximately 103 feet high in the air.

Engage NY Eureka Math 8th Grade Module 3 Lesson 13 Answer Key

Eureka Math Grade 8 Module 3 Lesson 13 Exercise Answer Key

Exercises
Use the Pythagorean theorem to determine the unknown length of the right triangle.

Exercise 1.
Determine the length of side c in each of the triangles below.

a.
Answer:
5²+12²=c²
25+144=c²
169=c²
13=c

b.
Answer:
0.5²+1.2²=c²
0.25+1.44=c²
1.69=c²
1.3=c

Exercise 2.
Determine the length of side b in each of the triangles below.
a.
Answer:
4²+b²=5²
16+b²=25
16-16+b²=25-16
b²=9
b=3

b.
Answer:
0.4²+b²=0.5²
0.16+b²=0.25
0.16-0.16+b²=0.25-0.16
b²=0.09
b=0.3

Exercise 3.
Determine the length of \(\overline{Q S}\). (Hint: Use the Pythagorean theorem twice.)

Answer:
15²+|QT|²=17²
225+|QT|²=289
225-225+|QT|²=289-225
|QT|²=64
|QT| = 8

15²+|TS|²=25²
225+|TS|²=625
225-225+|TS|²=625-225
|TS|²=400
|TS|=20
Since |QT|+|TS|=|QS|, then the length of side \(\overline{Q S}\) is 8+20, which is 28.

Eureka Math Grade 8 Module 3 Lesson 13 Exit Ticket Answer Key

Determine the length of side \(\overline{B D}\) in the triangle below.

Answer:
First, determine the length of side \(\overline{B C}\).
12²+BC²=15²
144+BC²=225
BC²=225-144
BC²=81
BC=9

Then, determine the length of side \(\overline{C D}\).
12²+CD²=13²
144+CD²=169
CD²=169-144
CD²=25
CD=5
Adding the lengths of sides \(\overline{B C}\) and \(\overline{C D}\) determines the length of side \(\overline{B D}\); therefore, 5+9=14. \(\overline{B D}\) has a length of 14.

Eureka Math Grade 8 Module 3 Lesson 13 Problem Set Answer Key

Students practice using the Pythagorean theorem to find unknown lengths of right triangles.

Use the Pythagorean theorem to determine the unknown length of the right triangle.

Question 1.
Determine the length of side c in each of the triangles below.
a.
Answer:
6²+8²=c²
36+64=c²
100=c²
10=c

b.
Answer:
0.6²+0.8²=c²
0.36+0.64=c²
1=c²
1=c

Question 2.
Determine the length of side a in each of the triangles below.
a.
Answer:
a²+8²=17²
a²+64=289
a²+64-64=289-64
a²=225
a=15

b.
Answer:
a²+0.8²=1.7²
a²+0.64=2.89
a²+0.64-0.64=2.89-0.64
a²=2.25
a=1.5

Question 3.
Determine the length of side b in each of the triangles below.
a.
Answer:
20²+b²=25²
400+b²=625
400-400+b²=625-400
b²=225
b=15

b.
Answer:
2²+b²=2.5²
4+b²=6.25
4-4+b²=6.25-4
b²=2.25
b=1.5

Question 4.
Determine the length of side a in each of the triangles below.
a.
Answer:
a²+12²=20²
a²+144=400
a²+144-144=400-144
a²=256
a=16

b.
Answer:
a²+1.2²=2²
a²+1.44=4
a²+1.44-1.44=4-1.44
a²=2.56
a=1.6

Question 5.
What did you notice in each of the pairs of Problems 1–4? How might what you noticed be helpful in solving problems like these?
Answer:
In each pair of problems, the problems and solutions were similar. For example, in Problem 1, part (a) showed the sides of the triangle were 6, 8, and 10, and in part (b), they were 0.6, 0.8, and 1. The side lengths in part (b) were a tenth of the value of the lengths in part (a). The same could be said about parts (a) and (b) of Problems 2–4. This might be helpful for solving problems in the future. If I am given side lengths that are decimals, then I could multiply them by a factor of 10 to make whole numbers, which are easier to work with. Also, if I know common numbers that satisfy the Pythagorean theorem, like side lengths of 3, 4, and 5, then I recognize them more easily in their decimal forms, that is, 0.3, 0.4, and 0.5.

Engage NY Eureka Math 8th Grade Module 3 Lesson 11 Answer Key

Eureka Math Grade 8 Module 3 Lesson 11 Exercise Answer Key

Exercise 1.
In the diagram below, you have △ABC and △AB’ C’. Use this information to answer parts (a)–(d).

a. Based on the information given, is △ABC~△AB’ C’? Explain.
Answer:
There is not enough information provided to determine if the triangles are similar. We would need information about a pair of corresponding angles or more information about the side lengths of each of the triangles.

b. Assume the line containing \(\overline{B C}\) is parallel to the line containing \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\). With this information, can you say that △ABC~△AB’ C’? Explain.
Answer:
If the line containing \(\overline{B C}\) is parallel to the line containing \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\), then △ABC~△AB’ C’. Both triangles share ∠A. Another pair of equal angles is ∠AB’C’and ∠ABC. They are equal because they are corresponding angles of parallel lines. By the AA criterion, △ABC~△AB’ C’.

c. Given that △ABC~△AB’ C’, determine the length of side \(\overline{A C^{\prime}}\).
Answer:
Let x represent the length of side \(\overline{A C^{\prime}}\).
\(\frac{x}{6}\)=\(\frac{2}{8}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 8x=12, and x=1.5.
The length of side \(\overline{A C^{\prime}}\) is 1.5.

d. Given that △ABC~△AB’ C’, determine the length of side \(\overline{A B}\).
Answer:
Let y represent the length of side \(\overline{A B}\).
\(\frac{2.7}{y}\)=\(\frac{2}{8}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 2y=21.6, and y=10.8. The length of side \(\overline{A B}\) is 10.8.

Exercise 2.
In the diagram below, you have △ABC and △A’B’C’. Use this information to answer parts (a)–(c).

a. Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
Yes, △ABC~△A’ B’C’. There are two pairs of corresponding angles that are equal in measure, namely, ∠A=∠A’=59°, and ∠B=∠B’=92°. By the AA criterion, these triangles are similar.

b. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{A^{\prime} C^{\prime}}\).
Answer:
Let x represent the length of side \(\overline{A^{\prime} C^{\prime}}\).
\(\frac{x}{6.1}\)=\(\frac{5.12}{3.2}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 3.2x=31.232, and
x=9.76. The length of side \(\overline{A^{\prime} C^{\prime}}\) is 9.76.

c. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{B C}\).
Answer:
Let y represent the length of side \(\overline{B C}\).
\(\frac{8.96}{y}\)=\(\frac{5.12}{3.2}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 5.12y=28.672, and y=5.6. The length of side \(\overline{B C}\) is 5.6.

Exercise 3.
In the diagram below, you have △ABC and △A’B’ C’. Use this information to answer the question below.

Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
No, △ABC is not similar to △A’ B’ C’. Since there is only information about one pair of corresponding angles, then we must check to see that the corresponding sides have equal ratios. That is, the following must be true:
\(\frac{10.58}{5.3}\) = \(\frac{11.66}{4.6}\)
When we compare products of each numerator with the denominator of the other fraction, we see that 48.668≠61.798. Since the corresponding sides do not have equal ratios, then the fractions are not equivalent, and the triangles are not similar.

Eureka Math Grade 8 Module 3 Lesson 11 Problem Set Answer Key

Students practice presenting informal arguments as to whether or not two given triangles are similar. Students practice finding measurements of similar triangles.

Question 1.
In the diagram below, you have △ABC and △A’B’ C’. Use this information to answer parts (a)–(b).

a. Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
Yes, △ABC~△A’B’ C’. Since there is only information about one pair of corresponding angles being equal, then the corresponding sides must be checked to see if their ratios are equal.
\(\frac{10.65}{7.1}\)=\(\frac{9}{6}\)
63.9=63.9
Since the cross products are equal, the triangles are similar.

b. Assume the length of side \(\overline{A C}\) is 4.3. What is the length of side \(\overline{A^{\prime} C^{\prime}}\)?
Answer:
Let x represent the length of side \(\overline{A^{\prime} C^{\prime}}\).
\(\frac{x}{4.3}\)=\(\frac{9}{6}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 6x=38.7, and x=6.45. The length of side \(\overline{A^{\prime} C^{\prime}}\) is 6.45.

Question 2.
In the diagram below, you have △ABC and △AB’ C’. Use this information to answer parts (a)–(d).

a. Based on the information given, is △ABC~△AB’ C’? Explain.
Answer:
There is not enough information provided to determine if the triangles are similar. We would need information about a pair of corresponding angles or more information about the side lengths of each of the triangles.

b. Assume the line containing \(\overline{B C}\) is parallel to the line containing \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\). With this information, can you say that △ABC~△AB’ C’? Explain.
Answer:
If the line containing \(\overline{B C}\) is parallel to the line containing \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\), then △ABC~△AB’ C’. Both triangles share ∠A. Another pair of equal angles are ∠AB’C’ and ∠ABC. They are equal because they are corresponding angles of parallel lines. By the AA criterion, △ABC~△AB’ C’.

c. Given that △ABC~△AB’ C’, determine the length of side \(\overline{A C^{\prime}}\).
Let x represent the length of side \(\overline{A C^{\prime}}\).
\(\frac{x}{16.1}\)=\(\frac{1.6}{11.2}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 11.2x=25.76, and x=2.3. The length of side \(\overline{A C^{\prime}}\) is 2.3.

d. Given that △ABC~△AB’ C’, determine the length of side \(\overline{A B^{\prime}}\).
Answer:
Let y represent the length of side \(\overline{A B^{\prime}}\).
\(\frac{y}{7.7}\)=\(\frac{1.6}{11.2}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 11.2y=12.32, and
y=1.1. The length of side \(\overline{A B^{\prime}}\) is 1.1.

Question 3.
In the diagram below, you have △ABC and △A’B’ C’. Use this information to answer parts (a)–(c).

a. Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
Yes, △ABC~△A’ B’C’. There are two pairs of corresponding angles that are equal in measure, namely, ∠A=∠A’=23°, and ∠C=∠C’=136°. By the AA criterion, these triangles are similar.

b. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\).
Answer:
Let x represent the length of side \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\).
\(\frac{x}{3.9}\)=\(\frac{8.75}{7}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 7x=34.125, and
x=4.875. The length of side \(\overline{\boldsymbol{B}^{\prime} \boldsymbol{C}^{\prime}}\) is 4.875.

c. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{A C}\).
Answer:
Let y represent the length of side \(\overline{A C}\).
\(\frac{5}{y}\)=\(\frac{8.75}{7}\)
We are looking for the value of y that makes the fractions equivalent. Therefore, 8.75y=35, and y=4. The length of side \(\overline{A C}\) is 4.

Question 4.
In the diagram below, you have △ABC and △AB’ C’. Use this information to answer the question below.

Based on the information given, is △ABC~△AB’ C’? Explain.
Answer:
No, △ABC is not similar to △AB’ C’. Since there is only information about one pair of corresponding angles, then we must check to see that the corresponding sides have equal ratios. That is, the following must be true:
\(\frac{9}{3}\)=\(\frac{12.6}{4.1}\)
When we compare products of each numerator with the denominator of the other fraction, we see that
36.9≠37.8. Since the corresponding sides do not have equal ratios, the fractions are not equivalent, and the triangles are not similar.

Question 5.
In the diagram below, you have △ABC and △A’B’C’. Use this information to answer parts (a)–(b).

a. Based on the information given, is △ABC~△A’B’ C’? Explain.
Answer:
Yes, △ABC~△A’B’ C’. Since there is only information about one pair of corresponding angles being equal, then the corresponding sides must be checked to see if their ratios are equal.
\(\frac{8.2}{20.5}\)=\(\frac{7.5}{18.75}\)
When we compare products of each numerator with the denominator of the other fraction, we see that 153.75=153.75. Since the products are equal, the fractions are equivalent, and the triangles are similar.

b. Given that △ABC~△A’B’ C’, determine the length of side \(\overline{\boldsymbol{A}^{\prime} \boldsymbol{B}^{\prime}}\).
Answer:
Let x represent the length of side \(\overline{\boldsymbol{A}^{\prime} \boldsymbol{B}^{\prime}}\).
\(\frac{x}{26}\)=\(\frac{7.5}{18.75}\)
We are looking for the value of x that makes the fractions equivalent. Therefore, 18.75x=195, and
x=10.4. The length of side \(\overline{\boldsymbol{A}^{\prime} \boldsymbol{B}^{\prime}}\) is 10.4.

Eureka Math Grade 8 Module 3 Lesson 11 Exit Ticket Answer Key

Question 1.
In the diagram below, you have △ABC and △A’B’ C’. Based on the information given, is △ABC~△A’B’ C’? Explain.

Answer:
Since there is only information about one pair of corresponding angles, we need to check to see if corresponding sides have equal ratios. That is, does \(\frac{|A B|}{\left|A^{\prime} B^{\prime}\right|}\) = \(\frac{|A C|}{\left|A^{\prime} C^{\prime}\right|^{\prime}}\), or does \(\frac{3.5}{8.75}\) = \(\frac{6}{21}\)? The products are not equal; 73.5≠52.5. Since the corresponding sides do not have equal ratios, the triangles are not similar.

Question 2.
In the diagram below, △ABC~△DEF. Use the information to answer parts (a)–(b).

a. Determine the length of side \(\overline{A B}\). Show work that leads to your answer.
Answer:
Let x represent the length of side \(\overline{A B}\).
Then, \(\frac{x}{17.64}\)=\(\frac{6.3}{13.23}\). We are looking for the value of x that makes the fractions equivalent. Therefore, 111.132=13.23x, and x=8.4. The length of side \(\overline{A B}\) is 8.4.

b. Determine the length of side \(\overline{D F}\). Show work that leads to your answer.
Answer:
Let y represent the length of side \(\overline{D F}\).
Then, \(\frac{4.1}{y}\)= \(\frac{6.3}{13.23}\). We are looking for the value of y that makes the fractions equivalent. Therefore, 54.243=6.3y, and 8.61=y. The length of side \(\overline{D F}\) is 8.61.

Engage NY Eureka Math 8th Grade Module 3 Lesson 10 Answer Key

Eureka Math Grade 8 Module 3 Lesson 10 Exercise Answer Key

Exercises 1–2.
Use a protractor to draw a pair of triangles with two pairs of equal angles. Then, measure the lengths of the sides, and verify that the lengths of their corresponding sides are equal in ratio.
Answer:
Sample student work is shown below.

Exercise 2.
Draw a new pair of triangles with two pairs of equal angles. Then, measure the lengths of the sides, and verify that the lengths of their corresponding sides are equal in ratio.
Answer:
Sample student work is shown below.

Exercises 3–5.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.
Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal, namely, |∠B|=|∠B’|=103°, and |∠A|=|∠A’|=31°.

Exercise 4.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
No, △ABC is not similar to △A’ B’ C’. They are not similar because they do not have two pairs of corresponding angles that are equal, just one, namely, |∠A|=|∠A’|, but |∠B|≠|∠B’ |.

Exercise 5.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B|=60° or |∠C’|=48°. Then, you can see that |∠A|=|∠A’|=72°, |∠B|=|∠B’|=60°, and |∠C|=|∠C’|=48°.

Eureka Math Grade 8 Module 3 Lesson 10 Problem Set Answer Key

Students practice presenting informal arguments to prove whether or not two triangles are similar.

Question 1.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal, namely, |∠B|=|∠B’|=103°, and |∠A|=|∠A’|=31°.

Question 2.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B’|=84° or |∠C|=32°. Then, you can see that |∠A|=|∠A’|=64°, |∠B|=|∠B’|=84°, and |∠C|=|∠C’|=32°.

Question 3.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
We do not know if △ABC is similar to △A’ B’ C’. We can use the triangle sum theorem to find out that |∠B|=44°, but we do not have any information about |∠A’| or |∠C’|. To be considered similar, the two triangles must have two pairs of corresponding angles that are equal. In this problem, we only know of one pair of corresponding angles, and that pair does not have equal measure.

Question 4.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal, namely, |∠C|=|∠C’|=46°, and |∠A|=|∠A’|=31°.

Question 5.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B|=81° or |∠C’|=29°. Then, you can see that |∠A|=|∠A’|=70°, |∠B|=|∠B’|=81°,
and |∠C|=|∠C’|=29°.

Question 6.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
No, △ABC is not similar to △A’ B’ C’. By the given information, |∠B|≠|∠B’|, and |∠A|≠|∠A’|.

Question 7.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B|=102° or |∠C’|=53°. Then, you can see that |∠A|=|∠A’|=25°, |∠B|=|∠B’|=102°, and |∠C|=|∠C’|=53°.

Eureka Math Grade 8 Module 3 Lesson 10 Exit Ticket Answer Key

Question 1.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
Yes, △ABC~△A’ B’ C’. They are similar because they have two pairs of corresponding angles that are equal. You have to use the triangle sum theorem to find out that |∠B’|=45˚or |∠A|=45˚. Then, you can see that |∠A|=|∠A’|=45˚, |∠B|=|∠B’|=45˚, and |∠C|=|∠C’|=90˚.

Question 2.
Are the triangles shown below similar? Present an informal argument as to why they are or are not similar.

Answer:
No, △ABC is not similar to △A’ B’ C’. They are not similar because they do not have two pairs of corresponding angles that are equal, namely, |∠A|≠|∠A’ |, and |∠B|≠|∠B’|.

Engage NY Eureka Math 8th Grade Module 7 Lesson 17 Answer Key

Eureka Math Grade 8 Module 7 Lesson 17 Example Answer Key

Example 1.
What is the distance between the two points A and B on the coordinate plane?

Answer:
What is the distance between the two points A and B on the coordinate plane?
The distance between points A and B is 6 units.

What is the distance between the two points A and B on the coordinate plane?

Answer:
What is the distance between the two points A and B on the coordinate plane?
The distance between points A and B is 2 units.

What is the distance between the two points A and B on the coordinate plane? Round your answer to the tenths place.

Answer:
What is the distance between the two points A and B on the coordinate plane? Round your answer to the tenths place.
Provide students time to solve the problem. Have students share their work and estimations of the distance between the points. The questions that follow can be used to guide students’ thinking.

We cannot simply count units between the points because the line that connects A to B is not horizontal or vertical. What have we done recently that allowed us to find the length of an unknown segment?

→ The Pythagorean theorem allows us to determine the length of an unknown side of a right triangle.
→ Use what you know about the Pythagorean theorem to determine the distance between points A and B.
Provide students time to solve the problem now that they know that the Pythagorean theorem can help them. If necessary, the questions below can guide students’ thinking.
We must draw a right triangle so that |AB| is the hypotenuse. How can we construct the right triangle that we need?

→ Draw a vertical line through B and a horizontal line through A. Or, draw a vertical line through A and a horizontal line through B.

Let’s mark the point of intersection of the horizontal and vertical lines we drew as point C. What is the length of \(\overline{A C}\)? \(\overline{B C}\)?

|AC| = 6 units, and |BC| = 2 units
Now that we know the lengths of the legs of the right triangle, we can determine the length of \(\overline{A B}\).
Remind students that because we are finding a length, we need only consider the positive value of the square root because a negative length does not make sense. If necessary, remind students of this fact throughout their work in this lesson.
Let c be the length of \(\overline{A B}\).
2² + 6² = c²
4 + 36 = c²
40 = c²
\(\sqrt{40}\) = c
6.3 ≈ c The distance between points A and B is approximately 6.3 units.

Example 2.
Given two points A and B on the coordinate plane, determine the distance between them. First, make an estimate; then, try to find a more precise answer. Round your answer to the tenths place.

Answer:
Provide students time to solve the problem. Have students share their work and estimations of the distance between the points. The questions below can be used to guide students’ thinking.
We know that we need a right triangle. How can we draw one?


→ Draw a vertical line through B and a horizontal line through A. Or draw a vertical line through A and a horizontal line through B.
Mark the point C at the intersection of the horizontal and vertical lines. What do we do next?

→ Count units to determine the lengths of the legs of the right triangle, and then use the Pythagorean theorem to find |AB|.
Show the last diagram, and ask a student to explain the answer.

|AC| = 3 units, and |BC| = 3 units. Let c be |AB|.
3² + 3² = c²
9 + 9 = c²
18 = c²
\(\sqrt{18}\) = c
4.2 ≈ c
The distance between points A and B is approximately 4.2 units.

Example 3.
Is the triangle formed by the points A, B, C a right triangle?

Answer:
→How can we verify if a triangle is a right triangle?
Use the converse of the Pythagorean theorem.

→ What information do we need about the triangle in order to use the converse of the Pythagorean theorem, and how would we use it?
We need to know the lengths of all three sides; then, we can check to see if the side lengths satisfy the Pythagorean theorem.

→ Clearly, |AB| = 10 units. How can we determine |AC|?
To find |AC|, follow the same steps used in the previous problem. Draw horizontal and vertical lines to form a right triangle, and use the Pythagorean theorem to determine the length.
→ Determine |AC|. Leave your answer in square root form unless it is a perfect square.

Let c represent |AC|.
1² + 3² = c²
1 + 9 = c²
10 = c²
\(\sqrt{10}\) = c

Now, determine |BC|. Again, leave your answer in square root form unless it is a perfect square.
Let c represent |BC|.
9² + 3² = c²
81 + 9 = c²
90 = c²
\(\sqrt{90}\) = c
→ The lengths of the three sides of the triangle are 10 units, \(\sqrt{10}\) units, and \(\sqrt{90}\) units. Which number represents the hypotenuse of the triangle? Explain.
The side \(\overline{A B}\) must be the hypotenuse because it is the longest side. When estimating the lengths of the other two sides, I know that \(\sqrt{10}\) is between 3 and 4, and \(\sqrt{90}\) is between 9 and 10. Therefore, the side that is 10 units in length is the hypotenuse.

→ Use the lengths 10, \(\sqrt{10}\), and \(\sqrt{90}\) to determine if the triangle is a right triangle.
Sample response:
(\(\sqrt{10}\))² + (\(\sqrt{90}\))² = 10²
10 + 90 = 100
100 = 100
Therefore, the points A, B, C form a right triangle.

Eureka Math Grade 8 Module 7 Lesson 17 Exercise Answer Key

Exercises 1–4
For each of the Exercises 1–4, determine the distance between points A and B on the coordinate plane. Round your answer to the tenths place.

Exercise 1.

Answer:

Let c represent |AB|.
5² + 6² = c²
25 + 36 = c²
61 = c²
\(\sqrt{61}\) = c
7.8 ≈ c
The distance between points A and B is about 7.8 units.

Exercise 2.

Answer:

Let c represent |AB|.
13² + 4² = c²
169 + 16 = c²
185 = c²
\(\sqrt{185}\) = c
13.6 ≈ c
The distance between points A and B is about 13.6 units.

Exercise 3.

Answer:

Let c represent |AB|.
3² + 5² = c²
9 + 25 = c²
34 = c²
\(\sqrt{34}\) = c
5.8 ≈ c
The distance between points A and B is about 5.8 units.

Exercise 4.

Answer:

Let c represent |AB|.
5² + 4² = c²
25 + 16 = c²
41 = c²
\(\sqrt{41}\) = c
6.4 ≈ c
The distance between points A and B is about 6.4 units.

Eureka Math Grade 8 Module 7 Lesson 17 Problem Set Answer Key

For each of the Problems 1–4, determine the distance between points A and B on the coordinate plane. Round your answer to the tenths place.
Question 1.

Answer:

Let c represent |AB|.
6² + 7² = c²
36 + 49 = c²
85 = c²
\(\sqrt{85}\) = c
9.2 ≈ c
The distance between points A and B is about 9.2 units.

Question 2.

Answer:

Let c represent |AB|.
9² + 4² = c²
81 + 16 = c²
97 = c²
\(\sqrt{97}\) = c
9.8 ≈ c
The distance between points A and B is about 9.8 units.

Question 3.

Answer:

Let c represent |AB|.
2² + 8² = c²
4 + 64 = c²
68 = c²
\(\sqrt{68}\) = c
8.2 ≈ c
The distance between points A and B is about 8.2 units.

Question 4.

Answer:

Let c represent |AB|.
11² + 4² = c²
121 + 16 = c²
137 = c²
\(\sqrt{137}\) = c
11.7 ≈ c
The distance between points A and B is about 11.7 units.

Question 5.
Is the triangle formed by points A, B, C a right triangle?

Answer:

Let c represent |AB|.
3² + 6² = c²
9 + 36 = c²
45 = c²
\(\sqrt{45}\) = c

Let c represent |AC|.
3² + 5² = c²
9 + 25 = c²
34 = c²
\(\sqrt{34}\) = c

Let c represent |BC|.
3² + 8² = c²
9 + 64 = c²
73 = c²
\(\sqrt{73}\) = c

(\(\sqrt{45}\))² + (\(\sqrt{34}\))² = (\(\sqrt{73}\))²
45 + 34 = 73
79 ≠ 73
No, the points do not form a right triangle.

Eureka Math Grade 8 Module 7 Lesson 17 Exit Ticket Answer Key

Use the following diagram to answer the questions below.

Question 1.
Determine |AC|. Leave your answer in square root form unless it is a perfect square.
Answer:
Let c represent |AC|.
4² + 4² = c²
16 + 16 = c²
32 = c²
\(\sqrt{32}\) = c

Question 2.
Determine |CB|. Leave your answer in square root form unless it is a perfect square.
Answer:
Let d represent |CB|.
3² + 4² = d²
9 + 16 = d²
25 = d²
\(\sqrt{25}\) = d
5 = d

Question 3.
Is the triangle formed by the points A, B, C a right triangle? Explain why or why not.
Answer:
Using the lengths 5,\(\sqrt{32}\), and |AB| = 7 to determine if the triangle is a right triangle, I have to check to see if
5² + (\(\sqrt{32}\))² = 7²
25 + 32 ≠ 49
Therefore, the triangle formed by the points A, B, C is not a right triangle because the lengths of the triangle do not satisfy the Pythagorean theorem.

Engage NY Eureka Math 8th Grade Module 7 Lesson 18 Answer Key

Eureka Math Grade 8 Module 7 Lesson 18 Exercise Answer Key

Exercises

Exercise 1.
The area of the right triangle shown below is 26.46 in². What is the perimeter of the right triangle? Round your answer to the tenths place.

Answer:
Let b in. represent the length of the base of the triangle where
h = 6.3.
A = latex]\frac{bh}{2}[/latex]
26.46 = \(\frac{6.3b}{2}\)
52.92 = 6.3b
\(\frac{52.92}{6.3}\) = \(\frac{6.3b}{6.3}\)
8.4 = b

Let c in. represent the length of the hypotenuse.
6.3² + 8.4² = c²
39.69 + 70.56 = c²
110.25 = c²
\(\sqrt{110.25}\) = \(\sqrt{c^{2}}\)
\(\sqrt{11.025}\) = c
The number √(110.25) is between 10 and 11. When comparing with tenths, the number is actually equal to 10.5 because 10.5² = 110.25. Therefore, the length of the hypotenuse is 10.5 in. The perimeter of the triangle is 6.3 in. + 8.4 in. + 10.5 in. = 25.2 in.

Exercise 2.
The diagram below is a representation of a soccer goal.

a. Determine the length of the bar, c, that would be needed to provide structure to the goal. Round your answer to the tenths place.
Answer:
Let c ft. represent the hypotenuse of the right triangle.
8² + 3² = c²
64 + 9 = c²
73 = c²
\(\sqrt{73}\) = \(\sqrt{c^{2}}\)
The number \(\sqrt{73}\) is between 8 and 9. In the sequence of tenths, it is between 8.5 and 8.6 because 8.5² < (\(\sqrt{73}\))² < 8.6². In the sequence of hundredths, the number is between 8.54 and 8.55 because 8.54² < (\(\sqrt{73}\))² < 8.55². Since the number \(\sqrt{73}\) is between 8.54 and 8.55, it would round to 8.5. The length of the bar that provides structure for the goal is approximately 8.5 ft.

b. How much netting (in square feet) is needed to cover the entire goal?
Answer:
The areas of the triangles are each 12 ft². The area of the rectangle in the back is approximately 85 ft². The total area of netting required to cover the goal is approximately 109 ft².

Exercise 3.
The typical ratio of length to width that is used to produce televisions is 4:3.

A TV with length 20 inches and width 15 inches, for example, has sides in a 4:3 ratio; as does any TV with length 4x inches and width 3x inches for any number x.
a. What is the advertised size of a TV with length 20 inches and width 15 inches?
Answer:
Let c in. be the length of the diagonal.
20² + 15² = c²
400 + 225 = c²
625 = c²
\(\sqrt{625}\) = \(\sqrt{c^{2}}\)
25 = c
Since the TV has a diagonal length of 25 inches, then it is a 25″ TV.

b. A 42″ TV was just given to your family. What are the length and width measurements of the TV?
Answer:
Let x be the factor applied to the ratio 4:3.
(3x)² + (4x)² = 42²
9x² + 16x² = 1764
(9 + 16) x² = 1764
25x² = 1764
\(\frac{25 x^{2}}{25}\) = \(\frac{1764}{25}\)
x² = 70.56
\(\sqrt{x^{2}}\) = \(\sqrt{70.56}\)
x = \(\sqrt{70.56}\)
The number \(\sqrt{70.56}\) is between 8 and 9. In working with the sequence of tenths, I realized the number \(\sqrt{70.56}\) is actually equal to 8.4 because 8.4² = 70.56. Therefore, x = 8.4, and the dimensions of the TV are (4 × 8.4) inches , which is 33.6 inches, and (3 × 8.4) inches, which is 25.2 inches.

c. Check that the dimensions you got in part (b) are correct using the Pythagorean theorem.
Answer:
33.6² + 25.2² = 42²
1128.96 + 635.04 = 1764
1764 = 1764

d. The table that your TV currently rests on is 30″ in length. Will the new TV fit on the table? Explain.
Answer:
The dimension for the length of the TV is 33.6 inches. It will not fit on a table that is 30 inches in length.

Exercise 4.
Determine the distance between the following pairs of points. Round your answer to the tenths place. Use graph paper if necessary.
a. (7,4) and ( – 3, – 2)
Answer:
Let c represent the distance between the two points.
10² + 6² = c²
100 + 36 = c²
136 = c²
\(\sqrt{136}\) = \(\sqrt{c^{2}}\)
\(\sqrt{136}\) = c
The number \(\sqrt{136}\) is between 11 and 12. In the sequence of tenths, it is between 11.6 and 11.7 because 11.6² < (\(\sqrt{136}\))² < 11.7². In the sequence of hundredths, it is between 11.66 and 11.67, which means the number will round in tenths to 11.7. The distance between the two points is approximately 11.7 units.

b. ( – 5,2) and (3,6)
Answer:
Let c represent the distance between the two points.
8² + 4² = c²
64 + 16 = c²
80 = c²
\(\sqrt{80}\) = \(\sqrt{c^{2}}\)
\(\sqrt{80}\) = c
The number \(\sqrt{80}\) is between 8 and 9. In the sequence of tenths, it is between 8.9 and 9 because
8.9² < (\(\sqrt{80}\))² < 9². In the sequence of hundredths, it is between 8.94 and 8.95, which means it will round to 8.9. The distance between the two points is approximately 8.9 units.

c. Challenge: (x₁,y₁) and (x₂,y₂). Explain your answer.
Answer:
Note: Deriving the distance formula using the Pythagorean theorem is not part of the standard but does present an interesting challenge to students. Assign it only to students who need a challenge.
Let c represent the distance between the two points.
(x₁ – x₂ )² + (y₁ – y₂ )² = c²
\(\sqrt{\left(x_{1} – x_{2}\right)^{2} + \left(y_{1} – y_{2}\right)^{2}}\) = \(\sqrt{c^{2}}\)
\(\sqrt{\left(x_{1} – x_{2}\right)^{2} + \left(y_{1} – y_{2}\right)^{2}}\) = c
I noticed that the dimensions of the right triangle were equal to the difference in x – values and the difference in y – values. Using those expressions and what I knew about solving radical equations, I was able to determine the length of c.

Exercise 5.
What length of ladder is needed to reach a height of 7 feet along the wall when the base of the ladder is 4 feet from the wall? Round your answer to the tenths place.

Answer:
Let c feet represent the length of the ladder.
7² + 4² = c²
49 + 16 = c²
65 = c²
\(\sqrt{65}\) = \(\sqrt{c^{2}}\)
\(\sqrt{65}\) = c
The number \(\sqrt{65}\) is between 8 and 9. In the sequence of tenths, it is between 8 and 8.1 because 8² < (\(\sqrt{65}\))² < 8.1². In the sequence of hundredths, it is between 8.06 and 8.07, which means the number will round to 8.1. The ladder must be approximately 8.1 feet long to reach 7 feet up a wall when placed 4 feet from the wall.

Eureka Math Grade 8 Module 7 Lesson 18 Problem Set Answer Key

Question 1.
A 70″ TV is advertised on sale at a local store. What are the length and width of the television?
Answer:
The TV is in the ratio of 4:3 and has measurements of 4x:3x, where x is the scale factor of enlargement.
(3x)² + (4x)² = 70²
9x² + 16x² = 4,900
25x² = 4,900
\(\frac{25 x^{2}}{25}\) = \(\frac{4,900}{25}\)
x² = 196
\(\sqrt{x^{2}}\) = \(\sqrt{196}\)
x = 14
The length of the TV is (4 × 14) inches, which is 56 inches, and the width is (3 × 14) inches, which is 42 inches.

Question 2.
There are two paths that one can use to go from Sarah’s house to James’ house. One way is to take C Street, and the other way requires you to use A Street and B Street. How much shorter is the direct path along C Street?

Answer:
Let c miles represent the length of the hypotenuse of the right triangle.
2² + 1.5² = c²
4 + 2.25 = c²
6.25 = c²
\(\sqrt{6.225}\) = \(\sqrt{c^{2}}\)
2.5 = c
The path using A Street and B Street is 3.5 miles. The path along C Street is 2.5 miles. The path along C Street is exactly 1 mile shorter than the path along A Street and B Street.

Question 3.
An isosceles right triangle refers to a right triangle with equal leg lengths, s, as shown below.

What is the length of the hypotenuse of an isosceles right triangle with a leg length of 9 cm? Write an exact answer using a square root and an approximate answer rounded to the tenths place.
Answer:
Let c be the length of the hypotenuse of the isosceles triangle in centimeters.
9² + 9² = c²
81 + 81 = c²
162 = c²
\(\sqrt{162}\) = \(\sqrt{c^{2}}\)
\(\sqrt{81 \times 2}\) = c
\(\sqrt{81}\) × \(\sqrt{2}\) = c
9\(\sqrt{2}\) = c
The number \(\sqrt{2}\) is between 1 and 2. In the sequence of tenths, it is between 1.4 and 1.5 because 1.4² < (\(\sqrt{2}\))² < 1.5². Since the number 2 is closer to 1.4² than 1.5², it would round to 1.4. 9 × 1.4 = 12.6.
So, 12.6 cm is the approximate length of the hypotenuse, and 9\(\sqrt{2}\) cm is the exact length.

Question 4.
The area of the right triangle shown to the right is 66.5 cm².
a. What is the height of the triangle?

Answer:
A = \(\frac{bh}{2}\)
66.5 = \(\frac{9.5h}{2}\)
133 = 9.5h
\(\frac{133}{9.5}\) = \(\frac{9.5h}{9.5}\)
14 = h
The height of the triangle is 14 cm.

b. What is the perimeter of the right triangle? Round your answer to the tenths place.
Answer:
Let c represent the length of the hypotenuse in centimeters.
9.5² + 14² = c²
90.25 + 196 = c²
286.25 = c²
\(\sqrt{286.25}\) = \(\sqrt{c^{2}}\)
\(\sqrt{286.25}\) = c
The number \(\sqrt{286.25}\) is between 16 and 17. In the sequence of tenths, the number is between 16.9 and 17 because 16.9² < (\(\sqrt{286.25}\))² < 17². Since 286.25 is closer to 16.9² than 17², then the approximate length of the hypotenuse is 16.9 cm.
The perimeter of the triangle is 9.5 cm + 14 cm + 16.9 cm = 40.4 cm.

Question 5.
What is the distance between points (1,9) and ( – 4, – 1)? Round your answer to the tenths place.
Answer:
Let c represent the distance between the points.
10² + 5² = c²
100 + 25 = c²
125 = c²
\(\sqrt{125}\) = \(\sqrt{c^{2}}\)
\(\sqrt{125}\) = c
11.2 ≈ c
The distance between the points is approximately 11.2 units.

Question 6.
An equilateral triangle is shown below. Determine the area of the triangle. Round your answer to the tenths place.

Answer:
Let h in. represent the height of the triangle.
4² + h² = 8²
16 + h² = 64
h² = 48
\(\sqrt{h^{2}}\) = \(\sqrt{48}\)
h = \(\sqrt{48}\)
h ≈ 6.9
A = \(\frac{(8)(6.9)}{2}\) = (4)(6.9) = 27.6
The area of the triangle is approximately 27.6 in².

Eureka Math Grade 8 Module 7 Lesson 18 Exit Ticket Answer Key

Use the diagram of the equilateral triangle shown below to answer the following questions. Show the work that leads to your answers.

a. What is the perimeter of the triangle?
Answer:
4 + 4 + 4 = 12
The perimeter is 12 mm.

b. What is the height, h mm, of the equilateral triangle? Write an exact answer using a square root and an approximate answer rounded to the tenths place.
Answer:
Using the fact that the height is one leg length of a right triangle, and I know the hypotenuse is 4 mm and the other leg length is 2 mm, I can use the Pythagorean theorem to find h.
2² + h² = 4²
4 + h² = 16
4 – 4 + h² = 16 – 4
h² = 12
h = \(\sqrt{12}\)
h = \(\sqrt{4 \times 3}\)
h = \(\sqrt{4}\) × \(\sqrt{3}\)
h = 2\(\sqrt{3}\)
The number \(\sqrt{3}\) is between 1 and 2. In the sequence of tenths, it is between 1.7 and 1.8 because
1.7² < (\(\sqrt{3}\))² < 1.8². In the sequence of hundredths, it is between 1.73 and 1.74. This would put h between 2 × 1.73 mm, which is 3.46 mm, and 2 × 1.74 mm, which is 3.48 mm. In terms of tenths, the approximate height is 3.5 mm. The exact height is \(\sqrt{12}\) mm, or 2\(\sqrt{3}\) mm.

c. Using the approximate height found in part (b), estimate the area of the equilateral triangle
Answer:
A = \(\frac{bh}{2}\)
A = \(\frac{4(3.5)}{2}\)
A = \(\frac{14}{2}\)
A = 7
The approximate area of the equilateral triangle is 7 mm².

Eureka Math Grade 8 Module 7 Lesson 18 Area and Volume II Answer Key

Question 1.
Find the area of the square shown below.

Answer:
A = (6 cm)²
= 36 cm²

Question 2.
Find the volume of the cube shown below.

Answer:
V = (6 cm)³
= 216 cm³

Question 3.
Find the area of the rectangle shown below.

Answer:
A = (9 m)(3 m)
= 27 m²

Question 4.
Find the volume of the rectangular prism shown below.

Answer:
V = (27 m²)(5 m)
= 135 m³

Question 5.
Find the area of the circle shown below.

Answer:
A = (5 m)² π
= 25π m²

Question 6.
Find the volume of the cylinder shown below.

Answer:
V = (25π m² )(11 m)
= 275π m³

Question 7.
Find the area of the circle shown below.

Answer:
A = (8 in.)² π
= 64π in²

Question 8.
Find the volume of the cone shown below.

Answer:
V = (\(\frac{1}{3}\))(64π in²)(12 in.)
= 256π in³

Question 9.
Find the area of the circle shown below.

Answer:
A = (6 mm)² π
= 36π mm²

Question 10.
Find the volume of the sphere shown below.

Answer:
V = (\(\frac{4}{3}\))π(6 mm)³
= \(\frac{864 \mathrm{~mm}^{3}}{3}\) π
= 288π mm³

Engage NY Eureka Math 8th Grade Module 7 Lesson 19 Answer Key

Eureka Math Grade 8 Module 7 Lesson 19 Example Answer Key

Example 1.
State as many facts as you can about a cone.

Answer:

Area of the base:
A = π(r²
Circumference of the base:
C = 2π(r) = π(d)
Volume of the cone:
V = \(\frac{1}{3}\) π(r²)h

Eureka Math Grade 8 Module 7 Lesson 19 Exercise Answer Key

Exercises 1–2
Note: Figures not drawn to scale.

Exercise 1.
Determine the volume for each figure below.
a. Write an expression that shows volume in terms of the area of the base, B, and the height of the figure. Explain the meaning of the expression, and then use it to determine the volume of the figure.

Answer:
The expression V = Bh means that the volume of the cylinder is found by multiplying the area of the base by the height. The base is a circle whose area can be found by squaring the radius, 6 in., and then multiplying by π. The volume is found by multiplying that area by the height of 10.
V = π(6)² (10)
= 360π
The volume of the cylinder is 360π in³.

b. Write an expression that shows volume in terms of the area of the base, B, and the height of the figure. Explain the meaning of the expression, and then use it to determine the volume of the figure.

Answer:
V = \(\frac{1}{3}\) Bh
The expression V = \(\frac{1}{3}\) Bh means that the volume of the cone is found by multiplying the area of the base by the height and then taking one-third of that product. The base is a circle whose area can be found by squaring the radius, 6 in., and then multiplying by π. The volume is found by multiplying that area by the height of 10 in. and then taking one-third of that product.
V = \(\frac{1}{3}\) π(6)² (10)
= \(\frac{360}{3}\) π
= 120 π
The volume of the cone is 120π in³.

Exercise 2.
a. Write an expression that shows volume in terms of the area of the base, B, and the height of the figure. Explain the meaning of the expression, and then use it to determine the volume of the figure.

Answer:
V = Bh
The expression V = Bh means that the volume of the prism is found by multiplying the area of the base by the height. The base is a square whose area can be found by multiplying 12×12. The volume is found by multiplying that area, 144, by the height of 10.
V = 12(12)(10)
= 1,440
The volume of the prism is 1,440 in³.

b. The volume of the square pyramid shown below is 480 in³. What might be a reasonable guess for the formula for the volume of a pyramid? What makes you suggest your particular guess?

Answer:
Since 480 = \(\frac{1440}{3}\), the formula to find the volume of a pyramid is likely \(\frac{1}{3}\) Bh, where B is the area of the base. This is similar to the volume of a cone compared to the volume of a cylinder with the same base and height. The volume of a square pyramid is \(\frac{1}{3}\) of the volume of the rectangular prism with the same base and height.

Exercises 3–10

Exercise 3.
What is the lateral length (slant height) of the cone shown below?

Answer:
Let c be the lateral length.
3² + 4² = c²
9 + 16 = c²
25 = c²
\(\sqrt{25}\) = \(\sqrt{c^{2}}\)
5 = c
The lateral length of the cone is 5 units.

Exercise 4.
Determine the exact volume of the cone shown below.

Answer:
Let r be the radius of the base.
6² + r² = 9²
36 + r² = 81
r² = 45
The area of the base is 45π units².
V = \(\frac{1}{3}\) Bh
V = \(\frac{1}{3}\)(45)π(6)
V = 90π
The volume of the cone is 90π units³.

Exercise 5.
What is the lateral length (slant height) of the pyramid shown below? Give an exact square root answer and an approximate answer rounded to the tenths place.

Answer:
Let c in. represent the lateral length of the pyramid.
4² + 8² = c²
16 + 64 = c²
80 = c²
\(\sqrt{80}\) = \(\sqrt{c^{2}}\)
\(\sqrt{80}\) = c
The number \(\sqrt{80}\) is between 8 and 9. In the sequence of tenths, it is between 8.9 and 9.0. Since 80 is closer to 8.9² than 9², the approximate lateral length is 8.9 inches.

Exercise 6.
Determine the volume of the square pyramid shown below. Give an exact answer using a square root.

Answer:
Let h be the height of the pyramid.
1² + h² = 2²
1 + h² = 4
h² = 3
\(\sqrt{h^{2}}\) = \(\sqrt{3}\)
h = \(\sqrt{3}\)
The area of the base is 4 units².
V = \(\frac{1}{3}\) (4)(\(\sqrt{3}\))
= \(\frac{4 \sqrt{3}}{3}\)
The volume of the pyramid is \(\frac{4 \sqrt{3}}{3}\) units³.

Exercise 7.
What is the length of the chord of the sphere shown below? Give an exact answer using a square root.

Answer:
Let c cm represent the length of the chord.
11² + 11² = c²
121 + 121 = c²
242 = c²
\(\sqrt{242}\) = \(\sqrt{c^{2}}\)
\(\sqrt{11^{2} \times 2}\) = c
11\(\sqrt{2}\) = c
The length of the chord is \(\sqrt{242}\) cm, or 11\(\sqrt{2}\) cm.

Exercise 8.
What is the length of the chord of the sphere shown below? Give an exact answer using a square root.

Answer:
Let c in. represent the length of the chord.
4² + 4² = c²
16 + 16 = c²
32 = c²
\(\sqrt{32}\) = \(\sqrt{c^{2}}\)
\(\sqrt{4^{2} \times 2}\) = c
4\(\sqrt{2}\) = c
The length of the chord is \(\sqrt{32}\) in., or 4\(\sqrt{2}\) in.

Exercise 9.
What is the volume of the sphere shown below? Give an exact answer using a square root.

Answer:
Let r cm represent the radius of the sphere.
r² + r² = 20²
2r² = 400
r² = 200
\(\sqrt{r^{2}}\) = \(\sqrt{200}\)
r = \(\sqrt{200}\)
r = \(\sqrt{10^{2} \times 2}\)
r = 10\(\sqrt{2}\)

V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(10√2)³
= \(\frac{4}{3}\) π(10³ ) (\(\sqrt{2}\))³
= \(\frac{4}{3}\) π(1000)(\(\sqrt{8}\))
= \(\frac{4}{3}\) π(1000)(\(\sqrt{2^{2} \times 2}\))
= \(\frac{4}{3}\) π(1000)(2)(\(\sqrt{2}\))
= \(\frac{8000 \sqrt{2}}{3}\) π

The volume of the sphere is
\(\frac{4000 \sqrt{8}}{3}\) π cm³, or \(\frac{8000 \sqrt{2}}{3}\) π cm³.

Eureka Math Grade 8 Module 7 Lesson 19 Problem Set Answer Key

Question 1.
What is the lateral length (slant height) of the cone shown below? Give an approximate answer rounded to the tenths place.

Answer:
Let c m be the lateral length.
10² + 4² = c²
100 + 16 = c²
116 = c²
\(\sqrt{116}\) = \(\sqrt{c^{2}}\)
\(\sqrt{116}\) = c
The number \(\sqrt{116}\) is between 10 and 11. In the sequence of tenths, it is between 10.7 and 10.8. Since 116 is closer to 10.8² than 10.7², the approximate value of the number is 10.8.
The lateral length of the cone is approximately 10.8 m.

Question 2.
What is the volume of the cone shown below? Give an exact answer.

Answer:
Let h represent the height of a cone.
5² + h² = 13²
25 + h² = 169
h² = 144
\(\sqrt{h^{2}}\) = \(\sqrt{144}\)
h = 12
The height of the cone is 12 units.
V = \(\frac{1}{3}\) π(25)(12)
= 100π
The volume of the cone is 00π units³.

Question 3.
Determine the volume and surface area of the square pyramid shown below. Give exact answers.

Answer:
V = \(\frac{1}{3}\) (64)(7)
= 448/3
The volume of the pyramid is 448/3 units³.
Let c represent the lateral length.
7² + 4² = c²
49 + 16 = c²
65 = c²
\(\sqrt{65}\) = \(\sqrt{c^{2}}\)
\(\sqrt{65}\) = c
The area of each face of the pyramid is 4\(\sqrt{65}\) units² (since \(\frac{1}{2}\)×8×\(\sqrt{65}\) = 4\(\sqrt{65}\)), so the area of all four faces is 6\(\sqrt{65}\) units². Since the base area is 4 units², the total surface area of the pyramid is (64 + 16\(\sqrt{65}\)) units².

Question 4.
Alejandra computed the volume of the cone shown below as 64π cm³. Her work is shown below. Is she correct?
If not, explain what she did wrong, and calculate the correct volume of the cone. Give an exact answer.

V = \(\frac{1}{3}\) π(4² )(12)
= \(\frac{(16)(12) \pi}{3}\)
= 64π
= 64
Answer:
The volume of the cone is 64π cm³.
Alejandra’s work is incorrect. She used the lateral length instead of the height of the cone to compute volume.
Let h cm represent the height.
4² + h² = 12²
16 + h² = 144
h² = 128
\(\sqrt{h^{2}}\) = \(\sqrt{128}\)
h = \(\sqrt{128}\)
h = \(\sqrt{8^{2} \times 2}\)
h = 8\(\sqrt{2}\)

V = \(\frac{1}{3}\) π(4)² (8\(\sqrt{2}\))
V = \(\frac{1}{3}\) π(128\(\sqrt{65}\))
V = \(\frac{128 \sqrt{2}}{3}\) π
The volume of the cone is \(\frac{128 \sqrt{2}}{3}\) π cm³.

Question 5.
What is the length of the chord of the sphere shown below? Give an exact answer using a square root.

Answer:
Let c m represent the length of the chord.
9² + 9² = c²
81 + 81 = c²
162 = c²
\(\sqrt{162}\) = \(\sqrt{c^{2}}\)
\(\sqrt{162}\) = c
\(\sqrt{9^{2} \times 2}\) = c
9\(\sqrt{2}\) = c
The length of the chord is \(\sqrt{162}\) m, or 9\(\sqrt{2}\) m.

Question 6.
What is the volume of the sphere shown below? Give an exact answer using a square root.

Answer:
Let r in. represent the radius.
r² + r² = 14²
2r² = 196
r² = 98
\(\sqrt{r^{2}}\) = \(\sqrt{98}\)
r = \(\sqrt{7^{2} \times 2}\)
r = 7\(\sqrt{2}\)

V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(7\(\sqrt{2}\))³
= \(\frac{4}{3}\) π(343)(\(\sqrt{8}\))
= \(\frac{4}{3}\) π(343)(2\(\sqrt{2}\))
= \(\frac{2744 \sqrt{2}}{3}\) π
The volume of the sphere is \(\frac{4}{3}\) (\(\sqrt{98}\))³ π in³, or \(\frac{2744 \sqrt{2}}{3}\) π in³.

Eureka Math Grade 8 Module 7 Lesson 19 Exit Ticket Answer Key

Question 1.
Which has the larger volume? Give an approximate answer rounded to the tenths place.

Answer:
Let h cm represent the height of the square pyramid.
h² + 6² = 10²
h² + 36 = 100
h² = 64
h = 8

V = \(\frac{1}{3}\) (12²)(8)
V = \(\frac{1}{3}\) (144)(8)
V = 384
The volume of the square pyramid is 384 cm³.

Let r represent the radius of the sphere in centimeters.
r² + r² = 6²
2r² = 36
r² = 18
\(\sqrt{r^{2}}\) = \(\sqrt{18}\)
r = \(\sqrt{3^{2} \times 2}\)
r = 3\(\sqrt{2}\)

V = \(\frac{4}{3}\) πr³
= \(\frac{4}{3}\) π(3\(\sqrt{2}\))³
= \(\frac{4}{3}\) π(3)³ (\(\sqrt{2}\))³
= \(\frac{4}{3}\) π(27)(\(\sqrt{8}\))
= \(\frac{4}{3}\) π(27)(\(\sqrt{2^{2} \times 2}\))
= \(\frac{4}{3}\) π(27)(2)(\(\sqrt{2}\))
= 72π\(\sqrt{2}\)

The volume of the sphere is 72π\(\sqrt{2}\) cm³.
The number \(\sqrt{2}\) is between 1 and 2. In the sequence of tenths, it is between 1.4 and 1.5. Since 2 is closer to 1.4² than 1.5², the number is approximately 1.4.
We know from previous lessons we can estimate π = 3.14.
Then, we can calculate the approximate volume of the sphere:
V ≈ (72)(1.4)(3.14)
V ≈ 316.512
The approximate volume of the sphere is 316.512 cm³. Therefore, the volume of the square pyramid is greater.

Engage NY Eureka Math 8th Grade Module 7 Lesson 20 Answer Key

Eureka Math Grade 8 Module 7 Lesson 20 Example Answer Key

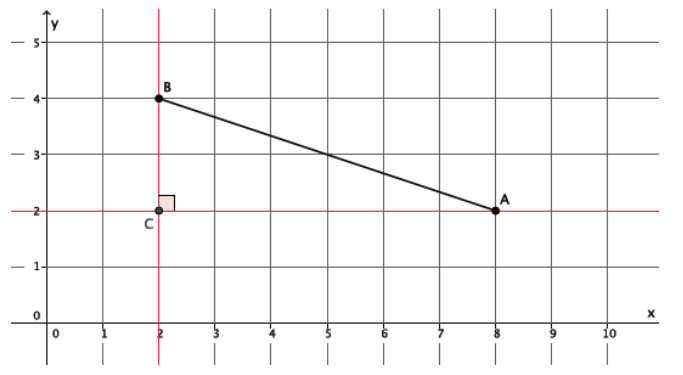
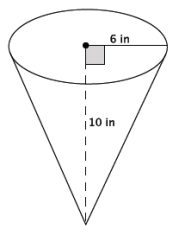
Example 1.
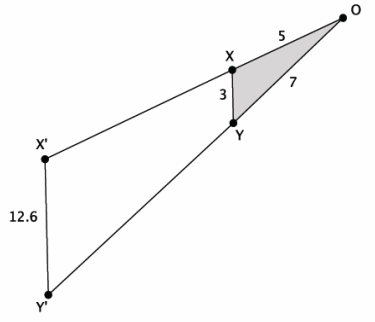
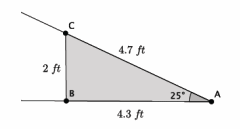
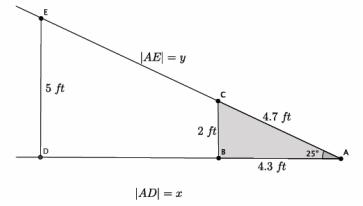
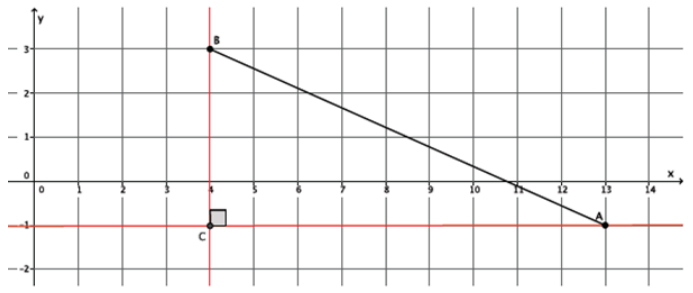
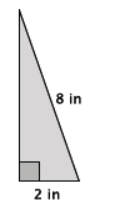
Determine the volume of the truncated cone shown below.

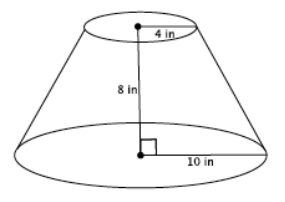
Answer:
Since we know that the original cone and the portion that has been removed to make this truncated cone are similar, let’s begin by drawing in the missing portion.

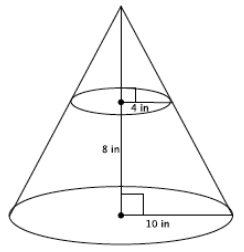
→ We know the formula to find the volume of a cone. Is there enough information in the new diagram for us to find the volume? Explain.
→ No, there’s not enough information. We would have to know the height of the cone, and at this point we only know the height of the truncated cone, 8 inches.
→ Recall our conversation about the similar right triangles. We can use what we know about similarity to determine the height of the cone with the following proportion. What does each part of the proportion represent in the diagram?
Since the triangles are similar, we will let x inches represent the height of the cone that has been removed.
\(\frac{4}{10}\) = \(\frac{x}{x + 8}\)
The 4 is the radius of the small cone. The 10 is the radius of the large cone. The x represents the height of the small cone. The expression x + 8 represents the height of the large cone.
Work in your groups to determine the height of the small cone.
4(x + 8) = 10x
4x + 32 = 10x
32 = 6x
\(\frac{32}{6}\) = x
\(5 . \overline{3}\) = x
→ Now that we know the height of the cone that has been removed, we also know the total height of the cone. How might we use these pieces of information to determine the volume of the truncated cone?
We can find the volume of the large cone, find the volume of the small cone that was removed, and then subtract the volumes. What will be left is the volume of the truncated cone.

→ Write an expression that represents the volume of the truncated cone. Use approximations for the heights since both are infinite decimals. Be prepared to explain what each part of the expression represents in the situation.
The volume of the truncated cone is given by the expression
\(\frac{1}{3}\) π(10)² (13.3) – \(\frac{1}{3}\) π(4)² (5.3),
where \(\frac{1}{3}\) π(10)² (13.3) is the volume of the large cone, and \(\frac{1}{3}\) π(4)² (5.3) is the volume of the smaller cone. The difference in the volumes will be the volume of the truncated cone.
Determine the volume of the truncated cone. Use the approximate value of the number \(5 . \overline{3}\) when you compute the volumes.

The volume of the small cone is
V ≈ \(\frac{1}{3}\) π(4)² (5.3)
≈ \(\frac{1}{3}\) π(84.8)
≈ \(\frac{84.8}{3}\) π
The volume of the large cone is
V ≈ \(\frac{1}{3}\)π(10)² (13.3)
≈ \(\frac{1330}{3}\) π
The volume of the truncated cone is
\(\frac{1330}{3}\) π – \(\frac{84.8}{3}\) π = (\(\frac{1330}{3}\) – \(\frac{84.8}{3}\))π
= \(\frac{1245.2}{3}\) π
The volume of the truncated cone is approximately \(\frac{1245.3}{3}\) π in ³.

Write an equivalent expression for the volume of a truncated cone that shows the volume is \(\frac{1}{3}\) of the difference between two cylinders. Explain how your expression shows this.
The expression \(\frac{1}{3}\) π(10)²(13.3) – \(\frac{1}{3}\) π(4)²(5.3) can be written as \(\frac{1}{3}\)(π(10)²(13.3) – π(4)²(5.3)), where π(10)²(13.3) is the volume of the larger cylinder, and π(4)²(5.3) is the volume of the smaller cylinder. One – third of the difference is the volume of a truncated cone with the same base and height measurements as the cylinders.

Eureka Math Grade 8 Module 7 Lesson 20 Exercise Answer Key

Exercises 1–5

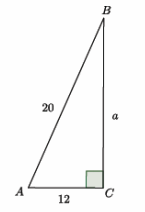
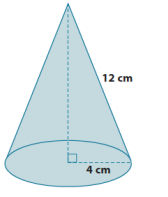
Exercise 1.
Find the volume of the truncated cone.

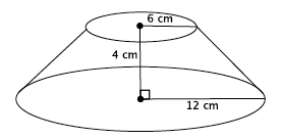
a. Write a proportion that will allow you to determine the height of the cone that has been removed. Explain what all parts of the proportion represent.
Answer:
\(\frac{6}{12}\) = \(\frac{x}{x + 4}\)
Let x cm represent the height of the small cone. Then, x + 4 is the height of the large cone (with the removed part included). The 6 represents the base radius of the removed cone, and the 12 represents the base radius of the large cone.

b. Solve your proportion to determine the height of the cone that has been removed.
Answer:
6(x + 4) = 12x
6x + 24 = 12x
24 = 6x
4 = x

c. Write an expression that can be used to determine the volume of the truncated cone. Explain what each part of the expression represents.
Answer:
\(\frac{1}{3}\) π(12)² (8) – \(\frac{1}{3}\) π(6)² (4)
The expression \(\frac{1}{3}\) π(12)² (8) is the volume of the large cone, and \(\frac{1}{3}\) π(6)² (4) is the volume of the small cone. The difference of the volumes gives the volume of the truncated cone.

d. Calculate the volume of the truncated cone.
Answer:
The volume of the small cone is
V = \(\frac{1}{3}\) π(6)² (4)
= \(\frac{144}{3}\) π.

The volume of the large cone is
V = \(\frac{1}{3}\) π(12)² (8)
= \(\frac{1152}{3}\) π.
The volume of the truncated cone is
\(\frac{1152}{3}\) π – \(\frac{144}{3}\) π = (\(\frac{1152}{3}\) – \(\frac{144}{3}\))π
= \(\frac{1008}{3}\) π
= 336π.
The volume of the truncated cone is 336π cm².

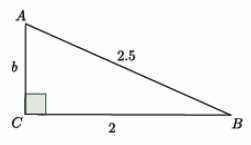
Exercise 2.
Find the volume of the truncated cone.

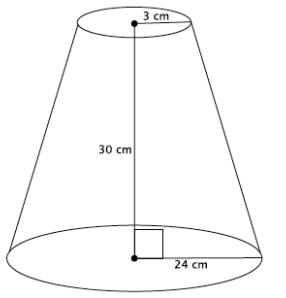
Answer:
Let x cm represent the height of the small cone.
\(\frac{3}{24}\) = \(\frac{x}{x + 30}\)
3x + 90 = 24x
90 = 21x
\(\frac{30}{7}\) = x
4.3 ≈ x

The volume of the small cone is
V ≈ \(\frac{1}{3}\) π(3)² (4.3)
≈ \(\frac{38.7}{3}\) π
= 12.9π.

The volume of the large cone is
V ≈ \(\frac{1}{3}\) π(24)² (34.3)
≈ \(\frac{19756.8}{3}\) π
= 6585.6π.

The volume of the truncated cone is
6585.6π – 12.9π = (6585.6 – 12.9)π
= 6572.7π.
The volume of the truncated cone is approximately 6572.7π cm³.

Exercise 3.
Find the volume of the truncated pyramid with a square base.

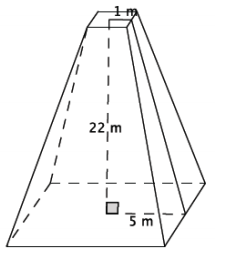
a. Write a proportion that will allow you to determine the height of the cone that has been removed. Explain what all parts of the proportion represent.
Answer:
\(\frac{1}{5}\) = \(\frac{x}{x + 22}\)
Let x m represent the height of the small pyramid. Then x + 22 is the height of the large pyramid. The 1 represents half of the length of the base of the small pyramid, and the 5 represents half of the length of the base of the large pyramid.

b. Solve your proportion to determine the height of the pyramid that has been removed.
Answer:
x + 22 = 5x
22 = 4x
5.5 = x

c. Write an expression that can be used to determine the volume of the truncated pyramid. Explain what each part of the expression represents.
Answer:
\(\frac{1}{3}\) (100)(27.5) – \(\frac{1}{3}\) (4)(5.5)
The expression \(\frac{1}{3}\) (100)(27.5) is the volume of the large pyramid, and \(\frac{1}{3}\) (4)(5.5) is the volume of the small pyramid. The difference of the volumes gives the volume of the truncated pyramid.

d. Calculate the volume of the truncated pyramid.
Answer:
The volume of the small pyramid is
V = \(\frac{1}{3}\) (4)(5.5)
= \(\frac{22}{3}\) .

The volume of the large pyramid is
V = \(\frac{1}{3}\) (100)(27.5)
= \(\frac{2750}{3}\) .

The volume of the truncated pyramid is
\(\frac{2750}{3}\) – \(\frac{22}{3}\) = \(\frac{2728}{3}\)

The volume of the truncated pyramid is \(\frac{2728}{3}\) m³.

Exercise 4.
A pastry bag is a tool used to decorate cakes and cupcakes. Pastry bags take the form of a truncated cone when filled with icing. What is the volume of a pastry bag with a height of 6 inches, large radius of 2 inches, and small radius of 0.5 inches?
Answer:
Let x in. represent the height of the small cone.
\(\frac{x}{x + 6}\) = \(\frac{0.5}{2}\)
2x = 0.5(x + 6)
2x = \(\frac{1}{2}\) x + 3
\(\frac{3}{2}\) x = 3
x = 2
The volume of the small cone is
V = \(\frac{1}{3}\) π(\(\frac{1}{2}\))² (2)
= \(\frac{1}{6}\) π.

The volume of the large cone is
V = \(\frac{1}{3}\) π(2)² (8)
= \(\frac{32}{3}\) π.

The volume of the truncated cone is
\(\frac{32}{3}\) π – \(\frac{1}{6}\) π = (\(\frac{32}{3}\) – \(\frac{1}{6}\))π
= \(\frac{63}{6}\) π
= \(\frac{21}{2}\) π.
The volume of the pastry bag is \(\frac{21}{2}\) π in³ when filled.

Exercise 5.
Explain in your own words what a truncated cone is and how to determine its volume.
Answer:
A truncated cone is a cone with a portion of the top cut off. The base of the portion that is cut off needs to be parallel to the base of the original cone. Since the portion that is cut off is in the shape of a cone, then to find the volume of a truncated cone, you must find the volume of the cone (without any portion cut off), find the volume of the cone that is cut off, and then find the difference between the two volumes. That difference is the volume of the truncated cone.

Eureka Math Grade 8 Module 7 Lesson 20 Problem Set Answer Key

Question 1.
Find the volume of the truncated cone.

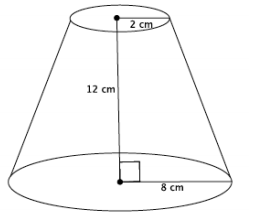
a. Write a proportion that will allow you to determine the height of the cone that has been removed. Explain what each part of the proportion represents.
Answer:
\(\frac{2}{8}\) = \(\frac{x}{x + 12}\)
Let x cm represent the height of the small cone. Then x + 12 is the height of the large cone. The 2 represents the base radius of the small cone, and the 8 represents the base radius of the large cone.

b. Solve your proportion to determine the height of the cone that has been removed.
Answer:
2(x + 12) = 8x
2x + 24 = 8x
24 = 6x
4 = x

c. Show a fact about the volume of the truncated cone using an expression. Explain what each part of the expression represents.
Answer:
\(\frac{1}{3}\) π(8)² (16) – \(\frac{1}{3}\) π(2)² (4)
The expression \(\frac{1}{3}\) π(8)² (16) represents the volume of the large cone, and \(\frac{1}{3}\) π(2)² (4) is the volume of the small cone. The difference in volumes gives the volume of the truncated cone.

d. Calculate the volume of the truncated cone.
Answer:
The volume of the small cone is
V = \(\frac{1}{3}\) π(2)² (4)
= \(\frac{16}{3}\) π.

The volume of the large cone is
V = \(\frac{1}{3}\) π(8)² (16)
= \(\frac{1024}{3}\) π.

The volume of the truncated cone is
\(\frac{1024}{3}\) π – \(\frac{16}{3}\) π = (\(\frac{1024}{3}\) – \(\frac{16}{3}\))π
= \(\frac{1008}{3}\) π
= 336π.
The volume of the truncated cone is 336π cm³.

Question 2.
Find the volume of the truncated cone.

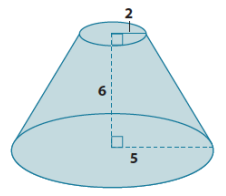
Answer:
Let x represent the height of the small cone.
\(\frac{2}{5}\) = \(\frac{x}{x + 6}\)
2(x + 6) = 5x
2x + 12 = 5x
12 = 3x
4 = x
The volume of the small cone is
V = \(\frac{1}{3}\) π(2)² (4)
= \(\frac{16}{3}\)π.

The volume of the large cone is
V = \(\frac{1}{3}\) π(5)² (10)
= \(\frac{250}{3}\) π.

The volume of the truncated cone is
\(\frac{250}{3}\) π – \(\frac{16}{3}\) π = (\(\frac{250}{3}\) – \(\frac{16}{3}\))π
= \(\frac{234}{3}\) π
= 78π.
The volume of the truncated cone is 8π units³.

Question 3.
Find the volume of the truncated pyramid with a square base.

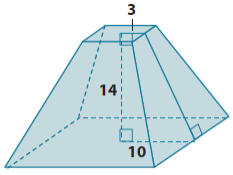
Answer:
Let x represent the height of the small pyramid.
\(\frac{3}{10}\) = \(\frac{x}{x + 14}\)
3(x + 14) = 10x
3x + 42 = 10x
42 = 7x
6 = x
The volume of the small pyramid is
V = \(\frac{1}{3}\) (36)(6)
= \(\frac{216}{3}\).

The volume of the large pyramid is
V = \(\frac{1}{3}\) (400)(20)
= \(\frac{8000}{3}\).

The volume of the truncated pyramid is
\(\frac{8000}{3}\) – \(\frac{216}{3}\) = \(\frac{7784}{3}\).

The volume of the truncated pyramid is \(\frac{7784}{3}\) units³.

Question 4.
Find the volume of the truncated pyramid with a square base. Note: 3 mm is the distance from the center to the edge of the square at the top of the figure.

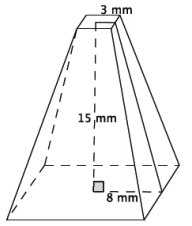
Answer:
Let x mm represent the height of the small pyramid.
\(\frac{3}{8}\) = \(\frac{x}{x + 15}\)
3(x + 15) = 8x
3x + 45 = 8x
45 = 5x
9 = x
The volume of the small pyramid is
V = \(\frac{1}{3}\) (36)(9)
= 108.

The volume of the large pyramid is
V = \(\frac{1}{3}\) (256)(24)
= 2048.

The volume of the truncated pyramid is
2048 – 108 = 1940.
The volume of the truncated pyramid is 1,940 mm³.

Question 5.
Find the volume of the truncated pyramid with a square base. Note: 0.5 cm is the distance from the center to the edge of the square at the top of the figure.

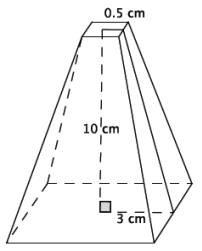
Answer:
Let x cm represent the height of the small pyramid.
\(\frac{0.5}{3}\) = \(\frac{x}{x + 10}\)
\(\frac{1}{2}\) (x + 10) = 3x
\(\frac{1}{2}\) x + 5 = 3x
5 = \(\frac{5}{2}\) x
2 = x
The volume of the small pyramid is
V = \(\frac{1}{3}\) (1)(2)
= \(\frac{2}{3}\).

The volume of the large pyramid is
V = \(\frac{1}{3}\) (36)(12)
= \(\frac{432}{3}\).

The volume of the truncated pyramid is
\(\frac{432}{3}\) – \(\frac{2}{3}\) = \(\frac{430}{3}\).

The volume of the truncated pyramid is \(\frac{430}{3}\) cm³.

Question 6.
Explain how to find the volume of a truncated cone.
Answer:
The first thing you have to do is use the ratios of corresponding sides of similar triangles to determine the height of the cone that was removed to make the truncated cone. Once you know the height of that cone, you can determine its volume. Then, you can find the height of the cone (the truncated cone and the portion that was removed). Once you know both volumes, you can subtract the smaller volume from the larger volume. The difference is the volume of the truncated cone.

Question 7.
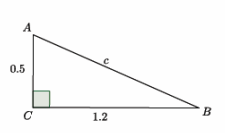
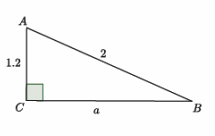
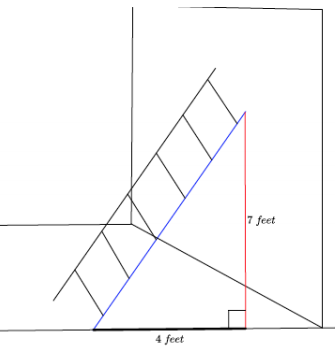
Challenge: Find the volume of the truncated cone.

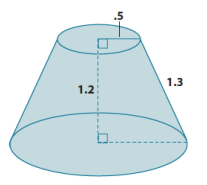
Answer:
Since the height of the truncated cone is 1.2 units, we can drop a perpendicular line from the top of the cone to the bottom of the cone so that we have a right triangle with a leg length of 1.2 units and a hypotenuse of 1.3 units. Then, by the Pythagorean theorem, if b is the length of the leg of the right triangle, then
1.2² + b² = 1.3²
1.44 + b² = 1.69
b² = 0.25
b = 0.5.
The part of the radius of the bottom base found by the Pythagorean theorem is 0.5. When we add the length of the upper radius (because if you translate along the height of the truncated cone, then it is equal to the remaining part of the lower base), then the radius of the lower base is 1.
Let x represent the height of the small cone.
\(\frac{0.5}{1}\) = \(\frac{x}{x + 1.2}\)
\(\frac{1}{2}\) (x + 1.2) = x
\(\frac{1}{2}\) x + 0.6 = x
0.6 = \(\frac{1}{2}\) x
1.2 = x
The volume of the small cone is
V = \(\frac{1}{3}\) π(0.5)² (1.2)
= \(\frac{0.3}{3}\) π
= 0.1π.

The volume of the large cone is
V = \(\frac{1}{3}\) π(1)² (2.4)
= \(\frac{2.4}{3}\) π
= 0.8π.

The volume of the truncated cone is
\(\frac{2.4}{3}\) π – \(\frac{0.3}{3}\) π = (\(\frac{2.4}{3}\) – \(\frac{0.3}{3}\))π
= \(\frac{2.1}{3}\) π
= 0.7π.
The volume of the truncated cone is 7π units³.

Eureka Math Grade 8 Module 7 Lesson 20 Exit Ticket Answer Key

Question 1.
Find the volume of the truncated cone.

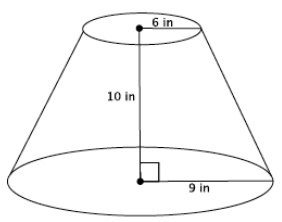
a. Write a proportion that will allow you to determine the height of the cone that has been removed. Explain what all parts of the proportion represent.
Answer:
\(\frac{6}{9}\) = \(\frac{x}{x + 10}\)
Let x in. represent the height of the small cone. Then
x + 10 is the height of the large cone. Then 6 is the base radius of the small cone, and 9 is the base radius of the large cone.

b. Solve your proportion to determine the height of the cone that has been removed.
Answer:
6(x + 10) = 9x
6x + 60 = 9x
60 = 3x
20 = x

c. Write an expression that can be used to determine the volume of the truncated cone. Explain what each part of the expression represents.
Answer:
\(\frac{1}{3}\) π(9)² (30) – \(\frac{1}{3}\) π(6)² (20)
The expression \(\frac{1}{3}\) π(9)² (30) represents the volume of the large cone, and \(\frac{1}{3}\) π(6)² (20) is the volume of the small cone. The difference in volumes represents the volume of the truncated cone.

d. Calculate the volume of the truncated cone.
Answer:
The volume of the small cone is
V = \(\frac{1}{3}\) π(6)² (20)
= \(\frac{720}{3}\) π.

The volume of the large cone is
V = \(\frac{1}{3}\) π(9)² (30)
= \(\frac{2430}{3}\) π.

The volume of the truncated cone is
\(\frac{2430}{3}\) π – \(\frac{720}{3}\) π = (\(\frac{2430}{3}\) – \(\frac{720}{3}\))π
= \(\frac{1710}{3}\) π
= 570π.
The volume of the truncated cone is 570π in³.

Engage NY Eureka Math 8th Grade Module 7 Lesson 16 Answer Key

Eureka Math Grade 8 Module 7 Lesson 16 Classwork Answer Key

Classwork
Proof of the Converse of the Pythagorean Theorem

Answer:
→ What do we know or not know about each of these triangles?
In the first triangle, ABC, we know that a² + b² = c². We do not know if angle C is a right angle.
In the second triangle, A’B’C’, we know that it is a right triangle.

→ What conclusions can we draw from this?
By applying the Pythagorean theorem to △A’B’C’, we get |A’B’|² = a² + b². Since we are given
c² = a² + b², then by substitution, |A’B’|² = c², and then |A’B’| = c. Since c is also |AB|, then |A’B’| = |AB|. That means that both triangles have sides a, b, and c that are the exact same lengths.

→ Recall that we would like to prove that ∠ACB is a right angle, that it maps to ∠A’ C’ B’. If we can translate
△ABC so that A goes to A’, B goes to B’, and C goes to C’, it follows that all three angles in the triangle will match. In particular, that ∠ACB maps to the right angle ∠A’ C’ B’, and so is a right angle, too.
→ We can certainly perform a translation that takes B to B’ and C to C’ because segments BC and B’C’ are the same length. Must this translation take A to A’? What goes wrong mathematically if it misses and translates to a different point A” as shown below?

In this picture, we’ve drawn A” to the left of \(\overline{A{\prime} C{\prime}}\). The reasoning that follows works just as well for a picture with A” to the right of \(\overline{A{\prime} C{\prime}}\) instead.

Provide time for students to think of what may go wrong mathematically. If needed, prompt them to notice the two isosceles triangles in the diagram, △A”C’A’ and △A”B’A’ and the four angles w₁,w₂,w₃,w₄ labeled as shown in the diagram below.

△A”C’A’ is isosceles and therefore has base angles that are equal in measure:
w₁ + w₂ = w₃.
△A”B’A’ is isosceles and therefore has base angles that are equal in measure:
w₂ = w₃ + w₄.
These two equations give w₁ + w₃ + w₄ = w₃, which is equal to w₁ + w₄ = 0, which is obviously not true.
Therefore, the translation must map A to A’, and since translations preserve the measures of angles, we can conclude that the measure of ∠ACB is equal to the measure of ∠A’C’B’, and ∠ACB is a right angle.
Finally, if a triangle has side lengths of a,b and c, with c the longest length, that don’t satisfy the equation a² + b² = c², then the triangle cannot be a right triangle.

Eureka Math Grade 8 Module 7 Lesson 16 Exercise Answer Key

Exercises 1–7

Exercise 1.
Is the triangle with leg lengths of 3 mi. and 8 mi. and hypotenuse of length \(\sqrt{73}\) mi. a right triangle? Show your work, and answer in a complete sentence.
Answer:
3² + 8² = (\(\sqrt{73}\))²
9 + 64 = 73
73 = 73
Yes, the triangle with leg lengths of 3 mi. and 8 mi. and hypotenuse of length \(\sqrt{73}\) mi. is a right triangle because it satisfies the Pythagorean theorem.

Exercise 2.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.

Answer:
Let c in. represent the length of the hypotenuse of the triangle.
1² + 4² = c²
1 + 16 = c²
17 = c²
\(\sqrt{17}\) = c
4.1≈c
The length of the hypotenuse of the right triangle is exactly \(\sqrt{17}\) inches and approximately 4.1 inches.

Exercise 3.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.

Answer:
Let c mm represent the length of the hypotenuse of the triangle.
2² + 6² = c²
4 + 36 = c²
40 = c²
\(\sqrt{40}\) = c
\(\sqrt{2^{3}}\)×\(\sqrt{5}\) = c
\(\sqrt{2^{2}}\)×\(\sqrt{2}\)×\(\sqrt{5}\) = c
2\(\sqrt{10}\) = c
The length of the hypotenuse of the right triangle is exactly 2\(\sqrt{10}\) mm and approximately 6.3 mm.

Exercise 4.
Is the triangle with leg lengths of 9 in. and 9 in. and hypotenuse of length \(\sqrt{175}\) in. a right triangle? Show your work, and answer in a complete sentence.
Answer:
9² + 9² = (\(\sqrt{175}\))²
81 + 81 = 175
162 ≠ 175
No, the triangle with leg lengths of 9 in. and 9 in. and hypotenuse of length \(\sqrt{175}\) in. is not a right triangle because the lengths do not satisfy the Pythagorean theorem.

Exercise 5.
Is the triangle with leg lengths of √(28 ) cm and 6 cm and hypotenuse of length 8 cm a right triangle? Show your work, and answer in a complete sentence.
Answer:
(\(\sqrt{28}\))² + 6² = 8²
28 + 36 = 64
64 = 64
Yes, the triangle with leg lengths of \(\sqrt{28}\) cm and 6 cm and hypotenuse of length 8 cm is a right triangle because the lengths satisfy the Pythagorean theorem.

Exercise 6.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence.

Answer:
Let c ft. represent the length of the hypotenuse of the triangle.
3² + (\(\sqrt{27}\))² = c²
9 + 27 = c²
36 = c²
\(\sqrt{36}\) = \(\sqrt{c^{2}}\)
6 = c
The length of the hypotenuse of the right triangle is 6 ft.

Exercise 7.
The triangle shown below is an isosceles right triangle. Determine the length of the legs of the triangle. Show your work, and answer in a complete sentence.

Answer:
Let x cm represent the length of each of the legs of the isosceles triangle.
x² + x² = (\(\sqrt{18}\))²
2x² = 18
\(\frac{2 x^{2}}{2}\) = \(\frac{18}{2}\)
x² = 9
\(\sqrt{x^{2}}\) = \(\sqrt{9}\)
x = 3
The leg lengths of the isosceles triangle are 3 cm.

Eureka Math Grade 8 Module 7 Lesson 16 Problem Set Answer Key

Question 1.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.

Answer:
Let c cm represent the length of the hypotenuse of the triangle.
1² + 1² = c²
1 + 1 = c²
2 = c²
\(\sqrt{2}\) = \(\sqrt{c^{2}}\)
1.4≈c
The length of the hypotenuse is exactly \(\sqrt{2}\) cm and approximately 1.4 cm.

Question 2.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.

Answer:
Let x ft. represent the unknown length of the triangle.
7² + x² = 11²
49 + x² = 121
49 – 49 + x² = 121 – 49
x² = 72
\(\sqrt{x^{2}}\) = \(\sqrt{72}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{2}\) ⋅ \(\sqrt{3^{2}}\)
x = 6\(\sqrt{2}\)
x≈8.5
The length of the unknown side of the triangle is exactly 6\(\sqrt{2}\) ft. and approximately 8.5 ft.

Question 3.
Is the triangle with leg lengths of \(\sqrt{3}\) cm and 9 cm and hypotenuse of length \(\sqrt{84}\) cm a right triangle? Show your work, and answer in a complete sentence.
Answer:
(\(\sqrt{3}\))² + 9² = (\(\sqrt{84}\))²
3 + 81 = 84
84 = 84
Yes, the triangle with leg lengths of \(\sqrt{3}\) cm and 9 cm and hypotenuse of length \(\sqrt{84}\) cm is a right triangle because the lengths satisfy the Pythagorean theorem.

Question 4.
Is the triangle with leg lengths of \(\sqrt{7}\) km and 5 km and hypotenuse of length \(\sqrt{48}\) km a right triangle? Show your work, and answer in a complete sentence.
Answer:
(\(\sqrt{7}\))² + 5² = (\(\sqrt{48}\))²
7 + 25 = 48
32 ≠ 48
No, the triangle with leg lengths of \(\sqrt{7}\) km and 5 km and hypotenuse of length \(\sqrt{48}\) km is not a right triangle because the lengths do not satisfy the Pythagorean theorem.

Question 5.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.

Answer:
Let c mm represent the length of the hypotenuse of the triangle.
5² + 10² = c²
25 + 100 = c²
125 = c²
\(\sqrt{125}\) = \(\sqrt{c^{2}}\)
\(\sqrt{5^{3}}\) = c
\(\sqrt{5^{2}}\)×\(\sqrt{5}\) = c
5\(\sqrt{5}\) = c
11.2≈c
The length of the hypotenuse is exactly 5\(\sqrt{5}\) mm and approximately 11.2 mm.

Question 6.
Is the triangle with leg lengths of 3 and 6 and hypotenuse of length \(\sqrt{45}\) a right triangle? Show your work, and answer in a complete sentence.
Answer:
3² + 6² = (\(\sqrt{45}\))²
9 + 36 = 45
45 = 45
Yes, the triangle with leg lengths of 3 and 6 and hypotenuse of length \(\sqrt{45}\) is a right triangle because the lengths satisfy the Pythagorean theorem.

Question 7.
What is the length of the unknown side of the right triangle shown below? Show your work, and answer in a complete sentence. Provide an exact answer and an approximate answer rounded to the tenths place.

Answer:
Let x in. represent the unknown side length of the triangle.
2² + x² = 8²
4 + x² = 64
4 – 4 + x² = 64 – 4
x² = 60
\(\sqrt{x^{2}}\) = \(\sqrt{60}\)
x = \(\sqrt{2^{2}}\) ⋅ \(\sqrt{3}\) ⋅ \(\sqrt{5}\)
x = 2\(\sqrt{15}\)
x≈7.7
The length of the unknown side of the triangle is exactly 2\(\sqrt{15}\) inches and approximately 7.7 inches.

Question 8.
Is the triangle with leg lengths of 1 and \(\sqrt{3}\) and hypotenuse of length 2 a right triangle? Show your work, and answer in a complete sentence.
Answer:
1² + (\(\sqrt{3}\))² = 2²
1 + 3 = 4
4 = 4
Yes, the triangle with leg lengths of 1 and \(\sqrt{3}\) and hypotenuse of length 2 is a right triangle because the lengths satisfy the Pythagorean theorem.

Question 9.
Corey found the hypotenuse of a right triangle with leg lengths of 2 and 3 to be \(\sqrt{13}\). Corey claims that since \(\sqrt{13}\) = 3.61 when estimating to two decimal digits, that a triangle with leg lengths of 2 and 3 and a hypotenuse of 3.61 is a right triangle. Is he correct? Explain.
Answer:
No, Corey is not correct.
2² + 3² = (3.61)²
4 + 9 = 13.0321
13 ≠ 13.0321
No, the triangle with leg lengths of 2 and 3 and hypotenuse of length 3.61 is not a right triangle because the lengths do not satisfy the Pythagorean theorem.

Question 10.
Explain a proof of the Pythagorean theorem.
Answer:
Consider having students share their proof with a partner while their partner critiques their reasoning. Accept any of the three proofs that students have seen.

Question 11.
Explain a proof of the converse of the Pythagorean theorem.
Answer:
Consider having students share their proof with a partner while their partner critiques their reasoning. Accept either of the proofs that students have seen.

Eureka Math Grade 8 Module 7 Lesson 16 Exit Ticket Answer Key

Question 1.
Is the triangle with leg lengths of 7 mm and 7 mm and a hypotenuse of length 10 mm a right triangle? Show your work, and answer in a complete sentence.
Answer:
7² + 7² = 10²
49 + 49 = 100
98≠100
No, the triangle with leg lengths of 7 mm and 7 mm and hypotenuse of length 10 mm is not a right triangle because the lengths do not satisfy the Pythagorean theorem.

Question 2.
What would the length of the hypotenuse need to be so that the triangle in Problem 1 would be a right triangle? Show work that leads to your answer.
Answer:
Let c mm represent the length of the hypotenuse.
Then,
7² + 7² = c²
49 + 49 = c²
98 = c²
\(\sqrt{98}\) = c
The hypotenuse would need to be \(\sqrt{98}\) mm for the triangle with sides of 7 mm and 7 mm to be a right triangle.

Question 3.
If one of the leg lengths is 7 mm, what would the other leg length need to be so that the triangle in Problem 1 would be a right triangle? Show work that leads to your answer.
Answer:
Let a mm represent the length of one leg.
Then,
a² + 7² = 10²
a² + 49 = 100
a² + 49 – 49 = 100 – 49
a² = 51
a = \(\sqrt{51}\)
The leg length would need to be \(\sqrt{51}\) mm so that the triangle with one leg length of 7 mm and the hypotenuse of 10 mm is a right triangle.