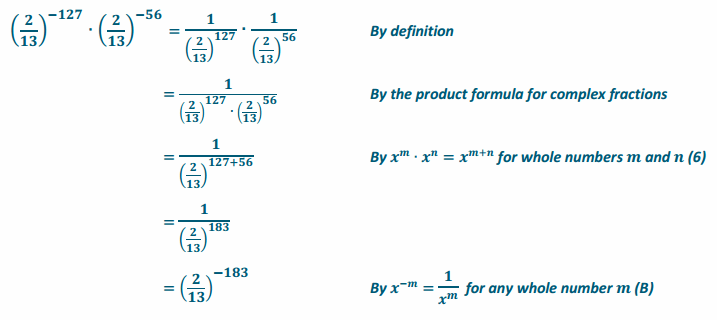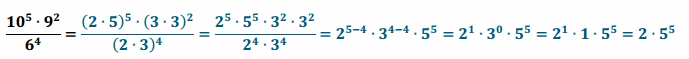Eureka Math

Engage NY Eureka Math 8th Grade Module 7 Lesson 3 Answer Key

Eureka Math Grade 8 Module 7 Lesson 3 Exercise Answer Key

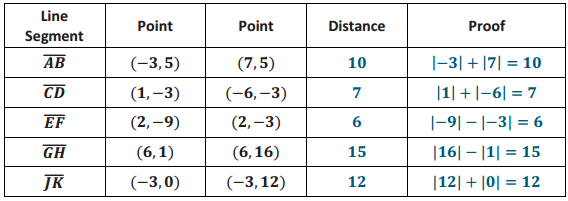
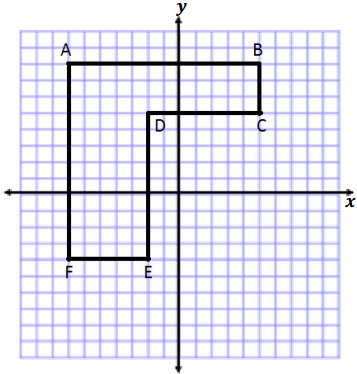
Opening
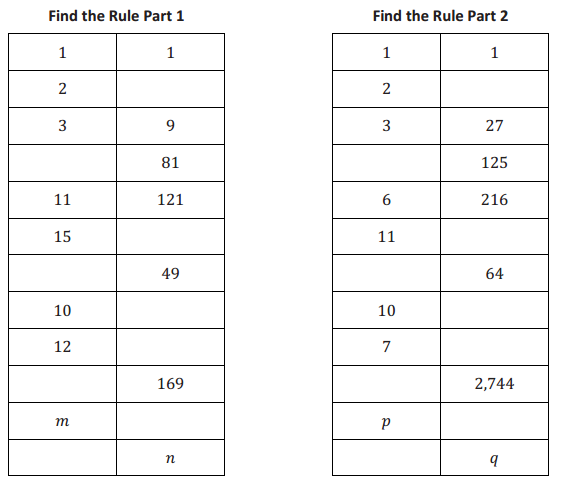
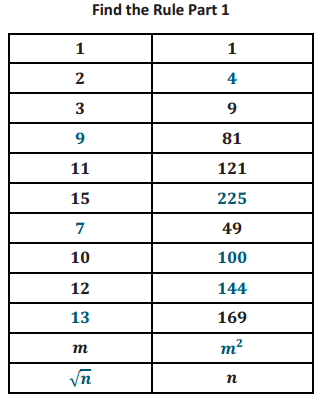
The numbers in each column are related. Your goal is to determine how they are related, determine which numbers belong in the blank parts of the columns, and write an explanation for how you know the numbers belong there.

Answer:

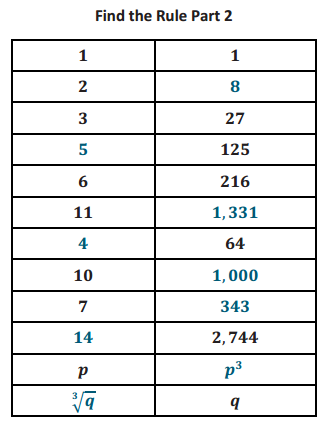
Exercises
Find the positive value of x that makes each equation true. Check your solution.

Exercise 1.
x² = 169
a. Explain the first step in solving this equation.
Answer:
The first step is to take the square root of both sides of the equation.

b. Solve the equation, and check your answer.
Answer:
x² = 169
\(\sqrt{x^{2}}\) = \(\sqrt{169}\)
x = \(\sqrt{169}\)
x = 13

Check:
13² = 169
169 = 169

Exercise 2.
A square-shaped park has an area of 324 yd². What are the dimensions of the park? Write and solve an equation.
x² = 324
\(\sqrt{x^{2}}\) = \(\sqrt{324}\)
x = \(\sqrt{324}\)
x = 18

Check:
18² = 324
324 = 324
The square park is 18 yd. in length and 18 yd. in width.

Exercise 3.
625 = x²
625 = x²
\(\sqrt{625}\) = \(\sqrt{x^{2}}\)
\(\sqrt{625}\) = x
25 = x

Check:
625 = 25²
625 = 625

Exercise 4.
A cube has a volume of 27 in³. What is the measure of one of its sides? Write and solve an equation.
27 = x³
\(\sqrt [ 3 ]{ 27 }\) = \(\sqrt[3]{x^{3}}\)
\(\sqrt [ 3 ]{ 27 }\) = x
3 = x

Check:
27 = 3³
27 = 27
The cube has side lengths of 3 in.

Exercise 5.
What positive value of x makes the following equation true: x² = 64? Explain.
x² = 64
\(\sqrt{x^{2}}\) = \(\sqrt{64}\)
x = \(\sqrt{64}\)
x = 8

Check:
8² = 64
64 = 64
To solve the equation, I need to find the positive value of x so that when it is squared, it is equal to 64. Therefore, I can take the square root of both sides of the equation. The square root of x², \(\sqrt{52}\), is x because x² = x ∙ x. The square root of 64, \(\sqrt{64}\), is 8 because 64 = 8 ∙ 8. Therefore, x = 8.

Exercise 6.
What positive value of x makes the following equation true: x³ = 64? Explain.
Answer:
x³ = 64
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 64 }\)
x = \(\sqrt [ 3 ]{ 64 }\)
x = 4 Check:
4³ = 64
64 = 64
To solve the equation, I need to find the positive value of x so that when it is cubed, it is equal to 64. Therefore, I can take the cube root of both sides of the equation. The cube root of x³, \(\sqrt[3]{x^{3}}\), is x because x³ = x ∙ x ∙ x. The cube root of 64, \(\sqrt [ 3 ]{ 64 }\), is 4 because 64 = 4 ∙ 4 ∙ 4. Therefore, x = 4.

Exercise 7.
Find the positive value of x that makes the equation true: x² = 256^-1.
Answer:
x² = 256^-1
\(\sqrt{x^{2}}\) = \(\sqrt{256^{-1}}\)
x = \(\sqrt{256^{-1}}\)
x = \(\sqrt{\frac{1}{256}}\)
x = \(\frac{1}{16}\)
x = 16^-1

Check:
(16^-1)² = 256^-1
16^-2 = 256^-1
\(\frac{1}{16^{2}}\) = 256^-1
\(\frac{1}{256}\) = 256^-1
256^-1 = 256^-1

Exercise 8.
Find the positive value of x that makes the equation true: x³ = 343^-1.
x³ = 343^-1
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{343^{-1}}\)
x = \(\sqrt[3]{343^{-1}}\)
x = \(\sqrt[3]{\frac{1}{343}}\)
x = \(\frac{1}{7}\)
x = 7^-1

Check:
(7^-1)³ = 343^-1
7³ = 343^-1
(\(\frac{1}{7}\))³ = 343^-1
\(\frac{1}{343}\) = 343^-1
343^-1 = 343^-1

Exercise 9.
Is 6 a solution to the equation x² – 4 = 5x? Explain why or why not.
Answer:
6² – 4 = 5(6)
36 – 4 = 30
32 ≠ 30
No, 6 is not a solution to the equation x² – 4 = 5x. When the number is substituted into the equation and simplified, the left side of the equation and the right side of the equation are not equal; in other words, it is not a true number sentence. Since the number 6 does not satisfy the equation, it is not a solution to the equation.

Eureka Math Grade 8 Module 7 Lesson 3 Problem Set Answer Key

Find the positive value of x that makes each equation true. Check your solution.
Question 1.
What positive value of x makes the following equation true: x² = 289? Explain.
Answer:
x² = 289
\(\sqrt{x^{2}}\) = \(\sqrt{289}\)
x = \(\sqrt{289}\)
x = 17

Check:
17² = 289
289 = 289
To solve the equation, I need to find the positive value of x so that when it is squared, it is equal to 289. Therefore, I can take the square root of both sides of the equation. The square root of x², \(\sqrt{x^{2}}\), is x because x² = x ⋅ x. The square root of 289, \(\sqrt{289}\) , is 17 because 289 = 17 ⋅ 17. Therefore, x = 17.

Question 2.
A square-shaped park has an area of 400 yd². What are the dimensions of the park? Write and solve an equation.
Answer:
x² = 400
\(\sqrt{x^{2}}\) = \(\sqrt{400}\)
x = \(\sqrt{400}\)
x = 20

Check:
20² = 400
400 = 400
The square park is 20 yd. in length and 20 yd. in width.

Question 3.
A cube has a volume of 64 in³. What is the measure of one of its sides? Write and solve an equation.
Answer:
x³ = 64
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 64 }\)
x = \(\sqrt [ 3 ]{ 64 }\)
x = 4

Check:
4³ = 64
64 = 64
The cube has a side length of 4 in.

Question 4.
What positive value of x makes the following equation true: 125 = x³? Explain.
Answer:
125 = x³
\(\sqrt [ 3 ]{ 125 }\) = \(\sqrt[3]{x^{3}}\)
\(\sqrt [ 3 ]{ 125 }\) = x
5 = x

Check:
125 = 5³
125 = 125
To solve the equation, I need to find the positive value of x so that when it is cubed, it is equal to 125. Therefore, I can take the cube root of both sides of the equation. The cube root of x³, \(\sqrt[3]{x^{3}}\), is x because x³ = x ⋅ x ⋅ x. The cube root of 125, \(\sqrt [ 3 ]{ 125 }\), is 5 because 125 = 5 ⋅ 5 ⋅ 5. Therefore, x = 5.

Question 5.
Find the positive value of x that makes the equation true: x² = 441^-1.
a. Explain the first step in solving this equation.
Answer:
The first step is to take the square root of both sides of the equation.

b. Solve and check your solution.
x² = 441^-1
\(\sqrt{x^{2}}\) = \(\sqrt{144^{-1}}\)
x = \(\sqrt{144^{-1}}\)
x = \(\sqrt{\frac{1}{441}}\)
x = \(\frac{1}{21}\)
x = 21^-1

Check:
(21^-1 )² = 441^-1
21^-2 = 441^-1
\(\frac{1}{21^{2}}\) = 441^-1
\(\frac{1}{441}\) = 441^-1
441^-1 = 441^-1

Question 6.
Find the positive value of x that makes the equation true: x³ = 125^-1.
Answer:
x³ = 125^-1
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{125^{-1}}\)
x = \(\sqrt[3]{125^{-1}}\)
x = \(\sqrt[3]{\frac{1}{125}}\)
x = \(\frac{1}{5}\)
x = 5^-1

Check:
(5^-1)³ = 125^-1
5^-3 = 125^-1
\(\frac{1}{5^{3}}\) = 125^-1
\(\frac{1}{125}\) = 125^-1
125^-1 = 125^-1

Question 7.
The area of a square is 196 in². What is the length of one side of the square? Write and solve an equation, and then check your solution.
Answer:
Let x in. represent the length of one side of the square.
x² = 196
\(\sqrt{x^{2}}\) = \(\sqrt{196}\)
x = \(\sqrt{196}\)
x = 14

Check:
14² = 196
196 = 196
The length of one side of the square is 14 in.

Question 8.
The volume of a cube is 729 cm³. What is the length of one side of the cube? Write and solve an equation, and then check your solution.
Answer:
Let x cm represent the length of one side of the cube.
x³ = 729
\(\sqrt[3]{x^{3}}\) = \(\sqrt [ 3 ]{ 729 }\)
x = \(\sqrt [ 3 ]{ 729 }\)
x = 9

Check:
9³ = 729
729 = 729
The length of one side of the cube is 9 cm.

Question 9.
What positive value of x would make the following equation true: 19 + x² = 68?
Answer:
19 + x² = 68
19 – 19 + x² = 68 – 19
x² = 49
x = 7
The positive value for x that makes the equation true is 7.

Eureka Math Grade 8 Module 7 Lesson 3 Exit Ticket Answer Key

Find the positive value of x that makes each equation true. Check your solution.
Question 1.
x² = 225
a. Explain the first step in solving this equation.
Answer:
The first step is to take the square root of both sides of the equation.

b. Solve and check your solution.
Answer:
x² = 225
\(\sqrt{x^{2}}\) = \(\sqrt{225}\)
x = \(\sqrt{225}\)
x = 15

Check:
15² = 225
225 = 225

Question 2.
x³ = 64
Answer:
x³ = 64
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{ 64 }\)
x = \(\sqrt [ 3 ]{ 64 }\)
x = 4

Check:
4³ = 64
64 = 64

Question 3.
x² = 361^-1
Answer:
x² = 361^-1
\(\sqrt{x^{2}}\) = \(\sqrt{361^{-1}}\)
x = \(\sqrt{361^{-1}}\)
x = \(\sqrt{\frac{1}{361}}\)
x = \(\frac{1}{19}\)
x = 19^-1

Check:
(19^-1)² = 361^-1
19^-2 = 361^-1
\(\frac{1}{19^{2}}\) = 361^-1
\(\frac{1}{361}\) = 361^-1
361^-1 = 361^-1

Question 4.
x³ = 1000^-1
Answer:
x³ = 1000^-1
\(\sqrt[3]{x^{3}}\) = \(\sqrt[3]{1000^{-1}}\)
x = \(\sqrt[3]{1000^{-1}}\)
x = \(\sqrt[3]{\frac{1}{1000}}\)
x = \(\frac{1}{10}\)
x = 10^-1

Check:
(10^-1 )³ = 1000^-1
10^-3 = 1000^-1
\(\frac{1}{10^{3}}\) = 1000^-1
\(\frac{1}{1000}\) = 1000^-1
1000^-1 = 1000^-1

Engage NY Eureka Math 8th Grade Module 7 Lesson 2 Answer Key

Eureka Math Grade 8 Module 7 Lesson 2 Exercise Answer Key

Exercise 1.
Determine the positive square root of 81, if it exists. Explain.
Answer:
The square root of 81 is 9 because 9²=81.

Exercise 2.
Determine the positive square root of 225, if it exists. Explain.
Answer:
The square root of 225 is 15 because 15²=225.

Exercise 3.
Determine the positive square root of -36, if it exists. Explain.
Answer:
The number -36 does not have a square root because there is no number squared that can produce a negative number.

Exercise 4.
Determine the positive square root of 49, if it exists. Explain.
Answer:
The square root of 49 is 7 because 7²=49.

Discussion

Answer:
Place the numbers \(\sqrt{1}\), \(\sqrt{4}\), \(\sqrt{9}\), and \(\sqrt{1}\)6 on the number line, and explain how you knew where to place them.
Solutions are shown below in red.

Place the numbers \(\sqrt{2}\) and \(\sqrt{3}\) on the number line. Be prepared to explain your reasoning.
Solutions are shown below in red. Students should reason that the numbers \(\sqrt{2}\) and \(\sqrt{3}\) belong on the number line between \(\sqrt{1}\) and \(\sqrt{4}\). They might be more specific and suggest that the numbers \(\sqrt{2}\) and \(\sqrt{3}\) sit equally spaced in the interval between 1 and 2. This idea suggests that 1 \(\frac{1}{3}\) might be a good approximation for \(\sqrt{2}\) and 1 \(\frac{2}{3}\) for \(\sqrt{3}\). Of course, this suggested spacing is just speculation for now.

Place the numbers \(\sqrt{5}\), \(\sqrt{6}\), \(\sqrt{7}\), and \(\sqrt{8}\) on the number line. Be prepared to explain your reasoning.
Solutions are shown below in red. The discussion about placement should be similar to the previous one.

Place the numbers \(\sqrt{1}\)0, \(\sqrt{1}\)1, \(\sqrt{1}\)2, \(\sqrt{1}\)3, \(\sqrt{1}\)4, and \(\sqrt{1}\)5 on the number line. Be prepared to explain your reasoning.
Solutions are shown below in red. The discussion about placement should be similar to the previous one.

Our work on the number line shows that there are many more square roots of whole numbers that are not perfect squares than those that are perfect squares. On the number line above, we have four perfect square numbers and twelve that are not! After we do some more work with roots, in general, we will cover exactly how to describe these numbers and how to approximate their values with greater precision. For now, we will estimate their locations on the number line using what we know about perfect squares.

Determine the positive square root of the number given. If the number is not a perfect square, determine which whole number the square root would be closest to, and then use guess and check to give an approximate answer to one or two decimal places.
Exercise 5.
\(\sqrt{49}\)
Answer:
7

Exercise 6.
\(\sqrt{62}\)
Answer:
The square root of 62 is close to 8. The square root of 62 is approximately 7.9 because 7.9²=62.41.

Exercise 7.
\(\sqrt{122}\)
Answer:
The square root of 122 is close to 11. Students may guess a number between 11 and 11.1 because 11.05²=122.1025.

Exercise 8.
\(\sqrt{400}\)
Answer:
20

Exercise 9.
Which of the numbers in Exercises 5–8 are not perfect squares? Explain.
Answer:
The numbers 62 and 122 are not perfect squares because there is no integer x to satisfy x²=62 or x²=122.

Eureka Math Grade 8 Module 7 Lesson 2 Problem Set Answer Key

Determine the positive square root of the number given. If the number is not a perfect square, determine the integer to which the square root would be closest.
Question 1.
\(\sqrt{169}\)
Answer:
13

Question 2.
\(\sqrt{256}\)
Answer:
16

Question 3.
\(\sqrt{81}\)
Answer:
9

Question 4.
\(\sqrt{147}\)
Answer:
The number 147 is not a perfect square. It is between the perfect squares 144 and 169 but closer to 144. Therefore, the square root of 147 is close to 12.

Question 5.
\(\sqrt{8}\)
Answer:
The number 8 is not a perfect square. It is between the perfect squares 4 and 9 but closer to 9. Therefore, the square root of 8 is close to 3.

Question 6.
Which of the numbers in Problems 1–5 are not perfect squares? Explain.
Answer:
The numbers 147 and 8 are not perfect squares because there is no integer x so that x²=147 or x²=8.

Question 7.
Place the following list of numbers in their approximate locations on a number line.
\(\sqrt{32}\), \(\sqrt{12}\), \(\sqrt{27}\), \(\sqrt{18}\), \(\sqrt{23}\), and \(\sqrt{50}\)
Answer:
Answers are noted in red.

Question 8.
Between which two integers will \(\sqrt{45}\) be located? Explain how you know.
Answer:
The number 45 is not a perfect square. It is between the perfect squares 36 and 49 but closer to 49. Therefore, the square root of 45 is between the integers 6 and 7 because \(\sqrt{36}\) = 6 and \(\sqrt{49}\) = 7 and \(\sqrt{36}\) < \(\sqrt{45}\) < \(\sqrt{49}\).

Eureka Math Grade 8 Module 7 Lesson 2 Exit Ticket Answer Key

Question 1.
Write the positive square root of a number x in symbolic notation.
Answer:
\(\sqrt{x}\)

Question 2.
Determine the positive square root of 196. Explain.
Answer:
\(\sqrt{196}\) = 14 because 14² = 196.

Question 3.
The positive square root of 50 is not an integer. Which whole number does the value of \(\sqrt{50}\) lie closest to? Explain.
Answer:
\(\sqrt{50}\) is between 7 and 8 but closer to 7. The reason is that 7²=49, and 8²=64. The number 50 is between 49 and 64 but closer to 49. Therefore, the square root of 50 is close to 7.

Question 4.
Place the following numbers on the number line in approximately the correct positions: \(\sqrt{16}\), \(\sqrt{9}\), \(\sqrt{11}\), and 3.5.

Answer:
Solutions are shown in red below.

Engage NY Eureka Math 8th Grade Module 2 Lesson 13 Answer Key

Eureka Math Grade 8 Module 2 Lesson 13 Exploratory Challenge Answer Key

Classwork
Concept Development

m∠1+m∠2+m∠3=m∠4+m∠5+m∠6=m∠7+m∠8+m∠9=180°
Note that the sum of the measures of angles 7 and 9 must equal 90° because of the known right angle in the right triangle.

We want to prove that the angle sum of any triangle is 180°. To do so, we use some facts that we already know about geometry:
→ A straight angle is 180° in measure.
→ Corresponding angles of parallel lines are equal in measure (corr. ∠’s, \(\overline{A B}\) || \(\overline{C D}\).
→ Alternate interior angles of parallel lines are equal in measure (alt. ∠’s, \(\overline{A B}\) || \(\overline{C D}\).

Exploratory Challenge 1.
Let triangle ABC be given. On the ray from B to C, take a point D so that C is between B and D. Through point C, draw a segment parallel to \(\overline{A B}\), as shown. Extend the segments AB and CE. Line AC is the transversal that intersects the parallel lines.

a. Name the three interior angles of triangle ABC.
Answer:
∠ABC, ∠BAC, ∠BCA

b. Name the straight angle.
Answer:
∠BCD
Our goal is to show that the measures of the three interior angles of triangle ABC are equal to the measures of the angles that make up the straight angle. We already know that a straight angle is 180° in measure.
If we can show that the interior angles of the triangle are the same as the angles of the straight angle, then we will have proven that the sum of the measures of the interior angles of the triangle have a sum of 180°.

c. What kinds of angles are ∠ABC and ∠ECD? What does that mean about their measures?
Answer:
∠ABC and ∠ECD are corresponding angles. Corresponding angles of parallel lines are equal in measure (corr. ∠’s, \(\overline{A B}\) || \(\overline{\boldsymbol{C E}}\)).

d. What kinds of angles are ∠BAC and ∠ECA? What does that mean about their measures?
Answer:
∠BAC and ∠ECA are alternate interior angles. Alternate interior angles of parallel lines are equal in measure (alt. ∠’s, \(\overline{\boldsymbol{A B}}\) || \(\overline{\boldsymbol{C E}}\)).

d. We know that m∠BCD=m∠BCA+m∠ECA+m∠ECD=180°. Use substitution to show that the measures of the three interior angles of the triangle have a sum of 180°.
Answer:
m∠BCD=m∠BCA+m∠BAC+m∠ABC=180° (∠ sum of △)

Exploratory Challenge 2.
The figure below shows parallel lines L₁ and L₂ . Let m and n be transversals that intersect L₁ at points B and C, respectively, and L₂ at point F, as shown. Let A be a point on L₁ to the left of B, D be a point on L₁ to the right of C, G be a point on L₂ to the left of F, and E be a point on L₂ to the right of F.

a. Name the triangle in the figure.
Answer:
△BCF

b. Name a straight angle that will be useful in proving that the sum of the measures of the interior angles of the triangle is 180°.
Answer:
∠GFE
As before, our goal is to show that the sum of the measures of the interior angles of the triangle are equal to the measure of the straight angle. Use what you learned from Exploratory Challenge 1 to show that the measures of the interior angles of a triangle have a sum of 180°.

c. Write your proof below.
Answer:
The straight angle ∠GFE is comprised of ∠GFB, ∠BFC, and ∠EFC. Alternate interior angles of parallel lines are equal in measure (alt. ∠’s, \(\overline{A D}\) || \(\overline{C E}\)). For that reason, ∠BCF=∠EFC and ∠CBF=∠GFB. Since ∠GFE is a straight angle, it is equal to 180°. Then, ∠GFE=∠GFB+∠BFC+∠EFC=180°.
By substitution, ∠GFE=∠CBF+∠BFC+∠BCF=180°. Therefore, the sum of the measures of the interior angles of a triangle is 180° (∠ sum of △).

Eureka Math Grade 8 Module 2 Lesson 13 Exit Ticket Answer Key

Question 1.
If L₁ || L₂ , and L₃ || L₄ , what is the measure of ∠1? Explain how you arrived at your answer.

Answer:
The measure of angle 1 is 29°. I know that the angle sum of triangles is 180°. I already know that two of the angles of the triangle are 90° and 61°.

Question 2.
Given that line AB is parallel to line CE, present an informal argument to prove that the measures of the interior angles of triangle ABC have a sum of 180°.

Answer:
Since \(\overleftrightarrow{A B}\) is parallel to \(\overleftrightarrow{C E}\), the corresponding angles ∠BAC and ∠ECD are equal in measure. Similarly, ∠ABC and ∠ECB are equal in measure because they are alternate interior angles. Since ∠ACD is a straight angle (i.e., equal to 180° in measure), substitution shows that triangle ABC has a sum of 180°. Specifically, the straight angle is made up of ∠ACB, ∠ECB, and ∠ECD. ∠ACB is one of the interior angles of the triangle and one of the angles of the straight angle. We know that ∠ABC has the same measure as ∠ECB and that ∠BAC has the same measure as ∠ECD. Therefore, the sum of the measures of the interior angles will be the same as the sum of the measures of the angles of the straight angle, which is 180°.

Eureka Math Grade 8 Module 2 Lesson 13 Problem Set Answer Key

Students practice presenting informal arguments about the sum of the angles of a triangle using the theorem to find the measures of missing angles.

Question 1.
In the diagram below, line AB is parallel to line CD, that is, L_AB ∥L_CD. The measure of ∠ABC is 28° and the measure of ∠EDC is 42°. Find the measure of ∠CED. Explain why you are correct by presenting an informal argument that uses the angle sum of a triangle.

Answer:
The measure of ∠CED is 110°. This is the correct measure for the angle because ∠ABC and ∠DCE are alternate interior angles of parallel lines. That means that the angles are congruent and have the same measure. Since the angle sum of a triangle is 180°, then ∠CED=180°-(28°+42°) and ∠CED is 110°.

Question 2.
In the diagram below, line AB is parallel to line CD, that is, L_AB || L_CD . The measure of ∠ABE is 38°, and the measure of ∠EDC is 16°. Find the measure of ∠BED. Explain why you are correct by presenting an informal argument that uses the angle sum of a triangle. (Hint: Find the measure of ∠CED first, and then use that measure to find the measure of ∠BED.)

Answer:
The measure of ∠BED is 54°. This is the correct measure for the angle because ∠ABC and ∠DCE are alternate interior angles of parallel lines. That means that the angles are congruent and have the same measure. Since the angle sum of a triangle is 180°, then ∠CED=180°-(38°+16°)=126°. The straight angle ∠BEC is made up of ∠CED and ∠BED. Since we know straight angles measure 180° and ∠CED=126°, then ∠BED is 54°.

Question 3.
In the diagram below, line AB is parallel to line CD, that is, L_AB || L_CD . The measure of ∠ABE is 56°, and the measure of ∠EDC is 22°. Find the measure of ∠BED. Explain why you are correct by presenting an informal argument that uses the angle sum of a triangle. (Hint: Extend the segment BE so that it intersects line CD.)

Answer:
The measure of ∠BED is 78°. This is the correct measure for the angle because ∠ABE and ∠DFE are alternate interior angles of parallel lines. That means that the angles are congruent and have the same measure. Since the angle sum of a triangle is 180°, then ∠FED=180°-(56°+22°)=102°. The straight angle ∠BEF is made up of ∠FED and ∠BED. Since straight angles measure 180° and ∠FED is 102°, then ∠BED is 78°.

Question 4.
What is the measure of ∠ACB?

Answer:
The measure of ∠ACB is 180°-(83°+64°), which is equal to 33°.

Question 5.
What is the measure of ∠EFD?

Answer:
The measure of ∠EFD is 180°-(101°+40°), which is equal to 39°.

Question 6.
What is the measure of ∠HIG?

Answer:
The measure of ∠HIG is 180°-(154°+14°), which is equal to 12°.

Question 7.
What is the measure of ∠ABC?

Answer:
The measure of ∠ABC is 60° because 60°+60°+60°, which is equal to 180°.

Question 8.
Triangle DEF is a right triangle. What is the measure of ∠EFD?

Answer:
The measure of ∠EFD is 90°-57°, which is equal to 33°.

Question 9.
In the diagram below, Lines L₁ and L₂ are parallel. Transversals r and s intersect both lines at the points shown below. Determine the measure of ∠JMK. Explain how you know you are correct.

Answer:
The Lines L₁ and L₂ are parallel, which means that the alternate interior angles formed by the transversals are equal. Specifically, ∠LMK=∠JKM=72°. Since △JKM has a sum of interior angles equal to 180°,
∠KJM+∠JMK+∠JKM=180°. By substitution, we have 39°+∠JMK+72°=180°; therefore, ∠JMK is 69°.

Engage NY Eureka Math 8th Grade Module 2 Lesson 14 Answer Key

Eureka Math Grade 8 Module 2 Lesson 14 Example Answer Key

Example 1
Find the measure of angle x.

Answer:
We need to find the sum of the measures of the remote interior angles to find the measure of the exterior angle x:
14+30=44. Therefore, the measure of ∠x is 44°.

→ Present an informal argument that proves you are correct.
→ We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠ABC must be 136°, which means that ∠x is 44°.

Example 2.
Find the measure of angle x.

Answer:
We need to find the sum of the measures of the remote interior angles to find the measure of the exterior angle x: 44+32=76. Therefore, the measure of ∠x is 76°.

→ Present an informal argument that proves you are correct.
→ We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠ACB must be 104°, which means that ∠x is 76°.

Example 3.
Find the measure of angle x.

Answer:
180-121=59. Therefore, the measure of ∠x is 59°.

Students should notice that they are not given the two remote interior angles associated with the exterior angle x.
For that reason, they must use what they know about straight angles (or supplementary angles) to find the measure of
angle x.

Example 4.
Find the measure of angle x.

Answer:
129-45=84. Therefore, the measure of ∠x is 84°.

Eureka Math Grade 8 Module 2 Lesson 14 Exercise Answer Key

Exercises 1–4
Use the diagram below to complete Exercises 1–4.

Exercise 1.
Name an exterior angle and the related remote interior angles.
Answer:
The exterior angle is ∠ZYP, and the related remote interior angles are ∠YZX and ∠ZXY.

Exercise 2.
Name a second exterior angle and the related remote interior angles.
Answer:
The exterior angle is ∠XZQ, and the related remote interior angles are ∠ZYX and ∠ZXY.

Exercise 3.
Name a third exterior angle and the related remote interior angles.
Answer:
The exterior angle is ∠RXY, and the related remote interior angles are ∠ZYX and ∠XZY.

Exercise 4.
Show that the measure of an exterior angle is equal to the sum of the measures of the related remote interior angles.
Answer:
Triangle XYZ has interior angles ∠XYZ, ∠YZX, and ∠ZXY. The sum of those angles is 180°. The straight angle ∠XYP also has a measure of 180° and is made up of angles ∠XYZ and ∠ZYP. Since the triangle and the straight angle have the same number of degrees, we can write the sum of their respective angles as an equality:
∠XYZ+∠YZX+∠ZXY=∠XYZ+ZYP.
Both the triangle and the straight angle share ∠XYZ. We can subtract the measure of that angle from the triangle and the straight angle. Then, we have
∠YZX+∠ZXY=∠ZYP,
where the angle ∠ZYP is the exterior angle, and the angles ∠YZX and ∠ZXY are the related remote interior angles of the triangle. Therefore, the sum of the measures of the remote interior angles of a triangle are equal to the measure of the exterior angle.

Exercise 5–10

Question 5.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 89+28 = 117, the measure of angle x is 117°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠ACB must be 63°, which means that ∠x is 117°.

Question 6.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 59+52=111, the measure of angle x is 111°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠CAB must be 69°, which means that ∠x is 111°.

Question 7.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 180-79=101, the measure of angle x is 101°. We know that straight angles are 180°, and the straight angle in the diagram is made up of ∠ABC and ∠x. ∠ABC is 79°, which means that ∠x is 101°.

Question 8.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 71+74=145, the measure of angle x is 145°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠ACB must be 35°, which means that ∠x is 145°.

Question 9.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 107+32=139, the measure of angle x is 139°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠CBA must be 41°, which means that x is 139°.

Question 10.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 156-81 = 75, the measure of angle x is 75°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BAC must be 24° because it is part of the straight angle. Then, ∠x=180°-(81°+24°), which means ∠x is 75°.

Eureka Math Grade 8 Module 2 Lesson 14 Exit Ticket Answer Key

Question 1.
Find the measure of angle p. Present an informal argument showing that your answer is correct.

Answer:
The measure of angle p is 67°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BAC must be 113°, which means that ∠p is 67°.

Question 2.
Find the measure of angle q. Present an informal argument showing that your answer is correct.

Answer:
The measure of angle q is 27°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠CAB must be 25°, which means that ∠q is 27°.

Question 3.
Find the measure of angle r. Present an informal argument showing that your answer is correct.

Answer:
The measure of angle r is 121°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BCA must be 59°, which means that ∠r is 121°.

Eureka Math Grade 8 Module 2 Lesson 14 Problem Set Answer Key

Students practice finding missing angle measures of triangles.

For each of the problems below, use the diagram to find the missing angle measure. Show your work.

Question 1.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 26+13=39, the measure of angle x is 39°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BCA must be 141°, which means that ∠x is 39°.

Question 2.
Find the measure of angle x.

Answer:
Since 52+44=96, the measure of angle x is 96°.

Question 3.
Find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since 76-25=51, the measure of ∠x is 51°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°. ∠BAC must be 104° because it is part of the straight angle. Then, x=180°-(104°+25°), which means ∠x is 51°.

Question 4.
Find the measure of angle x.

Answer:
Since 27+52 =79, the measure of angle x is 79°.

Question 5.
Find the measure of angle x.

Answer:
Since 180-104=76, the measure of angle x is 76°.

Question 6.
Find the measure of angle x.

Answer:
Since 52+53=105, the measure of angle x is 105°.

Question 7.
Find the measure of angle x.

Answer:
Since 48+83=131, the measure of angle x is 131°.

Question 8.
Find the measure of angle x.

Answer:
Since 100+26=126, the measure of angle x is 126°.

Question 9.
Find the measure of angle x.

Answer:
Since 126-47=79, the measure of angle x is 79°.

Question 10.
Write an equation that would allow you to find the measure of angle x. Present an informal argument showing that your answer is correct.

Answer:
Since y+z=x, the measure of angle x is (y+z)°. We know that triangles have a sum of interior angles that is equal to 180°. We also know that straight angles are 180°.
Then, ∠y+∠z+∠BAC=180°, and ∠x+∠BAC=180°. Since both equations are equal to 180°,
then ∠y+∠z+∠BAC=∠x+∠BAC. Subtract ∠BAC from each side of the equation, and you get ∠y+∠z=∠x.

Engage NY Eureka Math 8th Grade Module 2 Lesson 12 Answer Key

Eureka Math Grade 8 Module 2 Lesson 12 Exploratory Challenge Answer Key

Exploratory Challenge 1.
In the figure below, L₁ is not parallel to L₂, and m is a transversal. Use a protractor to measure angles 1–8. Which, if any, are equal in measure? Explain why. (Use your transparency if needed.)

Answer:

The following angle measures are equal: ∠1=∠3, ∠2=∠4, ∠5=∠7, and ∠6=∠8. The pairs of angles listed are equal because they are vertical angles. Vertical angles are always equal because a rotation of 180° around the vertex of the angle will map it to its opposite angle.

Exploratory Challenge 2.
In the figure below, L₁ || L₂, and m is a transversal. Use a protractor to measure angles 1–8. List the angles that are equal in measure.

Answer:

∠1=∠3=∠5=∠7 and ∠2=∠4=∠6=∠8

a. What did you notice about the measures of ∠1 and ∠5? Why do you think this is so? (Use your transparency if needed.)
Answer:
∠1 and ∠5 are equal in measure. We can translate ∠1 along a vector on line m so that the vertex of ∠1 maps onto the vertex of ∠5. Translations are angle-preserving, so the two angles will coincide.

b. What did you notice about the measures of ∠3 and ∠7? Why do you think this is so? (Use your transparency if needed.) Are there any other pairs of angles with this same relationship? If so, list them.
Answer:
∠3 and ∠7 are equal in measure. We can translate ∠3 along a vector on line m so that the vertex of ∠3 maps onto the vertex of ∠7. Translations are angle-preserving, so the two angles will coincide. Other pairs of angles with this same relationship are ∠4 and ∠8 and ∠2 and ∠6.

c. What did you notice about the measures of ∠4 and ∠6? Why do you think this is so? (Use your transparency if needed.) Is there another pair of angles with this same relationship?
Answer:
The measures of ∠4 and ∠6 are equal. A rotation of 180° around a center would map ∠4 to ∠6. Rotations are angle-preserving, so we know that ∠4 and ∠6 are equal. ∠3 and ∠5 have the same relationship.

Eureka Math Grade 8 Module 2 Lesson 12 Problem Set Answer Key

Students practice identifying corresponding, alternate interior, and alternate exterior angles from a diagram.

Use the diagram below to do Problems 1–10.

Question 1.
Identify all pairs of corresponding angles. Are the pairs of corresponding angles equal in measure? How do you know?
Answer:
∠1 and ∠5, ∠4 and ∠8, ∠2 and ∠6, ∠3 and ∠7
There is no information provided about the lines in the diagram being parallel. For that reason, we do not know if the pairs of corresponding angles are equal in measure. If we knew the lines were parallel, we could use translation to map one angle onto another.

Question 2.
Identify all pairs of alternate interior angles. Are the pairs of alternate interior angles equal in measure? How do you know?
Answer:
∠4 and ∠5, ∠3 and ∠6
There is no information provided about the lines in the diagram being parallel. For that reason, we do not know if the pairs of alternate interior angles are equal in measure. If the lines were parallel, we could use rotation to show that the pairs of angles would map onto one another, proving they are equal in measure.

Question 3.
Use an informal argument to describe why ∠1 and ∠8 are equal in measure if L₁ || L₂.
Answer:
The reason that angle 1 and angle 8 are equal in measure when the lines are parallel is because you can rotate around the midpoint of the segment between the parallel lines. A rotation would then map angle 1 onto angle 8, showing that they are congruent and equal in measure.

Question 4.
Assuming L₁∥L₂, if the measure of ∠4 is 73°, what is the measure of ∠8? How do you know?
Answer:
The measure of ∠8 is 73°. This must be true because they are corresponding angles of parallel lines.

Question 5.
Assuming L₁ || L₂, if the measure of ∠3 is 107° degrees, what is the measure of ∠6? How do you know?
Answer:
The measure of ∠6 is 107°. This must be true because they are alternate interior angles of parallel lines.

Question 6.
Assuming L₁ || L₂, if the measure of ∠2 is 107°, what is the measure of ∠7? How do you know?
Answer:
The measure of ∠7 is 107°. This must be true because they are alternate exterior angles of parallel lines.

Question 7.
Would your answers to Problems 4–6 be the same if you had not been informed that L₁ || L₂? Why or why not?
Answer:
No. The fact that the lines are parallel is the reason we can state that specific pairs of angles are equal in measure. We can use basic rigid motions to prove that angles associated with parallel lines have the property of being equal in measure when they are corresponding, alternate interior, or alternate exterior angles. If the lines are not parallel, then we could still classify the angles, but we would not know anything about their measures.

Question 8.
Use an informal argument to describe why ∠1 and ∠5 are equal in measure if L₁ || L₂.
Answer:
The reason that angle 1 and angle 5 are equal in measure when the lines are parallel is because you can translate along a vector equal in length of the segment between the parallel lines; then, angle 1 would map onto angle 5.

Question 9.
Use an informal argument to describe why ∠4 and ∠5 are equal in measure if L₁ || L₂.
Answer:
The reason that angle 4 and angle 5 are equal in measure when the lines are parallel is because when you rotate angle 4 around the midpoint of the segment between the parallel lines, angle 4 will map onto angle 5.

Question 10.
Assume that L₁ is not parallel to L₂. Explain why ∠3≠∠7.
Answer:
If the lines are not parallel, then all we know about angle 3 and angle 7 is that they are corresponding angles. If the lines are parallel, we could use translation to map one angle onto the other to show that they are equal in measure. However, we are to assume that the lines are not parallel, which means that their corresponding angles will not be equal in measure.

Eureka Math Grade 8 Module 2 Lesson 12 Exit Ticket Answer Key

Use the diagram to answer Questions 1 and 2. In the diagram, lines L₁ and L₂ are intersected by transversal m, forming angles 1–8, as shown.

Question 1.
If L₁ || L₂, what do you know about ∠2 and ∠6? Use informal arguments to support your claim.
Answer:
They are alternate interior angles because they are on opposite sides of the transversal and inside of lines L₁
and L₂. Also, the angles are equal in measure because the lines L₁ and L₂ are parallel. If we rotated angle 2 180° around the midpoint of the segment between the parallel lines, then it would map onto angle 6.

Question 2.
If L₁ || L₂, what do you know about ∠1 and ∠3? Use informal arguments to support your claim.
Answer:
They are corresponding angles because they are on the same side of the transversal and above each of lines L₁
and L₂. Also, the angles are equal in measure because the lines L₁ and L₂ are parallel. If we translated angle 1 along a vector (the same length as the segment between the parallel lines), then it would map onto angle 3.

Engage NY Eureka Math 8th Grade Module 2 Lesson 11 Answer Key

Eureka Math Grade 8 Module 2 Lesson 11 Example Answer Key

Example 1.
The advantage of the scientific notation becomes even more pronounced when we have to compute how many times heavier a proton is than an electron. Instead of writing the value of the ratio, r, as

we express it as
r=\(\frac{1.672622 \times 10^{-27}}{9.10938291 \times 10^{-31}}\).
→ Should we eliminate the power of 10 in the numerator or denominator? Explain.
→ Using the theorem on generalized equivalent fractions, we can eliminate the negative power of 10 in the numerator and denominator to see what we are doing more clearly. Anticipating that
10^-31×10³¹=1, we can multiply the numerator and denominator of the (complex) fraction by 10³¹

Using the first law of exponents (10) presented in Lesson 5, we get

Note that since we are using scientific notation, we can interpret an approximate value of r right away. For example, we see

so that r is approximately \(\frac{1}{5}\) ×10,000, which is 2,000. Thus, we expect a proton to be about two thousand times heavier than an electron.

Example 2.
The U.S. national debt as of March 23, 2013, rounded to the nearest dollar, is $16,755,133,009,522. According to the 2012 U.S. census, there are about 313,914,040 U.S. citizens. What is each citizen’s approximate share of the debt?
Answer:
\(\frac{1.6755 \times 10^{13}}{3.14 \times 10^{8}}\)=\(\frac{1.6755}{3.14}\)×\(\frac{10^{13}}{10^{8}}\)
=\(\frac{1.6755}{3.14}\)×10⁵
=0.533598…×10⁵
≈0.5336×10⁵
=53360
Each U.S. citizen’s share of the national debt is about $53,360.

Eureka Math Grade 8 Module 2 Lesson 11 Exercise Answer Key

Exercise 1.
The mass of a proton is
0.000 000 000 000 000 000 000 000 001 672 622 kg.
In scientific notation it is
Answer:
1.672622×10^-27 kg.

Exercise 2.
The mass of an electron is
0.000 000 000 000 000 000 000 000 000 000 910 938 291 kg.
In scientific notation it is
Answer:
9.10938291×10^-31 kg.

Exercise 3.
Write the ratio that compares the mass of a proton to the mass of an electron.
Answer:
Ratio: (1.672622×10^-27) :(9.10938291×10^-31)

Exercise 4.
Compute how many times heavier a proton is than an electron (i.e., find the value of the ratio). Round your final answer to the nearest one.
Answer:
Let r= the value of the ratio, then:
r=\(\frac{1.672622 \times 10^{-27}}{9.10938291 \times 10^{-31}}\)
=\(\frac{1.672622 \times 10^{-27} \times 10^{31}}{9.10938291 \times 10^{-31} \times 10^{31}}\)
=\(\frac{1.672622 \times 10^{4}}{9.10938291}\)×10⁴
=\(\frac{1.672622 \times 10^{8}}{9.10938291 \times 10^{8}}\) ×10⁴
=\(\frac{167,262,200}{910,938,291}\)×10⁴
=0.183615291675×10⁴
=1836.15291675
≈1836

Exercise 5.
The geographic area of California is 163,696 sq.mi., and the geographic area of the U.S. is 3,794,101 sq.mi. Let’s round off these figures to 1.637×10⁵ and 3.794×10⁶. In terms of area, roughly estimate how many Californias would make up one U.S. Then compute the answer to the nearest ones.
Answer:
\(\frac{3.794 \times 10^{6}}{1.637 \times 10^{5}}\)=\(\frac{3.794}{1.637}\)×\(\frac{10^{6}}{10^{5}}\)
=\(\frac{3.794}{1.637}\)×10
=2.3176…×10
≈2.318×10
=23.18
It would take about 23 Californias to make up one U.S.

Exercise 6.
The average distance from Earth to the moon is about 3.84×10⁵ km, and the distance from Earth to Mars is approximately 9.24×10⁷ km in year 2014. On this simplistic level, how much farther is traveling from Earth to Mars than from Earth to the moon?
9.24×10⁷-3.84×10⁵=924×10⁵-3.84×10⁵
=(924-3.84)×10⁵
=920.16×10⁵
=92 016 000
It is 92,016,000 km further to travel from Earth to Mars than from Earth to the moon.

Eureka Math Grade 8 Module 2 Lesson 11 Problem Set Answer Key

Question 1.
There are approximately 7.5×10¹⁸ grains of sand on Earth. There are approximately 7×10²7 atoms in an average human body. Are there more grains of sand on Earth or atoms in an average human body? How do you know?
Answer:
There are more atoms in the average human body. When comparing the order of magnitude of each number,
27>18; therefore, 7×10²⁷>7.5×10¹⁸.

Question 2.
About how many times more atoms are in a human body compared to grains of sand on Earth?
Answer:
\(\frac{7 \times 10^{27}}{7.5 \times 10^{18}}\)=\(\frac{7}{7.5}\)×\(\frac{10^{27}}{10^{18}}\)
≈1×10^27-18
≈1×10⁹
≈10⁹
There are about 1,000,000,000 times more atoms in the human body compared to grains of sand on Earth.

Question 3.
Suppose the geographic areas of California and the U.S. are 1.637×10⁵ and 3.794×10⁶ sq.mi., respectively. California’s population (as of 2012) is approximately 3.804×10⁷ people. If population were proportional to area, what would be the U.S. population?
Answer:
We already know from Exercise 5 that it would take about 23 Californias to make up one U.S. Then the population of the U.S. would be 23 times the population of California, which is
23×3.804×10⁷=87.492×10⁷
=8.7492×10⁸
=874,920,000.

Question 4.
The actual population of the U.S. (as of 2012) is approximately 3.14×10⁸. How does the population density of California (i.e., the number of people per square mile) compare with the population density of the U.S.?
Answer:
Population density of California per square mile:
\(\frac{3.804 \times 10^{7}}{1.637 \times 10^{5}}\)=\(\frac{3.804}{1.637}\)×\(\frac{10^{7}}{10^{5}}\)
=2.32376…×10²
≈2.32×10²
=232
Population density of the U.S. per square mile:
\(\frac{3.14 \times 10^{8}}{3.794 \times 10^{6}}\)=\(\frac{3.14}{3.794}\)×\(\frac{10^{8}}{10^{6}}\)
=0.8276…×10²
≈0.83×10²
=83
Population density of California compared to the population density of the U.S.:
\(\frac{232}{83}\)=2.7951…
≈2.8
California is about 3 times as dense as the U.S. in terms of population.

Eureka Math Grade 8 Module 2 Lesson 11 Exit Ticket Answer Key

Question 1.
Two of the largest mammals on earth are the blue whale and the elephant. An adult male blue whale weighs about 170 tonnes or long tons. (1 tonne = 1000 kg)
Show that the weight of an adult blue whale is 1.7×10⁵ kg.
Answer:
Let x (or any other symbol) represent the number of kilograms an adult blue whale weighs.
170×1000=x
1.7×10⁵=x

Question 2.
An adult male elephant weighs about 9.07×10³ kg.
Compute how many times heavier an adult male blue whale is than an adult male elephant (i.e., find the value of the ratio). Round your final answer to the nearest one.
Answer:
Let r be the value of the ratio.
r=\(\frac{1.7 \times 10^{5}}{9.07 \times 10^{3}}\)
=\(\frac{1.7}{9.07}\)×10²
=0.18743×10²
=18.743
≈19
The blue whale is 19 times heavier than the elephant.

Engage NY Eureka Math 8th Grade Module 2 Lesson 10 Answer Key

Eureka Math Grade 8 Module 2 Lesson 10 Example Answer Key

Example 1.
The world population is about 7 billion. There are 4.6× 10⁷ ants for every human on the planet. About how many ants are there in the world?
First, write 7 billion in scientific notation: (7× 10⁹).
To find the number of ants in the world, we need to multiply the world population by the known number of ants for each person: (7× 10⁹)(4.6× 10⁷ ).
(7× 10⁹)(4.6× 10⁷ )=(7×4.6)( 10⁹× 10⁷) By repeated use of the associative and commutative properties
=32.2× 10¹⁶ By the first law of exponents
=3.22×10× 10¹⁶
=3.22× 10¹⁷ By the first law of exponents
There are about 3.22× 10¹⁷ ants in the world!

Example 2.
A certain social media company processes about 990 billion likes per year. If the company has approximately 8.9× 10⁸ users of the social media, about how many likes is each user responsible for per year? Write your answer in scientific and standard notation.
First, write 990 billion in scientific notation: 9.9× 10¹¹.
To find the number of likes per person, divide the total number of likes by the total number of users: \(\frac{9.9 \times 10^{11}}{8.9 \times 10^{8}}\)
\(\frac{9.9 \times 10^{11}}{8.9 \times 10^{8}}\) = \(\frac{9.9}{8.9}\)×\(\frac{10^{11}}{10^{8}}\) By the product formula
=1.11235…× 10³ By the first law of exponents
≈1.1× 10³
≈1100
Each user is responsible for about 1.1× 10³, or 1,100, likes per year.

Example 3.
In 2010, Americans generated 2.5× 10⁸ tons of garbage. There are about 2,000 landfills in the United States. Assuming that each landfill is the same size and that trash is divided equally among them, determine how many tons of garbage were sent to each landfill in 2010.
First, write 2,000 in scientific notation: 2× 10³.
To find the number of tons of garbage sent to each landfill, divide the total weight of the garbage by the number of landfills: \(\frac{2.5 \times 10^{8}}{2 \times 10^{3}}\).
\(\frac{2.5 \times 10^{8}}{2 \times 10^{3}}\) = \(\frac{2.5}{2}\)× \(\frac{10^{8}}{10^{3}}\) By the product formula
=1.25× 10⁵ By the first law of exponents
Each landfill received 1.25× 10⁵ tons of garbage in 2010.
Actually, not all garbage went to landfills. Some of it was recycled and composted. The amount of recycled and composted material accounted for about 85 million tons of the 2.5× 10⁸ tons of garbage. Given this new information, how much garbage was actually sent to each landfill?
First, write 85 million in scientific notation: 8.5× 10⁷.
Next, subtract the amount of recycled and composted material from the garbage: 2.5× 10⁸-8.5× 10⁷. To subtract, we must give each number the same order of magnitude and then use the distributive property.
2.5× 10⁸-8.5× 10⁷=(2.5×10)× 10⁷-8.5× 10⁷ By the first law of exponents
=(2.5×10)-8.5))× 10⁷ By the distributive property
=(25-8.5)× 10⁷
=16.5× 10⁷
=1.65×10× 10⁷
=1.65× 10⁸ By the first law of exponents
Now, divide the new amount of garbage by the number of landfills: \(\frac{1.65 \times 10^{8}}{2 \times 10^{3}}\).
\(\frac{1.65 \times 10^{8}}{2 \times 10^{3}}\) = \(\frac{1.65}{2}\)× \(\frac{10^{8}}{10^{3}}\) By the product formula
=0.825× 10⁵ By the first law of exponents
=0.825×10× 10⁴ By the first law of exponents
=8.25× 10⁴
Each landfill actually received 8.25× 10⁴ tons of garbage in 2010.

Eureka Math Grade 8 Module 2 Lesson 10 Exercise Answer Key

Exercise 1.
The speed of light is 300,000,000 meters per second. The sun is approximately 1.5× 10¹¹ meters from Earth. How many seconds does it take for sunlight to reach Earth?
Answer:
300 000 000=3× 10⁸
\(\frac{1.5 \times 10^{11}}{3 \times 10^{8}}\) = \(\frac{1.5}{3}\)×\(\frac{10^{11}}{10^{8}}\)
=0.5× 10³
=0.5×10× 10²
=5× 10²
It takes 500 seconds for sunlight to reach Earth.

Exercise 2.
The mass of the moon is about 7.3× 10²² kg. It would take approximately 26,000,000 moons to equal the mass of the sun. Determine the mass of the sun.
Answer:
26 000 000=2.6× 10⁷
(2.6× 10⁷ )(7.3× 10²²)=(2.6×7.3)( 10⁷× 10²²)
=18.98× 10²⁹
=1.898×10× 10²⁹
=1.898× 10³⁰
The mass of the sun is 1.898× 10³⁰ kg.

Exercise 3.
The mass of Earth is 5.9× 10²4 kg. The mass of Pluto is 13,000,000,000,000,000,000,000 kg. Compared to Pluto, how much greater is Earth’s mass than Pluto’s mass?
Answer:
13 000 000 000 000 000 000 000=1.3× 10²²
5.9× 10²⁴-1.3× 10²²=(5.9× 10² )× 10²²-1.3× 10²²
=(590-1.3)× 10²²
=588.7× 10²²
=5.887× 10²× 10²²
=5.887× 10²⁴
The mass of Earth is 5.887× 10²⁴ kg greater than the mass of Pluto.

Exercise 4.
Using the information in Exercises 2 and 3, find the combined mass of the moon, Earth, and Pluto.
Answer:
7.3× 10²²+1.3× 10²²+5.9× 10²⁴=(7.3× 10²²+1.3× 10²²)+5.9× 10²⁴
=8.6× 10²²+5.9× 10²⁴
=(8.6+590)× 10²²
=598.6× 10²²
=5.986× 10²× 10²²
=5.986× 10²⁴
The combined mass of the moon, Earth, and Pluto is 5.986× 10²⁴ kg.

Exercise 5.
How many combined moon, Earth, and Pluto masses (i.e., the answer to Exercise 4) are needed to equal the mass of the sun (i.e., the answer to Exercise 2)?
Answer:
\(\frac{1.898 \times 10^{30}}{5.986 \times 10^{24}}\)=\(\frac{1.898}{5.986}\) × \(\frac{10^{30}}{10^{24}}\)
≈0.32× 10⁶
=0.32×10× 10⁵
=3.2× 10⁵
It would take 3.2× 10⁵ combined masses of the moon, Earth, and Pluto to equal the mass of the sun.

Eureka Math Grade 8 Module 2 Lesson 10 Problem Set Answer Key

Have students practice operations with numbers written in scientific notation and standard notation.

Question 1.
The sun produces 3.8× 10²⁷ joules of energy per second. How much energy is produced in a year? (Note: a year is approximately 31,000,000 seconds).
Answer:
31 000 000=3.1× 10⁷
(3.8× 10²7 )(3.1× 10⁷ )=(3.8×3.1)( 10²7× 10⁷ )
=11.78× 10³⁴
=1.178×10× 10³⁴
=1.178× 10³⁵
The sun produces 1.178× 10³⁵ joules of energy in a year.

Question 2.
On average, Mercury is about 57,000,000 km from the sun, whereas Neptune is about 4.5× 10⁹ km from the sun. What is the difference between Mercury’s and Neptune’s distances from the sun?
Answer:
57 000 000=5.7× 10⁷
4.5× 10⁹-5.7× 10⁷=(4.5× 10² )× 10⁷-5.7× 10⁷
=450× 10⁷-5.7× 10⁷
=(450-5.7)× 10⁷
=444.3× 10⁷
=4.443× 10²× 10⁷
=4.443× 10⁹
The difference in the distance of Mercury and Neptune from the sun is 4.443× 10⁹ km.

Question 3.
The mass of Earth is approximately 5.9× 10²⁴ kg, and the mass of Venus is approximately 4.9× 10²⁴ kg.
a. Find their combined mass.
Answer:
5.9× 10²⁴+4.9× 10²⁴=(5.9+4.9)× 10²⁴
=10.8× 10²⁴
=1.08×10× 10²⁴
=1.08× 10²⁵
The combined mass of Earth and Venus is 1.08× 10²⁵ kg.

b. Given that the mass of the sun is approximately 1.9× 10³⁰ kg, how many Venuses and Earths would it take to equal the mass of the sun?
Answer:
\(\frac{1.9 \times 10^{30}}{1.08 \times 10^{25}}\) = \(\frac{1.9}{1.08}\) × \(\frac{10^{30}}{10^{25}}\)
=1.75925…× 10⁵
≈1.8× 10⁵
It would take approximately 1.8× 10⁵ Venuses and Earths to equal the mass of the sun.

Eureka Math Grade 8 Module 2 Lesson 10 Exit Ticket Answer Key

Question 1.
The speed of light is 3× 10⁸ meters per second. The sun is approximately 230,000,000,000 meters from Mars. How many seconds does it take for sunlight to reach Mars?
Answer:
230 000 000 000=2.3× 10¹¹
\(\frac{2.3 \times 10^{11}}{3 \times 10^{8}}\) =\(\frac{2.3}{3}\)×\(\frac{10^{11}}{10^{8}}\)
=0.7666″…”× 10³
≈0.77×10× 10²
≈7.7× 10²
It takes approximately 770 seconds for sunlight to reach Mars.

Question 2.
If the sun is approximately 1.5× 10¹¹ meters from Earth, what is the approximate distance from Earth to Mars?
Answer:
(2.3× 10¹¹ )-(1.5× 10¹¹ )=(2.3-1.5)× 10¹¹
=0.8× 10¹¹
=0.8×10× 10¹⁰
=8× 10¹⁰
The distance from Earth to Mars is 8× 10¹⁰ meters.

Engage NY Eureka Math 8th Grade Module 2 Lesson 9 Answer Key

Eureka Math Grade 8 Module 2 Lesson 9 Exercise Answer Key

Are the following numbers written in scientific notation? If not, state the reason.
Exercise 1
1.908×10¹⁷
Answer:
yes

Exercise 2.
0.325×10^-2
Answer:
no, d<1

Exercise 3.
7.99×10³²
Answer:
yes

Exercise 4.
4.0701+10⁷
Answer:
no, it must be a product

Exercise 5.
18.432×5⁸
Answer:
no, d>10 and it is ×5 instead of ×10

Exercise 6.
8×10^-11
Answer:
yes

Use the table below to complete Exercises 7 and 8.

The table below shows the debt of the three most populous states and the three least populous states.

Exercise 7.
a. What is the sum of the debts for the three most populous states? Express your answer in scientific notation.
Answer:
(4.07×10¹¹ )+(3.37×10¹¹ )+(2.76×10¹¹ )=(4.07+3.37+2.76)×10¹¹
=10.2×10¹¹
=(1.02×10)×10¹¹
=1.02×10¹²

b. What is the sum of the debt for the three least populous states? Express your answer in scientific notation.
Answer:
(4×10⁹ )+(4×10⁹ )+(2×10⁹ )=(4+4+2)×10⁹
=10×10⁹
=(1×10)×10⁹
=1×10¹⁰

c. How much larger is the combined debt of the three most populous states than that of the three least populous states? Express your answer in scientific notation.
Answer:
(1.02×10¹² )-(1×10¹⁰ )=(1.02×10²×10¹⁰ )-(1×10¹⁰ )
=(102×10¹⁰ )-(1×10¹⁰ )
=(102-1)×10¹⁰
=101×10¹⁰
=(1.01×10²)×10¹⁰
=1.01×10¹²

Exercise 8.
a. What is the sum of the population of the three most populous states? Express your answer in scientific notation.
Answer:
(3.8×10⁷ )+(1.9×10⁷ )+(2.6×10⁷ )=(3.8+1.9+2.6)×10⁷
=8.3×10⁷

b. What is the sum of the population of the three least populous states? Express your answer in scientific notation.
Answer:
(6.9×10⁵ )+(6.26×10⁵ )+(5.76×10⁵ )=(6.9+6.26+5.76)×10⁵
=18.92×10⁵
=(1.892×10)×10⁵
=1.892×10⁶

c. Approximately how many times greater is the total population of California, New York, and Texas compared to the total population of North Dakota, Vermont, and Wyoming?
Answer:
\(\frac{8.3 \times 10^{7}}{1.892 \times 10^{6}}\) = \(\frac{8.3}{1.892}\) × \(\frac{10^{7}}{10^{6}}\)
≈4.39×10
=43.9
The combined population of California, New York, and Texas is about 43.9 times greater than the combined population of North Dakota, Vermont, and Wyoming.

Exercise 9.
All planets revolve around the sun in elliptical orbits. Uranus’s furthest distance from the sun is approximately 3.004×10⁹ km, and its closest distance is approximately 2.749×10⁹ km. Using this information, what is the average distance of Uranus from the sun?
Answer:
average distance = \(\frac{\left(3.004 \times 10^{9}\right)+\left(2.749 \times 10^{9}\right)}{2}\)
= \(\frac{(3.004+2.749) \times 10^{9}}{2}\)
= \(\frac{5.753 \times 10^{9}}{2}\)
=2.8765×10⁹
On average, Uranus is 2.8765×10⁹ km from the sun.

Eureka Math Grade 8 Module 2 Lesson 9 Problem Set Answer Key

Students practice working with numbers written in scientific notation.

Question 1.
Write the number 68,127,000,000,000,000 in scientific notation. Which of the two representations of this number do you prefer? Explain.
Answer:
68 127 000 000 000 000=6.8127×10¹⁶
Most likely, students will say that they like the scientific notation better because it allows them to write less. However, they should also take note of the fact that counting the number of zeros in 68,127,000,000,000,000 is a nightmare. A strong reason for using scientific notation is to circumvent this difficulty: right away, the exponent 16 shows that this is a 17-digit number.

Question 2.
Here are the masses of the so-called inner planets of the solar system.
Mercury: 3.3022×10²³ kg
Earth: 5.9722×10²⁴ kg
Venus: 4.8685×10²⁴ kg
Mars: 6.4185×10²³ kg
What is the average mass of all four inner planets? Write your answer in scientific notation.
Answer:

= 29.531925×10²³
= 2.9531925×10²⁴
The average mass of the inner planets is 2.9531925×10²⁴ kg.

Eureka Math Grade 8 Module 2 Lesson 9 Exit Ticket Answer Key

Question 1.
The approximate total surface area of Earth is 5.1×10⁸ km². All the salt water on Earth has an approximate surface area of 352,000,000 km², and all the fresh water on Earth has an approximate surface area of
9×10⁶ km². How much of Earth’s surface is covered by water, including both salt and fresh water? Write your answer in scientific notation.
Answer:
(3.52×10⁸ )+(9×10⁶ )=(3.52×10²×10⁶ )+(9×10⁶ )
=(352×10⁶ )+(9×10⁶ )
=(352+9)×10⁶
=361×10⁶
=3.61×10⁸
The Earth’s surface is covered by 3.61×10⁸ km² of water.

Question 2.
How much of Earth’s surface is covered by land? Write your answer in scientific notation.
Answer:
(5.1×10⁸ )-(3.61×10⁸ )=(5.1-3.61)×10⁸
=1.49×10⁸
The Earth’s surface is covered by 1.49×10⁸ km² of land.

Question 3.
Approximately how many times greater is the amount of Earth’s surface that is covered by water compared to the amount of Earth’s surface that is covered by land?
Answer:
\(\frac{3.61 \times 10^{8}}{1.49 \times 10^{8}}\)≈2.4
About 2.4 times more of the Earth’s surface is covered by water than by land.

Engage NY Eureka Math 8th Grade Module 2 Lesson 15 Answer Key

Eureka Math Grade 8 Module 2 Lesson 15 Example Answer Key

Example 1.
Now that we know what the Pythagorean theorem is, let’s practice using it to find the length of a hypotenuse of a right triangle.
Determine the length of the hypotenuse of the right triangle.

The Pythagorean theorem states that for right triangles a² +b² =c² , where a and b are the legs, and c is the hypotenuse. Then,
a² +b² =c²
6² +8² =c²
36+64=c²
100=c².
Since we know that 100=10², we can say that the hypotenuse c is 10.

Example 2.
Determine the length of the hypotenuse of the right triangle.

→ Based on our work in the last example, what should we do to find the length of the hypotenuse?
→ Use the Pythagorean theorem, and replace a and b with 3 and 7. Then,
a² + b² = c²
3² +7² =c²
9+49=c²
58=c²
→ Since we do not know what number times itself produces 58, for now we can leave our answer as 58=c² . Later this year, we learn how to determine the actual value for c for problems like this one.

Eureka Math Grade 8 Module 2 Lesson 15 Exercise Answer Key

Exercises 1–5
For each of the exercises, determine the length of the hypotenuse of the right triangle shown. Note: Figures are not drawn to scale.

Question 1.

Answer:
a² +b² =c²
3² +4² =c²
9+16=c²
25=c²
5=c

Question 2.

Answer:
a² +b² =c²
8² +11² =c²
64+121=c²
185=c²

Question 3.

Answer:
a² +b² =c²
4² +9² =c²
16+81=c²
97=c²

Question 4.

Answer:
a² +b² =c²
2² +5² =c²
4+25=c²
29=c²

Question 5.

Answer:
a² +b² =c²
1² +9² =c²
1+81=c²
82=c²

Eureka Math Grade 8 Module 2 Lesson 15 Problem Set Answer Key

Students practice using the Pythagorean theorem to find the length of the hypotenuse of a right triangle.

For each of the problems below, determine the length of the hypotenuse of the right triangle shown. Note: Figures are not drawn to scale.

Question 1.

Answer:
a² +b² =c²
3² +9² =c²
9+81=c²
90=c²

Question 2.

Answer:
a² +b² =c²
8² +2² =c²
64+4=c²
68=c²

Question 3.

Answer:
a² +b² =c²
9² +2² =c²
81+4=c²
85=c²

Question 4.

Answer:
a² +b² =c²
7² +1² =c²
49+1=c²
50=c²

Question 5.

Answer:
a² +b² =c²
6² +3² =c²
36+9=c²
45=c²

Question 6.

Answer:
a² +b² =c²
4² +3² =c²
16+9=c²
25=c²
5=c

Question 7.

Answer:
a² +b² =c²
4² +2² =c²
16+4=c²
20=c²

Question 8.

Answer:
a² +b² =c²
12² +5² =c²
144+25=c²
169=c²
13=c

Question 9.

Answer:
a² +b² =c²
13² +8² =c²
169+64=c²
233=c²

Question 10.

Answer:
a² +b² =c²
10² +7² =c²
100+49=c²
149=c²

Question 11.

Answer:
a² +b² =c²
12² +9² =c²
144+81=c²
225=c²
15=c

Question 12.

Answer:
a² +b² =c²
5² +1² =c²
25+1=c²
26=c²

Eureka Math Grade 8 Module 2 Lesson 15 Exit Ticket Answer Key

Question 1.
Label the sides of the right triangle with leg, leg, and hypotenuse.

Answer:

Question 2.
Determine the length of c in the triangle shown.

Answer:
a² +b² =c²
6² +8² =c²
36+64=c²
100=c²
10=c

Question 3.
Determine the length of c in the triangle shown.

Answer:
a² +b² =c²
4² +7² =c²
16+49=c²
65=c²

Engage NY Eureka Math 8th Grade Module 2 Lesson 16 Answer Key

Engage NY Math 8th Grade Module 2 Lesson 16 Example Answer Key

Example 1.
Given a right triangle with a hypotenuse with length 13 units and a leg with length 5 units, as shown, determine the length of the other leg.

Answer:
5² +b² =13²
5² – 5² + b² =13² -5²
b² =13² -5²
b² =169-25
b² =144
b=12
The length of the leg is 12 units.

→ Let b represent the missing leg of the right triangle; then, by the Pythagorean theorem:
5² +b² =13².
→ If we let a represent the missing leg of the right triangle, then by the Pythagorean theorem:
a² +5² =13².
→ Which of these two equations is correct: 5² +b² =13² or a² +5² =13² ?

→ It does not matter which equation we use as long as we are showing the sum of the squares of the legs as equal to the square of the hypotenuse.
→ Using the first of our two equations, 5² +b² =13², what can we do to solve for b in the equation?
→ We need to subtract 5² from both sides of the equation.
5² + b² =13²
5² – 5² + b² =13² -5²
b² =13² -5²
→ Point out to students that we are looking at the Pythagorean theorem in a form that allows us to find the length of one of the legs of the right triangle. That is, b² =c² -a² .
→ The length of the leg of the right triangle is 12 units.

Example 2.
The Pythagorean theorem as it applies to missing side lengths of triangles in a real-world problem:
→ Suppose you have a ladder of length 13 feet. Suppose that to make it sturdy enough to climb, you must place the ladder exactly 5 feet from the wall of a building. You need to post a banner on the building 10 feet above the ground. Is the ladder long enough for you to reach the location you need to post the banner?

The ladder against the wall forms a right angle. For that reason, we can use the Pythagorean theorem to find out how far up the wall the ladder will reach. If we let h represent the height the ladder can reach, what equation will represent this problem?
→ 5² +h² =13² or h² =13² -5²

→ Using either equation, we see that this is just like Example 1. We know that the missing side of the triangle is 12 feet. Is the ladder long enough for you to reach the 10-foot banner location?
→ Yes, the ladder allows us to reach 12 feet up the wall.

Example 3.
Pythagorean theorem as it applies to missing side lengths of a right triangle:
→ Given a right triangle with a hypotenuse of length 15 units and a leg of length 9, what is the length of the other leg?

→ If we let the length of the missing leg be represented by a, what equation will allow us to determine its value?
→ a² +9² =15² or a² =15² -9²
→ Finish the computation:
a² =225-81
a² =144
a=12
→ The length of the missing leg of this triangle is 12 units.

Eureka Math Grade 8 Module 2 Lesson 16 Exercise Answer Key

Exercises 1–2

Exercise 1.
Use the Pythagorean theorem to find the missing length of the leg in the right triangle.
Answer:

Let b represent the missing leg length; then,
15² +b² =25²
15² -15² +b² =25² -15²
b² =625-225
b² =400
b=20
The length of the leg is 20 units.

Exercise 2.
You have a 15-foot ladder and need to reach exactly 9 feet up the wall. How far away from the wall should you place the ladder so that you can reach your desired location?
Answer:

Let a represent the distance the ladder must be placed from the wall; then,
a² +9² =15²
a² +9² -9² =15² -9²
a² =225-81
a² =144
a=12.
The ladder must be placed exactly 12 feet from the wall.

Exercises 3–6

Exercise 3.
Find the length of the segment AB, if possible.

Answer:
If we let the length of segment AB be represented by c, then
3² +4² =c²
9+16=c²
25=c²
5=c.
The length of segment AB is 5 units.

Exercise 4.
Given a rectangle with dimensions 5 cm and 10 cm, as shown, find the length of the diagonal, if possible.

Answer:
Let c represent the length of the diagonal; then,
c² =5² +10²
c² =25+100
c² =125.
The measure of the length of the hypotenuse in centimeters is the positive number c that satisfies c² =125.

Exercise 5.
A right triangle has a hypotenuse of length 13 in. and a leg with length 4 in. What is the length of the other leg?
Answer:
If we let a represent the length of the other leg, then
a² +4² =13²
a² +4² -4² =13² -4²
a² =13² -4²
a² =169-16
a² =153
The measure of the length of the leg in inches is the positive number a that satisfies a² =153.

Exercise 6.
Find the length of b in the right triangle below, if possible.

Answer:
By the Pythagorean theorem,
4² +b² =11²
4² -4² +b² =11² -4²
b² =11² -4²
b² =121-16
a² =105.
The length of side AC is the positive number b that satisfies b² =105.

Eureka Math Grade 8 Module 2 Lesson 16 Problem Set Answer Key

Students practice using the Pythagorean theorem to find missing lengths in right triangles.

Question 1.
Find the length of the segment AB shown below, if possible.

Answer:
If we let the length of segment AB be represented by c units, then by the Pythagorean theorem
6² +8² =c²
36+48=c²
100=c²
10=c
The length of the segment AB is 10 units.

Question 2.
A 20-foot ladder is placed 12 feet from the wall, as shown. How high up the wall will the ladder reach?

Answer:
Let the height up the wall that the ladder will reach be a feet. Then,
a² +12² =20²
a² +12² -12² =20² -12²
a² =20² -12²
a² =400-144
a² =256
a=16
The ladder will reach 16 feet up the wall.

Question 3.
A rectangle has dimensions 6 in. by 12 in. What is the length of the diagonal of the rectangle?
Answer:
Let the length of the diagonal be c inches. Then c is a positive number that satisfies
6² +12² =c²
36+144=c²
80=c² .
The measure of the length of the diagonal in inches is the positive number c that satisfies c² =180.

Use the Pythagorean theorem to find the missing side lengths for the triangles shown in Problems 4–8.

Question 4.
Determine the length of the missing side, if possible.

12²+b²=13²
12²-12²+b²=〖13²-12²
b² =13²-12²
b²=169-144
b²=25
b=5
The length of the missing side is 5 units.

Question 5.
Determine the length of the missing side, if possible.

Answer:
a²+3²=8²
a²+3²-3²=8²-3²
a²=8²-3²
a²=64-9
a²=55)
The number of units of the side is given by the positive number a that satisfies a²=55.

Question 6.
Determine the length of the missing side, if possible.

Answer:
7²+b²=10²
7²-7²+b²=10²-7²
b²=10²-7²
b²=100-49
b²=51
The number of units of the side is given by the positive number b that satisfies b²=51.

Question 7.
Determine the length of the missing side, if possible.

Answer:
a²+1²=5²
a²+1²-1²=5²-1²
a²=5²-1²
a²=25-1
a²=24
The number of units of the side is given by the positive number a that satisfies a²=24.

Question 8.
Determine the length of the missing side, if possible.

Answer:
a²+9²=14²
a²+9²-9²=14²-9²
a²=14²-9²
a²=196-81
a²=115
The number of units of the side is given by the positive number a that satisfies a²=115.

Eureka Math Grade 8 Module 2 Lesson 16 Exit Ticket Answer Key

Question 1.
Find the length of the missing side of the rectangle shown below, if possible.

Answer:
Let the length of the unknown leg be a units. Then,
a² +7² =12²
a² +7² -7² =12² -7²
a² =12² -7²
a² =144-49
a² =95.
The number of units of the side is given by the positive number a that satisfies a² =95.

Question 2.
Find the length of all three sides of the right triangle shown below, if possible.

Answer:

The two legs are each 5 units in length. If the hypotenuse is c units in length, then c is a positive number that satisfies
5²+5²=c²
25+25=c²
50=c².
The length of the hypotenuse is given by the positive number c that satisfies c² =50 units.

Engage NY Eureka Math 8th Grade Module 2 Lesson 7 Answer Key

Eureka Math Grade 8 Module 2 Lesson 7 Exercise Answer Key

Exercise 1.
Let M=993,456,789,098,765. Find the smallest power of 10 that will exceed M.
Answer:
M=993 456 789 098 765<999 999 999 999 999 < 1 000 000 000 000 000=10¹⁵. Because M has 15 digits, 10¹⁵ will exceed it.

Exercise 2.
Let M=78,491\(\frac{899}{987}\). Find the smallest power of 10 that will exceed M.
Answer:
M=78491\(\frac{899}{987}\)<78492<99999<100 000=10⁵.
Therefore, 10⁵ will exceed M.

Exercise 3.
Let M be a positive integer. Explain how to find the smallest power of 10 that exceeds it.
Answer:
If M is a positive integer, then the power of 10 that exceeds it will be equal to the number of digits in M. For example, if M were a 10-digit number, then 10¹⁰ would exceed M. If M is a positive number, but not an integer, then the power of 10 that would exceed it would be the same power of 10 that would exceed the integer to the right of M on a number line. For example, if M=5678.9, the integer to the right of M is 5,679. Then based on the first explanation, 10⁴ exceeds both this integer and M; this is because M=5678.9<5679<10 000=10⁴.

Exercise 4.
The chance of you having the same DNA as another person (other than an identical twin) is approximately 1 in 10 trillion (one trillion is a 1 followed by 12 zeros). Given the fraction, express this very small number using a negative power of 10.
\(\frac{1}{10000000000000}\)=
Answer:
\(\frac{1}{10000000000000}\)=\(\frac{1}{10^{13}}\) =10¹³

Exercise 5.
The chance of winning a big lottery prize is about 10^-8, and the chance of being struck by lightning in the U.S. in any given year is about 0.000 001. Which do you have a greater chance of experiencing? Explain.
Answer:
0.000 001=10^-6
There is a greater chance of experiencing a lightning strike. On a number line, 10^-8 is to the left of 10^-6. Both numbers are less than one (one signifies 100% probability of occurring). Therefore, the probability of the event that is greater is 10^-6—that is, getting struck by lightning.

Exercise 6.
There are about 100 million smartphones in the U.S. Your teacher has one smartphone. What share of U.S. smartphones does your teacher have? Express your answer using a negative power of 10.
Answer:
\(\frac{1}{100000000}\) = \(\frac{1}{10^{8}}\) = 10^-8

Eureka Math Grade 8 Module 2 Lesson 7 Exit Ticket Answer Key

Question 1.
Let M=118,526.65902. Find the smallest power of 10 that will exceed M.
Answer:
Since M=118,526.65902<118,527<1,000,000<10⁶, then 10⁶will exceed M.

Question 2.
Scott said that 0.09 was a bigger number than 0.1. Use powers of 10 to show that he is wrong.
Answer:
We can rewrite 0.09 as \(\frac{9}{10^{2}}\) =9×10^-2 and rewrite 0.1 as \(\frac{1}{10^{1}}\) =1×10^-1. Because 0.09 has a smaller power of 10, 0.09 is closer to zero and is smaller than 0.1.

Eureka Math Grade 8 Module 2 Lesson 7 Problem Set Answer Key

Question 1.
What is the smallest power of 10 that would exceed 987,654,321,098,765,432?
Answer:
987 654 321 098 765 432<999 999 999 999 999 999<1 000 000 000 000 000 000=10¹⁸

Question 2.
What is the smallest power of 10 that would exceed 999,999,999,991?
Answer:
999 999 999 991<999 999 999 999<1 000 000 000 000=10¹²

Question 3.
Which number is equivalent to 0.000 000 1: 10⁷or 10^-7? How do you know?
Answer:
0.000 000 1=10^-7. Negative powers of 10 denote numbers greater than zero but less than 1. Also, the decimal 0.000 000 1 is equal to the fraction \(\frac{1}{10^{7}}\), which is equivalent to 10^-7.

Question 4.
Sarah said that 0.000 01 is bigger than 0.001 because the first number has more digits to the right of the decimal point. Is Sarah correct? Explain your thinking using negative powers of 10 and the number line.
Answer:
0.000 01= \(\frac{1}{100000}\) =10^-5 and 0.001= \(\frac{1}{1000}\) =10^-3. On a number line, 10^-5 is closer to zero than 10^-3; therefore, 10^-5 is the smaller number, and Sarah is incorrect.

Question 5.
Order the following numbers from least to greatest:

Answer:
10^-99<10^-17<10^-5<10⁵<10¹⁴<10³⁰

Engage NY Eureka Math 8th Grade Module 2 Lesson 6 Answer Key

Eureka Math Grade 8 Module 2 Lesson 6 Exercise Answer Key

Exercises 1–3

Exercise 1.
Show that (C) is implied by equation (5) of Lesson 4 when m>0, and explain why (C) continues to hold even when
m=0.
Answer:
Equation (5) says for any numbers x, y, (y≠0) and any positive integer n, the following holds: (\(\frac{x}{y}\))ⁿ= \(\frac{x^{n}}{y^{n}}\). So,
\(\left(\frac{1}{x}\right)^{m}\) = \(\frac{1^{m}}{x^{m}}\) By (\(\frac{x}{y}\))ⁿ=\(\frac{x^{n}}{y^{n}}\) for positive integer n and nonzero y (5)
= \(\frac{1}{x^{m}}\) Because 1^m=1
If m= 0, then the left side is
(\(\frac{x}{y}\))^m=(\(\frac{x}{y}\))⁰
=1 By definition of x⁰,
and the right side is
\(\frac{1}{x^{m}}\) =\(\frac{1}{x^{0}}\)
= \(\frac{1}{1}\) By definition of x⁰
=1.

Exercise 2.
Show that (B) is in fact a special case of (11) by rewriting it as (x^m)^-1=x^(-1)m for any whole number m, so that if b=m (where m is a whole number) and a=-1, (11) becomes (B).
Answer:
(B) says x^-m= \(\frac{1}{x^{m}}\).
The left side of (B), x^-m is equal to x^(-1)m).
The right side of (B), \(\frac{1}{x^{m}}\), is equal to (x^m)^-1 by the definition of (x^m)^-1 in Lesson 5.
Therefore, (B) says exactly that (x^m)^-1=x^(-1)m.

Exercise 3.
Show that (C) is a special case of (11) by rewriting (C) as (x^-1)^m=x^m(-1) for any whole number m. Thus, (C) is the special case of (11) when b=-1 and a=m, where m is a whole number.
Answer:
(C) says (\(\frac{1}{x}\))^m=\(\frac{1}{x^{m}}\) for any whole number m.
The left side of (C) is equal to
(\(\frac{1}{x}\))^m =(x^-1)^m By definition of x^-1,
and the right side of (C) is equal to
\(\frac{1}{x^{m}}\) = x^-m By definition of x^-m,
and the latter is equal to x^m(-1). Therefore, (C) says (x^-1)^m=x^m(-1) for any whole number m.

Exercise 4.
Proof of Case (iii): Show that when a<0 and b≥0, (x^b)^a=x^ab is still valid. Let a=-c for some positive integer c. Show that the left and right sides of (x^b)^a=x^ab are equal.
The left side is
(x^b)^a=(x^b)^-c
= \(\frac{1}{\left(x^{b}\right)^{c}}\) for any whole number m (B)
= \(\frac{1}{x^{c b}}\) . By (x^m)ⁿ=x^mn for all whole numbers m and n (A)
The right side is
x^ab=x^(-c)b
=x^-(cb)
= \(\frac{1}{x^{c b}}\). By x^-m= \(\frac{1}{x^{m}}\) for any whole number m (B)
So, the two sides are equal.

Eureka Math Grade 8 Module 2 Lesson 6 Problem Set Answer Key

Question 1.
You sent a photo of you and your family on vacation to seven Facebook friends. If each of them sends it to five of their friends, and each of those friends sends it to five of their friends, and those friends send it to five more, how many people (not counting yourself) will see your photo? No friend received the photo twice. Express your answer in exponential notation.

Answer:

The total number of people who viewed the photo is (5⁰+5¹+5²+5³)×7.

Question 2.
Show directly, without using (11), that (1.27^-36)^-85=1.27^-36.85.
Answer:
(1.27^-36)^-85= (\(\frac{1}{1.27^{36}}\))^-85 By definition
= \(\frac{1}{\left(1.27^{36}\right)^{85}}\) By \(\left(\frac{1}{x}\right)\)^m = \(\frac{1}{x^{m}}\) for any whole number m(c)
= \(\frac{1}{1.27^{36 \cdot 85}}\) By (x^m)ⁿ = m^mn for whole numbers m and (7)
= 1.27^-36.85 By x^-m=\(\frac{1}{x^{m}}\) for any whole number m(B)

Question 3.
Show directly that (\(\frac{2}{13}\))^-127∙(\(\frac{2}{13}\))^-56=(\(\frac{2}{13}\))^-183.
Answer:

Question 4.
Prove for any nonzero number x, x^-127∙x^-56=x^-183.
Answer:
x^-127∙x^-56 =\(\frac{1}{x^{127}}\)∙\(\frac{1}{x^{56}}\) By definition
= \(\frac{1}{x^{127} \cdot x^{56}}\) By the product formula for complex fractions
=\(\frac{1}{x^{127+56}}\) By x^m∙xⁿ=x^m+n for whole numbers m and n (6)
=\(\frac{1}{x^{183}}\)
= x^-183 By x^-m= \(\frac{1}{x^{m}}\)^m for any whole number m (B)

Question 5.
Prove for any nonzero number x, x^-m∙x^-n=x^-m-n for positive integers m and n.
Answer:
x^-m∙x^-n= \(\frac{1}{x^{m}}\)∙\(\frac{1}{x^{n}}\) By definition
= \(\frac{1}{x^{m \cdot x^{n}}}\) By the product formula for complex fractions
= \(\frac{1}{x^{m+n}}\) By x^m∙xⁿ =x^m+n for whole numbers m and n(6)
= x^-(m+n) By x^-m = \(\frac{1}{x^{m}}\) for any whole number m(B)
= x^-m-n

Question 6.
Which of the preceding four problems did you find easiest to do? Explain.
Answer:
Students will likely say that x^-m∙x^-n=x^-m-n (Problem 5) was the easiest problem to do. It requires the least amount of writing because the symbols are easier to write than decimal or fraction numbers.

Question 7.
Use the properties of exponents to write an equivalent expression that is a product of distinct primes, each raised to an integer power.
Answer:

Eureka Math Grade 8 Module 2 Lesson 6 Exit Ticket Answer Key

Question 1.
Show directly that for any nonzero integer x, x^-5∙x^-7=x^-12.
Answer:
x^-5∙x^-7 =\(\frac{1}{x^{5}}\)\(\frac{1}{x^{7}}\) By x^-m= \(\frac{1}{x^{m}}\) for any whole number m (B)
= \(\frac{1}{x^{5} \cdot x^{7}}\) By the product formula for complex fractions
=\(\frac{1}{x^{5+7}}\) By x^m∙xⁿ=x^m+n for whole numbers m and n (6)
=\(\frac{1}{x^{12}}\)
= x^-12 By x^-m= \(\frac{1}{x^{m}}\) for any whole number m (B)

Question 2.
Show directly that for any nonzero integer x, (x^-2)^-3=x⁶.
Answer:
(x^-2)^-3 =\(\frac{1}{\left(x^{-2}\right)^{3}}\) By x^-m= \(\frac{1}{x^{m}}\) for any whole number m (B)
=\(\frac{1}{x^{-(2 \cdot 3)}}\) By case (ii) of (11)
=\(\frac{1}{x^{-6}}\)
= x⁶ By x^-m= \(\frac{1}{x^{m}}\) for any whole number m (B)

Engage NY Eureka Math Grade 6 Module 5 Lesson 8 Answer Key

Eureka Math Grade 6 Module 5 Lesson 8 Example Answer Key

Question 1.
Plot and connect the points A(3, 2), B(3, 7), and C(8, 2). Name the shape, and determine the area of the polygon.

Answer:

Right Triangle

A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (5 units)(5 units)
A = \(\frac{1}{2}\) (25 units²)
A = 12.5 units²

Question 2.
Plot and connect the points E(-8, 8), F(-2, 5), and G(-7, 2). Then give the best name for the polygon, and determine the area.
Answer:

The shape is a triangle.

Area of Square
A = s²
A = (6 units)²
A = 36 units²

Area of Triangle 1

A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (1 unit) (6 units)
A = \(\frac{1}{2}\) (6 units²)
A = 3 units²

Area of Triangle 2

A = \(\frac{1}{2}\)bh
A = \(\frac{1}{2}\) (6 units)(3 units)
A = \(\frac{1}{2}\) (18 units²)
A = 9 units²

Area of Triangle 3

A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (5 units) (3 units)
A = \(\frac{1}{2}\) (15 units²)
A = 7.5 units²

Total Area of Triangle
A = 36 units² – 3 units² – 9 units² – 7.5 units²
A = 16.5 units²

Question 3.
Plot and connect the following points: K(-9, -7), L(-4, -2), M(-1, -5), and N(-5, -5). Give the best name for the polygon, and determine the area.
Answer:

This polygon has 4 sides and has no pairs of parallel sides.
Therefore, the best name for this shape is a quadrilateral.
To determine the area, I will separate the shape into two
triangles.
Area of Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (6 units) (3 units)
A = \(\frac{1}{2}\) (18 units²)
A = 9 units²

Area of Triangle 2
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (2 units) (2 units)
A = \(\frac{1}{2}\) (4 units²)
A = 2 units²

Total Area = 9 units² + 2 units²
Total Area = 11 units²

Question 4.
Plot and connect the following points: P(1, -4), Q(5, -2), R(9, -4), S(7, -8), and T(3, -8). Give the best name for the polygon, and determine the area.
Answer:

To determine the area, I will decompose this pentagon into four smaller shapes.

Area of Shape 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (8 units)(2 units)
A = \(\frac{1}{2}\) (16 units²)
A = 8 units²

Area of Shape 2 and Shape 4
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(2 units)
A = \(\frac{1}{2}\) (8 units²)
A = 4 units²

Because there are two of the same triangle, that makes a total of 8 units².

Area of Shape 3
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units) (4 units)
A = 16 units²
Total Area = 8 units² + 8 units² + 16 units²
Total Area = 32 units²

Question 5.
Two of the coordinates of a rectangle are A (3, 7) and B (3, 2). The rectangle has an area of 30 square units. Give the possible locations of the other two vertices by identifying their coordinates. (Use the coordinate plane to draw and check your answer.)

Answer:

One possible location of the other two vertices is (9, 2) and (9, 7). Using these coordinates will result in a distance, or side length, of 6 units. Since the height is 5 units, 5 units × 6 units = 30 units².

Another possible location of the other two vertices is (-3, 2) and (-3, 7). Using these coordinates will result in a distance, or side length, of 6 units. Since the height is 5 units, 5 units × 6 units = 30 units².

Eureka Math Grade 6 Module 5 Lesson 8 Exercise Answer Key

Exercise:

For Exercises 1 and 2, plot the points, name the shape, and determine the area of the shape. Then write an expression that could be used to determine the area of the figure. Explain how each part of the expression corresponds to the situation.

Question 1.
A(4, 6), B(8, 6), C(10, 2), D(8, -3), E(5, -3), and F(2, 2)
Answer:

This shape is a hexagon.

Area of Shape 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (2 units)(4 units)
A = \(\frac{1}{2}\) (8 units2)
A = 4 units²

Area of Shape 2
A = \(\frac{1}{2}\) bh
A = (1 unit) (4 units)
A = 4 units²

Area of Shape 3
A = \(\frac{1}{2}\) bh
A = (3 units) (9 units)
A = 27 units²

Area of Shape 4
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (3 units)(5 units)
A = \(\frac{1}{2}\) (15 units2)
A = 7.5 units²

Area of Shape 5
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (2 units)(9 units)
A = \(\frac{1}{2}\) (18 units2)
A = 9 units²

Total Area = 4 units² + 4 units² + 27 units² + 7.5 units² + 9 units²

Expression:
\(\frac{1}{2}\) (2) (4) + (1) (4) + (3) (9) + \(\frac{1}{2}\) (3)(5) +\(\frac{1}{2}\) (2)(9).
Each term represents the area of a section of the hexagon. They must be added together to get the total.

The first term is the area of triangle 1 on the left.
The second term is the area of rectangle 2.
The third term is the area of the large rectangle 3.
The fourth term is the area of triangle 4 on the left.
The fifth term is the area of triangle 5 on the right.

Question 2.
X (-9, 6), Y (-2, -1), and Z (-8, -7)
Answer:

This shape is a triangle.

Area of Outside Rectangle
A = lw
A = (7 units) (13 units)
A = 91 units²

Area of Triangle 1

A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (7 units)(7 units)
A = \(\frac{1}{2}\) (49 units²)
A = 24.5 units²

Area of Triangle 2

A = \(\frac{1}{2}\)bh
A = \(\frac{1}{2}\) (6 units)(6 units)
A = \(\frac{1}{2}\) (36 units²)
A = 18 units²

Area of Triangle 3
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (13 units)(1 unit)
A = \(\frac{1}{2}\) (13 units²)
A = 6.5 units²

Total Area = 91 units² – 24.5 units² – 18 units² – 6.5 units²
Total Area = 42 units²

Expression:

(7)(13) – \(\frac{1}{2}\) (7)(7) – \(\frac{1}{2}\) (6)(6) – \(\frac{1}{2}\) (13)(1)

The first term in the expression represents the area of the rectangle that goes around the outside of the triangle.
The next three terms represent the areas that need to be subtracted from the rectangle so that we are only left with the given triangle.
The second term is the area of the top right triangle.
The third term is the area of the bottom right triangle.
The fourth term is the area of the triangle on the left.

Question 3.
A rectangle with vertices located at (-3, 4) and (5, 4) has an area of 32 square units. Determine the location of the other two vertices.
Answer:
The other two points could be located at (-3, 8) and (5, 8) or (-3, 0) and (5, 0).

Question 4.
Challenge: A triangle with vertices located at (-2, -3) and (3, -3) has an area of 20 square units. Determine one possible location of the other vertex.
Answer:
Answers will vary. Possible solutions include points that are 8 units from the base. (-2, 5) or (3, -11).

Eureka Math Grade 6 Module 5 Lesson 8 Problem Set Answer Key

Plot the points for each shape, determine the area of the polygon, and then write an expression that could be used to determine the area of the figure. Explain how each part of the expression corresponds to the situation.

Question 1.
A(1, 3), B(2, 8), C(8, 8), D(10, 3), and E(5, -2)

Answer:

Area of Triangle 1
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (6 units) (5 units)
A = \(\frac{1}{2}\) (30 units²)
A = 15 units²

Area of Triangle 2
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (9 units)(5 units)
A = \(\frac{1}{2}\) (45 units²)
A = 22.5 units²

Area of Triangle 3
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (9 units)(5 units)
A = \(\frac{1}{2}\) (45 units²)
A = 22.5 units²

Pentagon total area = 15 units² + 22.5 units² + 22.5 units²
Total Area = 60 units²

Expression:
\(\frac{1}{2}\) (6)(5) + \(\frac{1}{2}\) (9)(5) + \(\frac{1}{2}\) (9)(5)

Each term in the expression represents the area of one of the triangular pieces that fits inside the pentagon. They are all added together to form the complete figure.

Question 2.
X(-10, 2), Y(-3, 6), and Z(-6, -5)

Answer:

Area of Outside Rectangle
A = lw
A = (11 units) (7 units)
A = 77 units²

Area of Top Triangle
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (7 units)(4 units)
A = \(\frac{1}{2}\) (28 units²)
A = 14 units²

Area of Bottom Left Triangle
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(7 units)
A = \(\frac{1}{2}\) (28 units²)
A = 14 units²

Area of Bottom Right Triangle
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (3 units)(11 units)
A = \(\frac{1}{2}\) (33 units²)
A = 16.5 units²

Area of center triangle = 77 units² – 14 units² – 14 units² – 16.5 units²
Area of center triangle = 32.5 units²
Expression:
(11)(7) – \(\frac{1}{2}\) (7)(4) – \(\frac{1}{2}\) (4)(7) – \(\frac{1}{2}\) (3)(11)
The first term in the expression represents the area of the rectangle that would enclose the triangle. Then the three terms after represent the areas of the triangles that need to be removed from the area of the rectangle to find the area of the given triangle.

Question 3.
E(5, 7), F(9, -5), and G(1, -3)

Answer:

Area of Triangle on the Left
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (11 units)(4 units)
A = 22 units

Area of Triangle on the Right
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (11 units)(4 units)
A = 22 units²
Total Area = 22 units² + 22 units² = 44 units²

Expression:
\(\frac{1}{2}\) (11)(4) + \(\frac{1}{2}\) (11)(4)
Each term in the expression represents the area of a triangle that makes up the total area. The first term is the area of the triangle on the left, and the second term is the area of the triangle on the right.

Question 4.
Find the area of the triangle In Problem 3 using a different method. Then, compare the expressions that can be used for both solutions in Problems 3 and 4.
Answer:

Area of Rectangle
A = lw
A = (12 units) (8 units)
A = 96 units²

Area of Triangle on Top Left
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(10 units)
A = 20 units²

Area of Triangle on Bottom Left
A =\(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (8 units)(2 units)
A = 8 units²

Area of Triangle on Right
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(12 units)
A = 24 units²

Total Area = 96 units² – 20 units² – 8 units² – 24 units²
Total Area = 44 units²

Expression: (12)(8) – \(\frac{1}{2}\) (4)(10) – \(\frac{1}{2}\) (8)(2) – \(\frac{1}{2}\) (4)(12)
The first term in the expression is the area of a rectangle around the outside of the figure. Then we subtracted all of the extra areas with the next three terms.

The two expressions are different because of the way we divided up the figure. In the first expression, we split the shape into two triangles that had to be added together to get the whole. In the second expression, we enclosed the triangle inside a new figure and then had to subtract the extra area.

Question 5.
Two vertices of a rectangle are (8, -5) and (8, 7). If the area of the rectangle is 72 square units, name the possible location of the other two vertices.
Answer:
(2, -5) and (2, 7) or (14, -5) and (14, 7)

Question 6.
A triangle with two vertices located at (5, -8) and (5, 4) has an area of 48 square units. Determine one possible location of the other vertex.
Answer:
Answers will vary. Possible solutions include points that are 8 units from the base such as (13, -2) or (-3, -2).

Eureka Math Grade 6 Module 5 Lesson 8 Exit Ticket Answer Key

Question 1.
Determine the area of both polygons on the coordinate plane, and explain why you chose the methods you used. Then write an expression that could be used to determine the area of the figure. Explain how each part of the expression corresponds to the situation.

Answer:

Methods to calculate the answer will vary.

#1 Area of shape a
A = lw
A = (2 units) (6 units)
A = 12 units²

Area of shape b
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (4 units)(2 units)
A = \(\frac{1}{2}\) (8 units²)
A = 4 units²

Total Area = 12 units² + 4 units² = 16 units²
Explanations will vary depending on the method chosen.

Expression: (2)(6) + latex]\frac{1}{2}[/latex] (4)(2)

The first term represents the area of the rectangle on the left, which makes up part of the figure.
The second term represents the area of the triangle on the right that completes the figure.

#2 Area of outside rectangle
A = lw
A = (7 units) (6 units)
A = 42 units²

Area of shape c
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (6 units)(3 units)
A = \(\frac{1}{2}\) (18 units²)
A = 9 units²

Area of shape d
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (7 units)(3 units)
A = \(\frac{1}{2}\) (21 units²)
A = 10.5 units²

Area of shape e
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) (1 units)(6 units)
A = \(\frac{1}{2}\) (6 units²)
A = 3 units²

Total Area = 42 units² – 9 units² – 10.5 units² – 3 units²
Total Area = 19.5 units²
Explanations will vary depending on method chosen.

Expression:
(7)(6) – \(\frac{1}{2}\) (6)(3) – \(\frac{1}{2}\) (7)(3) – \(\frac{1}{2}\) (1)(6)

The first term in the expression is the area of a rectangle that goes around the triangle.
Each of the other terms represents the triangles that need to be subtracted from the rectangle so that we are left with just the figure in the center.

Engage NY Eureka Math Grade 6 Module 5 Lesson 7 Answer Key

Eureka Math Grade 6 Module 5 Lesson 7 Example Answer Key

Question 1.
Determine the lengths of the given line segments by determining the distance between the two endpoints.

Answer:

Eureka Math Grade 6 Module 5 Lesson 7 Exercise Answer Key

Question 1.
complete the table using the diagram on the coordinate plane.

Answer:

Extension:

For each problem below, write the coordinates of two points that are S units apart with the segment connecting these points having the following characteristics.

Question a.
The segment is vertical.
Answer:
Answers may vary. One possible solution is (2, 1) and (2,6).

Question b.
The segment intersects the x-axis.
Answer:
Answers may vary. One possible solution is (3,-4) and (3, 1).

Question c.
The segment intersects the y-axis.
Answer:
Answers may wary. One possible solution is (-4, 3) and (1, 3).

Question d.
The segment is vertical and lies above the x-axis.
Answer:
Answers may wary. One possible solution is (-3, 5) and (-3, 10).

Eureka Math Grade 6 Module 5 Lesson 7 Problem Set Answer Key

Question 1.
Given the pairs of points, determine whether the segment that joins them is horizontal, vertical, or neither.
a. X(3, 5) and Y(-2, 5) _____
Answer:
Horizontal

b. M(-4, 9) and N(4, -9) ____
Answer:
Neither

c. E(-7, 1) and F(-7, 4) _____
Answer:
Vertical

Question 2.
Complete the table using absolute value to determine the lengths of the line segments.

Answer:

Question 3.
Complete the table using the diagram and absolute value to determine the lengths of the line segments.

Answer:

Question 4.
Complete the table using the diagram and absolute value to determine the lengths of the line segments.

Answer:

Question 5.
Name two points in different quadrants that form a vertical line segment that is 8 units in length.
Answer:
Answers will vary. One possible solution is (2, 5) and (2, -3).

Question 6.
Name two points in the same quadrant that form a horizontal line segment that is 5 units in length.
Answer:
Answers will vary. One possible solution is (-4, -11) and (-9, -11).

Eureka Math Grade 6 Module 5 Lesson 7 Exit Ticket Answer Key

Question 1.
Use absolute value to show the lengths of \(\overline{A B}\), \(\overline{B C}\), \(\overline{C D}\), \(\overline{D E}\),and \(\overline{E F}\).

Answer:

Eureka Math Grade 6 Module 5 Lesson 7 Addition of Decimals Answer Key

Addition of Decimals II – Round 1

Directions: Evaluate each expression.

Question 1.
2.5 + 4 =
Answer:
6.5

Question 2.
2.5 + 0.4 =
Answer:
2.9

Question 3.
2.5 + 0.04 =
Answer:
2.54

Question 4.
2.5 + 0.004 =
Answer:
2.504

Question 5.
2.5 + 0.0004 =
Answer:
2.5004

Question 6.
6 + 1.3 =
Answer:
7.3

Question 7.
0.6 + 1.3 =
Answer:
1.9

Question 8.
0.06 + 1.3 =
Answer:
1.36

Question 9.
0.006 + 1.3 =
Answer:
1.306

Question 10.
0.0006 + 1.3 =
Answer:
1.3006

Question 11.
0.6 + 13 =
Answer:
13.6

Question 12.
7 + 0.2 =
Answer:
7.2

Question 13.
0.7 + 0.02 =
Answer:
0.72

Question 14.
0.07 + 0.2 =
Answer:
0.27

Question 15.
0.7 + 2 =
Answer:
2.7

Question 16.
7 + 0.02 =
Answer:
7.02

Question 17.
6 + 0.3 =
Answer:
6.3

Question 18.
0.6 + 0.03 =
Answer:
0.63

Question 19.
0.06 + 0.3 =
Answer:
0.36

Question 20.
0.6 + 3 =
Answer:
3.6

Question 21.
6 + 0.03 =
Answer:
6.03

Question 22.
0.6 + 0.3 =
Answer:
0.9

Question 23.
4.5 + 3.1 =
Answer:
7.6

Question 24.
4.5 + 0.31 =
Answer:
4.81

Question 25.
4.5 + 0.031 =
Answer:
4.531

Question 26.
0.45 + 0.031 =
Answer:
0.481

Question 27.
0.045 + 0.031 =
Answer:
0.076

Question 28.
12 + 0.36 =
Answer:
12.36

Question 29.
1.2 + 3.6 =
Answer:
4.8

Question 30.
1.2 + 0.36 =
Answer:
1.56

Question 31.
1.2 + 0.036 =
Answer:
1.236

Question 32.
0.12 + 0.036 =
Answer:
0.156

Question 33.
0.012 + 0.036 =
Answer:
0.048

Question 34.
0.7 + 3 =
Answer:
3.7

Question 35.
0.7 + 0.3 =
Answer:
1

Question 36.
0.07 + 0.03 =
Answer:
0.1

Question 37.
0.007 + 0.003 =
Answer:
0.01

Question 38.
5 + 0.5 =
Answer:
5.5

Question 39.
0.5 + 0.5 =
Answer:
1

Question 40.
0.05 + 0.05 =
Answer:
0.1

Question 41.
0.005 + 0.005 =
Answer:
0.01

Question 42.
0.11 + 19 =
Answer:
19.11

Question 43.
1.1 + 1.9 =
Answer:
3

Question 44.
0.11 + 0.19 =
Answer:
0.3

Addition of Decimals II – Round 2

Directions: Evaluate each expression.

Question 1.
7.4 + 3 =
Answer:
10.4

Question 2.
7.4 + 0.3 =
Answer:
7.7

Question 3.
7.4 + 0.03 =
Answer:
7.43

Question 4.
7.4 + 0.003 =
Answer:
7.403

Question 5.
7.4 + 0.0003 =
Answer:
7.4003

Question 6.
6 + 2.2 =
Answer:
8.2

Question 7.
0.6 + 2.2 =
Answer:
2.8

Question 8.
0.06 + 2.2 =
Answer:
2.26

Question 9.
0.006 + 2.2 =
Answer:
2.206

Question 10.
0.0006 + 2.2 =
Answer:
2.2006

Question 11.
0.6 + 2.2 =
Answer:
2.8

Question 12.
7 + 0.8 =
Answer:
7.8

Question 13.
0.7 + 0.08 =
Answer:
0.78

Question 14.
0.07 + 0.8 =
Answer:
0.87

Question 15.
0.7 + 8 =
Answer:
8.7

Question 16.
7 + 0.08 =
Answer:
7.08

Question 17.
0.5 + 0.4 =
Answer:
0.9

Question 18.
0.5 + 0.04 =
Answer:
0.54

Question 19.
0.05 + 0.4 =
Answer:
0.45

Question 20.
0.5 + 4 =
Answer:
4.5

Question 21.
5 + 0.04 =
Answer:
5.04

Question 22.
5 + 0.4 =
Answer:
5.4

Question 23.
3.6 + 2.3 =
Answer:
5.9

Question 24.
3.6 + 0.23 =
Answer:
3.83

Question 25.
3.6 + 0.023 =
Answer:
3.623

Question 26.
0.36 + 0.023 =
Answer:
0.383

Question 27.
0.036 + 0.023 =
Answer:
0.059

Question 28.
0.13 + 56 =
Answer:
56.13

Question 29.
1.3 + 5.6 =
Answer:
6.9

Question 30.
1.3 + 0.56 =
Answer:
1.86

Question 31.
1.3 + 0.056 =
Answer:
1.356

Question 32.
0.13 + 0.056 =
Answer:
0.186

Question 33.
0.013 + 0.056 =
Answer:
0.069

Question 34.
2 + 0.8 =
Answer:
2.8

Question 35.
0.2 + 0.8 =
Answer:
1

Question 36.
0.02 + 0.08 =
Answer:
0.1

Question 37.
0.002 + 0.008 =
Answer:
0.01

Question 38.
0.16 + 14 =
Answer:
14.16

Question 39.
1.6 + 1.4 =
Answer:
3

Question 40.
0.16 + 0.14 =
Answer:
0.3

Question 41.
0.016 + 0.014 =
Answer:
0.03

Question 42.
15 + 0.15 =
Answer:
15.15

Question 43.
1.5 + 1.5 =
Answer:
3

Question 44.
0.15 + 0.15 =
Answer:
0.3

Engage NY Eureka Math 6th Grade Module 3 Lesson 3 Answer Key

Eureka Math Grade 6 Module 3 Lesson 3 Example Answer Key

Example 1.
A Look at Sea Level
The picture below shows three different people participating in activities at three different elevations. With a partner, discuss what you see. What do you think the word elevation means in this situation?

Answer:
Pose questions to the class, and define elevation. Students gain additional practice with elevation by completing Exercise 1 independently.
Possible discussion questions:
→ Looking at the picture, if you were to draw a vertical number line to model elevation, which person’s elevation do you think would be at zero? Explain.
Sea level should represent an elevation of zero. So, the person sailing would be at zero because he is sailing on the surface of the water, which is neither above nor below the surface. On a number line, zero is the point or number separating positive and negative numbers.

→ On the same vertical number line, which person’s elevation would be represented above zero?
The elevation of the person hiking would be above zero because she is moving higher above the water.
On a vertical number line, this is represented by a positive value above zero because she is above the surface.

→ On the same vertical number line, which person’s elevation do you think would be below zero?
The elevation of the person scuba diving would be below zero because he is swimming below the surface of the water. On a vertical number line, this is represented by a negative value below zero because he is below the surface.

→ What does zero represent in this situation?
Zero represents the top of the water (the water’s surface).

→ In this example, which numbers correspond to elevations above sea level?
Above sea level means to be above zero, which are positive numbers.

→ In this example, which numbers correspond to elevations below sea level?
Below sea level means to be below zero, which are negative numbers.

→ On a number line, what does it mean to be at sea level?
To be at zero means to be at sea level.

→ Elevation is the height of a person, place, or thing above or below a certain reference point. In this case, what is the reference point?
The reference point is sea level.

Eureka Math Grade 6 Module 3 Lesson 3 Exercise Answer Key

Refer back to Example 1. Use the following information to answer the questions.
→ The scuba diver is 30 feet below sea level.
→ The sailor is at sea level.
→ The hiker is 2 miles (10,560 feet) above sea level.

Exercises 1.
Write an integer to represent each situation.
Answer:
Scuba Diver: – 30
Sailor: 0
Hiker: 2 (to represent the elevation in miles) or 10, 560 (to represent the elevation in feet)

Exercises 2.
Use an appropriate scale to graph each of the following situations on the number line to the right. Also, write an Integer to represent both situations.

a. A hiker is 15 feet above sea level.
Answer:
15

b. A diver is 20 feet below sea level.
Answer:
– 20

Exercises 3.
For each statement, there are two related statements: (i) and (ii). Determine which related statement ((i) or (ii)) is expressed correctly, and circle it. Then, correct the other related statement so that both parts, (i) and (ii), are stated correctly.
a. A submarine is submerged 800 feet below sea level.
i. The depth of the submarine is – 800 feet below sea level.
Answer:
The depth of the submarine is 800 feet below sea level.

ii. 800 feet below sea level can be represented by the integer – 800.
Answer:

b. The elevation of a coral reef with respect to sea level is given as – 150 feet.
i. The coral reef is 150 feet below sea level.
Answer:

ii. The depth of the coral reef is – 150 feet below sea level.
Answer:
The depth of the coral reef is 150 feet below sea level.

Eureka Math Grade 6 Module 3 Lesson 3 Problem Set Answer Key

Question 1.
Write an integer to match the following descriptions.
a. A debit of $40
Answer:
– 40

b. A deposit of $225
Answer:
225

c. 14,000 feet above sea level
Answer:
14,000

d. A temperature increase of 40°F
Answer:
40

e. A withdrawal of $225
Answer:
– 225

f. 14,000 feet below sea level
Answer:
– 14,000

For Problems 2 – 4, read each statement about a real-world situation and the two related statements in parts (a) and (b) carefully. Circle the correct way to describe each real-world situation; possible answers include either (a), (b), or both (a) and (b).

Question 2.
A whale is 600 feet below the surface of the ocean.
a. The depth of the whale is 600 feet from the ocean’s surface.
b. The whale is – 600 feet below the surface of the ocean.
Answer:
a. The depth of the whale is 600 feet from the ocean’s surface.

Question 3.
The elevation of the bottom of an iceberg with respect to sea level is given as – 125 feet.
a. The iceberg is 125 feet above sea level.
b. The iceberg is 125 feet below sea level.
Answer:
b. The iceberg is 125 feet below sea level.

Question 4.
Alex’s body temperature decreased by 2°F.
a. Alex’s body temperature dropped 2°F.
b. The integer – 2 represents the change in Alex’s body temperature in degrees Fahrenheit.
Answer:

Question 5.
A credit of $35 and a debit of $40 are applied to your bank account.
a. What is an appropriate scale to graph a credit of $35 and a debit of $40? Explain your reasoning.
Answer:
Answers will vary. I would count by 5’s because both numbers are multiples of 5.

b. What integer represents “a credit of $35” If zero represents the original balance? Explain.
Answer:
35; a credit is greater than zero, and numbers greater than zero are positive numbers.

c. What integer describes “a debit of $40” if zero represents the original balance? Explain.
Answer:
– 40; a debit is less than zero, and numbers less than zero are negative numbers.

d. Based on your scale, describe the location of both integers on the number line.
Answer:
If the scale is multiples of 5, then 35 would be 7 units to the right of (or above) zero, and – 40 would be 8 units to the left of (or below) zero.

e. What does zero represent in this situation?
Answer:
Zero represents no change being made to the account balance. In other words, no amount is either subtracted or added to the account.

Eureka Math Grade 6 Module 3 Lesson 3 Exit Ticket Answer Key

Question 1.
Write a story problem using sea level that includes both integers – 110 and 120.
Answer:
Answers may vary. On the beach, a man’s kite flies at 120 feet above sea level, which is indicated by the water’s surface. In the ocean, a white shark swims at 110 feet below the water’s surface.

Question 2.
What does zero represent in your story problem?
Answer:
Zero represents the water’s surface level, or sea level

Question 3.
Choose and label an appropriate scale to graph both integers on the vertical number line.
Answer:
I chose a scale of 10.

Question 4.
Graph and label both points on the vertical number line.

Answer: