Eureka Math

Engage NY Eureka Math 7th Grade Module 4 Lesson 18 Answer Key

Eureka Math Grade 7 Module 4 Lesson 18 Example Answer Key

Example 1.
All of the 3-letter passwords that can be formed using the letters A and B are as follows: AAA, AAB, ABA, ABB, BAA, BAB, BBA, BBB.
a. What percent of passwords contain at least two B’s?
Answer:
There are four passwords that contain at least two B’s: ABB, BAB, BBA, and BBB. There are eight passwords total.
\(\frac{4}{8}\) = \(\frac{1}{2}\) = 50%, so 50% of the passwords contain at least two B’s.

b. What percent of passwords contain no A’s?
Answer:
There is one password that contains no A’s. There are eight passwords total.
\(\frac{1}{8}\) = 0.125 = 12.5%, so 12.5% of the passwords contain no A’s.

Example 2.
In a set of 3-letter passwords, 40% of the passwords contain the letter B and two of another letter. Which of the two sets below meets the criteria? Explain how you arrived at your answer.

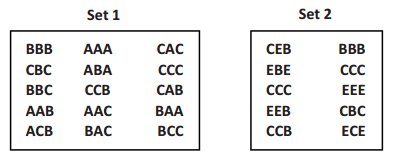
Answer:
For each set, I counted how many passwords have the letter B and two of another letter. Then, I checked to see if that quantity equaled 40% of the total number of passwords in the set.
In Set 1, CBC, AAB, ABA, CCB, BAA, and BCC are the passwords that contain a B and two of another letter. Set 1 meets the criteria since there are 15 passwords total and 40% of 15 is 6.
Quantity = Percent × Whole
6 = 0.4(15)
6 = 6 → True

In Set 2, EBE, EEB, CCB, and CBC are the only passwords that contain a B and two others of the same letter. Set 2 meets the criteria since there are 10 passwords total and 40% of 10 is 4.
Quantity = Percent × Whole
4 = 0.4(10)
4 = 4 → True
So, both Sets 1 and 2 meet the criteria.

Example 3.
Look at the 36 points on the coordinate plane with whole number coordinates between 1 and 6, inclusive.

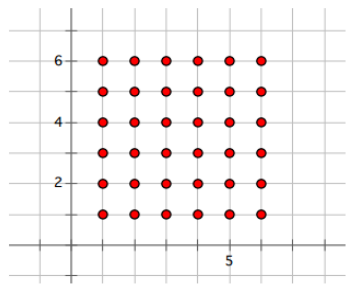
a. Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 7.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 6.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 5.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 4.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 3.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 2.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 8.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 9.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 10.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 11.
Draw a line through each of the points which have an x-coordinate and y-coordinate sum of 12.
Answer:

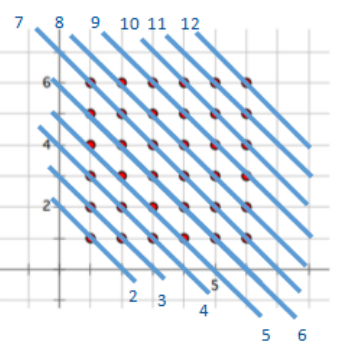
b. What percent of the 36 points have a coordinate sum of 7?
Answer:
\(\frac{6}{36}\) = \(\frac{1}{6}\) = 16 \(\frac{2}{3}\)%

c. Write a numerical expression that could be used to determine the percent of the 36 points that have a coordinate sum of 7.
Answer:
There are six coordinate points in which the sum of the x-coordinate and the y-coordinate is 7. So,
\(\frac{6}{36}\) × 100%.

d. What percent of the 36 points have a coordinate sum of 5 or less?
Answer:
\(\frac{10}{36}\) × 100% = 27 \(\frac{7}{9}\)%

e. What percent of the 36 points have a coordinate sum of 4 or 10?
Answer:
\(\frac{6}{36}\) × 100% = 16 \(\frac{2}{3}\)%

Eureka Math Grade 7 Module 4 Lesson 18 Exercise Answer Key

Opening Exercise
You are about to switch out your books from your locker during passing period but forget the order of your locker combination. You know that there are the numbers 3, 16, and 21 in some order. What is the percent of locker combinations that start with 3?
Locker Combination Possibilities:
3, 16, 21
21, 16, 3
16, 21, 3
21, 3, 16
16, 3, 21
3, 21, 16
Answer:
\(\frac{2}{6}\) = \(\frac{1}{3}\) = \(0.33 \overline{3}\) = \(33 . \overline{3} \%\)

Exercises 1–2

Exercise 1.
How many 4-letter passwords can be formed using the letters A and B?
Answer:
16: AAAA, AAAB, AABB, ABBB, AABA, ABAA, ABAB, ABBA,
BBBB, BBBA, BBAA, BAAA, BBAB, BABB, BABA, BAAB

Exercise 2.
What percent of the 4-letter passwords contain
a. No A’s?
Answer:
\(\frac{1}{16}\) = 0.0625 = 6.25%

b. Exactly one A?
Answer:
\(\frac{4}{16}\) = \(\frac{1}{4}\) = 25%

c. Exactly two A’s?
Answer:
\(\frac{6}{16}\) = 0.375 = 37.5%

d. Exactly three A’s?
Answer:
\(\frac{4}{16}\) = \(\frac{1}{4}\) = 25%

e. Four A’s?
Answer:
\(\frac{1}{16}\) = 0.0625 = 6.25%

f. The same number of A’s and B’s?
Answer:
\(\frac{6}{16}\) = 0.375 = 37.5%

→ Which categories have percents that are equal?
No A’s and four A’s have the same percents.
Exactly one A and exactly three A’s have the same percents.
Exactly two A’s and the same number of A’s and B’s also have the same percents.

→ Why do you think they are equal?
Four A’s is the same as saying no B’s, and since there are only two letters, no B’s is the same as no A’s.
The same reasoning can be used for exactly one A and exactly three A’s. If there are exactly three A’s, then this would mean that there is exactly one B, and since there are only two letters, exactly one B is the same as exactly one A.
Finally, exactly two A’s and the same number of A’s and B’s are the same because the same amount of A’s and B’s would be two of each.

Exercises 3–4

Exercise 3.
Shana read the following problem:
“How many letter arrangements can be formed from the word triangle that have two vowels and two consonants (order does not matter)?”
She answered that there are 30 letter arrangements.
Twenty percent of the letter arrangements that began with a vowel actually had an English definition. How many letter arrangements that begin with a vowel have an English definition?
Answer:
0.20 × 30 = 6
Six have a formal English definition.

Exercise 4.
Using three different keys on a piano, a songwriter makes the beginning of his melody with three notes, C, E, and G: CCE, EEE, EGC, GCE, CEG, GEE, CGE, GGE, EGG, EGE, GCG, EEC, ECC, ECG, GGG, GEC, CCG, CEE, CCC, GEG, CGC.
a. From the list above, what is the percent of melodies with all three notes that are different?
Answer:
\(\frac{6}{21}\) ≈ 28.6%

b. From the list above, what is the percent of melodies that have three of the same notes?
Answer:
\(\frac{3}{21}\) ≈ 14.3%

Eureka Math Grade 7 Module 4 Lesson 18 Problem Set Answer Key

Question 1.
A six-sided die (singular for dice) is thrown twice. The different rolls are as follows:
1 and 1, 1 and 2, 1 and 3, 1 and 4, 1 and 5, 1 and 6,
2 and 1, 2 and 2, 2 and 3, 2 and 4, 2 and 5, 2 and 6,
3 and 1, 3 and 2, 3 and 3, 3 and 4, 3 and 5, 3 and 6,
4 and 1, 4 and 2, 4 and 3, 4 and 4, 4 and 5, 4 and 6,
5 and 1, 5 and 2, 5 and 3, 5 and 4, 5 and 5, 5 and 6,
6 and 1, 6 and 2, 6 and 3, 6 and 4, 6 and 5, 6 and 6.
a. What is the percent that both throws will be even numbers?
Answer:
\(\frac{9}{36}\) = 25%

b. What is the percent that the second throw is a 5?
Answer:
\(\frac{6}{36}\) = 16 \(\frac{2}{3}\)%

c. What is the percent that the first throw is lower than a 6?
Answer:
\(\frac{30}{36}\) = 83 \(\frac{1}{3}\)%

Question 2.
You have the ability to choose three of your own classes, art, language, and physical education. There are three art classes (A1, A2, A3), two language classes (L1, L2), and two P.E. classes (P1, P2) to choose from. The order does not matter and you must choose one from each subject.

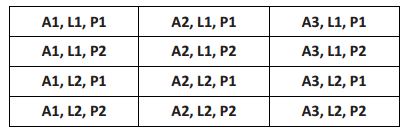
Compare the percent of possibilities with A1 in your schedule to the percent of possibilities with L1 in your schedule.
Answer:
A1: \(\frac{4}{12}\) = 33 \(\frac{1}{3}\)% L1: \(\frac{6}{12}\) = 50%
There is a greater percent with L1 in my schedule.

Question 3.
Fridays are selected to show your school pride. The colors of your school are orange, blue, and white, and you can show your spirit by wearing a top, a bottom, and an accessory with the colors of your school. During lunch, 11 students are chosen to play for a prize on stage. The table charts what the students wore.

a. What is the percent of outfits that are one color?
Answer:
\(\frac{2}{11}\) = 18 \(\frac{2}{11}\)%

b. What is the percent of outfits that include orange accessories?
Answer:
\(\frac{5}{11}\) = 45 \(\frac{5}{11}\)%

Question 4.
Shana wears two rings (G represents gold, and S represents silver) at all times on her hand. She likes fiddling with them and places them on different fingers (pinky, ring, middle, index) when she gets restless. The chart is tracking the movement of her rings.

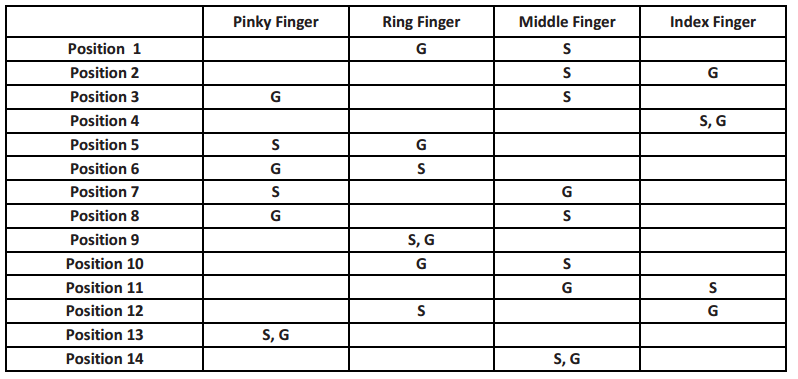
a. What percent of the positions shows the gold ring on her pinky finger?
Answer:
\(\frac{4}{14}\) ≈ 28.57%

b. What percent of the positions shows both rings on the same finger?
Answer:
\(\frac{4}{14}\) = 28 \(\frac{4}{7}\)%

Question 5.
Use the coordinate plane below to answer the following questions.

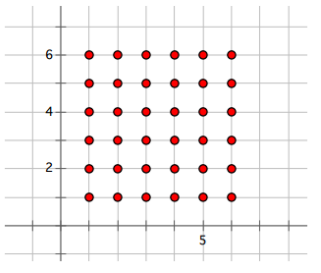
a. What is the percent of the 36 points whose quotient of \(\frac{x \text { -coordinate }}{y-\text { coordinate }}\) is greater than one?
Answer:
\(\frac{15}{36}\) = 41 \(\frac{2}{3}\)%

b. What is the percent of the 36 points whose coordinate quotient is equal to one?
Answer:
\(\frac{6}{36}\) = 16\(\frac{2}{3}\)%

Eureka Math Grade 7 Module 4 Lesson 18 Exit Ticket Answer Key

There are a van and a bus transporting students on a student camping trip. Arriving at the site, there are 3 parking spots. Let v represent the van and b represent the bus. The chart shows the different ways the vehicles can park.

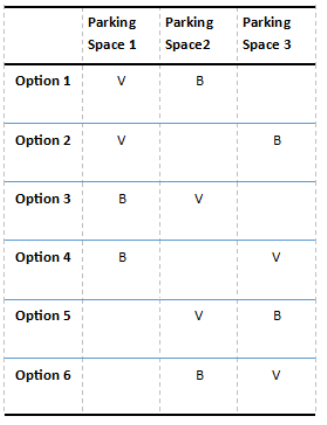
a. In what percent of the arrangements are the vehicles separated by an empty parking space?
Answer:
\(\frac{2}{6}\) = 33 \(\frac{1}{3}\)%

b. In what percent of the arrangements are the vehicles parked next to each other?
Answer:
\(\frac{4}{6}\) = 66 \(\frac{2}{3}\)%

c. In what percent of the arrangements does the left or right parking space remain vacant?
Answer:
\(\frac{4}{6}\) = 66 \(\frac{2}{3}\)%

Engage NY Eureka Math 7th Grade Module 3 Lesson 22 Answer Key

Eureka Math Grade 7 Module 3 Lesson 22 Example Answer Key

Example 1.
The pyramid in the picture has a square base, and its lateral faces are triangles that are exact copies of one another. Find the surface area of the pyramid.

Answer:
The surface area of the pyramid consists of one square base and four lateral triangular faces.
B = s²
B = (6 cm)²
B = 36 cm²
The pyramid’s base area is 36 cm².

LA = 4(\(\frac{1}{2}\) bh)
LA = 4 ∙ \(\frac{1}{2}\) (6 cm ∙ 7 cm)
LA = 2(6 cm ∙ 7 cm)
LA = 2(42 cm² )
LA = 84 cm²
The pyramid’s lateral area is 84 cm².
SA = LA + B
SA = 84 cm² + 36 cm²
SA = 120 cm²
The surface area of the pyramid is 120 cm².

Example 2: Using Cubes
There are 13 cubes glued together forming the solid in the diagram. The edges of each cube are \(\frac{1}{4}\) inch in length. Find the surface area of the solid.

Answer:
The surface area of the solid consists of 46 square faces, all having side lengths of \(\frac{1}{4}\) inch. The area of a square having sides of length \(\frac{1}{4}\) inch is \(\frac{1}{16}\) in² .
SA = 46 ∙ A_square
SA = 46 ∙ \(\frac{1}{16}\) in²
SA = \(\frac{46}{16}\) in²
SA = 2 \(\frac{14}{16}\) in²
SA = 2 \(\frac{7}{8}\) in² The surface are of the solid is 2 \(\frac{7}{8}\) in².

Example 3.
Find the total surface area of the wooden jewelry box. The sides and bottom of the box are all \(\frac{1}{4}\) inch thick.
What are the faces that make up this box?

Answer:
The box has a rectangular bottom, rectangular lateral faces, and a rectangular top that has a smaller rectangle removed from it. There are also rectangular faces that make up the inner lateral faces and the inner bottom of the box.

How does this box compare to other objects that you have found the surface area of?
Answer:
The box is a rectangular prism with a smaller rectangular prism removed from its inside. The total surface area is equal to the surface area of the larger right rectangular prism plus the lateral area of the smaller right rectangular prism.

Large Prism: The surface area of the large right rectangular prism makes up the outside faces of the box, the rim of the box, and the inside bottom face of the box.

SA = LA + 2B
LA = P ∙ h
LA = 32 in. ∙ 4 in.
LA = 128 in²

B = lw
B = 10 in. ∙ 6 in.
B = 60 in²
The lateral area is 128 in².
The base area is 60 in².

SA = LA + 2B
SA = 128 in² + 2(60 in²)
SA = 128 in² + 120 in²
SA = 248 in²
The surface area of the larger prism is 248 in².

Small Prism: The smaller prism is \(\frac{1}{2}\) in. smaller in length and width and \(\frac{1}{4}\) in. smaller in height due to the thickness of the sides of the box.
SA = LA + 1B
LA = P ∙ h
LA = 2(9 \(\frac{1}{2}\) in. + 5 \(\frac{1}{2}\) in.) ∙ 3 \(\frac{3}{4}\) in.
LA = 2(14 in. + 1 in.) ∙ 3 \(\frac{3}{4}\) in.
LA = 2(15 in.) ∙ 3 \(\frac{3}{4}\) in.
LA = 30 in. ∙ 3 \(\frac{3}{4}\) in.
LA = 90 in² + \(\frac{90}{4}\) in²
LA = 90 in² + 22 \(\frac{1}{2}\) in²
LA = 112 \(\frac{1}{2}\) in²
The lateral area is 112 \(\frac{1}{2}\) in².

Surface Area of the Box
SA_box = SA + LA
SA_box = 248 in² + 112 \(\frac{1}{2}\) in²
SA_box = 360 \(\frac{1}{2}\) in²
The total surface area of the box is 360 \(\frac{1}{2}\) in².

Eureka Math Grade 7 Module 3 Lesson 22 Exercise Answer Key

Opening Exercise
What is the area of the composite figure in the diagram? Is the diagram a net for a three-dimensional image? If so, sketch the image. If not, explain why.

Answer:
There are four unit squares in each square of the figure. There are 18 total squares that make up the figure, so the total area of the composite figure is
A = 18 ∙ 4 units² = 72 units².
The composite figure does represent the net of a three-dimensional figure. The figure is shown below.

Eureka Math Grade 7 Module 3 Lesson 22 Problem Set Answer Key

Question 1.
For each of the following nets, draw (or describe) the solid represented by the net and find its surface area.
a. The equilateral triangles are exact copies.

Answer:
The net represents a triangular pyramid where the three lateral faces are identical to each other and the triangular base.
SA = 4B since the faces are all the same size and shape.

SA = 4B
SA = 4(35 \(\frac{1}{10}\) mm² )
SA = 140 mm² + \(\frac{4}{10}\) mm²
SA = 140 \(\frac{2}{5}\) mm²

B = \(\frac{1}{2}\) bh
B = \(\frac{1}{2}\) ∙ 9 mm ∙ 7 \(\frac{4}{5}\) mm
B = \(\frac{9}{2}\) mm ∙ 7 \(\frac{4}{5}\) mm
B = \(\frac{63}{2}\) mm² + \(\frac{36}{10}\) mm²
B = \(\frac{315}{10}\) mm² + \(\frac{36}{10}\) mm²
B = \(\frac{351}{10}\) mm² The surface area of the triangular pyramid is 140 \(\frac{2}{5}\) mm².
B = 35 \(\frac{1}{10}\) mm²

b.

Answer:
The net represents a square pyramid that has four identical lateral faces that are triangles. The base is a square.
B = s²
B = (12 in.)²
B = 144 in²

LA = 2(12 in. ∙ 14 \(\frac{3}{4}\) in.)
SA = LA + B
LA = 4 ∙ \(\frac{1}{2}\) (bh)
LA = 4 ∙ \(\frac{1}{2}\) (12 in. ∙ 14 \(\frac{3}{4}\) in.)
LA = 2(168 in² + 9 in² )
LA = 336 in² + 18 in²
LA = 354 in²
SA = LA + B
SA = 354 in² + 144 in²
SA = 498 in²
The surface area of the square pyramid is 498 in².

Question 2.
Find the surface area of the following prism.

Answer:
SA = LA + 2B
LA = P ∙ h
LA = (4 cm + 6 \(\frac{1}{2}\) cm + 4 \(\frac{1}{5}\) cm + 5 \(\frac{1}{4}\) cm) ∙ 9 cm
LA = (19 cm + \(\frac{1}{2}\) cm + \(\frac{1}{5}\) cm + \(\frac{1}{4}\) cm) ∙ 9 cm
LA = (19 cm + \(\frac{10}{20}\) cm + \(\frac{4}{20}\) cm + \(\frac{5}{20}\) cm) ∙ 9 cm
LA = (19 cm + \(\frac{19}{20}\) cm) ∙ 9 cm
LA = 171 cm² + \(\frac{171}{20}\) cm²
LA = 171 cm² + 8 \(\frac{11}{20}\) cm²
LA = 179 \(\frac{11}{20}\) cm²

B = A_rectangle + A_triangle
B = (5 \(\frac{1}{4}\) cm ∙ 4 cm) + \(\frac{1}{2}\)(4 cm ∙ 1 \(\frac{1}{4}\) cm)
B = (20 cm² + 1 cm² ) + (2 cm ∙ 1 \(\frac{1}{4}\) cm)
B = 21 cm² + 2 \(\frac{1}{2}\) cm²
B = 23 \(\frac{1}{2}\) cm²

SA = LA + 2B
SA = 179 \(\frac{11}{20}\) cm² + 2(23 \(\frac{1}{2}\) cm² )
SA = 179 \(\frac{11}{20}\) cm² + 47 cm²
SA = 226 \(\frac{11}{20}\) cm²
The surface area of the prism is 226 \(\frac{11}{20}\) cm².

Question 3.
The net below is for a specific object. The measurements shown are in meters. Sketch (or describe) the object, and then find its surface area.

Answer:
SA = LA + 2B
LA = P ∙ h
LA = 6 cm ∙ \(\frac{1}{2}\) cm
LA = 3 cm²

B = (\(\frac{1}{2}\) cm ∙ \(\frac{1}{2}\) cm) + (\(\frac{1}{2}\) cm ∙ 1 cm) + (\(\frac{1}{2}\) cm ∙ 1 \(\frac{1}{2}\) cm)
B = (\(\frac{1}{4}\) cm²) + (\(\frac{1}{2}\) cm² ) + (\(\frac{3}{4}\) cm² )
B = (\(\frac{1}{4}\)cm²) + (\(\frac{2}{4}\) cm²) + (\(\frac{3}{4}\) cm²)
B = \(\frac{6}{4}\) cm²
B = 1 \(\frac{1}{2}\) cm²

SA = LA + 2B
SA = 3 cm² + 2(1 \(\frac{1}{2}\) cm² )
SA = 3 cm² + 3 cm²
SA = 6 cm²

The surface area of the object is 6 cm².

Question 4.
In the diagram, there are 14 cubes glued together to form a solid. Each cube has a volume of \(\frac{1}{8}\) in³. Find the surface area of the solid.

Answer:
The volume of a cube is s³, and 1/8 in³ is the same as (\(\frac{1}{2}\) in.)³, so the cubes have edges that are \(\frac{1}{2}\) in. long. The cube faces have area s², or (\(\frac{1}{2}\) in.)², or \(\frac{1}{4}\) in². There are 42 cube faces that make up the surface of the solid.
SA = \(\frac{1}{4}\) in² ∙ 42
SA = 10 \(\frac{1}{2}\) in²
The surface area of the solid is 10 \(\frac{1}{2}\) in².

Question 5.
The nets below represent three solids. Sketch (or describe) each solid, and find its surface area.
a.

Answer:
SA = LA + 2B
LA = P ∙ h
LA = 12 ∙ 3
LA = 36 cm²

B = s²
B = (3 cm)²
B = 9 cm²

SA =
36 cm² + 2(9 cm²)
SA = 36 cm² + 18 cm²
SA = 54 cm²

b.

Answer:
SA = 3A_square + 3A_{rt triangle} + A_{equ triangle}
A_square = s²
A_square = (3 cm)²
A_square = 9 cm²
A_{rt triangle} = \(\frac{1}{2}\) bh
A_{rt triangle} = \(\frac{1}{2}\) ∙ 3 cm ∙ 3 cm
A_{rt triangle} = \(\frac{9}{2}\)
A_{rt triangle} = 4 \(\frac{1}{2}\) cm²
A_{equ triangle} = \(\frac{1}{2}\) bh
A_{equ triangle} = \(\frac{1}{2}\) ∙ (4 \(\frac{1}{5}\) cm) ∙ (3 \(\frac{7}{10}\) cm)
A_{equ triangle} = 2 \(\frac{1}{10}\) cm ∙ 3 \(\frac{7}{10}\) cm
A_{equ triangle} = \(\frac{21}{10}\) cm ∙ \(\frac{37}{10}\) cm
A_{equ triangle} = 7 \(\frac{77}{100}\) cm²
A_{equ triangle} = 7 \(\frac{77}{100}\) cm²
SA = 3(9 cm² ) + 3(4 \(\frac{1}{2}\) cm² ) + 7 \(\frac{77}{100}\) cm²
SA = 27 cm² + (12 + \(\frac{3}{2}\)) cm² + 7 \(\frac{77}{100}\) cm²
SA = 47 cm² + \(\frac{1}{2}\) cm² + \(\frac{77}{100}\) cm²
SA = 47 cm² + \(\frac{50}{100}\) cm² + \(\frac{77}{100}\) cm²
SA = 47 cm² + \(\frac{127}{100}\) cm²
SA = 47 cm² + 1 cm² + \(\frac{27}{100}\) cm²
SA = 48 \(\frac{27}{100}\) cm²

c.

Answer:
SA = 3A_{rt triangle} + A_{equ triangle}
SA = 3(4 \(\frac{1}{2}\) ) cm² + 7 \(\frac{77}{100}\) cm²
SA = 12 cm² + \(\frac{3}{2}\) cm² + 7 cm² + \(\frac{77}{100}\) cm²
SA = 20 cm² + \(\frac{1}{2}\) cm² + \(\frac{77}{100}\) cm²
SA = 20 cm² + 1 cm² + \(\frac{27}{100}\) cm²
SA = 21 \(\frac{27}{100}\) cm²

d. How are figures (b) and (c) related to figure (a)?
Answer:
If the equilateral triangular faces of figures (b) and (c) were matched together, they would form the cube in part (a).

Question 6.
Find the surface area of the solid shown in the diagram. The solid is a right triangular prism (with right triangular bases) with a smaller right triangular prism removed from it.

Answer:
SA = LA + 2B
LA = P ∙ h
LA = (4 in. + 4 in. + 5 \(\frac{13}{20}\) in.) ∙ 2 in.
LA = (13 \(\frac{13}{20}\) in.) ∙ 2 in.
LA = 26 in² + \(\frac{13}{10}\) in²
LA = 26 in² + 1 in² + \(\frac{3}{10}\) in²
LA = 27 \(\frac{3}{10}\) in²
The \(\frac{1}{4}\)in. by 4 \(\frac{19}{20}\) in. rectangle has to be taken away from the lateral area:
A = lw
A = 4 \(\frac{19}{20}\) in ∙ \(\frac{1}{4}\) in
A = 1 in² + 19/80 in²
A = 1 19/80 in²

LA = 27 \(\frac{3}{10}\) in²-1 \(\frac{19}{80}\) in²
LA = 27 \(\frac{24}{80}\) in²-1 \(\frac{19}{80}\) in²
LA = 26 \(\frac{5}{80}\) in²
LA = 26 \(\frac{1}{16}\) in²

Two bases of the larger and smaller triangular prisms must be added:
SA = 26 \(\frac{1}{16}\) in² + 2(3 \(\frac{1}{2}\) in ∙ \(\frac{1}{4}\) in) + 2(\(\frac{1}{2}\) ∙ 4 in ∙ 4 in)
SA = 26 \(\frac{1}{16}\) in² + 2 ∙ \(\frac{1}{4}\) in ∙ 3 \(\frac{1}{2}\) in + 16 in²
SA = 26 \(\frac{1}{16}\) in² + \(\frac{1}{2}\) in ∙ 3 \(\frac{1}{2}\) in + 16 in²
SA = 26 \(\frac{1}{16}\) in² + (\(\frac{3}{2}\) in² + \(\frac{1}{4}\) in² ) + 16 in²
SA = 26 \(\frac{1}{16}\) in² + 1 in² + \(\frac{8}{16}\) in² + \(\frac{4}{16}\) in² + 16 in²
SA = 43 \(\frac{13}{16}\) in²
The surface area of the solid is 43 \(\frac{13}{16}\) in².

Question 7.
The diagram shows a cubic meter that has had three square holes punched completely through the cube on three perpendicular axes. Find the surface area of the remaining solid.

Answer:
Exterior surfaces of the cube (SA₁):
SA₁ = 6(1 m)²-6(\(\frac{1}{2}\) m)²
SA₁ = 6(1 m² )-6(\(\frac{1}{4}\) m²)
SA₁ = 6 m²–\(\frac{6}{4}\) m²
SA₁ = 6 m²-(1 \(\frac{1}{2}\) m²)
SA₁ = 4 \(\frac{1}{2}\) m²
Just inside each square hole are four intermediate surfaces that can be treated as the lateral area of a rectangular prism. Each has a height of \(\frac{1}{4}\) m and perimeter of \(\frac{1}{2}\) m + \(\frac{1}{2}\) m + \(\frac{1}{2}\) m + \(\frac{1}{2}\) m or 2 m.
SA₂ = 6(LA)
SA₂ = 6(2 m ∙ \(\frac{1}{4}\) m)
SA₂ = 6 ∙ \(\frac{1}{2}\) m²
SA₂ = 3 m²

The total surface area of the remaining solid is the sum of these two areas:
SA_T = SA₁ + SA₂.
SA_T = 4 \(\frac{1}{2}\) m² + 3 m²
SA_T = 7 \(\frac{1}{2}\) m²
The surface area of the remaining solid is 7 \(\frac{1}{2}\) m².

Eureka Math Grade 7 Module 3 Lesson 22 Exit Ticket Answer Key

Question 1.
The right hexagonal pyramid has a hexagon base with equal-length sides. The lateral faces of the pyramid are all triangles (that are exact copies of one another) with heights of 15 ft. Find the surface area of the pyramid.

Answer:
SA = LA + 1B
LA = 6 ∙ \(\frac{1}{2}\) (bh)
LA = 6 ∙ \(\frac{1}{2}\) (5 ft. ∙ 15 ft.)
LA = 3 ∙ 75 ft²
LA = 225 ft²

B = A_rectangle + 2A_triangle
B = (8 ft. ∙ 5 ft.) + 2 ∙ \(\frac{1}{2}\) (8 ft. ∙ 3 ft.)
B = 40 ft² + (8 ft. ∙ 3 ft.)
B = 40 ft² + 24 ft²

B = 64 ft²
SA = LA + 1B
SA = 225 ft² + 64 ft²
SA = 289 ft²
The surface area of the pyramid is 289 ft².

Question 2.
Six cubes are glued together to form the solid shown in the diagram. If the edges of each cube measure 1 \(\frac{1}{2}\) inches in length, what is the surface area of the solid?

Answer:
There are 26 square cube faces showing on the surface area of the solid (5 each from the top and bottom view, 4 each from the front and back view, 3 each from the left and right side views, and 2 from the “inside” of the front).
A = s²
A = (1 \(\frac{1}{2}\) in.)²
A = (1 \(\frac{1}{2}\) in.)(1 \(\frac{1}{2}\) in.)
A = 1 \(\frac{1}{2}\) in.(1 in. + \(\frac{1}{2}\) in.)
A = (1 \(\frac{1}{2}\) in. ∙ 1 in.) + (1 \(\frac{1}{2}\) in. ∙ \(\frac{1}{2}\) in.)
A = 1 \(\frac{1}{2}\) in² + \(\frac{3}{4}\) in²
A = 1 \(\frac{2}{4}\) in² + \(\frac{3}{4}\) in²
A = 1 \(\frac{5}{4}\) in² = 2 \(\frac{1}{4}\) in²

SA = 26 ∙ (2 \(\frac{1}{4}\) in²)
SA = 52 in² + \(\frac{26}{4}\) in²
SA = 52 in² + 6 in² + \(\frac{1}{2}\) in²
SA = 58 \(\frac{1}{2}\) in²
The surface area of the solid is 58 \(\frac{1}{2}\) in².

Engage NY Eureka Math 7th Grade Module 3 Lesson 21 Answer Key

Eureka Math Grade 7 Module 3 Lesson 21 Example Answer Key

Example 1: Lateral Area of a Right Prism
A right triangular prism, a right rectangular prism, and a right pentagonal prism are pictured below, and all have equal heights of h.

a. Write an expression that represents the lateral area of the right triangular prism as the sum of the areas of its lateral faces.
Answer:
a ∙ h + b ∙ h + c ∙ h

b. Write an expression that represents the lateral area of the right rectangular prism as the sum of the areas of its lateral faces.
Answer:
a ∙ h + b ∙ h + a ∙ h + b ∙ h

c. Write an expression that represents the lateral area of the right pentagonal prism as the sum of the areas of its lateral faces.
Answer:
a ∙ h + b ∙ h + c ∙ h + d ∙ h + e ∙ h

d. What value appears often in each expression and why?
Answer:
h; Each prism has a height of h; therefore, each lateral face has a height of h.

e. Rewrite each expression in factored form using the distributive property and the height of each lateral face.
Answer:
h(a + b + c)
h(a + b + a + b)
h(a + b + c + d + e)

f. What do the parentheses in each case represent with respect to the right prisms?
Answer:

The perimeter of the base of the corresponding prism.

g. How can we generalize the lateral area of a right prism into a formula that applies to all right prisms?
Answer:
If LA represents the lateral area of a right prism, P represents the perimeter of the right prism’s base, and h represents the distance between the right prism’s bases, then:
LA = P_base ∙ h.

Relevant Vocabulary
RIGHT PRISM: Let E and E’ be two parallel planes. Let B be a triangular or rectangular region or a region that is the union of such regions in the plane E. At each point P of B, consider the segment PP’ perpendicular to E, joining P to a point P’ of the plane E’. The union of all these segments is a solid called a right prism.

There is a region B’ in E’ that is an exact copy of the region B. The regions B and B’ are called the base faces (or just bases) of the prism. The rectangular regions between two corresponding sides of the bases are called lateral faces of the prism. In all, the boundary of a right rectangular prism has 6 faces: 2 base faces and 4 lateral faces. All adjacent faces intersect along segments called edges (base edges and lateral edges).

CUBE: A cube is a right rectangular prism all of whose edges are of equal length.
SURFACE: The surface of a prism is the union of all of its faces (the base faces and lateral faces).
NET: A net is a two-dimensional diagram of the surface of a prism.

1. Why are the lateral faces of right prisms always rectangular regions?
Answer:
Because along a base edge, the line segments PP’ are always perpendicular to the edge, forming a rectangular region.

2. What is the name of the right prism whose bases are rectangles?
Answer:
Right rectangular prism

3. How does this definition of right prism include the interior of the prism?
Answer:
The union of all the line segments fills out the interior.

Eureka Math Grade 7 Module 3 Lesson 21 Exercise Answer Key

Opening Exercise: Surface Area of a Right Rectangular Prism
On the provided grid, draw a net representing the surfaces of the right rectangular prism (assume each grid line represents 1 inch). Then, find the surface area of the prism by finding the area of the net.

Answer:
There are six rectangular faces that make up the net.
The four rectangles in the center form one long rectangle that is 20 in. by 3 in.
Area = lw
Area = 3 in ∙ 20 in
Area = 60 in²

Two rectangles form the wings, both 6 in by 4 in.
Area = lw
Area = 6 in ∙ 4 in
Area = 24 in²
The area of both wings is 2(24 in² ) = 48 in².

The total area of the net is
A = 60 in² + 48 in² = 108 in²

The net represents all the surfaces of the rectangular prism, so its area is equal to the surface area of the prism. The surface area of
the right rectangular prism is 108 in².

Exercise 1.
Marcus thinks that the surface area of the right triangular prism will be half that of the right rectangular prism and wants to use the modified formula SA = \(\frac{1}{2}\) (2lw + 2lh + 2wh). Do you agree or disagree with Marcus? Use nets of the prisms to support your argument.

Answer:
The surface area of the right rectangular prism is 108 in², so Marcus believes the surface areas of each right triangular prism is 54 in².

The net of the right triangular prism has one less face than the right rectangular prism. Two of the rectangular faces on the right triangular prism (rectangular regions 1 and 2 in the diagram) are the same faces from the right rectangular prism, so they are the same size. The areas of the triangular bases (triangular regions 3 and 4 in the diagram) are half the area of their corresponding rectangular faces of the right rectangular prism. These four faces of the right triangular prism make up half the surface area of the right rectangular prism before considering the fifth face; no, Marcus is incorrect.

The areas of rectangular faces 1 and 2, plus the areas of the triangular regions 3 and 4 is 54 in². The last rectangular region has an area of 30 in². The total area of the net is 54 in² + 30 in² or 84 in², which is far more than half the surface area of the right rectangular prism.

Eureka Math Grade 7 Module 3 Lesson 21 Problem Set Answer Key

Question 1.
For each of the following nets, highlight the perimeter of the lateral area, draw the solid represented by the net, indicate the type of solid, and then find the solid’s surface area.
a. Right rectangular prism

Answer:
SA = LA + 2B
LA = P ∙ h
LA = (2 \(\frac{1}{2}\) cm + 7 \(\frac{1}{2}\) cm + 2 \(\frac{1}{2}\) cm + 7 \(\frac{1}{2}\) cm) ∙ 5 cm
LA = 20 cm ∙ 5 cm
LA = 100 cm²

B = lw
B = 2 \(\frac{1}{2}\) cm ∙ 7 \(\frac{1}{2}\) cm
B = \(\frac{5}{2}\) cm ∙ \(\frac{15}{2}\) cm
B = \(\frac{75}{4}\) cm²

SA = 100 cm² + 2(\(\frac{75}{4}\) cm² )
SA = 100 cm² + 37.5 cm²
SA = 137.5 cm²
The surface area of the right rectangular prism is 137.5 cm²

b. Right triangular prism

Answer:
SA = LA + 2B
LA = P ∙ h
LA = (10 in. + 8 in. + 10 in.) ∙ 12 in.
LA = 28 in. ∙ 12 in.
LA = 336 in²

B = \(\frac{1}{2}\) bh
B = \(\frac{1}{2}\) (8 in.)(9 \(\frac{1}{5}\) in.)
B = 4 in.(9 \(\frac{1}{5}\) in.)
B = (36 + \(\frac{4}{5}\) )in²
B = 36 \(\frac{4}{5}\) in²

SA = 336 in² + 2(36 \(\frac{4}{5}\) in²)
SA = 336 in² + (72 + \(\frac{8}{5}\) )in²
SA = 408 in² + 1 \(\frac{3}{5}\) in²
SA = 409 \(\frac{3}{5}\) in²
The surface area of the right triangular prism is 409 3/5 in²2.

Question 2.
Given a cube with edges that are \(\frac{3}{4}\) inch long:
a. Find the surface area of the cube.
Answer:
SA = 6s²2
SA = 6(\(\frac{3}{4}\) in.)²
SA = 6 (\(\frac{3}{4}\) in.) ∙ (\(\frac{3}{4}\) in.)
SA = 6(\(\frac{9}{16}\) in²)
SA = \(\frac{27}{8}\) in² or 3 \(\frac{3}{8}\) in²

b. Joshua makes a scale drawing of the cube using a scale factor of 4. Find the surface area of the cube that Joshua drew.
Answer:
\(\frac{3}{4}\) in. ∙ 4 = 3 in.; The edge lengths of Joshua’s drawing would be 3 inches.
SA = 6(3 in.)²
SA = 6(9 in²)
SA = 54 in²

c. What is the ratio of the surface area of the scale drawing to the surface area of the actual cube, and how does the value of the ratio compare to the scale factor?
Answer:
54 ÷ 3 \(\frac{3}{8}\)
54 ÷ \(\frac{27}{8}\)
54 ∙ \(\frac{8}{27}\)
2 ∙ 8 = 16. The ratios of the surface area of the scale drawing to the surface area of the actual cube is 16:1. The value of the ratio is 16. The scale factor of the drawing is 4, and the value of the ratio of the surface area of the drawing to the surface area of the actual cube is 4² or 16.

Question 3.
Find the surface area of each of the following right prisms using the formula SA = LA + 2B.
a.

Answer:
SA = LA + 2B
LA = P ∙ h
LA = (12 \(\frac{1}{2}\) mm + 10 mm + 7 \(\frac{1}{2}\) mm) ∙ 15 mm
LA = 30 mm ∙ 15 mm
LA = 450 mm²

B = \(\frac{1}{2}\) bh
B = \(\frac{1}{2}\) ∙ (7 \(\frac{1}{2}\) mm) ∙ (10 mm)
B = \(\frac{1}{2}\) ∙ (70 + 5) mm²
B = \(\frac{1}{2}\) ∙ 75 mm²
B = 75/2 mm²

SA = 450 mm² + 2(\(\frac{75}{2}\) mm²)
SA = 450 mm² + 75 mm²
SA = 525 mm²

The surface area of the prism is 525 mm².

b.

SA = LA + 2B
LA = P ∙ h
LA = (9 \(\frac{3}{25}\) in. + 6 \(\frac{1}{2}\) in. + 4 in.) ∙ 5 in in. ∙ 2 \(\frac{1}{2}\) in.
LA = (\(\frac{228}{25}\) in. + \(\frac{13}{2}\) in. + 4 in.) ∙ 5 in
LA = (\(\frac{456}{50}\) in. + \(\frac{325}{50}\) in. + \(\frac{200}{50}\) in.) ∙ 5 in.
LA = (\(\frac{981}{50}\) in.) ∙ 5 in.
LA = \(\frac{49,050}{50}\) in²
LA = 98 \(\frac{1}{10}\) in²

B = \(\frac{1}{2}\) bh
B = \(\frac{1}{2}\) ∙ 9 \(\frac{3}{25}\)
B = \(\frac{1}{2}\) ∙ \(\frac{228}{25}\) in. ∙ \(\frac{5}{2}\) in.
B = \(\frac{1,140}{100}\) in²
B = 11 \(\frac{2}{5}\) in²
2B = 2 ∙ 11 \(\frac{2}{5}\) in²
2B = 22 \(\frac{4}{5}\) in²

SA = LA + 2B
SA = 98 \(\frac{1}{10}\) in² + 22 \(\frac{4}{5}\) in²
SA = 120 \(\frac{9}{10}\) in²
The surface area of the prism is 120 \(\frac{9}{10}\) in².

c.

SA = LA + 2B
LA = P ∙ h
LA = (\(\frac{1}{8}\) in. + \(\frac{1}{2}\) in. + \(\frac{1}{8}\) in. + \(\frac{1}{4}\) in. + \(\frac{1}{2}\) in. + \(\frac{1}{4}\) in.) ∙ 2 in.
LA = (1 \(\frac{3}{4}\) in.) ∙ 2 in.
LA = 2 in² + 1 \(\frac{1}{2}\) in²
LA = 3 \(\frac{1}{2}\) in²

B = A_rectangle + 2A_triangle
B = (\(\frac{1}{2}\) in. ∙ \(\frac{1}{5}\) in.) + 2 ∙ \(\frac{1}{2}\) (\(\frac{1}{8}\) in. ∙ \(\frac{1}{5}\) in.)
B = (\(\frac{1}{10}\) in² ) + (\(\frac{1}{40}\) in² )
B = \(\frac{1}{10}\) in² + \(\frac{1}{40}\)
B = \(\frac{4}{40}\) in² + \(\frac{1}{40}\) in²
B = \(\frac{5}{40}\) in²
B = \(\frac{1}{8}\) in²

SA = 3 \(\frac{1}{2}\) in² + 2(\(\frac{1}{8}\) in²) in²
SA = 3 \(\frac{1}{2}\) in² + \(\frac{1}{4}\) in²
SA = 3 \(\frac{2}{4}\) in² + \(\frac{1}{4}\) in²
SA = 3 \(\frac{3}{4}\) in²
The surface area of the prism is 3 \(\frac{3}{4}\) in².

d.

SA = LA + 2B
LA = P ∙ h
LA = (13 cm + 13 cm + 8.6 cm + 8.6 cm) ∙ 2 \(\frac{1}{4}\) cm
LA = (26 cm + 17.2 cm) ∙ 2 \(\frac{1}{4}\) cm
LA = (43.2)cm ∙ 2 \(\frac{1}{4}\) cm
LA = (86.4 cm² + 10.8 cm²)
LA = 97.2 cm²

SA = LA + 2B
SA = 97.2 cm² + 2(95 cm²)
SA = 97.2 cm² + 190 cm²
SA = 287.2 cm²

B = \(\frac{1}{2}\) (10 cm ∙ 7 cm ) + \(\frac{1}{2}\) (12 cm ∙ 10 cm)
B = \(\frac{1}{2}\) (190 cm²)
B = \(\frac{1}{2}\) (70 cm² + 120 cm²)
B = 95 cm²
The surface area of the prism is 287.2 cm².

Question 4.
A cube has a volume of 64 m³. What is the cube’s surface area?
Answer:
A cube’s length, width, and height must be equal. 64 = 4 ∙ 4 ∙ 4 = 4³, so the length, width, and height of the cube are all 4 m.
SA = 6s²
SA = 6(4 m)²
SA = 6(16 m²)
SA = 96 m²

Question 5.
The height of a right rectangular prism is 4 \(\frac{1}{2}\) ft. The length and width of the prism’s base are 2 ft. and 1 \(\frac{1}{2}\) ft. Use the formula SA = LA + 2B to find the surface area of the right rectangular prism.
Answer:
SA = LA + 2B
LA = P ∙ h
LA = (2 ft. + 2 ft. + 1 \(\frac{1}{2}\) ft. + 1 \(\frac{1}{2}\) ft.) ∙ 4 \(\frac{1}{2}\) ft.
LA = (2 ft + 2 ft. + 3 ft.) ∙ 4 \(\frac{1}{2}\) ft.
LA = 7 ft. ∙ 4 \(\frac{1}{2}\) ft.
LA = 28 ft² + 3 \(\frac{1}{2}\) ft²
LA = 31 \(\frac{1}{2}\) ft²

B = lw
B = 2 ft. ∙ 1 \(\frac{1}{2}\) ft.
B = 3 ft²

SA = LA + 2b
SA = 31 \(\frac{1}{2}\) ft² + 2(3 ft²)
SA = 31 \(\frac{1}{2}\) ft² + 6 ft²
SA = 37 \(\frac{1}{2}\) ft²
The surface area of the right rectangular prism is 37 \(\frac{1}{2}\) ft².

Question 6.
The surface area of a right rectangular prism is 68 \(\frac{2}{3}\) in². The dimensions of its base are 3 in and 7 in Use the formula SA = LA + 2B and LA = Ph to find the unknown height h of the prism.
Answer:
SA = LA + 2B
SA = P ∙ h + 2B
68 \(\frac{2}{3}\) in² = 20 in. ∙ (h) + 2(21 in²)
68 \(\frac{2}{3}\) in² = 20 in. ∙ (h) + 42 in²
68 \(\frac{2}{3}\) in² – 42 in² = 20 in. ∙ (h) + 42 in² – 42 in²
26 \(\frac{2}{3}\) in² = 20 in. ∙ (h) + 0 in²
26 \(\frac{2}{3}\) in² ∙ \(\frac{1}{20 \mathrm{in.}}\) = 20 in ∙ \(\frac{1}{20 \mathrm{in.}}\) ∙ (h)
\(\frac{80}{3}\) in² ∙ \(\frac{1}{20 \mathrm{in.}}\) = 1 ∙ h
\(\frac{4}{3}\) in. = h
h = \(\frac{4}{3}\) in. or 1 \(\frac{1}{3}\) in.
The height of the prism is 1 \(\frac{1}{3}\) in.

Question 7.
A given right triangular prism has an equilateral triangular base. The height of that equilateral triangle is approximately 7.1 cm. The distance between the bases is 9 cm. The surface area of the prism is 319 \(\frac{1}{2}\) cm². Find the approximate lengths of the sides of the base.
Answer:
SA = LA + 2B
LA = P ∙ h
LA = 3(x cm) ∙ 9 cm
LA = 27x cm²

Let x represent the number of centimeters in each side of the equilateral triangle.
B = \(\frac{1}{2}\) lw
B = \(\frac{1}{2}\) ∙ (x cm) ∙ 7.1 cm
B = 3.55x cm²

319 \(\frac{1}{2}\) cm² = LA + 2B
319 \(\frac{1}{2}\) cm² = 27x cm² + 2(3.55x cm²)
319 \(\frac{1}{2}\) cm² = 27x cm² + 7.1x cm²
319 \(\frac{1}{2}\) cm² = 34.1x cm²
319 \(\frac{1}{2}\) cm² = 34 \(\frac{1}{10}\) x cm²
\(\frac{639}{2}\) cm² = \(\frac{341}{10}\) x cm²
\(\frac{639}{2}\) cm² ∙ \(\frac{10}{341 \mathrm{~cm}}\) = \(\frac{341}{10}\) x cm² ∙ \(\frac{10}{341 \mathrm{~cm}}\)
\(\frac{3195}{341}\) cm = x
x = \(\frac{3195}{341}\) cm
x ≈ 9.4 cm
The lengths of the sides of the equilateral triangles are approximately 9.4 cm each.

Eureka Math Grade 7 Module 3 Lesson 21 Exit Ticket Answer Key

Question 1.
Find the surface area of the right trapezoidal prism. Show all necessary work.

Answer:
SA = LA + 2B
LA = P ∙ h
LA = (3 cm + 7 cm + 5 + 11 cm ) ∙ 6 cm
LA = 26 cm ∙ 6 cm
LA = 156 cm²
Each base consists of a 3 cm by 7 cm rectangle and right triangle with a base of 3 cm and a height of 4 cm. Therefore, the area of each base:
B = A_r + A_t
B = lw + \(\frac{1}{2}\) bh
B = (7 cm ∙ 3 cm) + (\(\frac{1}{2}\) ∙ 3 cm ∙ 4 cm)
B = 21 cm² + 6 cm²
B = 27 cm²

SA = LA + 2B
SA = 156 cm² + 2(27 cm² )
SA = 156 cm² + 54 cm²
SA = 210 cm²
The surface of the right trapezoidal prism is 210 cm².

Engage NY Eureka Math 7th Grade Module 3 Lesson 23 Answer Key

Eureka Math Grade 7 Module 3 Lesson 23 Exploratory Challenge Answer Key

Exploratory Challenge: The Volume of a Right Prism
What is the volume of the right prism pictured on the right? Explain.

Answer:

The volume of the right prism is 36 units³ because the prism is filled with 36 cubes that are 1 unit long, 1 unit wide, and 1 unit high, or 1 unit³.

Draw the same diagonal on the square base as done above; then, darken the grid lines on the lower right triangular prism. What is the volume of that right triangular prism? Explain.
Answer:
The volume of the right triangular prism is 18 units³. There are 15 cubes from the original right prism and 6 right triangular prisms that are each half of a cube. The 6 right triangular prisms can be paired together to form 3 cubes, or 3 units³. Altogether the area of the right triangular prism is (15+3) units³, or 18 units³.

How could we create a right triangular prism with five times the volume of the right triangular prism pictured to the right, without changing the base? Draw your solution on the diagram, give the volume of the solid, and explain why your solution has five times the volume of the triangular prism.

Answer:

If we stack five exact copies of the base (or bottom floor), the prism then has five times the number of unit cubes as the original, which means it has five times the volume, or 90 units³.

What could we do to cut the volume of the right triangular prism pictured on the right in half without changing the base? Draw your solution on the diagram, give the volume of the solid, and explain why your solution has half the volume of the given triangular prism.

Answer:

If we slice the height of the prism in half, each of the unit cubes that make up the triangular prism will have half the volume as in the original right triangular prism. The volume of the new right triangular prism is 9 units³.

To find the volume (V) of any right prism …
Answer:
Multiply the area of the right prism’s base (B) times the height of the right prism (h), V = Bh.

Eureka Math Grade 7 Module 3 Lesson 23 Example Answer Key

Example: The Volume of a Right Triangular Prism
Find the volume of the right triangular prism shown in the diagram using V = Bh.

Answer:
V = Bh
V = (\(\frac{1}{2}\) lw)h
V = (\(\frac{1}{2}\) ∙ 4 m ∙ \(\frac{1}{2}\) m) ∙ 6 \(\frac{1}{2}\) m
V = (2 m ∙ \(\frac{1}{2}\) m) ∙ 6 \(\frac{1}{2}\) m
V = 1 m² ∙ 6 \(\frac{1}{2}\) m
V = 6 \(\frac{1}{2}\) m³ The volume of the triangular prism is 6 \(\frac{1}{2}\) m³.

Eureka Math Grade 7 Module 3 Lesson 23 Exercise Answer Key

Opening Exercise
The volume of a solid is a quantity given by the number of unit cubes needed to fill the solid. Most solids—rocks, baseballs, people—cannot be filled with unit cubes or assembled from cubes. Yet such solids still have volume. Fortunately, we do not need to assemble solids from unit cubes in order to calculate their volume. One of the first interesting examples of a solid that cannot be assembled from cubes, but whose volume can still be calculated from a formula, is a right triangular prism.

What is the area of the square pictured on the right? Explain.

Answer:

The area of the square is 36 units² because the region is filled with 36 square regions that are 1 unit by 1 unit, or 1 unit².

Draw the diagonal joining the two given points; then, darken the grid lines within the lower triangular region. What is the area of that triangular region? Explain.
Answer:
The area of the triangular region is 18 units². There are 15 unit squares from the original square and 6 triangular regions that are \(\frac{1}{2}\) unit². The 6 triangles can be paired together to form 3 units². Altogether the area of the triangular region is (15+3) units², or 18 units².

Exercise: Multiple Volume Representations
The right pentagonal prism is composed of a right rectangular prism joined with a right triangular prism. Find the volume of the right pentagonal prism shown in the diagram using two different strategies.

Answer:
Strategy #1
The volume of the pentagonal prism is equal to the sum of the volumes of the rectangular and triangular prisms.
V = V_{rectangular prism} + V_{triangular prism}
V = Bh
V = (lw)h
V = (4 m ∙ 6 \(\frac{1}{2}\) m) ∙ 6 \(\frac{1}{2}\) m
V = (24 m²+2 m²) ∙ 6 \(\frac{1}{2}\) m
V = 26 m² ∙ 6 \(\frac{1}{2}\) m
V = 156 m³+13 m³
V = 169 m³

V = Bh
V = (\(\frac{1}{2}\) lw)h
V = (\(\frac{1}{2}\) ∙ 4 m ∙ \(\frac{1}{2}\) m) ∙ 6 \(\frac{1}{2}\) m
V = (2 m ∙ \(\frac{1}{2}\) m) ∙ 6 \(\frac{1}{2}\) m
V = (1 m² ) ∙ 6 \(\frac{1}{2}\) m
V = 6 \(\frac{1}{2}\) m³
So the total volume of the pentagonal prism is 169 m³+6 \(\frac{1}{2}\) m³, or 175 \(\frac{1}{2}\) m³ .

Strategy #2
The volume of a right prism is equal to the area of its base times its height. The base is a rectangle and a triangle.
V = Bh
B = A_rectangle + A_triangle
A_rectangle = 4 m ∙ 6 \(\frac{1}{2}\) m
A_rectangle = 24 m²+2 m²
A_rectangle = 26 m²

A_triangle = \(\frac{1}{2}\) ∙ 4 m ∙ \(\frac{1}{2}\) m
A_triangle = 2 m ∙ \(\frac{1}{2}\) m
A_triangle = 1 m²

V = Bh
V = 27 m² ∙ 6 \(\frac{1}{2}\) m
V = 162 m³+13 \(\frac{1}{2}\) m³
V = 175 \(\frac{1}{2}\) m³

B = 26 m²+1 m²
B = 27 m²
The volume of the right pentagonal prism is 175 \(\frac{1}{2}\) m³.

Eureka Math Grade 7 Module 3 Lesson 23 Problem Set Answer Key

Question 1.
Calculate the volume of each solid using the formula V = Bh (all angles are 90 degrees).
a.

Answer:
V = Bh
V = (8 cm ∙ 7 cm) ∙ 12 \(\frac{1}{2}\) cm
V = (56 ∙ 12 \(\frac{1}{2}\)) cm³
V = 672 cm³+28 cm³
V = 700 cm³
The volume of the solid is 700 cm³.

b.

Answer:
V = Bh
V = (\(\frac{3}{4}\) in. ∙ \(\frac{3}{4}\) in.) ∙ \(\frac{3}{4}\) in.
V = (9/16) ∙ \(\frac{3}{4}\) in³
V = \(\frac{27}{64}\) in³
The volume of the cube is \(\frac{27}{64}\) in³.

c.

Answer:
V = Bh
B = A_rectangle+A_square
B = lw+s²
B = (2 \(\frac{1}{2}\) in. ∙ 4 \(\frac{1}{2}\) in.)+(1 \(\frac{1}{2}\) in.)²
B = (10 in²+1 \(\frac{1}{4}\) in² )+(1 \(\frac{1}{2}\) in. ∙ 1 \(\frac{1}{2}\) in.)
B = 11 \(\frac{1}{4}\) in²+(1 \(\frac{1}{2}\) in²+\(\frac{3}{4}\) in² )
B = 11 \(\frac{1}{4}\) in²+\(\frac{3}{4}\) in²+1 \(\frac{1}{2}\) in²
B = 12 in²+1 \(\frac{1}{2}\) in²
B = 13 \(\frac{1}{2}\) in²

V = Bh
V = 13 \(\frac{1}{2}\) in² ∙ \(\frac{1}{2}\) in.
V = \(\frac{13}{2}\) in³+\(\frac{1}{4}\) in³
V = 6 in³+\(\frac{1}{2}\) in³+\(\frac{1}{4}\) in³
V = 6 \(\frac{3}{4}\) in³
The volume of the solid is 6 \(\frac{3}{4}\) in³.

d.

Answer:
V = Bh
B = (A_{(lg rectangle})-(A_{sm rectangle})
B = (lw)₁– (lw)₂
B = (6 yd. ∙ 4 yd.)-(1 \(\frac{1}{3}\) yd. ∙ 2 yd.)
B = 24 yd²-(2 yd²+\(\frac{2}{3}\) yd² )
B = 24 yd²-2 yd²–\(\frac{2}{3}\) yd²
B = 22 yd²–\(\frac{2}{3}\) yd²
B = 21 \(\frac{1}{3}\) yd²

V = Bh
V = (21 \(\frac{1}{3}\) yd²) ∙ \(\frac{2}{3}\) yd.
V = 14 yd³+(\(\frac{1}{3}\) yd² ∙ \(\frac{2}{3}\) yd.)
V = 14 yd³+\(\frac{2}{9}\) yd³
V = 14 \(\frac{2}{9}\) yd³
The volume of the solid is 14 \(\frac{2}{9}\) yd³.

e.

Answer:
V = Bh_prism
B = \(\frac{1}{2}\) bh_triangle
B = \(\frac{1}{2}\) ∙ 4 cm ∙ 4 cm
B = 2 ∙ 4 cm²
B = 8 cm²

V = Bh
V = 8 cm² ∙ 6 \(\frac{7}{10}\) cm
V = 48 cm³+\(\frac{56}{10}\) cm³
V = 48 cm³+5 cm³+6/10 cm³
V = 53 cm³+\(\frac{3}{5}\) cm³
V = 53 \(\frac{3}{5}\) cm³
The volume of the solid is 53 \(\frac{3}{5}\) cm³.

f.

Answer:
V = Bh_prism
B = \(\frac{1}{2}\) bh_triangle
B = \(\frac{1}{2}\) ∙ 9 \(\frac{3}{25}\) in. ∙ 2 \(\frac{1}{2}\) in.
B = \(\frac{1}{2}\) ∙ 2 \(\frac{1}{2}\) in. ∙ 9 3/25 in.
B = (1 \(\frac{1}{4}\) ) ∙ (9 \(\frac{3}{25}\) )in²
B = (\(\frac{5}{4}\) ∙ \(\frac{228}{25}\) )in²
B = \(\frac{57}{5}\) in²

V = Bh
V = (\(\frac{57}{5}\) in² ) ∙ 5 in
V = 57 in³
The volume of the solid is 57 in³.

g.

Answer:
V = Bh
B = A_rectangle + A_triangle
B = lw+\(\frac{1}{2}\) bh
B = (5 \(\frac{1}{4}\) cm ∙ 4 cm)+\(\frac{1}{2}\) (4 cm ∙ 1 \(\frac{1}{4}\) cm)
B = (20 cm²+1 cm² )+(2 cm ∙ 1 \(\frac{1}{4}\) cm)
B = 21 cm²+2 cm²+\(\frac{1}{2}\) cm²
B = 23 cm²+\(\frac{1}{2}\) cm²
B = 23 \(\frac{1}{2}\) cm²

V = Bh
V = 23 \(\frac{1}{2}\) cm² ∙ 9 cm
V = 207 cm³+\(\frac{9}{2}\) cm³
V = 207 cm³+4 cm³+\(\frac{1}{2}\) cm³
V = 211 \(\frac{1}{2}\) cm³
The volume of the solid is 211 \(\frac{1}{2}\) cm³.

h.

Answer:
V = Bh
V = \(\frac{1}{8}\) in² ∙ 2 in.
V = \(\frac{1}{4}\) in³

B = A_rectangle+2A_triangle
B = lw+2 ∙ \(\frac{1}{2}\) bh
B = (\(\frac{1}{2}\) in. ∙ \(\frac{1}{5}\) in.)+(1 ∙ \(\frac{1}{8}\) in. ∙ \(\frac{1}{5}\) in.)
B = \(\frac{1}{10}\) in²+\(\frac{1}{40}\) in²
B = \(\frac{4}{40}\) in²+\(\frac{1}{40}\) in²
The volume of the solid is \(\frac{1}{4}\) in³.
B = \(\frac{5}{40}\) in²
B = \(\frac{1}{8}\) in²

Question 2.
Let l represent the length, w the width, and h the height of a right rectangular prism. Find the volume of the prism when
a. l = 3 cm, w = 2 \(\frac{1}{2}\) cm, and h = 7 cm.
Answer:
V = lwh
V = 3 cm ∙ 2 \(\frac{1}{2}\) cm ∙ 7 cm
V = 21 ∙ (2 \(\frac{1}{2}\) ) cm³
V = 52 \(\frac{1}{2}\) cm³ The volume of the prism is 52 \(\frac{1}{2}\) cm³.

l = \(\frac{1}{4}\) cm, w = 4 cm, and h = 1 \(\frac{1}{2}\) cm.
V = lwh
V = \(\frac{1}{4}\) cm ∙ 4 cm ∙ 1 \(\frac{1}{2}\) cm
V = 1 \(\frac{1}{2}\) cm³ The volume of the prism is 1 \(\frac{1}{2}\) cm³.

Question 3.
Find the length of the edge indicated in each diagram.
a. V = Bh
Let h represent the number of inches in the height of the prism.

93 \(\frac{1}{2}\) in³ = 22 in² ∙ h
93 \(\frac{1}{2}\) in³ = 22h in²
22h = 93.5 in
h = 4.25 in
The height of the right rectangular prism is 4 \(\frac{1}{4}\) in.

What are possible dimensions of the base?
11 in by 2 in, or 22 in by 1 in

b. V = Bh
Let h represent the number of meters in the height of the triangular base of the prism.

V = (\(\frac{1}{2}\) bh_triangle) ∙ h_prism
4 \(\frac{1}{2}\) m³ = (\(\frac{1}{2}\) ∙ 3 m ∙ h) ∙ 6 m
4 \(\frac{1}{2}\) m³ = \(\frac{1}{2}\) ∙ 18 m² ∙ h
4 \(\frac{1}{2}\) m³ = 9h m²
9h = 4.5 m
h = 0.5 m
The height of the triangle is \(\frac{1}{2}\) m.

Question 4.
The volume of a cube is 3 \(\frac{3}{8}\) in³. Find the length of each edge of the cube.
Answer:
V = s³, and since the volume is a fraction, the edge length must also be fractional.
3 \(\frac{3}{8}\) in³ = \(\frac{27}{8}\) in³
3 \(\frac{3}{8}\) in³ = \(\frac{3}{2}\) in. ∙ \(\frac{3}{2}\) in. ∙ \(\frac{3}{2}\) in.
3 \(\frac{3}{8}\) in³ = (\(\frac{3}{2}\) in.)³
The lengths of the edges of the cube are \(\frac{3}{2}\) in., or 1 \(\frac{1}{2}\) in.

Question 5.
Given a right rectangular prism with a volume of 7 \(\frac{1}{2}\) ft³, a length of 5 ft., and a width of 2 ft., find the height of the prism.
Answer:
V = Bh
V = (lw)h Let h represent the number of feet in the height of the prism.
7 \(\frac{1}{2}\) ft³ = (5ft. ∙ 2ft.) ∙ h
7 \(\frac{1}{2}\) ft³ = 10 ft² ∙ h
7.5 ft³ = 10h ft²
h = 0.75 ft.
The height of the right rectangular prism is \(\frac{3}{4}\) ft. (or 9 in.).

Eureka Math Grade 7 Module 3 Lesson 23 Exit Ticket Answer Key

Question 1.
The base of the right prism is a hexagon composed of a rectangle and two triangles. Find the volume of the right hexagonal prism using the formula V = Bh.

Answer:
The area of the base is the sum of the areas of the rectangle and the two triangles.
B = A_rectangle+2 ∙ A_triangle
A_rectangle = lw
A_rectangle = 2 \(\frac{1}{4}\) in. ∙ 1 \(\frac{1}{2}\) in.
A_rectangle = (\(\frac{9}{4}\) ∙ \(\frac{3}{2}\)) in²
A_rectangle = \(\frac{27}{8}\) in²

A_triangle = \(\frac{1}{2}\) lw
A_triangle = \(\frac{1}{2}\) (1 \(\frac{1}{2}\) in. ∙ \(\frac{3}{4}\) in.)
A_triangle = (\(\frac{1}{2}\) ∙ \(\frac{3}{2}\) ∙ \(\frac{3}{4}\) )in²
A_triangle = \(\frac{9}{16}\) in²

B = \(\frac{27}{8}\) in²+2(\(\frac{9}{16}\) in² )
B = \(\frac{27}{8}\) in²+\(\frac{9}{8}\) in²
B = \(\frac{36}{8}\) in²
B = \(\frac{9}{2}\) in²

V = Bh
V = (\(\frac{9}{2}\) in² ) ∙ 3 in.
V = \(\frac{27}{2}\) in³
V = 13 \(\frac{1}{2}\) in³

The volume of the hexagonal prism is 13 \(\frac{1}{2}\) in³.

Engage NY Eureka Math 7th Grade Module 3 Lesson 24 Answer Key

Eureka Math Grade 7 Module 3 Lesson 24 Exploratory Challenge Answer Key

Exploratory Challenge: Measuring a Container’s Capacity
A box in the shape of a right rectangular prism has a length of 12 in, a width of 6 in., and a height of 8 in. The base and the walls of the container are \(\frac{1}{4}\) in thick, and its top is open. What is the capacity of the right rectangular prism?
(Hint: The capacity is equal to the volume of water needed to fill the prism to the top.)

If the prism is filled with water, the water will take the shape of a right rectangular prism slightly smaller than the container. The dimensions of the smaller prism are a length of 11 \(\frac{1}{2}\) in, a width of 5 \(\frac{1}{2}\) in, and a height of 7 \(\frac{3}{4}\) in.
V = Bh
V = (lw)h
V = (11 \(\frac{1}{2}\) in ∙ 5 \(\frac{1}{2}\) in) ∙ 7 \(\frac{3}{4}\) in
V = (\(\frac{23}{2}\) in ∙ \(\frac{11}{2}\) in) ∙ \(\frac{31}{4}\) in
V = (25\(\frac{3}{4}\) in²) ∙ \(\frac{31}{4}\) in
V = \(\frac{7843}{16}\) in³
V = 490 \(\frac{3}{16}\) in³
The capacity of the right rectangular prism is 490 \(\frac{3}{16}\) in³.

Eureka Math Grade 7 Module 3 Lesson 24 Example Answer Key

Example 1: Measuring Liquid in a Container in Three Dimensions
A glass container is in the form of a right rectangular prism. The container is 10 cm long, 8 cm wide, and 30 cm high. The top of the container is open, and the base and walls of the container are 3 mm (or 0.3 cm) thick. The water in the container is 6 cm from the top of the container. What is the volume of the water in the container?

Answer:
Because of the walls and base of the container, the water in the container forms a right rectangular prism that is 9.4 cm long, 7.4 cm wide, and 23.7 cm tall.
V = Bh
V = (lw)h
V = (9.4 cm ∙ 7.4 cm) ∙ 23.7 cm
V = (\(\frac{94}{10}\) cm ∙ \(\frac{74}{10}\) cm) ∙ \(\frac{237}{10}\) cm
V = (\(\frac{6,956}{100}\) cm² ) ∙ \(\frac{237}{10}\) cm
V = \(\frac{1,648,572}{1,000}\) cm³
V = 1,648.572 cm³
The volume of the water in the container is 1,648.6 cm³.

Example 2.
7.2 L of water are poured into a container in the shape of a right rectangular prism. The inside of the container is 50 cm long, 20 cm wide, and 25 cm tall. How far from the top of the container is the surface of the water? (1 L = 1,000 cm³)

Answer:
7.2 L = 7,200 cm³
V = Bh
V = (lw)h
7,200 cm³ = (50 cm)(20 cm)h
7,200 cm³ = 1,000 cm² ∙ h
7,200 cm³ ∙ \(\frac{1}{1,000 \mathrm{~cm}^{2}}\) = 1,000 cm² ∙ \(\frac{1}{1,000 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{7,200}{1,000}\) cm = 1 ∙ h
7.2 cm = h
The depth of the water is 7.2 cm. The height of the container is 25 cm.
25 cm – 7.2 cm = 17.8 cm
The surface of the water is 17.8 cm from the top of the container.

Example 3.
A fuel tank is the shape of a right rectangular prism and has 27 L of fuel in it. It is determined that the tank is \(\frac{3}{4}\) full. The inside dimensions of the base of the tank are 90 cm by 50 cm. What is the height of the fuel in the tank? How deep is the tank? (1 L = 1,000 cm³)
Answer:
Let the height of the fuel in the tank be h cm.
27 L = 27,000 cm³
V = Bh
V = (lw)h
27,000 cm³ = (90 cm ∙ 50 cm) ∙ h
27,000 cm³ = (4,500 cm² ) ∙ h
27,000 cm³ ∙ \(\frac{1}{4,500 \mathrm{~cm}^{2}}\) = 4,500 cm² ∙ \(\frac{1}{4,500 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{27,000}{4,500}\) cm = 1 ∙ h
6 cm = h
The height of the fuel in the tank is 6 cm. The height of the fuel is \(\frac{3}{4}\) the depth of the tank. Let d represent the depth of the tank in centimeters.
6 cm = \(\frac{3}{4}\) d
6 cm ∙ \(\frac{4}{3}\) = \(\frac{3}{4}\) ∙ \(\frac{4}{3}\) ∙ d
8 cm = d
The depth of the fuel tank is 8 cm.

Eureka Math Grade 7 Module 3 Lesson 24 Problem Set Answer Key

Question 1.
Mark wants to put some fish and decorative rocks in his new glass fish tank. He measured the outside dimensions of the right rectangular prism and recorded a length of 55 cm, width of 42 cm, and height of 38 cm. He calculates that the tank will hold 87.78 L of water. Why is Mark’s calculation of volume incorrect? What is the correct volume? Mark also failed to take into account the fish and decorative rocks he plans to add. How will this affect the volume of water in the tank? Explain.
Answer:
V = Bh = (lw)h
V = 55 cm ∙ 42 cm ∙ 38 cm
V = 2,310 cm² ∙ 38 cm
V = 87,780 cm³
87,780 cm³ = 87.78 L
Mark measured only the outside dimensions of the fish tank and did not account for the thickness of the sides of the tank. If he fills the tank with 87.78 L of water, the water will overflow the sides. Mark also plans to put fish and rocks in the tank, which will force water out of the tank if it is filled to capacity.

Question 2.
Leondra bought an aquarium that is a right rectangular prism. The inside dimensions of the aquarium are 90 cm long, by 48 cm wide, by 60 cm deep. She plans to put water in the aquarium before purchasing any pet fish. How many liters of water does she need to put in the aquarium so that the water level is 5 cm below the top?
Answer:
If the aquarium is 60 cm deep, then she wants the water to be 55 cm deep. Water takes on the shape of its container, so the water will form a right rectangular prism with a length of 90 cm, a width of 48 cm, and a height of 55 cm.
V = Bh = (lw)h
V = (90 cm ∙ 48 cm) ∙ 55 cm
V = 4,320 cm² ∙ 55 cm
V = 237,600 cm³
237,600 cm³ = 237.6 L
The volume of water needed is 237.6 L.

Question 3.
The inside space of two different water tanks are shown below. Which tank has a greater capacity? Justify your answer.

Answer:
V₁ = Bh = (lw)h
V₁ = (6 in. ∙ 1 \(\frac{1}{2}\) in.) ∙ 3 in.
V₁ = (6
V₁ = 9 in² ∙ 3 in.
V₁ = 27 in³

V₂ = Bh = (lw)h
V₂ = (1 \(\frac{1}{2}\) in. ∙ 2 in.) ∙ 9 in.
V₂ = (2 in² ÷ 1 in²) ∙ 9 in .
V₂ = 3 in² ∙ 9 in.
V₂ = 27 in³
The tanks have the same volume, 27 in³. Each prism has a face with an area of 18 in²(base) and a height that is 1 \(\frac{1}{2}\) in.

Question 4.
The inside of a tank is in the shape of a right rectangular prism. The base of that prism is 85 cm by 64 cm. What is the minimum height inside the tank if the volume of the liquid in the tank is 92 L ?
Answer:
V = Bh = (lw)h
92,000 cm³ = (85 cm ∙ 64 cm) ∙ h
92,000 cm³ = 5,440 cm² ∙ h
92,000 cm³ ∙ \(\frac{1}{5,440 \mathrm{~cm}^{2}}\) = 5,440 cm² ∙ \(\frac{1}{5,440 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{92,000}{5,440}\) cm = 1 ∙ h
16 \(\frac{31}{34}\) cm = h
The minimum height of the inside of the tank is 16 \(\frac{31}{34}\) cm.

Question 5.
An oil tank is the shape of a right rectangular prism. The inside of the tank is 36.5 cm long, 52 cm wide, and 29 cm high. If 45 liters of oil have been removed from the tank since it was full, what is the current depth of oil left in the tank?
Answer:
V = Bh = (lw)h
V = (36.5 cm ∙ 52 cm) ∙ 29 cm
V = 1,898 cm² ∙ 29 cm
V = 55,042 cm³
The tank has a capacity of 55,042 cm³, or 55.042 L.
55.042 L – 45 L = 10.042 L

If 45 L of oil have been removed from the tank, then 10.042 L are left in the tank.
V = Bh = (lw)h
10,042 cm³ = (36.5 cm ∙ 52 cm) ∙ h
10,042 cm³ = 1,898 cm² ∙ h
10,042 cm³ ∙ \(\frac{1}{1,898 \mathrm{~cm}^{2}}\) = 1,898 cm² ∙ \(\frac{1}{1,898 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{10,042}{1,898}\) cm = 1 ∙ h
5.29 cm ≈ h
The depth of oil left in the tank is approximately 5.29 cm.

Question 6.
The inside of a right rectangular prism – shaped tank has a base that is 14 cm by 24 cm and a height of 60 cm. The tank is filled to its capacity with water, and then 10.92 L of water is removed. How far did the water level drop?
Answer:
V = Bh = (lw)h
V = (14 cm ∙ 24 cm) ∙ 60 cm
V = 336 cm² ∙ 60 cm
V = 20,160 cm³
The capacity of the tank is 20,160 cm³ or 20.16 L.
20,160 cm³ – 10,920 cm³ = 9,240 cm³
When 10.92 L or 10,920 cm³ of water is removed from the tank, there remains 9,240 cm³ of water in the tank.

V = Bh = (lw)h
9,240 cm³ = (14 cm ∙ 24 cm) ∙ h
9,240 cm³ = 336 cm² ∙ h
9,240 cm³ ∙ \(\frac{1}{336 \mathrm{~cm}^{2}}\) = 336 cm² ∙ \(\frac{1}{336 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{9,240}{336}\) cm = 1 ∙ h
27 \(\frac{1}{2}\) cm = h
The depth of the water left in the tank is 27 \(\frac{1}{2}\) cm.
60 cm – 27 \(\frac{1}{2}\) cm = 32 \(\frac{1}{2}\) cm
This means that the water level has dropped 32 \(\frac{1}{2}\) cm.

Question 7.
A right rectangular prism – shaped container has inside dimensions of 7 \(\frac{1}{2}\) cm long and 4 \(\frac{3}{5}\) cm wide. The tank is \(\frac{3}{5}\) full of vegetable oil. It contains 0.414 L of oil. Find the height of the container.
Answer:
V = Bh = (lw)h
414 cm³ = (7 \(\frac{1}{2}\) cm ∙ 4 \(\frac{3}{5}\) cm) ∙ h
414 cm³ = 34 \(\frac{1}{2}\) cm² ∙ h
414 cm³ = \(\frac{69}{2}\) cm² ∙ h
414 cm³ ∙ \(\frac{2}{69 \mathrm{~cm}^{2}}\) = \(\frac{69}{2}\) cm² ∙ \(\frac{2}{69 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{828}{69}\) cm = 1 ∙ h
12 cm = h
The vegetable oil in the container is 12 cm deep, but this is only \(\frac{3}{5}\) of the container’s depth. Let d represent the depth of the container in centimeters.
12 cm = \(\frac{3}{5}\) ∙ d
12 cm ∙ \(\frac{5}{3}\) = \(\frac{3}{5}\) ∙ \(\frac{5}{3}\) ∙ d
\(\frac{60}{3}\) cm = 1 ∙ d
20 cm = d
The depth of the container is 20 cm.

Question 8.
A right rectangular prism with length of 10 in, width of 16 in, and height of 12 in is \(\frac{2}{3}\) filled with water. If the water is emptied into another right rectangular prism with a length of 12 in, a width of 12 in, and height of 9 in, will the second container hold all of the water? Explain why or why not. Determine how far (above or below) the water level would be from the top of the container.
Answer:
\(\frac{2}{3}\) ∙ 12 in = \(\frac{24}{3}\) in = 8 in The height of the water in the first prism is 8 in.
V = Bh = (lw)h
V = (10 in ∙ 16 in) ∙ 8 in
V = 160 in² ∙ 8 in
V = 1,280 in³
The volume of water is 1,280 in³.

V = Bh = (lw)h
V = (12 in ∙ 12 in) ∙ 9 in
V = 144 in² ∙ 9 in
V = 1,296 in³
The capacity of the second prism is 1,296 in³, which is greater than the volume of water, so the water will fit in the second prism.

V = Bh = (lw)h Let h represent the depth of the water in the second prism in inches.
1,280 in³ = (12 in ∙ 12 in) ∙ h
1,280 in³ = (144 in² ) ∙ h
1,280 in³ ∙ \(\frac{1}{144 \mathrm{in}^{2}}\) = 144 in² ∙ \(\frac{1}{144 \mathrm{in}^{2}}\) ∙ h
\(\frac{1,280}{144}\) in = 1 ∙ h
8 \(\frac{128}{144}\) in = h
8 \(\frac{8}{9}\) in = h
The depth of the water in the second prism is 8 \(\frac{8}{9}\) in.
9 in – 8 \(\frac{8}{9}\) in = \(\frac{1}{9}\) in
The water level will be \(\frac{1}{9}\) in from the top of the second prism.

Eureka Math Grade 7 Module 3 Lesson 24 Exit Ticket Answer Key

Lawrence poured 27.328 L of water into a right rectangular prism – shaped tank. The base of the tank is 40 cm by 28 cm. When he finished pouring the water, the tank was \(\frac{2}{3}\) full. (1 L = 1,000 cm³)
a. How deep is the water in the tank?
Answer:
27.328 L = 27,328 cm³
V = Bh
V = (lw)h
27,328 cm³ = (40 cm ∙ 28 cm) ∙ h
27,328 cm³ = 1,120 cm² ∙ h
27,328 cm³ ∙ \(\frac{1}{1,120 \mathrm{~cm}^{2}}\) = 1,120 cm² ∙ \(\frac{1}{1,120 \mathrm{~cm}^{2}}\) ∙ h
\(\frac{27,328}{1,120}\) cm = 1 ∙ h
24\(\frac{280}{1,120}\) cm = h
24 \(\frac{2}{5}\) cm = h
The depth of the water is 24 \(\frac{2}{5}\) cm.

b. How deep is the tank?
Answer:
The depth of the water is \(\frac{2}{3}\) the depth of the tank. Let d represent the depth of the tank in centimeters.
24 \(\frac{2}{5}\) cm = \(\frac{2}{3}\) ∙ d
24 \(\frac{2}{5}\) cm ∙ \(\frac{3}{2}\) = \(\frac{2}{3}\) ∙ \(\frac{3}{2}\) ∙ d
36 cm ÷ \(\frac{3}{5}\) cm = 1d
36 \(\frac{3}{5}\) cm = d
The depth of the tank is 36 \(\frac{3}{5}\) cm.

c. How many liters of water can the tank hold in total?
Answer:
V = Bh
V = (lw)h
V = (40 cm ∙ 28 cm) ∙ 36 \(\frac{3}{5}\) cm
V = 1,120 cm² ∙ 36 \(\frac{3}{5}\) cm
V = 40,320 cm³ ÷ 672 cm³
V = 40,992 cm³
40,992 cm³ = 40.992 L The tank can hold up to 41.0 L of water.

Engage NY Eureka Math 7th Grade Module 3 Lesson 25 Answer Key

Eureka Math Grade 7 Module 3 Lesson 25 Example Answer Key

Example 1: Volume of a Fish Tank
Jay has a small fish tank. It is the same shape and size as the right rectangular prism shown in the Opening Exercise.
a. The box it came in says that it is a 3-gallon tank. Is this claim true? Explain your reasoning. Recall that 1 gal = 231 in³.
Answer:
The volume of the tank is 715 in³. To convert cubic inches to gallons, divide by 231.
715 in³ ∙ \(\frac{1 \text { gallon }}{231 \mathrm{in}^{3}}\) = 3.09 gallons
The claim is true if you round to the nearest whole gallon.

b. The pet store recommends filling the tank to within 1.5 in of the top. How many gallons of water will the tank hold if it is filled to the recommended level?
Answer:
Use 8.5 in. instead of 10 in. to calculate the volume. V = 11 in ∙ 6.5 in ∙ 8.5 in = 607.75 in³.
607.75 in³ ∙ \(\frac{1 \text { gallon }}{231 \mathrm{in}^{3}}\) = 2.63 gallons

c. Jay wants to cover the back, left, and right sides of the tank with a background picture. How many square inches will be covered by the picture?
Answer:
Back side area = 10 in ∙ 11 in = 110 in²
Left and right side area = 2(6.5 in)(10 in) = 130 in²
The total area to be covered with the background picture is 240 in².

d. Water in the tank evaporates each day, causing the water level to drop. How many gallons of water have evaporated by the time the water in the tank is four inches deep? Assume the tank was filled to within
Answer:
1.5 in. of the top to start.
Volume when water is 4 in. deep:
11 in. ∙ 6.5 in. ∙ 4 in = 286in³
Difference in the two volumes:
607.75 in³-286 in³ = 321.75 in³
When the water is filled to within 1.5 in of the top, the volume is 607.75 in³. When the water is 4 in deep, the volume is 286 in³. The difference in the two volumes is 321.75 in³. Converting cubic inches to gallons by dividing by 231 gives a difference of 1.39 gal., which means 1.39 gal. of water have evaporated.

Eureka Math Grade 7 Module 3 Lesson 25 Exercise Answer Key

Opening Exercise
What is the surface area and volume of the right rectangular prism?

Answer:
Surface Area = 2(11 in)(6.5 in) + 2(10 in)(6.5 in) + 2(11 in)(10 in) = 493 in²
Volume = 11 in ∙ 6.5 in ∙ 10 in = 715 in³

Exercise 1: Fish Tank Designs
Two fish tanks are shown below, one in the shape of a right rectangular prism (R) and one in the shape of a right trapezoidal prism (T).

a. Which tank holds the most water? Let Vol(R) represent the volume of the right rectangular prism and Vol(T) represent the volume of the right trapezoidal prism. Use your answer to fill in the blanks with Vol(R) and Vol(T).
__________________ < __________________
Answer:
Volume of the right rectangular prism: (25 in × 10 in) × 15 in = 3,750 in³
Volume of the right trapezoidal prism: (31 in × 8 in) × 15 in = 3,720 in³
The right rectangular prism holds the most water.
Vol(T) < Vol(R)

b. Which tank has the most surface area? Let SA(R) represent the surface area of the right rectangular prism and SA(T) represent the surface area of the right trapezoidal prism. Use your answer to fill in the blanks with SA(R) and SA(T).
__________________ < __________________
Answer:
The surface area of the right rectangular prism:
2(25 in × 10 in) + 2(25 in × 15 in) + 2(10 in × 15 in) = 500 in² + 750 in² + 300 in² = 1,550 in²
The surface area of the right trapezoidal prism:
2(31 in × 8 in) + 2(10 in × 15 in) + (25 in × 15 in) + (31 in × 15 in) = 496 in² + 300 in² + 375 in² + 555 in² = 1726 in²
The right trapezoidal prism has the most surface area.
SA(R) < SA(T)

c. Water evaporates from each aquarium. After the water level has dropped \(\frac{1}{2}\) inch in each aquarium, how many cubic inches of water are required to fill up each aquarium? Show work to support your answers.
Answer:
The right rectangular prism will need 125 in³ of water. The right trapezoidal prism will need 124 in³ of water. First, decrease the height of each prism by a half inch and recalculate the volumes. Then, subtract each answer from the original volume of each prism.
NewVol(R) = (25 in)(10 in)(14.5 in) = 3,625 in³
NewVol(T) = (31 in)(8 in)(14.5 in) = 3,596 in³
3,750 in³-3,625 in³ = 125 in³
3,720 in³-3,596 in³ = 124 in³

Exercise 2: Design Your Own Fish Tank
Design at least three fish tanks that will hold approximately 10 gallons of water. All of the tanks should be shaped like right prisms. Make at least one tank have a base that is not a rectangle. For each tank, make a sketch, and calculate the volume in gallons to the nearest hundredth.
Answer:
Three possible designs are shown below.

10 gal. is 2,310 in³
Rectangular Base: Volume = 2,304 in³ or 9.97 gal.
Triangular Base: Volume = 2,240 in³ or 9.70 gal.
Hexagonal Base: Volume = 2,325 in³ or 10.06 gal.

Challenge: Each tank is to be constructed from glass that is \(\frac{1}{4}\) in. thick. Select one tank that you designed, and determine the difference between the volume of the total tank (including the glass) and the volume inside the tank. Do not include a glass top on your tank.
Answer:
Height = 12 in-\(\frac{1}{4}\) in = 11.75 in
Length = 24 in-\(\frac{1}{2}\) in = 23.5 in
Width = 8 in-\(\frac{1}{2}\) in = 7.5 in
Inside Volume = 2,070.9 in³
The difference between the two volumes is 233.1 in³, which is approximately 1 gal.

Eureka Math Grade 7 Module 3 Lesson 25 Problem Set Answer Key

Question 1.
The dimensions of several right rectangular fish tanks are listed below. Find the volume in cubic centimeters, the capacity in liters (1 L = 1000 cm³), and the surface area in square centimeters for each tank. What do you observe about the change in volume compared with the change in surface area between the small tank and the extra-large tank?

Answer:

While the volume of the extra-large tank is about five times the volume of the small tank, its surface area is less than three times that of the small tank.

Question 2.
A rectangular container 15 cm long by 25 cm wide contains 2.5 L of water.

a. Find the height of the water level in the container. (1 L = 1000 cm³)
2.5 L = 2,500 cm³
To find the height of the water level, divide the volume in cubic centimeters by the area of the base.
\(\frac{2,500 \mathrm{~cm}^{3}}{25 \mathrm{~cm} \cdot 15 \mathrm{~cm}}\) = 6 \(\frac{2}{3}\) cm

b. If the height of the container is 18 cm, how many more liters of water would it take to completely fill the container?
Answer:
Volume of tank: (25 cm × 15 cm) × 18 cm = 6,750 cm³
Capacity of tank: 6.75 L
Difference: 6.75 L- 2.5 L = 4.25 L

c. What percentage of the tank is filled when it contains 2.5 L of water?
Answer:
\(\frac{2.5 L}{6.75 L}\) = 0.37 = 37%

Question 3.
A rectangular container measuring 20 cm by 14.5 cm by 10.5 cm is filled with water to its brim. If 300 cm³ are drained out of the container, what will be the height of the water level? If necessary, round to the nearest tenth.

Answer:
Volume: (20 cm × 14.5 cm) × 10.5 cm = 3,045 cm³
Volume after draining: 2,745 cm³
Height (divide the volume by the area of the base):
\(\frac{2745 \mathrm{~cm}^{3}}{20 \mathrm{~cm} \times 14.5 \mathrm{~cm}}\) ≈ 9.5 cm

Question 4.
Two tanks are shown below. Both are filled to capacity, but the owner decides to drain them. Tank 1 is draining at a rate of 8 liters per minute. Tank 2 is draining at a rate of 10 liters per minute. Which tank empties first?

Answer:
Tank 1 Volume: 75 cm × 60 cm × 60 cm = 270,000 cm³
Tank 2 Volume: 90 cm × 40 cm × 85 cm = 306,000 cm³
Tank 1 Capacity: 270 L
Tank 2 Capacity: 306 L

To find the time to drain each tank, divide the capacity by the rate (liters per minute).
Time to drain tank 1: \(\frac{270 \mathrm{~L}}{8 \frac{\mathrm{L}}{\mathrm{min}}}\) = 33.75 min.
Time to drain tank 2: \(\frac{360 \mathrm{~L}}{10 \frac{\mathrm{L}}{\mathrm{min}}}\) = 30.6 min.
Tank 2 empties first.

Question 5.
Two tanks are shown below. One tank is draining at a rate of 8 liters per minute into the other one, which is empty. After 10 minutes, what will be the height of the water level in the second tank? If necessary, round to the nearest minute.

Answer:
Volume of the top tank: 45 cm × 50 cm × 55 cm = 123,750 cm³
Capacity of the top tank: 123.75 L
At 8 L/min for 10 minutes, 80 L will have drained into the bottom tank after 10 minutes.
That is 80,000 cm³. To find the height, divide the volume by the area of the base.
\(\frac{80,000 \mathrm{~cm}^{3}}{100 \mathrm{~cm} \cdot 35 \mathrm{~cm}}\) ≈ 22.9 cm
After 10 minutes, the height of the water in the bottom tank will be about 23 cm.

Question 6.
Two tanks with equal volumes are shown below. The tops are open. The owner wants to cover one tank with a glass top. The cost of glass is $0.05 per square inch. Which tank would be less expensive to cover? How much less?

Answer:
Dimensions: 12 in. long by 8 in. wide by 10 in. high
Surface area: 96 in²
Cost: \(\frac{\$ 0.05}{\mathrm{in}^{2}}\) ∙ 96 in² = $4.80

Dimensions: 15 in. long by 8 in. wide by 8 in. high
Surface area: 120 in²
Cost: \(\frac{\$ 0.05}{\mathrm{in}^{2}}\) ∙ 120 in² = $6.00

The first tank is less expensive. It is $1.20 cheaper.

Question 7.
Each prism below is a gift box sold at the craft store.

a. What is the volume of each prism?
Answer:
(a) Volume = 336 cm³
(b) Volume = 750 cm³
(c) Volume = 990 cm³
(d) Volume = 1130.5 cm³

b. Jenny wants to fill each box with jelly beans. If one ounce of jelly beans is approximately 30 cm^3, estimate how many ounces of jelly beans Jenny will need to fill all four boxes? Explain your estimates.
Answer:
Divide each volume in cubic centimeters by 30.
(a) 11.2 ounces
(b) 25 ounces
(c) 33 ounces
(d) 37.7 ounces
Jenny would need a total of 106.9 ounces.

Question 8.
Two rectangular tanks are filled at a rate of 0.5 cubic inches per minute. How long will it take each tank to be half-full?
a. Tank 1 Dimensions: 15 in. by 10 in. by 12.5 in.
Answer:
Volume: 1,875 in³
Half of the volume is 937.5 in³.
To find the number of minutes, divide the volume by the rate in cubic inches per minute.
Time: 1,875 minutes.

b. Tank 2 Dimensions: 2 \(\frac{1}{2}\) in. by 3 \(\frac{3}{4}\) in. by 4 \(\frac{3}{8}\) in.
Answer:
Volume: \(\frac{2625}{64}\) in³
Half of the volume is \(\frac{2625}{128}\) in³.
To find the number of minutes, divide the volume by the rate in cubic inches per minute.
Time: 41 minutes

Eureka Math Grade 7 Module 3 Lesson 25 Exit Ticket Answer Key

Melody is planning a raised bed for her vegetable garden.

a. How many square feet of wood does she need to create the bed?
Answer:
2(4 ft)(1.25 ft) + 2(2.5 ft)(1.25 ft) = 16.25 ft²
The dimensions in feet are 4 ft. by 1.25 ft. by 2.5 ft. The lateral area is 16.25 ft².

b. She needs to add soil. Each bag contains 1.5 cubic feet. How many bags will she need to fill the vegetable garden?
Answer:
V = 4 ft ∙ 1.25 ft ∙ 2.5 ft = 12.5 ft³
The volume is 12.5 ft³. Divide the total cubic feet by 1.5 ft³ to determine the number of bags.
12.5 ft³ ÷ 1.5 ft³ = 8 \(\frac{1}{3}\)
Melody will need to purchase 9 bags of soil to fill the garden bed.

Engage NY Eureka Math 7th Grade Module 3 Lesson 26 Answer Key

Eureka Math Grade 7 Module 3 Lesson 26 Example Answer Key

Example 1.

The insulated box shown is made from a large cube with a hollow inside that is a right rectangular prism with a square base. The figure on the right is what the box looks like from above.
a. Calculate the volume of the outer box.
Answer:
24 cm × 24 cm × 24 cm = 13,824 cm³

b. Calculate the volume of the inner prism.
Answer:
18 cm × 18 cm × 21 \(\frac{1}{4}\) cm = 6,885 cm³

c. Describe in words how you would find the volume of the insulation.
Answer:
Find the volume of the outer cube and the inner right rectangular prism, and then subtract the two volumes.

d. Calculate the volume of the insulation in cubic centimeters.
Answer:
13,824 cm³ – 6,885 cm³ = 6,939cm³

e. Calculate the amount of water the box can hold in liters.
Answer:
6939 cm³ = 6939 mL = \(\frac{(6939 \mathrm{~mL})}{1000 \frac{\mathrm{mL}}{\mathrm{L}}}\) = 6.939 L

Eureka Math Grade 7 Module 3 Lesson 26 Exercise Answer Key

Opening Exercise
Explain to your partner how you would calculate the area of the shaded region. Then, calculate the area.

Answer:
Find the area of the outer rectangle, and subtract the area of the inner rectangle.
6 cm × 3 cm – 5 cm × 2 cm = 8 cm²

Exercise 1: Brick Planter Design
You have been asked by your school to design a brick planter that will be used by classes to plant flowers. The planter will be built in the shape of a right rectangular prism with no bottom so water and roots can access the ground beneath. The exterior dimensions are to be 12 ft. × 9 ft. × 2 \(\frac{1}{2}\) ft. The bricks used to construct the planter are 6 in. long, 3 \(\frac{1}{2}\) in. wide, and 2 in. high.
a. What are the interior dimensions of the planter if the thickness of the planter’s walls is equal to the length of the bricks?
Answer:

6 in = \(\frac{1}{2}\) ft.
Interior length:
12 ft. – \(\frac{1}{2}\) ft. – \(\frac{1}{2}\) ft. = 11 ft.
Interior width:
9 ft. – \(\frac{1}{2}\) ft. – \(\frac{1}{2}\) ft. = 8 ft.
Interior dimensions:
11 ft. × 8 ft. × 2 \(\frac{1}{2}\) ft.

b. What is the volume of the bricks that form the planter?
Answer:
Solution 1
Subtract the volume of the smaller interior prism V_S from the volume of the large exterior prism V_L.
V_Brick = V_L – V_S
V_Brick = (12 ft. × 9 ft. × 2 \(\frac{1}{2}\) ft.) – (11 ft. × 8 ft. × 2 \(\frac{1}{2}\) ft.)
V_Brick = 270 ft³ – 220 ft³
V_Brick = 50 ft³

Solution 2
The volume of the brick is equal to the area of the base times the height.

B = \(\frac{1}{2}\) ft. × (8 \(\frac{1}{2}\) ft. + 11 \(\frac{1}{2}\) ft. + 8 \(\frac{1}{2}\) ft. + 11 \(\frac{1}{2}\) ft.)
B = \(\frac{1}{2}\) ft. × (40 ft.) = 20 ft²
V = Bh
V = (20 ft² )(2 \(\frac{1}{2}\) ft.) = 50 ft³

c. If you are going to fill the planter \(\frac{3}{4}\) full of soil, how much soil will you need to purchase, and what will be the height of the soil?
Answer:
The height of the soil will be \(\frac{3}{4}\) of 2 \(\frac{1}{2}\)feet.
\(\frac{3}{4}\) (\(\frac{5}{2}\) ft.) = \(\frac{15}{8}\) ft.; The height of the soil will be \(\frac{15}{8}\) ft. (or 1 \(\frac{7}{8}\) ft.).
The volume of the soil in the planter:
V = (11 ft × 8 ft. × \(\frac{15}{8}\) ft.)
V = (11 ft. × 15 ft² ) = 165 ft³

d. How many bricks are needed to construct the planter?
Answer:
P = 2(8 \(\frac{1}{2}\)ft.) + 2(11 \(\frac{1}{2}\)ft.)
P = 17 ft. + 23 ft. = 40 ft.

3 \(\frac{1}{2}\) in. = \(\frac{7}{24}\) ft.

We can then divide the perimeter by the width of each brick in order to determine the number of bricks needed for each layer of the planter.
40 ÷ \(\frac{7}{24}\) = \(\frac{960}{7}\)
40 × \(\frac{24}{7}\) = \(\frac{960}{7}\) ≈ 137.1

Each layer of the planter requires approximately 137.1 bricks.
2 in. = \(\frac{1}{6}\) ft.
The height of the planter, 2 \(\frac{1}{2}\) ft., is equal to the product of the number of layers of brick, n, and the height of each brick, \(\frac{1}{6}\) ft.
2\(\frac{1}{2}\) = l(\(\frac{1}{6}\))
6(2 \(\frac{1}{2}\)) = l
15 = l
There are 15 layers of bricks in the planter.

The total number of bricks, b, is equal to the product of the number of bricks in each layer (\(\frac{960}{7}\)) and the number of layers (15).
b = \(\frac{960}{7}\))(15)
b = \(\frac{14400}{7}\) ≈ 2057.1
It is not reasonable to purchase 0.1 brick; we must round up to the next whole brick, which is 2,058 bricks. Therefore, 2,058 bricks are needed to construct the planter.

e. Each brick used in this project costs $0.82 and weighs 4.5 lb. The supply company charges a delivery fee of $15 per whole ton (2000 lb) over 4000 lb How much will your school pay for the bricks (including delivery) to construct the planter?
Answer:
If the school purchases 2058 bricks, the total weight of the bricks for the planter,
2058(4.5 lb) = 9261 lb
The number of whole tons over 4,000 pounds,
9261 – 4000 = 5261
Since 1 ton = 2000 lb., there are 2 whole tons (4000 lb.) in 5,261 lb.
Total cost = cost of bricks + cost of delivery
Total cost = 0.82(2058) + 2(15)
Total cost = 1687.56 + 30 = 1717.56
The cost for bricks and delivery will be $1,717.56.

f. A cubic foot of topsoil weighs between 75 and 100 lb. How much will the soil in the planter weigh?
Answer:
The volume of the soil in the planter is 165 ft³.
Minimum weight:
Minimum weight = 75 lb(165)
Minimum weight = 12375 lb.

Maximum weight:
Maximum weight = 100 lb(165)
Maximum weight = 16500 lb.
The soil in the planter will weigh between 12,375 lb. and 16,500 lb.

g. If the topsoil costs $0.88 per cubic foot, calculate the total cost of materials that will be used to construct the planter.
Answer:
The total cost of the top soil:
Cost = 0.88(165) = 145.2; The cost of the top soil will be $145.20.
The total cost of materials for the brick planter project:
Cost = (cost of bricks) + (cost of soil)
Cost = $1,717.56 + $145.20
Cost = $1,862.76
The total cost of materials for the brick planter project will be $1,862.76.

Exercise 2: Design a Feeder
You did such a good job designing the planter that a local farmer has asked you to design a feeder for the animals on his farm. Your feeder must be able to contain at least 100,000 cubic centimeters, but not more than 200,000 cubic centimeters of grain when it is full. The feeder is to be built of stainless steel and must be in the shape of a right prism but not a right rectangular prism. Sketch your design below including dimensions. Calculate the volume of grain that it can hold and the amount of metal needed to construct the feeder.
The farmer needs a cost estimate. Calculate the cost of constructing the feeder if \(\frac{1}{2}\) cm thick stainless steel sells for $93.25 per square meter.
Answer:
Answers will vary. Below is an example using a right trapezoidal prism.
This feeder design consists of an open – top container in the shape of a right trapezoidal prism. The trapezoidal sides of the feeder will allow animals easier access to feed at its bottom. The dimensions of the feeder are shown in the diagram.

B = \(\frac{1}{2}\)(b₁ + b₂ )h
B = \(\frac{1}{2}\) (100 cm + 80 cm)∙30 cm
B = \(\frac{1}{2}\) (180 cm)∙30 cm
B = 90 cm∙30 cm
B = 2700 cm²

V = Bh
V = (2,700 cm² )(60 cm)
V = 162,000 cm³

The volume of the solid prism is 162,000 cm³, so the volume that the feeder can contain is slightly less, depending on the thickness of the metal used.

The exterior surface area of the feeder tells us the area of metal required to build the feeder.
SA = (LA – A_top) + 2B
SA = 60 cm∙(40 cm + 80 cm + 40 cm) + 2(2,700 cm² )
SA = 60 cm(160 cm) + 5,400 cm²
SA = 9,600 cm² + 5,400 cm²
SA = 15,000 cm²
The feeder will require 15,000 cm² of metal.
1 m² = 10,000 cm², so 15,000 cm² = 1.5 m²
Cost = 93.25(1.5) = 139.875
Since this is a measure of money, the cost must be rounded to the nearest cent, which is $139.88.

Eureka Math Grade 7 Module 3 Lesson 26 Problem Set Answer Key

Question 1.
A child’s toy is constructed by cutting a right triangular prism out of a right rectangular prism.

a. Calculate the volume of the rectangular prism.
Answer:
10 cm × 10 cm × 12 \(\frac{1}{2}\) cm = 1250 cm³

b. Calculate the volume of the triangular prism.
Answer:
\(\frac{1}{2}\) (5 cm × 2 \(\frac{1}{2}\) cm) × 12 \(\frac{1}{2}\) cm = 78 \(\frac{1}{8}\) cm³

c. Calculate the volume of the material remaining in the rectangular prism.
Answer:
1250 cm³ – 78 \(\frac{1}{8}\) cm³ = 1171 \(\frac{7}{8}\) cm³

d.
What is the largest number of triangular prisms that can be cut from the rectangular prism?
Answer:
\(\frac{1250 \mathrm{~cm}^{3}}{78 \frac{1}{8} \mathrm{~cm}^{3}}\) = 16

e. What is the surface area of the triangular prism (assume there is no top or bottom)?
Answer:
5.6 cm × 12 \(\frac{1}{2}\) cm + 2 \(\frac{1}{2}\) cm × 12 \(\frac{1}{2}\) cm + 5 cm × 12 \(\frac{1}{2}\) cm = 163 \(\frac{3}{4}\) cm²

Question 2.
A landscape designer is constructing a flower bed in the shape of a right trapezoidal prism. He needs to run three identical square prisms through the bed for drainage.

a. What is the volume of the bed without the drainage pipes?
Answer:
\(\frac{1}{2}\) (14 ft. + 12 ft.) × 3 ft. × 16 ft. = 624 ft³

b. What is the total volume of the three drainage pipes?
Answer:
3(\(\frac{1}{4}\) ft² × 16 ft.) = 12 ft³

c. What is the volume of soil if the planter is filled to 3/4 of its total capacity with the pipes in place?
Answer:
\(\frac{3}{4}\) (624 ft³ ) – 12 ft³ = 456 ft³

d. What is the height of the soil? If necessary, round to the nearest tenth.
Answer:
\(\frac{456 \mathrm{ft}^{3}}{\frac{1}{2}(14 \mathrm{ft} + 12 \mathrm{ft}) \times 16 \mathrm{ft}}\)≈ 2.2 ft.

e. If the bed is made of 8 ft. × 4 ft. pieces of plywood, how many pieces of plywood will the landscape designer need to construct the bed without the drainage pipes?
Answer:
2(3 \(\frac{1}{4}\) ft. × 16 ft.) + 12 ft. × 16 ft. + 2(\(\frac{1}{2}\) (12 ft. + 14 ft.) × 3 ft.) = 374 ft²
374 ft² ÷ \(\frac{(8 \mathrm{ft} \times 4 \mathrm{ft})}{\text { piece of plywood }}\) = 11.7, or 12 pieces of plywood

f. If the plywood needed to construct the bed costs $35 per 8 ft. × 4 ft. piece, the drainage pipes cost $125 each, and the soil costs $1.25/cubic foot, how much does it cost to construct and fill the bed?
Answer:
\(\frac{\$ 35}{\text { piece of plywood }}\)(12 pieces of plywood) + \(\frac{\$ 125}{\text { pipe }}\) (3 pipes) + \(\frac{\$ 1.25}{f t^{3} \text { soil }}\)(456 ft³ soil) = $1,365.00

Eureka Math Grade 7 Module 3 Lesson 26 Exit Ticket Answer Key

Lawrence is designing a cooling tank that is a square prism. A pipe in the shape of a smaller 2 ft × 2 ft square prism passes through the center of the tank as shown in the diagram, through which a coolant will flow.

a. What is the volume of the tank including the cooling pipe?
Answer:
7 ft. × 3 ft. × 3 ft. = 63 ft³

b. What is the volume of coolant that fits inside the cooling pipe?
Answer:
2 ft. × 2 ft. × 7 ft. = 28 ft³

c. What is the volume of the shell (the tank not including the cooling pipe)?
Answer:
63 ft³ – 28 ft³ = 35 ft³

d. Find the surface area of the cooling pipe.
Answer:
2 ft. × 7 ft. × 4 = 56 ft²

Engage NY Eureka Math 7th Grade Module 4 Lesson 17 Answer Key

Eureka Math Grade 7 Module 4 Lesson 17 Example Answer Key

Example 1.
A 5 – gallon container of trail mix is 20% nuts. Another trail mix is added to it, resulting in a 12 – gallon container of trail mix that is 40% nuts.
a. Write an equation to describe the relationships in this situation.
Answer:
Let j represent the percent of nuts in the second trail mix that is added to the first trail mix to create the resulting 12 – gallon container of trail mix.
0.4(12) = 0.2(5) + j(12 – 5)

b. Explain in words how each part of the equation relates to the situation.
Answer:
Quantity = Percent×Whole
(Resulting gallons of trail mix)(Resulting % of nuts) = (1^st trail mix in gallons)(% of nuts) + (2^nd trail mix in gallons)(% of nuts)

c. What percent of the second trail mix is nuts?
Answer:
4.8 = 1 + 7j
4.8 – 1 = 1 – 1 + 7j
3.8 = 7j
j ≈ 0.5429
About 54% of the second trail mix is nuts.

Example 2.
Soil that contains 30% clay is added to soil that contains 70% clay to create 10 gallons of soil containing 50% clay. How much of each of the soils was combined?
Answer:
Let x be the amount of soil with 30% clay.
(1^st soil amount)(% of clay) + (2^nd soil amount)(% of clay) = (resulting amount)(resulting % of clay)
(0.3)(x) + (0.7)(10 – x) = (0.5)(10)
0.3x + 7 – 0.7x = 5
– 0.4x + 7 – 7 = 5 – 7
– 0.4x = – 2
x = 5
5 gallons of the 30% clay soil and 10 – 5 = 5, so 5 gallons of the 70% clay soil must be mixed to make 10 gallons of 50% clay soil.

Eureka Math Grade 7 Module 4 Lesson 17 Exercise Answer Key

Opening Exercise
Imagine you have two equally – sized containers. One is pure water, and the other is 50% water and 50% juice. If you combined them, what percent of juice would be the result?

Answer:

25% of the resulting mixture is juice because \(\frac{0.5}{2}\) = \(\frac{1}{4}\).

If a 2 – gallon container of pure juice is added to 3 gallons of water, what percent of the mixture is pure juice?

Answer:
Let x represent the percent of pure juice in the resulting juice mixture.

If a 2 – gallon container of juice mixture that is 40% pure juice is added to 3 gallons of water, what percent of the mixture is pure juice?

Answer:

→ How many gallons of the juice mixture is pure juice?
(2 gallons)(0.40) = 0.8 gallons

→ What percent is pure juice out of the resulting mixture?
16%

→ Does this make sense relative to the prior problem?
Yes, because the mixture should have less juice than in the prior problem

If a 2 – gallon juice cocktail that is 40% pure juice is added to 3 gallons of pure juice, what percent of the resulting mixture is pure juice?

Answer:

What is the difference between this problem and the previous one?
Instead of adding water to the two gallons of juice mixture, pure juice is added, so the resulting liquid contains 3.8 gallons of pure juice.
What percent is pure juice out of the resulting mixture?
Let x represent the percent of pure juice in the resulting mixture.
x(5) = 40%(2) + 100%(3)
5x = 0.8 + 3
5x = 3.8
x = 0.76
The mixture is 76% pure juice.

Exercise 1.
Represent each situation using an equation, and show all steps in the solution process.
a. A 6 – pint mixture that is 25% oil is added to a 3 – pint mixture that is 40% oil. What percent of the resulting mixture is oil?
Answer:
Let x represent the percent of oil in the resulting mixture.
0.25(6) + 0.40(3) = x(9)
1.5 + 1.2 = 9x
2.7 = 9x
x = 0.3
The resulting 9 – pint mixture is 30% oil.

b. An 11 – ounce gold chain of 24% gold was made from a melted down 4 – ounce charm of 50% gold and a golden locket. What percent of the locket was pure gold?
Let x represent the percent of pure gold in the locket.
0.5(4) + (x)(7) = 0.24(11)
2 + 7x = 2.64
2 – 2 + 7x = 2.64 – 2
\(\frac{7x}{7}\) = \(\frac{0.64}{7}\)
x≈0.0914
The locket was about 9% gold.

c. In a science lab, two containers are filled with mixtures. The first container is filled with a mixture that is 30% acid. The second container is filled with a mixture that is 50% acid, and the second container is 50% larger than the first. The first and second containers are then emptied into a third container. What percent of acid is in the third container?
Answer:
Let m represent the total amount of mixture in the first container.
0.3m is the amount of acid in the first container.
0.5(m + 0.5m) is the amount of acid in the second container.
0.3m + 0.5(m + 0.5m) = 0.3m + 0.5(1.5m) = 1.05m is the amount of acid in the mixture in the third container.
m + 1.5m = 2.5m is the amount of mixture in the third container. So, \(\frac{1.05 m}{2.5 m}\) = 0.42 = 42% is the percent of acid in the third container.

Exercise 2.
The equation (0.2)(x) + (0.8)(6 – x) = (0.4)(6) is used to model a mixture problem.
a. How many units are in the total mixture?
Answer:
6 units

b. What percents relate to the two solutions that are combined to make the final mixture?
Answer:
20% and 80%

c. The two solutions combine to make 6 units of what percent solution?
Answer:
40%

d. When the amount of a resulting solution is given (for instance, 4 gallons) but the amounts of the mixing solutions are unknown, how are the amounts of the mixing solutions represented?
Answer:
If the amount of gallons of the first mixing solution is represented by the variable x, then the amount of gallons of the second mixing solution is 4 – x.

Eureka Math Grade 7 Module 4 Lesson 17 Problem Set Answer Key

Question 1.
A 5 – liter cleaning solution contains 30% bleach. A 3 – liter cleaning solution contains 50% bleach. What percent of bleach is obtained by putting the two mixtures together?
Answer:
Let x represent the percent of bleach in the resulting mixture.
0.3(5) + 0.5(3) = x(8)
1.5 + 1.5 = 8x
3 ÷ 8 = 8x ÷ 8
x = 0.375
The percent of bleach in the resulting cleaning solution is 37.5%.

Question 2.
A container is filled with 100 grams of bird feed that is 80% seed. How many grams of bird feed containing 5% seed must be added to get bird feed that is 40% seed?
Answer:
Let x represent the amount of bird feed, in grams, to be added.
0.8(100) + 0.05x = 0.4(100 + x)
80 + 0.05x = 40 + 0.4x
80 – 40 + 0.05x = 40 – 40 + 0.4x
40 + 0.05x = 0.4x
40 + 0.05x – 0.05x = 0.4x – 0.05x
40 ÷ 0.35 = 0.35x ÷ 0.35
x ≈ 114.3
About 114.3 grams of the bird seed containing 5% seed must be added.

Question 3.
A container is filled with 100 grams of bird feed that is 80% seed. Tom and Sally want to mix the 100 grams with bird feed that is 5% seed to get a mixture that is 40% seed. Tom wants to add 114 grams of the 5% seed, and Sally wants to add 115 grams of the 5% seed mix. What will be the percent of seed if Tom adds 114 grams? What will be the percent of seed if Sally adds 115 grams? How much do you think should be added to get 40% seed?
Answer:
If Tom adds 114 grams, then let x be the percent of seed in his new mixture. 214x = 0.8(100) + 0.05(114). Solving, we get the following:
x = \(\frac{80 + 5.7}{214}\) = \(\frac{85.7}{214}\) ≈ 0.4005 = 40.05%.
If Sally adds 115 grams, then let y be the percent of seed in her new mixture. 215y = 0.8(100) + 0.05(115). Solving, we get the following:
y = \(\frac{80 + 5.75}{215}\) = \(\frac{85.75}{215}\) ≈ 0.3988 = 39.88%.
The amount to be added should be between 114 and 115 grams. It should probably be closer to 114 because 40.05% is closer to 40% than 39.88%.

Question 4.
Jeanie likes mixing leftover salad dressings together to make new dressings. She combined 0.55 L of a 90% vinegar salad dressing with 0.45 L of another dressing to make 1 L of salad dressing that is 60% vinegar. What percent of the second salad dressing was vinegar?
Answer:
Let c represent the percent of vinegar in the second salad dressing.
0.55(0.9) + (0.45)(c) = 1(0.6)
0.495 + 0.45c = 0.6
0.495 – 0.495 + 0.45c = 0.6 – 0.495
0.45c = 0.105
0.45c ÷ 0.45 = 0.105 ÷ 0.45
c ≈ 0.233
The second salad dressing was around 23% vinegar.

Question 5.
Anna wants to make 30 mL of a 60% salt solution by mixing together a 72% salt solution and a 54% salt solution. How much of each solution must she use?
Answer:
Let s represent the amount, in milliliters, of the first salt solution.
0.72(s) + 0.54(30 – s) = 0.60(30)
0.72s + 16.2 – 0.54s = 18
0.18s + 16.2 = 18
0.18s + 16.2 – 16.2 = 18 – 16.2
0.18s = 1.8
s = 10
Anna needs 10 mL of the 72% solution and 20 mL of the 54% solution.

Question 6.
A mixed bag of candy is 25% chocolate bars and 75% other filler candy. Of the chocolate bars, 50% of them contain caramel. Of the other filler candy, 10% of them contain caramel. What percent of candy contains caramel?
Answer:
Let c represent the percent of candy containing caramel in the mixed bag of candy.
0.25(0.50) + (0.75)(0.10) = 1(c)
0.125 + 0.075 = c
0.2 = c
In the mixed bag of candy, 20% of the candy contains caramel.

Question 7.
A local fish market receives the daily catch of two local fishermen. The first fisherman’s catch was 84% fish while the rest was other non – fish items. The second fisherman’s catch was 76% fish while the rest was other non – fish items. If the fish market receives 75% of its catch from the first fisherman and 25% from the second, what was the percent of other non – fish items the local fish market bought from the fishermen altogether?
Answer:
Let n represent the percent of non – fish items of the total market items.
0.75(0.16) + 0.25(0.24) = n
0.12 + 0.06 = n
0.18 = n
The percent of non – fish items in the local fish market is 18%.

Eureka Math Grade 7 Module 4 Lesson 17 Exit Ticket Answer Key

A 25% vinegar solution is combined with triple the amount of a 45% vinegar solution and a 5% vinegar solution resulting in 20 milliliters of a 30% vinegar solution.
Question 1.
Determine an equation that models this situation, and explain what each part represents in the situation.
Answer:
Let s represent the number of milliliters of the first vinegar solution.
(0.25)(s) + (0.45)(3s) + (0.05)(20 – 4s) = (0.3)(20)
(0.25)(s) represents the amount of the 25% vinegar solution.
(0.45)(3s) represents the amount of the 45% vinegar solution, which is triple the amount of the 25% vinegar solution.
(0.05)(20 – 4s) represents the amount of the 5% vinegar solution, which is the amount of the remainder of the solution.
(0.3)(20) represents the result of the mixture, which is 20 mL of a 30% vinegar solution.

Question 2.
Solve the equation and find the amount of each of the solutions that were combined.
Answer:
0.25s + 1.35s + 1 – 0.2s = 6
1.6s – 0.2s + 1 = 6
1.4s + 1 – 1 = 6 – 1
1.4s ÷ 1.4 = 5 ÷ 1.4
s ≈ 3.57
3s ≈ 3(3.57) = 10.71
20 – 4s ≈ 20 – 4(3.57) = 5.72
Around 3.57 mL of the 25% vinegar solution, 10.71 mL of the 45% vinegar solution and 5.72 mL of the
5% vinegar solution were combined to make 20 mL of the 30% vinegar solution.

Engage NY Eureka Math 7th Grade Module 4 Lesson 15 Answer Key

Eureka Math Grade 7 Module 4 Lesson 15 Example Answer Key

Example 1.
What percent of the area of the large square is the area of the small square?

Answer:
Scale factor of the large square to the small square: \(\frac{1}{5}\)
Area of the large square to the small square: (\(\frac{1}{5}\))² = \(\frac{1}{25}\) = \(\frac{4}{100}\) = 0.04 = 4%
The area of the small square is only 4% of the area of the large square.

Example 2.
What percent of the area of the large disk lies outside the shaded disk?

Answer:
Radius of the shaded disk = 2
Radius of large disk = 4
Scale factor of the large disk to the shaded disk: \(\frac{2}{4}\) = \(\frac{1}{2}\)
Area of the large disk to the shaded disk:
(\(\frac{1}{2}\))² = \(\frac{1}{4}\) = 25%
Area outside shaded disk: \(\frac{3}{4}\) = 75%

Example 3.
If the area of the shaded region in the larger figure is approximately 21.5 square inches, write an equation that relates the areas using scale factor and explain what each quantity represents. Determine the area of the shaded region in the smaller scale drawing.

Answer:
Scale factor of corresponding sides:
\(\frac{6}{10}\) = \(\frac{3}{5}\) = 60%

Area of shaded region of smaller figure: Assume A is the area of the shaded region of the larger figure.
(\(\frac{3}{5}\))² A = \(\frac{9}{25}\) A
= \(\frac{9}{25}\)(21.5)
= 7.74
In this equation, the square of the scale factor, (\(\frac{3}{5}\))², multiplied by the area of the shaded region in the larger figure, 21.5 sq.in., is equal to the area of the shaded region of the smaller figure, 7.74 sq.in.
The area of shaded region of the smaller scale drawing is about 7.74 sq.in.

Example 4.
Use Figure 1 below and the enlarged scale drawing to justify why the area of the scale drawing is k² times the area of the original figure.

Answer:
Area of Figure 1: Area of scale drawing:
Area = lw Area = lw
Area = (kl)(kw)
Area = k² lw
Since the area of Figure 1 is lw, the area of the scale drawing is k² multiplied by the area of Figure 1.

Explain why the expressions (kl)(kw) and k² lw are equivalent. How do the expressions reveal different information about this situation?
Answer:
(kl)(kw) is equivalent to klkw by the associative property, which can be written kklw using the commutative property. This is sometimes known as “any order, any grouping.” kklw is equal to k² lw because k × k = k². (kl)(kw) shows the area as the product of each scaled dimension, while k² lw shows the area as the scale factor squared, times the original area (lw).

Eureka Math Grade 7 Module 4 Lesson 15 Exercise Answer Key

Opening Exercise
For each diagram, Drawing 2 is a scale drawing of Drawing 1. Complete the accompanying charts. For each drawing, identify the side lengths, determine the area, and compute the scale factor. Convert each scale factor into a fraction and percent, examine the results, and write a conclusion relating scale factors to area.

Answer:

Answer:

The length of each side in Drawing 1 is 12 units, and the length of each side in Drawing 2 is 6 units.


Answer:

Scale factor: \(\frac{1}{2}\)
Quotient of areas: \(\frac{1}{4}\)
Conclusion: (\(\frac{1}{2}\))(\(\frac{1}{2}\)) = (\(\frac{1}{2}\))² = \(\frac{1}{4}\)
The quotient of the areas is equal to the square of the scale factor.

Exercise 1.
The Lake Smith basketball team had a team picture taken of the players, the coaches, and the trophies from the season. The picture was 4 inches by 6 inches. The team decided to have the picture enlarged to a poster and then enlarged again to a banner measuring 48 inches by 72 inches.
a. Sketch drawings to illustrate the original picture and enlargements.
Answer:

b. If the scale factor from the picture to the poster is 500%, determine the dimensions of the poster.
Answer:
Quantity = Percent × Whole
Poster height = Percent × Picture height
Poster height = 500% × 4 in.
Poster height = (5.00)(4 in.)
Poster height = 20 in.

Quantity = Percent × Whole
Poster width = Percent × Picture width
Poster width = 500% × 6 in.
Poster width = (5.00)(6 in.)
Poster width = 30 in.

The dimensions of the poster are 20 in. by 30 in.

c. What scale factor is used to create the banner from the picture?
Answer:
Quantity = Percent × Whole
Banner width = Percent × Picture width
72 = Percent × 6
\(\frac{72}{6}\) = Percent
12 = 1,200%

Quantity = Percent × Whole
Banner height = Percent × Picture height
48 = Percent × 4
\(\frac{48}{4}\) = Percent
12 = 1,200%

The scale factor used to create the banner from the picture is 1,200%.

d. What percent of the area of the picture is the area of the poster? Justify your answer using the scale factor and by finding the actual areas.
Answer:
Area of picture:
A = lw
A = (4)(6)
A = 24
Area = 24 sq.in.

Area of poster:
A = lw
A = (20)(30)
A = 600
Area = 600 sq.in.

Quantity = Percent × Whole
Area of Poster = Percent × Area of Picture
600 = Percent × 24
\(\frac{600}{24}\) = Percent
25 = 2,500%

Using scale factor:
Scale factor from picture to poster was given earlier in the problem as 500% = \(\frac{500}{100}\) = 5.
The area of the poster is the square of the scale factor times the corresponding area of the picture. So, the area of the poster is ????,????????????% the area of the original picture.

e. Write an equation involving the scale factor that relates the area of the poster to the area of the picture.
Answer:
Quantity = Percent × Whole
Area of Poster = Percent × Area of Picture
A = 2,500% p
A = 25p

f. Assume you started with the banner and wanted to reduce it to the size of the poster. What would the scale factor as a percent be?
Answer:
Banner dimensions: 48 in. × 72 in.
Poster dimensions: 20 in. × 30 in.
Quantity = Percent × Whole
Poster = Percent × Banner
30 = Percent × 72
\(\frac{30}{72}\) = \(\frac{5}{12}\) = \(\frac{5}{12}\) × 100% = 41 \(\frac{2}{3}\)%

g. What scale factor would be used to reduce the poster to the size of the picture?
Answer:
Poster dimensions: 20 in. × 30 in.
Picture dimensions: 4 in. × 6 in.
Quantity = Percent × Whole
Picture width = Percent × Poster width
6 = Percent × 30
\(\frac{6}{30}\) = \(\frac{1}{5}\) = 0.2 = 20%

Eureka Math Grade 7 Module 4 Lesson 15 Problem Set Answer Key

Question 1.
What percent of the area of the larger circle is shaded?

a. Solve this problem using scale factors.
Answer:
Scale factors:
Shaded small circle: radius = 1 unit
Shaded medium circle: radius = 2 units
Large circle: radius = 3 units, area = A
Area of small circle: (\(\frac{1}{3}\))² A = \(\frac{1}{9}\) A
Area of medium circle: (\(\frac{2}{3}\))² A = \(\frac{4}{9}\) A
Area of shaded region: \(\frac{1}{9}\) A + 4/9 A = \(\frac{5}{9}\) A = \(\frac{5}{9}\) A × 100% = 55 \(\frac{5}{9}\)%A
The area of the shaded region is 55 \(\frac{5}{9}\)% of the area of the entire circle.

b. Verify your work in part (a) by finding the actual areas.
Areas:
Answer:
Small circle: A = πr²
A = π(1 unit)²
A = 1π unit²
Medium circle: A = πr²
A = π(2 units)²
A = 4π units²
Area of shaded circles: 1π unit² + 4π units² = 5π units²
Large circle: A = πr²
A = π(3 units)²
A = 9π units²
Percent of shaded to large circle: \(\frac{5 \pi \text { units }^{2}}{9 \pi \text { units }^{2}}\) = \(\frac{5}{9}\) = \(\frac{5}{9}\) × 100% = 55 \(\frac{5}{9}\)%

Question 2.
The area of the large disk is 50.24 units².

a. Find the area of the shaded region using scale factors. Use 3.14 as an estimate for π.
Answer:
Radius of small shaded circles = 1 unit
Radius of larger shaded circle = 2 units
Radius of large disk = 4 units
Scale factor of shaded region:
Small shaded circles: \(\frac{1}{4}\)
Large shaded circle: \(\frac{2}{4}\)
If A represents the area of the large disk, then the total shaded area:
(\(\frac{1}{4}\))² A + (\(\frac{1}{4}\))² A + (\(\frac{2}{4}\))² A
= \(\frac{1}{16}\) A + \(\frac{1}{16}\) A + \(\frac{4}{16}\) A
= \(\frac{6}{16}\) A
= \(\frac{6}{16}\)(50.24 units²)
The area of the shaded region is 18.84 units².

b. What percent of the large circular region is unshaded?
Answer:
Area of the shaded region is 18.84 square units. Area of total is 50.24 square units. Area of the unshaded region is 31.40 square units. Percent of large circular region that is unshaded is
\(\frac{31.4}{50.24}\) = \(\frac{5}{8}\) = 0.625 = 62.5%.

Question 3.
Ben cut the following rockets out of cardboard. The height from the base to the tip of the smaller rocket is 20 cm. The height from the base to the tip of the larger rocket is 120 cm. What percent of the area of the smaller rocket is the area of the larger rocket?

Answer:
Height of smaller rocket: 20 cm
Height of larger rocket: 120 cm
Scale factor:
Quantity = Percent × Whole
Actual height of larger rocket = Percent × height of smaller rocket
120 = Percent × 20
6 = Percent
600%
Area of larger rocket:
(scale factor)² (area of smaller rocket)
(6)² (area of smaller rocket)
36A
36 = 36 × 100% = 3,600%
The area of the larger rocket is 3,600% the area of the smaller rocket.

Question 4.
In the photo frame depicted below, three 5 inch by 5 inch squares are cut out for photographs. If these cut-out regions make up 3/16 of the area of the entire photo frame, what are the dimensions of the photo frame?

Answer:
Since the cut-out regions make up \(\frac{3}{16}\) of the entire photo frame, then each cut-out region makes up (\(\frac{\frac{3}{16}}{3}\) = \(\frac{1}{16}\) of the entire photo frame.
The relationship between the area of the scale drawing is
(square factor)² × area of original drawing.

The area of each cut-out is \(\frac{1}{16}\) of the area of the original photo frame. Therefore, the square of the scale factor is \(\frac{1}{16}\). Since (\(\frac{1}{4}\))² = \(\frac{1}{16}\), the scale factor that relates the cut-out to the entire photo frame is \(\frac{1}{4}\), or 25%.
To find the dimensions of the square photo frame:
Quantity = Percent × Whole
Small square side length = Percent × Photo frame side length
5 in. = 25% × Photo frame side length
5 in. = \(\frac{1}{4}\) × Photo frame side length
4(5) in. = 4(\(\frac{1}{4}\)) × Photo frame side length
20 in. = Photo frame side length
The dimensions of the square photo frame are 20 in. by 20 in.

Question 5.
Kelly was online shopping for envelopes for party invitations and saw these images on a website.

The website listed the dimensions of the small envelope as 6 in. by 8 in. and the medium envelope as 10 in. by 13 \(\frac{1}{3}\) in.
a. Compare the dimensions of the small and medium envelopes. If the medium envelope is a scale drawing of the small envelope, what is the scale factor?
Answer:
To find the scale factor,
Quantity = Percent × Whole
Medium height = Percent × small height
10 = Percent × 6
\(\frac{10}{6}\) = \(\frac{5}{3}\) = \(\frac{5}{3}\) × 100% = 166 \(\frac{2}{3}\)%

Quantity = Percent × Whole
Medium width = Percent × Small width
13 \(\frac{1}{3}\) = Percent × 8
\(\frac{13 \frac{1}{3}}{8}\) = \(\frac{5}{3}\) = \(\frac{5}{3}\) × 100% = 166 \(\frac{2}{3}\)%

b. If the large envelope was created based on the dimensions of the small envelope using a scale factor of 250%, find the dimensions of the large envelope.
ans;:
Scale factor is 250%, so multiply each dimension of the small envelope by 2.50.
Large envelope dimensions are as follows:
(6 in.)(2.5) = 15 in.
(8 in.)(2.5) = 20 in.

c. If the medium envelope was created based on the dimensions of the large envelope, what scale factor was used to create the medium envelope?
Answer:
Scale factor:
Quantity = Percent × Whole
Medium = Percent × Large
10 = Percent × 15
\(\frac{10}{15}\) = Percent
\(\frac{2}{3}\) = \(\frac{2}{3}\) × 100% = 66 \(\frac{2}{3}\)%

Quantity = Percent × Whole
Medium = Percent × Large
13 \(\frac{1}{3}\) = Percent × 20
\(\frac{13 \frac{1}{3}}{20}\) = Percent
\(\frac{2}{3}\) = \(\frac{2}{3}\) × 100% = 66 \(\frac{2}{3}\)%

d. What percent of the area of the larger envelope is the area of the medium envelope?
Answer:
Scale factor of larger to medium: 66 \(\frac{2}{3}\)% = \(\frac{2}{3}\)
Area: (\(\frac{2}{3}\))² = \(\frac{4}{9}\) = \(\frac{4}{9}\) × 100% = 44 \(\frac{4}{9}\)%
The area of the medium envelope is 44 \(\frac{4}{9}\)% of the larger envelope.

Eureka Math Grade 7 Module 4 Lesson 15 Exit Ticket Answer Key

Question 1.
Write an equation relating the area of the original (larger) drawing to its smaller scale drawing. Explain how you determined the equation. What percent of the area of the larger drawing is the smaller scale drawing?

Answer:
Scale factor:
Quantity = Percent × Whole
Scale Drawing Length = Percent × Original Length
6 = Percent × 15
\(\frac{6}{15}\) = \(\frac{2}{5}\) = \(\frac{4}{10}\) = 0.4
The area of the scale drawing is equal to the square of the scale factor times the area of the original drawing. Using A to represent the area of the original drawing, then the area of the scale is
(\(\frac{4}{10}\))² A = \(\frac{16}{100}\) A.
As a percent, \(\frac{16}{100}\) A = 0.16A .
Therefore, the area of the scale drawing is 16% of the area of the original drawing.

Engage NY Eureka Math 7th Grade Module 4 Lesson 14 Answer Key

Eureka Math Grade 7 Module 4 Lesson 14 Example Answer Key

Example 1.
The distance around the entire small boat is 28.4 units. The larger figure is a scale drawing of the smaller drawing of the boat. State the scale factor as a percent, and then use the scale factor to find the distance around the scale drawing.

Answer:
Scale factor:
Horizontal distance of the smaller boat: 8 units Vertical sail distance of smaller boat: 6 units
Horizontal distance of the larger boat: 22 units Vertical sail distance of larger boat: 16.5 units
Scale factor: Quantity = Percent × Whole
Smaller boat is the whole.
Total Distance:
Distance around smaller boat = 28.4 units
Distance around larger boat = 28.4(275%) = 28.4(2.75) = 78.1
The distance around the larger boat is 78.1 units.
Length in larger = Percent × Length in smaller
22 = P × 8
\(\frac{22}{8}\) = 2.75 = 275%

Length in larger = Percent × Length in smaller
16.5 = P × 6
\(\frac{16.5}{6}\) = 2.75 = 275%

Example 2: Time to Garden

Sherry designed her garden as shown in the diagram above. The distance between any two consecutive vertical grid lines is 1 foot, and the distance between any two consecutive horizontal grid lines is also 1 foot. Therefore, each grid square has an area of one square foot. After designing the garden, Sherry decided to actually build the garden 75% of the size represented in the diagram.
a. What are the outside dimensions shown in the blueprint?
Answer:
Blueprint dimensions: Length: 26 boxes = 26 ft.
Width: 12 boxes = 12 ft.

b. What will the overall dimensions be in the actual garden? Write an equation to find the dimensions. How does the problem relate to the scale factor?
Answer:
Actual garden dimensions (75% of blueprint): 19.5 ft. × 9 ft.
Length: (26 ft.)(0.75) = 19.5 ft.
Width: (12 ft.)(0.75) = 9 ft.
Since the scale factor was given as 75%, each dimension of the actual garden should be 75% of the original corresponding dimension. The actual length of the garden,19.5 ft., is 75% of 26 ft., and the actual width of the garden, 9 ft., is 75% of 12 ft.

c. If Sherry plans to use a wire fence to divide each section of the garden, how much fence does she need?
Answer:
Dimensions of the blueprint:

Total amount of wire needed for the blueprint:
26(4)+12(2)+4.5(4)+14 = 160
The amount of wire needed is 160 ft.
New dimensions of actual garden:
Length: 19.5 ft. (from part (b))
Width: 9 ft. (from part (b))
Inside borders: 4.5(0.75) = 3.375; 3.375 ft.
14(0.75) = 10.5; 10.5 ft.
The dimensions of the inside borders are 3.375 ft. by 10.5 ft.

Total wire with new dimensions:
19.5(4)+9(2)+3.375(4)+10.5 = 120
OR
160(0.75) = 120
Total wire with new dimensions is 120 ft.
Simpler way: 75% of 160 ft. is 120 ft.

d. If the fence costs $3.25 per foot plus 7% sales tax, how much would the fence cost in total?
Answer:
3.25(120) = 390
390(1.07) = 417.30
The total cost is $417.30.

Example 3.
Race Car #2 is a scale drawing of Race Car #1. The measurement from the front of Race Car #1 to the back of Race Car #1 is 12 feet, while the measurement from the front of Race Car #2 to the back of Race Car #2 is 39 feet. If the height of Race Car #1 is 4 feet, find the scale factor, and write an equation to find the height of Race Car #2. Explain what each part of the equation represents in the situation.

Answer:
Scale Factor: The larger race car is a scale drawing of the smaller. Therefore, the smaller race car is the whole in the relationship.
Quantity = Percent × Whole
Larger = Percent × Smaller
39 = Percent × 12
\(\frac{39}{12}\) = 3.25 = 325%
Height: 4(3.25) = 13
The height of Race Car #2 is 13 ft.
The equation shows that the smaller height, 4 ft., multiplied by the scale factor of 3.25, equals the larger height, 13 ft.

Eureka Math Grade 7 Module 4 Lesson 14 Exercise Answer Key

Exercise 1.
The length of the longer path is 32.4 units. The shorter path is a scale drawing of the longer path. Find the length of the shorter path, and explain how you arrived at your answer.

Answer:
First, determine the scale factor. Since the smaller path is a reduction of the original drawing, the scale factor should be less than 100%. Since the smaller path is a scale drawing of the larger, the larger path is the whole in the relationship.
Quantity = Percent × Whole
To determine the scale factor, compare the horizontal segments of the smaller path to the larger path.
Smaller = Percent × Larger
2 = Percent × 6
\(\frac{2}{6}\) = \(\frac{1}{3}\) = 33 \(\frac{1}{3}\)%
To determine the length of the smaller path, multiply the length of the larger path by the scale factor.
32.4(\(\frac{1}{3}\)) = 10.8
The length of the shorter path is 10.8 units.

Exercise 2.
Determine the scale factor, and write an equation that relates the height of side A in Drawing 1 and the height of side B in Drawing 2 to the scale factor. The height of side A is 1.1 cm. Explain how the equation illustrates the relationship.

Answer:
Equation: 1.1(scale factor) = height of side B in Drawing 2
First find the scale factor:
Quantity = Percent × Whole
Drawing 2 = Percent × Drawing 1
3.3 = Percent × 2
\(\frac{3.3}{2}\) = 1.65 = 165%
Equation: (1.1)(1.65) = 1.815
The height of side B in Drawing 2 is 1.815 cm.
Once we determine the scale factor, we can write an equation to find the unknown height of side B in Drawing 2 by multiplying the scale factor by the corresponding height in the original drawing.

Exercise 3.
The length of a rectangular picture is 8 inches, and the picture is to be reduced to be 45 \(\frac{1}{2}\)% of the original picture. Write an equation that relates the lengths of each picture. Explain how the equation illustrates the relationship.
Answer:
8(0.455) = 3.64
The length of the reduced picture is 3.64 in. The equation shows that the length of the reduced picture, 3.64, is equal to the original length, 8, multiplied by the scale factor, 0.455.

Eureka Math Grade 7 Module 4 Lesson 14 Problem Set Answer Key

Question 1.
The smaller train is a scale drawing of the larger train. If the length of the tire rod connecting the three tires of the larger train, as shown below, is 36 inches, write an equation to find the length of the tire rod of the smaller train. Interpret your solution in the context of the problem.

Answer:
Scale factor:
Smaller = Percent × Larger
6 = Percent × 16
\(\frac{6}{16}\) = 0.375 = 37.5%
Tire rod of smaller train: (36)(0.375) = 13.5
The length of the tire rod of the smaller train is 13.5 in.
Since the scale drawing is smaller than the original, the corresponding tire rod is the same percent smaller as the windows. Therefore, finding the scale factor using the windows of the trains allows us to then use the scale factor to find all other corresponding lengths.

Question 2.
The larger arrow is a scale drawing of the smaller arrow. If the distance around the smaller arrow is 25.66 units. What is the distance around the larger arrow? Use an equation to find the distance and interpret your solution in the context of the problem.

Answer:
Horizontal distance of smaller arrow: 8 units
Horizontal distance of larger arrow: 12 units
Scale factor:
Larger = Percent × Smaller
12 = Percent × 8
\(\frac{12}{8}\) = 1.5 = 150%
Distance around larger arrow:
(25.66)(1.5) = 38.49
The distance around the larger arrow is 38.49 units.
An equation where the distance of the smaller arrow is multiplied by the scale factor results in the distance around the larger arrow.

Question 3.
The smaller drawing below is a scale drawing of the larger. The distance around the larger drawing is 39.4 units. Using an equation, find the distance around the smaller drawing.

Answer:
Vertical distance of larger drawing: 10 units
Vertical distance of smaller drawing: 4 units
Scale factor:
Smaller = Percent × Larger
4 = Percent × 10
\(\frac{4}{10}\) = 0.4 = 40%
Total distance:
(39.4)(0.4) = 15.76
The total distance around the smaller drawing is 15.76 units.

Question 4.
The figure is a diagram of a model rocket and is a two-dimensional scale drawing of an actual rocket. The length of a model rocket is 2.5 feet, and the wing span is 1.25 feet. If the length of an actual rocket is 184 feet, use an equation to find the wing span of the actual rocket.

Answer:
Length of actual rocket: 184 ft.
Length of model rocket: 2.5 ft.
Scale Factor:
Actual = Percent × Model
184 = Percent × 2.5
\(\frac{184}{2.5}\) = 73.60 = 7,360%

Wing span:
Model rocket wing span: 1.25 ft.
Actual rocket wing span : (1.25)(73.60) = 92
The wing span of the actual rocket is 92 ft.

Eureka Math Grade 7 Module 4 Lesson 14 Exit Ticket Answer Key

Question 1.
Each of the designs shown below is to be displayed in a window using strands of white lights. The smaller design requires 225 feet of lights. How many feet of lights does the enlarged design require? Support your answer by showing all work and stating the scale factor used in your solution.

Answer:
Scale Factor:
Bottom horizontal distance of the smaller design: 8
Bottom horizontal distance of the larger design: 16
The smaller design represents the whole since we are going from the smaller to the larger.
Quantity = Percent × Whole
Larger = Percent × Smaller
16 = Percent × 8
\(\frac{16}{8}\) = 2 = 200%
Number of feet of lights needed for the larger design:
225 ft.(200%) = 225 ft.(2) = 450 ft.

Engage NY Eureka Math 7th Grade Module 4 Lesson 13 Answer Key

Eureka Math Grade 7 Module 4 Lesson 13 Example Answer Key

Example 1.
The scale factor from Drawing 1 to Drawing 2 is 60%. Find the scale factor from Drawing 2 to Drawing 1. Explain your reasoning.

Answer:
The scale drawing from Drawing 2 to Drawing 1 is an enlargement. Drawing 1 is represented by 100%, and Drawing 2, a reduction of Drawing 1, is represented by 60%. A length in Drawing 2 is the whole, so the scale factor from Drawing 2 to 1 is length in Drawing 1 = percent × length in Drawing 2.
100% = percent × 60%
\(\frac{100 \%}{60 \%}\) = \(\frac{1}{0.60}\) = \(\frac{1}{\frac{3}{5}}\) = \(\frac{5}{3}\) = 166 \(\frac{2}{3}\)%

Example 2.
A regular octagon is an eight-sided polygon with side lengths that are all equal. All three octagons are scale drawings of each other. Use the chart and the side lengths to compute each scale factor as a percent. How can we check our answers?



Answer:


To check our answers, we can start with 10 (the length of the original Drawing 1) and multiply by the scale factors we found to see whether we get the corresponding lengths in Drawings 2 and 3.
Drawing 1 to 2: 10(1.20) = 12
Drawing 2 to 3: 12(\(\frac{2}{3}\)) = 8

Example 3.
The scale factor from Drawing 1 to Drawing 2 is 112%, and the scale factor from Drawing 1 to Drawing 3 is 84%. Drawing 2 is also a scale drawing of Drawing 3. Is Drawing 2 a reduction or an enlargement of Drawing 3? Justify your answer using the scale factor. The drawing is not necessarily drawn to scale.

Answer:
First, I needed to find the scale factor of Drawing 3 to Drawing 2 by using the relationship
Quantity = Percent × Whole.
Drawing 3 is the whole. Therefore,
Drawing 2 = Percent × Drawing 3
112% = Percent × 84%
\(\frac{1.12}{0.84}\) = \(\frac{112}{84}\) = \(\frac{4}{3}\) = 133 \(\frac{1}{3}\)%
Since the scale factor is greater than 100%, Drawing 2 is an enlargement of Drawing 3.

Explain how you could use the scale factors from Drawing 1 to Drawing 2 (112%) and from Drawing 2 to Drawing 3 (75%) to show that the scale factor from Drawing 1 to Drawing 3 is 84%.
Answer:
The scale factor from Drawing 1 to Drawing 2 is 112%, and the scale factor from Drawing 2 to Drawing 3 is 75%; therefore, I must find 75% of 112% to get from Drawing 2 to Drawing 3. (0.75)(1.12) = 0.84. Comparing this answer to the original problem, the resulting scale factor is indeed what was given as the scale factor from Drawing 1 to
Drawing 3.

Eureka Math Grade 7 Module 4 Lesson 13 Exercise Answer Key

Opening Exercise
Scale factor: \(\frac{\text { length in SCALE drawing }}{\text { Corresponding length in ORIGINAL drawing }}\)
Describe, using percentages, the difference between a reduction and an enlargement.
Answer:
A scale drawing is a reduction of the original drawing when the lengths of the scale drawing are smaller than the lengths in the original drawing. The scale factor is less than 100%.
A scale drawing is an enlargement of the original drawing when the lengths of the scale drawing are greater than the lengths in the original drawing. The scale factor is greater than 100%.

Use the two drawings below to complete the chart. Calculate the first row (Drawing 1 to Drawing 2) only.


Answer:

Compare Drawing 2 to Drawing 1. Using the completed work in the first row, make a conjecture (statement) about what the second row of the chart will be. Justify your conjecture without computing the second row.
Answer:
Drawing 1 will be a reduction of Drawing 2. I know this because the corresponding lengths in Drawing 1 are smaller than the corresponding lengths in Drawing 2. Therefore, the scale factor from Drawing 2 to Drawing 1 would be less than 100%.

Compute the second row of the chart. Was your conjecture proven true? Explain how you know.
Answer:
The conjecture was true because the calculated scale factor from Drawing 2 to Drawing 1 was 62.5%. Since the scale factor is less than 100%, the scale drawing is indeed a reduction.

Eureka Math Grade 7 Module 4 Lesson 13 Problem Set Answer Key

Question 1.
The scale factor from Drawing 1 to Drawing 2 is 41 \(\frac{2}{3}\)%. Justify why Drawing 1 is a scale drawing of Drawing 2 and why it is an enlargement of Drawing 2. Include the scale factor in your justification.

Answer:
Quantity = Percent × Whole
Length in Drawing 1 = Percent × Length in Drawing 2
100% = Percent × 41 \(\frac{2}{3}\)%
\(\frac{100 \%}{41 \frac{2}{3} \%}\) = \(\frac{100 \cdot 3}{41 \frac{2}{3} \cdot 3}\) = \(\frac{300}{125}\) = \(\frac{12}{5}\) = 2.40 = 240%
Drawing 1 is a scale drawing of Drawing 2 because the lengths of Drawing 1 would be larger than the corresponding lengths of Drawing 2.
Since the scale factor is greater than 100%, the scale drawing is an enlargement of the original drawing.

Question 2.
The scale factor from Drawing 1 to Drawing 2 is 40%, and the scale factor from Drawing 2 to Drawing 3 is 37.5%. What is the scale factor from Drawing 1 to Drawing 3? Explain your reasoning, and check your answer using an example.

Answer:
To find the scale factor from Drawing 1 to 3, I needed to find 37.5% of 40%, so (0.375)(0.40) = 0.15. The scale factor from Drawing 1 to Drawing 3 would be 15%.
Check: Assume the length of Drawing 1 is 10. Then, using the scale factor for Drawing 2, the corresponding length of Drawing 2 would be 4. Then, applying the scale factor to Drawing 3, Drawing 3 would be 4(0.375) = 1.5. To go directly from Drawing 1 to Drawing 3, which was found to have a scale factor of 15%, then 10(0.15) = 1.5.

Question 3.
Traci took a photograph and printed it to be a size of 4 units by 4 units as indicated in the diagram. She wanted to enlarge the original photograph to a size of 5 units by 5 units and 10 units by 10 units.
a. Sketch the different sizes of photographs.

Answer:

b. What was the scale factor from the original photo to the photo that is 5 units by 5 units?
Answer:
The scale factor from the original to the 5 by 5 enlargement is \(\frac{5}{4}\) = 1.25 = 125%.

c. What was the scale factor from the original photo to the photo that is 10 units by 10 units?
Answer:
The scale factor from the original to the 10 by 10 photo is \(\frac{10}{4}\) = 2.5 = 250%.

d. What was the scale factor from the 5 × 5 photo to the 10 × 10 photo?
The scale factor from the 5 × 5 photo to the 10 × 10 photo is \(\frac{10}{5}\) = 2 = 200%.

e. Write an equation to verify how the scale factor from the original photo to the enlarged 10 × 10 photo can be calculated using the scale factors from the original to the 5 × 5 and then from the 5 × 5 to the 10 × 10.
Answer:
Scale factor original to 5 × 5: (125%)
Scale factor 5 × 5 to 10 × 10: (200%)
4(1.25) = 5
5(2.00) = 10
Original to 10 × 10, scale factor = 250%
4(2.50) = 10
The true equation 4(1.25)(2.00) = 4(2.50) verifies that a single scale factor of 250% is equivalent to a scale factor of 125% followed by a scale factor of 200%.

Question 4.
The scale factor from Drawing 1 to Drawing 2 is 30%, and the scale factor from Drawing 1 to Drawing 3 is 175%. What are the scale factors of each given relationship? Then, answer the question that follows. Drawings are not to scale.

a. Drawing 2 to Drawing 3
Answer:
The scale factor from Drawing 2 to Drawing 3 is
\(\frac{175 \%}{30 \%}\) = \(\frac{1.75}{0.30}\) = \(\frac{175}{30}\) = \(\frac{35}{6}\) = 5 \(\frac{5}{6}\) = 583 \(\frac{1}{3}\)%.

b. Drawing 3 to Drawing 1
Answer:
The scale factor from Drawing 3 to Drawing 1 is
\(\frac{1}{1.75}\) = \(\frac{100}{175}\) = \(\frac{4}{7}\) ≈ 57.14%.

c. Drawing 3 to Drawing 2
Answer:
The scale factor from Drawing 3 to Drawing 2 is
\(\frac{0.3}{1.75}\) = \(\frac{30}{175}\) = \(\frac{6}{35}\) ≈ 17.14%.

d. How can you check your answers?
Answer:
To check my answers, I can work backwards and multiply the scale factor from Drawing 1 to Drawing 3 of 175% to the scale factor from Drawing 3 to Drawing 2, and I should get the scale factor from Drawing 1 to Drawing 2.
(1.75)(0.1714) ≈ 0.29995 ≈ 0.30 = 30%

Eureka Math Grade 7 Module 4 Lesson 13 Exit Ticket Answer Key

Question 1.
Compute the scale factor, as a percent, for each given relationship. When necessary, round your answer to the nearest tenth of a percent.

a. Drawing 1 to Drawing 2
Answer:
Drawing 2 = Percent × Drawing 1
3.36 = Percent × 1.60
\(\frac{3.36}{1.60}\) = 2.10 = 210%

b. Drawing 2 to Drawing 1
Answer:
Drawing 1 = Percent × Drawing 2
1.60 = Percent × 3.36
\(\frac{1.60}{3.36}\) = \(\frac{1}{2.10}\) ≈ 0.476190476 ≈ 47.6%

c. Write two different equations that illustrate how each scale factor relates to the lengths in the diagram.
Answer:
Drawing 1 to Drawing 2:
1.60(2.10) = 3.36
Drawing 2 to Drawing 1:
3.36(0.476) = 1.60

Question 2.
Drawings 2 and 3 are scale drawings of Drawing 1. The scale factor from Drawing 1 to Drawing 2 is 75%, and the scale factor from Drawing 2 to Drawing 3 is 50%. Find the scale factor from Drawing 1 to Drawing 3.

Answer:
Drawing 1 to 2 is 75%. Drawing 2 to 3 is 50%. Therefore, Drawing 3 is 50% of 75%, so
(0.50)(0.75) = 0.375. To determine the scale factor from Drawing 1 to Drawing 3, we went from 100% to 37.5%. Therefore, the scale factor is 37.5%. Using the relationship:
Drawing 3 = Percent × Drawing 1
37.5% = Percent × 100%
0.375 = Percent
= 37.5%

Engage NY Eureka Math 7th Grade Module 4 Lesson 12 Answer Key

Eureka Math Grade 7 Module 4 Lesson 12 Example Answer Key

Example 1.
Create a snowman on the accompanying grid. Use the octagon given as the middle of the snowman with the following conditions:

a. Calculate the width, neck, and height, in units, for the figure to the right.
Answer:
Width: 20
Neck: 12
Height: 12

b. To create the head of the snowman, make a scale drawing of the middle of the snowman with a scale factor of 75%. Calculate the new lengths, in units, for the width, neck, and height.
Answer:
Width: 75%(20) = (0.75)(20) = 15
Neck: 75%(12) = (0.75)(12) = 9
Height : 75%(12) = (0.75)(12) = 9

c. To create the bottom of the snowman, make a scale drawing of the middle of the snowman with a scale factor of 125%. Calculate the new lengths, in units, for the width, waist, and height.
Answer:
Width: 125%(20) = (1.25)(20) = 25
Waist: 125%(12) = (1.25)(12) = 15
Height: 125%(12) = (1.25)(12) = 15

d. Is the head a reduction or an enlargement of the middle?
Answer:
The head is a reduction of the middle since the lengths of the sides are smaller than the lengths in the original drawing and the scale factor is less than 100% (75%).

e. Is the bottom a reduction or an enlargement of the middle?
Answer:
The bottom is an enlargement of the middle since the lengths of the scale drawing are larger than the lengths in the original drawing, and the scale factor is greater than 100% (125%).

f. What is the significance of the scale factor as it relates to 100%? What happens when such scale factors are applied?
Answer:
A scale factor of 100% would create a drawing that is the same size as the original drawing; therefore, it would be neither an enlargement nor reduction. A scale factor of less than 100% results in a scale drawing that is a reduction of the original drawing. A scale factor of greater than 100% results in a scale drawing that is an enlargement of the original drawing.

g. Use the dimensions you calculated in parts (b) and (c) to draw the complete snowman.
Answer:

Example 2.
Create a scale drawing of the arrow below using a scale factor of 150%.

Answer:

Example 3: Scale Drawings Where the Horizontal and Vertical Scale Factors Are Different
Sometimes it is helpful to make a scale drawing where the horizontal and vertical scale factors are different, such as when creating diagrams in the field of engineering. Having differing scale factors may distort some drawings.

For example, when you are working with a very large horizontal scale, you sometimes must exaggerate the vertical scale in order to make it readable. This can be accomplished by creating a drawing with two scales. Unlike the scale drawings with just one scale factor, these types of scale drawings may look distorted. Next to the drawing below is a scale drawing with a horizontal scale factor of 50% and vertical scale factor of 25% (given in two steps). Explain how each drawing is created.

Answer:
Each horizontal distance in the scale drawing is 50%
(or half) of the corresponding length in the original drawing. Each vertical distance in the scale drawing is 25% (or one-fourth) of the corresponding length in the original drawing.
Horizontal distance of house: 8(0.50) = 8(\(\frac{1}{2}\)) = 4
Vertical distance of house: 8(0.25) = 8(\(\frac{1}{4}\)) = 2
Vertical distance of top of house:
4(0.25) = 4(\(\frac{1}{4}\)) = 1

Eureka Math Grade 7 Module 4 Lesson 12 Exercise Answer Key

Opening Exercise:

Compare the corresponding lengths of Figure A to the original octagon in the middle. This is an example of a particular type of scale drawing called a _________. Explain why it is called that.
Answer:
reduction
A scale drawing is a reduction of the original drawing when the side lengths of the scale drawing are smaller than the corresponding side lengths of the original figure or drawing.

Compare the corresponding lengths of Figure B to the original octagon in the middle. This is an example of a particular type of scale drawing called an __________. Explain why it is called that.
Answer:
enlargement
A scale drawing is an enlargement of the original drawing when the side lengths of the scale drawing are larger than the corresponding side lengths of the original figure or drawing.

The scale factor is the quotient of any length in the scale drawing and its corresponding length in the original drawing.
Use what you recall from Module 1 to determine the scale factors between the original figure and Figure A and the original figure and Figure B.
Answer:
Scale factor between original and Figure A: \(\frac{1.5}{3}\) = \(\frac{1}{2}\) or \(\frac{2}{4}\) = \(\frac{1}{2}\)
Scale factor between original and Figure B: \(\frac{4.5}{3}\) = \(\frac{3}{2}\) or \(\frac{6}{4}\) = \(\frac{3}{2}\)

Use the diagram to complete the chart below to determine the horizontal and vertical scale factors. Write answers as a percent and as a concluding statement using the previously learned reduction and enlargement vocabulary.

Answer:

Exercise 1.
Create a scale drawing of the following drawing using a horizontal scale factor of 183 \(\frac{1}{3}\)% and a vertical scale factor of 25%.

Answer:

Horizontal scale factor: \(\frac{183 \frac{1}{3} \cdot 3}{100 \cdot 3}\) = \(\frac{550}{300}\) = \(\frac{11}{6}\)
Horizontal distance: 6(\(\frac{11}{6}\)) = 11
Vertical scale factor: \(\frac{25}{100}\) = \(\frac{1}{4}\)
Vertical distance: 4(\(\frac{1}{4}\)) = 1
New sketch:

Exercise 2.
Chris is building a rectangular pen for his dog. The dimensions are 12 units long and 5 units wide.

Chris is building a second pen that is 60% the length of the original and 125% the width of the original. Write equations to determine the length and width of the second pen.
Answer:
Length: 12 × 0.60 = 7.2
The length of the second pen is 7.2 units.
Width: 5 × 1.25 = 6.25
The width of the second pen is 6.25 units.

Eureka Math Grade 7 Module 4 Lesson 12 Problem Set Answer Key

Question 1.
Use the diagram below to create a scale drawing using a scale factor of 133 \(\frac{1}{3}\)%. Write numerical equations to find the horizontal and vertical distances in the scale drawing.

Answer:
Scale factor: 133 \(\frac{133 \frac{1}{3} \cdot 3}{100 \cdot 3}\) = \(\frac{400}{300}\) = \(\frac{4}{3}\)
Horizontal distance: 9(\(\frac{4}{3}\)) = 12
Vertical distance forks: 3(\(\frac{4}{3}\)) = 4
Vertical distance handle: 6(\(\frac{4}{3}\)) = 8
Scale drawing:

Question 2.
Create a scale drawing of the original drawing given below using a horizontal scale factor of 80% and a vertical scale factor of 175%. Write numerical equations to find the horizontal and vertical distances.

Answer:
Horizontal scale factor: 80% = \(\frac{80}{100}\) = \(\frac{4}{5}\)
Horizontal segment lengths: 10(0.80) = 8 or 10(\(\frac{4}{5}\)) = 8
Horizontal distance: 15(\(\frac{4}{5}\)) = 12
Vertical scale factor: 175% = \(\frac{175}{100}\) = \(\frac{7}{4}\)
Vertical distance: 8(\(\frac{7}{4}\)) = 14
Scale drawing:

Question 3.
The accompanying diagram shows that the length of a pencil from its eraser to its tip is 7 units and that the eraser is 1.5 units wide. The picture was placed on a photocopy machine and reduced to 66 2/3%. Find the new size of the pencil, and sketch a drawing. Write numerical equations to find the new dimensions.

Answer:
Scale factor: 66 \(\frac{2}{3}\)% = \(\frac{66 \frac{2}{3} \cdot 3}{100 \cdot 3}\) = \(\frac{200}{300}\) = \(\frac{2}{3}\)
Pencil length: 7(\(\frac{2}{3}\)) = 4 \(\frac{2}{3}\)
Eraser: (1 \(\frac{1}{2}\))(\(\frac{2}{3}\)) = (\(\frac{3}{2}\))(\(\frac{2}{3}\)) = 1

Question 4.
Use the diagram to answer each question.
a. What are the corresponding horizontal and vertical distances in a scale drawing if the scale factor is 25%? Use numerical equations to find your answers.

Answer:
Horizontal distance on original drawing: 14
Vertical distance on original drawing: 10
Scale drawing:
Scale factor: 25%
\(\frac{25}{100}\) = \(\frac{1}{4}\)
Horizontal distance: 14(\(\frac{1}{4}\)) = 3.5
Vertical distance: 10(\(\frac{1}{4}\)) = 2.5

b. What are the corresponding horizontal and vertical distances in a scale drawing if the scale factor is 160%? Use a numerical equation to find your answers.
Answer:
Horizontal distance on original drawing: 14
Vertical distance on original drawing: 10
Scale drawing:
Scale factor: 160%
\(\frac{160}{100}\) = \(\frac{8}{5}\)
Horizontal distance: 14(\(\frac{8}{5}\)) = 22.4
Vertical distance: 10(\(\frac{8}{5}\)) = 16

Question 5.
Create a scale drawing of the original drawing below using a horizontal scale factor of 200% and a vertical scale factor of 250%.

Answer:

Question 6.
Using the diagram below, on grid paper sketch the same drawing using a horizontal scale factor of 50% and a vertical scale factor of 150%.

Answer:

Eureka Math Grade 7 Module 4 Lesson 12 Exit Ticket Answer Key

Question 1.
Create a scale drawing of the picture below using a scale factor of 60%. Write three equations that show how you determined the lengths of three different parts of the resulting picture.

Answer:
Scale factor: 60% = \(\frac{60}{100}\) = \(\frac{3}{5}\)
Horizontal distances: 10(\(\frac{3}{5}\)) = 6
5(\(\frac{3}{5}\)) = 3
Vertical distances: 5(\(\frac{3}{5}\)) = 3
7 \(\frac{1}{2}\) (\(\frac{3}{5}\)) = \(\frac{15}{2}\) (\(\frac{3}{5}\)) = \(\frac{9}{2}\) = 4.5
Scale drawing:

Equations:
Left vertical distance: 5 × 0.60 = 3
Right vertical distance: 7.5 × 0.60 = 4.5
Top horizontal distance: 5 × 0.60 = 3
Bottom horizontal distance: 10 × 0.60 = 6

Question 2.
Sue wants to make two picture frames with lengths and widths that are proportional to the ones given below.
Note: The illustration shown below is not drawn to scale.

a. Sketch a scale drawing using a horizontal scale factor of 50% and a vertical scale factor of 75%. Determine the dimensions of the new picture frame.
Answer:

Horizontal measurement: 8(0.50) = 4
Vertical measurement: 12(0.75) = 9
4 in. by 9 in.

b. Sketch a scale drawing using a horizontal scale factor of 125% and a vertical scale factor of 140%. Determine the dimensions of the new picture frame.
Answer:

Horizontal measurement: 8(1.25) = 10
Vertical measurement: 12(1.40) = 16.8
10 in. by 16.8 in.