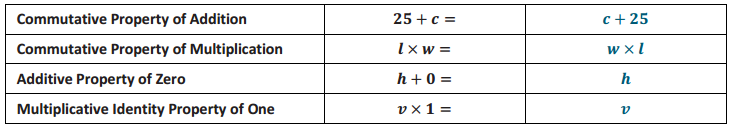Prasanna

Engage NY Eureka Math 6th Grade Module 4 Lesson 12 Answer Key

Eureka Math Grade 6 Module 4 Lesson 12 Example Answer Key

Example 1.
Write an expression that is equivalent to 2(a + b).
Answer:
→ In this example, we have been given the factored form of the expression.
→ To answer this question, we can create a model to represent 2(a + b).
→ Let’s start by creating a model to represent (a + b).

Create a model to represent (a + b).
Answer:

The expression 2(a + b) tells us that we have 2 of the (a + b)’s. Create a model that shows 2 groups of (a + b).
Answer:

How many a’s and how many b’s do you see in the diagram?
Answer:
There are 2 a’s and 2 b’s.

How would the model look if we grouped together the a’s and then grouped together the b’s?
Answer:

What expression could we write to represent the new diagram?
Answer:
2a + 2b

What conclusion can we draw from the models about equivalent expressions?
Answer:
2(a + b) = 2a + 2b

Let a = 3 and b = 4.
Answer:
2(a+b)                      2a + 2b
2(3 + 4)                    2(3) + 2(4)
2(7)                           6 + 8
14                              14

What happens when we double (a + b)?
Answer:
We double a, and we double b.

Example 2.
Write an expression that Is equivalent to double (3x + 4y).

How can we rewrite double (3x + 4y)?
Answer:
Double is the same as multiplying by two.
2(3x + 4y) or 6x + 8y

Is this expression In factored form, expanded form, or neither?
Answer:
The first expression is in factored form, and the second expression is in expanded form.

Let’s start this problem the same way that we started the first example. What should we do?
Answer:
We can make a model of 3x + 4y.

Are there terms that we can combine in this example?
Answer:

Yes. There are 6 x’s and 8y’s.
So, the model is showing 6x + 8y.

What is an equivalent expression that we can use to represent 2(3x + 4y)?
Answer:
2(3x + 4y) = 6x + 8y
This is the same as 2(3x) + 2(4y).

Summarize how you would solve this question without the model.
Answer:
When there is a number outside the parentheses, I would multiply it by all the terms on the inside of the parentheses.

Example 3.
Write an expression in expanded form that is equivalent to the model below.

What factored expression is represented in the model?
Answer:
y(4x + 5)

How can we rewrite this expression in expanded form?
Answer:
y(4x) + y(5)
4xy + 5y

Example 4.
Write an expression in expanded form that is equivalent to 3(7d + 4e).
Answer:
We will multiply 3 × 7d and 3 × 4e.
We would get 21d + 12e. So, 3(7d+ 4e) = 21d + 12e.

Eureka Math Grade 6 Module 4 Lesson 12 Exercise Answer Key

Exercises
Create a model for each expression below. Then, write another equivalent expression using the distributive property.

Exercise 1.
3(x + y)
Answer:

3x + 3y

Exercise 2.
4(2h + g)
Answer:

8h + 4g

Apply the distributive property to write equivalent expressions in expanded form.

Exercise 3.
8(h + 3)
Answer:
8k + 24

Exercise 4.
3(2h + 7)
Answer:
6k + 21

Exercise 5.
5(3x + 9y)
Answer:
15x + 45y

Exercise 6.
4(11k + 3g)
Answer:
44h + 12g

Exercise 7.

Answer:
7jk + 12jm

Exercise 8.
a(9b + 13)
Answer:
9ab + 13a

Eureka Math Grade 6 Module 4 Lesson 12 Problem Set Answer Key

Question 1.
Use the distributive property to write the following expressions in expanded form.
a. 4(x + y)
Answer:
4x + 4y

b. 8(a + 3b)
Answer:
8a + 24h

c. 3(2x + 11y)
Answer:
6x + 33y

d. 9(7a + 6b)
Answer:
63a + 54b

e. c(3a + b)
Answer:
3ac + bc

f. y(2x + 11z)
Answer:
2xy + 11yz

Question 2.
Create a model to show that 2(2x + 3y) = 4x + 6y.
Answer:

Eureka Math Grade 6 Module 4 Lesson 12 Exit Ticket Answer Key

Use the distributive property to write the following expressions in expanded form.
Question 1.
2(b + c)
2h + 2c

Question 2.
5(7h + 3m)
Answer:
35h + 15m

Question 3.
e(f + g)
Answer:
ef + eg

Eureka Math Grade 6 Module 4 Lesson 12 Opening Exercise Answer Key

a. Create a model to show 2 × 5.
Answer:

b. Create a model to show 2 × b, or 2b
Answer:

Engage NY Eureka Math 6th Grade Module 4 Lesson 13 Answer Key

Eureka Math Grade 6 Module 4 Lesson 13 Example Answer Key

Example 1.
Write an expression showing 1 ÷ 2 without the use of the division symbol.
Answer:

What can we determine from the model?
Answer:
1 ÷ 2 is the same as \(\frac{1}{2}\).

Example 2.
Write an expression showing a ÷ 2 without the use of the division symbol.
Answer:

What can we determine from the model?
Answer:
a ÷ 2 is the same as \(\frac{a}{2}\).

When we write division expressions using the division symbol, we represent
Answer:
dividend ÷ divisor.

How would this look when we write division expressions using a fraction?
Answer:

Example 3
a. Write an expression showing a ÷ b without the use of the division symbol.
Answer:
\(\frac{a}{b}\)

b. Write an expression for g divided by the quantity h plus 3.
Answer:
\(\frac{g}{h+3}\)

c. Write an expression for the quotient of the quantity m reduced by 3 and 5.
Answer:
\(\frac{m-3}{5}\)

Eureka Math Grade 6 Module 4 Lesson 13 Exercise Answer Key

Write each expression two ways: using the division symbol and as a fraction.

a. 12 divided by 4
Answer:
12 ÷ 4 and \(\frac{12}{4}\)

b. 3 divided by 5
Answer:
3÷ 5 and \(\frac{3}{5}\)

c. a divided by 4
Answer:
a ÷ 4 and \(\frac{a}{4}\)

d. The quotient of 6 and m
Answer:
6 ÷ m and \(\frac{6}{m}\)

e. Seven divided by the quantity x plus y
Answer:
7 ÷ (x + y) and \(\frac{7}{x+y}\)

f. y divided by the quantity x minus 11
Answer:
y ÷ (x – 11) and \(\frac{y}{x-11}\)

g. The sum of the quantity h and 3 divided by 4
Answer:
(h + 3) ÷ 4 and \(\frac{h+3}{4}\)

h. The quotient of the quantity k minus 10 and m
Answer:
(k – 10) ÷ m and \(\frac{k-10}{m}\)

Eureka Math Grade 6 Module 4 Lesson 13 Problem Set Answer Key

Question 1.
Rewrite the expressions using the division symbol and as a fraction.

a. Three divided by 4
Answer:
3 ÷ 4 and \(\frac{3}{4}\)

b. The quotient of m and 11
Answer:
m ÷ 11 and \(\frac{m}{11}\)

c. 4 divided by the sum of h and 7
Answer:
4 ÷ (h + 7) and \(\frac{4}{h+7}\)

d. The quantity x minus 3 divided by y
Answer:
(x – 3) ÷ y and \(\frac{x-3}{y}\)

Question 2.
Draw a model to show that x ÷ 3 s the same as \(\frac{x}{3}\).
Answer:

Eureka Math Grade 6 Module 4 Lesson 13 Exit Ticket Answer Key

Rewrite the expressions using the division symbol and as a fraction.

Question 1.
The quotient of m and 7
Answer:
m ÷ 7 and \(\frac{m}{7}\)

Question 2.
Five divided by the sum of a and b
Answer:
5 ÷ (a + b) and \(\frac{5}{a+b}\)

Question 3.
The quotient of k decreased by 4 and 9
Answer:
(k – 4) ÷ 9 and \(\frac{k-4}{9}\)

Engage NY Eureka Math 6th Grade Module 4 Lesson 9 Answer Key

Eureka Math Grade 6 Module 4 Lesson 9 Example Answer Key

Example 1.
Create a bar diagram to show 3 plus 5.
Answer:

How would this look it you were asked to show 5 plus 3?
Answer:
There would be 5 tiles and then 3 tiles.

Are these two expressions equivalent?
Answer:
Yes. Both 3 + 5 and 5 + 3 have a sum of 8.

Example 2.

How can we show a number increased by 2?
Answer:
a + 2 or 2 + a

Can you prove this using a model? If so, draw the model.
Answer:
Yes. I can use a bar diagram.

Example 3.
Write an expression to show the sum of m and k.
Answer:
m + k or k + m

Which property can be used in Examples 1 – 3 to show that both expressions given are equivalent?
Answer:
The commutative property of addition

Example 4
How can we show 10 minus 6?
Draw a bar diagram to model this expression.
Answer:

What expression would represent this model?
Answer:
10 – 6

Could we also use 6 – 10?
Answer:
No. If we started with 6 and tried to take 10 away the models would not match.

Example 5
How can we write an expression to show 3 less than a number?
Start by drawing a diagram to model the subtraction. Are we taking away from the 3 or the unknown number?
Answer:
We are taking 3 away from the unknown number.

What expression would represent this model?
Answer:
The expression is n – 3

Example 6
How would we write an expression to show the number c being subtracted from the sum of a and b?

Start by writing an expression for “the sum of a and b.”
Answer:
a + b or b + a

Now, show c being subtracted from the sum.
Answer:
a + b – c or b + a – c

Example 7
Write an expression to show c minus the sum of a and b.
Answer:
c – (a + b)

Why are parentheses necessary in this example and not the others?
Answer:
Without the parentheses, only a is being taken away from c, where the expression says that a + b should be taken away from c.

Replace the variables with numbers to see if c – (a + b) is the same as c – a + b.

Eureka Math Grade 6 Module 4 Lesson 9 Exercise Answer Key

Exercise 1.
Write an expression to show the sum of 7 and 1. 5.
Answer:
7 + 1.5 or 1.5 + 7

Exercise 2.
Write two expressions to show w increased by 4. Then, draw models to prove that both expressions represent the same thing.
Answer:
w + 4 and 4 + w

Exercise 3.
Write an expression to show the sum of a, b, and c.
Answer:
Answers will vary. Below are possible answers.
a + b + c               b + c + a           c + b + a
a + c + b               b + a + c           c + a + b

Exercise 4.
Write an expression and a model showing 3 less than p.
Answer:
p – 3

Exercise 5.
Write an expression to show the difference of 3 and p.
Answer:
3 – p

Exercise 6.
Write an expression to show 4 less than the sum of g and 5.
Answer:
g + 5 – 4 or 5 + g – 4

Exercise 7.
Write an expression to show 4 decreased by the sum of g and 5.
Answer:
4 – (g + 5) or 4 – (5 + g)

Exercise 8.
Should Exercises 6 and 7 have different expressions? Why or why not?
Answer:
The expressions are different because one includes the word “decreased by”and the other has the words ‘less than.” The words “less than” give the amount that was taken away first, whereas the word “decreased by” gives us a starting amount and then the amount that was taken away.

Eureka Math Grade 6 Module 4 Lesson 9 Problem Set Answer Key

Question 1.
Write two expressions to show a number increased by 11. Then, draw models to prove that both expressions represent the same thing.
Answer:
a + 11 and 11 + a

Question 2.
Write an expression to show the sum of x and y.
Answer:
x + y or y + x

Question 3.
Write an expression to show h decreased by 13.
Answer:
h – 13

Question 4.
Write an expression to show k less than 3. 5.
Answer:
3.5 – k

Question 5.
Write an expression to show the sum of g and h reduced by 11.
Answer:
g + h – 11

Question 6.
Write an expression to show 5 less than y, plus g.
Answer:
y – 5 + g

Question 7.
Write an expression to show 5 less than the sum of y and g.
Answer:
y + g – 5

Eureka Math Grade 6 Module 4 Lesson 9 Exit Ticket Answer Key

Question 1.
Write an expression showing the sum of 8 and a number f.
Answer:
8 + f or f + 8

Question 2.
Write an expression showing 5 less than the number k.
Answer:
k – 5

Question 3.
Write an expression showing the sum of a number h and a number w minus 11.
Answer:
h + w – 11

Engage NY Eureka Math 6th Grade Module 4 Lesson 8 Answer Key

Eureka Math Grade 6 Module 4 Lesson 8 Example Answer Key

Example 1.
Additive Identity Property of Zero
g + 0 = g

Remember a letter in a mathematical expression represents a number. Can we replace g with any number?
Answer:
Yes

Choose a value for g, and replace g with that number in the equation. What do you observe?
Answer:
The value of g does not change when 0 is added to g.

Repeat this process several times, each time choosing a different number for g.

Will all values of result in a true number sentence?
Answer:
Yes

Write the mathematical language for this property below:
Answer:
g + 0 = g, additive identity property of zero. Any number added to zero equals itself.

Example 2.
Multiplicative Identity Property of One
g × 1 = g
Remember a letter in a mathematical expression represents a number. Can we replace g with any number?
Answer:
Yes

Choose a value for g, and replace g with that number in the equation. What do you observe?
Answer:
The value of g does not change when g is multiplied by 1.

Will all values of result in a true number sentence? Experiment with different values before making your claim.
Answer:
Yes

Write the mathematical language for this property below:
Answer:
g × 1 = g, multiplicative identity property of one. Any number multiplied by one equals itself.

Example 3.
Commutative Property of Addition and Multiplication
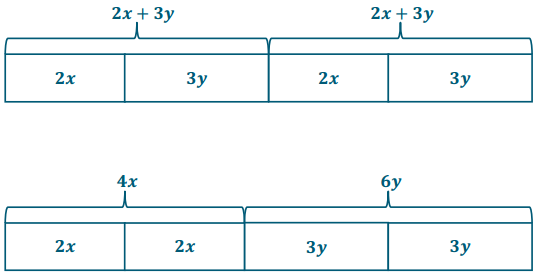
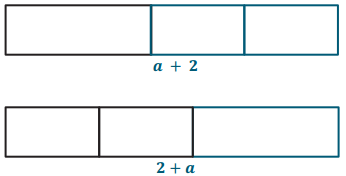
3 + 4 = 4 + 3
3 × 4 = 4 × 3

Replace the 3’s in these number sentences with the letter
Answer:
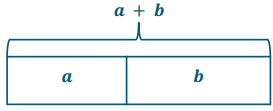
a + 4 = 4 + a
a × 4 = 4 × a

Choose a value for a, and replace with that number in each of the equations. What do you observe?
Answer:
The result is a true number sentence.

Will all values of result in a true number sentence? Experiment with different values before making your claim.
Answer:
Yes, any number, even zero, can be used in place of the variable

Now, write the equations again, this time replacing the number 4 with a variable, b.
Answer:
a + b = b + a
a × b = b × a

Will all values of and result in true number sentences for the first two equations? Experiment with different values before making your claim.
Answer:
Yes

Write the mathematical language for this property below:
Answer:
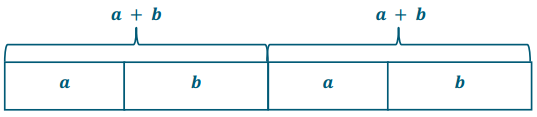
a + b = b + a commutative property of addition. Order does not matter when adding.
a × b = b × a commutative property of multiplication. Order does not matter when multiplying.

Example 4.
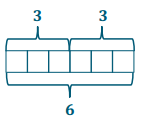
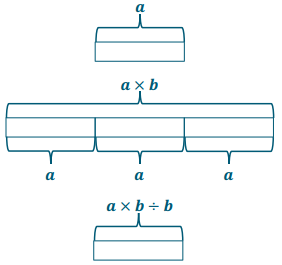
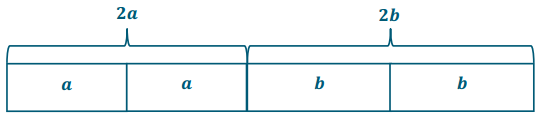
3 + 3 + 3 + 3 = 4 × 3
3 ÷ 4 = \(\frac{3}{4}\)

Replace the 3’s in these number sentences with the letter
Answer:
a + a + a + a = 4 × a
a ÷ 4 = \(\frac{a}{4}\)

Choose a value for a, and replace a with that number in each of the equations. What do you observe?
Answer:
The result is a true number sentence.

Will all values of a result in a true number sentence? Experiment with different values before making your claim.
Answer:
Yes, any number, even zero, can be used in place of the variable

Now, write the equations again, this time replacing the number 4 with a variable, b.
Answer:
a + a + a + a = b × a
a ÷ b = \(\frac{a}{b}\), b ≠ 0

Will all values of and result in true number sentences for the equations? Experiment with different values before making your claim.
Answer:
In the equation a + a + a + a = b × a, any value can be substituted for the variable a, but only 4 can be used for b since there are exactly 4 copies of a in the equation.
It is true for all values of and all values of b ≠ 0.

Eureka Math Grade 6 Module 4 Lesson 8 Problem Set Answer Key

Question 1.
State the commutative property of addition using the variables a and b.
Answer:
a + b = b + a

Question 2.
State the commutative property of multiplication using the variables a and b.
Answer:
a × b = b × a

Question 3.
State the additive property of zero using the variable b.
Answer:
b + 0 = b

Question 4.
State the multiplicative identity property of one using the variable b.
Answer:
b × 1 = b

Question 5.
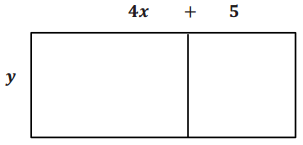
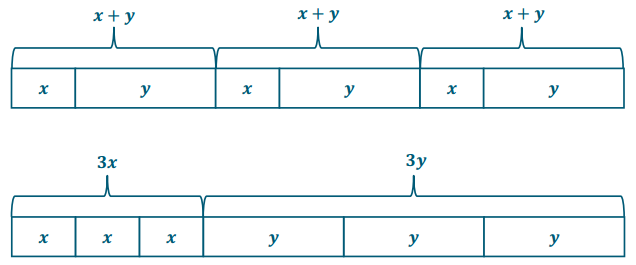
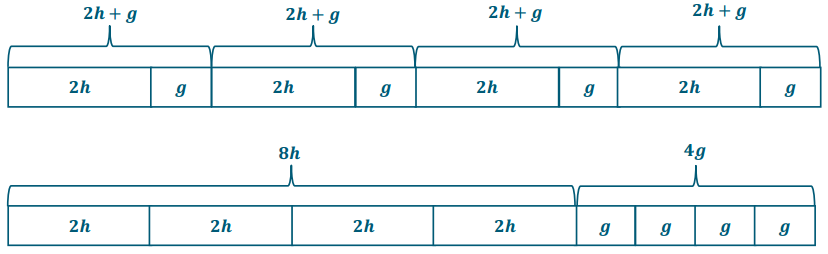
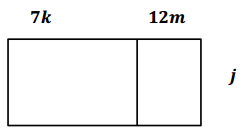
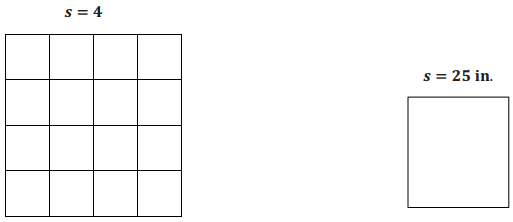
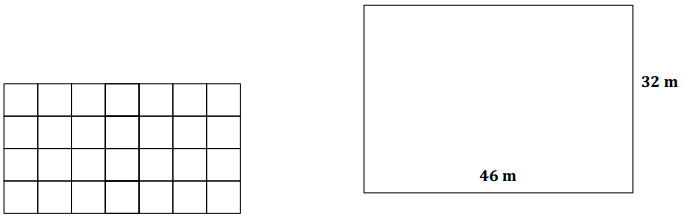
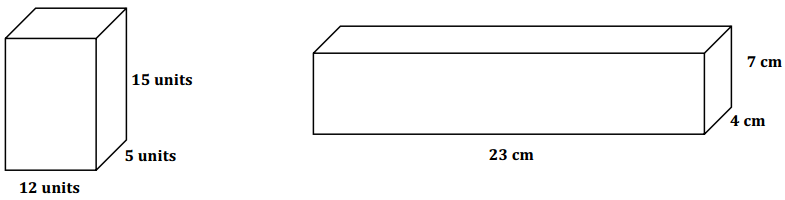
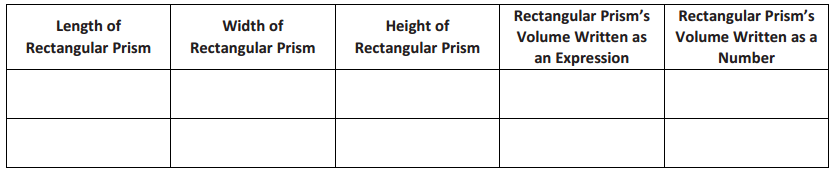
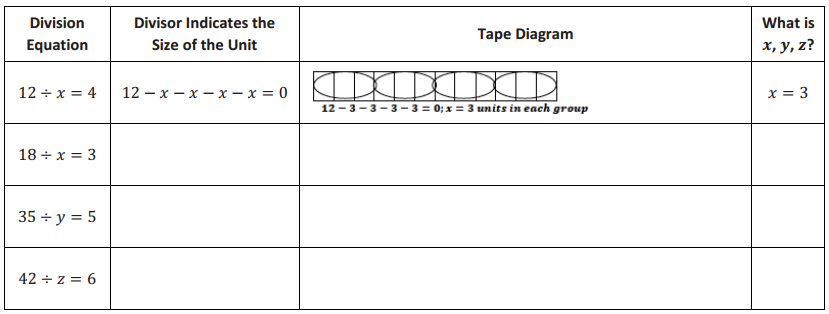
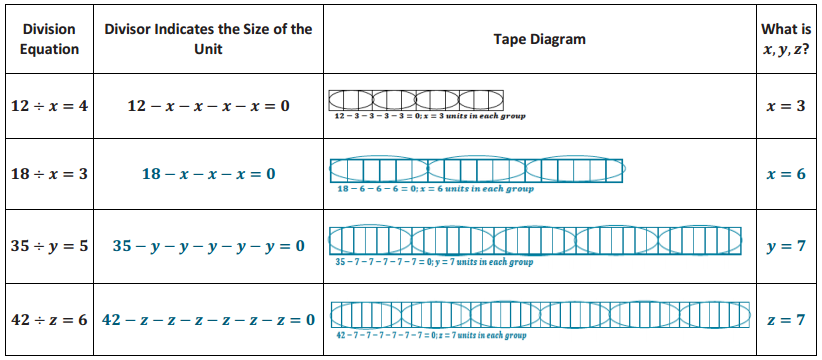
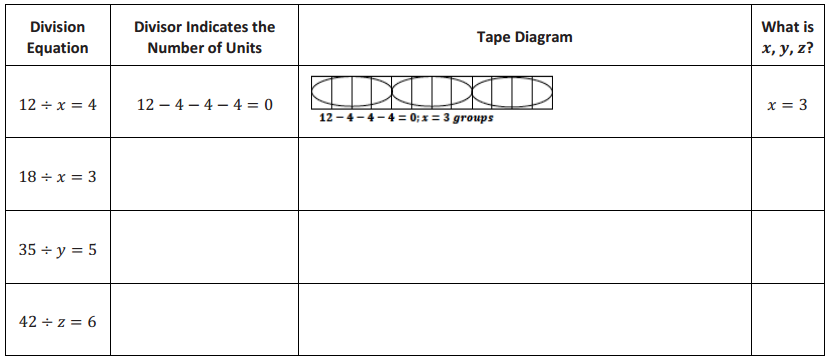
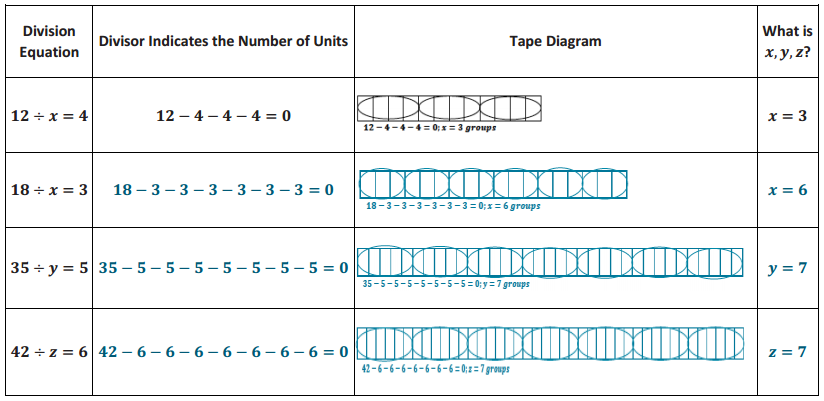
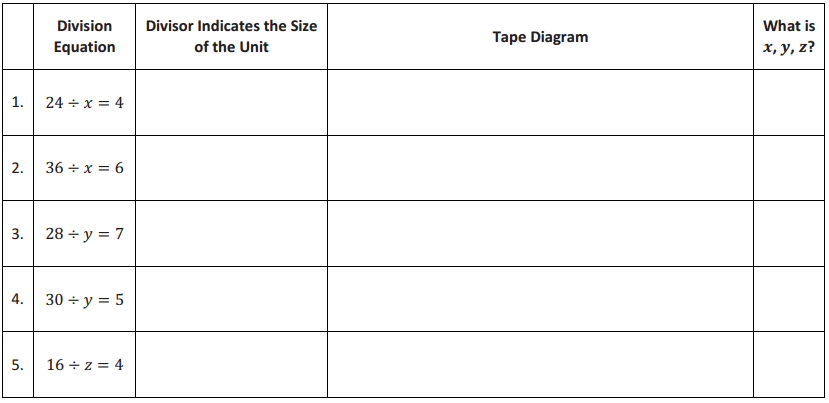
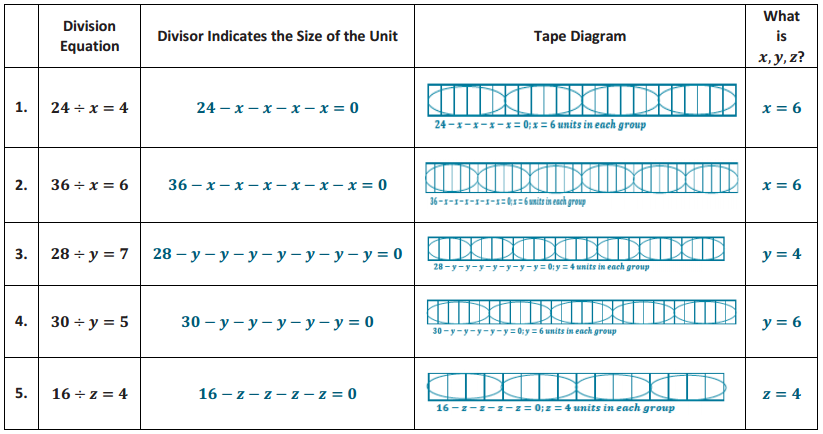
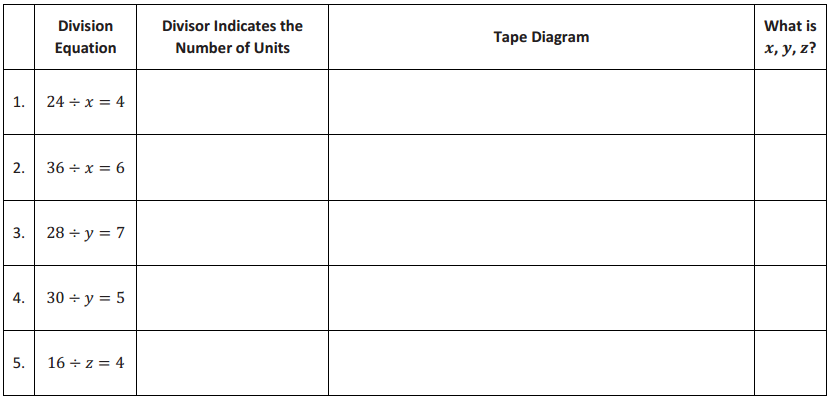
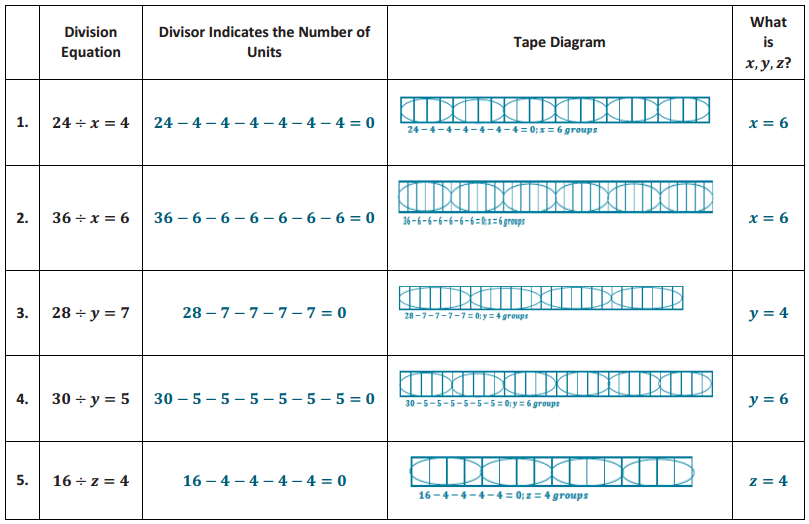
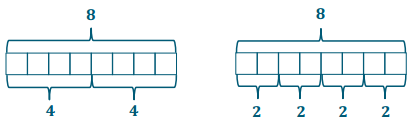
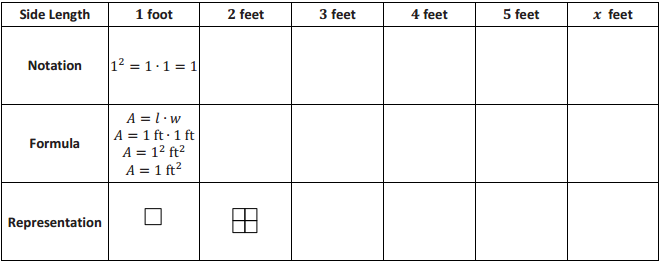
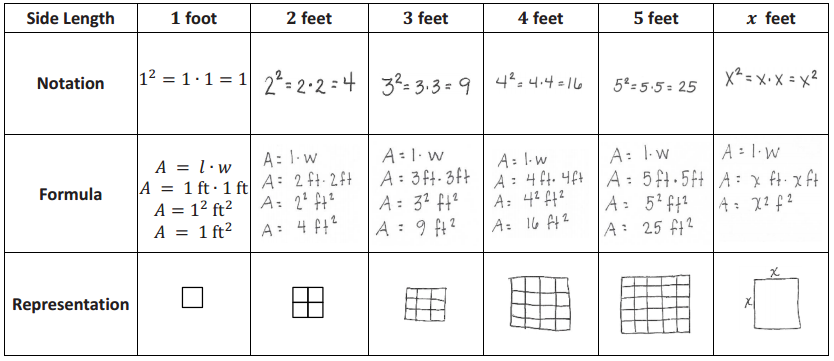
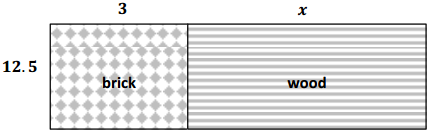
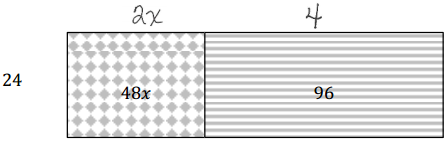
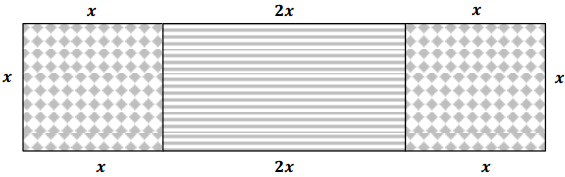
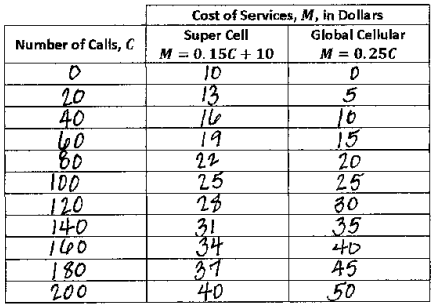
Demonstrate the property listed in the first column by filling in the third column of the table.

Answer:

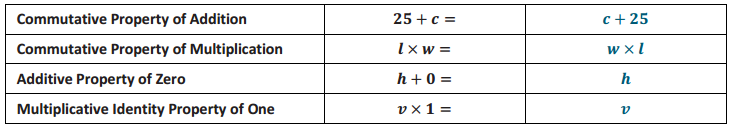
Question 6.
Why is there no commutative property for subtraction or division? Show examples.
Answer:
Answers will vary. Examples should show reasoning and proof that the commutative property does not work for subtraction and division. An example would be 8 ÷ 2 and 2 ÷ 8. 8 ÷ 2 = 4, but 2 ÷ 8 = \(\frac{1}{4}\).

Eureka Math Grade 6 Module 4 Lesson 8 Exit Ticket Answer Key

Question 1.
State the commutative property of addition, and provide an example using two different numbers.
Answer:
Any two different addends can be chosen, such as 5 + 6 = 6 + 5.

Question 2.
State the commutative property of multiplication, and provide an example using two different numbers.
Answer:
Any two different factors can be chosen, such as 4 × 9 = 9 × 4.

Question 3.
State the additive property of zero, and provide an example using any other number.
Answer:
Any nonzero addend can be chosen, such as 3 + 0 = 3.

Question 4.
State the multiplicative identity property of one, and provide an example using any other number.
Answer:
Any nonzero factor can be chosen, such as 12 × 1 = 12.

Eureka Math Grade 6 Module 4 Lesson 8 Opening Exercise Answer Key

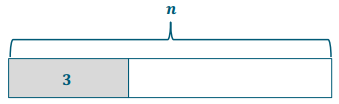
4 + 0 = 4
4 × 1 = 4
4 ÷ 1 = 4
4 × 0 = 0
1 ÷ 4 = \(\frac{1}{4}\)

How many of these statements are true?
Answer:
All of them

How many of those statements would be true if the number was replaced with the number in each of the number sentences?
Answer:
All of them

Would the number sentences be true if we were to replace the number with any other number?

What if we replaced the number 4 with the number 0? Would each of the number sentences be true?
Answer:
No. The first four are true, but the last one, dividing by zero, is not true.

What if we replace the number 4 with a letter g? Please write all 4 expressions below, replacing each 4 with a g.
Answer:
g + 0 = g
g × 1 = g
g ÷ 1 = g
g × 0 = 0
1 ÷ g = \(\frac{1}{g}\)

Are these all true (except for g= 0) when dividing?
Answer:
Yes

Eureka Math Grade 6 Module 4 Lesson 8 Division of Fractions II Answer Key

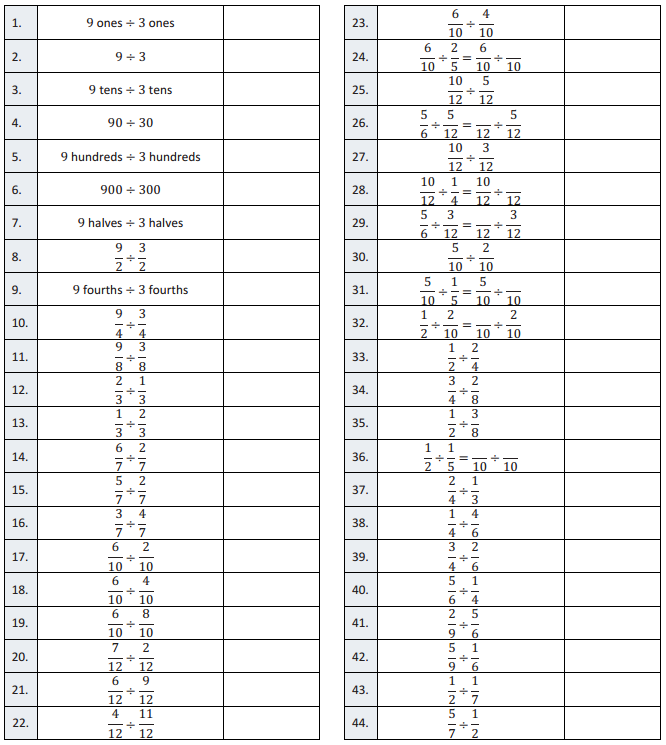
Division of Fractions II – Round 1

Directions: Determine the quotient of the fractions and simplify.

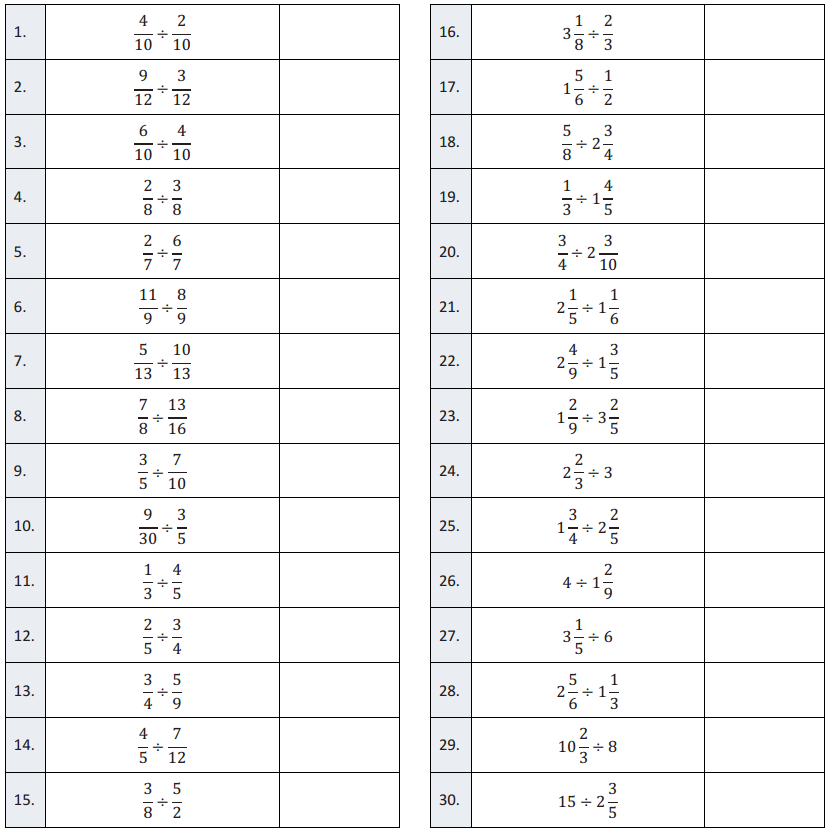
Question 1.
\(\frac{4}{10} \div \frac{2}{10}\)
Answer:
\(\frac{4}{2}\) = 2

Question 2.
\(\frac{9}{12} \div \frac{3}{12}\)
Answer:
\(\frac{9}{3}\) = 3

Question 3.
\(\frac{6}{10} \div \frac{4}{10}\)
Answer:
\(\frac{6}{4}=\frac{3}{2}=1 \frac{1}{2}\)

Question 4.
\(\frac{2}{8} \div \frac{3}{8}\)
Answer:
\(\frac{2}{3}\)

Question 5.
\(\frac{2}{7} \div \frac{6}{7}\)
Answer:
\(\frac{2}{6}=\frac{1}{3}\)

Question 6.
\(\frac{11}{9} \div \frac{8}{9}\)
Answer:
\(\frac{11}{8}=1 \frac{3}{8}\)

Question 7.
\(\frac{5}{13} \div \frac{10}{13}\)
Answer:
\(\frac{5}{10}=\frac{1}{2}\)

Question 8.
\(\frac{7}{8} \div \frac{13}{16}\)
Answer:
\(\frac{14}{13}=1 \frac{1}{13}\)

Question 9.
\(\frac{3}{5} \div \frac{7}{10}\)
Answer:
\(\frac{6}{7}\)

Question 10.
\(\frac{9}{30} \div \frac{3}{5}\)
Answer:
\(\frac{9}{18}=\frac{1}{2}\)

Question 11.
\(\frac{1}{3} \div \frac{4}{5}\)
Answer:
\(\frac{5}{12}\)

Question 12.
\(\frac{2}{5} \div \frac{3}{4}\)
Answer:
\(\frac{8}{15}\)

Question 13.
\(\frac{3}{4} \div \frac{5}{9}\)
Answer:
\(\frac{27}{20}=1 \frac{7}{20}\)

Question 14.
\(\frac{4}{5} \div \frac{7}{12}\)
Answer:
\(\frac{48}{35}=1 \frac{13}{35}\)

Question 15.
\(\frac{3}{8} \div \frac{5}{2}\)
Answer:
\(\frac{6}{40}=\frac{3}{20}\)

Question 16.
\(3 \frac{1}{8} \div \frac{2}{3}\)
Answer:
\(\frac{75}{16}=4 \frac{11}{16}\)

Question 17.
\(1 \frac{5}{6} \div \frac{1}{2}\)
Answer:
\(\frac{22}{6}=\frac{11}{3}=3 \frac{2}{3}\)

Question 18.
\(\frac{5}{8} \div 2 \frac{3}{4}\)
Answer:
\(\frac{20}{88}=\frac{5}{22}\)

Question 19.
\(\frac{1}{3} \div 1 \frac{4}{5}\)
Answer:
\(\frac{5}{27}\)

Question 20.
\(\frac{3}{4} \div 2 \frac{3}{10}\)
Answer:
\(\frac{30}{92}=\frac{15}{46}\)

Question 21.
\(2 \frac{1}{5} \div 1 \frac{1}{6}\)
Answer:
\(\frac{66}{35}=1 \frac{31}{35}\)

Question 22.
\(2 \frac{4}{9} \div 1 \frac{3}{5}\)
Answer:
\(\frac{110}{72}=\frac{55}{36}=1 \frac{19}{36}\)

Question 23.
\(1 \frac{2}{9} \div 3 \frac{2}{5}\)
Answer:
\(\frac{55}{153}\)

Question 24.
\(2 \frac{2}{3} \div 3\)
Answer:
\(\frac{8}{9}\)

Question 25.
\(1 \frac{3}{4} \div 2 \frac{2}{5}\)
Answer:
\(\frac{35}{48}\)

Question 26.
\(4 \div 1 \frac{2}{9}\)
Answer:
\(\frac{36}{11}=3 \frac{3}{11}\)

Question 27.
\(3 \frac{1}{5} \div 6\)
Answer:
\(\frac{16}{30}=\frac{8}{15}\)

Question 28.
\(2 \frac{5}{6} \div 1 \frac{1}{3}\)
Answer:
\(\frac{51}{24}=2 \frac{3}{24}=2 \frac{1}{8}\)

Question 29.
\(10 \frac{2}{3} \div 8\)
Answer:
\(\frac{32}{24}=\frac{4}{3}=1 \frac{1}{3}\)

Question 30.
\(15 \div 2 \frac{3}{5}\)
Answer:
\(\frac{75}{13}=5 \frac{10}{13}\)

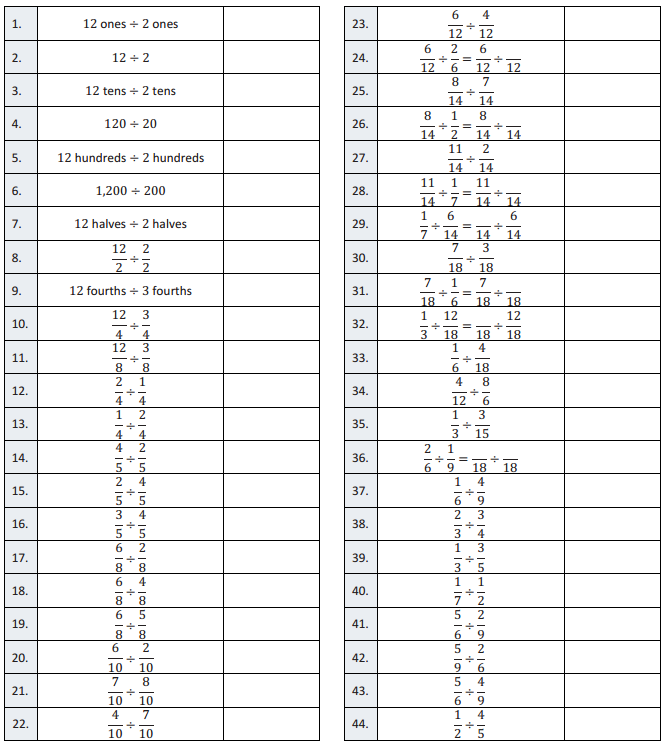
Division of Fractions II – Round 2

Directions: Determine the quotient of the fractions and simplify.

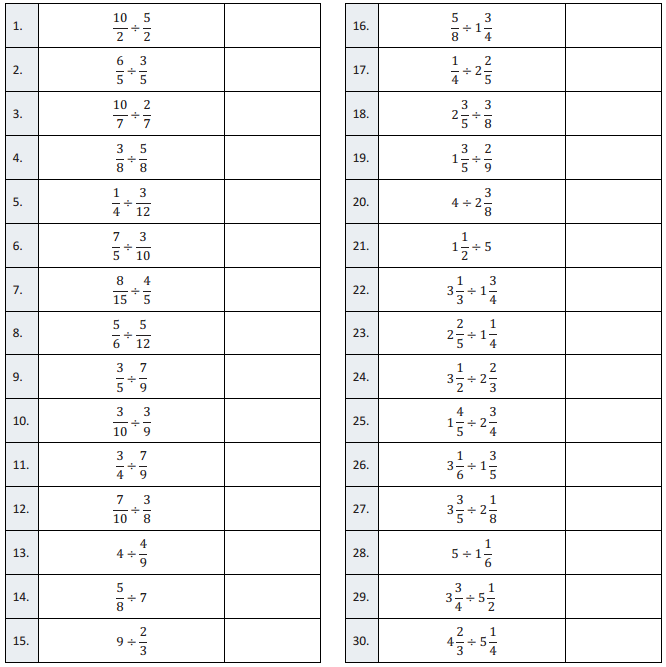
Question 1.
\(\frac{10}{2} \div \frac{5}{2}\)
Answer:
\(\frac{10}{5}\) = 2

Question 2.
\(\frac{6}{5} \div \frac{3}{5}\)
Answer:
\(\frac{6}{3}\) = 2

Question 3.
\(\frac{10}{7} \div \frac{2}{7}\)
Answer:
\(\frac{10}{2}\) = 5

Question 4.
\(\frac{3}{8} \div \frac{5}{8}\)
Answer:
\(\frac{3}{5}\)

Question 5.
\(\frac{1}{4} \div \frac{3}{12}\)
Answer:
\(\frac{3}{3}\) = 1

Question 6.
\(\frac{1}{4} \div \frac{3}{12}\)
Answer:
\(\frac{14}{3}=4 \frac{2}{3}\)

Question 7.
\(\frac{8}{15} \div \frac{4}{5}\)
Answer:
\(\frac{8}{12}=\frac{2}{3}\)

Question 8.
\(\frac{5}{6} \div \frac{5}{12}\)
Answer:
\(\frac{10}{5}\) = 2

Question 9.
\(\frac{3}{5} \div \frac{7}{9}\)
Answer:
\(\frac{27}{35}\)

Question 10.
\(\frac{3}{10} \div \frac{3}{9}\)
Answer:
\(\frac{27}{30}=\frac{9}{10}\)

Question 11.
\(\frac{3}{4} \div \frac{7}{9}\)
Answer:
\(\frac{27}{28}\)

Question 12.
\(\frac{7}{10} \div \frac{3}{8}\)
Answer:
\(\frac{56}{30}=\frac{28}{15}=1 \frac{13}{15}\)

Question 13.
\(4 \div \frac{4}{9}\)
Answer:
\(\frac{36}{4}\) = 9

Question 14.
\(\frac{5}{8} \div 7\)
Answer:
\(\frac{5}{56}\)

Question 15.
\(9 \div \frac{2}{3}\)
Answer:
\(\frac{27}{2}=13 \frac{1}{2}\)

Question 16.
\(\frac{5}{8} \div 1 \frac{3}{4}\)
Answer:
\(\frac{20}{56}=\frac{5}{14}\)

Question 17.
\(\frac{1}{4} \div 2 \frac{2}{5}\)
Answer:
\(\frac{5}{48}\)

Question 18.
\(2 \frac{3}{5} \div \frac{3}{8}\)
Answer:
\(\frac{104}{15}=6 \frac{14}{15}\)

Question 19.
\(1 \frac{3}{5} \div \frac{2}{9}\)
Answer:
\(\frac{72}{10}=7 \frac{2}{10}=7 \frac{1}{5}\)

Question 20.
\(4 \div 2 \frac{3}{8}\)
Answer:
\(\frac{32}{19}=1 \frac{13}{19}\)

Question 21.
\(1 \frac{1}{2} \div 5\)
Answer:
\(\frac{3}{10}\)

Question 22.
\(3 \frac{1}{3} \div 1 \frac{3}{4}\)
Answer:
\(\frac{40}{21}=1 \frac{19}{21}\)

Question 23.
\(2 \frac{2}{5} \div 1 \frac{1}{4}\)
Answer:
\(\frac{48}{25}=1 \frac{23}{25}\)

Question 24.
\(3 \frac{1}{2} \div 2 \frac{2}{3}\)
Answer:
\(\frac{21}{16}=1 \frac{5}{16}\)

Question 25.
\(1 \frac{4}{5} \div 2 \frac{3}{4}\)
Answer:
\(\frac{36}{55}\)

Question 26.
\(3 \frac{1}{6} \div 1 \frac{3}{5}\)
Answer:
\(\frac{95}{48}=1 \frac{47}{48}\)

Question 27.
\(3 \frac{3}{5} \div 2 \frac{1}{8}\)
Answer:
\(\frac{144}{85}=1 \frac{59}{85}\)

Question 28.
\(5 \div 1 \frac{1}{6}\)
Answer:
\(\frac{30}{7}=4 \frac{2}{7}\)

Question 29.
\(3 \frac{3}{4} \div 5 \frac{1}{2}\)
Answer:
\(\frac{30}{44}=\frac{15}{22}\)

Question 30.
\(4 \frac{2}{3} \div 5 \frac{1}{4}\)
Answer:
\(\frac{56}{63}=\frac{8}{9}\)

Engage NY Eureka Math 6th Grade Module 4 Lesson 7 Answer Key

Eureka Math Grade 6 Module 4 Lesson 7 Example Answer Key

Example 1.

What is the length of one side of this square?
Answer:
3 units

What is the formula for the area of a square?
Answer:
A = s²

What is the square’s area as a multiplication expression?
Answer:
3 units × 3 units

What is the square’s area?
Answer:
9 square units

We can count the units. However, look at this other square. Its side length is 23 That is just too many tiny units to draw. What expression can we build to find this square’s area?
Answer:
23 × 23 cm

What is the area of the square? Use a calculator if you need to.
Answer:
529 cm²

Example 2.

What does the letter represent in this blue rectangle?
Answer:
b = 8

With a partner, answer the following question: Given that the second rectangle is divided into four equal parts, what number does the x represent?
Answer:
x = 8

How did you arrive at this answer?
Answer:
We reasoned that each width of the 4 congruent rectangles must be the same. Two 4 lengths equals

What is the total length of the second rectangle? Tell a partner how you know.
Answer:
The length consists of 4 segments that each has a length of 4 cm. 4 × 4 cm = 16 cm.

If the two large rectangles have equal lengths and widths, find the area of each rectangle.
Answer:
8 cm × 16 cm = 128 cm²

Discuss with your partner how the formulas for the area of squares and rectangles can be used to evaluate area for a particular figure.
Answer:

Example 3.

What does the l represent in the first diagram?
Answer:
The length of the rectangular prism

What does the w represent in the first diagram?
Answer:
The width of the rectangular prism

What does the h represent in the first diagram?
Answer:
The height of the rectangular prism

Since we know the formula to find the volume is V = l × w ×h, what number can we substitute for the l in the formula? Why?
Answer:
6, because the length of the second right rectangular prism is 6 cm.

What other number can we substitute for the l?
Answer:
No other number can replace the l. Only one number can replace one letter.

What number can we substitute for the in the formula? Why?
Answer:
2, because the width of the second right rectangular prism is 2 cm.

What number can we substitute for the h in the formula?
Answer:
8 because the height of the second right rectangular prism is 8 cm.

Determine the volume of the second right rectangular prism by replacing the letters in the formula with their appropriate numbers.
Answer:
V = l × w × h; V = 6 cm × 2 cm × 8 cm = 96 cm³

Eureka Math Grade 6 Module 4 Lesson 7 Exercise Answer Key

Exercise 1.
Complete the table below for both squares. Note: These drawings are not to scale.


Answer:

Exercise 2.


Answer:

Exercise 3.
Complete the table for both figures. Using a calculator is appropriate.


Answer:

Eureka Math Grade 6 Module 4 Lesson 7 Problem Set Answer Key

Question 1.
Replace the side length of this square with 4 in., and find the area.

Answer:
The student should draw a square, label the side 4 in., and calculate the area to be 16 in².

Question 2.
Complete the table for each of the given figures.


Answer:

Question 3.
Find the perimeter of each quadrilateral in Problems 1 and 2.
Answer:
p = 16 in. p = 118 p = 35 yd.

Question 4.
Using the formula V = l × w × h, find the volume of a right rectangular prism when the length of the prism is 45 cm, the width is 12 cm, and the height is 10 cm.
Answer:
V = l × w × h; V = 45 cm × 12 cm × 10 cm = 5,400 cm³

Eureka Math Grade 6 Module 4 Lesson 7 Exit Ticket Answer Key

Question 1.
In the drawing below, what do the letters and represent?

Answer:
Length and width of the rectangle

Question 2.
What does the expression l + w + l + w represent?
Answer:
Perimeter of the rectangle, or the sum of the sides of the rectangle

Question 3.
What does the expression l ∙ w represent?
Answer:
Area of the rectangle

Question 4.
The rectangle below is congruent to the rectangle shown in Problem 1. Use this information to evaluate the expressions from Problems 2 and 3.

Answer:
l = 5 and w = 2 p = 14 units A = 10 units²

Engage NY Eureka Math 6th Grade Module 4 Lesson 6 Answer Key

Eureka Math Grade 6 Module 4 Lesson 6 Example Answer Key

Example 1.
Expressions with Only Addition, Subtraction, Multiplication, and Division

What operations are evaluated first?
Answer:
Multiplication and division are evaluated first, from left to right.

What operations are always evaluated last?
Answer:
Addition and subtraction are always evaluated last, from left to right.

Example 2.
Expressions with Four Operations and Exponents
4 + 9² ÷ 3 × 2 – 2

What operation is evaluated first?
Answer:
Exponents (9² = 9 × 9 = 81)

What operations are evaluated next?
Answer:
Multiplication and division, from left to right (81 ÷ 3 = 27; 27 × 2 = 54)

What operations are always evaluated last?
Answer:
Addition and subtraction, from left to right (4 + 54 = 58; 58 – 2 = 56)

What is the final answer?
Answer:
56

Example 3. Expressions with Parentheses
Consider a family of 4 that goes to a soccer game. Tickets are $5.00 each. The mom also buys a soft drink for $2.00. How would you write this expression?
Answer:
4 × 5 + 2

How much will this outing cost?
Answer:
$22

Consider a different scenario: The same family goes to the game as before, but each of the family members wants a drink. How would you write this expression?
Answer:
4 × (5 + 2)

Why would you add the 5 and 2 first?
Answer:
We need to determine how much each person spends. Each person spends $7; then, we multiply by 4 people to figure out the total cost.

How much will this outing cost?
Answer:
$28

How many groups are there?
Answer:
4

What does each group comprise?
Answer:
$5 + $2, or $7

Example 4.
Expressions with Parentheses and Exponents
2 × (3 + 4)²
Which value will we evaluate first within the parentheses? Evaluate.
Answer:
First, evaluate 4² which is 16; then, add 3.The value of the parentheses is 19.
2 × (3 + 4²)
2 × (3 + 16)
2 × 19

Evaluate the rest of the expression.
Answer:
2 × 19 = 38

What do you think will happen when the exponent in this expression is outside of the parentheses?
2 × (3 + 4)²

Will the answer be the same?
Answer:
Answers will vary.

Which should we evaluate first? Evaluate.
Answer:
Parentheses
2 × (3 + 4)²
2 × (7)²

What happened differently here than in our last example?
Answer:
The 4 was not raised to the second power because it did not have an exponent. We simply added the values inside the parentheses.

What should our next step be?

We need to evaluate the exponent next.
Answer:
7² = 7 × 7 = 49

Evaluate to find the final answer.
Answer:
2 × 49
98

What do you notice about the two answers?
Answer:
The final answers were not the same.

What was different between the two expressions?
Answer:
Answers may vary. In the first problem, a value inside the parentheses had an exponent, and that value was evaluated first because it was inside of the parentheses. In the second problem, the exponent was outside of the parentheses, which made us evaluate what was in the parentheses first; then, we raised that value to the power of the exponent.

What conclusions can you draw about evaluating expressions with parentheses and exponents?
Answer:
Answers may vary. Regardless of the location of the exponent in the expression, evaluate the parentheses first. Sometimes there will be values with exponents inside the parentheses. If the exponent is outside the parentheses, evaluate the parentheses first, and then evaluate to the power of the exponent.

Eureka Math Grade 6 Module 4 Lesson 6 Exercise Answer Key

Exercise 1.
4 + 2 × 7
Answer:
4 + 14
18

Exercise 2.
36 ÷ 3 × 4
Answer:
12 × 4
48

Exercise 3.
20 − 5 × 2
Answer:
20 − 10
10

Exercise 4.
90 − 5² × 3
Answer:
90 − 25 × 3
90 − 75
15

Exercise 5.
4³ + 2 × 8
Answer:
64 + 2 × 8
64 + 16
80

Exercise 6.
2 + (9²)
Answer:
2 + (81 – 4)
2 + 77
79

Exercise 7.
2 . (13 + 5 – 14 ÷ (3 + 4)
Answer:
2 . (13 + 5 – 14 ÷ 7)
2 . (13 + 5 – 2)
2 . 16
32

Exercise 8.
7 + (12 – 3²)
Answer:
7 + (12 – 9)
7 + 3
10

Exercise 9.
7 + (12 – 3)²
Answer:
7 + 9²
7 + 81
88

Eureka Math Grade 6 Module 4 Lesson 6 Problem Set Answer Key

Evaluate each expression.

Question 1.
3 × 5 + 2 × 8 + 2
Answer:
15 + 16 + 2
33

Question 2.
($1.75 + 2 × $0.25 + 5 × $0.05) × 24
Answer:
($1.75 + $0.50 + $0.25) × 24
$2.50 × 24
$60.00

Question 3.
(2 × 6) + (8 × 4) + 1
Answer:
12 + 32 + 1
45

Question 4.
((8 × 1.95) + (3 × 2.95) + 10.95) × 1.06
Answer:
(15.6 + 8.85 + 10.99) × 1.06
35.4 × 1.06
37.54

Question 5.
((12 ÷ 3)² – (18 ÷ 3²)) × (4 ÷ 2)
Answer:
(4² − (18 ÷ 9)) × (4 ÷ 2)
(16 – 2) × 2
14 × 2
28

Eureka Math Grade 6 Module 4 Lesson 6 Exit Ticket Answer Key

Question 1.
Evaluate this expression: 39 ÷ (2 + 1) – 2 × (4 + 1).
Answer:
39 ÷ 3 − 2 × 5
13 − 10
3

Question 2.
Evaluate this expression: 12 × (3 + 2² ÷ 2 − 10
Answer:
12 × (3 + 4) ÷2 − 10
12 × 7 ÷ 2 − 10
84 ÷ 2 − 10
42 − 10
32

Question 3.
Evaluate this expression: 12 × (3 + 2)² ÷ 2 – 10.
Answer:
12 × 5² ÷ 2 – 10
12 × 25 ÷ 2 − 10
300 ÷ 2 − 10
150 − 10
140

Engage NY Eureka Math 6th Grade Module 4 Lesson 5 Answer Key

Eureka Math Grade 6 Module 4 Lesson 5 Example Answer Key

Write each expression in exponential form.
Example 1.
5 × 5 × 5 × 5 × 5 =
Answer:
5⁵

Example 2.
2 × 2 × 2 × 2 =
Answer:
2⁴

Write each expression in expanded form.
Example 3.
8³ =
Answer:
8 × 8 × 8

Example 4.
10⁶ =
Answer:
10 × 10 × 10 × 10 × 10 × 10

Example 5.
g³ =
Answer:
g × g × g

Go back to Examples 1 – 4, and use a calculator to evaluate the expressions.

Example 1.
5 × 5 × 5 × 5 × 5 = 5⁵
Answer:
3,125

Example 2.
2 × 2 × 2 × 2 = 2⁴
Answer:
16

Example 3.
8³ = 8 × 8 × 8
Answer:
512

Example 4.
10⁶ = 10 × 10 × 10 × 10 × 10 × 10
Answer:
1,000,000

Example 5.
What is the difference between 3g and g³?
Answer:
3g = g + g + g or 3 times g; g³ = g × g × g

Example 6.
Write the expression in expanded form, and then evaluate.
(3.8)⁴ =
Answer:
3.8 × 3.8 × 3.8 × 3.8 = 208.5136

Example 7.
Write the expression in exponential form, and then evaluate.
Answer:
2.1 × 2.1 = (2.1)² = 4.41

Example 8.
Write the expression in exponential form, and then evaluate.
0.75 × 0.75 × 0.75
Answer:
= (0.75)³ = 0.421875

The base number can also be a fraction. Convert the decimals to fractions in Examples 7 and 8 and evaluate. Leave your answer as a fraction. Remember how to multiply fractions!

Example 7.
Answer:
\(\frac{21}{10} \times \frac{21}{10}=\left(\frac{21}{10}\right)^{2}=\frac{441}{100}=4 \frac{41}{100}\)

Example 8.
Answer:
\(\frac{3}{4} \times \frac{3}{4} \times \frac{3}{4}=\left(\frac{3}{4}\right)^{3}=\frac{27}{64}\)

Example 9.
Write the expression in exponential form, and then evaluate.
Answer:
\(\frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}=\left(\frac{1}{2}\right)^{3}=\frac{1}{8}\)

Example 10.
Write the expression in expanded form, and then evaluate.
Answer:
\(\left(\frac{2}{3}\right)^{2}=\frac{2}{3} \times \frac{2}{3}=\frac{4}{9}\)

Eureka Math Grade 6 Module 4 Lesson 5 Exercise Answer Key

Exercise 1.
Fill in the missing expressions for each row. For whole number and decimal bases, use a calculator to find the standard form of the number. For fraction bases, leave your answer as a fraction.

Answer:

Exercise 2.
Write five cubed in all three forms: exponential form, expanded form, and standard form.
Answer:
5³; 5 × 5 × 5; 125

Exercise 3.
Write fourteen and seven-tenths squared in all three forms.
Answer:
(14.7)²; 14.7 × 14.7; 216.09

Exercise 4.
One student thought two to the third power was equal to six. What mistake do you think he made, and how would you help him fix his mistake?
Answer:
The student multiplied the base, 2, by the exponent, 3. This is wrong because the exponent never multiplies the base; the exponent tells how many copies of the base are to be used as factors.

Eureka Math Grade 6 Module 4 Lesson 5 Problem Set Answer Key

Question 1.
Complete the table by filling in the blank cells. Use a calculator when needed.

Answer:

Question 2.
Why do whole numbers raised to an exponent get greater, while fractions raised to an exponent get smaller?
Answer:
As whole numbers are multiplied by themselves, products are larger because there are more groups. As fractions of fractions are taken, the product is smaller. A part of a part is less than how much we started with.

Question 3.
The powers of 2 that are in the range 2 through 1,000 are 2, 4, 8, 16, 32, 64, 128, 256, and 512. Find all the powers of that are in the range 3 through 1,000.
Answer:
3, 9, 27, 81, 243, 729

Question 4.
Find all the powers of 4 in the range 4 through 1,000.
Answer:
4, 16, 64, 256

Question 5.
Write an equivalent expression for n × a using only addition.
Answer:

Question 6.
Write an equivalent expression for w^b using only multiplication.
Answer:

a. Explain what w is in this new expression.
Answer:
w is the factor that will be repeatedly multiplied by itself.

b. Explain what b is in this new expression.
Answer:
b is the number of times w will be multiplied.

Question 7.
What is the advantage of using exponential notation?
Answer:
It is a shorthand way of writing a multiplication expression if the factors are all the same.

Question 8.
What is the difference between 4x and x⁴? Evaluate both of these expressions when x = 2
Answer:
4x means four times x; this is the same as x + x + x + x. On the other hand, x⁴ means x to the fourth power, or x × x × x × x.
When x = 2, 4x = 4 × 2 = 8.
When x = 2, x⁴ = 2 × 2 × 2 × 2 = 16.

Eureka Math Grade 6 Module 4 Lesson 5 Exit Ticket Answer Key

Question 1.
What is the difference between 6z and z⁶?
Answer:
6z = z + z + z + z + z + z or 6 times z; z⁶ = z × z × z × z × z × z

Question 2.
Write 10³ as a multiplication expression having repeated factors.
Answer:
10 × 10 × 10

Question 3.
Write 8 × 8 × 8 × 8 using an exponent.
Answer:
8⁴

Eureka Math Grade 6 Module 4 Lesson 5 Opening Exercise Answer Key

As you evaluate these expressions, pay attention to how you arrive at your answers.

Question 1.
4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4
Answer:
4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 + 4 = 4 × 10
= 4¹⁰

Question 2.
9 + 9 + 9 + 9 + 9
Answer:
9 + 9 + 9 + 9 + 9 = 9 × 5
= 9⁵

Question 3.
10 + 10 + 10 + 10 + 10
Answer:
10 + 10 + 10 + 10 + 10 = 10 × 5
= 10⁵

Eureka Math Grade 6 Module 4 Lesson 5 Multiplication of Decimals Answer Key

Progression of Exercises

Question 1.
0.5 × 0.5 =
Answer:
0.25

Question 2.
0.6 × 0.6 =
Answer:
0.36

Question 3.
0.7 × 0.7
Answer:
0.49

Question 4.
0.5 × 0.6 =
Answer:
0.3

Question 5.
1.5 × 1.5 =
Answer:
0.25

Question 6.
2.5 × 2.5 =
Answer:
6.25

Question 7.
0.25 × 0.25 =
Answer:
0.0625

Question 8.
0.1 × 0.1 =
Answer:
0.01

Question 9.
0.1 × 123.4 =
Answer:
12.34

Question 10.
0.01 × 123.4 =
Answer:
1.234

Engage NY Eureka Math 6th Grade Module 4 Lesson 4 Answer Key

Eureka Math Grade 6 Module 4 Lesson 4 Exercise Answer Key

Exercise 1.
Build subtraction equations using the indicated equations. The first example has been completed for you.

Answer:

Answer:

Exercise 2.
Answer each question using what you have learned about the relationship of division and subtraction.
a. If 12 ÷ x = 3 how many times would x have to be subtracted from 12 in order for the answer to be zero? What is the value of x?
Answer:
3; x = 4

b. 36 − f − f − f − f = 0. Write a division sentence for this repeated subtraction sentence. What is the value
of x?
Answer:
36 ÷ 4 = f or 36 ÷ f = 4; f = 9

c. If 24 ÷ b = 12, which number is being subtracted 12 times in order for the answer to be zero?
Answer:
Two

Eureka Math Grade 6 Module 4 Lesson 4 Problem Set Answer Key

Build subtraction equations using the indicated equations.

Answer:

Answer:

Eureka Math Grade 6 Module 4 Lesson 4 Exit Ticket Answer Key

Question 1.
Represent 56 ÷ 8 = 7 using subtraction. Explain your reasoning.
Answer:
56 – 7 – 7 – 7 – 7 – 7 – 7 – 7 – 7 = 0 because
56 – 7 = 49; 49 – 7 = 42; 42 – 7 = 35; 35 – 7 = 28; 28 – 7 = 21; 21 – 7 = 14; 14 – 7 = 7; 7 – 7 = 0.

OR

56 – 8 – 8 – 8 – 8 – 8 – 8 – 8 = 0 because
56 – 8 = 48; 48 – 8 = 40; 40 – 8 = 32; 32 – 8 = 24; 24 – 8 = 16; 16 – 8 = 8; 8 – 8 = 0.

Question 2.
Explain why 30 ÷ x = 6 is the same as 30 – x – x – x – x – x – x = 0. What is the value of x in this example?
Answer:
30 ÷ 5 = 6, so x = 5. When I subtract 5 from 30 six times, the result is zero. Division is a repeat operation of
subtraction.

Engage NY Eureka Math 6th Grade Module 4 Lesson 3 Answer Key

Eureka Math Grade 6 Module 4 Lesson 3 Exercise Answer Key

Exercise 1.
Write the addition sentence that describes the model and the multiplication sentence that describes the model.

Answer:
5 + 5 + 5 and 3 × 5

Exercise 2.
Write an equivalent expression to demonstrate the relationship of multiplication and addition.
a. 6 + 6
Answer:
2 × 6

b. 3 + 3 + 3 + 3 + 3 + 3
Answer:
6 × 3

c. 4 + 4 + 4 + 4 + 4
Answer:
5 × 4

d. 6 × 2
Answer:
2 + 2 + 2 + 2 + 2+ 2

e. 4 × 6
Answer:
6 + 6 + 6 + 6

f. 3 × 9
Answer:
9 + 9 + 9

g. h + h + h + h + h
Answer:
5h

h. 6y
Answer:
y + y + y + y + y + y

Exercise 3.
Roberto is not familiar with tape diagrams and believes that he can show the relationship of multiplication and addition on a number line. Help Roberto demonstrate that the expression 3 × 2 is equivalent to 2 + 2 + 2 on a number line.
Answer:
Possible answer: The first number line shows that there are 3 groups of 2, resulting in 6. The second number line shows the sum of 2 + 2 + 2, resulting in 6.

Since both number lines start at 0 and end at 6, the expressions are equivalent.

Exercise 4.
Tell whether the following equations are true or false. Then, explain your reasoning.
a. x + 6g − 6g = x
The equation is true because it demonstrates the addition identity.

b. 2f − 4e + 4e = 2f
Answer:
The equation is true because it demonstrates the subtraction identity.

Exercise 5.
Write an equivalent expression to demonstrate the relationship between addition and multiplication.
a. 6 + 6 + 6 + 6 + 6 + 6 + 6
Answer:
4 × 6 + 3 × 4

b. d + d + d + w + w + w + w + w
Answer:
3d + 5w

c. a + a + b + b + b + c + c + c + c
Answer:
2a + 3b + 4c

Eureka Math Grade 6 Module 4 Lesson 3 Problem Set Answer Key

Write an equivalent expression to show the relationship of multiplication and addition.

Question 1.
10 + 10 + 10
Answer:
3 × 10

Question 2.
4 + 4 + 4 + 4 + 4 + 4 + 4
Answer:
7 × 4

Question 3.
8 × 2
Answer:
2 + 2 + 2 + 2 + 2 + 2 + 2 + 2

Question 4.
3 × 9
Answer:
9 + 9 + 9

Question 5.
6m
Answer:
m + m + m + m + m + m

Question 6.
d + d + d + d + d
Answer:
5d

Eureka Math Grade 6 Module 4 Lesson 3 Exit Ticket Answer Key

Write an equivalent expression to show the relationship of multiplication and addition.

Question 1.
8 + 8 + 8 + 8 + 8 + 8 + 8 + 8 + 8
Answer:
9 × 8

Question 2.
4 × 9
Answer:
9 + 9 + 9 + 9

Question 3.
6 + 6 + 6
Answer:
3 × 6

Question 4.
7h
Answer:
h + h + h + h + h + h + h

Question 5.
j + j + j + j + j
Answer:
5j

Question 6.
u + u + u + u + u + u + u + u + u + u
Answer:
10u

Eureka Math Grade 6 Module 4 Lesson 3 Opening Exercise Answer Key

Write two different expressions that can be depicted by the tape diagram shown. One expression should include addition, while the other should include multiplication.

a.

Answer:
Possible answers: 3 + 3 + 3 or 3 × 3

b.

Answer:
Possible answers: 8 + 8 or 2 × 8

c.

Answer:
Possible answers: 5 + 5 + 5 or 3 × 5

Engage NY Eureka Math 6th Grade Module 4 Lesson 2 Answer Key

Eureka Math Grade 6 Module 4 Lesson 2 Problem Set Answer Key

Question 1.
Fill in each blank to make each equation true.
a. 132 ÷ 3 × 3 = __________
Answer:
132

b. _______ ÷ 25 × 25 = 225
Answer:
225

c. 56 × ______ ÷ 8 = 56
Answer:
8

d. 452 × 12 ÷ ___ = 452
Answer:
12

Question 2
How is the relationship of addition and subtraction similar to the relationship of multiplication and division?
Answer:
Possible answer: Both relationships create identities.

Eureka Math Grade 6 Module 4 Lesson 2 Exit Ticket Answer Key

Question 1.
Fill In the blanks to make each equation true.
a. 12 ÷ 3 × __________ = 12
Answer:
3

b. f × h ÷ h = __________
Answer:
f

c. 45 × _________ ÷ 15 = 45
Answer:
15

d. __________ ÷ r × r = p
Answer:
p

Question 2.
Draw a series of tape diagrams to represent the following number sentences.
a. 12 ÷ 3 × 3 = 12
Answer:

b. 4 × 5 ÷ 5 = 4
Answer:

Eureka Math Grade 6 Module 4 Lesson 2 Opening Exercise Answer Key

Draw a pictorial representation of the division and multiplication problems using a tape diagram.

a. 8 ÷ 2
Answer:

b. 3 × 2
Answer:

Eureka Math Grade 6 Module 4 Lesson 2 Exploratory Challenge Answer Key

Work in pairs or small groups to determine equations to show the relationship between multiplication and division. Use tape diagrams to provide support for your findings.

Question 1.
Create two equations to show the relationship between multiplication and division. These equations should be identities and Include variables. Use the squares to develop these equations.
Answer:

Question 2.
Write your equations on large paper. Show a series of tape diagrams to defend each of your equations.
Answer:
Only one number sentence is shown there; the second number sentence and series of tape diagrams are included in the optional Discussion.
Possible answer: a × b ÷ b = a

Possible answer: a ÷ b × b = a

Use the following rubric to critique other posters.
1. Name of the group you are critiquing
2. Equation you are critiquing
3. Whether or not you believe the equations are true and reasons why
Answer:

Eureka Math Grade 6 Module 4 Lesson 2 Division of Fractions Answer Key

Divisions of Fractions – Round 1

Question 1.
9 ones ÷ 3 ones
Answer:
\(\frac{9}{3}\) = 3

Question 2.
9 ÷ 3
Answer:
\(\frac{9}{3}\) = 3

Question 3.
9 tens ÷ 3 tens
Answer:
\(\frac{9}{3}\) = 3

Question 4.
90 ÷ 30
Answer:
\(\frac{9}{3}\) = 3

Question 5.
9 hundreds ÷ 3 hundreds
Answer:
\(\frac{9}{3}\) = 3

Question 6.
900 ÷ 300
Answer:
\(\frac{9}{3}\) = 3

Question 7.
9 halves ÷ 3 halves
Answer:
\(\frac{9}{3}\) = 3

Question 8.
\(\frac{9}{2} \div \frac{3}{2}\)
Answer:
\(\frac{9}{3}\) = 3

Question 9.
9 fourths ÷ 3 fourths
Answer:
\(\frac{9}{3}\)

Question 10.
\(\frac{9}{4} \div \frac{3}{4}\)
Answer:
\(\frac{9}{3}\) = 3

Question 11.
\(\frac{9}{8} \div \frac{3}{8}\)
Answer:
\(\frac{9}{3}\) = 3

Question 12.
\(\frac{2}{3} \div \frac{1}{3}\)
Answer:
\(\frac{2}{1}\) = 2

Question 13.
\(\frac{1}{3} \div \frac{2}{3}\)
Answer:
\(\frac{1}{2}\)

Question 14.
\(\frac{6}{7} \div \frac{2}{7}\)
Answer:
\(\frac{6}{2}\) = 3

Question 15.
\(\frac{5}{7} \div \frac{2}{7}\)
Answer:
\(\frac{5}{2}=2 \frac{1}{2}\)

Question 16.
\(\frac{3}{7} \div \frac{4}{7}\)
Answer:
\(\frac{3}{4}\)

Question 17.
\(\frac{6}{10} \div \frac{2}{10}\)
Answer:
\(\frac{6}{2}\) = 3

Question 18.
\(\frac{6}{10} \div \frac{4}{10}\)
Answer:
\(\frac{6}{4}=1 \frac{1}{2}\)

Question 19.
\(\frac{6}{10} \div \frac{8}{10}\)
Answer:
\(\frac{6}{8}=\frac{3}{4}\)

Question 20.
\(\frac{7}{12} \div \frac{2}{12} \)
Answer:
\(\frac{7}{2}=3 \frac{1}{2}\)

Question 21.
\(\frac{6}{12} \div \frac{9}{12}\)
Answer:
\(\frac{6}{9}=\frac{2}{3}\)

Question 22.
\(\frac{4}{12} \div \frac{11}{12}\)
Answer:
\(\frac{4}{11}\)

Question 23.
\(\frac{6}{10} \div \frac{4}{10}\)
Answer:
\(\frac{6}{4}=1 \frac{1}{2}\)

Question 24.
\(\frac{6}{10} \div \frac{2}{5}=\frac{6}{10} \div \frac{ }{10}\)
Answer:
\(\frac{6}{4}=1 \frac{1}{2}\)

Question 25.
\(\frac{10}{12} \div \frac{5}{12}\)
Answer:
\(\frac{10}{5}=2\)

Question 26.
\(\frac{5}{6} \div \frac{5}{12}=\frac{ }{12} \div \frac{5}{12}\)
Answer:
\(\frac{10}{5}=2\)

Question 27.
\(\frac{10}{12} \div \frac{3}{12}\)
Answer:
\(\frac{10}{3}=3 \frac{1}{3}\)

Question 28.
\(\frac{10}{12} \div \frac{1}{4}=\frac{10}{12} \div \frac{ }{12}\)
Answer:
\(\frac{10}{3}=3 \frac{1}{3}\)

Question 29.
\(\frac{5}{6} \div \frac{3}{12}=\frac{ }{12} \div \frac{3}{12}\)
Answer:
\(\frac{10}{3}=3 \frac{1}{3}\)

Question 30.
\(\frac{5}{10} \div \frac{2}{10}\)
Answer:
\(\frac{5}{2}=2 \frac{1}{2}\)

Question 31.
\(\frac{5}{10} \div \frac{1}{5}=\frac{5}{10} \div \frac{ }{10}\)
Answer:
\(\frac{5}{2}=2 \frac{1}{2}\)

Question 32.
\(\frac{1}{2} \div \frac{2}{10}=\frac{ }{10} \div \frac{2}{10}\)
Answer:
\(\frac{5}{2}=2 \frac{1}{2}\)

Question 33.
\(\frac{1}{2} \div \frac{2}{4}\)
Answer:
\(\frac{2}{2}=1\)

Question 34.
\(\frac{3}{4} \div \frac{2}{8}\)
Answer:
3

Question 35.
\(\frac{1}{2} \div \frac{3}{8}\)
Answer:
\(\frac{4}{3}=1 \frac{1}{3}\)

Question 36.
\(\frac{1}{2} \div \frac{1}{5}=\frac{1}{10} \div \frac{ }{10}\)
Answer:
\(\frac{5}{2}=2 \frac{1}{2}\)

Question 37.
\(\frac{2}{4} \div \frac{1}{3}\)
Answer:
\(\frac{6}{4}=1 \frac{1}{2}\)

Question 38.
\(\frac{1}{4} \div \frac{4}{6}\)
Answer:
\(\frac{3}{8}\)

Question 39.
\(\frac{3}{4} \div \frac{2}{6}\)
Answer:
\(\frac{9}{4}=2 \frac{1}{4}\)

Question 40.
\(\frac{5}{6} \div \frac{1}{4}\)
Answer:
\(\frac{10}{3}=3 \frac{1}{3}\)

Question 41.
\(\frac{2}{9} \div \frac{5}{6}\)
Answer:
\(\frac{4}{15}\)

Question 42.
\(\frac{5}{9} \div \frac{1}{6}\)
Answer:
\(\frac{15}{3}\) = 5

Question 43.
\(\frac{1}{2} \div \frac{1}{7}\)
Answer:
\(\frac{7}{2}=3 \frac{1}{2}\)

Question 44.
\(\frac{5}{7} \div \frac{1}{2}\)
Answer:
\(\frac{10}{7}=1 \frac{3}{7}\)

Divisions of Fractions – Round 2

Question 1.
12 ones ÷ 2 ones
Answer:
\(\frac{12}{2}\) = 6

Question 2.
12 ÷ 2
Answer:
\(\frac{12}{2}\) = 6

Question 3.
12 tens ÷ 2 tens
Answer:
\(\frac{12}{2}\) = 6

Question 4.
120 ÷ 20
Answer:
\(\frac{12}{2}\) = 6

Question 5.
12 hundreds ÷ 2 hundreds
Answer:
\(\frac{12}{2}\) = 6

Question 6.
1,200 ÷ 200
Answer:
\(\frac{12}{2}\) = 6

Question 7.
12 halves ÷ 2 halves
Answer:
\(\frac{12}{2}\) = 6

Question 8.
\(\frac{12}{2} \div \frac{2}{2}\)
Answer:
\(\frac{12}{2}\) =6

Question 9.
12 fourths ÷ 3 fourths
Answer:
\(\frac{12}{3}\) = 4

Question 10.
\(\frac{12}{4} \div \frac{3}{4}\)
Answer:
\(\frac{12}{3}\) = 4

Question 11.
\(\frac{12}{8} \div \frac{3}{8}\)
Answer:
\(\frac{12}{3}\) = 4

Question 12.
\(\frac{2}{4} \div \frac{1}{4}\)
Answer:
\(\frac{2}{1}\) = 2

Question 13.
\(\frac{1}{4} \div \frac{2}{4}\)
Answer:
\(\frac{1}{2}\)

Question 14.
\(\frac{4}{5} \div \frac{2}{5}\)
Answer:
\(\frac{4}{2}\) = 2

Question 15.
\(\frac{2}{5} \div \frac{4}{5}\)
Answer:
\(\frac{2}{4}=\frac{1}{2}\)

Question 16.
\(\frac{3}{5} \div \frac{4}{5}\)
Answer:
\(\frac{3}{4}\)

Question 17.
\(\frac{6}{8} \div \frac{2}{8}\)
Answer:
\(\frac{6}{2}\) = 3

Question 18.
\(\frac{6}{8} \div \frac{4}{8}\)
Answer:
\(\frac{6}{4}=1 \frac{1}{2}\)

Question 19.
\(\frac{6}{8} \div \frac{5}{8}\)
Answer:
\(\frac{6}{5}=1 \frac{1}{5}\)

Question 20.
\(\frac{6}{10} \div \frac{2}{10}\)
Answer:
\(\frac{6}{2}\) = 3

Question 21.
\(\frac{7}{10} \div \frac{8}{10}\)
Answer:
\(\frac{7}{8}\)

Question 22.
\(\frac{4}{10} \div \frac{7}{10}\)
Answer:
\(\frac{4}{7}\)

Question 23.
\(\frac{6}{12} \div \frac{4}{12}\)
Answer:
\(\frac{6}{4}=1 \frac{1}{2}\)

Question 24.
\(\frac{6}{12} \div \frac{2}{6}=\frac{6}{12} \div \frac{ }{12}\)
Answer:
\(\frac{6}{4}=1 \frac{1}{2}\)

Question 25.
\(\frac{8}{14} \div \frac{7}{14}\)
Answer:
\(\frac{8}{7}=1 \frac{1}{7}\)

Question 26.
\(\frac{8}{14} \div \frac{1}{2}=\frac{8}{14} \div \frac{ }{14}\)
Answer:
\(\frac{8}{7}=1 \frac{1}{7}\)

Question 27.
\(\frac{11}{14} \div \frac{2}{14}\)
Answer:
\(\frac{11}{2}=5 \frac{1}{2}\)

Question 28.
\(\frac{11}{14} \div \frac{1}{7}=\frac{11}{14} \div \frac{ }{14}\)
Answer:
\(\frac{11}{2}=5 \frac{1}{2}\)

Question 29.
\(\frac{1}{7} \div \frac{6}{14}=\frac{ }{14} \div \frac{6}{14}\)
Answer:
\(\frac{2}{6}=\frac{1}{3}\)

Question 30.
\(\frac{7}{18} \div \frac{3}{18}\)
Answer:
\(\frac{7}{3}=2 \frac{1}{3}\)

Question 31.
\(\frac{7}{18} \div \frac{1}{6}=\frac{7}{18} \div \frac{ }{18}\)
Answer:
\(\frac{7}{3}=2 \frac{1}{3}\)

Question 32.
\(\frac{1}{3} \div \frac{12}{18}=\frac{ }{18} \div \frac{12}{18}\)
Answer:
\(\frac{6}{12}=\frac{1}{2}\)

Question 33.
\(\frac{1}{6} \div \frac{4}{18}\)
Answer:
\(\frac{3}{4}\)

Question 34.
\(\frac{4}{12} \div \frac{8}{6}\)
Answer:
\(\frac{4}{16}=\frac{1}{4}\)

Question 35.
\(\frac{1}{3} \div \frac{3}{15}\)
Answer:
\(\frac{5}{3}=1 \frac{2}{3}\)

Question 36.
\(\frac{2}{6} \div \frac{1}{9}=\frac{1}{18} \div \frac{ }{18}\)
Answer:
\(\frac{6}{2}\)

Question 37.
\(\frac{1}{6} \div \frac{4}{9}\)
Answer:
\(\frac{3}{8}\)

Question 38.
\(\frac{2}{3} \div \frac{3}{4}\)
Answer:
\(\frac{8}{9}\)

Question 39.
\(\frac{1}{3} \div \frac{3}{5}\)
Answer:
\(\frac{5}{9}\)

Question 40.
\(\frac{1}{7} \div \frac{1}{2}\)
Answer:
\(\frac{2}{7}\)

Question 41.
\(\frac{5}{6} \div \frac{2}{9}\)
Answer:
\(\frac{15}{4}=3 \frac{3}{4}\)

Question 42.
\(\frac{5}{9} \div \frac{2}{6}\)
Answer:
\(\frac{10}{6}=1 \frac{2}{3}\)

Question 43.
\(\frac{5}{6} \div \frac{4}{9}\)
Answer:
\(\frac{15}{8}=1 \frac{7}{8}\)

Question 44.
\(\frac{1}{2} \div \frac{4}{5}\)
Answer:
\(\frac{5}{8}\)

Engage NY Eureka Math Grade 6 Module 4 Mid Module Assessment Answer Key

Eureka Math Grade 6 Module 4 Mid Module Assessment Answer Key

Question 1.
Yolanda is planning out her vegetable garden. She decides that her garden will be square. Below are possible sizes of the garden she will create.

a. Complete the table by continuing the pattern.

Answer:

b. Yolanda decides the length of her square vegetable garden will be 17 ft. She calculates that the area of the garden is 34 ft². Determine if Yolanda’s calculation is correct. Explain.
Answer:
A = l.w
A = 17 ft. . 17 ft.
A = 17² ft²
A = 289 ft²

Yolanda is incorrect. Instead of finding 17² (or 17 . 17), she multiplied 17 . 2, the base times the exponent.

Question 2.
Yolanda creates garden cubes to plant flowers. She will fill the cubes with soil and needs to know the amount of soil that will fill each garden cube. The volume of a cube is determined by the following formula: V = s³, where s equals the side length.

a. Represent the volume, in cubic inches, of the garden cube above using a numerical expression.
Answer:
32³ or 32 . 32 . 32

b. Evaluate the expression to determine the volume of the garden cube and the amount of soil, in cubic inches, she will need for each cube.
Answer:
32³ = 32 . 32 . 32 = 32,768

Question 3.
Explain why \(\left(\frac{1}{2}\right)^{4}=\frac{1}{16}\)
Answer:

Question 4.
Yolanda is building a patio in her backyard. She is interested in using both brick and wood for the flooring of the patio. Below is the plan she has created for the patio. All measurements are in feet.

a. Create an expression to represent the area of the patio.

Answer:
12.5(3 + x) or 37.5 + 12.5x

b. Yolanda’s husband develops another plan for the patio because he prefers the patio to be much wider than Yolanda’s plan. Determine the length of the brick section and the length of the wood section. Then, use the dimensions to write an expression that represents the area of the entire patio.

Answer:

24(2x + 4)

Question 5.
The landscaper hired for Yolanda’s lawn suggests a patio that has the same measure of wood as it has brick.

a. Express the perimeter of the patio in terms of x, first using addition and then using multiplication.
Answer:
x + x + x + 2x + 2x + x + x + x = 10x

b. Use substitution to determine if your expressions are equivalent. Explain.
Answer:
The expressions are equivalent.
Let x = 2
x + x + x + 2x + 2x + x + x + x
2 + 2 + 2 + 4 + 4 + 2 + 2 + 2 = 20
OR
10x = 10(2) = 20

Question 6.
Elena and Jorge have similar problems and find the same answer. Each determines that the solution to the problem is 24.
Elena: (14 + 42) ÷ 7 + 4²
Jorge: 14 + (42 ÷ 7) + 4²

a. Evaluate each expression to determine if both Elena and Jorge are correct.
Answer:
Elena: (14 + 42) ÷ 7 + 4²
= 56 ÷ 7 + 4²
= 56 ÷ 7 + 16
= 8 + 16 = 24

Jorge: 14 + (42 ÷ 7) + 4²
= 14 + 6 + 4²
= 14 + 6 + 16
= 20 + 16 = 36

b. Why would each find the solution of 24? What mistakes were made, if any?
Answer:
Elena followed the order of operations correctly. Jorge made a mistake. He added 14 + 42 first and then divided the sum by 7 to get 8. He did not follow the correct order of operations. He should have evaluated the parentheses first.

Question 7.
Jackson gave Lena this expression to evaluate: 14(8 + 12). Lena said that to evaluate the expression was simple; just multiply the factors 14 and 20. Jackson told Lena she was wrong. He solved it by finding the product of 14 and 8 and then adding that to the product of 14 and 12.

a. Evaluate the expression using each student’s method.

Answer:

b. Who was right in this discussion? why?
Answer:
They both were correct. Lena used the order of operations correctly to determine 280. Jackson used the distributive property to determine 280.

Engage NY Eureka Math Grade 6 Module 4 End of Module Assessment Answer Key

Eureka Math Grade 6 Module 4 End of Module Assessment Answer Key

Question 1.
Gertrude is deciding which cell phone plan is the best deal for her to buy. SuperCell charges a monthly fee of $10 and also charges $0.15 per call. She makes a note that the equation is M = 0.15C + 10, where M is the monthly charge, in dollars, and C is the number of calls placed. Global Cellular has a plan with no monthly fee but charges $0.25 per call. She makes a note that the equation is M = 0.25C, where M is the monthly charge, in dollars, and C is the number of calls placed. Both companies offer unlimited text messages.

a. Make a table for both companies showing the cost of service, M, for making from 0 to 200 calls per month. Use multiples of 20.

Answer:

b. Construct a graph for the two equations on the same graph. Use the number of calls, C, as the independent variable and the monthly charge, in dollars, M, as the dependent variable.

Answer:

c. Which cell phone plan is the best deal for Gertrude? Defend your answer with specific examples.
Answer:
The best deal depends on the number of calls placed in a month. The breakpoint is 100 calls per month. Supercell is a better deal if the number of monthly calls is less than 100. Global cellular is a better deal if the number of monthly calls is greater than 100.

Question 2.
Sadie is saving her money to buy a new pony, which costs $600. She has already saved $75. She earns $50 per week working at the stables and wonders how many weeks it will take to earn enough for a pony of her own.

a. Make a table showing the week number, W, and total savings, in dollars, S, in Sadie’s savings account.

Answer:

50w + 75

b. Show the relationship between the number of weeks and Sadie’s savings using an expression.
Answer:
If Sadie works 11 weeks, she will earn $625, which is $25 more than the cost of the pony.

Question 3.
The elevator at the local mall has a weight limit of 1,800 pounds and requires that the maximum person allowance be no more than nine people.

a. Let x represent the number of people. Write an inequality to describe the maximum allowance of people allowed in the elevator at one time.
Answer:
0 ≤ x ≤ 9

b. Draw a number line diagram to represent all possible solutions to part (a).
Answer:

c. Let w represent the amount of weight, in pounds. Write an inequality to describe the maximum weight allowance in the elevator at one time.
Answer:
0 ≤ W ≤ 1,800

d. Draw a number line to represent all possible solutions to part (c).
Answer:

Question 4.
Devin’s football team carpools for practice every week. This week is his parents’ turn to pick up team members and take them to the football field. While still staying on the roads, Devin’s parents always take the shortest route in order to save gasoline. Below is a map of their travels. Each grid line represents a street and the same distance.

Devin’s father checks his mileage and notices that he drove 18 miles between his house and Stop 3.

a. Create an equation and determine the amount of miles each gridline represents.
Answer:
Let G represent the number of grid lines passed on the map.
9G = 18
\(\frac{9G}{9}=\frac{18}{9}\)
C = 2 miles.

b. Using this information, determine how many total miles Devin’s father will travel from home to the football field, assuming he made every stop. Explain how you determined the answer.
Answer:
15 G = miles
15 (2 miles) = 30 miles

c. At the end of practice, Devin’s father dropped off team members at each stop and went back home. How many miles did Devin’s father travel altogether?
Answer:
30 G = miles
30(2 miles) = 60 miles

Question 5.
For a science experiment, Kenneth reflects a beam of a mirror. He is measuring the missing angle created when the light reflects off the mirror. (Note: The figure is not drawn to scale.)

Use an equation to determine the missing angle, labeled x in the diagram.
Answer:
A straight angle measures 180°
51° + x° + 51° = 180°
x° + 102° = 180°
x° + 102° – 102° = 180° – 102°
x° = 78°

Engage NY Eureka Math Grade 6 Module 5 End of Module Assessment Answer Key

Eureka Math Grade 6 Module 5 End of Module Assessment Answer Key

Question 1.
The juice box pictured below is 4 inches high, 3 inches long, and 2 inches wide.

a. In the grid above, the distance between grid lines represents one inch. Use the grid paper to sketch the net of the juice box.
Answer:

b. Find the surface area of the juice box. Show your work.
Answer:
SA = 2(l.w + l.h + w.h)
SA = 2(3 in. . 2 in. + 3 in. . 4 in. + 2 in. . 4 in.)
SA = 2(6 in² + 12 in² + 8 in²)
SA = 2(26 in²)
SA = 52 in²

c. Find the volume of the juice box. Show your work.
Answer:
V = l.w.h
V = 3 in. . 2 in. . 4 in.
V = 24 in²

Question 2.
The Cubic Crystal Company has a new Crystal Cube they want to sell. The packaging manager insists that the cubes be arranged to form a rectangular prism and that the package be designed to hold the Crystal Cubes exactly, with no leftover packaging. Each Crystal Cube measures 1 in. × 1 in. × 1 in. There are 24 Crystal Cubes to be sold in a box.

a. What are the dimensions of the possible box designs in inches?

Answer:

b. Which Crystal Cube box design will use the least amount of cardboard for packaging? Justify your answer as completely as you can.

Answer:

The minimum surface area is found to be on the 2 in × 3 in × 4 in box. That box needs the least amount of cardboard.

c. Another type of cube is the Mini Crystal Cube, which has an edge length of inch. What is the volume in cubic inches of one Mini Crystal Cube? Show your work.
Answer:
V = l.w.h
V = \(\frac{3}{4}\) in . \(\frac{3}{4}\) in . \(\frac{3}{4}\) in
V = \(\frac{27}{64}\) in³

Question 3.
Which of these nets can be folded to form a cube?

Answer:

Question 4.
Which box below has the larger surface area?


Answer:
SA = 2(l.w + l.h + w.h)
SA = 2(5 in. . 2 in. + 5 in. . 3in. + 2 in. . 3 in.)
SA = 2(10 in². + 15 in². + 6 in².)
SA = 2(31 in².)
SA = 62 in².

SA = 2(l.w + l.h + w.h)
SA = 2(10 in. . 1 in. + 10 in. 3 in. + 1 in. . 3 in.)
SA = 2(10 in² + 30 in². + 3 in².)
SA = 2(43 in².)
SA = 86 in²
This box has the larger surface area.

Question 5.

a. Draw a polygon in the coordinate plane using the given coordinates.

(4, -4)
(6, -2)
(8, -6)
Answer:

b. Calculate the area of the polygon.
Answer:
Area of Square:
A = l.w or S²
A = 4 u. 4 u or (4 u)²
A = 16 u²

Area of Triangle 1:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) 2 u . 2u
A = 2 u²

Area of Triangle 2:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) 2 u . 4 u
A = 4 u²

Area of Triangle 3:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\) . 2 u . 4 u
A = 4 u²

Area of Triangle 4 = 16 u² – 2 u² – 4 u² – 4 u² = 6 u²

Question 6.
Eaglecrest Elementary School is creating a vegetable garden at the school.

a. What is the area of the garden?

Answer:
A = b.h
A = 25 ft . 6 ft
A = 150 ft²

b. After more discussion, Eaglecrest decided to change the location of the garden so that the vegetables can get more sunlight. Below is the new garden.

In which garden can eagle crest students plant more vegetables? Explain your reasoning.
Answer:
A = \(\frac{1}{2}\) bh
A = \(\frac{1}{2}\)(7 ft. . 28 ft.)
A = \(\frac{1}{2}\) (194 ft²)
A = 98 ft²

The students of Eaglecrest can plant more vegetables in original garden in the shape of a parallelogram. It has a larger area than the triangular prism.