Prasanna

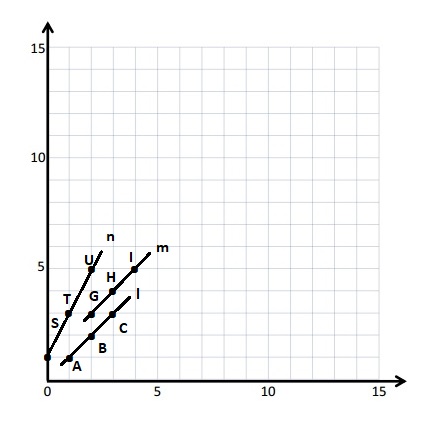
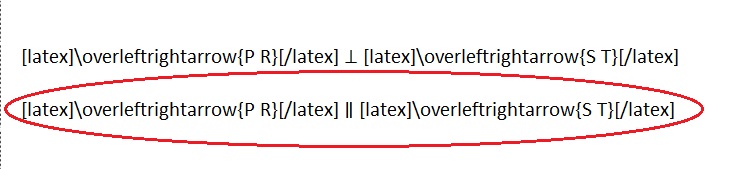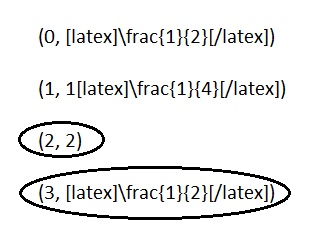Engage NY Eureka Math 5th Grade Module 6 Lesson 16 Answer Key

Eureka Math Grade 5 Module 6 Lesson 16 Problem Set Answer Key

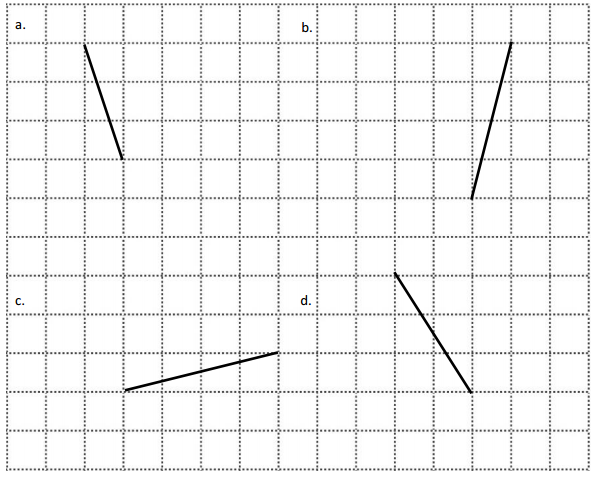
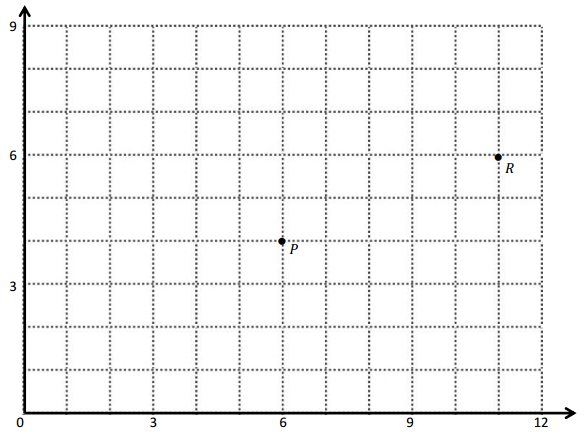
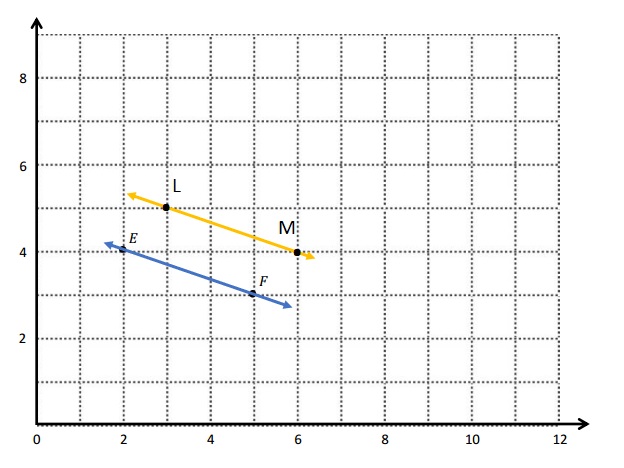
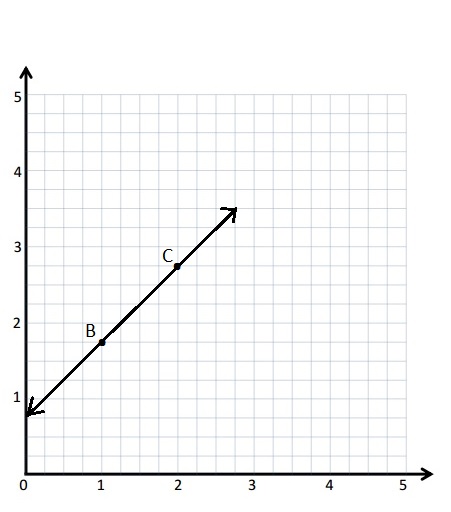
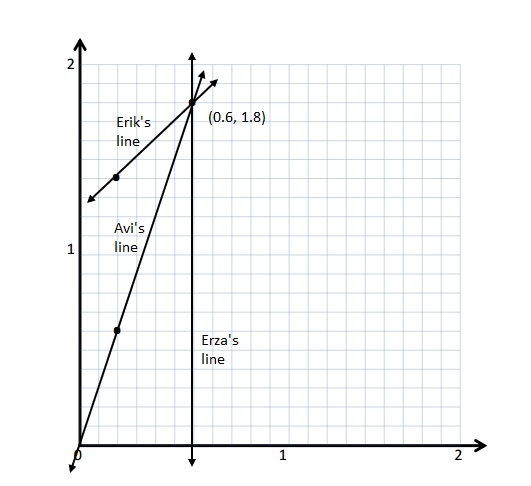
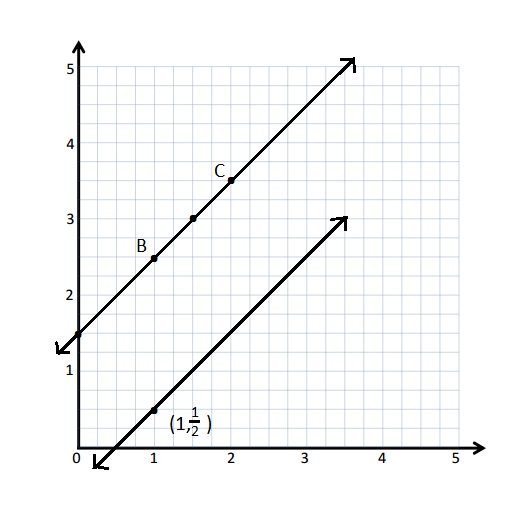
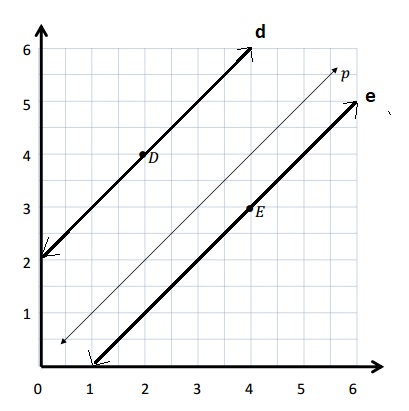
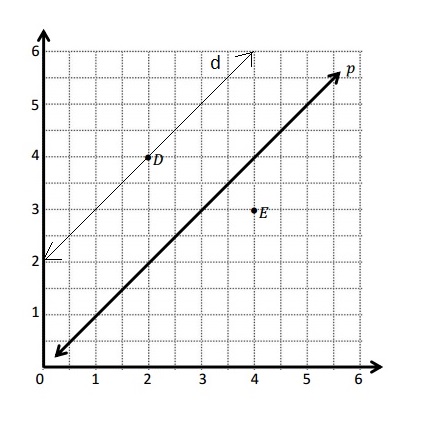
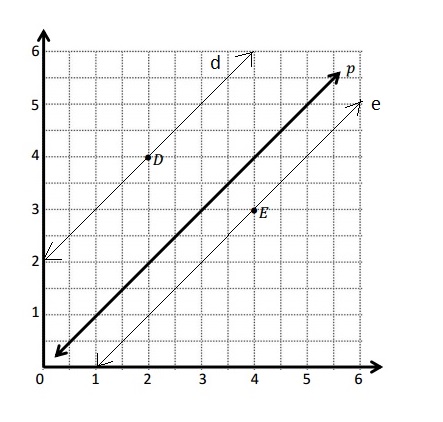
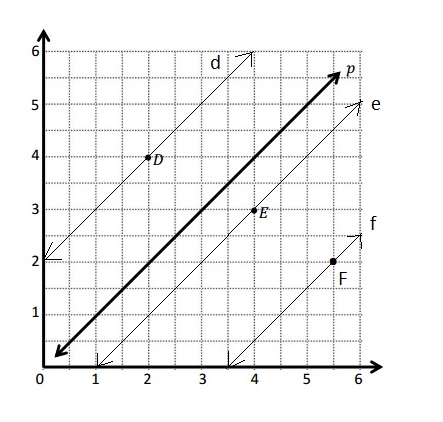
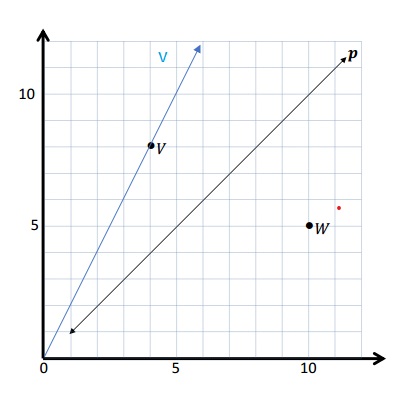
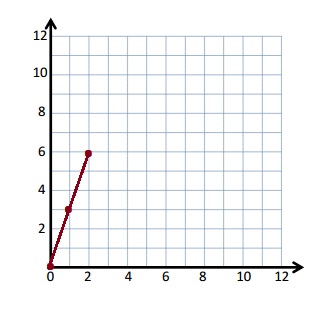
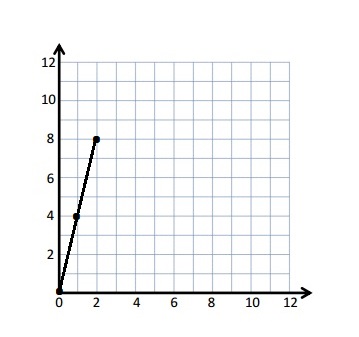
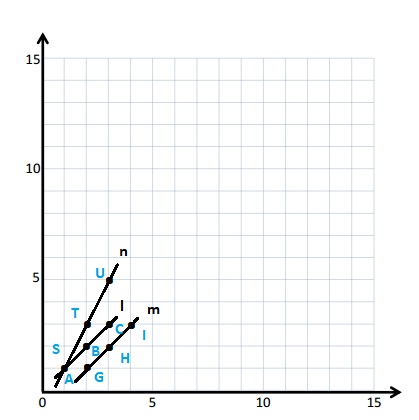
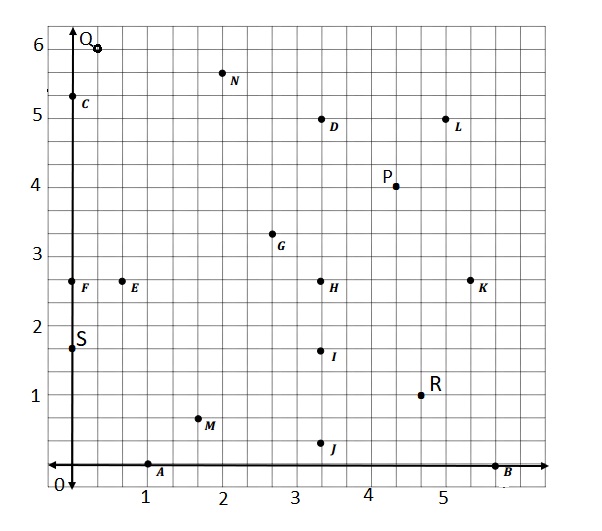
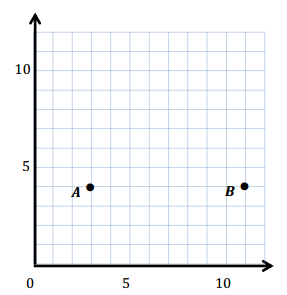
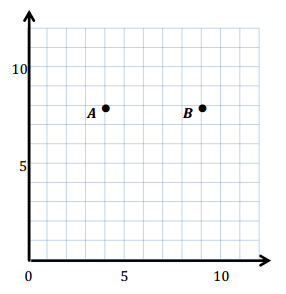
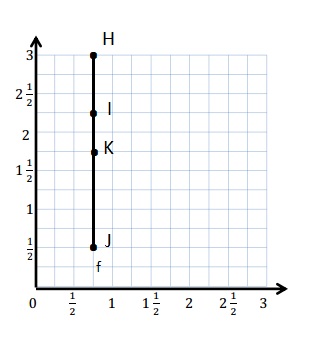
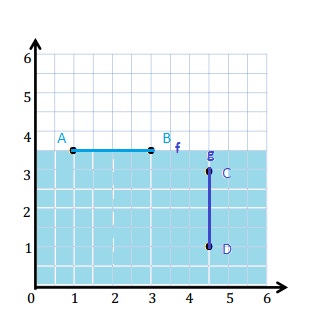
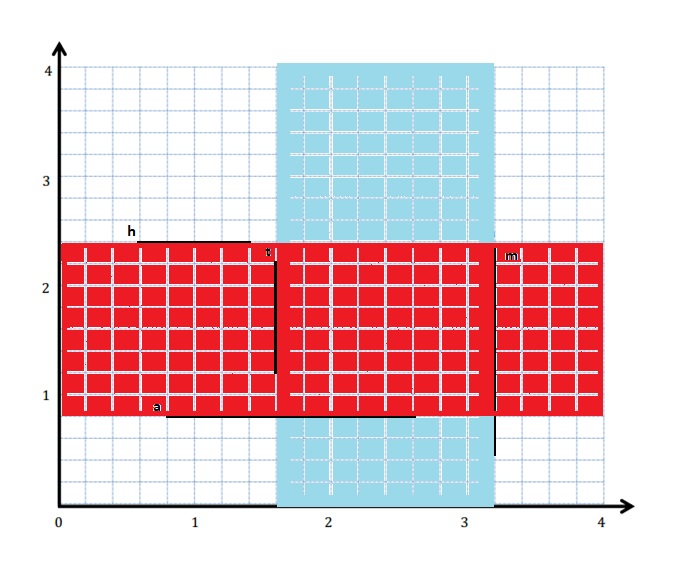
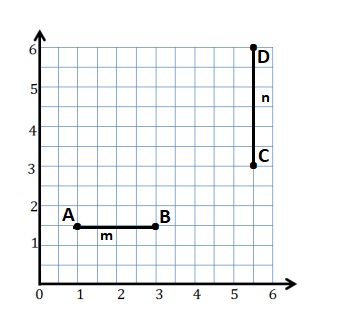
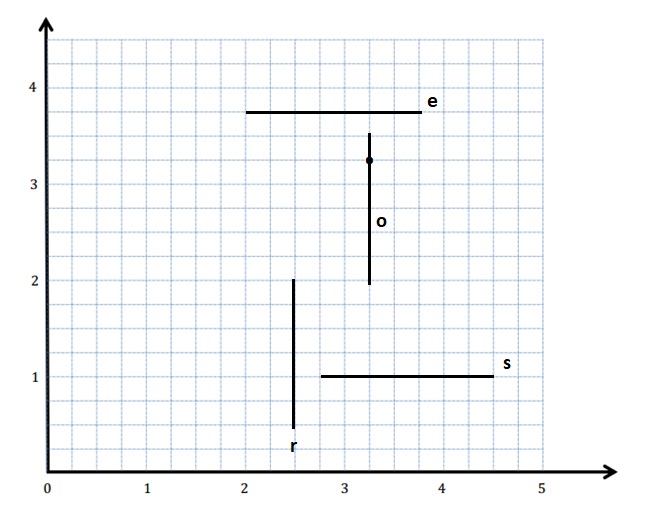
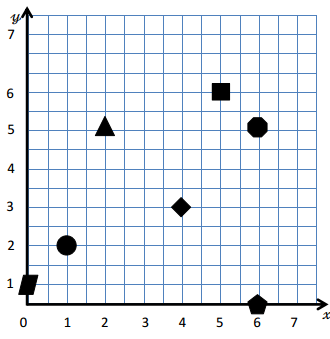
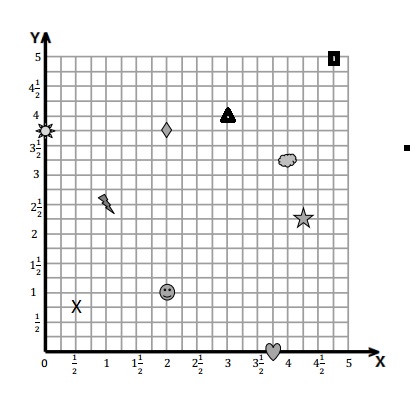
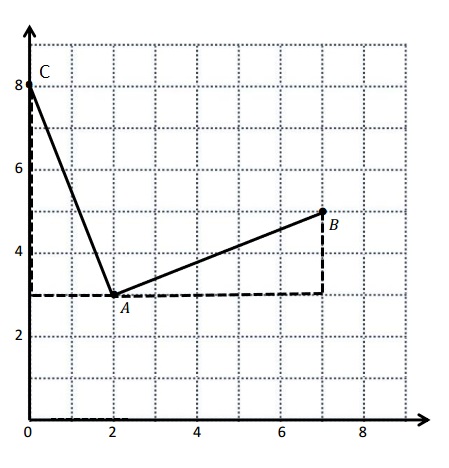
Question 1.
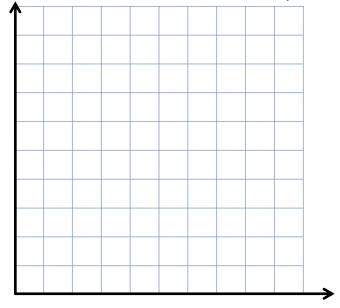
Use the coordinate plane below to complete the following tasks.

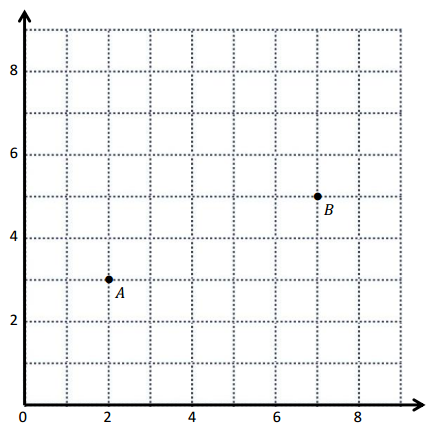
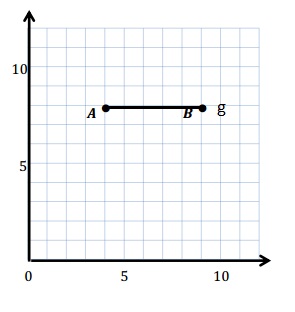
a. Draw \(\overline{A B}\).
b. Plot point C (0, 8).
c. Draw \(\overline{A C}\).
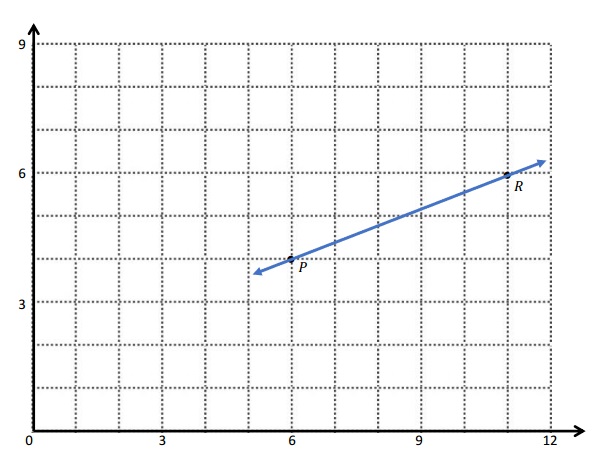
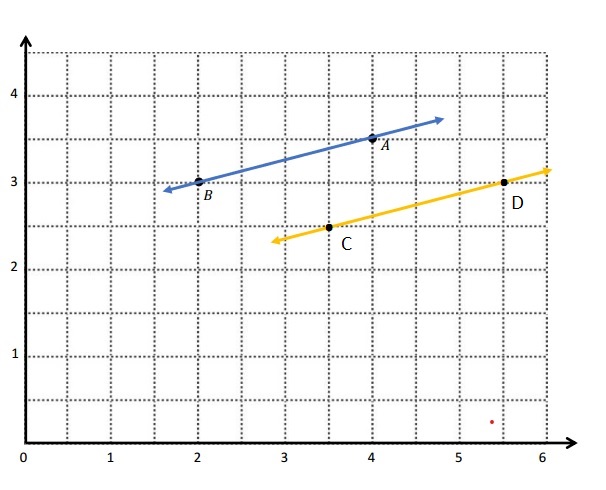
d. Explain how you know ∠CAB is a right angle without measuring it.
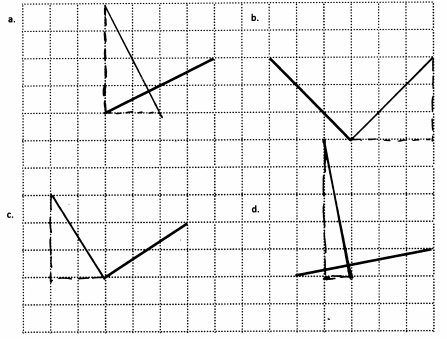
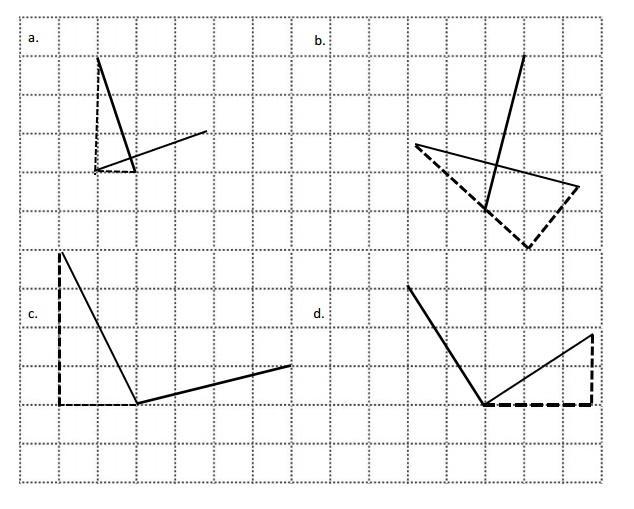
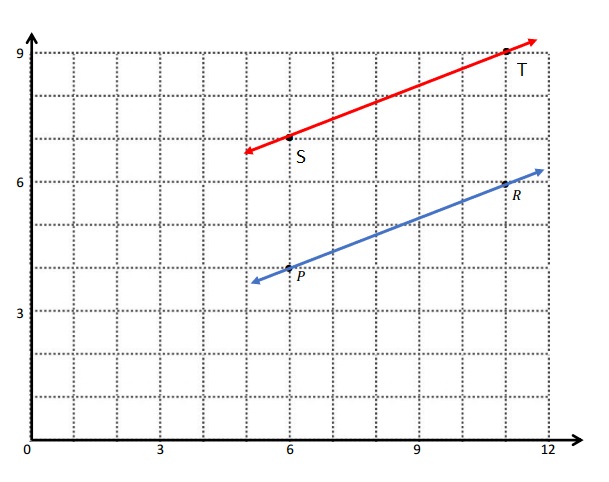
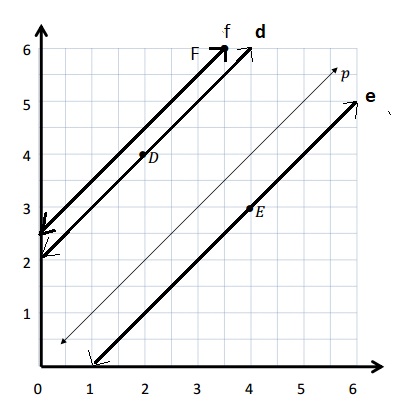
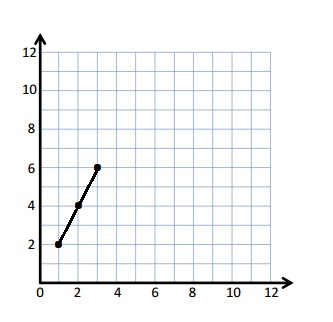
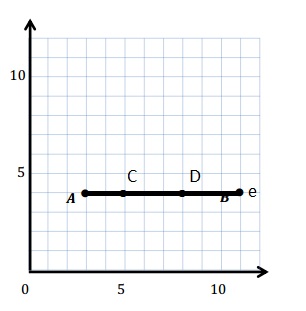
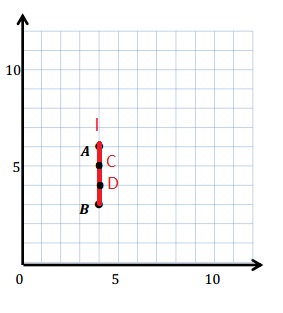
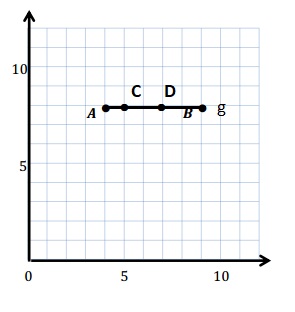
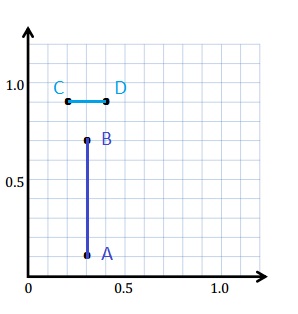
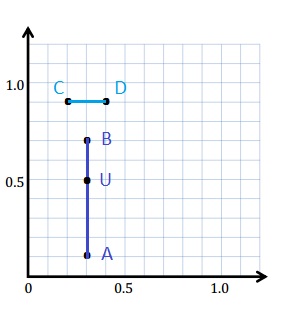
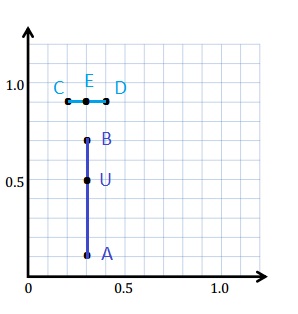
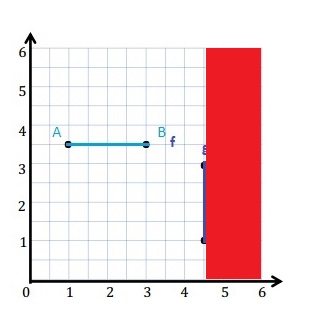
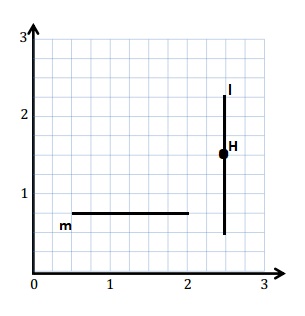
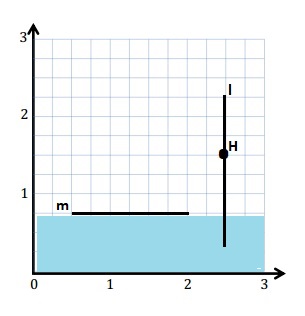
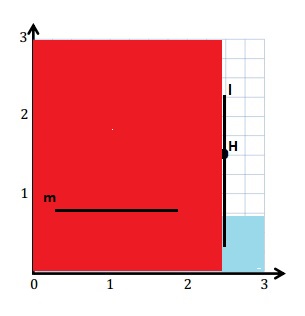
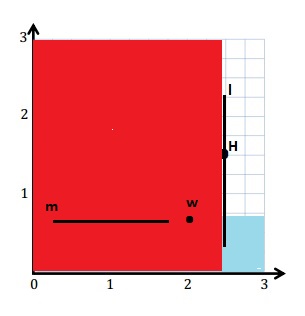
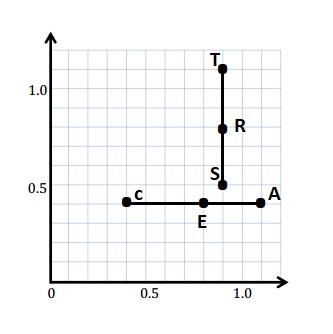
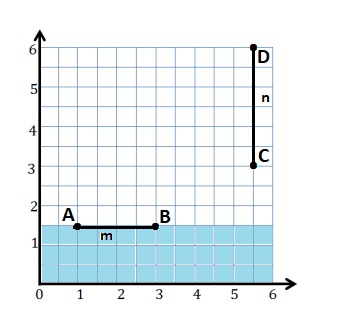
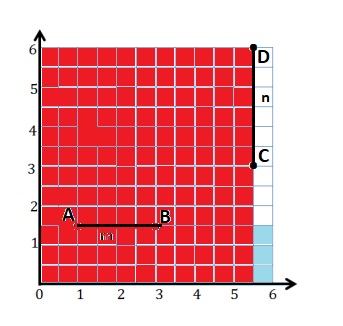
e. Sean drew the picture below to find a segment perpendicular to (AB) ̅. Explain why Sean is correct.

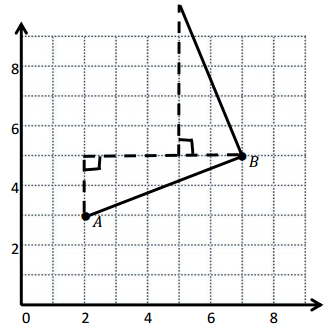
Answer:

d.
Explanation :
∠CAB is a right angle because I can Draw a triangle that has \(\overline{A B}\) has its long side. The length is 5 units and the Height is 2 units . When I slide the triangle to the left and rotated, I know 2 acute angles will form a 90 degrees or right angle .
e.
Sean is correct because I notice that he slid and rotated the triangle and the 2 acute angles form the right angle .

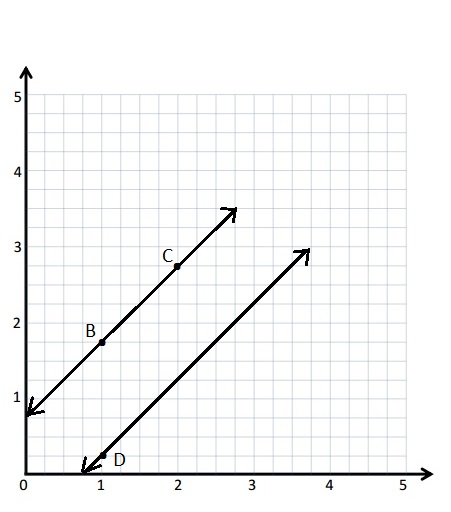
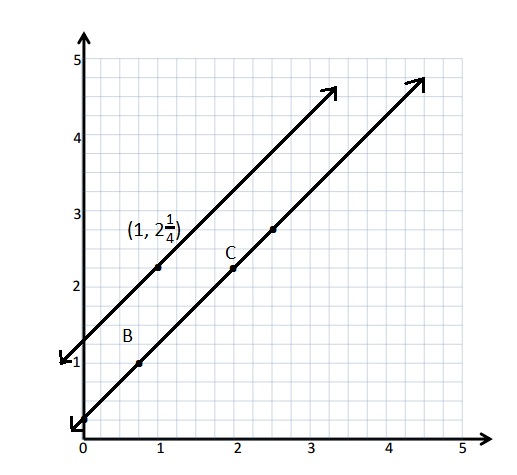
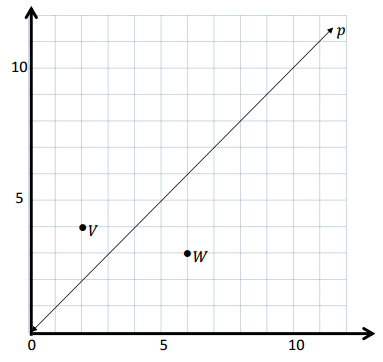
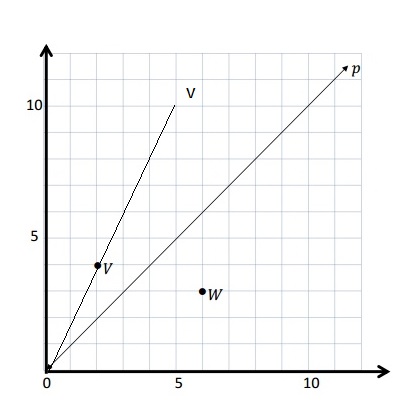
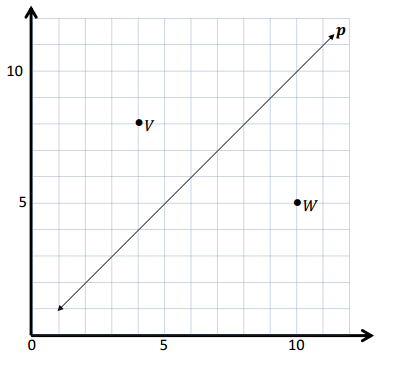
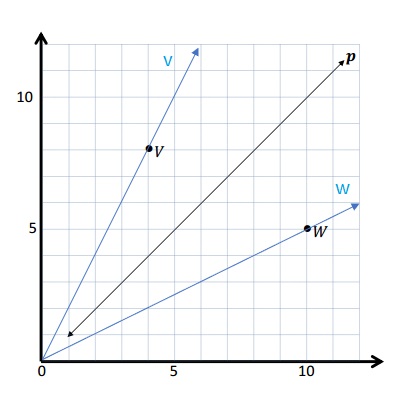
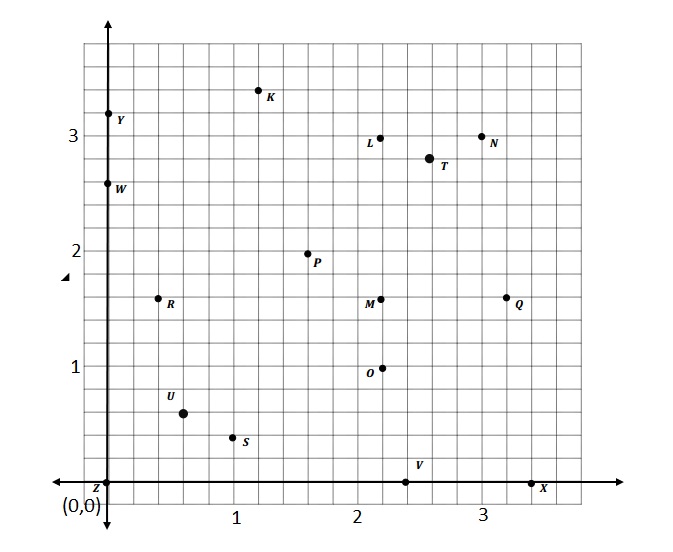
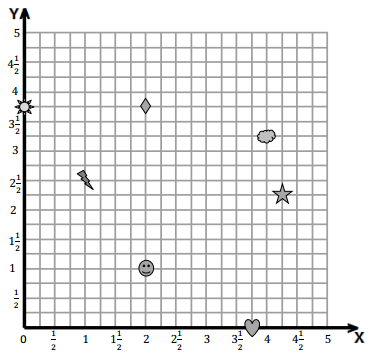
Question 2.
Use the coordinate plane below to complete the following tasks.

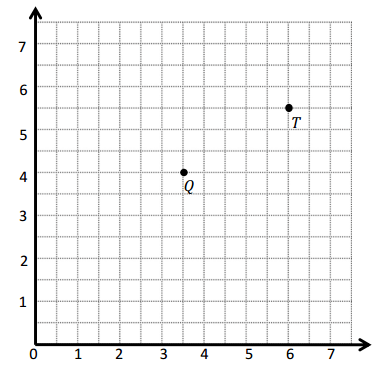
a. Draw \(\overline{Q T}\).
b. Plot point R (2, 6\(\frac{1}{2}\)).
c. Draw \(\overline{Q R}\).
d. Explain how you know ∠RQT is a right angle without measuring it.
e. Compare the coordinates of points Q and T. What is the difference of the x-coordinates? The y-coordinates?
f. Compare the coordinates of points Q and R. What is the difference of the x-coordinates? The y-coordinates?
g. What is the relationship of the differences you found in parts (e) and (f) to the triangles of which these two segments are a part?
Answer:

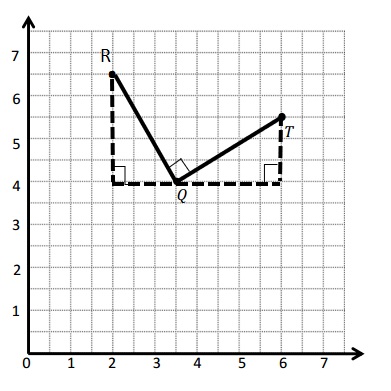
d.
Explanation :
Triangles are drawn when I slid and rotated the triangle. I know that 2 acute angles will form 90 degrees. If they form 90 degrees the angle between them , ∠RQT will be 90 degrees Since the 3 angles form a straight line .
e. The coordinates of points Q and T are ( 3\(\frac{1}{2}\) , 4 ) and (6, 5\(\frac{1}{2}\)) Respectively .
The differences of x- coordinate = 6 – 3\(\frac{1}{2}\)= 2\(\frac{1}{2}\) .
The difference of y-coordinate = 5\(\frac{1}{2}\) – 4 = 1\(\frac{1}{2}\).
f. The coordinates of points Q and R are ( 3\(\frac{1}{2}\) , 4 ) and (2, 6\(\frac{1}{2}\)) Respectively .
The differences of x- coordinate = 3\(\frac{1}{2}\) – 2 = 1\(\frac{1}{2}\) .
The difference of y-coordinate = 6\(\frac{1}{2}\) – 4 = 2\(\frac{1}{2}\).
g. The differences in the X-coordinate of the points Q and T is same as the differences in the Y-coordinate of the points Q and R .
The differences in the Y-coordinate of the points Q and T is same as the differences in the X-coordinate of the points Q and R. Just        the Numbers flipped.

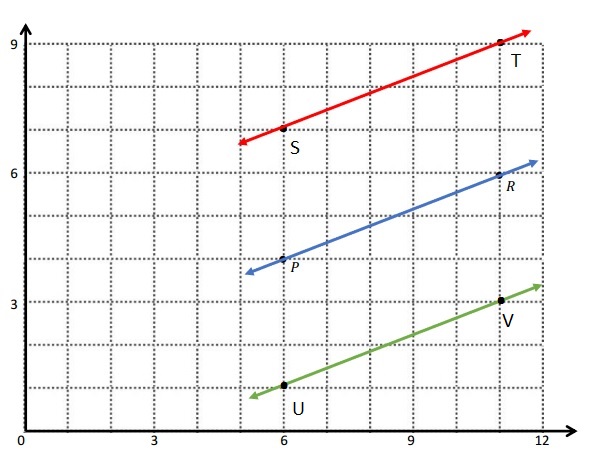
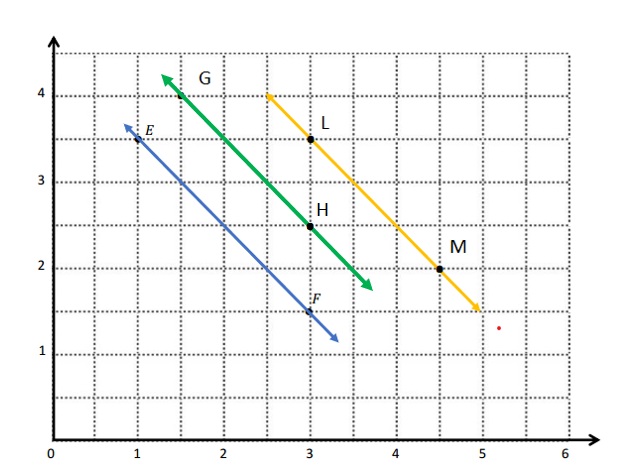
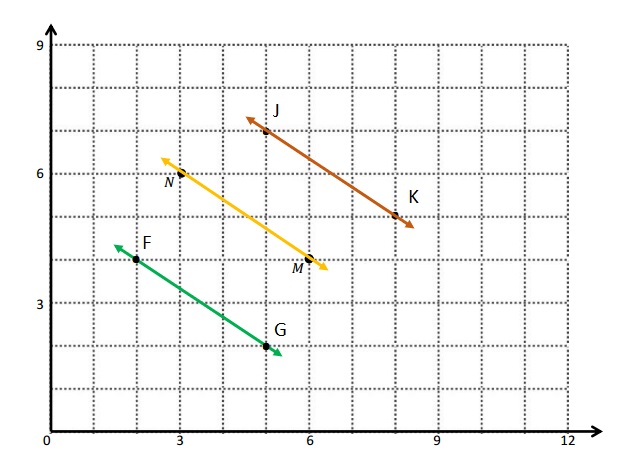
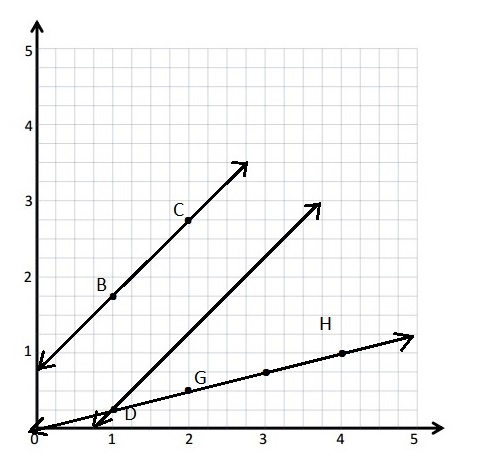
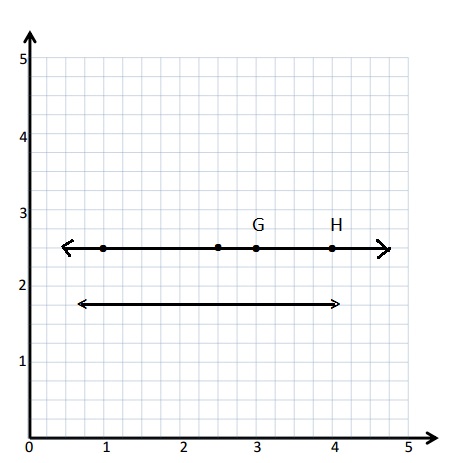
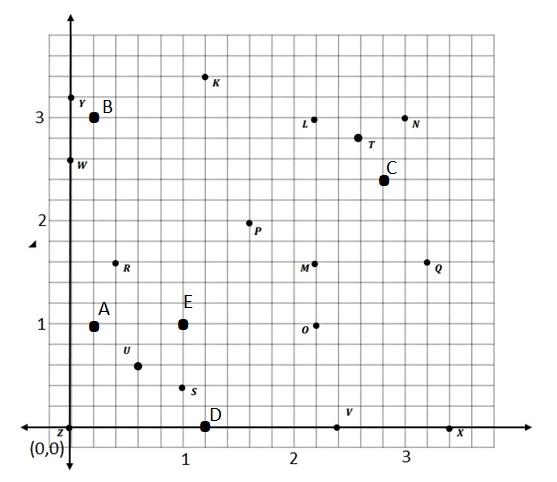
Question 3.
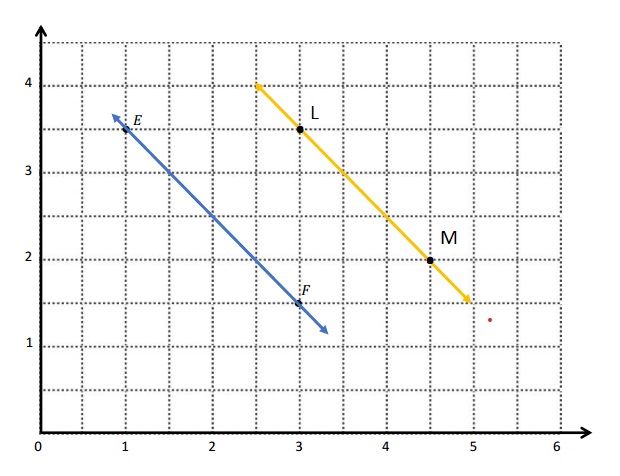
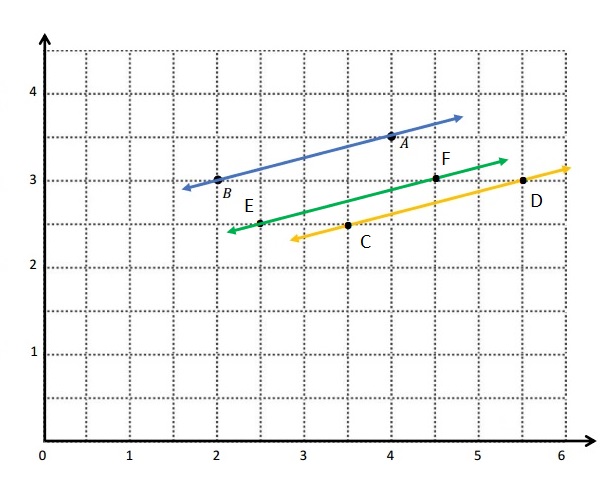
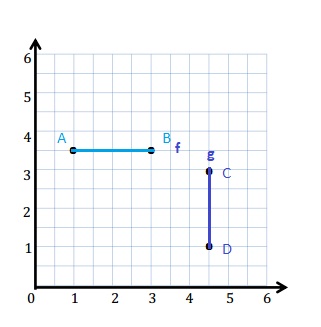
\(\overline{E F}\) contains the following points. E: (4, 1) F: (8, 7)
Give the coordinates of a pair of points G and H, such that \(\overline{E F}\) ⊥ \(\overline{G H}\).
G: (_____, _____) H: (_____, _____)
Answer:
As the above rule is applied of Question -2-g and the Coordinate of Points are written .
G: (1, 8) H: ( 7, 4)

Eureka Math Grade 5 Module 6 Lesson 16 Exit Ticket Answer Key

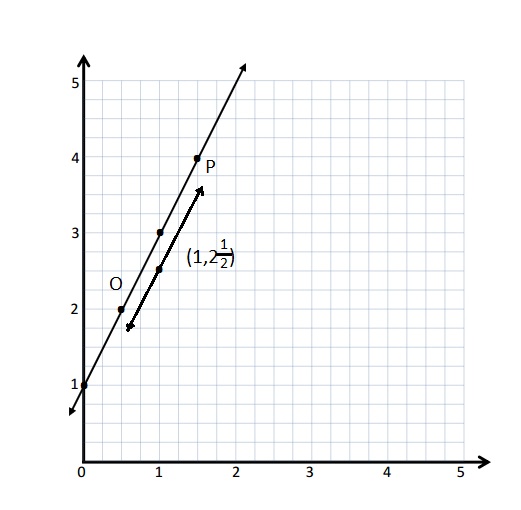
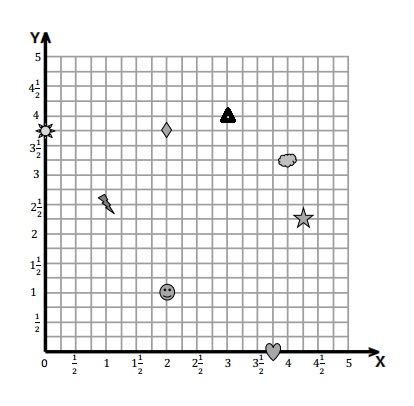
Use the coordinate plane below to complete the following tasks.
a. Draw \(\overline{U V}\).
b. Plot point W (4\(\frac{1}{2}\),6).
c. Draw \(\overline{V W}\).
d. Explain how you know that ∠UVW is a right angle without measuring it.

Answer:

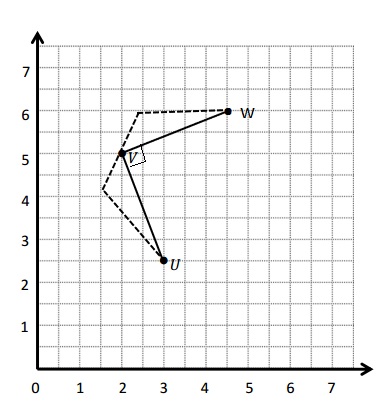
d.
Explanation :
Triangles are drawn when I slid and rotated the triangle. I know that 2 acute angles will form 90 degrees. If they form 90 degrees the angle between them , ∠UVW will be 90 degrees Since the 3 angles form a straight line .

Eureka Math Grade 5 Module 6 Lesson 16 Homework Answer Key

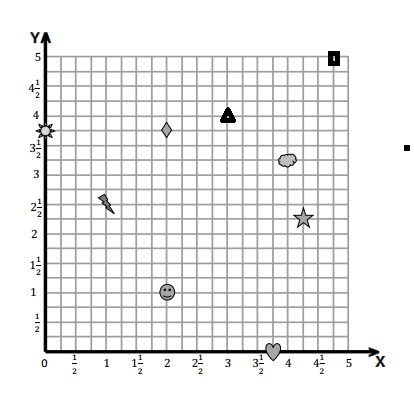
Question 1.
Use the coordinate plane below to complete the following tasks.

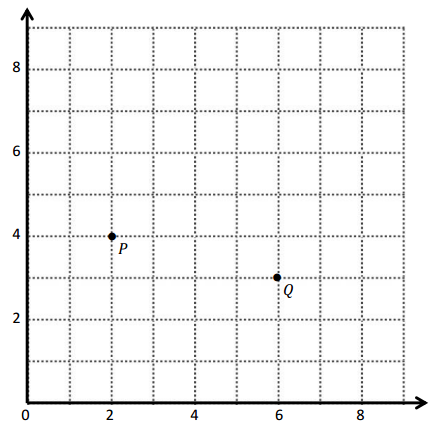
a. Draw \(\overline{P Q}\).
b. Plot point R (3, 8).
c. Draw \(\overline{P R}\).
d. Explain how you know ∠RPQ is a right angle without measuring it.
e. Compare the coordinates of points P and Q. What is the difference of the x-coordinates? The y-coordinates?
f. Compare the coordinates of points P and R. What is the difference of the x-coordinates? The y-coordinates?
g. What is the relationship of the differences you found in parts (e) and (f) to the triangles of which these two segments are a part?
Answer:

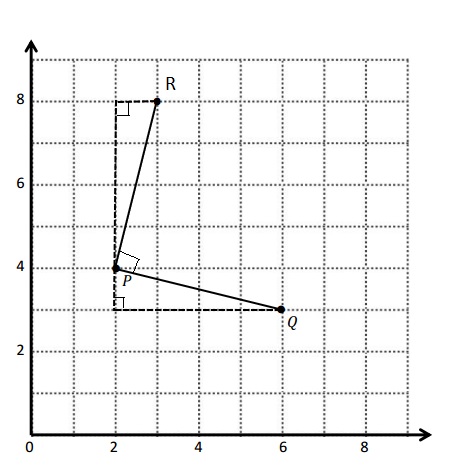
d. Explanation :
Triangles are drawn when I slid and rotated the triangle. I know that 2 acute angles will form 90 degrees. If they form 90 degrees the angle between them , ∠RPQ will be 90 degrees Since the 3 angles form a straight line .
e. The coordinates of points P and Q are ( 2, 4 ) and (6, 3) Respectively .
The differences of x- coordinate = 6 – 2= 4 .
The difference of y-coordinate = 4- 3 = 1.
f. The coordinates of points P and R are ( 2, 4 ) and ( 3, 8 ) Respectively .
The differences of x- coordinate = 3 – 2 = 1
The difference of y-coordinate = 8 – 4 = 4
g. The differences in the X-coordinate of the points P and Q  is same as the differences in the Y-coordinate of the points P and R .
The differences in the Y-coordinate of the points P and Q is same as the differences in the X-coordinate of the points P and R . Just        the Numbers flipped.

Question 2.
Use the coordinate plane below to complete the following tasks.

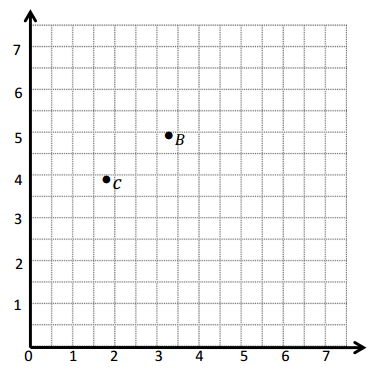
a. Draw \(\overline{C B}\).
b. Plot point D(\(\frac{1}{2}\), 5\(\frac{1}{2}\)).
c. Draw \(\overline{C D}\).
d. Explain how you know ∠DCB is a right angle without measuring it.
e. Compare the coordinates of points C and B. What is the difference of the x-coordinates? The y-coordinates?
f. Compare the coordinates of points C and D. What is the difference of the x-coordinates? The y-coordinates?
g. What is the relationship of the differences you found in parts (e) and (f) to the triangles of which these two segments are a part?
Answer:

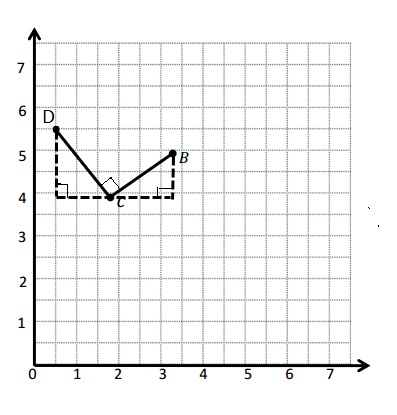
d. Explanation :
Triangles are drawn when I slid and rotated the triangle. I know that 2 acute angles will form 90 degrees. If they form 90 degrees the angle between them , ∠DCB will be 90 degrees Since the 3 angles form a straight line .
e. The coordinates of points C and B. are (1\(\frac{3}{4}\), 4 ) and (3\(\frac{1}{4}\), 5) Respectively .
The differences of x- coordinate = 3\(\frac{1}{4}\) – 1\(\frac{3}{4}\) = \(\frac{13}{4}\) –\(\frac{7}{4}\) = 1\(\frac{6}{4}\)=\(\frac{2}{3}\)
The difference of y-coordinate = 5 – 4 =1
f. The coordinates of points C and D are (1\(\frac{3}{4}\), 4 ) and (\(\frac{1}{2}\), 5\(\frac{1}{2}\)) Respectively .
The differences of x- coordinate = 1\(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{7}{4}\)– \(\frac{2}{4}\)= \(\frac{5}{4}\)= 1\(\frac{1}{4}\)
The difference of y-coordinate =5\(\frac{1}{2}\) – 4 = 1\(\frac{1}{2}\)
g. All the differences are different .No Relationship is formed .

Question 3.
\(\overline{S T}\) contains the following points. S: (2, 3) T: (9, 6)
Give the coordinates of a pair of points, U and V, such that \(\overline{S T}\) ⊥ \(\overline{S T}\).
U: (_____, _____) V: (_____, _____)
Answer:

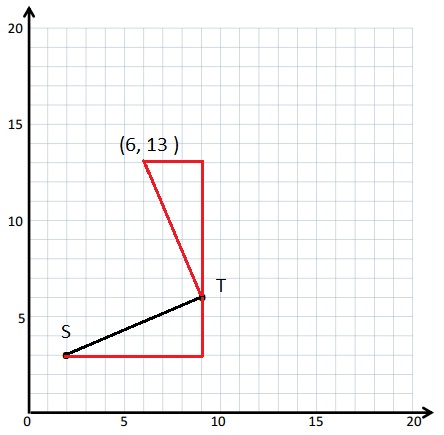
the coordinates of a pair of points, U and V, such that \(\overline{S T}\) ⊥ \(\overline{S T}\).
U: (, ) V: (_____, _____)
The coordinates of points S and T are(2, 3) and (9, 6) Respectively .
The differences of x- coordinate = 9 – 2= 7 .
The difference of y-coordinate = 6- 3 = 3.

The coordinates of points T and (6, 13) are (9, 6) and (6, 13)
The differences of x- coordinate = 9 – 6 = 3
The difference of y-coordinate = 13 – 6 = 7

The differences in the X-coordinate of the points S and T  is same as the differences in the Y-coordinate of the points T and (6, 13) .
The differences in the Y-coordinate of the points S and T is same as the differences in the X-coordinate of the points T and (6, 13) .        Just the Numbers flipped.
U: (3, 9) V: (6, 2)

Engage NY Eureka Math 5th Grade Module 6 Lesson 15 Answer Key

Eureka Math Grade 5 Module 6 Lesson 15 Problem Set Answer Key

Question 1.
Circle the pairs of segments that are perpendicular.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 2.
In the space below, use your right triangle templates to draw at least 3 different sets of perpendicular lines.
Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 3.
Draw a segment perpendicular to each given segment. Show your thinking by sketching triangles as needed.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 4.
Draw 2 different lines perpendicular to line e.

Explanation :

Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.
Answer:

Eureka Math Grade 5 Module 6 Lesson 15 Exit Ticket Answer Key

Draw a segment perpendicular to each given segment. Show your thinking by sketching triangles as needed.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Eureka Math Grade 5 Module 6 Lesson 15 Homework Answer Key

Question 1.
Circle the pairs of segments that are perpendicular.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 2.
In the space below, use your right triangle templates to draw at least 3 different sets of perpendicular lines.
Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 3.
Draw a segment perpendicular to each given segment. Show your thinking by sketching triangles as needed.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Question 4.
Draw 2 different lines perpendicular to line b.

Answer:

Explanation :
Perpendicular line means A line is said to be perpendicular to another line if the two lines intersect at a right angle.

Engage NY Eureka Math 5th Grade Module 6 Lesson 14 Answer Key

Eureka Math Grade 5 Module 6 Lesson 14 Problem Set Answer Key

Question 1.
Use the coordinate plane below to complete the following tasks.

a. Identify the locations of P and R. P: (_____, _____) R: (_____, _____)
b. Draw \(\overleftrightarrow{P R}\).
c. Plot the following coordinate pairs on the plane.
S: (6, 7) T: (11, 9)
d. Draw \(\overleftrightarrow{S T}\).
e. Circle the relationship between \(\overleftrightarrow{P R}\) and \(\overleftrightarrow{S T}\).
\(\overleftrightarrow{P R}\) ⊥ \(\overleftrightarrow{S T}\)
\(\overleftrightarrow{P R}\) ∥ \(\overleftrightarrow{S T}\)
f. Give the coordinates of a pair of points, U and V, such that \(\overleftrightarrow{U V}\) ∥ \(\overleftrightarrow{P R}\).
U: (_____, _____) V: (_____, _____)
g. Draw \(\overleftrightarrow{U V}\).
Answer:
a. The locations of P and R. P: (6, 4) R: (11, 6) .
b.

c.

e.

Explanation :
Both the lines are equidistant from each other so, the \(\overleftrightarrow{P R}\) is parallel to  \(\overleftrightarrow{S T}\) .
f. The coordinate points of u and v are U ( 6, 1) and V (11, 3)
g.

Question 2.
Use the coordinate plane below to complete the following tasks.

a. Identify the locations of E and F. E: (_____, _____) F: (_____, _____)
b. Draw \(\overleftrightarrow{E F}\).
c. Generate coordinate pairs for L and M, such that \(\overleftrightarrow{E F}\) ∥ \(\overleftrightarrow{L M}\).
L: (____, ____) M: (____, ____)
d. Draw \(\overleftrightarrow{L M}\).
e. Explain the pattern you made use of when generating coordinate pairs for L and M.
f. Give the coordinates of a point, H, such that \(\overleftrightarrow{E F}\) ∥ \(\overleftrightarrow{G H}\).
G: (1\(\frac{1}{2}\), 4) H: (____, ____)
g. Explain how you chose the coordinates for H.
Answer:
a. The locations of E and F. E: (1,3\(\frac{1}{2}\) ) F: (3, 1\(\frac{1}{2}\))
b.

c. The L and M points are L ( 3, 3\(\frac{1}{2}\)) and M ( 4\(\frac{1}{2}\), 2)
d.

e. The pattern made when generating coordinate pairs for L and M are parallel lines .
f. G: (1\(\frac{1}{2}\), 4) H: (3, 2\(\frac{1}{2}\))
g. The the coordinates for H is choose such that the latex]\overleftrightarrow{E F}[/latex] ∥ \(\overleftrightarrow{G H}\).
Explanation :
Plot the point G and then draw a parallel line from Point G such a way that it should be parallel to latex]\overleftrightarrow{E F}[/latex] .
After that take a point H on that parallel line .

Eureka Math Grade 5 Module 6 Lesson 14 Exit Ticket Answer Key

Use the coordinate plane below to complete the following tasks.

a. Identify the locations of E and F. E: (_____, _____) F: (_____, _____)
b. Draw \(\overleftrightarrow{E F}\).
c. Generate coordinate pairs for L and M, such that \(\overleftrightarrow{E F}\)∥\(\overleftrightarrow{L M}\).
L: (____, ____) M: (____, ____)
d. Draw \(\overleftrightarrow{L M}\).
Answer:
a. The locations of E and F. E: (2, 4) F: (5, 3) .
b.

c. The coordinate pairs for L and M, such that \(\overleftrightarrow{E F}\)∥\(\overleftrightarrow{L M}\) are
L: (3, 5) M: (6, 4)
d.

Eureka Math Grade 5 Module 6 Lesson 14 Homework Answer Key

Question 1.
Use the coordinate plane below to complete the following tasks.

a. Identify the locations of M and N. M: (_____, _____) N: (_____, _____)
b. Draw \(\overleftrightarrow{M N}\).
c. Plot the following coordinate pairs on the plane.
J: (5, 7) K: (8, 5)
d. Draw \(\overleftrightarrow{J K}\).
e. Circle the relationship between \(\overleftrightarrow{M N}\) and \(\overleftrightarrow{J K}\).
\(\overleftrightarrow{M N}\) ⊥ \(\overleftrightarrow{J K}\)
\(\overleftrightarrow{M N}\) ∥ \(\overleftrightarrow{J K}\)
f. Give the coordinates of a pair of points, F and G, such that \(\overleftrightarrow{F G}\) ∥ \(\overleftrightarrow{M N}\).
F: (_____, _____) G: (_____, _____)
g. Draw \(\overleftrightarrow{F G}\).
Answer:
a. The locations of M and N. M: (6, 4) N: (3, 6)
b.
c. The J and K are plotted on the graph .
d.

e.

Explanation :
\(\overleftrightarrow{M N}\) and \(\overleftrightarrow{J K}\) are Equidistant from each other so, parallel lines .

f. The coordinates of a pair of points, F and G, such that \(\overleftrightarrow{F G}\) ∥ \(\overleftrightarrow{M N}\).
F: (2, 4) G: (5, 2)
g.

Question 2.
Use the coordinate plane below to complete the following tasks.

a. Identify the locations of A and B. A: (____, ____) B: (____, ____)
b. Draw \(\overleftrightarrow{A B}\).
c. Generate coordinate pairs for C and D, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{C D}\).
C: (____, ____) D: (____, ____)
d. Draw \(\overleftrightarrow{C D}\).
e. Explain the pattern you used when generating coordinate pairs for C and D.
f. Give the coordinates of a point, F, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{E F}\).
E: (2\(\frac{1}{2}\), 2\(\frac{1}{2}\)) F: (____, ____)
g. Explain how you chose the coordinates for F.
Answer:
a. The locations of A and B. A: (4, 3\(\frac{1}{2}\)) B: (2 , 3)
b.

c. The coordinate pairs for C and D, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{C D}\).
C: (3\(\frac{1}{2}\), 2\(\frac{1}{2}\)) D: (5\(\frac{1}{2}\), 3)
d.

e. The pattern you used when generating coordinate pairs for C and D are \(\overleftrightarrow{A B}\) ∥     \(\overleftrightarrow{C D}\).
f. The coordinates of a point, F, such that \(\overleftrightarrow{A B}\) ∥ \(\overleftrightarrow{E F}\).
E: (2\(\frac{1}{2}\), 2\(\frac{1}{2}\)) F: (4\(\frac{1}{2}\) , 3)
g.

The the coordinates for F is choose such that the latex]\overleftrightarrow{E F}[/latex] ∥ \(\overleftrightarrow{A B}\).
Explanation :
Plot the point E and then draw a parallel line from Point E such a way that it should be parallel to latex]\overleftrightarrow{A B}[/latex] .
After that take a point F on that parallel line .

Engage NY Eureka Math 5th Grade Module 6 Lesson 11 Answer Key

Eureka Math Grade 5 Module 6 Lesson 11 Sprint Answer Key

A
Round to the Nearest One

Question 1.
3.1 ≈
Answer:
3.1 ≈ 3

Question 2.
3.2 ≈
Answer:
3.2 ≈ 3

Question 3.
3.3 ≈
Answer:
3.3 ≈ 3

Question 4.
3.4 ≈
Answer:
3.4 ≈ 3

Question 5.
3.5 ≈
Answer:
3.5 ≈ 4

Question 6.
3.6 ≈
Answer:
3.6 ≈ 4

Question 7.
3.9 ≈
Answer:
3.9 ≈ 4

Question 8.
13.9 ≈
Answer:
13.9 ≈ 14

Question 9.
13.1 ≈
Answer:
13.1 ≈ 13

Question 10.
13.5 ≈
Answer:
13.5 ≈ 14

Question 11.
7.5 ≈
Answer:
7.5 ≈ 8

Question 12.
8.5 ≈
Answer:
8.5 ≈ 9

Question 13.
9.5 ≈
Answer:
9.5 ≈ 10

Question 14.
19.5 ≈
Answer:
19.5 ≈ 20

Question 15.
29.5 ≈
Answer:
29.5 ≈ 30

Question 16.
89.5 ≈
Answer:
89.5 ≈ 90

Question 17.
2.4 ≈
Answer:
2.4 ≈ 2

Question 18.
2.41 ≈
Answer:
2.41 ≈ 2

Question 19.
2.42 ≈
Answer:
2.42 ≈ 2

Question 20.
2.45 ≈
Answer:
2.45 ≈ 2

Question 21.
2.49 ≈
Answer:
2.49 ≈ 2

Question 22.
2.51 ≈
Answer:
2.51 ≈ 3

Question 23.
12.51 ≈
Answer:
12.51 ≈ 13

Question 24.
16.61 ≈
Answer:
16.61 ≈ 17

Question 25.
17.41 ≈
Answer:
17.41 ≈ 17

Question 26.
11.51 ≈
Answer:
11.51 ≈ 12

Question 27.
11.49 ≈
Answer:
11.49 ≈ 11

Question 28.
13.49 ≈
Answer:
13.49 ≈ 13

Question 29.
13.51 ≈
Answer:
13.51 ≈ 14

Question 30.
15.51 ≈
Answer:
15.51 ≈ 16

Question 31.
15.49 ≈
Answer:
15.49 ≈ 16

Question 32.
6.3 ≈
Answer:
6.3 ≈ 6

Question 33.
7.6 ≈
Answer:
7.6 ≈ 8

Question 34.
49.5 ≈
Answer:
49.5 ≈ 50

Question 35.
3.45 ≈
Answer:
3.45 ≈ 3

Question 36.
17.46 ≈
Answer:
17.46 ≈ 17

Question 37.
11.76 ≈
Answer:
11.76 ≈ 12

Question 38.
5.2 ≈
Answer:
5.2 ≈ 5

Question 39.
12.8 ≈
Answer:
12.8 ≈ 13

Question 40.
59.5 ≈
Answer:
59.5 ≈ 60

Question 41.
5.45 ≈
Answer:
5.45 ≈ 5

Question 42.
19.47 ≈
Answer:
19.47 ≈ 19

Question 43.
19.87 ≈
Answer:
19.87 ≈ 20

Question 44.
69.51 ≈
Answer:
69.51 ≈ 70

B
Round to the Nearest One

Question 1.
4.1 ≈
Answer:
4.1 ≈ 4

Question 2.
4.2 ≈
Answer:
4.2 ≈ 4

Question 3.
4.3 ≈
Answer:
4.3 ≈ 4

Question 4.
4.4 ≈
Answer:
4.4 ≈ 4

Question 5.
4.5 ≈
Answer:
4.5 ≈ 5

Question 6.
4.6 ≈
Answer:
4.6 ≈ 5

Question 7.
4.9 ≈
Answer:
4.9 ≈ 5

Question 8.
14.9 ≈
Answer:
14.9 ≈ 15

Question 9.
14.1 ≈
Answer:
14.1 ≈ 14

Question 10.
14.5 ≈
Answer:
14.5 ≈ 15

Question 11.
7.5 ≈
Answer:
7.5 ≈ 8

Question 12.
8.5 ≈
Answer:
8.5 ≈ 9

Question 13.
9.5 ≈
Answer:
9.5 ≈ 10

Question 14.
19.5 ≈
Answer:
19.5 ≈ 20

Question 15.
29.5 ≈
Answer:
29.5 ≈ 30

Question 16.
79.5 ≈
Answer:
79.5 ≈ 80

Question 17.
3.4 ≈
Answer:
3.4 ≈ 3

Question 18.
3.41 ≈
Answer:
3.41 ≈ 3

Question 19.
3.42 ≈
Answer:
3.42 ≈ 3

Question 20.
3.45 ≈
Answer:
3.45 ≈ 3

Question 21.
3.49 ≈
Answer:
3.49 ≈ 3

Question 22.
3.51 ≈
Answer:
3.51 ≈ 4

Question 23.
13.51 ≈
Answer:
13.51 ≈ 14

Question 24.
17.61 ≈
Answer:
17.61 ≈ 18

Question 25.
18.41 ≈
Answer:
18.41 ≈ 18

Question 26.
12.51 ≈
Answer:
12.51 ≈ 13

Question 27.
12.49 ≈
Answer:
12.49 ≈ 12

Question 28.
14.49 ≈
Answer:
14.49 ≈ 14

Question 29.
14.51 ≈
Answer:
14.51 ≈ 15

Question 30.
16.51 ≈
Answer:
16.51 ≈ 17

Question 31.
16.49 ≈
Answer:
16.49 ≈ 16

Question 32.
7.3 ≈
Answer:
7.3 ≈ 7

Question 33.
8.6 ≈
Answer:
8.6 ≈ 9

Question 34.
39.5 ≈
Answer:
39.5 ≈ 40

Question 35.
4.45 ≈
Answer:
4.45 ≈ 4

Question 36.
18.46 ≈
Answer:
18.46 ≈ 18

Question 37.
12.76 ≈
Answer:
12.76 ≈ 13

Question 38.
6.2 ≈
Answer:
6.2 ≈ 6

Question 39.
13.8 ≈
Answer:
13.8 ≈ 14

Question 40.
49.5 ≈
Answer:
49.5 ≈ 50

Question 41.
6.45 ≈
Answer:
6.45 ≈ 6

Question 42.
19.48 ≈
Answer:
19.48 ≈ 19

Question 43.
19.78 ≈
Answer:
19.78 ≈ 20

Question 44.
59.51 ≈
Answer:
59.51 ≈ 60

Eureka Math Grade 5 Module 6 Lesson 11 Problem Set Answer Key

Question 1.
Complete the tables for the given rules.

Line l
Rule: Double x

Line m
Rule: Double x, and then add 1

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule double x, and then subtract 1 would look like. Draw the line on the plane above.
Answer:
Line l
Rule: Double x
y= 2x

Line m
Rule: Double x, and then add 1
y= 2x + 1

The given points are plotted on the graph .

b. The Line l and Line m are parallel to each other.
c.
Line n
Rule: double x, and then subtract 1
y= 2x – 1

Question 2.
Circle the point(s) that the line for the rule multiply x by \(\frac{1}{3}\), and then add 1 would contain.
(0, \(\frac{1}{3}\))
(2, 1\(\frac{2}{3}\))
(1\(\frac{1}{2}\), 1\(\frac{1}{2}\))
(2\(\frac{1}{4}\), 2\(\frac{1}{4}\))
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:
a.
Rule: multiply x by \(\frac{1}{3}\),
y= x \(\frac{1}{3}\) + 1

b. Two points that fall on this line are
x = \(\frac{1}{2}\)
y = 1\(\frac{1}{6}\)
Point ( \(\frac{1}{2}\) , 1\(\frac{1}{6}\) )
x = 1
y =1\(\frac{1}{3}\)
Point (1, 1\(\frac{1}{3}\)) .

Question 3.
Complete the tables for the given rules.

Line l
Rule: Halve x

Line m
Rule: Halve x, and then add 1\(\frac{1}{2}\)

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule halve x, and then subtract 1 would look like. Draw the line on the plane above.
Answer:
Line l
Rule: Halve x

Line m
Rule: Halve x, and then add 1\(\frac{1}{2}\)
y = \(\frac{x}{2}\) + \(\frac{3}{2}\) = \(\frac{x+3}{2}\)

a.

b. Both the lines l and m are parallel to each other.
c.
Line n
Rule: halve x, and then subtract 1
y = \(\frac{x}{2}\) – 1

Question 4.
Circle the point(s) that the line for the rule multiply x by \(\frac{2}{3}\), and then subtract 1 would contain.
(1\(\frac{1}{3}\), \(\frac{1}{9}\))
(2, \(\frac{1}{3}\))
(1\(\frac{3}{2}\), 1\(\frac{1}{2}\))
(3, 1)
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:

Explanation :
Line n
Rule: multiply x by \(\frac{2}{3}\), and then subtract 1
y = \(\frac{2x}{3}\) – 1 = \(\frac{2x – 3 }{3}\)

b. The other two points that fall on this line are (6 , 3 ) and (9, 5 ) .

Eureka Math Grade 5 Module 6 Lesson 11 Exit Ticket Answer Key

Question 1.
Complete the tables for the given rules.

Line l
Rule: Triple x

Line m
Rule: Triple x, and then add 1

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
Answer:
a.
Line l
Rule: Triple x
y = 3x

Line m
Rule: Triple x, and then add 1
y = 3x + 1

b. Line m is parallel to line m and is shown in above graph .

Question 2.
Circle the point(s) that the line for the rule multiply x by \(\frac{1}{3}\), and then add 1 would contain.
(0, \(\frac{1}{2}\))
(1, 1\(\frac{1}{3}\))
(2, 1\(\frac{2}{3}\))
(3, 2\(\frac{1}{2}\))
Answer:

Explanation :
Line n
Rule: x by \(\frac{1}{3}\), and then add 1
y = \(\frac{x}{3}\) + 1 = \(\frac{ x + 3 }{3}\)

Eureka Math Grade 5 Module 6 Lesson 11 Homework Answer Key

Question 1.
Complete the tables for the given rules.

Line l
Rule: Double x

Line m
Rule: Double x, and then subtract 1

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule double x, and then add 1 would look like. Draw your prediction on the plane above.
Answer:
a.
Line l
Rule: Double x
y = 2x

Line m
Rule: Double x, and then subtract 1
y = 2x – 1

b. The l and m are parallel lines . both lines are parallel to each other .
c.
Line n
Rule: Double x, and then add 1
y = 2x +1

Question 2.
Circle the point(s) that the line for the rule multiply x by \(\frac{1}{2}\), and then add 1 would contain.
(0, \(\frac{1}{2}\))
(1, 1\(\frac{1}{4}\))
(2, 2)
(3, \(\frac{1}{2}\))
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:
a.

Explanation :
Rule: x by \(\frac{1}{2}\), and then add 1
y = \(\frac{x}{2}\) + 1 = \(\frac{ x + 2 }{2}\)

b. The other two points are (4, 3) and ( 6, 4)

Question 3.
Complete the tables for the given rules.

Line l
Rule: Halve x, and then add 1

Line m
Rule: Halve x, and then add 1\(\frac{1}{4}\)

a. Draw each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what the line for the rule halve x, and then subtract 1 would look like. Draw your prediction on the plane above.
Answer:
a.
Line l
Rule: Halve x, and then add 1
y = \(\frac{x}{2}\) + 1 = \(\frac{ x + 2 }{2}\)

Line m
Rule: Halve x, and then add 1\(\frac{1}{4}\)
y = \(\frac{x}{2}\) + \(\frac{5}{4}\) = \(\frac{ 2x + 5 }{4}\)

b. Line l and line m are parallel to each other and is shown in above graph .
c.
Line n
Rule: halve x, and then subtract 1
y = \(\frac{x}{2}\) – 1 = \(\frac{ x – 2 }{2}\) .

Question 4.
Circle the point(s) that the line for the rule multiply x by \(\frac{3}{4}\), and then subtract \(\frac{1}{2}\) would contain.
(1, \(\frac{1}{4}\))
(2, \(\frac{1}{4}\))
(3, 1\(\frac{3}{4}\))
(3, 1)
a. Explain how you know.
b. Give two other points that fall on this line.
Answer:
a.

Explanation :
Rule: multiply x by \(\frac{3}{4}\), and then subtract \(\frac{1}{2}\)
y = x\(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{ 3x – 2 }{4}\) .

b. The other 2 points that fall on this line are (6, 4) and ( 8, 5\(\frac{ 1 }{2}\))
Explanation :
y = x\(\frac{3}{4}\) – \(\frac{1}{2}\) = \(\frac{ 3x – 2 }{4}\) .
x= 6
y = \(\frac{ 3 x 6 – 2 }{4}\) = 4
and
x = 8
y= \(\frac{ 3 x 8 – 2 }{4}\) = \(\frac{ 22 }{4}\) = \(\frac{ 11 }{2}\) = 5\(\frac{ 1 }{2}\)

Engage NY Eureka Math 5th Grade Module 6 Lesson 13 Answer Key

Eureka Math Grade 5 Module 6 Lesson 13 Problem Set Answer Key

Question 1.
Use a right angle template and straightedge to draw at least four sets of parallel lines in the space below.
Answer:

Explanation :
4 set of parallel lines are drawn and is shown in above figure .

Question 2.
Circle the segments that are parallel.

Answer:

Explanation :
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Question 3.
Use your straightedge to draw a segment parallel to each segment through the given point.

Answer:

Explanation :
Parallel lines are drawn from the given points and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Question 4.
Draw 2 different lines parallel to line b.

Answer:

Explanation :
Parallel lines m and n are drawn parallel to b and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Eureka Math Grade 5 Module 6 Lesson 13 Exit Ticket Answer Key

Use your straightedge to draw a segment parallel to each segment through the given point.

Answer:

Explanation :
Parallel lines are drawn from the given points and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Eureka Math Grade 5 Module 6 Lesson 13 Homework Answer Key

Question 1.
Use your right angle template and straightedge to draw at least three sets of parallel lines in the space below.
Answer:

Explanation :
Parallel lines are drawn from the given points and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Question 2.
Circle the segments that are parallel.

Answer:
Explanation :
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.
All the parallel lines are circled in the given figure .

Question 3.
Use your straightedge to draw a segment parallel to each segment through the given point.

Answer:

Explanation :
Parallel lines are drawn from the given points and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Question 4.
Draw 2 different lines parallel to line b.

Answer:

Explanation :
Parallel lines m and n are drawn parallel to b and is shown in above figure .
Parallel lines means two lines in the same plane that are at equal distance from each other and never meet.

Engage NY Eureka Math 5th Grade Module 6 Lesson 12 Answer Key

Eureka Math Grade 5 Module 6 Lesson 12 Sprint Answer Key

A
Subtract Decimals

Question 1.
5 – 1 =
Answer:
5 – 1 = 4

Question 2.
5.9 – 1 =
Answer:
5.9 – 1 = 4.9
Explanation :

Question 3.
5.93 – 1 =
Answer:
5.93 – 1 = 4.93
Explanation :

Question 4.
5.932 – 1 =
Answer:
5.932 -1 = 4.932

Explanation :

Question 5.
5.932 – 2 =
Answer:
5.932 – 2 = 3.932

Explanation :

Question 6.
5.932 – 4 =
Answer:
5.932 – 4 = 1.932

Explanation :

Question 7.
0.5 – 0.1 =
Answer:
0.5 – 0.1 = 0.4

Explanation :

Question 8.
0.53 – 0.1 =
Answer:
0.53 – 0.1 = 0.43
Explanation :

Question 9.
0.539 – 0.1 =
Answer:
0.539 – 0.1 = 0.439
Explanation :

Question 10.
8.539 – 0.1 =
Answer:
8.539 – 0.1 = 8.439

Explanation :

Question 11.
8.539 – 0.2 =
Answer:

Explanation :

Question 12.
8.539 – 0.4 =
Answer:
8.539 – 0.4 = 8.139

Explanation :

Question 13.
0.05 – 0.01 =
Answer:
0.05 – 0.01 = 0.04

Explanation :

Question 14.
0.057 – 0.01 =
Answer:
0.057 – 0.01 =0.047

Explanation :

Question 15.
1.057 – 0.01 =
Answer:
1.057 – 0.01 = 1.047
Explanation :

Question 16.
1.857 – 0.01 =
Answer:
1.857 – 0.01 = 1.847
Explanation :

Question 17.
1.857 – 0.02 =
Answer:
1.857 – 0.02 = 1.837

Question 18.
1.857 – 0.04 =
Answer:
1.857 – 0.04 = 1.817

Question 19.
0.005 – 0.001 =
Answer:
0.005 – 0.001 = 0.004
Explanation :

Question 20.
7.005 – 0.001 =
Answer:
7.005 – 0.001 = 7.004
Explanation :

Question 21.
7.905 – 0.001 =
Answer:
7.905 – 0.001 = 7.904

Question 22.
7.985 – 0.001 =
Answer:
7.985 – 0.001 = 7.984

Question 23.
7.985 – 0.002 =
Answer:
7.985 – 0.002 = 7.983

Question 24.
7.985 – 0.004 =
Answer:
7.985 – 0.004 =7.981

Question 25.
2.7 – 0.1 =
Answer:
2.7 – 0.1 = 2.6

Question 26.
2.785 – 0.1 =
Answer:
2.785 – 0.1 = 2.775
Explanation :

Question 27.
2.785 – 0.5 =
Answer:
2.785 – 0.5 = 2.285

Question 28.
4.913 – 0.4 =
Answer:
4.913 – 0.4 = 4.513

Question 29.
3.58 – 0.01 =
Answer:
3.58 – 0.01 = 3.47

Explanation :

Question 30.
3.586 – 0.01 =
Answer:
3.586 – 0.01 = 3.576

Question 31.
3.586 – 0.05 =
Answer:
3.586 – 0.05 = 3.536

Question 32.
7.982 – 0.04 =
Answer:
7.982 – 0.04 = 7.942

Question 33.
6.126 – 0.001 =
Answer:
6.126 – 0.001 = 6.125

Question 34.
6.126 – 0.004 =
Answer:
6.126 – 0.004 = 6.122

Question 35.
9.348 – 0.006 =
Answer:
9.348 – 0.006 = 9.342

Question 36.
8.347 – 0.3 =
Answer:
8.347 – 0.3 = 8.047

Question 37.
9.157 – 0.05 =
Answer:
9.157 – 0.05 = 9.107

Question 38.
6.879 – 0.009 =
Answer:
6.879 – 0.009 = 6.870

Question 39.
6.548 – 2 =
Answer:
6.548 – 2 = 6.348

Question 40.
6.548 – 0.2 =
Answer:
6.548 – 0.2 = 6.348

Question 41.
6.548 – 0.02 =
Answer:
6.548 – 0.02 = 6.528

Question 42.
6.548 – 0.002 =
Answer:
6.548 – 0.002 = 6.546

Question 43.
6.196 – 0.06 =
Answer:
6.196 – 0.06 = 6.136

Question 44.
9.517 – 0.004 =
Answer:
9.517 – 0.004 = 9.513

B
Subtract Decimals

Question 1.
6 – 1 =
Answer:
6 – 1 = 5

Question 2.
6.9 – 1 =
Answer:
6.9 – 1 = 5.9

Question 3.
6.93 – 1 =
Answer:
6.93 – 1 = 5.93

Question 4.
6.932 – 1 =
Answer:
6.932 – 1 = 5.932

Question 5.
6.932 – 2 =
Answer:
6.932 – 2 = 4.932

Question 6.
6.932 – 4 =
Answer:
6.932 – 4 = 2.932

Question 7.
0.6 – 0.1 =
Answer:
0.6 – 0.1 = 0.5

Question 8.
0.63 – 0.1 =
Answer:
0.63 – 0.1 = 0.53

Question 9.
0.639 – 0.1 =
Answer:
0.639 – 0.1 = 0.539

Question 10.
8.639 – 0.1 =
Answer:
8.639 – 0.1 = 8.539

Question 11.
8.639 – 0.2 =
Answer:
8.639 – 0.2 = 8.439

Question 12.
8.639 – 0.4 =
Answer:
8.639 – 0.4 = 8.239

Question 13.
0.06 – 0.01 =
Answer:
0.06 – 0.01 = 0.05

Question 14.
0.067 – 0.01 =
Answer:
0.067 – 0.01 = 0.057

Question 15.
1.067 – 0.01 =
Answer:
1.067 – 0.01 = 1.057

Question 16.
1.867 – 0.01 =
Answer:
1.867 – 0.01 = 1.857

Question 17.
1.867 – 0.02 =
Answer:
1.867 – 0.02 = 1.847

Question 18.
1.867 – 0.04 =
Answer:
1.867 – 0.04 = 1.827

Question 19.
0.006 – 0.001 =
Answer:
0.006 – 0.001 = 0.005

Question 20.
7.006 – 0.001 =
Answer:
7.006 – 0.001 = 7.005

Question 21.
7.906 – 0.001 =
Answer:
7.906 – 0.001 = 7.905

Question 22.
7.986 – 0.001 =
Answer:
7.986 – 0.001 = 7.985

Question 23.
7.986 – 0.002 =
Answer:
7.986 – 0.002 = 7.984

Question 24.
7.986 – 0.004 =
Answer:
7.986 – 0.004 = 7.982

Question 25.
3.7 – 0.1 =
Answer:
3.7 – 0.1 = 3.6

Question 26.
3.785 – 0.1 =
Answer:
3.785 – 0.1 = 3.685

Question 27.
3.785 – 0.5 =
Answer:
3.785 – 0.5 = 3.285

Question 28.
5.924 – 0.4 =
Answer:
5.924 – 0.4 = 5.524

Question 29.
4.58 – 0.01 =
Answer:
4.58 – 0.01 = 4.57

Question 30.
4.586 – 0.01 =
Answer:
4.586 – 0.01 = 4.576

Question 31.
4.586 – 0.05 =
Answer:
4.586 – 0.05 = 4.536

Question 32.
6.183 – 0.04 =
Answer:
6.183 – 0.04 =6.143

Question 33.
7.127 – 0.001 =
Answer:
7.127 – 0.001 = 7.126

Question 34.
7.127 – 0.004 =
Answer:
7.127 – 0.004 = 7.123

Question 35.
1.459 – 0.006 =
Answer:
1.459 – 0.006 = 1.453

Question 36.
8.457 – 0.4 =
Answer:
8.457 – 0.4 = 8.057

Question 37.
1.267 – 0.06 =
Answer:
1.267 – 0.06 = 1.207

Question 38.
7.981 – 0.001 =
Answer:
7.981 – 0.001 = 7.980

Question 39.
7.548 – 2 =
Answer:
7.548 – 2 = 5.548

Question 40.
7.548 – 0.2 =
Answer:
7.548 – 0.2 = 7.348

Question 41.
7.548 – 0.02 =
Answer:
7.548 – 0.02 = 7.528

Question 42.
7.548 – 0.002 =
Answer:
7.548 – 0.002 = 7.546

Question 43.
7.197 – 0.06 =
Answer:
7.197 – 0.06 = 7.191

Question 44.
1.627 – 0.004 =
Answer:
1.627 – 0.004 =1.623

Eureka Math Grade 5 Module 6 Lesson 12 Problem Set Answer Key

Question 1.
Write a rule for the line that contains the points (0, \(\frac{3}{4}\)) and (2\(\frac{1}{2}\), 3\(\frac{1}{4}\)).

a. Identify 2 more points on this line. Draw the line on the grid below.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{4}\)).
Answer:
a.
(0, \(\frac{3}{4}\)) and (2\(\frac{1}{2}\), 3\(\frac{1}{4}\)).
Rule : add \(\frac{3}{4}\) to x .
y = x + add \(\frac{3}{4}\)

b. A rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{4}\)).
Rule : subtract \(\frac{3}{4}\) from x .
D = (1, \(\frac{1}{4}\)).

Question 2.
Create a rule for the line that contains the points (1, \(\frac{1}{4}\) and (3, \(\frac{3}{4}\)).
a. Identify 2 more points on this line. Draw the line on the grid on the right.

b. Write a rule for a line that passes through the origin and lies between \(\overleftrightarrow{B C}\) and \(\overleftrightarrow{G H}\).
Answer:
a. Rule :Multiply x by \(\frac{1}{4}\)
(1, \(\frac{1}{4}\) and (3, \(\frac{3}{4}\))

b. Rule :Multiply x by \(\frac{3}{4}\) .

Question 3.
Create a rule for a line that contains the point (\(\frac{1}{4}\), 1\(\frac{1}{4}\)) using the operation or description below. Then, name 2 other points that would fall on each line.
a. Addition: _________

b. A line parallel to the x-axis: _________

c. Multiplication: _________

d. A line parallel to the y-axis: _________

e. Multiplication with addition: _________

Answer:

a. Addition:  add 1 to x

b. A line parallel to the x-axis: y is always 1\(\frac{1}{4}\).

c. Multiplication: multiply x by 5 .

d. A line parallel to the y-axis: x coordinate is always 4

e. Multiplication with addition: multiply x and add \(\frac{1}{4}\)

Question 4.
Mrs. Boyd asked her students to give a rule that could describe a line that contains the point (0.6, 1.8). Avi said the rule could be multiply x by 3. Ezra claims this could be a vertical line, and the rule could be x is always 0.6. Erik thinks the rule could be add 1.2 to x. Mrs. Boyd says that all the lines they are describing could describe a line that contains the point she gave. Explain how that is possible, and draw the lines on the coordinate plane to support your response.

Answer:

Explanation :
Mrs. Boyd’s gave only one point (0.6, 1.8) on the line .Many lines can be drawn from one point . With 2 points we can say the rule but without 2 points we cannot say the rule.

Question 5.
Create a mixed operation rule for the line that contains the points (0, 1) and (1, 3).

a. Identify 2 more points, O and P, on this line. Draw the line on the grid.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{O P}\) and goes through point (1, 2\(\frac{1}{2}\)).
Answer:
Rule : Multiply x by 2 and add 1 .
a.

b. Rule : Multiply by x and add 2.

Eureka Math Grade 5 Module 6 Lesson 12 Exit Ticket Answer Key

Write the rule for the line that contains the points (0, 1\(\frac{1}{2}\)) and (1\(\frac{1}{2}\), 3).

a. Identify 2 more points on this line. Draw the line on the grid.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{2}\)).
Answer:
Rule : add \(\frac{1}{2}\) to x .

b.
The Rule that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, \(\frac{1}{2}\)) is  Subtract \(\frac{1}{2}\) from x .

Eureka Math Grade 5 Module 6 Lesson 12 Homework Answer Key

Question 1.
Write a rule for the line that contains the points (0, \(\frac{1}{4}\)) and (2\(\frac{1}{2}\), 2\(\frac{3}{4}\)).

a. Identify 2 more points on this line. Draw the line on the grid below.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, 2\(\frac{1}{4}\).
Answer:
Rule : Add \(\frac{1}{4}\) to x .

b.
Rule for a line that is parallel to \(\overleftrightarrow{B C}\) and goes through point (1, 2\(\frac{1}{4}\) is add 1\(\frac{1}{4}\) to x .

Question 2.
Give the rule for the line that contains the points (1, 2\(\frac{1}{2}\)) and (2\(\frac{1}{2}\), 2\(\frac{1}{2}\)).
a. Identify 2 more points on this line. Draw the line on the grid above.

b. Write a rule for a line that is parallel to \(\overleftrightarrow{G H}\).
Answer:
a.
Rule : For all x-coordinates the y- coordinate is 2\(\frac{1}{2}\)

b. A rule for a line that is parallel to \(\overleftrightarrow{G H}\) is
For all x-coordinates the y- coordinate is 1\(\frac{3}{4}\) .

Question 3.
Give the rule for a line that contains the point (\(\frac{3}{4}\), 1\(\frac{1}{2}\)) using the operation or description below. Then, name 2 other points that would fall on each line.
a. Addition: ________________

b. A line parallel to the x-axis: ________________

c. Multiplication: ________________

d. A line parallel to the y-axis: ________________

e. Multiplication with addition: _____________

Answer:

a. Addition: add \(\frac{3}{4}\) to x

b. A line parallel to the x-axis: all x coordinate have y coordinate as 2

c. Multiplication: multiply by 2

d. A line parallel to the y-axis: All y coordinates have the same x coordinate 2

e. Multiplication with addition: multiply by 2 and add 1

Question 4.
On the grid, two lines intersect at (1.2, 1.2). If line a passes through the origin and line b contains the point (1.2, 0), write a rule for line a and line b.

Answer:

For line a the Rule is x coordinate . The y coordinate is same the x coordinate .
For line b the Rule is All y coordinates have the same x coordinate 1.2 .

Engage NY Eureka Math 5th Grade Module 6 Lesson 10 Answer Key

Eureka Math Grade 5 Module 6 Lesson 10 Problem Set Answer Key

Question 1.
Use the coordinate plane below to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, d, that is parallel to line p and contains point D.
c. Name 3 coordinate pairs on line d.
d. Identify a rule to describe line d.
e. Construct a line, e, that is parallel to line p and contains point E.
f. Name 3 points on line e.
g. Identify a rule to describe line e.
h. Compare and contrast lines d and e in terms of their relationship to line p.
Answer:
a. Yes, Line p represents the rule x and y are equal because all x and y coordinates are equal .
Some of the coordinate points on line p are ( 1, 1) , (2, 2) .
b. A  line, d, that is parallel to line p and contains point D is shown in below graph with coordinate points (1, 3)          and (3, 5)

c. The 3 coordinate pairs on line d are (1, 3) , (1\(\frac{1}{2}\), 3\(\frac{1}{2}\)) and                           (3\(\frac{1}{2}\), 5\(\frac{1}{2}\)) .
d. A rule for line d, is y is 2 more than x .
e. A line, e, that is parallel to line p and contains point E .

f . 3 points that are on line e are (2, 1) , ( 3, 2) and (5, 4).
g. A rule for line e, is y is 1 less than x .
h. Line p is parallel to line d and line p is parallel to line e .

Question 2.
Write a rule for a fourth line that would be parallel to those above and would contain the point (3\(\frac{1}{2}\), 6). Explain how you know.
Answer:
First plot the point F (3\(\frac{1}{2}\), 6) and draw a line that is parallel to line p , d and e.

Question 3.
Use the coordinate plane below to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, v, that contains the origin and point V.
c. Name 3 points on line v.
d. Identify a rule to describe line v.
e. Construct a line, w, that contains the origin and point W.
f. Name 3 points on line w.
g. Identify a rule to describe line w.
h. Compare and contrast lines v and w in terms of their relationship to line p.
i. What patterns do you see in lines that are generated by multiplication rules?
Answer:
a. Yes , Line p represents the rule x and y are equal because the coordinates of x and y are equal .
two coordinate points on line p are (1, 1) and (8, 8)
b.

c. The 3 points on line v are ( 2, 4) , (3,6) and ( 4, 8).
d. The rule to describe line v is the y coordinate is double the x coordinate .
e.

f. The 3 points on line w are (2, 1), (4, 2) and ( 10, 5)
g. The rule to describe line w is the y coordinate is half of x coordinate .
h. The line v is steeper and line w is shallower than p . The rule used is multiplication of x but line v multiplies by a      greater number .
i. They are not parallel lines because in line p the x and y coordinates are equal . The v and w lines are stepper and shallower respectively .

Question 4.
Circle the rules that generate lines that are parallel to each other.
add 5 to x
multiply x by \(\frac{2}{3}\)
x plus \(\frac{1}{2}\)
x times 1\(\frac{1}{2}\)
Answer:

Eureka Math Grade 5 Module 6 Lesson 10 Exit Ticket Answer Key

Use the coordinate plane below to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, a, that is parallel to line p and contains point A.
c. Name 3 points on line a.
d. Identify a rule to describe line a.
Answer:
b.

c. The 3 points on line a are (4, 1) , ( 5, 2) and (6, 3)
d. The rule to describe line a is the y coordinate is 3 less than x coordinate .

Eureka Math Grade 5 Module 6 Lesson 10 Homework Answer Key

Question 1.
Use the coordinate plane to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, d, that is parallel to line p and contains point D.
c. Name 3 coordinate pairs on line d.
d. Identify a rule to describe line d.
e. Construct a line, e, that is parallel to line p and contains point E.
f. Name 3 points on line e.
g. Identify a rule to describe line e.
h. Compare and contrast lines d and e in terms of their relationship to line p.
Answer:
b.

c. The 3 coordinates pairs of line d are (1, 3) , (2, 4) and (3, 5).
d. The rule to describe line d is the y coordinate is 2 more than the x coordinate .
e.

f. The 3 points on line e are (2, 1) , (3, 2) and (5, 4) .
g. The rule to describe line e is the y coordinate is 1 less than the x coordinate .
h. Line d and Line e are both parallel to line p .

Question 2.
Write a rule for a fourth line that would be parallel to those above and that would contain the point (5\(\frac{1}{2}\), 2). Explain how you know.
Answer:

Explanation :
First mark the point F ((5\(\frac{1}{2}\), 2)) and then draw a line that is parallel to line p .
The 3 coordinate points on line f are (4, \(\frac{1}{2}\)) , (4 \(\frac{1}{2}\), 1 ) and (6 , 2\(\frac{1}{2}\)).
The rule for line f is the y coordinate is 3\(\frac{1}{2}\) less than the x coordinate .

Question 3.
Use the coordinate plane below to complete the following tasks.

a. Line p represents the rule x and y are equal.
b. Construct a line, v, that contains the origin and point V.
c. Name 3 points on line v.
d. Identify a rule to describe line v.
e. Construct a line, w, that contains the origin and point W.
f. Name 3 points on line w.
g. Identify a rule to describe line w.
h. Compare and contrast lines v and w in terms of their relationship to line p.
i. What patterns do you see in lines that are generated by multiplication rules?
Answer:
b.

c. The 3 points on line v are (1, 2) , ( 2, 4) and (5, 10) .
d. The rule to describe the line v is the y coordinate is double the x coordinate .
e.

f. The 3 coordinate points on line w are ( 2, 1), (4, 2) and (6, 3) .
g. The rule to describe the line w is the y coordinate is half of x coordinate .
h. The line v is steeper and line w is shallower than p . The rule used is multiplication of x but line v multiplies by a      greater number .
i. They are not parallel lines because in line p the x and y coordinates are equal . The v and w lines are stepper and shallower respectively .

Engage NY Eureka Math 5th Grade Module 6 Lesson 9 Answer Key

Eureka Math Grade 5 Module 6 Lesson 9 Problem Set Answer Key

Question 1.
Complete the table for the given rules.

Line a
Rule: y is 1 more than x

Line b
Rule: y is 4 more than x

a. Construct each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what line c, whose rule is y is 7 more than x, would look like. Draw your prediction on the plane above.
Answer:
a.
Line a
Rule: y is 1 more than x
y = x + 1

Line b
Rule: y is 4 more than x
y = x + 4

b. Lines a and b are parallel lines .
c. The line c
rule: y is 7 more than x
y = x + 7

Even line c is parallel to line a and line b .

Question 2.
Complete the table for the given rules.

Line e
Rule: y is twice as much as x

Line f
Rule: y is half as much as x

a. Construct each line on the coordinate plane above.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what line g, whose rule is y is 4 times as much as x, would look like. Draw your prediction in the plane above.
Answer:
a.
Line e
Rule: y is twice as much as x
y = 2x

Line f
Rule: y is half as much as x
y = x/2

b. Both the lines e and f intersect at (0, 0)
c. line g
rule: y is 4 times as much as x
y = 4x

All 3 lines intersect at (0, 0)

Eureka Math Grade 5 Module 6 Lesson 9 Exit Ticket Answer Key

Complete the table for the given rules. Then, construct lines l and m on the coordinate plane.

Line l
Rule: y is 5 more than x

Line m
Rule: y is 5 times as much as x

Answer:
Line l
Rule: y is 5 more than x
y = x + 5

Line m
Rule: y is 5 times as much as x
y = 5x

Lines l and m are shown in the above graph .

Eureka Math Grade 5 Module 6 Lesson 9 Homework Answer Key

Question 1.
Complete the table for the given rules.

Line a
Rule: y is 1 less than x

Line b
Rule: y is 5 less than x

a. Construct each line on the coordinate plane.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what line c, whose rule is y is 7 less than x, would look like. Draw your prediction on the plane above.
Answer:
a.
Line a
Rule: y is 1 less than x
y = x – 1

Line b
Rule: y is 5 less than x
y = x – 5

b. Both the lines are a and b are parallel lines.
c.
Line c
Rule: y is 7 less than x
y = x – 7

All the 3 lines are parallel lines  and are shown in above graph .

Question 2.
Complete the table for the given rules.

Line e
Rule: y is 3 times as much as x

Line f
Rule: y is a third as much as x

a. Construct each line on the coordinate plane.
b. Compare and contrast these lines.
c. Based on the patterns you see, predict what line g, whose rule is y is 4 times as much as x, and line h, whose rule is y is one-fourth as much as x, would look like. Draw your prediction in the plane above.
Answer:
a.
Line e
Rule: y is 3 times as much as x
y = 3x

Line f
Rule: y is a third as much as x

b. Both the lines e and f intersect at (0, 0)
c.
Line g
Rule: y is 4 times as much as x
y = 4x

Line h
Rule: y is one-fourth as much as x
y = x/4

All the 4 lines intersect at (0, 0 ) and is shown in the above graph .

Engage NY Eureka Math 5th Grade Module 6 Lesson 8 Answer Key

Eureka Math Grade 5 Module 6 Lesson 8 Sprint Answer Key

A
Multiply Decimals by 10, 100, and 1,000

Question 1.
62.3 × 10 =
Answer:
62.3 × 10 = 623

Question 2.
62.3 × 100 =
Answer:
62.3 × 100 = 6230

Question 3.
62.3 × 1,000 =
Answer:
62.3 × 1,000 = 62300

Question 4.
73.6 × 10 =
Answer:
73.6 × 10 = 736

Question 5.
73.6 × 100 =
Answer:
73.6 × 100 = 7360

Question 6.
73.6 × 1,000 =
Answer:
73.6 × 1,000 = 73600

Question 7.
0.6 × 10 =
Answer:
0.6 × 10 = 6

Question 8.
0.06 × 10 =
Answer:
0.06 × 10 = 0.6

Question 9.
0.006 × 10 =
Answer:
0.006 × 10 = 0.06

Question 10.
0.3 × 10 =
Answer:
0.3 × 10 = 3

Question 11.
0.3 × 100 =
Answer:
0.3 × 100 = 30

Question 12.
0.3 × 1,000 =
Answer:
0.3 × 1,000 = 300

Question 13.
0.02 × 10 =
Answer:
0.02 × 10 = 0.2

Question 14.
0.02 × 100 =
Answer:
0.02 × 100 = 2

Question 15.
0.02 × 1,000 =
Answer:
0.02 × 1,000 = 20

Question 16.
0.008 × 10 =
Answer:
0.008 × 10 = 0.08

Question 17.
0.008 × 100 =
Answer:
0.008 × 100 = 0.8

Question 18.
0.008 × 1,000 =
Answer:
0.008 × 1,000 = 8

Question 19.
0.32 × 10 =
Answer:
0.32 × 10 = 3.2

Question 20.
0.67 × 10 =
Answer:
0.67 × 10 = 6.7

Question 21.
0.91 × 100 =
Answer:
0.91 × 100 = 91

Question 22.
0.74 × 100 =
Answer:
0.74 × 100 = 74

Question 23.
4.1 × 1,000 =
Answer:
4.1 × 1,000 = 4100

Question 24.
7.6 × 1,000 =
Answer:
7.6 × 1,000 = 7600

Question 25.
0.01 × 1,000 =
Answer:
0.01 × 1,000 = 10

Question 26.
0.07 × 1,000 =
Answer:
0.07 × 1,000 = 70

Question 27.
0.072 × 100 =
Answer:
0.072 × 100 = 7.2

Question 28.
0.802 × 10 =
Answer:
0.802 × 10 = 8.02

Question 29.
0.019 × 1,000 =
Answer:
0.019 × 1,000 = 19

Question 30.
7.412 × 1,000 =
Answer:
7.412 × 1,000 = 7412

Question 31.
6.8 × 100 =
Answer:
6.8 × 100 = 680

Question 32.
4.901 × 10 =
Answer:
4.901 × 10 = 49.01

Question 33.
16.07 × 100 =
Answer:
16.07 × 100 = 1607

Question 34.
9.19 × 10 =
Answer:
9.19 × 10 = 91.9

Question 35.
18.2 × 100 =
Answer:
18.2 × 100 = 1820

Question 36.
14.7 × 1,000 =
Answer:
14.7 × 1,000 = 14700

Question 37.
2.021 × 100 =
Answer:
2.021 × 100 = 202.1

Question 38.
172.1 × 10 =
Answer:
172.1 × 10 = 1721

Question 39.
3.2 × 20 =
Answer:
3.2 × 20 = 64

Question 40.
4.1 × 20 =
Answer:
4.1 × 20 = 82

Question 41.
3.2 × 30 =
Answer:
3.2 × 30 = 96

Question 42.
1.3 × 30 =
Answer:
1.3 × 30 = 39

Question 43.
3.12 × 40 =
Answer:
3.12 × 40 = 124.8

Question 44.
14.12 × 40 =
Answer:
14.12 × 40 = 564.8

B
Multiply Decimals by 10, 100, and 1,000

Question 1.
46.1 × 10 =
Answer:
46.1 × 10 = 461

Question 2.
46.1 × 100 =
Answer:
46.1 × 100 = 4610

Question 3.
46.1 × 1,000 =
Answer:
46.1 × 1,000 = 46100

Question 4.
89.2 × 10 =
Answer:
89.2 × 10 = 892

Question 5.
89.2 × 100 =
Answer:
89.2 × 100 = 8920

Question 6.
89.2 × 1,000 =
Answer:
89.2 × 1,000 = 89200

Question 7.
0.3 × 10 =
Answer:
0.3 × 10 = 3

Question 8.
0.03 × 10 =
Answer:
0.03 × 10 = 0.3

Question 9.
0.003 × 10 =
Answer:
0.003 × 10 = 0.03

Question 10.
0.9 × 10 =
Answer:
0.9 × 10 = 9

Question 11.
0.9 × 100 =
Answer:
0.9 × 100 =90

Question 12.
0.9 × 1,000 =
Answer:
0.9 × 1,000 = 900

Question 13.
0.04 × 10 =
Answer:
0.04 × 10 = 0.4

Question 14.
0.04 × 100 =
Answer:
0.04 × 100 = 4

Question 15.
0.04 × 1,000 =
Answer:
0.04 × 1,000 = 40

Question 16.
0.007 × 10 =
Answer:
0.007 × 10 = 0.07

Question 17.
0.007 × 100 =
Answer:
0.007 × 100 = 0.7

Question 18.
0.007 × 1,000 =
Answer:
0.007 × 1,000 = 7

Question 19.
0.45 × 10 =
Answer:
0.45 × 10 = 4.5

Question 20.
0.78 × 10 =
Answer:
0.78 × 10 = 7.8

Question 21.
0.28 × 100 =
Answer:
0.28 × 100 = 28

Question 22.
0.19 × 100 =
Answer:
0.19 × 100 = 19

Question 23.
5.2 × 1,000 =
Answer:
5.2 × 1,000 = 5200

Question 24.
8.7 × 1,000 =
Answer:
8.7 × 1,000 = 8700

Question 25.
0.01 × 1,000 =
Answer:
0.01 × 1,000 = 10

Question 26.
0.08 × 1,000 =
Answer:
0.08 × 1,000 = 80

Question 27.
0.083 × 10 =
Answer:
0.083 × 10 = 0.83

Question 28.
0.903 × 10 =
Answer:
0.903 × 10 =9.03

Question 29.
0.017 × 1,000 =
Answer:
0.017 × 1,000 = 17

Question 30.
8.523 × 1,000 =
Answer:
8.523 × 1,000 =8523

Question 31.
7.9 × 100 =
Answer:
7.9 × 100 = 790

Question 32.
5.802 × 10 =
Answer:
5.802 × 10 = 58.02

Question 33.
27.08 × 100 =
Answer:
27.08 × 100 = 2708

Question 34.
8.18 × 10 =
Answer:
8.18 × 10 = 81.8

Question 35.
29.3 × 100 =
Answer:
29.3 × 100 = 2930

Question 36.
25.8 × 1,000 =
Answer:
25.8 × 1,000 = 25800

Question 37.
3.032 × 100 =
Answer:
3.032 × 100 = 303.2

Question 38.
283.1 × 10 =
Answer:
283.1 × 10 = 2831

Question 39.
2.1 × 20 =
Answer:
2.1 × 20 = 42

Question 40.
3.3 × 20 =
Answer:
3.3 × 20 = 6.6

Question 41.
3.1 × 30 =
Answer:
3.1 × 30 = 93

Question 42.
1.2 × 30 =
Answer:
1.2 × 30 = 36

Question 43.
2.11 × 40 =
Answer:
2.11 × 40 = 84.4

Question 44.
13.11 × 40 =
Answer:
13.11 × 40 = 524.4

Eureka Math Grade 5 Module 6 Lesson 8 Problem Set Answer Key

Question 1.
Create a table of 3 values for x and y such that each y-coordinate is 3 more than the corresponding x-coordinate.

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Give the coordinates of 2 other points that fall on this line with x-coordinates greater than 12. (______ , ______) and (______ , ______)
Answer:
a. 3 points are plotted on the graph where each y-coordinate is 3 more than the corresponding x-coordinate.

b. 3 points are connected with a straight line .
c. The coordinates of 2 other points that fall on this line with x-coordinates greater than 12 and each y-coordinate is 3 more than the corresponding x-coordinate are (13 , 16) and ( 15 , 18)

Question 2.
Create a table of 3 values for x and y such that each y-coordinate is 3 times as much as its corresponding x-coordinate.

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Give the coordinates of 2 other points that fall on this line with y-coordinates greater than 25. (______ , ______) and (______ , ______)
Answer:
a. 3 Points are plotted on the graph where each y-coordinate is 3 times as much as its corresponding x

b. All the points are connected with a straight line .
c. The coordinates of 2 other points that fall on this line with y-coordinates greater than 25 and each y-coordinate is 3 times as much as its corresponding x – coordinate are (9, 27 ) and (10 , 30 )

Question 3.
Create a table of 5 values for x and y such that each y-coordinate is 1 more than 3 times as much as its corresponding x value.

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Give the coordinates of 2 other points that would fall on this line whose x-coordinates are greater than 12. (______ , ______) and (______ , ______)
Answer:
a. y = 3x + 1

b. A  straightedge line is drawn to connect these points is shown in above graph .
c. The coordinates of 2 other points that would fall on this line whose x-coordinates are greater than 12 and each      y-coordinate is 1 more than 3 times as much as its corresponding x value are (14 , 44 ) and (15 , 46 ) .

Question 4.
Use the coordinate plane below to complete the following tasks.

a. Graph the lines on the plane.
line l: x is equal to y

line m: y is 1 more than x

line n: y is 1 more than twice x

b. Which two lines intersect? Give the coordinates of their intersection.
c. Which two lines are parallel?
d. Give the rule for another line that would be parallel to the lines you listed in Problem 4(c).
Answer:
a.

line l: x is equal to y

line m: y is 1 more than x
y=x+1

line n: y is 1 more than twice x
y = 2x + 1

b. The two lines intersect are m and n lines .The coordinates of their intersection are ( 0, 1)
c. The two parallel lines are n and m lines.
d. The rule for another line that would be parallel to the lines you listed in Problem 4(c) is y is 2 more than x

Eureka Math Grade 5 Module 6 Lesson 8 Exit Ticket Answer Key

Complete this table with values for y such that each y-coordinate is 5 more than 2 times as much as its corresponding x-coordinate

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Name 2 other points that fall on this line with y-coordinates greater than 25.
Answer:
a.
Each y-coordinate is 5 more than 2 times as much as its corresponding x-coordinate
y = 2x + 5
All the points are plotted in the graph .

b. A straightedge line is drawn to connect all these points and is shown in above graph .
c. The 2 other points that fall on this line with y-coordinates greater than 25 and each y-coordinate is 5 more than 2 times as much as its corresponding x-coordinate are (11, 27) and ( 12, 29)

Eureka Math Grade 5 Module 6 Lesson 8 Homework Answer Key

Question 1.
Complete this table such that each y-coordinate is 4 more than the corresponding x-coordinate.

a. Plot each point on the coordinate plane.
b. Use a straightedge to construct a line connecting these points.
c. Give the coordinates of 2 other points that fall on this line with x-coordinates greater than 18. (______ , ______) and (______ , ______)
Answer:
a.
Each y-coordinate is 4 more than the corresponding x-coordinate.
y = 4x
The points are plotted on the the coordinate plane .

b. A straightedge line is drawn to connect all these points and is shown in above graph .
c. The coordinates of 2 other points that fall on this line with x-coordinates greater than 18 and each y-coordinate is 4 more than the corresponding x-coordinate  (19 , 76 ) and (20 , 80)

Question 2.
Complete this table such that each y-coordinate is 2 times as much as its corresponding x-coordinate.

a. Plot each point on the coordinate plane.
b. Use a straightedge to draw a line connecting these points.
c. Give the coordinates of 2 other points that fall on this line with y-coordinates greater than 25. (______ , ______) and (______ , ______)
Answer:
a.
Each y-coordinate is 2 times as much as its corresponding x-coordinate.
y = 2x
The points are plotted on the the coordinate plane .

b. A straightedge line is drawn to connect all these points and is shown in above graph .
c. The coordinates of 2 other points that fall on this line with y-coordinates greater than 25 and each y-coordinate is 2 times as much as its corresponding x-coordinate. (13, 26 ) and ( 15, 30) .

Question 3.
Use the coordinate plane below to complete the following tasks.

a. Graph these lines on the plane.
line l: x is equal to y

line m: y is 1 less than x

line n: y is 1 less than twice x

b. Do any of these lines intersect? If yes, identify which ones, and give the coordinates of their intersection.
c. Are any of these lines parallel? If yes, identify which ones.
d. Give the rule for another line that would be parallel to the lines you listed in Problem 3(c).
Answer:
a.
line l: x is equal to y
y = x

line m: y is 1 less than x
y = x – 1

line n: y is 1 less than twice x
y = 2x – 1

b.
Yes, The Two lines which intersect are line l and n.
They intersect at coordinate (1, 1).
c. Yes, We have parallel lines.
The parallel lines are line l and m.
d. The rule for another line that would be parallel to the lines you listed in Problem 3(c) is y is 2 less than x .

Engage NY Eureka Math 5th Grade Module 6 Lesson 7 Answer Key

Eureka Math Grade 5 Module 6 Lesson 7 Problem Set Answer Key

Question 1.
Complete the chart. Then, plot the points on the coordinate plane below.

a. Use a straightedge to draw a line connecting these points.
b. Write a rule showing the relationship between the x- and y-coordinates of points on the line.
c. Name 2 other points that are on this line.
Answer:

a.

Points are plotted and all points are connected with a straight line .
b. A rule showing the relationship between the x- and y-coordinates of points on the line is the difference between x and y coordinates of all points is 1 .
The x-coordinate and y-coordinate both are increased by 2 with respective to the x and y coordinates .
c. The other 2 points that are on the line are ( 3, 4) ( 5, 6)

Question 2.
Complete the chart. Then, plot the points on the coordinate plane below.

a. Use a straightedge to draw a line connecting these points.
b. Write a rule showing the relationship between the x- and y-coordinates.
c. Name 2 other points that are on this line.
Answer:
a.

b. A rule showing the relationship between the x- and y-coordinates of points on the line is Double the x coordinate is the y coordinates .
c. The 2 other points that are on this line are (\(\frac{3}{4}\), 1 \(\frac{3}{4}\)) and (1\(\frac{1}{4}\), 2\(\frac{1}{2}\))

Question 3.
Use the coordinate plane below to answer the following questions.

a. Give the coordinates for 3 points that are on line a. ________ ________ ________
b. Write a rule that describes the relationship between the x- and y-coordinates for the points on line a.
c. What do you notice about the y-coordinates of every point on line b?
d. Fill in the missing coordinates for points on line d.
(12, _____) (6, _____) (_____, 24) (28, _____) (_____, 28)
e. For any point on line c, the x-coordinate is _______.
f. Each of the points lies on at least 1 of the lines shown in the plane on the previous page. Identify a line that contains each of the following points.
i. (7, 7) a
ii. (14, 8) ______
iii. (5, 10) ______
iv. (0, 17) ______
v. (15.3, 9.3) ______
vi. (20, 40) ______
Answer:
a. The coordinates for 3 points that are on line a. (4, 4) ( 6, 6) and (8 , 8 )
b. A rule that describes the relationship between the x- and y-coordinates for the points on line a is Both the x          and y coordinates are equal.
c. The y-coordinates of every point on line b are equal that means the y – coordinate for all x-coordinates is 17 .
d. The missing coordinates for points on line d.
(12, 6 ) (6, 0 ) (30 , 24) (28, 30 ) (36 , 28)
e. For any point on line c, the x-coordinate is 5 .
f.
i. (7, 7)- a
ii. (14, 8) – d
iii. (5, 10) – c or e
iv. (0, 17) – b
v. (15.3, 9.3) – d
vi. (20, 40) – e

Eureka Math Grade 5 Module 6 Lesson 7 Exit Ticket Answer Key

Complete the chart. Then, plot the points on the coordinate plane.

Question 1.
Use a straightedge to draw a line connecting these points.
Answer:

Question 2.
Write a rule to show the relationship between the x- and y-coordinates for points on the line.
Answer:
A rule to show the relationship between the x- and y-coordinates for points on the line is the difference between x and y coordinate is 4

Question 3.
Name two other points that are also on this line. __________ __________
Answer:
The two other points that are also on this line are (1, 5) and (4, 8)

Eureka Math Grade 5 Module 6 Lesson 7 Homework Answer Key

Question 1.
Complete the chart. Then, plot the points on the coordinate plane.

a. Use a straightedge to draw a line connecting these points.
b. Write a rule showing the relationship between the x- and y-coordinates of points on this line.
c. Name two other points that are also on this line.
Answer:
a.

b. A rule showing the relationship between the x- and y-coordinates of points on this line is The difference                between x coordinate and y coordinate is 2
c . The two other points that are also on this line are (3, 1) and ( 4, 2) .

Question 2.
Complete the chart. Then, plot the points on the coordinate plane.

a. Use a straightedge to draw a line connecting these points.
b. Write a rule showing the relationship between the x- and y-coordinates for points on the line.
c. Name two other points that are also on this line. _____________ _____________
Answer:
a.

b. A rule showing the relationship between the x- and y-coordinates for points on the line is Increasing from 0 to (\(\frac{1}{2}\) , (\(\frac{1}{2}\) to 1 and 1 to 2 increasing by double the x coordinate .
c. The two other points that are also on this line are

Question 3.
Use the coordinate plane to answer the following questions.

a. For any point on line m, the x-coordinate is _______.
b. Give the coordinates for 3 points that are on line n.
c. Write a rule that describes the relationship between the x- and y-coordinates on line n.
d. Give the coordinates for 3 points that are on line q.
e. Write a rule that describes the relationship between the x- and y-coordinates on line q.
f. Identify a line on which each of these points lie.
i. (10, 3.2) ______
ii. (12.4, 18.4) ______
iii. (6.45, 12) ______
iv. (14, 7) ______
Answer:
a. For any point on line m, the x-coordinate is 10 .
b. The coordinates for 3 points that are on line n are ( 2, 8) , ( 4, 10) and (6, 12)
c. A rule that describes the relationship between the x- and y-coordinates on line n is the difference between the       all the x-coordinates and respective y – coordinates is 6 .
d. The coordinates for 3 points that are on line q are ( 4, 2) , (8, 4 ) and ( 12, 6).
e. A rule that describes the relationship between the x- and y-coordinates on line q is the differences is 2 multiple      2, 4, 6 . . . . . .
f. A line on which each of these points lie.
i. (10, 3.2) is m line
ii. (12.4, 18.4) is n line
iii. (6.45, 12) is l line
iv. (14, 7) is q line .

Engage NY Eureka Math 5th Grade Module 6 Lesson 3 Answer Key

Eureka Math Grade 5 Module 6 Lesson 3 Problem Set Answer Key

Question 1.
Use the grid below to complete the following tasks.
a. Construct an x-axis that passes through points A and B.
b. Construct a perpendicular y-axis that passes through points C and F.
c. Label the origin as 0.
d. The x-coordinate of B is 5\(\frac{2}{3}\). Label the whole numbers along the x-axis.
e. The y-coordinate of C is 5\(\frac{1}{3}\). Label the whole numbers along the y-axis.

Answer:

Question 2.
For all of the following problems, consider the points A through N on the previous page.
a. Identify all of the points that have an x-coordinate of 3\(\frac{1}{3}\).
Answer :
The points that have an x-coordinate of 3\(\frac{1}{3}\) are J, I, H and D .

b. Identify all of the points that have a y-coordinate of 2\(\frac{2}{3}\).
Answer :
The points that have a y-coordinate of 2\(\frac{2}{3}\) are E, F, H and K .

c. Which point is 3\(\frac{1}{3}\) units above the x-axis and 2\(\frac{2}{3}\) units to the right of the y-axis? Name the point, and give its coordinate pair.
Answer :
Point H and its coordinate pair is ( 3\(\frac{1}{3}\) , 2\(\frac{2}{3}\) )

d. Which point is located 5\(\frac{1}{3}\) units from the y-axis?
Answer :
Point C .

e. Which point is located 1\(\frac{2}{3}\) units along the x-axis?
Answer :
Point M .

f. Give the coordinate pair for each of the following points.
K: __
I: ______
B: ______
C: ______
Answer :
The coordinate pair of K is (5\(\frac{1}{3}\), 2\(\frac{2}{3}\))
The coordinate pair of I is (3\(\frac{1}{3}\), 1\(\frac{2}{3}\))
The coordinate pair of B is (5\(\frac{2}{3}\), 0)
The coordinate pair of C is (0, 5\(\frac{1}{3}\) )

g. Name the points located at the following coordinates.
(1\(\frac{2}{3}\), \(\frac{2}{3}\)) ______
(0, 2\(\frac{2}{3}\)) ______
(1, 0) ______
(2, 5\(\frac{2}{3}\)) ______
h. Which point has an equal x- and y-coordinate? ________
i. Give the coordinates for the intersection of the two axes. (____ , ____) Another name for this point on the plane is the ___________.
j. Plot the following points.
P: (4\(\frac{1}{3}\), 4)
Q: (\(\frac{1}{3}\), 6)
R: (4\(\frac{2}{3}\), 1)
S: (0, 1\(\frac{2}{3}\))
k. What is the distance between E and H, or EH?
l. What is the length of HD?
m. Would the length of ED be greater or less than EH+HD?
n. Jack was absent when the teacher explained how to describe the location of a point on the coordinate plane. Explain it to him using point J.
Answer:
(1\(\frac{2}{3}\), \(\frac{2}{3}\))  is Point M
(0, 2\(\frac{2}{3}\)) is Point F
(1, 0) is Point  A
(2, 5\(\frac{2}{3}\)) is Point N
h. The point L has an equal x- and y-coordinate
i. (0,0) Origin.
j.
P: (4\(\frac{1}{3}\), 4)
Q: (\(\frac{1}{3}\), 6)
R: (4\(\frac{2}{3}\), 1)
S: (0, 1\(\frac{2}{3}\))

Eureka Math Grade 5 Module 6 Lesson 3 Exit Ticket Answer Key

Question 1.
Use a ruler on the grid below to construct the axes for a coordinate plane. The x-axis should intersect points L and M. Construct the y-axis so that it contains points K and L. Label each axis.

a. Place a hash mark on each grid line on the x- and y-axis.
b. Label each hash mark so that A is located at (1, 1).
c. Plot the following points:

Answer:

Eureka Math Grade 5 Module 6 Lesson 3 Homework Answer Key

Question 1.
Use the grid below to complete the following tasks.
a. Construct a y-axis that passes through points Y and Z.
b. Construct a perpendicular x-axis that passes through points Z and X.
c. Label the origin as 0.
d. The y-coordinate of W is 2\(\frac{3}{5}\). Label the whole numbers along the y-axis.
e. The x-coordinate of V is 2\(\frac{2}{5}\). Label the whole numbers along the x-axis.

Answer:

Question 2.
For all of the following problems, consider the points K through X on the previous page.
a. Identify all of the points that have a y-coordinate of 1\(\frac{3}{5}\).
Answer :
The points that have a y-coordinate of 1\(\frac{3}{5}\) are R, M and Q.

b. Identify all of the points that have an x-coordinate of 2\(\frac{1}{5}\).
Answer :
The points that have an x-coordinate of 2\(\frac{1}{5}\) are O, M and L .

c. Which point is 1\(\frac{3}{5}\) units above the x-axis and 3\(\frac{1}{5}\) units to the right of the y-axis? Name the point, and give its coordinate pair.
Answer :
Point P and its coordinate pair is ( 1\(\frac{3}{5}\) , 3\(\frac{1}{5}\) )

d. Which point is located 1\(\frac{1}{5}\) units from the y-axis?
Answer :
Point K .

e. Which point is located \(\frac{2}{5}\) unit along the x-axis?
Answer :
Point R .

f. Give the coordinate pair for each of the following points.
T: ________
U: ________
S: ________
K: ________
Answer :
The coordinate pair of T is (2\(\frac{3}{5}\), 2\(\frac{4}{5}\))
The coordinate pair of U is ( \(\frac{3}{5}\), \(\frac{3}{5}\))
The coordinate pair of S is ( 1, \(\frac{2}{5}\))
The coordinate pair of K is (1\(\frac{1}{5}\), 3\(\frac{2}{5}\))

g. Name the points located at the following coordinates.
(\(\frac{3}{5}\), \(\frac{3}{5}\)) ______
(3\(\frac{2}{5}\), 0) ______
(2\(\frac{1}{5}\), 3) ______
(0, 2\(\frac{3}{5}\)) ______
Answer :
(\(\frac{3}{5}\), \(\frac{3}{5}\)) is Point U
(3\(\frac{2}{5}\), 0) is Point X
(2\(\frac{1}{5}\), 3) is Point L
(0, 2\(\frac{3}{5}\)) is Point W

h. Plot a point whose x- and y-coordinates are equal. Label your point E.
Answer :
Point is plotted at (1,1) where x and y coordinates are 1

i. What is the name for the point on the plane where the two axes intersect? ___________ Give the coordinates for this point. ( ____ , ____ )
Answer :
(0,0) ,Origin .

j. Plot the following points.
A: (1\(\frac{1}{5}\), 1)
B: (\(\frac{1}{5}\), 3)
C: (2\(\frac{4}{5}\), 2\(\frac{2}{5}\))
D: (1\(\frac{1}{5}\), 0)
Answer :

k. What is the distance between L and N, or LN?
Answer :
Point L is at 2\(\frac{1}{5}\)
Point N is at 3
Distance of LN = 3 – 2\(\frac{1}{5}\) = \(\frac{15}{5}\) – \(\frac{11}{5}\)= \(\frac{4}{5}\)

l. What is the distance of MQ?
Answer :
Same y coordinates so subtract only x coordinates .
Point M is at 2\(\frac{1}{5}\)
Point Q is at  3\(\frac{1}{5}\)
Distance of MQ = 3 \(\frac{1}{5}\) – 2\(\frac{1}{5}\) = \(\frac{16}{5}\) – \(\frac{11}{5}[/latex = [latex]\frac{5}{5}\) =1

m. Would RM be greater than, less than, or equal to LN+MQ?
Answer :
Same y coordinates so subtract only x coordinates .
Point M is at 2\(\frac{1}{5}\)
Point R is at  \(\frac{2}{5}\)
Distance of RM = 2 \(\frac{1}{5}\) – \(\frac{2}{5}\) = \(\frac{11}{5}\) – \(\frac{2}{5}\) = \(\frac{9}{5}\)
Distance of LN = \(\frac{4}{5}\)
Distance of MQ = 1
LN +MQ = 1 + \(\frac{4}{5}\) = \(\frac{9}{5}\)
RM is Equal to LN +MQ

n. Leslie was explaining how to plot points on the coordinate plane to a new student, but she left off some important information. Correct her explanation so that it is complete.
“All you have to do is read the coordinates; for example, if it says (4, 7), count four, then seven, and put a point where the two grid lines intersect.”
Answer:
Leslie should say how to specify which is x and y coordinates and how to plot the points .

Engage NY Eureka Math 5th Grade Module 6 Lesson 5 Answer Key

Eureka Math Grade 5 Module 6 Lesson 5 Problem Set Answer Key

Question 1.
Use the coordinate plane to the right to answer the following questions.

a. Use a straightedge to construct a line that goes through points A and B. Label the line e.
b. Line e is parallel to the ______-axis and is perpendicular to the ______-axis.
c. Plot two more points on line e. Name them C and D.
d. Give the coordinates of each point below.
A: ________
B: ________
C: ________
D: ________
e. What do all of the points of line e have in common?
f. Give the coordinates of another point that would fall on line e with an x-coordinate greater than 15.
Answer:

b. Line e is parallel to the X-axis and is perpendicular to the Y-axis.
d. The coordinates of each point below.
A: (3, 4)
B: (11, 4)
C: (5, 4)
D: (8, 4)
e. All of the points of line e have in common Y-Coordinate.
f. The coordinates of another point that would fall on line e with an x-coordinate greater than 15 is ( 16, 4 )

Question 2.
Plot the following points on the coordinate plane to the right.

P: (1\(\frac{1}{2}\), \(\frac{1}{2}\))
Q: (1\(\frac{1}{2}\), 2\(\frac{1}{2}\))
R: (1\(\frac{1}{2}\), 1\(\frac{1}{2}\))
S: (1\(\frac{1}{2}\), \(\frac{3}{4}\))
a. Use a straightedge to draw a line to connect these points. Label the line h.
b. In line h, x = _____ for all values of y.
c. Circle the correct word.
Line h is parallel perpendicular to the x-axis.
Line h is parallel perpendicular to the y-axis.
d. What pattern occurs in the coordinate pairs that let you know that line h is vertical?
Answer:

b. In line h, x =1\(\frac{1}{2}\)  for all values of y.
c.
d . All the coordinate pairs form a straight line .

Question 3.
For each pair of points below, think about the line that joins them. For which pairs is the line parallel to the x-axis? Circle your answer(s). Without plotting them, explain how you know.
a. (1.4, 2.2) and (4.1, 2.4)
b. (3, 9) and (8, 9)
c. (1\(\frac{1}{4}\), 2) and (1\(\frac{1}{4}\), 8)
Answer:
Option b
Explanation :
To form a parallel line to x -axis, the y-coordinates should be same for all x-coordinates. so in option c we have same y -coordinates b. (3, 9) and (8, 9).

Question 4.
For each pair of points below, think about the line that joins them. For which pairs is the line parallel to the y-axis? Circle your answer(s). Then, give 2 other coordinate pairs that would also fall on this line.
a. (4, 12) and (6, 12)
b. (\(\frac{3}{5}\), 2\(\frac{3}{5}\)) and (\(\frac{1}{5}\), 3 \(\frac{1}{5}\))
c. (0.8, 1.9) and (0.8, 2.3)
Answer:
Option c
Explanation :
To form a parallel line to y -axis, the x-coordinates should be same for all y-coordinates. so in option a we have same y -coordinates (0.8, 1.9) and (0.8, 2.3)
The 2 Other coordinate pairs that would also fall on this line are (0.8, 2) and (0.8, 2.1)

Question 5.
Write the coordinate pairs of 3 points that can be connected to construct a line that is 5\(\frac{1}{2}\) units to the right of and parallel to the y-axis.
a. ________________
b. ________________
c. ________________
Answer:
A (5\(\frac{1}{2}\) ,\(\frac{1}{2}\))
B (5\(\frac{1}{2}\), 2\(\frac{1}{2}\))
C (5\(\frac{1}{2}\), 3)
Explanation :
To form a parallel line to y -axis, the x-coordinates should be same for all y-coordinates.

Question 6.
Write the coordinate pairs of 3 points that lie on the x-axis.
a. ________________
b. ________________
c. ________________
Answer:
A ( 3, 0 )
B ( 5, 0)
C ( 7, 0)
Explanation :
To lie 3 points on x – axis y coordinates should be 0 . then any point with different x-coordinates lie on x-axis.

Question 7.
Adam and Janice are playing Battleship. Presented in the table is a record of Adam’s guesses so far.
He has hit Janice’s battleship using these coordinate pairs. What should he guess next? How do you know? Explain using words and pictures.
(3, 11) hit
(2, 11) miss
(3, 10) hit
(4, 11) miss
(3, 9) miss
Answer:
Next Coordinate will be (3, 8)

Explanation :
By plotting the 5 coordinate points above the shape formed is T . So, The next coordinate can be (3, 8) it completes the letter T.

Eureka Math Grade 5 Module 6 Lesson 5 Exit Ticket Answer Key

Question 1.
Use a straightedge to construct a line that goes through points A and B. Label the line l.

Answer:

Explanation :
A and B points are joined and labeled as line l

Question 2.
Which axis is parallel to line l?
Which axis is perpendicular to line l?
Answer:
y – axis is parallel to line l
x – axis is perpendicular to line l

Question 3.
Plot two more points on line l. Name them C and D.
Answer:

Explanation :
Two points are plotted on line l and named as C and D .
C is marked at ( 4, 5 )
D is marked at ( 4, 4)

Question 4.
Give the coordinates of each point below.
A: ___________
B: ___________
C: ___________
D: ___________
Answer:
A : ( 4, 6 )
B: ( 4, 3 )
C: ( 4, 5 )
D: ( 4, 4 )

Question 5.
Give the coordinates of another point that falls on line l with a y-coordinate greater than 20.
Answer:
( 4, 22 )
Explanation :
All the x- coordinates are the same it is parallel line to y – axis and given y – coordinate should be greater than 20 so, (4, 22) .

Eureka Math Grade 5 Module 6 Lesson 5 Homework Answer Key

Question 1.
Use the coordinate plane to answer the questions.

a. Use a straightedge to construct a line that goes through points A and B. Label the line g.
b. Line g is parallel to the ______-axis and is perpendicular to the ______-axis.
c. Draw two more points on line g. Name them C and D.
d. Give the coordinates of each point below.
A: ___________
B: ___________
C: ___________
D: ___________
e. What do all of the points on line g have in common?
f. Give the coordinates of another point that falls on line g with an x-coordinate greater than 25.
Answer:

b. Line g is parallel to the x-axis and is perpendicular to the y-axis.
c.

d. The Coordinates are written below
A: (4, 8)
B: (9, 8)
C: (5, 8)
D: (7, 8)
e. All of the points on line g have in common is y-coordinate .
f. The coordinates of another point that falls on line g with an x-coordinate greater than 25 is  ( 28 , 8) .
All of the points on line g have in common is y-coordinate .

Question 2.
Plot the following points on the coordinate plane to the right.

H: (\(\frac{3}{4}\), 3)
I: (\(\frac{3}{4}\), 2\(\frac{1}{4}\))
J: (\(\frac{3}{4}\), \(\frac{1}{2}\))
K: (\(\frac{3}{4}\), 1\(\frac{3}{4}\))
a. Use a straightedge to draw a line to connect these points. Label the line f.
b. In line f, x = ______ for all values of y.
c. Circle the correct word:
Line f is parallel perpendicular to the x-axis.
Line f is parallel perpendicular to the y-axis.
d. What pattern occurs in the coordinate pairs that make line f vertical?
Answer:
a.

b. In line f, x = \(\frac{3}{4}\) for all values of y.
c.
d. all the points form a straight line .

Question 3.
For each pair of points below, think about the line that joins them. For which pairs is the line parallel to the x-axis? Circle your answer(s). Without plotting them, explain how you know.
a. (3.2, 7) and (5, 7)
b. (8, 8.4) and (8, 8.8)
c. (6\(\frac{1}{2}\), 12) and (6.2, 11)
Answer:
a. (3.2, 7) and (5, 7)
Explanation :
To form a parallel line to x -axis, the y-coordinates should be same for all x-coordinates.
In  option a. (3.2, 7) and (5, 7) we have same x – coordinate .

Question 4.
For each pair of points below, think about the line that joins them. For which pairs is the line parallel to the y-axis? Circle your answer(s). Then, give 2 other coordinate pairs that would also fall on this line.
a. (3.2, 8.5) and (3.2, 24)
b. (13\(\frac{1}{2}\), 4\(\frac{2}{3}\)) and (13\(\frac{1}{3}\), 7)
c. (2.9, 5.4) and (7.2, 5.4)
Answer:
a. (3.2, 8.5) and (3.2, 24)
Explanation :
To form a parallel line to y -axis, the x-coordinates should be same for all y-coordinates.
In Option a. (3.2, 8.5) and (3.2, 24) we have same x-coordinates .

Question 5.
Write the coordinate pairs of 3 points that can be connected to construct a line that is 5\(\frac{1}{2}\) units to the right of and parallel to the y-axis.
a. ________________
b. ________________
c. ________________
Answer:
A ( 5\(\frac{1}{2}\), 2\(\frac{1}{2}\) )
B ( 5\(\frac{1}{2}\), 5\(\frac{1}{2}\))
C ( 5\(\frac{1}{2}\), 4)
Explanation :
To form a parallel line to y -axis, the x-coordinates should be same for all y-coordinates.

Question 6.
Write the coordinate pairs of 3 points that lie on the y-axis.
a. ________________
b. ________________
c. ________________
Answer:
A ( 0, 2 )
B ( 0, 4)
C ( 0, 6)
Explanation :
The 3 points that lie on the y-axis means x-coordinate should be 0 then all the points lie on y-axis .

Question 7.
Leslie and Peggy are playing Battleship on axes labeled in halves. Presented in the table is a record of Peggy’s guesses so far. What should she guess next? How do you know? Explain using words and pictures.
(5, 5) miss
(4, 5) hit
(3\(\frac{1}{2}\), 5) miss
(4\(\frac{1}{2}\), 5) miss
Answer:

Explanation :
All the above points form a straight line so, the next point should also form a straight line so, the next point is (3, 5 )

Engage NY Eureka Math 5th Grade Module 6 Lesson 6 Answer Key

Eureka Math Grade 5 Module 6 Lesson 6 Problem Set Answer Key

Question 1.
Plot the following points, and label them on the coordinate plane.

A: (0.3, 0.1)
B: (0.3, 0.7)
C: (0.2, 0.9)
D: (0.4, 0.9)
a. Use a straightedge to construct line segments \(\overline{A B}\) and \(\overline{C D}\).
b. Line segment _________ is parallel to the x-axis and is perpendicular to the y-axis.
c. Line segment _________ is parallel to the y-axis and is perpendicular to the x-axis.
d. Plot a point on line segment \(\overline{A B}\) that is not at the endpoints, and name it U. Write the coordinates. U ( _____ , _____ )
e. Plot a point on line segment \(\overline{C D}\) and name it V. Write the coordinates. V ( _____ , _____ )
Answer:
a.

b. Line segment \(\overline{C D}\) is parallel to the x-axis and is perpendicular to the y-axis.
c. Line segment \(\overline{A B}\) is parallel to the y-axis and is perpendicular to the x-axis.
d. The coordinates. U ( 0.3 , 0.5 )

e. The coordinates. V ( 0.3 , 0.9 )

Question 2.
Construct line f such that the y-coordinate of every point is 3\(\frac{1}{2}\), and construct line g such that the x-coordinate of every point is 4\(\frac{1}{2}\).

a. Line f is ________ units from the x-axis.
b. Give the coordinates of the point on line f that is \(\frac{1}{2}\) unit from the y-axis. ________
c. With a blue pencil, shade the portion of the grid that is less than 3\(\frac{1}{2}\) units from the x-axis.
d. Line g is _________ units from the y-axis.
e. Give the coordinates of the point on line g that is 5 units from the x-axis. ________
f. With a red pencil, shade the portion of the grid that is more than 4\(\frac{1}{2}\) units from the y-axis.
Answer:
Line f is drawn with points A and B with the y-coordinate of every point is 3\(\frac{1}{2}\) .
A : (1, 3\(\frac{1}{2}\))
B : (3,  3\(\frac{1}{2}\))
Line g is drawn with points C and D with the x-coordinate of every point is 4\(\frac{1}{2}\) .
C : (4\(\frac{1}{2}\) , 3 )
D : ( 4\(\frac{1}{2}\) , 1)

a. Line f is 4\(\frac{1}{2}\) units from the x-axis.
Explanation :
Distance between f and x-axis is the y-coordinate .

b. The coordinate of the point is ( \(\frac{1}{2}\) , 3\(\frac{1}{2}\) )
c.

d. Line g is 4\(\frac{1}{2}\) units from the y-axis.
Explanation :
Distance between g and y-axis is the x-coordinate .
e. The coordinates of the point on line g that is 5 units from the x-axis is ( 4\(\frac{1}{2}\) , 5 )
f.

Question 3.
Complete the following tasks on the plane below.
a. Construct a line m that is perpendicular to the x-axis and 3.2 units from the y-axis.
b. Construct a line a that is 0.8 unit from the x-axis.
c. Construct a line t that is parallel to line m and is halfway between line m and the y-axis.
d. Construct a line h that is perpendicular to line t and passes through the point (1.2, 2.4).
e. Using a blue pencil, shade the region that contains points that are more than 1.6 units and less than 3.2 units from the y-axis.
f. Using a red pencil, shade the region that contains points that are more than 0.8 unit and less than 2.4 units from the x-axis.
g. Give the coordinates of a point that lies in the double-shaded region.

Answer:


g. The coordinates of a point that lies in the double-shaded region is (1, 2)

Eureka Math Grade 5 Module 6 Lesson 6 Exit Ticket Answer Key

Question 1.
Plot the point H (2\(\frac{1}{2}\), 1\(\frac{1}{2}\)).
Answer:

Question 2.
Line l passes through point H and is parallel to the y-axis. Construct line l.
Answer:

Question 3.
Construct line m such that the y-coordinate of every point is \(\frac{3}{4}\).
Answer:

Explanation :
For same y -coordinate of every point is \(\frac{3}{4}\) then draw a line from \(\frac{3}{4}\) from x-axis .

Question 4.
Line m is ________ units from the x-axis.
Answer:
Line m is \(\frac{3}{4}\) units from the x-axis.
Explanation :
It is represented by y-coordinate of line m .

Question 5.
Give the coordinates of the point on line m that is \(\frac{1}{2}\) unit from the y-axis.
Answer:
The coordinates of the point on line m that is \(\frac{1}{2}\) unit from the y-axis is (\(\frac{1}{2}\) , \(\frac{3}{4}\) ).

Question 6.
With a blue pencil, shade the portion of the plane that is less than \(\frac{3}{4}\) unit from the x-axis.
Answer:

Question 7.
With a red pencil, shade the portion of the plane that is less than 2\(\frac{1}{2}\) units from the y-axis.
Answer:

Question 8.
Plot a point that lies in the double-shaded region. Give the coordinates of the point.
Answer:
The point that lies in the double-shaded region is W ( 2 , \(\frac{1}{2}\) )

Eureka Math Grade 5 Module 6 Lesson 6 Homework Answer Key

Question 1.
Plot and label the following points on the coordinate plane.

C: (0.4, 0.4)
A: (1.1, 0.4)
S: (0.9, 0.5)
T: (0.9, 1.1)
a. Use a straightedge to construct line segments \(\overline{C A}\) and \(\overline{S T}\).
b. Name the line segment that is perpendicular to the x-axis and parallel to the y-axis. _________
c. Name the line segment that is parallel to the x-axis and perpendicular to the y-axis. _________
d. Plot a point on \(\overline{C A}\), and name it E. Plot a point on line segment \(\overline{S T}\), and name it R.
e. Write the coordinates of points E and R.
E ( ____ , ____ ) R ( ____ , ____ )
Answer:

a.

c. The line segment that is perpendicular to the x-axis and parallel to the y-axis is \(\overline{S T}\)
d. The line segment that is parallel to the x-axis and perpendicular to the y-axis is \(\overline{C A}\)
e.

f. The coordinates of points E and R.
E ( 0.8 , 0.4 ) R ( 0.9 , 0.8 )

Question 2.
Construct line m such that the y-coordinate of every point is 1\(\frac{1}{2}\), and construct line n such that the x-coordinate of every point is 5\(\frac{1}{2}\).

a. Line m is ________ units from the x-axis.
b. Give the coordinates of the point on line m that is 2 units from the y-axis. ________
c. With a blue pencil, shade the portion of the grid that is less than 1\(\frac{1}{2}\) units from the x-axis.
d. Line n is _________ units from the y-axis.
e. Give the coordinates of the point on line n that is 3\(\frac{1}{2}\) units from the x-axis.
f. With a red pencil, shade the portion of the grid that is less than 5\(\frac{1}{2}\) units from the y-axis.
Answer:
Line m is drawn with points A and B with the y-coordinate of every point is 1\(\frac{1}{2}\) .
A : (1, 1\(\frac{1}{2}\))
B : (3,  1\(\frac{1}{2}\))
Line n is drawn with points C and D with the x-coordinate of every point is 5\(\frac{1}{2}\) .
C : (5\(\frac{1}{2}\) , 3 )
D : ( 5\(\frac{1}{2}\) , 6)

a. a. Line m is 1\(\frac{1}{2}\) units from the x-axis.
Explanation :
Distance between x-axis and line m is the y coordinate .

b. The coordinates of the point on line m that is 2 units from the y-axis is ( 2, 1\(\frac{1}{2}\) )
c.

d. Line n is 5\(\frac{1}{2}\) units from the y-axis.
Explanation :
Explanation :
Distance between y-axis and line n is the x – coordinate .

e. The coordinates of the point on line n that is 3\(\frac{1}{2}\) units from the x-axis is (5\(\frac{1}{2}\) , 3\(\frac{1}{2}\))
f.

Question 3.
Construct and label lines e, r, s, and o on the plane below.
a. Line e is 3.75 units above the x-axis.
b. Line r is 2.5 units from the y-axis.
c. Line s is parallel to line e but 0.75 farther from the x-axis.
d. Line o is perpendicular to lines s and e and passes through the point (3\(\frac{1}{4}\), 3\(\frac{1}{4}\)).
Answer:

Question 4.
Complete the following tasks on the plane.
a. Using a blue pencil, shade the region that contains points that are more than 2\(\frac{1}{2}\) units and less than 3\(\frac{1}{4}\) units from the y-axis.
b. Using a red pencil, shade the region that contains points that are more than 3\(\frac{3}{4}\) units and less than 4\(\frac{1}{2}\) units from the x-axis.
c. Plot a point that lies in the double-shaded region, and label its coordinates.

Answer:

Explanation :
In double shaded (3,4 ) is a point that is marked as shown in above figure .

Engage NY Eureka Math 5th Grade Module 6 Lesson 4 Answer Key

Eureka Math Grade 5 Module 6 Lesson 4 Problem Set Answer Key

Battleship Rules

Goal: To sink all of your opponent’s ships by correctly guessing their coordinates.
Materials

• 1 grid sheet (per person/per game)
• Red crayon/marker for hits
• Black crayon/marker for misses
• Folder to place between players

Ships

• Each player must mark 5 ships on the grid.
  • Aircraft carrier—plot 5 points.
  • Battleship—plot 4 points.
  • Cruiser—plot 3 points.
  • Submarine—plot 3 points.
  • Patrol boat—plot 2 points

Setup

• • With your opponent, choose a unit length and fractional unit for the coordinate plane.
  • Label the chosen units on both grid sheets.
  • Secretly select locations for each of the 5 ships on your My Ships grid.
  • All ships must be placed horizontally or vertically on the coordinate plane.
  • Ships can touch each other, but they may not occupy the same coordinate.

Play

• • Players take turns firing one shot to attack enemy ships.
  • On your turn, call out the coordinates of your attacking shot. Record the coordinates of each attack shot.
  • Your opponent checks his/her My Ships grid. If that coordinate is unoccupied, your opponent says, “Miss.” If you named a coordinate occupied by a ship, your opponent says, “Hit.”
  • Mark each attempted shot on your Enemy Ships grid. Mark a black ✖ on the coordinate if your opponent says, “Miss.” Mark a red ✓ on the coordinate if your opponent says, “Hit.”
  • On your opponent’s turn, if he/she hits one of your ships, mark a red ✓on that coordinate of your My Ships grid. When one of your ships has every coordinate marked with a ✓, say, “You’ve sunk my [name of ship].”

Victory

• • The first player to sink all (or the most) opposing ships, wins.
    
    Aircraft carrier—5 points
    Battleship—4 points
    Cruiser—3 points
    Submarine—3 points
    Patrol boat—2 points

Draw a red ✓over any coordinate your opponent hits.
Once all of the coordinates of any ship have been hit, say, “You’ve sunk my [name of ship].”

Attack Shots
Record the coordinates of each shot below and whether it was a ✓(hit) or an ✖ (miss).
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
( _____ , _____ ) ( _____ , _____ )
Enemy Ships

• Draw a black ✖ on the coordinate if your opponent says, “Miss.”
• Draw a red ✓ on the coordinate if your opponent says, “Hit.”
• Draw a circle around the coordinates of a sunken ship.
  

Eureka Math Grade 5 Module 6 Lesson 4 Exit Ticket Answer Key

Fatima and Rihana are playing Battleship. They labeled their axes using just whole numbers.
a. Fatima’s first guess is (2, 2). Rihana says, “Hit!” Give the coordinates of four points that Fatima might guess next.
b. Rihana says, “Hit!” for the points directly above and below (2, 2). What are the coordinates that Fatima guessed?
Answer:

Eureka Math Grade 5 Module 6 Lesson 4 Homework Answer Key

Your homework is to play at least one game of Battleship with a friend or family member. You can use the directions from class to teach your opponent. You and your opponent should record your guesses, hits, and misses on the sheet as you did in class.
When you have finished your game, answer these questions.
Question 1.
When you guess a point that is a hit, how do you decide which points to guess next?
Answer:

Question 2.
How could you change the coordinate plane to make the game easier or more challenging?
Answer:

Question 3.
Which strategies worked best for you when playing this game?
Answer:

Engage NY Eureka Math 5th Grade Module 6 Lesson 2 Answer Key

Eureka Math Grade 5 Module 6 Lesson 2 Problem Set Answer Key

Question 1.
a. Use a set square to draw a line perpendicular to the x-axes through points P, Q, and R. Label the new line as the y-axis.

Answer :

Explanation :
A line is said to be perpendicular to another line if the two lines intersect at a right angle.

b. Choose one of the sets of perpendicular lines above, and create a coordinate plane. Mark 7 units on each axis, and label them as whole numbers.
Answer:

Explanation :
7 units are marked on the first figure on both the axes .

Question 2.
Use the coordinate plane to answer the following.

a. Name the shape at each location.

Answer :

b. Which shape is 2 units from the y-axis?
Answer :
Circle is 2 units from y – axis .
c. Which shape is 1 units from the y-axis?
Answer :
Parallelogram is 1 units from the y-axis

d. Which shape is 4 units from the y-axis and 3 units from the x-axis?
Answer:
Diamond is 4 units from the y-axis and 3 units from the x-axis

Question 3.
Use the coordinate plane to answer the following.

a. Fill in the blanks.

b. Name the shape whose x-coordinate is \(\frac{1}{2}\) more than the value of the heart’s x-coordinate.
Answer :
Star shape

c. Plot a triangle at (3, 4).
Answer :

Explanation :
X- coordinate = 3
Y-coordinate = 4 .

d. Plot a square at (4 \(\frac{3}{4}\), 5).
Answer :

Explanation :
X- coordinate = 4 \(\frac{3}{4}\)
Y- coordinate = 5

e. Plot an X at (\(\frac{1}{2}\), \(\frac{3}{4}\)).
Answer:

Explanation :
X – Coordinate  = (\(\frac{1}{2}\)
Y- Coordinate  = \(\frac{3}{4}\)).

Question 4.
The pirate’s treasure is buried at the X on the map. How could a coordinate plane make describing its location easier?

Answer:
It would give you the exact location when you describe the position with x and y axis .
It would you draw x- axis along the island and y axis along the left side and mark the point for  x then the location would be exactly clear to find easier .

Eureka Math Grade 5 Module 6 Lesson 2 Exit Ticket Answer Key

Question 1.
Name the coordinates of the shapes below.

Answer:

Question 2.
Plot a square at (3, 3\(\frac{1}{2}\)).
Answer:

Question 3.
Plot a triangle at (4\(\frac{1}{2}\), 1).
Answer:

Eureka Math Grade 5 Module 6 Lesson 2 Homework Answer Key

Question 1.
a. Use a set square to draw a line perpendicular to the x-axis through point P. Label the new line as the y-axis.

Answer a :

b. Choose one of the sets of perpendicular lines above, and create a coordinate plane. Mark 5 units on each axis, and label them as whole numbers.
Answer:

Explanation :
In First figure the x-axis and y-axis is divided into 5 parts as shown in above figure .

Question 2.
Use the coordinate plane to answer the following.

a. Name the shape at each location.

Answer :

b. Which shape is 2 units from the x-axis?
Answer :
Star

c. Which shape has the same x- and y-coordinate?
Answer:
Square it is located at (3,3)

Question 3.
Use the coordinate plane to answer the following.

a. Name the coordinates of each shape.

Answer :

shape.

b. Which 2 shapes have the same y-coordinate?
Answer :
Heart and star have same y – coordinate as 2

c. Plot an X at (2, 3).
Answer :

d. Plot a square at (3, 2\(\frac{1}{2}\)).
Answer :

e. Plot a triangle at (6, 3\(\frac{1}{2}\)).
Answer:

Question 3.
Mr. Palmer plans to bury a time capsule 10 yards behind the school. What else should he do to make naming the location of the time capsule more accurate?

Answer:
If Palmer drew an x-axis and y-axis and a scale he would have the exact location of the time capsule .