Sruthi Reddy

Standard Sets of Numbers mean the set of common numbers. As we all know, a set is a collection of well-defined objects. Those well-defined objects can be all numbers also. Based on the elements present in the set, we will call them with some names. Let us check the following sections to know the generally used standard common number sets with examples. Students can also clear their doubts by reading the frequently asked questions section.

Standard Sets of Numbers

There are several standard sets of common numbers. We can represent those standard sets of numbers using three different forms names statement form, roster form, and set-builder form. All these sets are infinite sets, so it will extend infinitely and has no end number. We have represented all these sets in all three forms with definitions and examples.

1. Natural Numbers:

Natural Numbers are the numbers starting from 1 counting upward.

The set of natural numbers are N = {1, 2, 3, 4, 5, 6, 7, . . . }

The statement form is the set of natural numbers.

The set builder form is { x: x is a counting number starting from 1 }

2. Whole Numbers:

The whole numbers are the natural numbers including 0. It will start from 0.

The set of whole numbers are W = {0, 1, 2, 3, 4, 5, 6, . . .}

The statement form is the set of natural numbers including zero.

The set builder form is { x: x is zero and all-natural numbers }

3. Integers:

integers are the set of whole numbers along with the negative numbers means opposite to the natural numbers.

The set of integers are Z or I = { . . . -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, . . . }

The statement form is the set natural numbers, zero, and negative natural numbers.

The set builder form is Z = { x: x ∈ I}

4. Real Numbers:

Real numbers are also called measuring numbers. It includes all numbers and which can be written as decimals. It can include fractions and irrational numbers in the form of decimals.

The set of real numbers are R = {0.5, 0.25, 0.6, 0.07, 0.8}

The set builder form is { x: x is a decimal}

The statement form is the set of decimals.

5. Rational Numbers:

The rational numbers are the fractional numbers. The numerator and denominator of the fractions are integers. The numerator can be zero but the denominator cannot be 0.

The set of rational numbers are R = {\(\frac { 1 }{ 2 } \), \(\frac { -4 }{ 5 } \), \(\frac { 5 }{ 8 } \)}

The statement form is the set of fractions.

The set builder form is { x: x is a fraction }

6. Even Numbers:

Even numbers are the numbers that are divisible by 2.

The statement form of even numbers is the set of numbers divisible by 2.

The roster form is E = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, . . . }

The set builder form is { x : x is a even number}

7. Odd Numbers:

Odd numbers are the numbers that are not divisible by 2.

The set builder form of odd numbers is { x: x is a number that is not divisible by 2 }

The roster form is O = {1, 3, 5, 7, 9, 11, 13, 15, . . . . }

The statement form is “the set of numbers which are not even”.

8. Prime Numbers:

Prime numbers are the positive integers that have only two factors 1 and that integer itself.

The statement form of the prime numbers is “set of numbers has two factors 1 and the same integer”

The set builder form is P = { x: x is a positive integer has only two factors }

The roster form is P = {1, 2, 3, 5, 7, 11, 13, . . . }

9. Complex Numbers:

Complex numbers are the numbers that can be expressed in the form of a + bi. Here ‘i’ is the imaginary unit.

The statement form is “set of numbers in the form of a + bi”

The roster form is C = {1 +2i, 3 + 4i, 5 + 4i, . . . }

The set builder form is C = { x : x is a number in the form of a + bi }

10. Imaginary Numbers:

The imaginary numbers are the numbers which have square root or imaginary unit.

The statement form is “the set of numbers having either square root or imaginary unit”.

The set builder form is I = {x: x is an imaginary number}

The roster form is I = {√5, 3i, √6, √8, √15, . . . }

Also, Read:

FAQs on Standard Sets of Numbers

1. What are the sets of numbers?

The different sets of numbers are natural numbers, whole numbers, integers, real numbers, rational numbers, irrational numbers, even numbers, odd numbers, complex numbers, imaginary numbers, and prime numbers.

2. What are the 3 ways to describe a set?

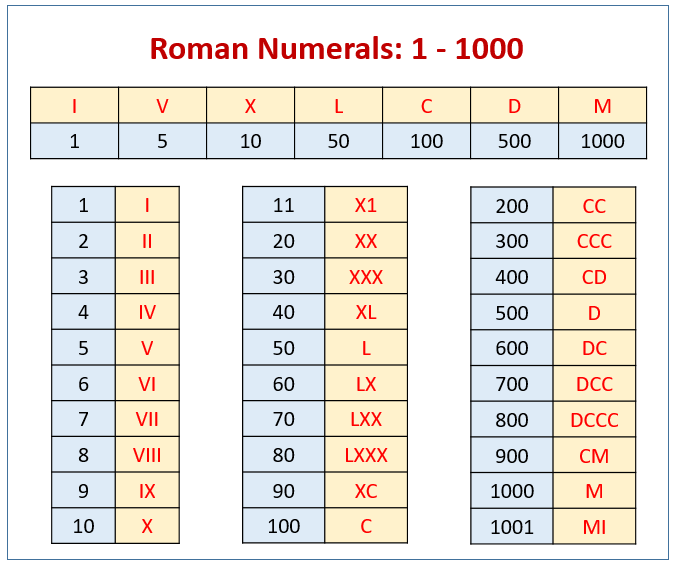
The 3 different ways to represent a set are statement form, set builder form, and roster form. The last 2 forms use curly braces. The roster form lists all the set elements. The set builder form uses a property and statement form that describes the set verbally.

3. What are the 4 operations of sets?

The four operations of sets are union, intersection, set difference, the complement of a set, and cartesian product.

4. What are sets and their types?

Set is a collection of well-defined objects. The various types of sets are finite set, infinite set, empty set, singleton set, equal sets, equivalent sets, subset, superset, disjoint sets, proper subset, and universal set.

In mathematics, a set is a collection of well-defined objects. Those objects are called members or elements of a set. The set elements are closed between the curly braces and each element is broken up by a comma. The sets are classified into various types. Interested students can go through the following sections to check useful information on set types. You can see definitions and examples for all sets.

Set Types

Based on the elements on the set, size of the set, and other factors, sets are divided into various types. They are listed here.

• Finite Set
• Null Set
• Infinite set
• Equal Sets
• Singleton Set
• Equivalent Sets
• Subset
• Proper Subset
• Cardinal Number of a set
• Power Set
• Superset
• Disjoint Sets
• Universal Set

Types of Sets

Let us discuss the definition and examples of all types of sets in the below sections.

1. Empty Set

If a set has no elements in it, then it is called the empty set. It is also known as the null set or void set. An empty set is represented by ϕ or {}.

Examples:

A = { x : x is a whole number that is not a natural number, x ≠ 0}

Zero is the only whole number that is not a natural number. If x ≠ 0, then there is no possible value for x. So, A = ϕ.

B = { y : 1 < y < 2, y is a natural number}

We know that a natural number cannot be a decimal. So, set y is a null set.

2. Finite Set

A finite set has a definite number of elements. We can find the size of the finite set easily.

Examples:

C = { x | x is a natural number, 20 > x > 10 }

D = { t, y, p, e, s, o, f, s, e, t, s }

3. Infinite Set

A set that has an infinite number of elements in it is called the infinite set. It is not possible to find the size of an infinite set.

Examples:

E = { x : x is a whole number, x > 50 }

The set of whole numbers greater than 50 are 51, 52, 53, 54, . . . . Therefore, set E is an infinite set.

F = { x | x is an even number and x >2 }

The set of even numbers greater than 2 are 4, 6, 8, 10, 12, 14, 16, 18, 20, . . . Hence, set F is an infinite set.

4. Singleton Set

Singleton set is also known as a unit set. If a set has only one element, then it is called the singleton set. The size of a unit set is always 1.

Examples:

G = {5}

As set G has only one element it is a singleton set.

H = {x : x is whole number but not natural number }

We have only one element which is the whole number, not a natural number i.e 0. So, H is a singleton set.

5. Equal Sets

If two sets contain the same elements, then they are equal sets. There is no need to have the same order of elements in both sets.

Examples:

Let I = {4, 14, 15, 5, 6, 18} and J = {15, 5, 18, 14, 4, 6} are two sets.

Then I = J

Here, two sets have the same elements i.e 4, 5, 6, 14, 15, 18

6. Equivalent Sets

If two sets have the same number of elements, then they are called equivalent sets. Two sets order or cardinality is equal.

Examples:

Let K = {8, 17, 25, 63}, L = {56, 5, 45, 28}

The order of K = n(k) = 4

The order of L = n(L) = 4

So, L and K are equivalent sets.

Let M = {p, o, w, e, r}, N = {1, 5, 6, 8, 12}

n(M) = 5

n(N) = 5

So, M and n are equivalent sets.

7. Subset

A set A is said to be a subset of B if all the elements of A are the elements B. Subset is denoted by the symbol ⊂ and A ⊂ B.

Examples:

If O = {0, 3, 6, 8, 14}, P = {15, 5, 0, 1, 2, 3, 6, 14, 7, 8, 9}

The elements of P are 0, 1, 2, 3, 5, 6, 7, 8, 9, 14, and 15.

The elements of O are 0, 3, 6, 8, and 14.

All the elements of O belong to set P. So, O ⊆ P.

8. Proper Subset

If A, B are two sets, A is called the proper subset of B if A ⊂ B but B ⊃ A i.e A ≠ B. The symbol ⊆ is used to represent the proper subset.

Examples:

Q = {7, 5, 2, 16} and R = {2, 5, 7}

All the elements of R are in Q.

n(R) = 3, n(Q) = 4 and Q ≠ R

So, R ⊆ Q

9. Superset

When set A is a subset of set B, then B is a superset of A and it can be represented as B ⊇ A. The symbol ⊇ means “is a superset of”.

Examples:

Let S = {p, o, w, e, r}, T = {p, o, w, e, r, f, u, l}

Here, S ⊂ T. So, T ⊇ S.

10. Universal Set

A set that has all the elements of other given sets is known as the universal set. The symbol is ∪ or ξ.

Examples:

Let P = {a, b, c, d, h},  V = {x, y, z}, W = {m, n, o , p}

∪ = {a, b, c d, e, f, g h, i, j, k, l, m, n, o, p, q, r, s, t, u, v w, x, y, z}

So, ∪ is the universal set.

11. Disjoint Sets

Two sets A and B are called disjoint sets if they do not have common elements between them. So, the properties of disjoint sets are n(A ∩ B) = { }, n(A U B) = n(A) + n(B)

Examples:

X = {1, 2, 5}, Y = {8, 6, 3}

Here, X and y sets has no common element. So X, Y are disjoint sets.

12. Cardinal Number of a set

The number of different elements in the set is called the cardinal number of a set. It is denoted by n(A).

Examples:

Y = { x : x is a natural number, n >10}

n(Y) = 9

Z = {n, u, m, b, e, r, o, f, e, l, e, m, e, n, t, s}

n(Z) = 16

13. Power Set

The set of all subsets is called the power sets. We know that an empty set is a subset of all sets and every set is a subset of itself.

Examples:

If set A = {1, 8, 15}, then power set of A is P(A) = {ϕ, {8}, {15, 8}, {1, 8}, {1, 15}, (8, 1, 15}, {15}, {1}}

Frequently Asked Questions on Set Types

1. How do you express an empty set?

An empty set has no element. it can be represented as ϕ or { }.

2. What are the two sets that contain the same elements?

If two sets have the same elements, then they are called equal sets. The example is A = {m, a, t, h, e, m, a, t, i, c, s} and B = {a, a, m, m, t, t, h, e, s, i, c}. So, A = B.

3. What is a Subset?

If A and B are two sets, and every element of set A is also an element of set B, then A is called a subset of B and expressed as A ⊂ B. B ⊇ A means B is a superset of A. A ⊆ B means A is a proper subset of B.

Read Similar Articles on Sets

In general, a set is a collection of well-defined objects. A set must have the same type of objects. The objects are also called the members or elements of the set. The number of the element present in a set is called the order of the set. The pairs of sets mean there is a relationship between two sets. Get the examples and various pairs of sets in the below sections of this article.

What are Pairs of Sets?

If there is some relationship between two sets then such sets are called pairs of sets. Various pairs of sets are mentioned below.

• Equal Sets
• Equivalent Sets
• Disjoint Sets
• Overlapping Sets

Pairs of Sets Examples

The relation between two sets is called pairs of sets. Let us know about each of the set pairs with the examples on the following modules.

1. Equal Sets:

Two sets P and Q are said to be equal sets if all the elements of the first set are in the second set irrespective of the position of the elements. The symbol to denote the equal sets is “=”.

Here P = Q means P is equal to Q and Q is equal to P.

Examples:

P = {12, 13, 14, 15, 16}

Q = {15, 12, 14, 13, 16}

The elements of P and Q are same. So, P = Q.

X = {a, e, l, , u}, Y = {e, q, u, a, l}

The elements of sets X and Y are the same. So, X = Y and Y = X.

2. Equivalent Sets:

Two sets P and Q are said to be equivalent if both sets have the same number of elements or same order or same cardinality. The symbol to denote equivalent sets is ↔. Equal sets are always equivalent. But equivalent sets may or may not be equal.

P ↔ Q means set P and Q have the same order.

Examples:

P = {10, 20, 30, 40, 50, 60, 70, 80, 90, 100}

Q = {11, 22, 33, 44, 55, 66, 77, 88, 99, 111}

The order of P = n(P) = 10

The order of Q = n(Q) = 10

n(P) = n(Q). So, P ↔ Q.

A = {a, p, p, l, e}, B = {p, o, w, e, r}

The number of elements of A = n(A) = 5

The number of elements of B = n(B) = 5

n(A) = n(B). So, A ↔ B i.e A is equivalent to B.

3. Disjoint Sets:

Two sets P and Q are said to be disjoint sets if they do not contain only one element in common.

Examples:

P = {x | x is an even number}

Q = {x : x is an odd number}

The set of even numbers are {2, 4, 6, 8, 10, 12, 14, . . . }

The set of odd numbers are {1, 3, 5, 7, 9, 11, 13, . . }

So, there is no common element in between P and Q. Therefore, P and Q are disjoint sets.

A = {5, 10, 15, 20, 25, 30, 35, 40}, B = {3, 6, 9, 18, 21, 24, 27}

Here, A and B has no common element. So, A and B are disjoint sets.

4. Overlapping Sets:

Two sets P and Q are said to be overlapping sets if they have at least one element in common.

Examples:

P = {x : x is a whole number}

Q = {x : x is a natural number}

The set of whole numbers are {0, 1, 2, 3, 4, 5, 6, 7, 8, . . . }

The set of natural numbers are {1, 2, 3, 4, 5, 6, . . . }

The common elements in both sets are {1, 2, 3, 4, 5, 6, 7, . . . }

So, P and Q are overlapping sets.

M = {p, i, n, e, a, p, p, l, e}

N = {c, u, s, t, a, r, d, a, p, p, l, e}

The common elements in both sets are {a, p, p, l, e}

Also, Read

Solved Example Questions on Pairs of Sets

Example 1:

State whether the sets A and B are equal sets or not?

A = {s, t, a, t, e s}

B = {a, e, s, s, t, t}

Solution:

Given two sets are

A = {s, t, a, t, e s}, B = {a, e, s, s, t, t}

The elements of both sets are the same. So, A and B are equal sets.

Therefore, A = B.

Example 2:

State whether the sets C and D are equivalent or not?

C = {5, 9, 10, 12, 16, 78}

D = {a, b, c, d, e, g}

Solution:

Given two sets are

C = {5, 9, 10, 12, 16, 78} and D = {a, b, c, d, e, g}

The number of elements of C = n(C) = 6

The order of D = n(D) = 6

n(C) = n(D)

So, C and D are equivalent sets i.e C ↔ D.

Example 3:

Find whether the following sets are disjoint sets or overlapping sets.

(i) X = {x : x is a multiple of 7 between 1 and 50}

Y = {x | x is a multiple of 11 between 1 and 50}

(ii) P = {x : x is a letter in ‘FLOOR’}

Q = {x | x is a letter in ‘FLOWER’}

Solution:

(i) Given two sets are X = {x : x is a multiple of 7 between 1 and 50} and Y = {x | x is a multiple of 11 between 1 and 50}

The roster form is X = {7, 14, 21, 28, 35, 42, 49}, Y = {11, 22, 33, 44}

Two sets X and Y have no common element.

So, X and Y are disjoint sets

(ii) Given two sets are P = {x : x is a letter in ‘FLOOR’} and Q = {x | x is a letter in ‘FLOWER’}

The roster form of P = {F, L, O, O, R}, Q = {F, L, O, W, E, R}

The common elements are F, L, O, R

So, P and Q are overlapping sets.

A set is a collection of well-defined objects. The best examples are set of even numbers between 2 and 20, set of whole numbers. The change in writing the order of elements in a set does not make any change. And if anyone or more elements of a set are repeated, then also the set remains the same. Check out the detailed information on the properties of set operations in the following sections along with the formulas.

Properties of Sets

If two or more sets are combined together to form another set under the provided constraints, then operations on the sets are carried out. the six important properties of set operations are along the lines.

1. Commutative Property

2. Associative Property

3. Distributive Property

4. Identity Property

5. Complement Property

6. Idempotent Property

What are the Basic Properties of Set Operations?

Here, we will discuss the six important set operations using the Venn diagrams.

To understand the following properties, let us take A, B, and C are three sets and U be the universal set.

Property 1: Commutative Property

Intersection and union of sets satisfy the commutative property.

(i) A U B = B U A

     = 

(ii) A ∩ B = B ∩ A

= 

Property 2: Associative Property

Intersection and union of sets satisfy the associative property.

(i) (A⋂B)⋂C = A⋂(B⋂C)

(ii) (A⋃B)⋃C = A⋃(B⋃C)

Property 3: Distributive Property

(i) A⋃(B⋂C) = (A⋃B)⋂(A⋃C)

(ii) A⋂(B⋃C) = (A⋂B)⋃(A⋂C)

Property 4: Identity Property

(i) A⋃∅ = A

(ii) A⋂U = A

Property 5: Complement Property

(i) A⋃A^c = U

(ii) A⋂A^c = ∅

Property 6: Idempotent Property

(i) A⋂A = A

(ii) A⋃A = A

Solved Examples on Properties of Sets

Example 1:

If A = {1, 4, 6}, U = {1, 2, 3, 4, 5, 6} prove the complement property.

Solution:

Given that,

A = {1, 4, 6}, U = {1, 2, 3, 4, 5, 6}

A’ = {2, 3, 5}

To prove that A⋃A’ = U

L.H.S = AUA’

= {1, 4, 6} U {2, 3, 5}

= {1, 4, 6, 2, 3, 5}

= R.H.S

To prove A⋂A’ = ∅

L.H.S = {1, 4, 6} ⋂ {2, 3, 5}

= { }

= R.H.S

Hence, proved.

Example 2:

If A = {4, 10, 25}, B = {1, 5, 8}, C = {2, 16, 18}, prove that A⋃(B⋂C) = (A⋃B)⋂(A⋃C).

Solution:

Given that,

A = {4, 10, 25}, B = {1, 4, 5, 8}, C = {5, 2, 4, 16, 18}

L.H.S = A⋃(B⋂C)

= {4, 10, 25} U ({1, 4, 5, 8} ⋂ {2, 5, 16, 4, 18})

= {4, 10, 25} U {4, 5}

= {4, 5, 10, 25}

R.H.S = (A⋃B)⋂(A⋃C)

= ({4, 10, 25} U {1, 4, 5, 8}) ⋂ ({4, 10, 25} ⋃ {5, 2, 4, 16, 18})

= {1, 4, 5, 8, 10, 25} ⋂ {2, 4, 5, 10, 16, 18, 25}

= {4, 5, 10, 25}

Therefore, L.H.S = R.H.S

Example 3:

If A = {2, 4, 6, 8}, B = {1, 3, 5, 7}, C = {1, 2, 5, 8}, then show that (A⋃B)⋃C = A⋃(B⋃C)

Solution:

Given that,

A = {2, 4, 6, 8}, B = {1, 3, 5, 7}, C = {1, 2, 5, 8}

L.H.S = (A⋃B)⋃C

= ({2, 4, 6, 8} U {1, 3, 5, 7}) U {1, 2, 5, 8}

= {1, 2, 3, 4, 5, 6, 7, 8} U {1, 2, 5, 8}

= {1, 2, 3, 4, 5, 6, 7, 8

R.H.S = A⋃(B⋃C)

= {2, 4, 6, 8} U ({1, 3, 5, 7} U {1, 2, 5, 8})

= {2, 4, 6, 8} U {1, 2, 3, 5, 7}

= {1, 2, 3, 4, 5, 6, 7, 8}

Hence, shown.

Also, Read

Interested students can see the process of representation of sets on this page. We have three different ways to represent a set. Get the solved examples on sets in the following sections. Check out the Representation of a Set in set-builder form, roster form, and statement form from the below sections of this page. Also, refer to solved examples on the representation of a set using different notations explained clearly.

What is Meant by Representation of a Set?

Sets are the collection of well-defined objects. The numbers, alphabets and others enclosed between the curly braces of a set are called the elements. The elements are separated by a comma symbol. Usually, sets are denoted by capital letters i.e A, B, C and so on. We have three ways for representing a set, they are

1. Descriptive Form

2. Set Builder Form

3. Roster Form

Also, Read

Descriptive Form

It is a way of representing a set in the verbal statement. It gives a description of elements in the set. The description must allow a concise determination of which elements belong to the set and which elements do not.

Examples:

• The set of natural numbers less than 25.
• The set of vowels in the alphabets.
• The set of all letters in English alphabets.
• The set of prime numbers less than 50.
• The set of even numbers between 20 and 40.

Roster Form or Tabular Form

Roster form means listing all the elements of a set inside a pair of curly braces {}.

Examples:

The natural numbers less than 15 are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14.

Let N be the set of natural numbers less than 15.

N = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14}

The prime numbers lesser than 50 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47

Let P be the set of prime numbers below 50.

P = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47}

Let M be the set of all months in a year.

Therefore, M = {January, February, March, April, May, June, July, August, September, October November, December}

Set-Builder Form or Rule Form

In the set-builder form, the statements are written inside a pair of braces. In this case, all the set elements must have a single property to become the set member. Here, the set elements are described by a symbol ‘x’ or any other variable followed by a colon “:” or slash “|”. After writing the symbol, you need to write a statement including the variable. In this, colon or slash stands for such that and braces stands for ‘set of all’.

Examples:

(i) Let P is the set of natural numbers between 15 and 25.

The set builder form is

P = { x : x is a natural number between 15 and 25 } or

P = { x | x is a natural number between 15 and 25 }

You can read this as P is a set of elements x such that x is a natural number between 15 and 25.

(ii) Let A denote the set of prime numbers between 5 and 50. It can be written in the set builder form as

A = { x | x is a prime number, 5 < x < 50 }

or A = { x : x ∈ P, 5 < x < 50 and P is an prime number }

(iii) The set B of all even natural numbers can be written as

B = {x : x is a natural number and x = 2n for n ∈ W}

Example Questions on Set Representation Using 3 Methods

Question 1:

The set of days of a week.

Solution:

Given that,

Set of days of a week.

The statement form is Set of seven days in a week.

The days in a week are Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday

The roster form is W ={Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday}

The set-builder notation is W = { x : x is a day of the week }

Question 2:

The set of whole numbers lying between 5 and 25.

Solution:

Given that,

The set of whole numbers lying between 5 and 25.

The description notation is Set of whole numbers between 5 and 25.

The whole numbers lying between 5 and 25 are 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, and 24.

The set-builder form is A = {x | x is a whole number, 5 < x <24}

The roster form is A = {6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24}

Question 3:

The set of all numbers lesser than 16 and greater than 8.

Solution:

Given that,

The set of all numbers lesser than 16 and greater than 8.

The numbers greater than 8 and less than 16 are 9, 10, 11, 12, 13, 14, 15

The roster form is N = {9, 10, 11, 12, 13, 14, 15}

The statement form is the set of numbers between 8 and 16.

The set builder form is N = { x : x ∈ A, 8 < x < 16, A is a natural number}

FAQs on Representation of a Set

1. What are the ways for representing a set?

The 3 various ways of set representation are statement form or description form, set-builder form or rule form, roster form or tabular form.

2. What is the formula to use rule form?

The rule form formula is { x : property}. Here property defines the elements of a set.

3. What is the best way to represent sets?

According to me, the best and most used way of writing a set is roster form. The advantage of using the roster form is we can just list the set elements between the curly braces and each element is separated by a comma.

4. What are the two methods of writing sets?

The two main methods of representation of a set are using a Venn diagram or listing the elements (roster form). Venn diagram is the pictorial representation and roster form is the mathematical representation.

Do you want to know what is meant by elements of a set? If yes, then stay tuned to this page. Students can see the example problems on how to find set elements and element definition. You can also check what is the size of a set. Set size and elements are related terms, one depends on the other. Generally, sets are represented using curly braces { }.

What are the Elements of a Set?

Elements of a set mean the numbers, alphabets, and others enclosed between curly braces. The set is a collection of elements or well-defined objects. Each element in a set is separated by a comma. The set elements are also called members of a set. The set name is always written in capital letters.

Examples:

set A = {2, 4, 6, 8, 10}

The elements of set A are 2, 4, 6, 8, and 10. It is a finite set as it has a finite number of elements.

set B = {-1, 0, 1, 2, 3, 4, . . . }

The elements of set B are -1, 0, 1, 2, 3, 4, 5, etc. It is an infinite set as we can’t count the number of elements in set B.

set C = {‘a’, ‘ab’, ‘c’, ‘d’}

The elements of set C are ‘a’, ‘ab’, ‘c’, and ‘d’.

Size of a Set

The size of a set means the number of elements or objects in the set. We can find the set size for the finite sets but infinite set size can’t be defined. The size of a set is also known as the order of sets. The order of a set is represented as n(set_name).

Examples:

P = {1, 3, 5, 7, 9}

The order of P is 5. n(P) = 5

Q = {“Apple”, “Orrange”, “Banana”, “Pomegranate”, “Pineapple”, “Papaya”}

Set Q has the names of fruits apple, orange, pomegranate, banana, papaya, and pineapple as the elements.

n(Q) = 6

Elements of a Set Examples

Question 1:

If set V = {‘a’, ‘e’, ‘i’, ‘o’, ‘u’}. State whether the following statements are ‘true’ or ‘false’:

(i) o ∈ V

(ii) m ∉ V

(iii) e ∈ B

Solution:

The elements of the given set V are ‘a’, ‘e’, ‘i’, ‘o’, and ‘u’.

(i) o ∈ V

It is a true statement. Because the letter o is present in the set V.

(ii) m ∉ V

True statement. Why because the letter m does not belongs to the set V.

(iii) e ∈ B

False statement. The reason is we don’t know about the elements of set B.

Question 2:

List out the members and order of each set in the following.

(i) A = {3, 6, 8, 10, 5, 7, 8}

(ii) B = {10, 12, 15, 7, 16}

(iii) C = {2, 8, 14, 20}

Solution:

(i) The given set is A = {3, 6, 8, 10, 5, 7, 8}

The members of set A is 3, 6, 8, 10, 5, and 7.

The order of A = n(A) = 7.

(ii) The given set is B = {10, 12, 15, 7, 16}

The elements of set B is 10, 7, 12, 15 and 16

n(B) = 5

(iii) The given set is C = {2, 8, 14, 20}

The elements of set C is 2, 8, 14, and 20.

n(C) = 4.

Question 3:

If set X = {2, 4, 6, 8, 10, 12, 14}. State which of the following statements are ‘correct’ and which are ‘wrong’ along with the correct explanations.

(i) X is a set of even numbers between 2 and 20.

(ii) 8, 4, 6, 12 are the members of set X.

(iii) 16 ∈ X

(iv) 10 ∈ X

(v) 1 ∉ X

Solution:

The given set is X = {2, 4, 6, , 10, 12, 14}

The elements of set X are 2, 4, 6, 8, 10, 12, and 14.

(i) X is a set of even numbers between 2 and 20.

Wrong. Since the set X contains even numbers till 14.

(ii) 8, 4, 6, 12 are the members of set X.

Correct. By checking the elements of X, we can say that 8, 6, and 12 belong to X.

(iii) 16 ∈ X

Wrong. As 16 does not belong to set X.

(iv) 10 ∈ X

Correct. As 10 belong to set X.

(v) 1 ∉ X

Correct. As the number 1 is not an element of set X.

Also, Check out

FAQ’s on Elements of a Set

1. Does a Null Set have elements?

Null set or empty set does not have members or elements. It is represented as {Ø} or { }.

2. What are the set members?

The members of a set are the objects or elements in it. For example the set A = {5, 8, 17, 25}. The elements or members of set A are 5, 8, 17, and 25. All the elements are locked between curly braces and they are separated by a comma.

3. What does ∈ mean?

The symbol ∈ is set membership. It means “is an element of”. The example B = {x, y, z, p, g}, g ∈ B means g is an element of B. ∉ means “is not an element of”. p ∉ B means p is not a member of set B.

4. What are elements and cardinality?

The cardinality is the number of elements in a set. If a set has 10 elements, then its cardinality becomes 10.

In maths, a set is a group of objects or elements. It deals with the properties & a collection of objects. Set theory is used in various concepts like fields, loops, groups, abstract algebra constructs, and closed part of one more operations. Here, we can check whether the given objects form a set or not? Get the conditions, and solved example problems in the following segments of this page.

What is a Set?

A set is a collection of objects or elements. The ways of describing sets are statement form, roster form, and set builder form. All the elements of the set are enclosed by curly braces. While forming a set the objects are grouped into a single entity. The example of a set are A = {“apple”, “custard apple”, “pineapple”, “orange”, “banana”, “grapes”, “papaya”}. The essential features of a set theory are along the lines.

• The relationship that may or may not exist between a set and an object is called a membership relationship.
• The principle of extension states that the set is defined by its objects instead of a single or defining group.

How to Confirm that Whether Objects Form a Set?

The following states help the students to check whether the group of objects form a set or not.

• A bunch of “lovely flowers” is not a set. As the object i.e flowers is not well defined. The reason is the word lovely is a relative term. What one person may feel lovely is not the same for other persons.
• A bunch of “red roses” is a set, because every red color rose is included in this set. It means set objects are well defined.
• A group of young actors” does not form a set. Because the particular rage of the young actor is not specified exactly. So, the objects are well defined.
• A group of “employees with age between 20 and 30 years” is a set. Because here the range of age of employees is provided. So, it can easily decide which employee is included and who is excluded.

Also, Read

Whether Objects Form a Set or Not Examples

State Whether the Objects Form a Set

Example 1:

The school has 45 students who know Telugu.

Solution:

The given objects form a set.

Reason: It can easily find the number of students in the school who can know the Telugu language by just asking them. Count those students. Hence, the objects form a set.

Example 2:

All the objects are heavier than 35 kg.

Solution:

The given objects form a set.

Every object’s weight is compared. If the weight is more than 28 kgs, then they are selected. It means objects are well defined.

Hence, the objects form a set.

Example 3:

All the number of books in the school bag is 6.

Solution:

The given objects form a set.

Reason: Check every student’s school bag, if the number of books is equal to 6 then take them into consideration. It says that objects are well defined.

Hence, the objects form a set.

Example 4:

All problems of this book, which are difficult to solve.

Solution:

The given objects do not form a set.

The problems one may difficult may not be difficult problems for other students. So, the objects not well defined.

Hence, the objects do not form a set.

Sets are a collection of organized objects. It can be represented using either roster or set-builder form. Students can read the further sections of this page to know the complete details like the definition, types, symbols, elements, and how to represent the sets. Few examples of sets are a collection of numbers, a list of fruits, a group of friends, and others.

Sets Definition

Sets are a collection of well-defined elements or objects. A set is represented by capital alphabets. The number of elements in a finite set is called the cardinal number of a set. The elements in the sets are separated by a comma.

Example:

A = {0, 1, 2, 3, 4, 5, . . .}

Here A is a set.

The elements or members of the set are 0, 1, 2, 3, . . .

The set of elements are here are whole numbers.

Representation of Sets

Generally, the elements of sets are enclosed by curly braces. Examples are {x, y, z}, {grapes, bananas, apples, oranges}. The sets can be represented in roster form or set builder form or statement form.

Statement Form:

The well-defined description of elements of a set is written and enclosed in the curly brackets. The set of odd numbers between 20 and 100 can be written in the statement form as {odd numbers between 20 and 100}.

Roster Form:

The roster form means all the members of the set are listed. The set of whole numbers is W = {0, 1, 2, 3, . . }

Set Builder Form:

The general form of set builder form is A = { x : property }. The example is A = {x : x = 5n, n ∈ N and 1 < n < 50}

Elements of a Set

The elements of a set mean the numbers or alphabets or objects in the set. The number of objects or items in a set is called the order of the set. The order of the set defines the set size. It is also known as cardinality.

Let us take a set M = {5, 8, 9, 15}

The elements of a set are 5, 8, 9 and 15.

As the set M has 4 elements, the size order of M is 4.

Types of Sets

In mathematics, the different types of sets are listed here.

Empty Set: A set that does not have elements in it is called an empty or null or void set. It is denoted by Ø or { }.

Finite Set: One which has a finite number of elements is called a finite set. An example is a set of natural numbers up to 6. A = {1, 2, 3, 4, 5, 6}

Singleton Set: One which has only one element is called a singleton set.

Equivalent Set: If two different sets have the same number of elements, then they are called equivalent sets.

Infinite Set: One which has an infinite number of elements is called an infinite set. Example is A = {5, 10, 15, . . .}

Equal Sets: If two sets have exactly the same elements irrespective of the elements order is called the equal sets. A = {Red, Green, Yellow, Orange}, B = {Green, Orange, Yellow, Red}. So, A = B.

Disjoint Sets: If two sets are disjoint, then they should not have common elements between them. Example is A = {2, 4, 6}, B = {1, 3, 5} are disjoint sets.

Subsets: Set A is the subset of set B means every element of A is also an element of B. It is denoted as A⊆ B.

Superset: If set X is a subset of another set Y and all the elements of set Y are the elements of set X, then X is a superset of Y. Superset can be represented as X⊃Y.

Proper Subset: If A ⊆ B and A ≠ B, then A is called the proper subset of B and it can be written as A⊂B.

Universal Set: One set which has all sets relevant to a condition is called a universal set.

Also, Read:

Sets Formulas

Check out the most important and commonly used Sets Formula from the below table. Use them during your calculations and make your work much simple.

Frequently Asked Questions on Sets

1. What is a set and example?

In mathematics, a set is a collection of objects, items, or elements. The set of all-natural numbers is an infinite set. The example of set is A = {5, 6, 8, 10}.

2. What are the different types of sets?

The sets are classified into various types. They are universal set, subset, proper subset, superset, equal sets, finite set, infinite set, disjoint sets, equivalent sets, empty set, and singleton set.

3. Why do we use sets?

Sets allow us to treat a collection of mathematical objects as an object. With the sets, you can develop further objects like constructing a continuous function.

4. What is the notation of a set?

We can represent sets in two forms roster form or set builder form. These two forms use curly braces to represent elements. The roster form is S = {a, b, c, d, e}, set builder form is S = {x : x +5n, n∈ N and 1  ≤ n ≤ 4}.

The basic four different arithmetic operations are addition, subtraction, multiplication, and division. To perform these arithmetic operations, you just need at least 2 numbers. Subtraction is one of the arithmetic operations that means removing objects from a group. It is represented using the minus sign “-“.

The other names of subtraction are minus, difference, deduct, less, decrease, and take away. For subtracting larger whole numbers, you can use subtraction with regrouping (borrowing) or quick subtraction or subtraction or addition methods. Interested candidates can read further sections to know five different properties of subtraction along with solved examples.

Also Check:

• Properties of Multiplication
• Properties of Division of Integers

How to Subtract Two Whole Numbers?

Students can subtract two larger whole numbers by following these steps.

• Let us take two numbers one is minuend, second is subtrahend.
• Write the number that is to be subtracted from on the top and the number that is to be subtracted on the bottom.
• Begin the process from the rightmost digits of the numbers.
• If the minuend digit is lesser than the subtrahend digit, then barrow 10 from the next digit of minuend which is on the left side.
• Add 10 to the minuend digit and subtract the result from the subtrahend’s digit.
• Don’t forget to mention the borrowed value on the top of the digit.
• Then the next digit becomes (digit – 1)
• Repeat the steps till you are left with nothing on the left side.

Properties of Subtraction

We are here to explain about five different properties of subtraction. Let us have a look at the following sections to get a clear idea about the topic.

Property 1: Closure Property

The difference between any two integers will also be an integer. If a, b are integers, then a – b is also an integer.

Examples:

15 – 5 = 10

259 – 8 = 251

45 – 48 = -3

16 – 0 = 16

Property 2: Identity Property

When a is an integer other than zero, then a – 0 = a but 0 – a is undefined.

Examples:

15 – 0 = 15 but 0 – 15 is not possibe

2 – 0 = 2 but 0 – 2 is undefined

84 – 0 = 84 but 0 – 84 is not defined

Property 3: Commutative Property

The commutative property of subtraction says that the swapping of terms will affect the difference value. If a and b are two integers, then (a – b) is never equal to (b – a).

Examples:

15 – 4 = 11 and 4 – 15 = -11

So, 15 – 4 ≠ 4 – 15

82 – 45 = 37 and 45 – 82 = -37

So, 82 – 45 ≠ 45 – 82

6 – 10 = -4 and 10 – 6 = 4

So, 6 – 10 ≠ 10 – 6

Property 4: Associative Property

The associative property of subtraction states that if you change the way of grouping numbers, then the result will be different. If a, b, c are three integers, then a – (b – c) is not equal to (a – b) – c.

Examples:

1. 15 – (10 – 2) = 15 – 8 = 7

(15 – 10) – 2 = 5 – 2 = 3

Therefore, 15 – (10 – 2) ≠ (15 – 10) – 2

2. 28 – (6 – 4) = 28 – 2 = 26

(28 – 6) – 4 = 22 – 4 = 18

Therefore, 28 – (6 – 4) ≠ (28 – 6) – 4

3. (156 – 120) – 10 = 36 – 10 = 26

156 – (120 – 10) = 156 – 110 = 46

Therefore, (156 – 120) – 10 ≠ 156 – (120 – 10)

Property 5: Distributive Property

The distributive property states that the integers are subtracted first and then multiplied by the result or multiply first and then subtraction later. If a, b, c are three integers, then a x (b – c) = a x b – a x c.

Examples:

1. 5 x (6 – 7) = 5 x (-1) = -5

5 x 6 – 5 x 7 = 30 – 35 = -5

So, 5 x (6 – 7) = 5 x 6 – 5 x 7

2. 16 x 25 – 16 x 20 = 400 – 320 = 80

16 x (25 – 20) = 16 x 5 = 80

So, 16 x 25 – 16 x 20 = 16 x (25 – 20)

Property 6:

If a, b, c are the whole numbers and a – b = c, then a = c + b.

Examples:

18 – 0 = 18 and 18 = 18 + 0

So, whenever zero is subtracted from any whole number, then we get the whole number.

18 – 18 = 0

So whenever a number is subtracted from the same number, then the difference is zero.

1850 – 1 = 1849 and 1849 + 1 = 1850.

Solved Examples on Properties of Subtraction

Example 1:

Solve the following.

(i) 415 – 0

(ii) 710 – 2

(iii) 5645 – 455

Solution:

(i) The given integers are 415, 0

As per the identity property, if any number is subtracted from 0, then the difference is a whole number.

So, 415 – 0 = 415.

(ii) The given integers are 710, 2

710 – 2 = 708.

(iii)

10

5 6 4 5

– 4 5 5

5 1 9 0

5645 – 455 = 5190.

Example 2:

Find the missed numbers from the following.

(i) 258 – _____ = 0

(ii) ______ – 90 = 88

(iii) 1652 – ______ = 10

Solution:

(i) 258 – x = 0

We already know that a – b = c, then a = c + b.

258 – 0 = x

As per the identity property, if any number is subtracted from 0, then the difference is a whole number.

So, 258 – 0 = 0

(ii) x – 90 = 88

We already know that a – b = c, then a = c + b.

x = 88 + 90

x = 178

So, 178 – 90 = 88.

(iii) 1652 – x = 10

We already know that a – b = c, then a = c + b.

1652 – 10 = x

x = 1642

So, 1652 – 1642 = 10.

Example 3:

State whether the following statements are correct or not.

(i) 56 x (85 – 25) = 56 x 85 – 56 x 25

(ii) 182 – (72 – 38) = (182 – 72) – 38

(iii) 546 – 546 = 1

Solution:

(i) The given statement is 56 x (85 – 25) = 56 x 85 – 56 x 25

L.H.S = 56 x (85 – 25)

= 56 x 60

= 3360

R.H.S = 56 x 85 – 56 x 25

= 4760 – 1400

= 3360

So, L.H.S = R.H.S

Therefore, the stament is true.

(ii) The given statement is 182 – (72 – 38) = (182 – 72) – 38

L.H.S = 182 – (72 – 38)

= 182 – 34

= 148

R.H.S = (182 – 72) – 38

= (110) – 38

= 72

L.H.S ≠ R.H.S

Therefore, the statement is false.

(iii) The given statement is 546 – 546 = 1

We know that, if a number is subtracted from the same whole number, then the result is zero.

Therefore, the statement is false.

FAQs on Properties of Subtraction

1. Write the different properties of subtraction?

The five various subtraction properties are closure property, identity property, distributive property, commutative property, and associative property.

2. Describe the terms minuend, subtrahend, and difference?

A minuend is a number that is to be subtracted from, a subtrahend is a number that is to be subtracted, and the difference is the result of subtracting one number from another number.

3. What is the difference between distributive property and associative property.

Distributive property for subtraction is true but associative property for subtraction is false. Distributive property is a x b – a x c = a x (b – c). Associative property is a – (b – c) ≠ (a – b) – c.

Roman Numerals are a special kind of numerical notations that were used by the Romans. Different combinations of symbols are used to represent the number. Both addition and subtraction are used to convert the roman numbers to the numbers. We are 4 different rules to form a roman numeral. The rules for forming the roman numerals with examples are mentioned in the following sections of this page.

Also, Read: Roman Numerals

Roman Numeral – Definition

A Roman numeral is a numeral in a system of notation that is based on the ancient Roman system. In this system, numbers are represented by the combination of letters from the Latin alphabet. The mostly used seven symbols and their values are I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000. Addition and subtraction operations are used to find other numbers. The first 10 roman numbers are I, II, III, IV, V, VI, VII, VIII, IX, and X.

Roman Numerals Chart 1-1000

Rules for Formation of Roman Numerals

In the Roman numerals system, there is no symbol to represent the digit 0. Roman numerals system has no place value. The digit or digits of lower value is placed after or before the digit of higher value. The value of digits of lower value is added to or subtracted from the value of digits of higher value. Using these rules, you can represent a number in the numeral system.

Rule 1: Repetition of roman numeral means addition.

(i) The symbols I, X, C, and M can be repeated more than once.

The value of I is 1, X is 10, C is 50, M is 1000.

(ii) The values I, X and C can be added as

II = 1 + 1 = 2

III = 1 + 1 + 1 = 3

XX = 10 + 10 = 20

XXX = 10 + 10 + 10 = 30

CC = 100 + 100 = 200

CCC = 100 + 100 + 100 = 300

(iii) The symbols V, L, D cannot be repeated. The repetition of V, L, and D is invalid in the formation of numbers.

(iv) None of the numeral symbols can be repeated more than 3 times.

Rule 2: If a smaller numeral is written to the right side of a larger numeral, then it is always added to the larger numeral.

(i) When a digit of lower value is written to the right side or after a digit of higher value, the values of all the digits are added.

VI = 5 + 1 = 6

VII = 5 + 1 + 1 = 7

XII = 10 + 1 + 1 = 12

XV = 10 + 5 = 15

LX = 50 + 10 = 60

(ii) Value of similar digits are also added as indicated in rule 1

XXX = 10 + 10 + 10 = 30

II = 1 + 1 = 2

Rule 3: If a small numeral is written to the left side of a larger numeral, then it is always subtracted from the larger value.

(i) V, L, D can never be subtracted

(ii) I can be subtracted only from V and X.

IV = 5 – 1 = 4

IX = 10 – 1 = 9

XIV = 10 + (5 – 1) = 10 + 4 = 14

CLIX = 100 + 50 + (10 – ) = 159

XXIX = 10 + 10 + (10 – 1) = 29

However, V is never written to the left of X.

Rule 4: If a smaller numeral is located between two large numerals, then the small numeral is subtracted from the bigger numeral immediately following it.

Rule 5: When a roman number has a straight horizontal line on the top of it, then its value becomes 1000 times.

XIV = 14 but XIV = 14000

CLV = 155 but CLV = 155000

Roman Numerals Examples

Example 1:

Write the Roman numerals for the following numbers:

(i) 55

(ii) 216

(iii) 517

Solution:

(i) The given number is 55

55 = 50 + 5

= LV

So, 55 = LV

(ii) The given number is 216

216 = 100 + 100 + 10 + 5 + 1

= CCXVI

So, 216 = CCXVI

(iii) The given number is 517

517 = 500 + 10 + 5 + 1 + 1

= DXVII

So, 517 = DXVII

Example 2:

Write the numbers for the following Roman numerals:

(i) XXXVII

(ii) DXLV

(iii) XLII

Solution:

(i) The given roman numeral is XXXVII

XXXVII = 10 + 10 + 10 + 5 + 1 + 1

= 37

So, XXXVII = 37

(ii) The given roman numeral is DXLV

DXLV = 500 + (-10 + 50) + 5

= 500 + 40 + 5

= 545

So, DXLV = 545

(iii) The given roman numeral is XLII

XLII = (-10 + 50) + 1 + 1

= 40 + 1 + 1

= 42

So, XLII = 42

Example 3:

Write the Roman numerals for the following numbers:

(i) 425

(ii) 159

(iii) 61

Solution:

(i) The given number is 425

425 = (500 – 100) + 10 + 10 + 5

= CDXXV

So, 425 = CDXXV

(ii) The given number is 159

159 = 100 + 50 + (10 – 1)

= C + L + (X – I)

= CLIX

So, 159 = CLIX

(iii) The given number is 61

61 = 50 + 10 + 1

= L + X + I

= LXI

So, 61 = LXI

Algebraic expressions are the expressions that have variables, constants, and arithmetic operators. Mainly, we have three different types of algebraic expressions. Get to know more about those algebraic expression types in the following sections. You can check what is meant by an algebraic expression, definitions of various algebraic expressions, examples, and worked out problems in this article.

Algebraic Expression Definition

An algebraic expression is a mathematical term that contains variables, constants along with mathematical operators like addition, subtraction, division, and multiplication. The example of an algebraic expression is 5x + 20y – 9. The different parts of an algebraic expression are variable, coefficient, operator, and constant. The definitions of these different parts of an algebraic expression are:

• Constant: It is a term whose value remains unchanged throughout the expression.
• Variable: It is an alphabetic letter whose value is unknown. It can take any value based on the situation.
• Coefficient: It is a numerical value added before the variable to modify the variable value.
• Operator: Mathematical operators are used in algebraic expressions to perform some math calculations on two or more expressions.

Types of Algebraic Expressions

The algebraic expressions are further divided into 5 different types. Let us discuss each of these types in the following sections.

1. Monomial Algebraic Expression

2. Polynomial Algebraic Expression

3. Binomial Algebraic Expression

4. Trinomial Algebraic Expression

5. Multinomial Algebraic Expression

Also, Read:

• Factorization when Monomial is Common
• Factors of Algebraic Expressions
• Factorization when Binomial is Common

Monomial Algebraic Expression

An algebraic expression that has only one non-zero term is known as the monomial.

Examples of monomials:

7a³b² is a monomial in two variables a, b

\(\frac { 2ax }{ 3y } \) is a monomial in three variables a, x and y.

x² is a monomial in one variable x.

2y is a monomial in one variable y.

Polynomial Algebraic Expression

An algebraic expression that has one, two, or more terms is known as the polynomial.

Examples of Polynomials:

3x + 4y is a polynomial in two variables x, y

4x² – 3xy + 6y² + 80 is a polynomial in two variables x, y

m + 5mn – 7mn² + nm² + 9 is a polynomial in two variables m, n

a³b + 4b²c + 6ab + 2ca + 5bc is a polynomial in three variables a, b, c

Binomial Algebraic Expression

An algebraic expression that has two non-zero terms is known as the binomial.

Examples of binomials:

5x + 6y³ is a binomial in two variables x, y

a + b is a binomial in two variables a, b

p – q² is a binomial in two variables p, q

m²n + 6 is a binomial in two variables m, n

Trinomial Algebraic Expression

An expression that has three non-zero terms is known as trinomial.

Examples of Trinomial:

p + q + r is a trinomial in three variables p, q, r

\(\frac { x² }{ 3 } \) + ay – 6bz is a trinomial in three variables x, y, z

xy + x + 2y2 is a trinomial in two variables x and y.

Multinomial Algebraic Expression

An algebraic expression that has two or more than three terms is known as the multinomial.

Examples of Multinomial:

w + x – y + 2z is a multinomial in four variables w, x, y, z.

a + ab + b + bc + cd is a multinomial of five terms in four variables a, b, c, and d.

5x⁸ + 3x⁷ + 2x⁶ + 5x⁵ – 2x⁴ – x³ + 7x² – x is a multinomial of eight terms in one variable x.

Formulas

The general algebraic formulas we use to solve the expressions or equations are:

• (a + b)² = a² + 2ab + b²
• (a – b)² = a² – 2ab + b²
• a2 – b² = (a – b)(a + b)
• (a + b)³ = a³ + b³ + 3ab(a + b)
• (a – b)³ = a³ – b³ – 3ab(a – b)
• a³ – b³ = (a – b)(a² + ab + b²)
• a³ + b³ = (a + b)(a² – ab + b²)

Algebraic Expressions Questions

Question 1:

Add algebraic expressions 3x + 5y – 6z and x – 4y + 2z.

Solution:

The given algebraic expressions are 3x + 5y – 6z and x – 4y + 2z

While adding two or more algebraic expressions, add the like terms together.

3x + 5y – 6z + x – 4y + 2z = (3x + x) + (5y – 4y) + (2z – 6z)

= 4x + y – 4z

Therefore, the sum is 4x + y – 4z

Question 2:

Subtract the algebraic expressions 3x² – 6x – 4 from x + 5 – 2x²

Solution:

The given algebraic expressions are 3x² – 6x – 4, x + 5 – 2x²

While subtracting two or more algebraic expressions, perform the operation only between the like terms.

x + 5 – 2x² – (3x² – 6x – 4) = x + 5 – 2x² – 3x² + 6x + 4

= (x + 6x) + 5 + 4 – (2x² + 3x²)

= 7x + 9 – 5x²

Therefore, x + 5 – 2x² – (3x² – 6x – 4) = 7x + 9 – 5x²

Question 3:

Simplify the algebraic expression by combining the like terms

4(2x+1) – 3x – 2

Solution:

The given algebraic expression is 4(2x+1) – 3x – 2

Remove the braces

4(2x+1) – 3x – 2 = 8x + 4 – 3x – 2

= (8x – 3x) + 4 – 2

= 5x + 2

Therefore, 4(2x+1) – 3x – 2 = 5x + 2

Question 4:

Reduce the algebraic expression to its lowest term

Solution:

The given algebraic expression is \(\frac { (x² – y²)}{ (x + y) } \)

We see that the numerator and denominator of the given algebraic fraction is polynomial, which can be factorized.

(x² – y²) = (x + y)(x – y)

\(\frac { (x² – y²)}{ (x + y) } \) = \(\frac { (x + y)(x – y)}{ (x + y) } \)

Cancel te like term (x + y)

= (x – y)

Therefore, \(\frac { (x² – y²)}{ (x + y) } \) = x – y.

FAQs on Types of Algebraic Expressions

1. What are the types of algebraic expressions?

The five different types of algebraic expressions are monomial, binomial, trinomial, multinomial, and polynomial.

2. What are the rules for algebraic expressions?

The basic rules are to combine the like terms, constants for addition or subtraction. Remove any grouping symbols like paranthesis, brackets by multiplying factors. Use the exponential rule to remove grouping.

3. Write examples of algebraic expressions?

The examples of algebraic expression is x + 2y + 1, x² + 5xy + y³ + 9, x⁴y + 4x³y² + 16xy.

4. How to derive algebraic expressions?

An algebraic expression is a combination of constants, variables and algebraic operations (+, -, ×, ÷). We can derive the algebraic expression for a given situation or condition by using these combinations.

Looking for any help to divide a decimal by a decimal number? Then stay on this page. Here we are giving solved example questions on how to divide two decimal numbers. Interested students can read this complete page to know more details about the topic. Not only the easy procedure Division of a Decimal by a Decimal but also you can check the definition of decimal numbers in the further sections.

Also, Read

• Dividing Decimal by a Whole Number
• Decimal Fractions
• Decimals

What are Decimals?

A decimal number is a number that has a whole number part and fractional part separated by a dot called a decimal point. The value of digits following the decimal point should be less than the value of 1. Some of the decimal numbers are 45.9, 708.3, etc.

How to Divide a Decimal by a Decimal?

Get the detailed steps on Dividing Decimal by a Decimal Number in the following sections. Follow these steps as it is to get the product easily and quickly.

• Take any two decimal numbers one as dividend and the other as the divisor.
• In general, dividend value should be more when compared to divisor value.
• Remove dot from the decimal numbers.
• Divide those two numbers.
• Place the decimal dot in the quotient.

Decimal Division Problems with Answers

Example 1:

Solve 15.5 ÷ 0.5 by eliminating the decimal places.

Solution:

The given divisor is 0.5 and the dividend is 15.5

Count the number of decimal digits in the divisor and we observe that after decimal there is 1 number so we divide the number by 10.

15.5 ÷ 0.5 = \(\frac { 155 }{ 10 } \) ÷ \(\frac { 5 }{ 10 } \)

= \(\frac { 155 }{ 10 } \) x \(\frac { 10 }{ 5 } \) [reverse it to multiplication]

= \(\frac { 155 x 10 }{ 5 x 10 } \)

= \(\frac { 1550 }{ 50 } \)

Now divide the numbers as usual.

Therefore, 15.5 ÷ 0.5 = 31

Example 2:

Solve 1.296 ÷ 0.108.

Solution:

The given divisor = 0.108, dividend = 1.296

Count the number of decimal digits in the divisor and we observe that after decimal there are 3 numbers so we divide the number by 1000

1.296 ÷ 0.108 = \(\frac { 1296 }{ 1000 } \) ÷ \(\frac { 108 }{ 1000 } \)

= \(\frac { 1296 }{ 1000 } \)  x \(\frac { 1000 }{ 108 } \) [reverse it to multiplication]

= \(\frac { 1296 x 1000 }{ 1000 x 108 } \)

= \(\frac { 1296000 }{ 108000 } \)

Now divide the numbers as usual.

Therefore, 1.296 ÷ 0.108 = 12

Example 3:

Solve 0.445 ÷ 0.05.

Solution:

The given divisor = 0.05, dividend = 0.445

Count the number of decimal digits in the divisor.

Move the decimal in a dividend that many places to the right.

So, 0.445 ÷ 0.05 = 44.5 ÷ 5

Write the divisor without the decimal. And add the decimal point to the quotient.

Therefore, 0.445 ÷ 0.05 = 8.9.

Example 4:

Solve 2.805 ÷ 0.11.

Solution:

The given divisor = 0.11, dividend = 2.805

Count the number of decimal digits in the divisor.

Move the decimal in a dividend that many places to the right.

So, 2.805 ÷ 0.11 = 280.5 ÷ 11

Write the divisor without the decimal. And add the decimal point to the quotient.

So, 2.805 ÷ 0.11 = 25.5.

FAQs on Division of a Decimal by a Decimal

1. How do you divide a decimal number by a decimal?

To divide two decimal numbers, move the decimal point in the divisor and dividend. The number we divide by is called the divisor and the number which divides is called the dividend. After removing the decimal point in the divisor, divide like normal. And add the decimal point to the obtained quotient.

2. How do you divide decimals without a calculator?

To divide the decimal by a decimal number without a calculator, follow the simple steps mentioned here.

3. What are the steps for dividing decimals?

Eliminate the decimal point in the divisor by moving the point to the left side. Just remove the decimal point in the dividend and divide those numbers as usual. And then add a decimal point to the quotient.

Worksheet on LCM is given here. Students can get the important questions on the least common multiples on this page. Along with the problems, you can also see the solutions, steps to solve all types of LCM questions. Check out the detailed explanation on solving the L.C.M of numbers, monomials, and polynomials in the following sections. By solving all the questions of Worksheet on Least Common Multiples, you can prepare well for the exams.

You can find the lowest common multiple of numbers by finding the common prime factors, prime factorization method, division method, listing multiples, and others. Practice the problems as much as possible to clear the exam.

Also, Read: Common Factors

What is L.C.M?

The least common multiple of two integers a, b is denoted as lcm(a, b), which means the smallest positive integer that is divisible by both a and b. As the division of integers by zero is undefined, the definition has meaning only if a and b are both different from zero. The lcm is the lowest common denominator (LCD) that can be used before adding, subtracting, or comparing the fractions. The L.C.M of two or more integers can be the smallest positive integer that is divisible by all of them.

Problem 1:

Find the L.C.M of the following integers by listing their multiples.

(i) 10, 15, 35

(ii) 6, 42, 54

(iii) 16, 24, 48

Problem 2:

Find the first 3 common multiples of the given using a number line.

(i) 2 and 3

(ii) 3 and 4

(iii) 9 and 12

Problem 3:

Find the Lowest Common Multiple of the following by finding common prime factors.

(i) 2, 8, 10

(ii) 56, 72

(iii) 25, 30, 150

Problem 4:

Find the L.C.M. of the given numbers by division method.

(i) 70, 110, 150

(ii) 36, 60, 120

(iii) 21, 49, 63

Problem 5:

Find the LCM of the given numbers by the prime factorization method.

(i) 10, 15 and 45

(ii) 36, 27 and 18

(iii) 18, 54, 72

Problem 6:

Calculate the LCM of integers using the Cake/Ladder method.

(i) 5, 27, 15

(ii) 48, 64 and 120

(iii) 12 and 20

Problem 7:

Calculate the least common multiple of numbers using the G.C.F method.

(i) 49, 14, 70

(ii) 84, 90

(iii) 10, 25, 60

Problem 8:

Find the lowest number which is less by 2 to be divided by 56 and 98 exactly.

Problem 9:

The H.C.F. two numbers are 6 and their L.C.M. is 36. If one of the numbers is 18, find the other number.

Problem 10:

The product of two numbers is 144. If the L.C.M. of these numbers is 12, find their H.C.F.

Problem 11:

Find the LCm of monomials 4mn, 10n

Problem 12:

Find the LCM of polynomials x² – 5², (x + 5)²

Students do you want to know that the number 13 is a prime number or not? Also, learn more about the 13 Times Table Multiplication Chart from this article. Here, you will find various options to understand, learn and remember the multiplication table of thirteen. So, read this complete page and gather the useful information that helps to learn the Math Tables from 0 to 25. These tables are mandatory at the time of prime classes. Hence have a look at the tips and tricks to memorize the 13 Times Table and the solved example questions.

Multiplication Table of 13 | Table of Thirteen

In the below sections, we have provided the 13 Times Table Multiplication Chart both in the image and tabular format. Students can download it from here and prepare offline too whenever they need it. By downloading Multiplication Table of 13 you can revise it regularly and remember it easily. You can get it free of cost from our site which is useful to make your math calculations quickly.

13 Times Multiplication Table up to 25

It is very easy to learn the Thirteen Times Table Multiplication Chart. Just we need to add 13 to the first multiple and get the next multiple. It is a process of repeated addition where 13 x 0 = 0 and then add 13 to get the next multiple results. So, go through the table and learn the writing the Multiplication Table of 13 up to 25 whole numbers. Also, you will find the section to learn how to read 13 times Multiplication Table on this page.

How to Read Thirteen Times Table

Zero time thirteen is 0

One time thirteen is 13

Two times thirteen is 26

Three times thirteen is 39

Four times thirteen is 52

Five times thirteen is 65

Six times thirteen is 78

Seven times thirteen is 91

Eight times thirteen is 104

Nine times thirteen is 117

Ten times thirteen is 130.

Get More Multiplication Tables

Why One Should Read 13 Times Table Multiplication Chart?

Learning 13 times Multiplication table is very important and it has several advantages for solving mathematical problems. There are many aspects of mathematics that require multiplication tables to spend less amount of time.

• Math Tables saves your time while doing arithmetical operations like multiplications, divisions, and reducing fractions, finding LCM, GCF, etc
• In this way, learning tables are helpful to solve math problems easily and quickly.
• 13 Times Table makes you perfect in performing the quick calculations.

Tips & Tricks to Remember 13th Table

We have 2 simple techniques to remember and memorize the Multiplication table of 13. So, interested students must check out these tips to learn the table quickly.

• To memorize the 13 Times Table Multiplication Chart, first, you need to remember the 3rd Table. The multiples of three are 3, 6, 9, 12, 15, 18, . . .
• And then add natural numbers to the ten’s digit of the 3 multiples. The obtaines 13 multiples are (1 + 0)3 = 13, (2 + 0)6 = 26, (3 + 0)9 = 39, (4 + 1)2 = 52, (5 + 1)5 = 65, (6 + 1)8 = 78, (7 + 2)1 = 91, (8 + 2)4 = 104, (9 + 2)7 = 117, (10 + 3)0 = 130, (11 + 3)3 = 143, . .
• Thirteen does not have any rules that make the multiplication table easier to memorize. Them here is a structure for every 10 multiples of 13. They are 13, 26, 39, 52, 65, 78, 91, 104, 117, 130. In all these multiples, the last digit i.e units place digit is repeating. So, one can remember this logic to memorize the table.

Solved Examples on 13 Times Multiplication Table

Example 1:

Calculate the value of 3 plus 13 times of 7 minus 4, using the 13 Times Table.

Solution:

Given, calculate the value using 13 Times Table

First, we have to write down the given statement plus 13 times of 7 minus 4

Now, solving the above expression by using 13 Times Table Multiplication Chart,

3 plus 13 times 7 minus 4 = 3 + 13 x 7 – 4

= 3 + 91 – 4

= 3 + 87

= 90

Therefore, the value of 3 plus 13 times 7 minus is 90.

Example 2:

Check using the table of 13 whether 8 times 13 minus 4 is 100?

Solution:

Given, calculate the value using 13 Times Table

First, we have to write down the given statement 8 times 13 minus 4

8 times 13 minus 4 = 8 x 13 – 4

= 104 – 4

= 100

Therefore, the given statement is true.

Example 3:

Use the 13 times table multiplication chart, and evaluate the value of 6 plus 13 times 5 minus 9.

Solution:

Given, calculate the value using 13 Times Table

First, we have to write down the given statement 6 plus 13 times 5 minus 9

6 plus 13 times 5 minus 9 = 6 + 13 x 5 – 9

= 6 + 65 – 9

= 6 + 56

= 62

Therefore, 6 plus 13 times 5 minus 9 is 62.

Example 4:

Using the Multiplication Table of 13, evaluate 13 times 15 plus 25 minus 4.

Solution:

Given, calculate the value using 13 Times Table

First, we have to write down the given statement 13 times 15 plus 25 minus 4

Now, solving the above expression by using 13 Times Table

13 times 15 plus 25 minus 4 = 13 x 15 + 25 – 4

= 195 + 25 – 4

= 195 + 21

= 216

Therefore, 13 times 15 plus 25 minus 4 is 216.

Numbers were invented for the purpose of counting. The number system is defined as a writing system to express the number in a consistent manner. The place values of digits express in the sequence of ones, tens, hundreds, thousands, ten thousand, hundred thousand, millions, ten million, and so on in the international number system. Students can also know more about the international numbering system with example questions in the following sections.

International Numbering System Definition

The international numbering system is followed by most of the countries in the world. In this system, a number is split into groups or periods. In the international number system, we use ones (1), tens (10), hundreds (100), thousands (1000), ten thousands (10,000), hundred thousand’s (100,000), one millions (1,000,000), ten millions (10,000,000), hundreds millions (100,000,000), etc. We place the numbers according to their place value. We place a comma after each period to differentiate the periods.

How to Express Numbers in International System?

Based on the number of digits in the number, it is divided into periods.

• The first period is known as one’s period, formed with the first 3 digits of the number.
• The second period is called the thousands period, formed with the next 3 digits of the number.
• The third period is called the millions period, formed with the digits after thousands.

Also, Read

• Roman Numerals

International Numbering System Examples

Question 1:

Write the following figures in the international system.

(i) Six hundred thousand

(ii) Fifty million

(iii) Six hundred million

Solution:

To represent the given figures in the international numbering system, we must identify the period.

(i) The given figure is six hundred thousand

The hundred thousand means 100,000

six hundred thousand is 600,000.

(ii) The given figure is fifty million

Million means the third period formed after three digits of the thousands period. One million is 1,000,000

So, fifty million means 50,000,000.

(iii) The given figure is six hundred million

Million means the third period formed after three digits of the thousands period. One million is 1,000,000 and one hundred million is 100,000,000.

So, five hundred million is 500,000,000.

Question 2:

Write the following in figures in the International system:

(i) Six thousand, five hundred and twenty-two.

(ii) Three hundred and twenty-five thousand, four hundred and two

(iii) Three hundred and fifteen million, one hundred and twenty-one thousand, eight hundred and ten

Solution:

To express these word figures into the international numbering system, we need to have a clear idea of the periods.

(i) The given figure is six thousand, five hundred and twenty-two

six thousand means 6,000

five hundred means 500

twenty means 20

two means 2.

So, six thousand, five hundred and twenty-two is 6,522.

(ii) The given figure is Three hundred and twenty-five thousand, four hundred and two

Three hundred and twenty-five thousand means 325,000

four hundred means 400

two means 2

So, Three hundred and twenty-five thousand, four hundred and two is 325,402.

(iii) The given figure is Three hundred and fifteen million, one hundred and twenty-one thousand, eight hundred and ten

Three hundred and fifteen million is 315,000,000

one hundred and twenty-one thousand means 125,000

eight hundred means 800

ten means 10

So, Three hundred and fifteen million, one hundred and twenty-one thousand, eight hundred and ten is 315,125,810.

Question 3:

Write the following figures in the international system.

(i) Five million six hundred and twenty-five thousand seven hundred

(ii) One hundred ninety-six thousand eight hundred sixty-seven

(iii) Four hundred and ten thousand one hundred and six

Solution:

To express these word figures into the international numbering system, we need to have a clear idea of the periods.

(i) The given figure is Five million six hundred and twenty-five thousand seven hundred

Five million six hundred means 560,000,000

twenty-five thousand means 25,000

seven hundred means 700.

So, Five million six hundred and twenty-five thousand seven hundred is 560,025,700.

(ii) The given figure is One hundred ninety-six thousand eight hundred sixty-seven

One hundred ninety-six thousand means 196,000

eight hundred sixty-seven means 867.

So, One hundred ninety-six thousand eight hundred sixty-seven is 196,867.

(iii) The given figure is Four hundred and ten thousand one hundred and six

Four hundred and ten thousand means 410,000

one hundred and six means 106

So, Four hundred and ten thousand one hundred and six is 410,106.

Question 4:

(i) 25,896

(ii) 185,200,604

(iii) 568,952

Solution:

Write the following figures in the international system.

(i) The given figure is 25,896

25,000 is twenty-five thousand.

896 is eight hundred and ninety-six.

So, 25,896 is twenty-five thousand eight hundred and ninety-six

(ii) The given figure is 185,200,604

185,000,000 is one hundred and eighty-five million

200,000 is two hundred thousand

604 is six hundred and four.

So, 185,200,604 is eighty-five million and two hundred thousand six hundred and four..

(iii) The given figure is 568,952

568,000 is five hundred and sixty-eight thousand

952 is nine hundred fifty-two.

So, 568,952 is five hundred and sixty-eight thousand nine hundred and fifty-two.

FAQs on International Numbering System

1. Compare Indian and International Number System?

The major difference between the Indian and international number systems is the placement of the separators and nomenclature of different place values. In the international system, nine places are grouped into three periods ones, thousands, and millions.

In the Indian system, nine places are grouped into four periods. The place values of the Indian system are ones, tens, hundreds, thousands, ten thousand, lakhs, ten lakhs, crores, and ten crores. The international system place values are ones, tens, hundreds, thousands, ten thousand, hundred thousand, millions, ten million, and hundred million.

2. How do you write 6 digit numbers in the international system?

The 1st digit is ones, 2nd is tens, 3rd is hundreds, fourth is thousand, the fifth digit is ten thousand and six-digit is hundred thousand. The six digits have 2 periods.

3. How many periods are there in an international number system?

The international number system has 3 periods. They are ones, thousands, and millions. One period has ones, tens, and hundreds.