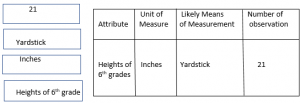
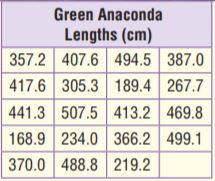
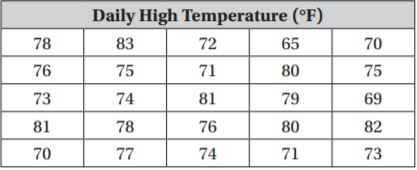
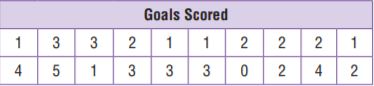
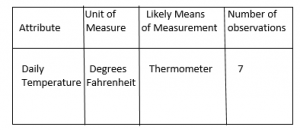
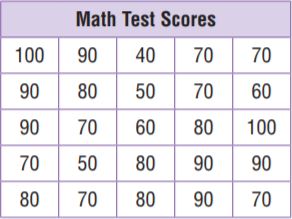
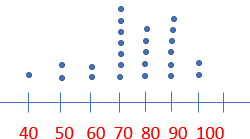
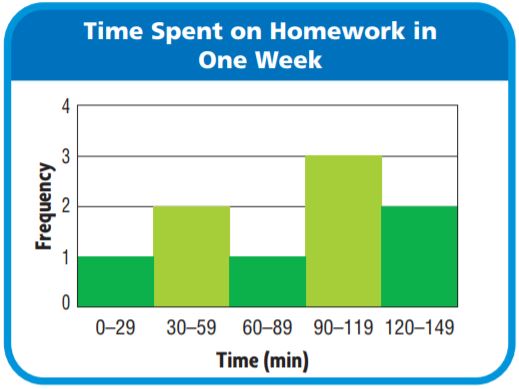
Go Math Grade 4 Answer Key Chapter 1 Place Value, Addition, and Subtraction to One Million pdf formatted download links are provided here for all concepts. Students of Grade 4 can take help from Go Math solutions for better preparation and score high marks in the exams. Want to help the students in offering immense knowledge? this is the best resource for them. So,
Go Math Grade 4 Answer Key Chapter 1 Place Value, Addition, and Subtraction to One Million is helpful and understandable by students. It includes each and every question with step by step explanation in a simple way.
Go Math Grade 4 Answer Key Chapter 1 Place Value, Addition, and Subtraction to One Million
Chapter 1 of Go Math 4th Grade Answer Keys includes topis like Place value relationships, Read and write numbers, Compare and Order numbers, Round numbers, Rename numbers, etc. All these topics are illustrated explicitly which addresses the toppers to learn quickly.
Go Math Grade 4 Answer Key Chapter 1 Place Value, Addition, and Subtraction to One Million Questions & Solutions are provided in a fundamental way that makes students not find any difficulty in learning & solving.
Chapter 1-Lesson 1:
Chapter 1-Lesson 2:
Chapter 1-Lesson 3:
Chapter 1-Lesson 4:
Chapter 1-Lesson 5:
Chapter 1-Lesson 6:
Chapter 1-Lesson 7:
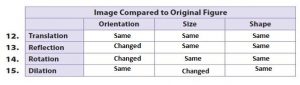
Chapter 1-Lesson 8:
Chapter 1-Lesson 9:
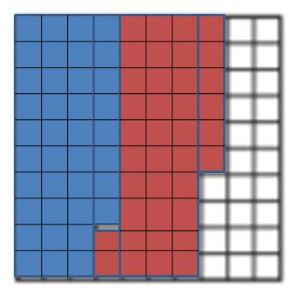
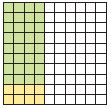
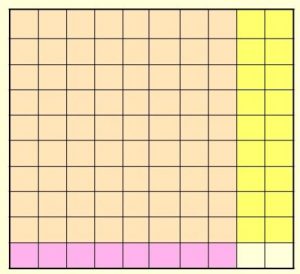
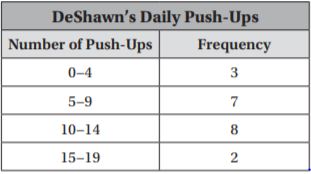
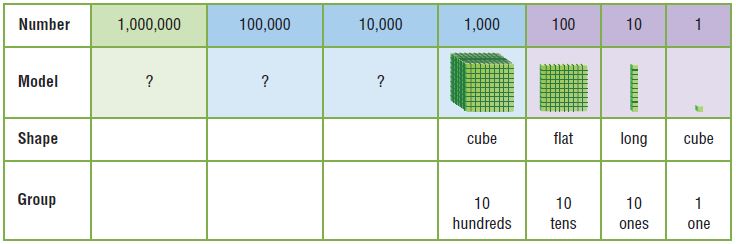
Common Core – Model Place Value Relationships (Page 5)
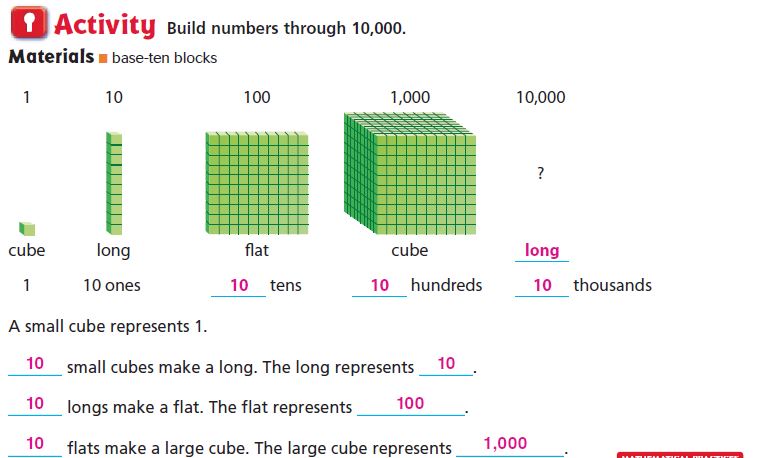
Question 1.
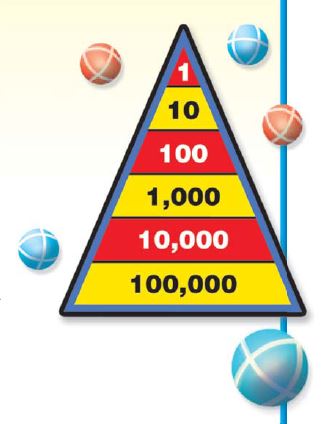
Describe the pattern in the shapes of the models. What will be the shape of the model for 10,000?
Answer: The pattern shows cube, long, flat, cube. So the shape of the model for 10,000 will be long.
Question 2.
Describe the pattern you see in the sizes of the models. How will the size of the model for 100,000 compare to the size of the model for 10,000?
Answer: Each model is 10 times the previous model, so the model for 100,000 will be 10 times the size of the model for 10,000.
Common Core – Model Place Value Relationships (Page 6)
Value of a Digit
The value of a digit depends on its place-value position in the number. A place-value chart can help you understand the value of each digit in a number. The value of each place is 10 times the value of the place to the right.
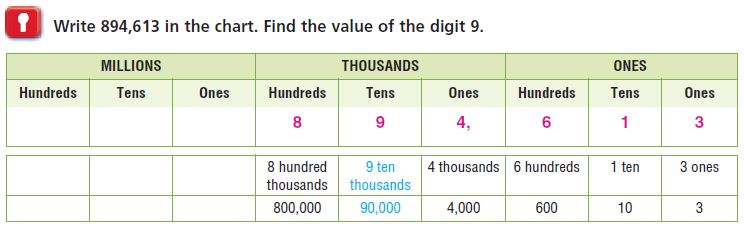
Question 1.
The value of the digit 9 is 9 ten thousands, or:
Answer: The place value of the digit 9 in 894,613 is 90,000.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 9 in 8,94,613 is 90,000.
Compare the values of the underlined digits.
2,304 16,135
Answer: The value of 3 in 2,304 is 10 times the value of 3 in 16,135.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 3 in 2,304 is 300. And the place value of the digit 3 in 16,135 is 30. As each hundred is 10 times as many as 10, so 3 hundreds are ten times as many as 3 tens. So, the value of 3 in 2,304 is 10 times the value of 3 in 16,135.
Question 2.
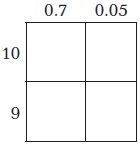
STEP 1 Find the value of 3 in 2,304.
Show 2,304 in a place-value chart.
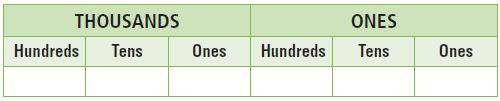
Answer: The value of 3 in 2,304 is 300
Explanation:
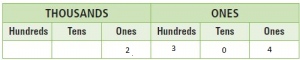
Question 2.
STEP 2 Find the value of 3 in 16,135.
Show 16,135 in a place-value chart.
So, the value of 3 in 2,304 is ___________ times the value of 3 in 16,135.
Answer: The value of 3 in 16,135 is 30. So, the value of 3 in 2,304 is 10 times the value of 3 in 16,135.
Explanation:
Each hundred is 10 times as many as 10, so 3 hundreds are ten times as many as 3 tens. So, the value of 3 in 16,135 is 30. So, the value of 3 in 2,304 is 10 times the value of 3 in 16,135.

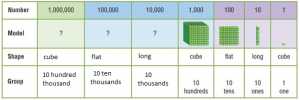
Common Core – Model Place Value Relationships (Page 7)
Question 1.
Complete the table below.
Answer:
Explanation:
Find the value of the underlined digit.
Question 2.
703,890
Answer: The value of the digit 7 in 703,890 is 700,000.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 7 in 703,890 is 700,000.
Question 3.
63,540
Answer: The value of the digit 4 in 63,540 is 40.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 4 in 63,540 is 40.
Question 4.
182,034
Answer: The value of the digit 8 in 182,034 is 80,000.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 7 in 703,890 is 700,000.
Question 5.
345,890
Answer: The value of the digit 5 in 345,890 is 5,000.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 5 in 345,890 is 5,000.
Compare the values of the underlined digits.
Question 6.
2,000 and 200
The value of 2 in 2,000 is ___________ times the value of 2 in 200
Answer: 10 times.
Explanation: The value of 2 in 2000 is 10 times the value of 2 in 200.
Question 7.
40 and 400
The value of 4 in 400 is ___________ times the value of 4 in 40
Answer: 10 times.
Explanation: The value of 4 in 400 is 10 times the value of 4 in 40.
Find the value of the underlined digit.
Question 8.
230,001
Answer: The place value of the digit 3 in 230,001 is 30,000.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 3 in 230,001 is 30,000.
Question 9.
803,040
Answer: The place value of the digit 3 in 230,001 is 30,000.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 3 in 230,001 is 30,000.
Question 10.
46,842
Answer: The place value of the digit 2 in 46,842 is 2.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 2 in 46,842 is 2.
Question 11.
980,650
Answer: The place value of the digit 9 in 980,650 is 900,000.
Explanation: Every digit in a number has a place value and the place value can be defined as the value represented by a digit in a number on the basis of its position in the number. So the place value of the digit 9 in 980,650 is 900,000.
Compare the values of the underlined digits.
Question 12.
67,908 and 76,908
Answer: The value of 7 in 76,908 is 10 times the value of 7 in 67,908.
Explanation: As the value of 7 in 76,908 is 70,000 and the value of 7 in 67,908 is 7,000. So the value of 7 in 76,908 is 10 times the value of 7 in 67,908.
Question 13.
546,300 and 3,456
Answer: The value of 3 in 3,456 is 10 times the value of 3 in 546,300.
Explanation: As the value of 3 in 3,456 is 3,000 and the value of 3 in 546,300 is 300. So the value of 3 in 3,456 is 10 times the value of 3 in 546,300.
Question 14.
Greg has collected 4,385 pennies and Hannah has collected 3,899 pennies. How many times as great as the value of 3 in 4,385 is the value of 3 in 3,899?
Answer: The value of the digit 3 in 3,899 is 10 times more than the value of the digit 3 in 4,385.
Explanation:
The value of the digit 3 is 4,385 is 300 and the value of 3 in 3,899 is 3000. So the value of the digit 3 in 3,899 is 10 times more than the value of the digit 3 in 4,385.
Question 15.
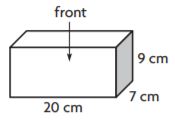
Shawn wants to model the number 13,450 using base-ten blocks. How many large cubes, flats, and longs does he need to model the number?
Answer: Shawn needs 13 large cubes, 4 flats, and 5 longs.
Explanation: Each large cube represents 1000, so 13 large cubes will represent 13×1000= 13,000, and each flat represent 100 so each 4 flats represent 4×100= 400, and each long represents 10 so 5 longs represent 5×10= 50.
So 13,000+400+50= 13,450.
Common Core – Model Place Value Relationships (Page 8)
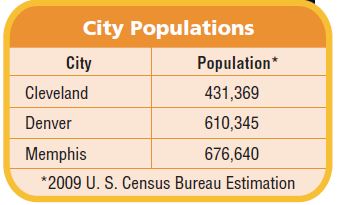
Question 14.
What is the value of the digit 7 in the population of Memphis?
Answer: The value of digit 7 in 676,640 is 70,000.
Explanation: The population of Memphis is 676,640, so the value of digit 7 in 676,640 is 70,000.
Question 14.
What is the value of the digit 1 in the population of Denver?
Answer: The value of the digit 1in 610,345 is 10,000.
Explanation: The population of Denver is 610,345, so the value of the digit 1in 610,345 is 10,000.
Question 14.
How many times as great as the value of the digit 1 in the population of Cleveland is this value?
Answer: The value of digit 1 in 431,369 is 1000.
Explanation: The population of Cleveland is 431,369, so the value of digit 1 in 431,369 is 1000.
Question 14.
Which city’s population has a 4 in the hundred thousands place?
Answer: Cleveland is the city with 4 in the hundred thousands place.
Explanation: Cleveland is the city with 4 in the hundred thousands place. As the population of Cleveland is 431,369 and the value of 4 in 431,369 is 400,000.
Question 15.
How many models of 100 do you need to model 3,200? Explain.
Answer: 32 hundreds.
Explanation: As 3 thousands are the same as 30 hundreds, so 30 hundreds+ 2 hundreds= 32 hundreds.
Question 16.
Sid wrote 541,309 on his paper. Using numbers and words, explain how the number would change if he switched the digits in the hundred thousands and tens places.
Answer: The number is 41,359.
Explanation: The number would be 041,359, but since zeros are not recorded when they are in the left-most place value position. So the number now is 41,359.
Question 17.
There are 686,147 books at the Greenville Library. What is the value of the digit 8 in this number?
(a) 80
(b) 8,000
(c) 80,000
(d) 800.000
Answer: The value of the digit 8 in 686,147 is 80,000.
Explanation: As there are 686,147 books in the library, so the value of the digit 8 in 686,147 is 80,000.
Question 18.
The value of 7 in 375,081 is 7,000.
(a) True
(b) False
Answer: False.
Explanation: As the digit 7 is in thousands place, so the value of 7 in 375,081 is 70,000.
Question 18.
The value of 6 in 269,480 is 600,000.
(a) True
(b) False
Answer: False.
Explanation: As the digit 6 is in thousands place, so the value of 6 in 269,480 is 60,000.
Question 18.
The value of 5 in 427,593 is 500.
(a) True
(b) False
Answer: True.
Explanation: As the digit 5 is in hundreds place, so the value of 5 in 427,593 is 500.
Question 18.
The value of 1 in 375,081 is 10.
(a) True
(b) False
Answer: False.
Explanation: As the digit 1 is in ones place, so the value of 1 in 375,081 is 1.
Question 18.
The value of 4 in 943,268 is 40,000.
(a) True
(b) False
Answer: True.
Explanation: As the digit 4 is in thousands place, so the value of 4 in 943,268 is 40,000.
Common Core – Model Place Value Relationships (Page 9)
Model Place Value Relationships
Find the value of the underlined digit.
Question 1.
6,035
30
Question 2.
43,782
Answer: The value of 7 in 43,782 is 700
Explanation: As the digit 7 is in hundreds place so the value of 7 in 43,782 is 700.
Question 3.
506,087
Answer: The value of 7 in 506,087 is 7.
Explanation: As the digit 7 is in ones place so the value of 7 in 506,087 is 7.
Question 4.
49,254
Answer: The value of 9 in 49,254 is 9,000.
Explanation: As the digit 9 is in thousands place so the value of 9 in 49,254 is 9,000.
Question 5.
136,422
Answer: The value of 3 in 136,422 is 30,000.
Explanation: As the digit 3 is in thousands place so the value of 3 in 136,422 is 30,000.
Question 6.
673,512
Answer: The value of 5 in 673,512 is 500.
Explanation: As the digit 5 is in hundreds place so the value of 5 in 673,512 is 500.
Question 7.
814,295
Answer: The value of 8 in 814,295 is 800,000.
Explanation: As the digit 8 is in hundred thousands place so the value of 8 in 814,295 is 800,000.
Question 8.
736,144
Answer: The value of 6 in 736,144 is 6,000.
Explanation: As the digit 6 is in thousands place so the value of 6 in 736,144 is 6,000.
Compare the values of the underlined digits.
Question 9.
6,300 and 530
The value of 3 in ___________ is ___________ times the value of 3 in ___________ .
Answer: The value of 3 in 6,300 is 10 times the value of 3 in 530.
Explanation:
The value of 3 in 6300 is 300 and the value of 3 in 530 is 30.
So the value of 3 in 6,300 is 10 times the value of 3 in 530.
Question 10.
2,783 and 7,283
The value of 2 in ___________ is ___________ times the value of 2 in ___________ .
Answer: The value of 2 in 2,738 is 10 times the value of 2 in 7,238.
Explanation:
The value of 2 in 2,738 is 2,000 and the value of 2 in 7,238 is 200.
So the value of 2 in 2,738 is 10 times the value of 2 in 7,238.
Question 11.
34,258 and 47,163
The value of 4 in ___________ is ___________ times the value of 4 in ___________.
Answer: The value of 4 in 47,163 is 10 times the value of 4 in 34,258.
Explanation:
The value of 4 in 47,163 is 40,000 and the value of 4 in 34,258 is 4000.
So the value of 4 in 47,163 is 10 times the value of 4 in 34,258.
Question 12.
503,497 and 26,475
The value of 7 in ___________ is ___________ times the value of 7 in ___________ .
Answer: The value of 7 in 26,475 is 10 times the value of 7 in 503,497.
Explanation:
The value of 7 in 26,475 is 70 and the value of 7 in 503,497 is 7.
So the value of 7 in 26,475 is 10 times the value of 7 in 503,497.
Problem Solving
Use the table for 13–14.
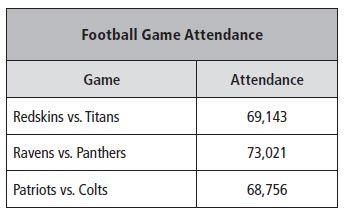
Question 13.
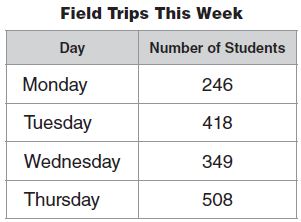
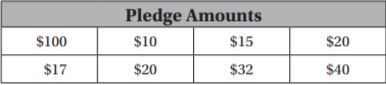
What is the value of the digit 9 in the attendance at the Redskins vs. Titans game?
The value of 9 is ___________ .
Answer: The value of 9 is 9,000.
Explanation: As the digit 9 is in thousands place, so the value of the digit 9 in 69,143 is 9,000.
Question 14.
The attendance at which game has a 7 in the ten thousands place?
Answer: Ravens vs. Panthers attendance is 73,021
Explanation: The attendance at Ravens vs. Panthers game has a 7 in the ten thousands place.
Common Core – Model Place Value Relationships (Page 10)
Lesson Check
Question 1.
During one season, a total of 453,193 people attended a baseball team’s games. What is the value of the digit 5 in the number of people?
(a) 500
(b) 5,000
(c) 50,000
(d) 500,000
Answer: c.
Explanation: The total number of people attended for baseball game are 453,193 and the value of the digit 5 in 453,193 is 5 ten thousands which is 50,000.
Question 2.
Hal forgot the number of people at the basketball game. He does remember that the number had a 3 in the tens place. Which number could Hal be thinking of?
(a) 7,321
(b) 3,172
(c) 2,713
(d) 1,237
Answer: d.
Explanation: The number which has 3 in tens place is 1,237.
Spiral Review
Question 3.
Hot dog buns come in packages of 8. For the school picnic, Mr. Spencer bought 30 packages of hot dog buns. How many hot dog buns did he buy?
(a) 24
(b) 38
(c) 110
(d) 240
Answer: d
Explanation: The number of hot dog buns in a package are 8 and Mr. Spencer bought 30 packages, so the total number of hot dog buns he bought is 8×30= 240.
Question 4.
There are 8 students on the minibus. Five of the students are boys. What fraction of the students are boys?
(a) \(\frac{3}{8}\)
(b) \(\frac{5}{8}\)
(c) \(\frac{5}{5}\)
(d) \(\frac{8}{8}\)
Answer: b.
Explanation: The total number of students are 8 and in that 5 are boys, so the fraction of the students are boys is \(\frac{5}{8}\)
Question 5.
The clock below shows the time when Amber leaves home for school. At what time does Amber leave home?

(a) 2:41
(b) 8:02
(c) 8:10
(d) 8:20
Answer: c
Explanation: Amber leaves home for school at 8:10.
Question 6.
Jeremy drew a polygon with four right angles and four sides with the same length.

What kind of polygon did Jeremy draw?
(a) hexagon
(b) square
(c) trapezoid
(d) triangle
Answer: b
Explanation: Jeremy draws a square, as it’s all sides are equal.
Common Core – Read and Write Numbers (Page 11)
Question 1.
The International Space Station uses 262,400 solar cells to change sunlight to electricity. Write 262,400 in standard form, word form, and expanded form.
Use a place-value chart. Each group of three digits separated by a comma is called a period. Each period has hundreds, tens, and ones. The greatest place-value position in the thousands period is hundred thousands.
Write 262,400 in the place-value chart below.
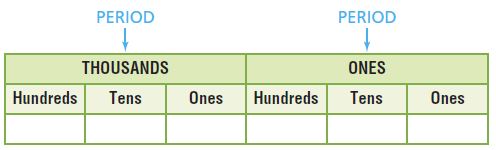
Answer:
The word form of 262,400 is two hundred sixty-two thousand, four hundred, and the expanded form of 262,400 is 200,000+60,000+2,000+400.
Explanation:
Use place value to read and write numbers.
Question 2.
Word Form: ninety-two thousand,one hundred seventy
Standard Form: ___________
Expanded Form: 90,000 + 2,000 + ___________ + 70
Answer:
Standard Form: 92,170.
Expanded Form: 90,000+2,000+100+70+0.
Explanation:
A standard form is a way to write large numbers in a short way. So the standard form of ninety-two thousand,one hundred seventy is 92,170.
The expanded form is a way to write numbers by showing the value of each digit. So the expanded form of ninety-two thousand,one hundred seventy is 90,000+2,000+100+70+0.
Question 2.
Standard Form: 200,007
Word Form: two hundred ___________
Expanded Form: ___________ + 7
Answer:
Word Form: Two hundred thousand, seven.
Expanded Form: 200,000+7
Explanation:
A word form is a way to write the numbers in words. So word form of 200,007 is two hundred thousand seven.
The expanded form is a way to write numbers by showing the value of each digit. So the expanded form of 200,007 is 200,000+7
Common Core – Read and Write Numbers (Page 12)
Question 1.
How can you use place value and period names to read and write 324,904 in word form?
Read and write the number in two other forms.
Answer:
The word form of 324,904 is three hundred twenty-four thousand nine hundred four.
The expanded form of 324,904 is 300,000+20,000+4,000+900+4.
Explanation:
A word form is a way to write the numbers in words. So word form of 324,904 is three hundred twenty-four thousand nine hundred four.
The expanded form is a way to write numbers by showing the value of each digit. So the expanded form of 324,904 is 300,000+20,000+4,000+900+4.
Question 2.
four hundred eight thousand, seventeen
Answer:
Standard Form: 408,017.
Expanded Form: 400,000+8,000+10+7.
Explanation:
A standard form is a way to write large numbers in a short way. So the standard form of four hundred eight thousand, seventeen is 408,017.
The expanded form is a way to write numbers by showing the value of each digit. So the expanded form of four hundred eight thousand, seventeen is 400,000+8,000+10+7.
Question 3.
65,058
Read and write the number in two other forms.
Answer:
The word form of 65,058 is sixty-five thousand, fifty-eight.
The expanded form of 65,058 is 60,000+5,000+50+8.
Explanation:
A word form is a way to write the numbers in words. So word form of 65,058 is sixty-five thousand, fifty-eight.
The expanded form is a way to write numbers by showing the value of each digit. So the expanded form of 65,058 is 60,000+5,000+50+8.
Question 4.
five hundred eight thousand
Answer:
Standard Form: 508,000.
Expanded Form: 500,000+8,000.
Explanation:
A standard form is a way to write large numbers in a short way. So the standard form of five hundred eight thousand is 508,000.
The expanded form is a way to write numbers by showing the value of each digit. So the expanded form of five hundred eight thousand is 500,000+8,000.
Question 5.
forty thousand, six hundred nineteen
Answer:
Standard Form: 40,619.
Expanded Form: 40,000+600+10+9.
Explanation:
A standard form is a way to write large numbers in a short way. So the standard form of forty thousand, six hundred nineteen is 40,619.
The expanded form is a way to write numbers by showing the value of each digit. So the expanded form of forty thousand, six hundred nineteen is 40,000+600+10+9.
Question 6.
570,020
Answer:
The word form of 570,020 is five hundred, seventy thousand, twenty.
The expanded form of 570,020 is 500,000+70,000+20.
Explanation:
A word form is a way to write the numbers in words. So word form of 570,020 is five hundred, seventy thousand, twenty.
The expanded form is a way to write numbers by showing the value of each digit. So the expanded form of 570,020 is 500,000+70,000+20.
Question 7.
400,000 + 60,000 + 5,000 + 100
Answer:
Standard Form: 465,100.
Word Form: Four hundred, sixty-five thousand, one hundred.
Explanation:
A standard form is a way to write large numbers in a short way. So the standard form of 400,000 + 60,000 + 5,000 + 100 is 465,100.
A word form is a way to write the numbers in words. So word form of 400,000 + 60,000 + 5,000 + 100 is Four hundred, sixty-five thousand, one hundred.
Question 8.
During the week of the county fair, fifteen thousand, six hundred nine entry tickets were sold. Is it correct to write the number as 15,069? Explain.
Answer: No.
Explanation: The standard form of fifteen thousand, six hundred nine is 15,609.
Question 9.
There were 94,172 people at a football game on Saturday. On Monday, 1,000 fewer people were at a football game. In word form, how many people were at the football game on Monday?
Answer: The word form of 93,172 is ninety-three thousand one hundred seventy-two.
Explanation: The total number of people are 94,172 as there are 1000 fewer people on Monday, so the total number of people are
94,172-1,000= 93,172. So the word form of 93,172 is ninety-three thousand one hundred seventy-two.
Question 10.
Richard got 263,148 hits when he did an Internet search. What is the value of the digit 6 in this number? Explain.
Answer: The value of 6 in 263,148 is 60,000.
Explanation: As Richard got 263,148 hits and the digit 6 is in the ten thousands place, so the value of 6 in 263,148 is 60,000.
Common Core – Read and Write Numbers (Page 13)
Question 11.
Yvonne wrote the numbers sixteen thousand, nine hundred eighteen and 64,704 on the board. Which of the numbers has a greater value in the thousands place?
Answer: 16,918 has a greater value in the thousands place.
Explanation: As Yvonne wrote sixteen thousand, nine hundred eighteen in word form, so standard form is 16,918. And 64,704 was written on board, so the number with greater value in thousands place is 16,918 as the digit 6 is in thousands place wherein 64,704 the digit 4 is in thousands place. So 16,918 has greater value in thousands place.
Question 12.
Matthew found the sum of 3 thousands 4 hundreds 3 tens 1 one + 4 thousands 8 hundreds 3 tens 5 ones. Victoria found the sum of 5 thousands 7 hundreds 4 ones + 3 thousands 2 hundreds 3 tens 1 one. Who had the greater sum? What was the greater sum?
Who had the greater sum?
What was the greater sum?
Answer: Victoria had a greater sum and the sum is 8,935.
Explanation: The sum of Matthew is 3 thousands 4 hundreds 3 tens 1 one (3431) + 4 thousands 8 hundreds 3 tens 5 ones (4835)= 8,266 and the sum of Victoria 5 thousands 7 hundreds 4 ones (5704) + 3 thousands 2 hundreds 3 tens 1 one (3231)= 8,935. So Victoria had the greater sum and the sum is 8,935.
Use the table for 13–15.
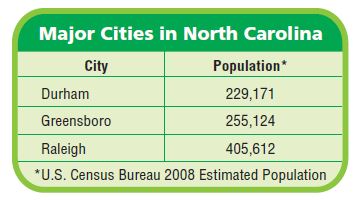
Question 13.
Use Graphs Which city has a population of two hundred fifty-five thousand, one hundred twenty-four?
Answer: Greensboro
Explanation: Greensboro has two hundred fifty-five thousand, one hundred twenty-four population and it was represented word form and the standard form of two hundred fifty-five thousand, one hundred twenty-four is 255,124.
Question 14.
Write the population of Raleigh in expanded form and word form.
Answer: The expanded form of 405,612 is 400,000+5,000+600+10+2 and the word form of 405,612 is four hundred five thousand, six hundred twelve.
Explanation: The population of Raleigh city is 405,612 and the expanded form of 405,612 is 400,000+5,000+600+10+2 and the word form of 405,612 is four hundred five thousand, six hundred twelve.
Question 15.
What’s the Error? Sophia said that the expanded form for 605,970 is 600,000 + 50,000 + 900 + 70. Describe Sophia’s error and give the correct answer.
Answer: The error in Sophia’s expanded form is 600,000+5,000+900+70.
Explanation: The error in Sophia’s expanded form is 600,000+5,000+900+70 as digit 5 is in the thousands place.
Common Core – Read and Write Numbers (Page 14)
Question 16.
Mark tossed six balls while playing a number game. Three balls landed in one section, and three balls landed in another section. His score is greater than one hundred thousand. What could his score be?
a. What do you know?
Answer: Mark’s score will be 300,000+30,000= 330,000.
Explanation: As Mark tossed six balls while playing a number game and that three balls landed in one section, and three balls landed in one section, and three balls landed in another section. Since his score is greater than one hundred thousand, which means that three of the balls landed in the section of 100,000 this will make the score 300,000. If the other three balls, landed in the section of 10,000 this will make the score of three balls to be 30,000. Therefore Mark’s score will be 300,000+30,000= 330,000.
Question 16.
b. How can you use what you know about place value to find what Mark’s score could be?
Answer: To find Mark’s score we will see where the ball will be landed. If the ball is landed in the 100,000 section then the score will be 100,000 and if the ball is landed in the 10,000 section then the score will be 10,000.
Question 16.
c. Draw a diagram to show one way to solve the problem.
Answer:
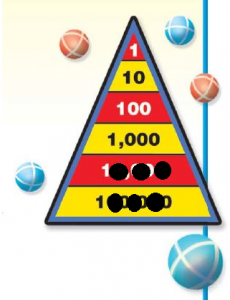
Question 16.
Complete the sentences.
Three balls could have landed in the ___________ section.
Three balls could have landed in the ___________ section.
Mark’s score could be ___________
Answer:
Three balls could have landed in the 100,000 section.
Three balls could have landed in the 10,000 section.
Mark’s score could be 330,000.
Question 17.
What is another way to write 615,004?
Mark all that apply.
(a) six hundred fifteen thousand, four
(b) six hundred five thousand, fourteen
(c) 60,000 + 10,000 + 5,000 + 4
(d) 600,000 + 10,000 + 5,000 + 4
Answer: a,c.
Explanation: The another way to write 615,004 is six hundred fifteen thousand, four and 600,000 + 10,000 + 5,000 + 4
Common Core – Read and Write Numbers (Page 15)
Read and Write Numbers
Read and write the number in two other forms.
Question 1.
six hundred ninety-two thousand, four
standard form: 692,004;
expanded form: 600,000 + 90,000 + 2,000 + 4
Question 2.
314,207
Answer:
Word Form: Three hundred fourteen, two hundred seven.
Expanded Form: 300,000+10,000+4,000+200+7.
Explanation:
A word form is a way to write the numbers in words. So word form of 314,207 is Three hundred fourteen, two hundred seven.
The expanded form is a way to write numbers by showing the value of each digit. So the expanded form of 314,207 is 300,000+10,000+4,000+200+7.
Question 3.
600,000 + 80,000 + 10
Answer:
Word Form: Six hundred eighty thousand ten.
Standard Form: 680,010.
Explanation:
A word form is a way to write the numbers in words. So word form of 314,207 is Three hundred fourteen, two hundred seven.
A standard form is a way to write large numbers in a short way. So the standard form of 600,000 + 80,000 + 10 is 680,010.
Use the number 913,256.
Question 4.
Write the name of the period that has the digits 913.
Answer: The name of the period that has the digits 913 is Thousand
Explanation: The name of the period that has the digits 913 is Thousand. As we got two periods and 913 are in thousands period and 256 are in units period.
Question 5.
Write the digit in the ten thousands place.
Answer: 1.
Explanation: In 913,256, the digit 1 is in the ten thousands place.
Question 6.
Write the value of the digit 9.
Answer: The value of 9 is nine hundred thousands.
Explanation: In 913,256 the digit 9 is in hundred thousands place, so the value of 9 is nine hundred thousands or 900,000.
Problem Solving
Use the table for 7 and 8.
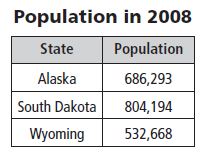
Question 7.
Which state had a population of eight hundred four thousand, one hundred ninety-four?
Answer: South Dakota
Explanation: The population of eight hundred four thousand, one hundred ninety-four is South Dakota which is 804,194.
Question 8.
What is the value of the digit 8 in Alaska’s population?
Answer: 80,000.
Explanation: The value of the digit 8 in Alaska’s population is 80,000.
Common Core – Read and Write Numbers (Page 16)
Lesson Check
Question 1.
Based on a 2008 study, children 6–11 years old spend sixty-nine thousand, one hundred eight minutes a year watching television. What is this number written in
standard form?
(a) 6,918
(b) 69,108
(c) 69,180
(d) 690,108
Answer: b
Explanation: As 6–11 years old spend sixty-nine thousand, one hundred eight minutes a year watching television, the standard form of sixty-nine thousand, one hundred eight is 69,108
Question 2.
What is the value of the digit 4 in the number 84,230?
(a) 4
(b) 400
(c) 4,000
(d) 40,000
Answer: c
Explanation: The value of the digit 4 in the number 84,230 is 4,000.
Spiral Review
Question 3.
An ant has 6 legs. How many legs do 8 ants have in all?
(a) 14
(b) 40
(c) 45
(d) 48
Answer: d
Explanation: As ant has 6 legs, so for 8 ants 6×8= 48 legs.
Question 4.
Latricia’s vacation is in 4 weeks. There are 7 days in a week. How many days is it until Latricia’s vacation?
(a) 9 days
(b) 11 days
(c) 20 days
(d) 28 days
Answer: d
Explanation: As Latricia’s vacation is in 4 weeks and a week has 7 days, so for 4 weeks it will be 4×7= 28 days.
Question 5.
Marta collected 363 cans. Diego collected 295 cans. How many cans did Marta and Diego collect in all?
(a) 668
(b) 658
(c) 568
(d) 178
Answer: b
Explanation: Marta collected 363 cans and Diego collected 295 cans, so total number of cans both collected are 363+295= 658.
Question 6.
The city Tim lives in has 106,534 people. What is the value of the 6 in 106,534?
(a) 6,000
(b) 600
(c) 60
(d) 6
Answer: a
Explanation: The value of 6 in 106,534 is 6,000.
Common Core – Compare and Order Numbers (Page 18)
Question 1.
Compare 15,327 and 15,341.
Write <, >, or =. Use the number line to help.

15,327 _______ 15,341
Answer: 15,327 < 15,341
Explanation: The number 15,327 < 15,341 as 327 is less than 341.
Compare. Write <, >, or =.
Question 2.
$631,328 _______ $640,009
Answer: $631,328 < $640,009.
Explanation: The number $631,328 < $640,009.
Question 3.
56,991 _______ 52,880
Answer: 56,991 > 52,880.
Explanation: The number 56,991 > 52,880.
Question 4.
708,561 _______ 629,672
Answer: 708,561 > 629,672.
Explanation: The number 708,561 > 629,672.
Question 5.
143,062 _______ 98,643
Answer: 143,062 > 98,643.
Explanation: The number 143,062 > 98,643.
Order from greatest to least.
Question 6.
20,650; 21,150; 20,890
________ ; ________ ; ________.
Answer: 21,150>20,890>20,650.
Explanation: The numbes from greatest to least are 21,150>20,890>20,650.
Common Core – Read and Write Numbers (Page 19)
Compare. Write <, >, or =.
Question 7.
$2,212 _______ $2,600
Answer: $2,212 < $2,600.
Explanation: The number $2,212 < $2,600.
Question 8.
88,304 _______ 88,304
Answer: 88,304 = 88,304.
Explanation: The number 88,304 = 88,304.
Question 9.
$524,116 _______ $61,090
Answer: $524,116 > $61,090.
Explanation: The number $524,116 > $61,090.
Question 10.
751,272 _______ 851,001
Answer: 751,272 < 851,001.
Explanation: The number 751,272 < 851,001.
Order from least to greatest.
Question 11.
41,090; 41,190; 40,009
_______ ; _______ ; _______
Answer: 40,009<41,090<41,190.
Explanation: The numbers from least to greatest are 40,009<41,090<41,190.
Question 12.
910,763; 912,005; 95,408
_______ ; _______ ; _______
Answer: 95,408<910,763<912,005.
Explanation: The numbers from least to greatest are 95,408<910,763<912,005.
Identify Relationships Algebra Write all of the digits that can replace each
Question 13.
567 < 5 _______ 5 < 582
Answer: 567<575<582.
Explanation: The suitable number to fit the equation is 7, so 567<575<582.
Question 14.
464,545 > 4 _______ 3,535 > 443,550
464,545 > 4 _______ 3,535 > 443,550
Answer:
464,545>453,535>443,550.
464,545>463,535>443,550.
Explanation: The suitable number to fit the equation is 5 or 6. So
464,545>453,535>443,550.
464,545>463,535>443,550.
Question 15.
Leah’s car has 156,261 miles on the odometer. Casey’s car has 165,002 miles on the odometer. Mike’s car has 145,834 miles on the odometer. Whose car has the most miles? Order the number of miles from least to greatest.
Answer: Casey’s car has the most miles and the order of the miles from least to greatest is 145,834<156,261<165,002.
Explanation: As Leah’s car has 156,261 miles and Casey’s car has 165,002 miles and Mike’s car has 145,834 miles. So Casey’s car has the most miles and the order of the miles from least to greatest is 145,834<156,261<165,002.
Question 16.
At Monica’s Used Cars, the sales staff set a goal of $25,500 in sales each week. The sales for three weeks were $28,288; $25,369; and $25,876. Which total did not meet the goal?
(a) $28,288
(b) $25,369
(c) $25,876
Answer: b
Explanation: $25,369 did not meet the goal. As the staff set the goal to $25,500 and $25,369 is less than $25,500.
Question 17.
What’s the Error? Max said that 36,594 is less than 5,980 because 3 is less than 5. Describe Max’s error and give the correct answer.
Answer: 3 is less than 5 but 30,000 is greater than 5,000 that is Max’s error.
Explanation: 3 is less than 5 but the digit 3 in 36,594 is in ten thousands place so the place value of 3 is 30,000 and the digit 5 in 5,980 is in thousands place and the place value of 5 is 5000. This is Max’s error.
Common Core – Compare and Order Numbers (Page 20)
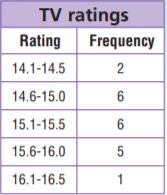
Use the picture graph for 18–20.

Question 18.
Use Graphs In which month shown did Grand Canyon National Park have about 7,500 tent campers?
Answer: September.
Explanation: We can see from the above figure that september month has 5000+2500= 7500.
Question 19.
How many more campers were there in July and August than in June and September?
Answer: 10,000 more campers in July and August.
Explanation:
The campers in July and August are 15,000+12,500= 27,500
The campers in June and September are 10,000+7,500= 17,500
So 27,500-17,500= 10,000 more campers in July and August.
Question 20.
What if during the month of October, the park had 22,500 tent campers? How many symbols would be placed on the pictograph for October?
Answer: There will be four full symbols and one half symbol.
Explanation: As each symbol represents 5,000 tent campers, for 22,500 tent campers there will be four full symbols and one half symbol which means 5,000+5,000+5,000+5,000+2,500= 22,500.
Question 21.
What’s the Question?
Compare: 643,251; 633,512; and 633,893.
The answer is 633,512.
Answer: What is the least number?
Explanation: As we can see in the given the answer that 633,512 is less than the other two numbers. So the question would be What is the least number?
Question 22.
Zachary’s school set a goal of collecting 12,155 cans of food each day. In the first 3 days the school collected 12,250 cans; 10,505 cans; and 12,434 cans. Write each number in the box that tells whether or not the school met its goal.
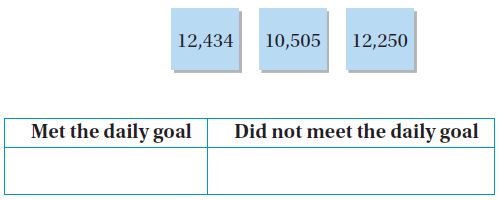
(a) 12,250 cans
(b) 10,505 cans
(c) 12,434 cans
Answer: 12,250 and 12,434 met the daily goal and 10,505 didn’t meet the daily goal.
Explanation: As Zachary’s school set a goal of collecting 12,155 cans of food each day, so 12,250 and 12,434 met the daily goal and 10,505 didn’t meet the daily goal.

Common Core – Compare and Order Numbers (Page 21)
Compare and Order Numbers
Compare. Write < .> or =.
Question 1.
3,273 < 3,279
Question 2.
$1,323 _______ $1,400
Answer: $1,323 < $1,400.
Explanation: The number $1,323 is less than $1,400.
Question 3.
52,692 _______ 52,692
Answer: 52,692 = 52,692.
Explanation: The number 52,692 is equal to 52,692.
Question 4.
$413,005 _______ $62,910
Answer: $413,005 > $62,910
Explanation: The number $413,005 is greater than $62,910
Question 5.
382,144 _______ 382,144
Answer: 382,144= 382,144
Explanation: The number 382,144 is equal to 382,144
Question 6.
157,932 _______ 200,013
Answer: 157,932 < 200,013
Explanation: The number 157,932 is less than 200,013.
Question 7.
401,322 _______ 410,322
Answer: 401,322 < 410,322.
Explanation: The number 401,322 is less than 410,322.
Question 8.
989,063 _______ 980,639
Answer: 989,063 > 980,639
Explanation: The number 989,063 is greater than 980,639.
Question 9.
258,766 _______ 258,596
Answer: 258,766 > 258,596.
Explanation: The number 258,766 is greater than 258,596.
Order from least to greatest.
Question 10.
23,710; 23,751; 23,715
_______< _______ < _______
Answer: 23,710<23,715<23,751
Explanation: The numbers from least to greatest are 23,710<23,715<23,751
Question 11.
52,701; 54,025; 5,206
_______ < _______ < _______
Answer: 5,206<52,701<54,025.
Explanation: The numbers from least to greatest are 5,206<52,701<54,025.
Question 12.
465,321; 456,321; 456,231
_______ < _______ < _______
Answer: 456,231<456,321<465,321.
Explanation: The numbers from least to greatest are 456,231<456,321<465,321.
Question 13.
$330,820; $329,854; $303,962
_______ < _______ < _______
Answer: $329,854<$303,962<$330,820.
Explanation: The numbers from least to greatest $329,854<$303,962<$330,820.
Problem Solving
Question 14.
An online newspaper had 350,080 visitors in October, 350,489 visitors in November, and 305,939 visitors in December. What is the order of the months from greatest to least number of visitors?
1. _______
2. _______
3. _______
Answer: November, October, December.
Explanation: As 350,489 is greater than 305,939. So the order of the months from greatest to the least number of visitors are November, October, and December.
Question 15.
The total land area in square miles of each of three states is shown below.
Colorado: 103,718
New Mexico: 121,356
Arizona: 113,635
What is the order of the states from least to greatest total land area?
1. _______
2. _______
3. _______
Answer: Colorado, Arizona, New Mexico.
Explanation: As 103,718 is less than 113,635 is less than 121,356. So the order of the state from least to greatest is Colorado, Arizona, New Mexico.
Common Core – Compare and Order Numbers (Page 22)
Lesson Check
Question 1.
At the yearly fund-raising drive, the nonprofit company’s goal was to raise $55,500 each day. After three days, it had raised $55,053; $56,482; and $55,593. Which amount was less than the daily goal?
(a) $55,500
(b) $55,053
(c) $55,593
(d) $56,482
Answer: b
Explanation: As the goal is to raise $55,500 each day and $55,053 didn’t reach the goal. As $55,053 is less than $55,550.
Question 2.
Which of the following lists of numbers is in order from greatest to least?
(a) 60,343; 60,433; 63,043
(b) 83,673; 86,733; 86,373
(c) 90,543; 90,048; 93,405
(d) 20,433; 20,343; 20,043
Answer: d
Explanation: The numbers in order from greatest to least is 20,433, 20,343, 20,043.
Spiral Review
Question 3.
Jess is comparing fractions. Which fraction is greater than \(\frac{5}{6}\)?
(a) \(\frac{7}{8}\)
(b) \(\frac{4}{5}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{2}{3}\)
Answer: a
Explanation: As \(\frac{5}{6}\) in decimals is 0.83 and
\(\frac{7}{8}\)= 0.875
\(\frac{4}{5}\)= 0.80
\(\frac{3}{4}\)= 0.75
\(\frac{2}{3}\)= 0.67
So, \(\frac{7}{8}\) is greater than \(\frac{5}{6}\).
Question 4.
What is the perimeter of the rectangle below?
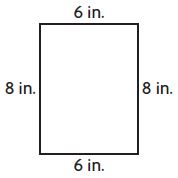
(a) 14 inches
(b) 26 inches
(c) 28 inches
(d) 48 inches
Answer: c.
Explanation: The perimeter of the rectangle is 2(l+w)
= 2(8+6)
= 2(14)
= 28 inches.
Question 5.
A website had 826,140 hits last month. What is the value of the 8 in 826,140?
(a) 800
(b) 8,000
(c) 80,000
(d) 800,000
Answer:
Explanation: The value of the digit 8 in 826,140 is 800,000.
Question 6.
Which is 680,705 written in expanded form?
(a) 680 + 705
(b) 68,000 + 700 + 5
(c) 600,000 + 8,000 + 700 + 5
(d) 600,000 + 80,000 + 700 + 5
Answer: d
Explanation: The expanded form of 680,705 is 600,000+80,000+700+5
Common Core – Round Numbers (Page 24)
Question 1.
What number is halfway between 100,000 and 200,000?
Answer: 150,000.
Explanation: The number is halfway between 100,000 and 200,000 is 150,000.
Question 2.
How does knowing where the halfway point is help you find which hundred thousand 138,202 is closest to? Explain.
Answer: The location of a number relative to the halfway point help you tell if it is closer to the lesser or the greater rounding number.
Question 3.
What number is halfway between 70,000 and 80,000?
Answer: 75,000.
Explanation: The number is halfway between 70,000 and 80,000 is 75,000.
Question 4.
What is 75,000 rounded to the nearest ten thousand? Explain.
Answer: 80,000.
Explanation: As 75,000 is exactly halfway between 70,000 and 80,000 rounds to the greater number.
Round to the place value of the underlined digit.
Question 5.
64,999
Answer: 60,000.
Explanation: The place value of 6 in 64,999 is 60,000.
Question 5.
850,000
Answer: 800,000.
Explanation: The place value of 8 in 850,000 is 800,000.
Question 5.
301,587
Answer: 1,000.
Explanation: The place value of 1 in 301,587 is 1,000.
Question 5.
10,832
Answer: 0.
Explanation: The place value of 0 in 10,832 is 0 because 0 is in thousands place, so 0×1000= 0.
Common Core – Round Numbers (Page 25)
Question 1.
Suppose 255,113 people live in a city. Is it reasonable to say that about 300,000 people live in the city? Use the number line to help you solve the problem. Explain.
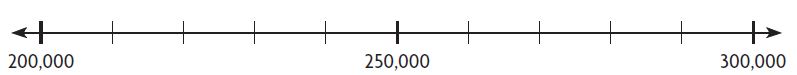
Answer: Yes, 300,000 is a reasonable estimate.
Explanation: As 255,113 is closer to 300,000 than 200,000. So 300,000 is a reasonable estimate.
Round to the place value of the underlined digit.
Question 2.
934,567
Answer: 935,000.
Explanation: Round off the value means making a number simpler but keeping its value close to what it was. The result is less accurate but easy to use. So round off 934,567 to 935,000.
Question 3.
641,267
Answer: 640,000.
Explanation: Round off the value means making a number simpler but keeping its value close to what it was. The result is less accurate but easy to use. So round off 641,267 to 640,000.
Question 4.
234,890
Answer: 200,000.
Explanation: Round off the value means making a number simpler but keeping its value close to what it was. The result is less accurate but easy to use. So round off 234,890 to 200,000.
Question 5.
347,456
Answer: 350,000.
Explanation: Round off the value means making a number simpler but keeping its value close to what it was. The result is less accurate but easy to use. So round off 347,456 to 350,000.
Question 6.
To the nearest hundred, a factory produced 3,600 jars of applesauce on Thursday and 4,200 jars of apple sauce on Friday. To the nearest thousand, how many jars of apple juice did they produce during the two days?
Answer: 7,800 jars.
Explanation:
The number of jars of apple sauce on Thursday= 3,600 jars
The number of jars of apple sauce on Friday= 4,200 jars.
So the total number of jars they produced during the two days is 3,600+4,200= 7,800 jars.
Question 7.
The number 2,000 is missing a digit. The number rounded to the nearest thousand is 3,000. List all of the possibilities for the missing digit. Explain your answer.
Answer: 5,6,7,8,9.
Explanation: If the digit in the hundreds place 5,6,7,8,9, then the number is closer to 3,000 than 2,000 and if the digit in the hundreds place is 5, the number is exactly halfway between 2,000 and 3,000. So we can round off to the greater number.
Common Core – Round Numbers (Page 26)
Question 8.
A male elephant weighs 6,728 pounds. A female elephant weighs 5,843 pounds. To the nearest hundred, what is the total weight of the two elephants?
Answer: 12,600 pounds.
Explanation:
The weight of a male elephant is 6,728 pounds
The weight of a female elephant is 5,843 pounds
So total weight is 6,728+5,843= 12,571.
Rounding off to the nearest hundred, so the value is 12,600.
Question 9.
About 300,000 people attended a festival. For numbers 9a–9e choose Yes or No to show whether each number could be the exact number of people that attended the festival.
a. 351,213
(a) yes
(b) no
Answer: No
Explanation: By rounding off 351,213 to the nearest thousands place then the value will be 351,000 which is more than 300,000. So the answer is No.
Question 9.
b. 249,899
(a) yes
(b) no
Answer: No.
Explanation: By rounding off 249,899 to the nearest thousands place then the value will be 250,000 which is less than 300,000. So the answer is No.
Question 9.
c. 252,348
(a) yes
(b) no
Answer: No.
Explanation: By rounding off 252,348 to the nearest thousands place then the value will be 252,000 which is less than 300,000. So the answer is No.
Question 9.
d. 389,001
(a) yes
(b) no
Answer: No
Explanation: By rounding off 389,001 we will get the value as 400,000 but not 300,000. So the answer is no.
Question 9.
e. 305,992
(a) yes
(b) no
Answer: Yes.
Explanation: By rounding off 305,992 we will get the value as 300,000 which is equal to 300,000. So the answer is yes.
Common Core – Round Numbers (Page 27)
Round Numbers
Round to the place value of the underlined digit.
Question 1.
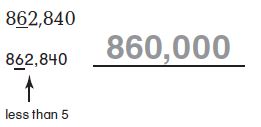
Look at the digit to the right. If the digit to the right is less than 5, the digit in the rounding place stays the same.
Change all the digits to the right of the rounding place to zero.
Question 2.
123,499
Answer: 123,000.
Explanation: The digit to the right to the underlined number is less than 5, so the digit in the rounding place stays the same, and all the digits to the right of the rounding place to zero. So the value will be 123,000.
Question 3.
552,945
Answer: 600,000.
Explanation: The digit to the right to the underlined number is equal to 5, so the underlined digit will be increased by 1 and will round up to the nearest hundred thousands place. So the value is 600,000.
Question 4.
389,422
Answer: 390,000.
Explanation: The digit to the right to the underlined number is greater than 5, so the underlined digit will be increased by 1 and will round up to the nearest hundred thousands place. So the value is 390,000.
Question 5.
209,767
Answer: 200,000.
Explanation: The digit to the right to the underlined number is less than 5, so the digit in the rounding place stays the same, and all the digits to the right of the rounding place to zero. So the value is 200,000.
Question 6.
191,306
Answer: 191,000.
Explanation: The digit to the right to the underlined number is less than 5, so the digit in the rounding place stays the same, and all the digits to the right of the rounding place to zero. So the value is 191,000.
Question 7.
66,098
Answer: 70,000.
Explanation: The digit to the right to the underlined number is greater than 5, so the underlined digit will be increased by 1 and will round up to the nearest hundred thousands place. So the value is 70,000.
Question 8.
73,590
Answer: 74,000.
Explanation: The digit to the right to the underlined number is equal to 5, so the underlined digit will be increased by 1 and will round up to the nearest hundred thousands place. So the value is 74,000.
Question 9.
149,903
Answer: 100,000.
Explanation: The digit to the right to the underlined number is less than 5, so the digit in the rounding place stays the same, and all the digits to the right of the rounding place to zero. So the value is 100,000.
Question 10.
684,303
Answer: 684,000.
Explanation: The digit to the right to the underlined number is less than 5, so the digit in the rounding place stays the same, and all the digits to the right of the rounding place to zero. So the value is 684,000.
Question 11.
499,553
Answer: 500,000.
Explanation: The digit to the right to the underlined number is greater than 5, so the underlined digit will be increased by 1 and will round up to the nearest hundred thousands place. So the value is 500,000.
Problem Solving
Use the table for 12–13.
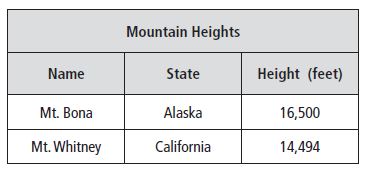
Question 12.
Find the height of Mt. Whitney in the table. Round the height to the nearest thousand feet.
_______ feet
Answer: 14,000 feet.
Explanation: The height of Mt. Whitney in the table is 14,494 feet, by rounding off to nearest thousand the height will be 14,000 feet.
Question 13.
What is the height of Mt. Bona rounded to the nearest ten thousand feet?
_______ feet
Answer: 20,000 feet.
Explanation: The height of Mt. Bona is 16,500 feet, by rounding off to the nearest ten thousand the height will be 20,000 feet.
Common Core – Round Numbers (Page 28)
Lesson Check
Question 1.
Which number is 247,039 rounded to the nearest thousand?
(a) 200,000
(b) 250,000
(c) 247,000
(d) 7,000
Answer: c
Explanation: The number rounded to the nearest thousand is 247,000.
Question 2.
To the nearest ten thousand, the population of Vermont was estimated to be about 620,000 in 2008. Which might have been the exact population of Vermont in 2008?
(a) 626,013
(b) 621,270
(c) 614,995
(d) 609,964
Answer: b
Explanation: The exact population of Vermont in 2008 is 621,270. As the estimated population is 620,000 and the number is rounded off to the nearest thousand, so the exact population of Vermont is 621,270.
Spiral Review
Question 3.
Which symbol makes the following number sentence true?
$546,322 Ο $540,997
(a) <
(b) >
(c) =
(d) +
Answer: b
Explanation: The number $546,322 is greater than $540,997.
Question 4.
Pittsburgh International Airport had approximately 714,587 passengers in August 2009. Which number is greater than 714,587?
(a) 714,578
(b) 704,988
(c) 714,601
(d) 714,099
Answer: c
Explanation: 714,601 is greater than 714,587.
Question 5.
June made a design with 6 equal tiles. One tile is yellow, 2 tiles are blue, and 3 tiles are purple. What fraction of the tiles are yellow or purple?
(a) \(\frac{1}{6}\)
(b) \(\frac{2}{6}\)
(c) \(\frac{3}{6}\)
(d) \(\frac{4}{6}\)
Answer: d
Explanation: Total tiles are 6 tiles and in that one tile is yellow and 3 purple tiles and the total yellow and purple tiles are 4 tiles. So the fraction of the yellow tile and purple tile is \(\frac{4}{6}\).
Question 6.
The fourth grade collected 40,583 cans and plastic bottles. Which of the following shows that number in word form?
(a) forty thousand, five hundred eighty
(b) forty thousand, five hundred eighty-three
(c) four thousand, five hundred eighty-three
(d) four hundred thousand, five hundred eighty
Answer: b.
Explanation: The word form of 40,583 is forty thousand, five hundred eighty-three.
Common Core – Chapter 1 -Mid-Chapter Checkpoint (Page 29)
Choose the best term from the box.
Question 1.
The _______ of 23,850 is 20,000 + 3,000 + 800 + 50.
Answer: Expanded form.
Explanation: The expanded form of 23,850 is 20,000 + 3,000 + 800 + 50.
Question 2.
You can _______ to find about how much or how many.
Answer: Round.
Explanation: You can round to find about how much or how many.
Question 3.
In 192,860 the digits 1, 9, and 2 are in the same _________
Answer: Period.
Explanation: In 192,860 the digits 1, 9, and 2 are in the same period.
Find the value of the underlined digit.
Question 4.
380,671
Answer: 80,000.
Explanation: The place value of the digit 8 in 380,671 is 80,000.
Question 5.
10,698
Answer: 90.
Explanation: The place value of the digit 9 in 10,698 is 90.
Question 6.
650,234
Answer: 600,000
Explanation: The place value of the digit 6 in 650,234 is 600,00.
Write the number in two other forms.
Question 7.
293,805
Answer:
Expanded form: 200,000+90,000+3,000+800+5.
Word form: two hundred ninety three thousand,eight hundred five.
Explanation:
The expanded form of 293,805 is 200,000+90,000+3,000+800+5.
The word form of 293,805 is two hundred ninety three thousand,eight hundred five.
Question 8.
300,000 + 5,000 + 20 + 6
Answer:
Standard form: 305,026.
Word form: three hundred five thousand twenty six.
Explanation:
The standard form of 300,000 + 5,000 + 20 + 6 is 305,026.
The word form of 300,000 + 5,000 + 20 + 6 is three hundred five thousand twenty six.
Compare. Write <, >, or =.
Question 9.
457,380 _______ 458,590
Answer:
457,380 < 458,590
Explanation:
The number 457,380 is less than 458,590.
Question 10.
390,040 _______ 39,040
Answer:
390,040 > 39,040
Explanation:
The number 390,040 is greater than 39,040.
Question 11.
11,809 _______ 11,980
Answer:
11,809 > 11,980
Explanation:
The number 11,809 is greater than 11,980.
Round to the place of the underlined digit.
Question 12.
140,250
Answer: 100,000.
Explanation: The place value of the digit 1 in 140,250 is 100,000.
Question 13.
10,450
Answer: 400.
Explanation: The place value of the digit 4 in 10,450 is 400.
Question 14.
126,234
Answer: 6,000.
Explanation: The place value of the digit 6 in 126,234 is 6,000.
Common Core – Chapter 1 -Mid-Chapter Checkpoint (Page 30)
Question 15.
Last year, three hundred twenty-three thousand people visited the museum. What is this number written in standard form?
Answer: 323,000.
Explanation: The standard form of three hundred twenty-three thousand is 323,000.
Question 16.
Rachael rounded 16,473 to the nearest hundred. Then she rounded her answer to the nearest thousand. What is the final number?
Answer: 17,000.
Explanation: When we round a number to the nearest we check the tens place digit, if the digit is less than 5 then the number is rounded to the previous hundred while if it is 5 or more than 5 then the number is rounded to the next hundred. As tens place digit is 7, so
16,473= 16,500. And when we need to round the number to the nearest thousand and will check the hundred place digit which is 5. So when 16,500 is rounded off to the nearest thousand the value will be 17,000.
Question 17.
What is the highest volcano in the Cascade Range?
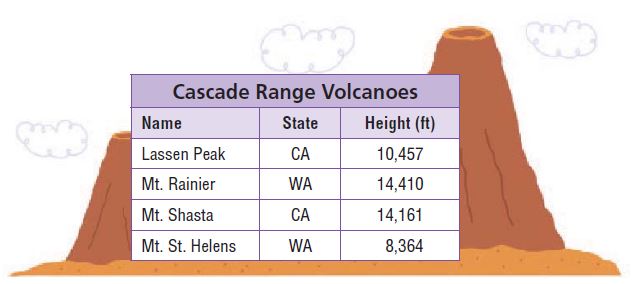
Answer: Mt. Rainier
Explanation: Mt. Rainier is the highest volcano in the Cascade Range with a height of 14,410 ft.
Question 18.
Richard got 263,148 hits when he did an Internet search. What is the value of the digit 6 in this number?
Answer:
Explanation: Richard got 263,148 which is in standard form, so we will convert into expanded form to find the value of the digit 6. The expanded form of 263,148 is 200,000+60,000+3,000+100+40+8. The value of the digit 6 is 60,000.
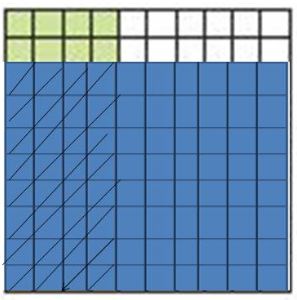
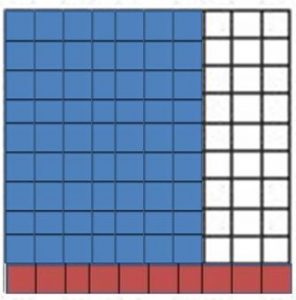
Common Core – Investigate • Rename Numbers (Page 32)
Question 1.
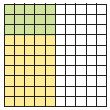
How is the number of large cubes and flats in the first model related to the number of flats in the second model?
Answer: 10 flats.
Explanation: We need 10 flats to make a large cube, so 1 large cube and 2 flats are the same as 10 flats and 2 flats or 12 flats.
Question 2.
Can you model 1,200 using only longs? Explain.
Answer: Yes.
Explanation: We need 12 flats to model 1,200. Since there are 10 longs in each flat, you need 120 longs.
Question 3.
You renamed 1,200 as hundreds. How can you rename 1,200 as tens? Explain.
Answer: 120 tens.
Explanation: As each long is a ten, and we need 120 longs to model 1,200. So we will rename as 120 tens.
Question 4.
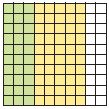
What would the models in Step A and Step B look like for 5,200? How can you rename 5,200 as hundreds?
Answer: We can rename 5,200 as 52 hundred.
Explanation: In Step A, the model would have 5 large cubes and 2 flats to model 5 thousands and 2 hundreds. In step B, the model would have 52 flats. So we can rename 5,200 as 52 hundred.
Common Core – Investigate • Rename Numbers (Page 33)
Rename the number. Draw a quick picture to help.
Question 1.
150
_______ tens
Answer: 15 tens.
Explanation: As each long is a ten, so we need 15 longs to model 150.

Question 2 (request help)
1,400
_______ hundreds
Answer: 14 hundreds.
Explanation: As each box is a hundred, so we need 14 box to model 1,400.
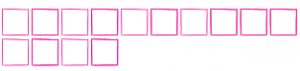
Question 3.
2 thousands 3 hundreds
_______ hundreds
Answer: 23 hundred.
Explanation: As each box is a hundred, so we need 23 box to model 2,300.

Question 4.
13 hundreds
_______ thousand _______ hundreds
Answer: 1 thousand and 3 hundred.
Explanation: The group of 10 boxes are equal to thousand, so for 13 hundreds we need 1 thousand and 3 hundred.

Rename the number. Use the place-value chart to help.
Question 5.
18 thousands = _______
Answer: 18,000.
Explanation:
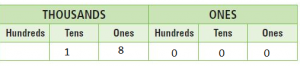
Question 6.
570,000 = 57 _______
Answer: 57 ten thousand.
Explanation:
Rename the number.
Question 7 (request help)
580= _______ tens
Answer: 58 tens.
Question 8.
740,000= _______ten thousands
Answer: 74 ten thousand.
Question 9.
8 hundreds 4 tens = 84 _______
Answer: 84 tens.
Question 10.
29 thousands = _______
Answer: 29,000.
Common Core – Investigate • Rename Numbers (Page 34)
Question 11.
A toy store is ordering 3,000 remote control cars. The store can order the cars in sets of 10. How many sets of 10 does the store need to order?
_______ sets
Answer: 300 sets.
Explanaton: Number of cars ordering by the toy store are 3,000 and the store can order the sets of 10, so number of sets are 3000/10 = 300 sets.
Question 11.
a. What information do you need to use?
Answer: The store is ordering 3,000 remote control cars and the cars come in the set of 10.
Question 11.
b. What do you need to find?
Answer: We need to find how many sets of 10 the store need to order.
Question 11.
c. How can renaming numbers help you solve this problem?
Answer: We can rename 3,000 as tens to find how many sets of 10 make 3,000.
Question 11.
d. Describe a strategy you can use to solve the problem.
Answer: We can use place value chart to see how many tens are in 3,000.
Question 11.
e. How many sets of 10 remote control cars does the store need to buy?
_______ sets
Answer: 300 sets.
Explanation: 300 sets of 10 remote control cars store needs to buy.
Question 12.
Ivan sold 53 boxes of oranges on Friday and 27 boxes on Saturday during a citrus sale. There were 10 oranges in each box. How many oranges did he sell in all?
_______ oranges
Answer:
Explanation: Ivan sold 53 boxes of oranges on Friday and 27 boxes on Saturday, so total number of boxes are 53+27= 80. As each box contains 10 oranges, so total number of oranges he sold is 80×10= 800 oranges.
Question 12.
Use Reasoning A store sold a total of 15,000 boxes of buttons last month, and 12,000 boxes this month. If the store sold 270,000 buttons, how many buttons were in each box?
_______ buttons
Answer: 10 buttons.
Explanation: As store sold a total of 15,000 boxes of buttons last month, and 12,000 boxes this month, so total number of button boxes sold are 15,000+12,000= 27,000 boxes. And the store sold 270,000 buttons, so total number of buttons in each box are
270,000/27,000= 10 buttons.
For numbers 14a–14d, select True or False for each statement.
Question 14.
a. 9 hundreds 3 tens can be renamed as 39 tens.
(a) True
(b) False
Answer: False
Explanation: 9 hundreds 3 tens can rename as 93 tens.
Question 14.
b. 370,000 can be renamed as 37 ten thousands.
(a) True
(b) False
Answer: True.
Explanation: Yes, 370,000 can be renamed as 37 ten thousands.
Question 14.
c. 780 can be renamed as 78 tens.
(a) True
(b) False
Answer: True.
Explanation: Yes, 780 can be renamed as 78 tens.
Question 14.
d. 42,000 can be renamed as 42 thousands.
(a) True
(b) False
Answer: True
Explanation: Yes, 42,000 can be renamed as 42 thousands.
Common Core – Investigate • Rename Numbers (Page 35)
Rename Numbers
Rename the number. Use the place-value chart to help.
Question 1.
760 hundreds = 76,000
Question 2.
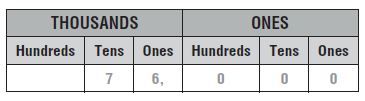
805 tens = _______
Answer: 8,050.
Explanation:
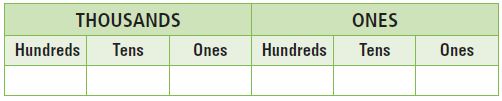
| THOUSANDS | ONES |
| Hundreds | Tens | Ones | Hundreds | Tens | Ones |
| | 8 | 0 | 5 | 0 |
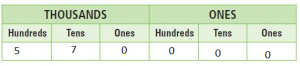
Question 3.
24 ten thousands = ________
Answer: 240,000.
Explanation:
| THOUSANDS | ONES |
| Hundreds | Tens | Ones | Hundreds | Tens | Ones |
| 2 | 4 | 0 | 0 | 0 | 0 |
Rename the number.
Question 4.
720 = _______ tens
Answer: 72 tens.
Explanation: The number 720 can be rename as 72 tens.
Question 5.
4 thousands 7 hundreds = 47 _______
Answer: 47 hundred.
Explanation: 4 thousands 7 hundreds can rename as 47 hundred.
Question 6.
25,600 = _______ hundreds
Answer: 256 hundred.
Explanation: 25,600 can rename as 256 hundred.
Question 7.
204 thousands = _______
Answer: 204,000.
Explaantion: 204 thousands can rename as 204,000.
Problem Solving
Question 8.
For the fair, the organizers ordered 32 rolls of tickets. Each roll of tickets has 100 tickets. How many tickets were ordered in all?
_______ tickets
Answer: 3200 tickets.
Explanation: Total number of rolls of tickets ordered by the organizers are 32 rolls and each roll contains 100 tickets. So number of tickets were ordered are 32×100= 3200 tickets.
Question 9.
An apple orchard sells apples in bags of 10. The orchard sold a total of 2,430 apples one day. How many bags of apples was this?
_______ bags
Answer: 243 bags.
Explantion: Total number of apples sold by orchard are 2,430 apples, and the orchard sells apples in a bag of 10, so number of apples are 2,430÷10= 243 bags.
Question 10.
Explain how you can rename 5,400 as hundreds. Include a quick picture or a place-value chart in your explanation.
_______ hundreds
Answer: 54 hundred.
Explanation: In 5,400 there are 2 zeros and also in 100 there are 2 zeros, so 2 zeros equals hundred and 100= 1 hundred, because it has a 1 front of the 2 zeros. So 5,400= 54 hundreds, because it has a 54 in front of the 2 zeros.
Common Core – Investigate • Rename Numbers (Page 36)
Lesson Check
Question 1.
A dime has the same value as 10 pennies. Marley brought 290 pennies to the bank. How many dimes did Marley get?
(a) 29
(b) 290
(c) 2,900
(d) 29,000
Answer: a.
Explanation: As a dime has the same value as 10 pennies, Marley brought 290 pennies. So their will be 290/10= 29 dimes MArley will get.
Question 2.
A citrus grower ships grapefruit in boxes of 10. One season, the grower shipped 20,400 boxes of grapefruit. How many grapefruit were shipped?
(a) 204
(b) 2,040
(c) 20,400
(d) 204,000
Answer: d.
Explanation: Number of boxes are 10 and the grower shipped 20,400 boxes of grapefruit. So number of grapefruits were shipped are 20,400×10= 204,000.
Spiral Review
Question 3.
There were 2,605 people at the basketball game. A reporter rounded this number to the nearest hundred for a newspaper article. What number did the reporter use?
(a) 2,600
(b) 2,610
(c) 2,700
(d) 3,000
Answer: a.
Explanation: Number of people at the basketball game are 2,605 as reporter rounded to nearest hundred, so the number will be 2,600.
Question 4.
To get to Level 3 in a game, a player must score 14,175 points. Ann scores 14,205 points, Ben scores 14,089 points, and Chuck scores 10,463 points. Which score is greater than the Level 3 score?
(a) 14,205
(b) 14,175
(c) 14,089
(d) 10,463
Answer: a.
Explanation: Ann score is greater than the level 3 score and the score is 14,205.
Question 5.
Henry counted 350 lockers in his school. Hayley counted 403 lockers in her school. Which statement is true?
(a) The 3 in 350 is 10 times the value of the 3 in 403.
(b) The 3 in 350 is 100 times the value of the 3 in 403.
(c) The 3 in 403 is 10 times the value of the 3 in 350.
(d) The 3 in 403 is 100 times the value of the 3 in 350.
Answer: b
Explanation: The statement b is correct, as 3 in 350 is 100 times the value of the 3 in 403.
Question 6.
There are 4 muffins on each plate. There are 0 plates of lemon muffins. How many lemon muffins are there?
(a) 4
(b) 2
(c) 1
(d) 0
Answer:d.
Explanation: 0 lemon muffins are there.
Common Core – Add Whole Numbers (Page 39)
Question 1.
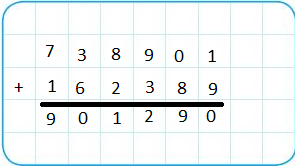
Use the grid to find 738,901 + 162,389.

Use the grid to align the addends by place value.
Answer: 901,290
Explanation:
Estimate. Then find the sum.
Question 2.
72,931 + 18,563
Estimate: _______
Sum: _______
Answer:
Estimate: 90,000.
Sum: 91,494.
Explanation: The sum of 72,931 + 18,563= 91,494.
Question 3.
432,068 + 239,576
Estimate: _______
Sum: _______
Answer:
Estimate: 700,000.
Sum: 671,644.
Explanation: The sum of 432,068 + 239,576= 671,644.
Question 4.
64,505 + 38,972
Estimate: _______
Sum: _______
Answer:
Estimate: 100,000.
Sum: 103,477.
Explanation: The sum of 64,505 + 38,972= 103,477.
Question 5.
839,136 + 120,193
Estimate: _______
Sum: _______
Answer:
Estimate: 960,000.
Sum: 959,329.
Explanation: The sum of 839,136 + 120,193= 959,329.
Question 6.
186,231 + 88,941
Estimate: _______
Sum: _______
Answer:
Estimate: 280,000.
Sum: 275,172.
EXplanation: The sum of 186,231 + 88,941= 275,172.
Question 7.
744,201 + 168,900
Estimate: _______
Sum: _______
Answer:
Estimate: 900,000.
Sum: 913,101.
Explanation: The sum of 744,201 + 168,900= 913,101.
Question 8.
For the first football game of the season, 62,732 fans attended. The number of fans at the second game was 469 more than at the first game. What is the total number of fans that attended the first two games?
_______ fans
Answer: 125,933 fans.
Explanation: The first game had 62,732 fans, the second game was 469 more, so the second game fans attended is 62,732+469= 63,201. The total number of fans attended are 62,732+63,201= 125,933.
Question 9.
Daisy’s Flower Shop sold 135,649 flowers during its first year. The second year, the shop sold 9,754 more flowers than it did its first year. The third year, it sold 1,343 more flowers than it did in the second year. How many flowers did the shop sell during the three years?
_______ flowers
Answer:
Explanation:
Reason Abstractly Algebra Find the missing number and name the property you used to find it. Write Commutative or Associative.
Question 10.
(4,580 + 5,008) + 2,351 = 4,580 + ( _______ +2,351)
Answer: Associative property.
Explanation: (4,580 + 5,008) + 2,351 = 4,580 + ( 5,008 +2,351). The associative property states that when three or more numbers are added or multiplied. The sum or the product is the same regardless of the grouping of the addends.
Question 11.
7,801+ _______ =4,890+7,801
Answer: Commutative property.
Explanation: 7,801+ 4,890 = 4,890+7,801. Commutative property states that the numbers on which we operate can be moved or swapped from their position without making any difference to the answer.
Question 12.
2,592 + 3,385 = 3,385+ _______
Answer: Commutative property.
Explanation: 2,592 + 3,385 = 3,385+ 2,592. Commutative property states that the numbers on which we operate can be moved or swapped from their position without making any difference to the answer.
Common Core – Add Whole Numbers (Page 40)
Use the table for 13–14.
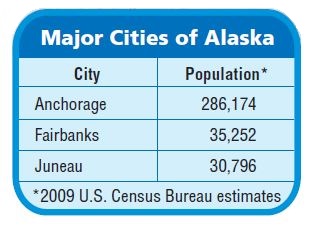
Question 13.
What is the combined population of the three major Alaskan cities? Estimate to verify your answer.
Estimate: _______
Sum: _______
Answer:
Estimate: 350,000.
Sum: 352,222.
Explanation: The combined population of the three major Alaskan cities are 352,222.
Question 14.
The digit 5 occurs two times in the population of Fairbanks. What is the value of each 5? Explain your answer.
First 5: _______
Second 5: _______
Answer:
First 5: 5,000.
Second 5: 50.
Explanation: To find the value of the digit 5 we will expand the 35,252, the expanded form of 35,252 is 30,000+5,000+200+50+2. So the value of first digit 5 is 5,000 and the second digit 5 is 50.
Question 15.
Kaylie has 164 stamps in her collection. Her friend Nellie has 229 more stamps than Kaylie. How many stamps do Kaylie and Nellie have?
_______ stamps
Answer: 393 stamps.
Explanation: Number of stamps did Kaylie has are 164 stamps and Nellie has 229 more stamps, so total stamps Kaylie and Nellie has 164+229= 393 stamps.
Question 16.
Alaska’s Glacier Bay National Park had 431,986 visitors one year. The next year, the park had 22,351 more visitors than the year before. How many people visited during the two years? Show your work and explain how you found your answer.
_______ visitors
Answer: 886,503 Visitors.
Explanation: The number of visitors in Alaska’s Glacier Bay is 431,986 in one year and in the next year the number of visitors is 22,351 more. So the number of people visited in the second year is 431,986+22,351= 454,517. And the number of visitors in two years are 431,986+454,517= 886,503.
Common Core – Add Whole Numbers (Page 41)
Add Whole Numbers
Estimate. Then find the sum.
Question 1.
Estimate: 90,000
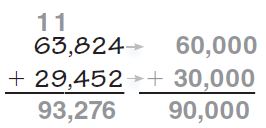
Question 2.
73,404 + 27,865
Estimate: _______
Sum: _______
Answer:
Estimate: 100,000.
Sum: 101,269.
Explanation:
73,404 –> 70,000
+27,865 –>+ 30,000
———– ———–
101,269 100,000
Question 3.
404,446 + 396,755
Estimate: _______
Sum: _______
Answer:
Estimate: 800,000.
Sum: 801,201.
Explanation:
404,446 –> 400,000
+396,755 –>+ 400,000
———– ———–
801,201 800,000
Question 4.
137,638 + 52,091
Estimate: _______
Sum: _______
Answer:
Estimate: 200,000.
Sum: 189,729.
Explanation:
137,638 –> 100,000
+ 52,091 –>+ 100,000
———– ———–
189,729 200,000
Question 5.
200,629 + 28,542
Estimate: _______
Sum: _______
Answer:
Estimate: 250,000.
Sum: 229,171.
Explanation:
200,629 –> 200,000
+ 28,542 –>+ 50,000
———– ———–
229,171 250,000
Question 6.
212,514 + 396,705
Estimate: _______
Sum: _______
Estimate: 600,000.
Sum: 609,219.
Explanation:
212,514 –> 200,000
+ 396,705 –>+ 400,000
———– ———–
609,219 600,000
Question 7.
324,867 + 6,233
Estimate: _______
Sum: _______
Estimate: 331,000
Sum: 331,100
Explanation:
324,867 –> 325,000
+ 6,233 –>+ 6,000
———– ———–
331,100 331,000
Question 8.
462,809 + 256,738
Estimate: _______
Sum: _______
Estimate: 800,000.
Sum: 719,547.
Explanation:
462,809 –> 500,000
+ 256,738 –>+ 300,000
———– ———–
719,547 800,000.
Question 9.
624,836 + 282,189
Estimate: _______
Sum: _______
Estimate: 900,000
Sum: 907,025
Explanation:
624,836 –> 600,000
+ 282,189 –>+ 300,000
———– ———–
907,025 900,000.
Problem Solving
Use the table for 10–12.
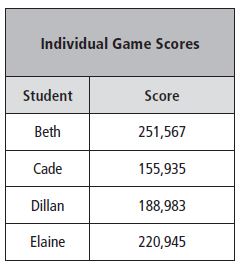
Question 10.
Beth and Cade were on one team. What was their total score?
_______
Answer: The total score is 407,502.
Explanation: Beth scores 251,567 and Cade scores 155,935. So the total score is 251,567+155,935= 407,502.
Question 11.
Dillan and Elaine were on the other team. What was their total score?
_______
Answer: 409,928
Explanation: Dillan score is 188,983 and Elaine score is 220,945. So the total score is 188,983+220,945= 409,928.
Question 12.
Which team scored the most points?
_______
Answer: Second-team scores the most points.
Explanation: Second-team scores the most points which are 409,928 whereas 1st team scores 407,502.
Question 13.
Have students write a story problem that can be solved by finding the sum of 506,211 and 424,809. Have them solve the problem.
Answer: 931,020.
Explanation: Town A has a population of 506,211 and town B has a population of 424,809. What is the total population?
Town A population is 506,211 and the town B population is 424,809. So the total population is 506,211+424,809= 931,020.
Common Core – Add Whole Numbers (Page 42)
Lesson Check
Question 1.
The coastline of the United States is 12,383 miles long. Canada’s coastline is 113,211 miles longer than the coastline of the United States. How long is the coastline of Canada?
(a) 100,828 miles
(b) 115,594 miles
(c) 125,594 miles
(d) 237,041 miles
Answer: 125,594 miles.
Explanation: Coastline of the United States is 12,383 miles long and Canada’s coastline is 113,211 miles longer than the coastline of the United States, so the total length of the coastline of Canada is 12,383+113,211= 125,594.
Question 2.
Germany is the seventh largest European country and is slightly smaller by area than Montana. Germany has a land area of 134,835 square miles and a water area of 3,011 square miles. What is the total area of Germany?
(a) 7,846 square miles
(b) 131,824 square miles
(c) 137,846 square miles
(d) 435,935 square miles
Answer: 137,846 miles.
Explanation: The land area of Germany is 134,835 square miles and the water area is 3,011 square miles, so the total area of Germany is 134,835+3,011= 137,846 miles.
Spiral Review
Question 3.
In an election, about 500,000 people voted in all. Which number could be the exact number of people who voted in the election?
(a) 429,455
(b) 441,689
(c) 533,736
(d) 550,198
Answer: 533,736
Explanation: As 500,000 people are voted so the exact number of people who voted in the election is 533,736.
Question 4.
In 2007, Pennsylvania had approximately 121,580 miles of public roads. What is 121,580 rounded to the nearest thousand?
(a) 100,000
(b) 120,000
(c) 121,000
(d) 122,000
Answer: 122,000.
Explanation: The number 121,580 is rounded to the nearest thousand is 122,000.
Question 5.
Which of the following lists of numbers is in order from greatest to least?
(a) 33,093; 33,903; 33,309
(b) 42,539; 24,995; 43,539
(c) 682,131; 628,000; 682,129
(d) 749,340; 740,999; 740,256
Answer: 749,340; 740,999; 740,256.
Explanation: The numbers in order from greatest to least is 749,340; 740,999; 740,256.
Question 6.
Which symbol makes the following statement true?
$413,115 ________ $431,511
(a) <
(b) >
(c) =
(d) +
Answer: a
Explanation: $413,115 < $431,511.
Common Core – Subtract Whole Numbers (Page 44)
Question 1.
Subtract. Use the grid to record the problem.
637,350 − 43,832

Answer: 1,076,182.
Explanation:
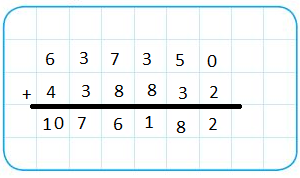
Estimate. Then find the difference.
Question 2.
14,659 − 11,584
Estimate: _______
Difference: _______
Estimate: 3,000
Sum: 3,075
Explanation:
14,659 –> 15,000
– 11,584 –> -12,000
———– ———–
3,075 3,000
Question 3.
456,912 − 37,800
Estimate: _______
Difference: _______
Estimate: 420,000.
Sum: 419,112.
Explanation:
456,912 –> 460,000
– 37,800 –> – 40,000
———– ———–
419,112 420,000
Question 4.
407,001 − 184,652
Estimate: _______
Difference: _______
Estimate: 210,000.
Sum: 222,349.
Explanation:
407,001 –> 410,000
– 184,652 –> – 200,000
———– ———–
222,349 210,000
Question 5.
942,385 − 461,803
Estimate: _______
Difference: _______
Estimate: 400,000.
Sum: 480,582.
Explanation:
942,385 –> 900,000
– 461,803 –> -500,000
———– ———–
480,582 400,000
Question 6.
798,300 − 348,659
Estimate: _______
Difference: _______
Estimate: 500,000.
Sum: 449,641.
Explanation:
798,300 –> 800,000
– 348,659 –> -300,000
———– ———–
449,641 500,000
Question 7.
300,980 − 159,000
Estimate: _______
Difference: _______
Estimate: 141,000.
Sum: 141,980.
Explanation:
300,980 –> 301,000
– 159,000 –> -160,000
———– ———–
141,980 141,000
Common Core – Subtract Whole Numbers (Page 45)
Practice: Copy and Solve Subtract. Add to check.
Question 8.
653,809 – 256,034 = _______
Answer: 397,775.
Explanation: 653,809 – 256,034 = 397,775.
Question 9.
258,197 – 64,500 = _______’
Answer: 163,697.
Explanation: 258,197 – 64,500 = 163,697.
Question 10.
496,004 – 398,450 = _______
Answer:
Explanation: 496,004 – 398,450 = 97,554.
Question 11.
500,000 – 145,609 = _______
Answer: 354,391.
Explanation: 500,000 – 145,609= 354,391.
Reason Abstractly Algebra Find the missing digit.
Question 12.
6,532 − 4,1_5 = 2,407
Answer: 2
Explanation: To find the missing digit we will subtract 6,532-2,407= 4,125.
Question 13.
_08,665−659,420 = 149,245
Answer: 8
Explanation: To find the missing digit we will add 149,245+659,420= 808,665.
Question 14.
697,320 − 432,_08 = 264,712
Answer: 6
Explanation: To find the missing digit we will subtract 697,320-264,712= 432,608.
Use the table for 15–16.

Question 15.
Estimate Reasonableness How many more acres were grown in 1996 than in 1986? Estimate to check the reasonableness of your answer.
_______ acres
Answer: 200,000 acres.
Explanation: The number of acres in 1986 is 466,256 and the number of acres in 1996 is 656,598. So the number of acres grown in 1996 is 656,598- 466,256= 190,342. So the estimated answer is 200,000 acres.
Question 16.
What is the difference between the greatest number of acres and the least number of acres used for growing oranges?
_______ acres
Answer: 206,830.
Explanation: The greatest number of acres is 673,086 and the least number of acres is 466,256. So the difference between the greatest number of acres and the least number of acres are 673,086- 466,256= 206,830.
Question 17.
Workers at a paper company count the number of boxes of paper in the warehouse each month. In January, there were 106,341 boxes of paper. In February, there were 32,798 fewer boxes than there were in January. In March, there were 25,762 fewer boxes than there were in February. How many boxes were in the warehouse in March?
_______ boxes
Answer: 106,341-58,560= 47,781 boxes.
Explanation: Total number of boxes is 106,341 in January and in February there were 32,798 boxes and in march, there were 25,762 fewer boxes. Total boxes are 32,798+25,762= 58,560, so the number of boxes were in the warehouse in March is 106,341-58,560= 47,781 boxes.
Question 18.
There are 135,663 kilometers of U.S. coastline that border the Pacific Ocean. There are 111,866 kilometers of U.S. coastline that border the Atlantic Ocean. How many more kilometers of U.S. coastline border the Pacific Ocean than the Atlantic Ocean? Solve the problem and show how to check your answer.
_______ km
Answer: 23,797 km.
Explanation: There are 135,663 kilometers of US coastline in the Pacific Ocean and 111,866 kilometers in the Atlantic ocean. So the number of kilometers of US coastline border the Pacific Ocean than the Atlantic Ocean is 135,663- 111,866= 23,797 km.
Common Core – Subtract Whole Numbers (Page 46)
Question 19.
What’s the Error? Maryland has an area of 12,407 square miles. Texas has an area of 268,601 square miles. How much larger is Texas than Maryland?
Read how Janice solved the problem.
Find her error.
Texas: 268,601 square miles
Maryland: 12,407 square miles
I can subtract to find the difference.
268,601
–12,407
144,531
Solve the problem and correct her error.
Answer: Texas is 256,194 square miles larger than Maryland.
Explanation:
Texas: 268,601 square miles
Maryland: 12,407 square miles
I can subtract to find the difference.
268,601- 12,407= 256,194.
So Texas is 256,194 square miles larger than Maryland.
Question 20.
Verify Reasoning of Others Describe Janice’s error.
Answer: Janice did not align the digits by place value when subtracted the numbers.
Common Core – Subtract Whole Numbers (Page 47)
Subtract Whole Numbers
Estimate. Then find the difference.
Question 1.

Question 2.
428,731 – 175,842
Estimate: ______
Difference: ______
Answer:
Estimate: 200,000.
Difference: 252,889.
Explanation:
428,731 – 175,842= 252,889
400,000 – 200,000= 200,000.
Question 3.
920,026 – 535,722
Estimate: ______
Difference: ______
Answer:
Estimate: 400,000.
Difference: 384,304.
Explanation:
920,026 – 535,722= 384,304
900,000 – 500,000= 400,000.
Question 4.
253,495 – 48,617
Estimate: ______
Difference: ______
Answer:
Estimate: 200,000.
Difference: 204,878.
Explanation:
253,495 – 48,617= 204,878.
250,000 – 50,000= 200,000.
Subtract. Add to check.
Question 5.
735,249 – 575,388 = ______
______ + ______ = ______
Answer: 159,861.
575,388+159,861= 735,249.
Explanation:
735,249 – 575,388= 159,861.
575,388+159,861= 735,249.
Question 6.
512,724 – 96,473 = ______
______ + ______ = ______
Answer: 416,251
96,473+416,251= 512,724.
Explanation:
512,724 – 96,473 = 416,251
96,473+416,251= 512,724.
Question 7.
600,000 – 145,782 = _______
_______ + ______ = _______
Answer: 454,218.
145,782+454,218= 600,000.
Explanation:
600,000 – 145,782 = 454,218.
145,782+454,218= 600,000.
Problem Solving
Use the table for 8 and 9.
Question 8.
How many more people attended the Magic’s games than attended the Pacers’ games?
_______ people
Answer: 133,606 people.
Explanation: The number of people attended for Magic’s game is 715,901 and the number of people attended for Pacer’s games is 582,295. So the number of people more attended for the Magic’s games than attended the Pacers’ games are 715,901-582,295=133,606.
Question 9.
How many fewer people attended the Pacers’ games than attended the Clippers’ games?
_______ people
Answer: 87,768 people
Explanation: The number of people attended for Indiana Pacers game is 582,295 and the number of people attended for Los Angeles Clippers is 670,063. So 670,063- 582,295= 87,768 people attended the Pacers’ games than attended the Clippers’ games.
Question 10.
Have students write a story problem that can be solved by finding the difference of 432,906 and 61,827. Then have them solve the problem.
Answer: The number of people who attended the football game is 432,906 and the number of people who attended the basketball game is 61,287. How many fewer people attended the football game than attended the basketball game?
Explanation: The number of people who attended the football game is 432,906 and the number of people who attended the basketball game is 61,287. So 432,906- 61,287= 371,619 people attended the Pacers’ games than attended the Clippers’ games.
Common Core – Subtract Whole Numbers (Page 48)
Lesson Check
Question 1.
This year, a farm planted 400,000 corn stalks. Last year, the farm planted 275,650 corn stalks. How many more corn stalks did the farm plant this year than last year?
(a) 124,350
(b) 125,450
(c) 235,450
(d) 275,650
Answer: 124,350.
Explanation: A farm planted 400,000 corn stalks this year and 275,650 corn stalks last year, so 400,000-275,650= 124,350 many more corn stalks did the farm plant this year than last year.
Question 2.
One machine can make 138,800 small paper clips in one day. Another machine can make 84,250 large paper clips in one day. How many more small paper clips than large paper clips are made by the two machines in one day?
(a) 44,550
(b) 54,550
(c) 54,650
(d) 154,650
Answer: 54,550.
Explanation: As machine one makes 138,800 small paper clips in one day and the machine makes 84,250 paper clips in one day, so
138,800-84,250= 54,550 many more small paper clips than large paper clips are made by the two machines in one day.
Spiral Review
Question 3.
In three baseball games over a weekend, 125,429 people came to watch. The next weekend, 86,353 came to watch the games. How many people in all watched the six baseball games?
(a) 201,782
(b) 211,772
(c) 211,782
(d) 211,882
Answer: 211,782.
Explanation: The number of people attended for three baseball games is 125,429 and 86,353 in next weekend, so
125,429+86,353= 211,782 people watched the six baseball games.
Question 4.
Kevin read the number “two hundred seven thousand, forty-eight” in a book. What is this number in standard form?
(a) 27,048
(b) 27,480
(c) 207,048
(d) 207,480
Answer: 207,048.
Explanation: The standard form of “two hundred seven thousand, forty-eight” is 207,048.
Question 5.
A museum had 275,608 visitors last year. What is this number rounded to the nearest thousand?
(a) 275,600
(b) 276,000
(c) 280,000
(d) 300,000
Answer: 276,000.
Explanation: The nearest thousand of the number 275,608 is 276,000.
Question 6.
At the Millville Theater, a play ran for several weeks. In all, 28,175 people saw the play. What is the value of the digit 8 in 28,175?
(a) 8
(b) 800
(c) 8,000
(d) 80,000
Answer: 8,000.
Explanation: The value of the digit 8 in 28,175 is 8,000.
Problem Solving • Comparison Problems with Addition and Subtraction (Page 50)
During an event, a hot air balloon traveled a distance of 5,110 feet during the first trip and 850 feet more during the second trip. How far did it travel during the second trip?
Question 1.
What do I need to find?
Answer: We need to find the number of feet the balloon traveled during the second trip.
Question 2.
What information do I need to use?
Answer: We will use the facts that the ballon traveled 5,110 feet during the first trip and 850 feet more during the second trip.
Question 3.
How will I use the information?
Answer: We can draw a diagram or use a bar model to help me find how many feet the ballons traveled during the second trip.
Explanation: As hot air balloon traveled a distance of 5,110 feet in the first trip and 850 more in the second trip, so the second trip is 5,110+850= 5,960 feet. So, the balloon traveled 5,960 feet during the second trip.
Question 4.
How far did it travel during the second trip? And
______ feet
Answer: The ballon traveled 5,960 feet during the second trip.
Explanation: As hot air balloon traveled a distance of 5,110 feet in the first trip and 850 more in the second trip, so the second trip is 5,110+850= 5,960 feet. So, the balloon traveled 5,960 feet during the second trip.
Question 5.
Is your answer reasonable? Explain how you know.
Answer: Yes, the answer is reasonable.
Explanation: As 5,960 feet is reasonable because 5,000+1,000= 6,000 and 5,960 is close to 6,000. Since addition and subtraction are inverse operations, we can subtract 850 from the sum to see if we get 5,110.
Problem Solving • Comparison Problems with Addition and Subtraction (Page 51)
Hot air balloons are able to fly at very high altitudes. A world record height of 64,997 feet was set in 1988. In 2005, a new record of 68,986 feet was set. How many feet higher was the 2005 record than the 1988 record?
Question 1.
First, draw a diagram to show the parts of the problem.
Answer: 3,989 feet higher.
Explanation: 68,986-64,997= 3,989 feet.
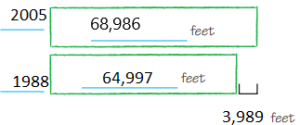
Question 1.
Next, write the problem you need to solve.
Answer: 3,989 feet higher.
Explanation: The 2005 record was 68,986-64,997= 3,989 feet higher.
Question 1.
Last, solve the problem to find how many feet higher the 2005 record was than the 1988 record
______ feet higher
Answer: 3,989 feet higher.
Explanation: The 2005 record was 68,986-64,997= 3,989 feet higher.
Question 2.
What if a new world altitude record of 70,000 feet was set? How many feet higher would the new record be than the 2005 record?
______ feet
Answer: 1,014 feet.
Explanation: The new world altitude record is 70,000 feet, so the new record is 70,000-68,986= 1,014 feet higher.

Question 3.
Last year, the ticket sales for a commercial hot air balloon ride were $109,076. This year, the ticket sales were $125,805. How much more were the ticket sales this year?
$ ______
Answer: $16,729.
Explanation: The ticket sale for last year is $109,076 and this year is $125,805, so $125,805- $109,076= $16,729 much more tickets are sold this year.
Question 4.
There were 665 hot air balloon pilots at a hot air balloon race. There were 1,550 more ground crew members than there were pilots. How many ground crew members were there in all?
______ ground crew members
Answer: 2,215 ground crew members.
Explanation: There were 1,550 more ground crew members and 665 hot air ballon pilots at a hot air ballon. So 1,550+665= 2,215 ground crew members.

Problem Solving • Comparison Problems with Addition and Subtraction (Page 52)
Question 5.
Steve Fossett attempted to fly around the world in a balloon several times before he succeeded in 2002. How many more miles did he fly during the 2002 flight than during the August 1998 flight?
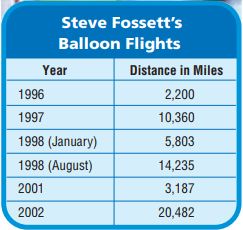
______ miles
Answer: 6,247 miles.
Explanation: Number of miles did he flew are during 2002 are 20,482-14,235= 6,247 miles.
Question 6.
Is the combined distance for the 1998 flights more or less than the distance for the 2002 flight?
Answer: The combined distance is 20,038 miles, which is less than 20,482 miles.
Question 7.
Estimate the total number of miles Fossett flew during the six hot air balloon flights. Explain how you estimated.
______ miles
Answer: 55,000 miles.
Explanation: Round off each distance to the greatest place value position, then add 2,000+10,000+6,000+14,000+3,000+20,000= 55,000 miles.
Question 8.
Rusty wants to buy a small hot air balloon that costs $23,950. The cost of training for a license is $2,750. How much will Rusty pay for the balloon and the training?
(a) $21,200
(b) $26,600
(c) $26,700
(d) $36,700
Answer: $26,700
Explanation: Rusty wants to buy a small hot air balloon that costs $23,950 and the cost of training for a license is $2,750, so total Rusty pay is $23,950+$2,750= $26,700.
Problem Solving • Comparasion Problems with Addition and Substraction (Page 53)
Problem Solving • Comparasion Problems with Addition and Substraction
Use the information in the table for 1–3.
Question 1.
How many square miles larger is the surface area of Lake Huron than the surface area of Lake Erie?
Think: How can a bar model help represent the problem? What equation can be written?

Question 1.
Question 2.
Which lake has a surface area that is 14,938 square miles greater than the surface area of Lake Ontario? Draw a model and write a number sentence to solve the problem.
Answer: Lake Michigan 22,278 square miles.
Explanation: 7,340+14,938= 22,278.

Question 3.
Lake Victoria has the largest surface area of all lakes in Africa. Its surface area is 26,828 square miles. How much larger is the surface area of Lake Superior than that of Lake Victoria?
______ square milles
Answer: 4,872 square miles.
Explanation: The Surface area of Lake Victoria is 26,828 square miles and the surface area of the Lake Superior is 31,700 square miles. So 31,700-26,828= 4,872 square miles larger.
Question 4.
At 840,000 square miles, Greenland is the largest island in the world. The second-largest island is New Guinea, at 306,000 square miles. How much larger is Greenland than New Guinea?
______ square miles
Answer: 534,000 square miles.
Explanation: The surface area of Greenland is 840,000 square miles and New Guinea is 306,000 square miles. So 840,000-306,000= 534,000 square miles.
Problem Solving • Comparison Problems with Addition and Subtraction (Page 54)
Lesson Check
Question 1.
The Mariana Trench in the Pacific Ocean is about 36,201 feet deep. The Puerto Rico Trench in the Atlantic Ocean is about 27,493 feet deep. Based on these data, how many feet deeper is the Mariana Trench than the Puerto Rico Trench?
(a) 8,708 feet
(b) 9,718 feet
(c) 9,808 feet
(d) 63,694 feet
Answer: 8,708 feet.
Explanation: The Mariana Trench in the Pacific Ocean is about 36,201 feet deep and the Atlantic Ocean is about 27,493 feet deep. So 36,201-27,493= 8,708 feet.
Question 2.
At 1,932 feet, Crater Lake, Oregon, is the deepest lake in the United States. The world’s deepest lake, Lake Baykal in Russia, is 3,383 feet deeper. How deep is Lake Baykal?
(a) 3,383 feet
(b) 4,215 feet
(c) 4,315 feet
(d) 5,315 feet
Answer: 5,315 feet
Explanation: Crater Lake is 1,932 feet and Lake Baykal is 3,383 feet, so 1,932+3,383= 5,315 feet deeper.
Spiral Review
Question 3.
Which of the following amounts is greater than $832,458?
(a) $82,845
(b) $832,458
(c) $823,845
(d) $832,485
Answer: $832,485.
Explanation: $832,458 is greater than $832,485.
Question 4.
A stadium in Pennsylvania seats 107,282 people. A stadium in Arizona seats 71,706 people. Based on these facts, how many more people does the stadium in Pennsylvania seat than the stadium in Arizona?
(a) 35,576
(b) 35,586
(c) 36,576
(d) 178,988
Answer: 35,576.
Explanation: A stadium in Pennsylvania seats 107,282 people and a stadium in Arizona seats 71,706 people. So 107,282-71,706= 35,576 people seat in the stadium in Arizona.
Question 5.
Which of the following numbers is 399,713 rounded to the place value of the underlined digit?
(a) 390,000
(b) 398,000
(c) 399,800
(d) 400,000
Answer: 400,000.
Explanation: The number 399,713 rounded to the nearest thousand is 400,000.
Question 6.
About 400,000 people visited an art museum in December. Which number could be the exact number of people who visited the art museum?
(a) 478,051
(b) 452,223
(c) 352,483
(d) 348,998
Answer: 352,483.
Explanation: The exact number of people who visited the art museum is 352,483.
Problem Solving • Comparasion Problems with Addition and Substraction (Page 55)
Question 1.
Select a number for ■ that will make a true comparison. Mark all that apply.
703,209 > ■
Options:
(a) 702,309
(b) 703,029
(c) 703,209
(d) 703,290
(e) 730,029
(f) 730,209
Answer: 703,209>702,309, 703,209>703,029.
Explanation: The numbers 702,309, 703,029 are less than 703,209.
Question 2.
Nancy wrote the greatest number that can be made using each of these digits exactly once.

Part A
What was Nancy’s number? How do you know this is the greatest possible number for these digits?
Answer: 985,431.
Explanation: Here we will use place value and we will take the greatest digit and place it in the spot furthest to the left, the hundred thousands column. And place the next greatest digit in the ten thousands column and so on. We know that the place value of each digit to the left is ten times the place value of the digit to its right.
Question 2.
Part B
What is the least number that can be made using each digit exactly once? Explain why the value of the 4 is greater than the value of the 5.
Answer: 134,589.
Explanation: The 4 represents 4,000 and 5 represents 500.
Problem Solving • Comparasion Problems with Addition and Substraction (Page 56)
For 3–4, use the table.
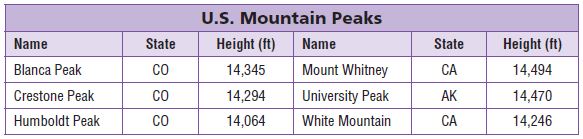
Question 3.
Write the name of each mountain peak in the box that describes its height, in feet.
Between 14,000 feet and Between 14,301 feet and
14,300 feet 14,500 feet
Answer:
Between 14,000 feet and 14,300 feet- Crestone Peak, Humboldt Peak, White Mountain.
Between 14,301 feet and 14,500 feet- Blanca Peak, University Peak, Mount Whitney.
Explanation:
Between 14,000 feet and 14,300 feet- Crestone Peak 14,294 ft, Humboldt Peak 14,064 ft, White Mountain 14,246 ft.
Between 14,301 feet and 14,500 feet- Blanca Peak 14,345 ft, University Peak 14,470 ft, Mount Whitney 14,494 ft.
Question 4.
Circle the name of the tallest peak. Explain how you know which of the mountain peaks is the tallest.
Answer: Mount Whitney.
Explanation: Comparing the heights by place value position.
Question 5.
Mr. Rodriguez bought 420 pencils for the school. If there are 10 pencils in a box, how many boxes did he buy?
Options:
(a) 42
(b) 420
(c) 430
(d) 4,200
Answer: 42 boxes.
Explanation: Mr. Rodriguez bought 420 pencils and in a box, there are 10 pencils. So the number of boxes did he bought is
420÷10= 42 boxes.
Question 6.
Bobby and Cheryl each rounded 745,829 to the nearest ten thousand. Bobby wrote 750,000 and Cheryl wrote 740,000. Who is correct? Explain the error that was made.
_________
Answer: Bobby is correct.
Explanation: Cheryl left the ten thousands digit the same instead of increasing it by 1. The digit in the thousands place is 5, so to round to the nearest ten thousand, Cheryl should have increased the ten thousands digit, 4 by 1.
Problem Solving • Comparasion Problems with Addition and Substraction (Page 57)
Question 7.
The total season attendance for a college team’s home games, rounded to the nearest ten thousand, was 270,000. For numbers 7a–7d, select Yes or No to tell whether the number could be the exact attendance.
a. 265,888
i. yes
ii. no
Answer: Yes.
Explanation: When 265,888 is rounded off to the nearest ten thousand we will get 270,000.
Question 7.
b. 260,987
i. yes
ii. no
Answer: No.
Explanation: When 260,987 is rounded off to the nearest ten thousand we will get 260,000.
Question 7.
c. 274,499
i. yes
ii. no
Answer: Yes.
Explanation: When 274,499 is rounded off to the nearest ten thousand we will get 270,000.
Question 7.
d. 206,636
i. yes
ii. no
Answer: No.
Explanation: When 206,636 is rounded off to the nearest ten thousand we will get 210,000.
For 8–10, use the table.
The table shows recent population data for Sacramento, California.
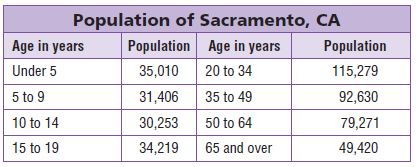
Question 8.
How many children are under 10 years old? Show your work.
_____ children
Answer: 66,416 children.
Explanation: Children under 10 years old are 35,010+31,406= 66,416 children.
Question 9.
How many people are between the ages of 20 and 49? Show your work.
_____ people
Answer: 207,909 people.
Explanation: People between the ages of 20 and 49 are 115,279+92,630= 207,909 people.
Question 10.
How many more children are under the age of 5 than between the ages of 10 and 14? Show your work.
_____ children
Answer: 4,757 children.
Explanation: The children 35,010-30,253= 4,757 children are under the age of 5 than between the ages of 10 and 14.
Problem Solving • Comparasion Problems with Addition and Substraction (Page 58)
Question 11.
For numbers 11a–11d, select True or False for each sentence.
a. The value of 7 in 375,092 is 7,000.
i. True
ii. False
Answer: False.
Explanation: False, because the value of the digit 7 in 375,092 is 70,000.
Question 11.
b. The value of 5 in 427,593 is 500.
i. True
ii. False
Answer: True.
Explanation: As 5 is in hundreds place, so the value of the digit 5 in 427,593 is 500.
Question 11.
c. The value of 2 in 749,021 is 200.
i. True
ii. False
Answer: False.
Explanation: False, because the value of the digit 2 in 749,021 is 20.
Question 11.
d. The value of 4 in 842,063 is 40,000.
i. True
ii. False
Answer: True.
Explanation: The value of the digit 4 in the digit 842,063 is 40,000.
Question 12.
Select another way to show 403,871. Mark all that apply.
Options:
(a) four hundred three thousand, eight hundred one
(b) four hundred three thousand, seventy-one
(c) four hundred three thousand, eight hundred seventy-one
(d) 400,000 + 38,000 + 800 + 70 + 1
(e) 400,000 + 3,000 + 800 + 70 + 1
(f) 4 hundred thousands + 3 thousands + 8 hundreds + 7 tens + 1 one
Answer: c, e, f
Explanation: four hundred three thousand, eight hundred seventy-one, 400,000 + 3,000 + 800 + 70 + 1, 4 hundred thousands + 3 thousands + 8 hundreds + 7 tens + 1 one are the another way of 403,871.
Question 13.
Lexi, Susie, and Rial are playing an online word game. Rial scores 100,034 points. Lexi scores 9,348 fewer points than Rial and Susie scores 9,749 more points than Lexi. What is Susie’s score? Show your work.
_____
Answer: 100,435 points.
Explanation: Rial score is 100,034 points and Lexi scores 9,348 fewer points which means 100,034-9,348= 90686 and Susie scores 9,749 more points than Lexi which means 90,686+9,749= 100,435 points are scored by Susie.
Question 14.
There were 13,501 visitors to a museum in June. What is this number rounded to the nearest ten thousand? Explain how you rounded.
_____
Answer: 10,000.
Explanation: There is a 1 in the ten thousands place. The digit to its right is 3, so the 1 stays the same.
Problem Solving • Comparasion Problems with Addition and Substraction (Page 59)
Question 15.
New Mexico has an area of 121,298 square miles. California has an area of 155,779 square miles. How much greater is the area, in square miles, of California than the area of New Mexico? Show your work and explain how you know the answer is reasonable.
______ square miles
Answer: 34,481 square miles.
Explanation: The area of New Mexico is 121,298 square miles and the area of California is 155,779 square miles. So
155,779- 121,298= 34,481 square miles greater.
Question 16.
Circle the choice that completes the statement.
10,000 less than 24,576 is  1,000 less than 14,576.
1,000 less than 14,576.
_________
Answer: 10,000 less than 24,576 is greater than 1,000 less than 14,576.
Explanation:
10,000 less than 24,576 is  1,000 less than 14,576.
1,000 less than 14,576.
Question 17.
Match the number to the value of its 5.

Type below:
__________
Answer: 45,678 – 5,000 757,234 – 50,000 13,564 – 500. 3,450 – 50.
Explanation:
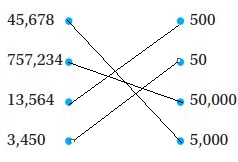
Problem Solving • Comparasion Problems with Addition and Substraction (Page 60)
Question 18.
During September and October, a total of 825,150 visitors went to Grand Canyon National Park. If 448,925 visitors went to the park in September, how many visitors went to the park in October? Show your work.
_____ people
Answer:
Explanation: The total number of visitors in September and October is 825,150 visitors and 448,925 visitors visited the park in September, so 825,150-448,925= 376,225 visitors visited in October.
Question 19.
A college baseball team had 3 games in April. Game one had an attendance of 14,753 people. Game two had an attendance of 20,320 people. Game three had an attendance of 14,505 people. Write the games in order from the least attendance to the greatest attendance. Use pictures, words, or numbers to show how you know.
Game _____ ; _____ ; _____
Answer: Game 3; Game 1; Game2.
Explanation: The number of people who attended for game one is 14,753 and game two is 20,320 people, game three is 14,505 people. So the order from the least attendance to the greatest attendance is 14,505<14,753<20,320.
Question 20.
Caden made a four-digit number with a 5 in the thousands place, a 5 in the ones place, a 6 in the tens place, and a 4 in the hundreds place. What was the number?
_____
Answer: 5,465.
Explanation: The four-digit number with 5 in the thousands place, 4 in the hundreds place, 6 in the tens place, and 5 in the ones place made by Caden is 5,465.
Problem Solving • Comparasion Problems with Addition and Substraction (Page 65)
Question 1.
There are 8 students in the art club. There are 3 times as many students in chorus. How many students are in chorus?
So, there are _____ students in chorus.
Answer: There are 24 students in the chorus.
Explanation: The number of students in the art club is 8 students and there are 3 times as many students in the chorus. So number of students in the chorus is 8×3= 24 students. So, there are 24 students in the chorus.
Draw a model and write an equation.
Question 2.
6 times as many as 2 is 12.
Answer: 6×2= 12
Explanation: 6×2= 12
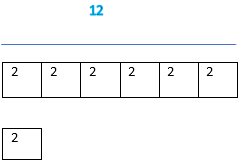
Question 3.
20 is 4 times as many as 5.
Answer: 20= 4×5.
Explanation: 20= 4×5.
Write a comparison sentence.
Question 4.
18 = 9 × 2
_____ is _____ times as many as _____ .
Answer: 18 is 9 times as many as 2.
Question 5.
8 × 4 = 32
_____ times as many as _____ is _____
Answer: 8 times as many as 4 is 32.
Write a comparison sentence.
Question 6.
5 × 7 = 35
_____ times as many as _____ is _____ .
Answer: 5 times as many as 7 is 35.
Question 7.
54 = 6 × 9
_____ is _____ times as many as _____ .
Answer: 54 is 6 times as many as 9.
Question 8.
One week, Jake and Sally collected canned goods for a food drive. On Monday, Jake collected 4 boxes and Sally collected 2 boxes. At the end of the week, Jake had 3 times as many boxes as he had on Monday. Sally had 4 times as many boxes as she had on Monday. Together, how many boxes of canned goods did they have at the end of the week?
_____ boxes
Answer: 20 boxes.
Explanation:
The number of boxes Jake collected on Monday is 4 boxes and at the end of the week, he collected 3 times as many boxes as he had on Monday, which means 3×4= 12. Sally collected 2 boxes on Monday and at the end of the week, Sally collected 4 times as many boxes as she had on Monday which means 4×2= 8 boxes. So 12 boxes+8 boxes= 20 boxes of canned goods they have collected at the end of the week.
Question 9.
Nando has 4 goldfish. Jill has 3 goldfish. Cooper has 2 times as many goldfish as Nando and Jill combined. Write an equation that compares the number of goldfish Cooper has with the number of goldfish that Nando and Jill have.
Answer: 14 goldfish.
Explanation: Nando has 4 goldfish, Jill has 3 goldfish and Cooper has 2 times as many goldfish as Nando and Jill combined which means the total goldfish Nando and Cooper has are 4+3= 7, so Cooper had 2×7= 14 goldfish.
Question 10.
Represent a Problem Write a comparison sentence about pet food that could be represented using the equation 12 = 4 × 3.
Answer: Cooper bought 12 cans of cat food, which is 4 times the number of cans that he has now.
Problem Solving • Comparasion Problems with Addition and Substraction (Page 66)
Question 11.
Luca has 72 baseball cards. This is 8 times as many cards as Han has. How many baseball cards does Han have?

a. What do you need to find?
Answer: We need to find how many baseball cards Han has.
Question 11.
b. How can you use a model to find the number of cards Han has?
Answer: By drawing a comparison model we can find the number of cards Han has.
Question 11.
c. Draw the model.
Answer:
Question 11.
d. Write an equation and solve.
Answer: Han has 9 baseball cards.
Explanation:
72= 8×n
n= 72÷8
= 9.
So, Han has 9 baseball cards.
Question 12.
Complete the statements to describe each model.
24 is _____ times as many as _____ . 24 is _____ times as many as _____ .
Answer:
24 is 6 times as many as 4.
24 is 4 times as many as 6.
Conclusion:
Enhance your math skills by preparing from the Go Math Answer Key Chapter 1. Also, get some subject knowledge after performing the chapter practice test in the HMH Go Math Grade 4 Answer Key Chapter 1 Place Value, Addition, and Subtraction to One Million.

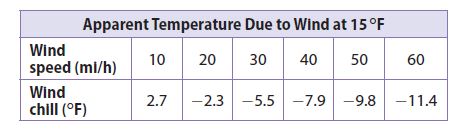

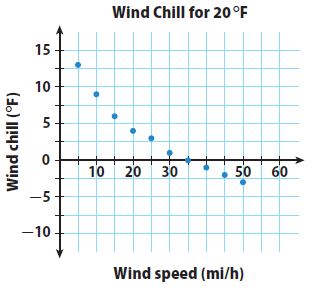
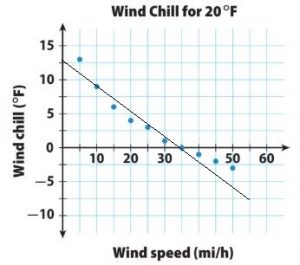



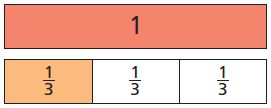



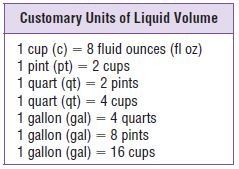


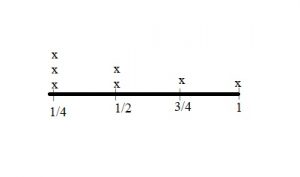

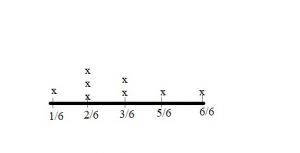

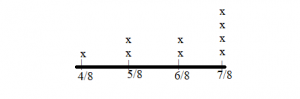

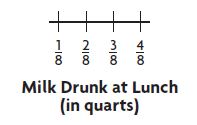
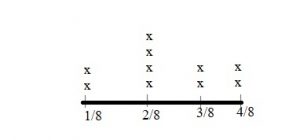





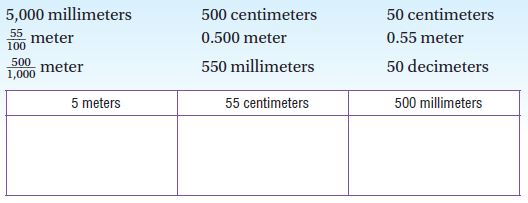

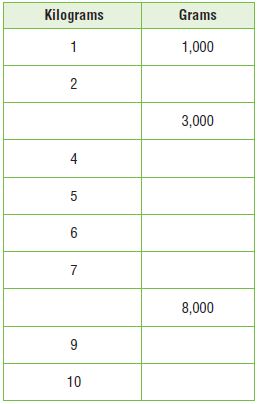








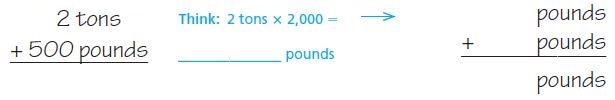

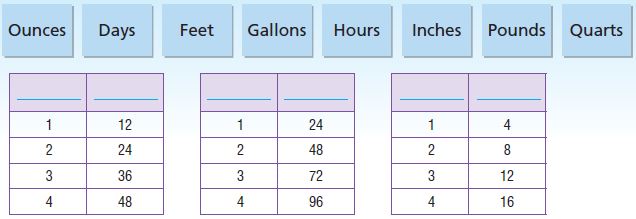



 of water.
of water.

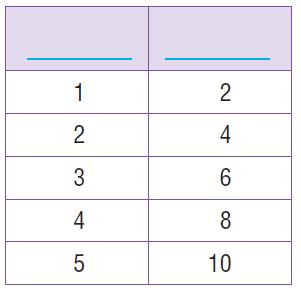




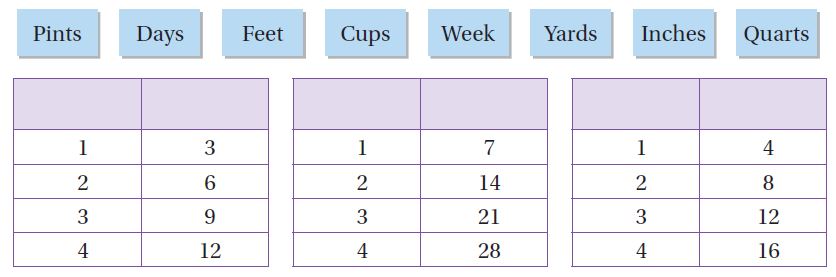
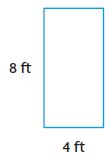




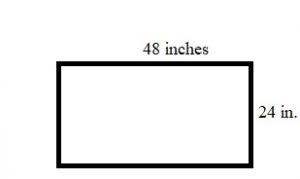

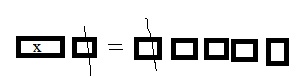
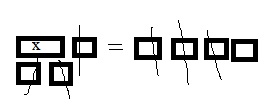
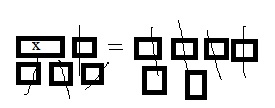
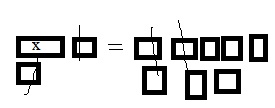
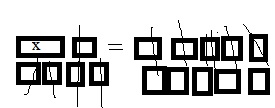

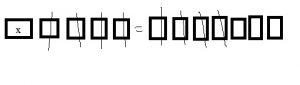
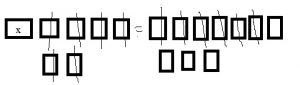



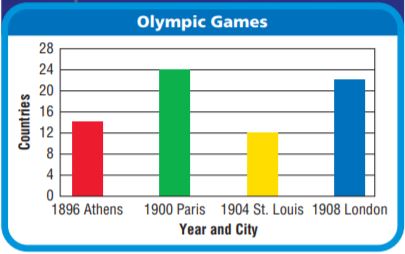














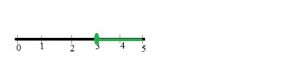




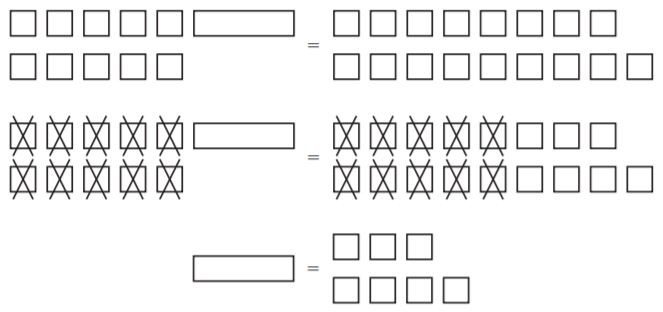
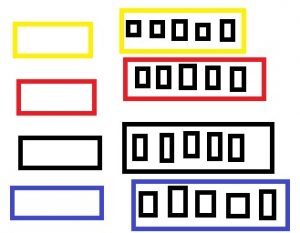





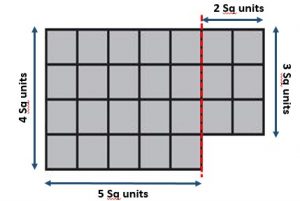

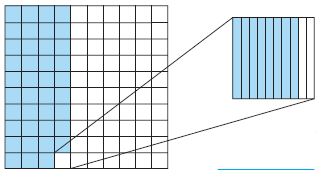
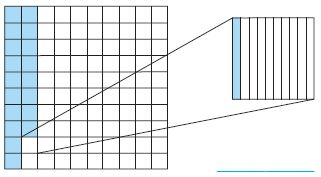
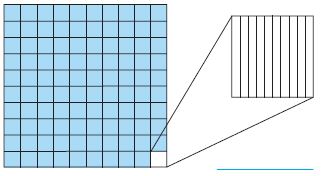
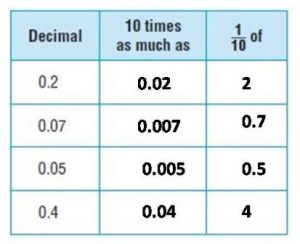

 and \(\frac{1}{10}\) of
and \(\frac{1}{10}\) of 
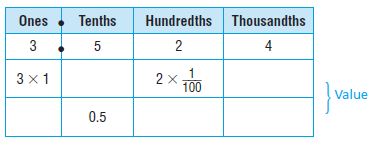
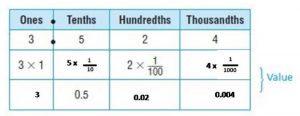
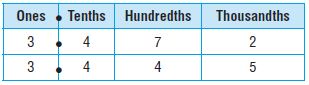

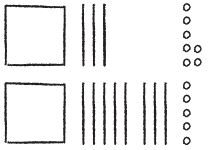


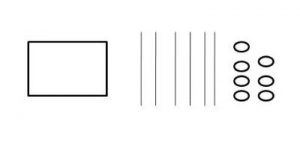






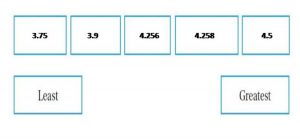
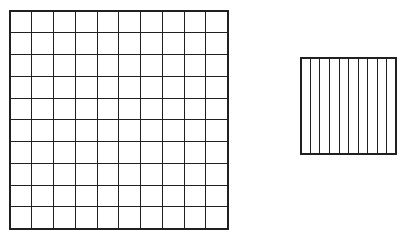
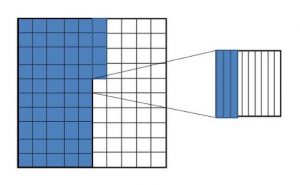
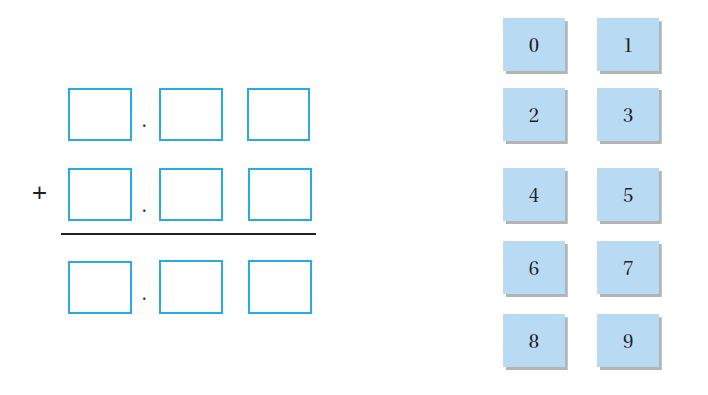
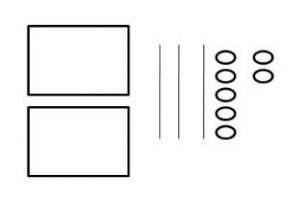


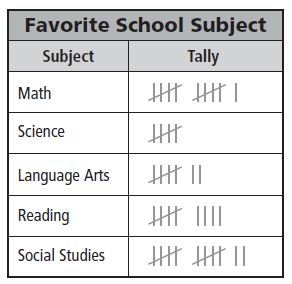
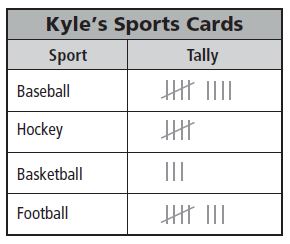

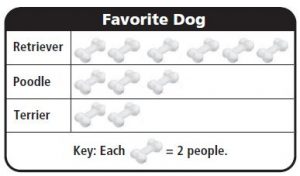
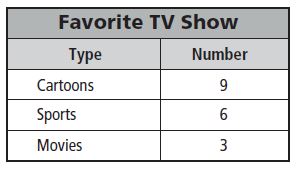



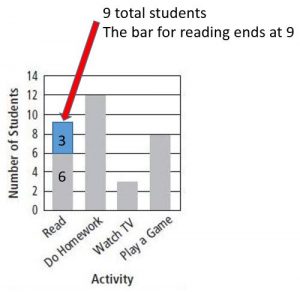
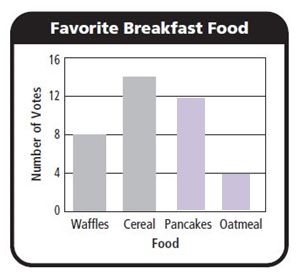
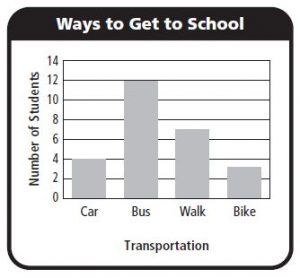
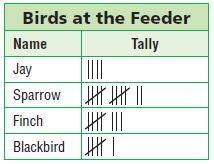
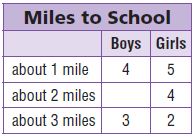
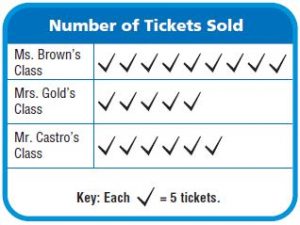
 class than
class than  class.
class.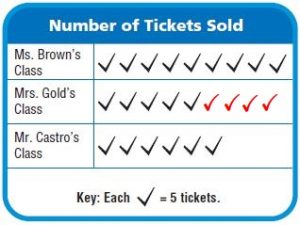
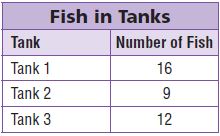


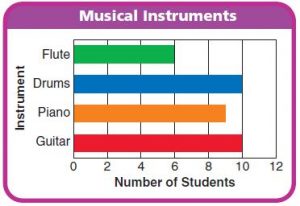
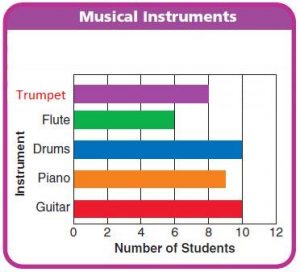
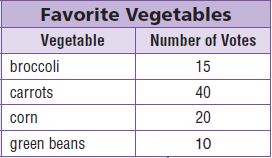
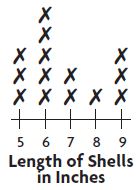










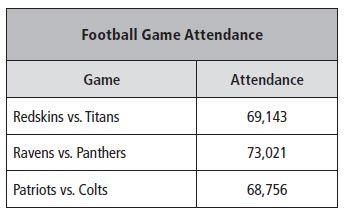













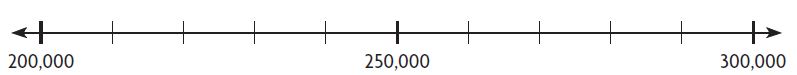
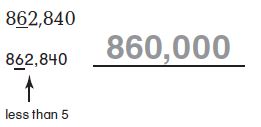















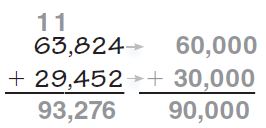

















 1,000 less than 14,576.
1,000 less than 14,576.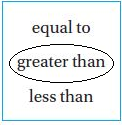 1,000 less than 14,576.
1,000 less than 14,576.








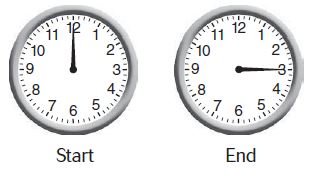
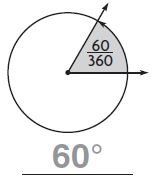
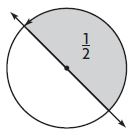
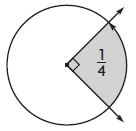
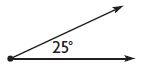






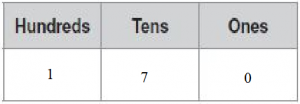
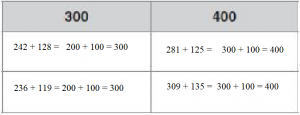
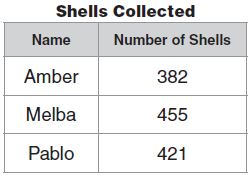
 Property of Addition describes the number sentence 17 + 1 = 1 + 17.
Property of Addition describes the number sentence 17 + 1 = 1 + 17. Property of Addition describes the number sentence 17 + 1 = 1 + 17.
Property of Addition describes the number sentence 17 + 1 = 1 + 17.