Prasanna

Engage NY Eureka Math 3rd Grade Module 5 Lesson 20 Answer Key

Eureka Math Grade 3 Module 5 Lesson 20 Pattern Sheet Answer Key

Multiply.

Answer :

Explanation :
Here we see the seven table
7 × 1 = 7
7 × 2 = 14
7 × 3 = 21
7 × 4 = 28
7 × 5 = 35

Eureka Math Grade 3 Module 5 Lesson 20 Problem Set Answer Key

Question 1.
Label what fraction of each shape is shaded. Then, circle the fractions that are equal.

Answer :

Explanation :
The Fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
fraction of each shape shaded are written and the fractions which are same are circled as shown in the above figure .

Question 2.
Label the shaded fraction. Draw 2 different representations of the same fractional amount.

Answer :

Explanation :
In figure a the Fraction of shaded = \(\frac{1}{4}\) the same fraction is represented with a circle divided into 4 equal parts and 1 part is shaded
In figure b the Fraction of shaded = \(\frac{1}{7}\) the same fraction is represented with a Rectangle which is divided into 7 equal parts and 1 part is shaded .

Question 3.
Ann has 6 small square pieces of paper. 2 squares are grey. Ann cuts the 2 grey squares in half with a diagonal line from one corner to the other.

a. What shapes does she have now?
b. How many of each shape does she have?
c. Use all the shapes with no overlaps. Draw at least 2 different ways Ann’s set of shapes might look. What fraction of the figure is grey?
Answer :

a. The shapes does she have now is Triangles and Squares.
b. 4 Triangles and 4 Squares .
c.
Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
Fraction = \(\frac{2}{6}\) .

Question 4.
Laura has 2 different beakers that hold exactly 1 liter. She pours \(\frac{1}{2}\) liter of blue liquid into Beaker A. She pours \(\frac{1}{2}\) liter of orange liquid into Beaker B. Susan says the amounts are not equal. Cristina says they are. Explain who you think is correct and why.

Answer :
Cristine is Correct .
Explanation :
Here the Breaker A contains Blue Liquid of \(\frac{1}{2}\) liter
Breaker B contains Orange liquid of \(\frac{1}{2}\) liter .
Whatever may be the shapes of the breaker but both the Amount of Quantities are same .
Where as , Susan Comparing the breakers Shape and saying the quantities are different . But she is Wrong .

Eureka Math Grade 3 Module 5 Lesson 20 Exit Ticket Answer Key

Question 1.
Label what fraction of the figure is shaded. Then, circle the fractions that are equal.

Answer :

Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .

Question 2.
Label the shaded fraction. Draw 2 different representations of the same fractional amount.

Answer :
Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
The figure a has shaded fraction = \(\frac{5}{11}\)
The fraction is represented with 2 different shapes . The first is a small rectangular strip with 11 parts and 5 parts are shaded and another figure is Longer rectangular strip with 11 parts and 5 parts are shaded .
The figure b has shaded fraction = \(\frac{2}{10}\)
The fraction is represented with 2 different shapes . The first is a small rectangular strip with 10 parts and 2 parts are shaded and another figure is star shape with 10 parts of Triangles and 2 parts are shaded .

Eureka Math Grade 3 Module 5 Lesson 20 Homework Answer Key

Question 1.
Label the shaded fraction. Draw 2 different representations of the same fractional amount.

Answer :

Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
The figure a has shaded fraction = \(\frac{3}{7}\)
The fraction is represented with 2 different shapes . The first is a Triangular strip with 7 parts and 3 parts are shaded and another figure is rectangular strip with 7 parts and 3 parts are shaded .

Question 2.
These two shapes both show \(\frac{4}{5}\).

a. Are the shapes equivalent? Why or why not?
b. Draw two different representations of \(\frac{4}{5}\) that are equivalent.
Answer :
a. No, The Shapes are not Equivalent , Both the shapes are \(\frac{4}{5}\) units but both the shapes are different .
b.

Explanation :
2 Different shapes of \(\frac{4}{5}\) units are represented in the above figure .

Question 3.
Diana ran a quarter mile straight down the street. Becky ran a quarter mile on a track. Who ran more? Explain your thinking.

Answer :
If the length of the down street and the track is same then
Diana and Becky both ran Quarter that means both ran same length .
Whereas if the length of the down street and the track is different , Then length of the Quarter will be different then both Ran different miles . The one who ran more can be known by if the length of the down street and track mile if given .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 22 Answer Key

Eureka Math Grade 3 Module 5 Lesson 22 Problem Set Answer Key

Write the shaded fraction of each figure on the blank. Then, draw a line to match the equivalent fractions.

Answer :

Explanations :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
All the fractions are written and the respective fractions are matched .

Question 2.
Write the missing parts of the fractions.

Answer :

Explanations :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
The Shaded fractions are written .

Question 3.
Why does it take 2 copies of \(\frac{1}{8}\) to show the same amount as 1 copy of \(\frac{1}{4}\)? Explain your answer in words and pictures.
Answer :

Explanation :
Because, the parts in 1/8 is doubled than 1/4, so, we need to double the copies.
Since, by the Above diagram,

Thus, the parts in 1/8 is doubled than 1/4, so, we need to double the copies.

Question 4.
How many sixths does it take to make the same amount as \(\frac{1}{3}\) ? Explain your answer in words and pictures.
Answer :

Explanation :
The Rectangular strip is divided into 3 parts and 6 parts . The first strip is marked \(\frac{1}{3}\) and the second is marked \(\frac{2}{6}\) which means \(\frac{1}{3}\) is equal to \(\frac{2}{6}\).
It takes two one-sixths to make a third.

Question 5.
Why does it take 10 copies of 1 sixth to make the same amount as 5 copies of 1 third? Explain your answer in words and pictures.
Answer :

Explanation :
The Sixths have as many as units as thirds .
So, \(\frac{10}{6}\) are as equal as \(\frac{5}{3}\) copies as shown in above figure .

Eureka Math Grade 3 Module 5 Lesson 22 Exit Ticket Answer Key

Question 1.
Draw and label two models that show equivalent fractions.
Answer :

Explanation :
From The above figure we notice
The First rectangular strip is divided into 2 equal parts and fraction shaded is \(\frac{1}{2}\) .
The Second rectangular strip is divided into 6 equal parts and the fraction shaded is \(\frac{3}{6}\) .
Both show the equivalent fraction \(\frac{1}{2}\) = \(\frac{3}{6}\) .

Question 2.
Draw a number line that proves your thinking about Problem 1.
Answer :

Explanation :
The number is represented for the above equivalent Fraction \(\frac{1}{2}\) = \(\frac{3}{6}\) .

Eureka Math Grade 3 Module 5 Lesson 22 Homework Answer Key

Question 1.
Write the shaded fraction of each figure on the blank. Then, draw a line to match the equivalent fractions.

Answer :

Explanation :
The fraction of shaded parts = Number of shaded parts ÷ Total Number of Parts .
All the fractions are written and the respective fractions are matched .

Question 2.
Complete the fractions to make true statements.
Answer :
Answer :

Explanation :
The Figures are divided into double and the shaded Fractions are compared .

Question 3.
Why does it take 3 copies of \(\frac{1}{6}\) to show the same amount as 1 copy of \(\frac{1}{2}\)? Explain your answer in words and pictures.
Answer :

Explanation :
The Two tape Diagram Shows 3 copies of \(\frac{3}{6}\) is the same length as 1 copy of \(\frac{1}{2}\) .

Question 4.
How many ninths does it take to make the same amount as \(\frac{1}{3}\)? Explain your answer in words and pictures.
Answer :

Explanation :
The Two tape Diagram Shows 3 ninths ( \(\frac{3}{9}\)) is the same length as 1Thirds (\(\frac{1}{3}\)) .

Question 5.
A pie was cut into 8 equal slices. If Ruben ate \(\frac{3}{4}\) of the pie, how many slices did he eat? Explain your answer using a number line and words.
Answer :

Explanation :
\(\frac{3}{4}\) is the same length as \(\frac{6}{8}\)
Ruben ate 6 slices which is \(\frac{6}{8}\) = \(\frac{3}{4}\).

Engage NY Eureka Math 3rd Grade Module 5 Lesson 23 Answer Key

Eureka Math Grade 3 Module 5 Lesson 23 Sprint Answer Key

A
Add by Six

Question 1.
0 + 6 =

Question 2.
1 + 6 =

Question 3.
2 + 6 =

Question 4.
3 + 6 =

Question 5.
4 + 6 =

Question 6.
6 + 4 =

Question 7.
6 + 3 =

Question 8.
6 + 2 =

Question 9.
6 + 1 =

Question 10.
6 + 0 =

Question 11.
15 + 6 =

Question 12.
25 + 6 =

Question 13.
35 + 6 =

Question 14.
45 + 6 =

Question 15.
55 + 6 =

Question 16.
85 + 6 =

Question 17.
6 + 6 =

Question 18.
16 + 6 =

Question 19.
26 + 6 =

Question 20.
36 + 6 =

Question 21.
46 + 6 =

Question 22.
76 + 6 =

Question 23.
7 + 6 =

Question 24.
17 + 6 =

Question 25.
27 + 6 =

Question 26.
37 + 6 =

Question 27.
47 + 6 =

Question 28.
77 + 6 =

Question 29.
8 + 6 =

Question 30.
18 + 6 =

Question 31.
28 + 6 =

Question 32.
38 + 6 =

Question 33.
48 + 6 =

Question 34.
78 + 6 =

Question 35.
9 + 6 =

Question 36.
19 + 6 =

Question 37.
29 + 6 =

Question 38.
39 + 6 =

Question 39.
89 + 6 =

Question 40.
6 + 75 =

Question 41.
6 + 56 =

Question 42.
6 + 77 =

Question 43.
6 + 88 =

Question 44.
6 + 99 =

B
Add by Six

Question 1.
6 + 0 =

Question 2.
6 + 1 =

Question 3.
6 + 2 =

Question 4.
6 + 3 =

Question 5.
6 + 4 =

Question 6.
4 + 6 =

Question 7.
3 + 6 =

Question 8.
2 + 6 =

Question 9.
1 + 6 =

Question 10.
0 + 6 =

Question 11.
5 + 6 =

Question 12.
15 + 6 =

Question 13.
25 + 6 =

Question 14.
35 + 6 =

Question 15.
45 + 6 =

Question 16.
75 + 6 =

Question 17.
6 + 6 =

Question 18.
16 + 6 =

Question 19.
26 + 6 =

Question 20.
36 + 6 =

Question 21.
46 + 6 =

Question 22.
86 + 6 =

Question 23.
7 + 6 =

Question 24.
17 + 6 =

Question 25.
27 + 6 =

Question 26.
37 + 6 =

Question 27.
47 + 6 =

Question 28.
67 + 6 =

Question 29.
8 + 6 =

Question 30.
18 + 6 =

Question 31.
28 + 6 =

Question 32.
38 + 6 =

Question 33.
48 + 6 =

Question 34.
88 + 6 =

Question 35.
9 + 6 =

Question 36.
19 + 6 =

Question 37.
29 + 6 =

Question 38.
39 + 6 =

Question 39.
79 + 6 =

Question 40.
6 + 55 =

Question 41.
6 + 76 =

Question 42.
6 + 57 =

Question 43.
6 + 98 =

Question 44.
6 + 89 =

Eureka Math Grade 3 Module 5 Lesson 23 Problem Set Answer Key

Question 1.
On the number line above, use a red colored pencil to divide each whole into fourths, and label each fraction above the line. Use a fraction strip to help you estimate, if necessary.
Answer :

Question 2.
On the number line above, use a blue colored pencil to divide each whole into eighths, and label each fraction below the line. Refold your fraction strip from Problem 1 to help you estimate.
Answer :

Question 3.
List the fractions that name the same place on the number line.
Answer :
The Fractions that have same place on the number line are
\(\frac{1}{4}\) = \(\frac{2}{8}\)
\(\frac{2}{4}\) = \(\frac{4}{8}\)
\(\frac{3}{4}\) = \(\frac{6}{8}\)
\(\frac{4}{4}\) = \(\frac{8}{8}\)
\(\frac{5}{4}\) = \(\frac{10}{8}\)
\(\frac{6}{4}\) = \(\frac{12}{8}\)
\(\frac{7}{4}\) = \(\frac{14}{8}\)
\(\frac{8}{4}\) = \(\frac{16}{8}\)
\(\frac{9}{4}\) = \(\frac{18}{8}\)
\(\frac{10}{4}\) = \(\frac{20}{8}\)
\(\frac{11}{4}\) = \(\frac{22}{8}\)
\(\frac{12}{4}\) = \(\frac{24}{8}\)

Question 4.
Using your number line to help, what red fraction and what blue fraction would be equal to \(\frac{7}{2}\)? Draw the part of the number line below that would include these fractions, and label it.
Answer :
\(\frac{7}{2}\) = \(\frac{14}{4}\) = \(\frac{28}{8}\).

Question 5.
Write two different fractions for the dot on the number line. You may use halves, thirds, fourths, fifths, sixths, or eighths. Use fraction strips to help you, if necessary.

_____________ = _____________

_____________ = _____________

_____________ = _____________
Answer :

Explanation :
The given 1 st number line is divided into 3 parts that means it can be partitioned into thirds and sixths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{2}{6}\) = \(\frac{1}{3}\) .
The given 2nd number line is divided into 4 parts that means it can be partitioned intoFourths and Eighths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{2}{4}\) = \(\frac{4}{8}\) .

Question 6.
Cameron and Terrance plan to run in the city race on Saturday. Cameron has decided that he will divide his race into 3 equal parts and will stop to rest after running 2 of them. Terrance divides his race into 6 equal parts and will stop and rest after running 2 of them. Will the boys rest at the same spot in the race? Why or why not? Draw a number line to explain your answer.
Answer :
No, they don’t spot in the same place .

Explanation :
The number line is divided into thirds and sixths .
The Cameron partitioned the race into 3 parts and fraction values are written below the number line .
The Cameron stop and rest after running 2 of them = \(\frac{2}{3}\) .
The Terrance partitioned the race into 6 parts and fraction values are written above the number line .
The Terrance stop and rest after running 2 of them = \(\frac{2}{6}\) .
That means they don’t spot the same place for rest .

Question 7.
Henry and Maddie were in a pie-eating contest. The pies were cut either into thirds or sixths. Henry picked up a pie cut into sixths and ate \(\frac{4}{6}\) of it in 1 minute. Maddie picked up a pie cut into thirds. What fraction of her pie does Maddie have to eat in 1 minute to tie with Henry? Draw a number line, and use words to explain your answer.
Answer :

Explanation :
Henry pie is cut in sixths.
Number of of pies ate by henry in 1 minute= \(\frac{4}{6}\)
Maddie pie cut in thirds.
Number of of pies ate by Maddie in 1 minute= ?
For tie Maddie should eat same quantity as Henry that means the point \(\frac{4}{6}\) is marked says number of pies Maddie should eat in thirds .
Number of of pies ate by Maddie in 1 minute=\(\frac{2}{3}\) .

Eureka Math Grade 3 Module 5 Lesson 23 Homework Answer Key

Question 1.
On the number line above, use a colored pencil to divide each whole into thirds and label each fraction above the line.
Answer :

Explanation :
Number line from 0 to 3 is partitioned into thirds . and all the fraction values are written above the number line .

Question 2.
On the number line above, use a different colored pencil to divide each whole into sixths and label each fraction below the line.
Answer :

Explanation :
Number line from 0 to 3 is partitioned into sixths . and all the fraction values are written below the number line .

Question 3.
Write the fractions that name the same place on the number line.
Answer :
The Fractions that have same place on the number line are
\(\frac{1}{3}\) = \(\frac{2}{6}\)
\(\frac{2}{3}\) = \(\frac{4}{6}\)
\(\frac{3}{3}\) = \(\frac{6}{6}\)
\(\frac{4}{3}\) = \(\frac{8}{6}\)
\(\frac{5}{3}\) = \(\frac{10}{6}\)
\(\frac{6}{3}\) = \(\frac{12}{6}\)
\(\frac{7}{3}\) = \(\frac{14}{6}\)
\(\frac{8}{3}\) = \(\frac{16}{6}\)
\(\frac{9}{3}\) = \(\frac{18}{6}\)

Question 4.
Using your number line to help, name the fraction equivalent to \(\frac{20}{6}\). Name the fraction equivalent to \(\frac{12}{3}\). Draw the part of the number line that would include these fractions below, and label it.

Answer :

Explanation :
Number line is partitioned from 3 to 4 into thirds and sixths and all the thirds fraction values are written above number line and  sixths fraction values are written below the number line .
We notice \(\frac{20}{6}\) = \(\frac{10}{3}\) and \(\frac{12}{3}\) = \(\frac{24}{6}\) .

Question 5.
Write two different fraction names for the dot on the number line. You may use halves, thirds, fourths, fifths, sixths, eighths, or tenths.

Answer :

Explanation :
The given 1 st number line is divided into 3 parts that means it can be partitioned into thirds and sixths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{4}{6}\) = \(\frac{2}{3}\) .
The given 2nd number line is divided into 4 parts that means it can be partitioned into Fourths and Eighths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{2}{8}\) = \(\frac{1}{4}\) .
The given 3rd number line is divided into 4 parts that means it can be partitioned into Fourths and Eighths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{7}{4}\) = \(\frac{14}{8}\) .
The given 4th number line is divided into 5 parts that means it can be partitioned into fifths and tenths .
All fraction numbers are written and at a given point we notice the fraction value is \(\frac{7}{5}\) = \(\frac{14}{10}\) .

Question 6.
Danielle and Mandy each ordered a large pizza for dinner. Danielle’s pizza was cut into sixths, and Mandy’s pizza was cut into twelfths. Danielle ate 2 sixths of her pizza. If Mandy wants to eat the same amount of pizza as Danielle, how many slices of pizza will she have to eat? Write the answer as a fraction. Draw a number line to explain your answer.
Answer :

Explanation :
Danielle pizza is cut in sixths.
Number of pizza pieces ate by Danielle = \(\frac{2}{6}\)
Mandy pizza cut in twelfths.
Number of pizza pieces ate by Mandy= ?
For same Quantity Mandy should eat same quantity as Danielle that means the point \(\frac{2}{6}\) is marked says number of pizza pieces Mandy should eat in twelfths .
Number of pizza pieces should eat by mandy =\(\frac{4}{12}\) .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 24 Answer Key

Eureka Math Grade 3 Module 5 Lesson 24 Sprint Answer Key

A
Add by Seven

Question 1.
0 + 7 =
Answer :
0 + 7 = 7
Explanation :

Question 2.
1 + 7 =
Answer :
1 + 7 = 8
Explanation :

Question 3.
2 + 7 =
Answer :
2 + 7 = 9
Explanation :

Question 4.
3 + 7 =
Answer :
3 + 7 = 10
Explanation :

Question 5.
7 + 3 =
Answer :
7 + 3 = 10
Explanation :

Question 6.
7 + 2 =
Answer :
7 + 2 = 9
Explanation :

Question 7.
7 + 1 =
Answer :
7 + 1 = 8

Question 8.
7 + 0 =
Answer :
7 + 0 = 7

Question 9.
4 + 7 =
Answer :
4 + 7 = 11

Explanation :

Question 10.
14 + 7 =
Answer :
14 + 7 = 21

Explanation :

Question 11.
24 + 7 =
Answer :
24 + 7 = 31

Explanation :

Question 12.
34 + 7 =
Answer :
34 + 7 = 41

Explanation :

Question 13.
44 + 7 =
Answer :
44 + 7 = 51

Explanation :

Question 14.
84 + 7 =
Answer :
84 + 7 = 91

Explanation :

Question 15.
64 + 7 =
Answer :
64 + 7 = 71

Explanation :

Question 16.
5 + 7 =
Answer :
5 + 7 = 12

Explanation :

Question 17.
15 + 7 =
Answer :
15 + 7 = 22

Explanation :

Question 18.
25 + 7 =
Answer :
25 + 7 = 32

Explanation :

Question 19.
35 + 7 =
Answer :
35 + 7 = 42

Explanation :

Question 20.
45 + 7 =
Answer :
45 + 7 = 52

Explanation :

Question 21.
75 + 7 =
Answer :
75 + 7 = 82

Explanation :

Question 22.
55 + 7 =
Answer :
55 + 7 = 62

Explanation :

Question23.
6 + 7 =

Question 24.
16 + 7 =
Answer :
16 + 7 = 23

Explanation :

Question 25.
26 + 7 =
Answer :
26 + 7 = 33

Explanation :

Question 26.
36 + 7 =
Answer :
36 + 7 = 43

Explanation :

Question 27.
46 + 7 =
Answer :
46 + 7 = 53

Explanation :

Question 28.
66 + 7 =
Answer :
66 + 7 = 73

Explanation :

Question 29.
7 + 7 =
Answer :
7 + 7 = 14

Question 30.
17 + 7 =
Answer :
17 + 7 = 24

Explanation :

Question 31.
27 + 7 =
Answer :
27 + 7 = 34

Explanation :

Question 32.
37 + 7 =
Answer :
37 + 7 = 44

Explanation :

Question 33.
87 + 7 =
Answer :
87 + 7 = 94

Explanation :

Question 34.
8 + 7 =
Answer :
8 + 7 = 15

Question 35.
18 + 7 =
Answer :
18 + 7 = 25
Explanation :

Question 36.
28 + 7 =
Answer :
28 + 7 = 35

Explanation :

Question 37.
38 + 7 =
Answer :
38 + 7 = 45
Explanation :

Question 38.
78 + 7 =
Answer :
78 + 7 = 85

Explanation :

Question 39.
9 + 7 =
Answer :
9 + 7 =
Answer :
9 + 7 =  16

Question 40.
19 + 7 =
Answer :
19 + 7 = 26
Explanation :

Question 41.
29 + 7 =
Answer :
29 + 7 = 36

Explanation :

Question 42.
39 + 7 =
Answer :
39 + 7 = 46

Explanation :

Question 43.
49 + 7 =
Answer :
49 + 7 = 56
Explanation :

Question 44.
79 + 7 =
Answer :
79 + 7 = 86

Explanation :

B
Add by Seven

Question 1.
7 + 0 =
Answer :
7 + 0 = 7

Question 2.
7 + 1 =
Answer :
7 + 1 = 8

Question 3.
7 + 2 =
Answer :
7 + 2 = 9

Question 4.
7 + 3 =
Answer :
7 + 3 = 10

Question 5.
3 + 7 =
Answer :
3 + 7 = 10

Question 6.
2 + 7 =
Answer :
2 + 7 = 9

Question 7.
1 + 7 =
Answer :
1 + 7 = 8

Question 8.
0 + 7 =
Answer :
0 + 7 = 7

Question 9.
4 + 7 =
Answer :
4 + 7 = 11

Question 10.
14 + 7 =
Answer :
14 + 7 = 21

Question 11.
24 + 7 =
Answer :
24 + 7 = 31

Question 12.
34 + 7 =
Answer :
34 + 7 = 41

Question 13.
44 + 7 =
Answer :
44 + 7 = 51

Question 14.
74 + 7 =
Answer :
74 + 7 = 81

Question 15.
54 + 7 =
Answer :
54 + 7 = 61

Question 16.
5 + 7 =
Answer :
5 + 7 = 12

Question 17.
15 + 7 =
Answer :
15 + 7 = 22

Question 18.
25 + 7 =
Answer :
25 + 7 = 32

Question 19.
35 + 7 =
Answer :
35 + 7 = 42

Question 20.
45 + 7 =
Answer :
45 + 7 = 52

Question 21.
85 + 7 =
Answer :
85 + 7 = 92

Question 22.
65 + 7 =
Answer :
65 + 7 = 72

Question 23.
6 + 7 =
Answer :
6 + 7 = 13

Question 24.
16 + 7 =
Answer :
16 + 7 = 23

Question 25.
26 + 7 =
Answer :
26 + 7 = 33

Question 26.
36 + 7 =
Answer :
36 + 7 = 43

Question 27.
46 + 7 =
Answer :
46 + 7 = 53

Question 28.
76 + 7 =
Answer :
76 + 7 = 83

Question 29.
7 + 7 =
Answer :
7 + 7 = 14

Question 30.
17 + 7 =
Answer :
17 + 7 = 24

Question 31.
27 + 7 =
Answer :
27 + 7 = 34

Question 32.
37 + 7 =
Answer :
37 + 7 = 44

Question 33.
67 + 7 =
Answer :
67 + 7 = 74

Question 34.
8 + 7 =
Answer :
8 + 7 = 15

Question 35.
18 + 7 =
Answer :
18 + 7 = 25

Question 36.
28 + 7 =
Answer :
28 + 7 = 35

Question 37.
38 + 7 =
Answer :
38 + 7 = 45

Question 38.
88 + 7 =
Answer :
88 + 7 = 95

Question 39.
9 + 7 =
Answer :
9 + 7 = 16

Question 40.
19 + 7 =
Answer :
19 + 7 = 26

Question 41.
29 + 7 =
Answer :
29 + 7 = 36

Question 42.
39 + 7 =
Answer :
39 + 7 = 46

Question 43.
49 + 7 =
Answer :
49 + 7 = 56

Question 44.
89 + 7 =
Answer :
89 + 7 = 96

Eureka Math Grade 3 Module 5 Lesson 24 Problem Set Answer Key

Question 1.
Complete the number bond as indicated by the fractional unit. Partition the number line into the given fractional unit, and label the fractions. Rename 0 and 1 as fractions of the given unit. The first one is done for you.

Answer :

Explanation :
The number line is divided into halves , thirds , Fourths and fifths and respective number bond is represented in the above figure .
Thirds: Number bond showing 3 units of \(\frac{1}{3}\) ; number line partitioned and labeled from 0 to 1
Fourths: Number bond showing 4 units of \(\frac{1}{4}\) ;number line partitioned and labeled from 0 to 1
Fifths: Number bond showing 5 units of \(\frac{1}{5}\) ; number line partitioned and labeled from 0 to 1

Question 2.
Circle all the fractions in Problem 1 that are equal to 1. Write them in a number sentence below.

Answer :

Question 3.
What pattern do you notice in the fractions that are equivalent to 1?
Answer :
The fractions that are equivalent to 1 have The Numerator and the Denominator same .

Question 4.
Taylor took his little brother to get pizza. Each boy ordered a small pizza. Taylor’s pizza was cut in fourths, and his brother’s was cut in thirds. After they had both eaten all of their pizza, Taylor’s little brother said, “Hey that was no fair! You got more than me! You got 4 pieces, and I only got 3.”
Should Taylor’s little brother be mad? What could you say to explain the situation to him? Use words, pictures, or a number line.
Answer :

Explanation :
The Taylor’s pizza and His brother pizza ordered small size pizza. Both the pizza’s are of same length.
The Taylor’s pizza is divided into fourths that means into 4 parts.
His Brother’s pizza is divided into thirds that means into 3 parts.
The slice of Taylor’s pizza is smaller than compared to his brother’s pizza .
The size doesn’t depends on the number of slices .

Eureka Math Grade 3 Module 5 Lesson 24 Exit Ticket Answer Key

Question 1.
Complete the number bond as indicated by the fractional unit. Partition the number line into the given fractional unit, and label the fractions. Rename 0 and 1 as fractions of the given unit.

Answer :

Explanation :
Fourths: Number bond showing 4 units of \(\frac{1}{4}\) ; number line partitioned and labeled from 0 to 1

Question 2.
How many copies of \(\frac{1}{4}\) does it take to make 1 whole? What’s the fraction for 1 whole in this case? Use the number line or the number bond in Problem 1 to help you explain.
Answer :
Fourths: Number bond showing 4 units of \(\frac{1}{4}\) ; number line partitioned and labeled from 0 to 1 in the above figure .
For 1 whole we notice \(\frac{4}{4}\) Fraction in the figure that means we require 4 \(\frac{1}{4}\) copies to make 1 Whole .

Eureka Math Grade 3 Module 5 Lesson 24 Homework Answer Key

Question 1.
Complete the number bond as indicated by the fractional unit. Partition the number line into the given fractional unit, and label the fractions. Rename 0 and 1 as fractions of the given unit.

Answer :

Explanation :
The number line is divided into fifths, Sixths, Sevenths and Eighths and respective number bond is represented in the above figure .
Fifths: Number bond showing 5 units of \(\frac{1}{5}\) ; number line partitioned and labeled from 0 to 1
Sixths: Number bond showing 6 units of \(\frac{1}{6}\) ; number line partitioned and labeled from 0 to 1
Seventhss: Number bond showing 7 units of \(\frac{1}{7}\) ;number line partitioned and labeled from 0 to 1
Eigths: Number bond showing 8 units of \(\frac{1}{8}\) ; number line partitioned and labeled from 0 to 1

Question 2.
Circle all the fractions in Problem 1 that are equal to 1. Write them in a number sentence below.

Answer :
\(\frac{5}{5}\) = \(\frac{6}{6}\) = \(\frac{7}{7}\) = \(\frac{8}{8}\) .

Question 3.
What pattern do you notice in the fractions that are equivalent to 1? Following this pattern, how would you represent ninths as 1 whole?
Answer :
The Fractions that are equivalent to 1 follow the pattern have Numerator and Denominator Equal .
To represent Ninths are 1 whole = \(\frac{9}{9}\) .

Question 4.
In Art class, Mr. Joselyn gave everyone a 1-foot stick to measure and cut. Vivian measured and cut her stick into 5 equal pieces. Scott measured and cut his into 7 equal pieces. Scott said to Vivian, “The total length of my stick is longer than yours because I have 7 pieces, and you only have 5.” Is Scott correct? Use words, pictures, or a number line to help you explain.
Answer :

Explanation :
Scott is wrong , Even though he has more pieces than Vivian Both the Lengths of Sticks = 1 foot .
Scott pieces are smaller because his stick is broken into more pieces .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 25 Answer Key

Eureka Math Grade 3 Module 5 Lesson 25 Problem Set Answer Key

A
Subtract by Six

Question 1.
16 – 6 =

Question 2.
6 – 6 =

Question 3.
26 – 6 =

Question 4.
7 – 6 =

Question 5.
17 – 6 =

Question 6.
37 – 6 =

Question 7.
8 – 6 =

Question 8.
18 – 6 =

Question 9.
48 – 6 =

Question 10.
9 – 6 =

Question 11.
19 – 6 =

Question 12.
59 – 6 =

Question 13.
10 – 6 =

Question 14.
20 – 6 =

Question 15.
70 – 6 =

Question 16.
11 – 6 =

Question 17.
21 – 6 =

Question 18.
81 – 6 =

Question 19.
12 – 6 =

Question 20.
22 – 6 =

Question 21.
82 – 6 =

Question 22.
13 – 6 =

Question 23.
23 – 6 =

Question 24.
33 – 6 =

Question 25.
63 – 6 =

Question 26.
83 – 6 =

Question 27.
14 – 6 =

Question 28.
24 – 6 =

Question 29.
34 – 6 =

Question 30.
74 – 6 =

Question 31.
54 – 6 =

Question 32.
15 – 6 =

Question 33.
25 – 6 =

Question 34.
35 – 6 =

Question 35.
85 – 6 =

Question 36.
65 – 6 =

Question 37.
90 – 6 =

Question 38.
53 – 6 =

Question 39.
42 – 6 =

Question 40.
71 – 6 =

Question 41.
74 – 6 =

Question 42.
95 – 6 =

Question 43.
51 – 6 =

Question 44.
92 – 6 =

B
Subtract by Six

Question 1.
6 – 6 =

Question 2.
16 – 6 =

Question 3.
26 – 6 =

Question 4.
7 – 6 =

Question 5.
17 – 6 =

Question 6.
67 – 6 =

Question 7.
8 – 6 =

Question 8.
18 – 6 =

Question 9.
78 – 6 =

Question 10.
9 – 6 =

Question 11.
19 – 6 =

Question 12.
89 – 6 =

Question 13.
10 – 6 =

Question 14.
20 – 6 =

Question 15.
90 – 6 =

Question 16.
11 – 6 =

Question 17.
21 – 6 =

Question 18.
41 – 6 =

Question 19.
12 – 6 =

Question 20.
22 – 6 =

Question 21.
42 – 6 =

Question 22.
13 – 6 =

Question 23.
23 – 6 =

Question 24.
33 – 6 =

Question 25.
53 – 6 =

Question 26.
73 – 6 =

Question 27.
14 – 6 =

Question 28.
24 – 6 =

Question 29.
34 – 6 =

Question 30.
64 – 6 =

Question 31.
44 – 6 =

Question 32.
15 – 6 =

Question 33.
25 – 6 =

Question 34.
35 – 6 =

Question 35.
75 – 6 =

Question 36.
55 – 6 =

Question 37.
70 – 6 =

Question 38.
63 – 6 =

Question 39.
52 – 6 =

Question 40.
81 – 6 =

Question 41.
64 – 6 =

Question 42.
85 – 6 =

Question 43.
91 – 6 =

Question 44.
52 – 6 =

Eureka Math Grade 3 Module 5 Lesson 25 Problem Set Answer Key

Question 1.
Label the following models as a fraction inside the dotted box. The first one has been done for you.

Answer :

Explanation :
\(\frac{4}{1}\) means it is 4 whole . ( you have 4 copies of 1 whole ).
\(\frac{4}{4}\) means you have 1 whole . ( you have 4 copies of \(\frac{1}{4}\) ) .
\(\frac{4}{2}\) means you have 2 whole .( you have 4 copies of \(\frac{1}{2}\) ) .
and similar for others .

Question 2.
Fill in the missing whole numbers in the boxes below the number line. Rename the whole numbers as fractions in the boxes above the number line.

Answer :

Question 3.
Explain the difference between these two fractions with words and pictures.

Answer :

Explanation :
\(\frac{2}{1}\) means it is 2 whole . ( you have 2 copies of 1 whole ).
\(\frac{2}{2}\) means you have 1 whole . ( you have 2 copies of \(\frac{1}{2}\) ) .

Eureka Math Grade 3 Module 5 Lesson 25 Exit Ticket Answer Key

Question 1.
Label the model as a fraction inside the box.

Answer :

Question 2.
Partition the wholes into thirds. Rename the fraction for 3 wholes. Use the number line and words to explain your answer.

Answer :

Explanation :
Number line partitioned into thirds; fraction for 3 wholes renamed as \(\frac{9}{3}\)

Eureka Math Grade 3 Module 5 Lesson 25 Homework Answer Key

Question 1.
Label the following models as fractions inside the boxes.

Answer :

Explanation :
\(\frac{4}{1}\) means it is 4 whole . ( you have 4 copies of 1 whole ).
\(\frac{4}{4}\) means you have 1 whole . ( you have 4 copies of \(\frac{1}{4}\) ) .
\(\frac{4}{2}\) means you have 2 whole .( you have 4 copies of \(\frac{1}{2}\) ) .

\(\frac{8}{1}\) means it is 8 whole . ( you have 8 copies of 1 whole ).
\(\frac{8}{8}\) means you have 1 whole . ( you have 8 copies of \(\frac{1}{8}\) ) .
\(\frac{8}{2}\) means you have 2 whole .( you have 8 copies of \(\frac{1}{4}\) ) .

Fill in the missing whole numbers in the boxes below the number line. Rename the wholes as fractions in the boxes above the number line.

Answer :

Answer :
Number is represented from 0 to 12 and from 15 to 21 .the whole numbers are renamed in fraction form. All the missing whole numbers and fraction numbers are written .

Question 3.
Explain the difference between these fractions with words and pictures.

Answer :

Explanation :
\(\frac{5}{1}\) means it is 5 whole . ( you have 5 copies of 1 whole ).
\(\frac{5}{5}\) means you have 1 whole . ( you have 5 copies of \(\frac{1}{5}\) ) .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 26 Answer Key

Eureka Math Grade 3 Module 5 Lesson 26 Sprint Answer Key

A
Add by Eight

Question 1.
0 + 8 =

Question 2.
1 + 8 =

Question 3.
2 + 8 =

Question 4.
8 + 2 =

Question 5.
1 + 8 =

Question 6.
0 + 8 =

Question 7.
3 + 8 =

Question 8.
13 + 8 =

Question 9.
23 + 8 =

Question 10.
33 + 8 =

Question 11.
43 + 8 =

Question 12.
83 + 8 =

Question 13.
4 + 8 =

Question 14.
14 + 8 =

Question 15.
24 + 8 =

Question 16.
34 + 8 =

Question 17.
44 + 8 =

Question 18.
74 + 8 =

Question 19.
5 + 8 =

Question 20.
15 + 8 =

Question 21.
25 + 8 =

Question 22.
35 + 8 =

Question 23.
65 + 8 =

Question 24.
6 + 8 =

Question 25.
16 + 8 =

Question 26.
26 + 8 =

Question 27.
36 + 8 =

Question 28.
86 + 8 =

Question 29.
46 + 8 =

Question 30.
7 + 8 =

Question 31.
17 + 8 =

Question 32.
27 + 8 =

Question 33.
37 + 8 =

Question 34.
77 + 8 =

Question 35.
8 + 8 =

Question 36.
18 + 8 =

Question 37.
28 + 8 =

Question 38.
38 + 8 =

Question 39.
68 + 8 =

Question 40.
9 + 8 =

Question 41.
19 + 8 =

Question 42.
29 + 8 =

Question 43.
39 + 8 =

Question 44.
89 + 8 =

B
Add by Eight

Question 1.
8 + 0 =

Question 2.
8 + 1 =

Question 3.
8 + 2 =

Question 4.
2 + 8 =

Question 5.
1 + 8 =

Question 6.
0 + 8 =

Question 7.
3 + 8 =

Question 8.
13 + 8 =

Question 9.
23 + 8 =

Question 10.
33 + 8 =

Question 11.
43 + 8 =

Question 12.
73 + 8 =

Question 13.
4 + 8 =

Question 14.
14 + 8 =

Question 15.
24 + 8 =

Question 16.
34 + 8 =

Question 17.
44 + 8 =

Question 18.
84 + 8 =

Question 19.
5 + 8 =

Question 20.
15 + 8 =

Question 21.
25 + 8 =

Question 22.
35 + 8 =

Question 23.
55 + 8 =

Question 24.
6 + 8 =

Question 25.
16 + 8 =

Question 26.
26 + 8 =

Question 27.
36 + 8 =

Question 28.
66 + 8 =

Question 29.
56 + 8 =

Question 30.
7 + 8 =

Question 31.
17 + 8 =

Question 32.
27 + 8 =

Question 33.
37 + 8 =

Question 34.
67 + 8 =

Question 35.
8 + 8 =

Question 36.
18 + 8 =

Question 37.
28 + 8 =

Question 38.
38 + 8 =

Question 39.
78 + 8 =

Question 40.
9 + 8 =

Question 41.
19 + 8 =

Question 42.
29 + 8 =

Question 43.
39 + 8 =

Question 44.
89 + 8 =

Eureka Math Grade 3 Module 5 Lesson 26 Problem Set Answer Key

Question 1.
Partition the number line to show the fractional units. Then, draw number bonds using copies of 1 whole for the circled whole numbers.

Answer :

Explanation :
The number line is divided into halves from 0 to 2 and whole numbers are represented in fraction form and number bond is completed .
The number line is divided into thirds from 2 to 4  and whole numbers are represented in fraction form and number bond is completed .

Question 2.
Write the fractions that name the whole numbers for each fractional unit. The first one has been done.

Answer :

Question 3.
Sammy uses \(\frac{1}{4}\) meter of wire each day to make things.
a. Draw a number line to represent 1 meter of wire. Partition the number line to represent how much Sammy uses each day. How many days does the wire last?
b. How many days will 3 meters of wire last?
Answer :
a.

Explanation :
Number line is partitioned into Fourths . Each day he does \(\frac{1}{4}\) . In four days he completes the 1 meter work .
b.
Each day he works \(\frac{1}{4}\).
In 4 days he completes 1 meter work .
For 3 meter work it takes 4 × 3 = 12 days .

Question 4.
Cindy feeds her dog \(\frac{1}{3}\) pound of food each day.
a. Draw a number line to represent 1 pound of food. Partition the number line to represent how much food she uses each day.
b. Draw another number line to represent 4 pounds of food. After 3 days, how many pounds of food has she given her dog?
c. After 6 days, how many pounds of food has she given her dog?
Answer :
a.

Explanation :
A number of 1 pound food is partitioned into thirds . Each day Cindy feeds her dog \(\frac{1}{3}\) pound of food . She can feed for 3 days of 1 pound food .
b.

Explanation
The Number Line is partitioned in thirds for 4 pounds of food .Each day Cindy feeds her dog \(\frac{1}{3}\) pound of food .After 3 days she feeds 1 pound of food to her dog  .
c.
After 6 days she feeds 2 pound of food to her dog .
For Every 3 days she completes 1 pound of food .

Eureka Math Grade 3 Module 5 Lesson 26 Exit Ticket Answer Key

Irene has 2 yards of fabric.
a. Draw a number line to represent the total length of Irene’s fabric.
b. Irene cuts her fabric into pieces of \(\frac{1}{5}\) yard in length. Partition the number line to show her cuts.
c. How many \(\frac{1}{5}\)-yard pieces does she cut altogether? Use number bonds with copies of wholes to help you explain.
Answer :

Explanation :
a. Number line drawn to represent 2 yards of fabric
b. Number line partitioned and labeled to show fifths
c. 10peices are cut al together ; number bond completed

Eureka Math Grade 3 Module 5 Lesson 26 Homework Answer Key

Question 1.
Partition the number line to show the fractional units. Then, draw number bonds with copies of 1 whole for the circled whole numbers.

Answer :

Explanation :
The number line is divided into sixths from 0 to 2 and whole numbers are represented in fraction form and number bond is completed .
The number line is divided into Fifths from 2 to 4  and whole numbers are represented in fraction form and number bond is completed .

Question 2.
Write the fractions that name the whole numbers for each fractional unit. The first one has been done for you.

Answer :

Question 3.
Rider dribbles the ball down \(\frac{1}{3}\) of the basketball court on the first day of practice. Each day after that, he dribbles \(\frac{1}{3}\) of the way more than he did the day before. Draw a number line to represent the court. Partition the number line to represent how far Rider dribbles on Day 1, Day 2, and Day 3 of practice. What fraction of the way does he dribble on Day 3?
Answer :

Explanation :
Number line drawn to represent the basketball court, partitioned into thirds, and labeled correctly;
Day 1: \(\frac{1}{3}\)
Day 2: \(\frac{2}{3}\)
Day 3: \(\frac{3}{3}\)
The Fraction that dribble on Day 3 is \(\frac{3}{3}\) . He dribbles the complete way .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 27 Answer Key

Eureka Math Grade 3 Module 5 Lesson 27 Sprint Answer Key

A
Subtract by Seven

Question 1.
17 – 7 =

Question 2.
7 – 7 =

Question 3.
27 – 7 =

Question 4.
8 – 7 =

Question 5.
18 – 7 =

Question 6.
38 – 7 =

Question 7.
9 – 7 =

Question 8.
19 – 7 =

Question 9.
49 – 7 =

Question 10.
10 – 7 =

Question 11.
20 – 7 =

Question 12.
60 – 7 =

Question 13.
11 – 7 =

Question 14.
21 – 7 =

Question 15.
71 – 7 =

Question 16.
12 – 7 =

Question 17.
22 – 7 =

Question 18.
82 – 7 =

Question 19.
13 – 7 =

Question 20.
23 – 7 =

Question 21.
83 – 7 =

Question 22.
14 – 7 =

Question 23.
24 – 7 =

Question 24.
34 – 7 =

Question 25.
64 – 7 =

Question 26.
84 – 7 =

Question 27.
15 – 7 =

Question 28.
25 – 7 =

Question 29.
35 – 7 =

Question 30.
75 – 7 =

Question 31.
55 – 7 =

Question 32.
16 – 7 =

Question 33.
26 – 7 =

Question 34.
36 – 7 =

Question 35.
86 – 7 =

Question 36.
66 – 7 =

Question 37.
90 – 7 =

Question 38.
53 – 7 =

Question 39.
42 – 7 =

Question 40.
71 – 7 =

Question 41.
74 – 7 =

Question 42.
56 – 7 =

Question 43.
95 – 7 =

Question 44.
92 – 7 =

B
Subtract by Seven

Question 1.
7 – 7 =

Question 2.
17 – 7 =

Question 3.
27 – 7 =

Question 4.
8 – 7 =

Question 5.
18 – 7 =

Question 6.
68 – 7 =

Question 7.
9 – 7 =

Question 8.
19 – 7 =

Question 9.
79 – 7 =

Question 10.
10 – 7 =

Question 11.
20 – 7 =

Question 12.
90 – 7 =

Question 13.
11 – 7 =

Question 14.
21 – 7 =

Question 15.
91 – 7 =

Question 16.
12 – 7 =

Question 17.
22 – 7 =

Question 18.
42 – 7 =

Question 19.
13 – 7 =

Question 20.
23 – 7 =

Question 21.
43 – 7 =

Question 22.
14 – 7 =

Question 23.
24 – 7 =

Question 24.
34 – 7 =

Question 25.
54 – 7 =

Question 26.
74 – 7 =

Question 27.
15 – 7 =

Question 28.
25 – 7 =

Question 29.
35 – 7 =

Question 30.
65 – 7 =

Question 31.
45 – 7 =

Question 32.
16 – 7 =

Question 33.
26 – 7 =

Question 34.
36 – 7 =

Question 35.
76 – 7 =

Question 36.
56 – 7 =

Question 37.
70 – 7 =

Question 38.
63 – 7 =

Question 39.
52 – 7 =

Question 40.
81 – 7 =

Question 41.
74 – 7 =

Question 42.
66 – 7 =

Question 43.
85 – 7 =

Question 44.
52 – 7 =

Eureka Math Grade 3 Module 5 Lesson 27 Problem Set Answer Key

Question 1.
Use the pictures to model equivalent fractions. Fill in the blanks, and answer the questions.

What happened to the size of the equal parts when there were fewer equal parts?
What happened to the number of equal parts when the equal parts became larger?

What happened to the size of the equal parts when there were more equal parts?
What happened to the number of equal parts when the equal parts became smaller?
Answer :

Explanation :
In figure a
When there are fewer parts the size of the equal parts are bigger .
When the equal parts became larger The number of equal parts will become fewer .
In figure b
when there were more equal parts the size of the equal parts are smaller .
when the equal parts became smaller the number of equal parts will become more .

Question 2.
6 friends want to share 3 chocolate bars that are all the same size, which are represented by the 3 rectangles below. When the bars are unwrapped, the friends notice that the first chocolate bar is cut into 2 equal parts, the second is cut into 4 equal parts, and the third is cut into 6 equal parts. How can the 6 friends share the chocolate bars equally without breaking any of the pieces?

Answer :

Explanation :
The First Chocolate is shared by 2 friend’s with \(\frac{1}{2}\) part each .
The Second chocolate is shared by 2 friend’s with\(\frac{2}{4}\) part each .
The Third chocolate is shared by 2 friend’s with\(\frac{3}{6}\) part each .
That means each friend will get \(\frac{1}{2}\) of one chocolate .

Question 3.
When the whole is the same, why does it take 6 copies of 1 eighth to equal 3 copies of 1 fourth? Draw a model to support your answer.
Answer :

Explanation :
It takes Six one-Eighths to make Three one Fourths.
\(\frac{3}{4}\) is equivalent to \(\frac{6}{8}\) .

Question 4.
When the whole is the same, how many sixths does it take to equal 1 third? Draw a model to support your answer.
Answer :

Explanation :
It takes two one-sixths to make a third. and we can see that there are \(\frac{1}{6}\) = 6 sixths in a whole.

Question 5.
You have a magic wand that doubles the number of equal parts but keeps the whole the same size. Use your magic wand. In the space below, draw to show what happens to a rectangle that is partitioned in fourths after you tap it with your wand. Use words and numbers to explain what happened.

Answer :

Explanation :
Both the wholes have same length .
The Rectangular strip is partitioned in Fourths. after magic the Rectangular strip is partitioned into eigths with same length by dividing the rectangular strip in middle  as shown in above figure .

Eureka Math Grade 3 Module 5 Lesson 27 Exit Ticket Answer Key

Question 1.
Solve.
2 thirds is equal to __ twelfths

Answer :
2 thirds is equal to 8 twelfths

Question 2.
Draw and label two models that show fractions equivalent to those in Problem 1.
Answer :

Explanation :
2 thirds is equal to 8 twelfths

Question 3.
Use words to explain why the two fractions in Problem 1 are equal.
Answer :
Both the wholes have same length .
The Rectangular strip is partitioned in Thirds. The Same Rectangular strip is partitioned into twelfths with same length by dividing the rectangular strip in middle into by 2 strips as shown in above figure .

Eureka Math Grade 3 Module 5 Lesson 27 Homework Answer Key

Question 1.
Use the pictures to model equivalent fractions. Fill in the blanks, and answer the questions.

What happened to the size of the equal parts when there were fewer equal parts?

What happened to the size of the equal parts when there were more equal parts?
Answer :

Explanation :
when there were fewer equal parts the number of parts are bigger .
when there were more equal parts the number of parts are smaller .

Question 2.
8 students share 2 pizzas that are the same size, which are represented by the 2 circles below. They notice that the first pizza is cut into 4 equal slices, and the second is cut into 8 equal slices. How can the 8 students share the pizzas equally without cutting any of the pieces?

Answer :

Explanation :
Each student gets \(\frac{1}{4}\) or \(\frac{2}{8}\) of the pizza . From 1 st pizza 4 students get \(\frac{1}{4}\) of the pizza and from 2nd pizza 4 students get \(\frac{2}{8}\) of the pizza .

Question 3.
When the whole is the same, why does it take 4 copies of 1 tenth to equal 2 copies of 1 fifth? Draw a model to support your answer.
Answer :

Explanation :
Both the wholes have same length .
The Rectangular strip is partitioned in fifths. The Another Rectangular strip is partitioned into tenths with same length by dividing the rectangular strip in middle as shown in above figure .
two one fifths is equal to four one tenths .

Question 4.
When the whole is the same, how many eighths does it take to equal 1 fourth? Draw a model to support your Answer.

Explanation :
Both the wholes have same length .
The Rectangular strip is partitioned in fourths. The Another Rectangular strip is partitioned into Eigths with same length by dividing the rectangular strip in middle as shown in above figure .
one fourths is equal to four two Eighths .

Question 5.
Mr. Pham cuts a cake into 8 equal slices. Then, he cuts every slice in half. How many of the smaller slices does he have? Use words and numbers to explain your answer.
Answer :

Explanation :
The figure shows a cake of 8 slices .the middle orange line shows the cake is sliced in half , creating 16 small slices .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 28 Answer Key

Eureka Math Grade 3 Module 5 Lesson 28 Sprint Answer Key

A
Subtract by Eight

Question 1.
18 – 8 =

Question 2.
8 – 8 =

Question 3.
28 – 8 =

Question 4.
9 – 8 =

Question 5.
19 – 8 =

Question 6.
39 – 8 =

Question 7.
10 – 8 =

Question 8.
20 – 8 =

Question 9.
50 – 8 =

Question 10.
11 – 8 =

Question 11.
21 – 8 =

Question 12.
71 – 8 =

Question 13.
12 – 8 =

Question 14.
22 – 8 =

Question 15.
82 – 8 =

Question 16.
13 – 8 =

Question 17.
23 – 8 =

Question 18.
83 – 8 =

Question 19.
14 – 8 =

Question 20.
24 – 8 =

Question 21.
34 – 8 =

Question 22.
54 – 8 =

Question 23.
74 – 8 =

Question 24.
15 – 8 =

Question 25.
25 – 8 =

Question 26.
35 – 8 =

Question 27.
85 – 8 =

Question 28.
65 – 8 =

Question 29.
16 – 8 =

Question 30.
26 – 8 =

Question 31.
36 – 8 =

Question 32.
96 – 8 =

Question 33.
76 – 8 =

Question 34.
17 – 8 =

Question 35.
27 – 8 =

Question 36.
37 – 8 =

Question 37.
87 – 8 =

Question 38.
67 – 8 =

Question 39.
70 – 8 =

Question 40.
62 – 8 =

Question 41.
84 – 8 =

Question 42.
66 – 8 =

Question 43.
91 – 8 =

Question 44.
75 – 8 =

B
Subtract by Eight

Question 1.
8 – 8 =

Question 2.
18 – 8 =

Question 3.
28 – 8 =

Question 4.
9 – 8 =

Question 5.
19 – 8 =

Question 6.
69 – 8 =

Question 7.
10 – 8 =

Question 8.
20 – 8 =

Question 9.
60 – 8 =

Question 10.
11 – 8 =

Question 11.
21 – 8 =

Question 12.
81 – 8 =

Question 13.
12 – 8 =

Question 14.
22 – 8 =

Question 15.
52 – 8 =

Question 16.
13 – 8 =

Question 17.
23 – 8 =

Question 18.
93 – 8 =

Question 19.
14 – 8 =

Question 20.
24 – 8 =

Question 21.
34 – 8 =

Question 22.
74 – 8 =

Question 23.
94 – 8 =

Question 24.
15 – 8 =

Question 25.
25 – 8 =

Question 26.
35 – 8 =

Question 27.
95 – 8 =

Question 28.
75 – 8 =

Question 29.
16 – 8 =

Question 30.
26 – 8 =

Question 31.
36 – 8 =

Question 32.
66 – 8 =

Question 33.
46 – 8 =

Question 34.
17 – 8 =

Question 35.
27 – 8 =

Question 36.
37 – 8 =

Question 37.
97 – 8 =

Question 38.
77 – 8 =

Question 39.
80 – 8 =

Question 40.
71 – 8 =

Question 41.
53 – 8 =

Question 42.
45 – 8 =

Question 43.
87 – 8 =

Question 44.
54 – 8 =

Eureka Math Grade 3 Module 5 Lesson 28 Problem Set Answer Key

Shade the models to compare the fractions. Circle the larger fraction for each problem.

Question 1.
2 fifths
2 thirds
Answer :

Explanation :
The Length of 2 thirds is greater than the length of the 2 fifths that means \(\frac{2}{3}\) is greater than \(\frac{2}{5}\) .

Question 2.
2 tenths
2 eighths
Answer :

Explanation :
The Length of 2 Eighths is longer than the length of the 2 Tenths that means \(\frac{2}{8}\) is greater than \(\frac{2}{10}\) .

Question 3.
3 fourths
3 eighths
Answer :

Explanation :
The Length of 3 Fourths is longer than the length of the 3 eighths that means \(\frac{3}{4}\) is greater than \(\frac{3}{8}\) .

Question 4.
4 eighths
4 sixths
Answer :

Explanation :
The Length of 4 sixths is longer than the length of the 4 eighths that means \(\frac{4}{6}\) is greater than \(\frac{4}{8}\) .

Question 5.
3 thirds
3 sixths
Answer :

Explanation :
The Length of 3 thirds is longer than the length of the 3 sixths that means \(\frac{3}{3}\) is 1 whole is greater than \(\frac{3}{6}\) .

Question 6.
After softball, Leslie and Kelly each buy a half-liter bottle of water. Leslie drinks 3 fourths of her water. Kelly drinks 3 fifths of her water. Who drinks the least amount of water? Draw a picture to support your answer.
Answer :
Kelly drinks least amount of water .

Explanation :
Leslie drinks \(\frac{3}{4}\) amount of half litre water .
Kelly drinks \(\frac{3}{5}\) amount of half litre water .
The Length of 3 fourths s is longer than the length of the 3 fifths
that means \(\frac{3}{5}\) is smaller than \(\frac{3}{4}\) .
So, Kelly drinks least amount of water .

Question 7.
Becky and Malory get matching piggy banks. Becky fills \(\frac{2}{3}\) of her piggy bank with pennies. Malory fills \(\frac{2}{4}\) of her piggy bank with pennies. Whose piggy bank has more pennies? Draw a picture to support your answer.
Answer :

Explanation :
Length of becky piggy bank filled = \(\frac{2}{3}\)
Length of Malory piggy bank filled = \(\frac{2}{4}\)
The length of becky bank is more than length of malory bank  that means more the length more number of pennies .
So, becky piggy bank has more pennies .

Question 8.
Heidi lines up her dolls in order from shortest to tallest. Doll A is \(\frac{2}{4}\) foot tall, Doll B is \(\frac{2}{6}\) foot tall, and Doll C is \(\frac{2}{3}\) foot tall. Compare the heights of the dolls to show how Heidi puts them in order. Draw a picture to support your answer.
Answer :

Explanation :
The Height of Doll A is \(\frac{2}{4}\)
The Height of Doll B is \(\frac{2}{6}\)
The height of Doll C is \(\frac{2}{3}\)
Longer the Length of Doll more than fraction value .
Therefore , \(\frac{2}{3}\) > \(\frac{2}{4}\)

Eureka Math Grade 3 Module 5 Lesson 28 Exit Ticket Answer Key

Question 1.
Shade the models to compare the fractions.
2 thirds
2 eighths
Which is larger, 2 thirds or 2 eighths? Why? Use words to explain.
Answer :

Explanation :
The Length of 2 thirds is longer than the length of the 2 eigths that means \(\frac{2}{3}\) is greater than \(\frac{2}{8}\) .

Question 2.
Draw a model for each fraction. Circle the smaller fraction.
3 sevenths

3 fourths
Answer :

Explanation :
The Length of 3 fourths is longer than the length of the 3 sevenths that means \(\frac{3}{4}\) is greater than \(\frac{3}{7}\) .

Eureka Math Grade 3 Module 5 Lesson 28 Homework Answer Key

Shade the models to compare the fractions. Circle the larger fraction for each problem.

Question 1.
1 half
1 fifth
Answer :

Explanation :
The Length of 1 Halfs is longer than the length of the 1 fifths that means \(\frac{1}{2}\) is greater than \(\frac{1}{5}\) .

Question 2.
2 sevenths
2 fourths
Answer :

Explanation :
The Length of 2 sevenths is longer than the length of the 2 fourths that means \(\frac{2}{7}\) is greater than \(\frac{2}{4}\) .

Question 3.
4 fifths
4 ninths

Answer:

Explanation :
The Length of 4 fifths is longer than the length of the 4 ninths that means \(\frac{4}{5}\) is greater than \(\frac{4}{9}\) .

Question 4.
5 sevenths
5 tenths

Answer :

Explanation :
The Length of 5 sevenths is longer than the length of the 5 tenths that means \(\frac{5}{7}\) is greater than \(\frac{5}{10}\) .

Question 5.
4 sixths
4 fourths

Answer :

Explanation :
The Length of 4 sixths is smaller than the length of the 4 fourths that means \(\frac{4}{4}\) is greater than \(\frac{4}{6}\) .

Question 6.
Saleem and Edwin use inch rulers to measure the lengths of their caterpillars. Saleem’s caterpillar measures 3 fourths of an inch. Edwin’s caterpillar measures 3 eighths of an inch. Whose caterpillar is longer? Draw a picture to support your answer.
Answer :

Explanation :
Length of Saleem’s caterpillar = 3 fourths
Length of Edwin’s caterpillar = 3 eighths
Length of Saleem’s caterpillar is longer than Edwin’s caterpillar
So, \(\frac{3}{4}\) is greater than \(\frac{3}{8}\) .

Question 7.
Lily and Jasmine each bake the same-sized chocolate cake. Lily puts \(\frac{5}{10}\) of a cup of sugar into her cake. Jasmine puts \(\frac{5}{6}\) of a cup of sugar into her cake. Who uses less sugar? Draw a picture to support your answer.
Answer :

Explanation :
Amount of sugar used by lily = \(\frac{5}{10}\)
Amount of sugar used by Jasmine = \(\frac{5}{6}\)
\(\frac{5}{10}\)  is less than \(\frac{5}{6}\) .
So, lily used less sugar than jasmine .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 30 Answer Key

Eureka Math Grade 3 Module 5 Lesson 30 Pattern Sheet Answer Key

Multiply.

multiply by 9 (1–5)
Answer :

Explanation :
multiply by 9 (1–5)
9 × 1 = 9
9 × 2 = 18
9 × 3 = 27
9 × 4 = 36
9 × 5 = 45

Eureka Math Grade 3 Module 5 Lesson 30 Homework Answer Key

Describe step by step the experience you had of partitioning a length into equal units by simply using a piece of notebook paper and a straight edge. Illustrate the process.

Answer :

Explanation :
Turn the page into vertical lines .
Mark 0 at one point and make equal differences in the above figure i am leaving 4 vertical lines and marking the next point  as \(\frac{1}{4}\), and next leave another 4 vertical lines and mark the next point as \(\frac{2}{4}\) mark all the points in the same way till 1 that means \(\frac{4}{4}\).
Mark all the points and draw the vertical lines from these points .
Next take a rectangular strip point one the end on point 0 and put another end on the vertical line of point 1.
Mark the points where the rectangular strip are touching these points .
Then take the same strip and place it horizontal then the strip is divided into 4 equal parts .

Engage NY Eureka Math 3rd Grade Module 5 Lesson 29 Answer Key

Eureka Math Grade 3 Module 5 Lesson 29 Pattern Sheet Answer Key

Multiply.

multiply by 8 (5–9)
Answer :

Explanation :
MULTIPLICATION of 8 (5 – 9 ) are given here .
8 × 5 = 40
8 × 6 = 48
8 × 7 = 56
8 × 8 = 64
8 × 9 = 72

Eureka Math Grade 3 Module 5 Lesson 29 Problem Set Answer Key

Label each shaded fraction. Use >, <, or = to compare. The first one has been done for you.

Question 1.

Question 2.

Answer :

Question 3.

Answer :

Question 4.

Answer :

Question 5.
Partition each number line into the units labeled on the left. Then, use the number lines to compare the fractions.

Answer :

Explanation :
The number lines are partitioned with the respective given units and compared the fractions .

Draw your own model to compare the following fractions.

Question 6.

Answer :

Explanation :
The number lines are partitioned with the respective given units and compared the fractions .
The length of \(\frac{3}{10}\) is shorter than the length of \(\frac{3}{5}\) .
That means \(\frac{3}{5}\) is greater than \(\frac{3}{10}\) .

Question 7.

Answer :

Explanation :
The number lines are partitioned with the respective given units and compared the fractions .
The length of \(\frac{3}{10}\) is shorter than the length of \(\frac{3}{5}\) .
That means \(\frac{3}{5}\) is greater than \(\frac{3}{10}\) .

Question 8.
John ran 2 thirds of a kilometer after school. Nicholas ran 2 fifths of a kilometer after school. Who ran the shorter distance? Use the model below to support your answer. Be sure to label 1 whole as 1 kilometer.

Answer :

Explanation :
Distance ran by John = \(\frac{2}{3}\)
Distance ran by Nicholas = \(\frac{2}{5}\)
The distance traveled by John is more than Nicholas .
Therefore, \(\frac{2}{3}\) > \(\frac{2}{5}\) .

Question 9.
Erica ate 2 ninths of a licorice stick. Robbie ate 2 fifths of an identical licorice stick. Who ate more?
Use the model below to support your answer.

Answer :

Explanation :
Licorice stick ate by Erica = \(\frac{2}{9}\)
Licorice stick ate by Robbie = \(\frac{2}{5}\)
From the above image we notice that Robbie ate more than Erica which means more length of orange strip is marked by Robbie .
Therefore, \(\frac{2}{9}\) < \(\frac{2}{5}\) .

Eureka Math Grade 3 Module 5 Lesson 29 Exit Ticket Answer Key

Question 1.
Complete the number sentence by writing >, <, or =.

Answer :
\(\frac{3}{5}\) > \(\frac{3}{9}\)

Question 2.
Draw 2 number lines with endpoints 0 and 1 to show each fraction in Problem 1. Use the number lines to explain how you know your comparison in Problem 1 is correct.
Answer :

Explanation :
The length of strip marked for \(\frac{3}{5}\) in the above number line is longer than the length of strip marked for \(\frac{3}{9}\).
More the length of strip marked on the number line means greater is the number .
Therefore \(\frac{3}{5}\) > \(\frac{3}{9}\)

Eureka Math Grade 3 Module 5 Lesson 29 Homework Answer Key

Label each shaded fraction. Use >, <, or = to compare.

Question 1.

Answer :

Question 2.

Answer :

Question 3.

Answer :

Question 4.

Answer :

Question 5.
Partition each number line into the units labeled on the left. Then, use the number lines to compare the fractions.

Answer :

Explanation :
The number lines are partitioned with the respective given units and compared the fractions .

Draw your own models to compare the following fractions.
Question 6.

Answer :

Explanation :
The length of strip marked for \(\frac{7}{8}\) in the above figure is longer than the length of strip marked for \(\frac{7}{10}\).
More the length of strip marked on the rectangular strip means greater is the number .
Therefore \(\frac{7}{8}\) > \(\frac{7}{10}\)

Question 7.

Answer :

Explanation :
The length of strip marked for \(\frac{4}{6}\) in the above figure is longer than the length of strip marked for \(\frac{4}{9}\).
More the length of strip marked on the rectangular strip means greater is the number .
Therefore \(\frac{4}{6}\) > \(\frac{4}{9}\)

Question 8.
For an art project, Michello used \(\frac{3}{4}\) of a glue stick. Yamin used \(\frac{3}{6}\) of an identical glue stick. Who used more of the glue stick? Use the model below to support your answer. Be sure to label 1 whole as 1 glue stick.

Answer :

Explanation :
Glue stick Used by Michello = \(\frac{3}{4}\)
Glue stick used by Yamin = \(\frac{3}{6}\)
The length of strip marked for \(\frac{3}{4}\) in the above figure is longer than the length of strip marked for \(\frac{3}{6}\).
More the length of strip marked on the rectangular strip means greater is the number .
Therefore \(\frac{3}{4}\) > \(\frac{3}{6}\)

Question 9.
After gym class, Jahsir drank 2 eighths of a bottle of water. Jade drank 2 fifths of an identical bottle of water. Who drank less water? Use the model below to support your answer.

Answer :

Explanation :
Quantity of Water drank by Jahsir = \(\frac{2}{8}\)
Quantity of water drank by Jade = \(\frac{2}{5}\)
The length of strip marked for \(\frac{2}{5}\) in the above figure is longer than the length of strip marked for \(\frac{2}{8}\).
Less the length of strip marked on the rectangular strip means lesser is the number .
Therefore \(\frac{2}{8}\) < \(\frac{2}{5}\) .

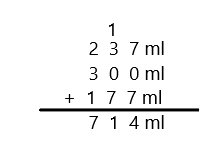
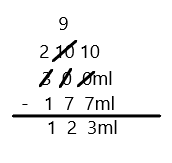
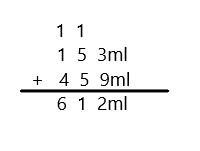
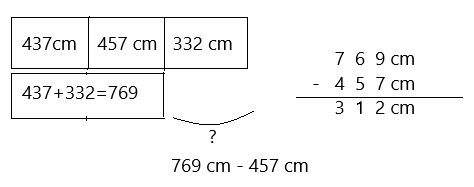
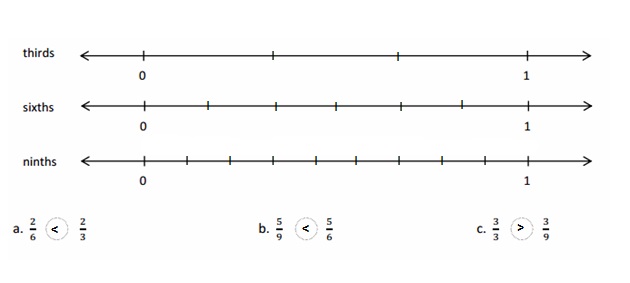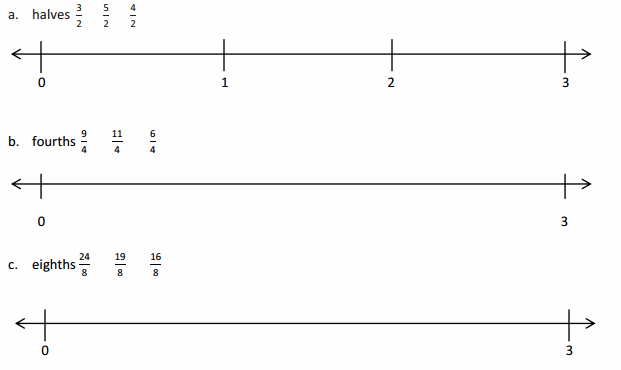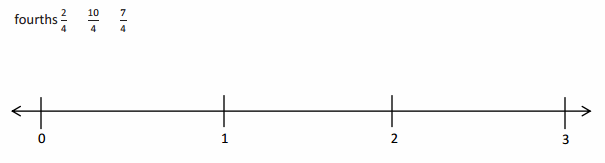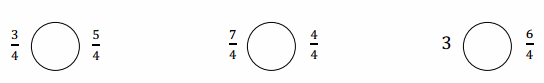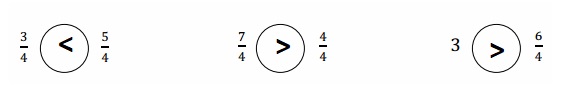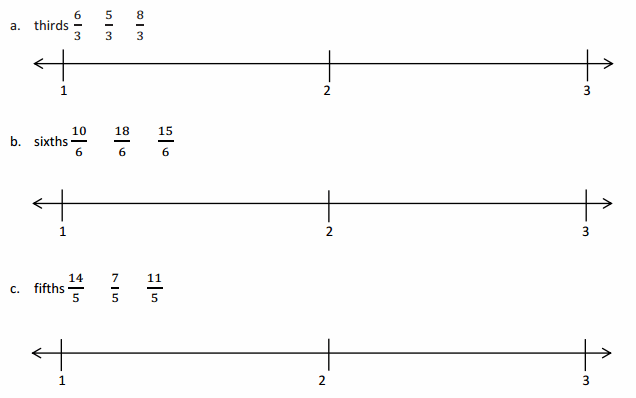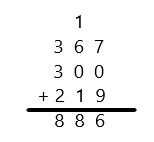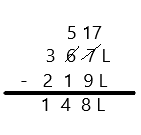Engage NY Eureka Math 3rd Grade Module 5 Lesson 19 Answer Key

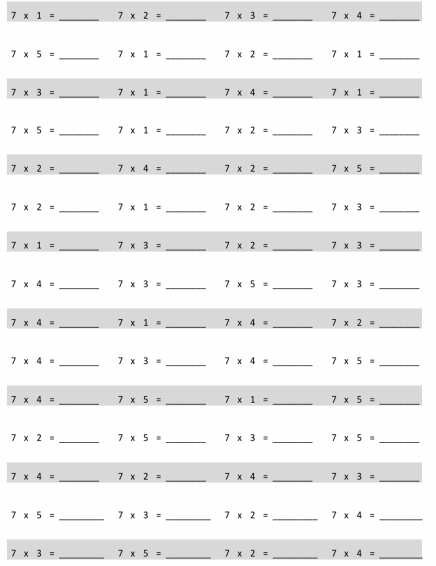
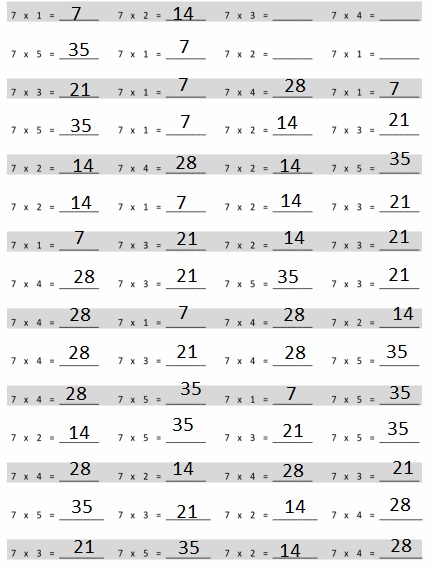
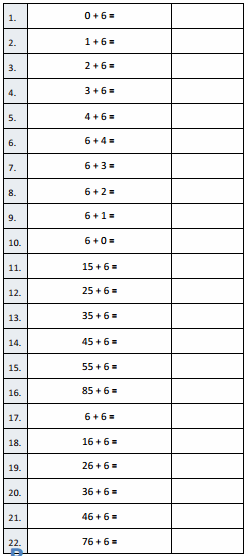
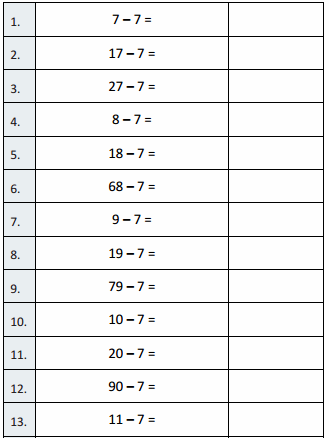
Eureka Math Grade 3 Module 5 Lesson 19 Sprint Answer Key

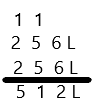
A
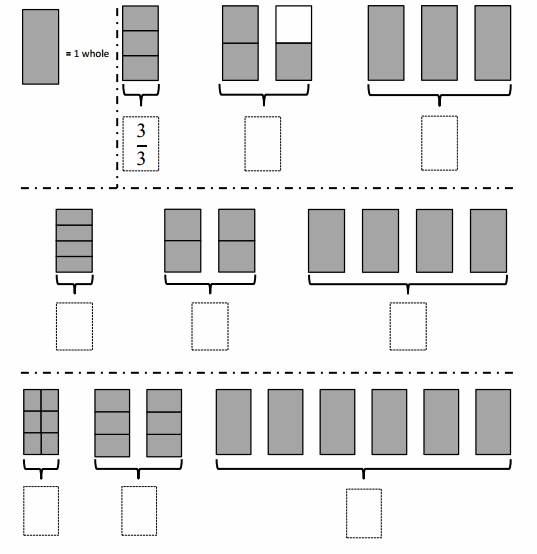
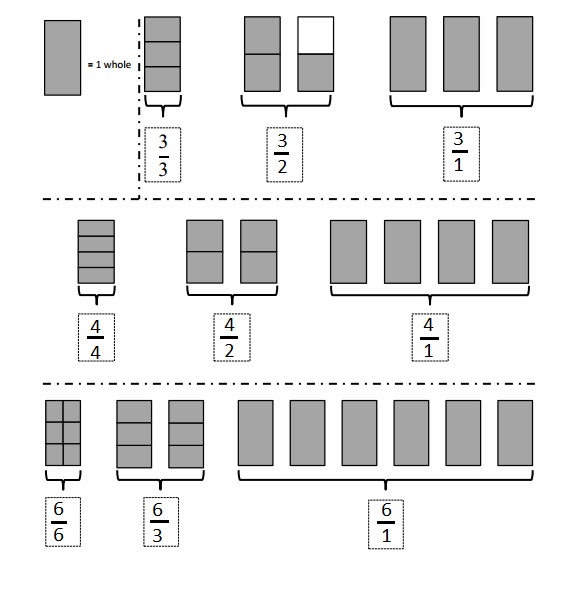
Express Fractions as Whole Numbers

Question 1.
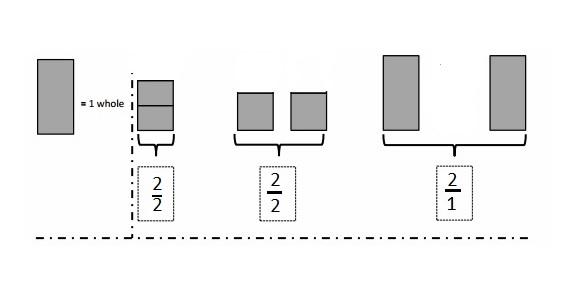
\(\frac { 2 }{ 1 }\) =
Answer :
\(\frac { 2 }{ 1 }\) = 2

Question 2.
\(\frac { 2 }{ 2 }\) =
Answer :
\(\frac { 2 }{ 2 }\) = 1

Question 3.
\(\frac { 4 }{ 2 }\) =
Answer :
\(\frac { 4 }{ 2 }\) = 2
Explanation :
2 x 2 = 4

Question 4.
\(\frac { 6 }{ 2 }\) =
Answer :
\(\frac { 6 }{ 2 }\) = 3
Explanation :
2 x 3 = 6

Question 5.
\(\frac { 10 }{ 2 }\) =
Answer :
\(\frac { 10 }{ 2 }\) = 5
Explanation :
2  ×  5  = 10

Question 6.
\(\frac { 8 }{ 2 }\) =
Answer :
\(\frac { 8 }{ 2 }\) = 4
Explanation :
2  × 4  = 8

Question 7.
\(\frac { 5 }{ 1 }\) =
Answer :
\(\frac { 5 }{ 1 }\) = 5
Explanation :
1  × 5 = 5

Question 8.
\(\frac { 5 }{ 5 }\) =
Answer :
\(\frac { 5 }{ 5 }\) = 1
Explanation :
1  × 5 = 5

Question 9.
\(\frac { 10 }{ 5 }\) =
Answer :
\(\frac { 10 }{ 5 }\) = 2
Explanation :
2  × 5 = 10

Question 10.
\(\frac { 15 }{ 5 }\) =
Answer :
\(\frac { 15 }{ 5 }\) = 3
Explanation :
3  × 5 = 15

Question 11.
\(\frac { 25 }{ 5 }\) =
Answer :
\(\frac { 25 }{ 5 }\) = 5
Explanation :
5  × 5 = 25

Question 12.
\(\frac { 20 }{ 5 }\) =
Answer :
\(\frac { 20 }{ 5 }\) = 4
Explanation :
4  × 5 = 20

Question 13.
\(\frac { 10 }{ 10 }\) =
Answer :
\(\frac { 10 }{ 10 }\) = 1
Explanation :
1  × 10 = 10

Question 14.
\(\frac { 50 }{ 10 }\) =
Answer :
\(\frac { 50 }{ 10 }\) = 5
Explanation :
10  × 5 = 50

Question 15.
\(\frac { 30 }{ 10 }\) =
Answer :
\(\frac { 30 }{ 10 }\) = 3
Explanation :
10  × 3 = 30

Question 16.
\(\frac { 10 }{ 1 }\) =
Answer :
\(\frac { 10 }{ 1 }\) = 10
Explanation :
10  × 1 = 10

Question 17.
\(\frac { 20 }{ 10 }\) =
Answer :
\(\frac { 20 }{ 10 }\) = 2
Explanation :
10  × 2 = 20

Question 18.
\(\frac { 40 }{ 10 }\) =
Answer :
\(\frac { 40 }{ 10 }\) = 4
Explanation :
10  × 4 = 40

Question 19.
\(\frac { 8 }{ 4 }\) =
Answer :
\(\frac { 8 }{ 4 }\) = 2
Explanation :
2  × 4 = 8

Question 20.
\(\frac { 4 }{ 4 }\) =
Answer :
\(\frac { 4 }{ 4 }\) = 1
Explanation :
1  × 4 = 4

Question 21.
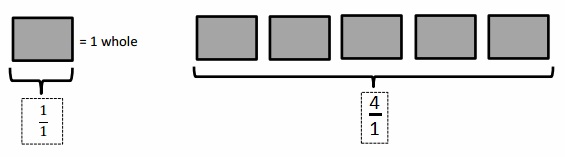
\(\frac { 4 }{ 1 }\) =
Answer :
\(\frac { 4 }{ 1 }\) = 4
Explanation :
1  × 4 = 4

Question 22.
\(\frac { 12 }{ 4 }\) =
Answer :
\(\frac { 12 }{ 4 }\) = 3
Explanation :
3  × 4 = 12

Question 23.
\(\frac { 6 }{ 3 }\) =
Answer :
\(\frac { 6 }{ 3 }\) = 2
Explanation :
3  × 2 = 6

Question 24.
\(\frac { 3 }{ 3 }\) =
Answer :
\(\frac { 3 }{ 3 }\) = 1
Explanation :
1  × 3 = 3

Question 25.
\(\frac { 3 }{ 1 }\) =
Answer :
\(\frac { 3 }{ 1 }\) = 3
Explanation :
1  × 3 = 3

Question 26.
\(\frac { 9 }{ 3 }\) =
Answer :
\(\frac { 9 }{ 3 }\) = 3
Explanation :
3  × 3 = 9

Question 27.
\(\frac { 16 }{ 4 }\) =
Answer :
\(\frac { 16 }{ 4 }\) = 4
Explanation :
4  × 4 = 16

Question 28.
\(\frac { 20 }{ 4 }\) =
Answer :
\(\frac { 20 }{ 4 }\) = 5
Explanation :
4  × 5 = 20

Question 29.
\(\frac { 12 }{ 3 }\) =
Answer :
\(\frac { 12 }{ 3 }\) = 4
Explanation :
4  × 3 = 12

Question 30.
\(\frac { 15 }{ 3 }\) =
Answer :
\(\frac { 15 }{ 3 }\) = 5
Explanation :
3  × 5 = 15

Question 31.
\(\frac { 70 }{ 10 }\) =
Answer :
\(\frac { 70 }{ 10 }\) = 7
Explanation :
10  × 7 = 70

Question 32.
\(\frac { 12 }{ 2 }\) =
Answer :
\(\frac { 12 }{ 2 }\) = 6
Explanation :
2  × 6 = 12

Question 33.
\(\frac { 14 }{ 2 }\) =
Answer :
\(\frac { 14 }{ 2 }\) = 7
Explanation :
2  × 7 = 14

Question 34.
\(\frac { 90 }{ 10 }\) =
Answer :
\(\frac { 90 }{ 10 }\) = 9
Explanation :
10  × 9 = 90

Question 35.
\(\frac { 30 }{ 5 }\) =
Answer :
\(\frac { 30 }{ 5 }\) = 6
Explanation :
5  × 6 = 30

Question 36.
\(\frac { 35 }{ 5 }\) =
Answer :
\(\frac { 35 }{ 5 }\) = 7
Explanation :
5  × 7 = 35

Question 37.
\(\frac { 60 }{ 10 }\) =
Answer :
\(\frac { 60 }{ 10 }\) = 6
Explanation :
10  × 6 = 60

Question 38.
\(\frac { 18 }{ 2 }\) =
Answer :
\(\frac { 18 }{ 2 }\) = 9
Explanation :
2 × 9 = 18

Question 39.
\(\frac { 40 }{ 5 }\) =
Answer :
\(\frac { 40 }{ 5 }\) = 8
Explanation :
5  × 8 = 40

Question 40.
\(\frac { 80 }{ 10 }\) =
Answer :
\(\frac { 80 }{ 10 }\) = 8
Explanation :
10  × 8 = 80

Question 41.
\(\frac { 16 }{ 2 }\) =
Answer :
\(\frac { 16 }{ 2 }\) = 8
Explanation :
2  × 8 = 16

Question 42.
\(\frac { 45 }{ 5 }\) =
Answer :
\(\frac { 45 }{ 5 }\) = 9
Explanation :
5  × 9 = 45

Question 43.
\(\frac { 27 }{ 3 }\) =
Answer :
\(\frac { 27 }{ 3 }\) = 9
Explanation :
3 × 9 = 27

Question 44.
\(\frac { 32 }{ 4 }\) =
Answer :
\(\frac { 32 }{ 4 }\) = 8
Explanation :
3  × 8 = 32

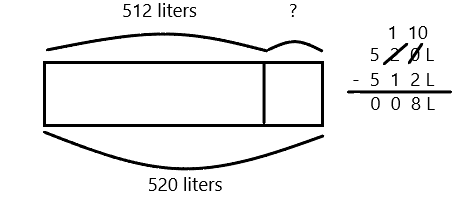
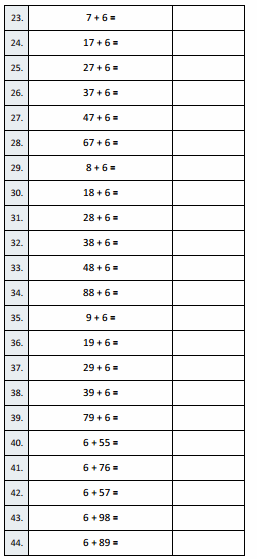
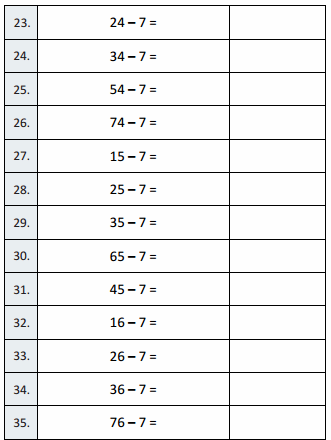
B
Express Fractions as Whole Numbers

Question 1.
\(\frac { 5 }{ 1 }\) =
Answer :
\(\frac { 5 }{ 1 }\) = 5
Explanation :
5  × 1 = 5

Question 2.
\(\frac { 5 }{ 5 }\) =
Answer :
\(\frac { 5 }{ 5 }\) = 1
Explanation :
5  × 1 = 5

Question 3.
\(\frac { 10 }{ 5 }\) =
Answer :
\(\frac { 10 }{ 5 }\) = 2
Explanation :
5  × 2 = 10

Question 4.
\(\frac { 15 }{ 5 }\) =
Answer :
\(\frac { 15 }{ 5 }\) = 3
Explanation :
5  × 3 = 1

Question 5.
\(\frac { 25 }{ 5 }\) =
Answer :
\(\frac { 25 }{ 5 }\) = 5
Explanation :
5  × 5 = 25

Question 6.
\(\frac { 20 }{ 5 }\) =
Answer :
\(\frac { 20 }{ 5 }\) = 4
Explanation :
5  × 4 = 20

Question 7.
\(\frac { 2 }{ 1 }\) =
Answer :
\(\frac { 2 }{ 1 }\) = 2
Explanation :
1  × 2 = 2

Question 8.
\(\frac { 2 }{ 2 }\) =
Answer :
\(\frac { 2 }{ 2 }\) = 1
Explanation :
1  × 2 = 2

Question 9.
\(\frac { 4 }{ 2 }\) =
Answer :
\(\frac { 4 }{ 2 }\) = 2
Explanation :
2 × 2 = 4

Question 10.
\(\frac { 6 }{ 2 }\) =
Answer :
\(\frac { 6 }{ 2 }\) = 3
Explanation :
2 × 3 = 6

Question 11.
\(\frac { 10 }{ 2 }\) =
Answer :
\(\frac { 10 }{ 2 }\) = 5
Explanation :
2 × 5 = 10

Question 12.
\(\frac { 8 }{ 2 }\) =
Answer :
\(\frac { 8 }{ 2 }\) = 4
Explanation :
2 × 4 = 8

Question 13.
\(\frac { 10 }{ 1 }\) =
Answer :
\(\frac { 10 }{ 1 }\) = 10
Explanation :
1 × 10 = 10

Question 14.
\(\frac { 10 }{ 10 }\) =
Answer :
\(\frac { 10 }{ 10 }\) = 1
Explanation :
1 × 10 = 10

Question 15.
\(\frac { 50 }{ 10 }\) =
Answer :
\(\frac { 50 }{ 10 }\) = 5
Explanation :
10 × 5 = 50

Question 16.
\(\frac { 30 }{ 10 }\) =
Answer :
\(\frac { 30 }{ 10 }\) = 3
Explanation :
10 × 3 = 30

Question 17.
\(\frac { 20 }{ 10 }\) =
Answer :
\(\frac { 20 }{ 10 }\) = 2
Explanation :
10 × 2 = 20

Question 18.
\(\frac { 40 }{ 10 }\) =
Answer :
\(\frac { 40 }{ 10 }\) = 4
Explanation :
10 × 4 = 40

Question 19.
\(\frac { 6 }{ 3 }\) =
Answer :
\(\frac { 6 }{ 3 }\) = 2
Explanation :
2 × 3 = 6

Question 20.
\(\frac { 3 }{ 3 }\) =
Answer :
\(\frac { 3 }{ 3 }\) = 1
Explanation :
1 × 3 = 3

Question 21.
\(\frac { 3 }{ 1 }\) =
Answer :
\(\frac { 3 }{ 1 }\) = 3
Explanation :
1 × 3 = 3

Question 22.
\(\frac { 9 }{ 3 }\) =
Answer :
\(\frac { 9 }{ 3 }\) =3
Explanation :
3 × 3 = 9

Question 23.
\(\frac { 8 }{ 4 }\) =
Answer :
\(\frac { 8 }{ 4 }\) = 2
Explanation :
2 × 4 = 8

Question 24.
\(\frac { 4 }{ 4 }\) =
Answer :
\(\frac { 4 }{ 4 }\) = 1
Explanation :
1 × 4 = 4

Question 25.
\(\frac { 4 }{ 1 }\) =
Answer :
\(\frac { 4 }{ 1 }\) = 4
Explanation :
1 × 4 = 4

Question 26.
\(\frac { 12 }{ 4 }\) =
Answer :
\(\frac { 12 }{ 4 }\) = 3
Explanation :
3 × 4 = 12

Question 27.
\(\frac { 12 }{ 3 }\) =
Answer :
\(\frac { 12 }{ 3 }\) = 4
Explanation :
3 × 4 = 12

Question 28.
\(\frac { 15 }{ 3 }\) =
Answer :
\(\frac { 15 }{ 3 }\) = 5
Explanation :
5 × 3 = 15

Question 29.
\(\frac { 16 }{ 4 }\) =
Answer :
\(\frac { 16 }{ 4 }\) = 4
Explanation :
4 × 4 = 16

Question 30.
\(\frac { 20 }{ 4 }\) =
Answer :
\(\frac { 20 }{ 4 }\) = 5
Explanation :
5 × 4 = 20

Question 31.
\(\frac { 90 }{ 10 }\) =
Answer :
\(\frac { 90 }{ 10 }\) = 9
Explanation :
10 × 9 = 90

Question 32.
\(\frac { 30 }{ 5 }\) =
Answer :
\(\frac { 30 }{ 5 }\) = 6
Explanation :
5 × 6 = 30

Question 33.
\(\frac { 35 }{ 5 }\) =
Answer :
\(\frac { 35 }{ 5 }\) = 7
Explanation :
5 × 7 = 35

Question 34.
\(\frac { 70 }{ 10 }\) =
Answer :
\(\frac { 70 }{ 10 }\) = 7
Explanation :
10 × 7 = 70

Question 35.
\(\frac { 12 }{ 2 }\) =
Answer :
\(\frac { 12 }{ 2 }\) = 6
Explanation :
2 × 6 = 12

Question 36.
\(\frac { 14 }{ 2 }\) =
Answer :
\(\frac { 14 }{ 2 }\) = 7
Explanation :
2 × 7 = 14

Question 37.
\(\frac { 80 }{ 10 }\) =
Answer :
\(\frac { 80 }{ 10 }\) = 8
Explanation :
10 × 9 = 90

Question 38.
\(\frac { 45 }{ 5 }\) =
Answer :
\(\frac { 45 }{ 5 }\) = 9
Explanation :
5 × 9 = 45

Question 39.
\(\frac { 16 }{ 2 }\) =
Answer :
\(\frac { 16 }{ 2 }\) = 8
Explanation :
2 × 8 = 16

Question 40.
\(\frac { 60 }{ 10 }\) =
Answer :
\(\frac { 60 }{ 10 }\) = 6
Explanation :
10 × 6 = 60

Question 41.
\(\frac { 18 }{ 2 }\) =
Answer :
\(\frac { 18 }{ 2 }\) = 9
Explanation :
2 × 9 = 18

Question 42.
\(\frac { 40 }{ 5 }\) =
Answer :
\(\frac { 40 }{ 5 }\) =8
Explanation :
5 × 8 = 40

Question 43.
\(\frac { 36 }{ 4 }\) =
Answer :
\(\frac { 36 }{ 4 }\) = 9
Explanation :
4 × 9 = 36

Question 44.
\(\frac { 24 }{ 3 }\) =
Answer :
\(\frac { 24 }{ 3 }\) = 8
Explanation :
4 × 8 = 32

Eureka Math Grade 3 Module 5 Lesson 19 Problem Set Answer Key

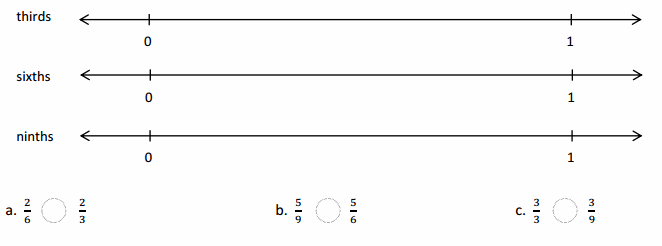
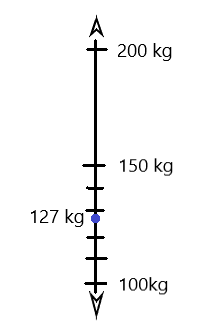
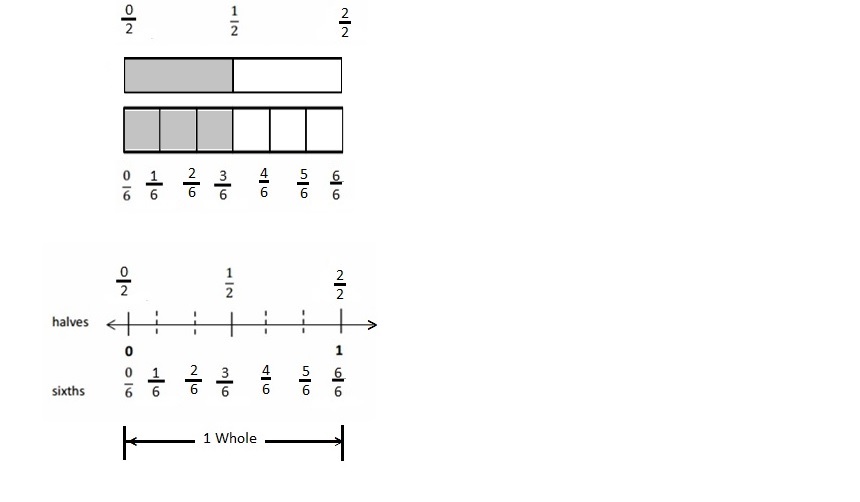
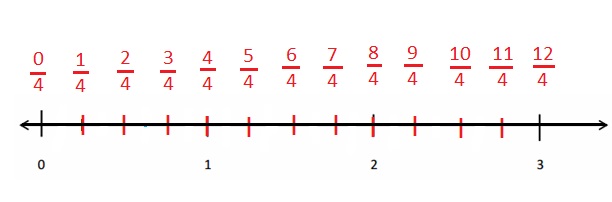
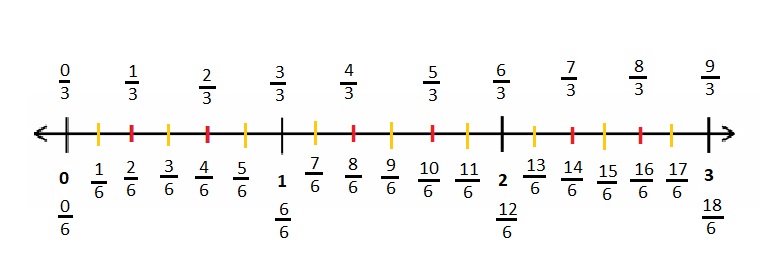
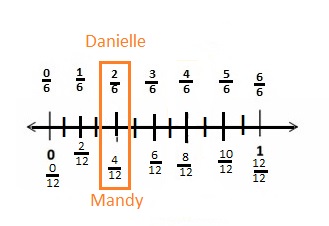
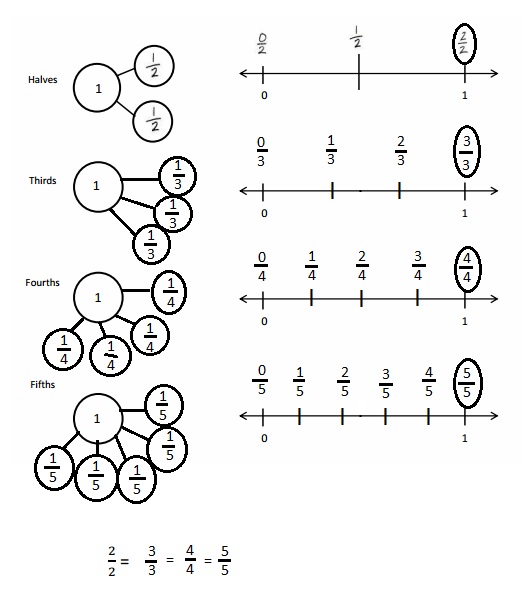
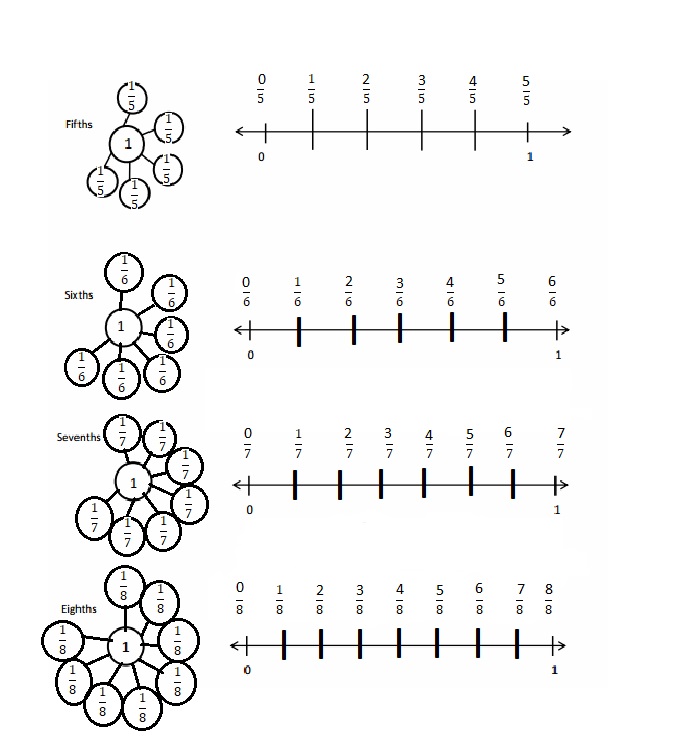
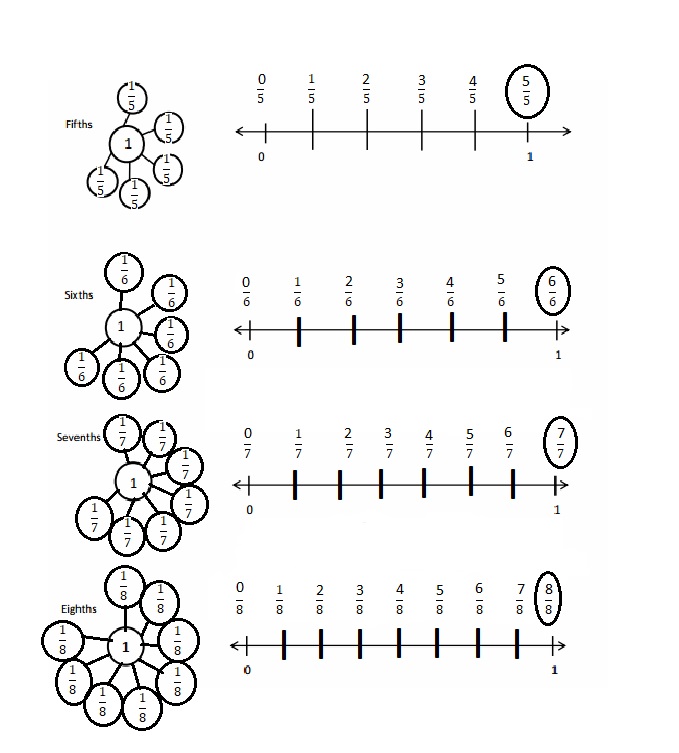
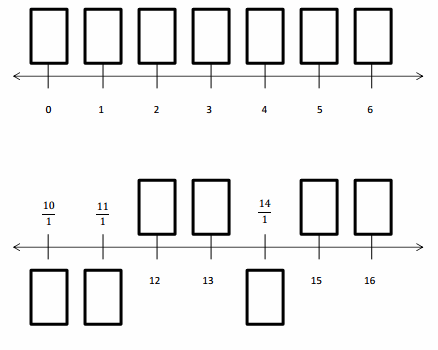
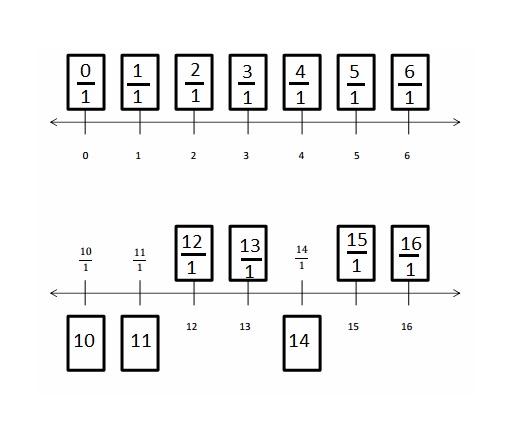
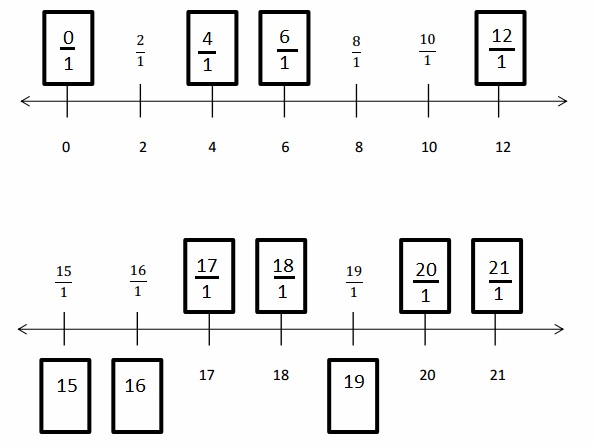
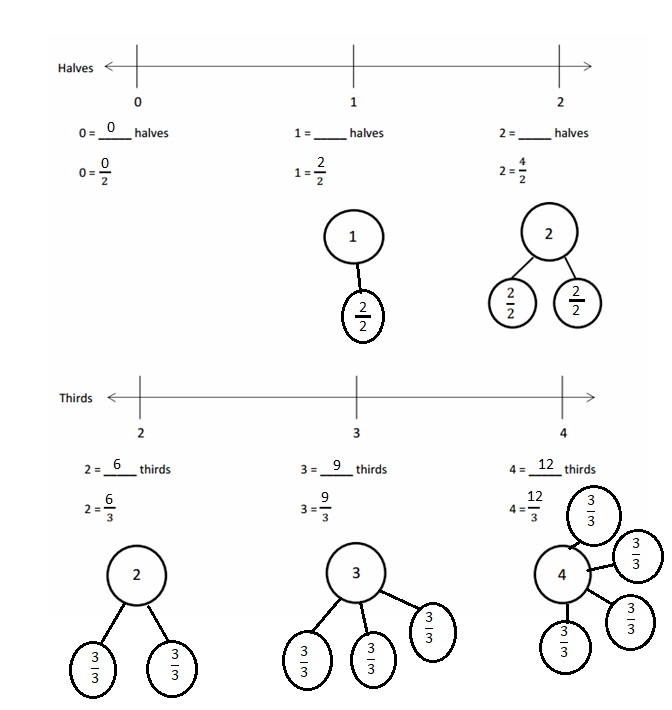
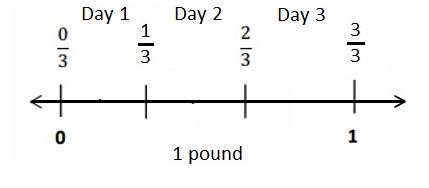
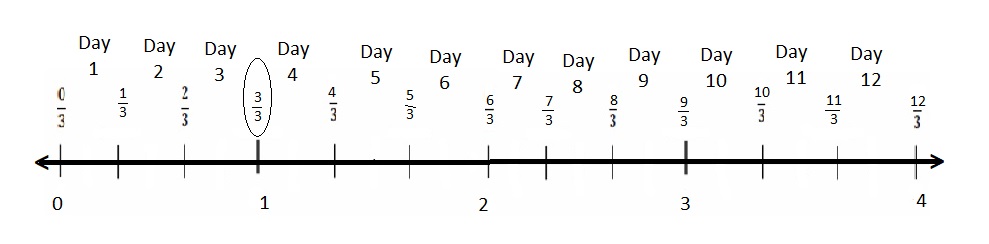
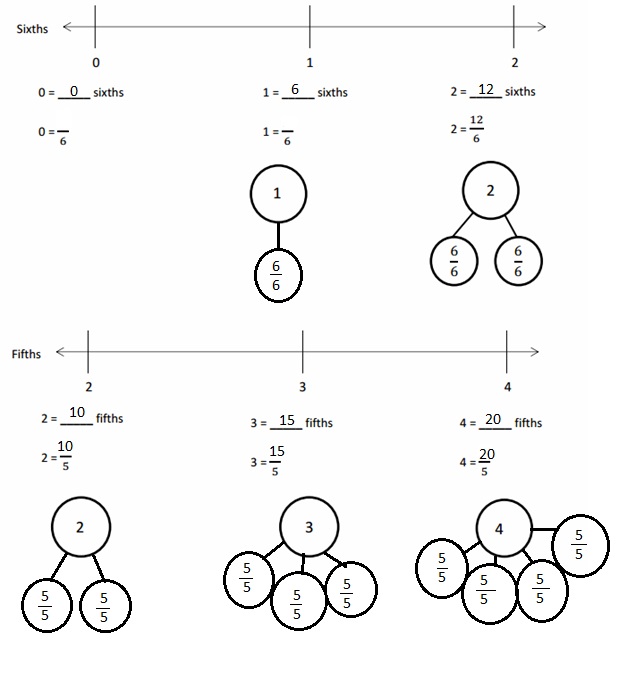
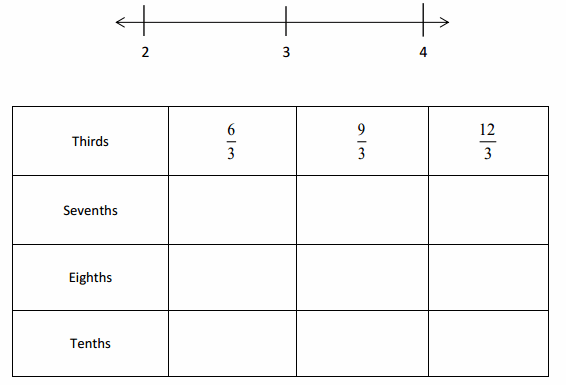
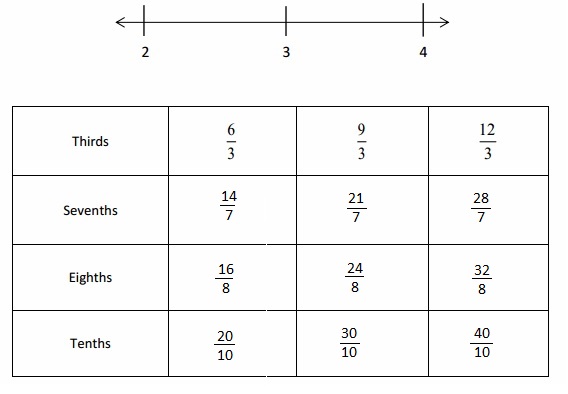
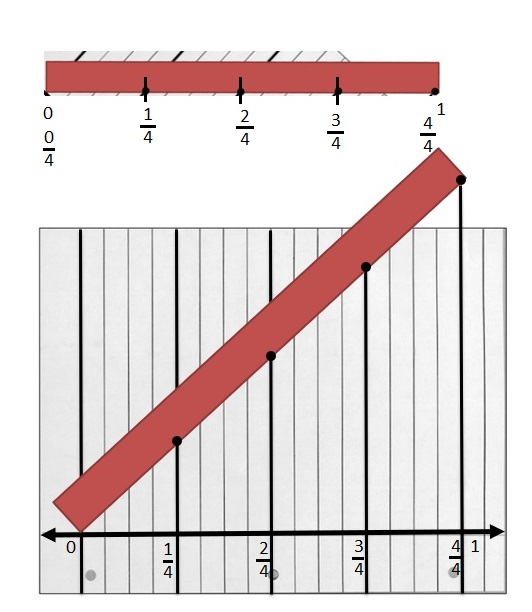
Question 1.
Divide each number line into the given fractional unit. Then, place the fractions. Write each whole as a fraction.

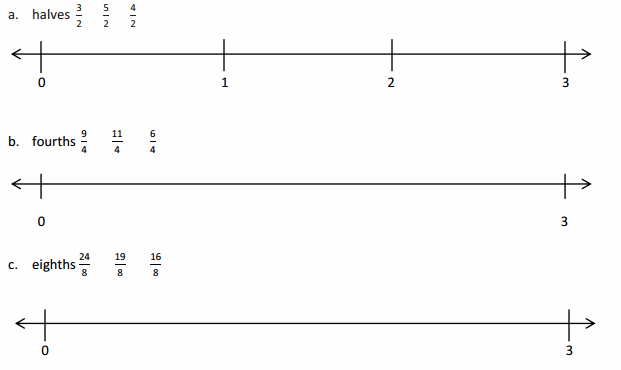
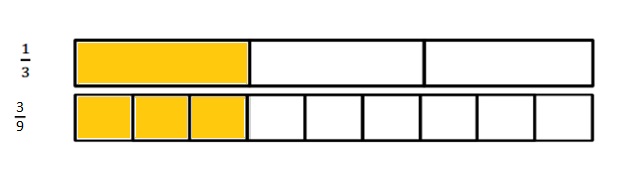
Answer :

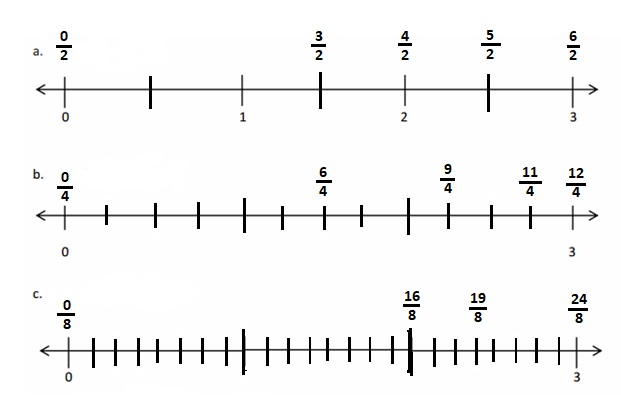
Explanation :
Number lines are represented and the given fractions are located and labeled .

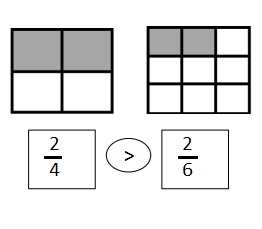
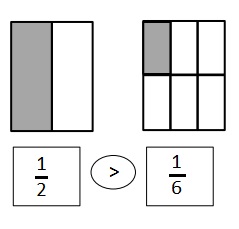
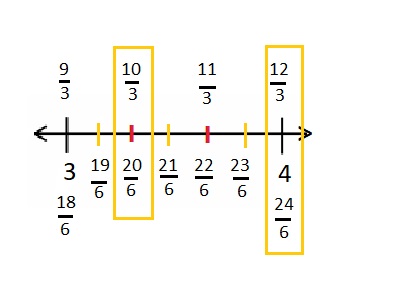
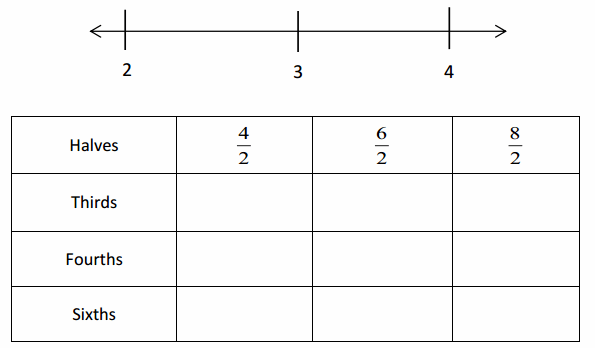
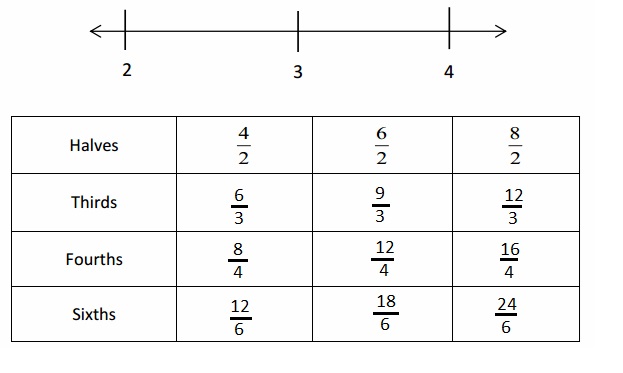
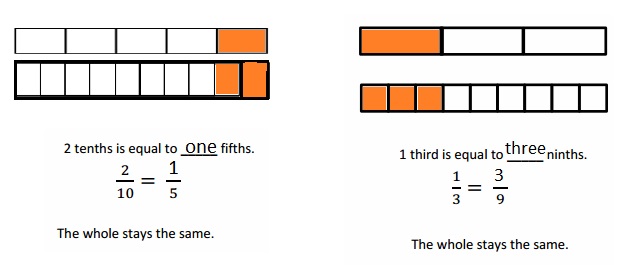
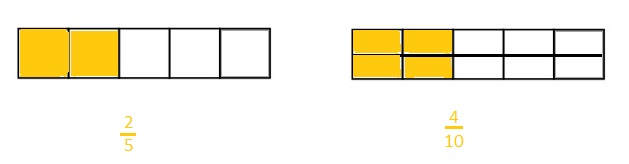
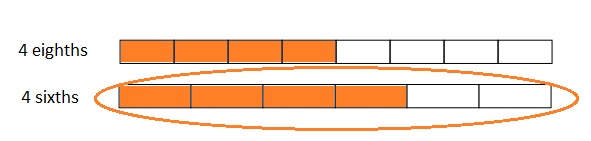
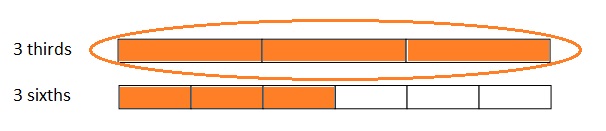
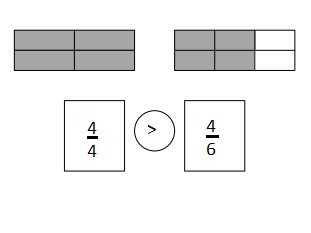
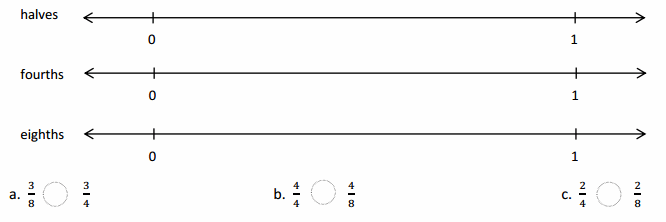
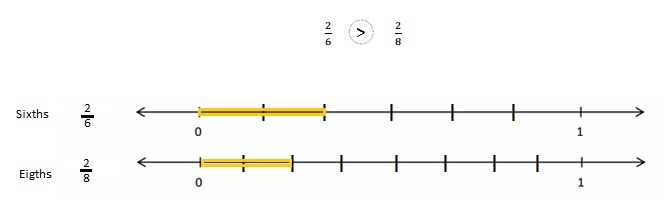
Question 2.
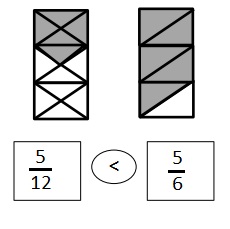
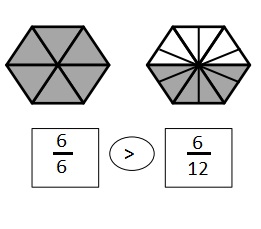
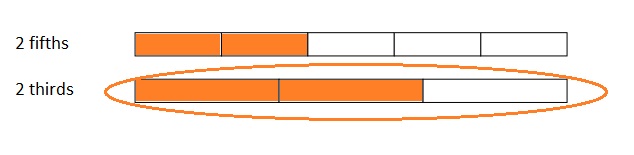
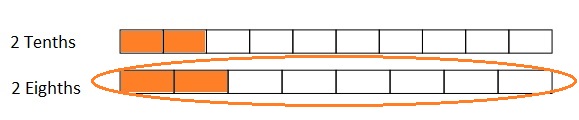
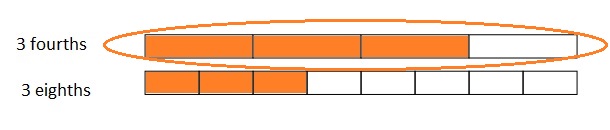
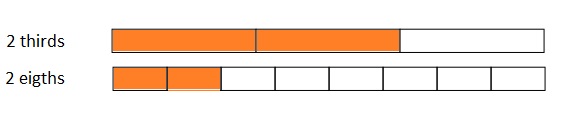
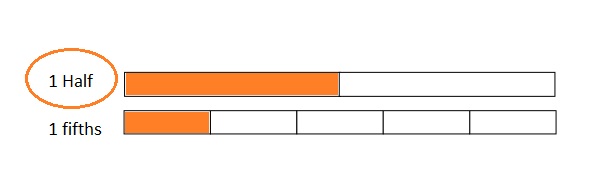
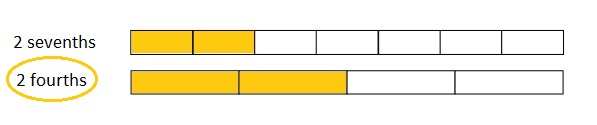
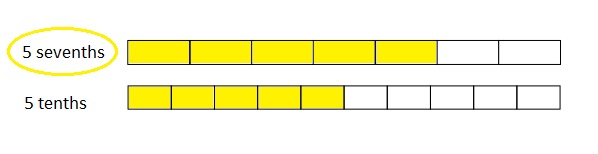
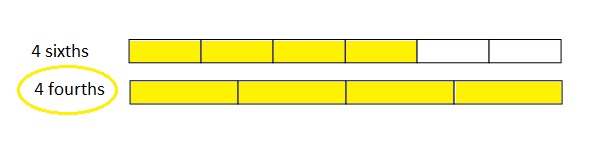
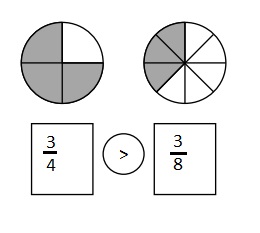
Use the number lines above to compare the following fractions using >, <, or =.

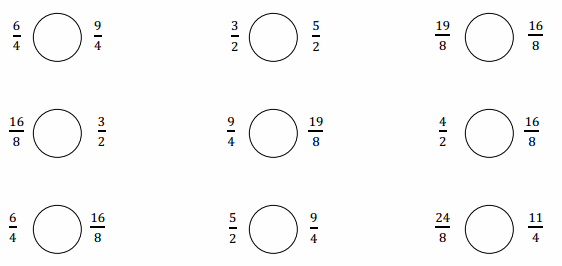
Answer :

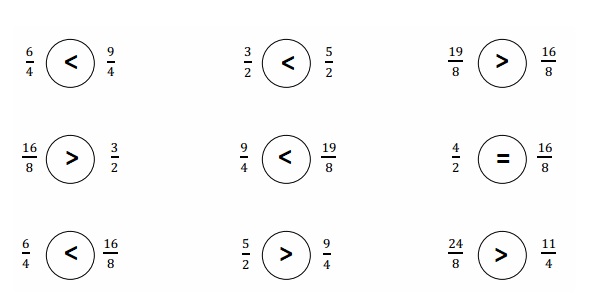
Explanation :
From the above figure the comparisons are done .

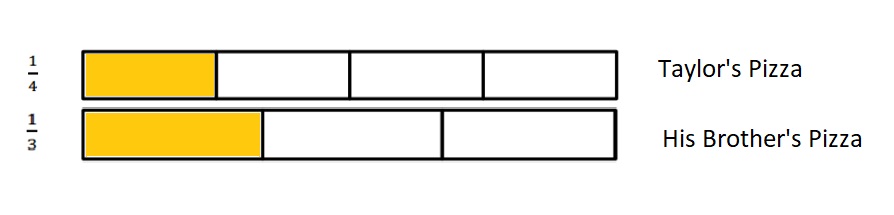
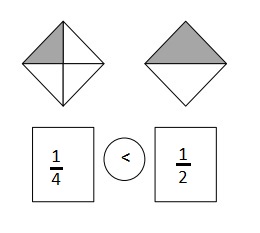
Question 3.
Choose a greater than comparison you made in Problem 2. Use pictures, numbers, and words to explain how you made that comparison.
Answer :

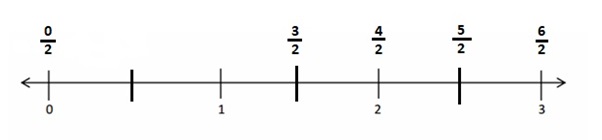
\(\frac {5 }{ 2 }\) is greater than \(\frac { 3 }{ 2 }\)
Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac {5 }{ 2 }\) is right on the number of \(\frac {3 }{ 2 }\)
So, \(\frac {5 }{ 2 }\) is greater than \(\frac { 3 }{ 2 }\)

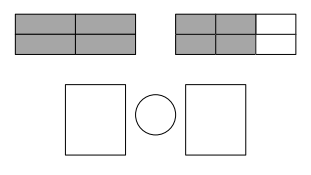
Question 4.
Choose a less than comparison you made in Problem 2. Use pictures, numbers, and words to explain a different way of thinking about the comparison than what you wrote in Problem 3.
Answer :

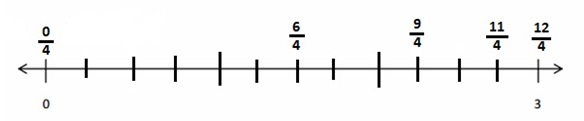
\(\frac {6 }{ 4 }\) is lesser than \(\frac {11 }{ 4 }\)
Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac {6 }{ 4 }\) is left of the number of \(\frac {11 }{ 4 }\)
So, \(\frac {6 }{ 4 }\) is lesser than \(\frac {11 }{ 4 }\)

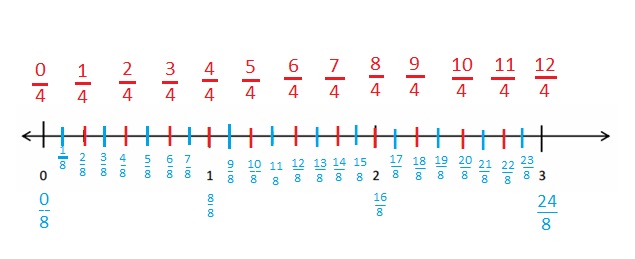
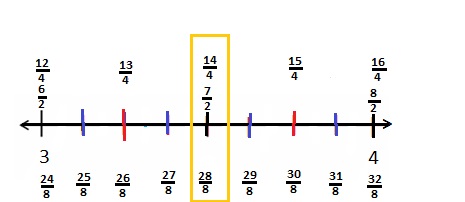
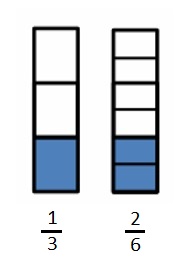
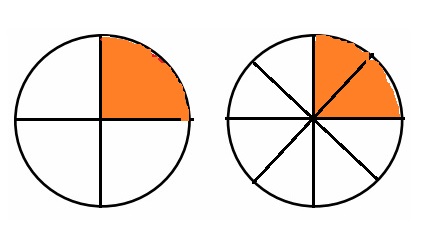
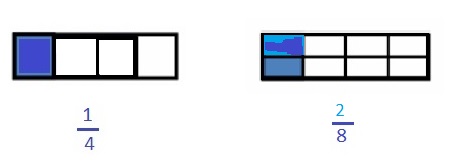
Question 5.
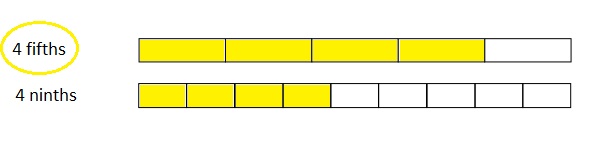
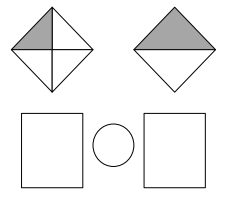
Choose an equal to comparison you made in Problem 2. Use pictures, numbers, and words to explain two ways that you can prove your comparison is true.
Answer :

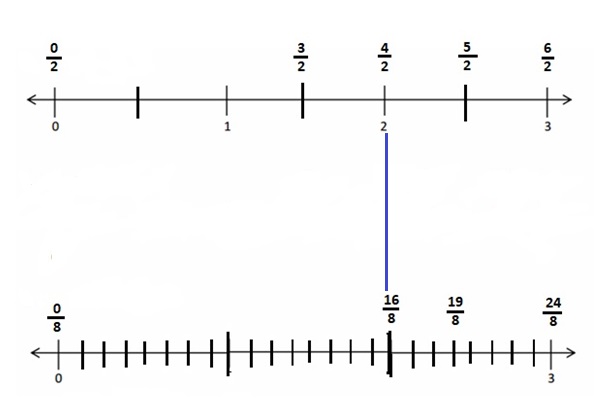
Explanation :
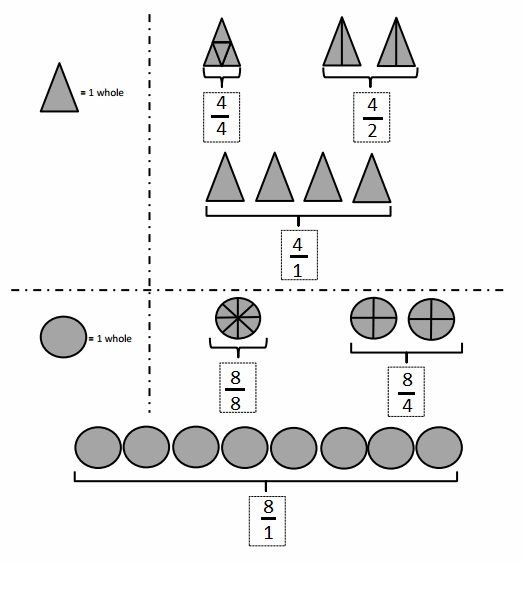
\(\frac { 4 }{ 2 }\) = \(\frac { 16 }{ 8 }\) both the points intersect as shown in above figure .

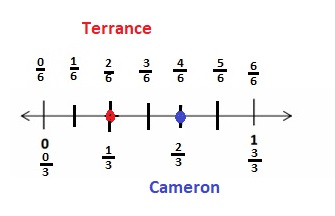
Eureka Math Grade 3 Module 5 Lesson 19 Exit Ticket Answer Key

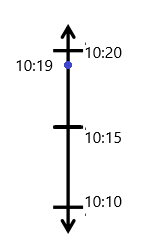
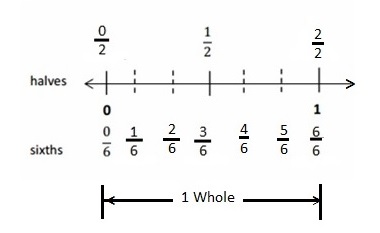
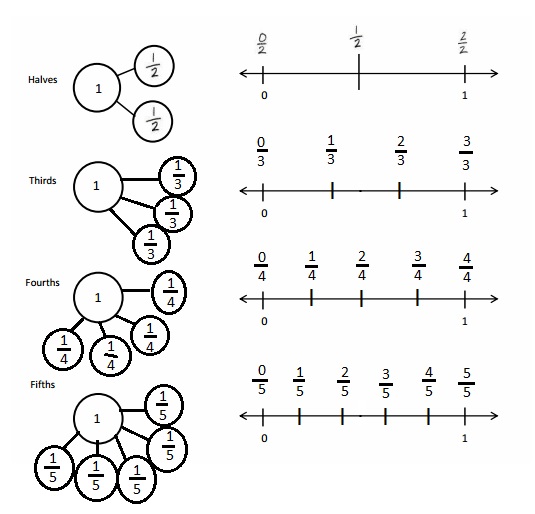
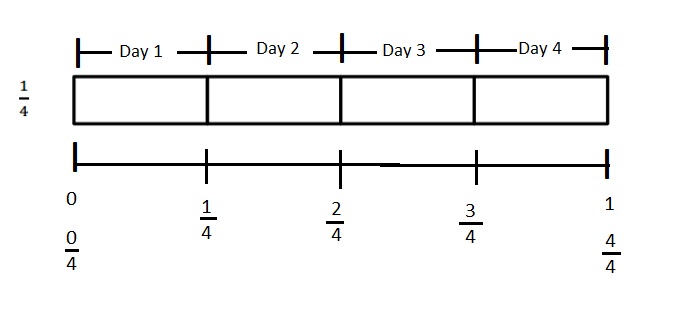
Question 1.
Divide the number line into the given fractional unit. Then, place the fractions. Write each whole as a fraction.

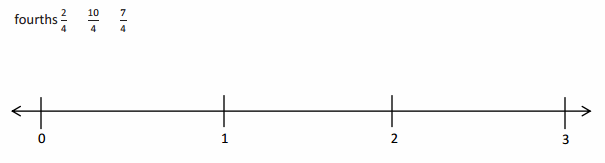
Answer :

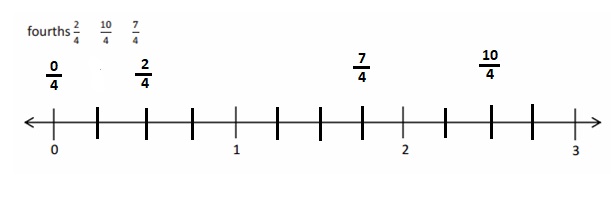
Question 2.
Use the number line above to compare the following fractions using >, <, or =.

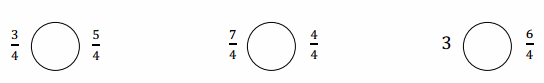
Answer :

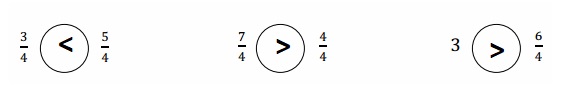
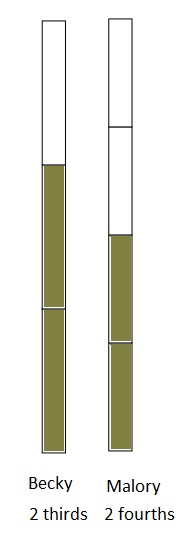
Question 3.
Use the number line from Problem 1. Which is larger: 2 wholes or \(\frac{9}{4}\)? Use words, pictures, and numbers to explain your answer.
Answer :

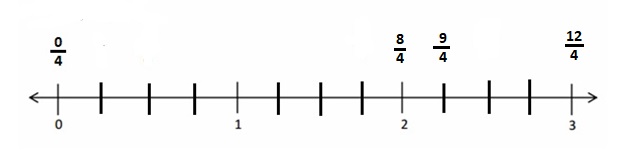
Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac {9 }{ 4 }\) is right of the number of 2 wholes
So, \(\frac {9 }{ 4 }\) > 2 wholes .

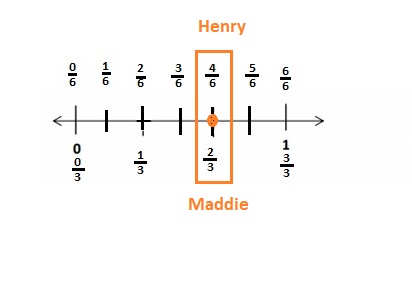
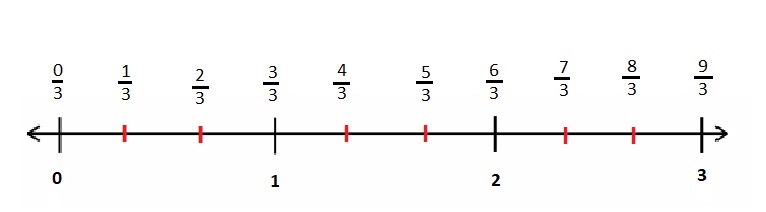
Eureka Math Grade 3 Module 5 Lesson 19 Homework Answer Key

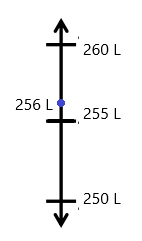
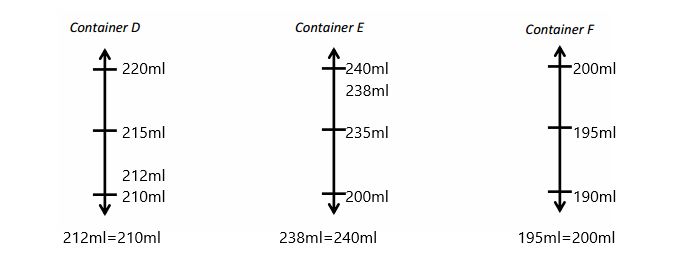
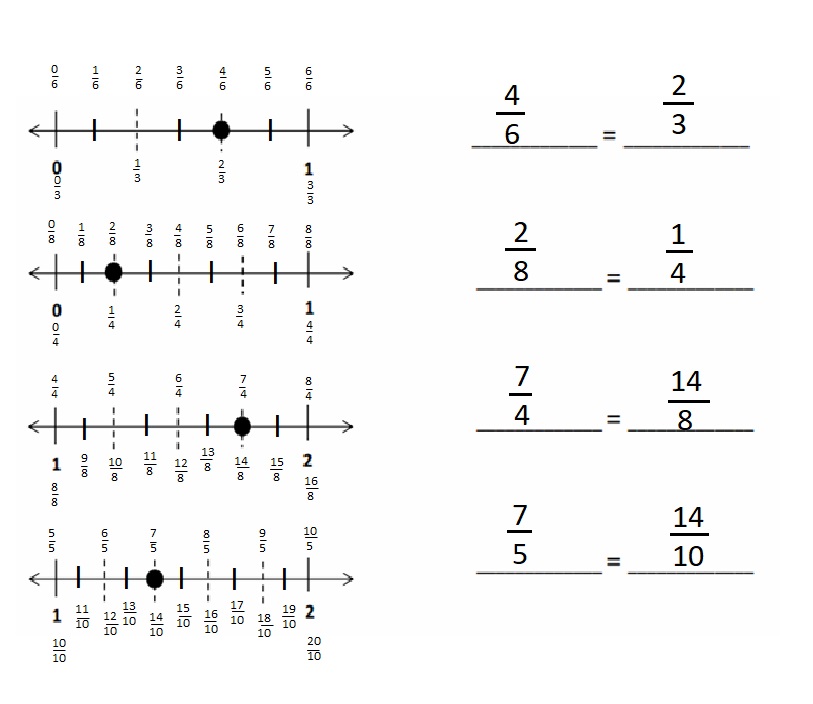
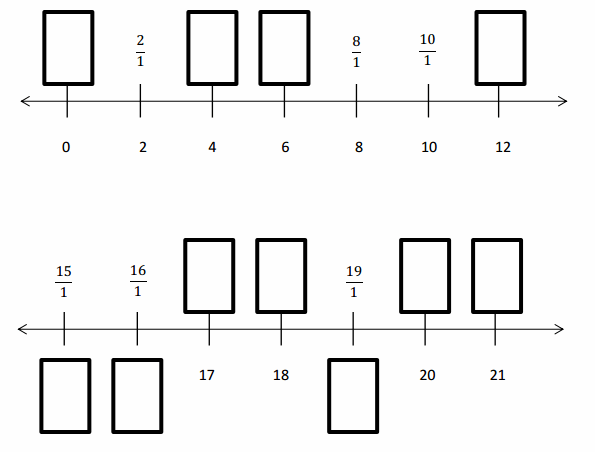
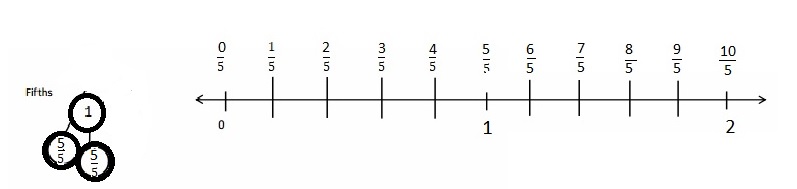
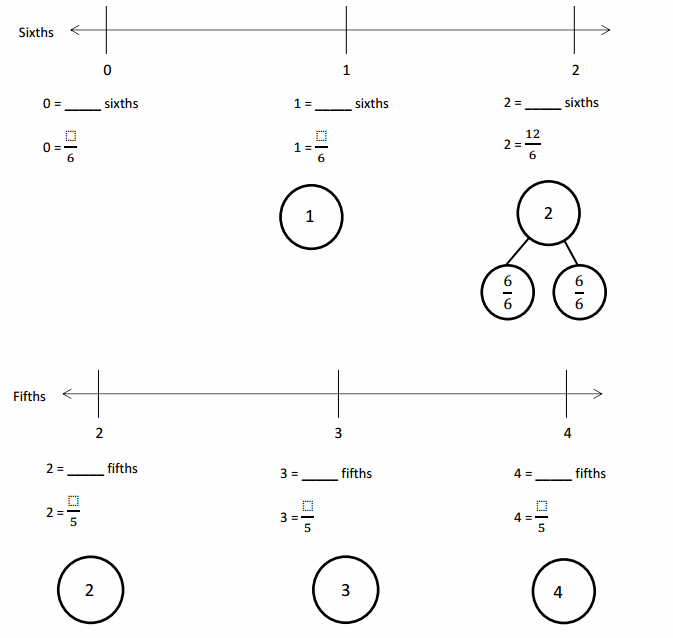
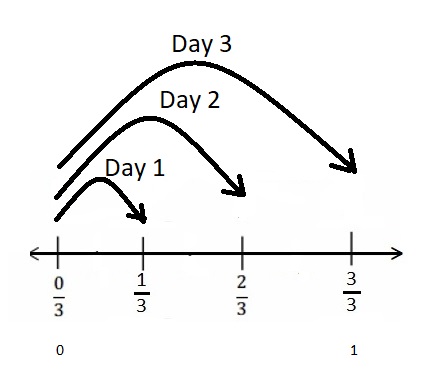
Question 1.
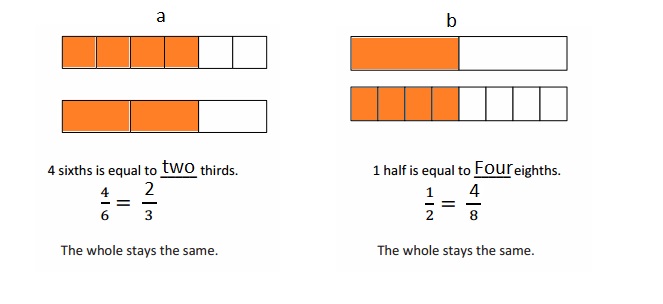
Divide each number line into the given fractional unit. Then, place the fractions. Write each whole as a fraction.

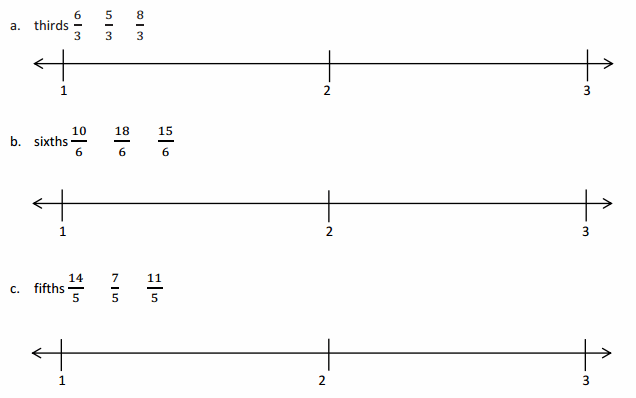
Answer :

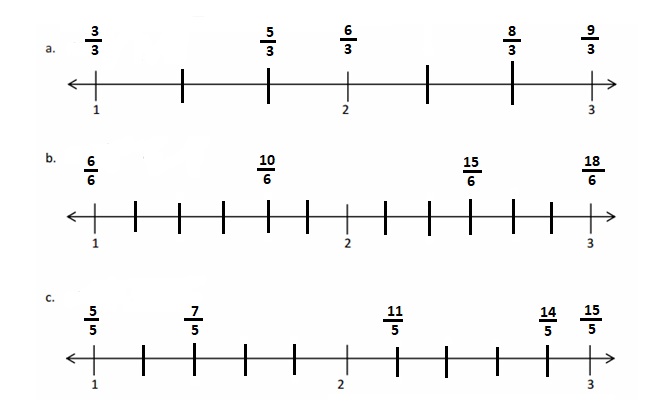
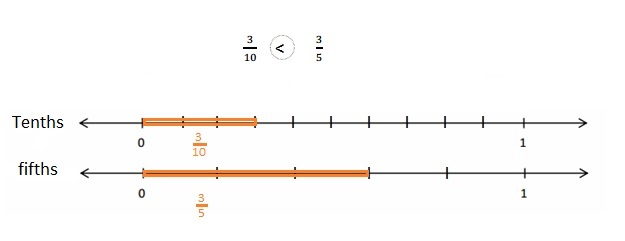
Question 2.
Use the number lines above to compare the following fractions using >, <, or =.

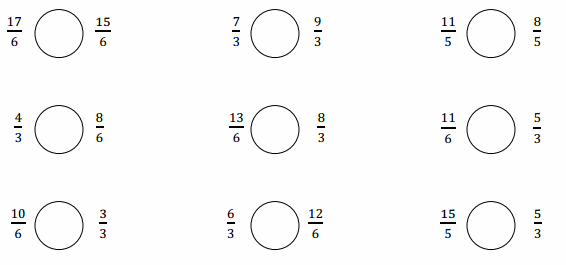
Answer :

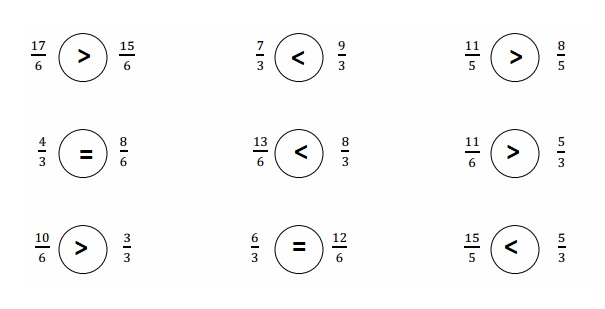
Question 3.
Use fractions from the number lines in Problem 1. Complete the sentence. Use words, pictures, or numbers to explain how you made that comparison.
____________ is greater than ____________.
Answer :
\(\frac { 18 }{ 6 }\) is greater than \(\frac { 15 }{ 6 }\)
Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac { 18 }{ 6 }\) is right of the number of \(\frac { 15 }{ 6 }\)
So, \(\frac { 18 }{ 6 }\) > \(\frac { 15 }{ 6 }\)

Question 4.
Use fractions from the number lines in Problem 1. Complete the sentence. Use words, pictures, or numbers to explain how you made that comparison.
____________ is less than ____________.
Answer :
\(\frac { 5 }{ 3 }\) is lesser than \(\frac { 6 }{ 3 }\)
Explanation :
The number which is on the right of the number is greater and the number which is on the left of the other number is lesser.
\(\frac { 5 }{ 3 }\) is right of the number of \(\frac { 6 }{ 3 }\)
So, \(\frac { 5 }{ 3 }\) < \(\frac { 6 }{ 3 }\)

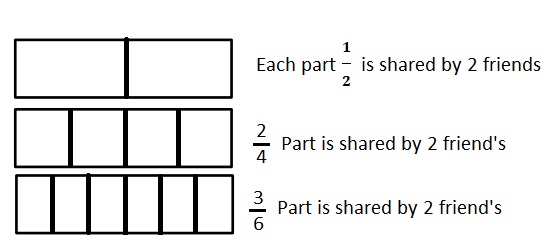
Question 5.
Use fractions from the number lines in Problem 1. Complete the sentence. Use words, pictures, or numbers to explain how you made that comparison.
____________ is equal to ____________.

Answer :
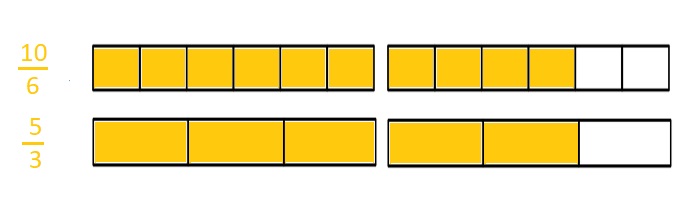
\(\frac { 5 }{ 3 }\) is Equal to \(\frac { 10 }{ 6 }\)

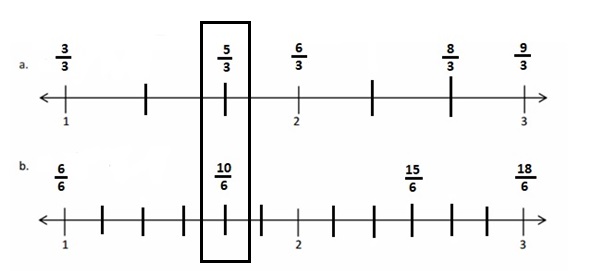
Explanation :
\(\frac { 5 }{ 3 }\) = \(\frac { 10 }{ 6 }\)
Both the numbers are of equal distance and lies at the point as shown in the above figure .

Engage NY Eureka Math 3rd Grade Module 7 Lesson 28 Answer Key

Eureka Math Grade 3 Module 7 Lesson 28 Pattern Sheet Answer Key

Multiply.

multiply by 8 (6–10)
Answer:

Eureka Math Grade 3 Module 7 Lesson 28 Problem Set Answer Key

Question 1.
Gia measures her rectangular garden and finds the width is 9 yards and the length is 7 yards.
a. Estimate to draw Gia’s garden, and label the side lengths.
b. What is the area of Gia’s garden?
c. What is the perimeter of Gia’s garden?
Answer:

Question 2.
Elijah draws a square that has side lengths of 8 centimeters.
a. Estimate to draw Elijah’s square, and label the side lengths.
b. What is the area of Elijah’s square?
c. What is the perimeter of Elijah’s square?
d. Elijah connects three of these squares to make one long rectangle. What is the perimeter of this rectangle?
Answer:

Question 3.
The area of Mason’s rectangular painting is 72 square inches. The width of the painting is 8 inches.
a. Estimate to draw Mason’s painting, and label the side lengths.
b. What is the length of the painting?
c. What is the perimeter of Mason’s painting?
d. Mason’s mom hangs the painting on a wall that already has two of Mason’s other paintings. The areas of the other paintings are 64 square inches and 81 square inches. What is the total area of the wall that is covered with Mason’s paintings?
Answer:

Question 4.
The perimeter of Jillian’s rectangular bedroom is 34 feet. The length of her bedroom is 9 feet.
a. Estimate to draw Jillian’s bedroom, and label the side lengths.
b. What is the width of Jillian’s bedroom?
c. What is the area of Jillian’s bedroom?
d. Jillian has a 4-foot by 6-foot rug in her room. What is the area of the floor that is not covered by the rug?
Answer:

Eureka Math Grade 3 Module 7 Lesson 28 Exit Ticket Answer Key

Jennifer measures her rectangular sandbox and finds the width is 8 feet and the length is 6 feet.
a. Estimate to draw Jennifer’s sandbox, and label the side lengths.
b. What is the area of Jennifer’s sandbox?
c. What is the perimeter of Jennifer’s sandbox?
Answer:

Eureka Math Grade 3 Module 7 Lesson 28 Homework Answer Key

Question 1.
Carl draws a square that has side lengths of 7 centimeters.
a. Estimate to draw Carl’s square, and label the side lengths.
b. What is the area of Carl’s square?
c. What is the perimeter of Carl’s square?
d. Carl draws two of these squares to make one long rectangle. What is the perimeter of this rectangle?
Answer:

Question 2.
Mr. Briggs puts food for the class party on a rectangular table. The table has a perimeter of 18 feet and a width of 3 feet.
a. Estimate to draw the table, and label the side lengths.
b. What is the length of the table?
c. What is the area of the table?
d. Mr. Briggs puts three of these tables together side by side to make 1 long table. What is the area of the long table?
Answer:

Engage NY Eureka Math 3rd Grade Module 2 End of Module Assessment Answer Key

Eureka Math Grade 3 Module 2 End of Module Assessment Task Answer Key

Question 1.
Paul is moving to Australia. The total weight of his 4 suitcases is shown on the scale to the right. On a number line, round the total weight to the nearest 100 kilograms.

Answer:

Explanation:
Paul is moving to Australia. The total weight of his 4 suitcases is 127 kg.
Rounded to the nearest 100 kg, his suit cases weighs 100kg.

Question 2.
Paul buys snacks for his flight. He compares cashews to yogurt raisins. The cashews weigh 205 grams, and the yogurt raisins weigh 186 grams. What is the difference between the weight of the cashews and yogurt raisins?

Answer:

Explanation:
Paul buys snacks for his flight, The cashews weigh 205 grams, and the yogurt raisins weigh 186 grams.
The difference between the weight of the cashews and yogurt raisins is 205-186=19 grams.

Question 3.
The clock to the right shows what time it is now.
a. Estimate the time to the nearest 10 minutes.

Answer:

Explanation:
10:19
The time is 10:20 rounded to the nearest 10 minutes.

b. The clock to the right show Paul’s departure time. Estimate the time to the nearest 10 minutes.

Answer:

Explanation:
10:53
Paul’s departure time is 10:50 rounded to the nearest 10 minutes.

c. Use your answers from Parts (a) and (b) to estimate how long Paul has before his flight leaves.

Answer:
The time is 10:20, Paul’s departure time is 10:50.
To find how long Paul has before his flight leaves subtract 20 from 50
50 min – 20 min = 30 min
Therefore, Paul has about 30 minutes before his flight leaves.

Question 4.
A large airplane uses about 256 liters of fuel every minute.
a. Round to the nearest ten liters to estimate how many liters of fuel get used every minute.

Answer:

Explanation:
A large airplane uses about 256 liters of fuel every minute, rounding to nearest tens.
About 260 L of fuel is used every minute.

b. Use your estimate to find about how many liters of fuel are used every 2 minutes.

Answer:

Explanation:
To find the fuel  used every 2 minutes add the fuel used in 1 minute with it again.
260+260=520L
About 520 L of fuel is used for every 2 minutes.

c. Calculate precisely how many liters of fuel are used every 2 minutes.

Answer:

Explanation:
The actual fuel used in a minute is 256.
To find the actual fuel used add 256+256=512 L
Therefore 512 liters of fuel are used every 2 minutes.

d. Draw a tape diagram to find the difference between your estimate and the precise calculation.

Answer:

Explanation:

The difference between the calculation and the estimate is 8 liters.

Question 5.
Baggage handlers lift heavy luggage into the plane. The weight of one bag is shown on the scale to the right.
a. One baggage handler lifts 3 bags of the same weight. Round to estimate the total weight he lifts. Then, calculate exactly.

Answer:

Explanation:
65 kg is about 70 kg
Baggage handler lifts about 210 kgs in total
Baggage handle lifts exactly 195 kg.

b. Another baggage handler lifts luggage that weighs a total of 200 kilograms. Write and solve an equation to show how much more weight he lifts than the first handler in Part (a).

Answer:

Explanation:
If another baggage handler lifts luggage that weighs a total of 200 kilograms then             200kg-195kg=5 kg
Therefore, another baggage handler lifts 5kg moe than the first handler.

c. The baggage handlers load luggage for 18 minutes. If they start at 10:25 p.m., what time do they finish?

Answer:

Explanation:
The baggage handlers load luggage for 18 minutes
If they start at 10:25 p.m., they will finish at 18+25=43
Therefore, they finish at 10:43pm.

d. One baggage handler drinks the amount of water shown below every day at work. How many liters of water does he drink during all 7 days of the week?

Answer:
One baggage handler drinks 4 L of water every day at work,
To find the number of liters of water he drinks in 7 days of the week is
7 x 4L = 28 L
Therefore, One baggage handler drinks 28 Liters of water in 7 days of the week.

Question 6.
Complete as many problems as you can in 100 seconds. The teacher will time you and tell you when to stop.

Answer:

Engage NY Eureka Math 3rd Grade Module 2 Mid Module Assessment Answer Key

Eureka Math Grade 3 Module 2 Mid Module Assessment Task Answer Key

Question 1.
Fatima runs errands.
a. The clock to the right shows what time she leaves home. What time does she leave?

Answer:
Famita leaves at 2:07 pm.

Explanation:
In the above clock the hours hand on 2 and the minutes hand is on 7.So, the time is 2:07pm.

b. It takes Fatima 17 minutes to go from her home to the market. Use the number line below to show what time she gets to the market.

Answer:

Explanation:
Famita leaves at 2:07 pm
It takes Fatima 17 minutes to go from her home to the market,
Add 7 and 17
7+17=24
She gets to the market at 2:24pm.
c. The clock to the right shows what time Fatima leaves the market. What time does she leave the market?

Answer:
Fatima leaves the market at 2:53pm

Explanation:
In the above clock the hours hand is on 2 and the minutes hand is on 53.So, the time is 2:53pm.

d. How long does Fatima spend at the market?

Answer:

Explanation:
Fatima leaves the market at 2:53pm, She gets to the market at 2:24pm.
Subtract 24 from 53 to find the number of minutes fatima spends in the store.
Fatima is at the store for 29 minutes.

Question 2.
At the market, Fatima uses a scale to weigh a bag of almonds and a bag of raisins, shown below. What is the total weight of the almonds and raisins?

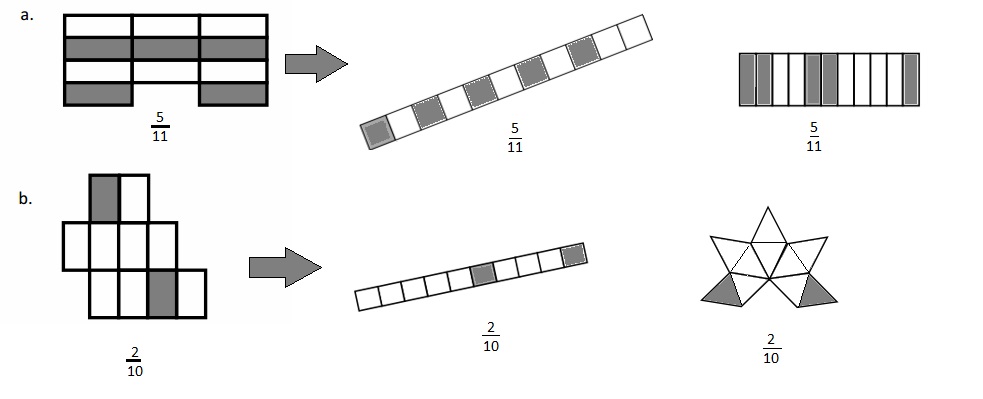
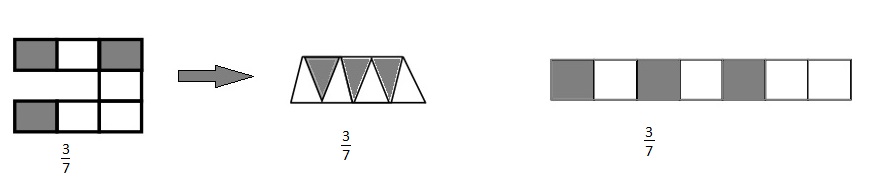
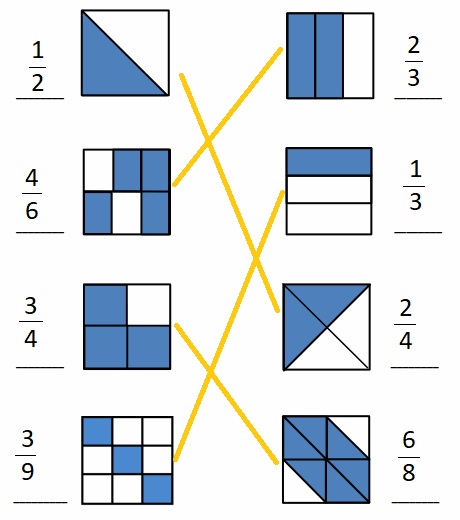
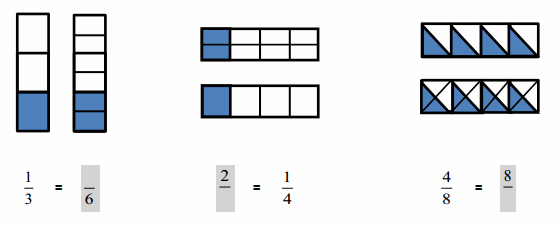
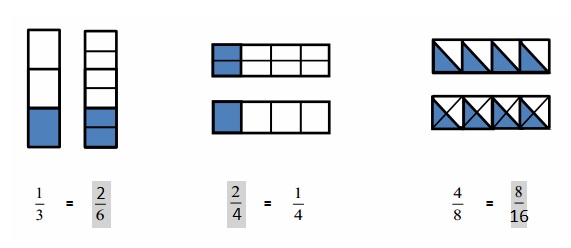
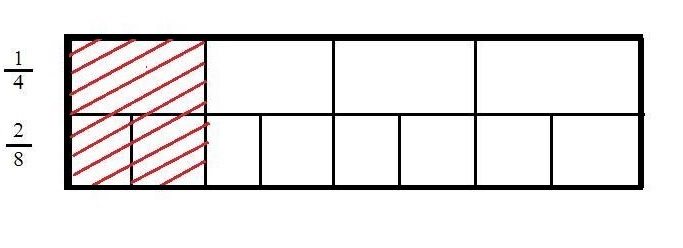
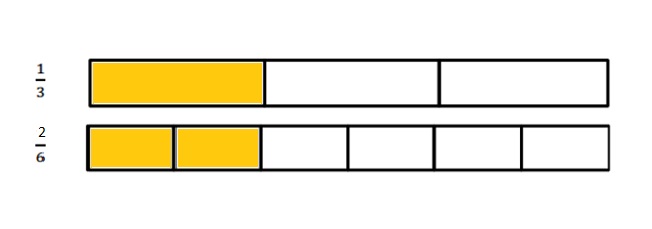
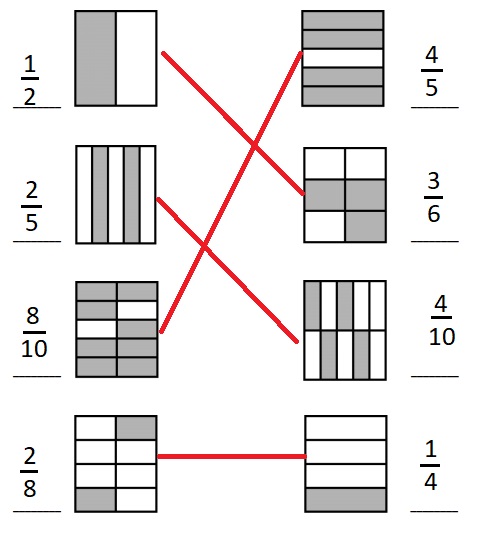
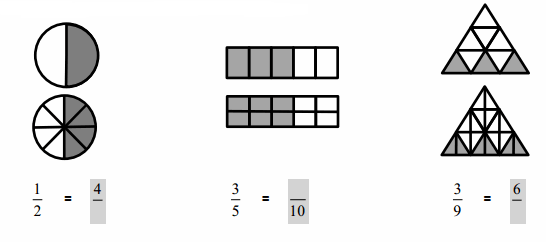Answer: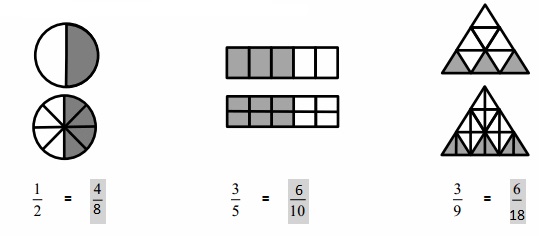
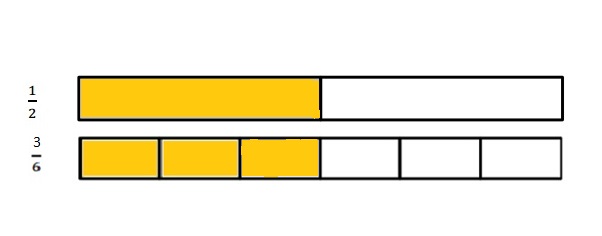
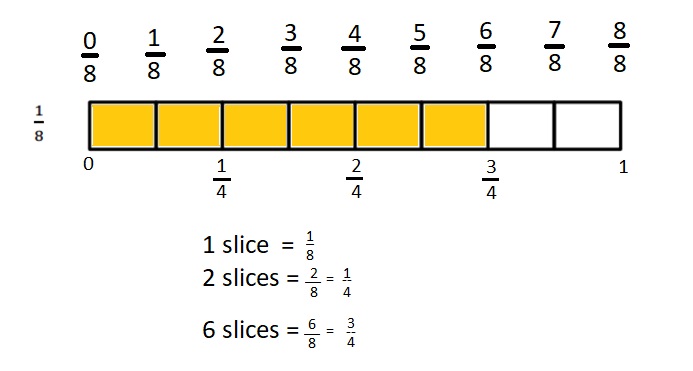
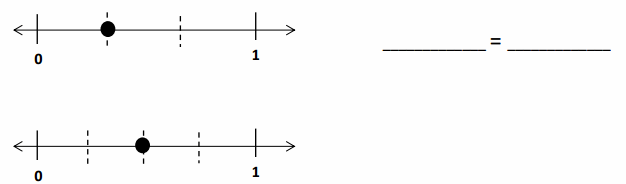
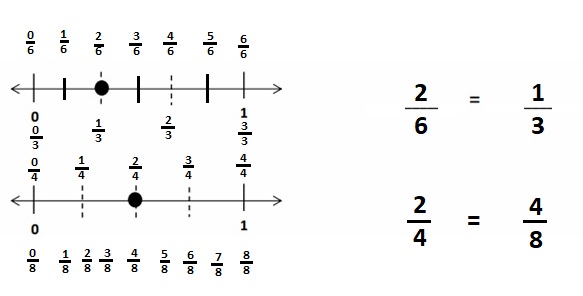
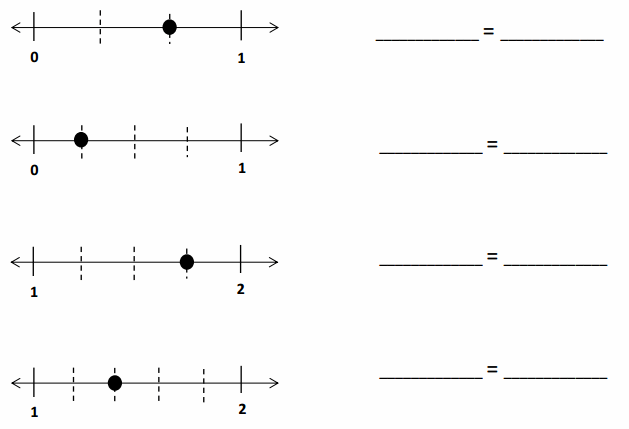
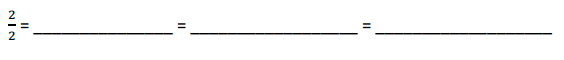
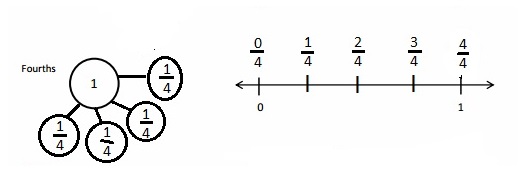
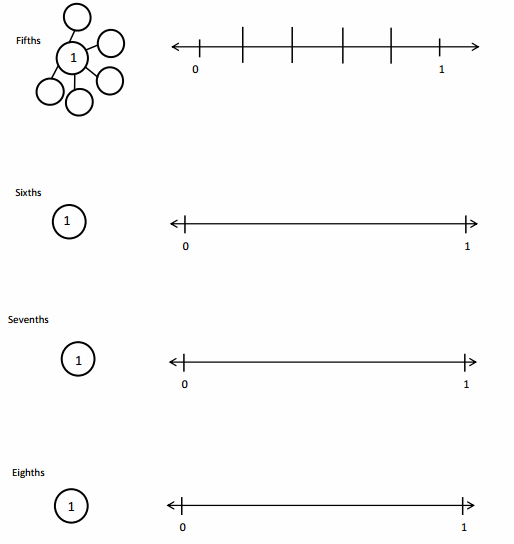
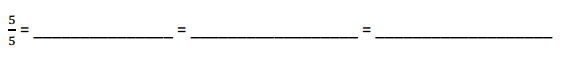
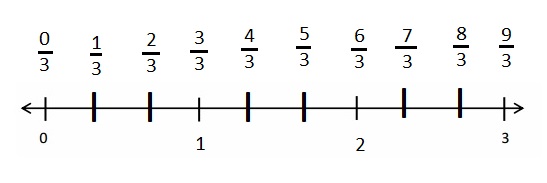
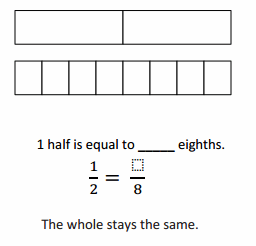
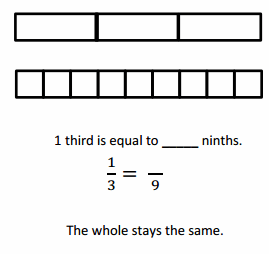
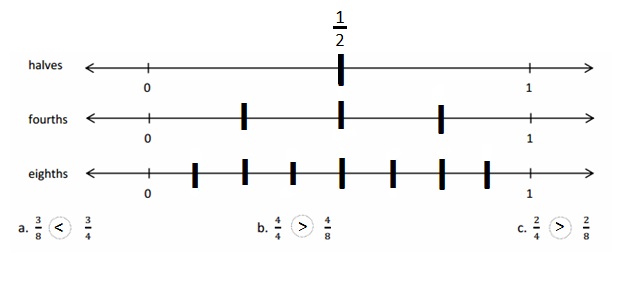
We know from the above picture,
The weight of Almonds is 223 grams,
The weight of Raisins is 355 grams.

The total weight of the almonds and the raisins is 578 grams.

Question 3.
The amount of juice in 1 bottle is shown to the right. Fatima needs 18 liters for a party. Draw and label a tape diagram to find how many bottles of juice she should buy.

Answer:

Explanation:
The amount of juice in 1 bottle is shown to the right. Fatima needs 18 liters for a party
To find the bottles of juice she should buy divide
18/2=9
Fatima needs to buy 9 bottles of juice for the party.

Question 4.
Altogether, Fatima’s lettuce, broccoli, and peas weigh 968 grams. The total weight of her lettuce and broccoli is shown to the right. Write and solve a number sentence to find how much the peas weigh.

Answer:
Fatima’s lettuce, broccoli, and peas weigh 968 grams.
The total weight of her lettuce and broccoli is 744 grams.
To find the weight of peas subtract 744 from 968

Fatima’s Peas weighs 244 grams.

Question 5.
Fatima weighs a watermelon, shown to the right.
a. How much does the watermelon weigh?

Answer:
From the above picture we know that the weight of watermelon is 3 kg.

b. Leaving the store Fatima thinks, “Each bag of groceries seems as heavy as a watermelon!” Use Fatima’s idea about the weight of the watermelon to estimate the total weight of 7 bags.

Answer:
Each bag of groceries seems as heavy as a watermelon
Fatima’s idea about the weight of the watermelon to estimate the total weight of 7 bags
7 x 3 = 21 kg
Fatima estimates the bags weigh about 21 kg altogether.

c. The grocer helps carry about 9 kilograms. Fatima carries the rest. Estimate how many kilograms of groceries Fatima carries.

Answer:
The grocer helps carry about 9 kilograms,Fatima’s bags weigh about 21 kg altogether.
Fatima carries the rest
To find the weight Fatima carries subtract 9 from 21.

Fatima carries about 12 kg of groceries.

d. It takes Fatima 12 minutes to drive to the bank after she leaves the store and then 34 more minutes to drive home. How many minutes does Fatima drive after she leaves the store?

Answer:
It takes Fatima 12 minutes to drive to the bank, 34 more minutes to drive home.
To find the number of minutes famita drives after she leaves the store then
Add 12 and 34
12 minutes + 34 minutes= 46 minutes.
Fatima drives for 46 minutes after she leaves the store.

Engage NY Eureka Math 3rd Grade Module 2 Lesson 21 Answer Key

Question 1.
Weigh the bags of beans and rice on the scale. Then, write the weight on the scales below.

a. Estimate, and then find the total weight of the beans and rice.
Estimate:________ + ________ ≈ ________ + ________ = _________
Actual: ________ + ________ = _________

Answer:
Estimate: 91g+58g ≈ 90g+60g=150g
Actual:91g+58g=149g

b. Estimate, and then find the difference between the weight of the beans and rice.
Estimate: ________ – ________ ≈ ________ – ________ = _________
Actual: ________ – ________ = _________

Answer:
Estimate:91g-58g ≈ 90g-60g=30g
Actual:91g-58g=33g

c. Are your answers reasonable? Explain why.

Answer:
My answers are reasonable because 150g is only 1 more than 149g and 30g is only 3 less than 33g.

Question 2.
Measure the lengths of the three pieces of yarn.
a. Estimate the total length of Yarn A and Yarn C. Then, find the actual total length.

Estimate:60cm+40cm=100cm

The estimated total is 100cm and the actual total is 102cm.

b. Subtract to estimate the difference between the total length of Yarns A and C, and the length of Yarn B. Then, find the actual difference. Model the problem with a tape diagram.

Answer:
Estimate:
100cm-90cm=10cm
Actual:102cm-88cm=14cm
Yarn A+Yarn C=102cm, Yarn B=88cm

Difference between the total length of Yarns A and C, and the length of Yarn B is 102-88=14cm.

Question 3.
Plot the amount of liquid in the three containers on the number lines below. Then, round to the nearest 10 milliliters.

Answer:

a. Estimate the total amount of liquid in three containers. Then, find the actual amount.

Answer:
Estimate:210+240+200=650ml

The estimated total 650ml and the actual total is 645ml.

b. Estimate to find the difference between the amount of water in Containers D and E. Then, find the actual difference. Model the problem with a tape diagram.

Answer:

The estimated difference is 30ml and the actual difference is 26ml.

Question 4.
Shane watches a movie in the theater that is 115 minutes long, including the trailers. The chart to the right shows the length in minutes of each trailer.
a. Find the total number of minutes for all 5 trailers.

Answer:
The total is 5+4+3+5+4=21 minutes

b. Estimate to find the length of the movie without trailers. Then, find the actual length of the movie by calculating the difference between 115 minutes and the total minutes of trailers.

Answer:
115min – 21 min    120-20=100min
115min-21min=94min
The estimated length is 100 minutes and the actual length is 94minutes.

c. Is your answer reasonable? Explain why.

Answer:
Yes, it is reasonable because 94minutes is close to 100minutes.

Eureka Math Grade 3 Module 2 Lesson 21 Exit Ticket Answer Key

Rogelio drinks water at every meal. At breakfast, he drinks 237 milliliters. At lunch, he drinks 300 milliliters. At dinner, he drinks 177 milliliters.
a. Estimate the total amount of water Rogelio drinks. Then, find the actual amount of water he drinks at all three meals.

Answer:
Estimate:
237 ml  ≈ 200 ml
300 ml ≈ 300 ml
177 ml ≈ 177 ml
200+300+177=677ml
About 677ml amount of water Rogelio drinks

Actual:
237+300+177ml=714 ml

Therefore, the actual amount of water he drinks at all three meals is 714.

b. Estimate how much more water Rogelio drinks at lunch than at dinner. Then, find how much more water Rogelio actually drinks at lunch than at dinner.

Answer:
Estimate:
300 ml ≈ 300 ml
177 ml ≈ 200 ml
300-200=100 ml
About 100ml more water Rogelio drinks at lunch than at dinner

Actual:
300 ml- 177 ml=123ml.

123 ml of water Rogelio actually drinks at lunch than at dinner

Eureka Math Grade 3 Module 2 Lesson 21 Homework Answer Key

Question 1.
There are 153 milliliters of juice in 1 carton. A three-pack of juice boxes contains a total of 459 milliliters. Estimate, and then find the actual total amount of juice in 1 carton and in a three-pack of juice boxes.
153 mL + 459 mL ≈ ______ + ______ =______
153 mL + 459 mL = ______

Answer:
153 ml + 459 ml ≈ 200 ml + 500 ml=700ml
153 ml + 459 ml =612 ml

b. Estimate, and then find the actual difference between the amount in 1 carton and in a three-pack of juice boxes.
459 mL − 153 mL ≈ ______ − ______ = ______
459 mL − 153 mL = ______

Answer:
459 ml – 153 ml ≈ 500 ml – 200 ml=300ml
459 ml – 153 ml = 306 ml

c. Are your answers reasonable? Why?
Answer:
No, my answer in addition is not reasonable as it is not close to the actual answer.
Yes, my answers in subtraction is reasonable as it is close to the actual answer.

Question 2.
Mr. Williams owns a gas station. He sells 367 liters of gas in the morning, 300 liters of gas in the afternoon, and 219 liters of gas in the evening.
a. Estimate, and then find the actual total amount of gas he sells in one day.

Answer:
Estimate:
367 L + 300 L + 219 L ≈ 400 L + 300 L + 200 L = 900 L
The estimated total amount of gas Mr.Williams sells in one day is 900L.

Actual:
367 L + 300 L + 219 L =886 L

The actual total amount of gas Mr.Williams sells in one day is 886 L.

b. Estimate, and then find the actual difference between the amount of gas Mr. Williams sells in the morning and the amount he sells in the evening.

Answer:
367 L – 219 L ≈ 400 L – 200 L = 200 L
The estimated difference between the amount of gas Mr. Williams sells in the morning and the amount he sells in the evening

Actual:
367 L – 219 L = 148 L

The actual difference between the amount of gas Mr. Williams sells in the morning and the amount he sells in the evening

Question 3.
The Blue Team runs a relay. The chart shows the time, in minutes, that each team member spends running.
a. How many minutes does it take the Blue Team to run the relay?

Answer:
The Blue Team took 28 minutes to run the relay.

b. It takes the Red Team 37 minutes to run the relay. Estimate, and then find the actual difference in time between the two teams.

Answer:
Estimate:
37 min ≈ 40 min
26 min ≈ 30min
40-30=10min
The estimated difference in time between the two teams is 10 minutes

Actual:
37 min – 26 min=11 min

The actual difference in time between the two teams is 11 minutes.

Question 4.
The lengths of three banners are shown to the right.
a. Estimate, and then find the actual total length of Banner A and Banner C.

Answer:
Estimate:
437 cm + 332 cm ≈ 400 L + 300 L =700 L
The estimate total length of Banner A and Banner C = 700 cm.

Actual:
437 cm + 332 cm = 769 cm

The actual total length of Banner A and Banner C = 769 cm.

b. Estimate, and then find the actual difference in length between Banner B and the combined length of Banner A and Banner C. Model the problem with a tape diagram.

Answer:
Estimate:
(437 cm+332 cm) – 457 L ≈ (400+300cm) – 400 L = 700 cm – 400 L =300 L
The estimated difference in length between Banner B and the combined length of Banner A and Banner C is 300 cm

Actual:
(437 cm+332 cm) – 457 L = 769 cm – 457 cm = 312 cm.

The actual difference in length between Banner B and the combined length of Banner A and Banner C is 312 cm