Prasanna

Engage NY Eureka Math 6th Grade Module 2 Mid Module Assessment Answer Key

Eureka Math Grade 6 Module 2 Mid Module Assessment Answer Key

Question 1.
Yasmine is having a birthday party with snacks and activities for her guests. At one table, five people are sharing three-quarters of a pizza. What equal-sized portion of the whole pizza will each of the five people receive?
a. Use a model (e.g., picture, number line, or manipulative materials) to represent the quotient.
Answer:

b. Write a number sentence to represent the situation. Explain your reasoning.
Answer:
Because there are 5 people, we found I out of the 5, which is \(\frac{1}{5}\). I can represent the situation as:
\(\frac{3}{2}\) ÷ 5 = \(\frac{3}{4}\) . \(\frac{1}{5}\) = \(\frac{3}{20}\)

c. If three-quarters of the pizza provided 12 pieces to the table, how many pieces were in the pizza when it was full? Support your answer with models.
Answer:

Question 2.
Yasmine needs to create invitations for the party. She has \(\frac{3}{4}\) of an hour to make the invitations. It takes her \(\frac{1}{12}\) of an hour to make each card. How many invitations can Yasmine create?
a. Use a number line to represent the quotient.
Answer:

b. Draw a model to represent the quotient.
Answer:

c. Compute the quotient without models. Show your work.
Answer:

Question 3.
Yasmine is serving ice cream with the birthday cake at her party. She has purchased 19\(\frac{1}{2}\) pints of ice cream. She will serve \(\frac{3}{4}\) of a pint to each guest.
a. How many guests can be served ice cream?
Answer:

b. Will there be any ice cream left? Justify your answer.
Answer:
My answer, 26, is a whole number, so there will be no ice cream left over. If my answer was 26\(\frac{1}{4}\) or any mixed number, there would be ice cream left over.

Question 4.
L.B. Johnson Middle School held a track and field event during the school year. Miguel took part in a four person shot put team. Shot put is a track and field event where athletes throw (or “put”) a heavy sphere, called a “shot,” as far as possible. To determine a team score, the distances of all team members are added. The team with the greatest score wins first place. The current winning team’s final score at the shot put is 52.08 ft. Miguel’s teammates threw the shot put the following distances: 12.26 ft., 12.82 ft., and 13.75 ft. Exactly how many feet will Miguel need to throw the shot put in order to tie the current first-place score? Show your work.

Answer:

Miguel will need to throw the shot put 13.25 feet to he the current first place score.

Question 5.
The sand pit for the long jump has a width of 2.75 meters and a length of 9.54 meters. Just in case it rains, the principal wants to cover the sand pit with a piece of plastic the night before the event. How many square meters of plastic will the principal need to cover the sand pit?

Answer:

Question 6.
The chess club is selling drinks during the track and field event. The club purchased water, juice boxes, and pouches of lemonade for the event. They spent $138.52 on juice boxes and $75.00 on lemonade. The club purchased three cases of water. Each case of water costs $6.80. What ¡s the total cost of the drinks?
Answer:

Engage NY Eureka Math 6th Grade Module 3 Lesson 1 Answer Key

Eureka Math Grade 6 Module 3 Lesson 1 Exercise Answer Key

Complete the diagrams. Count by ones to label the number lines.

Exercise 1.
Plot your point on both number lines.
Answer:
Answers may vary.

Exercise 2.
Show and explain how to find the opposite of your number on both number lines.
Answer:
In this example, the number chosen was – 4. So – 4 is the first number plotted, and the opposite is 4. Horizontal Number Line: I found my point by starting at zero and counting four units to the left to end on – 4. Then, to find the opposite of my number, I started on zero and counted to the right four units to end on 4. Vertical Number Line: I found my point by starting at zero and counting four units down to end on – 4. I found the opposite of my number by starting at zero and counting four units up to end on 4.

Exercise 3.
Mark the opposite on both number lines.
Answer:
Answers may vary.

Exercise 4.
Choose a group representative to place the opposite number on the class number lines.
Answer:

Exercise 5.
Which group had the opposite of the number on your index card?
Answer:
Answers may vary. Jackie’s group had the opposite of the number on my index card. They had 4.

Eureka Math Grade 6 Module 3 Lesson 1 Problem Set Answer Key

Question 1.
Draw a number line, and create a scale for the number line in order to plot the points – 2, 4, and 6.
a. Graph each point and its opposite on the number line.
Answer:

b. Explain how you found the opposite of each point.
Answer:
To graph each point, I started at zero and moved right or left based on the sign and number (to the right for a positive number and to the left for a negative number). To graph the opposites, I started at zero, but this time I moved in the opposite direction the same number of times.

Question 2.
Carlos uses a vertical number line to graph the points – 4, – 2, 3, and 4. He notices that – 4 is closer to zero than – 2. He is not sure about his diagram. Use what you know about a vertical number line to determine if Carlos made a mistake or not. Support your explanation with a number line diagram.
Answer:
Carlos made a mistake because – 4 is less than – 2, so it should be farther down the number line. Starting at zero, negative numbers decrease as we look farther below zero. So, – 2 lies before – 4 on a number line since – 2 is 2 units below zero and – 4 is 4 units below zero.

Question 3.
Create a scale in order to graph the numbers – 12 through 12 on a number line. What does each tick mark represent?
Answer:
Each tick mark represents 1 unit.

Question 4.
Choose an integer between – 5 and – 10. Label it R on the number line created in Problem 3, and complete the following tasks.
Answers may vary. Refer to the number line above for sample student work. – 6, – 7, – 8, or – 9
a. What is the opposite of R? Label it Q.
Answer:
Answers will vary. 6

b. State a positive integer greater than Q. Label it T.
Answer:
Answers will vary. 11

c. State a negative integer greater than R. Label it S.
Answer:
Answers will vary. – 3

d. State a negative integer less than R. Label it U.
Answer:
Answers will vary. 9

e. State an integer between R and Q. Label it V.
Answer:
Answers will vary. 2

Question 5.
Will the opposite of a positive number always, sometimes, or never be a positive number? Explain your reasoning.
Answer:
The opposite of a positive number will never be a positive number. For two nonzero numbers to be opposites, zero has to be in between both numbers, and the distance from zero to one number has to equal the distance between zero and the other number.

Question 6.
Will the opposite of zero always, sometimes, or never be zero? Explain your reasoning.
Answer:
The opposite of zero will always be zero because zero is its own opposite.

Question 7.
Will the opposite of a number always, sometimes, or never be greater than the number itself? Explain your reasoning. Provide an example to support your reasoning.
Answer:
The opposite of a number will sometimes be greater than the number itself because it depends on the given number. For example, if the number given is – 6, then the opposite is 6, which is greater than – 6. If the number given is 5, then the opposite is – 5, which is not greater than 5. If the number given is 0, then the opposite is 0, which is never greater than itself.

Eureka Math Grade 6 Module 3 Lesson 1 Exit Ticket Answer Key

Question 1.
Draw a number line, and create a scale for the number line in order to plot the points —2, 4, and 6.
a. Graph each point and its opposite on the number line.

Answer:
Answers will vary. One possible answer is a: – 4; b: – 1; C: 1; d: 4.

Question 2.
Below is a list of numbers in order from least to greatest. Use what you know about the number line to complete the list of numbers by filling in the blanks with the missing integers.
– 6, – 5, ________, – 3, – 2, – 1, ________, 1, 2, _______, 4, ________, 6
Answer:
– 6, – 5,   – 4,     – 3, – 2, – 1,    0,    1, 2,    3,    4,     5,      6

Question 3.
Complete the number line scale. Explain and show how to find 2 and the opposite of 2 on a number line.
Answer:
I would start at zero and move 2 units to the left to locate the number – 2 on the number line. So, to locate 2, 1 would start at zero and move 2 units to the right (the opposite direction).

Eureka Math Grade 6 Module 3 Lesson 1 Exploratory Challenge Answer Key

Exploratory Challenge: Constructing the Number Line
Answer:
The purpose of this exercise is to let students construct the number line (positive and negative numbers and zero) using a compass.

Have students draw a line, place a point on the line, and label it 0.

Have students use the compass to locate and label the next point 1, thus creating the scale. Students continue to locate other whole numbers to the right of zero using the same unit measure.

Using the same process, have students locate the opposites of the whole numbers. Have students label the first point to the left of zero – 1.

Introduce to the class the definition of the opposite of a number.

Sample student work is shown below.

Engage NY Eureka Math 6th Grade Module 2 End of Module Assessment Answer Key

Eureka Math Grade 6 Module 2 End of Module Assessment Answer Key

Question 1.
LB. Johnson Middle School held a track and field event during the school year. The chess club sold various drink and snack items for the participants and the audience. Altogether, they sold 486 items that totaled $2,673.
a. If the chess club sold each item for the same price, calculate the price of each item.
Answer:

Each item’s price is $5.50

b. Explain the value of each digit in your answer to 1(a) using place value terms.
Answer:

Question 2.
The long-jump pit was recently rebuilt to make it level with the runway. Volunteers provided pieces of
wood to frame the pit. Each piece of wood provided measures 6 feet, which is approximately 1.8287
meters.

a. Determine the amount of wood, in meters, needed to rebuild the frame.
Answer:

b. How many boards did the volunteers supply? Round your calculations to the nearest hundredth, and then provide the whole number of boards supplied.
Answer:

Question 3.
Andy runs 436.8 meters in 62.08 seconds.
a. If Andy runs at a constant speed, how far does he run in one second? Give your answer to the nearest tenth of a second.
Answer:

b. Use place value, multiplication with powers of 10, or equivalent fractions to explain what is happening mathematically to the decimal points in the divisor and dividend before dividing.
Answer:

When you write the problem as a fraction, multiply the numerator and denominator by 100. Multiplying each by 100 resulted in both numbers being whole numbers.
436.8 ÷ 62.08 is the same as 43,680 ÷ 6,208.

c. In the following expression, place a decimal point in the divisor and the dividend to create a new problem with the same answer as in 3(a). Then, explain how you know the answer will be the same.
43.68 ÷ 6.208
Answer:

Multiplying or dividing the dividend and divisor by the same power of ten yields the same quotient.

Question 4.
The PTA created a cross-country trail for the meet.
a. The PTA placed a trail marker in the ground every four hundred yards. Every nine hundred yards, the PTA set up a water station. What is the shortest distance a runner will have to run to see both a water station and trail marker at the same location?
Answer:

LCM 2 . 2 . 3 . 3 = 36 hundred
36 hundred yards

b. There are 1,760 yards in one mile. About how many miles will a runner have to run before seeing both a water station and trail marker at the same location? Calculate the answer to the nearest hundredth of a mile.
Answer:

c. The PTA wants to cover the wet areas of the trail with wood chips. They find that one bag of wood
chips covers a 3\(\frac{1}{2}\)-yard section of the trail. If there is a wet section of the trail that is approximately 50\(\frac{1}{4}\) yards long, how many bags of wood chips are needed to cover the wet section of the trail?
Answer:

Question 5.
The Art Club wants to paint a rectangle-shaped mural to celebrate the winners of the track and field meet. They design a checkerboard background for the mural where they will write the winners’ names. The rectangle measures 432 inches in length and 360 inches in width. Apply Euclid’s algorithm to determine the side length of the largest square they can use to fill the checkerboard pattern completely without overlap or gaps.
Answer:

Engage NY Eureka Math 6th Grade Module 2 Lesson 19 Answer Key

Eureka Math Grade 6 Module 2 Lesson 19 Opening Exercise Answer Key

Euclid’s algorithm is used to find the greatest common factor (GCF) of two whole numbers.
1. Divide the larger of the two numbers by the smaller one.
2. If there is a remainder, divide it into the divisor.
3. Continue dividing the last divisor by the last remainder until the remainder is zero.
4. The final divisor is the GCF of the original pair of numbers.

383 ÷ 4 =
Answer:
95.75

432 ÷ 12 =
Answer:
36

403 ÷ 13 =
Answer:
31

Eureka Math Grade 6 Module 2 Lesson 19 Example Answer Key

Example 1:
Euclid’s Algorithm Conceptualized

Answer:
→ Notice that we can use the GCF of 20 to create the largest square tile that covers the rectangle without any overlap or gaps. We used a 20 × 20 tile.
→ But, what if we did not know that? We could start by guessing. What is the biggest square tile that we can guess?
60 × 60

Display the following diagram:

→ It fits, but there are 40 units left over. Do the division problem to prove this.
→ What is the leftover area?
60 × 40
→ What is the largest square tile that we can fit in the leftover area?
40 × 40

Display the following diagram:

→ What is the leftover area?
20 × 40
→ What is the largest square tile that we can fit in the leftover area? 20)40
20 × 20
→ When we divide 40 by 20, there is no remainder. So, we have tiled the entire rectangle.
→ If we had started tiling the whole rectangle with squares, the largest square we could have used would be 20 by 20.

Example 2.
a. Let’s apply Euclid’s algorithm to some of the problems from our last lesson.
i. What is the GCF of 30 and 50?
Answer:
10

ii. Using Euclid’s algorithm, we follow the steps that are listed In the Opening Exercise.
Answer:

When the remainder is zero, the final divisor is the GCF.

b. Apply Euclid’s algorithm to find the GCF (30, 45).
Answer:

15

Example 3.
Larger Numbers
GCF (96, 144)
Answer:

Example 4:
Area Problems
The greatest common factor has many uses. Among them, the GCF lets us find out the maximum size of squares that cover a rectangle. When we solve problems like this, we cannot have any gaps or any overlapping squares. Of course, the maximum size squares is the minimum number of squares needed.

A rectangular computer table measures 30 inches by 50 inches. We need to cover it with square tiles. What is the side length of the largest square tile we can use to completely cover the table without overlap or gaps?
Answer:

a. If we use squares that are 10 by 10, how many do we need?
Answer:
3 . 5, or 15 squares

b. If this were a giant chunk of cheese ¡n a factory, would ¡t change the thinking or the calculations we just did?
Answer:
No

c. How many 10 inch × 10 inch squares of cheese could be cut from the giant 30 inch × 50 inch slab?
Answer:
15

Eureka Math Grade 6 Module 2 Lesson 19 Problem Set Answer Key

Question 1.
Use Euclid’s algorithm to find the greatest common factor of the following pairs of numbers:
a. GCF(12, 78)
Answer:

GCF (12, 78) = 6

b. GCF(18, 176)
Answer:

GCF (18, 176) = 2

Question 2.
Juanita and Samuel are planning a pizza party. They order a rectangular sheet pizza that measures 21 inches by 36 inches. They tell the pizza maker not to cut it because they want to cut it themselves.
a. All pieces of pizza must be square with none left over. What is the side length of the largest square pieces into which Juanita and Samuel can cut the pizza?
Answer:
GCF (21, 36) = 3 They can cut the pizza into 3 inch by 3 inch squares.

b. How many pieces of this size can be cut?
Answer:
7. 12 = 84 Juanita and Samuel can cut 84 pieces.

Question 3.
Shelly and Mickelle are making a quilt. They have a piece of fabric that measures 48 inches by 168 inches.
a. All pieces of fabric must be square with none left over. What is the side length of the largest square pieces into which Shelly and Mickelle can cut the fabric?
Answer:
GCF (48, 168) = 24

b. How many pieces of this size can Shelly and Mickelle cut?
Answer:
2 . 7 = 14 They can cut 14 pieces.

Eureka Math Grade 6 Module 2 Lesson 19 Exit Ticket Answer Key

Question 1.
Use Euclid’s algorithm to find the greatest common factor of 45 and 75.
Answer:

GCF (45, 75) = 15

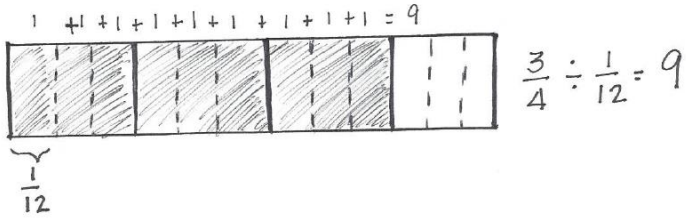
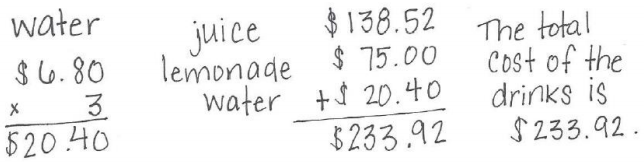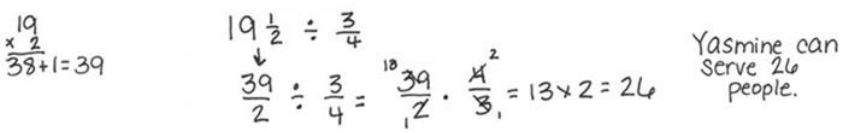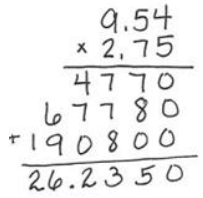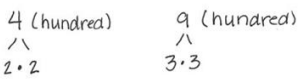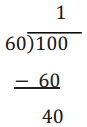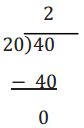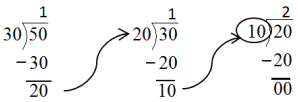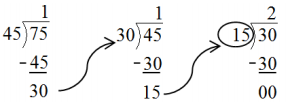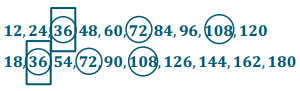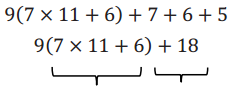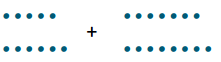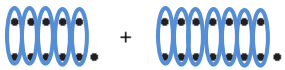Engage NY Eureka Math 6th Grade Module 2 Lesson 18 Answer Key

Eureka Math Grade 6 Module 2 Lesson 18 Example Answer Key

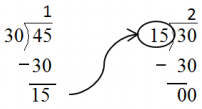
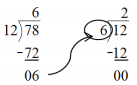
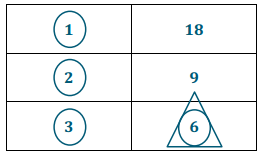
Find the greatest common factor of 12 and 18.
→ Listing these factor pairs in order helps ensure that no common factors are missed. Start with 1 multiplied by the number.
→ Circle all factors that appear on both lists.
→ Place a triangle around the greatest of these common factors.
GCF (12, 18)

12

Answer:

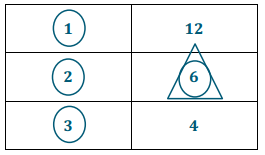
18

Answer:

Example 2.
Least Common Multiple
Find the least common multiple of 12 and 18.
LCM (12, 18)
Write the first 10 multiples of 12.
Answer:
12, 24, 36, 48, 60, 72, 84, 96, 108, 120

Write the first 10 multiples of 18.
Answer:
18, 36, 54, 72, 90, 108, 126, 144, 162, 180

Circle the multiples that appear on both lists.
Answer:

Put a rectangle around the least of these common multiples.
Answer:

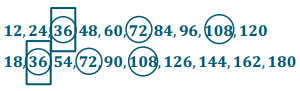
Eureka Math Grade 6 Module 2 Lesson 18 Exercise Answer Key

Exercise 1.
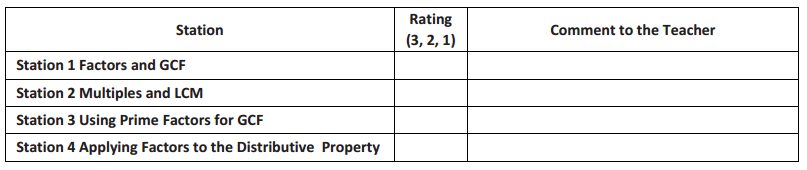
Station 1: Factors and GCF
Choose one of these problems that has not yet been solved. Solve It together on your student page. Then, use your marker to copy your work neatly on the chart paper. Use your marker to cross out your choice so that the next group solves a different problem.
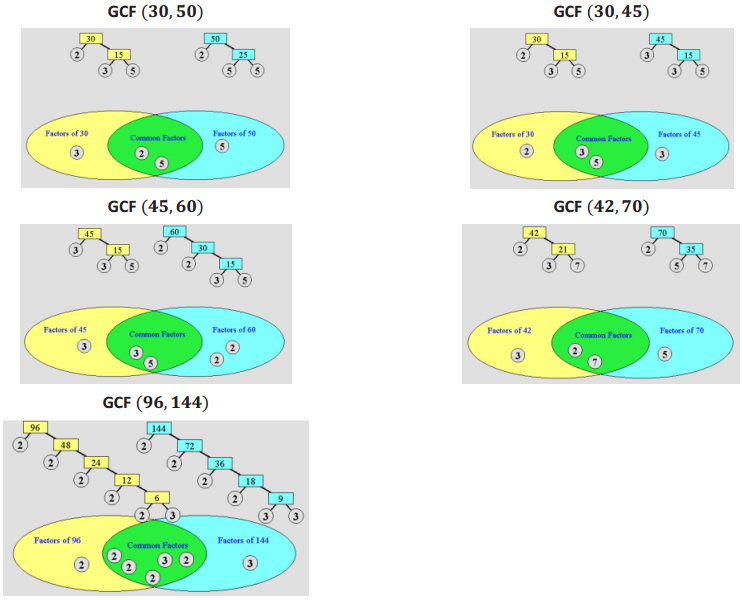
GCF (30, 50)
Answer:
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30                       Factors of 50: 1, 2, 5, 10, 25, 50
Common Factors: 1, 2, 5, 10                                   Greatest Common Factor: 10

GCF (30, 45)
Answer:
Factors of 30: 1, 2, 3, 5, 6, 10, 15, 30                        Factors of 45: 1, 3, 5, 9, 15, 45
Common Factors: 1, 3, 5, 15                                     Greatest Common Factor: 15

GCF (45, 60)
Answer:
Factors of 45: 1, 3, 5, 9, 15, 45                        Factors of 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Common Factors: 1, 3, 5, 15                           Greatest Common Factor: 15

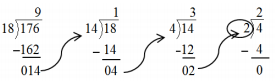
GCF (42, 70)
Answer:
Factors of 42: 1, 2, 3, 6, 7, 14, 21, 42                       Factors of 70: 1, 2, 5, 7, 10, 14, 35, 70
Common Factors: 1, 2, 7, 14                                   Greatest Common Factor: 14

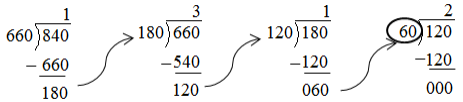
GCF (96, 144)
Answer:
Factors of 96: 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96                       Factors of 144: 1, 2, 3, 4, 6, 8, 9, 12, 16, 18, 24, 36, 48, 72, 144
Common Factors: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48                            Greatest Common Factor: 48

Next, choose one of these problems that has not yet been solved:

a. There are 18 girls and 24 boys who want to participate in a Trivia Challenge. If each team must have the same ratio of girls and boys, what is the greatest number of teams that can enter? Find how many boys and girls each team would have.
Answer:
6 teams can enter the Trivia Challenge, each having 3 girls and 4 boys.

b. Ski Club members are preparing Identical welcome kits for new skiers. The Ski Club has 60 hand-warmer packets and 48 foot-warmer packets. Find the greatest number of identical kits they can prepare using all of the hand-warmer and foot-warmer packets. How many hand-warmer packets and foot-warmer packets would each welcome kit have?
Answer:
There would be 12 welcome kits, each having 5 hand-warmer packets and 4 foot-warmer packets.

c. There are 435 representatives and 100 senators serving in the United States Congress. How many Identical groups with the same numbers of representative and senators could be formed from all of Congress if we want the largest groups possible? How many representatives and senators would be In each group?
Answer:
5 identical groups with the same numbers of representatives and senators can be formed, each group with 87 representatives and 20 senators.

d. Is the GCF of a pair of numbers ever equal to one of the numbers? Explain with an example.
Answer:
Yes. Valid examples should show a pair of numbers where the lesser of the two numbers is a factor of the greater number; the greater of the two numbers is a multiple of the lesser number.

e. Is the GCF of a pair of numbers ever greater than both numbers? Explain with an example.
Answer:
No. Factors are, by definition, less than or equal to the number. Therefore, the GCF cannot be greater than both numbers.

Station 2: Multiples and LCM
Choose one of these problems that has not yet been solved. Solve it together on your student page. Then, use your marker to copy your work neatly on the chart paper. Use your marker to cross out your choice so that the next group solves a different problem.
LCM (9, 12)
Answer:
Multiples of 9: 9, 18, 27, 36                                                                    Multiples of 12: 12, 24, 36
Least Common Multiple: 36

LCM (8, 18)
Multiples of 8: 8, 16, 24, 32, 40, 48, 56, 64, 72                                         Multiples of 18: 18, 36, 54, 72
Least Common Multiple: 72

LCM (4, 30)
Multiples of 4: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60         Multiples of 30: 30, 60
Least Common Multiple: 60

LCM (12, 30)
Multiples of 12: 12, 24, 36, 48, 60                                                              Multiples of 30: 30 ,60
Least Common Multiple: 60

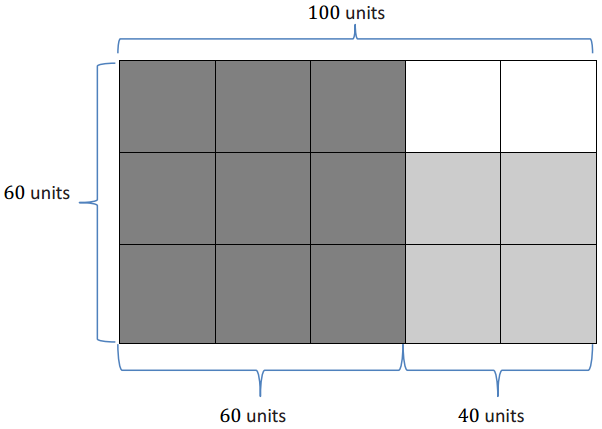
LCM (20, 50)
Multiples of 20: 20, 40, 60, 80, 100                                                             Multiples of 50: 50, 100
Least Common Multiple: 100

Next, choose one of these problems that has not yet been solved. Solve it together on your student page. Then, use your marker to copy your work neatly on this chart paper and to cross out your choice so that the next group solves a different problem.

a. Hot dogs come packed 10 in a package. Hot dog buns come packed 8 in a package. If we want one hot dog for each bun for a picnic with none left over, what is the least amount of each we need to buy? How many packages of each item would we have to buy?
Answer:
Four packages of hot dogs = 40 hot dogs. Five packages of buns = 40 buns. LCM (8, 10) = 40.

b. Starting at 6:00 a.m., a bus stops at my street corner every 15 minutes. Also starting at 6:00 a.m., a taxi cab comes by every 12 minutes. What is the next time both a bus and a taxi are at the corner at the same time?
Answer:
Both o bus and a taxi arrive at the corner at 7:00 a.m., which is 60 minutes after 6:00 a.m.
LCM (12, 15) = 60.

c. Two gears in a machine are aligned by a mark drawn from the center of one gear to the center of the other. If the first gear has 24 teeth, and the second gear has 40 teeth, how many revolutions of the first gear are needed until the marks line up again?
Answer:
The first gear needs five revolutions. During this time, 120 teeth pass by. The second gear revolves three times. LCM(24, 40) = 120.

d. Is the LCM of a pair of numbers ever equal to one of the numbers? Explain with an example.
Answer:
Yes. Valid examples should show of a pair of numbers where the lesser of the two numbers is a factor of the greater number; the greater of the two numbers is a multiple of the lesser number.

e. Is the LCM of a pair of numbers ever less than both numbers? Explain with an example.
Answer:
No. Multiples are, by definition, equal to or greater than the number.

Station 3: Using Prime Factors to Determine GCF
Choose one of these problems that has not yet been solved. Solve it together on your student page. Then, use your marker to copy your work neatly on the chart paper and to cross out your choice so that the next group solves a different problem.

Next, choose one of these problems that has not yet been solved:

a. Would you rather find all the factors of a number or find all the prime factors of a number? Why?
Answer:
Accept opinions. Students should defend their answer and use accurate mathematical terms in their response.

b. Find the GCF of your original pair of numbers.
Answer:
See answers listed in Exploratory Challenge 1.

c. Is the product of your LCM and GCF less than, greater than, or equal to the product of your numbers?
Answer:
In all cases, GCF (a, b) . LCM (a, b) = a . b.

d. Glenn’s favorite number is very special because it reminds him of the day his daughter, Sarah, was born. The factors of this number do not repeat, and all of the prime numbers are less than 12. What is Glenn’s number? When was Sarah born?
Answer:
2 . 3 . 5 . 7 . 11 = 2,310 Sarah’s birth date is 2/3/10.

Station 4: Applying Factors to the Distributive Property

Choose one of these problems that has not yet been solved. Solve it together on your student page. Then, use your marker to copy your work neatly on the chart paper and to cross out your choice so that the next group solves a different problem.

Find the GCF from the two numbers, and rewrite the sum using the distributive property.

1. 12 + 18 =
Answer:
6(2) + 6(3) = 6(2 + 3) = 6(5) = 30

2. 42 + 14 =
Answer:
7(6) + 7(2) = 7(6 + 2) = 7(8) = 56

3. 36 + 27 =
Answer:
9(4) + 9(3) = 9(4 + 3) = 9(7) = 63

4. 16 + 72 =
Answer:
8(2) + 8(9) = 8(2 + 9) = 8(11) = 88

5. 44 + 33 =
Answer:
11(4) + 11(3) = 11(4 + 3) = 11(7) = 77

Next, add another example to one of these two statements applying factors to the distributive property.

Choose any numbers for n, a, and b.

n(a) + n(b) = n(a + b)
Answer:
Accept all mathematically correct responses.

n(a) – n(b) = n(a – b)
Answer:
The distributive property holds for addition as well as subtraction. Accept all mathematically correct responses.

Eureka Math Grade 6 Module 2 Lesson 18 Problem Set Answer Key

Station 1: Factors and GCF
Choose one of these problems that has not yet been solved. Solve it together on your student page. Then, use your marker to copy your work neatly on the chart paper and to cross out your choice so that the next group solves a different problem.
Find the greatest common factor of one of these pairs: 30, 50; 30, 45; 45, 60; 42, 70; 96, 144.
Answer:

Next, choose one of these problems that has not yet been solved:
a. There are 18 girls and 24 boys who want to participate in a Trivia Challenge. If each team must have the same ratio of girls and boys, what is the greatest number of teams that can enter? Find how many boys and girls each team would have.
Answer:

b. Ski Club members are preparing identical welcome kits for new skiers. The Ski Club has 60 hand-warmer packets and 48 foot-warmer packets. Find the greatest number of identical kits they can prepare using all of the hand-warmer and foot-warmer packets. How many hand-warmer packets and foot-warmer packets would each welcome kit have?
Answer:

c. There are 435 representatives and loo senators serving in the United States Congress. How many identical groups with the same numbers of representatives and senators could be formed from all of Congress if we want the largest groups possible? How many representatives and senators would be in each group?
Answer:

d. Is the GCF of a pair of numbers ever equal to one of the numbers? Explain with an example.
Answer:

e. Is the GCF of a pair of numbers ever greater than both numbers? Explain with an example.
Answer:

Station 2: Multiples and LCM
Choose one of these problems that has not yet been solved. Solve it together on your student page. Then, use your marker to copy your work neatly on the chart paper and to cross out your choice so that the next group solves a different problem.
Find the least common multiple of one of these pairs: 9, 12; 8, 18; 4, 30; 12, 30; 20, 50.
Answer:

Next, choose one of these problems that has not yet been solved:
a. Hot dogs come packed 10 in a package. Hot dog buns come packed 8 in a package. If we want one hot dog for each bun for a picnic, with none left over, what is the least amount of each we need to buy? How many packages of each item would we have to buy?
Answer:

b. Starting at 6:00 a.m., a bus stops at my street corner every 15 minutes. Also starting at 6:00 a.m., a taxi cab comes by every 12 minutes. What is the next time both a bus and a taxi are at the corner at the same time?
Answer:

c. Two gears in a machine are aligned by a mark drawn from the center of one gear to the center of the other. If the first gear has 24 teeth, and the second gear has 40 teeth, how many revolutions of the first gear are needed until the marks line up again?
Answer:

d. Is the LCM of a pair of numbers ever equal to one of the numbers? Explain with an example.
Answer:

e. Is the LCM of a pair of numbers ever less than both numbers? Explain with an example.
Answer:

Solve it together on your student page. Then, use your marker to copy your work neatly on this chart paper and to cross out your choice so that the next group solves a different problem.

Station 3: Using Prime Factors to Determine GCF

Choose one of these problems that has not yet been solved. Solve it together on your student page. Then, use your marker to copy your work neatly on the chart paper and to cross out your choice so that the next group solves a different problem.

Use prime factors to find the greatest common factor of one of the following pairs of numbers:
30, 50 30, 45 45, 60 42, 70 96, 144
Answer:

Next choose one of these problems that has not yet been solved:
a. Would you rather find all the factors of a number or find all the prime factors of a number? Why?
Answer:

b. Find the GCF of your original pair of numbers.
Answer:

c. Is the product of your LCM and GCF less than, greater than, or equal to the product of your numbers?
Answer:

d. Glenn’s favorite number is very special because it reminds him of the day his daughter, Sarah, was born. The factors of this number do not repeat, and all of the prime numbers are less than 12. What is Glenn’s number? When was Sarah born?
Answer:

Station 4: Applying Factors to the Distributive Property
Study these examples of how factors apply to the distributive property.

8 + 12 = 4(2) + 4(3) = 4(2 + 3) = 20
4(2) + 4(3) = 4(5) = 20

15 + 25 = 5(3) + 5(5) = 5(3 + 5) = 40
5(3) + 5(5) = 5(8) = 40

36 – 24 = 4(9) – 4(6) = 4(9 – 6) = 12
4(9) – 4(6) = 4(3) = 12

Choose one of these problems that has not yet been solved. Solve it together on your student page. Then, use your marker to copy your work neatly on the chart paper and to cross out your choice so that the next group solves a different problem.

Find the GCF from the two numbers, and rewrite the sum using the distributive property.
Question 1.
12 + 18 =
Answer:

Question 2.
42 + 14 =
Answer:

Question 3.
36 + 27 =
Answer:

Question 4.
16 + 72 =
Answer:

Question 5.
44 + 33 =
Answer:

Next, add another example to one of these two statements applying factors to the distributive property.
Choose any numbers for n, a, and b.
n(a) + n(b) = n(a + b)
Answer:

n(a) – n(b) = n(a – b)
Answer:

Eureka Math Grade 6 Module 2 Lesson 18 Exit Ticket Answer Key

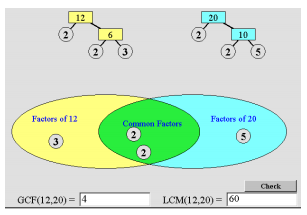
Question 1.
Find the LCM and GCF of 12 and 15.
Answer:
LCM: 60; GCF: 3

Question 2.
Write two numbers, neither of which is 8, whose GCF is 8.
Answer:
Answers will vary (e.g., 16 and 24, or 24 and 32).

Question 3.
Write two numbers, neither of which is 28, whose LCM is 28.
Answer:
Answers will vary (e.g., 4 and 14, or 4 and 7).

Rate each of the stations you visited today. Use this scale:
3 – Easy – I’ve got It, I don’t need any help.
2 – Medium – I need more practice, but I understand some of It.
1 – Hard – I’m not getting this yet.

Complete the following chart:

Engage NY Eureka Math 6th Grade Module 2 Lesson 17 Answer Key

Eureka Math Grade 6 Module 2 Lesson 17 Opening Exercise Answer Key

Below is a list of 10 numbers. Place each number in the circle(s) that is a factor of the number. Some numbers can be placed in more than one circle. For example, if 32 were on the list, it would be placed in the circles with 2, 4, and 8 because they are all factors of 32.
24; 36; 80; 115; 214; 360; 975; 4,678; 29,785; 414, 940

Answer:

Discussion:

Divisibility rule for 2: If and only if its unit digit is 0, 2, 4, 6, or 8

Divisibility rule for 4: If and only if its last two digits are a number divisible by 4

Divisibility rule for 5: If and only if its unit digit is 0 or 5

Divisibility rule for 8: If and only if its last three digits are a number divisible by 8

Divisibility rule for 10: If and only if its unit digit is 0

Decimal numbers with fraction parts do not follow the divisibility tests:
Students learn two new divisibility rules today. The rules are used to determine if numbers are divisible by 3 or 9. Start with students who already know the factors of 3 and 9, so they can see that the rule works.

→ What do the numbers 12, 18, 30, 66, and 93 all have in common?
Each is divisible by 3.

→ Calculate the sum of the digits for each given number. For example, the sum of the digits in the number 12 is 3 because 1 + 2 = 3.

Give students time to find the sums. Record the sums on the board.
→ What do these sums have in common?
They are divisible by 3.

→ When the sum of a number’s digits is divisible by 3, the entire number is divisible by 3. Now let’s examine a different set of numbers: 27, 36, 54, 72, and 99. What do these numbers have in common?
They are divisible by 9.

→ Calculate the sum of the digits for each given number.
Provide time for students to find the sums. Record the sums on the board.

→ What do all the sums have in common?
They are divisible by 9.

→ When the sum of the digits is divisible by 3 and 9, the entire number is divisible by 9. Let’s use this knowledge to determine if a large number is divisible by 3, 9, or both. The number 765 is divisible by both 3 and 9.

→ We can use what we know about the distributive property to prove that 765 is divisible by 3 and by 9.
→ Let’s begin by expanding 765.

Display the following progression.
→ We can represent 765 as:
7 × 100 + 6 × 10 + 5 × 1

→ We can further decompose the numbers that are easily seen as divisible by 3 and 9.
→ Let’s decompose 100 to 99 + 1. Why would we do this?
Because we already know that 99 is divisible by 3 and 9.
7(99 + 1) + 6 × 10 + 5

→ We can also decompose 10 to 9 + 1. Why would we do this?
Because we already know that 9 is divisible by 3 and 9.
7(99 + 1) + 6(9+ 1) + 5

→ Let’s use the distributive property further to distribute the factor 7 in the expression. We can represent 7
times the quantity (99 + 1) as 7(99) + 7 × 1, or 7(99) + 7.
7(99) + 7+ 6(9 + 1) + 5

→ We can distribute the factor 6 in the same fashion. How can we distribute the factor 6 in the expression?
We can represent 6 times the quantity (9 + 1) as 6(9) + 6 × 1, or 6(9) + 6.
7(99) + 7 + 6(9) + 6 + 5

→ Since we know that 9 is divisible by both 3 and 9, let’s factor the 9 out of the expression. We can use the commutative and associative properties to easily see this.
7(99) + 7 + 6(9) + 6 + 5
7(9 × 11) + 6(9 × 1) + 7 + 6 + 5
9(7 × 11 + 6) + 7 + 6 + 5

→ Let’s investigate our current expression. Obviously the product of 9(7 × 11 + 6) is divisible by 9 since the 9 is already factored out.

→ What about the sum of 7 + 6 + 5? What is the sum? Is this sum divisible by 3 and 9?
7 + 6 + 5 = 18.
This sum is divisible by 3 and 9.

→ Are 3 and 9 both factors of 18?
Yes

→ What do you notice about the addends 7 + 6 + 5?
They are the digits of our original number 765.

Let’s look once more at the expression:

→ Since the first term is divisible by 3 and 9, the number 765 is divisible by 3 and 9 if and only if 7 + 6 + 5 is also divisible by 3 and 9.
→ This process can be used for any decimal whole number!
Introduce the divisibility rules for 3 and 9. Have students record the rules in their student materials.

Divisibility rule for 3: If the sum of the digits is divisible by 3, then the number is divisible by 3.

Divisibility rule for 9: If the sum of the digits is divisible by 9, then the number is divisible by 9.

Eureka Math Grade 6 Module 2 Lesson 17 Example Answer Key

Example 1.
This example shows how to apply the two new divisibility rules we just discussed.
Explain why 378 is divisible by 3 and 9.

a. Expand 378.
Answer:
300 + 70 + 8
3 × 100 + 7 × 1o + 8

b. Decompose the expression to factor by 9.
Answer:
3(99 + 1) + 7(9 + 1) + 8
3(99) + 3 + 7(9) + 7 + 8

c. Factor the 9.
Answer:
3(9 × 11) + 3 + 7(9 × 1) + 7 + 8
9(3 × 11 + 7) + 3 + 7 + 8

d. What is the sum of the three digits?
Answer:
3 + 7 + 8 = 18; the sum of the three digits is 18.

e. Is 18 divisible by 9?
Answer:
Yes

f. Is the entire number 378 divisible by 9? Why or why not?
Answer:
The number 378 is divisible by 9 because the sum of the digits is divisible by 9.

g. Is the number 378 divisible by 3? Why or why not?
Answer:
Three is a factor of 378 because if 9 is a factor of 378, then 3 will also be a factor. OR
The number 378 is divisible by 3 because the sum of the digits is divisible by 3.

Example 2.
Is 3,822 divisible by 3 or 9? Why or why not?
Answer:
The number 3,822 is divisible by 3 but not by 9 because the sum of the digits is 3 + 8 + 2 + 2 = 15, and 15 is divisible by 3 but not by 9.

Eureka Math Grade 6 Module 2 Lesson 17 Exercise Answer Key

Circle ALL the numbers that are factors of the given number. Complete any necessary work in the space provided.

Exercise 1.
2,838 is divisible by

Answer:

Explain your reasoning for your choice(s).
Answer:
The number 2,838 is divisible by 3 because 3 is a factor of 2,838. I know this because the sum of the digits is 21, which is divisible by 3. The number 2,838 is not divisible by 9 because 21 is not divisible by 9, and 2,838 is not divisible by 4 because the last two digits (38) are not divisible by 4.

Exercise 2.
34,515 is divisible by

Answer:

Explain your reasoning for your choice (s).
Answer:
The number 34,515 is divisible by 3 and 9 because both 3 and 9 are factors of 34,515. I know this because the sum of the digits is 18, and 18 is divisible by both 3 and 9. The number 34,515 is also divisible by 5 because the unit digit is a 5.

Exercise 3.
10,534,341 is divisible by

Answer:

Explain your reasoning for your choice(s).
Answer:
The number 10,534,341 is divisible by 3 but not 9 because 3 is afactor of 10,534,341, but 9 is not. I know this because the sum of the digits is 21, which is divisible by 3 but not 9. The number 10, 534, 341 is not divisible by 2 because it does not end with 0, 2, 4, 6, or 8.

Exercise 4.
4,320 is divisible by

Answer:

Explain your reasoning for your choice(s).
Answer:
The number 4,320 is divisible by 3 and 9 because 3 and 9 are factors of 4,320. I know this because the sum of the digits is 9, which is divisible by 3 and 9. The number 4,320 is also divisible by 10 because 10 is a factor of 4,320. I know this because the unit digit is 0.

Exercise 5.
6,240 is divisible by

Answer:

Explain your reasoning for your choice(s).
Answer:
The number 6,240 is divisible by 3 but not divisible by 9 because 3 is a factor of 6,240, but 9 is not. I know this because the sum of the digits is 12, which is divisible by 3 but not divisible by 9. The number 6,240 is divisible by 8 because the last three digits (240) is divisible by 8.

Eureka Math Grade 6 Module 2 Lesson 17 Problem Set Answer Key

Question 1.
Is 32, 643 divisible by both 3 and 9? Why or why not?
Answer:
The number 32,643 is divisible by both 3 and 9 because the sum of the digits is 18, which is divisible by 3 and 9.

Question 2.
Circle all the factors of 424,380 from the list below.
Answer:

Question 3.
Circle all the factors of 322,875 from the list below.
Answer:

Question 4.
Write a 3-digit number that ¡s divisible by both 3 and 4. Explain how you know this number is divisible by 3 and 4.
Answer:
Answers will vary. Possible student response: The sum of the digits is divisible by 3, and that’s how I know the number is divisible by 3. The last 2 digits are divisible by 4, so the entire number is divisible by 4.

Question 5.
Write a 4-digit number that Is divisible by both 5 and 9. Explain how you know this number Is divisible by 5 and 9.
Answer:
Answers will vary. Possible student response: The number ends with a 5 or 0, so the entire number is divisible by 5. The sum of the digits is divisible by 9, so the entire number is divisible by 9.

Eureka Math Grade 6 Module 2 Lesson 17 Exit Ticket Answer Key

Question 1.
Is 26, 341 divisible by 3? If it is, write the number as the product of 3 and another factor. If not, explain.
Answer:
The number 26,341 is not divisible by 3 because the sum of the digits is 16, which is not divisible by 3.

Question 2.
Is 8,397 divisible by 9? If it is, write the number as the product of 9 and another factor. If not, explain.
Answer:
The number 8,397 is divisible by 9 because the sum of the digits is 27, which is divisible by 9. Nine is a factor of 8,397 because 9 × 933 = 8,397.

Question 3.
Explain why 186,426 is divisible by both 3 and 9.
Answer:
The number 186, 426 is divisible by both 3 and 9 because the sum of the digits is 27, which is divisible by both 3 and 9.

Engage NY Eureka Math 6th Grade Module 2 Lesson 16 Answer Key

Eureka Math Grade 6 Module 2 Lesson 16 Opening Exercise Answer Key

a. What is an even number?
Answer:
Possible student responses:
An integer that can be evenly divided by 2
A number whose unit digit is 0, 2, 4, 6, or 8
All the multiples of 2

b. List some examples of even numbers.
Answer:
Answers will vary.

c. What is an odd number?
Answer:
Possible student responses:
An integer that CANNOT be evenly divided by 2
A number whose unit digit is 1, 3, 5, 7, or 9
All the numbers that are NOT multiples of 2

d. List some examples of odd numbers.
Answer:
Answers will vary.

What happens when we add two even numbers? Do we always get an even number?
Answer:
Before holding a discussion about the process to answer the following questions, have students write or share their predictions.

Eureka Math Grade 6 Module 2 Lesson 16 Exercise Answer Key

Exercise 1.
Why is the sum of two even numbers even?
a. Think of the problem 12 + 14. Draw dots to represent each number.
Answer:

b. Circle pairs of dots to determine if any of the dots are left over.
Answer:

c. Is this true every time two even numbers are added together? Why or why not?
Answer:
Since 12 is represented by 6 sets of two dots, and 14 is represented by 7 sets of two dots, the sum is 13 sets of two dots. This is true every time two even numbers are added together because even numbers never have dots left over when we are circling pairs. Therefore, the answer is always even.

Exercise 2.
Why is the sum of two odd numbers even?
a. Think of the problem 11 + 15. Draw dots to represent each number.
Answer:

b. Circle pairs of dots to determine if any of the dots are left over.
Answer:

When we circle groups of two dots, there is one dot remaining in each representation because each addend is an odd number. When we look at the sum, however, the two remaining dots can form a pair, leaving us with a sum that is represented by groups of two dots. The sum is, therefore, even. Since each addend is odd, there is one dot for each addend that does not have a pair. However, these two dots can be paired together, which means there are no dots without a pair, making the sum an even number.

c. Is this true every time two odd numbers are added together? Why or why not?
Answer:
This is true every time two odd numbers are added together because every odd number has one dot remaining when we circle pairs of dots. Since each number has one dot remaining, these dots can be combined to make another pair. Therefore, no dots remain, resulting in an even sum.

Exercise 3.
Why is the sum of an even number and an odd number odd?
a. Think of the problem 14 + 11. Draw dots to represent each number.
Answer:
Students draw dots to represent each number. After circling pairs of dots, there is one dot left for the number 11, and the number 14 has no dots remaining. Since there is one dot left over, the sum is odd because not every dot has a pair.

b. Circle pairs of dots to determine if any of the dots are left over.
Answer:
Students draw dots to represent each number. After circling pairs of dots, there is one dot left for the number 11, and the number 14 has no dots remaining. Since there is one dot left over, the sum is odd because not every dot has a pair.

C. Is this true every time an even number and an odd number are added together? Why or why not?
Answer:
This is always true when an even number and an odd number are added together because only the odd number will have a dot remaining after we circle pairs of dots. Since this dot does not have a pair, the sum is odd.

d. What if the first addend is odd and the second is even? Is the sum still odd? Why or why not? For example, If we had 11 + 14, would the sum be odd?
Answer:
The sum is still odd for two reasons. First, the commutative property states that changing the order of an addition problem does not change the answer. Because an even number plus an odd number is odd, then an odd number plus an even number is also odd. Second, it does not matter which addend is odd; there is still one dot remaining, making the sum odd.

Let’s sum it up:
Answer:
→ “Even” + “even” = “even”
→ “Odd” + “odd” = “even”
→ “Odd” + “even” = “odd”

Exploratory Challenge/Exercises 4-6

Exercise 4.
The product of two even numbers is even.
Answer:
Answers will vary, but one example answer is provided.

Using the problem 6 × 14, students know that this is equivalent to six groups of fourteen, or
14 + 14 + 14 + 14 + 14 + 14. Students also know that the sum of two even numbers is even; therefore, when adding the addends two at a time, the sum is always even. This means the sum of six even numbers is even, making the product even since It is equivalent to the sum.

Using the problem 6 × 14, students can use the dots from previous examples.

From here, students can circle dots and see that there are no dots remaining, so the answer must be even.

Exercise 5.
The product of two odd numbers is odd.
Answer:
Answers will vary, but an example answer is provided.
Using the problem 5 × 15, students know that this is equivalent to five groups of fifteen, or
15 + 15 + 15 + 15 + 15. Students also know that the sum of two odd numbers is even, and the sum of an odd and even number is odd. When adding two of the addends together at a time, the answer rotates between even and odd. When the final two numbers are added together, one is even and the other odd. Therefore, the sum is odd, which makes the product odd since it is equivalent to the sum.

Using the problem 5 × 15, students may also use the dot method.

After students circle the pairs of dots, one dot from each set of 15 remains, for a total of 5 dots. Students can group these together and circle more pairs, as shown below.

Since there is still one dot remaining, the product of two odd numbers is odd.

Exercise 6.
The product of an even number and an odd number is even.
Answer:
Answers will vary, but one example is provided.
Using the problem 6 × 7, students know that this is equivalent to the sum of six sevens, or 7 + 7 + 7 + 7 + 7 + 7.
Students also know that the sum of two odd numbers is even, and the sum of two even numbers is even. Therefore, when adding two addends at a time, the result is an even number. The sum of these even numbers is also even, which means the total sum is even. This also Implies the product is even since the sum and product are equivalent.

Using the problem 6 × 7, students may also use the dot method.

After students circle the pairs of dots, one dot from each set of 7 remains, for a total of 6 dots. Students can group these together and circle more pairs, as shown below.

Since there are no dots remaining, the product of an even number and an odd number is even.

Eureka Math Grade 6 Module 2 Lesson 16 Problem Set Answer Key

Without solving, tell whether each sum or product Is even or odd. Explain your reasoning.

Question 1.
346 + 721
Answer:
The sum is odd because the sum of an even and an odd number is odd.

Question 2.
4,690 × 141
Answer:
The product is even because the product of an even and an odd number is even.

Question 3.
1,462,891 × 745,629
Answer:
The product is odd because the product of two odd numbers is odd.

Question 4.
425,922 + 32,481,064
Answer:
The sum is even because the sum of two even numbers is even.

Question 5.
32 + 45 + 67 + 91 + 34 + 56
Answer:
The first two addends are odd because an even and an odd is odd.
Odd number +67 is even because the sum of two odd numbers is even.
Even number +91 is odd because the sum of an even and an odd number is odd.
Odd number +34 is odd because the sum of an odd and an even number is odd.
Odd number +56 is odd because the sum of an odd andan even number is odd.
Therefore, the final sum is odd.

Eureka Math Grade 6 Module 2 Lesson 16 Exit Ticket Answer Key

Determine whether each sum or product is even or odd. Explain your reasoning.

Question 1.
56,426+17,895
Answer:
The sum is odd because the sum of an even number and an odd number is odd.

Question 2.
317,362 × 129,324
Answer:
The product is even because the product of two even numbers is even.

Question 3.
104,81 + 4,569
Answer:
The sum is even because the sum of two odd numbers is even.

Question 4.
32,457 × 12,781
Answer:
The product is odd because the product of two odd numbers is odd.

Question 5.
Show or explain why 12 + 13 + 14 + 15 + 16 results in an even sum.
Answer:
12 + 13 is odd because even + odd is odd.
Odd number +14 is odd because odd + even is odd.
Odd number +15 is even because odd + odd is even.
Even number +16 is even because even + even is even.
OR
Students may group even numbers together, 12 + 14 + 16, which results in an even number. Then, when students combine the two odd numbers, 13 + 15, the result is another even number. We know that the sum of two evens results in another even number.

Engage NY Eureka Math 8th Grade Module 2 Lesson 5 Answer Key

Eureka Math Grade 8 Module 2 Lesson 5 Exercise Answer Key

Exercise 1.
Let there be a rotation of d degrees around center O. Let P be a point other than O. Select d so that d≥0. Find P’ (i.e., the rotation of point P) using a transparency.

Answer:
Verify that students have rotated around center O in the counterclockwise direction.

Exercise 2.
Let there be a rotation of d degrees around center O. Let P be a point other than O. Select d so that d<0. Find P’ (i.e., the rotation of point P) using a transparency.

Answer:
Verify that students have rotated around center O in the clockwise direction.

Exercise 3.
Which direction did the point P rotate when d≥0?
Answer:
It rotated counterclockwise, or to the left of the original point.

Exercise 4.
Which direction did the point P rotate when d<0?
Answer:
It rotated clockwise, or to the right of the original point.

Exercises 5–6

Exercise 5.
Let L be a line, \(\overrightarrow{A B}\) be a ray, \(\overline{\boldsymbol{C D}}\) be a segment, and ∠EFG be an angle, as shown. Let there be a rotation of d degrees around point O. Find the images of all figures when d≥0.

Answer:

Verify that students have rotated around center O in the counterclockwise direction.

Exercise 6.
Let \(\overline{A B}\) be a segment of length 4 units and ∠CDE be an angle of size 45°. Let there be a rotation by d degrees, where d<0, about O. Find the images of the given figures. Answer the questions that follow.

Answer:

Verify that students have rotated around center O in the clockwise direction.

a. What is the length of the rotated segment Rotation(AB)?
Answer:
The length of the rotated segment is 4 units.

b. What is the degree of the rotated angle Rotation (∠CDE)?
Answer:
The degree of the rotated angle is 45°.

Exercises 7–8

Exercise 7.
Let L₁ and L₂ be parallel lines. Let there be a rotation by d degrees, where -360<d<360, about O.
Is (L₁ )’∥(L₂)’?

Answer:

Verify that students have rotated around center O in either direction. Students should respond that (L₁)’ || (L₂)’.

Exercise 8.
Let L be a line and O be the center of rotation. Let there be a rotation by d degrees, where d≠180 about O. Are the lines L and L’ parallel?

Answer:

Verify that students have rotated around center O in either direction any degree other than 180. Students should respond that L and L’ are not parallel.

Eureka Math Grade 8 Module 2 Lesson 5 Exit Ticket Answer Key

Question 1.
Given the figure H, let there be a rotation by d degrees, where d≥0, about O. Let Rotation(H) be H’.

Answer:

Sample rotation shown above. Verify that the figure H’ has been rotated counterclockwise with center O.

Question 2.
Using the drawing above, let Rotation₁ be the rotation d degrees with d<0, about O. Let Rotation_1 (H) be H”.
Answer:
Sample rotation shown above. Verify that the figure H” has been rotated clockwise with center O.

Eureka Math Grade 8 Module 2 Lesson 5 Problem Set Answer Key

Question 1.
Let there be a rotation by -90° around the center O.

Answer:
Rotated figures are shown in red.

Question 2.
Explain why a rotation of 90 degrees around any point O never maps a line to a line parallel to itself.
Answer:
A 90-degree rotation around point O will move a given line L to L’. Parallel lines never intersect, so it is obvious that a 90-degree rotation in either direction does not make lines L and L’ parallel. Additionally, we know that there exists just one line parallel to the given line L that goes through a point not on L. If we let P be a point not on L, the line L’ must go through it in order to be parallel to L. L’ does not go through point P; therefore, L and L’ are not parallel lines. Assume we rotate line L first and then place a point P on line L’ to get the desired effect (a line through P). This contradicts our definition of parallel (i.e., parallel lines never intersect); so, again, we know that line L is not parallel to L’.

Question 3.
A segment of length 94 cm has been rotated d degrees around a center O. What is the length of the rotated segment? How do you know?
Answer:
The rotated segment will be 94 cm in length. (Rotation 2) states that rotations preserve lengths of segments, so the length of the rotated segment will remain the same as the original.

Question 4.
An angle of size 124° has been rotated d degrees around a center O. What is the size of the rotated angle? How do you know?
Answer:
The rotated angle will be 124°. (Rotation 3) states that rotations preserve the degrees of angles, so the rotated angle will be the same size as the original.

Engage NY Eureka Math 8th Grade Module 2 Lesson 3 Answer Key

Eureka Math Grade 8 Module 2 Lesson 3 Exercise Answer Key

Exercise 1.
Draw a line passing through point P that is parallel to line L. Draw a second line passing through point P that is parallel to line L and that is distinct (i.e., different) from the first one. What do you notice?

Answer:

Students should realize that they can only draw one line through point P that is parallel to L.

Exercises 2–4 (9 minutes)
Students complete Exercises 2–4 independently in preparation for the discussion that follows.

Exercise 2.
Translate line L along the vector \(\overrightarrow{A B}\). What do you notice about L and its image, L’?

Answer:

L and L’ coincide. L=L’.

Exercise 3.
Line L is parallel to vector \(\overrightarrow{A B}\). Translate line L along vector (AB) ⃗. What do you notice about L and its image, L’?

Answer:

L and L’ coincide, again. L=L’.

Exercise 4.
Translate line L along the vector \(\overrightarrow{A B}\). What do you notice about L and its image, L’?

Answer:

L || L’

Exercises 5–6 (5 minutes)
Students complete Exercises 5 and 6 in pairs or small groups.

Exercise 5.
Line L has been translated along vector \(\overrightarrow{A B}\), resulting in L’. What do you know about lines L and L’?

Answer:
L || T(L)

Question 6.
Translate L₁ and L₂ along vector \(\overrightarrow{D E}\). Label the images of the lines. If lines L₁ and L₂ are parallel, what do you know about their translated images?

Answer:

Since L₁ || L₁, then (L₁)’ || (L₂)’.

Eureka Math Grade 8 Module 2 Lesson 3 Exit Ticket Answer Key

Question 1.
Translate point Z along vector \(\overrightarrow{A B}\). What do you know about the line containing vector \(\overrightarrow{A B}\) and the line formed when you connect Z to its image Z’?

Answer:
The line containing vector \(\overrightarrow{A B}\) and ZZ’ is parallel.

Question 2.
Using the above diagram, what do you know about the lengths of segment ZZ’ and segment AB?
Answer:
The lengths are equal: |ZZ’|=|AB|.

Question 3.
Let points A and B be on line L and the vector \(\overrightarrow{A C}\) be given, as shown below. Translate line L along vector \(\overrightarrow{A C}\). What do you know about line L and its image, L’? How many other lines can you draw through point C that have the same relationship as L and L’? How do you know?

Answer:

L and L’ are parallel. There is only one line parallel to line L that goes through point C. The fact that there is only one line through a point parallel to a given line guarantees it.

Eureka Math Grade 8 Module 2 Lesson 3 Problem Set Answer Key

Question 1.
Translate ∠XYZ, point A, point B, and rectangle HIJK along vector \(\overrightarrow{E F}\). Sketch the images, and label all points using prime notation.

Answer:

Question 2.
What is the measure of the translated image of ∠XYZ? How do you know?
Answer:
The measure is 38°. Translations preserve angle measure.

Question 3.
Connect B to B’. What do you know about the line that contains the segment formed by BB’ and the line containing the vector \(\overrightarrow{E F}\)?
Answer:
\(\overleftrightarrow{\boldsymbol{B B}^{\prime}} \| \overleftrightarrow{\boldsymbol{E F}}\)

Question 4.
Connect A to A’. What do you know about the line that contains the segment formed by AA’ and the line containing the vector \(\overrightarrow{\boldsymbol{E F}}\)?
Answer:
\(\overleftrightarrow{A A^{\prime}}\) and \(\overleftrightarrow{\boldsymbol{E F}}\) coincide.

Question 5.
Given that figure HIJK is a rectangle, what do you know about lines that contain segments HI and JK and their translated images? Explain.
Answer:
Since HIJK is a rectangle, I know that \(\overleftrightarrow{\boldsymbol{H} \boldsymbol{I}}\) || \(\overleftrightarrow{\boldsymbol{J K}}\). Since translations map parallel lines to parallel lines, then \(\overleftrightarrow{\boldsymbol{H}^{\prime} \boldsymbol{I}^{\prime}}\)||\(\overleftrightarrow{\boldsymbol{J}^{\prime} \boldsymbol{K}^{\prime}}\).

Engage NY Eureka Math 8th Grade Module 2 Lesson 2 Answer Key

Eureka Math Grade 8 Module 2 Lesson 2 Exercise Answer Key

Exercise 1.
Draw at least three different vectors, and show what a translation of the plane along each vector looks like. Describe what happens to the following figures under each translation using appropriate vocabulary and notation as needed.

Answer:
Answers will vary.

Exercise 2.
The diagram below shows figures and their images under a translation along \(\overrightarrow{H I}\). Use the original figures and the translated images to fill in missing labels for points and measures.

Answer:
Solutions are in red, below.

Eureka Math Grade 8 Module 2 Lesson 2 Exit Ticket Answer Key

Question 1.
Name the vector in the picture below.

Answer:
\(\overrightarrow{Q P}\)

Question 2.
Name the vector along which a translation of a plane would map point A to its image T(A).

Answer:
\(\overrightarrow{S R}\)

Question 3.
Is Maria correct when she says that there is a translation along a vector that maps segment AB to segment CD? If so, draw the vector. If not, explain why not.

Answer:

Yes. Accept any vector that would translate the segment AB to segment CD. A possible vector is shown in red, above.

Question 4.
Assume there is a translation that maps segment AB to segment CD shown above. If the length of segment CD is 8 units, what is the length of segment AB? How do you know?
Answer:
The length of CD must be 8 units in length because translations preserve the lengths of segments.

Eureka Math Grade 8 Module 2 Lesson 2 Problem Set Answer Key

Question 1.
Translate the plane containing Figure A along \(\overrightarrow{A B}\). Use your transparency to sketch the image of Figure A by this translation. Mark points on Figure A, and label the image of Figure A accordingly.

Answer:
Marked points will vary. Verify that students have labeled their points and images appropriately.

Question 2.
Translate the plane containing Figure B along \(\overrightarrow{B A}\). Use your transparency to sketch the image of Figure B by this translation. Mark points on Figure B, and label the image of Figure B accordingly.

Answer:
Marked points will vary. Verify that students have labeled their points and images appropriately.

Question 3.
Draw an acute angle (your choice of degree), a segment with length 3 cm, a point, a circle with radius 1 in., and a vector (your choice of length, i.e., starting point and ending point). Label points and measures (measurements do not need to be precise, but your figure must be labeled correctly). Use your transparency to translate all of the figures you have drawn along the vector. Sketch the images of the translated figures and label them.
Answer:
Drawings will vary. Note: Drawing is not to scale.

Question 4.
What is the length of the translated segment? How does this length compare to the length of the original segment? Explain.
Answer:
The length is 3 cm. The length is the same as the original because translations preserve the lengths of segments.

Question 5.
What is the length of the radius in the translated circle? How does this radius length compare to the radius of the original circle? Explain.
Answer:
The length is 1 in. The length is the same as the original because translations preserve lengths of segments.

Question 6.
What is the degree of the translated angle? How does this degree compare to the degree of the original angle? Explain.
Answer:
Answers will vary based on the original size of the angle drawn. The angles will have the same measure because translations preserve degrees of angles.

Question 7.
Translate point D along vector \(\overrightarrow{A B}\), and label the image D’. What do you notice about the line containing vector \(\overrightarrow{A B}\) and the line containing points D and D’? (Hint: Will the lines ever intersect?)

Answer:

The lines will be parallel.

Question 8.
Translate point E along vector \(\overrightarrow{A B}\), and label the image E’. What do you notice about the line containing vector \(\overrightarrow{A B}\) and the line containing points E and E’?

Answer:

The lines will coincide.

Engage NY Eureka Math 8th Grade Module 2 Lesson 1 Answer Key

Eureka Math Grade 8 Module 2 Lesson 1 Exploratory Challenge Answer Key

a. Describe, intuitively, what kind of transformation is required to move the figure on the left to each of the figures (1)–(3) on the right. To help with this exercise, use a transparency to copy the figure on the left. Note: Begin by moving the left figure to each of the locations in (1), (2), and (3).

Answer:
Slide the original figure to the image (1) until they coincide. Slide the original figure to (2), and then flip it so they coincide. Slide the original figure to (3), and then turn it until they coincide.

b. Given two segments AB and CD, which could be very far apart, how can we find out if they have the same length without measuring them individually? Do you think they have the same length? How do you check? In other words, why do you think we need to move things around on the plane?

Answer:
We can trace one of the segments on the transparency and slide it to see if it coincides with the other segment. We move things around in the plane to see if they are exactly the same. This way, we don’t have to do any measuring.

Eureka Math Grade 8 Module 2 Lesson 1 Problem Set Answer Key

Question 1.
Using as much of the new vocabulary as you can, try to describe what you see in the diagram below.

Answer:
There was a transformation, F, that moved point A to its image F(A) and point B to its image F(B). Since a transformation preserves distance, the distance between points A and B is the same as the distance between points F(A) and F(B).

Question 2.
Describe, intuitively, what kind of transformation is required to move Figure A on the left to its image on the right.

Answer:
First, I have to slide Figure A so that the point containing two dots maps onto the Image of A in the same location; next, I have to turn (rotate) it so that Figure A maps onto Image of A; finally, I have to flip the figure over so the part of the star with the single dot maps onto the image.

Eureka Math Grade 8 Module 2 Lesson 1 Exit Ticket Answer Key

First, draw a simple figure and name it Figure W. Next, draw its image under some transformation (i.e., trace your
Figure W on the transparency), and then move it. Finally, draw its image somewhere else on the paper.
Describe, intuitively, how you moved the figure. Use complete sentences.
Answer:
Accept any figure and transformation that is correct. Check for the same size and shape. Students should describe the movement of the figure as sliding to the left or right, turning to the left or right, or flipping, similar to how they described the movement of figures in the exercises of the lesson.

Engage NY Eureka Math 8th Grade Module 1 End of Module Assessment Answer Key

Eureka Math Grade 8 Module 1 End of Module Assessment Task Answer Key

Question 1.
You have been hired by a company to write a report on Internet companies’ Wi-Fi ranges. They have requested that all values be reported in feet using scientific notation.

Ivan’s Internet Company boasts that its wireless access points have the greatest range. The company claims that you can access its signal up to 2,640 feet from its device. A competing company, Winnie’s Wi-Fi, has devices that extend to up to 2\(\frac{1}{2}\) miles.

a. Rewrite the range of each company’s wireless access devices in feet using scientific notation, and state which company actually has the greater range (5,280 feet =1 mile).
Answer:
Ivan’s Range: 2,640 = 2.64 × 10³ ft.
Winner’s Range: (2.5)5280 = 13200 = 1.32 × 10⁴ ft.
Winner’s wi-fi has the greater range.

b. You can determine how many times greater the range of one Internet company is than the other by writing their ranges as a ratio. Write and find the value of the ratio that compares the range of Winnie’s wireless access devices to the range of Ivan’s wireless access devices. Write a complete sentence describing how many times greater Winnie’s Wi-Fi range is than Ivan’s Wi-Fi range.
Answer:
winnie to ivan’s ratio – (1.32 × 10⁴) : (2.64 × 10³)
Value of ratio – \(\frac{1.32 \times 10^{4}}{2.64 \times 10^{3}}\) = \(\frac{1.32}{2.64}\) × \(\frac{10^{4}}{10^{3}}\) = \(\frac{1}{2}\) × 10 = 5
winnie’s wi-fi is 5 times greater in range than ivan’s internet company.

c. UC Berkeley uses Wi-Fi over Long Distances (WiLD) to create long-distance, point-to-point links. UC Berkeley claims that connections can be made up to 10 miles away from its device. Write and find the value of the ratio that compares the range of Ivan’s wireless access devices to the range of Berkeley’s WiLD devices. Write your answer in a complete sentence.
Answer:
(10)5280 = 52800 = 5.28 × 10⁴
Ivan’s to berkeley ratio: (2.64 × 10³): (5.28 × 10⁴)
Value of ratio- \(\frac{2.64 \times 10^{3}}{5.28 \times 10^{4}}\) = \(\frac{2.64}{5.28}\)×\(\frac{10^{3}}{10^{4}}\)= \(\frac{1}{2}\)×\(\frac{1}{10}\)= \(\frac{1}{20}\)
Ivan’s internet devices have a range \(\frac{1}{20}\) the range of UC Berkeley wild devices.

Question 2.
There is still controversy about whether or not Pluto should be considered a planet. Although planets are mainly defined by their orbital path (the condition that prevented Pluto from remaining a planet), the issue of size is something to consider. The table below lists the planets, including Pluto, and their approximate diameters in meters.

a. Name the planets (including Pluto) in order from smallest to largest.
Answer:
Pluto, mercury, mars, venus, earth, neptune, uranus, saturn, jupiter.

b. Comparing only diameters, about how many times larger is Jupiter than Pluto?
Answer:
\(\frac{1.43 \times 10^{8}}{2.3 \times 10^{6}}\) = \(\frac{1.43}{2.3}\) × \(\frac{10^{8}}{10^{6}}\)
≈ 0.622 × 10²
≈ 62.2
The diameter of jupiter is about 62 times larger than pluto.

c. Again, comparing only diameters, find out about how many times larger Jupiter is compared to Mercury.
Answer:
\(\frac{1.43 \times 10^{8}}{4.88 \times 10^{6}}\) = \(\frac{1.43}{4.88}\) × \(\frac{10^{8}}{10^{6}}\)
≈ 0.293 × 10²
≈ 29.3
The diameter of jupiter is about 29 times larger than mercury.

d. Assume you are a voting member of the International Astronomical Union (IAU) and the classification of Pluto is based entirely on the length of the diameter. Would you vote to keep Pluto a planet or reclassify it? Why or why not?
Answer:
I would vote to reclassify it. Knowing that jupiter is 29 times larger than mercury means mercury is pretty small. Jupiter is 42 times larger than pluto, which means pluto is even. Smaller than mercury. For that reason vote that the length of the diameter of pluto is too small compared to other planets (Even the small one).

e. Just for fun, Scott wondered how big a planet would be if its diameter was the square of Pluto’s diameter. If the diameter of Pluto in terms of meters were squared, what would the diameter of the new planet be? (Write answer in scientific notation.) Do you think it would meet any size requirement to remain a planet? Would it be larger or smaller than Jupiter?
Answer:
(2.3 × 10⁶)² = 2.3² × (10⁶)²
= 5.29 × 10¹²
Yes, 5.29 × 10¹² would likely meet any size requirement for planets. It would be larger than jupiter.

Question 3.
Your friend Pat bought a fish tank that has a volume of 175 liters. The brochure for Pat’s tank lists a “fun fact” that it would take 7.43×10¹⁸ tanks of that size to fill all the oceans in the world. Pat thinks the both of you can quickly calculate the volume of all the oceans in the world using the fun fact and the size of her tank.

a. Given that 1 liter =1.0×10^-12 cubic kilometers, rewrite the size of the tank in cubic kilometers using scientific notation.
Answer:
175 litres = 175(1.0×10^-12) cubic kilometers
= 175 ×10^-12 km³
= 1.75 × 10^-10 km³

b. Determine the volume of all the oceans in the world in cubic kilometers using the “fun fact.”
Answer:
(1.75 × 10^-10)(7.43×10¹⁸) = (1.75× 7.43)(10^-10×10¹⁸)
= 13.0025×10⁸
= 1.30025×10⁹
The volume of all the oceans in the world is (1.30025×10⁹)km³.

c. You liked Pat’s fish so much you bought a fish tank of your own that holds an additional 75 liters. Pat asked you to figure out a different “fun fact” for your fish tank. Pat wants to know how many tanks of this new size would be needed to fill the Atlantic Ocean. The Atlantic Ocean has a volume of 323,600,000 cubic kilometers.
Answer:
Tank: 175+75 = 250 liters
250 liters = 250(1.0×10^-12) km³
= 2.50 ×10^-12
= 2.5 × 10^-10
Atlantic ocean: 323,600,000
= 3.236 × 10⁸ km³

\(\frac{3.236 \times 10^{8}}{2.5 \times 10^{-10}}\) = \(\frac{3.236}{2.5}\) × \(\frac{10^{8}}{10^{-10}}\)
= 1.2944×10¹⁸
It would take 1.2944×10¹⁸ tanks (of size 250 liters) to fill the atlantic ocean.

Engage NY Eureka Math 8th Grade Module 1 Mid Module Assessment Answer Key

Eureka Math Grade 8 Module 1 Mid Module Assessment Task Answer Key

Question 1.
The number of users of social media has increased significantly since the year 2001. In fact, the approximate number of users has tripled each year. It was reported that in 2005 there were 3 million users of social media.

a. Assuming that the number of users continues to triple each year, for the next three years, determine the number of users in 2006, 2007, and 2008.
Answer:
2006-9 MILLION
2007-27 MILLION
2008-81 MILLION

b. Assume the trend in the numbers of users tripling each year was true for all years from 2001 to 2009. Complete the table below using 2005 as year 1 with 3 million as the number of users that year.

Answer:

c. Given only the number of users in 2005 and the assumption that the number of users triples each year, how did you determine the number of users for years 2, 3, 4, and 5?
Answer:
I MULTIPLIED THE PRECEDING YEAR’S NUMBER OF USERS BY 3.

d. Given only the number of users in 2005 and the assumption that the number of users triples each year, how did you determine the number of users for years 0, -1, -2, and -3?
Answer:
I Divided The Next Year’s Number of users by 3.

e. Write an equation to represent the number of users in millions, N, for year t, t≥-3.
Answer:
N=3t

f. Using the context of the problem, explain whether or not the formula N=3^t would work for finding the number of users in millions in year t, for all t≤0.
Answer:
We only know that the number of users has tripled each year in the time frame of 2001 to 2009. For that reason, we cannot rely on the formula, N = 3t, to work for all t≤0, just to t=-3, which is the year 2001.

g. Assume the total number of users continues to triple each year after 2009. Determine the number of users in 2012. Given that the world population at the end of 2011 was approximately 7 billion, is this assumption reasonable? Explain your reasoning.
Answer:
2012 is t=8, so when t=8 in N=6,561,000,000. The number of users in 2012, 6,561,000,000. Does not exceed the world population of 7 billion, therefore it is possible to have that number of users. But 6,561,000,000 is Approximately 94%. of the world’s population. The number of users is likely less than that due to poverty, illness, infancy, etc. The Assumption is possible, but not reasonable.

Question 2.
Let m be a whole number.
a. Use the properties of exponents to write an equivalent expression that is a product of unique primes, each raised to an integer power.
\(\frac{6^{21} \cdot 10^{7}}{30^{7}}\)
Answer:
\(\frac{(3 \cdot 2)^{21} \cdot 10^{7}}{(3 \cdot 10)^{7}}\)=\(\frac{3^{21} \cdot 2^{21} \cdot 10^{7}}{3^{7} \cdot 10^{7}}\)
= 3^21-7.2²¹.10^7-7
= 3¹⁴.2²¹.10⁰
= 3¹⁴.2²¹

b. Use the properties of exponents to prove the following identity:
\(\frac{6^{3 m} \cdot 10^{m}}{30^{m}}\) = 2^3m.3^2m
Answer:
\(\frac{6^{3 m} \cdot 10^{m}}{30^{m}}\) = \(\frac{(3.2)^{3 m} \cdot 10^{m}}{(3 \cdot 10)^{m}}\)
= \(\frac{3^{3 m} \cdot 2^{3 m} \cdot 10^{m}}{3^{m} \cdot 10^{m}}\)
= 3^3m-3.2^3m.10^m-m
= 3^2m.2^3m
= 2^3m.3^2m

c. What value of m could be substituted into the identity in part (b) to find the answer to part (a)?
Answer:
2^3m.3^2m = 2²¹.3¹⁴
3m = 21
m = 7
2m = 14
m = 7
Therefore, m = 7

Question 3.
Jill writes 2³ ∙4³ =8⁶ and the teacher marked it wrong. Explain Jill’s error.
Answer:
Jill multiplied the bases, 2 and 4, and added the exponents. You can only add the exponents when the bases being multiplied are the same.

b. Find n so that the number sentence below is true:
2³ ∙4³ =2³ ∙2ⁿ =2⁹
Answer:
4³ = 4.4.4
= (2.2)(2.2)(2.2)
= 2⁶
Therefore
2³.4³ = 2³.2⁶ = 2⁹
so
n = 6

c. Use the definition of exponential notation to demonstrate why 2³ ∙4³ =2⁹ is true.
Answer:
4³=2⁶, 2³.4³ = 2⁹ is equivalent to 2³.2⁶ = 2⁹
By definition of exponential notation:

d. You write 7⁵ ∙7^-9 =7^-4 . Keisha challenges you, “Prove it!” Show directly why your answer is correct without referencing the laws of exponents for integers; in other words, x^a ∙x^b =x^a+b for positive numbers x and integers a and b.
Answer:
7⁵.7^-9 = 7⁵.\(\frac{1}{7^{9}}\) by definition
= \(\frac{7^{5}}{7^{9}}\) by product formula
= \(\frac{7^{5}}{7^{5.7^{4}}}\) by x^m.xⁿ = x^m+n for x>0, m,n≥0
= \(\frac{1}{7^{4}}\) by equivalent fractions
= 7^-4 by definition.

Engage NY Eureka Math 8th Grade Module 1 Lesson 13 Answer Key

Eureka Math Grade 8 Module 1 Lesson 13 Exercise Answer Key

Exercise 1.
The Fornax Dwarf galaxy is 4.6×10⁵ light-years away from Earth, while Andromeda I is 2.430×10⁶ light-years away from Earth. Which is closer to Earth?
Answer:
2.430×10⁶=2.430×10×10⁵=24.30×10⁵
Because 4.6<24.30, then 4.6×10⁵<24.30×10⁵, and since 24.30×10⁵=2.430×10⁶, we know that 4.6×10⁵<2.430×10⁶. Therefore, Fornax Dwarf is closer to Earth.

Exercise 2.
The average lifetime of the tau lepton is 2.906×10^-13 seconds, and the average lifetime of the neutral pion is 8.4×10^-17 seconds. Explain which subatomic particle has a longer average lifetime.
Answer:
2.906×10^-13=2.906×10⁴×10^-17=29,060×10^-17
Since 8.4<29,060, then 8.4×10^-17<29,060×10^-17, and since 29,060×10^-17=2.906×10^-13, we know that 8.4×10^-17< 2.906×10^-13. Therefore, tau lepton has a longer average lifetime.
This problem, as well as others, can be solved using an alternate method. Our goal is to make the magnitude of the numbers we are comparing the same, which will allow us to reduce the comparison to that of whole numbers.
Here is an alternate solution:
8.4×10^-17=8.4×10^-4×10^-13=0.000 84×10^-13.
Since 0.00084<2.906, then 0.000 84×10^-13<2.906×10^-13, and since 0.000 84×10^-13=8.4×10^-17, we know that 8.4×10^-17< 2.906×10^-13. Therefore, tau lepton has a longer average lifetime.

Exploratory Challenge 1/Exercise 3.
THEOREM: Given two positive numbers in scientific notation, a×10^m and b×10ⁿ, if m<n, then a×10^m<b×10ⁿ.

Prove the theorem.
If m<n, then there is a positive integer k so that n=k+m.
By the first law of exponents (10) in Lesson 5, b×10ⁿ=b×10^k×10^m=(b×10^k)×10^m. Because we are comparing with a×10^m, we know by (1) that we only need to prove a<(b×10^k). By the definition of scientific notation, a<10 and also (b×10^k)≥10 because k≥1 and b≥1, so that (b×10^k)≥1×10=10. This proves a<(b×10^k), and therefore, a×10^m<b×10ⁿ.
Explain to students that we know that a<10 because of the statement given that a×10^m is a number expressed in scientific notation. That is not enough information to convince students that a<b×10^k; therefore, we need to say something about the right side of the inequality. We know that k≥1 because k is a positive integer so that n=k+m. We also know that b≥1 because of the definition of scientific notation. That means that the minimum possible value of b×10^k is 10 because 1×10¹=10. Therefore, we can be certain that a<b×10^k.
Therefore, by (1), a×10^m<(b×10^k)×10^m. Since n=k+m, we can rewrite the right side of the inequality as
b×10ⁿ, and finally a×10^m<b×10ⁿ.

Exercise 4.
Compare 9.3×10²8 and 9.2879×10²8.
Answer:
We only need to compare 9.3 and 9.2879. 9.3×10⁴=93,000 and 9.2879×10⁴=92,879, so we see that
93,000>92,879. Therefore, 9.3×10²⁸>9.2879×10²⁸.

Exercise 5.
Chris said that 5.3×10⁴¹<5.301×10⁴1 because 5.3 has fewer digits than 5.301. Show that even though his answer is correct, his reasoning is flawed. Show him an example to illustrate that his reasoning would result in an incorrect answer. Explain.
Answer:
Chris is correct that 5.3×10⁴¹<5.301×10⁴¹, but that is because when we compare 5.3 and 5.301, we only need to compare 5.3×10³ and 5.301×10³ (by (1) above). But, 5.3×10³<5.301×10³ or rather 5,300<5,301, and this is the reason that 5.3×10⁴¹<5.301×10⁴¹. However, Chris’s reasoning would lead to an incorrect answer for a problem that compares 5.9×10⁴¹ and 5.199×10⁴¹. His reasoning would lead him to conclude that
5.9×10⁴¹<5.199×10⁴¹, but 5,900>5,199, which is equivalent to 5.9×10³>5.199×10³. By (1) again, 5.9>5.199, meaning that 5.9×10⁴¹>5.199×10⁴¹.

Exploratory Challenge 2/Exercise 6.
You have been asked to determine the exact number of Google searches that are made each year. The only information you are provided is that there are 35,939,938,877 searches performed each week. Assuming the exact same number of searches are performed each week for the 52 weeks in a year, how many total searches will have been performed in one year? Your calculator does not display enough digits to get the exact answer. Therefore, you must break down the problem into smaller parts. Remember, you cannot approximate an answer because you need to find an exact answer. Use the screen shots below to help you reach your answer.

Answer:
First, I need to rewrite the number of searches for each week using numbers that can be computed using my calculator.
35 939 938 877=35 939 000 000+938 877
=35 939×10⁶+938 877
Next, I need to multiply each term of the sum by 52, using the distributive law.
(35 939×10⁶+938 877)×52=(35 939×10⁶)×52+(938 877×52)
By repeated use of the commutative and associative properties, I can rewrite the problem as
(35 939×52)×10⁶+(938 877×52).
According to the screen shots, I get
1 868 828×10⁶+48 821 604=1 868 828 000 000+48 821 604
=1 868 876 821 604.
Therefore, 1,868,876,821,604 Google searches are performed each year.

Yahoo! is another popular search engine. Yahoo! receives requests for 1,792,671,335 searches each month. Assuming the same number of searches are performed each month, how many searches are performed on Yahoo! each year? Use the screen shots below to help determine the answer.

Answer:
First, I need to rewrite the number of searches for each month using numbers that can be computed using my calculator.
1 792 671 335=1 792 000 000+671 335
=1 792×10⁶+671 335.
Next, I need to multiply each term of the sum by 12, using the distributive law.
(1 792×10⁶+671 335)×12=(1 792×10⁶)×12+(671 335×12).
By repeated use of the commutative and associative properties, I can rewrite the problem as
(1 792×12)×10⁶+(671 335×12)
According to the screen shots, I get
21 504×10⁶+8 056 020=21 504 000 000+8 056 020
=21 512 056 020
Therefore, 21,512,056,020 Yahoo! searches are performed each year.

Eureka Math Grade 8 Module 1 Lesson 13 Exit Ticket Answer Key

Question 1.
Compare 2.01×10¹5 and 2.8×10¹3. Which number is larger?
Answer:
2.01×10¹⁵=2.01×10²×10¹³=201×10¹³
Since 201>2.8, we have 201×10¹³>2.8×10¹³, and since 201×10¹³=2.01×10¹⁵, we conclude 2.01×10¹⁵>2.8×10¹³.

Question 2.
The wavelength of the color red is about 6.5×10^^-9 m. The wavelength of the color blue is about 4.75×10^-9 m. Show that the wavelength of red is longer than the wavelength of blue.
Answer:
We only need to compare 6.5 and 4.75:
6.5×10^-9=650×10^-7 and 4.75×10^-9=475×10^-7, so we see that 650>475.
Therefore, 6.5×10^-9>4.75×10^-9.

Eureka Math Grade 8 Module 1 Lesson 13 Problem Set Answer Key

Question 1.
Write out a detailed proof of the fact that, given two numbers in scientific notation, a×10ⁿ and b×10ⁿ, a<b, if and only if a×10ⁿ<b×10ⁿ.
Answer:
Because 10ⁿ>0, we can use inequality (A) (i.e., (1) above) twice to draw the necessary conclusions. First, if a<b, then by inequality (A), a×10ⁿ<b×10ⁿ. Second, given a×10ⁿ<b×10ⁿ, we can use inequality (A) again to show an<b×10ⁿ by 10^-n.

a. Let A and B be two positive numbers, with no restrictions on their size. Is it true that A×10^-5<B×10⁵?
Answer:
No, it is not true that A×10^-5<B×10⁵. Using inequality (A), we can write
A×10^-5×10⁵<B×10⁵×10⁵, which is the same as A<B×10¹⁰. To disprove the statement, all we would need to do is find a value of A that exceeds B×10¹⁰.

b. Now, if A×10^-5 and B×10⁵ are written in scientific notation, is it true that A×10^-5<B×10⁵? Explain.
Answer:
Yes, since the numbers are written in scientific notation, we know that the restrictions for A and B are
1≤A<10 and 1≤B<10. The maximum value for A, when multiplied by 10^-5, will still be less than 1. The minimum value of B will produce a number at least 10⁵ in size.

Question 2.
The mass of a neutron is approximately 1.674927×10^-27 kg. Recall that the mass of a proton is
1.672622×10^-27 kg. Explain which is heavier.
Answer:
Since both numbers have a factor of 10^-27, we only need to look at 1.674927 and 1.672622. When we multiply each number by 10⁶, we get
1.674927×10⁶ and 1.672622×10⁶,
which is the same as
1,674,927 and 1,672,622.
Now that we are looking at whole numbers, we can see that 1,674,927>1,672,622 (by (2b) above), which means that 1.674927×10^-27>1.672622×10^-27. Therefore, the mass of a neutron is heavier.

Question 3.
The average lifetime of the Z boson is approximately 3×10^-25 seconds, and the average lifetime of a neutral rho meson is approximately 4.5×10^-24 seconds.
a. Without using the theorem from today’s lesson, explain why the neutral rho meson has a longer average lifetime.
Answer:
Since 3×10^-25=3×10^-1×10^-24, we can compare 3×10^-1×10^-24 and 4.5×10^-24. Based on Example 3 or by use of (1) above, we only need to compare 3×10^-1 and 4.5, which is the same as 0.3 and 4.5. If we multiply each number by 10, we get whole numbers 3 and 45. Since 3<45, then
3×10^-25<4.5×10^-24. Therefore, the neutral rho meson has a longer average lifetime.

b. Approximately how much longer is the lifetime of a neutral rho meson than a Z boson?
Answer:
45:3 or 15 times longer

Rapid White Board Exchange: Operations with Numbers Expressed in Scientific Notation

Question 1.
(5×10⁴)²=
Answer:
2.5×10⁹

Question 2.
(2×10⁹)⁴=
Answer:
1.6×10³7

Question 3.
\(\frac{\left(1.2 \times 10^{4}\right)+\left(2 \times 10^{4}\right)+\left(2.8 \times 10^{4}\right)}{3}\)=
Answer:
2×10⁴

Question 4.
\(\frac{7 \times 10^{15}}{14 \times 10^{9}}\) =
Answer:
5×10⁵

Question 5.
\(\frac{4 \times 10^{2}}{2 \times 10^{8}}\)=
Answer:
2×10^-6

Question 6.
\(\frac{\left(7 \times 10^{9}\right)+\left(6 \times 10^{9}\right)}{2}\)=
Answer:
6.5×10⁹

Question 7.
(9×10^-4)²=
Answer:
8.1×10^-7

Question 8.
(9.3×10¹⁰)-(9×10¹⁰)=
Answer:
3×10⁹