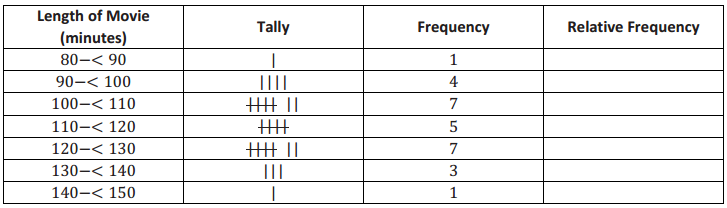
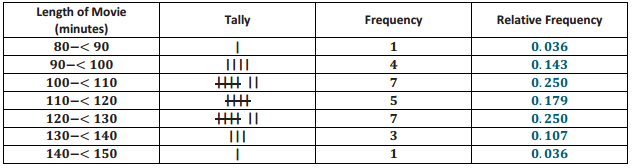
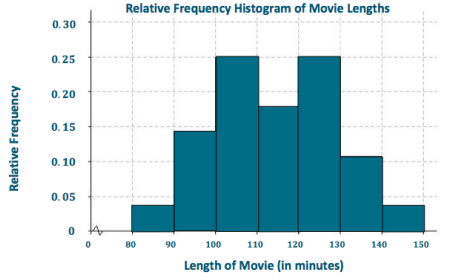
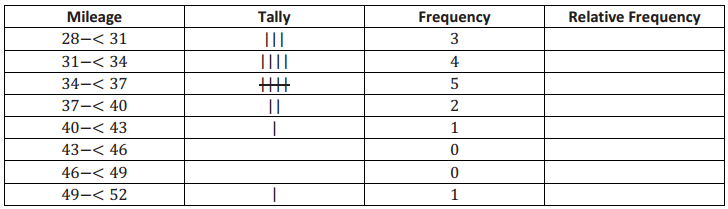
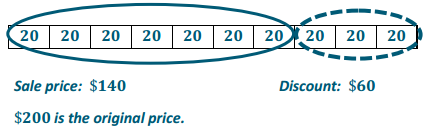
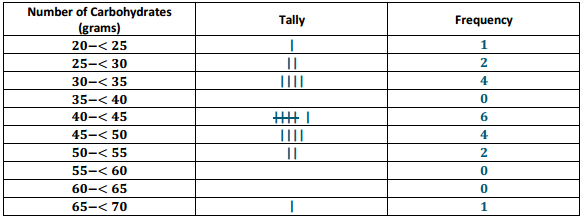
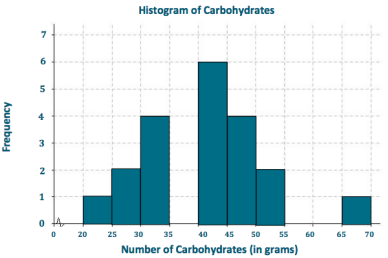
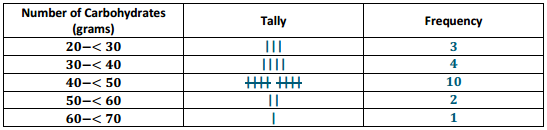
Students who are searching for different problems on Discounts can get them in one place. Get all the problems on discounts along with the answers here. Use the Worksheet on Discounts and kick start your preparation. Students can assess their strengths and weaknesses by solving all questions from Discounts Worksheet with Answers. Make use of these Discount Questions and understand different formulas and ways of solving problems related to all discount problems.
Different Questions are covered in the Discount Worksheets. Get the formulas and step-by-step process to solve each and every question. Here, we are offering a detailed solution along with an explanation for each and every problem for a better understanding of concepts.
Do Read:
- Practice Test on Profit and Loss
- Examples on Calculating Profit or Loss
- Word Problems on Profit and Loss
Discounts Problems with Solutions
1. The marked price of a washing machine is $ 3650. The shopkeeper offers an off-season discount of 18% on it. Find its selling price.
Solution:
Given that the market price of a washing machine is $ 3650. The shopkeeper offers an off-season discount of 18% on it.
The price of a washing machine is $ 3650.
The discount percent on a washing machine is 18%
Firstly, find out the discount on the washing machine.
Discount on washing machine = (18 * $3650)/100 = $657
To find the selling price of the washing machine, subtract the discount on the washing machine from The price of a washing machine.
Selling price = $ 3650 – $657 = $2993
Therefore, the selling price of a washing machine is $2993.
2. The price of a sweater was slashed from $ 860 to $ 716 by a shopkeeper in the winter season. Find the rate of discount given by him.
Solution:
Given that the price of a sweater was slashed from $ 860 to $ 716 by a shopkeeper in the winter season.
Cost Price = Price of the Sweater in the starting = ₹ 860
Selling Price = Price of the Sweater after slashing = ₹ 716
To Find the Rate of discount which is given by him, first, we have to find the amount that has been discounted.
The discount on the sweater = Cost Price – Selling Price
Substitute the Cost Price and Selling Price in the above equation.
The discount on the sweater = 860 – 716 = ₹ 144
Now, We need to calculate the discount percentage.
To find out the discount percentage we use the formula,
Discount Percentage = Discounted Price / Cost Price x 100
Now, Substitute the Discounted Price and Cost Price in the above equation.
Discount Percentage = ₹ 144/₹ 860 x 100 = 16.7% (approximately)
Therefore, the rate of discount that is given to him is 16.7%.
3. Find the rate of discount is given on a shirt whose selling price is $ 1092 after deducting a discount of $ 208 on its marked price.
Solution:
Given that a shirt whose selling price is $ 1092 after deducting a discount of $ 208 on its marked price.
Selling Price of the Shirt = $ 1092
Discounted Price = $ 208
To Find the Rate of discount on a shirt, first, we have to find the Marked Price of the Shirt.
The formula for the Marked Price is
Marked Price = Selling Price + Discount Price
Substitute the Selling Price and Discount Price in the above equation.
Marked Price = $ 1092 + $ 208 = $1300
Now, We need to calculate the rate of discount on the shirt.
To find out the rate of discount on the shirt we use the formula,
Rate of Discount = Discount Price / Marked Price x 100
Now, Substitute the Discount Price and Marked Price in the above equation.
Rate of Discount = $ 208/$1300 x 100 = 16%
Therefore, the rate of discount on the trouser is 16 %.
4. After allowing a discount of 76% on a toy, it is sold for $ 582. Find the marked price of the toy.
Solution:
Given that after allowing a discount of 76% on a toy, it is sold for $ 582.
The discount on a toy = 76%
The selling price of the toy = $ 582
Also, the Selling price of = 100 – 76% = 24%
To find the cost price of the toy,
Selling Price = 24%
Selling Price = $ 582
24% = $ 582
1% = $ 582 ÷ 24 = $ 24.25
100% = $ 24.25 x 100 = $ 2425
Therefore, the marked price of the toy is $ 2425.
5. A tea set was bought for $ 344 after getting a discount of 14% on its marked price. Find the marked price of the tea set.
Solution:
Given that a tea set was bought for $ 344 after getting a discount of 14% on its marked price.
Let the marked price of tea set be Rs = X
The selling price = $ 344
Also, the discount = 14%
Marked Price – Discount on Marked Price = $ 344
X – 14X/100 = $ 344
100X – 14X = $ 344 * 100
86X = $34400
X = $34400/86
X = $400
Therefore, the marked price of the tea set is $ 400.
6. A dealer marks his goods at 45% above the cost price and allows a discount of 30% on the marked price. Find his gain or loss percent.
Solution:
Given that a dealer marks his goods at 45% above the cost price and allows a discount of 30% on the marked price.
Let the Cost Price of the goods be X
The Marked price of the goods = X + (45/100 of x) = Rs 1.45 X
Also, the discount = 30%
Marked Price – Discount on Marked Price = Selling Price
Substitute the values in the above equation.
Discount = 30% of 1.45X = 1.45X × 0.3 = Rs 0.435X
Selling Price = 1.45 X – 0.435X = 1.015X
Selling Price = 1.015X
As Selling Price is more than Cost Price, there is a profit.
So, Profit = Selling Price – Cost Price
= 1.015X – X
= 0.015X
Profit percentage = (Profit / Cost Price) x 100
= (0.015X / X) x 100
= 1.5%
Therefore, the Profit percentage is 1.5%.
7. A cell phone was marked at 50% above the cost price and a discount of 20% was given on its marked price. Find the gain or loss percent made by the shopkeeper.
Solution:
Given that a cell phone was marked at 10% above the cost price and a discount of 20% was given on its marked price.
Let the Cost Price of the cell phone is Rs. 100.
The Marked price of the cell phone = (100 +10)%
The Marked price of the cell phone = (110)%
Also, the discount = 10% of 130 = 10/100 * 130
The Discount = 13
Selling Price = Marked price – Discount
Substitute the values in the above equation.
Selling Price = 110 – 13 = 97
Loss = 3
Loss % = (Loss × 100)/ CP
Loss% = 3%
Therefore, the Loss percentage is 3%.
8. A dealer purchased a fan for $ 620. After allowing a discount of 35% on its marked price, he gains 35%. Find the marked price of the fan?
Solution:
Given that a dealer purchased a fan for $ 620. After allowing a discount of 35% on its marked price, he gains 35%.
Let the Cost Price of a fan is $ 620.
The Discount on its marked price = 35%
The Profit % = 35%
Selling price = C.P + Profit% of C.P
Substitute the values in the above equation.
Selling price = 620 + 35% of 620
= 620 + 0.35 × 620
= 620 + 217
= 867
Selling Price = $867
Now, the next step is to find the marked price of the fan.
M.P = (S.P × 100)/(100 – discount)
= (867 × 100)/(100 – 35)
= 86700/65
= 1333.84
Therefore, the marked price of the fan is 1333.84.
9. A dealer bought a refrigerator for $ 23030. After allowing a discount of 32% on its marked price, he gains 40%. Find the marked price of the refrigerator.
Solution:
Given that a dealer bought a refrigerator for $ 23030. After allowing a discount of 32% on its marked price, he gains 40%.
Let the Cost Price of a fan is $ 23030.
The Discount on its marked price = 32%
The Profit % = 40%
Selling price = C.P + Profit% of C.P
Substitute the values in the above equation.
Selling price = 23030 + 40% of 23030
= 23030 + 0.4 × 23030
= 23030 + 9212
= 32242
Selling Price = $32242
Now, the next step is to find the marked price of the fan.
M.P = (S.P × 100)/(100 – discount)
= (32242 × 100)/(100 – 32)
= 3224200/68
= 47414.70
Therefore, the marked price of the refrigerator is 47414.70.
10. A carpenter allows a discount of 32% to his customers and still gains 40%. Find the marked price of a dining table which costs the carpenter $ 2380.
Solution:
Given that a carpenter allows a discount of 32% to his customers and still gains 40%.
Let the Marked Price of a dining table is M.
The Discount on its marked price = 32%
Selling price = Marked Price – Discount on its marked price
Substitute the values in the above equation.
Selling price = M – 0.32M = 0.68M
Cost = $ 2380
Gain 40% = 0.4 * 2380 = 952
Selling price = 2380 + 952 = 3332
Selling price = 0.68M = 3332
M = 3332/0.68
M = 4900
Therefore, the marked price of the dining table costs the carpenter $ 2380. is 4900.
11. After allowing a discount of 20% on the marked price, a trader still makes a gain of 34%. By what percent is the marked price above the cost price?
Solution:
Given that after allowing a discount of 20% on the marked price, a trader still makes a gain of 34%.
Let the cost price be 100 Rupees.
There is a gain of 34%.
So, the Selling price will be 100 + 34 Rupees.
Selling price = 134 Rupees.
Let marked price be M
Then 80% of M = 134
0.8M = 134
M = 134/0.8
M = 167.5
Above cost price =167.5 – 100 = 67.5
So, the marked price is 67.5 rupees more than CP.
Therefore, the shopkeeper must mark his good’s price 67.5% more than the cost price.
12. How much percent above the cost price should a shopkeeper mark his goods so that after allowing a discount of 20% on the marked price, he gains 16%?
Solution:
Given that after allowing a discount of 20% on the marked price, he gains 16%.
Let the cost price be 100 Rupees and also the marked price be M.
There is a gain of 16%.
So, the selling price of the article = Cost Price + Gain
Substitute the values in the above equation.
The selling price will be 100 + 16 Rupees.
Selling price = 116 Rupees.
Discount % = 20%
Discount = 20% of Marked Price
= Rs.20/100 * M
= Rs. 20M/100
= Rs. M/5
Marked Price – Discount = Selling price
=> M – M/5 = 116
=> (5M – M)/5 = 116
=> 4M/5 = 116
=> M = 116 * 5/4 = Rs. 145
Marked Price = Rs. 145
The amount marked above the CP = MP – CP
= Rs. (145 – 100)
= Rs. 45
∴ % amount marked above the CP
= Amount increased/CP * 100
= 45/100 * 100
= 45%
Therefore, the shopkeeper must mark his good’s price 45% more than the cost price.
13. The marked price of a television is $ 37000. A dealer allows two successive discounts of 10% and 5%. For how much is the television available?
Solution:
Given that the marked price of a television is $ 37000. A dealer allows two successive discounts of 10% and 5%.
The Price after 10% discount.
= $ 37000 – 10/100 * $ 37000
= $ 37000 – 0.05 * $ 37000 = $ 37000 – 3700 = 33300
The Price after 5% discount.
= $ 37000 – 5/100 * $ 37000
= $ 37000 – 0.1 * $ 37000 = $ 37000 – 1850 = 35150
Therefore, tv is available at price = 35150
14. Find the single discount which is equivalent to two successive discounts of 30% and 10%.
Solution:
Given that two successive discounts of 30% and 10%.
The marked price = 100
1st discount = 30% of 100 = 30
since, 100 – 30 = 70
2nd discount = 10% of 70 = 7
Selling price = 70 – 7 = 63
Single Equivalent Discount = MP – SP = 100 -63= 37
Since the discount of 37 is on 100
Required single discount = 37%