Practice Test on Framing the Formula let you know about the different problems available on the Framing the Formula. Most of the below questions appear on the exam which helps you to get good marks in the exam. Practice all the questions available below and have a perfect grip on Framing the Formula Problems.
All the concepts such as formulas, framing a formula, find the value of the variable using a change of subject of formula or an equation, change the subject of the formula, and method of substitution are included in the below article. Learn Tricks to solve Formula and Framing the Formula problems easily.
1. Write the formulas for the following statements.
(a) Area of the square is equal to the square of its side (b)
(b) Area B of the rhombus is equal to half the product of its diagonals (s₁, s₂).
(c) Perimeter (p) of a parallelogram is thrice the sum of its adjacent sides.
(d) Area of four walls (D) of a room is the product of two times the sum of length (l), breadth (b) and height (h).
(e) Profit (P) is calculated by taking the difference of cost price (C) and selling price (S).
Solution:
(a) Given that Area of the square is equal to the square of its side (b)
Area of the square = A
A = b²
(b) Area B of the rhombus is equal to half the product of its diagonals (s₁, s₂).
B = s₁ × s₂
(c) Perimeter (p) of a parallelogram is thrice the sum of its adjacent sides.
sum of its adjacent sides = x
p = 3(x)
(d) Area of four walls (D) of a room is the product of two times the sum of length (l), breadth (b) and height (h).
D = 2 (l + b + h)
(e) Profit (P) is calculated by taking the difference of cost price (C) and selling price (S).
P = S – C
2. Mention the formulas for the following statements.
(a) A side of a chessboard (D) is 3.14 times the side of a board (e).
(b) The difference between the two different variables is 36.
(c) The sum (X) of all the interior angles of a regular polygon of m sides is 2 less than m times 180°.
(d) Subtracting 2/5 from a number and multiplying this difference by 4 gives two times the same number.
(e) Fourteen years from now Sam’s age will be three times her present age.
Solution:
(a) Given that A side of a chessboard (D) is 3.14 times the side of a board (e).
D = 3.14e
(b) The difference between the two different variables is 36.
Two different variables are a and b
a – b = 36
(c) The sum (X) of all the interior angles of a regular polygon of m sides is 2 less than m times 180°.
X = (m – 2) × 180°
(d) Subtracting 2/5 from a number and multiplying this difference by 4 gives two times the same number.
Let the number is X.
X = 4(X – 2/5)
(e) Fourteen years from now Sam’s age will be three times her present age.
Sam’s age is C
C + 14 = 3C
3. Change the subject of the formula and find the value of the new subject.
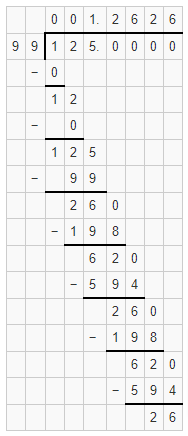
(a) X = 2YZ make the subject Z. X = 20, Y = 5
(b) l² = r² + h², l is the height of the cone, h is the height and r is the radius. Make the subject h when l = 12 and r = 6.
(c) M = 1/2 × b × h where M is the area of a triangle with base b and height h. Make h the subject, find h when M = 50, b = 24.
(d) D = d × q + r where D is the dividend, q is the quotient, d the divisor, and r is the remainder. Make the subject r, when D = x² – x, d = x – 2, q = x + 3.
(e) M × N = c × d, Make N as the subject where M = 2, c = 4, d = 10.
Solution:
(a) X = 2YZ make the subject Z. X = 20, Y = 5
Given that X = 2YZ
Divide both sides with 2Y
X/2Y = 2YZ/2Y
X/2Y = Z
Therefore, Z = X/2Y
Substitute the given values X = 20, Y = 5
Z = 20/2(5) = 20/10 = 2
Z = 2.
The final answer is Z = 2.
(b) l² = r² + h², l is the height of the cone, h is the height and r is the radius. Make the subject h when l = 12 and r = 6.
Given that l² = r² + h², l is the height of the cone, h is the height and r is the radius.
l² = r² + h²
Subtract r² on both sides
l² – r² = r² – r² + h²
l² – r² = h²
h = √(l² – r²)
Substitute the given values l = 12 and r = 6
h = √((12)² – (6)²) = √144 – 36 = √108
The final answer is h = √108
(c) M = 1/2 × b × h where M is the area of a triangle with base b and height h. Make h the subject, find h when M = 50, b = 24.
Given that M = 1/2 × b × h where M is the area of a triangle with base b and height h. Make h the subject, find h when M = 50, b = 24.
M = 1/2 × b × h
Divide 1/2 × b on both sides.
M/(1/2 × b) = (1/2 × b × h)/(1/2 × b)
M/(1/2 × b) = h
Therefore, h = M/(1/2 × b)
Substitute the given values M = 50, b = 24.
h = 50/(1/2 × 24)
h = 50/12
The final answer is h = 50/12
(d) D = (d × q) + r where D is the dividend, q is the quotient, d the divisor, and r is the remainder. Make the subject r, when D = x² – x, d = x – 2, q = x + 3.
Given that D = d × q + r where D is the dividend, q is the quotient, d the divisor, and r is the remainder. Make the subject r, when D = x² – x, d = x – 2, q = x + 3.
D = (d × q) + r
Subtract (d × q) on both sides
D – (d × q) = (d × q) – (d × q) + r
D – (d × q) = r
Therefore, r = D – (d × q)
Substitute the given values D = x² – x, d = x – 2, q = x + 3.
r = (x² – x) – ((x – 2)(x + 3))
r = (x² – x) – (x² + 3x – 2x – 6)
r = x² – x – x² – x + 6
r = -2x + 6
The final answer is r = -2x + 6
(e) M × N = c × d, Make N as the subject where M = 2, c = 4, d = 10.
Given that M × N = c × d
Divide M on both sides
MN/M = cd/M
N = cd/M
Substitute the given values M = 2, c = 4, d = 10
N = (4 × 10)/2
N = 40/2
N = 20
The final answer is N = 20.
3. If the base of the triangle is 3/2 times its height, then find the area of the triangle.
Solution:
Given that the base of the triangle is 3/2 times its height, then find the area of the triangle.
The base of the triangle = b
Height of the triangle = h
The area of the triangle = A
A = 1/2 × b × h
Base of the triangle is 3/2 times its height
b = 3/2 × h
A = 1/2 × 3/2 × h × h
A = 3/4 × h²
4. If ‘S’ is equal to the 3/4 of the r, then find r.
Solution:
Given that If ‘S’ is equal to the 3/4 of the r, then find r.
S = 3/4 r
Divide 3/4 on both sides.
S/(3/4) = (3/4)/(3/4) . r
4S/3 = r
The final answer is r = 4S/3
5. If x, y, z are in continued proportion, then find the value of z.
Solution:
Given that If x, y, z are in continued proportion, then find the value of z.
x/y = y/z
x . z = y . y
xz = y²
y² = xz
y = √xz
The final answer is y = √xz
6. If y workers can build a wall in 24 days, in how many days will 16 workers take to build a same wall.
Solution: Given that y workers can build a wall in 24 days
So, find the time taken to build a wall by one worker.
y workers = 24 days
1 worker = 24y days
Now, the time taken by 16 workers to build a wall.
1 worker = 24y days
16 worker = 24y/16 = 3/4y
Therefore, The time taken to build a wall by 16 workers is 3/4y.
The final answer is 3/4y.
7. A shirt is marked $ y and the shopkeeper allows 100 rupees off as a discount on it. What is its selling price?
Solution:
Given that a shirt is marked $ y and the shopkeeper allows $100 off as a discount on it.
Subtract $100 from $y to get the selling price.
$y – $100
The selling price is $y – $100.
8. A weighs 3 kg more than B and B weighs 6 kg less than C. If the weights of A, B, C is n, find the weights of A, B, C separately.
Solution:
Given that A weighs 3 kg more than B
A = 3 + B
B weighs 6 kg less than C
B = C – 6; C = B + 6
A + B + C = n
3 + B + B + B + 6 = n
3 + 3B + 6 = n
3B + 9 = n
3B = n – 9
B = (n – 9)/3
A = 3 + B
A = 3 + (n – 9)/3
C = B + 6
C = (n – 9)/3 + 6
The values of A, B, and C is A = 3 + (n – 9)/3, B = (n – 9)/3, and C = (n – 9)/3 + 6.
9. Half of a herd of deer are grazing in the field and 2/3 of the remaining are playing nearby. The rest 8 are drinking water from the pond. Find the number of deer in the herd?
Solution:
Let the total no.of deer = y
Half of a herd = y/2
2/3 of remaining half herd = (y/2)(2/3) = y/3
remaining deer = 8
From the given information, y = (y/2) + (y/3) + 8
y = (3y + 2y)/6 + 8
y = (5y + 48)/6
Multiply 6 on both sides
6y = (5y + 48)/6 × 6
6y = 5y + 48
Move 5y to the left side
6y – 5y = 48
y = 48.
The total number of deers is 48.
10. Arun is twice as old as Sam six years ago his age was four times Shriya’s age. Find their present ages.
Solution:
Let Arun age is x and Sam age is y
Arun age is twice as old as Sam
x = 2y if it is five years ago
x – 5 = 4(y – 5)
x – 5 = 4y – 20
x – 4y + 15 = 0
Substitute x = 2y in x – 4y + 15 = 0
2y – 4y + 15 = 0
-2y + 15 = 0
2y – 15 = 0
2y = 15
y = 15/2 = 7.5
x = 2y = 2 (15/2) = 15
Arun’s age is 15 and Sam’s age is 7.5
11. A car travels 12 km at the speed of x km/hr. Find the time taken by the car to reach the destination.
Solution:
Given that a car travels 12 km at the speed of x km/hr.
We know that Speed = Distance/Time
Time = Distance/Speed
Time = 12km/x km/hr.
The time = 12 hrs.
The time taken by the car to reach the destination is 12 hrs.
12. Ram had $192 with him. He purchased x kg potatoes for $40 a kg and y kg tomatoes for $45 a kg and z kg onions at $43 a kg. Find the money left with him?
Solution:
Given that Ram had $192 with him.
He purchased x kg potatoes for $40 a kg and y kg tomatoes for $45 a kg and z kg onions at $43 a kg.
Total cost of potatoes = 40x
The total cost of tomatoes = 45y
Total cost of onions = 43z
Total amount spent = 40x + 45y + 43z.
Money left with Ram is $192 – (40x + 45y + 43z)
Total Money left with Ram is $192 – (40x + 45y + 43z).