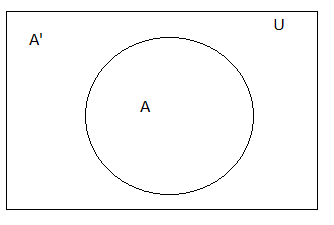
In general, a set is a collection of well-defined objects. A set must have the same type of objects. The objects are also called the members or elements of the set. The number of the element present in a set is called the order of the set. The pairs of sets mean there is a relationship between two sets. Get the examples and various pairs of sets in the below sections of this article.
What are Pairs of Sets?
If there is some relationship between two sets then such sets are called pairs of sets. Various pairs of sets are mentioned below.
- Equal Sets
- Equivalent Sets
- Disjoint Sets
- Overlapping Sets
Pairs of Sets Examples
The relation between two sets is called pairs of sets. Let us know about each of the set pairs with the examples on the following modules.
1. Equal Sets:
Two sets P and Q are said to be equal sets if all the elements of the first set are in the second set irrespective of the position of the elements. The symbol to denote the equal sets is “=”.
Here P = Q means P is equal to Q and Q is equal to P.
Examples:
P = {12, 13, 14, 15, 16}
Q = {15, 12, 14, 13, 16}
The elements of P and Q are same. So, P = Q.
X = {a, e, l, , u}, Y = {e, q, u, a, l}
The elements of sets X and Y are the same. So, X = Y and Y = X.
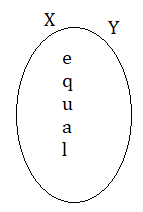
2. Equivalent Sets:
Two sets P and Q are said to be equivalent if both sets have the same number of elements or same order or same cardinality. The symbol to denote equivalent sets is ↔. Equal sets are always equivalent. But equivalent sets may or may not be equal.
P ↔ Q means set P and Q have the same order.
Examples:
P = {10, 20, 30, 40, 50, 60, 70, 80, 90, 100}
Q = {11, 22, 33, 44, 55, 66, 77, 88, 99, 111}
The order of P = n(P) = 10
The order of Q = n(Q) = 10
n(P) = n(Q). So, P ↔ Q.
A = {a, p, p, l, e}, B = {p, o, w, e, r}
The number of elements of A = n(A) = 5
The number of elements of B = n(B) = 5
n(A) = n(B). So, A ↔ B i.e A is equivalent to B.
3. Disjoint Sets:
Two sets P and Q are said to be disjoint sets if they do not contain only one element in common.
Examples:
P = {x | x is an even number}
Q = {x : x is an odd number}
The set of even numbers are {2, 4, 6, 8, 10, 12, 14, . . . }
The set of odd numbers are {1, 3, 5, 7, 9, 11, 13, . . }
So, there is no common element in between P and Q. Therefore, P and Q are disjoint sets.
A = {5, 10, 15, 20, 25, 30, 35, 40}, B = {3, 6, 9, 18, 21, 24, 27}
Here, A and B has no common element. So, A and B are disjoint sets.
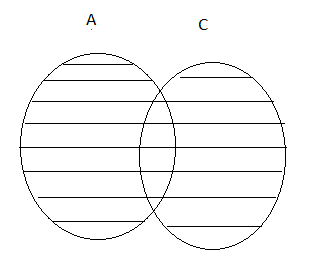
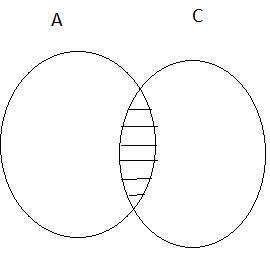
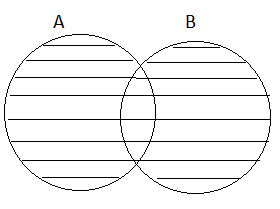
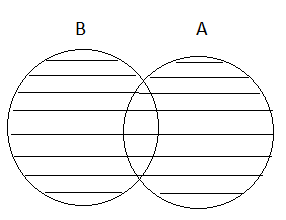
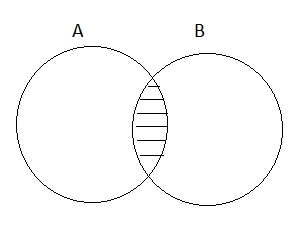
4. Overlapping Sets:
Two sets P and Q are said to be overlapping sets if they have at least one element in common.
Examples:
P = {x : x is a whole number}
Q = {x : x is a natural number}
The set of whole numbers are {0, 1, 2, 3, 4, 5, 6, 7, 8, . . . }
The set of natural numbers are {1, 2, 3, 4, 5, 6, . . . }
The common elements in both sets are {1, 2, 3, 4, 5, 6, 7, . . . }
So, P and Q are overlapping sets.
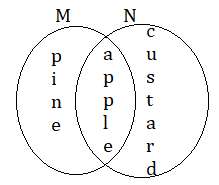
M = {p, i, n, e, a, p, p, l, e}
N = {c, u, s, t, a, r, d, a, p, p, l, e}
The common elements in both sets are {a, p, p, l, e}
Also, Read
Solved Example Questions on Pairs of Sets
Example 1:
State whether the sets A and B are equal sets or not?
A = {s, t, a, t, e s}
B = {a, e, s, s, t, t}
Solution:
Given two sets are
A = {s, t, a, t, e s}, B = {a, e, s, s, t, t}
The elements of both sets are the same. So, A and B are equal sets.
Therefore, A = B.
Example 2:
State whether the sets C and D are equivalent or not?
C = {5, 9, 10, 12, 16, 78}
D = {a, b, c, d, e, g}
Solution:
Given two sets are
C = {5, 9, 10, 12, 16, 78} and D = {a, b, c, d, e, g}
The number of elements of C = n(C) = 6
The order of D = n(D) = 6
n(C) = n(D)
So, C and D are equivalent sets i.e C ↔ D.
Example 3:
Find whether the following sets are disjoint sets or overlapping sets.
(i) X = {x : x is a multiple of 7 between 1 and 50}
Y = {x | x is a multiple of 11 between 1 and 50}
(ii) P = {x : x is a letter in ‘FLOOR’}
Q = {x | x is a letter in ‘FLOWER’}
Solution:
(i) Given two sets are X = {x : x is a multiple of 7 between 1 and 50} and Y = {x | x is a multiple of 11 between 1 and 50}
The roster form is X = {7, 14, 21, 28, 35, 42, 49}, Y = {11, 22, 33, 44}
Two sets X and Y have no common element.
So, X and Y are disjoint sets
(ii) Given two sets are P = {x : x is a letter in ‘FLOOR’} and Q = {x | x is a letter in ‘FLOWER’}
The roster form of P = {F, L, O, O, R}, Q = {F, L, O, W, E, R}
The common elements are F, L, O, R
So, P and Q are overlapping sets.




 =
= 
 =
=