Common Core Math

Angles are formed when two lines intersect each other at a point. The pair of angles are nothing but two angles. The angle pairs can relate to each other in various ways. Those are complementary angles, supplementary angles, vertical angles, adjacent angles, alternate interior angles, alternate exterior angles, and corresponding angles.

Pairs of Angles – Definition

The region between two infinitely long lines pointing a certain direction from a common vertex is called an angle. Which is the amount of turn is measured by an angle. The pairs of angles mean two angles. If there is one common line for two angles, it is known as angle pairs. Get the definitions and examples of all pairs of angles in the following section.

1. Complementary Angles

Two angles whose sum is 90° are called complementary angles and one angle is the complement of another angle.

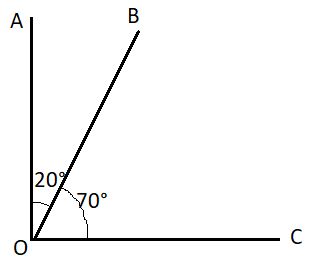
Here, ∠AOB = 20°, ∠BOC = 70°

So, ∠AOB + ∠BOC = 20° + 70° = 90°

Therefore, ∠AOB and ∠BOC are called complementary angles.

∠AOB is a complement of ∠BOC and ∠BOC is the complement of ∠AOB.

Example:

(i) Angles of measure 50° and 40° are complementary angles because 50° + 40° = 90°.

Thus, the complementary angle of 50° is the angle measure 40°. The complementary angle of 40° is the angle measure 50°.

(ii) Complementary of 60° is 90° – 60° = 30°

(iii) Complementary of 45° is 90° – 45°= 45°

(vi) Complementary of 25° is 90 – 25° = 65°

Working rule: To find the complementary angle of a given angle subtracts the measure of an angle from 90°.

So, the complementary angle = 90° – given angle

Also, Read:

• Complementary and Supplementary Angles
• Linear Pair of Angles
• Classification of Angles

2. Supplementary Angles

The pair of angles whose sum is 180° is called the supplementary angles and one angle is called the supplement of the other angle.

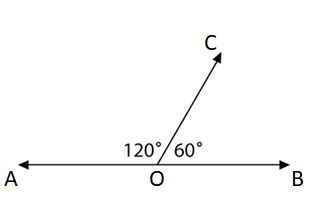
Here, ∠AOC = 120°, ∠COB = 60°

∠AOC + ∠COB = 120° + 60° = 180°

Therefore, ∠AOC, ∠COB are called supplementary angles.

∠AOC is the supplement of ∠COB, ∠COB is a supplement of ∠AOC.

Example:

(i) Angles of measure 90° and 90° are supplementary angles because 90°+ 90° = 180°

Thus, the supplementary angle of 90° is the angle of measure 90°.

(ii) Supplement of 100° is 180° – 100° = 80°

(iii) Supplement of 50° is 180° – 50° = 130°

(iv) Supplement of 95° is 180° – 95°= 85°

(v) Supplement of 140° is 180°- 140° = 40°

Working rule: To find the supplementary angle of the given angle, subtract the measure of angle from 180°.

So, the supplementary angle = 180° – given angle

3. Adjacent Angles

Two non-overlapping angles are said to be adjacent angles if they have a common vertex, common arm, and other two arms lying on the opposite side of this common arm so that their interiors do not overlap.

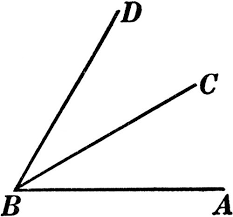
In the above figure, ∠DBC and ∠CBA are non-overlapping, have BC as the common arm and B as the common vertex. The other arms BD, AB of the angles ∠DBC and ∠CBA are opposite sides of the common arm BC.

Hence, the arm ∠DBC and ∠CBA form a pair of adjacent angles.

4. Linear Pair of Angles

The angles are called liner pairs of angles when they are adjacent to each other after the intersection of two lines. Two adjacent angles are said to form a linear pair if their sum is 180°. The types of linear pairs of angles are alternate exterior angles, alternate interior angles, and corresponding angles.

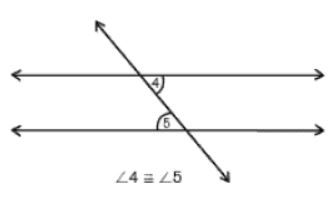
Alternate interior angles

Two angles in the interior of the parallel lines and on opposite sides of the transversal. Alternate interior angles are non-adjacent and congruent.

Alternate exterior angles

Two angles in the exterior of the parallel lines, and on the opposite sides of the transversal. Alternate exterior angles are non-adjacent and congruent.

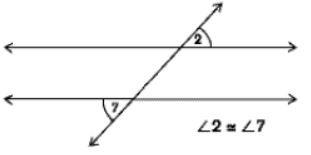
Corresponding angles

The pair of angles, one in the interior and another in the exterior that is on the same side of the transversal. Corresponding angles are non-adjacent and congruent.

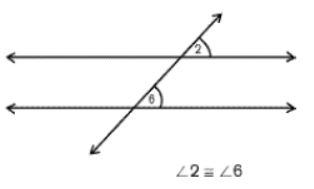
5. Vertical Angles

Two angles formed by two intersecting lines having no common arm are called the vertically opposite angles.

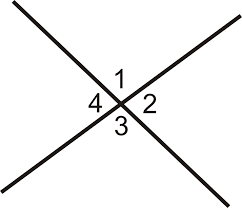
When two lines intersect, then vertically opposite angles are always equal.

∠1 = ∠3

∠2 = ∠4

Pair of Angles Examples

Example 1:

Suppose two angles ∠AOC and ∠ BOC form a linear pair at point O in a line segment AB. If the difference between the two angles is 40°. Then find both the angles.

Solution:

Given that,

∠AOC and ∠BOC form a linear pair

so, ∠AOC + ∠BOC = 180° —- (i)

∠AOC – ∠BOC = 40° —- (ii)

Add both equations

∠AOC + ∠BOC + ∠AOC – ∠BOC = 180° + 40°

2∠AOC = 220°

∠AOC = 220° / 2

∠AOC = 110°

Now, substitute ∠AOC in (i)

110° + ∠ BOC = 180°

∠BOC = 180° – 110°

∠BOC = 70°

Therefore, two angles are 70°, 110°.

Example 2:

Find the values of the angles x, y, and z in the following figure.

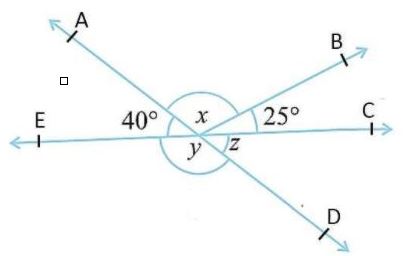
Solution:

From the given figure,

lines AD and EC intersect each other and ∠DOC and ∠AOE are vertically opposite angles

When two lines intersect, then vertically opposite angles are always equal.

So, ∠DOC = ∠AOE

Therefore, z = 40°

AD is a line

∠DOE and ∠AOE are adjacent angles. The sum of adjacent angles are 180°

So, ∠DOE + ∠AOE = 180°

y + 40° = 180°

y = 180°- 40°

y = 140°

And, lines AD and CE intersect

∠DOE, ∠COA are vertically opposite.

When two lines intersect, then vertically opposite angles are always equal.

So, ∠DOE = ∠COA

y = ∠COB + ∠BOAA

140° = x + 25°

140° – 25° = x

x = 115°

Hence, x = 115°, y = 140°, z = 40°

Example 3:

Identify the five pairs of adjacent angles in the following figure.

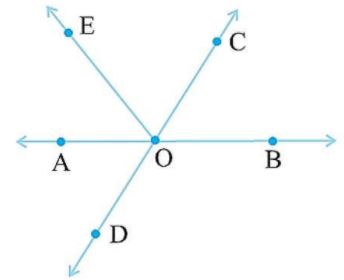
Solution:

Adjacent angles are the angles that have a common side, vertex, and no overlap.

So, (i) ∠AOD, ∠AOE are the adjacent angles

The common side is AO, the common vertex is O and OE, OD is not overlapping.

(ii) ∠AOD, ∠DOB is the adjacent angles

The common vertex is O, the common side is OD and OA, OB is not overlapping.

(iii) ∠DOB, ∠BOC is the adjacent angles

The common side is OB, the common vertex is O, and OD, OC are not overlapping.

(iv) ∠COE, ∠BOC are adjacent angles

The common side is OC, the common vertex is O, and OE, OB are not overlapping.

(v) ∠COE, ∠EOA are adjacent angles

The common vertex is O, the common side is OE, and OC, OA is not overlapping.

Read a Watch or Clock: Reading a clock or watch is an ability to master easily in a short time and with less effort. There are various types of clocks like Analogue clock, Digital clock, electronic word clock, musical clock, etc. Analogue clocks are distributed over a circle and move the hour hand and minute hand individually. This helps people to read a time from a clock or watch.

Whereas in the digital type of clock, you can easily read the hour and minutes. Well, reading a watch or clock can be confused when it comes to Roman numerals and military time. With a bit of hard work and smart work, you guys can read a clock or watch with ease. So, practice more by viewing the below modules regarding How to Read a Watch or a Clock.

How to Read a Watch or a Clock?

There are two methods to read a watch or clock. The first method is reading an Analogue clock and the second method is reading a Digital clock. Let’s start the process of the first method and learn the concept to read a watch or clock easily.

Method 1: Reading an Analogue Clock

• In step 1, we will discuss learning how a clock is divided. A clock is split into 12 sections. At the top, you will see the number ’12’. On the right-hand side, you will see a ‘1’ followed by 2, 3, 4, 5, ..so on up to 11 in a clockwise direction.
• Here the numbers labelling each section are the hours.
• The sections between the two numbers are divided into 5 divisions/segments.
• Above we have seen the numbers arranged in the clock.
• In a clock, there are 2 hands. A little hand indicated the hours and a big hand indicates minutes. For instance, if the little hand is showing ‘1’, then we have to read the time like this 1 o’clock.
• Now, use the big hand and read the minutes. To read the minutes, first, take the indicated number and multiply it by 5 to get the minutes.
  • If the big hand is pointing to “3,” you’ll know that it is 15 minutes past the hour.
  • If the big hand is between “1” and “2,” note what dash it is pointing to. For example, if it is on the 3rd dash after the “1,” it is 8 minutes past the hour. (1 x 5 + the number of dashes).
• After learning how to read hour and minutes, you can tell time easily. For instance,
  • If the little hand is pointing to “2” and the big hand is pointing to “12,” it is “two o’clock.”
  • If the little hand is pointing to “3” and the big hand is pointing to “2,” it is “3 hours 10 minutes” or “ten minutes past three.”
• To tell AM or PM, first, we have to know the time of day. From midnight to noon the next day, the time is in AM. From noon to midnight, the time is in PM.

Method 2: Reading a Digital Clock

• The digital clock is the opposite of the analogue clock. It displays only two numbers separated by a colon.
• The first number on a digital clock indicates the hours. If the first number reads “7”, then it is read as 7 o’clock hour.
• Now, come to the second number on a digital clock or watch, which is found after the colon, tells the minutes into the hour. For instance, if it displays 12, then it is read as 12 minutes into the hour.
• Finally, put them together to read the exact time. For example, if the clock displays ‘7:12’ then it means 7 hours 12 minutes, or seven-twelve, or twelve past seven.
• Also, to identify whether its AM or PM, some digital clocks show AM or PM directly on the clock.

Solved Examples on How to Tell Time in English?

1. Read the time shown in the given clock?

Solution:

In the given figure, the hour hand is showing the number 10 then 10 hours and the minute hand is showing the number 12 then 0 minutes. So, we can read it as a 10 o’clock.

2. Read the time shown in the below clock image?

Solution:

From the given clock image, the hour hand is indicating between 4 and 5. It is almost near to 5 but for now, we will read as a 4 hour or 4 o’clock.

The minute hand is indicating 7 then 7 x 5 is 40. So, we read as 40 minutes.

By joining both together, we read it as 4 hours 40 minutes or 40 minutes past 4. 

Cardinal Numbers are Numbers that are used for counting something. They are also called the Cardinals. Cardinals are meant by how many of anything is existing in a group. In other words, cardinal numbers are a collection of ordinal numbers. Learn about the Cardinal Number of a Set Definition, Solved Examples explained in detail in the further modules.

Cardinal Number of a Set – Definition

The Number of Distinct Elements present in a finite set is called the Cardinal Number of a Set. Usually, we define the size of a set using cardinality. The Cardinal Number of a Set A is denoted as n(A) where A is any set and n(A) represents the number of members in Set A.

Consider a set of even numbers less than 15.

Set A = {2, 4, 6, 8, 10, 12, 14}

As Set A has 7 elements, the Cardinal Number of the Set is n(A) = 7

Note:

(i) Cardinal number of an infinite set is not defined.

(ii) Cardinal number of the empty set is 0 since it has no element.

Also, Check:

• Different Notations in Sets
• Subset
• Intersection of Sets

How to find the Cardinal Number of a Set?

1. Find the cardinal number of the following set

E = { x : x < 0, x ∈ N }

Solution:

x<0 means negative integers and they don’t fall under Natural Numbers.

Therefore, the above set will not have any elements

Cardinal Number of Set E is n(E) =0

2. Find the Cardinal Number of the Following Set

Q = { x : – 4 ≤ x ≤ 3, x ∈ Z }

Solution:

Given Q = { x : – 4 ≤ x ≤ 3, x ∈ Z }

x={-4, -3, -2, -1, 0, 1, 2, 3 }

Number of Elements in the above set is 8

Therefore, Cardinal Number of Set Q is n(Q) = 8

3. Find the Cardinal Number of the Set

A = { x : x is even prime number }

Solution:

Among all the prime numbers 2 is the only even prime number and the set has only one element

A ={2}

Cardinal Number of a Set n(A) = 1

4. Set D = {3, 4, 4, 5, 6, 7, 8, 8, 9}

Solution:

We know the cardinal number of a set is nothing but the number of distinct elements in the set

Cardinal Number of Set D is n(D) = 7

5. Find the Cardinal Number of a Set X = {letters in the word APPLE}

Solution:

Set X = {letters in the word APPLE}

We know the cardinal number of a set is nothing but the number of distinct elements in the set

x = {A, P, L, E}

Cardinal Number of Set n(X) = 4

6. Find the Cardinal Number of a Set

P = {x | x ∈ N and x² <25}

Solution:

Given P = {x | x ∈ N and x² <25}

Then P = {1, 2, 3, 4}

Cardinal Number of Set P is 4 and is denoted by n(P) = 4

Polygons are the most important topic among all math concepts. One of the simplest polygons is Triangle and the easiest way to work with polygons is by calculating their perimeter. The term perimeter is a path that encloses an area. It completely refers total length of the edges or sides of a given polygon or a two-dimensional figure with angles. So, make sure you move down the page till to an end and learn the perimeter of a triangle definition, formula, and how to calculate the triangle perimeter easily & quickly.

What is the Perimeter of a Triangle?

The definition of Perimeter of a Triangle is the sum of the lengths of the side of the Triangle. It denotes as,

Perimeter = Sum of the three sides

In real-life problems, a perimeter of a triangle can be useful in building a fence around the triangular parcel, tying up a triangular box with ribbon, or estimating the lace required for binding a triangular pennant, etc.

Always, the result of the triangle perimeter should be represented in units. If the side lengths of the triangle are measured in centimeters, then the final result needs to be in centimeters.

Formula to Calculate Perimeter of Triangle

The basic formula is surprisingly uncomplicated. Simply add up the lengths of all of the triangle sides and you get the perimeter value of the given triangle. In the case of the triangle, if the sides are a,b,c then the perimeter of a triangle formula is P = a + b + c.

How to Find the Perimeter of a Triangle?

Between Area and Perimeter of a Triangle calculation, finding the perimeter of the triangle is the easiest one and it has three ways to calculate the triangle perimeter. All the three ways used to find the triangle perimeter are mentioned here for your sake of knowledge and understanding the concept efficiently. The ways to find the perimeter of a triangle are as follows:

1. The first & simple way is when side lengths are given, then we have to add them together to get the perimeter of the given triangle.
2. If we have two sides and then solve for a missing side using the Pythagorean theorem.
3. In case, we have the side-angle-side information in the given question, then we can solve for the missing side with the help of the Law of Cosines.

For a better explanation of the concept, we have listed out some worked-out examples of calculating the perimeter of a triangle below. Have a look at the solved examples and understand the concept behind solving the perimeter of a polygon ie., a Triangle.

Solved Examples on Finding Perimeter of a Triangle

1. Find the perimeter of the triangle where the three sides of the triangle are 20 cm, 34 cm, 15 cm?

Solution:

Given Sides of the triangle are a = 20 cm, b = 34 c, c = 15 cm

Now, use the Perimeter of Triangle Formula and find the result,

Perimeter = (a + b + c) 

= 20 + 34 + 15 = 69 cm.

2. Find the missing side whose perimeter is 40 cm and two sides of the triangles are 15 cm?

Solution:

Given,

a = 15 cm
b = 15 cm
P = 40 cm

Find c, Let’s assume c=x

Perimeter of the triangle P = a + b + c

40 cm = 15 cm + 15 cm + x

40 cm = 30 cm + x

x = 40 cm – 30 cm

x = 10 cm

Therefore, the length of the third side of the triangle is 10 cm.

FAQs on Calculating Triangle Perimeter

1. What are the types of Triangles and their perimeter formulas?

There are 4 types of triangles. They are listed below with their perimeter formulas:

1. Equilateral triangle: Perimeter (P) = 3 x l
2. Right triangle: Perimeter (P) = a + b + c
3. Isosceles triangle: Perimeter (P) = 2 x l + b
4. Scalene triangle: Perimeter (P) = b + p + h where h² = b² + p²

2. What is the formula of the perimeter of a triangle?

If a triangle has three sides a, b and c, then, the formula for the perimeter of a triangle is Perimeter, P = a + b +c.

3. How do you calculate the perimeter of a triangle with known sides?

If we knew the sides of a triangle, then finding the perimeter is so simple, just apply the perimeter of a triangle formula ie., P = a + b +c. and substitute all the sides and add them together.

In real-life mathematical tasks, we always do measuring the lengths in various situations. To learn about what is measuring length and what are the units for measuring length, this guide will help you a lot. Hence, gain knowledge about measuring length by understanding various units to measure the length from this page. Also, you may grasp some important information about units of measurements like temperature, time, mass, volume, etc. from our provided Math Conversion Chart.

What is Measuring Length?

Measuring of Length of any object includes in our daily life, we always measure the length of the cloth for dresses, wall-length for wallpapers, and many more other tasks.

You all want to know what is measuring length? Measuring length is a measurement of an object in a unit of length by using measuring tools such as scale or ruler.

For instance, the length of a pen can be measured in inches with the help of a ruler.

What is Length?

Length is determined as “Distance between two points” OR “The maximum extended dimension of an object”. Some of the tools used to measure length are Vernier caliper and Tapes.

Also Check: Units of Mass and Weight Conversion Chart 

What is a Unit of Length?

A unit of length refers any arbitrarily chosen and accepted reference standard for measurement of length. In modern use, the most common units are the metric units, which are utilized across the world. In the United States, the U.S. Customary units are also used mostly. For some purposes in the UK & other countries, British Imperial units are used. The metric system is classified into SI and non-SI units.

Units for Measuring Length

According to the metric system, the standard unit of length is a meter (m). Based upon the measuring of length, the meter can be converted into various units like millimeters (mm), centimeter (cm), and kilometer (km). In accordance with the length conversion charts, the different units of lengths and their equivalents are tabulated below:

See Related Articles:

• Units of Capacity and Volume Conversion Chart
• Units Of Length Conversion Charts
• Conversion of Units of Speed

Units of Length Definitions & Examples

Length describes how long a thing is from one end to the other.

FAQs on Unit of Measuring Length

1. What is the standard unit of measuring length?

‘Meter(m)’ is the standard unit of measuring length

2. Which is the standard tool to measure the length?

The standard tool among all to measure the length of any object is a ‘Ruler’. Just by placing the ruler beside the object and measure the object from start to end with the help of readings given on the ruler or scale.

3. What are the basic units of measurements?

There are seven SI base units and they are as follows:

• Length – meter (m)
• Mass – kilogram (kg)
• Temperature – kelvin (K)
• Time – second (s)
• Electric current – ampere (A)
• Luminous intensity – candela (cd)
• Amount of substance – mole (mole)

Converting Fractions to Decimals means you need to press the fractional numbers in the form of exact decimals. You can use different methods like just divide the numerator by the denominator of the fraction apply the long division method or any other simple method. Check out those different forms of converting a fraction into a decimal and apply the best one to get the answers quickly and effortlessly.

What is meant by a Fraction?

The fraction is a part of the whole number and it is also expressed as a ratio of two numbers. The form of the fraction is a/b where ais the numerator, b is the denominator and it is not equal to 0. The different types of fractions are mixed, proper, improper fractions. A fraction is also known as the rational number.

Examples: 2/5, 10/8, 120/150.

What is meant by a Decimal?

A decimal is a number that has a dot or point in between the digits. In simple words, we can say that decimals are fractions with denominators as multiples of 10.

Examples: 5.26, 1.25, 0.06

Methods of Converting Fractions to Decimals

The three different ways of converting fractions to decimals are mentioned here.

Method 1: Divide the numerator by denominator

• Get the fraction or mixed fraction
• Convert the mixed fraction into a fraction
• Just divide the numerator of the fraction by the denominator
• While dividing add a dot to the quotient when you reach a point where the remainder is lesser than the divisor.

Example:

Convert 1/4 into decimal form

1/4 = 0.25

Method 2: Multiply both numerators, denominators by the same number 

• Identify the fraction, you need to convert to the decimal number.
• Multiply the denominator of the fraction by some number to get the denominator as the multiple of 10.
• Find that number and multiply both the numerator and denominator by the same number.
• Then, you will get the denominator as the multiple of 10.
• After that, mark the decimal point after one place or two places or three places from right towards left if the given fraction’s denominator is 10 or 100 or 1000 respectively.

Example:

Convert 1/4 into the decimal form?

Given fraction is 1/4

1/4 = (1 x 25)/(4 x 25) = 25/100

= 0.25

Method 3: Using Long Division

• Find the fractional number.
• Divide the numerator of the fraction by denominator using the long division.
• Then, you will get the decimal number as a quotient.

Example:

Convert 1/4 into the decimal form?

Given fraction is 1/4

Divide 1/4 using long division.

So, 1/4 = 0.25

Have a look at the related articles

• Converting Decimals to Fractions
• Conversion of Fractions
• Conversion of a Decimal Fraction into a Fractional Number

Example Questions on Fractions to Decimal Conversion

Example 1:

Convert the following fractions to decimals.

(i) 9(1/2)

(ii) 14/5

(iii) 125/6

Solution:

(i) The given mied fraction is 9(1/2)

= 19/2

= 9.5 using the division method

So, 9(1/2) = 9.5

(ii) The given fraction is 14/5

Multiply both numerator and denominator by 2

= (14 x 2)/(5 x 2)

= 28/10

= 2.8

So, 14/5 = 2.8

(iii) The given fraction is 125/6

Using the long division method

So, 125/6 = 20.83333

Example 2:

Convert the following fractions to decimals.

(i) 3/10

(ii) 101/100

(iii) 856/9

Solution:

(i) The given fraction is 3/10

As the denominator is the multiple of 10, add point to the numerator.

So, 3/10 = 0.3

(ii) The given fraction is 101/100

As the denomintaor is 100, add point after two digits from the left side

So, 101/00 = 1.01

(iii) The given fraction is 856/9

Using the long division method

So, 856/9 = 95.11111

Example 3:

Convert the following fractions to decimals.

(i) 18/7

(ii) 2/5

(iii) 3/5

Solution:

(i) The given fraction is 18/7

Using the long division method

So, 18/7 = 2.571428571

(ii) The given fraction is 2/5

Multiply both numerator and denominator by 2

2/5 = (2 x 2)/(5 x 2)

= 4/10 = 0.4

So, 2/5 = 0.4

(iii) The given fraction is 3/5

Multiply both numerator and denominator by 2

3/5 = (3 x 2)/(5 x 2)

= 6/10 = 0.6

So, 3/5 = 0.6

Polygon is a two-dimensional geometric figure which has a finite number of sides. Each side of the polygon is a straight line and all line segments form a closed figure. Convex and Concave Polygons are the two different types of polygons. A polygon that has all the interior angles lesser than 180°, then it is called the convex polygon. If the polygon contains one or more interior angles greater than 180°, then it is called the concave polygon. Check out the definitions, properties, and examples in the remaining sections of this article.

Convex and Concave Polygons

A polygon is said to be a convex polygon when the measures of the interior angles are lesser than 180 degrees. The vertices of the convex polygon always point outwards.

A polygon that measures at least one angle greater than 180 degrees is called the concave polygon. The vertices of this are inwards and outwards also. Convex, concave polygons are opposite to each other.

Other Types of Polygons

The various types of polygons are described here with their definitions.

• Regular polygons: All sides of the polygons measure equal dimensions.
• Irregular Polygons: All sides of the polygons measure unequal dimensions.
• Quadrilateral Polygons: It is a four-sided quadrilateral
• Convex Polygons: Examples are rhombus, parallelogram, square, rectangle, pentagon, etc
• Concave Polygons

Also, read Regular and Irregular Polygons

Regular Convex Polygons

A regular convex polygon has all sides of equal length, all interior angles are the same and below 180 degrees. The distance between the center point to all vertices is equal. An example is square.

Irregular, Regular Concave Polygons

All the concave polygons are irregular concave polygons. Because concave polygons must have at least one angle greater than 180 degrees and irregular polygons measure interior angles differently. There is no concave polygon that is regular.

Convex and Concave Polygons – Formulas

The perimeter of a convex and concave polygon is the sum of all sides or the total region coved around the boundary.

Perimeter = Sum of all sides

Area of convex polygon is given as A = ½ | (x₁ • y₂ – x₂ • y₁) + (x₂ • y₃ – x₃ • y₂) + . . . + (x_n • y₁ – x₁ • y_n) |

Where (x₁, y₁), (x₂, y₂), (x₃, y₃), . . . (x_n, y_n) are the vertices of the convex polygon

Area of a concave polygon

Like regular polygons, there is no formula to calculate the area of the irregular concave polygons. Here, on each side, interior angles will be of different lengths. So, we need to split the polygons into triangles or other shapes to find the area.

Properties of Concave and Convex Polygons

• The interior angles of convex polygons have to be less than 180 degrees. The concave polygon should have at least one reflex angle.
• A concave polygon must have one vertex that points inwards to give the concave shape.
• Sum of all interior angles of the convex polygon of n sides = (n – 2) x 180°
• If a line segment is drawn crossing the concave polygon, then it will intersect the boundary more than two times.
• Concave polygons have more than one diagonal that lie outside the boundary.
• Concave polygons need to have one pair of sides joining a vertex that goes outside the vertex.

Interior, Exterior Angles

The interior angles are defined as the angles inside the polygon. The number of interior and exterior angles in a polygon are the same. According to the convex and concave polygon sum formula, for any n sided polygon, the sum of interior angles is (n – 2)180°. By knowing the sum, divide the sum by a total number of sides to get each interior angle measurement.

The exterior angle is defined as the angle formed by extending the side of the polygon. We already know that the sum of exterior angles of any polygon is 360°. Divide the sum by the total number of sides to get the measure of each exterior angle of Convex and Concave Polygons.

Examples of Convex and Concave Polygon

Example 1:

Find the area of the convex polygon with three sides, and vertices are (5, 7), (8, 4), (-2, 1).

Solution:

Given that,

Vertices of the polygon are (5, 7), (8, 4), (-2, 1).

(x₁, y₁) = (5, 7), (x₂, y₂) = (8, 4), (x₃, y₃) = (-2, 1)

The formula to calculate the area of a convex polygon is A = ½ | (x₁ • y₂ – x₂ • y₁) + (x₂ • y₃ – x₃ • y₂) + (x₃ • y₁ – x₁ • y₃) |

= ½ | (5 • 4 – 8 • 7) + (8 • 1 – (-2) • 4) + (-2 • 7 – 5 • 1) |

= ½ | (20 – 56) + (8 + 8) + (-14 – 5) |

= ½ | -36 + 16 – 19 |

= ½ | -55 + 16 |

= ½ | -39 |

= 19.5

Therefore, the area is 19.5 sq units.

Example 2:

Calculate the perimeter and area of the pentagon has a side length of 4 cm.

Solution:

Given that,

The side length of pentagon s = 4 cm

n = 5

The regular polygon area formula is A = n x s² x cot(π/n) / 4

A = 5 x 4² x cot(π/5) / 4

= 5 x 16 x 1.3763 / 4

= 110.104 / 4

= 27.526 cm²

Perimeter p = Sum of all sides

= 4 + 4 + 4 + 4 + 4

= 20 cm

Hence the area, perimeter of the pentagon is 27.526 cm², 20 cm.

Example 3:

Find the perimeter, area of the below given concave polygon.

Solution:

The perimeter of the polygon = sum of all sides

= 4 + 5 + 2 + 2 + 5

= 18 cm

To find the area divide the given polygon into a square and two triangles by drawing a dotted line.

Area of square = side²

= 4² = 16 cm²

Area of triangle = 1/2 x base x height

hypotenuese² = base² + height²

2² =1² + height²

4 = 1 + h²

h² = 4 – 1

h² = 3

h = √3

So, area = 1/2 x 1 x √3

= √3/2 cm²

So, area of polygon = area of square + 2 x area of the triangle

= 16 + 2(√3/2)

= 16 + √3

Therefore, the perimeter, area of the concave polygon is 18 cm, (16 + √3) cm²

Example 4:

Find the measure of each interior, exterior angle of a regular octagon.

Solution:

Octagon has 8 sides

The sum of interior angles of polygon = (n – 2)180°

= (8 – 2) 180°

= 6 x 180°

= 1080°

The measure of each interior angle of an octagon = sum of interior angles/ number of sides

= 1080°/8

= 135°

The sum of exterior angles = 360°

The measure of each exterior angle of an octagon = sum of exterior angles/ number of sides

= 360/8

= 45°

So, the measure of each interior angle, exterior angle of the octagon is 135°, 45°. Hence, it is a convex polygon.

FAQs on Convex and Concave Polygons

1. Write the differences between concave and convex polygons?

Each and every polygon is either convex or concave. The main difference between them is angles. For a polygon to be convex, it must have all interior angles lower than 180 degrees. If any of the interior angles is greater than 180 degrees, then it is a concave polygon.

2. How do you know if a polygon is convex?

Get the measure of each interior angle of the polygon. If all the angles are below 180 degrees, then you can say it is a convex polygon.

Roman Numerals are the numeral system which is originated in ancient Rome. It is a decimal or base 10 number system. It is an additive or subtractive system in which letters are used to denote some base numbers and arbitrary numbers in the number system and denoted using a different combination of symbols. Here, students can check the Roman Numerals Chart, how to convert roman numerals to numbers, and solved examples in the following sections.

Roman Numerals List

Here provided are some basic roman numerals.

Roman Numerals Chart:

Roman numerals Chart has particular roman numbers for the decimal numbers from 1 to 1000.

Rules for formation of Numbers

We have three different rules to form the roman numerals as numbers. They are multiplication rule, addition rule, and subtraction rule.

Multiplication Rule:

When a roman symbol is repeated in sequence, then we have to multiply the value of the numeral by the number of times it is repeated. A symbol cannot be repeated more than three times in series.

Example:

II = 1 x 2 = 2

XX = 10 x 2 = 20

III = 1 x 3 = 3

We cannot express 4 as IIII. Because the symbol cannot be repeated more than three times.

Addition Rule:

If a smaller number is located to the right of a larger number, then you need to add numbers.

Example:

VII = 5 + 1 + 1 = 7

VIII = 5 + 1 + 1 + 1 = 8

XXII = 10 + 10 + 1 + 1 = 22

Subtraction Rule:

Writing a smaller number to the left side of a larger number means that the smaller number has to be subtracted from the larger number. The symbol I can be subtracted from V and X and X can be subtracted from L and C.

Example:

IV = 5 – 1 = 4

IL = 50 – 1 = 49

We do not repeat V twice to get 10. We already have a symbol for 10. So VV for writing 10 is not correct.

We do not subtract 5 from any symbol. VX is not correct.

Roman Numerals Questions with Solutions

Example 1:

Write the Roman Numerals for 57.

Solution:

The given decimal number is 57

Break up the number into Tens and Ones.

57 = 50 + 7

The symbol for 50 is L

7 = 5 + 2 = 5 + 1 + 1

The symbol for 7 is VII.

57 convert roman numerals as LVII.

Example 2:

Write the number for XXIV.

Solution:

Given roman numeral is XXIV

V = 5

IV = 5 – 1 = 4

X = 10

XX = 10 + 10 = 20

Therefore, XXIV = 20 + 4

XXIV = 24.

Example 3:

Write the Roman Numerals for 18.

Solution:

The given decimal number is 18.

Break up the number into Tens and Ones.

18 = 10 + 8

The symbol for 10 is X.

8 = 5 + 1 + 1 + 1

The symbol for 5 is V, 1 is I

So, the symbol for 8 is VIII

18 convert roman numerals as XVIII.

Example 4:

Write the number for XXXIX.

Solution:

Given roman numeral is XXXIX

X = 10

IX = 10 – 1 = 9

XXX = 10 x 3 = 30

Therefore, XXXIX = 30 + 9 = 39

FAQs on Roman Numerals

1. How do you write roman numerals?
Roman numerals can be written by using seven different alphabets. They are I for 1, V for 5, X for 10, L for 50, C for 100, D for 500, M for 1000. By using these symbols, you can write all roman numerals easily.

2. How to evaluate 550 in roman numerals?

550 = 500 + 50

500 = D, 50 = L

Therefore, 550 = DL.

3. What is the use of roman numerals?

Roman numerals can be used for labeling the name or position of a person or an object. Examples are Kiran came IInd in the class. Prince Charles III, Schools have Classes from VIth to Xth.

4. Write roman numerals from 1 to 10?

The roman numerals from 1 to 10 are I, II, III, IV, V, VI, VII, VIII, IX, and X.

Looking for help on Correcting Decimals to 2 Places? If so, you have arrived at the right place and get complete knowledge regarding the Rounding Off Decimals to Hundredths Place. Here you will find how to round off to hundredths place or Correct to Two Decimal Places. Get the definition, rules, detailed step-by-step process of rounding numbers to the nearest hundredths place. Solved Examples on Rounding Decimals to 2 Places help you understand the concept clearly and learn the approach used to solve them.

Correct to Two Decimal Places – Definition

The process of Correct to Two Decimal Places is nothing but rounding the to hundredths. Rounding off to decimal places is a technique used to find the approximate values of the decimal number. Here, the decimal numbers are rounded off to 2 decimal places to make them easy to read, understand, and manageable instead of having lengthy string decimal places. We will keep the original 1st decimal number as it is, may change the second decimal number, and eliminate the remaining decimal numbers.

Rules for Rounding off to Two Decimal Places

For rounding the given numbers to the nearest hundredths, you need to check the below-provided rules.

• Rule 1: If the digit in the thousands place is less than 5, then remove the following digits or place 0 in place of them
• Rule 2: When the digit in the thousands place is equal to or more than 5, then the digit in the hundredths place is increased by 1 and the following digits are replaced by 0.

Also, check:

• Rounding Numbers to the nearest 100
• Rounding Decimals to the Nearest Whole Number

How to Correct to Two Decimal Places?

Follow the below-listed procedure to learn Rounding Decimals to Two Places. They are along the lines

• Identify the number for which you need to round off to two decimal places.
• See the digit in the thousands place of the given number.
• If the digit is equal to or greater than 5, then add 1 to the digit in the hundredth place of the number and remove the following digits.
• When the digit is smaller than 5, then replace the following digits with 0.

Solved Examples on Correcting Decimals to 2 Places

Example 1:

Round off the following to the two decimal places.

(i) 186. 256

(ii) 25. 532

Solution:

(i) 186. 256

The given number is 186. 256

We can see the digit in the thousandths place is 6 then round it to the nearest hundredths which is greater than the given decimal number. Since 6 > 5 then the decimal number is rounded to 186.260.

Therefore, the solution is 186.260.

(ii) 25. 532

The given number is 25. 53256

We can identify the digit in the thousandths place is 2 then round it to the nearest hundredths which is smaller than the given decimal number. Since 2 < 5 then the decimal number is rounded to 25.5300.

Therefore, the solution is 25.53.

Example 2:

(i) 120.085

(ii) 12,856.558

Solution:

(i) 120.085

The given number is 120.085

The digit in the thousands place is 5 which is equal to 5.

So, increase the hundreds place digit by 1 i.e 8 + 1 = 9, and remove the following digits.

Therefore, the solution is 120.09.

(ii) 12,856.558

The given number is 12,856.558

We can see the digit in the thousandths place is 5 then round it to the nearest hundredths which is greater than the given decimal number. Since 5 = 5 then the decimal number is rounded to 12,856.56.

Therefore, the solution is 12,856.56.

Example 3:

(i) 0.042

(ii) 12.567

Solution:

(i) 0.042

The given number is 0.042

The digit in the thousand’s place of the given number is 2

Since 2 is less than 5, then replace the following digits with 0.

Therefore, the solution is 0.04.

(ii) 12.567

The given number is 12.567

The digit in the thousand’s place of the given number is 7

Since 2 > 5 add 1 to the hundredths place of the number and remove the following digits.

So, the rounds off number is 12.57.

In the hexadecimal number system, the numbers are expressed with the base 16. Hexadecimal is also called as Hex. It is like decimal, binary or octal numbers. The list of 16 hexadecimal numbers are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. Here, we are going to learn how to perform addition, subtraction operations in between two hexadecimal numbers with the examples for the better understanding of the concept. So, interested people can check out this complete page.

What is Hexadecimal Number System?

A hexadecimal number is a number having a base of 16. These numbers are also called the 16 number system. It has 16 different symbols, 0 to 9 represent the binary values, A, B, C, D, E, F represent 10 to 15 values respectively. Each position in the hexadecimal number represents 0 power of the base 16. The last position in the number represents an x power of base 16.

Examples of Hexadecimal Numbers:

1. B84F

The decimal value of B84F is 11 x 16 + 8 x 16 + 4 x 16 + 16 x 16

= 176 + 128 + 64 + 256

= 624

2. Convert 857 to hexadecimal

857 ÷ 16 = 53.5625

0.5625 x 16 = 9 (Remainder 9)

53 ÷ 16 = 3.3125

0.3125 x 16 = 5 (Remainder 5)

3 ÷ 16 = 0.1875

0.1875 x 16 = 3 (Remainder 3)

Read remainders from bottom to top

So, 857 = (359)₁₆

Also, Read: Binary Subtraction

Procedure for Adding & Subtracting in Hexadecimal

Below provided are the simple steps that are helpful to compute the addtion and subtraction of two hexadecimal numbers.

1. Hexadecimal Numbers Addition

• Write two hexadecimal numbers one after another in two different lines
• Begin adding from the rightmost digits.
• If the digit is in the form of an alphabet then convert it to the respective decimal number to make the process easy
• Add those digits and convert the sum to the hexadecimal
• If you got the carry, then represent it on the top of the first number next digit and result on the bottom of the second number added digit.
• Continue the process until you left nothing on the left side.

We can also add two hexadecimal numbers by following this table.

For Example:

926 + 1A2

9 2 6

(+) 1 A 2

=    A C 8

So, 926 + 1A2 = AC8

2. Hexadecimal Numbers Subtraction

• Write two hexadecimal numbers in different lines
• Subtraction starts from the rightmost digits of the numbers.
• Convert the alphabets into decimals and subtract two digits and again convert the difference value as hexadecimal.
• In case the first number digit is smaller than the second number digit, then barrow from the left side digit.
• The borrowed value is always 16 as its base is 16. Then add borrowed value and first number digit and subtract.
• Don’t forget to mention the borrowed value on the top of the first number digit.
• After borrowing, the left side digit decreased by 1.
• Repeat the process till you have nothing remaining on the left side.

For Example:

938 – 1A2

8 – 2 = 6

3 – A(10) = (16 + 3) – 10 = 19 – 10 = 9

(9 – 1) – 1 = 8 – 1 = 7

So,  938 – 1A2 = 796.

Hexadecimal Addition and Subtraction Examples

Example 1:

Evaluate (1AB2)₁₆ + (2198)₁₆

Solution:

Given expression is (1AB2)₁₆ + (2198)₁₆

From the table,

2 + 8 = A

B + 9 = 4 and 1 is carry

1 + A + 1 = C

1 + 2 = 3

Therefore, (1AB2)₁₆ + (2198)₁₆ = 3C4A

Example 2:

Find subtraction of (B84F)₁₆ and (A53)₁₆.

Solution:

F means 15. F – 3 = 15 – 3 = 12 = C

4 + 16 = 20 – 5 = 15 = F

8 – 1 = 7

7 + 16 = 23 – A = 23 – 10 = 13 = D

8 – 1 = 7
23
10 7 20

B 8 4 F

(-) 0 A 5 3

= 7 D F C

So, (B84F)₁₆ – (A53)₁₆ = (7DFC)₁₆

Example 3:

Find the addition, subtraction of (AB53)₁₆, (155)₁₆

Solution:

The addition of numbers is (AB53)₁₆ + (155)₁₆

3 + 5 = 8

5 + 5 = 10 = A

B + 1 = 11 + 1 = 12 = C

A + 0 = 10 + 0 = 10 = A

So, (AB53)₁₆ + (155)₁₆ = (ACA8)₁₆

Subtraction of numbers is (AB53)₁₆ – (155)₁₆

(3 + 16) – 5 = 19 – 5 = 14 = E

(5 – 1) – 5 = 4 – 5

(4 + 16) – 5 = 20 – 5 = 15 = F

(B – 1) – 1 = (11 – 1) – 1 = 10 – 1 = 9

A – 0 = A

A B 5 3

(-) 0 1 5 5

= A 9 F E

So, (AB53)₁₆ – (155)₁₆ = (A9FE)₁₆

Example 4:

(i) Calculate (9AB)₁₆ + (12C)₁₆

(ii) Compute (CB5)₁₆ – (223)₁₆

Solution:

(i) (9AB)₁₆ + (12C)₁₆

B + C = 11 + 12 = 23 = 7 and 1 is carry

1 + A + 2 = 3 + 10 = 13 = D

9 + 1 = 10 = A

So, (9AB)₁₆ + (12C)₁₆ = (AD7)₁₆

(ii) (CB5)₁₆ – (223)₁₆

5 – 3 = 2

B – 2 = 11 – 2 = 9

C – 2 = 12 – 2 = A

So, (CB5)₁₆ – (223)₁₆ = (A92)₁₆

Are you looking for any material to know the relation between all Trigonometrical Ratios of 90 Degree Minus Theta? Then, you can relax now. On this page, we have enclosed the detailed information on the relation between Trigonometric Ratios of (90° – θ) along with the proofs. Get the example questions and step-by-step solutions in the following sections of this article. Check out the simple formula to memorize the Trigonometric Functions.

How to Determine the Trigonometric Ratios of 90 Degree Minus Theta?

Here, you can see Trigonometrical Functions of 90 Degree Minus Theta can be determined. As per the ASTC “All Silver Tea Cups” or “All Students Take Calculus”

A means All, S means “Sinθ, Cosecθ”, T means “Tanθ, Cotθ”, C means Cosθ, Secθ.

The pictorial representation of the ASTC formula is as follows:

From the above picture, (90° – θ) falls in the first quadrant.

sin (90° – θ) = cos θ

cos (90° – θ) = sin θ

tan (90° – θ) = cot θ

cosec (90° – θ) = sec θ

sec (90° – θ) = cosec θ

cot (90° – θ) = tan θ

Evaluate Trigonometrical Ratios of 90 Degree Minus Theta

1. Evaluate Sin(90° – θ)?

To evaluate sin (90° – θ), we have to consider the following important points.

•  (90° – θ) will fall in the 1st quadrant.
•  When we have 90°, “sin” will become “cos”.
•  In the 1st quadrant, the sign of “sin” is positive.

Considering the above points, we have

Sin (90° – θ) = Cos θ

2. Evaluate Cos(90° – θ)?

To evaluate cos (90° – θ), we have to consider the following important points.

• (90° – θ) will fall in the 1st quadrant.
•  When we have 90°, “cos” will become “sin”.
•  In the 1st quadrant, the sign of “cos” is positive.

Considering the above points, we have

Cos (90° – θ) = Sin θ

3. Evaluate Tan(90° – θ)?

To evaluate tan (90° – θ), we have to consider the following important points.

•  (90° – θ) will fall in the 1st quadrant.
•  When we have 90°, “tan” will become “cot”.
•  In the 1st quadrant, the sign of “tan” is positive.

Considering the above points, we have

Tan (90° – θ) = Cot θ

4. Evaluate Cot(90° – θ)?

To evaluate cot (90° – θ), we have to consider the following important points.

•  (90° – θ) will fall in the 1st quadrant.
•  When we have 90°, “cot” will become “tan”
•  In the 1st quadrant, the sign of “cot” is positive.

Considering the above points, we have

Cot (90° – θ) = Tan θ

5. Evaluate Cosec(90° – θ)?

To evaluate Cosec (90° – θ), we have to consider the following important points.

• (90° – θ) will fall in the 1st quadrant.
•  When we have 90°, “Cosec” will become “sec”.
•  In the 1st quadrant, the sign of “Cosec” is positive.

Considering the above points, we have

Cosec (90° – θ) = Sec θ

6. Evaluate Sec(90° – θ)?

To evaluate sec (90° – θ), we have to consider the following important points.

•  (90° – θ) will fall in the 1st quadrant.
•  When we have 90°, “sec” will become “cosec”.
•  In the 1st quadrant, the sign of “sec” is positive.

Considering the above points, we have

Sec (90° – θ) = Cosec θ

More Related Articles:

• Trigonometrical Ratios of 90 Degree Plus Theta
• Trigonometric Functions of 180 Minus Theta
• Trigonometrical Ratios Table
• Worksheet on Trigonometric Identities

Solved Examples on Trigonometric Ratios of 90° – θ

Example 1:

Find the value of Tan 45°?

Solution:

Tan 45° = Tan (90° – 45°)

We know that Tan (90° – θ) = Cot θ

So, Tan 45° = Cot 45°

= 1  [Cot 45° = 1]

Therefore, Tan 45° = 1.

Example 2:

Find the value of Sin 65°?

Solution:

Sin 65° = Sin (90° – 25°)

We know that Sin (90° – θ) = Cos θ

So, Sin 65° = Cos 25°

= 0.906308 [ Cos 25° = 0.906308]

Therefore, Sin 65° = 0.906308

Example 3:

Find the value of Cot 80°?

Solution:

Cot 80° = Cot (90° – 10°)

We know that Cot (90° – θ) = Tan θ

So, Cot 80° = Tan 10°

= 0.17633 [ Tan 10° = 0.17633]

Therefore, Cot 80° = 0.17633

Example 4:

Find the value of Cos 50°?

Solution:

Cos 50° = Cos (90° – 40°)

We know that Cos (90° – θ) = Sin θ

So, Cos 50° = Sin(40°)

= 0.64278760968 [ Sin(40°) = 0.64278760968]

Therefore, Cos 50° = 0.64278760968.

In this logarithm rules or log rules guide, students and teachers will learn the presented common laws of logarithms, also called ‘log rules’. Mainly, there are four log rules that are helpful in expanding logarithms, condensing logarithms, and solving logarithmic equations. Along with this, you will also find the proofs of these four log rules and additional laws of logarithms for a better understanding of the basic logarithm concept. Whenever you get confused during homework help please check out the basic logarithm rules or log rules prevailing here in this article.

Logarithm Rules Or Log Rules

There are four following math logarithm formulas:

• Product Rule Law: log_a (MN) = log_a M + log_a N
• Power Rule Law: log_a Mⁿ = n log_a M
• Quotient Rule Law: log_a (M/N) = log_a M – log_a N
• Change of Base Rule Law: log_a M = log_b M × log_a b

Also Check: Convert Exponentials and Logarithms

Descriptions of Logarithm Rules

Here, we have discussed four log rules along with proofs to grasp the concepts easily and become pro in calculating the logarithm problems. Let’s start with proof 1:

1. Logarithm Product Rule:

The logarithm of the multiplication of x and y is the sum of the logarithm of x and the logarithm of y.

log_b(x ∙ y) = log_b(x) + log_b(y)

Proof of Log Product Rule Law: 

log_a(MN) = log_a M + log_a N

Let log_a M = x ⇒ a sup>x = M

and log_a N= y ⇒ ay = N

Now a^x ∙ a^y = MN or, a^x+y = MN

Therefore from definition, we have,

log_a (MN) = x + y = log_a M + log_a N [putting the values of x and y]

Corollary: The law is true for more than two positive factors i.e.,

log_a (MNP) = log_a M + log_a N + log_a P

since, log_a (MNP) = log_a (MN) + log_a P = log_a M+ log_a N+ log_a P

Therefore in general, log_a (MNP ……. )= log_a M + log_a N + log_a P + …….

So, the product logarithm of two or more positive factors to any positive base other than 1 is equal to the sum of the logarithms of the factors to the same base.

Example: Calculate log₁₀(8 ∙ 4)?

The given expression matches the logarithm product rule.

So apply the log rule and get the result,

log₁₀(8 ∙ 4) = log₁₀(8) + log₁₀(4)

2. Logarithm Power Rule:

The logarithm of x raised to the power of y is y times the logarithm of x.

log_b(x^y) = y ∙ log_b(x)

Proof of Log Power Rule Law:

log_aMⁿ = n log_a M

Let log_a Mⁿ = x ⇒ a^x = Mⁿ

and log_a M = y ⇒ a^y = M

Now, a^x = Mⁿ = (a^y)n = a^ny

Therefore, x = ny or, log_a Mⁿ = n log_a M [putting the values of x and y].

Example: Find log₁₀(2⁹)?

Given log₁₀(2⁹) is in logarithm power rule. So, apply the log rule and calculate the output:

Hence, log₁₀(2⁹) = 9∙ log₁₀(2).

3. Logarithm Quotient Rule Formula

The logarithm of the ratio of two numbers is the logarithm of the numerator minus the logarithm of the denominator.

log_a(x / y) = log_a(x) – log_a(y)

Proof of Log Quotient Rule Formula:

Let M = a^x and N = a^y, then it follows that log_a(M) = x and log_a(N) = y,

We can now prove the quotient rule as follows:

log_a (M/N) = log_a (a^x/a^y)

= log_a(a^x-y)

= x – y [Put the values of x and y]

= log_a M – log_a N

Corollary: log_a [(M × N × P)/(R × S × T)] = log_a (M × N × P) – log_a (R × S × T)

= log_a M + log_a N + log_a P – (log_a R + log_a S + log_a T)

Example: Calculate log₁₀(10 / 5)

Now apply the log quotient rule and get the result,

Therefore, log₁₀(10 / 5) = log₁₀(10) – log₁₀(5).

4. Logarithm Base Change Rule:

The logarithm of M for base b is equal to the base a log of M divided by the base a log of b.

log_b M = log_a M/log_a b

Proof of Change of base Rule Law:

log_a M = log_b M × log_a b

Assume log_a M = x ⇒ a^x = M,

log_b M = y ⇒ b^y = M,

and log_a b = z ⇒ a^z = b.

Now, a^x= M = b^y – (a^z)y = a^yz

Therefore x = yz or, log_a M = log_b M × log_a b [putting the values of x, y, and z].

Corollary:

(i) Putting M = a on both sides of the change of base rule formula [log_a M = log_b M × log_a b] we get,

log_a a = log_b a × log_a b or, log_b a × log_a b = 1 [since, log_a a = 1]

or, log_b a = 1/log_a b

In other words, the logarithm of a positive number a with respect to a positive base b (≠ 1) is equal to the reciprocal of logarithm of b with respect to the base a.

(ii) On the basis of the log change of base rule formula we get,

log_b M = log_a M/log_a b

In other terms, the logarithm of a positive number M in respect of a positive base b (≠ 1) is equal to the quotient of the logarithm of the number M and the logarithm of the number b both with respect to any positive base a (≠1).

List of Some Other Logarithm Rules or Log Rules:

If M > 0, N > 0, a > 0, b > 0 and a ≠ 1, b ≠ 1 and n is any real number, then

(i) log_a 1 = 0

(ii) log_a a = 1

(iii) a ^{log_a M} = M

(iv) log_a (MN) = log_a M + log_a N

(v) log_a (M/N) = log_a M – log_a N

(vi) log_a Mⁿ = n log_a M

(vii) log_a M = log_b M × log_a b

(viii) log_b a × log_a b = 1

(ix) log_b a = 1/log_a b

(x) log_b M = log_a M/log_a b

Solved Examples of How to Apply the Log Rules or Logarithm Rules

1. Evaluate the expression ie., log₂ 4 + log₂ 8 by using log rules.

Solution:

Given expression is log₂ 4 + log₂ 8

First, express 4 and 8 as exponential numbers with a base of 2. Next, apply the logarithm power rule formula followed by the identity rule. Once you finished that, add the resulting values to find the final answer.

log₂ 4 + log₂ 8
= log₂ 2² + log₂2³ [apply power rule]
= 2 log₂ 2 + 3 log₂ 2 [apply identity rule]
= 2(1) + 3(1)
= 2+3
= 5
Hence, the answer for the given expression log₂ 4 + log₂ 8 is 5.

2. Evaluate the expression with Log Rules: log₃ 162 – log₃ 6

Solution:

log₃ 162 – log₃ 6

Now, we can’t express the 162 as an exponential number with base 3. Don’t worry, we have another way of solving the expression.

It is possible by applying the log rules in the reverse process. Yes, we can also apply the logarithm rules in reverse if not solved in a direct manner.

Remember that the log expression can be stated as one or a single logarithm number via using the backward Quotient Rule Law. Sounds different right, but so easy to calculate.

Take the given expression, log₃ 162 – log₃ 6
= log₃ (162/6)
= log₃ (27)
= log₃ (3³)
= 3 log₃ 3
= 3(1)
= 3

By applying the rules in reverse, we get the result as 3 for the given expression log₃ 162 – log₃ 6.

Hence, log₃ 162 – log₃ 6 = 3.

Are you looking for ways on how to convert from Exponential Form to Logarithmic Form? Then, don’t panic as we will discuss how to change Exponential Form to Logarithmic Form or Vice Versa. Get to know the Definitions of Exponential and Logarithmic Forms. Find Solved Examples on Converting between Exponential and Logarithmic Forms and learn the entire procedure.

Logarithmic Form – Definition

Logarithmic Functions are inverse of Exponential Functions. It tells us how many times we need to multiply a number to get another number. To give us the ability to solve the problem x = b^y for y

For x>0, b>0 b≠ 1, y = log_b x is equivalent to b^y = x

Example: When asked how many times we’ll need to multiply 2 in order to get 32, the answer is the logarithm 5.

Exponential Form – Definition

Exponents are when a number is raised to a certain power that tells you how many times to repeat the multiplication of a number by itself.

b^y = x

How to Convert from Exponential Form to Logarithmic Form?

To convert from exponential form to logarithmic form, identify the base of the exponential equation
and move the base to the other side of the equal to sign, and add the word “log”. Do not change anything
but the base, the other numbers or variables will not change sides.

Consider the equation b^y = x

The equation y = log_b x is said to be the Logarithmic Form

b^y = x is said to be Exponential Form

Two Equations are different ways of writing the same thing.

Solved Examples on Converting Between Exponential Form to Logarithmic Form

1. Convert the 10³ = 1000 Exponential Form to Logarithmic Form?

Solution:

10³ = 1000

log₁₀1000 = 3

In this example, the base is 10 and the base moved from the left side of the exponential equation to the right side of the logarithmic equation, and the word “log” was added.

2. Write the Exponential Equation 3^x = 27 in Logarithmic Form?

Solution:

3^x = 27

In this example, the base is 3 and the base moved from the left side of the exponential equation to the right side of the logarithmic equation, and the word “log” was added.

x = log₃27

= log₃3³

= 3log₃3

= 3.1

= 3

3. Write the Exponential Equation  6^y = 98 in Logarithmic Form?

Solution:

Given Equation is 6^y = 98

In this example, the base is 6 and the base moved from the left side of the exponential equation to the right side of the logarithmic equation, and the word “log” was added.

y = log₆ 98

Have you ever seen Tossing a Coin before Commencement of a Cricket Match? This is usually done in Matches and the Captain who predicts the Toss Correctly can choose on what his team could defend. It is the most common application of the Coin Toss Experiment. Tossing a Coin is quite useful as the Probability of obtaining Heads is as likely as Tail. There are only two outcomes when you flip a coin i.e. Head(H) and Tail(T).

However, if you Toss 2, 3, 4, or more coins than that at the same time the Probability is Different. Let us learn about the Coin Toss Probability Formula in detail in the later sections. You can check out Solved Examples on Tossing a Coin and their Probabilities here.

Tossing a Coin Probability

When Tossed a Coin you will have only two possible outcomes i.e. Head or Tail. However, you will not know which outcome you will get among Heads or Tails. Tossing a Coin is a Random Experiment and you do know the set of Outcomes but not the exact outcomes.

General Formula to Determine the Probability = \(\frac { No.\; of\; Favorable\; Outcomes }{  Total\; Number\; of\; Possible\; Outcomes } \)

On Tossing, we do have only two possible outcomes

Probability of getting Head = \(\frac { No.\;of \;Outcomes\; to\; get\; Head }{  Total\; Number\; of\; Possible\; Outcomes } \)

= \(\frac { 1 }{ 2 } \)

Probability of getting Tail = \(\frac { No.\; of\; Outcomes\; to\; get\; Tail }{  Total\; Number\; of\; Possible\; Outcomes } \)

= \(\frac { 1 }{ 2 } \)

How to Predict Heads or Tails?

• If a coin is fair or unbiased, i.e. no outcome is particularly preferred, then it is difficult to predict heads or tails. Both the outcomes are equally likely to show up.
• If a coin is unfair or biased, i.e. an outcome is preferred, then we can predict the outcome by choosing the side that has a higher probability.
  • If the probability of a head showing up is greater than 1/2, then we can predict the next outcome as a head.
  • If the probability of a tail showing up is greater than 1/2, then we can predict the next outcome as a tail.

Solved Examples on Coin Toss Probability

1. On tossing a coin twice, what is the probability of getting only one Head?

Solution:

On tossing a coin twice, the possible outcomes are {HH, TT, HT, TH}

Therefore, the total number of outcomes is 4

Getting only one Head includes {HT, TH}

Thus, the number of favorable outcomes is 2

Hence, the probability of getting exactly one head =  Probability of Favorable Outcomes/Total Number of Outcomes

= \(\frac { 1 }{ 2 } \)

2. Three fair coins are tossed simultaneously. What is the probability of getting at least three tails?

Solution:

When 3 coins are tossed, the possible outcomes are {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}.

Thus, the total number of possible outcomes = 8
Getting at least 3 tails include the outcomes = {TTT}

No. of Favorable Outcomes = 1

Probability of getting at least three tails include = Probability of Favorable Outcomes/Total Number of Outcomes

= \(\frac { 1 }{ 8 } \)

Do you want to learn about the Relation among All Trigonometric Ratios of (180° – θ)? Then, halt your search here as we have explained the Relationship between Trigonometric Functions of 180 Minus Theta in detail along with their proofs. Find Solved Examples on finding the Trigonometric Ratios with Step by Step Explanation making it easy for you to solve related problems in no time. Know a Simple Formula to memorize the Trigonometric Functions.

How to Determine the Trigonometric Ratios of (180° – θ)?

Before diving deep into the article to understand how trigonometric ratios of (180° – θ) are determined you need to understand the ASTC Formula.

The ASTC Formula can be easily remembered by considering the Phrases provided below

“All Silver Tea Cups” or ” All Students Take Calculus”

You will better understand the concept by having a glance at the below picture. From the picture, it is clearly evident that 180 degrees minus theta fall under the 2nd Quandrant. In the 2nd Quadrant, only sin and cosecant are Positive.

sin(180° – θ)=sinθ
cos(180° – θ)=−cosθ
tan(180° – θ)=−tanθ
cosec (180° – θ)=cosec θ
sec(180° – θ)=−secθ
cot(180° – θ)=−cotθ

Read More Articles:

• Trigonometrical Ratios of 90 Degree Plus Theta
• Trigonometrical Ratios Table
• Worksheet on Trigonometric Identities

Evaluate Trigonometric Functions of (180° – θ)

1. Evaluate Sin(180° – θ)?

Solution:

Sin(180° – θ) = Sin (90° + 90° – θ)

= Sin [90° + (90° – θ)]

= Cos (90° – θ), [since Sin (90° + θ) = Cos θ]

= Sin θ[since Cos (90° – θ) = Sin θ]

Therefore, Sin (180° – θ) = Sin θ

2. Evaluate Cos(180° – θ)?

Cos (180° – θ) = Cos (90° + 90° – θ)

= Cos [90° + (90° – θ)]

= – Sin (90° – θ), [since Cos (90° + θ) = -Sin θ]

= -Cos θ [since sin (90° – θ) = cos θ]

Therefore, Cos (180° – θ) = – Cos θ

3. Evaluate Tan (180° – θ)?

Solution:

Tan (180° – θ) = Tan (90° + 90° – θ)

= Tan [90° + (90° – θ)] [since Tan (90° + θ) = -Cot θ]

= – Cot (90° – θ)

= Tan θ [since Cot (90° – θ) = Tan θ]

Therefore, Tan (180° – θ) = – Tan θ

4. Evaluate Csc (180° – θ)?

Solution:

Csc (180° – θ) = \(\frac { 1 }{ Sin(180° – θ) } \)

= \(\frac { 1 }{ Sin θ } \) [Since Sin(180° – θ) = Sin θ]

Therefore, Csc (180° – θ) = \(\frac { 1 }{ Sin θ } \)

5. Evaluate Sec (180° – θ)?

Solution:

Sec (180° – θ) = \(\frac { 1 }{ Cos(180° – θ) } \)

= = \(\frac { 1 }{ -Cos θ } \) [Since Cos(180° – θ) = -Cos θ]

= -Sec θ

Therefore, Sec (180° – θ) = -Sec θ

6. Evaluate Cot (180° – θ)?

Solution:

Cot (180° – θ) = \(\frac { 1 }{ Tan(180° – θ) } \)

= \(\frac { 1 }{ -Tan θ } \) [Since Tan(180° – θ) = -Tan θ]

= -Cot θ

Solved Examples on Trigonometric Ratios

1. Find the Value of Cos 150°?

Solution:

Cos 150° = Cos(180° – 30°)

= – Cos 30°

= – \(\frac { √3 }{ 2 } \)

2. Find the value of Cot 135°?

Solution:

Cot 135° = Cot(180° – 45°)

= -Cot 45°

= -1