Eureka Math

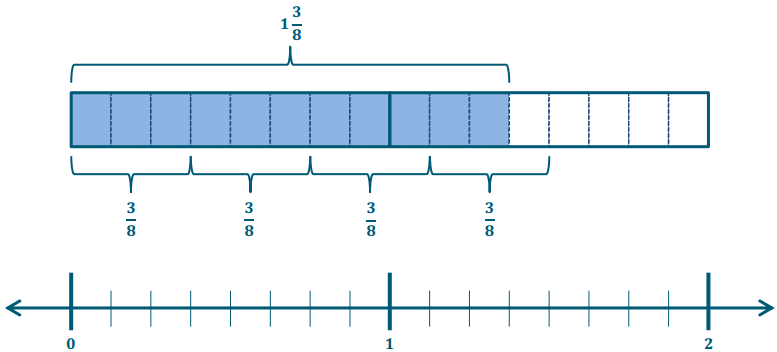
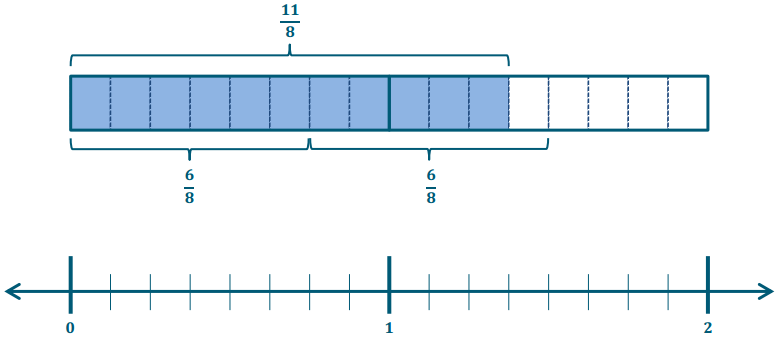
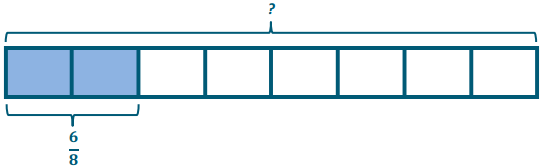
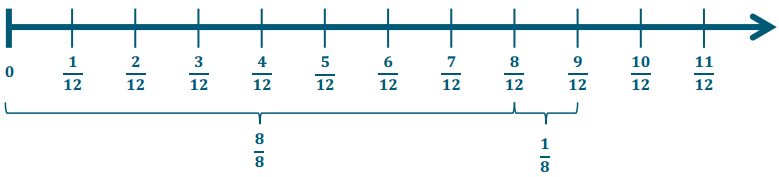
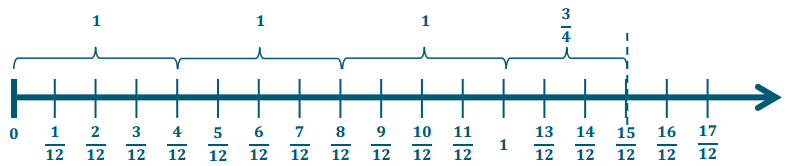
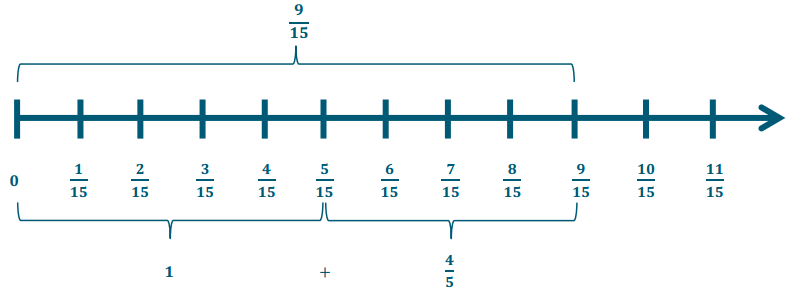
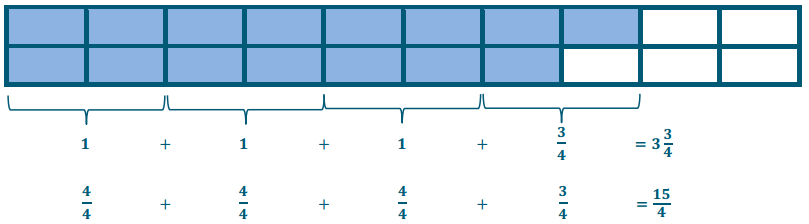
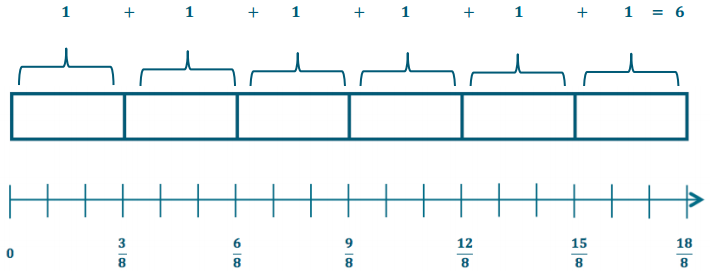
Engage NY Eureka Math 7th Grade Module 3 Lesson 6 Answer Key

Eureka Math Grade 7 Module 3 Lesson 6 Example Answer Key

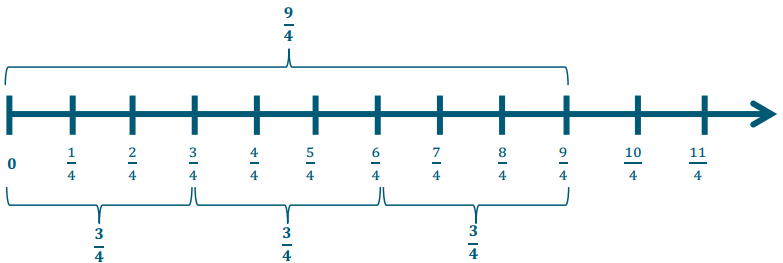
Example 1.
Rewrite the expression in standard form by collecting like terms.
\(\frac{2}{3}\) n-\(\frac{3}{4}\) n+\(\frac{1}{6}\) n+2 \(\frac{2}{9}\) n
Answer:
\(\frac{2}{3}\) n-\(\frac{3}{4}\) n+\(\frac{1}{6}\) n+2 \(\frac{2}{9}\) n
\(\frac{24}{36}\) n-\(\frac{27}{36}\) n+\(\frac{6}{36}\) n+2 \(\frac{8}{36}\) n
2 \(\frac{11}{36}\) n

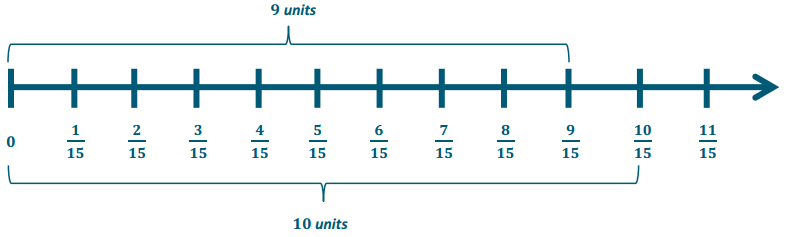
→ What are various strategies for adding, subtracting, multiplying, and dividing rational numbers?
→ Find common denominators; change from mixed numbers and whole numbers to improper fractions, and then convert back.

Example 2.
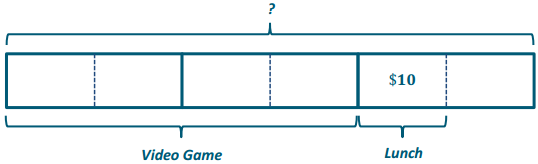
At a store, a shirt was marked down in price by $10.00. A pair of pants doubled in price. Following these changes, the price of every item in the store was cut in half. Write two different expressions that represent the new cost of the items, using s for the cost of each shirt and p for the cost of a pair of pants. Explain the different information each one shows.
Answer:
For the cost of a shirt:
\(\frac{1}{2}\) (s-10) The cost of each shirt is \(\frac{1}{2}\) of the quantity of the original cost of the shirt, minus 10.
\(\frac{1}{2}\) s-5 The cost of each shirt is half off the original price, minus 5, since half of 10 is 5.
For the cost of a pair of pants:
\(\frac{1}{2}\) (2p) The cost of each pair of pants is half off double the price.
p The cost of each pair of pants is the original cost because \(\frac{1}{2}\) is the multiplicative inverse of 2.

→ Describe a situation in which either of the two expressions in each case would be more useful.
→ Answers may vary. For example, p would be more useful than \(\frac{1}{2}\)(2p) because it is converted back to an isolated variable, in this case the original cost.

Example 3.
Write this expression in standard form by collecting like terms. Justify each step.
5 \(\frac{1}{3}\)-(3 \(\frac{1}{3}\))(\(\frac{1}{2}\) x-\(\frac{1}{4}\))
Answer:
\(\frac{16}{3}\)+(-\(\frac{10}{3}\))(\(\frac{1}{2}\) x)+(-\(\frac{10}{3}\))(-\(\frac{1}{4}\)) Write mixed numbers as improper fractions, then distribute.
\(\frac{16}{3}\)+(-\(\frac{5}{3}\) x)+\(\frac{5}{6}\) Any grouping (associative) and arithmetic rules for multiplying rational numbers
–\(\frac{5}{3}\) x+(\(\frac{36}{6}\)+\(\frac{5}{6}\)) Commutative property and associative property of addition, collect like terms
–\(\frac{5}{3}\) x+\(\frac{37}{6}\) Apply arithmetic rule for adding rational numbers

→ A student says he created an equivalent expression by first finding this difference: 5 \(\frac{1}{3}\)-3 \(\frac{1}{3}\) . Is he correct? Why or why not?
→ Although they do appear to be like terms, taking the difference would be incorrect. In the expression (3 \(\frac{1}{3}\))(\(\frac{1}{2}\) x-\(\frac{1}{4}\)), 3 \(\frac{1}{3}\) must be distributed before applying any other operation in this problem.

→ How should 3 \(\frac{1}{3}\) be written before being distributed?
→ The mixed number can be rewritten as an improper fraction \(\frac{10}{3}\). It is not necessary to convert the mixed number, but it makes the process more efficient and increases the likelihood of getting a correct answer.

Example 4.
Model how to write the expression in standard form using rules of rational numbers.
\(\frac{x}{20}\)+\(\frac{2x}{5}\)+\(\frac{(x+1)}{2}\)+\(\frac{(3x-1)}{10}\)

→ What are other equivalent expressions of \(\frac{x}{20}\)? How do you know?
→ Other expressions include 1\(\frac{x}{20}\) and \(\frac{1}{2}\)0 x because of the arithmetic rules of rational numbers.
→ What about \(\frac{1}{20x}\)? How do you know?
→ It is not equivalent because if x=2, the value of the expression is \(\frac{1}{40}\), which does not equal \(\frac{1}{10}\).
→ How can the distributive property be used in this problem?
→ For example, it can be used to factor out \(\frac{1}{20}\) from each term of the expression.
→ Or, for example, it can be used to distribute \(\frac{1}{10}\): \(\frac{3x-1}{10}\)=\(\frac{1}{10}\) (3x-1) = \(\frac{3x}{10}\)–\(\frac{1}{10}\).
Below are two solutions. Explore both with the class.

\(\frac{x}{20}\)+\(\frac{4(2x)}{20}\)+\(\frac{10(x+1)}{20}\)+\(\frac{2(3x-1)}{20}\)
\(\frac{x+8 x+10 x+10+6 x-2}{20}\)
\(\frac{25 x+8}{20}\)
\(\frac{5}{4}\)x + \(\frac{2}{5}\)

\(\frac{1}{20}\)x+\(\frac{2}{5}\) x+\(\frac{1}{2}\) x+\(\frac{1}{2}\)+\(\frac{3}{10}\) x-\(\frac{1}{10}\)
(\(\frac{1}{20}\)+\(\frac{2}{5}\)+\(\frac{1}{2}\)+\(\frac{3}{10}\))x+(\(\frac{1}{2}\)–\(\frac{1}{10}\))
(\(\frac{1}{20}\)+\(\frac{8}{20}\)+\(\frac{10}{20}\)+\(\frac{6}{20}\))x+(\(\frac{5}{10}\)–\(\frac{1}{10}\))
\(\frac{5}{4}\) x+\(\frac{2}{5}\)

Ask students to evaluate the original expression and the answers when x=20 to see if they get the same number.

Evaluate the original expression and the answers when x=20. Do you get the same number?
\(\frac{x}{20}\)+\(\frac{2x}{5}\)+\(\frac{x+1}{2}\)+\(\frac{3x-1}{10}\)
\(\frac{20}{20}\)+\(\frac{2(20)}{5}\)+\(\frac{20+1}{2}\)+\(\frac{3(20)-1}{10}\)
1+8+\(\frac{21}{2}\)+\(\frac{59}{10}\)
9+\(\frac{105}{10}\)+\(\frac{59}{10}\)
9+\(\frac{164}{10}\)
9+\(\frac{164}{10}\)
25 \(\frac{2}{5}\)
\(\frac{5}{4}\) x+\(\frac{2}{5}\)
\(\frac{5}{4}\) (20)+\(\frac{2}{5}\)
25+\(\frac{2}{5}\)
25 \(\frac{2}{5}\)

Example 5.
Rewrite the following expression in standard form.
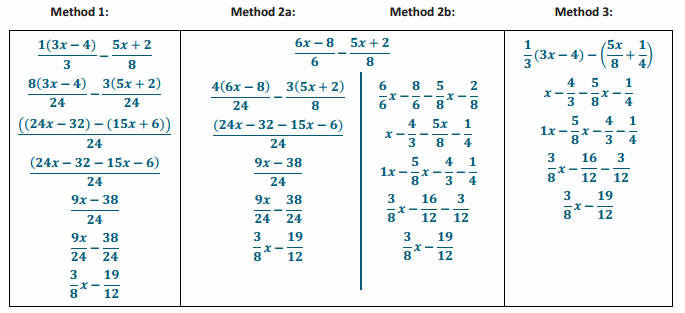
\(\frac{2(3 x-4)}{6}-\frac{5 x+2}{8}\)
Answer:
→ How can we start to rewrite this problem?
→ There are various ways to start rewriting this expression, including using the distributive property, renaming \(\frac{2}{6}\), rewriting the subtraction as an addition, distributing the negative in the second term, rewriting each term as a fraction (e.g., \(\frac{2}{6}\)(3x-4)-(\(\frac{5x}{8}\)+\(\frac{2}{8}\))), or finding the lowest common denominator.

Eureka Math Grade 7 Module 3 Lesson 6 Opening Exercise Answer Key

Solve each problem, leaving your answers in standard form. Show your steps.
a. Terry weighs 40 kg. Janice weighs 2 \(\frac{3}{4}\) kg less than Terry. What is their combined weight?
Answer:
40+(40-2 \(\frac{3}{4}\))=80-2\(\frac{3}{4}\)=78-\(\frac{3}{4}\)=77 \(\frac{1}{4}\). Their combined weight is 77 \(\frac{1}{4}\) kg.

b. 2\(\frac{2}{3}\)-1 \(\frac{1}{2}\)–\(\frac{4}{5}\)
Answer:
\(\frac{8}{3}\)–\(\frac{3}{2}\)–\(\frac{4}{5}\)
\(\frac{80}{30}\)–\(\frac{45}{30}\)–\(\frac{24}{30}\)
\(\frac{11}{30}\)

c. \(\frac{1}{5}\)+(-4)
Answer:
-3 \(\frac{4}{5}\)

d. 4(\(\frac{3}{5}\))
Answer:
\(\frac{4}{1}\) (\(\frac{3}{5}\))
\(\frac{12}{5}\)
2 \(\frac{2}{5}\)

e. Mr. Jackson bought 1 \(\frac{3}{5}\) lb. of beef. He cooked \(\frac{3}{4}\) of it for lunch. How much does he have left?
Answer:
If he cooked \(\frac{3}{4}\) of it for lunch, he had \(\frac{1}{4}\) of the original amount left. Since (1 \(\frac{3}{5}\))(\(\frac{1}{4}\))=\(\frac{8}{5}\)⋅\(\frac{1}{4}\)=\(\frac{2}{5}\), he had \(\frac{2}{5}\) lb. left. Teachers: You can also show your students how to write the answer as one expression.
(1\(\frac{3}{5}\))(1-\(\frac{3}{4}\))

→ How is the process of writing equivalent expressions by combining like terms in this Opening Exercise different from the previous lesson?
→ There are additional steps to find common denominators, convert mixed numbers to improper numbers (in some cases), and convert back.

Eureka Math Grade 7 Module 3 Lesson 6 Exercise Answer Key

Exercise 1.
For the following exercises, predict how many terms the resulting expression will have after collecting like terms. Then, write the expression in standard form by collecting like terms.
a. \(\frac{2}{5}\) g-\(\frac{1}{6}\)-g+\(\frac{3}{10}\) g-\(\frac{4}{5}\)
Answer:
There will be two terms.
\(\frac{2}{5}\) g-1g+\(\frac{3}{10}\) g-\(\frac{1}{6}\)–\(\frac{4}{5}\)
(\(\frac{2}{5}\)-1+\(\frac{3}{10}\))g-(\(\frac{1}{6}\)+\(\frac{4}{5}\))
–\(\frac{3}{10}\) g-\(\frac{29}{30}\)

b. i+6i-\(\frac{3}{7}\) i+\(\frac{1}{3}\) h+\(\frac{1}{2}\) i-h+\(\frac{1}{4}\) h
Answer:
i+6i-\(\frac{3}{7}\) i+\(\frac{1}{3}\) h+\(\frac{1}{2}\) i-h+\(\frac{1}{4}\) h
There will be two terms.
\(\frac{1}{3}\) h+\(\frac{1}{4}\) h-h+i-\(\frac{3}{7}\) i+6i+\(\frac{1}{2}\) i
(\(\frac{1}{3}\)+\(\frac{1}{4}\)+(-1))h+(1-\(\frac{3}{7}\)+6+\(\frac{1}{2}\))i
–\(\frac{5}{12}\) h+7 \(\frac{1}{14}\) i

Exercise 2.
Write two different expressions that represent the total cost of the items if tax was \(\frac{1}{10}\) of the original price. Explain the different information each shows.
For the cost of a shirt:
\(\frac{1}{2}\) (s-10)+\(\frac{1}{10}\) s The cost of each shirt is \(\frac{1}{2}\) of the quantity of the original cost of the shirt, minus 10, plus \(\frac{1}{10}\) of the cost of the shirt.
\(\frac{3}{5}\) s-5 The cost of each shirt is \(\frac{3}{5}\) of the original price (because it is \(\frac{1}{2}\) s+\(\frac{1}{10}\) s=\(\frac{6}{10}\) s), minus 5, since half of 10 is 5.
For the cost of a pair of pants:
\(\frac{1}{2}\) (2p)+\(\frac{1}{10}\) p The cost of each pair of pants is half off double the price plus \(\frac{1}{10}\) of the cost of a pair of pants.
1 \(\frac{1}{10}\) p The cost of each pair of pants is 1 \(\frac{1}{10}\) (because 1p+\(\frac{1}{10}\) p=1 \(\frac{1}{10}\) p) times the number of pair of pants.

Exercise 3.
Rewrite the following expressions in standard form by finding the product and collecting like terms.
a. -6 \(\frac{1}{3}\)–\(\frac{1}{2}\) (\(\frac{1}{2}\)+y)
Answer:
-6 \(\frac{1}{3}\)+(-\(\frac{1}{2}\))(\(\frac{1}{2}\))+(-\(\frac{1}{2}\))y
-6 \(\frac{1}{3}\)+(-\(\frac{1}{4}\))+(-\(\frac{1}{2}\) y)
–\(\frac{1}{2}\) y-(6 \(\frac{1}{3}\)+\(\frac{1}{4}\))
–\(\frac{1}{2}\) y-(6 \(\frac{4}{12}\)+\(\frac{3}{12}\))
–\(\frac{1}{2}\) y-6 \(\frac{7}{12}\)

b. \(\frac{2}{3}\)+\(\frac{1}{3}\) (\(\frac{1}{4}\) f-1 \(\frac{1}{3}\))
Answer:
\(\frac{2}{3}\)+\(\frac{1}{3}\) (\(\frac{1}{4}\) f)+\(\frac{1}{3}\) (-\(\frac{4}{3}\))
\(\frac{2}{3}\)+\(\frac{1}{12}\) f-\(\frac{4}{9}\)
\(\frac{1}{12}\) f+(\(\frac{6}{9}\)–\(\frac{4}{9}\))
\(\frac{1}{12}\) f+\(\frac{2}{9}\)

Exercise 4.
Rewrite the following expression in standard form by finding common denominators and collecting like terms.
\(\frac{2h}{3}\)–\(\frac{h}{9}\)+\(\frac{h-4}{6}\)
Answer:
\(\frac{6(2h)}{18}\)–\(\frac{2(h)}{18}\)+\(\frac{3(h-4)}{18}\)
\(\frac{12 h-2 h+3 h-12}{18}\)
\(\frac{13 h-12}{18}\)
\(\frac{13}{18}\)h – \(\frac{2}{3}\)

Exercise 5.
Write the following expression in standard form.
\(\frac{2 x-11}{4}-\frac{3(x-2)}{10}\)
Answer:
\(\frac{5(2 x-11)}{20}-\frac{2 \cdot 3(x-2)}{20}\)
\(\frac{(10 x-55)-6(x-2)}{20}\)
\(\frac{10 x-55-6 x+12}{20}\)
\(\frac{4 x-43}{20}\)
\(\frac{1}{5} x-2 \frac{3}{20}\)

Eureka Math Grade 7 Module 3 Lesson 6 Exit Ticket Answer Key

For the problem \(\frac{1}{5}\) g-\(\frac{1}{10}\)-g+1 \(\frac{3}{10}\) g-\(\frac{1}{10}\) , Tyson created an equivalent expression using the following steps.
Answer:
\(\frac{1}{5}\) g+-1g+1 \(\frac{3}{10}\) g+-\(\frac{1}{10}\)+-\(\frac{1}{10}\)
–\(\frac{4}{5}\) g+1 \(\frac{1}{10}\)
Is his final expression equivalent to the initial expression? Show how you know. If the two expressions are not equivalent, find Tyson’s mistake and correct it.

For the problem \(\frac{1}{5}\) g-\(\frac{1}{10}\)-g+1 \(\frac{3}{10}\) g-\(\frac{1}{10}\) , Tyson created an equivalent expression using the following steps.
\(\frac{1}{5}\) g+-1g+1 \(\frac{3}{10}\) g+-\(\frac{1}{10}\)+-\(\frac{1}{10}\)
–\(\frac{4}{5}\) g+1 \(\frac{1}{10}\)
Is his final expression equivalent to the initial expression? Show how you know. If the two expressions are not equivalent, find Tyson’s mistake and correct it.
Answer:
No, he added the first two terms correctly, but he forgot the third term and added to the other like terms.
If g=10,
\(\frac{1}{5}\) g+-1g+1 \(\frac{3}{10}\) g+-\(\frac{1}{10}\)+-\(\frac{1}{10}\)
\(\frac{1}{5}\)(10)+-1(10)+1 \(\frac{3}{10}\) (10)+-\(\frac{1}{10}\)+-\(\frac{1}{10}\)
2+(-10)+13+(-\(\frac{2}{10}\))
4\(\frac{4}{5}\)

–\(\frac{4}{5}\)g +1 \(\frac{1}{10}\)
–\(\frac{4}{5}\)(10)+1 \(\frac{1}{10}\)
-8+1 \(\frac{1}{10}\)
-6\(\frac{9}{10}\)
The expressions are not equal.
He should factor out the g and place parentheses around the values using the distributive property in order to make it obvious which rational numbers need to be combined.
\(\frac{1}{5}\) g+-1g+1 \(\frac{3}{10}\) g+-\(\frac{1}{10}\)+-\(\frac{1}{10}\)
(\(\frac{1}{5}\) g+-1g+1 \(\frac{3}{10}\) g)+(-\(\frac{1}{10}\)+-\(\frac{1}{10}\))
(\(\frac{1}{5}\)+-1+1 \(\frac{3}{10}\))g+(-\(\frac{2}{10}\))
(\(\frac{2}{10}\)+\(\frac{3}{10}\))g+(-\(\frac{1}{5}\))
\(\frac{1}{2}\) g-\(\frac{1}{5}\)

Eureka Math Grade 7 Module 3 Lesson 6 Problem Set Answer Key

Question 1.
Write the indicated expressions.
a. \(\frac{1}{2}\) m inches in feet
Answer:
\(\frac{1}{2}\) m×\(\frac{1}{12}\)=\(\frac{1}{24}\)m. It is \(\frac{1}{24}\)m ft.

b. The perimeter of a square with \(\frac{2}{3}\) g cm sides
Answer:
4×\(\frac{2}{3}\) g=\(\frac{8}{3}\) g. The perimeter is \(\frac{8}{3}\) g cm.

c. The number of pounds in 9 oz.
Answer:
9×\(\frac{1}{16}\)=\(\frac{9}{16}\). It is \(\frac{9}{16}\) lb.

d. The average speed of a train that travels x miles in \(\frac{3}{4}\) hour
Answer:
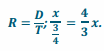. The average speed of the train is \(\frac{4}{3}\) x miles per hour.

e. Devin is 1 \(\frac{1}{4}\) years younger than Eli. April is \(\frac{1}{5}\) as old as Devin. Jill is 5 years older than April. If Eli is E years old, what is Jill’s age in terms of E?
Answer:
D=E-1 \(\frac{1}{4}\), A=\(\frac{D}{5}\), A+5=J, so J=(\(\frac{D}{5}\))+5. J=\(\frac{1}{5}\)(E-1 \(\frac{1}{4}\))+5. J=\(\frac{E}{5}\)+4 \(\frac{3}{4}\).

Question 2.
Rewrite the expressions by collecting like terms.
a. \(\frac{1}{2}\) k-\(\frac{3}{8}\) k
Answer:
\(\frac{4}{8}\) k-\(\frac{3}{8}\) k
\(\frac{1}{8}\) k

b. \(\frac{2r}{5}\)+\(\frac{7r}{15}\)
Answer:
\(\frac{6r}{15}\)+\(\frac{7r}{15}\)
\(\frac{13r}{15}\)

c. –\(\frac{1}{3}\) a-\(\frac{1}{2}\) b-\(\frac{3}{4}\)+\(\frac{1}{2}\) b-\(\frac{2}{3}\) b+\(\frac{5}{6}\) a
Answer:
–\(\frac{1}{3}\) a+\(\frac{5}{6}\) a-\(\frac{1}{2}\) b+\(\frac{1}{2}\) b-\(\frac{2}{3}\) b-\(\frac{3}{4}\)
–\(\frac{2}{6}\) a+\(\frac{5}{6}\) a-\(\frac{2}{3}\) b-\(\frac{3}{4}\)
\(\frac{1}{2}\) a-\(\frac{2}{3}\) b-\(\frac{3}{4}\)

d. -p+\(\frac{3}{5}\) q-\(\frac{1}{10}\) q+\(\frac{1}{9}\)–\(\frac{1}{9}\) p+2 \(\frac{1}{3}\) p
Answer:
-p-\(\frac{1}{9}\) p+2 \(\frac{1}{3}\) p+\(\frac{3}{5}\) q-\(\frac{1}{10}\) q+\(\frac{1}{9}\)
–\(\frac{9}{9}\) p-\(\frac{1}{9}\) p+2 \(\frac{3}{9}\) p+\(\frac{6}{10}\) q-\(\frac{1}{10}\) q+\(\frac{1}{9}\)
1\(\frac{1}{9}\) p+\(\frac{5}{10}\)q+\(\frac{1}{9}\)
1 \(\frac{2}{9}\) p+\(\frac{1}{2}\) q+\(\frac{1}{9}\)

e. \(\frac{5}{7}\) y-\(\frac{y}{14}\)
Answer:
\(\frac{10}{14}\) y-\(\frac{1}{14}\) y
\(\frac{9}{14}\)y

f. \(\frac{3n}{8}\)–\(\frac{n}{4}\)+2 \(\frac{n}{2}\)
Answer:
\(\frac{3n}{8}\)–\(\frac{2n}{8}\)+2\(\frac{4n}{8}\)
2\(\frac{5n}{8}\)

Question 3.
Rewrite the expressions by using the distributive property and collecting like terms.
a. \(\frac{4}{5}\) (15x-5)
Answer:
12x-4

b. \(\frac{4}{5}\) (\(\frac{1}{4}\) c-5)
Answer:
\(\frac{1}{5}\)c-4

c. 2 \(\frac{4}{5}\) v-\(\frac{2}{3}\) (4v+1 \(\frac{1}{6}\))
Answer:
\(\frac{2}{5}\) v-\(\frac{7}{9}\)

d. 8-4(\(\frac{1}{8}\) r-3 \(\frac{1}{2}\))
Answer:
–\(\frac{1}{2}\) r+22

e. \(\frac{1}{7}\) (14x+7)-5
Answer:
2x-4

f. \(\frac{1}{5}\) (5x-15)-2x
Answer:
-x-3

g. \(\frac{1}{4}\) (p+4)+\(\frac{3}{5}\) (p-1)
Answer:
\(\frac{17}{20}\) p+\(\frac{2}{5}\)

h. \(\frac{7}{8}\) (w+1)+\(\frac{5}{6}\)(w-3)
Answer:
\(\frac{41}{24}\)w-\(\frac{39}{24}\) or \(\frac{41}{24}\) w-\(\frac{13}{8}\)

i. \(\frac{4}{5}\) (c-1)-\(\frac{1}{8}\)(2c+1)
Answer:
\(\frac{11}{20}\)c – \(\frac{37}{40}\)

j. \(\frac{2}{3}\) (h+\(\frac{3}{4}\))-\(\frac{1}{3}\) (h+\(\frac{3}{4}\))
Answer:
\(\frac{1}{3}\) h+\(\frac{1}{4}\)

k. \(\frac{2}{3}\) (h+\(\frac{3}{4}\))-\(\frac{2}{3}\) (h-\(\frac{3}{4}\))
Answer:
1

l. \(\frac{2}{3}\) (h+\(\frac{3}{4}\))+\(\frac{2}{3}\) (h-\(\frac{3}{4}\))
Answer:
\(\frac{4}{3}\) h

m. \(\frac{k}{2}\)–\(\frac{4k}{5}\)-3
Answer:
–\(\frac{3k}{10}\)-3

n. \(\frac{3t+2}{7}\)+\(\frac{t-4}{14}\)
Answer:
\(\frac{1}{2}\) t

o. \(\frac{9x-4}{10}\)+\(\frac{3x+2}{5}\)
Answer:
\(\frac{3x}{2}\) or 1 \(\frac{1}{2}\)x

p. \(\frac{3(5 g-1)}{4}\) – \(\frac{2 g+7}{6}\)
Answer:
3\(\frac{5}{12}\)g – 1\(\frac{11}{12}\)

q. \(\frac{3 d+1}{5}\) + \(\frac{d-5}{2}\) + \(\frac{7}{10}\)
Answer:
\(\frac{-d}{10}\)-2

r. \(\frac{9 w}{6}+\frac{2 w-7}{3}-\frac{w-5}{4}\)
Answer:
\(\frac{23 w-13}{12}\)
\(\frac{23}{12}\)w-\(\frac{13}{12}\)

s. \(\frac{1+f}{5}-\frac{1+f}{3}+\frac{3-f}{6}\)
Answer:
\(\frac{11}{30}\)–\(\frac{3}{10}\)f

Engage NY Eureka Math 6th Grade Module 2 Lesson 15 Answer Key

Eureka Math Grade 6 Module 2 Lesson 15 Example Answer Key

Use Mental Math to Find Quotients

Example 1.
Use mental math to evaluate 105 ÷ 35.
Answer:
\(\frac{105 \times 2}{35 \times 2}=\frac{210}{70}=\frac{21}{7}=3\)

Example 2.
Mental Math and Division of Decimals
Evaluate the expression 175 ÷ 3. 5 using mental math techniques.
Answer:
\(\frac{175 \times 2}{3.5 \times 2}\) = 50

Example 3:
Mental Math and the Division Algorithm
Evaluate the expression 4,564 ÷ 3. 5 using mental math techniques and the division algorithm.
Answer:
\(\frac{4,564 \times 2}{3.5 \times 2}=\frac{9,128}{7}\)

Example 4:
Mental Math and Reasonable Work
Shelly was given this number sentence and was asked to place the decimal point correctly in the quotient.
55. 6875 ÷ 6.75 = 0.825
Do you agree with Shelly?
Answer:
No, I do not agree with Shelly. When I round the dividend to 54 and the divisor to 6, the quotient is 9. I know that 91 is in the ones place, so the decimal should be placed after the 8 in the quotient.

Divide to prove your answer is correct.
Answer:

Eureka Math Grade 6 Module 2 Lesson 15 Exercise Answer Key

Use mental math techniques to evaluate the expressions.

Exercise 1.
770 ÷ 14
Answer:
\(\frac{770 \div 7}{14 \div 7}=\frac{110}{2}=55\)

Exercise 2.
1005 ÷ 5
Answer:
\(\frac{1,005 \times 2}{5 \times 2}=\frac{2010}{10}=201\)

Exercise 3.
1,500 ÷ 8
Answer:
\(\frac{1,500 \div 2}{8 \div 2}=\frac{750 \div 2}{4 \div 2}=\frac{375}{2}=187.5\)

Exercise 4.
1,260 ÷ 5
Answer:
\(\frac{1,250}{10}\) = 126 × 2 = 252

Use mental math techniques to evaluate the expressions.

Exercise 5.
25 ÷ 6.25
Answer:
\(\frac{25 \times 4}{6.25 \times 4}=\frac{100}{25}=4\)

Exercise 6.
6.3 ÷ 1.5
Answer:
\(\frac{6.3 \times 2}{1.5 \times 2}=\frac{12.6}{3}=4.2\)

Exercise 7.
425 ÷ 2.5
Answer:
\(\frac{425 \times 2}{2.5 \times 2}=\frac{850}{5}=170\)

Eureka Math Grade 6 Module 2 Lesson 15 Problem Set Answer Key

Use mental math, estimation, and the division algorithm to evaluate the expressions.
Question 1.
118.4 ÷ 6.4
Answer:
18.5

Question 2.
314.944 ÷ 3.7
Answer:
85. 12

Question 3.
1,840.5072 ÷ 23.56
Answer:
78. 12

Question 4.
325 ÷ 2.5
Answer:
130

Question 5.
196 ÷ 3.5
Answer:
56

Question 6.
405 ÷ 4.5
Answer:
90

Question 7.
3,437.5 ÷ 5.5
Answer:
625

Question 8.
393.75 ÷ 5.25
Answer:
75

Question 9.
2,625 ÷ 6.25
Answer:
420

Question 10.
231 ÷ 8.25
Answer:
28

Question 11.
92 ÷ 5.75
Answer:
16

Question 12.
196 ÷ 12.25
Answer:
16

Question 13.
117÷6.5
Answer:
18

Question 14.
936 ÷ 9.75
Answer:
96

Question 15.
305 ÷ 12.2
Answer:
25

Place the decimal point in the correct place to make the number sentence true.

Question 16.
83.375 ÷ 2.3 = 3,625
Answer:
83.375 ÷ 2.3 = 36.25

Question 17.
183.575 ÷ 5,245 = 3.5
Answer:
183.575 ÷ 52.45 = 3.5

Question 18.
326,025 ÷ 9.45 = 3.45
Answer:
32.6025 ÷ 9.45 = 3.45

Question 19.
449.5 ÷ 725 = 6.2
Answer:
449.5 ÷ 72.5 = 6.2

Question 20.
446,642 ÷ 85.4 = 52.3
Answer:
4,466.42 ÷ 85.4 = 52.3

Eureka Math Grade 6 Module 2 Lesson 15 Exit Ticket Answer Key

Question 1.
Evaluate the expression using mental math techniques and the division algorithm. Explain your reasoning.
18.75 ÷ 2.5
Answer:
\(\frac{18.75 \times 2}{2.5 \times 2}=\frac{37.5}{5}\)
I find it easier to divide by 5, so I doubled both the divisor and the dividend. I knew that the dividend would be divisible by 5 since it has a 5 in the hundredths place.

18.75 ÷ 2.5 = 7.5

Eureka Math Grade 6 Module 2 Lesson 15 Opening Exercise Answer Key

Use mental math to evaluate the numeric expressions.

a. 99 + 44
Answer:
44 gives 1 to 99.
100 + 43 = 143

b. 86 – 39
Answer:
Increase both by 1.
87 – 40 = 47

c. 50 × 14
Answer:
Double 50; halve 14.
100 × 7 = 700

d. 180 ÷ 5
Answer:
Double both.
360 ÷ 10 = 36

Engage NY Eureka Math 6th Grade Module 2 Lesson 14 Answer Key

Eureka Math Grade 6 Module 2 Lesson 14 Example Answer Key

Evaluate the expression. Use a tape diagram to support your answer.

Example 1.
0.5 ÷ 0.1
Answer:

Rewrite 0. 5 ÷ 0.1 as a fraction.
Answer:
\(\frac{0.5}{0.1}\)

Express the divisor as a whole number.
Answer:
\(\frac{0.5}{0.1} \times \frac{10}{10}=\frac{5}{1}=5\)

Example 2.
Evaluate the expression. First, convert the decimal division expression to a fractional division expression in order to create a whole number divisor.
25.2 ÷ 0.72
Answer:
\(\frac{25.2}{0.72} \times \frac{100}{100}=\frac{2,520}{72}\)

Use the division algorithm to find the quotient.
Answer:
25.2 ÷ 0.72 = 35

Example 3.
A plane travels 3, 625. 26 miles in 6. 9 hours. What is the plane’s unit rate?
Represent this situation with a fraction.
Answer:
\(\frac{3,625.26}{6.9}\)

Represent this situation using the same units.
Answer:
36,252.6 tenths ÷ 69 tenths

Estimate the quotient.
Answer:
35,000 ÷ 70 = 500

Express the divisor as a whole number.
Answer:
\(\frac{3,625.26}{6.9} \times \frac{10}{10}=\frac{36,252.6}{69}\)

Use the division algorithm to find the quotient.
Answer:

Use multiplication to check your work.
Answer:
525.4 × 69 = 36,252.6

Eureka Math Grade 6 Module 2 Lesson 14 Exercise Answer Key

Convert the decimal division expressions to fractional division expressions in order to create whole number divisors. You do not need to find the quotients. Explain the movement of the decimal point. The first exercise has been completed for you.

Exercise 1.
18.6 ÷ 2.3
Answer:
\(\frac{18.6}{2.3} \times \frac{10}{10}=\frac{186}{23}\)
18.6 ÷ 23
I multiplied both the dividend and the divisor by ten, or by one power of ten, so each decimal point moved one place to the right because they grew larger by ten.

Exercise 2.
14.04 ÷ 4.68
Answer:
\(\frac{14.04}{4.86} \times \frac{100}{100}=\frac{1404}{486}\)
1,404 ÷ 486
I multiplied both the dividend and divisor by one hundred, or by two powers of ten, so each decimal point moved two places to the right because they grew larger by two powers of ten.

Exercise 3.
0.162 ÷ 0036
Answer:
\(\frac{0.162}{0.036} \times \frac{1,000}{1,000}=\frac{162}{36}\)
162 ÷ 36
I multiplied both the dividend and divisor by one thousand, or three powers often, so each decimal point moved three places to the right because they grew larger by three powers of ten.

Convert the decimal division expressions to fractional division expressions in order to create whole number divisors. Compute the quotients using the division algorithm. Check your work with a calculator.

Exercise 4.
2,000 ÷ 3.2
Answer:
\(\frac{2,000}{3.2} \times \frac{10}{10}=\frac{20,000}{32}\)

20000 ÷ 32 = 625
625 × 32 = 20000
2,000 ÷ 3.2 = 625
625 × 3.2 = 2,000

Exercise 5.
3,581.9 ÷ 4.9
Answer:
\(\frac{3,581.9}{4.9} \times \frac{10}{10}=\frac{35,819}{49}\)

35,819 ÷ 49 = 731
731 × 49 = 35,819
3,581.9 ÷ 4.9 = 731
731 × 4.9 = 3,581.9

Exercise 6.
893.76 ÷ 0.21
Answer:
\(\frac{893.76}{0.21} \times \frac{100}{100}=\frac{89,376}{21}\)

89,376 ÷ 21 = 4,256
4,256 × 21 = 89,376
893.76 ÷ 0.21 = 4,256
4,256 × 0.21 = 893.76

Exercise 7.
6.194 ÷ 0.326
Answer:
\(\frac{6.194}{0.326} \times \frac{1,000}{1,000}=\frac{6,194}{326}\)

6,194 ÷ 326 = 19
19 × 326 = 6,194
6.194 ÷ 0.326 = 19
19 × 0.326 = 6.194

Eureka Math Grade 6 Module 2 Lesson 14 Problem Set Answer Key

Convert decimal division expressions to fractional division expressions to create whole number divisors.

Question 1.
35.7 ÷ 0.07
Answer:
\(\frac{35.7}{0.07} \times \frac{100}{100}=\frac{3570}{7}\)

Question 2.
486.12 ÷ 0.6
Answer:
\(\frac{486.12}{0.6} \times \frac{10}{10}=\frac{4,861.2}{6}\)

Question 3.
3.43 ÷ 0.035
Answer:
\(\frac{3.43}{0.035} \times \frac{1,000}{1,000}=\frac{3430}{35}\)

Question 4.
5418.54 ÷ 0.009
Answer:
\(\frac{5,418.54}{0.009} \times \frac{1,000}{1,000}=\frac{5,418,540}{9}\)

Question 5.
812.5 ÷ 1.25
Answer:
\(\frac{812.5}{125} \times \frac{100}{100}=\frac{81,250}{125}\)

Question 6.
17.343 ÷ 36.9
Answer:
\(\frac{17.343}{36.9} \times \frac{10}{10}=\frac{173.43}{369}\)

Estimate quotients. Convert decimal division expressions to fractional division expressions to create whole number divisors. Compute the quotients using the division algorithm. Check your work with a calculator and your estimates.

Question 7.
Norman purchased 3. 5 lb. of his favorite mixture of dried fruits to use in a trail mix. The total cost was $16.87. How much does the fruit cost per pound?
Answer:
\(\frac{16.87}{3.5} \times \frac{10}{10}=\frac{168.7}{35}\)
Estimate 16 ÷ 4 = 4
The dried fruit costs $4.82 per pound. This is close to my estimate of 4.

Question 8.
Divide: 994.14÷ 18.9
Answer:
\(\frac{994.14}{18.9} \times \frac{10}{10}=\frac{9,941.4}{189}\)
Estimate: 100 ÷ 2 = 50
The quotient is 52.6. This is close to my estimate of 50.

Question 9.
Daryl spent $4. 68 on each pound of trail mix. He spent a total of $14. 04. How many pounds of trail mix did he purchase?
Answer:
\(\frac{14.04}{4.68} \times \frac{100}{100}=\frac{1,404}{468}\)
Estimate: 15 ÷ 5 = 3
Daryl purchased 3 pounds of trail mix. This is my estimate.

Question 10.
Mamie saved $161. 25. This is 25% of the amount she needs to save. How much money does Mamie need to save?
Answer:
\(\frac{161.25}{0.25} \times \frac{100}{100}=\frac{16,125}{25}\)
Estimate: 1,600 ÷ 2 = 800
Mamie needs to save $645. This Is close to my estimate of 800.

Question 11.
Kareem purchased several packs of gum to place in gift baskets for $1.26 each. He spent a total of $8. 82. How many packs of gum did he buy?
Answer:
\(\frac{8.82}{1.26} \times \frac{100}{100}=\frac{882}{126}\)
Estimate: 9 ÷ 1 = 9
Kareem bought 7 packs of gum. This is close to my estimate of 9.

Question 12.
Jerod is making candles from beeswax. He has 132. 72 ounces of beeswax. If each candle uses 8.4 ounces of beeswax, how many candles can he make? Will there be any wax left over?
Answer:
\(\frac{132.72}{8.4} \times \frac{10}{10}=\frac{1,327.2}{84}\)
Estimate: 120 ÷ 8 = 15
The quotient is 15.8. This means that Jerod can make 15 candles. This is close to my estimate. There will be wax left over.

Question 13.
There are 20. 5 cups of batter in the bowl. This represents 0.4 of the entire amount of batter needed for a recipe. How many cups of batter are needed?
Answer:
\(\frac{20.5}{0.4} \times \frac{10}{10}=\frac{205}{4}\)
Estimate: 200 ÷ 4 = 50
The number of cups of batter needed for the recipe is 51.25. This is close to my estimate.

Question 14.
Divide: 159.12 ÷ 6.8
Answer:
\(\frac{159.12}{6.8} \times \frac{10}{10}=\frac{1,591.2}{68}\)
Estimate: 160 ÷ 8 = 20
The quotient is 23.4. This is close to my estimate.

Question 15.
Divide: 167.67 ÷ 8.1
Answer:
\(\frac{167.67}{8.1} \times \frac{10}{10}=\frac{1,676.7}{81}\)
Estimate: 160 ÷ 8 = 20
The quotient is 20.7. This is close to my estimate.

Eureka Math Grade 6 Module 2 Lesson 14 Exit Ticket Answer Key

Estimate quotients. Convert decimal division expressions to fractional division expressions to create whole number divisor. Compute the quotient using the division algorithm. Check your work with a calculator and your estimate.

Question 1.
Lisa purchased almonds for $3. 50 per pound. She spent a total of $24. 50. How many pounds of almonds did she purchase?
Answer:
\(\frac{24.50}{3.50} \times \frac{100}{100}=\frac{245}{35}\)
Estimate: 270 ÷ 30 = 9

Lisa purchased 7 pounds of almonds. This is close to my estimate of 9.
7 × 35 = 245
7 × 3.5 = 24.5

Question 2.
Divide: 125.01 ÷ 5.4.
Answer:
\(\frac{125.01}{5.4} \times \frac{10}{10}=\frac{1250.1}{54}\)
Estimate: 125 ÷ 5 = 25

The quotient of 125.01 and 5.4 is 23.15. This is close to my estimate of 25.
23.15 × 54 = 1250.1
23.15 × 5.4 = 125.01

Eureka Math Grade 6 Module 2 Lesson 14 Opening Exercise Answer Key

Divide \(\frac{1}{2} \div \frac{1}{10}\) Use a tape diagram to support your reasoning.
Answer:
This question is asking the following: \(\frac{1}{2} \text { is } \frac{1}{10}\) of what number?

Relate the model to the invert and multiply rule.
Answer:
\(\frac{1}{2} \div \frac{1}{10}=\frac{1}{2} \times \frac{10}{1}=\frac{10}{2}=5\)

Another way \(\frac{1}{2} \div \frac{1}{10}\)
Answer:
→ Let’s look at the Opening Exercise another way. We can represent \(\frac{1}{2} \div \frac{1}{10}\) using decimals.
→ We can represent the fractions \(\frac{1}{2}\) and \(\frac{1}{10}\) with which decimals?
One-half can be represented with 0.5, and one-tenth can be represented by 0.1.
→ Display the following:
\(\frac{1}{2} \div \frac{1}{10}\)
0.5 ÷ 0.1
→ This expression can be represented with the same interpretation as the Opening Exercise: 5 tenths is 1 tenth of what number?
→ Let’s model this question with a tape diagram.

1 unit → 0.5
10 units → 10 × 0.5 = 5

→ What do you notice about the diagram and the quotient?
The diagram is set up exactly the same as in the Opening Exercise with the fraction, and the quotient is the same. Since \(\frac{1}{2}\) is equivalent to 0.5, and \(\frac{1}{10}\) is equivalent to 0.1, the quotients must be the same.

→ Look back at the problem: 0.5 ÷ 0.1. Rewrite this division expression as a fraction.
\(\frac{0.5}{0.1}\)

→ How can we express the divisor as a whole number?
Multiply by a fraction equal to one.

→ Choose a fraction to multiply in order to express the divisor as a whole number.
I could multiply by \(\frac{0.5}{0.1}\) by \(\frac{10}{10}\) to represent the divisor as the whole number 1.

→ Find the Product of \(\frac{0.5}{0.1} \times \frac{10}{10}\)
\(\frac{0.5}{0.1} \times \frac{10}{10}=\frac{5}{1}=5\)

→ What do you notice about the quotient?
It is the same as when we used a tape diagram to determine the quotient.

→ Why do you think the quotients are the same?
They are the same because I multiplied the divisor and the dividend by the same power of ten.

→ What conjecture can you make?
Because the divisor and the dividend both became ten times greater, when we write the numbers as ten times as much, we move the decimal to the right one place.

Engage NY Eureka Math 6th Grade Module 2 Lesson 13 Answer Key

Eureka Math Grade 6 Module 2 Lesson 13 Example Answer Key

Example 1.
Divide 70,072 ÷ 19.
a. Estimate:
Answer:
70,000 ÷ 20
70,000 ÷ 10 ÷ 2
7,000 ÷ 2 = 3,500

b. Create a table to show the multiple of 19.

Answer:

c. Use the algorithm to divide 70,072 ÷ 19. Check your work.
Answer:

Example 2.
Divide 14,175 ÷ 315.
a. Estimate:
Answer:
15, 000 ÷ 300
15,000 ÷ 100 ÷ 3
150 ÷ 3 = 50

b. Use the algorithm to divide 14, 175 ÷ 315. Check your work.
Answer:

Eureka Math Grade 6 Module 2 Lesson 13 Exercise Answer Key

For each exercise,
a. Estimate
b. Divide using the algorithm explaining your work using place value.

Exercise 1.
484,692 ÷ 78
Answer:
a. Estimate: 480,000 ÷ 80 = 6,000

b.

Exercise 2.
281,886 ÷ 33
Answer:
a. Estimate: 270,000 ÷ 30 = 9,000

b.

Exercise 3.
2,295,517 ÷ 37
Answer:
a. Estimate: 2,400,000 ÷ 40 = 60,000

b.

Exercise 4.
952,448 ÷ 112
Answer:
a. Estimate: 1,000,000 ÷ 100 = 10,000

b.

Exercise 5.
1,823,535 ÷ 245
Answer:
a. Estimate: 1,800,000 ÷ 200 = 9,000

b.

Eureka Math Grade 6 Module 2 Lesson 13 Problem Set Answer Key

Divide using the division algorithm.

Question 1.
1,634 ÷ 19
Answer:
86

Question 2.
2,450 ÷ 25
Answer:
98

Question 3.
22,274 ÷ 37
Answer:
602

Question 4.
21,361 ÷ 41
Answer:
521

Question 5.
34,874 ÷ 53
Answer:
658

Question 6.
50,902 ÷ 62
Answer:
821

Question 7.
70,434 ÷ 78
Answer:
903

Question 8.
91,047 ÷ 89
Answer:
1,023

Question 9.
115,785 ÷ 93
Answer:
1,245

Question 10.
207,968 ÷ 97
Answer:
2,144

Question 11.
7,735 ÷ 119
Answer:
65

Question 12.
21,948 ÷ 354
Answer:
62

Question 13.
72,372 ÷ 111
Answer:
652

Question 14.
74,152 ÷ 124
Answer:
598

Question 15.
182,727 ÷ 257
Answer:
711

Question 16.
396,256 ÷ 488
Answer:
812

Question 17.
730,730 ÷ 715
Answer:
1,022

Question 18.
1,434,342 ÷ 923
Answer:
1,554

Question 19.
1,775,296 ÷ 32
Answer:
55,478

Question 20.
1,144,932 ÷ 12
Answer:
95,411

Eureka Math Grade 6 Module 2 Lesson 13 Exit Ticket Answer Key

Question 1.
Divide using the division algorithm: 392,196 ÷ 87.
Answer:

Engage NY Eureka Math 6th Grade Module 2 Lesson 11 Answer Key

Eureka Math Grade 6 Module 2 Lesson 11 Exercise Answer Key

Exercise 1.
Calculate the product. 324.56 × 54.82
Answer:
324.56 × 54.82 = 17, 792. 3792

Exercise 2.
Kevin spends $11.25 on lunch every week during the school year. If there are 35.5 weeks during the school year, how much does Kevin spend on lunch over the entire school year? Remember to round to the nearest penny.
Answer:
11.25 × 35.5 = 399. 375 ≈ 399.38
Kevin would spend $399.38 on lunch over the entire school year.

Exercise 3.
Gunnar’s car gets 22.4 miles per gallon, and his gas tank can hold 17.82 gallons of gas. How many miles can Gunnar travel If he uses all of the gas in the gas tank?
Answer:
22.4 × 17.82 = 399. 168
Gunnar can drive 399. 168 miles on an entire tank of gas.

Exercise 4.
The principal of East High School wants to buy a new cover for the sand pit used in the long-jump competition. He measured the sand pit and found that the length is 29.2 feet and the width is 9. 8 feet. What will the area of the new cover be?
Answer:
29.2 × 9.8 = 286.16
The cover should have an area of 286. 16 square feet.

Eureka Math Grade 6 Module 2 Lesson 11 Problem Set Answer Key

Solve each problem. Remember to round to the nearest penny when necessary.

Question 1.
Calculate the product. 45.67 × 32.58
Answer:
45.67 × 32.58 = 1,487.9286

Question 2.
Deprina buys a large cup of coffee for $4. 70 on her way to work every day. If there are 24 workdays in the month, how much does Deprina spend on coffee throughout the entire month?
Answer:
4.70 × 24 = 112.80
Deprina would spend $112.80 a month on coffee.

Question 3.
Krego earns $2, 456.75 every month. He also earns an extra $4. 75 every time he sells a new gym membership. Last month, Krego sold 32 new gym memberships. How much money did Krego earn last month?
Answer:
2,456.75 + (4.75 × 32) = 2,608.75
Krego earned $2, 608.75 last month.

Question 4.
Kendra just bought a new house and needs to buy new sod for her backyard. If the dimensions of her yard are 24.6 feet by 14. 8 feet, what is the area of her yard?
Answer:
24.6 × 14.8 = 364.08
The area of Kendra’s yard is 364.08 square feet.

Eureka Math Grade 6 Module 2 Lesson 11 Exit Ticket Answer Key

Use estimation or fraction multiplication to determine if your answer is reasonable.

Question 1.
Calculate the product. 78.93 × 32.45
Answer:
78.93 × 32.45 = 2,561.2785

Question 2.
Paint costs $29.95 per gallon. Nikki needs 12. 25 gallons to complete a painting project. How much will Nikki spend on paint? Remember to round to the nearest penny.
Answer:
29.95 × 12.25 = 366.89
Nikki would spend $366.89 on paint to complete her project.

Eureka Math Grade 6 Module 2 Lesson 11 Exploratory Challenge Answer Key

You not only need to solve each problem, but your groups also need to prove to the class that the decimal in the product is located in the correct place. As a group, you are expected to present your Informal proof to the class.

a. Calculate the product. 34.62 × 12.8
Answer:
34.62 × 12.8 = 443. 136

Some possible proofs:
Using estimation: 35 × 13 = 455 If the decimal was located in a different place, the product would not be close to 455.

Using fractions: \(34 \frac{62}{100} \times 12 \frac{8}{10}=\frac{3,462}{100} \times \frac{128}{10}=\frac{443,136}{1,000}\) Because the denominator is 1,000, the last digit should be in the thousandths place when writing the fraction as a decimal. Therefore, the answer would be 443. 136.

b. Xavier earns $11. 50 per hour working at the nearby grocery store. Last week, Xavier worked 13. 5 hours. How much money did Xavier earn last week? Remember to round to the nearest penny.
Answer:
11.5 × 13.5 = 155.25

Some possible proofs:
Using estimation: 12 × 14 = 168 If the decimal was located In a different place, the product would not be close to 168.

Using fractions: \(11 \frac{5}{10} \times 13 \frac{5}{10}=\frac{115}{10} \times \frac{135}{10}=\frac{15,525}{100}\) Because the denominator is 100, the last digit should be In the hundredths place when writing the fraction as a decimal. Therefore, the answer would be $155. 25.

Discussion

Record notes from the Discussion in the box below.

Answer:
→ Do you see a connection between the number of decimal digits in the factors and the product?

→ In the first problem, there are two decimal digits in the first factor and one decimal digit in the second factor, which is a total of three decimal digits. The product has three decimal digits.

→ In the second problem, both factors have one decimal digit for a total of two decimal digits in the factors. The product also has two decimal digits.

Show students that this is another way to determine if their decimal points are in the correct place. If this point was brought up by students in their presentations, the discussion can reiterate this method to find the correct placement of the decimal. Remind students to place the decimal before eliminating any unnecessary zeros from the answer.

At the end of the discussion, have students record notes on decimal placement in the student materials.

Engage NY Eureka Math 6th Grade Module 2 Lesson 12 Answer Key

Eureka Math Grade 6 Module 2 Lesson 12 Example Answer Key

Estimate and apply the division algorithm to evaluate the expression 918 ÷ 27.
Answer:

Eureka Math Grade 6 Module 2 Lesson 12 Exercise Answer Key

Round to estimate the quotient. Then, compute the quotient using a calculator, and compare the estimation to the quotient.

Exercise 1.
2,970 ÷ 11
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:

Estimate: 300

b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
2,970 ÷ 11 = 270
The quotient is very close to the estimate.

Exercise 2.
4,752 ÷ 12
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:

Estimate: 500

b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
4,752 ÷ 12 = 396
The quotient is close to the estimate but not as close as the estimate in the first exercise.

Exercise 3.
11,647 ÷ 19
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:

Estimate: 600

b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
11,647 ÷ 19 = 613
The quotient is very close to the estimate.

Exercise 4.
40,644 ÷ 18
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:

Estimate: 2,000

b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
40,644 ÷ 18 = 2,258
The quotient is close to the estimate but not as close as the estimate in the third exercise.

Exercise 5.
49,170 ÷ 15
a. Round to a one-digit arithmetic fact. Estimate the quotient.
Answer:

Estimates may vary but could include 5,000 or 2,000.

b. Use a calculator to find the quotient. Compare the quotient to the estimate.
Answer:
49,170 ÷ 15 = 3,278
The quotient is somewhat close to the estimate; however, it is not as accurate as previous exercises and examples where the divisors were closer to a multiple of 10.

Eureka Math Grade 6 Module 2 Lesson 12 Problem Set Answer Key

Round to estimate the quotient. Then, compute the quotient using a calculator, and compare the estimate to the quotient.

Estimates may vary.

Question 1.
715 ÷ 11
Answer:
Estimate:. 700 ÷ 10 = 70
Quotient: 715 ÷ 11 = 65
Comparison: Since the dividend is very close to a multiple of ten, the quotient is very close to the estimate.

Question 2.
7,884 ÷ 12
Answer:
Estimate: 8,000 ÷ 10 = 800
Quotient: 7,884 ÷ 12 = 657
Comparison: The dividend is close to a multiple of ten, so the quotient is close to the estimate.

Question 3.
9,646 ÷ 13
Answer:
Estimate: 10,000 ÷ 10 = 1,000
Quotient: 9,646 ÷ 13 = 742
Comparison: The dividend is somewhat close to a multiple of ten, so me quotient is fairly close to the estimate.

Question 4.
11,942 ÷ 14
Answer:
Estimate: 12,000 ÷ 10 = 1,200
Quotient: 11,942 ÷ 14 = 853
Comparison: The dividend is not as close to a multiple of ten, so the quotient is not nearly as close to the estimate as dividends that are closer to a multiple of ten.

Question 5.
48,825 ÷ 15
Answer:
Estimate: 50,000 ÷ 10 = 5,000
Quotient: 48,825 ÷ 15 = 3,255
Comparison: The dividend is midway between multiples often. The quotient is in the same place value but is not as close to the estimate as dividends that are closer to a multiple of ten.

Question 6.
135,296 ÷ 16
Answer:
Estimate: 140,000 ÷ 20 = 7,000
Quotient: 135,296 ÷ 16 = 8,456
Comparison: The dividend is not as close to a multiple of ten, so the quotient is not nearly as close to the estimate as dividends that are closer to a multiple of ten.

Question 7.
199,988 ÷ 17
Answer:
Estimate: 200,000 ÷ 20 = 10,000
Quotient: 199,998 ÷ 17 = 11,764
Comparison: The dividend is somewhat close to a multiple of ten, so the quotient is fairly close to the estimate.

Question 8.
116,478 ÷ 18
Answer:
Estimate: 120,000 ÷ 20 = 6,000
Quotient: 116,478 ÷ 18 = 6,471
Comparison: The dividend is close to a multiple of ten, so the quotient is close to the estimate.

Question 9.
99,066÷ 19
Answer:
Estimate: 100,000 ÷ 20 = 5,000
Quotient: 99,066 ÷ 19 = 5,214
Comparison: Since the dividend is very close to a multiple of ten, the quotient is very close to the estimate.

Question 10.
181,800 ÷ 20
Answer:
Estimate: 180,000 ÷ 20 = 9,000
Quotient: 181,800 ÷ 20 = 9,090
Comparison: Since the divisor is a multiple of ten, the quotient is almost exactly the same as the estimate.

Eureka Math Grade 6 Module 2 Lesson 12 Exit Ticket Answer Key

Round to estimate the quotient. Then, compute the quotient using a calculator, and compare the estimation to the quotient.

Question 1.
4,732 ÷ 13
Answer:
Answers may vary.

Estimate: 500
4732 ÷ 13 = 364
The quotient 364 is somewhat close to the estimate. Both numbers are in the hundreds. If the divisor was closer to a multiple of 10, the estimate would have been closer to the quotient.

Question 2.
22,752 ÷ 16
Answer:

Estimate: 1,000
22,752 ÷ 16 = 1,422
The quotient 1,422 is somewhat close to the estimate. Both numbers are in the thousands place. The quotient is almost 1.5 times the estimate. The estimate would have been much closer to the quotient had the divisor been closer to a multiple of 10.

Eureka Math Grade 6 Module 2 Lesson 12 Discussion Answer Key

Divide 150 by 30.
Answer:

Engage NY Eureka Math 6th Grade Module 2 Lesson 7 Answer Key

Eureka Math Grade 6 Module 2 Lesson 7 Example Answer Key

Example 1.
Model the following using a partitive interpretation.
\(\frac{3}{4} \div \frac{2}{5}\)
Answer:
\(\frac{2}{5}\) of what number is \(\frac{3}{4}\)?

Shade 2 of the 5 sections \(\left(\frac{2}{5}\right)\).
Label the part that is known \(\left(\frac{3}{4}\right)\).
Make notes below on the math sentences needed to solve the problem.
Answer:
→ Let’s relate what we just did to multiplication.
Look back at the model. What was the first thing you did? What was the next thing you did?
We found half of \(\frac{3}{4}\). Then we took the result and multiplied by 5.

→ We can record this process using multiplication:
\(\frac{3}{4} \div \frac{2}{5}=\left(\frac{1}{2} \cdot \frac{3}{4}\right) \cdot 5\)

→ How can you show that \(\left(\frac{1}{2} \cdot \frac{3}{4}\right)\) . 5 is equivalent to \(\frac{3}{4} \cdot \frac{5}{2}\)? What does that tell you about \(\frac{3}{4} \div \frac{2}{5}\) and \(\frac{3}{4} \times \frac{5}{2}\)?
Since we are multiplying, we can rearrange the order of our factors:
\(\frac{1}{2} \cdot \frac{3}{4} \cdot 5=\frac{3}{4} \cdot\left(\frac{1}{2} \cdot 5\right)=\frac{3}{4} \cdot \frac{5}{2}\)
Since \(\frac{3}{4} \div \frac{2}{5}\) is equal to \(\left(\frac{1}{2} \cdot \frac{3}{4}\right)\) . 5, and that’s equal to \(\frac{3}{4} \cdot \frac{5}{2}\), we can say that \(\frac{3}{4} \div \frac{2}{5}=\frac{3}{4} \cdot \frac{5}{2}\).

→ To solve this division problem, we can invert the divisor and multiply. This is called the invert and multiply
method.

Example 2.
Model the following using a measurement interpretation.
\(\frac{3}{5} \div \frac{1}{4}\)
Answer:
\(\frac{3}{5}\) is how many fourths?

Convert the whole and the divisor to the same fractional units first. Then divide the numerators.
\(\frac{3}{5} \div \frac{1}{4}=\frac{12}{20} \div \frac{5}{20}\) = 12 twentieths ÷ 5 twentieths \(\frac{12}{5}=2 \frac{2}{5}\)

Example 3.
\(\frac{2}{3} \div \frac{3}{4}\)
Answer:
Answer may vary.

Show the number sentences below.
Answer:
\(\frac{2}{3} \div \frac{3}{4}=\frac{8}{12} \div \frac{9}{12}=\frac{8}{9}\)
\(\frac{1}{3} \cdot \frac{2}{3} \cdot 4=\frac{8}{9}\)
\(\frac{2}{3} \div \frac{3}{4}=\frac{2}{3} \cdot \frac{4}{3}=\frac{8}{9}\)

Eureka Math Grade 6 Module 2 Lesson 7 Problem Set Answer Key

Invert and multiply to divide.

Question 1.
a. \(\frac{2}{3} \div \frac{1}{4}\)
Answer:
= \(\frac{2}{3} \times \frac{4}{1}=\frac{8}{3}\)

b. \(\frac{2}{3}\) ÷ 4
Answer:
= \(\frac{2}{3} \times \frac{1}{4}=\frac{1}{6}\)

c. 4 ÷ \(\frac{2}{3}\)
Answer:
= 4 × \(\frac{3}{2}\) = 6

Question 2.
a. \(\frac{1}{3} \div \frac{1}{4}\)
Answer:
= \(\frac{1}{3} \times \frac{4}{1}=\frac{4}{3}\)

b. \(\frac{1}{8} \div \frac{3}{4}\)
Answer:
= \(\frac{1}{8} \times \frac{4}{3}=\frac{1}{6}\)

c. \(\frac{9}{4} \div \frac{6}{5}\)
Answer:
= \(\frac{9}{4} \times \frac{5}{6}=\frac{15}{8}\)

Question 3.
a. \(\frac{2}{3} \div \frac{3}{4}\)
Answer:
= \(\frac{2}{3} \times \frac{4}{3}=\frac{8}{9}\)

b. \(\frac{3}{5} \div \frac{3}{2}\)
Answer:
= \(\frac{3}{5} \times \frac{2}{3}=\frac{2}{5}\)

c. \(\frac{22}{4} \div \frac{2}{5}\)
Answer:
= \(\frac{22}{4} \times \frac{5}{2}=\frac{55}{4}\)

Question 4.
Summer used \(\frac{2}{5}\) of her ground beef to make burgers. If she used \(\frac{3}{4}\) pounds of beef, how much beef did she have at first?
Answer:
\(\frac{3}{4}\) is \(\frac{2}{5}\) of what? So, \(\frac{3}{4} \div \frac{2}{5}=\frac{3}{4} \times \frac{5}{2}=\frac{15}{8}=1 \frac{7}{8}\)

Question 5.
Alistair has 5 half-pound chocolate bars. It takes 1\(\frac{1}{2}\) pounds of chocolate, broken into chunks, to make a batch of cookies. How many batches can Alistair make with the chocolate he has on hand?
Answer:
\(1 \frac{1}{2}=\frac{3}{2}\)
\(\frac{5}{2}\) is how many \(\frac{3}{2}\)
\(\frac{5}{2} \div \frac{3}{2}=\frac{5}{2} \times \frac{2}{3}=\frac{5}{3}\)
Alistair can only make 1 full batch, but he has enough to make another \(\frac{2}{3}\) batch.

Question 6.
Draw a model that shows \(\frac{2}{5} \div \frac{1}{3}\). Find the answer as well.
Answer:

\(\frac{2}{5} \div \frac{1}{3}=\frac{2}{5} \cdot \frac{3}{1}=\frac{6}{5}\) or 1\(\frac{1}{5}\)

Question 7.
Draw a model that shows \(\frac{3}{4} \div \frac{1}{2}\). Find the answer as well.
Answer:

\(\frac{3}{4} \div \frac{1}{2}=\frac{3}{4} \cdot \frac{2}{1}=\frac{6}{4}\) or 1\(\frac{1}{2}\)

Eureka Math Grade 6 Module 2 Lesson 7 Exit Ticket Answer Key

Question 1.
Write the reciprocal of the following numbers.

Answer:

Question 2.
Rewrite this division expression as an equivalent multiplication expression: \(\frac{5}{8} \div \frac{2}{3}\)
Answer:
\(\frac{5}{8} \cdot \frac{3}{2} \text { or } \frac{1}{2} \cdot \frac{5}{8} \cdot 3\)

Question 3.
Solve problem 2. Draw a model to support your solution.
Answer:

\(\frac{5}{8} \div \frac{2}{3}=\frac{5}{8} \cdot \frac{3}{2}=\frac{15}{16}\)

Engage NY Eureka Math 6th Grade Module 2 Lesson 10 Answer Key

Eureka Math Grade 6 Module 2 Lesson 10 Example Answer Key

Example 1.
IntroductIon to Partial Products
Use partial products and the distributive property to calculate the product.
200 × 32.6
Answer:
200(32) + 200(0.6) = 6,400 + 120 = 6,520

Example 2.
Introduction to Partial Products
Use partial products and the distributive property to calculate the area of the rectangular patio shown below.

Answer:

500 × 22. 12 = 500(22 + 0. 12) = 500(22) + 500(0. 12) = 11,000 + 60 = 11,060
The area of the patio would be 11,060 square feet.

Eureka Math Grade 6 Module 2 Lesson 10 Exercise Answer Key

Exercise 1.
Use the boxes below to show your work for each station. Make sure that you are putting the solution for each station in the correct box.

Answer:

Eureka Math Grade 6 Module 2 Lesson 10 Problem Set Answer Key

Calculate the product using partial products.

Question 1.
400 × 45.2
Answer:
400(45) + 400(0.2) = 18,000 + 80 = 18,080

Question 2.
149 × 100
Answer:
100(14) + 100(0. 9) = 1,400 + 90 = 1,490

Question 3.
200 × 38.4
Answer:
200(38) + 200(0.4) = 7,600 + 80 = 7,680

Question 4.
900 × 20.7
Answer:
900(20) + 900(0.7) = 18,000 + 630 = 18,630

Question 5.
762 × 200
Answer:
200(76) + 200(0.2) = 15,200 + 40 = 15,240

Eureka Math Grade 6 Module 2 Lesson 10 Exit Ticket Answer Key

Complete the problem using partial products.

Question 1.
500 × 12.7
Answer:
500 × 12.7 = 500(12) + 500(0.7) = 6,000 + 350 = 6,350

Eureka Math Grade 6 Module 2 Lesson 10 Opening Exercise Answer Key

Calculate the product.

a. 200 × 32.6
Answer:
6,250

b. 500 × 22.12
Answer:
11.060

Engage NY Eureka Math 6th Grade Module 2 Lesson 9 Answer Key

Eureka Math Grade 6 Module 2 Lesson 9 Example Answer Key

Example 1.
25\(\frac{3}{10}\) + 376\(\frac{77}{100}\)
Answer:
Convert the mixed numbers into decimals.
→ 25.3 + 376.77

→ Round the addends to the nearest whole number. Then, find the estimated sum.
25 + 377 = 402

→ Line up the addends appropriately using place value, and add.

Example 2.
426\(\frac{1}{5}\) – 275\(\frac{1}{2}\)
Answer:
Each group should get the same value as their answer; however, the fraction group has 150\(\frac{7}{10}\) and the decimal group has 150.7.

It is important for students to see that these numbers have the same value. Students solving the problem using fractions most likely take longer to solve the problem and make more mistakes. Point out to students that the answers represent the same value, but using decimals made the problem easier to solve.

When discussing the problem, use the correct vocabulary. 426\(\frac{1}{5}\) is the minuend, 275\(\frac{1}{2}\) is the subtrahend, and 150\(\frac{7}{10}\) is the difference.

Eureka Math Grade 6 Module 2 Lesson 9 Exercise Answer Key

Calculate each sum or difference.

Exercise 1.
Samantha and her friends are going on a road trip that is 245\(\frac{7}{50}\) miles long. They have already driven How much farther do they have to drive?
Answer:
Expression: 245\(\frac{7}{50}\) – 128\(\frac{53}{100}\)                Estimated answer: 245 – 129 = 116
Actual answer: 245. 14 – 128.53 = 116.61

Exercise 2.
Ben needs to replace two sides of his fence. One side is 367\(\frac{9}{100}\) meters long, and the other is 329 meters long. How much fence does Ben need to buy?
Answer:
Expression: 367\(\frac{9}{100}\) + 329\(\frac{3}{10}\)               Estimated answer: 367 + 329 = 696
Actual answer: 367.09 + 329.3 = 696.39

Exercise 3.
Mike wants to paint his new office with two different colors. If he needs 4\(\frac{4}{5}\) gallons of red paint and 3\(\frac{1}{10}\) gallons of brown paint, how much paint does he need in total?
Answer:
This problem is an example of where it may not be easiest to convert mixed numbers into decimals. Either method would result in a correct answer, but discuss with students why it may just be easier to find the sum by keeping the addends as mixed numbers.
Expression: 4\(\frac{4}{5}\) + 3\(\frac{1}{10}\)               Estimated answer: 5 + 3 = 8
Actual answer: \(4 \frac{8}{10}+3 \frac{1}{10}=7 \frac{9}{10}\)

Exercise 4.
After Arianna completed some work, she figured she still had 78\(\frac{21}{100}\) pictures to paint. If she completed another 34\(\frac{23}{25}\) pictures, how many pictures does Arianna still have to paint?
Answer:
Expression: 78\(\frac{21}{100}\) – 34\(\frac{23}{25}\)               Estimated answer: 78 – 35 = 43
Actual answer: 78.21 – 34.92 = 43.29

Use a calculator to convert the fractions into decimals before calculating the sum or difference.

Exercise 5.
Rahzel wants to determine how much gasoline he and his wife use In a month. He calculated that he used
78\(\frac{1}{3}\) gallons of gas last month. Rahzel’s wife used 41\(\frac{3}{8}\) gallons of gas last month. How much total gas did Rahzel and his wife use last month? Round your answer to the nearest hundredth.
Answer:
Expression: 78\(\frac{1}{3}\) + 41\(\frac{3}{8}\)               Estimated answer: 78 + 41 = 119
Actual answer: 78.333 + 41. 375 ≈ 119.71

Eureka Math Grade 6 Module 2 Lesson 9 Problem Set Answer Key

Question 1.
Find each sum or difference.
a. 381\(\frac{1}{10}\) – 214\(\frac{43}{100}\)
Answer:
381.1 – 214.43 = 166.67

b. 32\(\frac{3}{4}\) – 12\(\frac{1}{2}\)
Answer:
32\(\frac{3}{4}\) – 12\(\frac{2}{4}\) = 20\(\frac{1}{4}\) or 20.25

c. 517\(\frac{37}{50}\) + 312\(\frac{3}{100}\)
Answer:
517.74 + 312.03 = 829.77

d. 632\(\frac{16}{25}\) + 32\(\frac{3}{10}\)
Answer:
632. 64 + 32.3 = 664.94

e. 421\(\frac{3}{50}\) – 212\(\frac{9}{10}\)
Answer:
421.06 – 212.9 = 208.16

Question 2.
Use a calculator to find each sum or difference. Round your answer to the nearest hundredth.
a. 422\(\frac{3}{7}\) – 367\(\frac{5}{9}\)
Answer:
422. 428571 – 367.555556 ≈ 54.87

b. 23\(\frac{1}{5}\) + 45\(\frac{7}{8}\)
Answer:
23.2 + 45.875 ≈ 69.08

Eureka Math Grade 6 Module 2 Lesson 9 Exit Ticket Answer Key

Solve each problem. Show that the placement of the decimal is correct through either estimation or fraction calculation.

Question 1.
382\(\frac{3}{10}\) – 191\(\frac{87}{100}\)
Answer:
Estimation: 382 – 192 = 190
382.3 – 191.87 = 190.43

Question 2.
594\(\frac{7}{25}\) + 89\(\frac{37}{100}\)
Answer:
Estimation: 594 + 89 = 683
594.28 + 89.37 = 683.65

Engage NY Eureka Math 6th Grade Module 2 Lesson 8 Answer Key

Eureka Math Grade 6 Module 2 Lesson 8 Example Answer Key

Example 1: Introduction to Calculating the Quotient of a Mixed Number and a Fraction

a. Carll has 4\(\frac{1}{2}\) walls left to paint in order for all the bedrooms in her house to have the same color paint.
However, she has used almost all of her paint and only has \(\frac{5}{6}\) of a gallon left.
How much paint can she use on each wall in order to have enough to paint the remaining wails?
Answer:
Write the expression: \(\frac{5}{6}\) ÷ 4\(\frac{1}{2}\)
Convert into a fraction: \(\frac{9}{2}\)
Divide fractions: \(\frac{5}{6} \div \frac{9}{2}=\frac{5}{6} \times \frac{2}{9}=\frac{10}{54} \text { or } \frac{5}{27}\)
Carli can use \(\frac{5}{27}\) of a gallon paint on each of the remaining walls.

b. Calculate the quoitent.
\(\frac{2}{5} \div 3 \frac{4}{7}\)
Answer:
Convert into a fraction: \(\frac{25}{7}\)
Divide fractions: \(\frac{2}{5} \div \frac{25}{7}=\frac{2}{5} \times \frac{7}{25}=\frac{14}{125}\)

Eureka Math Grade 6 Module 2 Lesson 8 Exercise Answer Key

Exercise 1.
Show your work for the memory game in the boxes provided below.

Answer:

Eureka Math Grade 6 Module 2 Lesson 8 Problem Set Answer Key

Calculate each quoitent.

Question 1.
\(\frac{2}{5} \div 3 \frac{1}{10}\)
Answer:
\(\frac{2}{5} \div \frac{31}{10}=\frac{2}{5} \times \frac{10}{31}=\frac{20}{155} \text { or } \frac{4}{31}\)

Question 2.
\(4 \frac{1}{3} \div \frac{4}{7}\)
Answer:
\(\frac{13}{3} \div \frac{4}{7}=\frac{13}{3} \times \frac{7}{4}=\frac{91}{12} \text { or } 7 \frac{7}{12}\)

Question 3.
\(3 \frac{1}{6} \div \frac{9}{10}\)
Answer:
\(\frac{19}{6} \div \frac{9}{10}=\frac{19}{6} \times \frac{10}{9}=\frac{190}{54} \text { or } \frac{95}{27} \text { or } 3 \frac{28}{54} \text { or } 3 \frac{14}{27}\)

Question 4.
\(\frac{5}{8} \div 2 \frac{7}{12}\)
Answer:
\(\frac{5}{8} \div \frac{31}{12}=\frac{5}{8} \times \frac{12}{31}=\frac{60}{248} \text { or } \frac{15}{62}\)

Eureka Math Grade 6 Module 2 Lesson 8 Exit Ticket Answer Key

Calculate the quoitent.

Question 1.
\(\frac{3}{4} \div 5 \frac{1}{5}\)
Answer:
\(\frac{3}{4} \div 5 \frac{1}{5}=\frac{3}{4} \div \frac{26}{5}=\frac{3}{4} \times \frac{5}{26}=\frac{15}{104}\)

Question 2.
\(\frac{3}{7} \div 2 \frac{1}{2}\)
Answer:
\(\frac{3}{7} \div 2 \frac{1}{2}=\frac{3}{7} \div \frac{5}{2}=\frac{3}{7} \times \frac{2}{5}=\frac{6}{35}\)

Question 3.
\(\frac{5}{8} \div 6 \frac{5}{6}\)
Answer:
\(\frac{5}{8} \div 6 \frac{5}{6}=\frac{5}{8} \div \frac{41}{6}=\frac{5}{8} \times \frac{6}{41}=\frac{30}{328} \text { or } \frac{15}{164}\)

Question 4.
\(\frac{5}{8} \div 8 \frac{3}{10}\)
Answer:
\(\frac{5}{8} \div 8 \frac{3}{10}=\frac{5}{8} \div \frac{83}{10}=\frac{5}{8} \times \frac{10}{83}=\frac{50}{664} \text { or } \frac{25}{332}\)

Engage NY Eureka Math 6th Grade Module 2 Lesson 6 Answer Key

Eureka Math Grade 6 Module 2 Lesson 6 Example Answer Key

Example 1.
Divide 50 ÷ \(\frac{2}{3}\).
Answer:
Step 1: Decide on an Interpretation.
Today, we use the partitive interpretation and Interpret the divisor, 2 thirds, to be the number of groups. I’m asking myself, “50 is 2 thirds group of what size?”

Step 2: Draw a model.

Step 3: Find the answer.
2 units = 50
1 unit = 50 ÷ 2 = 25
3 units = 3 × 25 = 75

Step 4: Choose a unit.
Answers will vary, but dollars will be used throughout the discussion below.

Step 5: Set up a situation based upon the model.
Answers will vary, but there is a story problem provided in the discussion.

Example 2.
Divide \(\frac{1}{2} \div \frac{3}{4}\)
Answer:
Step 1: Decide on an interpretation.
Today, we use the partitive interpretation and Interpret the divisor, 3 fourths, to be the number of groups. I’m asking myself, “1 half is 3 fourths of what number?”

Step 2: Draw a model.

Step 3: Find the answer.
3 units = \(\frac{1}{2}\)
1 unit = \(\frac{1}{2}\) ÷ 3 = \(\frac{1}{3}\) of \(\frac{1}{2}\) = \(\frac{1}{6}\)
4 units = 4 × 1 sixth = 4 sixths = \(\frac{4}{6}\)

Step 4: Choose a unit.
Answers will vary.

Step 5: Set up a situation based upon the model.
Answers will vary.

Eureka Math Grade 6 Module 2 Lesson 6 Exercise Answer Key

Exercise 1.
Using the same dividend and divisor, work with a partner to create your own story problem. You may use the same unit, dollars, but your situation must be unique. You could try another unit, such as miles, If you prefer.
Answer:
Possible story problems:
1. Ronaldo has ridden 50 miles during his bicycle race and is \(\frac{2}{3}\) of the way to the finish line. How long is the race?
2. Samantha used 50 tickets (\(\frac{2}{3}\) of her total) to trade for a kewpie doll at the fair. How many tickets did she start with?

Exercise 2.
Using the same dividend and divisor, work with a partner to create your own story problem. Try a different unit.
Answer:
Possible story problems:
1. Daryl completed 3 fourths of his homework in a half hour. How long does it take Daryl to complete all of his homework?
2. A snail saw food sitting a distance away. After traveling for a half foot, a snail had covered \(\frac{3}{4}\) the distance. How far away was the food?

Eureka Math Grade 6 Module 2 Lesson 6 Problem Set Answer Key

Question 1.
\(\frac{15}{16}\) is 1 sixteenth groups of what size?
Answer:
15 sixteenths ÷ 1 sixteenth = 15. The size of the group is 15.

Question 2.
\(\frac{7}{8}\) teaspoons is \(\frac{1}{4}\) groups of what size?
Answer:
7 eighths ÷ 2 eighths = \(\frac{7}{2}\) = 3\(\frac{1}{2}\). The size of the group is 3\(\frac{1}{2}\).

Question 3.
A 4-cup container of food is \(\frac{2}{3}\) groups of what size?
Answer:
12 thirds ÷ 2 thirds = 6. The size of the group is 6.

Question 4.
Write a partitive division story problem for 6 ÷ \(\frac{3}{4}\).
Answer:
Answers will vary.

Question 5.
Write a partitive division story problem for \(\frac{5}{12}\) ÷ \(\frac{1}{6}\)
Answer:
Answers will vary.

Question 6.
Fill In the blank to complete the equation. Then, find the quotient, and draw a model to support your solution.
a.

Answer:
\(\frac{1}{4} \div 7=\frac{1}{7} \text { of } \frac{1}{4}=\frac{1}{28}\)

b.

Answer:
\(\frac{5}{6} \div 4=\frac{1}{4} \text { of } \frac{5}{6}=\frac{5}{24}\)

Question 7.
There is \(\frac{3}{5}\) of a pie left. If 4 friends wanted to share the pie equally, how much would each friend receive?
Answer:
\(\frac{3}{5} \div 4=\frac{3}{5} \times \frac{1}{4}=\frac{3}{20}\)
Each friend would receive \(\frac{3}{20}\) of the pie.

Question 8.
In two hours, Holden completed \(\frac{3}{4}\) of his race. How long will it take Holden to complete the entire race?
Answer:
2 ÷ \(\frac{3}{4}\) = 8 fourths = \(\frac{8}{3}\) = 2\(\frac{2}{3}\)
It will take Holden 2\(\frac{2}{3}\) hews to complete the race.

Question 9.
Sam cleaned \(\frac{1}{3}\) of his house in 50 minutes. How many hours will it take him to clean his entire house?
Answer:
50 minutes = \(\frac{1}{60} \frac{\text { hour }}{\text { minutes }}\) = \(\frac{5}{6}\) hours
\(\frac{5}{6} \div \frac{1}{3}\) = 5 sixths ÷ 2 sixths = \(\frac{5}{2}\) = 2\(\frac{1}{2}\)
It will take Sam 2\(\frac{1}{2}\) hours to clean his entire house.

Question 10.
It took Mario 10 months to beat \(\frac{5}{8}\) of the levels on his new video game. How many years will it take for Mario to beat all the levels?
Answer:
10 months = \(\frac{1}{12} \frac{\text { year }}{\text { month } s}\) = \(\frac{10}{12}\) years = \(\frac{5}{6}\) years
\(\frac{5}{6} \div \frac{5}{8}=\frac{20}{24} \div \frac{15}{24}=\frac{20}{15}=1 \frac{1}{3}\)
Mario will need 1\(\frac{1}{3}\) years to beat all the levels.

Question 11.
A recipe calls for 1\(\frac{1}{2}\) cups of sugar. Marley only has measuring cups that measure \(\frac{1}{4}\) cup. How many times will Marley have to fill the measuring cup?
Answer:
\(1 \frac{1}{2} \div \frac{1}{4}=\frac{3}{2} \div \frac{1}{4}=\frac{6}{4} \div \frac{1}{4}=6\)
Marley will have to use the measuring cup 6 times.

Eureka Math Grade 6 Module 2 Lesson 6 Exit Ticket Answer Key

Question 1.
Write a story problem using the partitive Interpretation of division for the following: 25 ÷ \(\frac{5}{8}\) = 40.

Answer:
Zolanda spent \(\frac{5}{8}\) of her class period, or 25 minutes, taking notes. How long was the class period? (Accept any other reasonable story problem showing 25 ÷ \(\frac{5}{8}\) = 40.)

Engage NY Eureka Math 6th Grade Module 2 Lesson 3 Answer Key

Eureka Math Grade 6 Module 2 Lesson 3 Example Answer Key

Example 1.
\(\frac{8}{9} \div \frac{2}{9}\)
Write the expression in unit form, and then draw a model to solve.
Answer:

Here we have 4 groups of \(\frac{2}{9}\). Therefore, the quotient is 4.

Example 2.
\(\frac{9}{12} \div \frac{3}{12}\)
Write the expression in unit form, and then draw a model to solve.
Answer:

9 twelfths ÷ 3 twelfths = 9 ÷ 3 = 3

Example 3.
\(\frac{7}{9} \div \frac{3}{9}\)
Answer:

→ Look at your model. How many units of \(\frac{3}{9}\) can you see in \(\frac{3}{9}\)?
→2 complete units and then part of another

→ How can we name the part of the incomplete unit?
→There is one out of the three needed pieces to make another whole. So, it is \(\frac{1}{3}\)
→This means that \(\frac{7}{9} \div \frac{3}{9}\) = 2\(\frac{1}{3}\).
→This is the same as 7 ÷ 3.

→Do we get the same result solving \(\frac{7}{9} \div \frac{3}{9}\) as we do when solving \(\frac{7}{9} \times \frac{9}{3}\) ?

Eureka Math Grade 6 Module 2 Lesson 3 Exercise Answer Key

Write an expression to represent each problem. Then, draw a model to solve.

Exercise 1.
How many fourths are In 3 fourths?
Answer:
I need to divide three fourths by one fourth, which is 3.
\(\frac{3}{4} \div \frac{1}{4}\) = 3 fourth = 3 ÷ 1

There are 3 one-fourths in three-fourths.

Exercise 2.
\(\frac{4}{5} \div \frac{2}{5}\)
Answer:

This is really 4 fifths ÷ 2 fifths, which is 2.

Exercise 3.
\(\frac{9}{4} \div \frac{3}{4}\)
Answer:

This is really 9 fourths ÷ 3 fourths, which is 3.

Exercise 4.
\(\frac{7}{8} \div \frac{2}{8}\)
Answer:

This is really 7 eighths ÷ 2 eighths, which is \(\frac{7}{8}\) or 3\(\frac{1}{2}\)

Exercise 5.
\(\frac{13}{10} \div \frac{2}{10}\)
Answer:

This is really 13 tenths ÷ 2 tenths, which is \(\frac{13}{2}\) or 6\(\frac{1}{2}\)

Exercise 6.
\(\frac{11}{9} \div \frac{3}{9}\)
Answer:

This is really 11 ninths ÷ 3 ninths, which is \(\frac{11}{3}\) or 3\(\frac{2}{3}\).

Eureka Math Grade 6 Module 2 Lesson 3 Problem Set Answer Key

For the following exercises, rewrite the division expression in unit form. Then, find the quotient. Draw a model to support your answer.

Question 1.
\(\frac{4}{5} \div \frac{1}{5}\)
Answer:
4 fifths ÷ 1 fifth = 4

Question 2.
\(\frac{8}{9} \div \frac{4}{9}\)
Answer:
8 ninths ÷ 4 ninths = 2

Question 3.
\(\frac{15}{4} \div \frac{3}{4}\)
Answer:
15 fourths ÷ 3 fourths = 5

Question 4.
\(\frac{13}{5} \div \frac{4}{5}\)
Answer:
13 fifths ÷ 4fifths = ÷=3

Rewrite the expression In unit form, and find the quotient.

Question 5.
\(\frac{10}{3} \div \frac{2}{3}\)
Answer:
10 thirds ÷ 2 thirds = 5

Question 6.
\(\frac{8}{5} \div \frac{3}{5}\)
Answer:
8 fifths ÷ 3 fifths = = 2

Question 7.
\(\frac{12}{7} \div \frac{12}{7}\)
Answer:
12 sevenths ÷ 12 sevenths = 1

Represent the division expression using unit form. Find the quotient. Show all necessary work.

Question 8.
A runner is \(\) mile from the finish line. If she can travel \(\) mile per minute, how long will it take her to finish the race?
Answer:
7 eighths ÷ 3 eighths = \(\frac{7}{3}=2 \frac{1}{3}\)
It will take her 2\(\frac{1}{3}\) minutes to finish the race.

Question 9.
An electrician has 4. 1 meters of wire.
a. How many strips m long can he cut?
Answer:
41 tenths ÷ 7 tenths = \(\frac{41}{7}\) = 5\(\frac{6}{7}\)
He can cut 5 complete strips.

b. How much wire will he have left over?
Answer:
He will have \(\frac{6}{10}\)m left over.

Question 10.
Saeed bought 21\(\frac{1}{2}\) lb. of ground beef. He used \(\frac{1}{4}\) of the beef to make tacos and \(\frac{2}{3}\) of the remainder to make quarter-pound burgers. How many burgers did he make?
Answer:
\(\frac{1}{2}\) of 21\(\frac{1}{2}\) = 10\(\frac{3}{4}\) → 10\(\frac{3}{4}\) Ib. of beef is used for burgers.
43 fourths ÷ 1 fourth = 43
Saeed made 43 burgers.

Question 11.
A baker bought some flour. He used \(\frac{2}{5}\) of the flour to make bread and used the rest to make batches of muffins. If he used 16 lb. of flour making bread and \(\frac{2}{3}\) lb. for each batch of muffins, how many batches of muffins did he make?
Answer:
16 is \(\frac{2}{5}\) group of what size?
2 units = 16
1 unit = 16 ÷ 2 = 8
3 units = 3 × 8 = 24
The baker used 24 ib. of flour for muffins.

24 ÷ \(\frac{2}{3}\)
72 thirds ÷ 2 thirds = 36
The baker made 36 batches of muffins.

Eureka Math Grade 6 Module 2 Lesson 3 Exit Ticket Answer Key

Find the quotient. Draw a model to support your solution.

Question 1.
\(\frac{9}{4} \div \frac{3}{4}\)
This is really 9 fourths ÷ 3 fourths, which is 3.
Answer:

Question 2.
\(\frac{7}{3} \div \frac{2}{3}\)
Answer:
This is really 7 thirds ÷ 2 thirds, which is \(\frac{7}{2}\) or 3\(\frac{1}{2}\).

Eureka Math Grade 6 Module 2 Lesson 3 Opening Exercise Answer Key

Question 1.
Draw a model to represent 12 ÷ 3.
Answer:
There are two interpretations:
Partitive Division

Measurement Division

Question 2.
Create a question or word problem that matches your model.
Answer:
Answers will vary.
Sample Solutions for Partitive Division Model:
12 cards are shared with 3 people. How many cards does each person get?
12 is 3 of what number?

Sample Solutions for Measurement Division Model:
12 balls are put in groups of 3. How many groups are made?
How many 3’s are in 12?

Engage NY Eureka Math 6th Grade Module 2 Lesson 5 Answer Key

Eureka Math Grade 6 Module 2 Lesson 1 Example Answer Key

Example 1:
\(\frac{1}{2} \div \frac{1}{8}\)
Answer:
Step 1: Decide on an interpretation.
For today, we will only use the measurement interpretation and consider the divisor, 1 eighth, to be the size of the group.

Step 2: Draw a model

Step 3: Find the answer.
\(\frac{1}{2} \div \frac{1}{8}=\frac{4}{8} \div \frac{1}{8}\) = 4 eighths ÷ 1 eighth = 4
So, the answer is 4. There are four \(\frac{1}{8}\) in \(\frac{1}{2}\).

Step 4: Choose a unit.
Answers will vary, but pounds will be used throughout the discussion below.

Step 5: Set up a situation based upon the model.
Answers will vary, but there is a story problem provided in the discussion.

Example 2.
\(\frac{3}{4} \div \frac{1}{2}\)
Answer:
Step 1: Decide on an interpretation.
For today, we’ll only use the measurement interpretation and consider the divisor, 1 half, to be the size of the group.

Step 2: Draw a diagram.

Step 3: Find the answer.
\(\frac{3}{4} \div \frac{1}{2}=\frac{3}{4} \div \frac{2}{4}\) = 3 fourths ÷ 2 fourths = \(\frac{3}{2}\) = 1\(\frac{1}{2}\)
So, the answer is \(\frac{1}{2}\). There are 1\(\frac{1}{2}\) halves in \(\frac{3}{4}\).

Step 4: Choose a unit.
Answers will vary, but ounces will be used throughout the discussion below.

Step 5: Set up a situation based on the model.
Answers will vary, but there is a story problem provided in the discussion.

Eureka Math Grade 6 Module 2 Lesson 1 Exercise Answer Key

Exercise 1.
Using the same dividend and divisor, work with a partner to create your own story problem. You may use the same unit, but your situation must be unique. You could try another unit such as ounces, yards, or miles If you prefer.
Answer:
Possible story problems:
1. Tina uses \(\frac{1}{8}\) oz. of cinnamon each time she makes a batch of coffee cake topping. How many batches can she make if she has \(\frac{1}{2}\)oz. left in her spice jar?
2. Eugenia has \(\frac{1}{2}\) yard of ribbon. For each party decoration, she needs \(\frac{1}{8}\) yard. How many party decorations can she make?

Exercise 2.
Using the same dividend and divisor, work with a partner to create your own story problem. You may use the same unit, but your situation must be unique. You could try another unit such as cups, yards, or miles if you prefer.
Answer:
Possible story problems:
1. Tiffany uses \(\frac{1}{2}\) cup of glycerin each time she makes a batch of soap bubble mixture. How many batches can she make if she has \(\frac{3}{4}\) cup left In her glycerin bottle?
2. Each jug holds \(\frac{3}{4}\) gallon. Each bottle holds \(\frac{1}{2}\) gallon. One jug has the same capacity as how many bottles?

Eureka Math Grade 6 Module 2 Lesson 1 Problem Set Answer Key

Solve.
Question 1.
How many sixteenths are in \(\frac{15}{16}\)?
Answer:
15 sixteenths ÷ 1 sixteenth = 15
There are 15 sixteenths in \(\frac{15}{16}\).

Question 2.
How many \(\frac{1}{4}\) teaspoon doses are in \(\frac{7}{8}\) teaspoon of medicine?
Answer:
7 eighths ÷ 2 eighths = \(\frac{7}{2}\) = 3\(\frac{1}{2}\)
There are 3\(\frac{1}{2}\) doses.

Question 3.
How many cups servings are in a 4 cup container of food?
Answer:
12 thirds ÷ 2 thirds = 6
There are 6 servings in the container.

Question 4.
Write a measurement division story problem for 6 ÷ \(\frac{3}{4}\)
Answer:
Answers will vary.

Question 5
Write a measurement division story problem for \(\frac{5}{12} \div \frac{1}{6}\)
Answer:
Answers will vary.

Question 6.
Fill in the blank to complete the equation. Then, find the quotient, and draw a model to support your solution.
a.

Answer:
\(\frac{1}{2} \div 5=\frac{1}{5} \text { of } \frac{1}{2}=\frac{1}{10}\)

b.

Answer:
\(\frac{3}{4} \div 6=\frac{1}{6} \text { of } \frac{3}{4}=\frac{3}{24}\)

Question 7.
\(\frac{4}{5}\) of the money collected from a fund rasier was divided equally among 8 grades. What fraction of the money did each grade receive?
Answer:
\(\frac{4}{5} \div 8=\frac{4}{5} \times \frac{1}{8}=\frac{4}{40}=\frac{1}{10}\)
Each grade got 1 tenth of the money.

Question 8.
Meyer used 6 loads of gravel to cover \(\frac{2}{5}\) of his driveway. How many loads of gravel will he need to cover his entire driveway?
Answer:
6 is \(\frac{2}{5}\) group of what size?
2 units = 6
1 unit = 6 ÷ 2 = 3
5 units = 5 × 3 = 15
Meyer will need 15 loads.

Question 9.
An athlete plans to run 3 miles. Each lap around the school yard is \(\frac{3}{7}\) mile. How many laps will the athlete run?
Answer:
How many \(\frac{3}{7}\) in 3?
21 sevenths ÷ 3 sevenths = 7
The athlete will run 7 laps.

Question 10.
Parks spent \(\frac{1}{3}\) of his money on a sweater. He spent \(\frac{3}{5}\) of the remainder on a pair of jeans. If he has $36 left, how much did the sweater cost?
Answer:
\(\frac{2}{5} \text { of } \frac{2}{3}=\frac{6}{15}\)
\(\frac{1}{3}+\frac{6}{15}=\frac{11}{15}\)
\(\frac{4}{15}\) of Parks’s money is left over.

$36 is \(\frac{4}{15}\) of what number?
4 units = 36
1 unit = 36 ÷ 4 = 9
5 units = 5 × 9 = 45
The sweater cost $45.

Eureka Math Grade 6 Module 2 Lesson 1 Exit Ticket Answer Key

Question 1.
Write a story problem using the measurement interpretation of division for the following: \(\frac{3}{4} \div \frac{1}{8}\) = 6.

Answer:
Arthur divided \(\frac{3}{4}\) of his kingdom into parcels of land, each being \(\frac{1}{8}\) of the entire kingdom. How many parcels did he make?
(Accept any other reasonable story problem showing \(\frac{3}{4} \div \frac{1}{8}\) = 6.)

Eureka Math Grade 6 Module 2 Lesson 1 Opening Exercise Answer Key

Tape Diagram:
\(\frac{8}{9} \div \frac{2}{9}\)
Answer:

Here we have 4 groups of \(\frac{2}{9}\). Therefore, the answer is 4.

Number Line:
Molly’s friend, Xavier, also has \(\frac{11}{8}\) cups of strawberries. He needs \(\frac{3}{4}\) cup of strawberries to make a batch of tarts. How many batches can he make? Draw a model to support your solution.
Answer:

Xavier has enough to make 1 and \(\frac{5}{6}\) batches.

Engage NY Eureka Math 6th Grade Module 2 Lesson 4 Answer Key

Eureka Math Grade 6 Module 2 Lesson 4 Example Answer Key

Example 1.
Molly has 1\(\frac{3}{8}\) cups of strawberries. She needs \(\frac{3}{8}\) cup of strawberries to make one batch of muffins. How many batches can Molly make?
Use a model to support your answer.
Answer:

\(\frac{11}{8} \div \frac{3}{8}\) = 11 eighths ÷ 3 eighths = \(\frac{11}{3}\) = 3\(\frac{2}{3}\)
Molly can make 3\(\frac{2}{3}\) batches of muffins.

Example 2.
Molly’s friend, Xavier, also has \(\frac{11}{8}\) cups of strawberries. He needs \(\frac{3}{4}\) cup of strawberries to make a batch of tarts. How many batches can he make? Draw a model to support your solution.
Answer:

\(\frac{11}{8} \div \frac{6}{8}\) = 11 eighths ÷ 6 eighths = \(\frac{11}{6}\) = 1\(\frac{5}{6}\)
Xavier has enough to make 1 and \(\frac{5}{6}\) batches.

Example 3.
Find the quotient: \(\frac{6}{8} \div \frac{2}{8}\). Use a model to show your answer.
Answer:

2 units = 6 eighths
1 unit = 6 eighths ÷ 2 = 3 eighths
8 units = 8 × 3 eIghths = 24 eighths = 3

Example 4.
Find the quotient: \(\frac{3}{4} \div \frac{2}{3}\). Use a model to show your answer.
Answer:

We could rewrite this problem to ask \(\frac{9}{12} \div \frac{8}{12}\) = 9 twelfths ÷ 8 twelfths = \(\frac{9}{8}\) = 1\(\frac{1}{8}\).

Eureka Math Grade 6 Module 2 Lesson 4 Exercise Answer Key

Find each quotient.

Exercise 1.
\(\frac{6}{2} \div \frac{3}{4}\)
Answer:
We could rewrite this expression and solve as \(\frac{12}{4} \div \frac{3}{4}=\frac{12}{3}\) = 4.

Exercise 2.
\(\frac{2}{3} \div \frac{2}{5}\)
Answer:
We could rewrite this expression and solve as \(\frac{10}{15} \div \frac{6}{15}=\frac{10}{6}=1 \frac{4}{6}\)

Exercise 3.
\(\frac{7}{8} \div \frac{1}{2}\)
Answer:
We could rewrite this as \(\frac{7}{8} \div \frac{4}{8}=\frac{7}{4}=1 \frac{3}{4}\)

Exercise 4.
\(\frac{3}{5} \div \frac{1}{4}\)
Answer:
This can be rewritten as \(\frac{12}{20} \div \frac{5}{20}=\frac{12}{5}=2 \frac{2}{5}\)

Exercise 5.
\(\frac{5}{4} \div \frac{1}{3}\)
Answer:
We can be written this as \(\frac{15}{12} \div \frac{4}{12}=\frac{15}{4}=3 \frac{3}{4}\)

Eureka Math Grade 6 Module 2 Lesson 4 Problem Set Answer Key

Calculate the quotient. If needed, draw a model.

Question 1.
\(\frac{8}{9} \div \frac{4}{9}\)
Answer:
8 ninths ÷ 4 ninths = 2

Question 2.
\(\frac{9}{10} \div \frac{4}{10}\)
Answer:
9 tenths ÷ 4 tenths = 2\(\frac{1}{4}\)

Question 3.
\(\frac{3}{5} \div \frac{1}{3}\)
Answer:
\(\frac{9}{15} \div \frac{5}{15}\) = 9 fifteenths ÷ 5 fifteenths = \(\frac{9}{5}=1 \frac{4}{5}\)

Question 4.
\(\frac{3}{4} \div \frac{1}{5}\)
Answer:
\(\frac{15}{20} \div \frac{4}{20}\) = 15 twentieths ÷ 4 twentieths = \(\frac{15}{4}\)

Eureka Math Grade 6 Module 2 Lesson 4 Exit Ticket Answer Key

Calculate each quotient. If needed, draw a model.

Question 1.
\(\frac{9}{4} \div \frac{3}{8}\)
Answer:
This can be rewritten as \(\frac{18}{8} \div \frac{3}{8}\) = 18 eighths divided by 3 eighths = \(\frac{18}{3}\) = 6.

Question 2.
\(\frac{3}{5} \div \frac{2}{3}\)
Answer:
This can be rewritten as \(\frac{9}{15} \div \frac{10}{15}\) = 9fifteenths divided by 10 fifteenths, or 9 units ÷ 10 units. So, this is equal to \(\frac{9}{10}\).

Eureka Math Grade 6 Module 2 Lesson 4 Opening Exercise Answer Key

Write at least three equivalent fractions for each fraction below.

a. \(\frac{2}{3}\)
Answer:
Sample solution include \(\frac{4}{6}, \frac{6}{9}, \frac{8}{12}, \frac{10}{15}, \frac{12}{18}\)

b. \(\frac{10}{12}\)
Answer:
Sample solution include \(\frac{5}{6}, \frac{15}{18}, \frac{20}{24}, \frac{25}{30^{\prime}} \frac{30}{36}\)

Engage NY Eureka Math 6th Grade Module 2 Lesson 2 Answer Key

Eureka Math Grade 6 Module 2 Lesson 2 Example Answer Key

Example 1.
Question # _________
Write It as a division expression. ______________
Write It as a multiplication expression. ______________
Make a rough draft of a model to represent the problem:
As you travel to each model, be sure to answer the following questions:

Answer:

Example 2.
Molly has 9 cups of flour. If this is \(\frac{3}{4}\) of the amount she needs to make bread, how many cups does she need?
a. Construct the tape diagram by reading it backward. Draw a tape diagram and label the unknown.
Answer:

b. Next, shade in \(\frac{3}{4}\).
Answer:

c. Label the shaded region to show that 9 is equal to \(\frac{3}{4}\) of the total.
Answer:

d. Analyze the model to determine the quotient.
Answer:
3 units = 9
1 unit = 9 ÷ 3 = 3
4units = 4 × 3 = 12
Molly needs 12 cups of flour to make bread.

Eureka Math Grade 6 Module 2 Lesson 2 Exercise Answer Key

Exercise 1.
A construction company is setting up signs on 2 miles of a road. If the company places a sign at every mile, how many signs will it use?
Answer:
2 ÷ \(\frac{1}{4}\) → Haw many \(\frac{1}{4}\) in 2?

2 ÷ \(\frac{1}{4}\) = 8 fourths ÷ 1 fourth = 8
There are 8 fourths in 2. The company will use 8 signs.

Exercise 2.
George bought 4 submarine sandwiches for a birthday party. If each person will eat \(\frac{2}{3}\) of a sandwich, how many people can George feed?
Answer:
4 ÷ \(\frac{2}{3}\) → Haw many \(\frac{2}{3}\) in 2?

4 ÷ \(\frac{2}{3}\) = 12 thirds ÷ 2 thirds = 8
There are 6 two-thirds in 4. George can feed 6 people.

Exercise 3.
Miranda buys 6 pounds of nuts. If she puts \(\frac{3}{4}\) pound In each bag, how many bags can she make?
Answer:
6 ÷ \(\frac{3}{4}\) → Haw many \(\frac{3}{4}\) in 6?

6 ÷ \(\frac{3}{4}\) = 24 fourths ÷ 3 fourths = 8
There are 8 three-fourths in 6. Miranda can make 8 bags.

Exercise 4.
Margo freezes 8 cups of strawberries. If this is \(\frac{2}{3}\) of the total strawberries that she picked, how many cups of strawberries did Margo pick?
Answer:
8 ÷ \(\frac{2}{3}\) → 8 is \(\frac{2}{3}\) group of what size?

2 units = 8
1 unit = 8 ÷ 2 = 4
3 units = 3 × 4 = 12
Margo picked 12 cups of strawberries.

Exercise 5.
Regina is chopping up wood. She has chopped 10 logs so far. If the 10 logs represent \(\frac{5}{8}\) of all the logs that need to be chopped, how many logs need to be chopped in all?
Answer:
10 ÷ \(\frac{5}{8}\) → 10 is 6 ÷ \(\frac{5}{8}\) group of what size?

5 units = 10
1 unit = 10 ÷ 5 = 2
B units = 8 × 2 = 16
Regina will chop 16 logs.

Eureka Math Grade 6 Module 2 Lesson 2 Problem Set Answer Key

Rewrite each problem as a multiplication question. Model your answer.

Question 1.
Nicole used \(\frac{3}{8}\) of her ribbon to wrap a present. If she used 6 feet of ribbon for the present, how much ribbon did Nicole have at first?
Answer:
6 ÷ \(\frac{3}{8}\)
6 is \(\frac{3}{8}\) of what number?

3 units = 6
1 unit = 6 ÷ 3 = 2
8 units = 8 × 2 = 16
Nicole started with 16 feet of ribbon.

Question 2.
A Boy Scout has 3 meters of rope. He cuts the rope into cords \(\frac{3}{5}\)m long. How many cords will he make?
Answer:
How many \(\frac{3}{5}\) are in 3?

3 ÷ \(\frac{3}{5}\) = 15 fifths ÷ 3 fifths = \(\frac{15}{3}\) = 5
The Boy Scout can make 5 cords.

Question 3.
12 gallons of water fill a tank to \(\frac{3}{4}\) capacity.
a. What is the capacity of the tank?
Answer:
12 ÷ \(\frac{3}{4}\)
12 is \(\frac{3}{4}\) of what number?

3units = 12
1 unit = 12 ÷ 3 = 4
4 units = 4 × 4 = 16
The tank’s capacity is 16 gallons.

b. If the tank is then filled to capacity, how many half-gallon bottles can be filled with the water in the tank?
Answer:
How many \(\frac{1}{2}\) are in 16?
16 ÷ \(\frac{1}{2}\) = 32 halves ÷ 1 half = 32
32 bottles can be filled.

Question 4.
Hunter spent \(\frac{2}{3}\) of his money on a video game before spending half of his remaining money on lunch. If his lunch costs $10, how much money did he have at first?
Answer:
$10 is \(\frac{1}{6}\) of what number?
10 ÷ \(\frac{1}{6}\)

1 unit = $ 10
6 units = 6 × $10 = $60
Hunter had $60 at first.

Question 5.
Students were surveyed about their favorite colors. \(\frac{1}{4}\) of the students preferred red, \(\frac{1}{8}\) of the students preferred blue, and of the remaining students preferred green. If 15 students preferred green, how many students were surveyed?
Answer:
15 is \(\frac{3}{8}\) of what number?
15 ÷ \(\frac{3}{8}\)

3 units = 15
1 unit = 15 ÷ 3 = 5
8 units = 8 × 5 = 40
40 students were surveyed.

Question 6.
Mr. Scruggs got some money for his birthday. He spent \(\frac{1}{5}\) of it on dog treats. Then, he divided the remainder equally among his 3 favorite charities.
a. What fraction of his money did each charity receive?
Answer:
\(\frac{4}{5} \div 3=\frac{1}{3} \times \frac{4}{5}=\frac{4}{15}\) Each charity received \(\frac{4}{15}\) of Mr. Scruggs’ birthday money.

b. If he donated $60 to each charity, how much money did he receive for his birthday?
Answer:
60 is \(\frac{4}{15}\) of what number?
60 ÷ \(\frac{4}{15}\)

4 units = $60
1 unit = $60 ÷ 4 = $15
15 units = 15 × $15 = $225
Mr. Scruggs got $225 for his birthday.

Eureka Math Grade 6 Module 2 Lesson 2 Exit Ticket Answer Key

Solve each division problem using a model.

Question 1.
Henry bought 4 pies, which he plans to share with a group of his friends. If there Is exactly enough to give each member of the group one-sixth of the pie, how many people are In the group?
Answer:
4 ÷ \(\frac{1}{6}\) → How many \(\frac{1}{6}\) in 4?

There are 6 sixths in 1, and 24 sixths in 4. Henry can share the pies with 24 people.

Question 2.
Rachel finished \(\frac{3}{4}\) of the race in 6 hours. How long was the entire race?
Answer:
6 ÷ \(\frac{3}{4}\) → \(\frac{3}{4}\) of what number is 6?

3 units = 6
1 units = 6 ÷ 3 = 2
4 units = 4 × 2 = 8
The race was 8 hours.